Serious analytical inconsistencies challenge the validity of the energy balance theory

Abstract

Energy metabolism theory affirms that body weight stability is achieved as over time the average energy intake equals the average energy expenditure, a state known as energy balance. Here it is demonstrated, however, that weight stability coexists with a persistent energy imbalance. Such unexpected result emerges as a consequence of the answers to three fundamental problems: 1. Is it possible to model body weight fluctuations without the energy balance theory? And if so, what are the benefits over the energy balance strategy? 2. During energy balance, how the oxidized macronutrient distribution that underlies the average energy expenditure is related to the macronutrient distribution of the average energy intake? 3. Is energy balance possible under a low-fat diet that simultaneously satisfies the following conditions? (a) The fat fraction of the absorbed energy intake is always less than the oxidized fat fraction of the energy expenditure. (b) The carbohydrate fraction of the absorbed energy intake is always greater or equal to the oxidized carbohydrate fraction of the energy expenditure. The first of these issues is addressed with the axiomatic method while the rest are managed through analythical arguments. On the whole, this analysis identifies inconsistencies in the principle of energy balance. The axiomatic approach results also in a simple mass balance model that fits experimental data and explains body composition alterations. This model gives rise to a convincing argument that appears to elucidate the advantage of low-carbohydrate diets over isocaloric low-fat diets. It is concluded, according to the aforementioned model, that weight fluctuations are ultimately dependent on the difference between daily food mass intake and daily mass loss (e.g., excretion of macronutrient oxidation products) and not on energy imbalance. In effect, it is shown that assuming otherwise may caused unintended weight gain.

Applied Mathematics; Metabolism; Physiology; Biological Sciences; Pathophysiology; Health Sciences; Body weight; Energy Balance; Low-Fat Diet; Low-Carbohydrate Diet; Mass Balance

1. Introduction

Weight management literature asserts that body weight increases as energy intake (EI) exceeds energy expenditure (EE) but diminishes as dissipated energy surpasses consumed energy [1]. Weight stability is therefore expected as over time the average absorbed energy intake ($E{I}_{avg}$) equals the average expended energy ($E{E}_{avg}$) [2]. Such notion is termed energy balance and currently stands as a fundamental theory in obesity research [1, 2, 3, 4].

In stable weight individuals doubly labeled water EE measurements are frequently significantly greater than self-reported EI [3, 4]. The energy balance theory (EBT) interpretation of these data is that self-reports underestimate EI [3, 4] since the acceptance of the former finding is perceived as a violation of the First Law of Thermodynamics [2, 5, 6, 7]. This point of view fails to acknowledge, however, that according to this same principle, in close (Figure 1 A) or open (Figure 1 B) systems, a non-zero energy balance can coincide with a null mass change [8]. In line with such fact this work demonstrates that the EBT's proposed correspondence between energy balance and weight stability is unattainable, i.e., weight stability coexists with a persistent energy imbalance. The inconsistencies that sentence the EBT as a flawed rule emerged as existing knowledge is challenged by questions whose answers are unexpectedly revealing: First, is it possible to model weight loss data without taking into account energy balance? If so, does it offer any benefit over the energy balance method? Second, at energy balance, what can be said about the oxidized macronutrient distribution that results in the $E{E}_{avg}$ relative to the macronutrient distribution in the $E{I}_{avg}$? Third, is it possible to be at energy balance under a low-fat diet (LFD) that simultaneously satisfies the following conditions? (i) The fat fraction of the absorbed EI is always less than the oxidized fat fraction of the EE. (ii) The carbohydrate fraction of the absorbed EI is always greater or equal to the oxidized carbohydrate fraction of the EE. This article explains how the answers to these fundamental issues identify contradictions in the EBT and concludes that the conservation law that describes body weight dynamics is the Law of Conservation of Mass and not the First Law of Thermodynamics.

Figure 1.

A non-zero energy balance can coincide with a null mass change. A. When heat (Q) is supplied, work (W) is done as the expanding gas lifts the mass m through a distance h; energy balance is positive (ΔE > 0) yet the gas mass (m_gas) has not changed since the number of gas molecules is constant during expansion. B. Energy balance may be positive or negative yet the mass change that may occur during energy flux is not required by the First Law of Thermodynamics to mirror the energy balance direction. As illustrated, when a fixed amount of hot water is taken out of a water-heater and simultaneously replaced by the same amount of cold water, energy balance is negative (ΔE < 0) yet the system's mass remains constant.

The starting point of this is work is question number one and thus the next section starts by justifying why a mass balance perspective may be of importance in the attempt to model body weight fluctuations without invoking the EBT.

2. Methods and results

2.1. A mass balance approach to body weight dynamics

As the energy fraction from fat increases, in a fixed number of Calories, mass intake decreases due to the high energy density (ρ) of fat in contrast to other substrates. A 2,500 kcal = 10.465 MJ EI, for example, with energy distributed as 30% fat (F, ρ_F = 9.4 kcal/g = 39.33 MJ/kg), 55% carbohydrate (C, ρ_C = 4.2 kcal/g = 17.6 MJ/kg) and 15% protein (P, ρ_P = 4.7 kcal/g = 19.7 MJ/kg) corresponds to a mass intake of ~487g (energy densities as in [9]); whereas the same EI sorted as 60% F, 30% C and 10% P reduces mass ingestion by ~96g. Such difference merits careful attention as a constant daily loss (or gain) of this amount will result in the removal (or augmentation) of 35kg of body mass in a year. A low-carbohydrate diet (LCD) is, therefore, associated with a significant decrease in daily mass intake relative to an isocaloric LFD.

In numerous publications LCDs lead to greater weight loss in comparison to isocaloric LFDs [10, 11, 12, 13, 14, 15]. Whether the diminished mass intake, present in LCDs relative to isocaloric LFDs, explains or contributes to this apparent advantage remains unknown. The axiomatic method is next used to describe body weight fluctuations as a mass balance process instead of the predominant energy balance approach. Five axioms are sufficient to define the mass balance dynamics as their computational implementation simulates weight loss dietary interventions. These axioms also lead to a simple mathematical model that is used to contrast LCDs against isocaloric LFDs. According to the EBT the most probable explanation for the superior weight loss evoked by LCDs vs. LFDs is EI underreporting by low-fat dieters as typically no substantial differences are found between the EEs of both groups [14]. A recent in-patient study defies this hypothesis as the LCD advantage persists even when the energy intake is precisely measured and no energy imbalance differences are found [15]. The mass balance model proposed here predicts the LCD advantage and accurately fits experimental data.

2.1.1. Axioms of daily weight fluctuations

According to the Law of Conservation of Mass, as we eat daily meals, absorbed nutrients are incorporated as part of our body mass. At the same time each day our bodies excrete CO₂, water, minerals, urea, SO₃ and many other wastes products. This leads to the following five axioms:

• 1.Axiom of daily weight gain: Each day we experience a weight gain ($W_{gain}$) given by the weight of the energy-providing mass (EPM) plus the weight of the non-energy providing mass (nEPM) plus the weight of the daily O₂ uptake ($M_{O_2}$; consumed O₂ accumulates transiently in metabolically-produced water during cellular respiration [16]):

$$W_{gain}=EPM+nEPM+M_{O_2}=EPM+nEPM+{\rho }_{O_2}\cdot PAL\cdot v_{O_2}\cdot w$$

where EPM is the daily intake of F, C, P, soluble fiber and alcohol; nEPM is the daily intake of insoluble fiber, water, vitamins and minerals; ${\rho }_{O_2}=\frac{1\text{kg}}{n_{O_2}RT/P}=\frac{1\text{kg}}{\left(31.25\text{mol}\right)\left(0.0821\frac{\text{L}\cdot \text{ATM}}{\text{K}\cdot \text{mol}}\right)\left(300\text{K}\right)/1\text{ATM}}\approx \left(\frac{1}{770}\right)\text{kg}/\text{L}$ is the O₂ density at 27 °C and 1 ATM; PAL is the physical activity level defined as PAL = Total O₂ uptake (in L/day)/Resting O₂ uptake (in L/day); $v_{O_2}$ is the resting O₂ uptake (in L/[kg·day]); and w is the body weight (in kg).

• 2.Axiom of daily weight loss: Each day we experience a weight loss ($W_{loss}$) given by the weight of the EE-dependent mass loss (EEDML) plus the weight of the EE-independent mass loss (EEIML).

EEDML is given by the daily excretion of EPM oxidation byproducts (e.g., CO₂, water, urea and SO₃); whereas EEIML represents the daily weight loss that results from: the daily elimination of non-metabolically produced water (in respiration, in sweat, in urine and in feces); minerals loss in sweat and urine; fecal matter elimination; and mass loss from renewal of skin, hair and nails.

• 3.Axiom of daily weight change: At kth day body weight changes ($\Delta w_k$) by

$$\Delta w_k=W_{gain,k}-W_{loss,k}=W_{gain,k}-F_{loss,k}\cdot w_k=EP{M}_k+nEP{M}_k-[F_{loss,k}-{\rho }_{O_2}\cdot PA{L}_k\cdot v_{O_2{,}_k}]\cdot w_k$$

where $w_k$ is the body weight measured at some convenient time (e.g., weight after eight hours of night sleep) and $0<F_{loss,k}<1$ is the $w_k$ fraction equal to $W_{loss,k}$ or more precisely the relative daily rate of mass excretion. Notice that as O₂ accumulation is transient, the triple product ${\rho }_{O_2}\cdot PA{L}_k\cdot v_{O_2{,}_k}=M_{O_2,k}/w_k$ also represents the relative rate at which consumed O₂ is excreted. Thus, $[F_{loss,k}-{\rho }_{O_2}\cdot PA{L}_k\cdot v_{O_2{,}_k}]$ is the relative rate of mass excretion free of consumed O₂.

• 4.Axiom of consecutive fluctuations: Body weight fluctuations between consecutive days are given by

$$w_{k+1}=w_k+\Delta w_k=EP{M}_k+nEP{M}_k+(1-[F_{loss,k}-{\rho }_{O_2}\cdot PA{L}_k\cdot v_{O_2{,}_k}])\cdot w_k$$

where the change in body weight $\Delta w_k$ may result from overfeeding, underfeeding or other normal factors (e.g., constipation, water retention, menstrual cycle, etc.).

• 5.Axiom of mass balance: Body weight stability occurs when, on average, the daily mass input equals daily mass output, i.e., the average daily weight change (${\left[\Delta w\right]}_{avg}$) is zero

$${\left[\Delta w\right]}_{avg}=\underset{N\to \infty }{\lim }\frac{1}{N+1}\sum _{k=0}^N\Delta w_k=\overline{EPM}+\overline{nEPM}-[{\overline{F}}_{loss}-\rho {}_{O_2}\cdot \overline{PAL}\cdot \overline{v_{O_2}}]w_{avg}=0$$

where

• $\overline{EPM}=\underset{N\to \infty }{\lim }\frac{1}{N+1}\sum _{k=0}^{N}EP{M}_k$ is the average EPM value;

• $\overline{nEPM}=\underset{N\to \infty }{\lim }\frac{1}{N+1}\sum _{k=0}^{N}nEP{M}_k$ is the average nEPM value;

• ${\overline{F}}_{loss}=\underset{N\to \infty }{\lim }\sum _{k=0}^N{F}_{loss,k}\cdot w_k/\sum _{k=0}^N{w}_k$ is the average relative daily rate of mass excretion;

• $\overline{PAL}=\underset{N\to \infty }{\lim }\sum _{k=0}^{N}PA{L}_k\cdot v_{O2,k}\cdot w_k/\sum _{k=0}^N{v}_{O2,k}\cdot w_k$ is the average PAL value;

• $\overline{v_{O2}}=\underset{N\to \infty }{\lim }\sum _{k=0}^N{v}_{O2,k}\cdot w_k/\sum _{k=0}^N{w}_k$ is the average $v_{O2}$ value; and

• $w_{avg}=\underset{N\to \infty }{\lim }\frac{1}{N+1}\sum _{k=0}^N{w}_k$ is the stable average body weight.

2.1.2. Axioms of daily weight fluctuations reproduce typical weight loss dynamics

The previous set axioms may serve as a theoretical tool in the study of body weight regulation. The axiom of consecutive fluctuations, for example, can be used to simulate various dietary treatments. Figure 2 A illustrates, as an instance, three weight loss interventions that decreased $\overline{EPM}$ by 15% ($\overline{EPM}=528.7\text{g;}E{I}_{avg}=\mathrm{2,732}\text{kcal}=11.44\text{MJ}$), 30% ($\overline{EPM}=435.4\text{g;}E{I}_{avg}=\mathrm{2,250}\text{kcal}=9.42\text{MJ}$) and 55% ($\overline{EPM}=280\text{g;}E{I}_{avg}=\mathrm{1,447}\text{kcal}=6.06\text{MJ}$) while macronutrient distribution and $\overline{nEPM}$ were fixed (changes in the latter two parameters are treated in the next section). Notice that the evoked relative weight losses were much less than the relative $\overline{EPM}$ reductions. Such observation follows directly from the axiom of mass balance since as time progresses, ${\left[\Delta w\right]}_{avg}$ approaches zero and so

$$w_{avg}=\frac{\overline{EPM}+\overline{nEMP}}{{\overline{F}}_{loss}-{\rho }_{O_2}\cdot \overline{PAL}\cdot {\overline{v}}_{O_2}}$$ (1)

Figure 2.

Axioms of body weight fluctuations describe weight loss dynamics. A. Body weight (BW) remains stable around 100kg (gray trace) when $\overline{EMP}=\left[E{I}_{avg}\left(F/100\right)\right]/{\rho }_F+\left[E{I}_{avg}\left(C/100\right)\right]/{\rho }_C+\left[E{I}_{avg}\left(P/100\right)\right]/{\rho }_P\approx 0.622\text{kg}$ where $E{I}_{avg}=3\text{,}214\text{kcal}=13.454\text{MJ}\left(30\text{\% F,}50\text{\% C,}20\text{\% P}\right)$. If $\overline{EMP}$ is decreased by 15%, 30% and 55% BW stabilizes at the corresponding reduced mean weight (dashed lines). All simulations contain 730 days or iterations. The kth-iteration consisted of the following computations: First, three random numbers $\{x_k,y_k,z_k\}$ were drawn from a normal standard distribution. Second, $x_k$, $y_k$ and $z_k$ were used to compute: $EM{P}_k=\overline{EMP}(1+\frac{CVar}{100}{x}_k);nEM{P}_k=\overline{nEMP}(1+\frac{CVar}{100}{y}_k);F_{loss,k}=\overline{F}{}_{loss}(1+\frac{CVar}{100}{z}_k)$, where $\overline{nEMP}=1\mathrm{kg}$, ${\overline{F}}_{loss}=0.02492$ and CVar (coefficient of variation) = 10%. Finally, body weight was updated according to $w_{k+1}=EP{M}_k+nEP{M}_k+(1-[F_{loss,k}-{\rho }_{O_2}PAL{v}_{O_2}])\cdot w_k$, where ${\rho }_{O_2}=(1/770)\text{kg/L}$, PAL = 1.5 and $v_{O_2}=3.1\text{ml/}\left(\text{kg×min.}\right)\approx 4.49\text{L/}\left(\text{kg×day}\right)$ are fixed. B.Eq. (2) (continuous version, black curve) approximates the weight loss trajectory (gray trace as in A). The red curve is the absolute value of the continuous form of Eq. (3) (|Δw|). As |Δw| approaches zero BW stabilizes. According to Eq. (2) this happens in about 5τ days. Black curve: $w\left(d\right)=\frac{1.28}{0.01622}+\left(100-\frac{1.28}{0.01622}\right){\left(1-0.01622\right)}^d$, d: days; Red curve: $\left|\Delta w\left(d\right)\right|=0.01622\left(100-\frac{1.28}{0.01622}\right){\left(1-0.01622\right)}^d$. C. To simulate process of metabolic adaptation (black trace) the body weight updating formula is change to $w_{k+1}=EP{M}_k+nEP{M}_k+(1-(1-a)[F_{loss,k}-{\rho }_{O_2}PAL{v}_{O_2}])\cdot w_k$ where $a=f(0.622,0.280,\mathrm{1,1})=0.031628$. As shown, the inclusion of this physiological response limits the amount of lost weight (black trace vs. gray trace). The gray trace is the same as in part A where there is no metabolic adaptation. Red curve: $w\left(d\right)=\frac{1.28}{0.0157}+\left(100-\frac{1.28}{0.0157}\right){\left(1-0.0157\right)}^d$. D. The change in fat mass that underlies the weight loss trajectory depicted in part C (black trace) is computed with Eq. (6) generating the shown graph. The initial fat mass (FM) was 35kg and the dashed line represents the average fat mass computed with all FM values after day 300.

That is, at weight stability, the average body weight is equal to the mean daily weight of food and liquid intake divided by the mean relative daily rate of mass excretion free of consumed O₂. Accordingly, a 55% drop in $\overline{EPM}$ results in a 21.1% weight reduction since body weight becomes stable at

$$w_{avg}=\frac{\left(1-\frac{\%}{100}\right)\overline{EPM}+\overline{nEMP}}{{\overline{F}}_{loss}-{\rho }_{O_2}\cdot \overline{PAL}\cdot {\overline{v}}_{O_2}}=\frac{\left(1-\frac{55}{100}\right)0.622+1}{0.01622}\approx 78.9\text{kg.}$$

Consecutive body weight fluctuations can be approximated by

$$w_{k+1}\approx \overline{EPM}+\overline{nEPM}+(1-[{\overline{F}}_{loss}-{\rho }_{O_2}\cdot \overline{PAL}\cdot {\overline{v}}_{O_2}])w_k=\overline{M}+(1-\overline{R})w_k$$

where $\overline{M}=\overline{EPM}+\overline{nEPM}$ is the mean daily mass intake and $\overline{R}={\overline{F}}_{loss}-{\rho }_{O_2}\cdot \overline{PAL}\cdot {\overline{v}}_{O_2}$ is the mean daily rate of mass excretion free of consumed O₂. Iterations starting from the initial weight $w_0$ reveal that

$$\begin{gathered} w_k=\overline{M}+\left(1-\overline{R}\right)w_{k-1} \\ =\overline{M}\sum _{j=1}^k{\left(1-\overline{R}\right)}^{j-1}+{\left(1-\overline{R}\right)}^k{w}_0=\frac{\overline{M}}{\overline{R}}+\left(w_0-\frac{\overline{M}}{\overline{R}}\right){\left(1-\overline{R}\right)}^k \end{gathered}$$ (2)

This expression describes weight gain if $w_0<\overline{M}/\overline{R}$, weight loss if $w_0>\overline{M}/\overline{R}$, remains constant if $w_0=\overline{M}/\overline{R}$, converges to Eq. (1) and reaches a qualitative steady state in about $5/\left|\ln (1-\overline{R})\right|$ days since ${(1-\overline{R})}^k=\exp \left[-k/\tau \right]$ where $\tau =1/\left|\ln (1-\overline{R})\right|$.

By Eq. (2) the kth weight change becomes

$$\Delta w_k=\overline{EPM}+\overline{nEPM}-\left[{\overline{F}}_{loss}-{\rho }_{O_2}\cdot \overline{PAL}\cdot {\overline{v}}_{O_2}\right]w_k=-\overline{R}\left(w_0-\frac{\overline{M}}{\overline{R}}\right){\left(1-\overline{R}\right)}^k$$ (3)

Moreover, the net change in weight over n days (NCW_n) is

$$NC{W}_n=w_n-w_0=\sum _{k=0}^n\Delta w_k=\left(\frac{\overline{M}}{\overline{R}}-w_0\right)\left(1-{(1-\overline{R})}^n\right)$$ (4)

Eqs. (2) and (3) are plotted in Figure 2 B.

Dietary food restriction is known to diminish the mass-specific basal metabolic rate in proportion to the size of the reduction in food intake [17]; overfeeding, however, appears not to have a significant effect on this measurement [18, 19]. Such phenomenon is termed metabolic adaptation or adaptive thermogenesis [20] and manifests a very fast onset that correlates with alterations in blood levels of thyroid hormones or catecholamines [21, 22]. Thus, the axiom of mass balance can be modified to incorporate metabolic adaptation (a) as follows

$$w_{avg}=\frac{\left(1\pm \frac{X_1}{100}\right)\overline{EPM}+\left(1\pm \frac{X_2}{100}\right)\overline{nEMP}}{\left(1-a\right)\left[{\overline{F}}_{loss}-{\rho }_{O_2}\cdot \overline{PAL}\cdot {\overline{v}}_{O_2}\right]}$$ (5)

where X₁ ≥ 0 is the percent of change in $\overline{EPM}$ that is added to one for increments or subtracted for reductions; X₂ ≥ 0 is the percent of change in $\overline{nEPM}$ that is added to one for increments or subtracted for reductions; and 0 ≤ a < 1 is a function that models metabolic adaptation as a depression in the magnitude of $\overline{R}$ that depends on the relative change in$\overline{EPM}$. A possible form for a, adapted from the work Westerterp et al. [17], is

$$\begin{gathered} a=f\left({\overline{EPM}}_{old},{\overline{EPM}}_{new},{\overline{nEPM}}_{old},{\overline{nEPM}}_{new}\right) \\ =\{\begin{array}{l}0.15\left(1-\frac{{\overline{EPM}}_{new}+{\overline{nEPM}}_{new}}{{\overline{EPM}}_{old}+{\overline{nEPM}}_{old}}\right)0<\frac{{\overline{EPM}}_{new}}{{\overline{EPM}}_{old}}\le 0.5\\ 0.3\frac{{\overline{EPM}}_{new}}{{\overline{EPM}}_{old}}\left(1-\frac{{\overline{EPM}}_{new}+{\overline{nEPM}}_{new}}{{\overline{EPM}}_{old}+{\overline{nEPM}}_{old}}\right)0.5<\frac{{\overline{EPM}}_{new}}{{\overline{EPM}}_{old}}<1\\ 0\frac{{\overline{EPM}}_{new}}{{\overline{EPM}}_{old}}\ge 1\end{array} \end{gathered}$$

Figure 2 C shows the inclusion of the latter function into the axiom of consecutive fluctuations when only $\overline{EPM}$ is reduced by 55%, i.e., ${\overline{EPM}}_{new}/{\overline{EPM}}_{old}=0.45;{\overline{nEPM}}_{new}={\overline{nEPM}}_{old}$.

Alterations in body composition as a result of food intake restriction appear to depend primarily on the initial fat mass (FM) and on the magnitude of weight loss [23, 24, 25]. Hall [25] has shown, based on an empirical expression developed by Forbes [23, 24], that an excellent approximation of this relationship is given by

$$F{M}_{final}=10.4W\left\{\frac{F{M}_{initial}}{10.4}\exp \left(\frac{w_{final}-w_{initial}+F{M}_{initial}}{10.4}\right)\right\}$$

where the uppercase W is the Lambert W function. Therefore, changes in body composition over n = 1, 2, 3, …. consecutive days can be approximated by

$$F{M}_{k+n}=10.4W\left\{\frac{F{M}_k}{10.4}\exp \left(\frac{w_{k+n}-w_k+F{M}_k}{10.4}\right)\right\}$$ (6)

$$FF{M}_{k+n}=w_{k+n}-F{M}_{k+n}$$ (7)

where $FF{M}_{k+n}$ represents the fat-free mass. Figure 2 D simulates how fat mass evolves over time after $\overline{EPM}$ is reduced by 55%.

In summary, the axiomatic method shows that as food and liquid consumption are reduced, body weight decreases towards a new steady average value predicted by Eq. (5). The temporal progression of body weight, cumulative weight change, fat mass and fat-free mass can be approximated by Eqs. (2), (4), (6), and (7), respectively.

2.1.3. A mass balance contrast: low-fat diets vs. low-carbohydrate diets

Implicit between any two isocaloric diets, is the fact that the diet with largest energy proportion from fat will always contain the least macronutrient mass (Figure 3). Such difference can explain the LCD advantage as shown next.

Figure 3.

The energy proportion from fat, under a clamped caloric intake, determines the amount of ingested mass. The figure exemplifies how the energy proportion from fat impacts the amount of ingested nutrient mass. In the figure the energy densities of F, C and P are as in [9]: ρ_F = 9.4 kcal/g, ρ_C = 4.2 kcal/g, ρ_F = 4.7 kcal/g. A. The graph illustrates that, under clamped energy intake (2,500 kcal = 10.465 MJ), as the fat fraction increases the ingested nutrient mass decreases (black line). B. The effect observed in A is due to the fact that as the fat fraction increases the energy density (black curve) also increases meaning that a same level of energy intake can be achieved with the ingestion of less nutrient mass.

Imagine two 90kg obese subjects with identical weight maintenance EIs ($E{I}_{avg}=\mathrm{2,300}\text{kcal}=9.63\text{MJ}$), body composition (FFM = 55kg, FM = 35kg), macronutrient distribution (F: 35%, C: 50%, P: 15%; $\overline{EPM}=\left[E{I}_{avg}\left(F/100\right)\right]/{\rho }_F+\left[E{I}_{avg}\left(C/100\right)\right]/{\rho }_C+\left[E{I}_{avg}\left(P/100\right)\right]/{\rho }_P\approx 433\text{g}$), $\overline{nEPM}=1.567\text{kg}$, ${\rho }_{O_2}\cdot \overline{PAL}\cdot {\overline{v}}_{O_2}=0.008$ and ${\overline{F}}_{loss}={\rho }_{O_2}\cdot \overline{PAL}\cdot {\overline{v}}_{O_2}+\frac{\overline{EPM}+\overline{nEMP}}{w_{avg}}\approx 0.03$. Now the two individuals cut 1,000kcal = 4.186 MJ from their current EI but one consumes a LFD (1,300 kcal = 5.44 MJ, F: 30%, C: 55%, P: 15%; ${\overline{EPM}}_{LFD}\approx 253\text{g}$) while the other a LCD (1,300 kcal = 5.44 MJ, F: 70%, C: 15%, P: 15%; ${\overline{EPM}}_{LCD}\approx 185\text{g}$). Thus,

$${\overline{M}}_{LFD}={\overline{EPM}}_{LFD}+{\overline{nEPM}}_{LFD}=0.253+1.567=1.82\text{kg}$$

$${\overline{R}}_{LFD}={\overline{F}}_{loss,LFD}-{({\rho }_{O_2}\cdot \overline{PAL}\cdot {\overline{v}}_{O_2})}_{LFD}=0.03-0.008=0.022$$

$$a_{LFD}=f_{LFD}(0.433,0.253,1.567,1.567)\approx 0.01578$$

$${\overline{M}}_{LCD}={\overline{EPM}}_{LCD}+{\overline{nEPM}}_{LCD}=0.185+1.567=1.752\text{kg}$$

$${\overline{R}}_{LCD}={\overline{F}}_{loss,LCD}-{({\rho }_{O_2}\cdot \overline{PAL}\cdot {\overline{v}}_{O_2})}_{LCD}=0.03-0.008=0.022$$

$$a_{LCD}=f_{LCD}(0.433,0.185,1.567,1.567)=0.0186$$

where $\overline{nEPM}$ values are, for now, unaltered in order to isolate the body weight response to reductions in $\overline{EPM}$. This corresponds to assuming that the intake of water (in foods and drinks), insoluble fiber, vitamins and minerals have not been substantially affected by the dietary interventions.

Dietary treatments have reduced EI by ~43% and hence by the EBT we expect, under perfect diet adherence, similar weigh loss among subjects. Axioms of body weight fluctuations affirm, however, that the LCD will lead to greater weight loss since its mean daily mass intake is 68g smaller than that in the LFD, i.e.,

$${\overline{M}}_{LCD}-{\overline{M}}_{LFD}=1.752\text{kg}-1.82\text{kg}=-0.068\text{kg}=-68g.$$

To be more precise, let us input the presented data into Eq. (2)

$$\begin{gathered} \begin{array}{c}{w}_k^{LFD}=\frac{{\overline{M}}_{LFD}}{\left(1-a_{LFD}\right){\overline{R}}_{LFD}}+\left(w_0-\frac{{\overline{M}}_{LFD}}{\left(1-a_{LFD}\right){\overline{R}}_{LFD}}\right){\left(1-\left(1-a_{LFD}\right){\overline{R}}_{LFD}\right)}^k\end{array} \\ \approx 84.05+5.95\cdot {\left(0.97834716\right)}^k \end{gathered}$$ (8)

$$w_k^{LCD}\approx 81.16+8.84\cdot {\left(0.9784092\right)}^k$$ (9)

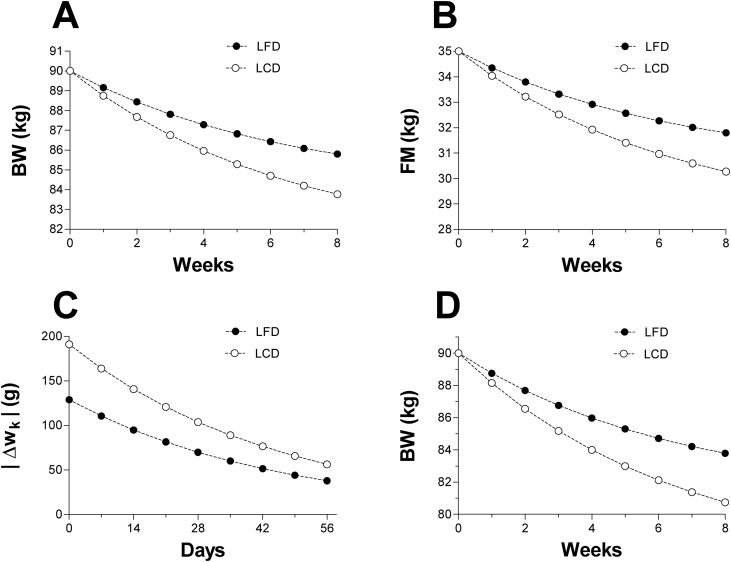
and plot the resulting formulas for the first 8 weeks into each diet (Figure 4 A). At week 8^th the LCD results in a lost weight of 6.24kg vs. 4.2kg in the LFD. Fat mass has also decreased by 4.73kg in the LCD vs. 3.2kg in the LFD (Figure 4 B). Eqs. (8) and (9) predict, on the long run, a weight loss close to$\underset{k\to \infty }{\lim }(90-w_k^{LCD})=8.84\text{kg}$ in the LCD vs. $\underset{k\to \infty }{\lim }(90-w_k^{LFD})=5.95\text{kg}$ in the LFD. These differences, which are in close agreement with experimental data [10, 11, 12, 13, 14, 15], emerge from the interaction between the variables governing the weight loss kinetics, namely, $\overline{M}$and $\overline{R}$.To appreciate this, let us apply Eq. (3) to each diet

$$\begin{gathered} \Delta w_k^{LFD}=-\left(1-a_{LFD}\right){\overline{R}}_{LFD}\left(w_0-\frac{{\overline{M}}_{LFD}}{\left(1-a_{LFD}\right){\overline{R}}_{LFD}}\right){\left(1-(1-a_{LFD}){\overline{R}}_{LFD}\right)}^k \\ \approx -0.1288\cdot {\left(0.97834716\right)}^k \end{gathered}$$ (10)

$$\Delta w_k^{LCD}\approx -0.191\cdot {\left(0.9784092\right)}^k$$ (11)

Figure 4.

Simulation: low-fat diet vs. low-carbohydrate diet. A. First eight weeks of two simulated 90kg obese individuals under different isocaloric diets: low-fat diet (LFD; 1,300 kcal = 5.44 MJ, F: 30%, C: 55%, P: 15%) vs. low-carbohydrate diet (LCD; 1,300 kcal = 5.44 MJ, F: 70%, C: 15%, P: 15%). The EI of both subjects before the intervention was 2,300 kcal = 9.63 MJ (F: 35%, C: 50%, P: 15%). Although both subjects are expected to experience similar levels of energy imbalance, the LCD resulted in greater weight loss in contrast to the LFD. Plots were computed with Eqs. (8) and (9) by letting k = 0, 7, 14, …, 56. B. The mass balance model predicts a greater decline in fat mass for the LCD in contrast to the LFD. Plots were computed with Eq. (6) using the weight loss sequences depicted in A. C. The figure illustrates the absolute value of the daily weight change ($\left|\Delta w_k\right|$) for both diets. The LCD's daily weight change is greater than that in the LFD. Over time this yields a much faster and greater weight loss as observed in A. Plots were computed with Eqs. (10) and (11) by letting k = 0, 7, 14, …, 56. D. Simulation similar to part A but with reductions in $\overline{nEMP}$ (4% in LFD vs. 6% LCD). Notice that small reductions in $\overline{nEMP}$ enhance the weight loss evoked by reductions in $\overline{EMP}$. This is expected as the $\overline{nEMP}$ is typically the largest component of $\overline{M}$. Such behavior is consistent with experimental data since changes in water intake and minerals result in detectable changes in body weight [26]. FM: fat mass, BW: body weight.

Notice that $\left|\Delta w_k^{LCD}\right|>\left|\Delta w_k^{LFD}\right|$ for all k and hence the LCD manifests a daily weight loss that is greater than that in the LFD (Figure 4 C). The LCD's daily mass intake is therefore small relative to the daily mass excretion and so the net daily mass loss becomes amplified. In the LFD such amplification is not as efficient since diet's mass intake cancels out a large fraction of the excreted mass, which decelerates daily weight loss. The next calculations illustrate this point:

At day 14 the LFD subject weighs

$$w_{14}^{LFD}=84.05+5.95\cdot {\left(0.97834716\right)}^{14}\approx 88.43\text{kg}$$

from which 2.165% (1.915kg) will be lost on day 14. However, as ${\overline{M}}_{LFD}=1.82\text{kg}$ the weight change becomes

$$\Delta w_{14}^{LFD}=\stackrel{{\overline{M}}_{LFD}=1.82}{\overbrace{\overline{EPM}+\overline{nEPM}}}-\stackrel{\approx 0.02165}{\overbrace{(1-a_{LFD})\left[{\overline{F}}_{loss}-{\rho }_{O_2}\cdot \overline{PAL}\cdot {\overline{v}}_{O_2}\right]}}{w}_{14}^{LFD}=1.82-1.915=-0.095\text{kg}=-95\text{g.}$$

In contrast, at day 14 the LCD subject weighs

$$w_{14}^{LCD}=81.16+8.84\cdot {\left(0.9784092\right)}^{14}=87.67\text{kg.}$$

Similarly, a 2.159% of this weight will be lost on day 14. Hence,

$$\Delta w_{14}^{LCD}=\stackrel{{\overline{M}}_{LCD}=1.752}{\overbrace{\overline{EPM}+\overline{nEPM}}}-\stackrel{\approx 0.02159}{\overbrace{(1-a_{LFD})\left[{\overline{F}}_{loss}-{\rho }_{O_2}\cdot \overline{PAL}\cdot {\overline{v}}_{O_2}\right]}}{w}_{14}^{LCD}=1.752-1.893=-0.141\text{kg}=-141\text{g.}$$

LCDs are, therefore, more effective in minimizing the daily mass intake relative to LFDs and consequently the former manifest a substantially larger daily weight loss than the latter. Ultimately such difference translates into greater weight loss in LCDs vs. isocaloric LFDs. In this model, the underlying mechanism that explains the advantage of LCDs over LFDs is independent of the difference in the physiology of each diet; the difference simply emerges from dissimilar mass intakes. Particularly, if two persons eliminate body mass at about the same daily rate, then the one ingesting less mass will express a greater daily weight loss which over time results in a much larger body weight reduction.

In the above calculations the $\overline{nEPM}$ was unaltered to better appreciate the body weight sensitivity to perturbations in $\overline{EPM}$. In many diets, however, this parameter is likely to be decreased. Fruits portions, for example, are reduced and salt content is limited, which results in the decline of the $\overline{nEPM}$. This is expected since smaller fruit portions and low-salt meals imply a reduced intake of water, insoluble fiber, vitamins and minerals. This effect is probably more pronounced in LCD than in LDF as the reduction in fruits and vegetables is usually more drastic in the former than the latter. In any case, according to the mass balance model, when the $\overline{nEPM}$ is decreased the amount of lost weight is projected to increased (Figure 4D). This enhanced weight loss follows mainly from the obligatory reduction in total body water that is needed in order to avoid dilution of electrolytes (e.g., sodium) since now they are being consumed in smaller quantities [26].

2.1.4. Eqs. (2) and (6) fit experimental data

In a first report Brehm et al. [13] published that obese women in LCDs lost more than twice as much weight than those that follow LFDs during a 6 months treatment period. This difference was not caused by distinct levels of energy consumption since women in both interventions reported statistically similar EIs. Guided by the EBT, they tested the hypothesis that the greater weight loss in LCDs vs. LFDs resulted from differences in the total EE evoked by each diet. After a second study [14] they found that weight loss variation could not be explained by differences in resting EE, thermic effect of food or PAL. These data led them to conclude that the most likely explanation for their findings was EI underreporting by the LFD group. Figure 5 A₁ and B₁ show, nonetheless, that the fit of Eq. (2) to these investigations is remarkable. As no differences were found in the level of metabolic and physical activity of both diets, it is fair to say that the disparity among fitted $\overline{R}$ values is likely to be non-significant. The dissimilarity between $\overline{M}$ estimates, however, substantiates the claim that the superior weight loss observed in LCDs vs. LFDs is mainly the result of differences in daily mass intake. In terms of body composition, Brehm et al. [13, 14] performed dual energy x-ray absorptiometry (DEXA) measurements and found that LCDs resulted in a grater reduction in fat mass in contrast to LFDs. Consistent with this observation when Eq. (6) was used to approximate the fat mass data in both studies, computed estimates were surprisingly close to the reported values (Table 1). As a consequence, with the use of solid curves in Figure 5 A₁ and B₁, is possible to predict the temporal decline in fat mass by fitting Eq. (6) to data in both studies (Figure 5 A₂ and B₂).

Figure 5.

Eqs. (2) and (6) fit experimental data. The figure illustrates fits of the continuous version of Eq. (2) to weight loss data from Brehm et al. [13] in A₁ and Brehm et al. [14] in B₁. Estimates of parameters in Eq. (2) are rounded to four decimal places. The fat mass data from Brehm et al. [13] (A₂) and Brehm et al. [14] (B₂) was fitted with following version of Eq. (6)$F{M}_{k+1}=\beta W\left\{\frac{F{M}_k}{\beta }\exp \left(\frac{w_{k+1}-w_k+F{M}_k}{\beta }\right)\right\}$. During curve-fitting procedure body weights $w_{k+1}$ and $w_k$ were obtained from solid curves in A₁ and B₁. Estimates of β are rounded to two decimal figures. Scatter data in panels A₁ and B₁ were extracted from graphs in the original publications using GetData Graph Digitizer version 2.26.0.20. FM: fat mass, BW: body weight.

Table 1.

Eq. (6)^§ estimates of DEXA fat mass data from Berhm et al. [13, 14].

Very Low-carbohydrate Diet (Brehm et al. [13])
w0	FFM0	FM0	Months (k)	wk	FFMk	DEXA FMk	Eq. (6) FMk
87.712	50.385	37.327	3	80.6005	47.5653	33.0352	31.8619∗
			6	80.972	48.418	32.554	32.1423∗
Low-fat Diet (Brehm et al. [13])
w0	FFM0	FM0	Months (k)	wk	FFMk	DEXA FMk	Eq. (6) FMk
88.8547	51.0268	37.8279	3	85.4868	50.1813	35.3055	35.2068∗
			6	86.1492	50.2959	35.8533	35.7190∗
Low-carbohydrate Diet (Brehm et al. [14])
w0	FFM0	FM0	Months (k)	wk	FFMk	DEXA FMk	Eq. (6) FMk
87.45	49.56	37.89	2	81.19	47.48	33.71	33.05∗∗
			4	77.92	46.22	31.7	30.59∗∗
Low-fat Diet (Brehm et al. [14])
w0	FFM0	FM0	Months (k)	wk	FFMk	DEXA FMk	Eq. (6) FMk
87.92	50.77	37.15	2	83.63	49.12	34.51	33.83∗∗
			4	82.74	48.83	33.91	33.15∗∗

^§All estimates in the table were computed with Eq. (6) in its current form without any numerical correction, i.e.,$F{M}_k=10.4W\left\{\frac{F{M}_0}{10.4}\exp \left(\frac{w_k-w_0+F{M}_0}{10.4}\right)\right\}$.

^∗Estimate rounded to four decimal places.

^∗∗estimate rounded to two decimal places.

In sum, the good fit of Eqs. (2) and (6) to experimental data support the argument that is possible to model body weight dynamics without invoking the EBT. A mass balance model gives, therefore, a parsimonious explanation for the well documented advantage of LCDs over LFDs. This difference, once again, emerges from distinct daily mass intakes and appears to be independent of the diet's physiology.

2.2. Mathematical reasoning indentifies inconsistencies in the EBT

The first question that this work set to answer was:

Is it possible to model weight loss data without taking into account energy balance? If so, does it offer any benefit over the energy balance method?

A mass balance model was created as an answer to the first part of this inquiry which in itself is not surprising as it is always possible to postulate alternative models for a particular phenomenon. This model, as a response to the second part of the query, gave an excellent fit to LCDs vs. LFDs data leading to a parsimonious explanation for the apparent advantage of LCDs over LFDs. The LCD superior weight loss, fundamentally, appears to result from a substantial reduction in daily mass intake in contrast to an isocaloric LFD as in both diets daily mass excretion seems to be non-significantly different. The second and third questions are now explicitly addressed and the interpretation of their answers identifies inconsistencies in the EBT.

2.2.1. At energy balance the oxidized macronutrient distribution that results in the $E{E}_{avg}$ is equal to macronutrient distribution in the $E{I}_{avg}$

It is generally assumed that when the $E{I}_{avg}$ equals the $E{E}_{avg}$ body weight remains stable [1, 2]. If so the corresponding energy densities are identical

$${\rho }_{E{I}_{avg}}={\rho }_{E{E}_{avg}}$$ (12)

Otherwise, we run into contradictions since energy is balanced but not mass. The analysis below determines the necessary condition for the existence of identity (12). This, in turn, leads to the answer of the second question posed in the introduction.

Let E be the absorbed or expended energy. The E energy density $\left({\rho }_E\right)$ is then

$${\rho }_E={\left(\frac{1}{{\rho }_F}{x}_{F,E}+\frac{1}{{\rho }_C}{x}_{C,E}+\frac{1}{{\rho }_P}{x}_{P,E}\right)}^{-1}$$ (13)

where $0\le x_{i,E}\le 1$ is the E fraction derived from $i=F,C,P$ and $x_{F,E}+x_{C,E}+x_{P,E}=1$.

Before we advanced further it is important clarify the next point. Observe that if Eq. (13) is applied to the EE there is no need to include an extra term for the EE fraction derived from ketones (i.e., $x_{Ketones,EE}$). This is so as the oxidation of these intermediates is essentially fat oxidation [16]. In liver cells, during the fasting state, for instance, the β-oxidation of one palmitic acid molecule yields 8 acetyl-coenzyme A molecules. Subsequently, every 2 of these substrates react to generate a total of 4 acetoacetate molecules [16]. These ketones then diffuse into circulation serving as energy fuel for non-liver cells. The oxidation of 4 molecules of acetoacetate is therefore equivalent to the oxidation of one palmitic acid molecule. Consequently, $x_{F,EE}$ term in Eq. (13) takes into account ketones oxidation.

Notice next that identity (12) can be rewritten using Eq. (13) as

$${\rho }_{E{I}_{avg}}={\rho }_{E{E}_{avg}}={\left(\frac{1}{{\rho }_F}{x}_{F,E{E}_{avg}}+\frac{1}{{\rho }_C}{x}_{C,E{E}_{avg}}+\frac{1}{{\rho }_P}{x}_{P,E{E}_{avg}}\right)}^{-1}$$

illustrating that when energy balance coincides with weight stability the macronutrient distribution in $E{E}_{avg}$ has to account for the $E{I}_{avg}$ energy density. This distribution also explains the mean daily O₂ consumption (${\overline{V}}_{O_2}$, in liters) and mean daily CO₂ production (${\overline{V}}_{C{O}_2}$, in liters) since there exists analytical constants $k_F,k_C,k_P$ that convert grams of F, C and P to O₂ liters necessary for oxidation, respectively [16]. Thus, the ${\overline{V}}_{O_2}$corresponding to $E{E}_{avg}$ is

$$\begin{gathered} {\overline{V}}_{O_2}=k_F\left(\frac{E{E}_{avg}\cdot x_{F,E{E}_{avg}}}{{\rho }_F}\right)+k_C\left(\frac{E{E}_{avg}\cdot x_{C,E{E}_{avg}}}{{\rho }_C}\right)+k_P\left(\frac{E{E}_{avg}\cdot x_{P,E{E}_{avg}}}{{\rho }_P}\right) \\ =E{E}_{avg}\left(\frac{k_F}{{\rho }_F}{x}_{F,E{E}_{avg}}+\frac{k_C}{{\rho }_C}{x}_{C,E{E}_{avg}}+\frac{k_P}{{\rho }_P}{x}_{P,E{E}_{avg}}\right) \end{gathered}$$ (14)

Likewise, the ${\overline{V}}_{C{O}_2}$associated with $E{E}_{avg}$ is

$${\overline{V}}_{C{O}_2}=E{E}_{avg}\left(\frac{r_F{k}_F}{{\rho }_F}{x}_{F,E{E}_{avg}}+\frac{r_C{k}_C}{{\rho }_C}{x}_{C,E{E}_{avg}}+\frac{r_P{k}_P}{{\rho }_P}{x}_{P,E{E}_{avg}}\right)$$ (15)

where $r_F,r_C,r_P$ are respiratory quotients for F, C and P, respectively.

The preceding analysis implies that if energy balance coincides with weight stability then the following system of linear equations has, at least, one solution

$$\begin{array}{c}{x}_{F,E{E}_{avg}}+x_{C,E{E}_{avg}}+x_{P,E{E}_{avg}}=1\\ \frac{1}{{\rho }_F}{x}_{F,E{E}_{avg}}+\frac{1}{{\rho }_C}{x}_{C,E{E}_{avg}}+\frac{1}{{\rho }_P}{x}_{P,E{E}_{avg}}=\frac{1}{{\rho }_{E{I}_{avg}}}\\ \frac{k_F}{{\rho }_F}{x}_{F,E{E}_{avg}}+\frac{k_C}{{\rho }_C}{x}_{C,E{E}_{avg}}+\frac{k_P}{{\rho }_P}{x}_{P,E{E}_{avg}}=\frac{{\overline{V}}_{O_2}}{E{E}_{avg}}\\ \frac{r_F{k}_F}{{\rho }_F}{x}_{F,E{E}_{avg}}+\frac{r_C{k}_C}{{\rho }_C}{x}_{C,E{E}_{avg}}+\frac{r_P{k}_P}{{\rho }_P}{x}_{P,E{E}_{avg}}=\frac{{\overline{V}}_{C{O}_2}}{E{E}_{avg}}\end{array}$$ (16)

such that $0\le x_{i,E{E}_{avg}}\le 1$ for all i.

In other words, if system (16) can be solved, then energy balance coincides with weight stability and thus it is possible for the macronutrient distribution in the $E{E}_{avg}$ (first equation) to simultaneously account for the $E{I}_{avg}$ energy density (second equation), the mean daily O₂ uptake (third equation) and the mean daily CO₂ production (fourth equation).

Row operations on the augmented matrix of system (16) give

$$\left[\begin{array}{cccc}1& 1& 1& 1\\ 0& \left(\frac{1}{{\rho }_C}-\frac{1}{{\rho }_F}\right)& \left(\frac{1}{{\rho }_P}-\frac{1}{{\rho }_F}\right)& \left(\frac{1}{{\rho }_{\overline{EI}}}-\frac{1}{{\rho }_F}\right)\\ 0& 0& 1& \frac{\left(\frac{1}{{\rho }_C}-\frac{1}{{\rho }_F}\right)\left(\frac{{\overline{V}}_{O_2}}{E{E}_{avg}}-\frac{k_F}{{\rho }_F}\right)-\left(\frac{k_C}{{\rho }_C}-\frac{k_F}{{\rho }_F}\right)\left(\frac{1}{{\rho }_{E{I}_{avg}}}-\frac{1}{{\rho }_F}\right)}{\left(\frac{1}{{\rho }_C}-\frac{1}{{\rho }_F}\right)\left(\frac{k_P}{{\rho }_P}-\frac{k_F}{{\rho }_F}\right)-\left(\frac{k_C}{{\rho }_C}-\frac{k_F}{{\rho }_F}\right)\left(\frac{1}{{\rho }_P}-\frac{1}{{\rho }_F}\right)}\\ 0& 0& 0& \alpha \end{array}\right]$$

where

$$\begin{gathered} \alpha =\frac{\left(\frac{{\overline{V}}_{C{O}_2}}{E{E}_{avg}}-\frac{r_F{k}_F}{{\rho }_F}\right)\left(\frac{1}{{\rho }_C}-\frac{1}{{\rho }_F}\right)-\left(\frac{r_C{k}_C}{{\rho }_C}-\frac{r_F{k}_F}{{\rho }_F}\right)\left(\frac{1}{{\rho }_{E{I}_{avg}}}-\frac{1}{{\rho }_F}\right)}{\left(\frac{1}{{\rho }_C}-\frac{1}{{\rho }_F}\right)\left(\frac{r_P{k}_P}{{\rho }_P}-\frac{r_F{k}_F}{{\rho }_F}\right)-\left(\frac{r_C{k}_C}{{\rho }_C}-\frac{r_F{k}_F}{{\rho }_F}\right)\left(\frac{1}{{\rho }_P}-\frac{1}{{\rho }_F}\right)} \\ -\frac{\left(\frac{1}{{\rho }_C}-\frac{1}{{\rho }_F}\right)\left(\frac{{\overline{V}}_{O_2}}{E{E}_{avg}}-\frac{k_F}{{\rho }_F}\right)-\left(\frac{k_C}{{\rho }_C}-\frac{k_F}{{\rho }_F}\right)\left(\frac{1}{{\rho }_{E{I}_{avg}}}-\frac{1}{{\rho }_F}\right)}{\left(\frac{1}{{\rho }_C}-\frac{1}{{\rho }_F}\right)\left(\frac{k_P}{{\rho }_P}-\frac{k_F}{{\rho }_F}\right)-\left(\frac{k_C}{{\rho }_C}-\frac{k_F}{{\rho }_F}\right)\left(\frac{1}{{\rho }_P}-\frac{1}{{\rho }_F}\right)}. \end{gathered}$$

The solution of system (16) only exists when $\alpha =0$, and under energy balance this is the case as explained below.

If $E{I}_{avg}=E{E}_{avg}$ and body weight is stable then, on average, the daily absorbed macronutrients mass is oxidized. Hence, ${\overline{V}}_{O_2}$ and ${\overline{V}}_{C{O}_2}$ are given by the nutrients distribution in the $E{I}_{avg}$. Thus, by Eqs. (14) and (15)

$$\begin{array}{l}\frac{{\overline{V}}_{O_2}}{E{E}_{avg}}=\frac{k_F}{{\rho }_F}{x}_{F,E{I}_{avg}}+\frac{k_C}{{\rho }_C}{x}_{C,E{I}_{avg}}+\frac{k_P}{{\rho }_P}{x}_{P,E{I}_{avg}}\\ \\ \frac{{\overline{V}}_{C{O}_2}}{E{E}_{avg}}=\frac{r_F{k}_F}{{\rho }_F}{x}_{F,E{I}_{avg}}+\frac{r_C{k}_C}{{\rho }_C}{x}_{C,E{I}_{avg}}+\frac{r_P{k}_P}{{\rho }_P}{x}_{P,E{I}_{avg}}\end{array}$$

Substitution of these expressions into $\alpha$ while recognizing that $\frac{1}{{\rho }_{E{I}_{avg}}}=\frac{1}{{\rho }_F}{x}_{F,E{I}_{avg}}+\frac{1}{{\rho }_C}{x}_{C,E{I}_{avg}}+\frac{1}{{\rho }_P}{x}_{P,E{I}_{avg}}$ simplifies to

$$\alpha =\frac{\left(\begin{array}{l}\left(\frac{r_F{k}_F}{{\rho }_F}{x}_{F,E{I}_{avg}}+\frac{r_C{k}_C}{{\rho }_C}{x}_{C,E{I}_{avg}}+\frac{r_P{k}_P}{{\rho }_P}{x}_{P,E{I}_{avg}}-\frac{r_F{k}_F}{{\rho }_F}\right)\left(\frac{1}{{\rho }_C}-\frac{1}{{\rho }_F}\right)\\ -\left(\frac{r_C{k}_C}{{\rho }_C}-\frac{r_F{k}_F}{{\rho }_F}\right)\left(\frac{1}{{\rho }_F}{x}_{F,E{I}_{avg}}+\frac{1}{{\rho }_C}{x}_{C,E{I}_{avg}}+\frac{1}{{\rho }_P}{x}_{P,E{I}_{avg}}-\frac{1}{{\rho }_F}\right)\end{array}\right)}{\left(\frac{1}{{\rho }_C}-\frac{1}{{\rho }_F}\right)\left(\frac{r_P{k}_P}{{\rho }_P}-\frac{r_F{k}_F}{{\rho }_F}\right)-\left(\frac{r_C{k}_C}{{\rho }_C}-\frac{r_F{k}_F}{{\rho }_F}\right)\left(\frac{1}{{\rho }_P}-\frac{1}{{\rho }_F}\right)}-\frac{\left(\begin{array}{l}\left(\frac{1}{{\rho }_C}-\frac{1}{{\rho }_F}\right)\left(\frac{k_F}{{\rho }_F}{x}_{F,E{I}_{avg}}+\frac{k_C}{{\rho }_C}{x}_{C,E{I}_{avg}}+\frac{k_P}{{\rho }_P}{x}_{P,E{I}_{avg}}\frac{k_F}{{\rho }_F}\right)\\ -\left(\frac{k_C}{{\rho }_C}-\frac{k_F}{{\rho }_F}\right)\left(\frac{1}{{\rho }_F}{x}_{F,E{I}_{avg}}+\frac{1}{{\rho }_C}{x}_{C,E{I}_{avg}}+\frac{1}{{\rho }_P}{x}_{P,E{I}_{avg}}-\frac{1}{{\rho }_F}\right)\end{array}\right)}{\left(\frac{1}{{\rho }_C}-\frac{1}{{\rho }_F}\right)\left(\frac{k_P}{{\rho }_P}-\frac{k_F}{{\rho }_F}\right)-\left(\frac{k_C}{{\rho }_C}-\frac{k_F}{{\rho }_F}\right)\left(\frac{1}{{\rho }_P}-\frac{1}{{\rho }_F}\right)}=\frac{\left(\begin{array}{l}\left(\frac{r_F{k}_F}{{\rho }_F}\left[x_{F,E{I}_{avg}}-1\right]+\frac{r_C{k}_C}{{\rho }_C}{x}_{C,E{I}_{avg}}+\frac{r_P{k}_P}{{\rho }_P}{x}_{P,E{I}_{avg}}\right)\left(\frac{1}{{\rho }_C}-\frac{1}{{\rho }_F}\right)\\ -\left(\frac{r_C{k}_C}{{\rho }_C}-\frac{r_F{k}_F}{{\rho }_F}\right)\left(\frac{1}{{\rho }_F}\left[x{x}_{F,E{I}_{avg}}-1\right]+\frac{1}{{\rho }_C}x{x}_{C,E{I}_{avg}}+\frac{1}{{\rho }_P}{x}_{P,E{I}_{avg}}\right)\end{array}\right)}{\left(\frac{1}{{\rho }_C}-\frac{1}{{\rho }_F}\right)\left(\frac{r_P{k}_P}{{\rho }_P}-\frac{r_F{k}_F}{{\rho }_F}\right)-\left(\frac{r_C{k}_C}{{\rho }_C}-\frac{r_F{k}_F}{{\rho }_F}\right)\left(\frac{1}{{\rho }_P}-\frac{1}{{\rho }_F}\right)}-\frac{\left(\begin{array}{l}\left(\frac{1}{{\rho }_C}-\frac{1}{{\rho }_F}\right)\left(\frac{k_F}{{\rho }_F}\left[x_{F,E{I}_{avg}}-1\right]+\frac{k_C}{{\rho }_C}{x}_{C,E{I}_{avg}}+\frac{k_P}{{\rho }_P}{x}_{P,E{I}_{avg}}\right)\\ -\left(\frac{k_C}{{\rho }_C}-\frac{k_F}{{\rho }_F}\right)\left(\frac{1}{{\rho }_F}\left[x_{F,E{I}_{avg}}-1\right]+\frac{1}{{\rho }_C}{x}_{C,E{I}_{avg}}+\frac{1}{{\rho }_P}{x}_{P,E{I}_{avg}}\right)\end{array}\right)}{\left(\frac{1}{{\rho }_C}-\frac{1}{{\rho }_F}\right)\left(\frac{k_P}{{\rho }_P}-\frac{k_F}{{\rho }_F}\right)-\left(\frac{k_C}{{\rho }_C}-\frac{k_F}{{\rho }_F}\right)\left(\frac{1}{{\rho }_P}-\frac{1}{{\rho }_F}\right)}=\frac{\left\{\left(\frac{1}{{\rho }_C}-\frac{1}{{\rho }_F}\right)\left(\frac{r_P{k}_P}{{\rho }_P}-\frac{r_F{k}_F}{{\rho }_F}\right)-\left(\frac{r_C{k}_C}{{\rho }_C}-\frac{r_F{k}_F}{{\rho }_F}\right)\left(\frac{1}{{\rho }_P}-\frac{1}{{\rho }_F}\right)\right\}{x}_{P,E{I}_{avg}}}{\left(\frac{1}{{\rho }_C}-\frac{1}{{\rho }_F}\right)\left(\frac{r_P{k}_P}{{\rho }_P}-\frac{r_F{k}_F}{{\rho }_F}\right)-\left(\frac{r_C{k}_C}{{\rho }_C}-\frac{r_F{k}_F}{{\rho }_F}\right)\left(\frac{1}{{\rho }_P}-\frac{1}{{\rho }_F}\right)}-\frac{\left\{\left(\frac{1}{{\rho }_C}-\frac{1}{{\rho }_F}\right)\left(\frac{k_P}{{\rho }_P}-\frac{k_F}{{\rho }_F}\right)-\left(\frac{k_C}{{\rho }_C}-\frac{k_F}{{\rho }_F}\right)\left(\frac{1}{{\rho }_P}-\frac{1}{{\rho }_F}\right)\right\}{x}_{P,E{I}_{avg}}}{\left(\frac{1}{{\rho }_C}-\frac{1}{{\rho }_F}\right)\left(\frac{k_P}{{\rho }_P}-\frac{k_F}{{\rho }_F}\right)-\left(\frac{k_C}{{\rho }_C}-\frac{k_F}{{\rho }_F}\right)\left(\frac{1}{{\rho }_P}-\frac{1}{{\rho }_F}\right)}=x_{P,E{I}_{avg}}-x_{P,E{I}_{avg}}=0$$

Thus, system (16) is equivalent to

$$\begin{array}{l}{x}_{F,E{E}_{avg}}+x_{C,E{E}_{avg}}+x_{P,E{E}_{avg}}=1\\ \left(\frac{1}{{\rho }_C}-\frac{1}{{\rho }_F}\right)x_{C,E{E}_{avg}}+\left(\frac{1}{{\rho }_P}-\frac{1}{{\rho }_F}\right)x_{P,E{E}_{avg}}=\frac{1}{{\rho }_{E{I}_{avg}}}-\frac{1}{{\rho }_F}\\ x_{P,E{E}_{avg}}=x_{P,E{I}_{avg}}\end{array}$$

With back-substitution and simplification, the solution of system (16) turns out to be

$$\begin{array}{l}{x}_{F,E{E}_{avg}}=x_{F,E{I}_{avg}}\\ x_{C,E{E}_{avg}}=x_{C,E{I}_{avg}}\\ x_{P,E{E}_{avg}}=x_{P,E{I}_{avg}}\end{array}$$ (17)

This analytical result is the answer to second question posed at the introduction; it states that energy balance coincides with weight stability if and only if the oxidized nutrient distribution in the $E{E}_{avg}$ is identical to that in the $E{I}_{avg}$ as such condition guarantees the existence of identity (12). Not meeting the requirement in (17) results in serious contradictions as exemplified in the answer to the introduction's third question which is explained below.

In accordance to the Law of Conservation of Mass each day we experience a mass change $\Delta m$ given by

$$\Delta m=m_{\text{intake}}-m_{\text{loss}}$$ (18)

where $m_{\text{intake}}$ is the mass of the daily absorbed nutrients and $m_{\text{loss}}$ is the daily mass loss that results from the excretion of byproducts of nutrients oxidation.

By Eq. (13) at energy equilibrium $\left(E{I}_{avg}=E{E}_{avg}=E_{eq}>0\right)$ Eq. (18) becomes

$$\begin{gathered} \Delta m=m_{\text{intake}}-m_{\text{loss}} \\ =\frac{E{I}_{avg}}{{\rho }_{E{I}_{avg}}}-\frac{E{E}_{avg}}{{\rho }_{E{E}_{avg}}} \\ =E_{eq}\left(\frac{1}{{\rho }_F}-\frac{1}{{\rho }_P}\right)\left(x_{F,E{I}_{avg}}-x_{F,E{E}_{avg}}\right)+E_{eq}\left(\frac{1}{{\rho }_C}-\frac{1}{{\rho }_P}\right)\left(x_{C,E{I}_{avg}}-x_{C,E{E}_{avg}}\right) \end{gathered}$$ (19)

Inspection of Eq. (19) answers the third question. Observe that

$$\frac{1}{{\rho }_F}-\frac{1}{{\rho }_P}<0\text{and}\frac{1}{{\rho }_C}-\frac{1}{{\rho }_P}>0$$

since ${\rho }_C<{\rho }_P<{\rho }_F$ [9].

Additionally, conditions (i) and (ii) imply

$$\begin{array}{l}{x}_{F,E{I}_{avg}}-x_{F,E{E}_{avg}}<0\\ x_{C,E{I}_{avg}}-x_{C,E{E}_{avg}}\ge 0\end{array}$$

This indicates that body weight increases over time since the satisfaction of both conditions result in a persistent positive mass balance, i.e.,

$$\Delta m=\stackrel{>0}{\overbrace{E_{eq}}}\stackrel{<0}{\overbrace{\left(\frac{1}{{\rho }_F}-\frac{1}{{\rho }_P}\right)}}\stackrel{<0}{\overbrace{(x_{F,E{I}_{avg}}-x_{F,E{E}_{avg}})}}+\stackrel{>0}{\overbrace{E_{eq}}}\stackrel{>0}{\overbrace{\left(\frac{1}{{\rho }_C}-\frac{1}{{\rho }_P}\right)}}\stackrel{\ge 0}{\overbrace{\left(x_{C,E{I}_{avg}}-x_{C,E{E}_{avg}}\right)}}>0$$

Yet this is impossible as body weight is supposed to be stable since $E{I}_{avg}=E{E}_{avg}$. Consequently, as indicated by system (17), for energy balance to coincide with weight stability, the oxidized nutrient distribution in $E{E}_{avg}$ has to be equal to that in $E{I}_{avg}$; otherwise we run into contradictions as ${\rho }_{E{I}_{avg}}\ne {\rho }_{E{E}_{avg}}$ (see Eq. (13)).

2.2.2. Energy balance is unattainable at weight stability

In accordance to the EBT, body weight stability requires that the average daily absorbed nutrients mass equals the average daily oxidized nutrients mass since if not, weight is increasing (absorbed mass > oxidized mass) or decreasing (absorbed mass < oxidized mass). As implied in system (17) such equilibrium only happens when the mean absorbed mass of each macronutrient (${\overline{m}}_{i,\text{ab}}$) equals its respective mean oxidized mass (${\overline{m}}_{i\text{,}\text{ox}}$) since

$${\overline{m}}_{i,\text{ab}}=\frac{E{I}_{avg}\cdot x_{i,E{I}_{avg}}}{{\rho }_i}=\frac{E{E}_{avg}\cdot x_{i,E{E}_{avg}}}{{\rho }_i}={\overline{m}}_{i,\text{ox}},i=F,C,P.$$

Yet, if ${\overline{m}}_{P,\text{ab}}={\overline{m}}_{P,\text{ox}}$ is true then, in general, all absorbed dietary protein is only utilized for EE; and thus, over time, total body protein persistently decreases because the EE-independent protein loss is not being compensated by dietary intake. EE-independent protein loss occurs in feces (e.g., excretion of mucin, an indigestible protein secreted by the intestinal mucosa [27]), in sweat (e.g., amino acids may be excreted during physical exertion [28]), in urine (e.g., urinary excretion of glycine in creatinine [29] and C-peptide [30], a 31 amino acid polypeptide generated from insulin secretion) and during renewal of skin, hair and nails (e.g., shedding of dead cells filled with keratin [31, 32, 33]). As a consequence, we run into a contradiction since body weight is simultaneously stable (true absorbed-oxidation identities imply mass balance) and decreasing (body protein is continuously diminishing). The constitutive processes of gluconeogenesis [34] and de novo lipogenesis [35] plus the fact that absorbed amino acids can exit the body without serving as EE fuel renders absorbed-oxidation identities impossible (Figure 6). Hence, energy balance is unattainable at weight stability.

Figure 6.

Mass balance may occur in the absence of energy balance. Hypothetical macronutrient mass input-output pattern that illustrates that it is possible to achieve weight stability without energy balance. Circles in the diagram represent macronutrient body reserves. The left dashed box contains the input mass while the right box encloses the output mass. Energy densities are ρ_F = 9.4 kcal/g = 39.33 MJ/kg, ρ_C = 4.2 kcal/g = 17.6 MJ/kg, ρ_P = 4.7 kcal/g = 19.7 MJ/kg [9]. Although mass balance is achieved, energy balance is not since some of the absorbed or stored protein may be transformed into glucose (gluconeogenesis, GNG) or lost through EE-independent routs (EEIPL); absorbed or stored fat may also undergo gluconeogenesis; and some of the absorbed glucose may be transformed into fat (de novo lipogenesis, DNL). All these metabolic processes render energy balance not possible. AEI: absorbed EI; EEF: EE fuel; EEIPL: EE-independent protein loss.

2.2.3. At weight stability energy balance may be positive or negative

The preceding analysis has shown that weight stability coincides with energy imbalance since the absorbed-oxidation macronutrient identities are unachievable (i.e., ${\overline{m}}_{i,\text{ab}}\ne {\overline{m}}_{i,\text{ox}}$). By system (17) this indicates that the macronutrient distribution in the $E{I}_{avg}$ is unequal to that in the $E{E}_{avg}$ and thus by Eq. (13) ${\rho }_{E{I}_{avg}}-{\rho }_{E{E}_{avg}}\ne 0$. Hence, at steady weight only two possibilities exist:

• 1.${\rho }_{E{I}_{avg}}-{\rho }_{E{E}_{avg}}<0$
• 2.${\rho }_{E{I}_{avg}}-{\rho }_{E{E}_{avg}}>0$

The first happens when $x_{F,E{I}_{avg}}<x_{F,E{E}_{avg}}$ since energy density increases as the fat fraction increases (see Eq. (13)). This is likely to happen in a LFD (e.g., $0.2\le x_{F,E{I}_{avg}}\le 0.3$). Conversely, the second occurs when $x_{F,E{I}_{avg}}>x_{F,E{E}_{avg}}$. Such situation is possible in a LCD (e.g., $x_{F,E{I}_{avg}}\gg 0.3$).

Recall now

$$E{I}_{avg}-E{E}_{avg}={\rho }_{E{I}_{avg}}{m}_{E{I}_{avg}}-{\rho }_{E{E}_{avg}}{m}_{E{E}_{avg}}$$

where $m_{E{I}_{avg}}$ is the average absorbed daily mass associated to the $E{I}_{avg}$ and $m_{E{E}_{avg}}$ is the average daily oxidized mass corresponding to the $E{E}_{avg}$.

At weight stability, mass is balanced and so $m_{E{I}_{avg}}$ is equal to average daily mass loss. The latter consists of the average daily excreted byproducts of oxidation ($m_{E{E}_{avg}}$) plus the average daily EEIML ($m_{EEIML}$)

$$m_{E{I}_{avg}}=m_{E{E}_{avg}}+m_{EEIML}$$

Therefore, the coincidence of energy imbalance and mass balance implies

$$E{I}_{avg}-E{E}_{avg}=m_{E{E}_{avg}}({\rho }_{E{I}_{avg}}-{\rho }_{E{E}_{avg}})+m_{EEIML}{\rho }_{E{I}_{avg}}\ne 0$$ (20)

Eq. (20) is only negative or positive, and consequently a negative energy balance coincides with weight stability only if ${\rho }_{E{I}_{avg}}-{\rho }_{E{E}_{avg}}<0$; otherwise (i.e., ${\rho }_{E{I}_{avg}}-{\rho }_{E{E}_{avg}}>0$ ), a positive energy balance coexists with weight stability. For example, in Figure 6

$$\begin{array}{ll}{\rho }_{E{I}_{avg}}-{\rho }_{E{E}_{avg}}\hfill & =\frac{E{I}_{avg}}{m_{E{I}_{avg}}}-\frac{E{E}_{avg}}{m_{E{E}_{avg}}}\hfill \\ \hfill & =\frac{E{I}_{avg}}{m_{E{I}_{avg}}}-\frac{E{I}_{avg}}{m_{E{I}_{avg}}-m_{EEIML}}\hfill \\ \hfill & =\frac{\mathrm{2,574.5}\text{kcal}}{500\text{g}}-\frac{\mathrm{2,768.3}\text{kcal}}{499\text{g}}\approx -0.3987\text{kcal}/\text{g}\hfill \end{array}$$

and thus

$$\begin{array}{ll}E{I}_{avg}-E{E}_{avg}& =m_{E{E}_{avg}}\left({\rho }_{E{I}_{avg}}-{\rho }_{E{E}_{avg}}\right)+m_{EEIML}{\rho }_{E{I}_{avg}}\\ & =499\text{g}\left(-0.3987\text{kcal}/\text{g}\right)+\left(1\text{g}\right)\left(5.149\text{kcal}/\text{g}\right)\\ & \approx -193.8\text{kcal.}\end{array}$$

Therefore, at weight stability the sign of ${\rho }_{E{I}_{avg}}-{\rho }_{E{E}_{avg}}\ne 0$ predicts the energy imbalance direction. As a result, during steady weight periods, the energy balance is likely to be negative under a LFD but positive under a LCD.

3. Discussion

The present work used the axiomatic method to described body weight fluctuations as a mass balance process. This approach resulted in a parsimonious account for the apparent advantage of LCDs over isocaloric LFDs. According to this model, the mechanism that explains the LCDs superiority is not the diet's physiology; the LCD dominance follows from its high-fat content which allows the same EI as in a LFD but at a much lower mass intake. Consequently, since the daily rate of mass excretion in both diets appear to be similar (inferred from published weight loss data [13, 14, 15]), a large weight reduction will be measured in subjects were mass intake is substantially reduced as occurs in LCDs. This hypothesis seems reasonable as Eqs. (2) and (6) fitted LCDs vs. LFDs data and so they may serve as a simple weight control model.

One of the most complex models of energy metabolism and weight change is that form Hall [15, 18, 19, 20]. This computational model shows improved weight loss in LCDs vs. isocaloric LFDs for only few weeks, but not over longer time intervals (e.g., 6 months) [15]. This is so as the model formulation was done to be consistent with the EBT; and hence, on the long run, both simulated diets result in the same level of weight loss as both interventions experience the same degree of energy imbalance [15, 19]. Such initial rapid weight loss, as predicted by Hall's model, is secondary to water excretion as a result of carbohydrate restriction and not a consequence of greater fat loss [15]. In Brehm et al. [13], nonetheless, the LCD superior weight loss persisted over 6 months and was associated with a substantial drop in fat mass as evidenced by DEXA measurements. The aforesaid model prediction is therefore open to discussion as it lacks of broader generality. The mass balance model proposed here, in contrast, gives excellent fits to weight loss data and its interpretation is straightforward. These characteristics had lead, as previously explained, to a much simpler and general hypothesis of the LCD advantage compared to the one offer by Hall's model. Consequently, according to Ockham's razor, the odds are in favor of the mass balance theory and not in favor of the EBT. Further experimentation is thus needed to resolve this controversial issue.

According to the EBT, the explanation behind the LCDs superior weight loss vs. LFDs is that people in the latter diets underreport EI as normally no substantial differences are found between the EE in both diets [14]. A recent in-patient study confronts such view. Hall et al. [15] confined obese adult men and women into a metabolic ward and randomly placed them into isocaloric LCDs or LFDs for 6 days. Statistical analysis of the negative energy balance of each diet showed non-significant differences over the 6 days, yet the LCD group lost significantly more weight than the LFD subjects (–1.85kg ± 0.15 (SEM) vs. –1.3kg ± 0.16 (SEM), respectively). This suggests that the one-to-one correspondence, implicit in the EBT, between energy imbalance magnitude and weight loss (or weight gain) appears to be absent. Moreover, fitting the mass balance model to Hall et al. [15] results in excellent estimates of the reported cumulative weight loss measurements

$$NC{W}_6^{LCD}=\left(\frac{{\overline{M}}_{LCD}}{{\overline{R}}_{LCD}}-w_0\right)\left(1-{(1-{\overline{R}}_{LCD})}^6\right)=\left(\frac{1.8496}{0.0205109}-106\right)\left(1-{(1-0.0205109)}^6\right)\approx -1.85017\text{kg}$$

$$NC{W}_6^{LFD}=\left(\frac{2.1005}{0.0219753}-106\right)\left(1-{(1-0.0219753)}^6\right)\approx -1.30002\text{kg}$$

Hence, it is likely that the LCDs advantage is predominantly explained by different mass intake levels. Likewise, the feature of the Western lifestyle that may explain the current obesity epidemic is today's super-size portions of food and drinks as the rising incidence in obesity appears not to be explained by diminished EE levels [36, 37, 38]. This suggests, therefore, that a mass balance model is better suited to describe our present obesity crisis.

This work has shown that Eq. (6), originally derived by Hall [25] from Forbes's theory [23, 24], is able to accurately reproduce the decline in fat mass induced by an arbitrary diet. According to this formula, however, the diet's macronutrient distribution appears to have no direct impact on the final body composition after weight loss. To illustrate this idea, consider two hypothetical subjects with identical body weights (100kg) and initial fat mass ($F{M}_k=35\text{kg}$). Suppose, next, that both subjects had lost 25kg ($w_{k+n}-w_k=-25$) through very distinct diets (e.g., LFD vs. LCD). Then according to Eq. (6) the new fat mass in both subjects is

$$F{M}_{k+n}=10.4W\left\{\frac{35}{10.4}\exp \left(\frac{-25+35}{10.4}\right)\right\}\approx 17.3\text{kg.}$$

Consequently, the effect of any diet on an initial state of body composition appears to be only dependent on the amount of weight lost and not in the diet's macronutrient contents. The diet composition, however, may have a positive or negative effect on the subject's diet adherence which is clearly an important determinant of the final weight loss amount.

This work demonstrated that for energy balance to coincide with weight stability, the average absorbed mass of each macronutrient has to be equal to its respective average oxidized mass. Such absorbed-oxidation identities are, however, unattainable due to the constitutive processes of gluconeogenesis and de novo lipogenesis plus the fact that absorbed amino acids can exit the body through EE-independent routes. The EBT is consequently rendered impossible and so weight stability coincides with energy imbalance whose direction is given by the sign of ${\rho }_{E{I}_{avg}}-{\rho }_{E{E}_{avg}}\ne 0$. Weight stability under a LFD is therefore likely to coexist with a negative energy balance as energy density is directly proportional to fat content. This conclusion provides an alternative explanation to the apparent EI underreporting observed in populations at steady weight [3, 4].

In nutrition science, EI represents the heat release upon food oxidation [39] and as such it has no contribution to body mass. Einstein's energy-mass equation shows, for instance, that 2,500 kcal = 10.465 MJ of heat energy are equivalent to

$$m=\frac{E}{c^2}=\frac{10.465\times {10}^6\text{J}}{{(3\times {10}^{8}m/s)}^2}\approx 1.16\times {10}^{-10}\text{kg.}$$

Daily accumulation of this amount for 100 years would increase body weight by 0.0000042kg. Food's Calories have, therefore, no impact on body mass. It is food mass that augments body weight; the absorption of 1g of glucose, protein or fat increases body mass by exactly 1g independent of the substrate's Calories; a consequence of the Law of Conservation of Mass. The level of daily of food mass intake is, however, influenced by the ever present interplay between the environment and genes and by how food's intrinsic biochemistry relates to satiety [39].

Macronutrients oxidation byproducts are CO₂, water, urea, SO₃ and heat [16]. Hence, body weight decreases through the excretion of all byproducts except heat. This is exemplified in glucose oxidation

$$C_6{H}_{12}{O}_6+6O_2\to 6C{O}_2+6H_{2}O+\text{Heat}(\sim 720\text{kcal}/\mathrm{mol}{C}_6{H}_{12}{O}_6)$$

as the mass entering the reaction (in g/mol) is

$$\underset{C_6{H}_{12}{O}_6}{180\text{g}}+\underset{6O_2}{192\text{g}}=372\text{g}$$

while the mass release after oxidation is only present in the reaction products and not in the dissipated heat

$$\underset{6C{O}_2}{264}+\underset{6H_{2}O}{108}=372\text{g}$$

Therefore, body mass decreases as we excrete CO₂, water, urea and SO₃ but not as consequence of the heat content in the EE [40]. The amount of daily mass excretion is, nonetheless, modulated by neural, gastric and endocrine signaling systems that direct body weight regulation [39].

Research by Ebbeling et al. [41, 42] has shown that LCDs increase EE in contrast to isocaloric LFDs. This according to EBT should increase the daily rate of mass loss (DRML) accounting in this manner for the deferential weight loss among diets. As previously explained, EE is a measurement of the heat release upon macronutrient oxidation, that as such, has no impact on body mass. Hence, in order to equate an increased EE with an increased DRML we need to determine how diet composition alters ${\rho }_{EE}$ since $DRML=EE/{\rho }_{EE}$. Inspection of Eq. (13) suggests, however, that ${\rho }_{EE}$ increases in LCDs but decreases in LFDs. It follows then, that the DRML in both diets could be similar since as EE increases in LCDs (or decreases in LFDs) ${\rho }_{EE}$ also increases (or decreases in LFDs). The next computation gives a concrete illustration of such possibility. Suppose that in the LCD the EE is 3,483 kcal/day with energy distributed as: 55% F oxidation, 35% C oxidation and 10% P oxidation. In contrast, for the LFD the EE is 3,200 kcal/day with energy distributed as: 45% F oxidation, 50% C oxidation and 5% P oxidation. Thus, by Eq. (13) we get

$$\begin{gathered} \begin{array}{c}{\rho }_{EE}^{LCD}={\left(\frac{1}{9.4}\left(0.55\right)+\frac{1}{4.2}\left(0.35\right)+\frac{1}{4.7}\left(0.1\right)\right)}^{-1}\approx 6.13\text{kcal/g}\\ \end{array} \\ {\rho }_{EE}^{LFD}={\left(\frac{1}{9.4}\left(0.45\right)+\frac{1}{4.2}\left(0.5\right)+\frac{1}{4.7}\left(0.05\right)\right)}^{-1}\approx 5.63\text{kcal/g} \end{gathered}$$

Implying,

$$\begin{array}{l}DRM{L}_{LCD}=\frac{E{E}_{LCD}}{{\rho }_{E{E}_{LCD}}}=\frac{\mathrm{3,483}\text{kcal/day}}{6.13\text{kcal/g}}\approx 568\text{g/day}\\ \\ DRM{L}_{LFD}=\frac{E{E}_{LFD}}{{\rho }_{E{E}_{LFD}}}=\frac{\mathrm{3,200}\text{kcal/day}}{5.63\text{kcal/g}}\approx 568\text{g/day}\end{array}$$

Therefore, as suggested by the mass balance model proposed here, the enhance weight loss observed in LCDs vs. isocaloric LFDs is mainly given by distinct levels in mass intake since the DRML appears to be similar between diets. Further experimentation is needed to confirm this hypothesis.

4. Conclusion

In conclusion, the food property that increases body weight is its mass and not its Calories. The physiological activity that decreases body weight is the excretion of food oxidation byproducts and not heat dissipation. Daily weight fluctuations are thus dependent on the difference between daily mass intake and daily mass excretion indicating that the conservation law that describes body weight dynamics is the Law of Conservation of Mass and not the First Law of Thermodynamics. According to the latter Law, in a closed (Figure 1 A) or open (Figure 1 B) systems, a positive or negative energy balance is not always followed by a similar sign mass change as required by the EBT. This theory is therefore not a corollary of First Law of Thermodynamics; assuming otherwise may have unintended consequences (Figure 7).

Figure 7.

The application of the EBT may lead to unintended weight gain. Current dietary guidelines advise subjects with adequate body weight to minimize health risks and avoid weight gain by adopting isocaloric LFDs [43]. Such practice may, however, result in unplanned weight gain. The figure simulates the possible effect of exchanging a high-fat diet (HFD; F: 50%, C: 40%, P: 10%) for an isocaloric LFD (F: 20%, C: 65%, P: 15%). Under the HFD, body weight was stable at ~70kg. After beginning the isocaloric LFD (day 250), body weight increases towards a steady value of ~74.3kg in order to accommodate the increased mass intake (77g) inherent to this diet. The application of the EBT may, therefore, caused unintended consequences as it fails to account the mass balance state and thus it cannot properly predict body weight evolution. Simulation algorithm was similar to that in Figure 2 A. Here $w_0=70\text{kg}$; ${\rho }_{O_2}\cdot PAL\cdot v_{O_2}=0.0087$; $nEM{P}_k=(1+0.05\cdot y_k)$;$F_{loss,k}=0.0278285(1+0.05\cdot z_k)$; and if k < 250 then $EM{P}_k=0.339(1+0.05\cdot x_k)$, otherwise $EM{P}_k=0.416(1+0.05\cdot x_k)$.

Declarations

Author contribution statement

Francisco Arencibia-Albite: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Funding statement

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Competing interest statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.