Energy optimization of Multiple Stage Evaporator system using Water Cycle Algorithm

Abstract

Black liquor, a residual stream from the Kraft recovery process of paper mills is an incipient biomass energy resource which finds prospective biofuel-based industrial applications to ensure process self-sufficiency and sustainability. Black liquor is concentrated using Multiple Stage Evaporator, the utmost energy intensive unit, before using it as biofuel. Pertaining to the contemporary global energy scenario, improvement in energy efficiency of Multiple Stage Evaporator becomes indispensable. The present work investigates the non-linear modeling and simulation-based optimization of Heptads' stage based Multiple Stage Evaporator in backward feed flow configuration integrated with various energy saving strategies. A novel metaheuristic approach, Water Cycle Algorithm has been employed to search the optimum estimates of unknown process variables and therefore, the optimum energy efficiency parameters. The optimization results demonstrate the efficiency of Water Cycle Algorithm in screening the most appropriate operating strategy, i.e., hybrid model of all energy saving strategies (steam-split, feed-split and feed-preheating) with optimum energy efficiency i.e. Steam Economy of 7.092 and Steam Consumption of 1.919 kg/s. Moreover, a comparative analysis of the results with previous literature and real-time plant estimates reveal that the hybrid model offers improvement of 52.84% in Steam Economy and reduction in Steam Consumption by 28.13% when compared to the real plant data.

Energy; Computing methodology; Biofuel; Energy economics; Renewable energy resources; Energy sustainability; Multiple Stage Evaporator; Energy optimization; Energy saving strategies; Steam economy; Steam consumption; Water Cycle Algorithm.

1. Introduction

The present energy scenario encompassing gargantuan proliferation of energy requirements, blooming cost of energy supplies and global warming concerns, dictates the transference from non-renewable to renewable energy to ensure sustainability. As a result of the escalating cost of oil and the uninterruptedly intensifying necessity for automotive transport fuels, the progression of a dependable and cost-effective practice for the production of biofuels for transport applications is a global requirement. With the intention to accomplish climate change commitments and ameliorate the security of energy supplies worldwide, bioenergy is frequently endorsed as a fossil fuel alternative owing to the CO₂-neutral trait of biomass. In recent years, there has been considerable interest in the utilization of biomass in a cost-efficient manner for the production of CO₂-neutral automotive fuels as CO₂ is the leading gas accountable for climate change (Akia et al., 2014; Chandel et al., 2012; Chum and Overend, 2001; Raheem et al., 2015; Zhu et al., 2010). In addition, there are voluminous improvements towards extraction of biofuels, biochemicals and biopolymers from biomass throughout the world (CH et al., 2012; Lee et al., 2012; Oh et al., 2015; Prasetyo and Park, 2013). Many researchers have shown great interest towards the production of clean and renewable fuels from biomass such as bio-ethanol (Baeyens et al., 2015; Kang et al., 2014; Taghizadeh-Alisaraei et al., 2019), aviation fuels (Wang et al., 2019) and others (Nie et al., 2017a, 2017b; Yao et al., 2020).

As per the report of International Energy Agency, the pulp and paper industry forming a vivacious fragment of the global economic cluster harvests about 170 million tonnes of black liquor (measured as dry solids) globally on yearly basis. This black liquor drained as a waste encompasses an aggregate energy content of about 2EJ and hence, black liquor corroborates to be a very noteworthy source of biomass. In this perspective, black liquor amassed as a discarded deposit from the Kraft recovery process in the production of paper is an eye-catching asset for sustainable development. The conversion of black liquor to biofuels unquestionably causes a decrease in emissions of greenhouse gases and pollutants (Johansson, 2016; Naqvi et al., 2010; Teske et al., 2011). Consequently, the transformation of primary energy in the residual black liquor to a high value energy transporter (for instance, thermal energy in the form of steam, electrical energy and biofuels for transport applications) is of prodigious attention (Al-Kaabi et al., 2017; Andersson et al., 2016; Carvalho et al., 2018; Ong et al., 2018). Black liquor can be transformed into a number of transport fuels such as DME, methanol, hydrogen, etc. Table 1 presents the calorific value (in MJ/kg) of various fuels including standard diesel and petrol, and the transport fuels obtained from black liquor (World Nuclear Association, 2018). Evidently, the primary energy in black liquor can be transformed into a high calorific value energy carrier.

Table 1.

Calorific (Heat) values of various fuels^∗.

Fuel	Calorific Value (in MJ/kg)
Hydrogen (H2)	120–142
Methane (CH4)	50–55
Methanol (CH3OH)	22.7
Dimethyl ether - DME (CH3OCH3)	29
Petrol/gasoline	44–46
Diesel fuel	42–46

^∗Data presented in this table has been taken from the website of World Nuclear Association (World Nuclear Association, 2018).

A growing body of literature has analyzed the possibilities of making humongous energy savings by using black liquor as an energy source, thereby, achieving process self-sufficiency (Darmawan et al., 2017; Hamaguchi et al., 2012). In the light of the above considerations, Black Liquor Gasification (BLG) emerges out as an attention-grabbing substitute for the production of synthesis gas and its subsequent conversion to a variety of motor fuels (Chum and Overend, 2001; Naqvi et al., 2010, 2012). In terms of CO₂-neutral fuels for automotive applications, amalgamation of BLG in a modern, eco-cyclic, pulp mill bio-refinery for the production of renewable energy sources proves to be a well-organized alternative.

Black liquor, which is an aqueous solution of lignin deposits, hemicellulose and the inorganic compounds utilized in the Kraft Recovery process, usually encompasses relatively low solids content (15–17%) when it is withdrawn from the digester. With the intention of producing a combustible material via black liquor as a biomass source, the black liquor is evaporated to high dryness in a Multiple Stage Evaporator (MSE) system which is the utmost energy intensive unit among all other units in the paper and pulp mills (Naqvi et al., 2010). This puts emphasis on energy optimization of MSE and on the investigation of numerous Energy Saving Strategies (ESSs). In general, the energy efficiency of MSE is administered by two energy efficiency parameters, namely Steam Economy (SE) and Steam Consumption (SC). The SE is highly influenced by various unknown process variables including liquor flow rates, amount of steam supplied (SC) and the heat transfer due to temperature difference between two stages. Hence, the optimum values of these parameters reflect the optimum process energy efficiency. Evidently, the above-all focus is on optimizing the energy efficiency parameters (SE and SC) by exploring several ESSs proposed for MSE and to delineate erstwhile research accomplishments in the arena of modeling and simulation of MSE under steady-state. Such energy-intensive systems have drawn considerable interest in terms of modeling, simulation, optimization and control (Bhargava et al., 2008b; Kaya and Ibrahim Sarac, 2007; Verma et al., 2018c, 2018b). Additionally, there is a considerable amount of literature on simulation of MSE with various ESSs and feed flow configurations via steady and dynamic state modeling (Bhargava et al., 2008a; Gautami and Khanam, 2012; Khanam and Mohanty, 2010; Kumar et al., 2013; Verma et al., 2016, 2017a).

Owing to the non-linear relationship between temperature of each stage of a MSE and the thermo-physical parameters (such as latent heat of vaporization (λ), enthalpy of vapor (H) and enthalpy of black liquor (h_L)), the energy models of MSE systems in real-time exhibit non-linear behavior to some extent. The steady-state non-linear energy models of MSE usually comprise of Simultaneous Non-Linear Algebraic Equations (SNLAEs). In order to obtain the solution of these SNLAEs and for accurate analysis of the overall MSE system, the selection of optimum temperature of each MSE stage is to be carried out to estimate the optimal energy efficiency parameters.

In the literature, there are a surprising number of methods for solving SNLAEs including various classical numerical iterative techniques, for instance, Gauss elimination method (Lambert et al., 1987), Secant and Newton-Raphson (NR) Methods. Other approaches include MIND method (Method for analysis of INDustrial energy systems) based on Mixed-Integer Linear Programming (MILP) (Karlsson, 2011) and Pinch analysis used for the identification of the optimum heat recovery of MSE process and the selection of the best suitable ESSs and configuration options concerning cost steam utility in MSE (Higa et al., 2009; Hillenbrand and Westerberg, 1988; Sharan and Bandyopadhyay, 2016). However, the classical numerical approaches are quite inefficient and inaccurate in solving the complex SNLAEs. Furthermore, the exhaustive computation of Jacobian Matrix and the dependency on the initial guess turn out to be drawbacks of the NR Method (Verma et al., 2017b). Besides, various approaches have been proposed to solve these issues of optimization of SE and SC including the Interior-Point Method (I-PM), a dynamic programming approach, GA, a nature-inspired approach (Verma et al., 2019; Verma et al., 2018d, 2017b, 2017c) and other nature-inspired algorithms (Pati et al., 2020).

On the other hand, in recent years, in the field of artificial intelligence, metaheuristic algorithms have ascertained their potential in application to an eclectic range of combinatorial optimization problems, improvement in the existing algorithms, and generation of innovative ones. For solving such complex numerical optimization problems as involved in MSE, researchers are relying on metaheuristic algorithms based on simulations and nature inspired approaches owing to the inefficiency and inaccuracy of prevailing numerical techniques (Eskandar et al., 2012; Kaveh and Bakhshpoori, 2016). A growing body of literature has investigated the efficiency of a number of nature-inspired optimization techniques for solving the non-linear optimization problems including Particle Swarm Optimization (PSO), Genetic Algorithms (GA), Differential Evolution (DE), Ant Colony Optimization (ACO), Cuckoo Search (CS) algorithm and many more. However, Water Cycle Algorithm (WCA), an innovative metaheuristic optimization technique for the solution of single as well as multi-objective engineering optimization problems including their constraints, has been widely investigated and addressed by many researchers (Eskandar et al., 2012; Sadollah et al., 2015c, 2015b). WCA emerges as an attractive optimization technique for those working in the field of optimization owing to its capability to yield improved optimal solutions and implementation as compared to the aforementioned metaheuristic algorithms. Much work on the potential of WCA has been carried out (Sadollah et al., 2015a, 2015b), however concerns have been raised which call into question the efficiency of WCA in solving non-linear complex optimization problems (for instance, in MSE) as WCA has been employed in a few benchmark functions only. Thus, pertaining to the above discussion and, attributable to the inefficiency of classical optimization approaches and the growing applications of metaheuristic approaches, the energy optimization of MSE via WCA, a novel metaheuristic technique, corroborates as a research area seeking exhaustive investigation.

With this insight, we shed new light on the mathematical modeling, steady-state performance analysis and optimization of energy efficiency of MSE for Backward Feed Flow (BFF) configuration in conjunction with various ESSs. This paper presents an innovative solution to search the optimum unknown process operating parameters via WCA, a novel metaheuristic optimization method that decide the prime energy efficiency parameters, SE and SC. The Heptads' stage based MSE system or Heptads' Effect Evaporator (HEE) has been considered for the present investigation which is being driven nearby North Indian Pulp and Paper Mill. With the intention of estimating the optimal values of SE and SC, the optimum selection of unknown process parameters: temperature and liquor flow rate of each stage of MSE is highly required. Therefore, non-linear mathematical models for BFF configuration integrated with various ESSs viz. Steam-split, Feed-split and Feed-Preheating have been formulated. A set of fourteen non-linear algebraic equations with fourteen unknown operating variables (6–Vapor temperatures, T_i, i = 2–7, 7–Liquor flow rates, L_i, i = 1–7 and steam consumption V₁) is obtained for each model configuration. Furthermore, for each proposed model, the optimization problem is formulated through the developed non-linear model via the transformation of the SNLAEs into the objective function. In quest of the optimum solution of the formulated optimization problem, the present work exploits WCA for finding the optimum temperature of the vapor produced and the liquor flow rate for each MSE stage along with optimum SC. The vigorous implementation of WCA to solve the non-linear optimization problems result in their global optimum solutions. This work, consequently, exhibits the effectiveness of WCA as a maiden attempt in solving such a complex SNLAEs and in this manner, successfully assists in screening the best operating strategy of MSE with reference to SE and SC.

Conclusively, the prime objectives of the present investigation consist of:

• 1.Searching the optimal solution of non-linear energy models for various operating schemes of MSE by WCA.
• 2.Validation of the competence of WCA in solving complex non-linear optimization problem involved in MSE.
• 3.Screening of the best operating scheme of MSE in terms of energy-efficient performance.
• 4.Comparative analysis of performance parameters (SE and SC) obtained by WCA with real-time plant estimates and erstwhile research endeavors.

In this work, the simulations have been carried out on MATLAB (R2016a) programming platform on an AMD A8-7410 APU with AMD Radeon R5 Graphics (2.20 GHz and 4.00 GB RAM) on a 64-bit OS, x64-based processor. The remaining of this article is organized as follows. Section 2 gives details about the development of steady-state mathematical model of HEE System for different MSE configurations combined with various ESSs. Then, Section 3 describes the Energy Optimization of HEE via WCA by transforming the SNLAEs into the Objective Function. The results are discussed in Section 4. Our conclusions are drawn in Section 5.

2. Mathematical modeling of Heptads' Effect Evaporator system

A growing body of literature has demonstrated the BFF configuration (attributable to its optimal energy performance parameters, SE and SC) to be more appropriate as compared to the forward-feed and mixed-feed configurations (Bhargava et al., 2008a; Verma et al., 2017b, 2018a). With this fact kept in consideration, the Heptads' Effect Falling Film Evaporator with the BFF configuration has been considered in the present investigation to inspect the steady-state response of the MSE via Mathematical Modeling. In this work, the steady-state analysis has been carried out via the data in operation picked up from a paper mill near Saharanpur (U.P., India) presented in Tables 2 and 3 (Verma et al., 2017b). The variability of SE with the inclusion of various ESSs dictates the examination of the effect of each proposed ESS on the energy efficiency with an eye to select an optimal MSE configuration. Figure 1 illustrates a typical sketch of HEE based Falling Film Evaporator with the BFF configuration along with the inclusion of various ESSs.

Table 2.

Operating process parameters of Heptads' Effect MSE^∗.

Operating process parameter(s)	Value (s)
Total number of effect(s)/stage(s)	7
Temperature of weak black liquor to be fed (°C)	65
Concentration of weak black liquor to be fed, xf	0.118
Feed flow rate of weak black liquor to be fed, Lf (kg/sec)	15.611
Vapor temperature generated at 7th (last) stage (°C)	52
Effective Heat Transfer Area A1 and A2, A3 – A6, and A7 (m2)	540, 660 and 690
Enthalpy of weak black liquor to be fed, hf (kJ/kg)	254.81

^∗Data presented in this table has been taken from operated paper mill nearby Saharanpur, U.P., India.

Table 3.

Steady-state values of various parameters of the considered HEE.

Parameter	Stage 1	Stage 2	Stage 3	Stage 4	Stage 5	Stage 6	Stage 7
Ui	0.165	0.296	0.985	1.08	1.676	1.792	2.369
xi	0.5286	0.4321	0.3285	0.2465	0.1954	0.1625	0.1394

Figure 1.

Layout of a HEE in BFF configuration with Steam-split, Feed-split and preheater.

For the development of the mathematical model of the MSE system, the basic mass, component and energy balance equations are exploited. With the purpose of construing the mathematical model for each proposed configuration, these mass, component, energy and heat transfer balance equations are applied to each stage of the MSE. Each proposed configuration for N number of stages yields 2N number of non-linear equations which highly influence the unknown process parameters: the extent of live steam supplied V₁, the liquor flow rates L_i (i = 1–7) and temperature of generated vapor at each stage, T_i (i = 1–7). Consequently, each model configuration yields fourteen non-linear equations with an equal number of unknown operating variables to be estimated. The various proposed model configurations of MSE along with numerous ESSs such as steam-split, feed-split, feed pre-heating and their combinations are comprehensively described in Table 4.

Table 4.

Model description of backward feed flow configured MSE with various ESSs.

Model Number	Model Configuration with various ESSs	Characteristics of the proposed model configuration
Model-I	Backward feed (Base model)	Weak black liquor is fed/entered to the last (seventh) stage and live steam is supplied to the first stage.
Model-II	Backward feed with Steam-split	Incorporated with the Base model having extra provision of splitting the amount of live steam supply in the first two stages with split ratios y and (1– y) respectively.
Model-III	Backward feed with Feed-split	Incorporated with the Base model having extra provision of splitting the amount of weak black liquor to be fed in the last two stages simultaneously with feed ratios k and (1– k) respectively.
Model-IV	Backward feed with Feed-preheating	Incorporated with the Base model having extra provision of a pre-heater (PH). This PH has been installed before feeding the weak black liquor to MSE at the last stage. The vapor generated from the last stage together with (1– m) fraction of vapor generated from the second last stage is sent to feed PH and hence, concentrate the liquor at some extent before feeding to the MSE.
Model-V	Backward feed coupled with Feed-split and Feed-preheating	Incorporates the provision of Base model, Feed-split (Model-III) and Feed-preheating (Model-IV).
Model-VI	Backward feed coupled with Feed-split and Steam-split	Incorporates the provision of Base model, Feed-split (Model-III) and Steam-split (Model-II).
Model-VII	Backward feed coupled with Steam-split and Feed-preheating	Hybrid the properties of Base model, Steam-split (Model-II) and Feed-preheating model (Model-IV).
Model-VIII	Backward feed coupled with Feed-split, Steam-split and Feed-preheating	Hybrid the characteristics of all the above mentioned ESSs (Base model, Steam-split (Model-II), Feed-split (Model-III) and Feed-preheating model (Model-IV))

2.1. Development of mathematical model

For the development of Simultaneous Non-Linear Algebraic Equations (SNLAEs) for model formulation of MSE, the assumptions made under ideal conditions are enumerated below:

• •Negligible loss of heat to the surroundings.
• •Negligible deviation in composition and boiling point elevation in each stage.
• •Negligible fouling and scaling effect.
• •Dependence of black liquor enthalpy on the temperature and concentration.
• •Thermal equilibrium between black liquor and vapor produced at each stage.

Apart from these assumptions, some useful thermo-physical correlations including latent heat of vaporization, λ, enthalpies of vapor produced, H and liquor concentrated, h_L respectively at each stage are also required for the simulation of MSE. These correlations are highly dependent on the vapor temperature and slightly dependent on the concentration of the liquor, thereby resulting in a non-linear model. These correlations have been reported (Verma et al., 2017b) which are exploited afterwards en route for thorough modeling of the proposed configurations. The development of these non-linear models for various ESSs has been previously carried out (Verma et al., 2017b) and is elaborated in the Supplementary Material. These SNLAEs for the developed non-linear models have been utilized and simulated in this work for energy optimization of MSE.

2.2. Problem formulation

With the intention of optimizing the energy efficiency of the HEE system utilized in the Kraft Recovery process in Pulp and Paper mill, firstly, the objective function J(z) is to be formulated. The objective function, J(z) is chosen in an attempt to evaluate the optimum values of these decision variables z so as to optimize the process parameters and performance of the MSE system.

2.2.1. Formulation of objective function: transformation of SNLAEs into the optimization problem

In the present investigation, the objective function J(z) is formulated by transforming the SNLAEs developed for each of the proposed model configurations (Model-I to Model-VIII) into optimization problem. For the formulation of optimization model, the merit function, J(z) is formulated as the summation of square of non-linear equations and is given by Eq. (1).

$$J\left(z\right)=\sum _{e=1}^{14}{f}_e^2\left(z\right)$$ (1)

where, J(z) is the objective function and f_e(z) (e = 1–14) represent the non-linear algebraic equations developed for each stage of the MSE system by setting the energy balance equations equal to zero. Thus, J(z) is the anticipated objective function to be optimized with the aim of tracking down the optimum values of the unknown process parameters, z, i.e., T_i (i = 2–7), L_i (i = 1–7) and V₁.

For the different model configurations put forward in this work, the conditions for bounds of vapor temperature at each stage, T_i (i = 2–7) are to be defined to yield the inequality constraints. These constraints are defined by considering the plant operating data (as presented in Table 2). This demonstrates that the produced vapor from the last stage is held at a constant temperature, 52 °C (i.e. T₈) and also, the live steam has been supplied at a fixed temperature, 147 °C (i.e. T₁). For the maximum heat transfer through MSE stages, the temperature of the earlier stage should be higher than later stage. Therefore, in order to convincingly coordinate with the steady drop in temperature T_i from the first stage to the last stage, the feasible constraints are given by Eq. (2). For the steam consumption, feasible bound for V₁ in kg/s has been defined in region of [0:3 in kg/s].

T_i > T_i+1 (i = 1–6) and T₇ > 52 (T₈) (2)

Each stage of the MSE may possibly operate at optimal values of input steam flow rate (V₁), liquor flow rate (L_i) and vapor temperature (T_i) in order to achieve maximum energy efficiency of MSE. With the aim of finding these optimum parameters, the objective function J(z) is optimized via WCA. With the proper realistic bounds picked up from the real-time data in operation from the aforesaid paper mill and from the earlier reported literature work (Verma et al., 2017b), WCA is employed for computation of the optimal values of the decision variables z. Table 5 illustrates a detailed description of the bounds on generated vapor temperatures (T_i) and liquor flow rates (L_i) respectively for various model configurations mentioned in Table 4.

Table 5.

Feasible bounds of generated vapor temperature and liquor flow rate for i^th stage for various proposed MSE model configurations.

Vapor Temperatures
Model-I, Model-III, Model-IV, Model V	$T_i\left(°C\right)\in \left[100:110;70:85;66:74;60:70;55:65;52:63\right],\left(i=2-7\right)$
Model-II	$T_i\left(°C\right)\in \left[115:125;113:125;66:74;60:70;55:65;52:63\right],\left(i=2-7\right)$
Model-VI	$T_i\left(°C\right)\in \left[115:125;113:125;66:100;60:70;55:95;52:85\right],\left(i=2-7\right)$
Model-VII, Model-VIII	$T_i\left(°C\right)\in \left[115:125;113:125;66:115;60:100;55:95;52:85\right],\left(i=2-7\right)$
Liquor Flow rates
Model-I, Model-II, Model-IV, Model-VII	$L_i\left(\frac{kg}{s}\right)\in \left[2:5;3.5:6;4.5:7;6.5:9;9:11;10.5:13;13:15\right],\left(i=1-7\right)$
Model-III, Model-V, Model-VI, Model-VIII	$L_i\left(\frac{kg}{s}\right)\in \left[2:5;3.5:6;4.5:7;6.5:9;9:11.5;6:8;6:8\right],\left(i=1-7\right)$

The formulated optimization problem, J(z) has been simulated using WCA in MATLAB programming environment. Finally, in order to compute the optimum performance parameter, SE, the optimum values of the decision variables are exploited. As described earlier, SE and SC are the performance parameters which govern the energy efficiency of MSE. The optimization task via WCA yields the optimum estimates of liquor flow rates, vapor temperatures and the performance parameter, SC. The Steam Consumption, SC (in kg/s) is the amount of fresh steam supplied to the MSE and is represented here by V₁. Moreover, the Steam Economy, SE for HEE based MSE system is referred as the amount of total vapor produced from all the seven stages for a supplied fixed amount of live and fresh steam, and is mathematically expressed by Eq. (3). From Eq. (3), it is clear that SE is a dimensionless and unit less quantity. Evidently, the optimum L₁ and V₁ are used to evaluate the optimum SE.

$$SE=\frac{\sum _{i=2}^8{V}_i}{V_1}=\frac{L_f-L_1}{V_1}$$ (3)

SE and SC show an inverse relationship as evident from Eq. (3). Thus, minimum SC and maximum SE are desirable for improved energy efficiency of MSE system.

3. Optimization strategy: Water Cycle Algorithm

In this work, WCA, a nature-inspired metaheuristic optimization method, has been employed to optimize the objective function, J(z) for the estimation of optimum performance energy efficiency parameters. For each of the proposed model configurations, the optimization has been initiated with the formulation of objective function, J(z). The central ideas and concepts underlying WCA are enthused by nature and are centered on the characteristics of hydrological (water) cycle and downhill course of rivers and streams headed for the sea in the real world. Like other metaheuristic approaches for optimization, WCA initiates with an initial population of raindrops. After raining, the random generation of an initial population of design variables (population of streams) takes place. The best stream, i.e. the stream with the minimum cost function, is chosen as the sea (Eskandar et al., 2012). Thereafter, a certain number of good streams (i.e., the values of cost function closer to the existing best) are selected as rivers and the remaining streams flow towards the chosen rivers and the sea. An all-inclusive description of WCA is available in a voluminous literature and hence, an in-depth analysis has not been provided here. Nevertheless, the generalized step-by-step pseudo code for the WCA is comprehensively demonstrated in Pseudo code-1.

Pseudo code-1. Steps for Water Cycle Algorithm.

• Objective function J(z)

1. Set the parameters

• •N_var (number of design/decision variables = 14)
• •N_sr ((Number of rivers + sea) = 4)
• •N_pop (Population size = 50)
• •d_max (evaporation condition constant = 10⁻⁵)
• •max_iteration (Maximum number of Iterations = 1000)

2. Create random initial population and form the initial streams (raindrops), rivers, and sea as

$$\text{Population}\text{of}\text{raindrops}=\left[\begin{array}{c}\mathit{Raindro}{p}_1\\ \mathit{Raindro}{p}_2\\ ⋮\\ \mathit{Raindro}{p}_{N_{\mathit{pop}}}\end{array}\right]=\left[\begin{array}{cccc}{z}_1^1& z_2^1& \cdots & z_{N_{\mathrm{var}}}^1\\ z_1^2& z_2^2& \cdots & z_{N_{\mathrm{var}}}^2\\ ⋮& ⋮& \ddots & ⋮\\ z_1^{N_{pop}}& z_2^{N_{pop}}& \cdots & z_{N_{\mathrm{var}}}^{N_{pop}}\end{array}\right]$$

N_sr = Number of Rivers +1(Sea) and N_Raindrops = N_pop - N_sr

3. Evaluate the value (cost) of each raindrop as

$$C_i=Cos{t}_i=J\left(z_1^i,z_1^i,\cdots z_{N_{\mathrm{var}}}^i\right),i=1,2\cdots N_{pop}$$

4. Compute the intensity of flow for rivers and sea via

$$N{S}_n=round\left\{\left|\frac{Cos{t}_n}{\sum _{i=1}^{N_{sr}}Cos{t}_i}\right|\times N_{Raindrops}\right\},n=1,2\cdots N_{sr}$$

where NS_n denotes the number of streams flowing towards the specific rivers or sea.

5. The flow of streams to the rivers is given as

$$z_{Stream}^{i+1}=Z_{Stram}^i+\left\{rand\times C\times \left(z_{River}^i-z_{Stream}^i\right)\right\}$$

The flow of rivers to the sea (situated at the utmost downhill location) is given as

$$z_{River}^{i+1}=Z_{River}^i+\left\{rand\times C\times \left(z_{Sea}^i-z_{River}^i\right)\right\}$$

where rand is a uniformly distributed random number between 0 and 1 and C = 2.

6. Interchange the position of river with a stream yielding the best solution. Similarly, interchange the position of river with the sea in case a river finds better solution than the sea.

7. Check the evaporation condition using

$$d_{\max }^{i+1}=d_{\max }^i-\frac{d_{\max }^i}{\max \_iteration}$$

8. Start the raining process (if the evaporation condition is met) using

$$z_{Stream}^{new}=LB-\left\{rand\times \left(UB-LB\right)\right\}$$

For the streams which directly flow to the sea,

$$z_{Stream}^{new}=Z_{Sea}-\left\{\sqrt{\mu }\times rand\left(1,N_{\mathrm{var}}\right)\right\}$$

where LB and UB signify the respective lower and upper bounds well-defined by the given problem. μ (set to 0.1) is a coefficient indicating the range of exploration region near the sea. ‘randn’ indicates a normally distributed random number.

9. Reduce the value of the user defined parameter d_max using the relation given in step 7.

10. Check the stopping criterion (convergence criteria). If it is fulfilled, end the algorithm. If not, go back to Step 5.

Alt-text: Pseudo code-1

In the present investigation, the performance of WCA has been investigated by solving the formulated optimization problems for each of the proposed model configurations of MSE. The optimization of J(z) for each model has been accomplished by means of 20 independent runs. Consequently, the optimal values of the process variables, T_i, L_i and V₁ in the feasible operating range and bounds are achieved which are further utilized for the computation of SE. Algorithm 1 illustrates a self-explanatory summary of the solution procedure for the estimation of optimum process parameters of various MSE Configurations.

Algorithm 1. Estimation of Steam Economy.

• Objective function J(z)

• Set A_i, U_i, x_i, ∀i = 1 to 7 and the other operating parameters

• Set the lower and upper bounds of decision variables i.e. V₁, L_i (i = 1–7) and T_i (i = 2–7)

• Optimize J(z)//using Water Cycle Algorithm

• Display T_i, V₁, L_i, λ_i, H_i, h_i

• Evaluate optimum SE using Eq. (3)

• return SE

• End

Alt-text: Algorithm 1

4. Results and discussion

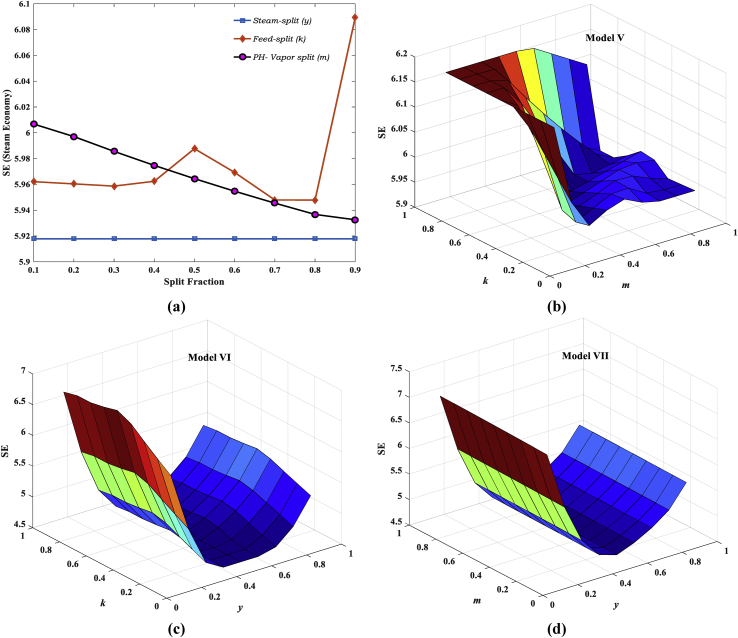
The mathematical models of backward feed configured HEE incorporated with proposed ESSs (viz. steam-split, feed-split and feed-preheating and its hybrid) employed in Indian paper industries have been developed in the earlier sections. With the purpose of tracking down the optimum values of the unknown process parameters (T_i, L_i and V₁), WCA has been implemented to optimize the formulated optimization problem. The optimum estimates of SE and SC are computed by exploiting the optimum values of these unknown operating variables. For each of the proposed model configurations and for different realistic bounds in the feasible region of various split fractions (y, k and m) in the range 10–90%, the energy performance parameters, SE and SC have been computed. These evaluated performance parameters in search of the optimal operating conditions yield the maximum energy efficiency of HEE system. Figure 2 shows the effect of these split-fractions on the SE for different model configurations. The optimum performance parameters have been computed based on the optimum values of various proposed split-fractions (y, k and m) using WCA. These optimum values of y, k and m can be visualized via Figure 2. For Model-V, the maximum SE of 6.172 is obtained at m = 0.1 and k = 0.3 while the minimum SE (less than 6) is at m = 0.9 and k = 0.8 (Figure 2(b)). Likewise, the minimum and maximum values of SE are obtained for y = 0.5 and k = 0.7 and y = 0.1 and k = 0.5 respectively for Model-VI (Figure 2(c)). Also, from Figure 2(d), it can be visualized that y = 0.1 and m = 0.9 results in maximum SE while the minimum SE is obtained for y = 0.5 and m = 0.1.

Figure 2.

Variation in SE with (a) independent variations in steam-split (y), feed-split (k) and vapor-split (m) fractions (b) collective variations in feed-split (k) and vapor-split (m) fractions (Model-V) (c) collective variations in feed-split (k) and steam-split (y) fractions (Model-VI) (d) collective variations in steam-split (y) and vapor-split (m) fractions (Model-VII).

The corresponding values of SC and SE pertaining to the optimum y, k and m for various model configurations are presented in Table 6. Also, for a well-organized comparison of different models (Model-I to Model-VIII), the various unknown process variables including T_i, L_i and V₁ have been evaluated. Also, the various thermo-physical parameters (λ_i, H_i, and h_Li) which depend on these computed unknown process variables have been evaluated as portrayed in Table 6.

Table 6.

Results of the proposed model configurations of MSE system (Model-I to Model-VIII) for the considered data.

Model No.	Process Parameters	Effect(s)/Stage(s) Number
		1	2	3	4	5	6	7
Model-I	Flow rate of concentrated exit liquor (in kg/s)	3.34	5.20	6.91	8.63	10.33	12.02	13.67
	Generated vapor Temperature (in ˚C)	147.00	100.00	73.22	67.08	61.41	57.77	54.39
	λi (in kJ/kg)	2109.51	2251.53	2324.34	2340.41	2355.06	2364.35	2372.93
	Hi (in kJ/kg)	2749.09	2672.65	2628.99	2618.85	2609.43	2603.36	2597.68
	hLi (in kJ/kg)	439.80	321.00	252.81	244.10	230.48	221.03	210.77
	Performance parameter, SE	5.768
	Performance parameter, SC (in kg/s)	2.126
Model-II	Flow rate of concentrated exit liquor (in kg/s)	2.00	5.18	6.82	9.00	11.00	12.79	14.21
	Generated vapor Temperature (in ˚C)	147.00	115.00	113.00	74.00	64.37	59.07	54.55
	λi (in kJ/kg)	2109.51	2208.05	2213.95	2322.77	2347.81	2361.31	2372.63
	Hi (in kJ/kg)	2749.09	2697.15	2693.88	2629.97	2614.11	2605.35	2597.88
	hLi (in kJ/kg)	439.80	369.15	389.20	268.59	241.10	225.63	211.24
	Performance parameter, SE	5.917
	Performance parameter, SC (in kg/s)	2.300
Model-III	Flow rate of concentrated exit liquor (in kg/s)	3.43	5.23	6.76	8.16	9.00	8.00	7.99
	Generated vapor Temperature (in ˚C)	147.00	100.00	71.66	66.00	60.00	55.50	55.33
	λi (in kJ/kg)	2109.51	2251.53	2328.91	2343.64	2358.97	2370.28	2370.71
	Hi (in kJ/kg)	2749.09	2672.65	2626.13	2616.79	2606.88	2599.44	2599.16
	hLi (in kJ/kg)	439.80	321.00	246.83	239.55	224.71	211.98	214.23
	Performance parameter, SE	6.089
	Performance parameter, SC (in kg/s)	2.000
Model-IV	Flow rate of concentrated exit liquor (in kg/s)	3.29	5.17	7.00	8.95	10.95	12.99	15.00
	Generated vapor Temperature (in ˚C)	147.00	100.00	73.64	67.11	60.71	56.44	52.36
	λi (in kJ/kg)	2109.51	2251.52	2323.69	2340.74	2357.14	2367.92	2378.07
	Hi (in kJ/kg)	2749.09	2672.65	2629.39	2618.64	2608.07	2601.00	2594.25
	hLi (in kJ/kg)	439.80	321.00	253.66	243.63	227.42	215.60	202.74
	Performance parameter, SE	6.006
	Performance parameter, SC (in kg/s)	2.050
Model-V	Flow rate of concentrated exit liquor (in kg/s)	3.26	5.07	6.63	8.07	9.00	8.00	6.00
	Generated vapor Temperature (in ˚C)	147.00	100.00	71.74	66.00	60.00	55.00	54.69
	λi (in kJ/kg)	2109.51	2251.53	2328.71	2343.64	2358.97	2371.53	2372.28
	Hi (in kJ/kg)	2749.09	2672.65	2626.25	2616.79	2606.88	2598.61	2598.11
	hLi (in kJ/kg)	439.80	321.00	247.09	239.55	224.71	210.07	211.78
	Performance parameter, SE	6.172
	Performance parameter, SC (in kg/s)	2.000
Model-VI	Flow rate of concentrated exit liquor (in kg/s)	2.00	3.50	5.67	8.32	9.00	8.00	6.00
	Generated vapor Temperature (in ˚C)	147.00	115.00	113.00	88.25	69.40	63.68	62.31
	λi (in kJ/kg)	2109.51	2178.10	2213.95	2284.36	2334.81	2349.58	2353.07
	Hi (in kJ/kg)	2749.09	2713.42	2693.88	2653.40	2622.41	2612.97	2610.70
	hLi (in kJ/kg)	439.80	401.25	389.20	320.32	259.95	243.26	241.27
	Performance parameter, SE	6.890
	Performance parameter, SC (in kg/s)	1.975
Model-VII	Flow rate of concentrated exit liquor (in kg/s)	2.00	3.50	5.59	8.74	11.00	13.00	14.61
	Generated vapor Temperature (in ˚C)	147.00	125.00	113.00	90.22	71.35	62.99	55.86
	λi (in kJ/kg)	2109.51	2178.10	2213.95	2278.93	2329.74	2351.36	2369.38
	Hi (in kJ/kg)	2749.09	2713.42	2693.88	2656.63	2625.61	2611.82	2600.03
	hLi (in kJ/kg)	439.80	401.25	389.20	327.48	267.22	240.60	216.28
	Performance parameter, SE	7.059
	Performance parameter, SC (in kg/s)	1.928
Model-VIII	Flow rate of concentrated exit liquor (in kg/s)	2.00	3.50	5.58	8.22	9.00	7.99	6.00
	Generated vapor Temperature (in ˚C)	147.00	125.00	113.00	91.27	74.73	69.71	69.43
	λi (in kJ/kg)	2109.51	2178.10	2213.95	2276.02	2320.83	2334.00	2334.74
	Hi (in kJ/kg)	2749.09	2713.42	2693.88	2658.35	2631.18	2622.92	2622.45
	hLi (in kJ/kg)	439.80	401.25	389.20	331.28	279.89	266.29	268.84
	Performance parameter, SE	7.092
	Performance parameter, SC (in kg/s)	1.919

SE and SC are the key performance parameters of the MSE system. They reflect the energy efficiency of the MSE. Also, the result analysis has been made by utilizing these values are mentioned in bold.

A comparative visualization of optimum values of these performance parameters, SE and SC for different proposed model configurations is illustrated in Figure 3.

Figure 3.

Comparative analysis of various proposed model configurations based on SE and SC.

As rendered in Table 6, the results reveal that Model-I yields a SE of 5.768 and SC of 2.126 kg/s. With the inclusion of steam-split strategy to the BFF Configuration (Model-II), there is an improvement in SE to 5.917 (i.e. an increase of 2.5%) at a steam-split fraction y of 90%. Owing to the steam-split strategy of splitting the input steam among stages 1^st and 2^nd, the effective heat transfer in the successive stages is improved, thereby yielding an improvement in SE over Model-I.

From Table 6, it can also be inferred that the inclusion of feed-split strategy to the BFF configuration (Model-III) yields an improved SE of 6.089 (i.e. an increase of ~5.6%) and a reduction in SC by ~6% to 2.0 kg/s at a feed-split fraction k of 90% when compared with Base model (Model-I). The incorporation of Feed-split strategy contributes to an improved SE owing to the splitting of feed among 6^th and 7^th stages which results in an increased heat transfer in the last stage. It may be noted that for the case when k = 0, the process becomes a 6-stage evaporator system with a reduced energy efficiency. The selection of k as 90% validates the increase in SE with an increased number of stages i.e., 7 (in this case). This fact also holds true for the steam-split strategy. However, the increased number of stages leads to greater installation and maintenance costs of the MSE unit as a whole. Model-IV (the BFF configuration integrated with Feed-preheating strategy) enhances the SE by ~4% and attains the optimum SE of 6.006. It reduces the SC (2.05 kg/s) by 3.6% at a vapor-split fraction m of 10% when compared to Base model. These mentioned results reveal that the energy efficiency of the MSE system is highly affected by the inclusion of feed-split strategy to the BFF configuration than other ESSs (i.e. Steam-split and Feed-preheating strategies).

The Base model combined with both the feed-split and feed-preheating strategies (Model-V) provides an optimal SE of 6.172 and SC of 2.00 kg/s at a feed-split fraction k of 30% and vapor-split fraction m of 10%. This points toward an increase of ~7% in SE and a decrease of ~6% in SC, i.e. a better result than that obtained in Model-I. It is to be noted that these results are convincingly better in comparison with the feed-split and feed-preheating strategies added separately to BFF configuration (i.e. Model-III and Model-IV). Model-VI (BFF with steam-split and feed-split ESSs) yields a SE of 6.890 and SC of 1.975 kg/s at steam-split fraction y of 10% and feed-split fraction k of 50%. These values correspond to an increase in SE by 19.45% and a reduction in SC by 7.1% when compared to Model-I. Undoubtedly, the inclusion of steam-split and feed-split ESSs to Model-I results in an improved SE (of 6.890) which is more than the SEs obtained for individual ESSs (5.917 and 6.089).

The addition of steam-split and feed-preheating ESSs to the Base model result in a SE of 7.059 and a SC of 1.928 kg/s. Conclusively, there is improvement in SE and SC by 22.38% and 9.31% respectively with respect to Model-I at an optimum steam-split fraction y of 10% and vapor-split fraction m of 90%. The values are better than the ESSs incorporated individually to Model-I as clearly indicated in Table 6. In Model-VIII, all the three ESSs (steam-split, feed-split and feed-preheating) combined to the base case yield a SE and SC of 7.092 and 1.919 kg/s respectively. These optimum values are obtained for a steam-split fraction y of 10%, feed-split fraction k of 10% and vapor-split fraction m of 90%. Compared to the base case, the SE and SC are significantly improved with an increment of 22.95% in SE and reduction of 9.73% in SC. This effect is as a result of the improvement in heat transfer rates in stages 3^rd – 7^th due to steam-split operation and in stages 6^th – 7^th due to feed-split and feed-preheating operations.

With reference to the above discussion, it is quite obvious that the maximum SE and minimum SC are acquired via the utilization of all three ESSs (steam-split, feed-split and feed-preheating). Thus, it can be concluded that the optimal operating strategy for optimum SE and SC is that of Model-VIII. This work presents significantly improved values of SE and SC for various model configurations than those reported earlier (Verma et al., 2017b). Table 7 provides a comparative analysis of the simulation results obtained via WCA with the earlier reported literature work for analogous MSE system at similar operating conditions (Verma et al., 2017b). As evidently revealed by Table 7, the results presented in this work by WCA offer improved solutions compared to those mentioned in previous work by I-PM (Interior-Point Method) (Verma et al., 2017b). Model-VIII proposed in this work yields a SE of 7.092 i.e. an improvement of 9.27% compared to the Model-G proposed by (Verma et al., 2017b). Also, when compared to the model proposed by (Bhargava et al., 2008b), the SE for Model-VIII shows an improvement of ~37%.

Table 7.

Comparative summary of various proposed MSE model configurations with earlier reported works and with Real-time plant.

Model Description and SE						% Enhancement in SE∗
Present Work (WCA)		(Verma et al., 2017b) (I-PM)		(Bhargava et al., 2008b)	Real-time Plant SE (MSE installed at paper mill)
Model-I	5.768	Model-A	5.39	5.15	4.64	24.31
Model-II	5.917	Model-B	5.60			27.52
Model-III	6.089	Model-C	6.11			31.22
Model-IV	6.006	Model-D	5.71			29.43
Model-V	6.172	-				33.01
Model-VI	6.890	Model-E	6.21			48.49
Model-VII	7.059	Model-F	5.89			52.13
Model-VIII	7.092	Model-G	6.49			52.84

^∗Results have been computed by comparing the SE in the present work with Real-time Plant SE.

Furthermore, when compared to the real-time plant estimate of SC of 2.67 kg/s (Verma et al., 2018d), it can be observed that Model-VIII proposed in this work (i.e., hybrid model of all ESSs) offers SC of 1.919 kg/s, thereby significantly reducing the SC by 28.13%. In view of that, WCA provides an effective search methodology for finding the optimum values of SE and SC.

The real-time plant data (SE and SC) have been taken from the specified real-time plant (at Saharanpur, India) and reported works (Verma et al., 2018d, 2019). For enhanced assessment of the SE and SC obtained by WCA (for various operating schemes of MSE) with real-time plant data and previous research chronicles, a graphical illustration (as shown in Figure 4) has also been presented. From Figure 4, it is clear that the SE and SC obtained by WCA exhibit significant improvement than previous works and real plant data. This verifies that WCA provides optimum SE and SC in the present investigation and endorses the BFF configured MSE with steam-split, feed-split and feed-preheating ESSs as the best operating scheme for optimum performance.

Figure 4.

Comparative analysis of present simulation results with real plant data and existing literature.

These simulation results (steady-state process parameters and performance parameters) of MSE may be undoubtedly utilized for the analysis of open-loop and closed-loop system dynamics and further, for the development of advanced controllers for necessary control actions along with set-point tracking, disturbance rejection and noise suppression.

5. Conclusions

The HEE system considered in the present investigation operating with the BFF configuration amalgamated with various proposed ESSs operated in the Kraft recovery process in the Indian Paper and Pulp mills yields a set of complex non-linear mathematical models. These formulated models, after being transformed into the optimization problems, are further solved using an efficient metaheuristic optimization strategy, WCA. In quest of the optimum values of the process parameters, WCA is employed to obtain the optimum temperature, liquor flow rates and SC, thereby assisting in the selection of the best MSE configuration in terms of optimum SE and SC. The simulations are carried out with the aid of real-time plant data and feasible bounds of various process parameters. The results reveal that the highest SE of 7.092 is obtained for the BFF configuration combined with steam-split (y = 0.1), feed-split (k = 0.1) and feed-preheating (m = 0.9) ESSs (i.e. Model-VIII). Model-VII also provides a high SE of 7.059 but slightly lower than that of Model-VIII. WCA efficiently estimates the optimal values of split-fractions (y = 0.1, k = 0.1 and m = 0.9) to yield maximum SE of 7.092 and minimum SC of 1.919 kg/s among all other proposed model configurations. This work demonstrates the robustness, efficiency and exploratory capability of WCA in solving such complex sets of non-linear algebraic equations via effective exploration of best operating conditions. Thus, WCA can be effectively employed for modeling and simulation of various complex non-linear engineering problems that are frequently encountered in many industrial processes. The effect of inclusion of various parameters including boiling point rise, fouling effects, loss of heat, etc. can be investigated further in future works.

Declarations

Author contribution statement

Drishti Yadav & Om Prakash Verma: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Funding statement

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Competing interest statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.

Appendix A. Supplementary data

The following is the supplementary data related to this article:

Supplementary Material