Abstract.
The Aedes aegypti mosquito inhabits most tropical and subtropical regions of the globe, where it transmits arboviral diseases of substantial public health relevance, such as dengue fever. In subtropical regions, Ae. aegypti often presents an annual abundance cycle driven by weather conditions. Because different population states may show varying responses to control, we are interested in studying what time of the year is most appropriate for control. To do so, we developed two dynamic site-occupancy models based on more than 200 weeks of mosquito trapping data from nearly 900 sites in a subtropical Brazilian city. Our phenomenological, Markovian models, fitted to data in a Bayesian framework, accounted for failure to detect mosquitoes in two alternative ways and for temporal variation in dynamic rates of local extinction and colonization of new sites. Infestation varied from nearly full cover of the city area in late summer, to between 10% and 67% of sites occupied in winter depending on the model. Sensitivity analysis reveals that changes in dynamic rates should have the greatest impact on site occupancy during autumn and early winter months, when the mosquito population is declining. We discuss the implications of this finding to the timing of mosquito control.
INTRODUCTION
Control of the mosquito and disease vector Aedes aegypti is an important public health challenge.1 Originated in Africa and unintentionally dispersed by humans around the world, Ae. aegypti is currently present in tropical and subtropical regions of Africa, Asia, Oceania, and the Americas.2 It is well adapted to urban environments because it can breed in artificial water containers and feed on human blood.2 Although dormant eggs can survive unfavorably cold and dry seasons, the survival, growth, and reproduction of the other life stages is dependent on rainy and hot weather.3 Thus, Ae. aegypti populations present high year-round abundances in tropical humid regions and annual cycles of abundance in most other regions where the species occurs.3 When sufficiently abundant, Ae. aegypti is a vector of many disease-causing arboviruses, including chikungunya,4 Zika,5 yellow fever,6 and dengue.7 Dengue fever is of particular concern because it is the most common human arboviral disease.8 More than one-third of the world population is at risk of contracting dengue,9 with yearly numbers of 58 million people infected, 10 thousand deaths, and 1.14 million disability-adjusted life years (DALY) lost because of the disease.8 Given the efficacy and safety concerns about the only commercially available vaccine,10,11 vector control is still the most reliable way to prevent dengue epidemics.12
Since the 1970’s, control of Ae. aegypti has relied mostly on ultralow-volume insecticide spraying and community-based removal of breeding sites.7 However, with all the effort that has been spent on control, the number of people infected by the disease is still increasing, doubling every 10 years since 1990.8 Brazil and Mexico, for example, have not managed to contain the disease despite spending yearly amounts of, respectively, US$450 million13 and US$83 million14 during the last decade. The growth of dengue incidence over the last 40 years makes it clear that vector control has been insufficient.15 Acknowledging the need to improve vector control, the scientific community and public health agencies routinely discuss existing and potential control strategies.12,16,17 These discussions usually emphasize development and introduction of new control methods, such as biocontrol, sterile male release, or genetic modifications that render mosquitoes incapable of transmitting dengue.
Our interest here is not on how but when to apply control measures: an aspect of control planning that is easily overlooked. Appropriate timing matters regardless of the method of choice and requires knowledge of mosquito population dynamics. Control interventions applied at distinct times of a mosquito’s annual population cycle may result in very different consequences. Modeling results suggest that intervening when abundance reaches above a threshold may not be the most efficient timing strategy.18 Poor timing of control measures leading to reduced density dependence at the larval stage may even induce mosquito population growth via the “Hydra effect.”19 Time enters analyses of mosquito population dynamics and dengue transmission in a variety of important ways, ranging from empirical epidemiological models of the timing of disease outbreak20,21 to numerical simulations of the effect of control frequency on mosquito populations and their resistance to insecticides.22,23 What we could not find, however, were studies about the time-related question that is most interesting to us: what time of the year is most appropriate for vector control?
Direct study of control timing requires experimenting with different control schedules while monitoring mosquito populations. Such experiments are costly and complex to implement. We believe, however, that costs may be reduced and experiments simplified by the indirect a priori identification of optimal control times, via the study of mosquito population dynamics. Sensitivity analysis is a tool developed for the study of age- or size-structured populations, by which one may ask how a small change in one of the population parameters, such as immature survival or adult fertility, impacts on a descriptor of the population state, such as size or growth rate.24 Sensitivity analysis, thus, helps identify which parameters, when modified, produce the most cost-effective impact on a state variable of interest. Tran et al.,25 Ellis et al.,26 and Luz et al.,23 for example, used sensitivity analysis of mosquito population models to infer what were the life stage–specific demographic rates to which different metrics of mosquito population state are most sensitive. This approach is applicable in a variety of systems, whenever a metric of population state may be affected by the manipulation of different population parameters at different times. Emery and Gross,27 for example, used sensitivity analysis to infer the best time of the year for controlled burning of an invasive plant species. In our study, we apply sensitivity analysis to a site-occupancy model of adult mosquito infestation. Our analysis, informed by field observations from the Brazilian city of Porto Alegre, identifies the time of the year when predicted infestation is most sensitive to changes in the occupancy dynamics parameters that explain expansion and contraction in the number of infested sites. Effective control measures affect those occupancy dynamics parameters, and, therefore, our sensitivity results offer hypothetical best control times that can be tested by vector control experiments in the field.
MATERIALS AND METHODS
Study setting.
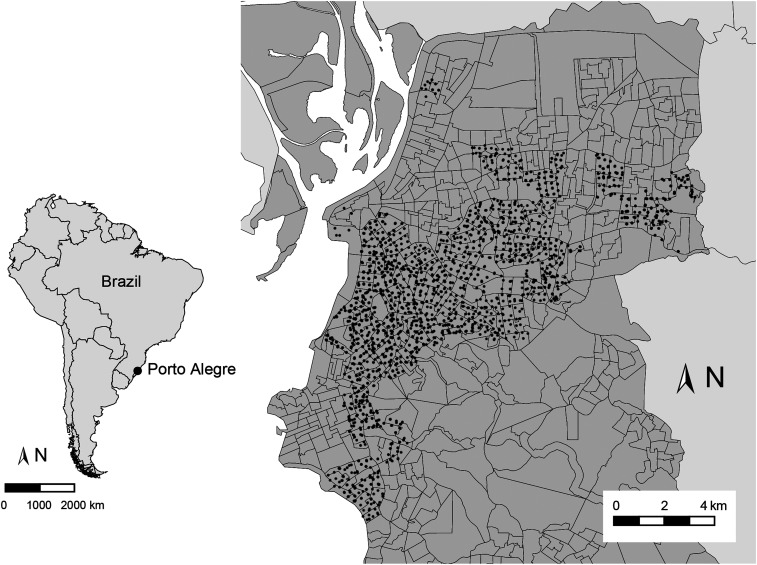
Our study examines Ae. aegypti infestation in Porto Alegre, the largest city of Rio Grande do Sul, the southernmost state in Brazil (Figure 1). The city proper has approximately one and a half million habitants, whereas the metropolitan area has more than 4 million. The city’s climate is subtropical humid, with hot summers, mild winters, and rainfall evenly distributed throughout the year. Aedes aegypti was first recorded in Porto Alegre in 2001, and it is now present in all the city’s neighborhoods. Locally transmitted dengue cases have been recorded since 2010, mostly in late summer and early fall. The largest outbreak happened in 2016, with 301 confirmed cases. Currently, municipal dengue control relies on peridomestic ultralow-volume insecticide spraying as well as on community-based actions to eliminate breeding sites. Spraying is applied within a radius of 200 m from the residence (and in some cases, the workplace) of infected patients, with the objective of suppressing further infections.28
Figure 1.
The city of Porto Alegre, with its location in South America (left) and the distribution of adult mosquito-trapping sites throughout the city (right). Map lines show sampling site boundaries. Black dots show all the locations where a trap was deployed at least once throughout the 4 years of monitoring included in this study.
Data collection.
We analyze data collected by the Núcleo de Vigilância de Roedores e Vetores (NVRV) of the Porto Alegre Municipal Department of Health, from September 23, 2012 to August 14, 2016. Sampling spanned 204 weeks and consisted of weekly deployment of hundreds of adult mosquito traps throughout the city. The number of traps deployed in one week ranged from 481, in September 23, 2012, to 893, in October 8, 2016, increasing through time according to the availability of resources and the monitoring priorities of the NVRV. Trap locations were kept constant after the first deployment, with only minor changes between adjacent properties due to accessibility problems beyond the control of the NVRV. The choice of trapping locations followed the spatial distribution of confirmed dengue cases and evidence of Aedes spp. infestation from household surveys of larvae-bearing containers. Traps were deployed outdoors either in public or private places and with a minimum distance of 250 meters from each other.
The NVRV uses a commercially available adult mosquito trap (Mosquitraps®; Ecovec, Belo Horizonte, Brazil), which consists of a 30-cm-high black plastic cylinder with a funnel-shaped opening on top. When deployed, traps were half filled with water treated with a slow-release chemical attractive that mimics the effects of a hay infusion (AtrAedes®, Ecovec, Belo Horizonte, Brazil). Female mosquitoes attracted by the odor enter the cylinder to lay eggs, get trapped by the funnel access, and eventually stick to an adhesive ribbon that lines the inner wall of the trap. Each NVRV agent is responsible for approximately 55 traps that she visits once a week, from Monday to Friday. On each visit to each trap, agents remove the adhesive ribbon and check for glued mosquitoes. If the ribbon has any mosquitoes that the agent identifies as being a female Ae. aegypti, the mosquito is sent to a laboratory to test for dengue, chikungunya, and Zika viruses.
For the purpose of our analysis, we outlined 756 sampling sites (Figure 1) on a map of Porto Alegre land cover and use (the Porto Alegre Environmental Diagnostic map29) overlaid with a map of the Brazilian federal government human socioeconomic census sectors.30 Our sites consist of one to eighteen (mean ± SD of 4 ± 2.8) adjacent census sectors with similar land cover and use characteristics. Whenever possible, we avoided mixing green areas with built-up areas, as well as areas of regular and irregular residential buildings. We sought to keep site area as constant as possible (28.9 ± 16.9 ha), but the geography of land cover and use combined with limits of census sectors resulted in a range of areas spanning three orders of magnitude, from approximately 5–150 ha. Nonetheless, more than half of the sites have between 20 and 32 ha in area. Our data set contains mosquito trapping data from 286 of the 756 sites in the city. Of these 286 sites, there was an average of 2.5 ± 2.1 traps per site per week. Traps deployed in the same site and week are treated as replicate samples of a closed system, so that if trap j detects Ae. aegypti on site i and week t, any failure to detect mosquitoes in other traps from the same site and week will be treated as a false-negative result. We will refer to the deployment of one set of traps in one site and week as a trapping event. The result from one trapping event is said to be positive if at least one of the traps captures one mosquito during that event.
Data analysis.
We modelled trapping data using Royle and Kéry’s31 Bayesian state-space implementation of the site-occupancy dynamics model developed by MacKenzie et al.32 This model formally separates the biological process of site infestation from the sampling process of mosquito trapping, with the latter conditioned on the former. Our analysis considers two alternative descriptions of the sampling process (model I and model II) based on the same description of the biological process. We represent the infestation state by the partially observable variable , which takes the value 1 when site i is infested by Ae. aegypti at time t, and the value 0 otherwise. The trapping data are represented by the variable , which takes the value 1 when trap j detects Ae. aegypti mosquitoes on site i and week t, and the value 0 otherwise. We say that is conditioned on because there can be no positive trap results for when .
The dynamic component of the model describes changes in infestation through time as a first-order Markov process, where the value of depends on the value of . At the outset, when t = 1, we model the infestation state as a Bernoulli trial with infestation probability , estimated from the data:
| (1) |
Subsequently, changes in infestation are given by the probabilities of local extinction, , and colonization, , also estimated from the data. The parameter represents the probability that a site infested at time t will not be infested at time t + 1; conversely, represents the probability that a site that is not infested at time t will be infested at time t + 1. Thus, the infestation state after the first week will be a Bernoulli trial with probability given by the following equation:
| (2) |
Thus, if a site is not infested at time t, equals ; if it is infested, equals , which can also be described as a probability of local persistence
We also want to take into account, however, that and are not constant through time. In fact, they must vary cyclically throughout the year because the infestation follows a year-long cycle. To capture this periodic cycling in a mathematical form, we adapted the model to represent temporal change in and by two cosine trigonometric functions33 in logit space:
| (3) |
| (4) |
These functions measure time as a continuous variable τ, which varies between 0 and 1. Our dataset keeps track of time with an integer week counter; therefore, for a given week t, is the mean Julian day of the week divided by the total number of days in the year. The parameters , , and , indexed by dynamic parameters or in Equations (3) and (4), respectively, are estimated from the data. Parameter gives the corresponding dynamic parameter mean value, gives the amplitude of the cycle, and gives the time—in τ units—at which the dynamic parameter takes its maximum value.
Our simplest description of the sampling process (under model I) treats the probability of detecting Ae. aegypti mosquitoes at trap j of infested site i on time t as being constant through time, across sites, and between traps of the same site. Formally, this consists of modeling the binary detection data as a Bernoulli trial with probability :
| (5) |
This equation captures the hierarchical nature of the model as it conditions the possibility of a nonzero detection probability on the biological state of the system. Model II follows the same logic but inserts a random temporal effect on , which will now be indexed by time, so that,
| (6) |
The underlying variation of in model II is modeled on the logit scale, as the realization of a random process with mean and normally distributed deviations from the mean, :
| (7) |
where is a logit-scale SD from the mean, which equals zero. We express and its SD on the probability scale using, respectively, an inverse logit function and a delta method approximation34:
| (8) |
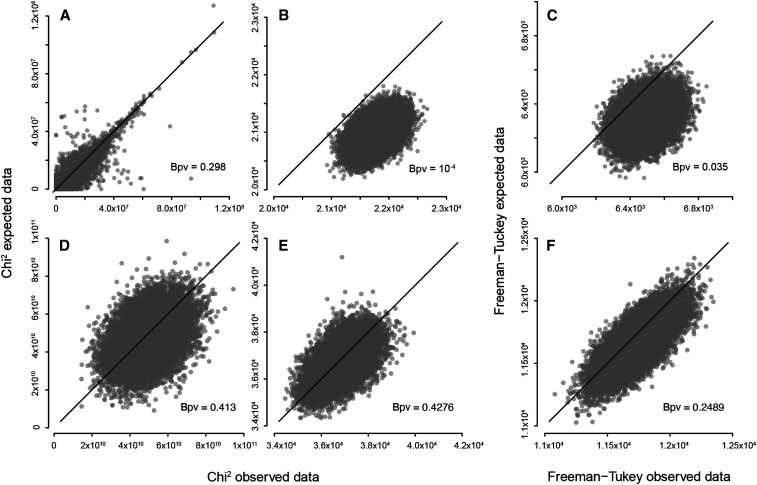
We fit our models to data in a Bayesian framework with vague priors, sampling from the posterior distribution of model parameters with a Markov chain Monte Carlo (MCMC) algorithm.35 To assess model fit, we use the Bayesian posterior predictive distributions approach proposed by Kéry and Royle.36 The approach compares two metrics of discrepancy: one between model predictions and observed data and the other between model predictions and data expected under the model. The more similar the discrepancies, the better the fit. We compute discrepancies separately for the occupancy dynamics and the detection parts of the model. Occupancy dynamics data are summarized as counts of the four possible types of transition between occupied and non-occupied states at each time, whereas detection data are summarized as number of traps that returned a positive result in each site and time. We use a chi-square discrepancy metric for both the occupancy and detection parts of the model and a Freeman–Tukey metric for the detection part alone.36 These lead to three discrepancy-comparison plots per model, two for occupancy and one for detection. Because the expected data are simulated within the MCMC algorithm, each plot shows one point per MCMC iteration; the proportion of points above the diagonal can be interpreted as a Bayesian p-value, with low values denoting higher discrepancy with observed than expected data, which implies poor fit. The MCMC algorithm was implemented with the software JAGS,37 accessed through R38 with the library jagsUI.39 We ran three chains with 15,000 iterations and a burn-in of 2,500 iterations. Model code can be found in Supplemental Material Appendix 1.
Part of our inference is based on metrics derived from the dynamic parameters of the site-occupancy model. We derived three infestation and two sensitivity metrics from the posterior samples given by the MCMC for both models. The infestation metrics are also described in Royle and Kéry31 as general occupancy metrics. The predicted equilibrium infestation denoted that is the infestation probability that the system converges to if and remain constant for a sufficient time. We obtained for each week of the study period, from the respective values of and ,
| (9) |
A second infestation metric, infestation probability, represents the expected infestation rate on the theoretical infinite statistical population of sites from which our sample was obtained. This metric is equal to when t = 1 and in all subsequent times is given by the following equation:
| (10) |
The third infestation metric is the finite sample infestation, which expresses the actual proportion of sample sites infested at time t. We denoted this metric and obtained it from a function of the latent variables:
| (11) |
with M representing the total number of sampling sites, in this case 286.
To evaluate how changes in the dynamic parameters—eventually provoked by control measures—affect the equilibrium infestation probability, we also obtained two sensitivity metrics, and , which measure the sensitivity of to infinitesimal changes in, respectively, and . We derived sensitivities as proposed by Martin et al.,40 using the following equations:
| (12) |
and
| (13) |
which give the derivatives of , respectively, on and .
RESULTS
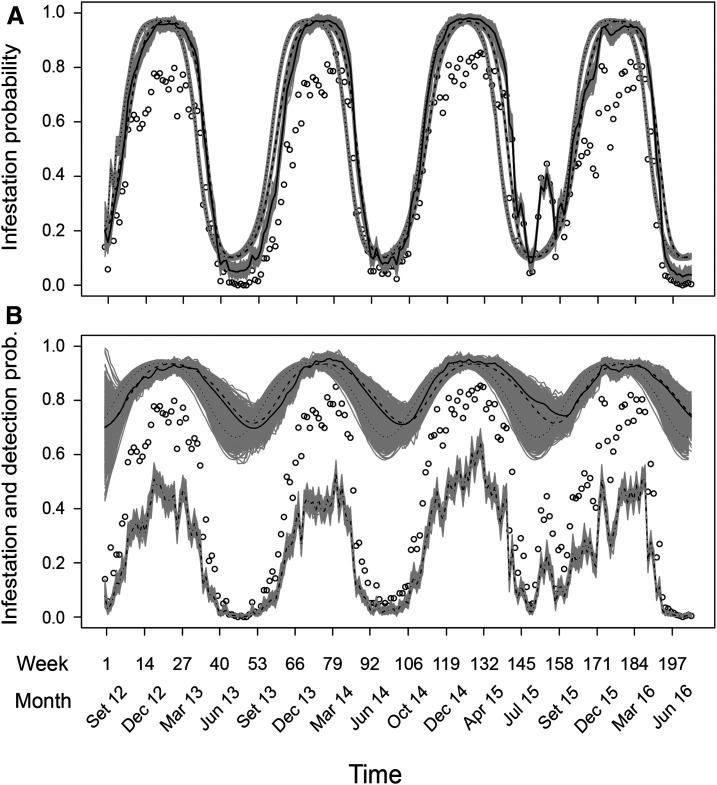
We gathered data from 150,453 trapping events, 33,499 (∼22%) of which returned positive results. The greatest proportion of positive results on any given week was 0.627, in week 131, the last week of March 2015. Throughout the whole 204-week study period, there were only 4 weeks with no positive traps at all. This happened in weeks 47, 49, 50—August and early September 2013—and in week 201, at the end of July 2016. Observed infestation, the ratio of sites with positive results to all sites sampled in one week, ranged from 0.854, in week 131, to 0, in weeks 47, 49, 50, and 201. The mean observed infestation was 0.434.
Both models I and II fit the occupancy part of the data reasonably well, but model II fits the detection data better. Posterior predictive checks of goodness of fit for model I show small Bayesian p-values in Figure 2B and C, indicating a low probability of obtaining a more extreme discrepancy between model prediction and observed data, under the null hypothesis of a fitting model. The Freeman–Tuckey metric returns a better fit than the chi-square, but both are lower than 0.04. Otherwise, Bayesian p-values are always higher than 0.24, both for the occupancy and detection parts of model II and for the occupancy part of model I. Detection probability estimates differ substantially between models. Model I estimates that approximately one in three traps deployed in an infested area will return a positive result (p = 0.37 ± 0.002; Table 1). That is, if only one trap were set per location, the observed infestation would be less than half its true value. With three traps, which is close to the average number of traps per sampled site in this study, the probability of obtaining at least one positive result at an infested site is approximately 0.75. Model II, with random temporal effects on detection, estimates that varies around a probability-scale mean of = 0.15 ± 0.02 and SD of = 0.22 ± 0.02 (Table 1). The resulting temporal variation has rising above 0.4 every summer and dipping below 0.04 every winter (Figure 3B). With = 0.04 and three traps, the probability of obtaining at least one positive result at an infested site is approximately 0.11, it would take 34 traps to bring that probability up to 0.75.
Figure 2.
Goodness-of-fit results for model I (A–C) and model II (D–F) under the posterior predictive distributions approach. Each panel compares two measures of discrepancy: one between model prediction and observed data (on the x axis) and the other between model prediction and expected data (on the y axis). Each dot on a plot represents one sample from the posterior in the corresponding Markov chain Monte Carlo (MCMC) algorithm. A, B, D, and E use a chi-square metric of discrepancy on occupancy dynamics data (A and D) and on detection data (B and E). C and F use the Freeman–Tukey metric of discrepancy, applicable to detection data alone. “Bpv” stands for “Bayesian p-value,” computed as the proportion of MCMC samples where discrepancy with expected data exceeds discrepancy with observed data.
Table 1.
Posterior mean ± SD for parameters estimated under models I and II, with their respective verbal descriptions.
| Model I | Model II | Parameter description | |||
|---|---|---|---|---|---|
| 0.20 ± 0.037 | 0.63 ± 0.121 | Initial infestation probability | |||
| −1.36 ± 0.048 | −1.65 ± 0.106 | Mean logit colonization | |||
| −1.05 ± 0.048 | −0.90 ± 0.150 | Amplitude logit colonization | |||
| 0.53 ± 0.009 | 0.54 ± 0.019 | Maximum colonization time | |||
| −1.64 ± 0.043 | −3.55 ± 0.101 | Mean logit local extinction | |||
| 2.91 ± 0.071 | 0.50 ± 0.124 | Amplitude logit local extinction | |||
| 0.61 ± 0.002 | 0.73 ± 0.048 | Maximum local extinction time | |||
| 0.37 ± 0.002 | – | Fixed detection probability | |||
| – | 0.15 ± 0.016 | Random-effect mean detection | |||
| – | 0.22 ± 0.022 | Random-effect standard deviation detection | |||
| 0.97 ± 0.002 | Febuary 4–7 | 0.94 ± 0.005 | Febuary 1–26 | Maximum equilibrium infestation probability. | |
| 0.10 ± 0.003 | July 21–28 | 0.66 ± 0.033 | Jul 30–August 21 | Minimum equilibrium infestation probability. | |
| 1.95 ± 0.119 | May 15–21 | 3.10 ± 0.777 | July 13–August 5 | Sensitivity to change in colonization | |
| 3.45 ± 0.249 | April 3–9 | 7.20 ± 1.323 | May 22–July 8 | Sensitivity to change in local extinction | |
Parameters are organized in three groups: the first (–, from Equations 1–4) describes occupancy dynamics; the second (–, from Equations 5–8) describes detection; and the third ( – , based on Equations 9, 12, and 13) shows extreme values of equilibrium occupancy (maximum and minimum) and sensitivity (only maximum). Time intervals indicate the 95% credible intervals for the date with the most extreme value of the corresponding parameter and model. The first two groups of parameters are directly estimated from the data, the third is derived.
Figure 3.
Different metrics of infestation by Aedes aegypti throughout the sampling period, according to model I (A) and model II (B). Empty circles show observed infestation, the proportion of sampled sites which had at least one Ae. aegypti capture in the corresponding week; they convey exactly the same information in both panels. Three black lines on each panel show posterior mean values for three metrics of infestation probability: finite sample infestation (; solid line), population infestation (; dashed line), and equilibrium infestation predicted under current dynamic parameter (εt, ) estimates (; dotted line). Gray shading around the black lines represents 250 infestation predictions for each black line, each based on one random sample of parameters (, , and ) from the posterior. The jagged dashed-and-dotted line on the lower part of (B) shows detection probability as it varies in time according to model II. Gray shading around this line represents 250 random samples from the posterior distribution of . The fixed value of estimated by model I as 0.37 ± 0.002 is omitted from the upper panel for simplicity of representation.
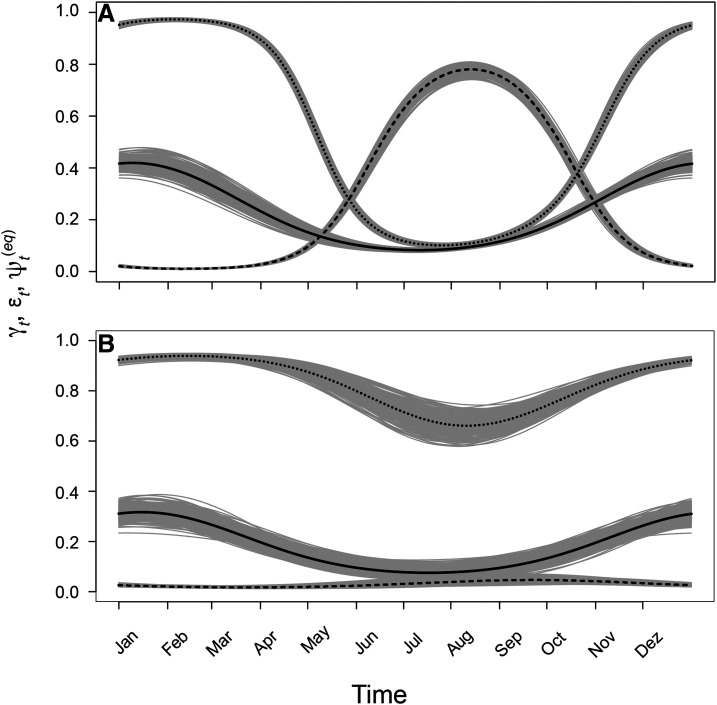
The annual oscillation in mosquito infestation is evident from the temporal variation of under both models (Figure 4). On average, model II oscillates about one to two weeks later than model I, but both peak in February and reach minimum values in late July to early August (Table 1). The key difference in predictions between models is in the amplitude of the oscillation, not its timing. Both models predict peak infestation of more than 90% of the sites; however, whereas model I predicts a minimum of 10%, model II—accounting for lower detection probability in winter—puts the minimum at more than 60%. Qualitatively, the values of behave similarly to those of (population infestation) and (finite sample infestation), but they tend to change earlier. Such anticipation is higher on average for model II, but with substantial overlap in the credible intervals of the three metrics for any given time (Figure 3). Observed infestation was almost always lower than both and . During weeks 150–156, in the abnormally warm winter of 2015, however, observed infestation was exceptionally high (Figure 3). For model I, it was even higher than the posterior means of or , which do not express variation between years. In both models, the infestation metric that best captures inter-annual variation is . The year 2015, with higher values of during winter, had the lowest variance of of all years, according to both models.
Figure 4.
Colonization probability (γt; solid line), local extinction probability (εt; dashed line), and equilibrium occupancy (; dotted line) estimated by model I (A) and model II (B) throughout the year. Black lines (solid, dashed, or dotted) show mean predicted values for each day; gray shading around the black lines represents uncertainty about the predicted values. Each shade includes 250 predictions of the respective variation, each resulting from one sample of underlying (, , and ) parameters from their respective posterior distributions.
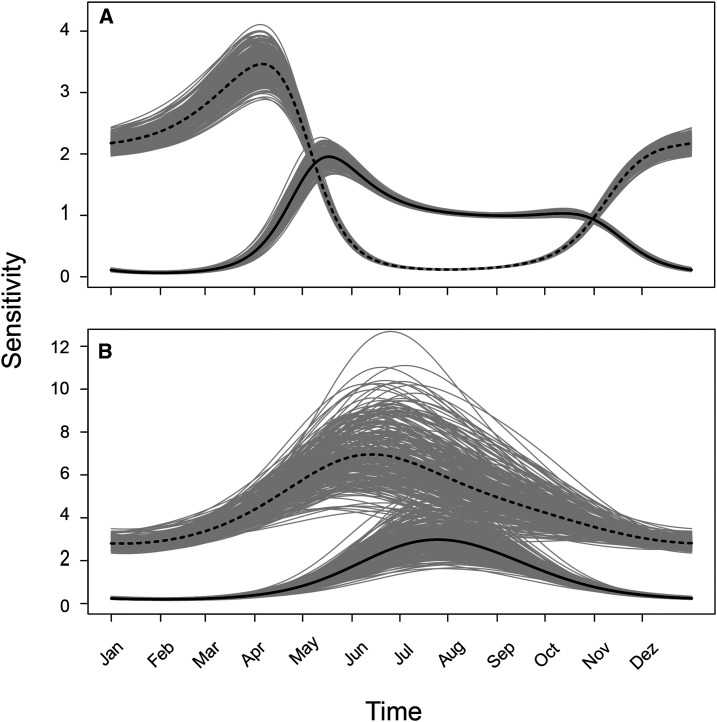
Variability in infestation metrics reflects variability in local extinction and colonization rates (Figure 4). On average and for both models, peaks in early summer, during the second week of January, a few weeks before the maximum value of . The amplitude of variation in is slightly higher for model I than for model II, but the biggest difference in dynamics parameters between models is the amplitude of variation in . According to model II, the probability of local extinction never rises above 0.05. For model I, it reaches near zero in summer and almost 0.8 in winter, driving the wider oscillation in infestation metrics. The variation of sensitivity throughout the year has lower amplitude for than for (; Figure 5) under both models. Maximum values of both and are higher and occur later for model II than for model I. Nevertheless, under both models, equilibrium occupancy is most sensitive to changes in dynamic parameters during the fall and early winter months, when it is declining or reaching its lowest value.
Figure 5.
Sensitivity of equilibrium occupancy to changes in probability of colonization (solid line) and probability of extinction (dashed line) as it varies throughout the year according to model I (A) and model II (B). Gray shading around the black lines represents 250 predictions of the same variation, based on random samples of underlying parameters (, , and ) from their respective posterior distributions.
DISCUSSION
Hierarchical modeling enabled us to account for the inevitable imperfection of the observation process. Some traps deployed in sites that are infested may not detect mosquitoes. By aggregating data from more than one trap per site, we estimated the probability that a trap does detect mosquitoes at an infested site and, concomitantly, the probability that mosquitoes are present in sites where they were not detected. On this footing, we built two models that differ in their treatment of temporal variation in detection probability: model I held it constant and model II let it vary according to a random effect. Both treated variation of infestation as a Markov process where changes between infested and noninfested states are ruled by occupancy dynamics parameters that oscillate throughout the year. Because we aim to predict appropriate timing for application of control measures in future years—for which we have no environmental data—we opted for a simple phenomenological representation of oscillation based on a trigonometric function. Thus, we prioritized general prediction of what may happen in the near future, over the mechanistic understanding of what did happen in the recent past.
Both models predicted cyclical variation in infestation with a maximum in February and a minimum in July–August; the population of Ae. aegypti never completely disappeared during the winter. This result places the city of Porto Alegre in Scenario 2 of classification of intra-annual occurrence of Ae. aegypti by Eisen et al.3 These locations have “year-around activity but potential for high abundance of the active stages only during the most favorable part of the year.”3 Because model I bars temporal variation in detection, it more readily takes absence of mosquito captures as evidence of mosquito absence. As a result, (austral) winter infestation estimates are much lower for model I than for model II. Underlying this difference, there is a sharp contrast between estimates of local extinction probability, with model I predicting steep oscillation, whereas model II predicts low and much more constant values. Despite the differences, however, the two models produce qualitatively similar sensitivity results. Sensitivity of equilibrium infestation to changes in dynamic parameters peaks in autumn and early winter months, when infestation is declining or reaching its lowest values.
Given the sensitivity results, one is tempted to conclude that control measures will be most effective from April to July, when sensitivity is at its highest. But that depends on the meaning of “effective control.” Permanence of infestation throughout the year in Scenario 2 locations motivates constant monitoring of disease cases and application of reactive mosquito control measures whenever needed to suppress further infections. This happens in Porto Alegre,41 and in other Scenario 2 cities such as Cairns, Australia.42 It seems reasonable, in this context, to evaluate effectiveness of control by some assessment of transmission avoidance. Indeed, Marini et al.28 fitted a model of Ae. aegypti abundance and disease transmission to Porto Alegre data on mosquito captures and transmission clusters,41 inferring that vector control avoided nearly one-quarter of potential disease cases for their study period. Reactive control measures are necessary whenever transmission is occurring, and their effectiveness should be measured by transmission avoidance. But preventive vector control can play an important part in epidemics prevention, and its effectiveness should be gauged by impact on the vector population.
Does occupancy provide a reasonable gauge to effectiveness of mosquito control? Abundance is arguably the most important state variable in population biology,43 and vector abundance plays a key role in the propagation of infectious disease.44 Egg quiescence,45 larvae interspecific interactions,46 and climate influences on survival and reproduction47 are only a few of the fascinating processes that drive mosquito abundance and are not directly captured by an occupancy model. Our reason to favor occupancy instead of abundance, in the context of this study, is twofold: first, unbiased estimation of abundance for small, elusive, and highly mobile animals is exceedingly difficult, especially over the space of an entire city; second, occupancy modeling offers a direct link to the analytical tools of metapopulation biology,48 originally developed for the study of insect populations49 and well suited for investigating sensitivity to change in dynamic parameters.40 Occupancy dynamics models are easy to fit within the hierarchical modeling framework32 and, although abstracting away from demographic detail, they estimate a quantity—occupancy—that is strongly correlated to abundance.50–52
Shifting the focus of analysis from the individual to the site requires delimiting sites. Our main delimitation concerns were area, identifiability in the field, and homogeneity of land cover and use. Metapopulation models often define sites as discrete habitat patches that may contain one local population of the study species. This is not our case but does not preclude an occupancy approach because site occupancy can be usefully interpreted as the probability that a site is used by at least one individual of the study species during all or part of a time period.53 There is no loss from animals frequently crossing between adjacent sites that are not large enough to sustain an isolated population. Likewise, inhomogeneous distribution of mosquitoes within a site, as resulting from clustering of infested houses, is entirely compatible with our approach. That is, as long as traps are located randomly with respect to the position of clusters,54 which cannot be far from our case because agents have no information about infestation clusters before choosing trap locations. Clustering will decrease detection probability as some traps will not coincide with clusters, but it should not bias occupancy estimation.
“All models are wrong,”55 but some are useful. Models I and II agree on a few important aspects but differ with respect to oscillation amplitude and minimum infestation. Which is closer to the truth? Model I is a better match to the intuition of Porto Alegre residents, who will hardly find mosquitoes during the winter. However, the better fit of model II, and the soundness of allowing for variation in detection, must give one pause. Seasonal variation in occupancy necessarily follows variation in within-site abundance. Such variation affects detection, as the probability of trapping at least one mosquito (i.e., detecting the species) goes up with the number available for trapping.56 As drops below 0.1 in the winter, however, the minimum probability of site occupancy by adult mosquitoes is estimated at more than 0.6. This is at odds with field perception but appears more reasonable if one considers that low-abundance occupancy is still occupancy. The truth is likely somewhere between the two models. We could learn more about winter detection probability from a study design with more traps per site57 and use the outcome of such study as an informative prior in future analysis of NVRV data.
Predicted equilibrium occupancy of the Porto Alegre Ae. aegypti population is most sensitive to small changes in occupancy dynamics parameters during the autumn and early winter months. Whether this finding leads to improved preventive control depends on the availability and application of measures that actually change the parameters. Reports of the low duration of ultralow-volume insecticide spraying effects28,58 reveal the difficulty of impacting local extinction or colonization. We do not know what control measures most directly affect one or the other dynamic parameter, but the idea of applying preventive control when occupancy is declining makes good biological sense. All else being equal, when control succeeds in eliminating mosquitoes from one site, recolonization will happen sooner when more sites are occupied. It is also reasonable to think that control measures in the fall will reduce the winter egg stock and, thus, limit infestation through the whole next year. Coincidentally or not, a study of spatiotemporal patterns of dengue epidemic events in Argentina found a positive relationship between average fall temperature and the number of dengue cases reported in the subsequent year.59 Perhaps, the most serious challenge to autumn/winter control is the cost of obtaining sufficient coverage to reach the relatively few occupied sites. Cost can be factored into sensitivity analysis of occupancy dynamics models to evaluate whether increased sensitivity merits the additional spending.40 At the same time, some control measures may improve coverage at reasonable cost such as indoor spraying60 and mosquito-disseminated larvicides.61
Supplemental material appendix
Acknowledgments:
We thank the Porto Alegre City Council for authorizing our use of mosquito trapping data. This work would not be possible without the effort of dozens of sanitary agents who checked traps weekly throughout Porto Alegre. We also thank Daniel A. Simões and three anonymous reviewers who made important contributions throughout the review process.
Note: Supplemental appendix appears at www.ajtmh.org.
REFERENCES
- 1.WHO , 2017. Global Vector Control Response 2017–2030. Geneva, Switzerland: World Health Organization. [Google Scholar]
- 2.Powell JR, Tabachnick WJ, 2013. History of domestication and spread of Aedes aegypti - a review. Mem Inst Oswaldo Cruz 108 (Suppl 1): 11–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Eisen L, Monaghan AJ, Lozano-Fuentes S, Steinhoff DF, Hayden MH, Bieringer PE, 2014. The impact of temperature on the bionomics of Aedes (Stegomyia) aegypti, with special reference to the cool geographic range margins. J Med Entomol 51: 496–516. [DOI] [PubMed] [Google Scholar]
- 4.Weaver SC, 2014. Arrival of chikungunya virus in the new world: prospects for spread and impact on public health. PLoS Negl Trop Dis 8: e2921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Fauci AS, Morens DM, 2016. Zika virus in the Americas–yet another arbovirus threat. N Engl J Med 374: 601–604. [DOI] [PubMed] [Google Scholar]
- 6.Soper FL, 1963. The elimination of urban yellow fever in the Americas through the eradication of Aedes aegypti. Am J Public Health Nations Health 53: 7–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Gubler DJ, 1998. Dengue and dengue hemorrhagic fever. Clin Microbiol Rev 11: 480–496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Stanaway JD, et al. 2016. The global burden of dengue: an analysis from the Global Burden of Disease Study 2013. Lancet Infect Dis 16: 712–723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Brady OJ, Gething PW, Bhatt S, Messina JP, Brownstein JS, Hoen AG, Moyes CL, Farlow AW, Scott TW, Hay SI, 2012. Refining the global spatial limits of dengue virus transmission by evidence-based consensus. PLoS Negl Trop Dis 6: e1760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Tremblay N, Freppel W, Sow AA, Chatel-Chaix L, 2019. The interplay between dengue virus and the human innate immune system: a game of hide and seek. Vaccines (Basel) 7: e145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Coudeville L, Baurin N, Shepard DS, 2020. The potential impact of dengue vaccination with, and without, pre-vaccination screening. Vaccine 38: 1363–1369. [DOI] [PubMed] [Google Scholar]
- 12.WHO , 2012. Global Strategy for Dengue Prevention and Control 2012–2020. Geneva, Switzerland: World Health Organization. [Google Scholar]
- 13.Teich V, Arinelli R, Fahham L, 2017. Aedes aegypti e sociedade: o impacto econômico das arboviroses no Brasil. J Bras Econ Saúde 9: 267–276. [Google Scholar]
- 14.Undurraga EA, et al. 2015. Economic and disease burden of dengue in Mexico. PLoS Negl Trop Dis 9: e0003547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Gubler DJ, 2011. Control of Aedes aegypti-borne diseases: lesson learned from past successes and failures. Asia Pac J Mol Biol 19: 111–114. [Google Scholar]
- 16.Gubler DJ, 2011. Dengue, urbanization and globalization: the unholy trinity of the 21st century. Trop Med Health 39 (Suppl 4): S3–S11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Achee NL, Gould F, Perkins TA, Reiner RC, Jr., Morrison AC, Ritchie SA, Gubler DJ, Teyssou R, Scott TW, 2015. A critical assessment of vector control for dengue prevention. PLoS Negl Trop Dis 9: e0003655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Cailly P, Tran A, Balenghiene T, L’Ambert G, Toty C, Ezanno P, 2012. A climate-driven abundance model to assess mosquito control strategies. Ecol Model 227: 7–17. [Google Scholar]
- 19.McIntire KM, Juliano SA, 2018. How can mortality increase population size? A test of two mechanistic hypotheses. Ecology 99: 1660–1670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Racloz V, Ramsey R, Tong S, Hu W, 2012. Surveillance of dengue fever virus: a review of epidemiological models and early warning systems. PLoS Negl Trop Dis 6: e1648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Campbell KM, Lin CD, Iamsirithaworn S, Scott TW, 2013. The complex relationship between weather and dengue virus transmission in Thailand. Am J Trop Med Hyg 89: 1066–1080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Zheng B, Yu J, Xi Z, Tang M, 2018. The annual abundance of dengue and Zika vector Aedes albopictus and its stubbornness to suppression. Ecol Model 387: 38–48. [Google Scholar]
- 23.Luz PM, Codeço CT, Medlock J, Struchiner CJ, Valle D, Galvani AP, 2009. Impact of insecticide interventions on the abundance and resistance profile of Aedes aegypti. Epidemiol Infect 137: 1203–1215. [DOI] [PubMed] [Google Scholar]
- 24.Caswell H, 2019. Sensitivity Analysis: Matrix Methods in Demography and Ecology. Cham, Switzerland: Springer. [Google Scholar]
- 25.Tran A, L’Ambert G, Lacour G, Benoît R, Demarchi M, Cros M, Cailly P, Aubry-Kientz M, Balenghien T, Ezanno P, 2013. A rainfall- and temperature-driven abundance model for Aedes albopictus populations. Int J Environ Res Public Health 10: 1698–1719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ellis AM, Garcia AJ, Focks DA, Morrison AC, Scott TW, 2011. Parameterization and sensitivity analysis of a complex simulation model for mosquito population dynamics, dengue transmission, and their control. Am J Trop Med Hyg 85: 257–264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Emery SM, Gross KL, 2005. Effects of timing of prescribed fire on the demography of an invasive plant, spotted knapweed Centaurea maculosa. J Appl Ecol 42: 60–69. [Google Scholar]
- 28.Marini G, Guzzetta G, Toledo CAM, Texeira M, Rosà R, Merler S, 2019. Effectiveness of ultralow volume insecticide spraying to prevent dengue in a non-endemic metropolitan area of Brazil. PLoS Comput Biol 15: e1006831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Hasenack H, Cordeiro JLP, Boldrini I, Trevisan R, Brack P, Weber EJ, 2008. Vegetação/ocupação. Hasenack H, ed. Diagnóstico Ambiental de Porto Alegre: Geologia, Solo, Drenagem, Vegetação/Ocupação e Paisagem. Porto Alegre, Brazil: Secretaria Municipal do Meio Ambiente, 56–71. [Google Scholar]
- 30.IBGE [Instituto Brasileiro de Geografia e Estatistica] , 2010. Malha Municipal Digital de Setores Censitários do Censo 2010. Available at: https://censo2010.ibge.gov.br. Accessed January 31, 2020. [Google Scholar]
- 31.Royle JA, Kéry M, 2007. A Bayesian state-space formulation of dynamic occupancy models. Ecology 88: 1813–1823. [DOI] [PubMed] [Google Scholar]
- 32.MacKenzie DI, Nichols JD, Hines JE, Knutson MG, Franklin AB, 2003. Estimating site occupancy, colonization, and local extinction when a species is detected imperfectly. Ecology 84: 2200–2207. [Google Scholar]
- 33.Matthiopoulos J, 2011. How to be a Quantitative Ecologist: the ‘A to R’ of Green Mathematics and Statistics. West Sussex, United Kingdom: John Wiley & Sons, 93–96. [Google Scholar]
- 34.Kéry M, Schaub M, 2012. Bayesian Population Analysis Using WinBUGS. Waltham, MA: Academic Press, 185. [Google Scholar]
- 35.Casella G, George EI, 1992. Explaining the gibbs sampler. Am Stat 46: 167–174. [Google Scholar]
- 36.Kéry M, Royle JA, 2020. Applied Hierarchical Modeling in Ecology: Analysis of Distribution, Abundance and Species Richness in R and BUGS, Volume 2, Dynamic and Advanced Models. Cambridge, MA: Academic Press, 235–331. [Google Scholar]
- 37.Plummer M, 2003. JAGS: a program for analysis of Bayesian graphical models using Gibbs sampling. Hornik K, Leisch F, Zeileis A, eds. Proceedings of the 3rd International Workshop on Distributed Statistical Computing (DSC 2003) Vienna, Austria: Technische Universität Wien, 1–10. [Google Scholar]
- 38.R Core Team , 2019. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing; Available at: https://www.R-project.org/. Accessed January 31, 2020. [Google Scholar]
- 39.Kellner K. 2017. JagsUI: A Wrapper Around ‘rjags’ to Streamline ‘JAGS’ Analyses. Available at: https://CRAN.R-project.org/package=jagsUI. Accessed January 31, 2020. [Google Scholar]
- 40.Martin J, Nichols JD, McIntyre CL, Ferraz G, Hines JE, 2009. Perturbation analysis for patch occupancy dynamics. Ecology 90: 10–16. [DOI] [PubMed] [Google Scholar]
- 41.Guzzetta G, Marques-Toledo CA, Rosà R, Teixeira M, Merler S, 2018. Quantifying the spatial spread of dengue in a non-endemic Brazilian metropolis via transmission chain reconstruction. Nat Commun 9: 2837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Vazquez-Prokopec GM, Montgomery BL, Horne P, Clennon JA, Ritchie SA, 2017. Combining contact tracing with targeted indoor residual spraying significantly reduces dengue transmission. Sci Adv 3: e1602024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Gaston KJ, 1994. Rarity. London, United Kingdom: Chapman & Hall, 94–113. [Google Scholar]
- 44.May RM, Anderson RM, 1979. Population biology of infectious diseases: part II. Nature 280: 455–461. [DOI] [PubMed] [Google Scholar]
- 45.Diniz DFA, de Albuquerque CMR, Oliva LO, de Melo-Santos MAV, Ayres CFJ, 2017. Diapause and quiescence: dormancy mechanisms that contribute to the geographical expansion of mosquitoes and their evolutionary success. Parasit Vector 10: 310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Juliano SA, 2009. Species interactions among larval mosquitoes: context dependence across habitat gradients. Annu Rev Entomol 54: 37–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Morin CW, Comrie AC, Ernst K, 2013. Climate and dengue transmission: evidence and implications. Environ Health Persp 121: 1264–1272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Hanski I, 1999. Metapopulation Ecology. Oxford, United Kingdom: Oxford University Press. [Google Scholar]
- 49.Levins R, 1969. Some demographic and genetic consequences of environmental heterogeneity for biological control. Bull Entomol Soc Am 15: 237–240. [Google Scholar]
- 50.Gaston KJ, Blackburn TM, Greenwood JJD, Gregory RD, Quinn RM, Lawton JH, 2000. Abundance-occupancy relationships. J Appl Ecol 37: 39–59. [Google Scholar]
- 51.Mogi M, Choochote W, Khamboonruang C, Suwanpanit P, 1990. Applicability of presence–absence and sequential sampling for ovitrap surveillance of Aedes (Diptera: culicidae) in Chiang Mai, Northern Thailand. J Med Entomol 27: 509–514. [DOI] [PubMed] [Google Scholar]
- 52.Tun-Lin W, Kay BH, Barnes A, Forsyth S, 1996. Critical examination of Aedes aegypti indices: correlations with abundance. Am J Trop Med Hyg 54: 543–547. [DOI] [PubMed] [Google Scholar]
- 53.MacKenzie DI, 2006. Modeling the probability of resource use: the effect of, and dealing with, detecting a species imperfectly. J Wildl Manage 70: 367–374. [Google Scholar]
- 54.Kendall WL, White GC, 2009. A cautionary note on substituting spatial subunits for repeated temporal sampling in studies of site occupancy. J Appl Ecol 46: 1182–1188. [Google Scholar]
- 55.Box GP, 1976. Science and statistics. J Am Stat Assoc 71: 791–799. [Google Scholar]
- 56.Royle JA, Nichols JD, 2003. Estimating abundance from repeated presence-absence data or point counts. Ecology 84: 777–790. [Google Scholar]
- 57.MacKenzie DI, Royle JA, 2005. Designing occupancy studies: general advice and allocating survey effort. J Appl Ecol 42: 1105–1114. [Google Scholar]
- 58.Focks DA, Kloter KO, Carmichael GT, 1987. The impact of ultra-low volume ground aerosol applications of malathion on the population of Aedes aegypti (L.). Am J Trop Med Hyg 36: 639–647. [DOI] [PubMed] [Google Scholar]
- 59.Carbajo AE, Cardo MV, Guimarey PC, Lizuain AA, Buyayisqui MP, Varela T, Utgés ME, Giovacchini CM, Santini MS, 2018. Is autumn the key for dengue epidemics in non endemic regions? The case of Argentina. PeerJ 6: e5196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Gunning CE, et al. 2018. Efficacy of Aedes aegypti control by indoor ultra low volume (ULV) insecticide spraying in iquitos, Peru. PLoS Negl Trop Dis 12: e0006378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Abad-Franch F, Zamora-Perea E, Ferraz G, Padilla-Torres SD, Luz SLB, 2015. Mosquito-disseminated pyriproxyfen yields high breeding-site coverage and boosts juvenile mosquito mortality at the neighborhood scale. PLoS Negl Trop Dis 9: e0003702. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.