Quantitative prediction of respiratory tidal volume based on the external torso volume change: a potential volumetric surrogate

Abstract

An external respiratory surrogate that not only highly correlates with but also quantitatively predicts internal tidal volume should be useful in guiding four-dimensional computed tomography (4DCT), as well as 4D radiation therapy (4DRT). A volumetric surrogate should have advantages over external fiducial point(s) for monitoring respiration-induced motion of the torso, which deforms in synchronization with a patient-specific breathing pattern. This study establishes a linear relationship between the external torso volume change (TVC) and lung air volume change (AVC) by validating a proposed volume conservation hypothesis (TVC = AVC) throughout the respiratory cycle using 4DCT and spirometry. Fourteen patients’ torso 4DCT images and corresponding spirometric tidal volumes were acquired to examine this hypothesis. The 4DCT images were acquired using dual surrogates in ciné mode and amplitude-based binning in 12 respiratory stages, minimizing residual motion artifacts. Torso and lung volumes were calculated using threshold-based segmentation algorithms and volume changes were calculated relative to the full-exhalation stage. The TVC and AVC, as functions of respiratory stages, were compared, showing a high correlation (r = 0.992 ± 0.005, p < 0.0001) as well as a linear relationship (slope = 1.027 ± 0.061, R² = 0.980) without phase shift. The AVC was also compared to the spirometric tidal volumes, showing a similar linearity (slope = 1.030 ± 0.092, R² = 0.947). In contrast, the thoracic and abdominal heights measured from 4DCT showed relatively low correlation (0.28 ± 0.44 and 0.82 ± 0.30, respectively) and location-dependent phase shifts. This novel approach establishes the foundation for developing an external volumetric respiratory surrogate.

1. Introduction

External respiratory surrogates have been studied and applied in radiation therapy, serving as correlative indicators for retrospective reconstruction of four-dimensional computed tomography (4DCT) (Vedam et al 2003a, Low et al 2003, Keall et al 2004, Mageras et al 2004, Rietzel et al 2005), as well as for respiratory gating or motion tracking during 4D radiation therapy (4DRT) (Shirato et al 2000, Schweikard et al 2000, 2004, Keall et al 2001, 2005, Ozhasoglu and Murphy 2002, Vedam et al 2003b, 2004, Hoisak et al 2004, Korreman et al 2006, Ionascu et al 2007, Li et al 2008a). They provide an attractive alternative to x-ray-based imaging by minimizing the radiation dose from imaging to patients. The foundation for such a working surrogate is the establishment of a correlation between the deformable motions of the external body and those of internal organs during respiration. Three external parameters have so far been utilized to establish such a clinically relevant correlation. These are (1) the height variation of a fiducial(s) on a patient’s upper abdomen, (2) the tension variation of a bellows around the upper abdomen and (3) the dynamic airflow (volume) into and out of the lungs. These surrogates are commercially available and are currently employed in the clinic to varying extents depending on their accuracy, simplicity and convenience.

Systems based on the change in height of one or more optical reflector(s) placed on the lower thorax or upper abdomen during respiration, such as the real-time positioning management (RPM) system, have been widely used for respiratory gating and tracking during radiation therapy. The variation in height depends on the position of the fiducial placed on patients (Yan et al 2006, Baroni et al 2007). In the presence of breathing irregularities, the presumed cyclical respiratory motion is disrupted and the correlation between phase and amplitude can be reduced dramatically, resulting in inadequate phase-based 4DCT reconstructions as high as 30–40% (Rietzel and Chen 2006, Lu et al 2005b, Mutaf et al 2007) and correlation coefficients as low as 0.39 when used for respiratory gated radiotherapy (Hoisak et al 2004, Vedam et al 2004, Korreman et al 2006, Ionascu et al 2007). Bellows systems measure the tension produced by the expansion of upper abdomen (change in circumference of a transverse body contour) during respiration. They have been primarily used as a surrogate for phase-based retrospective 4DCT imaging. Similar to the RPM system, the bellows response can be affected by both sensor placement and patient positioning (Lu et al 2006). Spirometry directly measures the airflow volume into and out of the lungs. It is considered to provide superior accuracy to the temporal variation of abdominal height (Hoisak et al 2004, Lu et al 2006). However, it suffers from substantial drift and requires frequent recalibration (Low et al 2003, Lu et al 2005b). The source of the drift has been recently identified as differential response of the spirometer to different flow rates (Ha et al 2008) and it is difficult to eliminate. The drift could result in variations as much as 40% per breathing cycle. Spirometry is also inconvenient to patients (Hoisak et al 2004), requiring that breathing be performed solely through the mouth, with the nose closed to avoid air leakage. Although all these existing surrogates produce respiratory waveforms that correlate (to a certain degree) with patient-specific breathing patterns, they often suffer from phase shifts (delayed or advanced signal), as indicated by cross-correlation studies (Vedam et al 2003b, Hoisak et al 2004, Korreman et al 2006, Lu et al 2006). Furthermore, the established external–internal correlation can be a function of the respiratory stage (Ionascu et al 2007). It can also suffer due to breathing irregularities (Rietzel et al 2005, Rietzel and Chen 2006, Lu et al 2006, Korreman et al 2006). Fundamentally, local point(s) or line(s) are indeterminate fiducials for volumetric and deformable moving anatomical structures. Their reliability and reproducibility vary with the condition of each patient, such as changes in abdominal muscle engagement (active or passive) during respiration. Practically, inadequate correlation and phase shifts can produce a false indication of the respiratory stage in real time, especially for irregular breathers, resulting in potentially unrealized problems in 4DCT imaging as well as in 4DRT respiratory gating or tracking (Rietzel and Chen 2006, Hoisak et al 2004, Korreman et al 2006). Therefore, it is necessary to find an alternative to these existing surrogates that addresses the problems of reliability and convenience in the clinic.

In this paper, we present a novel volumetric approach for establishing a highly correlative, as well as quantitative, relationship between the external torso volume change (TVC or ΔV_Torso) and the lung air volume change (AVC or ΔV_Air). We propose a volume conservation hypothesis in which the airflow (AVC) is the sole contributor to the TVC. Physiologically, quiet respiration involves not only thoracic but also abdominal motion and deformation, with minor pressure variations (∼3–11 mmHg or <1–2%) in both cavities (Applegate 2000, Agostoni and Rahn 1960). Physically, the tissue volume, except for the lungs, does not change with respiration and the gastrointestinal (GI) gas volume change (GVC) is negligible. Using the torso 4DCT images and spirometric measurements from 14 patients, this hypothesis is validated using correlation analysis as well as linear regression analysis. This linear volumetric relationship establishes the foundation for developing a novel surrogate with higher accuracy and reliability.

2. Methods and materials

2.1. A volume conservation hypothesis

Tissues in the human body are composed of materials in solid, liquid and gaseous phases. Solids (bone and soft tissue) and liquids (blood and other bodily fluids) do not change in volume with physiological pressure variations. Gases can be contained in either a closed (GI tract) or an open (lung) system. The airflow (dynamic tidal volume) changes lung volume and density during respiration. However, the amount of air in the expiratory reserve and residual volumes (reserve air volume in brief hereafter) remains unchanged through a dynamic equilibrium, which can be regarded as a pseudo-closed system in quiet respiration. Therefore, the gas volume in the closed and pseudo-closed systems should obey the ideal gas law:

$$P\cdot V=n\cdot R\cdot T,$$ (1)

where P, V, n, R and T represent pressure, volume, the mole of the gas molecules, ideal gas constant and temperature (in K), respectively.

Under quiet respiration, the lung pressure varies from −2 to +3 mmHg (Applegate 2000) or <1% of the ambient atmosphere pressure. The gastric pressure variation during the respiratory cycle for a patient in the supine position is normally between 10 and 15 cmH₂O (Agostoni and Rahn 1960) or 7.5 and 11 mmHg, <2% of the ambient pressure. Hence, the volume change of the air ‘sealed’ in these closed systems should be within 3%. Therefore, a clinically relevant hypothesis of torso volume conservation was proposed as TVC = AVC, which links the lung AVC (ΔV_Air) to the external TVC (ΔV_Torso), which covers motions in both thorax and abdomen (Konno and Mead 1966).

2.2. Patient 4DCT image acquisition using dual respiratory surrogates

4DCT torso images were acquired for 14 patients under quiet breathing conditions using a 16-slice CT scanner (Philips Medical Systems, Bothell, WA) operated under a special research protocol, which was described previously (Lu et al 2006). In brief, 25 scans in ciné mode were acquired at each abutting couch position (24 mm span) for 18 s, and the entire torso was scanned. Two respiratory surrogates, a bellows and a spirometer, were used to enhance the fidelity of respiratory measurement and the reliability of retrospective binning. The bellows (pressure transducer) was placed around each patient’s upper abdomen for monitoring the expansion/contraction pressure change during respiration. The spirometer was used to measure the amount of air flowing into and out of the patient’s lungs. Both bellows pressure and spirometry volume were used as external surrogates for determining the pseudo tidal volume (in cm³), which was converted from the bellows signal by multiplying the average ratio between a drift-corrected spirometer-measured tidal volume and the bellows signal during the scan session (Lu et al 2006). Based on the amplitude of the tidal volume (and airflow direction) within the respiratory cycle, all image projections were sorted into 12-stage bins for retrospective 4D image reconstruction. The respiratory cycle started and ended at full exhalation (stages 1 and 12), with full inhalation at stage 6 or 7. Each of the 12-stage 4DCT images contained 464, 1.5 mm thick slices. The pixel size in the 512 × 512 slices is 0.98 × 0.98 mm². The actual torso image volume used in this study was selected anatomically, from the clavicles to the pubic crest, including both the thoracic and the abdominal cavities.

2.3. Automatic threshold-based segmentation of the 4DCT images

Two automatic threshold-based segmentation tools were applied using an edge-tracing algorithm and a voxel-counting algorithm. External contours were automatically generated across the entire torso using the edge-tracing algorithm: each slice contour was defined by up to 800 points, after two times smoothing with an erosion-dilation (size conservative) filter. Multiple thresholds were tested (−250 to −400 Hounsfield Units, or HU) for defining tissue/air and tissue/lung interfaces, and −350 HU was used in this study. Within the body contour, tissue volumes and densities could be calculated using the voxel-counting algorithm. Depending upon the threshold, body volume (all CT# inside body contour) and lung volume (CT# ≤ −350 HU inside the thoracic body contours excluding GI gas) were obtained. This strategy does not need lung segmentation, reducing workload as well as gaining accuracy and reproducibility. The GI gas volume was calculated by subtracting the lung volume from the total air volume in the torso. The volume changes were calculated with reference to the full exhalation stage.

2.4. Lung air volume change (AVC) based on lung density correction

It is well known that lung density changes during respiration due to air dilution in the alveoli. Therefore, the lung volume change (LVC, ΔV_Lung) does not fully reflect the AVC (ΔV_Air). The fraction of air content can be calculated as (Lu et al 2005b)

$$f_{\text{Air}}=1.0-\left(\frac{{\text{CT}}_{\text{Lung}}-{\overline{\text{CT}}}_{\text{Air}}}{{\overline{\text{CT}}}_{\text{Tissue}}-{\overline{\text{CT}}}_{\text{Air}}}\right),$$ (2)

where CT_Lung, ${\overline{\text{CT}}}_{\text{Tissue}}$ and ${\overline{\text{CT}}}_{\text{Air}}$ are the CT# of lung voxels and average CT# for tissue and air. Assuming that air density is negligible and the tidal volume is much smaller than the lung volume, the AVC at stage i can be calculated as

$$\begin{gathered} \Delta V_{\text{Air}}=f_{\text{Air}}^i\cdot V_{\text{Lung}}^i-f_{\text{Air}}^0\cdot V_{\text{Lung}}^0 \\ \hspace{1em}\hspace{1em}\hspace{0.17em}\cong \Delta V_{\text{Lung}}-\left({\text{CT}}_{\text{Lung}}^i\cdot V_{\text{Lung}}^i-{\text{CT}}_{\text{Lung}}^0\cdot V_{\text{Lung}}^0\right), \end{gathered}$$ (3)

where ΔV_Air, ΔV_Lung, V_Lung and CT_Lung are the AVC, the LVC, the lung volume and density. The superscripts refer to two respiratory stages (0 is the reference).

2.5. Lung air volume change using spirometry measurement data

The pseudo tidal volume in a respiratory cycle was measured using a spirometer and a bellows with correction for instrumental drift (Lu et al 2006). The rate of the AVC showed a linear relationship with the rate of airflow into the lungs through the spirometer. The conversion factor is expressed as (Lu et al 2005b)

$$\frac{\Delta V}{\Delta \upsilon }\approx \frac{\Delta V_{\text{Air}}}{\Delta V_{\text{Spirom}}}=\frac{T_l\cdot \left(P_s-P_{s,\text{water}}\right)}{T_s\cdot \left(P_l-P_{l,\text{water}}\right)}=1.11,$$ (4)

where T_l, T_s, P_l, P_s, P_l,water and P_s,water are the temperatures, total pressures and partial pressures of water vapor in lungs and spirometer, respectively. Thus, the AVC (ΔV_Air) can be calculated from the spirometry data, with a theoretical correction factor of 1.11 (measured as 1.08) (Lu et al 2005b). The volume increases as air enters the lungs due to increased temperature and humidity compared with ambient room conditions.

2.6. Lung temperature kinetics and gastrointestinal pressure variation

Equation (4) assumes instant thermal equilibrium. This assumption can overestimate the air volume in the lungs by about 1%. When the reserve air volume is known (based on 4DCT), the temperature of the mixed air in the pseudo-closed lung system can be calculated based on equation (1), assuming that the lung pressure variation (<1%) is negligible:

$$T_i=\frac{V_{\text{Reserve}}+V_{\text{Tidal}}^i}{{\left(273+37\right)}^{-1}\cdot V_{\text{Reserve}}+{\left(273+22\right)}^{-1}\cdot V_{\text{Tidal}}^i}\left(\text{K}\right),$$ (5)

where V_Reserve and $V_{\text{tidal}}^i$ are the reserve air volume (assumed at ∼37 °C) and inhaling tidal volume (assumed at ∼22 °C) at inspiration stage i. In the expiration stages, the thermal equilibrium is gradually approached, resulting in an equilibrium temperature of 37 °C at the end of exhalation. Between the full exhalation and full inhalation stages, the maximum temperature variation is estimated to be less than 1% in K (given the ratio of V_Reserve/V_Tidal about 10 in equation (5)).

The lung air volume changes with the slight temperature variation, following Charles’s Law (reduced from equation (1)) in a constant pressure (isobaric) process:

$$\frac{T_0}{T_i}=\frac{V_0}{V_i},$$ (6)

where the subscripts i and 0 are any respiratory stage and the reference stage. Using this equation, the <1% temperature variation can be translated to <1% volume variation. Together with the variation of the partial pressure of vapor as the temperature changes in the lungs, this non-equilibrium correction provides a conversion factor of 1.10.

The bowel gas would follow Boyle’s law (reduced from equation (1)) between two respiratory stages i and 0 in a constant temperature (isothermal) process:

$$\frac{P_i}{P_0}=\frac{V_0}{V_i}.$$ (7)

Namely, the pressure variation is reciprocal to the volume variation.

2.7. Measurements of thoracic and abdominal heights

Two skin areas in the mid-sagittal plane are selected to track their heights in 4DCT. Anatomically, the lower thoracic point is defined as five slices (0.75 cm) superior to the inferior end of the sternum body, while the upper abdominal point is selected as ten slices (1.5 cm) inferior to the tip of the xiphoid process of the sternum. The ‘fiducial’ height changes (ΔH_Thorax and ΔH_Abdomen) are averaged from the skin heights in five consecutive slices for each of the 4DCT stage images. The measurement is performed manually based on body contours with a precision of about 0.5 mm.

2.8. Quantitative assessments of breathing patterns

Determination of breathing pattern (BP) can be subjective and lack quantification, since most patients are combined (thoracic and abdominal) breathers, utilizing both costal muscle and diaphragm. To quantify the complex breathing pattern and provide a comprehensive view on the thoracic and abdominal involvements, three descriptors are introduced: a volume ratio (BP_V), a point array (BP₅) and a height ratio (BP_H):

$${\text{BP}}_V=\frac{{\left(\text{thoracic Volume Change}\right)}^{\text{Max}}}{{\left(\text{Torso Volume Change}\right)}^{\text{Max}}}=\frac{{\left(\text{tVC}\right)}^{\text{Max}}}{{\left(\text{TVC}\right)}^{\text{Max}}}.$$ (8)

The volumetric involvement of the thorax and abdomen can be estimated from BP_V and (1.0 − BP_V), respectively. The thorax is above the xiphoid process of the sternum.

The array of five points (BP₅) on the skin, as shown in figure 1, is another descriptor of the breathing pattern: two points are on the thorax and three on the abdomen. This is a visually preferable descriptor. A ratio of average height (BP_H) is the third descriptor:

$${\text{BP}}_H=\frac{{\left(\overline{\text{thoracic Height Variation}}\right)}^{\text{Max}}}{{\left(\overline{\text{abdominal Height Variation}}\right)}^{\text{Max}}}=\frac{{\left(\overline{H_{\text{tho}}}\right)}^{\text{Max}}}{{\left(\overline{H_{\text{abd}}}\right)}^{\text{Max}}}.$$ (9)

Figure 1.

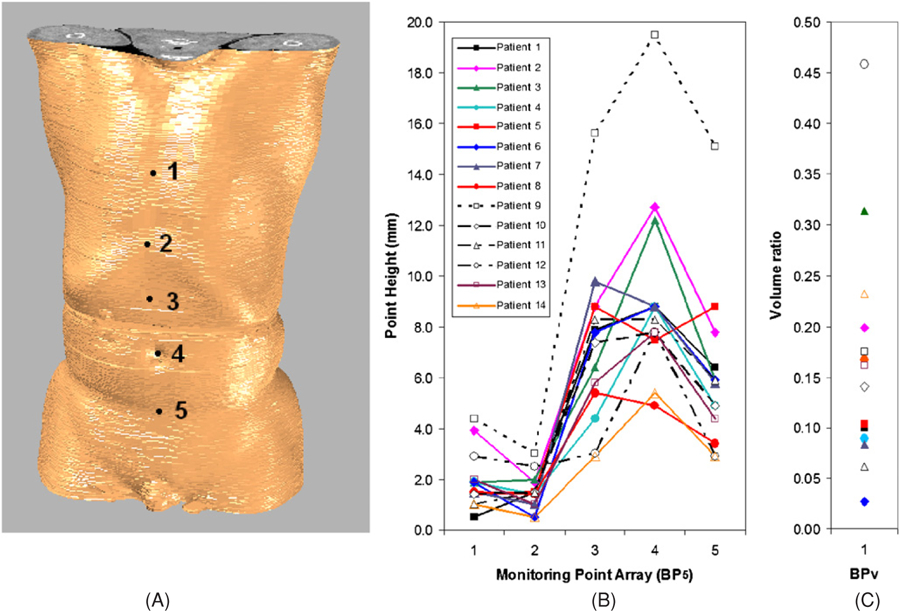
A volumetric image of a patient’s torso with an array of five anatomical sites (A) and two descriptors of the breathing pattern: the array–height descriptor (B) and the volumetric descriptor (C). The array contains (1) mid-point of the sternum, (2) inferior end-point of the sternum, (2) mid-point between points 2 and 4, (4) the biblical point and (5) mid-point between point 4 and the pubic bone.

2.9. Quantitative correlation and linear regression analyses

Correlation coefficient, linear regression and cross-correlation analyses were implemented using Matlab (The MathWorks, Natick, MA) and Excel (Microsoft, Redmond, WA). Twelve pairs of data, x (ΔV_Torso, ΔV_Spirom, ΔV_{GI Gas}, ΔH_Thorax, or ΔH_Abdomen) versus y (ΔV_Air), were analyzed for each patient to determine the correlation coefficient (r_{x, y}):

$$r_{x,y}=\frac{\mathrm{cov}\left(x,y\right)}{\sqrt{\mathrm{cov}\left(x,x\right)\cdot \mathrm{cov}\left(y,y\right)}},$$ (10)

where cov(x, y) is a covariance matrix of x and y in the 12-stage respiratory cycle.

A linear relationship between external and internal volume changes based on the volume conservation hypothesis was assumed as

$$Y=\alpha \cdot X+\beta ,$$ (11)

where the slope α provides a quantitative assessment of the hypothetical one-to-one relationship, and the intercept β provides an assessment of any systematic bias between the two quantities. Ideally, α should be close to unity and β should be close to null, independent of patients, including gender and breathing pattern.

The cross-correlation analysis was performed between x(i) and y(i) (as functions of respiratory stage i) to examine any phase shift by fitting the two curves for maximum overlap. A fractional phase shift could be obtained by analyzing linearly interpolated data between stages (i), making the discrete functions x(i) and y(i) continuous.

3. Results

3.1. Assessments of patients’ breathing patterns based on 4DCT images

Table 1 shows patients’ gender, ranges of the TVC and AVC, as well as the quantitative descriptors of breathing pattern based on volume and height variations on the thorax and abdomen. The external volumetric descriptor (BP_V) estimates that the thoracic involvement is 16 ± 11%, ranging from 3% to 46%. In parallel, the height descriptor (BP_H) shows that the ratio of thoracic height variation to abdominal variation is 16 ± 8%, ranging from 9% to 39%. Both descriptors suggest a large variation in the thoracic motion over the abdominal motion, and detailed height variations of the five skin points (BP₅) for all patients are plotted in figure 1. Given the differences in patients’ gender and breathing pattern, the maximum TVC and AVC are in close agreement: on average the relative difference is −2.7 ± 7.3%, as shown in table 1.

Table 1.

Quantitative, external–internal volumetric relationship and quantitative descriptors of breathing pattern. The maximum torso volume change (TVC) and lung air volume change (AVC) are in close agreement. The volume descriptor is the volume ratio: (tVC/TVC)^Max (as defined in equation (8)), while the height descriptors are the maximum height variation at five anatomical sites (as shown in figure 1), and the height ratio ${\left(\overline{H_{\text{tho}}}/\overline{H_{\text{abd}}}\right)}^{\text{Max}}$ (as defined in equation (9)).

Patient	Gender	Ext–int volumetric relationship Max volume changes (cm3)			Volume and height descriptors of breathing pattern
					Volume ratio (tVC/TVC)Max	Maximum height variation (mm)					Height ratio ${\left(\overline{H_{\text{tho}}}/\overline{H_{\text{abd}}}\right)}^{\text{Max}}$b
		TVC Max	AVCMax	Δ/Avg a		ΔH1	ΔH2	ΔH3	ΔH4	ΔH5
1	M	506.6	559.3	−9.9%	0.100	0.5	1.5	7.9	8.8	6.4	0.087
2	M	619.2	637.8	−3.0%	0.199	3.9	1.9	8.8	12.7	7.8	0.198
3	M	694.0	724.5	−4.3%	0.314	1.9	2.0	6.4	12.2	5.9	0.159
4	F	322.5	287.9	11.3%	0.089	1.9	1.4	4.4	8.8	4.9	0.182
5	F	530.8	505.7	4.8%	0.103	1.4	1.5	8.8	7.5	8.8	0.116
6	M	500.2	485.4	3.0%	0.027	1.9	0.5	7.8	8.8	5.9	0.107
7	M	477.0	514.8	−7.6%	0.083	1.5	1.0	9.8	8.8	5.8	0.102
8	F	345.2	384.5	−10.8%	0.167	1.5	1.4	5.4	4.9	3.4	0.212
9	M	1742.5	1655.2	5.1%	0.175	4.4	3.0	15.6	19.5	15.1	0.147
10	F	374.2	388.6	−3.8%	0.140	1.4	1.5	7.4	7.8	4.9	0.144
11	M	558.9	638.6	−13.3%	0.062	1.0	1.5	8.3	8.3	5.9	0.111
12	M	468.6	487.1	−3.9%	0.458	2.9	2.5	3.0	7.8	2.9	0.394
13	M	467.7	452.8	3.2%	0.161	2.0	1.0	5.8	7.8	4.4	0.167
14	M	257.2	282.1	−9.2%	0.231	1.0	0.5	2.9	5.4	2.9	0.134
Average		561.8	571.7	−2.7%	0.16	1.9	1.5	7.3	9.2	6.1	0.16
St. Dev.		359.4	336.9	7.3%	0.11	1.1	0.7	3.2	3.6	3.1	0.08

^aIn the relative difference (Δ/Avg), Δ = TVC − AVC and Avg = (TVC + AVC)/2.

^bIn the height ratio $\left(\overline{H_{\text{tho}}}/\overline{H_{\text{abd}}}\right)$, $\overline{H_{\text{tho}}}=\left(\Delta H_1+\Delta H_2\right)/2$ and $\overline{H_{\text{abd}}}=\left(\Delta H_3+\Delta H_4+\Delta H_5\right)/3$.

3.2. Linear regression and correlation analyses of the AVC and the TVC

Table 2 shows the linear regression results between the AVC and the TVC for all patients. The average slope is 1.027 ± 0.061 (R² = 0.985 ± 0.011), supporting the hypothetical relationship. The apparent intercept of −11.9 ± 25.3 cm³, or −2.1 ± 3.8% relative to the maximum tidal volumes, indicates a small systematic bias between the two measures. Figure 2(A) shows a linear regression plot of the data from all patients, showing that the linear relationship holds sufficiently well across the patient spectrum. Figure 3 shows four examples of the dynamic plot of internal and external volumetric variables versus respiratory stages. According to table 2, these four patients are statistical representatives of the pool of 14 patients. Cross-correlation analysis and visual examination find no phase shift.

Table 2.

Linear regression and correlation coefficient analyses of external parameters versus internal lung air volume change (AVC) obtained from the 4DCT images. The slopes are close to unity (α = 1.027 ± 0.061, R² = 0.985 ± 0.011), and the intercepts are relatively small in comparison with the maximum AVC (−2.0% ± 3.7%). The torso volume change (TVC), thoracic and abdominal heights are used against the AVC for calculating correlation coefficient, r_X,AVC. The GI-gas volume change (GVC) apparently is independent of respiratory stages with relatively small variation (2.8% ± 1.9%).

Patient	Quantitative volumetric relationship of the TVC and the AVC						Point height correlation analysisa		The GVC variation (cm3) statistical analysis
	Linear regression analysis				Correlation analysis
	Slope (α)	Intercept (β)	R2	β/AVCMax	rTVC	p-value	rAbdomen	rThorax	$\text{Average}\langle V\rangle$	St. Dev. (σ)	$\sigma /\langle V\rangle$
1	1.0914	1.80	0.9953	0.32%	0.9976	<0.0001	0.9773	0.1008	607.79	20.62	3.39%
2	1.0096	−35.97	0.9637	−5.64%	0.9817	<0.0001	0.8663	0.7079	194.72	4.05	2.08%
3	1.0313	22.49	0.9903	3.10%	0.9951	<0.0001	0.9732	0.6441	452.32	11.43	2.53%
4	0.9208	−19.48	0.9650	−6.77%	0.9823	<0.0001	0.6552	−0.5459	134.22	3.67	2.73%
5	0.9484	0.37	0.9878	0.07%	0.9939	<0.0001	−0.1943	0.0816	195.08	14.94	7.66%
6	0.9793	−34.92	0.9776	−7.19%	0.9887	<0.0001	0.9819	0.3059	411.34	5.82	1.41%
7	1.0056	−22.19	0.9763	−4.31%	0.9881	<0.0001	0.9786	−0.0343	106.01	1.75	1.65%
8	1.1324	−6.91	0.9908	−1.80%	0.9954	<0.0001	0.9405	0.4073	95.08	2.19	2.31%
9	0.9689	−69.98	0.9916	−4.23%	0.9958	<0.0001	0.9879	0.6144	433.37	8.51	1.96%
10	1.0670	5.47	0.9934	1.41%	0.9967	<0.0001	0.9814	0.1535	461.80	8.42	1.82%
11	1.0844	27.27	0.9839	4.27%	0.9919	<0.0001	0.8776	0.3343	458.02	7.58	1.66%
12	1.0490	−24.93	0.9832	−5.12%	0.9916	<0.0001	0.8376	0.8583	93.92	6.14	6.54%
13	1.0033	−9.83	0.9925	−2.17%	0.9962	<0.0001	0.8464	0.8397	1384.56	17.59	1.27%
14	1.0876	0.23	0.9968	0.08%	0.9984	<0.0001	0.7267	−0.6001	158.99	2.54	1.59%
Average	1.027	−11.9	0.985	−2.0%	0.992	0.000	0.82	0.28	370	8.2	2.8%
St. Dev.	0.061	25.3	0.011	3.7%	0.005	0.000	0.30	0.44	339	5.9	1.9%

^aNegative correlation coefficients suggest large phase-shifts of the height curve relative to the AVC curve.

Figure 2.

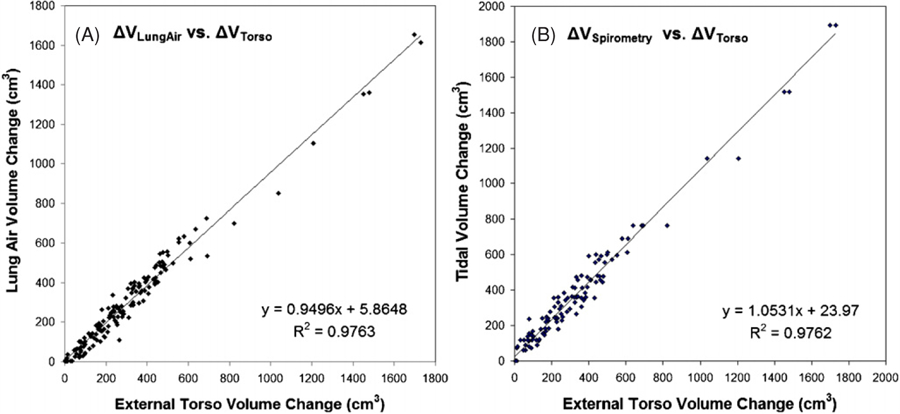
Linear regression analyses for all data in 14 patients: (A) internal lung air volume change (AVC) versus external torso volume change (TVC) and (B) the spirometric tidal volume versus the TVC. The slopes (α = 0.950 and 1.053) are slightly off unity, largely due to patient #9 who has an unusually large maximum tidal volume in the fitting scale.

Figure 3.

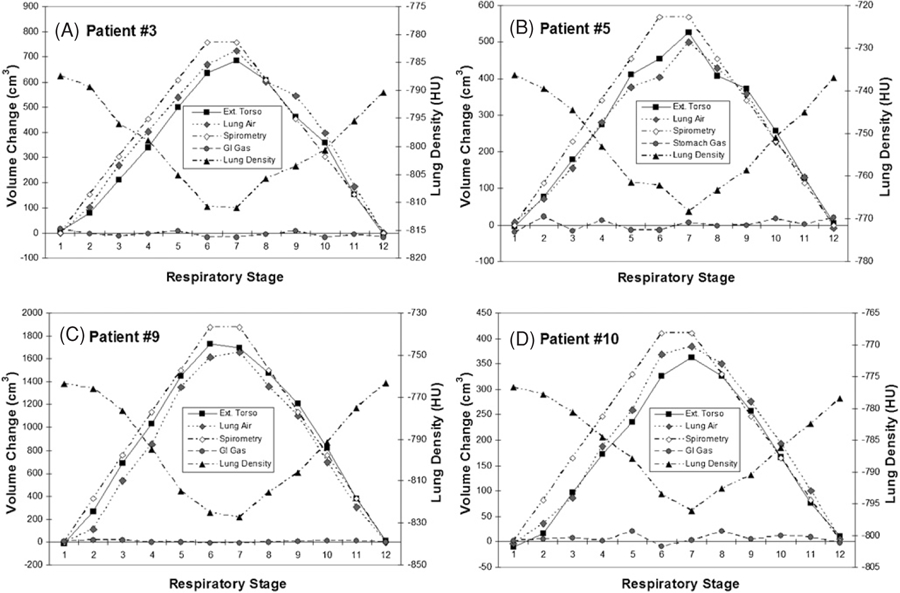
Four typical examples of the external and internal volume changes (the TVC and the AVC), spirometric tidal volume and lung density as functions of respiratory stage. The GI gas volume change (GVC) does not correlate with the respiratory stage. A phase shift (0.1–0.4 stage advance) is shown for the spirometric curve.

Table 2 also shows correlation results for the TVC versus the AVC, and for the thoracic and abdominal heights versus the AVC. The TVC–AVC correlation coefficients are high (r = 0.992 ± 0.005) with a p-value of <0.0001, independent of patient gender and breathing pattern. In contrast, the correlation for abdominal height versus the AVC (r = 0.82 ± 0.30) is higher than that of the thoracic height (r = 0.28 ± 0.44), but inferior to that of the TVC. Figure 4 shows four examples, comparing the AVC with the point height measurements.

Figure 4.

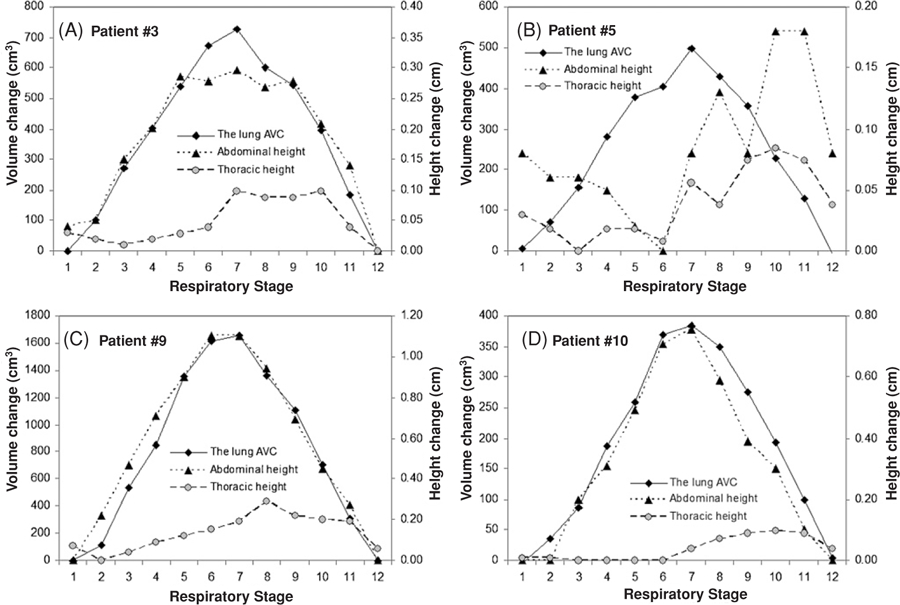
Four typical examples of comparison of the lung air volume change (AVC) with thoracic and abdominal heights. Most thoracic curves possess a phase shift of >1 stage. All heights are average of five measurements in the consecutive slices.

3.3. Volume and pressure variations of gas in the gastrointestinal tract

Table 2 also shows that the bowel gas volumes (ranging from 95 to 1385 cm³) have very small changes during respiration. The average relative variation is 2.8 ± 1.9%. Figure 3 shows four examples of the minute GVC variation during respiration. Little correlation (r = −0.05 ± 0.31) was found between the GVC and the TVC in the patients. Based on equation (7), the small volume variation indicates a small pressure variation in a similar scale (∼3%), consistent with measured values (∼2%) (Agostoni and Rahn 1960). This indicates that the GI gas volume is conserved during respiration.

3.4. Linear regression and correlation analyses of the AVC and spirometry data

Table 3 shows linear regression and correlation coefficient results of the AVC and the spirometric tidal volume. The close-to-unity slope (1.030 ± 0.092, R² = 0.947 ± 0.024) and small intercept (4.5 ± 5.0%) are similar to those in the TVC–AVC results. Figure 2(B) shows the linear fitting of the spirometry data versus the TVC across all patients. Table 3 also shows a high correlation (r = 0.973 ± 0.012) between the two data sets. Figure 3 shows four plots of the spirometric tidal volume versus the other volumetric variables as a function of respiratory stage. An average phase shift of 0.3 stages in the spirometric tidal volumes compared with the AVC data is observed based on cross-correlation analysis, possibly due to dynamic pressure imbalance between the bronchi and the alveoli (Lu et al 2006).

Table 3.

Correlation coefficient and linear regression analyses of spirometric tidal volume and the lung air volume change (AVC). The average correlation coefficient (r = 0.973 ± 0.012 with p < 0.0001) and linear relationship (α = 1.030 ± 0.092, R² = 0.947 ± 0.024) provide a quantitative assessment on the agreement between the two sets of volumetric data. Experimental spirometry data for patients 4, 6 and 13 were not available for these analyses.

Patient no.	Correlation coefficient (r)	Linear regression analysis
		Slope (α)	Intercept (β)	R2	$\Delta V_{\text{Air}}^{\text{Max}}$	$\beta /\Delta V_{\text{Air}}^{\text{Max}}$
1	0.9736	1.0667	24.78	0.9479	600.40	4.13%
2	0.9654	1.0680	74.67	0.9320	692.63	10.78%
3	0.9775	1.0407	−1.83	0.9555	764.13	−0.24%
5	0.9733	1.1523	4.76	0.9473	571.13	0.83%
7	0.9619	0.8733	34.39	0.9253	444.46	7.74%
8	0.9691	0.9019	25.21	0.9391	365.79	6.89%
9	0.9891	1.0829	85.04	0.9783	1893.59	4.49%
10	0.9628	1.0012	20.59	0.9269	414.22	4.97%
11	0.9898	0.9309	−7.41	0.9797	597.53	−1.24%
12	0.9532	1.1362	84.25	0.9086	594.21	14.18%
14	0.9894	1.0736	−4.04	0.9789	309.09	−1.31%
Average	0.973	1.030	30.95	0.947	658.83	4.7%
St. Dev.	0.012	0.092	35.11	0.024	432.42	5.0%

3.5. Comparison between the external volumetric and point-fiducial surrogates

As shown in table 1, the patient-specific maximum TVC and AVC are quantitatively comparable with a relative difference of ∼3%, while the five point heights have different motion ranges, depending upon anatomical locations (figures 1(A) and (B)). The dynamic curves of the TVC, the AVC and the tidal volume are similar to each other, indicated by the near-unity slope in the linear regression results (figure 2) and illustrated in the four examples (figure 3). No phase shift is observed for the TVC–AVC curves. In contrast, the dynamic curves of the thoracic and abdominal heights differ from each other, including the shape, phase and amplitude. Most of the thoracic curves show a phase shift (>1 stage), as shown in figure 4. Although the abdominal height can correlate well with the AVC, its curve can be dissimilar to the AVC curve. For instance, figure 4(A) shows a high correlation coefficient case (r = 0.973 for patient #3 in table 2) with flatter inhalation stages (stages 6, 7 and 8) in the abdominal height curve, differing from the peaked inhalation in the AVC curve. The precision of the height measurement is about 0.5 mm, limited by segmentation accuracy, manual precision, as well as minute residual motion artifacts (<1 mm) in the 4DCT due to breathing irregularity.

4. Discussion

4.1. Minimization of residual motions and motion artifacts in 4DCT imaging

The validation of the volume conservation hypothesis is primarily based on 4DCT imaging with confirmation from the spirometry measurements. So the quality of the 4DCT imaging plays an important role in determining the accuracy and reliability of the result. In summary, the following five efforts were devoted to minimize the residual motion artifacts in the 4DCT images (Lu et al 2006). These are as follows.

1. Dual surrogates (bellows and spirometer) were employed to monitor respiratory motions for higher accuracy and reliability (Mutaf et al 2007).

2. Ciné mode scanning was utilized with repetitive and redundant (25) scans in each couch position to minimize possible breathing irregularity (Pan 2005).

3. Amplitude-based retrospective binning was used to further suppress residual motion artifacts in the presence of breathing irregularity (Lu et al 2006).

4. Twelve-stage binning (versus ten) was applied to have slightly better time resolution with reduced residual motion in each stage of CT (with 1.5 mm slice thickness).

5. Patients were pre-instructed on their control of breathing regularity, which was established prior to the image acquisitions.

The amplitude-based binning with the dual surrogates can improve the reliability and accuracy of 4DCT imaging (Lu et al 2006, Mutaf et al 2007). Although there are minor residual motion artifacts due to breathing irregularity (occasionally between ciné sections in the mid abdomen) and fast motion (diaphragm), these 4DCT images provide a most reliable and accurate basis for assessing the volume conservation hypothesis.

4.2. Uncertainties in the quantitative volumetric approach

It is worthwhile to emphasize that the torso coverage should be anatomically complete since the respiration-induced motion involves tissues in both thorax and abdomen (Konno and Mead 1966); otherwise a gross underestimate of the volume change will lead to incorrect conclusion as tissues often deform out of the thoracic region. In both table 1 and figure 1, the volume and height descriptors of breathing pattern show that the maximum thoracic volume change only accounts for a fraction (0.03–0.46) of the maximum TVC (≈AVC) and the respiratory motion extends into the pelvis. By far, almost all 4DCT images reported in the literature cover only the thorax and upper abdomen (Jaffray et al 2007, Li et al 2008a), and they cannot be used to study the external–internal volumetric relationship.

The TVC and LVC obtained from segmentation are highly reproducible (< ±1 cm³). The edge-tracing algorithm is suitable to segment topologically simple anatomy, such as the torso, and the voxel-counting algorithm is utilized for calculation of the torso and lung volumes with different thresholds within the body contour. Inclusion of foreign objects in the torso contour, such as the bellows and body supports, could introduce some uncertainty (<±10 cm³) in the TVC calculation, although most of such random noises are cancelled out in calculating the volume change to a reference stage. In addition, different residual motion artifacts in the 4DCT introduce different uncertainties in the TVC and AVC calculation. In the diaphragm region, residual motion blurring introduces uncertainty to the AVC, rather than the TVC. In abdominal regions, residual motions between abutting ciné sections introduce uncertainty in TVC, but not the AVC.

The volume conservation hypothesis is validated only for quiet respiration. The negligible bowel gas pressure variation (∼3%) is consistent with experimental results (Agostoni and Rahn 1960). It is likely caused by a slight internal tension variation as the abdomen expands and contracts. For labored respiration, heavy muscular engagement can cause substantial pressure change, making the GVC a significant factor in the TVC. Hence, quiet respiration is required, consistent with the current clinical practice. After all, these above uncertainties are responsible for the non-unity slope (1.027), standard deviations (∼6%) and intercept (∼2% relative to the maximum tidal volume) as shown in table 2. This linear volumetric relationship is confirmed by cross-verification from independent spirometric tidal volume measurement. To the best of our knowledge, it is the first time that the one-to-one volumetric relationship has been established between external and internal organ motions during respiration.

4.3. Volumetric approaches versus fiducial point(s) approaches

The correlation between the respiratory phase and the height of upper abdomen or lower thorax has been intensively studied (Vedam et al 2003b, 2004, Hoisak et al 2004, Lu et al 2005a, 2005b, Chi et al 2006, Ionascu et al 2007) and widely utilized in clinical respiratory monitoring devices, such as the RPM. However, due to the diversity and complexity of breathing motions, which cause deformation in the thorax as well as the abdomen, point-fiducial-based motion monitoring systems may not provide a reliable, real-time signal for quantitative linking of external and internal motions (Chi et al 2006, Lu et al 2005b, Ionascu et al 2007, Gierga et al 2005), resulting in possible phase shifts and/or potential low correlative indications. The sensitivity of fiducial placement that was reported previously is confirmed in this study with two different positions. These two positions were selected based on the commonality of RPM placement (lower thorax and upper abdomen) in the clinic, and the continuity of the adjacent neighboring ciné sections in the 4DCT across all patients, avoiding potential residual motion artifacts. It was not our intention to simulate the RPM reflector’s motion (which is more complicated than height averaging within the 3.5 × 6.5 cm² area), but to demonstrate the location dependence of the height-based surrogates. As a matter of fact, the abdominal and thoracic heights in response to the respiratory motion are dramatically different from each other due to body deformation, as shown in both table 2 and figure 4. Although fiducial arrays were tried as an alternative, marginal improvements were demonstrated (Yan et al 2006, Baroni et al 2007). Instead, the dissimilar, complex motion patterns among the individual points due to the torso deformation (as shown in figure 1) may complicate the signal processing.

The superiority of this volumetric approach (the TVC–AVC–spirometry linearity) over the fiducial height method discussed above is consistent with previous reports on the superiority of spirometric tidal volume over the fiducial height (Hoisak et al 2004, Lu et al 2006). One or a few point fiducial(s) are fundamentally insufficient representation(s) of the deformable moving anatomy (the torso). In contrast, the volume-to-volume (1-to-1) relationship is quantitatively predictable and patient independent, whereas the height-to-volume (X-to-αX) correlation is empirical and patient specific. The linear coefficient (α) could be obtained through a patient-based calibration. This volumetric approach also provides an advantage over spirometry, which is inconvenient, demands frequent calibration and requires baseline drift correction (Lu et al 2006, Ha et al 2008).

4.4. A potential volumetric respiratory surrogate

The physiological process of respiration involves tidal volume change due to airflow into and out of the lungs, driven by minute intrapulmonary pressure variations from the ambient atmospheric pressure. As shown in this study, the one-to-one relationship is validated using the TVC, AVC and spirometric tidal volume. The external–internal linear volumetric relationship is naturally one of the most direct and most straightforward assessments of respiratory process.

In order to apply this predictable volumetric relationship to establish a clinically useful respiratory surrogate, we are investigating the use of a commercially available optical surface imaging system to acquire the external torso volume during respiration to replace the use of 4DCT imaging and spirometry. Such optical camera systems have been reportedly used for image-guided patient setup based on surface matching (Djajaputra and Li 2005, Bert et al 2006). The surface imaging resolution could reach 1280 × 1024 pixels with a speed of up to 15 Hz (Schoffel et al 2007). As the technology advances, the spatial and temporal resolutions of the surface imaging could soon become comparable to or even exceed those of 4DCT imaging in the coming years. On the other hand, computational techniques for real-time volumetric analysis of 3D multimodality images are available (Li et al 2005, 2008b). Although the implementation of the volumetric respiratory surrogate based on this fundamental study remains to be seen in the future, it is considered to be both desirable and feasible. Such a potential respiratory surrogate can provide more reliable guidance to 4DCT as well as 4DRT without ionizing radiation.

5. Conclusion

This study proposes and validates the volume conservation hypothesis within human torso during respiration. It demonstrates a new, one-to-one relationship between the volume changes of the external torso and the internal lung air content (the tidal volume). Based on this quantitative volumetric relationship, a potential torso respiratory surrogate could be implemented to provide accurate and reliable guidance for 4DCT imaging as well as 4DRT treatment.