Abstract
The measurement and simulation of water vapor isotopic composition has matured rapidly over the last decade, with long-term datasets and comprehensive modeling capabilities now available. Theories for water vapor isotopic composition have been developed by extending the theories that have been used for the isotopic composition of precipitation to include a more nuanced understanding of evaporation, large-scale mixing, deep convection, and kinetic fractionation. The technologies for in-situ and remote sensing measurements of water vapor isotopic composition have developed especially rapidly over the last decade, with discrete water vapor sampling methods, based on mass spectroscopy, giving way to laser spectroscopic methods and satellite- and ground-based infrared absorption techniques. The simulation of water vapor isotopic composition has evolved from General Circulation Model (GCM) methods for simulating precipitation isotopic composition to sophisticated isotope-enabled microphysics schemes using higher-order moments for water- and ice-size distributions. The incorporation of isotopes into GCMs has enabled more detailed diagnostics of the water cycle and has led to improvements in its simulation. The combination of improved measurement and modeling of water vapor isotopic composition opens the door to new advances in our understanding of the atmospheric water cycle, in processes ranging from the marine boundary layer, through deep convection and tropospheric mixing, and into the water cycle of the stratosphere. Finally, studies of the processes governing modern water vapor isotopic composition provide an improved framework for the interpretation of paleoclimate proxy records of the hydrological cycle.
1. Introduction
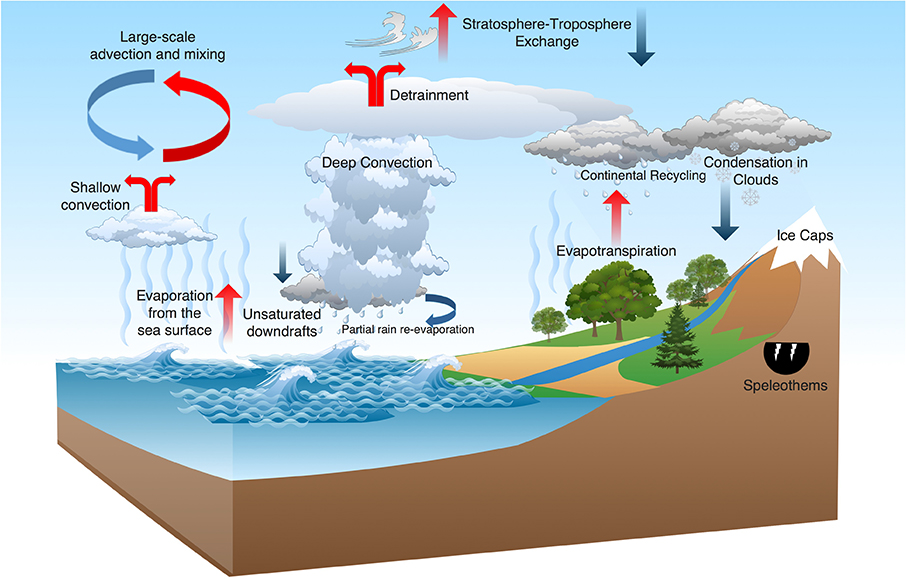
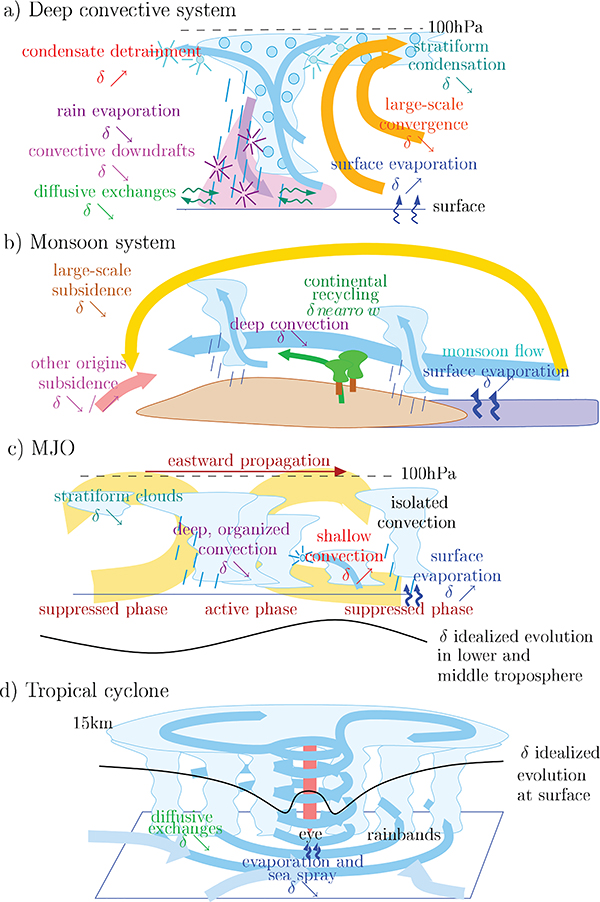
Stable isotopes have been used in hydrology since the late 1950s and early 1960s, beginning with the pioneering studies of Dansgaard [1954, 1964] and others. Until recently, such studies were restricted primarily to investigations of the isotopic composition of precipitation, which integrates the history of the atmospheric hydrologic cycle from evaporation to surface precipitation. Studies of the isotopic composition of atmospheric water vapor can provide unique constraints on how water is transported, mixed, and changes phase in the atmosphere and are thus a useful tool in the study of the Earth’s hydrologic cycle, and for improved understanding of paleoclimate proxies (Figure 1).
Figure 1.
Cartoon illustrating key processes governing the isotopic composition of atmospheric water vapor. Blue arrows indicate processes that tend to isotopically deplete water vapor and red arrows indicate processes that tend to isotopically enrich water vapor. The paleoclimate archives in glacial ice and in speleothems are also influenced by these processes, which are discussed in detail in Section 6.
In the last several years, there has been a tremendous expansion in the number of datasets of water vapor isotopic composition and a substantially improved set of theories and models for interpreting them. Studies of atmospheric water vapor isotopic composition can provide first-order constraints on the modern atmospheric hydrological cycle by constraining the relative roles of phase changes, transport, and mixing in ways that are difficult with measurements of water vapor mixing ratio alone. These studies can also inform paleoclimate interpretations from proxy records by improving our understanding of the whole suite of atmospheric processes that govern the isotopic composition of precipitation that is recorded in such proxies. Comparisons between observations and numerical models of water vapor isotopic composition can lead to improved interpretations of the governing hydrological processes, and can also help diagnose deficiencies within the models themselves.
The earliest studies of water vapor isotopic composition relied on cryogenic and mass spectrometric techniques, which dominated the field until the mid-1990s, when the first space-based measurements were obtained with the Atmospheric Trace Molecule Spectroscopy (ATMOS) instrument which flew aboard the space shuttle in 1994 [Gunson et al., 1996]. This was followed by the advent of laser absorption spectroscopic techniques [e.g.,, Scherer et al., 1997] in the 1990s. General circulation models with isotope-enabled microphysics schemes first became available in the 1980s, with more widespread use beginning in the 1990s [e.g., Joussaume et al., 1984a; Hoffmann et al., 1998].
Many of the major advances in the field have occurred within the last decade, which is part of the motivation for the present review. In the mid-2000s, relatively low-cost commercial laser absorption spectrometers became available [e.g.,, Baer et al., 2002; Crosson et al., 2002], along with nearly global satellite measurements of water vapor isotopic composition [e.g., Worden et al., 2006; Frankenberg et al., 2009] and ground-based remote sensing data using spectra measured within global networks [Schneider et al., 2012; Rokotyan et al., 2014]. The increased capacity to measure water vapor isotopic composition has spawned dozens of observational studies, many of which are discussed below, [e.g. Worden et al., 2007; Noone et al., 2011; Steen-Larsen et al., 2013; Galewsky et al., 2011; González et al., 2016]. Concurrently, there have been significant advances in the numerical modeling of stable water isotopologues through increased use of isotope-enabled general circulation [e.g., Schmidt et al., 2005; Risi et al., 2012a; Sturm et al., 2010] and limited-area [Sturm et al., 2005; Smith et al., 2006; Blossey et al., 2010] models.
To date, review papers of stable isotopes in hydrology have focused primarily on precipitation and were written before the recent expansion of studies in water vapor isotopic composition [e.g., Gat, 1996]; furthermore, studies of stable isotopes in atmospheric water vapor have remained mostly separate from work on, for example, the distribution [Pierrehumbert et al., 2006], or role [Held and Soden, 2000; Schneider et al., 2010] of water vapor itself in the climate system. The goal of this review paper is thus to collect and synthesize the state-of-the-art in our understanding of atmospheric water vapor isotopic composition, including measurement methods, modeling techniques, interpretive frameworks, and applications to the atmospheric hydrologic cycle.
The paper is organized as follows: Section 2 provides background material on stable isotopologues of water, including isotopic fractionation, Rayleigh distillation, mixing and techniques for visualizing water vapor isotopic composition. Section 3 describes techniques for measuring water vapor isotopic composition, including mass spectrometric, cavity-enhanced, and remote sensing approaches. Section 4 provides an overview of water vapor isotopic composition in the troposphere, focusing on in situ and remote sensing datasets, and on the so-called amount and temperature effects. Section 5 presents an overview of techniques for modeling water vapor isotopic composition, including global, regional and idealized models as well as Lagrangian approaches. Section 6 discusses the applications of water vapor isotopic measurements and simulations to understanding atmospheric processes in the modern and past climate system. In section 7, we present some perspectives and opportunities in the field and present some potential future research directions.
2. Theory and interpretive frameworks
2.1. Abundance of natural isotopologues of water and δ notation
There are two naturally-occurring stable isotopes of hydrogen (1H and 2H, or D) and three naturally-occurring stable isotopes of oxygen (16O;17 O;18 O), with the lightest isotope of each element being the most abundant. Molecules composed of different combinations of isotopes are called isotopologues. Of the nine possible isotopologues of water, is the most common (99.73098%), with , , and HD16O, and existing in much smaller, but still measurable quantities (0.199978%, 0.037888%, and 0.031460%, respectively) [Sharp, 2006].
Isotopic quantities are expressed as a ratio (R) of concentrations of the heavy, rare isotope to the abundant, light isotope. The stable isotopic composition of water is further expressed relative to the International Atomic Energy Agency (IAEA) Vienna Standard Mean Ocean Water (VSMOW) standard, which for the two main rare isotopes are D/H = 155.95 × 10−6 and 18O/16O = 2005.2 × 10−6, respectively [Araguás-Araguás et al., 2000; Sharp, 2006]. The oxygen isotope composition of a sample Rsamp, for example, is expressed using δ-notation in units of permil (%o), as:
| (1) |
Samples with lower, more negative δ18O or δD values have fewer of the heavy isotopes, and are sometimes referred to as being ‘more depleted’ in the heavy isotope. Samples with higher, less negative δ values are sometimes referred to as being ‘more enriched’ in the heavy isotope, although the term ‘less depleted’ is also used. One may also refer to δ values as being higher or lower rather than ‘enriched’ or ‘depleted’ in heavy isotopes.
δD and δ18O in meteoric waters vary nearly linearly and can be fit to the equation δD = 8 × δ18O+ d-excess [Craig, 1961] where d-excess is the deuterium-excess parameter [Dansgaard, 1964]. In precipitation, d-excess results from different evaporation rates for the different isotopologues of water [Dansgaard, 1964]. Globally, the average d-excess in meteoric water is 10%o [Craig, 1961]. Deviations from the slope of 8 and d-excess of 10%o provide important information about non-equilibrium processes involved in evapotranspiration, moisture transport and precipitation. The interpretation of d-excess in water vapor will be discussed in detail below.
Recently, measurements of the triple isotope composition of oxygen (17O/16O and 18O/16O) have been obtained in meteoric waters [e.g., Landais et al., 2006] and, even more recently, in marine boundary layer water vapor [Uemura et al., 2010]. Barkan and Luz [2007] defined the 17O-excess (also referred to as the Δ17O anomaly) to be:
| (2) |
where δ′ is a modified delta notation, where, for example, δ18O = ln(δ 8O + 1), and is defined analagously for 17O. Because the magnitude of the Δ17O is very small, it is typically multiplied by 106 and is reported in per meg rather than per mil with respect to VSMOW.
2.2. Isotopic fractionation
Evaporation and condensation are mass-dependent processes, which influences how different isotopologues of a substance change phase. In a liquid, water molecules with heavy oxygen or hydrogen isotopes will have greater binding energies and lower diffusive velocities, which causes them to evaporate less readily than the light isotopologue. As a result, when evaporation takes place, the resulting vapor has fewer, by proportion, of the heavy isotopes than the reservoir and a lower isotopic ratio, Rv. Conversely, the isotopic ratio Rl of the (liquid) reservoir will increase due to the preferential evaporation of the light isotopologues. When net condensation occurs from a vapor reservoir, there is a preferential transfer of the heavy isotopologue to the condensate, resulting in fewer of the heavy isotopologue in the vapor and more of the heavy isotopologues in the condensate. This separation of different isotopologues during phase changes is called fractionation. The isotopic composition of water in the atmosphere is determined by the fractionation that occurs at all stages of the hydrological cycle.
The extent of fractionation that takes place during evaporation from liquid to vapor is expressed as the fractionation factor :
| (3) |
where Rl is the isotopic ratio of the liquid, and Rv the isotopic ratio of the vapor in equilibrium with the liquid. Under equilibrium conditions, the fractionation factor for vapor condensing to liquid is simply the inverse of that for liquid to vapor:
| (4) |
The distinction must be made between time-independent, equilibrium fractionation in a closed system and time-dependent kinetic fractionation in an open system, especially for evaporation into an unsaturated, ventilated environment, ice deposition under supersaturated conditions, and for re-evaporation of condensate into unsaturated air. The theory of kinetic fractionation is an active research area [Casado et al., 2016], but here we summarize some of the most important kinetic effects.
The isotopic composition of water evaporated from oceans or lakes is an essential part of our understanding of water vapor isotopic composition and is governed by kinetic effects. Craig and Gordon [1965] developed the first comprehensive model of the isotopic composition of evaporation, and Horita et al. [2008] provide a recent summary. The isotopic composition Re of vapor evaporated from open water depends on the isotopic composition of the liquid water reservoir, the isotopic composition of water vapor in the free atmosphere, the relative humidity, the equilibrium fractionation factor and a kinetic fraction factor reflecting the ratio of diffusivities of the heavy and light isotopes. Knowledge of these processes can also be used to interpret d-excess measurements and make inferences about source conditions.
Condensate falling through unsaturated air in a convective downdraft or below cloud-base can partially or fully evaporate. Fractionation will occur, with the evaporate containing less of the heavy isotope, similar to what occurs during evaporation from the ocean. The effective fractionation factor includes equilibrium and kinetic effects that depend on the relative humidity and the different diffusivities of the heavy and light isotope.
When water vapor is deposited onto ice crystals, there is a kinetic effect due to the lower diffusivity of the heavy isotopes. This effect is present only during supersaturation (i.e. when the relative humidity exceeds 100%) [Jouzel and Merlivat, 1984], which is negligible above 0°C [Jouzel et al., 1987].
Representative descriptions of how equilibrium and kinetic processes are approximated in atmospheric applications are given by Gedzelman and Arnold [1994] and Hoffmann et al. [1998]. An example of a more detailed, modern treatment for more explicit cloud microphysics is presented in Blossey et al. [2010].
2.3. Rayleigh Distillation
The progressive effects of fractionation on the isotopic composition of water in the atmosphere is best understood in an idealized sense using the Rayleigh model of isotopic depletion of Dansgaard [1964]. Along the path of an idealized, precipitating air parcel in which condensate is removed as soon as it forms, the ratio Rr of heavy to light isotope in the vapor reservoir is described by:
| (5) |
where Rr is the isotopic ratio of the vapor, α(T) is the temperature-dependent fractionation factor between phases, and q is the water vapor mixing ratio. This equation can be integrated from initial conditions for Rr and q [Gat, 1996] to obtain:
| (6) |
where Ro is the initial isotopic ratio of the vapor and f is the fraction of original vapor remaining.
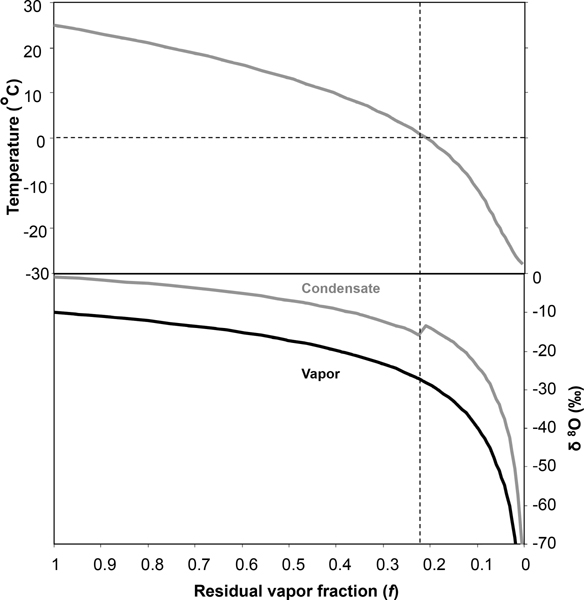
Rayleigh distillation is arguably the most important framework for interpreting isotopes in the atmospheric water cycle. Figure 2 shows the idealized Rayleigh depletion of a cooling, precipitating moisture mass with an initial vapor composition of δ18O = −10%o, typical of fresh evaporate from the ocean. When condensate forms as liquid from the vapor reservoir, there is about a 10 enrichment that occurs as a result of the heavy isotope condensing preferentially, indicated by the difference between the black (vapor) and grey (condensate) curves. As rainout occurs with decreasing f, this preferential removal leads to a progressive depletion of heavy isotopes in the vapor and also the condensate forming from it. When the precipitation changes from rainfall to snow at T = 0°C, the fractionation factor increases, resulting in a further offset between vapor and condensate. Over the remaining moisture loss from snowfall, the increase in fractionation factor results in more rapid depletion of the vapor reservoir and of subsequent condensate. In its simplest form, the Rayleigh distillation model is based on the assumption that condensate is irreversibly removed from the cloud as soon as it is formed. Jouzel [1986] and Noone [2012] describe how the basic concept can be extended to other cases, such as the retention of some condensate in the cloud (corresponding to small cloud droplets), below cloud-base isotopic exchange and recycling, and mixing between air masses.
Figure 2.
Isotopic composition of a precipitating air mass with vapor depleting according to the Rayleigh model with an initial vapor composition of −10 %o at T = 25°C, following Clark and Fritz [1997]. The dashed lines indicate the transition from rain to snow.
2.4. Mixing
If two air parcels mix, the resulting parcel will be less depleted in heavy isotopes than would be expected from a parcel at the same mixing ratio subject to Rayleigh distillation alone [Galewsky and Hurley, 2010]. The mixing ratio, q, of the mixed parcel is the weighted average of the mixing ratio of the two parcels:
| (7) |
where f is the mixing fraction. The δ value of the mixed parcel is not a simple weighted fraction of the two parcels, though, because the resulting ratio of heavy to light isotopic abundance Rmix is given by:
| (8) |
2.5. q — δ diagrams
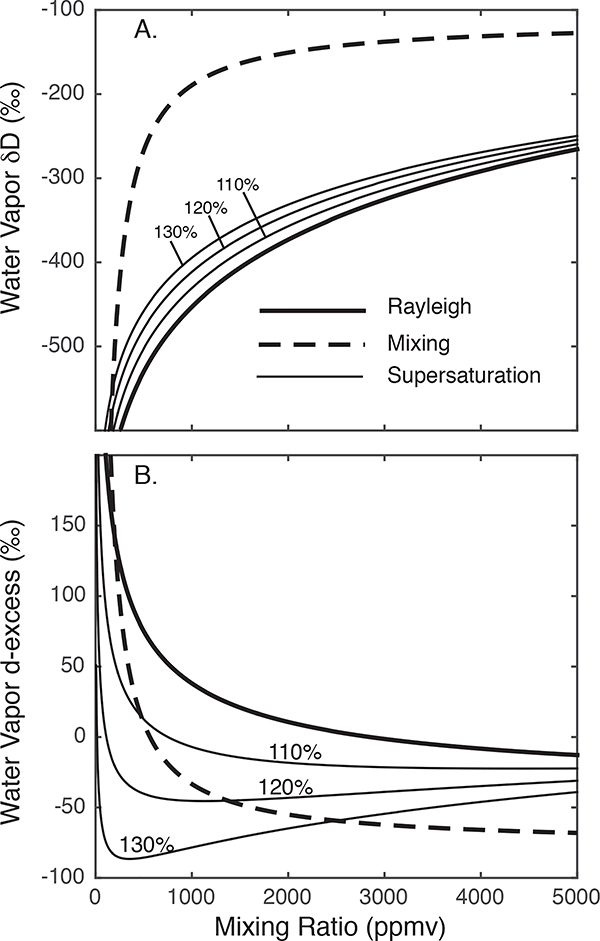
The relationships between water vapor mixing ratio and its isotopic composition can be visualized on a q — δ diagram. Such diagrams serve as the foundation of many studies of measurements of water vapor isotopic composition [e.g., Worden et al., 2007; Noone, 2012; Samuels-Crow et al., 2014a]. Figure 3 shows the relationships between Rayleigh distillation, mixing, and condensation under ice supersaturation for water vapor δD and d-excess, plotted as a function of the water vapor mixing ratio in ppmv. The mixing ratio can be expressed in different units, such as g/kg or mmol/mol, but the basic relationships remain the same.
Figure 3.
Example of a q — δ plot for interpreting water vapor isotopic data. Idealized relationships between Rayleigh distillation (heavy solid line), condensation under ice supersaturation (light solid lines; RHi indicated in percent), and mixing (dashed lines) for (A) water vapor δD and (B) water vapor d-excess, as a function of water vapor mixing ratio (ppmv).
Within this framework, the Rayleigh curve can be considered a reference process. Mixing yields water vapor δ values that are higher than expected for Rayleigh distillation [Galewsky and Hurley, 2010] and d-excess values that are lower than expected for Rayleigh distillation. Vapor deposition under ice supersaturation can also yield δ values that are higher than expected for Rayleigh distillation, leading to an important non-uniqueness in the interpretation of water vapor isotopic composition [e.g., Galewsky et al., 2011; Samuels-Crow et al., 2014a].
Subcloud remoistening associated with partial evaporation of condensate and the so-called isotope amount effect (see below) can yield δ values that are lower than expected for Rayleigh distillation and thus lie below the Rayleigh curve on a q — δ diagram [e.g., Noone, 2012]. This relationship has been used to diagnose the role of convective processes in setting the humidity upstream in remote-sensing [Samuels-Crow et al., 2014b] and in-situ [Galewsky and Samuels-Crow, 2015] datasets.
3. Techniques of measurement
3.1. Discrete water vapor sampling techniques
Dansgaard [1954] presented one of the first atmospheric water vapor isotopic records, which was compared to climate parameters. He collected water vapor by pumping atmospheric air through a glass trap submerged in a mixture of dry ice and alcohol thereby freezing out the majority of the water vapor without fractionation. This technique has since been used extensively to sample marine boundary layer water vapor [Craig and Gordon, 1965], and also in very dry regions like the Tibetan plateau [Yu et al., 2015] and on top of the Greenland Ice Sheet [Grootes and Stuiver, 1997; Steen-Larsen et al., 2011]. Different types of cryogenic sampling devices and protocols have been developed [Uemura et al., 2008; Helliker et al., 2002; Ehhalt, 1971]. Franz and Röckmann [2005] developed a specific sampler and protocol to collect stratospheric water vapor, which exists in only very small mixing ratios (< 10 ppm).
Water vapor isotopic composition has also been measured directly from air samples collected in flasks evacuated prior to sampling [Strong et al., 2007]. Since the sampling time is normally less than one second, this method allows one to make an instantaneous water vapor isotope measurement, which is useful for aircraft or gradient measurements. Han et al. [2006] presented a water vapor trap, which used a molecular sieve instead of cryogenically collecting the vapor in the field. However, in order to measure the sample using isotope-ratio mass spectrometry (IRMS), the collected water vapor had to be released and then cryogenically collected in the laboratory.
Combined precision and accuracy (1 standard deviation) for cryogenically sampled water vapor is in general 0.2 %o for δ18O and 1.5 %o for δD [Helliker et al., 2002], while for flask samples it is 0.2–0.3%o for δl8O and 2%o for δD [Strong et al., 2007]. Tests comparing samples using a cryogenic trap and a molecular sieve trap showed mean differences of 0.3 +/− 0.2 %o for δl8O and 2.6 +/− 1.5%o for δl8O [Han et al., 2006]. The uncertainty of water vapor samples collected in the stratosphere was determined to be 2–3 %o on δ18O but owing to the correlation between noise on the δ18O and δl7O, the 17O-excess precision was determined to be between 30 and 200 per meg [Franz and Röckmann, 2005].
3.2. Cavity enhanced spectroscopy
Some of the first water vapor isotope measurements using commercially-available cavity-enhanced spectroscopic techniques were carried out using a Cambell Scientific TDL trace gas analyzer [Lee et al., 2005]. In recent years, two commercial water vapor isotope analyzers have dominated the literature: Picarro CRDS (cavity ring down spectroscopy)-analyzers and Los Gatos Research Inc. ICOS (integrated cavity output spectroscopy)-analyzers. Common to both of these two types of analyzers is the use of cavity-enhanced, near-infrared laser absorption spectroscopy (CEAS) techniques. The analyzer produced by Picarro Inc. is based on cavity-ring-down-spectroscopy [Crosson et al., 2002] which uses time-based measurements of the exponential decay of light resonating in the optical cavity to quantify the optical loss at different optical wavelengths across a molecular absorption feature. The Los Gatos Inc. analyzer uses off-axis integrated-cavity-output spectroscopy [Baer et al., 2002], which is based on measurement of the transmitted intensity through the cavity, and typically averages several hundred continuous sweeps per second through a molecular absorption feature. After each sweep, a ring-down measurement is made to verify the baseline absorption. Both techniques use the Beer-Lambert law to calculate the concentrations of each species, with key differences being that CRDS allows smaller cavity volumes due to its on-axis beam geometry while ICOS offers much faster scan speeds and wider dynamical ranges. Measurement uncertainties of field-based measurements have been estimated by comparing discrete flask-based measurements with simultaneous measurements from the water vapor isotope analyzer [Johnson et al., 2011], and, more recently, by directly comparing observations carried out by two independently calibrated water vapor isotope analyzers. The latter approach has shown that using 10 min average data, the uncertainty of 0.23%o in δ18O, 2.4%o in δD, and 3%o in d-excess was achieved for humidity ranges between 1500–4000 ppmv [Steen-Larsen et al., 2013] while much improved uncertainty was achieved for measurements in the subtropical North Atlantic of 0.14%o in δ18O, 0.85%o in δD, and 1.1 %o in d-excess for humidity ranges between 20,000–30,000 ppmv [Steen-Larsen et al., 2014a]. An approach has been outlined for estimating the combined uncertainties from each of the steps of the calibration routine and by the measurements themselves by Bailey et al. [2015a].
Custom made water vapor isotope spectral analyzers have been deployed on aircraft to measure the upper troposphere and lower stratosphere e.g., [Sayres et al., 2009; St Clair et al., 2008; Kerstel et al., 2006; Hanisco et al., 2007; Dyroff et al., 2010]. The uncertainty of these instruments at the low water vapor concentrations found in the lower stratosphere down to 5 ppmv have been determined for 4 s averages to be 30%o for δ18O and 50%o for δD [Sayres et al., 2009] and at 200 ppmv for 30 s averages to be 1%o for δ18O and 9%o for δD [Kerstel et al., 2006]. A custom made water vapor isotope analyzer was recently developed with the aim of being able to study fractionation processes at low temperatures [Landsberg et al., 2014]. To meet this goal, the analyzer was developed to optimize precision and stability at low humidity concentration. Precision levels for δ18O and δD between 20–600 ppmv was found to be between 4.4 — 0.18%o for δ18O and 54 — 1.7%o for δD for 4 s averages but between 0.5 — 0.02%o for δ18O and 5 — 0.5%o for δD for 30–70 minute averaging time, depending on the optimal integration time of a given humidity level.
3.2.1. Instrumental setup
In general, an atmospheric water vapor isotope monitoring system consists of 4 parts: An inlet, which prevents rain and insects from being drawn into the system; a tube connecting the inlet with the analyzer consisting of a material that does not create fractionation by interacting with the water vapor molecules (materials such as copper, stainless steel, PFA, and PTFE have been used in previous studies) and which is heated well above the dew-point temperature of that atmospheric air in order to prevent condensation in the line; a calibration unit, which is able to generate a constant stream of water vapor with a known isotopic composition at different humidity levels; and a commercial or custom-made water vapor isotope analyzer. An extra pump connected to the inlet tubing is often installed to ensure a quick transport from inlet to analyzer. Steen-Larsen et al. [2014a] characterized the damping of the atmospheric water vapor isotope signal in the complete system from inlet to analyzer caused by mixing and interaction with the inside of the tube walls. This showed that 95% of a normalized response would be achieved after 10 min for δ18O and 20 min for δD and a signal with a periodicity of 100 s would be dampened by 98.5% for δ18O and 99.7% for δD, effectively removing all high frequency signal. It is therefore important to notice that without placing special attention on the attenuation of the signal it is not possible to report data resolution on the order of minutes. Furthermore, due to the attenuation difference between δ18O and δD, an artificial measured d-excess signal is likely to occur during fast changes in the atmospheric water vapor isotopic composition for example occurring immediately before and during rain events or when carrying out aircraft measurements in isotopically varying conditions. To improve data resolution two aspects have to be improved: The analyzer itself and the part of the inlet system bringing the ambient air to the analyzer. To change the data resolution of a commercial analyzer, the simplest approach is to change the flow-rate through the cavity. This approach has been used when limited air samples are available [Stowasser et al., 2012]. To minimize the damping of the ambient signal by the inlet tubing, the ratio between the inside surface area and the airflow volume should be minimized. Special attention should be place on minimizing the length of tubing between the main inlet line and the analyzer itself.
3.2.2. Calibration systems
The commercial water vapor isotope analyzers from respectively Picarro Inc. and Los Gatos Research Inc. both have their own calibration unit: the Standards Delivery Modules (SDM) and the Water Vapor Isotope Standard Source (WVISS). The SDM uses a syringe system to push a constant amount of liquid water into a vaporizer, which produces a stream of water vapor with constant isotopic composition. The syringe system is connected to two collapsible aluminum bags, which allow one to perform calibrations with two distinct isotope standards without the risk of evaporation and fractionation. Dry air from either a tank of compressed dry air or air pushed through a container of a desiccant transports the vapor into the analyzer cavity. The WVISS system uses a nebulizer to push water into a hot chamber where the small droplets evaporate completely without fractionation. A built-in compressor and regenerating drying system generates dry air, which transports the water vapor into the analyzer. The isotopic composition of the vapor can be changed manually by simply changing the standard bottle. Both of these systems suffer from the lack of ability to run autonomously for periods of several months. Changes have therefore been made to the SDM system e.g. [Bastrikov and Steen-Larsen, 2014] and custom calibration systems have been developed e.g. [Steen-Larsen et al., 2014a; Bailey et al., 2015a].
3.2.3. Calibration protocols
The reader is referred to Bailey et al. [2015a] for a comprehensive review of calibration protocols and techniques. We briefly summarize the necessary steps needed in order to calibrate the water vapor isotope measurements against the international VSMOW-SLAP scale. The protocol is identical irrespective of the instrument used and is based on the approach used to calibrate IRMS measurements. Four steps are needed:
1. Humidity-induced bias
All measurements must be corrected for instrumental humidity-induced bias in the measured isotopes. The humidity-isotope-response or concentration-dependence must be determined before and at frequent intervals throughout a measurement campaign. The humidity-isotope-response/concentration-dependence is instrument-dependent and might not be stable in time [Bailey et al., 2015a; Steen-Larsen et al., 2014a]. The humidity-isotope-response/concentration-dependence is estimated by generating a stream of water vapor with constant isotopic composition, which is then diluted by different amounts of dry air [Lee et al., 2005; Rambo et al., 2011; Schmidt et al., 2010]. Bastrikov and Steen-Larsen [2014] illustrated the influence of using air dried with Drierite as a desiccant, which does not result in completely dry air (down to about 150 ppmv), compared to dry air from a compressed air bottle. Johnson et al. [2011] used a bubbler apparatus with an open-split configuration and dry nitrogen gas as a carrier and were able to obtain reliable gas streams down to about 100 ppmv. Caution should be taken when the humidity from the dry air source constitute more than 10 — 20% of the measured humidity.
2. VSMOW-SLAP Calibration
After correcting all the measurements for the humidity-induced bias, the measurements must be calibrated against the international VSMOW-SLAP scale. Measuring multiple standards of known isotopic composition with isotopic values that span the range of the measurements allows one to establish the instrumental VSMOW-SLAP scale. The correction is instrument dependent and some degree of long-term variation has been observed [Bastrikov and Steen-Larsen, 2014; Steen-Larsen et al., 2014a]. Linear drift in the VSMOW-SLAP slope has been assumed in previous work. It is essential that multiple standards be used in order to generate the necessary calibrations [Sharp et al., 2001].
3. Drift Correction
The measurements are drift-corrected by comparing the measured values of the standards through time with the true value of the standards. Depending on the magnitude of the drift, the measurements can either be corrected by assuming a linear drift between standard measurements, or by accounting for uncertainty in the measurements of the drift by fitting the measured drift to a polynomial or using a running mean value.
4. Humidity Calibration
The measured water vapor mixing ratio should be calibrated either against atmospheric humidity measurements from a local meteorological station or by using a calibrated dew-point generator. No drift in the measured water vapor mixing ratio calibration has been reported. Some early models of the Picarro L-2130i reported a 23% moist bias in mixing ratio measurements [Samuels-Crow et al., 2014a] that has been corrected in later versions of that model but should still be verified for each instrument.
3.3. Aircraft-based in-situ measurements
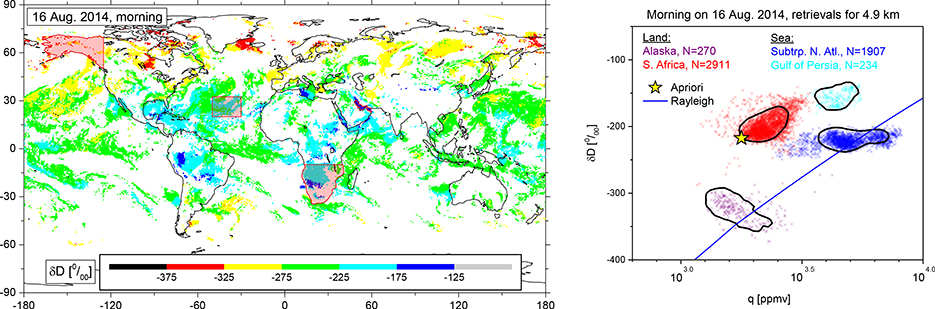
In situ airborne measurements have been performed with different techniques and on various platforms [Taylor, 1972; Ehhalt, 1973; Ehhalt et al., 2005; Webster and Heymsfield, 2003; Sayres et al., 2009; Iannone et al., 2009]. Even FTIR (Fourier-Transfrom InfraRed) spectrometers have been deployed on high-altitude research balloons [Notholt et al., 2010] and on aircraft [Coffey et al., 2006; Hanisco et al., 2007] for studies of water vapor in the stratosphere. Recently, Herman et al. [2014] and Dyroff et al. [2015] made the first lower and middle tropospheric observations at high vertical resolution and with inflight instrument-performance analyses by measuring a calibration-gas standard.
While Herman et al. [2014] worked with a commercially available Picarro L1115-i isotopic water analyzer, the observations of Dyroff et al. [2015] were made with the ISOWAT-II instrument [Dyroff et al., 2010], which has been developed for aircraft-based observations. The left panel of Fig. 6 shows vertical δD profiles measured by ISOWAT-II in the Northern Atlantic subtropics during two consecutive days in August 2013 (they represent two examples of the seven profiles measured during the summer 2013 MUSICA campaign; Dyroff et al. [2015]). The high vertical and temporal variability of δD in the lower and middle troposphere becomes clearly evident. In order to detect this high variability, aircraft instruments should be able to provide high quality data at high temporal resolution and for very different humidity conditions and air temperatures.
Figure 6.
Example of vertical distribution of tropospheric δD measured on two consecutive days in coincidence by three different techniques. Day 24th of August can be identified by red and day 25th of August by green color. Dashed black line with yellow stars is the apriori used by the remote sensing retrievals. Left: In-situ measurements by ISOWAT from aircraft; Middle: Circles and error bars represent MUSICA NDACC/FTIR remote sensing observations and their uncertainty, colored dashed line and shaded area represent the in-situ references and their confidence range after considering the vertical resolution and sensitivity of the FTIR retrievals; Right: same as before, but for the MUSICA MetOp/IASI remote sensing observations. For more details please refer to Dyroff et al. [2015] and Schneider et al. [2016].
Since 2010, the predecessor instrument, ISOWAT-I, has been employed aboard the CARIBIC passenger aircraft, an Airbus A340–600 by Lufthansa [Brenninkmeijer et al., 2007]. δD has been measured in the upper troposphere during 60 long-distance CARIBIC flights. A modified ISOWAT-II instrument will be deployed as of 2017 for four consecutive flights per month to also accurately sample the tropospheric profiles of vapor isotopologues (A. Zahn, personal communication, 2016).
3.4. Remote sensing
3.4.1. Overview
Continuous and/or global observations can be best achieved by remote sensing techniques; however, it is important for users to understand the nature of this kind of data. Remotely sensed measurements of water vapor and its isotopologues (or other atmospheric trace gases) are inferred by how these molecules spectrally affect light as it is transferred from a source (e.g., the Sun or the Earth), through the atmosphere, to a detector. The remote sensing retrieval calculates the atmospheric water vapor isotopologue state from the measured radiances, which is generally an ill-posed problem because many different atmospheric water vapor isotopologue states can explain a given measurement. In this sense the remote sensing data product should be understood as a statistical interpretation of the measured radiances and it is generally dependent on the assumptions needed for performing the interpretation.
Consequently, the use of satellite or ground based remotely sensed measurements of water vapor isotopic composition to investigate different components of the global water cycle depends on the viewing geometry, photon source, and instrument characteristics as well as on the retrieval setup (i.e., the assumptions made for interpreting the measured radiances).
Space based measurements of water vapor isotopic composition were first demonstrated with the Atmospheric Trace Molecule Spectroscopy (ATMOS) instrument which flew aboard the space shuttle in 1994 [Gunson et al., 1996]. The ATMOS instruments views the Sun through different levels of the upper troposphere and stratosphere to build a profile of trace gases. Measurements of HDO/H2O in the upper troposphere and lower stratosphere were used to reject the hypothesis that gradual dehydration is primarily responsible for the distribution of water vapor in the tropical lower-most stratosphere [Kuang et al., 2003] and support the hypothesis that convective uplift brings water into the stratosphere. The isotopic composition of the upper troposphere, stratosphere and mesosphere has also been retrieved from other space based limb sounders, like measurements from the SciSat Atmospheric Chemistry Experiment (ACE) [e.g., Nassar et al., 2007] and the Envisat Michelson Interferometer for Passive Atmospheric Sounding (MIPAS) [e.g., Payne et al., 2007; Steinwagner et al., 2007].
Zakharov et al. [2004] first demonstrated the potential for quantifying the global distribution of tropospheric water vapor isotopic composition using thermal infrared measurements; however, the use of remotely sensed measurements for investigating the global tropospheric water cycle greatly accelerated with downward looking (nadir) global satellite measurements based on thermal IR radiances [Worden et al., 2006, 2007] from the Aura Tropospheric Emission Spectrometer (TES) and reflected sunlight measurements from the Envisat Scanning Imaging Absorption Spectometer for Atmospheric Chartography (SCIAMACHY) instrument in the near-IR [Frankenberg et al., 2009]. For example, Worden et al. [2007] provided estimates on the effects of mixing and rainfall evaporation on the tropical water cycle while [Frankenberg et al., 2009] looked at the role of large scale dynamical effects on the subtropical water vapor distribution. Herbin et al. [2009] presented independent retrievals for the two water vapor isotopologues and HDO using the Infrared Atmospheric Sounding Interferometer (IASI) aboard the operational meteorological satellite MetOp. Optimal water vapor and isotopologue ratio retrievals ( and ) using MetOp/IASI were reported by Schneider and Hase [2011] and Lacour et al. [2012].
In addition, solar absorption spectra measured by ground-based high resolution Fourier transform spectrometers allow retrievals of the tropospheric water vapor isotopologue composition [e.g., Schneider et al., 2006a, 2012].
3.4.2. Retrieval techniques
Estimates of the distribution of HDO and H2O are typically derived from radiances using a non-linear estimation approach that minimizes the differences between an observed radiance and that from a radiation transfer model. Here we focus on techniques that allow detecting the lower and middle tropospheric water vapor isotopologues and we do not discuss retrievals for upper troposphere, the stratosphere and the mesosphere, which is possible by using limb sounders like MIPAS, ACE, or ATMOS. For a detailed description of the limb sounding retrievals we refer to the literature [Kuang et al., 2003; Nassar et al., 2007; Payne et al., 2007; Steinwagner et al., 2007; Lossow et al., 2011].
Remote sensing of HDO and H2O in the middle troposphere is typically an ill-posed problem, meaning that there are more parameters estimated than information in the radiances. For example, a retrieval might estimate more than 10 vertical levels for HDO and H2O because we know a priori that we need at least that many parameters to fit their logarithmic variation with altitude. However, the radiances may only have enough information to resolve either the total atmospheric column or two large layers. For these reasons some form of regularization is needed for each estimate.
If the non-linear estimation approach used to minimize the difference between the observed radiance and a forward model of that radiance converges to a global minimum, then the estimated quantity (typically a profile of a trace gas) may be related to the true distribution of that quantity and corresponding uncertainties associated with the measurement in the following manner [Rodgers, 2000]:
| (9) |
where , xa, and x are the retrieved (or estimated), a priori, and the ‘true’ state vectors respectively and represent the altitude distribution of HDO, H2O and any co-retrieved parameters such as albedo, temperature, or interfering gases.
The vector n describes the measurement noise on the spectral radiances. The is the gain matrix, which describes the sensitivity of each element of x to each element of the radiance L. The averaging kernel describes the sensitivity of the retrieved state to the true state. The matrix describes the sensitivity of the radiance to the true state. The last component of equation 9 describes the set of other possible errors (given as δi and the sensitivity of the radiance to these errors Ki) that can affect the retrieval such as temperature, clouds, surface emissivity etc. [Worden et al., 2006]. The parameters xa, A and G explicitly contain the regularization used to constrain the ill-posed nature of the remote sensing retrieval problem [e.g., Rodgers, 2000; Bowman et al., 2006] if an optimal estimation approach is used to guide the retrieval. For practical applications, the averaging kernel is central to making appropriate inferences from the data, described further in section 3.4.5.
3.4.3. Observations from space
Frankenberg et al. [2009, 2013] and Boesch et al. [2013] used sunlight reflected in the short wave infrared (SWIR) spectral region to independently estimate x = qHDO and , where qHDO and are vectors containing the altitude (or pressure) dependent concentrations of HDO and H2O respectively. Their retrieval processes use reanalysis data for and a fixed profile as background input. The retrieval products are the total column amounts (or C) for both HDO and H2O, which can then be used for an aposteriori calculation of the ratio (calculation after the retrieval process). This aposteriori calculation relies on the fact that for SWIR observation the sensitivity with respect to atmospheric H2O and HDO are similar. Nevertheless, it is important to remark that the sensitivities are similar but not identical, and one has to be careful when interpreting such aposteriori calculated ratios R [Boesch et al., 2013]. Scheepmaker et al. [2015] discusses the potential and limitations of such SWIR ratio product as complement to the SWIR product.
In the thermal infrared (TIR) the sensitivities with respect to HDO and H2O are significantly different and furthermore depend on their vertical distribution, atmospheric temperature, and surface temperature. Interferences from other trace gases can also increase uncertainty in these estimates. Consequently, the ratio R = HDO/H2O if calculated from independent estimations of H2O and HDO will mainly reflect the different uncertainties and sensitivities with respect to H2O and HDO and not real atmospheric variation of R. To overcome this problem the solution space for the ratio has to be constrained. For this purpose, Worden et al. [2006] and Schneider et al. [2006a] suggested a retrieval on the logarithmic scale together with a constraint for and ln(qHDO) as well as a cross-constraint for . It can be shown that such constraints are actually constraints for and [Schneider et al., 2012].
In this review we focus on discussing the version 5 of JPL TES retrievals and the MUSICA MetOp/IASI retrievals (MUSICA: MUlti-platform remote Sensing of Isotopologues for investigating the Cycle of Atmospheric water). Both use a similar retrieval strategy, like a simultaneous fit of all interfering gases and a broad spectral window [Schneider and Hase, 2011; Worden et al., 2012]. This is different from the MetOp/IASI retrieval strategy applied by a group of the University of Brussels [Lacour et al., 2012], which is similar to the TES version 4 retrieval [Worden et al., 2006], uses small microwindows, and is less computationally intensive.
The reason for focusing on TES is because the TES data set is currently most abundant tropospheric water vapor isotopologue data set. It has been already used in a variety of different studies, therefore it must play an important role in this review. IASI is very interesting because the two instruments currently in space measure about 1.3 million nadir spectra each 24 hours. A third sensor will be launched during the next few years, and follow-up missions are already approved. IASI offers a huge potential for tropospheric water vapor isotopologue studies; however, global water vapor isotopologue IASI retrievals have been performed only for a limited number of days to date.
3.4.4. Observations from ground
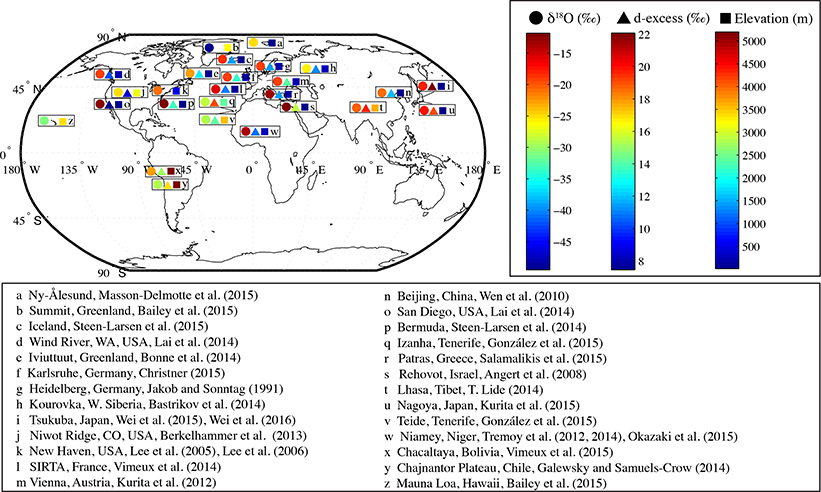
Ground-based, solar-viewing, high-resolution, infrared Fourier Transform Infrared (FTIR) spectrometers can provide daily total-column and profiles of water vapor, its isotopologues, and about 30 other atmospheric species [Hannigan et al., 2009]. There are currently about 19 FTIR installations as part of the Network for the Detection of Atmospheric Composition Change (NDACC) that have been measuring solar absorption spectra in the mid-infrared (750–4200 cm−1), with some sites beginning measurements in the 1990s. As part of the MUSICA project, a dedicated water vapor isotopologue retrieval has been applied to a subset of 12 sites (Table 1; Schneider et al. [2012]; Barthlott et al. [2016]) using the simultaneous optimal estimation of H2O and HDO as well as δD. This retrieval is very similar to that described above for the TIR satellite sensors.
Table 1.
List of current MUSICA NDACC/FTIR sites (ordered from North to South) and available aposteriori processed {q,δD} data record. DOFS (Degree Of Freedom for Signal) is a parameter of the information content in the retrieved data, whereby DOFS> 1.0 means weak profiling capability. This table is adopted from Barthlott et al. [2016].
| Site | Location | Altitude | Data Record | DOFS |
|---|---|---|---|---|
| Eureka, Canada | 80.1°N, 86.4°W | 610m a.s.l. | 2006–2014 | 1.7 |
| Ny Alesund, Norway | 78.9°N, 11.9°E | 21 m a.s.l. | 2005–2014 | 1.6 |
| Kiruna, Sweden | 67.8°N, 20.4°E | 419 m a.s.l. | 1996–2014 | 1.6 |
| Bremen, Germany | 53.1°N, 8.9°E | 27m a.s.l. | 2004–2014 | 1.6 |
| Karlsruhe, Germany | 49.1°N, 8.4°E | 110m a.s.l. | 2010–2014 | 1.6 |
| Jungfraujoch, Switzerland | 46.6°N, 8.0°E | 3580m a.s.l. | 1996–2014 | 1.6 |
| Izaña/Tenerife, Spain | 28.3°N, 16.5°W | 2367 m a.s.l. | 1999–2014 | 1.7 |
| Altzomoni, Mexico | 19.1°N, 98.7°W | 3985m a.s.l. | 2012–2014 | 1.7 |
| Addis Ababa, Ethiopia | 9.0°N, 38.8°E | 2443 m a.s.l. | 2009–2013 | 1.6 |
| Wollongong, Australia | 34.5°S, 150.9°E | 30 m a.s.l. | 2007–2014 | 1.6 |
| Lauder, New Zealand | 45.1°S, 169.7°E | 370m a.s.l. | 1997–2014 | 1.6 |
| Arrival Heights, Antarctica | 77.8°S, 166.7°E | 250m a.s.l. | 2002–2014 | 1.4 |
The Total Carbon Column Observing Network (TCCON) is a network of ground-based FTIR sites that measure solar absorption spectra in the near infrared region (3800–9000 cm−1). In this spectral region, the absorption signatures of HDO are much weaker than in the mid-infrared, but H2O and HDO column abundances can be obtained. Then after the retrieval process the column integrated δD values are calculated [Risi et al., 2012a]. To first order, these retrievals are similar to that described above for the space based SWIR sensors. Rokotyan et al. [2014] discusses problems that can occur when using δD that has been calculated after the retrieval process from the retrieved HDO and H2O amounts.
An advantage of FTIR over satellite-based remote sensing is the opportunity to develop relatively high-precision, long (decadal) datasets at key sites. In contrast to the cavity-enhanced methods described above, FTIR provides measurements of total column abundances and profiles of water vapor and its isotopologues.
3.4.5. Characterising and comparing remote sensing retrievals
Equation 9 is the basis for theoretical uncertainty calculations. The uncertainty in the estimated atmospheric state is given by the expectation of the estimate relative to the ‘true’ state:
| (10) |
where I is the identity matrix, S stands for covariance matrices that describe the statistics of the corresponding parameters (a for apriori knowledge, n for measurement noise, i for parameter i) and usually is determined from a model or an uncertainty calculation.
When comparing remote sensing data with in-situ data or with model data, the retrieval’s regularization should be taken into account [Rodgers, 2000]. The effect of the regularization is described by the averaging kernels. By convolving the in-situ data or the model data with the averaging kernels we can estimate the remote sensing observation that corresponds to the in-situ/model data. For this purpose the in-situ or modelled profile is mapped to the same altitude grid used by the retrieval and then convolved by the averaging kernel:
| (11) |
where xair is the in-situ/model profile mapped to the retrieval altitude (or pressure) grid.
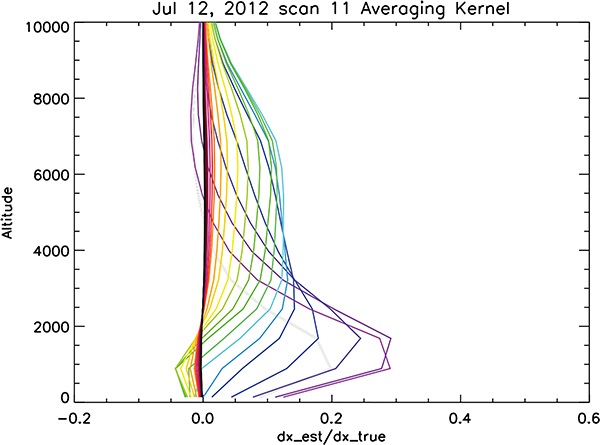
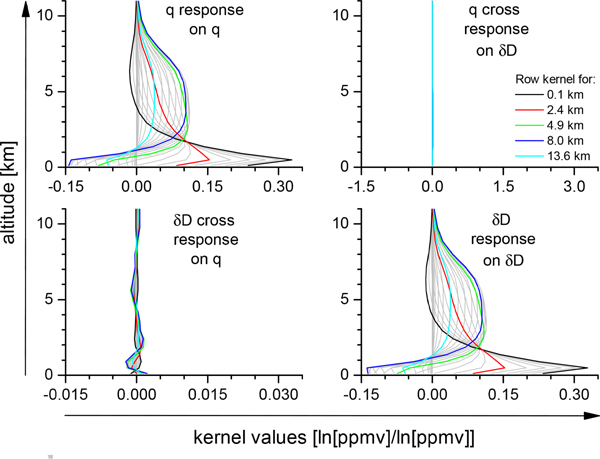
Figure 4 shows the rows of the HDO component of the averaging kernel as produced by the TES retrieval for an observation over the tropical ocean. The HDO component of the kernel is generally the limiting component for the estimate of R. As can be seen in Figure 4, the sensitivity of TES’s estimate of HDO (or R) peaks in approximately two altitude ranges with the first altitude range between 500 and 2500 meters and the second altitude range between 2000 and 9000 meters. The averaging kernel therefore shows that this TES estimate can resolve the isotopic composition of the atmosphere in these two altitude regions. As can be deduced by Equation 9, if the diagonal of the averaging kernel has a value of unity, then the estimate can resolve that level of the atmosphere perfectly, but with the uncertainties described by noise and interferences. If a diagonal term of the averaging kernel has a value of 0.5, for example, then the estimate can only resolve about half the variability of the HDO/H2O ratio at the corresponding level. Another feature of each row of the averaging kernel is that it need not have a peak value at its corresponding diagonal element. For example, the first row of the averaging kernel, which describes the sensitivity of the surface level to the rest of the HDO profile, peaks at 1000 meters indicating that most of the information comes from HDO at 1000 meters. As can be seen in Figure 4, the averaging kernel rows typically peak at 0.3 for the higher pressures and about 0.1 at the lower pressures. The trace of the averaging kernel gives the degrees-of-freedom (DOFS) for signal of the retrieval and is approximately 1.5 for this retrieval with approximately 0.9 DOFS in the lower layer with an altitude range between the surface and 2500 meters and 0.6 DOFS for the layer with an altitude range between 2000 and 9000 meters. That means we can almost perfectly resolve the lower layer (to within its errors) and resolve about 60% of the variability of R in the upper layer (plus the uncertainties).
Figure 4.
Rows of the averaging kernel for an observation taken over South America in the fall of 2006.
When working with the state vector , the error estimations and convolution operations for the ratio are obtained by rewriting the equations 10 and 11 as a function of R:
| (12) |
where Ahh and ADD are the averaging kernels for and ln(qHDO), respectively. Adh and Adh are the cross kernels (response of atmospheric on ln(qHDO) and vice versa). GR is the gain matrix for R. Rair is the in-situ/modelled profile mapped to the retrieval altitude (or pressure) grid and Ra the apriori profile. More details on this error calculations and convolution operations can be found in a variety of TES papers (e.g. Worden et al. [2006]; Risi et al. [2013]; Sutanto et al. [2015]).
An alternative approach is to perform a basis transformation from the basis system to the basis system. These new bases are good proxies for the q and δD (or R) states. In the new basis system we can directly use Equations 10 and 11 for performing error estimations and convolution operations for q and δD [Schneider et al., 2012; Wiegele et al., 2014; Barthlott et al., 2016].
In addition, the transformation to the proxy basis system makes transparent how the remote sensing system interprets the real atmospheric {q,δD} pair distribution, because the transformed averaging kernels are the averaging kernels for the q and δD proxies. The proxy kernels clearly reveal that generally the sensitivities of the q and δD products are significantly different. In order to get a q and δD product that represents the same atmospheric structures an aposteriori processing is required. It is motivated and explained in detail in Schneider et al. [2012], Wiegele et al. [2014] and Barthlott et al. [2016]. The processing assures that the averaging kernels of the q and δD proxy states are almost identical. Without the aposteriori processing the remote sensing {q,δD} pair diagrams can be rather misleading [Schneider et al., 2016].
An example of a kernel in the {q,δD} proxy basis system is given in Figure 5. It shows the situation for a typical MUSICA NDACC/FTIR retrieval for the Izana FTIR instrument, situated at 2370 m a.s.l., and after performing the aposteriori processing, which is the reason that the kernels for the q and δD proxies are almost identical. The kernels reveal that with the NDACC/FTIR systems we can observe a first layer expanding up to 2000 meters and a layer between 1500 and 8500 meters above the instrument. The DOFS for these {q,δD} pair products is typically 1.7 [Barthlott et al., 2016]), i.e. we can almost observe the two layers independently.
Figure 5.
Example of row entries of the Karlsruhe MUSICA NDACC/FTIR averaging kernels in the {q,δD} proxy basis system and after aposteriori correction. Please note that the q proxy kernels (upper left plot) and the δD proxy kernels (bottom right plot) are almost identical. The different scales on the x-axis consider the different magnitudes of ln[q] and δD variations. For more details please refer to Schneider et al. [2012] and Barthlott et al. [2016].
The MUSICA MetOp/IASI retrievals provide also q and δD proxy kernels that are almost identical (after the aposteriori processing; Wiegele et al. [2014]). The DOFS for the respective {q,δD} pair products is between 0.5 and 1.2 (data with less sensitivity are filtered out), whereby the DOFS is typically higher in the tropics than at high latitudes.
3.4.6. Validating remote sensing data
A typical purpose for comparing remotely sensed measurements (or retrievals) to aircraft data is to evaluate biases in the retrieval and to validate the retrieval’s calculated uncertainties.
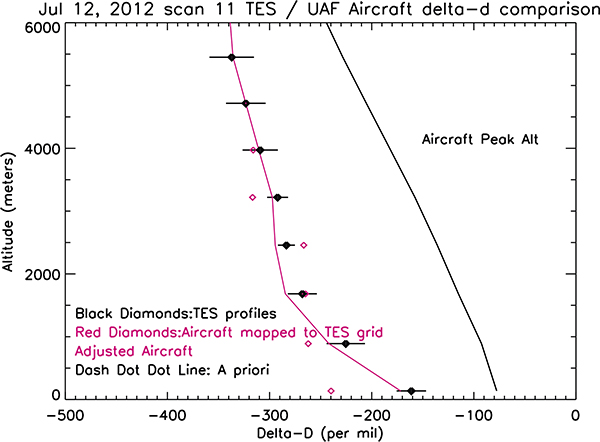
Figure 7 shows the comparison between an aircraft profile of the HDO/H2O ratio over Alaska in the summer of 2011 and a TES measurement that was taken to coincide with the aircraft. The a priori profile for R is given by the dashed line, the red diamonds are the aircraft measurements mapped to the TES retrieval grid, the black diamonds are the TES estimate for R, and the solid red line is the aircraft profile after being passed through the instrument operator shown in Equation 13.
Figure 7.
Comparison of a TES retrieval to aircraft measurements. The dashed line is the a priori used for the TES retrieval. The red diamonds are the raw aircraft measurements, mapped to the TES retrieval grid. The solid red line is the aircraft measurement after passing through the TES instrument operator. The black diamonds show the TES HDO/H2O profile (in units of per mil relative to SMOW)
As shown in Equation 12, the estimate at any given level is a combination of the difference between a priori and true state (modulated by the averaging kernel), and the uncertainties. For this reason, the bottom-most level for the TES estimate is a weighted sum of the true value of −240%o, as measured by the aircraft, and the tropical a priori used in the retrieval of approximately −77%o. The retrieval and ‘true’ are much closer for the altitude region where the diagonal of the averaging kernel is large. The smoothness of aircraft profile, adjusted with the TES averaging kernel, reflects the convolution of the aircraft profile with the averaging kernel matrix.
Figure 6 shows comparisons of the MUSICA NDACC/FTIR (middle panel) and MUSICA MetOp/IASI δD products (right panel) with two exemplary aircraft in-situ profiles measured between sea level and almost 7000 meters above sea level during the MUSICA validation campaign in summer 2013. The colored dashed lines and shaded areas depict the smoothed aircraft reference profiles (smoothing according to Equation 11) and their respective confidence range. The confidence range of the reference data is largely determined by the fact that there are no reference observations above 7000 meters. The corresponding large uncertainty above 7000 meter propagates to lower altitudes due to the smoothing with the averaging kernel. The circles and error bars represent the remote sensing data and their respective uncertainties.
The plot in the middle panel reveals the good agreement between the reference data and the MUSICA NDACC/FTIR retrievals and confirms the weak profiling capability of the ground based NDACC/FTIR systems. On 25th of August and below 3500 meter δD is lower than on 24th of August. Above 3500 meter it is the other way round. There δD is higher on the 25th than on the 24th. The different vertical structures in δD for the two exemplary days are similarly observed in the aircraft reference profiles.
The plot in the right panel shows that MUSICA MetOp/IASI δD retrievals are in good agreement with the aircraft reference data. This plot also reveals that the MetOp/IASI data represent averages over a rather deep layer between 2000 and 8000 meter (typical MUSICA MetOp/IASI kernels for this comparison study are shown in Schneider et al. [2016]).
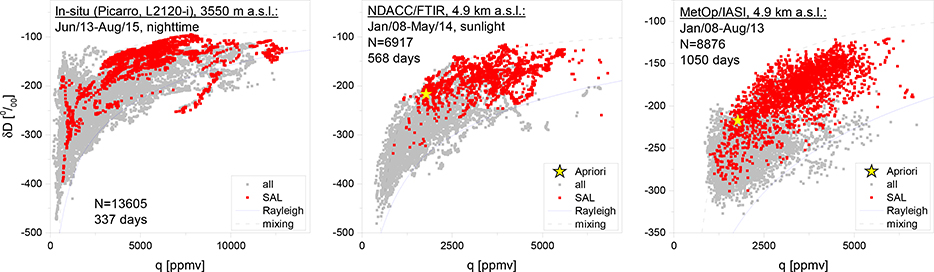
For the scientific interpretation of lower and middle tropospheric water isotopologue data, q-δ distribution plots are in particularly useful (see discussion in the context of Figure 3). This means that a validation of the q-δ distribution as obtained from the remote sensing data is important. Figure 8 gives an example of such validation exercise. It shows {q,δD} pair distributions as observed in in-situ as well as in MUSICA NDACC/FTIR and MUSICA MetOp/IASI remote sensing data (aposteriori processed data). The different data sets have a very similar {q,δD} pair distributions: most {q,δD} pairs lie between the plotted exemplary Rayleigh and mixing curves (solid blue and dashed black lines), a few data points are above the mixing curve (mainly for dry conditions) and a few data points are below the Rayleigh curve (mainly for humid conditions). The good agreement becomes even more evident if we identify observations made during Saharan Air Layer (SAL, respective data points are marked by red color) conditions. SAL means that we detect a dust laden air mass that has experienced dry convection over the Sahara. Such air masses have a {q,δD} pair distributions that approximates a mixing curve (mixing between boundary layer and middle/upper tropospheric air; González et al. [2016]). This distinct {q,δD} pair distribution is clearly identified in the three different data sets. The smaller variability in the MetOp/IASI data for q < 2000 ppmv is due to the retrieval’s reduced sensitivity for dry conditions.
Figure 8.
Example of {q,δD} pair distributions observed in the North Atlantic subtropical free troposphere during several years and by three different techniques, from the left to the right: in-situ, ground-based remote sensing (MUSICA NDACC/FTIR) and space-based remote sensing (MUSICA MetOp/IASI). Grey dots represent all observations, red dots observations during Saharan Air Layer (SAL) events and the yellow star is the apriori {q,δD} pair used for all remote sensing retrievals. In addition the plots show two simulated curves: (1) A Rayleigh curve (blue line) for initialisation with T=25C, RH=80% and δD=−80%o. (2) A mixing curve (black dashed line) for mixing between {25000ppmv,−80%o} and {500ppmv,−500%o}. For more details please refer to González et al. [2016].
3.4.7. Using remote sensing data for validating models
Provided that the uncertainties and biases in the remotely sensed measurement have been evaluated and validated, we can also use Equations 9, 10 and 11 to evaluate modeled profiles of water vapor and HDO in global hydrological models. First a model HDO/H2O profiles is mapped to the retrieval grid and passed through the instrument operator (Equation 11). If the model meteorology is expected to agree reasonably well with that seen by the retrieval, the averaging kernels from the retrievals can be applied directly to model profiles [e.g., Risi et al., 2012a].
However, if we do not know whether the modeled and observed atmospheric situation reasonably agree, a simple application of the averaging kernels (corresponding to the observed situation) to the model profiles (corresponding to the model situation) can be misleading. It could happen that the model-measurement differences are strongly camouflaged by the averaging kernel calculations. The effect of the averaging kernels to the model {q,δD} pair distribution is in particularly strong. In particularly, if the considered retrieval product is not aposteriori processed, then the sensitivities for q and δD are significantly different and the kernels are rather complex.
The problem of averaging kernels that are not representative for the model situation can be overcome by using a statistical approach for estimating the instrument operator (the averaging kernels) from the model’s temperature and humidity fields [e.g., Field et al., 2012, 2014]. This means that the averaging kernel will correspond to the atmospheric situation of the model. Testing hypotheses with the remote sensing data becomes a matter of relating the modeled HDO/H2O profiles to the physics that must be tested and passing that profile through the instrument operator [e.g., Jiang et al., 2013; Jones et al., 2003, and references therein].
The effect of the averaging kernels on model data validation studies is especially strong if {q,δD} pair distributions are of interest. The situation can be significantly improved by working with the aposteriori processed data [Schneider et al., 2012]. The aposteriori processing reduces the complexity of the averaging kernels. Then atmospheric {q,δD} pair variations that take place over deep layers are weakly affected by the averaging kernels, making the application of the averaging kernel to the model data less critical and a first order comparison between modeled and measured {q,δD} pair distributions is even possible without applying the averaging kernels to the model (see discussions in Schneider et al. [2016]). This possibility becomes evident from Figure 8: there the in-situ data as depicted in the left panel correspond to point measurements made at 3550 meter, whereas the NDACC/FTIR and MetOp/IASI data reflect the atmosphere according to their averaging kernels. The aposteriori processed NDACC/FTIR and MetOp/IASI {q,δD} pair data well compare to the in-situ data that are not affected by averaging kernels, so they can be used as a direct reference for a first order validation of model outputs.
4. Water vapor isotopic composition in the troposphere
In this section we review the spatial distribution of global water vapor isotopic composition, related aspects of which have been observed in precipitation isotopes, but have only recently been observed in vapor with the availability of remote sensing and in situ data described in the previous section.
4.1. Temperature and continental effects
The decrease of δ values in precipitation as latitude or altitude increase has long been observed [Dansgaard, 1964; Rozanski et al., 1993]. More generally, δ-values decrease as temperature decreases, a pattern called the “temperature effect”. The same pattern can now be observed for δ-values in water vapor with the new measurement techniques described in section 3 [Worden et al., 2007; Frankenberg et al., 2009]. This can be interpreted, to first order, in terms of Rayleigh distillation: as temperature decreases, the specific humidity at saturation decreases, leading to the decrease in δ-values in both the vapor and the subsequent precipitation. Mixing processes along trajectories and isotopic exchange with the underlying surface can modulate the temperature effect. For example, if the contribution of turbulent eddies to the equator-to-pole transport increases, the δ-values are expected to decrease less steeply with latitude [Hendricks et al., 2000].
The δ-value minimum that is observed in the water vapor over desert regions [Frankenberg et al., 2009] can also be interpreted in terms of the temperature effect: air masses subsiding over desert regions have undergone condensation at high altitude where the temperature is low. In this case, the control on the δ-values is not the local temperature, but rather the temperature at the point of last saturation [Galewsky and Hurley, 2010; Risi et al., 2010a; Hurley et al., 2012; Galewsky, 2015].
A decrease of δ-values in precipitation as air masses move inland has also long been observed and named “continental effect” [Dansgaard, 1964]. The same pattern can also be observed for δ in the water vapor [Frankenberg et al., 2009]. This can also be interpreted in terms of Rayleigh distillation along air mass trajectories. The magnitude of the continental effect varies greatly in space, with a smoother decrease of vapor and precipitation δ-values over tropical land forests (e.g., the Amazon) than over mid-latitude continentals, particularly during winter (e.g., Eurasia) [Salati et al., 1979; Rozanski et al., 1993]. This is because over tropical land forests, and during extratropical summer, evapotranspiration efficiently recharges air masses in water vapor as they move inland, a process called continental recycling [Budyko, 1974; Burde et al., 1996; Trenberth, 1999]. This recycling partially compensates for the δ-value decrease by Rayleigh distillation [Winnick et al., 2014]. As for the temperature effect, the magnitude of the continental effect may vary depending on the relative importance of eddy diffusion and large-scale advection for the transport of water vapor [Winnick et al., 2014].
4.2. Amount effect
In the tropics, precipitation δ-values are observed to be anti-correlated with the amount of precipitation. This is called the “amount effect” [Dansgaard, 1964; Rozanski et al., 1993]. This effect is especially pronounced over the ocean and can be well observed on tropical islands. The traditional Rayleigh distillation framework is not sufficient to interpret isotopic variations in the tropics, where most of the precipitation arises from deep convection and vertical motions dominate over horizontal transport. Dansgaard [1964] cited several potential explanations for the amount effect. First, when convection is more intense, rain drops are larger and the fraction of these drops that reevaporate is smaller. Therefore, the rain drops become less enriched by reevaporation as they fall [Stewart, 1975]. Second, when convection is more intense, the air is usually moister, which limits rain reevaporation and favors diffusive isotopic exchanges between rain drops and vapor. This limits the reenrichment of rain drops as they fall. These effects were confirmed by several modeling studies [Risi et al., 2008a; Lee and Fung, 2008; Yoshimura et al., 2010].
The amount effect can also be observed in water vapor δ-values [Worden et al., 2007; Lawrence et al., 2004; Tremoy et al., 2012]. Deep convection acts to isotopically deplete the low-level water vapor through several possible mechanisms. First, deep convection is associated with intense vertical mixing, bringing isotopically depleted water vapor from the mid-troposphere downwards. This mixing is undertaken by unsaturated or meso-scale downdrafts [Risi et al., 2008a, 2010b; Kurita et al., 2011]. Second, partial reevaporation of raindrops isotopically deplete the water vapor [Worden et al., 2007; Field et al., 2010], as long as the reevaporation fraction is small enough [Risi et al., 2010b]. Third, when the air is saturated, diffusive exchanges between rain drops and vapor deplete the vapor [Lawrence et al., 2004]. Fourth, deep convection is associated with convergence of air masses. According to a vertically-integrated water vapor budget, as convergence increases, more of the vapor originates from the surrounding atmospheric columns and less originates from fresh surface evaporation. The former being more isotopically depleted, as convergence increases the water vapor is more depleted [Lee et al., 2007a; Moore et al., 2014]. The amount effect can be modulated by convective or large-scale properties: deep convection depletes the low-level water vapor all the more as the degree of organization of convection is high [Lawrence and Gedzelman, 2003; Lawrence et al., 2004; Risi et al., 2008b], as the relative proportion of stratiform to convective precipitation is high [Kurita et al., 2011; Kurita, 2013] or as the vertical profile of air convergence is more top-heavy [Moore et al., 2014].
Deep convection has a cumulative effect on the water vapor composition [Risi et al., 2008a]. Observed δ-values in precipitation and water vapor integrate convective activity over both time and space. Therefore, the amount effect is not a purely local phenomenon. In monsoon regions, for example, deep convection is associated with more isotopically depleted water vapor and precipitation in downstream air mass trajectories [Vuille et al., 2003; Vuille and Werner, 2005; Vimeux et al., 2005; Risi et al., 2008b; Vimeux et al., 2011; Gao et al., 2011; Tremoy et al., 2012; Samuels-Crow et al., 2014b; Galewsky and Samuels-Crow, 2015; He et al., 2015], and also with the degree of organization of the precipitation [Lekshmy et al., 2014; Pausata et al., 2011].
4.3. Evaporation and re-evaporation in the marine boundary layer
Evaporation from the oceans constitutes one of the key components in the global hydrological cycle and being able to constrain the processes involved is critical for simulating accurately the climate. Understanding the isotopic fingerprint of evaporation was therefore among the first goals of water vapor isotopic studies. Craig and Gordon [1965] carried out the first comprehensive study of water vapor isotopic composition in the marine boundary layer and their relation with evaporation and exchange between the lower atmosphere and sea surface. They were able to conclude, contrary to earlier suggestions from Epstein and Mayeda [1953], that the water vapor was more isotopically depleted than vapor in isotopic equilibrium with the sea surface. Their data from several different oceanic regions showed the isotopic composition to have a higher correlation with respect to the relative humidity calculated relative to saturated vapor pressure at the sea surface temperature (RHsst) instead of the relative humidity calculated relative to the saturated vapor pressure at the air temperature (RHair). The isotopic composition of the flux from an evaporating water body is governed by the isotopic transfer rates during molecular diffusion and eddy diffusion/turbulent transport. To simplify the description of the transfer rates Craig and Gordon developed a two-layer model based on the work of Rideal and Langmuir on liquid-vapor exchange [Rideal, 1925; Langmuir and Langmuir, 1927]. They defined a laminar layer above the air-water interface in which the molecular transfer is dominated by molecular diffusion and a turbulent layer above the laminar layer in which molecular transfer is dominated by eddy/turbulent diffusion. In their model, the water vapor flux for the different isotopes through the laminar layer is proportional to the vapor pressure difference of the given isotopes between the interphace of the laminar and turbulent layer and the interface of the ocean skin layer (the air-ocean interface) and the laminar layer. The eddy/turbulent diffusion in the turbulent layer is normally assumed to be the same for all isotopes. Humidity and isotopic equilibrium is assumed at the ocean skin layer (the air-ocean interface). Under these assumptions and the assumption that no divergence or convergence in the air column above the ocean occur the isotopic flux can be described as
| (13) |
| (14) |
| (15) |
where δL is the isotopic composition of the ocean surface; δa is the isotopic composition of the free atmosphere; α* is the fractionation coefficient defined as RV _ α*RL, where RV and Rl are the isotopic ratios of the vapor and the liquid; RHsst is the relative humidity compared to saturation at sea surface temperature, θ is a weighting term determined by the influence of the evaporation flux on the free atmosphere. According to Gat [1996], the value of θ is equal to 1 for a small body of water with little influence on the free troposphere but close to 0.5 for regions such as the eastern Mediterranean, where the measurements were obtained, which may be representative for conditions over the open ocean. n is the exponent on the molecular diffusivities of the different isotopes governing the vapor transfer rate in the air. In a fully laminar domain, the value of n becomes 1, while going from smooth conditions to conditions where strong turbulent mixing occurs, the value of n will decrease from 0.75 to 0.5 [Brutsaert, 1975, 1965; Merlivat and Coantic, 1975]. The molecular diffusivities in air of the heavy isotopes compared to the light isotope are shown in Table 2. For placing the development of the Craig-Gordon model into a historical perspective the reader is referred to Gat [2008].
Table 2.
The molecular diffusivities in air of the heavy isotopologues compared to the light isotopologues
| D[HDO]/D[H2O] | 0.9755 [Merlivat, 1978] 0.9839 [Cappa et al., 2003] |
| D[H217O]/D[H2O] | 0.9856 [Barkan and Luz, 2007] |
| D[H218O]/D[H2O] | 0.9723 [Merlivat, 1978] 0.9691 [Cappa et al., 2003] 0.9725 [Barkan and Luz, 2007] |
Jouzel [1979], based on the work of Merlivat and Coantic [1975], simplified the expression for the isotopic value of the evaporation flux by prescribing the kinetic effects through a parameter k defined for a smooth regime and a rough regime with a separation of the two regimes for wind speeds around 6–7 m/s. The value of k varies between 6.2%o and 3.5%o [Brutsaert, 1975; Merlivat, 1978] and the expression becomes
| (16) |
where , δocean, and is the isotopic value of the evaporation flux, the ocean, and the water vapor in the ambient air.
4.4. Deuterium excess
With the definition of the Global Meteoric Water line [Craig, 1961; Dansgaard, 1964], the d-excess of both present day and archived water samples (ice core and ground water) can be calculated. Jouzel [1979] approached this problem by simplifying the assumptions of the Craig-Gordon model. They took a global point of view and considered an isolated air parcel that is filled by evaporation and then precipitates totally along its trajectory. The water budget is closed so that the weighted mean isotopic composition of the evaporation flux is equal to that of the precipitation. In addition, if all the water vapor from the boundary layer at the evaporative source precipitates, then the isotopic composition of the precipitation is equal to that of the boundary layer vapor. Therefore, the isotopic composition of the evaporation flux is equal to that of the boundary layer vapor. This is also called the closure assumption, referring to the assumption of a closed water budget. A similar relationship can also be achieved by taking a local point of view, assuming that all the water vapor in the boundary layer originates from the evaporation flux.
Using the closure assumption, Equation 16 can be simplified to:
| (17) |
at 3 m/s is 6.4 and at 8 m/s is 3.5, , .
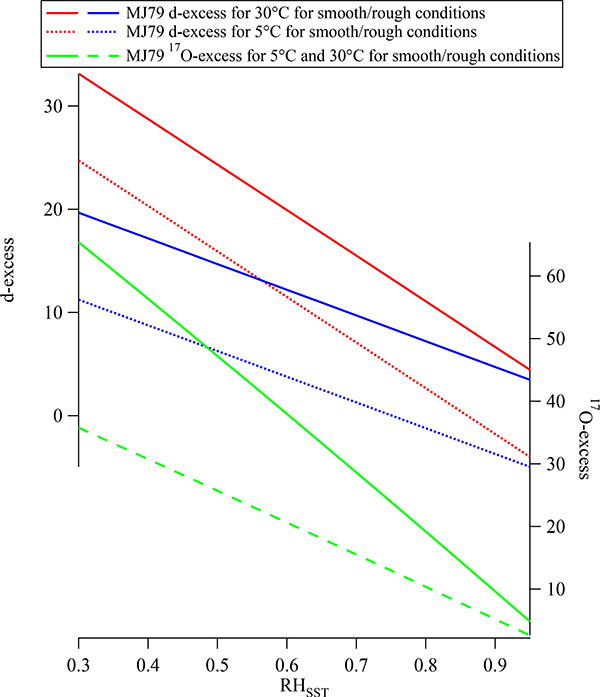
Under the closure assumption it was shown by Jouzel [1979] that the d-excess in the boundary-layer water vapor should theoretically depend strongly on the SST, RHsst, and the wind speed (sea surface condition; Figure 9). This allowed Jouzel [1979] to speculate that it would be possible to deduce glacial source region conditions from ice cores obtained in Polar Regions. Johnsen et al. [1989] deduced source region conditions for glacial and interglacial conditions for snow accumulating in Greenland using this framework. The added value of using the d-excess of air masses to deduce moisture source conditions lies in the assumption that the d-excess is conserved during transport and distillation as long as no kinetic fractionation or too much distillation occurs. This assumption was empirically verified by Bonne et al. [2014], who combined simultaneous water vapor isotope measurements from three measuring stations along an atmospheric river bringing moisture from the sub-tropics up on the Greenland Ice Sheet. Using the d-excess fingerprint in water vapor Kurita [2011] and Steen-Larsen et al. [2013] showed that Arctic moisture carried a distinctly higher d-excess than moisture in the mid-latitudes. Measurements from South France showed distinct d-excess levels in air masses from the Mediterranean compared to air masses from the North Atlantic [Delattre et al., 2015].
Figure 9.
The initial water vapor d-excess (upper panel) and 17O-excess (lower panel) above the ocean calculated as function of RHsst and SST for a smooth and rough ocean surface assuming the closure assumption defined by Merlivat and Jouzel [1979].
While marine boundary-layer d-excess has received much attention, especially as a tool for identifying marine source regions for ice core records, there have been far fewer studies of water vapor d-excess in free tropospheric water vapor. Rayleigh distillation predicts that air in the upper troposphere should have high d-excess (150 — 200%o) [Bony et al., 2008] and may serve as a tracer of subsiding upper-tropospheric water vapor [Blossey et al., 2010]. Samuels-Crow et al. [2014a] presented measurements of d-excess from the high altitude (5 km or 550 hPa) subtropical Chajnantor Plateau in the Chilean Andes that were as high as 234%o, consistent with expectations from Rayleigh distillation. Their back-trajectory analysis showed that there was no link between marine source area and d-excess, suggesting that free-tropospheric d-excess is controlled by a different set of processes than boundary-layer d-excess.
A pure Rayleigh distillation process should always yield high d-excess at low mixing ratios, but Samuels-Crow et al. [2014a] showed that the average d-excess on the Chajnantor was 46%o when the mixing ratio was below 500 ppm, much lower than would be expected for Rayleigh distillation. Their analysis showed that observations of low d-excess under dry conditions required vapor deposition under ice supersaturation, followed by a small degree of moistening during transport to Chajnantor. During a cold-air outbreak on Chajnantor [Galewsky, 2015], the d-excess reached the relatively low value of 35 ± 6%o at a mixing ratio of only 195 ppmv, a result significantly at odds with pure Rayleigh distillation, which would predict a d-excess of 150%o at that mixing ratio. Galewsky [2015] showed that those measurements required vapor deposition under supersaturation with RHice of between 112% and 118%, consistent with Samuels-Crow et al. [2014a]. These studies suggest that the d-excess in the free troposphere is strongly tied to in-cloud microphysical processes.
4.5. 17O-excess
Due to the definition of the 17O-excess and the laboratory finding relating the fractionation coefficient of compared to as , no effect of SST exists on the 17O-excess of the marine boundary layer. However due to the different molecular diffusivity of and , RHsst will continue to have strong influence as illustrated in Figure 9. The combined measurements of 17O-excess and d-excess will make it possible to use the difference in molecular diffusion between and 1H 2H16O to constrain kinetic effects caused by forced molecular diffusion along a vapor pressure gradient during, for example, evaporation or deposition, a problem that is otherwise under-constrained. The large d-excess variability at the synoptic scale of up to 30 %o and at the inter-seasonal scale of up to 8 %o observed in the North Atlantic Steen-Larsen et al. [2014a, 2015] implies that a 17O-excess variability on synoptic to seasonal scale will be up to 65 per meg and up to 20 per meg. This is several times larger than the current reported analytical precision using IRMS, CRDS, or OA-ICOS [Barkan and Luz, 2005; Schoenemann et al., 2013; Steig et al., 2014; Berman et al., 2013] and should therefore be possible to measure. The lack of SST effect on 17O-excess means that concomitant measurements of δ18O, δ17O, and δD will allow one to separate the influence of RHsst and SST [Landais et al., 2008]
4.6. Observations of water vapor isotopic composition in the troposphere
Having outlined some of the first-order processes that govern the spatial distribution of water vapor isotopologues in the troposphere, we now present remote sensing data from TES and in-situ data that illustrate some of these processes.
Figure 10 shows the distribution of in-situ stations with at least one full year of measurement of sufficient data and calibration quality to allow for calculating the mean annual water vapor isotopic value δ18O and d-excess. The reader is referred to the individual publications for details about the specific datasets. All of the water vapor isotopic values have either been obtained or published after year 2000 and most of the isotopic measurements have been obtained using water vapor isotope spectrometers. A noticeable overrepresentation of stations in the Northern hemisphere exists. Among stations in the planetary boundary layer, there is a clear meridional gradient between the subtropics and Arctic regions. The map documents a surprising homogeneity in the mean annual d-excess in the North American, North Atlantic, and European stations within the planetary boundary layer. Both stations in Japan show an elevated level in the d-excess likely as a result of evaporation from the Sea of Japan. It is interesting to note that for the stations in the Pacific region, the Andes, and the North Atlantic region, which are above the planetary boundary layer there is a clear uniformity in δ18O values, which is significantly different from the stations in the planetary boundary layer.
Figure 10.
Mean annual in-situ water vapor δ18O and d-excess (where data is available) from stations with at least one full year of measurements together with elevation of measurement station. The δ18O value is given by the color scale of the filled circle (spanning −11%o to −50%o), the d-excess is given by the color scale of the filled triangle (spanning 8%o to 22%o), and the elevation is given by the color scale of the filled square (spanning sea level to 5200 m). [Berkelhammer et al., 2013; Okazaki et al., 2015; Kurita et al., 2015; Salamalikis et al., 2015; Kurita et al., 2012; Lee et al., 2006, 2005; Wei et al., 2016; Christner, 2015; Lai et al., 2014; Bailey et al., 2015b; González et al., 2016]
Figures 11 and 12 show seasonal averages of TES measurements from the year 2006. In the lower troposphere (Figure 11 ), measured δD values range from −250%o in extratropical regions to nearly 0%o over Africa, likely due to significant transpiration over the Congo basin. Over the northern hemispheric continents, isotopic variations can primarily be explained in terms of the temperature and continent effects. For example, water vapor becomes gradually more depleted with lower temperature (higher latitudes) or as air parcels travel from from Europe to Siberia [Gryazin et al., 2014]. Important differences in isotopic variations are apparent in tropical regions. For example isotopic values over India during the summer monsoon are similar to the nearby ocean, but over Asia isotopic values are lower than the ocean, reflecting key differences in the moisture sources and processes affecting summertime rains in these regions [Lee et al., 2012a]. In contrast, water vapor over South America is most enriched in boreal fall in the lower and middle troposphere, likely indicating that transpiration and shallow convection are affecting the observed air parcels. While the isotopic distribution of the boreal winter rainy season over the Amazon is similar to that in boreal summer, comparison of δD versus mixing ratio show that much of the vapor during the Amazonian rainy season is affected by convection [Brown et al., 2008a]. In the middle troposphere (Figure 12), the TES water vapor δD ranges from −350%o in the extratropics to −150%o in the tropics and in monsoon areas. The intertropical convergence zone (ITCZ) appears as a band of higher δ values (about 50%o higher than surrounding regions) near the equator. Monsoonal regions (South Asia and South America) show a nearly 100%o increase in δD values during the peak monsoon months.
Figure 11.
Seasonal average δD for the lower troposphere from TES measurements, averaged over the lowermost 175 hPa, for the year 2006.
Figure 12.
Seasonal average δD for the middle troposphere defined as the layer between between 300 hPa and the top of the ”lower troposphere” shown in Figure 11.
So far there are few studies that use MetOp/IASI water vapor isotopologue data. However, it is important to note the huge potential of this sensor, since it can provide global maps (twice daily: morning and evening) and its operation and follow-up missions are guaranteed for more than two decades. The left panel of Figure 13 shows a middle tropospheric δD map with the global coverage that can be produced from daily morning overpasses, plotted are only retrievals with reasonable sensitivity: it is required that at least 50% of real middle tropospheric {q,δD} pair variations are detectable by the remote sensor, which is the case for typically 120000 pixels during one morning overpass (IASI-A and -B together). This snapshot observation for the morning of 16th of August 2014 agrees with the most important patterns as observed in the TES climatology for SON (bottom right plot in Figure 12).
Figure 13.
Example of MUSICA MetOp/IASI {q,δD} pair observations in the middle troposphere during a single morning overpass (at about 10 local time). Left: daily δD morning overpass map (similar coverage is achieved for an evening overpass at about 22 local time). Right: distinct {q,δD} pair distributions observed in the four different regions as marked by reddish color in the left map. The black lines envelop the {q,δD} area with the highest data point density and with 66% of all data points. N gives the number of individual observations in each region. The blue line is an exemplary Rayleigh curve (same as in Figure 8). For more details please refer to Schneider et al. [2016].
The right panel of Figure 13 shows some details of the daily MetOp/IASI {q,δD} pair observations with high spatial and temporal resolution. It depicts the {q,δD} pairs as observed during the morning of 16th August 2014 at the four different geophysical locations marked by reddish color in the map on the left. The plot is made for q on the logarithmic scale since then a Rayleigh curve describes almost a straight line (the blue solid line is the exemplary Rayleigh curve as specified in the caption of Figure 8). At the four regions the middle tropospheric {q,δD} pair distributions are significantly different. For similar q, the air over Alaska and the North Atlantic is significantly more depleted than the air over South Africa and the Persian Gulf. A reason could be that the less depleted air comes from a source region where during evaporation the temperature or the relative humidity has been rather low or that it is significantly affected by air mass mixing. It is likely that over South Africa the air is dried due to mixing with upper tropospheric air (large scale subsidence over the subtropics) and over the Gulf of Persia it is especially wet due to mixing of very warm air from the boundary layer (moistening without reaching condensation). The strongly depleted North Atlantic air might also indicate rain reevaporation.
5. Techniques of modeling
Beyond a simple Rayleigh framework, most interpretations of water vapor isotopic composition require some degree of modeling, ranging from full simulation in general circulation models to simple one dimensional models. In this section, we review the state-of-the-art in modeling approaches for water vapor isotopic composition. Table 4 provides a representative list of models, selected for the key advances that each represents.
Table 4.
Selected advances in the development of water-isotope equipped climate models.
| Name | Horizontal resolution | Key technical advance | Reference |
|---|---|---|---|
| LMD | 11.25°x7.5° | First isotopically-equipped AGCM with reproduction of global precipitation δ18O distribution and spatial temperature effect. | Joussaume et al. [1984] |
| GISS | 10°x8° | First combination of water isotopes and source region tracers, used by Charles et al. [1994] to estimate contributions of changing moisture source regions to Greenland ice core record. | Koster et al. [1992] |
| LMD | 11.25°x7.5° | First forward modeling of water isotopes under paleoclimate conditions (LGM). | Joussaume and Jouzel [1993] |
| ECHAM3 | T42 | Separate equilibration for cumulus and stratiform clouds, first model estimates of temporal temperature and amount effects. | Hoffmann et al. [1998] |
| CLIMBER | 51° x10° | First intermediate-complexity climate model with water isotopes | Roche et al. [2004] |
| REMOiso | 0.5°x0.5° | First high-resolution regional model with water isotopes. | Sturm et al. [2005] |
| GISS | 5°x4° | First coupled atmosphere-ocean model with water isotopes. | Schmidt et al. [2007] |
| NCAR CAM2 | T42 | First comparison to satellite water isotope retrievals. | Lee et al. [2009] |
| LMDz | 2.75°x3.5° | First GCM with stretchedgrid zoom functionality with water isotopes. | Risi et al. [2010] |
| COSMOiso | 40 | First non-hydrostatic, forecasting model. | Pfahl et al. [2012] |
| SPEEDY-IER | T30 | Fast physics AGCM. | Dee et al. [2015] |
5.1. General Circulation Models
5.1.1. Overview
General circulation models (GCMs) equipped with stable water isotopologue tracers simulate the effects of fractionation and transport on the isotopic composition of water in all branches of the hydrological cycle, from evaporation from seawater, evapotranspiration from the land surface, transport and mixing in the atmosphere, precipitation from clouds, and the return of water to the Earth’s surface. Isotopically equipped GCMs were originally developed to interpret paleoisotope proxy signals using experiments and diagnosis under pre-industrial conditions, identify the controls on water isotope variability at the surface in the absence of dense and long-term observational networks, and mechanistically understand controls on isotopic variability using sensitivity tests. Sturm et al. [2010] review the rationale for these models in paleoclimate applications. Noone and Sturm [2010] and Werner et al. [2011] review the development of isotopically-equipped GCMs, addressing practical considerations involved in their implementation for different host models. In this section, we focus on selected advances since their introduction in the 1980s.
5.1.2. Isotopic GCM history and development
Stable isotope tracers were first incorporated into the Laboratoire de Meteorologie Dynamique (LMD) atmospheric GCM by Joussaume et al. [1984b]. They successfully simulated the main global geographic patterns observed in precipitation δ18O and also reproduced the spatial slope between precipitation δ18O and surface temperature for GNIP locations resulting from the temperature effect, for temperatures less than 15°C. This was followed by implementation of isotopic tracers in the NASA Goddard Institute for Space Studies (GISS) II GCM by Jouzel et al. [1987]. Subsequently, the first forward-modeling studies of precipitation δ18O under Last Glacial Maximum (LGM) conditions were conducted [Joussaume and Jouzel, 1993; Jouzel et al., 1994] with those models, showing that simulated differences between modern and glacial δ18O agreed reasonably well with ice core data from Antarctica and Greenland. The temporal temperature effect [Rozanski et al., 1992] was modeled toward continental interiors, albeit weakly, in ECHAM3 [Hoffmann et al., 1998] and GISS II [Cole et al., 1999], along with the temporal precipitation-amount effect in the tropics.
Schmidt et al. [2007] made an important advance by equipping the fully coupled atmosphere-ocean general circulation version of the GISS with stable isotope tracers. The isotopic composition of ocean water is modeled prognostically as it circulates, is lost to evaporation, and is recharged through precipitation and runoff.
GCMs can also be relaxed, or ‘nudged’, toward large-scale meteorological fields from reanalyses, as in Risi et al. [2012a], for example, rather than allowing the atmosphere to run freely. These are useful if trying to simulate observed interannual variability, or a particular meteorological event, such as a storm [Yoshimura et al., 2010], for which isotopic observations exist. The single -column models (SCMs) of convection used in GCMs have been used offline from their host GCMs to study specific isotopic behavior, for example the amount effect using the SCM version of LMD [Risi et al., 2008a]. Water vapor isotopic measurements can also be assimilated into GCMs using for example, ensemble Kalman filter techniques, with promising evidence from idealized experiments that such techniques can improve overall simulation of the hydrologic cycle [Yoshimura et al., 2014].
Efforts to systematically compare water isotopologue simulations across GCMs have been made through the Stable Water Isotope Inter-comparison Group, now in its second phase (SWING2) [Risi et al., 2012a; Sturm et al., 2010]. The SWING2 data archive consists of water-isotope equipped model simulations ranging in length for 20–50 years, for free-running and nudged atmospheres, and with data available at monthly temporal resolution. The SWING2 archive is particularly useful for assessing the robustness of different isotopic interpretations [Conroy et al., 2013; Risi et al., 2012a].
GCMs with reduced complexity are a computationally cheaper alternative to the current generation of isotopically equipped general circulation models. At the expense of higher-resolution details, they permit more numerical experiments and over longer integration times. Roche et al. [2004] equipped the CLIMBER model with isotopic tracers in a coupled model with simplified ocean and atmosphere components. Other intermediate complexity models equipped with isotope tracers are the University of Victoria Earth System Climate Model [Brennan et al., 2012], the iLOVECLIM model [Roche, 2013], and the Simplified Parameterizations, Primitive Equation Dynamics Isotope-Enabled Reconstructions Model (SPEEDY-IER) [Dee et al., 2015].
Werner et al. [2011] and Noone and Sturm [2010] provide overviews of what is involved in equipping different GCMs with stable water isotope tracers. The details will be model-specific, but common to all will be the requirement that the isotope tracers be conserved and track the prognostic water through all branches of the model’s hydrological cycle. In a technical sense, this requires adding duplicate code for the rare ( and HDO) isotopes whenever the state of the prognostic, abundant water isotope changes, whether from advection or a transfer between reservoirs. The isotopic change is different only during phase changes where fractionation occurs. Hoffman et al. [1998] and Schmidt et al. [2005] describe fractionation physics representative of how stable water isotope tracers are implemented in numerical models, capturing, for example, slow equilibrium fractionation (representing that of small droplets in stratiform clouds), and kinetic fractionation in subsaturated environments or during evaporation from the ocean surface. Noone and Sturm [2010] point out that the complexity of this tracking reflects that of the model’s underlying hydrological cycle. In cumulus schemes, for example, this relates to how the parameterizations approximate unresolved processes such as updrafts, downdrafts, entrainment and detrainment into either, and re-evaporation from cloud condensate and rain.
The sophistication of the isotopic microphysics will also be tied to that of the underlying cloud microphysics. In current isotopically-equipped GCMs, these tend to be simplified bulk schemes, but isotope physics have been implemented in more sophisticated limited-domain models [Smith et al., 2006; Blossey et al., 2010] using higher order moments of water and ice-size distributions. At the other end of the spectrum of complexity, Galewsky [2009]; Galewsky and Hurley [2010] implemented a simplified isotopic parameterization into a perfect precipitation warm rain microphysics scheme in which no condensate was carried in the model, and Wright et al. [2009] implemented a similar perfect precipitation isotope scheme in the GISS model in order to quantitatively evaluate the impact of condensate evaporation on the atmospheric hydrologic cycle. Such semi-idealized approaches are useful for exploring the first-order impacts of circulation on the isotopic composition of precipitation and vapor.
5.1.3. Isotopic GCM evaluation
Evaluation of the simulation of stable isotopologues of water has mostly focused on precipitation rather than vapor, owing to the abundance of precipitation isotopic measurements. Isotopic simulations have improved along with the underlying model and increased resolution. Over Greenland, for example, Joussaume et al. [1984b] found that modeled minimum precipitation δ18O was 18 %o higher than observations compared to high biases of, for example, 2 %o for ECHAM-3 [Hoffmann et al., 1998] and 3 %o for HadCM3 [Tindall et al., 2009].
There has been far less evaluation of modeled water vapor isotopic composition due to a lack of data, particularly in the free troposphere. Tropospheric vapor δD profiles of Ehhalt [1973] over the US Midwest have been used for evaluation of the GISS Model II [Jouzel et al., 1987] and ModelE [Schmidt et al., 2005], both showing a decrease from −100 to −150 %o in the lower troposphere to −400 to −450 %o in the upper troposphere, slightly higher than, but inside the variability of, the observed values. Noone and Simmonds [2002] found similar agreement for the Melbourne University GCM (MUGCM). Schmidt et al. [2005] further compared δD in the tropical tropopause layer to CRYSTAL-FACE measurements from Webster and Heymsfield [2003], finding that a −650 %o minimum near 10 hPa in reasonable agreement with observations, but against considerable background variability. The lack of model evaluation against measurements of water vapor isotopic composition has been a shortcoming, in the sense of trying to evaluate quantities more closely connected to model state variables (humidity) rather than fluxes of those quantities (precipitation and evaporation) [Noone and Sturm, 2010].
This has changed with the availability of satellite estimates of water vapor isotopic composition. Using the NCAR CAM2 model, Lee et al. [2009a] performed the first model evaluation against satellite water vapor isotope estimates, comparing simulated δD in the lower troposphere to retrievals from the Aura TES satellite instrument. They showed that model-data agreement was sensitive to parameter settings in the convective scheme, hinting at the potential for stable water isotope data to act as a complementary observational tool for evaluating climate models, as suggested by Schmidt et al. [2005].
Quantitative comparison between simulated and remotely sensed water vapor isotope profiles requires taking into account the limitations of the retrievals, touched upon in section 3.4.7. These are: low quality under certain conditions such as thick clouds, limited vertical resolution, influence of the prior profile, and limited sampling coverage. This helps to attribute model-data discrepancies to model performance rather than limitations in the retrieval. The key technical step is the choice of averaging kernels from equation 13, which has been approached differently depending on the type of model experiment. For their nudged atmosphere experiments, Risi et al. [2012a] used maps of mean averaging kernels estimated from satellite retrievals. This was based on the assumption that the modeled meteorology was close enough to the actual meteorology that the factors contributing to averaging kernel structure would be similar.
Figure 14 illustrates such a comparison between TES and the LMDz model for a nudged atmosphere. The top panel shows the annual mean global distribution of the column integrated TES measurements for the year 2007. The middle panel shows the corresponding raw values from the LMDz model. The bottom panel shows the corresponding values when the LMDz model HDO/H2O profiles have been passed through the TES instrument operator. The LMDz field with the instrument operator reflects the greater sensitivity of TES to lower tropospheric δD and also the sparseness of the TES sampling, and is what should be compared to TES. When the retrieval sensitivity and orbital sampling are accounted for, we can conclude that the LMDz model underestimates the HDO/H2O in the tropics and overestimates it at high-latitudes such that the modeled latitudinal gradient is smaller than observed. This underestimate of the latitudinal gradient is a consistent feature with global hydrological models [e.g., Field et al., 2010; Risi et al., 2013; Gryazin et al., 2014]. We can test whether a hypothesis related to some aspect of the model physics by adjusting the corresponding parameter in the model and determining if the difference between the adjusted model and data is improved.
Figure 14.
(Top) Global distribution of the column integrated TES HDO/H2O measurements. (Middle) column integrated HDO/H2O values from the LMDz model. (Bottom) Column integrated LMDz model values after passing HDO/H2O profiles through the corresponding TES instrument operators.
This was done for experiments with a free-running atmosphere for the NASA GISS ModelE2. In that case, they instead estimated the averaging kernels statistically from model conditions using a simple retrieval simulator embedded within their model, as described in Field et al. [2012]. Without a retrieval simulator, it is difficult to make comparisons between freely-running atmospheric models and satellite data, given that there is no expectation that the model will reproduce short timescale meteorological conditions affecting retrieval quality, such as the distribution of thick clouds. In these instances, nudged simulations are more suitable, but this leads to a different set of questions that can be examined.
5.1.4. Improving general circulation models and their simulations
Climate models exhibit a persistent spread in their temperature and precipitation changes in response to a given scenario for the emissions of greenhouse gases and aerosols [Meehl et al., 2007; Knutti and Sedlacek, 2013]. The representation of sub-grid scale processes (such as convective and cloud processes) by parameterizations in atmospheric GCMs play a key role in this spread [Bony and Dufresne, 2005; Sherwood et al., 2014]). Several studies have attempted to use water isotopic measurements to evaluate and improve the representation of physical processes simulated by models. These studies exploit the opportunities given by the increasing number of water vapor isotopic observations and the increasing number of GCMs now equipped with isotopic parameterizations, allowing model comparisons with data.
Using isotopes for improving the representation of physical processes by models is possible only if the representation of isotopic processes is less uncertain than the representation of physical processes. The equilibrium fractionation coefficients are well known, except for very low temperature [Merlivat and Nief, 1967; Ellehϕj et al., 2013; Lamb et al., 2015], while the kinetic fractionation coefficients are less certain. The Rayleigh and mixing lines are well established, while the representation of reevaporation processes, especially associated kinetic fractionation processes, are less certain. The major difficulty in the simulation of δD or δl8O is how to combine Rayleigh distillation, mixing and evaporation lines to reproduce observations. This depends mainly on macrophysical processes, such as turbulent and convective processes or the large-scale circulation. The uncertainty in isotopic processes plays a very minor role. For d-excess, in contrast, the uncertainty on isotopic processes cannot be completely neglected.
Water vapor isotope measurements can be used to understand the cause of model biases. For example, combining various water vapor δD measurements, sensitivity tests with a GCM and model outputs from the SWING2 archive, Risi et al. [2012b] argued that the moist bias that GCMs exhibit in the tropical and subtropical middle and upper troposphere is due to excessive vertical diffusion.
Water vapor isotope measurements can also be used to detect shortcomings in the representation of physical processes that do not arise in conventional meteorological or climatological variables. For example, all isotopic GCMs underestimate the observed latitudinal gradient in upper tropospheric water vapor [Risi et al., 2012b], the variability in water vapor and precipitation d-excess at the daily scale in polar regions [Steen-Larsen et al., 2013] and the isotopic depletion recorded at LGM in tropical archives [Jouzel et al., 2000; Werner et al., 2001; Risi et al., 2010c]. These may reveal common biases in the representation of physical processes in GCMs, or the absence of certain key processes in the models. If a climate simulation seems correct when compared to conventional climate variables, it could be for the wrong reasons because of compensating errors. Such errors may not always compensate for water isotopes, so that water isotopes are helpful to detect shortcomings in the representation of physical processes. This opportunity remains largely unexplored.
Water vapor isotope measurements could also be used to tune the physical parameters on which GCM simulations rely [Mauritsen et al., 2012; Hourdin et al., 2013]. Several studies have shown the sensitivity of simulated water isotopic composition of vapor or precipitation to model parameters in cloud or convective parameterizations [Schmidt et al., 2005; Bony et al., 2008; Lee et al., 2009b]. Field et al. [2014] conducted a small set of perturbed physics experiments with the GISS GCM evaluated against different observations over the tropics. Indeed, they found that model-data agreement across the different experiments varied more strongly for mid-tropospheric δD (compared to TES), relative to more conventional observations such as precipitation, temperature and humidity (Figure 15). The spread in agreement between modeled and observed δD, for example, is more than twice that of the relative humidity in the mid-troposphere or precipitation amount. Understanding why this is the case requires further investigation, but the results do suggest that water vapor isotopic measurements may provide unique value for model evaluation.
Figure 15.
GISS GCM agreement across a small ensemble of 18 perturbed physics experiments for different observation types across the tropics for 2005–2011 [Field et al., 2014]. The metric of model-data agreement is the spatial pattern correlation between model and observations in the annual mean. The greater spread in agreement for δD suggests these measurements have unique potential beyond conventional observations for model evaluation.
5.2. Limited domain models
As with GCMs in general, isotopically-equipped GCMs are limited in performance by coarse resolution. An important development in this regard has been the implementation of water isotopologue tracers in high-resolution limited domain models, boundary conditions for which are provided by an isotopically-equipped GCM. This was first done for the regional climate model (RCM) REMOiso, by Sturm et al. [2005] at 0.5° × 0.5° resolution. The most apparent improvement was in the ability of REMOiso to capture orographic gradients in precipitation δ18O over the Alps, Pyrenees and Scandinavian Mountains that would not have been resolved by isotopically-equipped GCMs at the time. REMOiso has subsequently been applied to isotopic simulations over France [Genty et al., 2014; Labuhn et al., 2014], South America [Insel et al., 2013; Sturm et al., 2007a, b], Greenland [Sjolte et al., 2011], and Svalbard [Divine et al., 2011]. Over South America [Sturm et al., 2007a], the most significant performance improvement relative to the host ECHAM-4 GCM was a more realistic dry-season altitude effect over the Andes compared to GNIP precipitation δ18O. Similar improvements were seen in the REMOiso δ18O-temperature slope over GNIP and ice core sites in Greenland relative to the ECHAM-4 GCM [Sjolte et al., 2011]. Pfahl et al. [2012] equipped the COSMO non-hydrostatic weather forecasting model with stable water isotopologues, with a grid-size of 0:0625°, which is suitable for short integrations. They analyzed a single storm in 1986 during which snow and precipitation δ18O samples were taken along the east Coast of the US [Gedzelman and Lawrence, 1990]. COSMOiso simulations of 3-hourly accumulated precipitation δ18O were considerably better than the outer global model, accurately capturing specific synoptic features of the precipitation and vapor δ18O for a single site. The Scripps Experimental Climate Prediction Center’s Regional Spectral Model (RSM) equipped with isotopes was used to study an atmospheric river event [Yoshimura et al., 2010].
As a compromise between global models with lower resolution and limited domain models requiring externally-prescribed boundary conditions, the latest version of the isotopically-equipped LMD GCM (LMDz) [Risi et al., 2010c] has the functionality of a higher resolution regional grid nested within a coarser resolution global grid. Particularly for free-running simulations, the advantage is greater internal consistency compared to a regional model, because the fields on the coarse global model grid cannot respond to changes on the finer grid of the regional model.
General circulation models and regional models rely on physical parameterizations, e.g., a single-column, statistical representation of physical processes whose horizontal scale is smaller than that of the grid box. In particular, shallow and deep convection or boundary layer turbulence need to be parameterized. As a consequence, the isotopic composition simulated by GCMs, RCMs or SCMs are sensitive to empirical parameters involved in these parameterizations [Bony et al., 2008; Lee et al., 2009a]. This is a limitation when using such models to investigate the effect of convection or turbulence on the isotopic composition of water vapor.
In cloud resolving models (CRMs), the horizontal scale is fine enough (shorter than a few km) for deep convection to be represented explicitly [Redelsperger and Lafore, 1988]. To investigate the effect of deep convection on troposphere-to-stratosphere exchanges, Smith et al. [2006] and Blossey et al. [2010] implemented water isotopologues in the Distributed Hydrodynamic Aerosol and Radiation Modeling Application (DHARMA, Stevens and Bretherton [1996]) and in the System for Atmospheric Modeling (SAM, Khairoutdinov and Randall [2003]), respectively. The isotopic version SAM was also used to investigate the amount effect [Moore et al., 2014].
Most CRMs remain too coarse for explicitly representing shallow convection and boundary layer turbulent structures. This requires models with an even finer horizontal resolution (a few tens of meters), called large eddy simulation (LES) models. To investigate the effect of boundary layer processes on the isotopic composition of low-level vapor, Lee et al. [2012c] implemented water isotopologues in the National Center for Atmospheric Research (NCAR)-LES model [Patton et al., 2005]. In the same way that GCMs can be equipped with satellite simulators, the high horizontal (50m) and vetical (20m) resolution of their LES allowed them to simulate Keeling plots (see section 6.1.2) as would be obtained from a flux tower, and thus to test some of the assumptions underlying the method to estimate the isotopic composition of evapotranspiration. Such high-resolution simulations offer the unique opportunity to explore the interpretation of observations over small horizontal and vertical scales.
To date, only a few CRMs or LES models are equipped with water isotopologoues, though projects are ongoing to implement water isotopologues in other models such as the Weather Research and Forecasting (WRF) or the Mesoscale Non-hydrostatic (Meso-NH) models (pers. comm. J.-P. Pinty). Even for the CRMs or LES models that do have water isotopologues, the opportunities offered by these tools remain largely unexplored. CRMs and LESs have been extensively and successfully used for investigating convective and cloud processes, but for only a few cases with water isotopologues. Furthermore, CRMs or LES are valuable as a link between observations and parameterized models [Randall et al., 1996]. They can be directly compared to SCMs and thus help in the evaluation and development of parameterizations [Rio et al., 2009; Couvreux et al., 2010; Hourdin et al., 2013]. Again, this opportunity has been unexplored so far for water isotopologues.
CRMs or LES are often applied for case studies, such as those derived from observational campaigns [Bechtold et al., 2000]. The limitation in this case is that these models require initial and boundary conditions based on observations, which are often lacking for water isotopologues. Therefore, to date, the application of CRMs or LES is most promising for idealized cases [e.g., Moore et al., 2014].
5.3. Lagrangian models
GCMs, RCMs, CRMs and LESs are all Eulerian in the sense that mass is exchanged between fixed, discrete volumes. Alternatively, Lagrangian models are used to calculate the trajectory and composition of an infinitesimal air parcel in the atmosphere and, in contrast to Eulerian models, are not subject to numerical diffusion. They also more explicitly retain information about a parcel’s history, which is useful for understanding controls on the isotopic composition of vapor arriving at a site of interest. For a review of the implementation, calculations, and use of trajectories the reader is referred to Stohl et al. [1998]; Wilson and Sawford [1996]. Lagrangian trajectories can either be calculated forward or backward starting from a point in space and time and using the three-dimensional wind field to calculate the displacement either forward or backward in time. Several different Lagrangian trajectory models exist: e.g., FLEXPART [Stohl et al., 2005], HYSPLIT [Draxler and Hess, 1998], KNMI trajectory model [Scheele et al., 1996], LANGRANTO [Wernli and Davies, 1997], NAME [Jones et al., 2007], and TRAJ3D [Bowman and Carrie, 2002].
One advantage of Lagrangian models compared to Eulerian models is that estimating moisture sources [e.g., Dirmeyer and Brubaker, 1999] is computationally cheaper. This has for example been used to characterize the global hydrological cycle [Dirmeyer and Brubaker, 2007], and to estimate moisture sources for the snow that falls on top of the Greenland and Antarctic Ice Sheets under Last Glacial Maximum and at present day [Sodemann et al., 2008; Rhines and Huybers, 2014; Reijmer et al., 2002].
Lagrangian models have also been equipped with water isotopes [e.g., Helsen et al., 2004] by following the approach of Ciais [1994] simulating the isotopic fractionation during moisture uptake into an air parcel or phase transition occurring in an isolated air parcel being simulated. This has been used in trajectory calculations to simulate the isotopic composition of precipitation in Antarctica and Greenland [Helsen et al., 2006; Sodemann et al., 2008] and in water vapor in Hawaii [Hurley et al., 2012]. However, due to limited understanding and ability to parameterize post-depositional processes [e.g., Steen-Larsen et al., 2014b] several caveats have to be taken into considerations when interpreting the results together with ice core isotope records. It is therefore important to compare combined trajectory and isotope modeling directly with atmospheric water vapor isotope observations. This was carried out by Pfahl and Wernli [2008], who compared individual observed water vapor d-excess in Rehovot (Israel) with RHsst and SST in the regions where backwards trajectories simulated moisture uptake. This thereby revealed the controls on the d-excess signal. Instead of deducing the drivers on the d-excess, Steen-Larsen et al. [2015] calculated the spatial distribution of mean annual d-excess in the North Atlantic by combining the moisture uptake-weighted d-excess signal from two independent monitoring stations. It is however clear that the added value from Lagrangian trajectories can be achieved when two or more continuous water vapor monitoring stations can be connected by an air mass trajectory. A first attempt to do this was carried out by [Bonne et al., 2015], who characterized moisture uptake and transport of an atmospheric river passing over three atmospheric water vapor isotope monitoring stations. They compared the change in measured water vapor isotopic composition between monitoring stations with expected changes calculated by a distillation model using the observed changes in specific humidity and temperature to drive the model.
Hurley et al. [2012] used Lagrangian trajectories along with Eulerian last-saturation tracers [Galewsky and Hurley, 2010] to test an advection-condensation model of subtropical water vapor at Mauna Loa, Hawaii. They found that the Lagrangian and Eulerian frameworks could only be reconciled through the inclusion of moistening free tropospheric air with water vapor from the boundary layer. Their study showed how measurements of water vapor isotopic composition can be used to reconcile Lagrangian and Eulerian models for the humidity of the free troposphere.
While there have been many different approaches to forward modeling of water vapor isotopic composition, as described above, there have been fewer attempts at inverse modeling. One approach to inverse modeling of in-situ isotopic measurements was presented by Galewsky and Rabanus [2016]. Their technique used a genetic algorithm to invert observations from the Chajnantor Plateau in northern Chile to obtain the spectrum of last-saturation temperatures and moistening fractions that best fit the observations. While inverse techniques for isotopic measurements are still in their infancy, they show promise for using such datasets to obtain parameters of broad climatological interest.
With future organization of water vapor isotope monitoring stations into networks such as the NEON network (www.neonscience.org) it will be possible to combine multiple station with transport models and carry out inverse modeling to constrain processes such as surface evapotranspiration. This approach has previously been used to constrain CO2 sinks and sources [Gurney et al., 2002, e.g.].
6. Applications to atmospheric processes
One of the goals of much research into water vapor isotopic composition has been to use such measurements to understand broader issues in the atmospheric water cycle. In this section, we review several of those studies to illustrate the scope and potential of such applications. Figure 1 shows many of the processes discussed below and places them into context within the hydrologic cycle.
6.1. Boundary layer processes
6.1.1. Marine boundary layer
Due to the influence of kinetic effects, studies of water vapor isotopic composition in the marine boundary layer have particularly focused on the ability to model observed variations in the d-excess. These studies have also had the added value of improving the paleoclimate community’s ability to reconstruct past variations in the ocean conditions.
Craig and Gordon [1965] developed an expression for the isotopic composition of the evaporative flux, which was later simplified by Jouzel [1979] under the closure assumption. Due to the ease-of-use description of Jouzel [1979], significant effort has gone into benchmarking the closure assumption. The closure assumption is based on the assumption that locally all the water vapor in the boundary layer originates from the local evaporation flux. It was found using isotope-enabled GCM simulations that the closure assumption resulted in excessively low δ18O and δD of the marine boundary layer vapor but d-excess values that were too high [Jouzel and Koster, 1996]. Uemura et al. [2008] carried out one of the first studies to benchmark directly the description of Jouzel [1979] by collecting water vapor from the marine boundary layer in the Southern Ocean. They found a strong correlation with RHsst with a slope of −0.58 %o(d-excess) RHsst, which was however significantly steeper than the value prescribed for a smooth ocean surface (wind speed 3 m/s) by Jouzel [1979] of −0.43 %o(d-excess)% RHsst and the value prescribed for a rough ocean surface (wind speed 8 m/s) of −0.28%o(d-excess)/ RHsst. Using in-situ continuous observations spanning more than a full year from the Bermuda Islands and Iceland, a near perfect agreement with Jouzel [1979] was achieved (see Table 3) with slope of - 0.426 +/− 0.004 %o(d-excess) /RHsst (Bermuda Islands) and −0.466 +/−0.013 %o(d-excess) /RHsst (Iceland) [Steen-Larsen et al., 2015, 2014a]. Subdividing the dataset it was found that the slope would vary depending on season and wind direction. Surprisingly the observations from the Bermuda Islands and Iceland showed a nearly identical relationship between d-excess and RHsst indicating, contrary to earlier predictions [Jouzel, 1979], limited influence of SST [Steen-Larsen et al., 2015]. No influence of wind speed on the observed relationship between d-excess and RHsst was observed, however, a finding also supported by Benetti et al. [2015]. The strong linear correlation between d-excess and RHsst was also found from a one-month long ship-based campaign in subtropical Eastern North Atlantic Ocean (slope −0.45 %o(d-excess)/ RHsst) [Benetti et al., 2014]. An indirect estimate of the relationship between d-excess and RHsst was carried out using backwards trajectories [Pfahl and Wernli, 2008]. They obtained a slope of −0.53%o(d-excess)/ RHsst for the eastern Mediterranean, but were not able to document any relationship with SST. The documented strong relationship between d-excess and RHsst illustrates that under the assumption that the d-excess signal is conserved during transport [Bonne et al., 2015], the d-excess in paleo-climatic archives can be used to reconstruct source region conditions.
Table 3.
Slope of d-excess (per mil) versus RHsst (percent), calculated and observed.
| Value | Reference | Note |
|---|---|---|
| −0.43 | Jouzel [1979] | Calculated, for smooth surface |
| −0.28 | Jouzel [1979] | Calculated, for rough surface |
| −0.58 | Uemura et al. [2008] | Observed |
| −0.53 | Pfahl and Wernli [2008] | Observed |
| −0.464 | Steen-Larsen et al. [2015] | Observed |
| −0.426 | Steen-Larsen et al. [2014a] | Observed |
| −0.45 | Benetti et al. [2015] | Observed |
Benetti et al. [2015] introduced a multi-layer mixing model in order to account for entrainment of the lower tropospheric air into the marine boundary layer. They showed that by doing this it was possible to correctly simulate the d-excess as well as the water vapor isotopic composition, which was not possible when using the closure assumption. They used lower tropospheric water vapor isotopic composition simulated by an isotope-enabled GCM (LMDZiso) as input to their one-dimension model.
While Benetti et al. [2015] focused on the short-term (hourly) temporal variation of water vapor isotopic composition and d-excess, Steen-Larsen et al. [2015] focused on the relationship between d-excess and the water isotopologues on synoptic time scales. Using the isotopic flux described by Craig and Gordon [1965] and a box-model developed by Gat et al. [2003], previously used to describe observed isotopic variation in the Mediterranean, Steen-Larsen et al. [2015] were able to explain the observed relationship between d-excess and the isotopic composition in the marine boundary layer of the North Atlantic.
The marine boundary layer in the subtropics is strongly influenced by the trade-wind inversion. Shallow convection can transport boundary layer water vapor across the inversion, while entraining dry free tropospheric air into the boundary layer [e.g., Albrecht et al., 1979]. Bailey et al. [2013] obtained profiles of water vapor mixing ratio and isotopic composition across the trade inversion on the Island of Hawaii and showed that cloud condensate re-evaporation from clouds associated with daytime convection was required to explain the isotopic composition near the top of the mixed layer. They also found that water vapor transport from the boundary layer into the free troposphere could be understood in terms of a vertical mixing model modulated by residual layers that formed during previous mixing events.
Only one study has so far measured 17O-excess in the marine boundary layer [Uemura et al., 2010]. They showed, in agreement with theory [Craig and Gordon, 1965; Jouzel, 1979], that the 17O-excess is controlled by kinetic fraction during evaporation, and they showed a strong linear relationship between 17O-excess and RHsst. However their data are not conclusive on the effect of wind speed on the kinetic fractionation.
6.1.2. Continental boundary layer and recycling
Water vapor isotopic measurements at continental sites have been used to identify the sources of boundary layer water vapor, including continental evapotranspiration, free tropospheric water vapor, or from rainfall reevaporation [Wen et al., 2010].
Surface water vapor isotopic composition reflects the relative proportion of free tropospheric vapor, which depends on the intensity of boundary layer mixing. At the diurnal scale, surface water vapor is most depleted and has maximum d-excess during the afternoon, when boundary layer mixing is at its maximum [Lai and Ehleringer, 2010; Angert et al., 2008; Wen et al., 2010; Welp et al., 2012]. For δD and δ18O, this is consistent with free tropospheric water vapor being more depleted with altitude. For d-excess, this could be consistent either with a diurnal change in the evapotranspiration composition, or with an increasing d-excess with altitude. Measurements of d-excess profiles reaching above the boundary layer would be necessary to check the latter hypothesis. Several studies suggest that water vapor isotopic measurements could help characterize boundary layer mixing and associated structures [Noone et al., 2012; Lee et al., 2012c], but quantitative estimates have not yet been done.
Quantitative estimates based on water vapor isotopic measurements have been more successful for the partitioning of the evapotranspiration flux into its different components: bare soil evaporation and transpiration [Moreira et al., 1997; Yepez et al., 2003; Williams et al., 2004] or standing water evaporation and snow sublimation [Noone et al., 2012]. These studies rely on the estimate of the isotopic composition of the total evapotranspiration flux. This can be done through the Keeling plot approach [Keeling, 1961], in which the measured water vapor δD or δl8O is regressed against the inverse of specific humidity [Griffis, 2013]. Different values for water vapor δD or δl8O may correspond to different times of day [e.g., Moreira et al., 1997] or to different altitudes within the boundary layer [Noone et al., 2012]. This approach has several limitations [Good et al., 2012; Griffis, 2013] which could potentially be lifted with an improvement in the temporal and vertical resolution of the measurements [Noone et al., 2012]. An alternative approach is the eddy covariance method applied to isotopic measurements [Saleska et al., 2006; Sturm et al., 2012], which would outperform the Keeling plot approach if a response time shorter than a few seconds could be achieved with laser instruments [Good et al., 2012; Griffis, 2013]. The residence time in the sampling device is however a limitation.
Once the isotopic composition of the total evapotranspiration flux is estimated, the flux can be partitioned into two components, as long as the isotopic composition of these components are known. For example, in the case of the partitioning into bare soil evaporation and transpiration, the isotopic composition of bare soil evaporation can be estimated using the equation of Craig and Gordon [1965] and measurements of surface soil composition, whereas the isotopic composition of transpiration can be estimated using isotopic measurements in plant tissues [Moreira et al., 1997]. The isotopic composition of transpiration and of its variations through the day has been the subject of many studies [e.g., Flanagan and Ehleringer, 1991], to which laboratory measurements using water vapor in-situ analyzers have also contributed [Lee et al., 2007b].
At the continental scale, an important component of the water cycle is continental recycling, which is the partial return of continental precipitation back to the atmosphere through evapotranspiration. For example, the proportion of the precipitation arising from evapotranspiration over land can reach up to 85% in Siberia in summer or remain above 60% in the Congo basin all year long [Koster et al., 1986; Yoshimura et al., 2004; van der Ent et al., 2010; Gimeno et al., 2010; Goessling and Reick, 2011]. Quantifying continental recycling usually involves regional atmospheric water budgets based on reanalyses, observations or models [Brubaker et al., 1994; Eltahir and Bras, 1996; Gong and Eltahir, 1996; Bosilovich and Schubert, 2002; Dirmeyer and Brubaker, 2007; Dirmeyer et al., 2009; Gimeno et al., 2012]. A drawback of such methods is that it is difficult to accurately take into account the effect of mixing and of sub-grid scale water vapor transport, sources and sinks. Some studies used the water tagging technique to overcome this issue [Koster et al., 1986; Numaguti, 1999; Yoshimura et al., 2004], but in all cases, such water budgets remain difficult to evaluate observationally. In this context, water vapor isotopic measurements have been suggested as a way to observationally constrain continental recycling.
Water originating from the land is more enriched in heavy isotopes than the ambient water vapor [Gat, 1996]. This property contributes to the maximum enrichment that is observed by satellites over tropical land masses [Worden et al., 2007; Brown et al., 2008b; Frankenberg et al., 2009]. While lighter isotopes evaporate more easily from the ocean [Craig and Gordon, 1965], transpiration is not associated with fractionation relative to soil water because there is no fractionation during root extraction [Washburn and Smith, 1934; Barnes and Allison, 1988; Flanagan and Ehleringer, 1991] and all water extracted by the root needs to be transpired when steady state is reached after extraction [Brunel et al., 1995; Walker et al., 2001]. Soil water originates from precipitation, which is to first order at equilibrium with the ambient vapor [Field et al., 2010] and thus more isotopically enriched than the water vapor. For example, Figure 16 shows how the isotopic signature of transpired water vapor over tropical lands is distinct from that of the oceanic vapor [Risi et al., 2013]. Several studies have tried to exploit this property to infer continental recycling using isotopic measurements in the precipitation [Salati et al., 1979]. Measurements of water vapor isotopic composition should, in principle, allow us to more directly infer the evaporative origin without being disturbed by post-condensational processes [Stewart, 1975; Lee and Fung, 2008; Risi et al., 2010b], opening the prospect to more precisely constraining continental recycling [Risi et al., 2013; Sutanto et al., 2015]. Note that attempts have also been made to partition continental recycling into its transpiration and evaporation components using isotopic composition in lakes and rivers [Jasechko et al., 2013], an approach that is beyond the scope of this paper.
Figure 16.
Probability density function of the isotopic composition (δ18O and d-excess) of water vapor at the lowest model level for all tropical land locations and for all days in 2006, for total vapor (black), vapor originating from ocean evaporation (blue), vapor originating from land surface transpiration (green) and vapor originating from bare soil evaporation (pink). These probability density functions are calculated from a model simulation equipped with the water tagging technique [Risi et al., 2013].
Evaporation from bare soil is characterized by a higher d-excess (Figure 16) because kinetic fractionation during the evaporation of soil water is very strong [Mathieu and Bariac, 1996; Braud et al., 2009a, b]. In this case, the evaporation of HDO is favored by its high diffusivity. This property is the basis of studies trying to partition continental recycling into its transpiration and evaporation components [Gat and Matsui, 1991; Aemisegger et al., 2013].
Despite the potential advantages of isotopic measurements, it has proven difficult to use water vapor isotopic measurements to estimate continental recycling with a better precision than classical water budget methods [Risi et al., 2010a] because water vapor isotopic composition over land is not a single function of continental recycling, but also depends on boundary layer processes, deep convection and large-scale circulation [Frankenberg et al., 2009; Risi et al., 2010a; Lee et al., 2012c; Welp et al., 2012]. The water vapor isotopic composition is an integral over all of the relevant processes active along the trajectory, so it can be difficult to parse the contributions from individual processes. Several studies have tried to circumvent this problem by focusing on daily variability rather than on mean values, but difficulties remain [Risi et al., 2013; Aemisegger et al., 2013]. Better understanding of the combination of processes that control the isotopic composition is necessary before we can make a more quantitative use of water vapor isotopic measurements to constrain continental recycling. In this perspective, the uncertainties in the representation of moist processes in general circulation models or regional models limits our ability to understand the isotopic impact of this combination of processes [Risi et al., 2013].
6.2. Free atmosphere
6.2.1. Water vapor transport and mixing in the subtropical free troposphere
To first order, the humidity of the arid subtropical free troposphere can be understood in terms of large-scale mixing between air parcels that have been subjected to a variety of condensation and moistening histories [e.g Galewsky et al., 2005]. Predicting changes in subtropical humidity under global warming is challenging, but essential for a full picture of the water vapor feedback [Pierrehumbert et al., 2006]. Our understanding of the humidity of the free troposphere has been substantially clarified by the so-called ‘last-saturation’ concept, which approximates the water vapor mixing ratio of air by its saturation value when it was last in a cloud [Pierrehumbert et al., 2006; Hurley and Galewsky, 2010]. This concept has proved very useful, especially for understanding the controls on subtropical humidity, which is influenced by far-field processes and nonlocal mixing [Galewsky et al., 2005; Cau et al., 2007; Wright et al., 2010].
Most studies that make use of the last-saturation concept rely on reanalysis or GCM output. Given the importance of the subtropical humidity for understanding the water vapor feedback [e.g., Held and Soden, 2000], it would be useful to identify an independent dataset that could be used to constrain the processes that influence free tropospheric humidity. In principle, measurements of the stable isotopic composition of water vapor can provide such a dataset.
Galewsky and Hurley [2010] used an idealized GCM and transilient turbulence theory to place water vapor isotopic composition into a last-saturation framework and showed how water vapor isotopic composition simulated in an isotope-enabled GCM can be understood in terms of last-saturation, mixing, and moistening from the boundary layer. Their study predated datasets large enough to fully explore the implications of the theory, but such datasets are currently being collected.
Early, flask-based, measurements of water vapor isotopic composition from the summit of Mauna Kea, Hawaii, [Galewsky et al., 2007] were supplemented by an idealized GCM to show how subtropical humidity is largely controlled by mixing, but those studies consisted only of water vapor δD measurements. Some of the first continuous CRDS measurements of subtropical water vapor isotopic composition on Mauna Loa, Hawaii, and Tenerife, Canary Islands, affirmed the primacy of mixing and the last-saturation concept for subtropical humidity [Hurley et al., 2012; Noone et al., 2011; González et al., 2016]. Dyroff et al. [2015] found relatively high water vapor δ-values (δD close to −125%o) up to almost 5500 meters in several high resolution aircraft profiles measured over the Northern Subtropical Atlantic, which is consistent with strong mixing from the boundary layer.
As CRDS techniques improved, reliable measurements of water vapor d-excess became available from arid, high-altitude subtropical sites such as the Chajnantor Plateau in the northern Chilean Andes. Galewsky et al. [2011] first showed how interpretations of mixing in isotopic measurements from arid subtropical sites can be confounded by the isotopic effects of vapor deposition under supersaturated conditions at remote last-saturation sites. A conceptual model of last-saturation under supersaturated conditions followed by moistening was used to explain d-excess measurements from the Chajnantor Plateau in Samuels-Crow et al. [2014a] and was used to quantitatively constrain the supersaturation and mixing in measurements from a South American cold-air outbreak [Galewsky, 2015] using a genetic algorithm to fit a simple model to the data. Galewsky and Rabanus [2016] extended the genetic algorithm approach and applied to a longer period of the dataset to obtain the spectrum of last-saturation temperatures and moistening fractions governing the humidity at the site, thereby directly linking in-situ measurements to the last-saturation paradigm.
These studies have shown how continuous, long-term monitoring of water vapor isotopic composition can provide constraints on mixing and moistening at subtropical sites that will be useful for monitoring the water vapor feedback and will be a useful complement to other climatological measurements.
6.2.2. Stratosphere-troposphere exchange
Water in the stratosphere plays an important role in climate through its influences on radiation and ozone chemistry [Forster and Shine, 2002; Kirk-Davidoff et al., 1999]. The mechanisms for transport of water vapor from the troposphere into the stratosphere depend on transport processes in the tropical tropopause layer ”cold trap” [Fueglistaler et al., 2005; Holton and Gettleman, 2001], within the stratosphere on the speed of the slow poleward component of the Brewer-Dobson Circulation [Butchart, 2014], and between the stratosphere and troposphere in the extratropics on different exchange processes [Gettelman et al., 2011]. Rosenlof et al. [2001] showed that stratospheric humidity has increased over the last 50 years at about 1% per year, indicative of a long-term change in the transport of water vapor into the stratosphere, and water vapor isotopic studies have been brought to bear in an attempt to diagnose the mechanisms for this increase in stratospheric humidity.
There is a longstanding debate about the relative importance of the processes that govern the entry of water vapor into the stratosphere. Above about 13–14 km in the tropics, at the base of the tropical tropopause layer (TTL), the clear sky radiative heating is positive, and this diabatic heating causes air to ascend gradually. In the troposphere, convection is responsible for the vertical mixing of air and most, but not all, of the condensing water is removed by rain formation or sedimentation of cloud droplets. Air that detrains below the level of zero radiative heating (LZRH) will subside, but air that detrains above the LZRH can enter the stratosphere. If convection detrains near the LZRH, it enters the TTL and the air will be further dehydrated during its ascent to the tropopause by in-situ formation of cirrus clouds, which leads to more isotopic depletion before the water enters the stratosphere. In this scenario, the humidity of the air entering the stratosphere is controlled by the coldest temperature encountered during transport. Water detraining from deep convection can either be injected directly into the stratosphere [Sherwood and Dessler, 2000] or mix with the ambient reservoir below the tropopause [Dessler and Sherwood, 2003]. Mixing of older stratospheric air from higher latitudes that has experienced in-situ formation of H2O from CH4 oxidation can also contribute to the water budget near the tropical tropopause. Distinguishing between these processes is important, because their relative balance may have changed, and may change in the future as the climate warms.
The isotopic composition of water vapor in the upper troposphere and lower stratosphere (UTLS) is a potentially useful (and measurable) tracer of these processes. Early measurements of stratospheric water vapor isotopic composition [Johnson et al., 2001a; Moyer et al., 1996] suggested a δD of about −670%o for water vapor entering the stratosphere, which is substantially higher than would be expected for a simple Rayleigh distillation model of dehydration down to stratospheric mixing ratios. This apparent ”underdepletion” was variously interpreted in terms of the lofting and sublimation of isotopically enriched cloud ice [Moyer et al., 1996] or in terms of mixing slowly rising air from the bottom of the TTL with drier air detrained from convection [Dessler and Sherwood, 2003].
High resolution measurements of water vapor δD across the TTL have helped provide additional constraints. Kuang et al. [2003] presented remote sensing data spanning the UT and LS and showed that the water vapor δD values did not decrease in the region, despite a 4–5 fold decrease in the mixing ratio, a result that is inconsistent with a simple gradual dehydration mechanism. Webster and Heymsfield [2003] showed substantial variability below the tropopause in their in-situ measurements of δD, which they interpreted to represent a combination of both convective and gradual dehydration mechanisms.
In the UTLS over the southwest US, Hanisco et al. [2007] measured stratospheric δD between −400%o to −600%o, higher than would be expected from Rayleigh distillation to stratospheric mixing ratios. Using a simple model including the contributions of a tropical vapor source and a convective ice source, they estimated that up to 45% of the summertime stratospheric vapor over North America was of convective (but not necessarily local) origin and with considerable uncertainty related to assumptions about the tropical stratospheric δD entry value and variability in the δD of ice. Dessler et al. [2007] used a trajectory model of last saturation with a probabilistic estimate of the contributions of deep convection to ice water. They found that with the contribution of convectively lofted ice, stratospheric δD was brought into better agreement with the ATMOS retrievals when convection was capped below the cold point (but was unrealistically high, along with H2O concentrations, when convection was capped at higher altitudes). They further argued that mixing was a key process for accurately simulating TTL δD. Sayres et al. [2010] used a trajectory-based Rayleigh model that accounted for convective influence to argue that high δD over Central America could be explained by convectively lofted ice.
Several studies have examined long-term trends in H2O and δD in the stratosphere, but with sparse coverage and different measurement techniques. With aircraft-based FTIR-based retrievals, Coffey et al. [2006] found a decrease of 5 — 6%o per year between 1978 and 2005, in contrast to a well-established increase in H2O. These measurements have yet to be explained [Sherwood et al., 2010; Lossow et al., 2011], but the simple interpretation most consistent with the above studies is that an increasing stratospheric H2O trend is not due to an increase in convectively lofted ice particles sublimating in the stratosphere. Notholt et al. [2010] argued from balloon-based solar FTIR δD measurements from 1991 to 2007 at mid- and high-latitudes that ice transported through the tropopause has only a minor role in the amount of water entering the stratosphere.
More recent satellite measurements have added substantial detail to our picture of how water vapor enters the stratosphere. Steinwagner et al. [2010] presented data from the Michelson Interferomter for Passive Atmospheric Sounding (MIPAS) that showed a clear seasonal cycle in water vapor δD propagating upward from the tropical tropopause layer into the tropical stratosphere. This upward propagating signal is sometimes referred to as a ‘tape recorder’. They interpreted their results to represent a combination of gradual dehydration of air by in-situ cirrus cloud formation and seasonally varying contributions from sublimated, convectively lofted cloud ice. Using an earlier MIPAS retrieval, Payne et al. [2007] did not detect a strong stratospheric δD seasonal signal, which was partially attributed to the sparseness of the data at the time and possible data biases toward dry, more depleted conditions. This tape recorder signal was also not evident above 20 km in the ACE-FTS measurements presented by Randel et al. [2012], but they showed an overall vertical structure of δD in the tropics with a minimum near 15km of about −675%o, a small increase above this level to about −600%o and nearly constant values in the stratosphere above. They linked this structure to sublimation of lofted ice and to mixing of air from the extratropics, while Payne et al. [2007] emphasized the role of methane oxidation above the lower stratosphere.
Modeling studies have complemented these observational studies. In their GCM study of stratosphere-troposphere exchange, Schmidt et al. [2005] emphasized the role of mixing in generating water vapor δ values higher than expected from Rayleigh distillation. Their model did not include the impacts of ice lofting or convective overshooting, and they suggested that estimates of their importance may have been exaggerated. Alternatively, to the extent that such models can be compared, simulations with large-eddy [Smith et al., 2006] and cloud resolving [Blossey et al., 2010] showed that convective overshooting and ice sublimation can increase high-altitude δD, in fair agreement with observations compared to Rayleigh distillation. Eichinger et al. [2015a] also focused on stratospheric δD in their GCM simulations, suggesting that a 100%o low bias relative to MIPAS was partly due to too little ice sublimation, and also partly because the oxidation of molecular hydrogen was not included in their model. Like Schmidt et al. [2005], Eichinger et al. [2015a] detected a stratospheric δD tape recorder. They found, however, that when the model was sampled according to the ACE-FTS coverage, that the tape recorder was absent, which possibly explains the lack of that feature in Randel et al. [2012]. With further diagnosis and sensitivity testing, Eichinger et al. [2015b] found that that the tape recorder resulted from a mixing of moisture from the TTL and extratropical air with higher δD from methane oxidation. Somewhat in contrast to previous analytical and Lagrangian models, however, they found that the effect of parameterized convection was to lower stratospheric δD, but that large-scale cloud activity caused an increase in stratospheric δD. It is possible that these results are parameterization specific, having to do, for instance, with how convectively-originating moisture is transferred to the large-scale cloud reservoir as it detrains from the tops of parameterized deep convective clouds.
While the above discussion focused on transport of water vapor from the troposphere into the stratosphere, intrusions of stratospheric air into the troposphere can be generated by Rossby wave breaking on the subtropical tropopause [Chen, 1995; Postel and Hitchman, 1999] and are responsible for mixing very dry, ozone rich stratospheric air into the tropical upper troposphere (UT). This process is an important mechanism for stratosphere-troposphere exchange and is associated with the generation of thin tongues of high potential vorticity (PV) air that can intrude into the subtropics and tropics [McIntyre and Palmer, 1983]. Stratospheric air intrusions are also linked with the transport of very dry, ozone-rich air from the stratosphere into the troposphere [Yoneyama and Parsons, 1999; Waugh, 2005]. Galewsky and Samuels-Crow [2014] used surface measurements of the isotopic composition of water vapor in a stratospheric intrusion to constrain the dilution of such intrusions as they mix into the troposphere. Modeling of those measurements using the FLEXPART model [Stohl et al., 2005] showed that the stratospheric intrusion mixed with an upper-tropospheric background air mass before additionally mixing with boundary layer air.
6.2.3. Stratospheric processes
Air entering the stratosphere has only about 3–4 ppmv of water vapor and increases by about 1–2 ppmv within the stratosphere owing to the photochemical oxidation of methane [e.g., Dessler et al., 1994] and to a lesser extent molecular hydrogen [Payne et al., 2007]. The isotopic composition of this photochemically produced water vapor is controlled primarily by the [D]/[H] ratios of the methane and the oxygen isotopic composition of the oxygen reservoir. The mixing and transport pathways of tropospheric water vapor entering the stratosphere and how that mixing ratio is altered by photochemical effects are poorly constrained, and several studies have used measurements of water vapor isotopic composition to elucidate the processes [Johnson et al., 2001a, b; Zahn et al., 1998; Zahn, 2001].
Within the stratosphere, water vapor δD increases from −660%o at the tropopause to about −440%o above 40 km, with the increase in δ values attributed to about 40% of water vapor produced from the oxidation of methane [Ridal, 2002; Zahn et al., 2006]. Oxygen isotope ratios in water vapor also show a vertical increase in the stratosphere even more pronounced than the increase in hydrogen isotope ratios [Zahn et al., 2006, and references therein], with δ17O and δ18O reaching positive values with a vertical increase of 85%o and 150%o, respectively. Modeling studies suggest that photochemical effects are expected to induce a Δ17O anomaly of between 0 — 30%o depending on a variety of oxygen isotope exchange rates [Zahn et al., 2006; Franz and Röckmann, 2005]. Franz and Röckmann [2005] presented measurements of Δ17O that averaged about 0.13%o, with a standard deviation of only 0.95%o, suggesting that the exchange between NO2 and water vapor is negligible.
Intriguingly, these studies of stratospheric water vapor Δ17O have been invoked to suggest stratospheric inputs into the troposphere in studies of snow pit data from Vostok, Antarctica [Winkler et al., 2013] and water vapor from Alert, Canada [Lin et al., 2013]. The use of Δ17O as a tracer of stratospheric water vapor in the troposphere is still in its infancy and warrants further study.
6.3. Tropical weather and climate
6.3.1. Deep convection
In the tropics, most of the precipitation arises from deep convection. The observed isotopic variability for most weather and climate phenomena is dominated by convective processes. The effects of deep convection on water vapor isotopic composition are summarized in Figure 17a. Deep convection depletes the lower-tropospheric water vapor, through rain reevaporation and unsaturated downdrafts, contributing to the amount effect. Deep convection is also known to enrich the isotopic composition of the upper troposphere, through detrainment and sublimation of ice crystals. In the mid-troposphere, the impact of convection is probably a mixture of the effects occurring in the lower and in the upper troposphere, in proportions that depend on the depth of the convective mixing and on the height of convective detrainment [Lacour, 2015].
Figure 17.
Effect of deep convection and several tropical weather and climate features on the isotopic composition of water vapor: a) deep convection, b) monsoon, c) Madden-Julian Oscillation, d) tropical cyclone.
Based on sensitivity of the isotopic composition of water vapor to convective processes, several studies have tried to use water vapor isotope measurements to better understand convective processes. For example, using TES measurements, Worden et al. [2007] tried to estimate the fraction of the vapor arising from rain reevaporation over tropical oceans. A difficulty of such studies is to bridge the gap between the very simple, q-δD framework and the complexity of the underlying processes. Observed mixing ratios result from the mixture of diverse air masses with different origins, all of which may have been subjected to different processes. The gap can be partially bridged by analyzing processes along air mass trajectories. Assuming air masses are isolated along their trajectories, idealized curves in the q-δD framework can then be applied [Brown et al., 2008b].
6.3.2. Monsoons
Water vapor isotopic composition in monsoon regions have been studied with the aim of better understanding the present-day water budget of these regions (Figure 17b). Water vapor in monsoon regions comes from evaporation over nearby oceanic basins, and is depleted by deep convection along its way [Vimeux et al., 2005; Risi et al., 2008b; Gao et al., 2011]. Continental recycling recharges air masses with enriched water vapor [Yoshimura et al., 2004; Risi et al., 2010a; Tierney et al., 2011a; Lee et al., 2012b]. Large-scale subsidence at the edges of monsoon regions, or in monsoon regions during the dry season or dry spells of monsoon seasons, dehydrate the air and deplete the water vapor [Frankenberg et al., 2009; Risi et al., 2010a]. Other sources of water vapor, such as sources from mid-latitudes westerlies, can also provide their own isotopic signatures [Tian et al., 2001]. Due to the specific isotopic signatures of these different water sources (Figure 17b), several studies have tried to use water vapor isotopic measurements to provide information on the contributions of the different water sources to the water budget [e.g., Risi et al., 2010a; Lee et al., 2012b; Galewsky and Samuels-Crow, 2015]. Such studies typically combine water vapor measurements and modeling experiments using the water tracking capability. However, so far, obtaining quantitative information with a precision greater than that obtained from more conventional methods (e.g., water budgets based on reanalyses) has been hampered by the difficulty to estimate the exact effect of each process on the water isotopic composition.
6.3.3. Madden-Julian Oscillation
The Madden-Julian Oscillation (MJO) is the dominant mode of intraseasonal variability in the tropics [Madden and Julian, 1971, 1972; Zhang, 2005]. It is characterized by the propagation of a zone of active convection from the western Indian ocean to the central Pacific, with a typical periodicity of 30 to 90 days. Typically, an MJO event starts with deepening shallow convection, followed by deep and organized convection, stratiform clouds and then back to a quiescent weather occasionally disturbed by isolated deep convective systems [Benedict and Randall, 2007], (Figure 17c). Climate models have persistent difficulties in simulating the MJO and its characteristics [Lin et al., 2006; Hung et al., 2013]. Initiation and propagation of the MJO involve processes that are difficult to simulate by models, such as shallow to deep convection transition, convection-humidity interactions, sea-atmosphere interactions or cloud-radiative interactions [Bony and Emanuel, 2005; Del Genio et al., 2012; Kim et al., 2012; DeMott et al., 2015]. Therefore, it has been proposed that the measurement and simulation of water isotopologues could help better document the sequence of physical processes during an MJO event and better quantify their relative contributions [Berkelhammer et al., 2012].
To do so, composites of meteorological and isotopic variables during MJO events have been computed based on observations, and the added value of water isotopic measurements has been assessed in the q-δD framework [Berkelhammer et al., 2012]. The typical evolution of δD in the lower and middle troposphere during MJO events reflect the evolution of moistening processes and cloud types (Figure 17c). Water vapor δ values increase during the suppressed and shallow convection phases while humidity builds up and decrease during the convective phase while humidity is maximum. It remains low during the stratiform phase, while humidity recovers its low value. Finally, δD returns to higher values several days later while humidity is minimum [Kurita et al., 2011]. The fact that the isotopic evolution reflects the relative timing of convective and cloud processes is promising and may help to better document the associated physical processes and evaluate their representation in models.
6.3.4. Organized convective systems: squall lines, tropical cyclones
Water vapor and precipitation isotopic measurements have been made at the intra-event time scale within organized convective systems with the aim of understanding how convective processes affect water isotopic composition, and in turn assess the extent to which isotopic measurement can help better constrain convective processes. The advantage of such systems is that the different processes vary in space with a standard pattern. For example, water vapor and precipitation composition along squall lines has been analyzed [Taupin and Gallaire, 1998; Risi et al., 2010b; Tremoy et al., 2014], and has allowed a better understanding of the isotopic effects of rain reevaporation, unsaturated downdrafts and meso-scale downdrafts.
Water vapor has also been analyzed within [Lawrence and Gedzelman, 1996; Fudeyasu et al., 2008] or in the vicinity of tropical cyclones [Herbin et al., 2009]. Water vapor is isotopically depleted as air masses converge within the rain bands (Figure 17d), reaching extremely low δ values in the inner rain bands [Fudeyasu et al., 2008]. It has been shown that in tropical cyclones, diffusive exchanges between rain drops and water vapor deplete the vapor very efficiently, due to the very moist air and to the intense flux of rain [Lawrence et al., 2002]. In contrast, the water vapor is isotopically enriched in the eye. Evaporation of sea spray droplets, which does not fractionate as long as droplets evaporate in totality, enriched the water vapor [Lawrence et al., 2004; Fudeyasu et al., 2008].
6.4. Mid-latitude systems
Compared to tropical and polar settings, there have been relatively few studies focusing on the application of water vapor isotopic measurements to mid-latitude weather systems. Yoshimura et al. [2010] used an isotope-enabled regional model and measurements of precipitation isotopic composition to study the microphysics of an atmospheric river event that affected California in 2005. They linked the observed initially high δ values in precipitation, and their subsequent drop, to kinetic isotopic exchange between rain drops and the water vapor below cloud base. While their modeling approach was somewhat limited, the study shows some of the promise for using isotopic measurements to constrain microphysical processes in mid-latitude weather systems.
Galewsky [2015] used in-situ measurements of water vapor isotopic composition from a high altitude subtropical site in Chile to constrain the long-range transport of water vapor from a midlatitude wave train during a South American cold-air outbreak. By combining isotopic measurements and modeling with numerical weather simulations and back-trajectory calculations, they were able to constrain the last-saturation temperature over the South Pacific, the supersaturation at the point of last saturation, and the degree of moistening during isentropic transport to the subtropics. This study marked one of the first applications of water vapor isotopic measurements to the last-saturation paradigm of free tropospheric humidity.
6.5. Polar weather and climate
Water vapor isotope observations in polar regions have been focused on understanding the climate fingerprint in ice core isotope records and, more generally, characterization of the polar atmospheric hydrological cycle. With the use of backwards trajectories and water tagging in GCM simulations, it is possible to combine the measured water vapor isotopic composition with estimates of moisture origin to show that water vapor originating from the Arctic carries a high d-excess fingerprint [Steen-Larsen et al., 2015, 2013; Kurita, 2011]. Kopec et al. [2014] used water vapor isotopic observations from the west coast of Greenland to characterize the diurnal structure and variability of the katabatic wind. Concomitant water vapor isotope measurements (Bermuda, South Greenland, and North-West Greenland Ice Sheet) along an atmospheric river event starting from the subtropical western North Atlantic region and transporting moisture up on the Greenland Ice Sheet showed a clear water vapor isotopic signal as the warm moist air mass from the subtropical region displaced the cold dry Arctic air masses [Bonne et al., 2015]. These finding have offered the potential to trace and differentiate the atmospheric water vapor contributions that make up the Arctic hydrological cycle.
The cause of high d-excess in Arctic water vapor is not clear. It has been hypothesized that the high d-excess is formed at the sea ice margin and coastline along adjacent continents, where cold dry air masses meet the relatively warm ocean, thereby creating strong kinetic evaporation due to the vapor pressure difference between the air and the saturated skin layer of the ocean. This strong kinetic evaporation is then expected to result in kinetic fractionation and high d-excess levels in the water vapor. Simulations using an isotope-enabled GCM nudged to reanalysis wind pattern cannot accurately simulate the observed d-excess [Steen-Larsen et al., 2014a, 2013; Bonne et al., 2014]. It was hypothesized that the model shortfall is related to treatment of the evaporation from the Arctic Ocean. Bintanja and Selten [2014] showed that for the simulated future Arctic evaporation a large inter-model variability exists in the sensitivity to temperature increase caused by greenhouse gas emissions. It was shown that for a RCP 4.5 scenario using 33 CMIP5 climate models that the model dependent climate sensitivity for evaporation in the Arctic varied between 5 and 15%/K. This large inter-model variation results in increased uncertainty for projections of future Arctic climate.
Only a few Δ17O measurements of the atmospheric water vapor in the Arctic have been obtained [Steen-Larsen et al., 2014b; Landais et al., 2012; Lin et al., 2013]. It was argued that high Δ17O measurements in water vapor collected at Alert station were indicative of stratospheric air inflow [Lin et al., 2013], a conclusion that has been debated [Miller, 2013]. The relatively few cryogenically collected samples presented by Steen-Larsen et al. [2014b] and Landais et al. [2012] show a positive correlation between the Δ17O and d-excess, in agreement with the expected influence of kinetic fractionation effects during evaporation and snow crystal formation. This illustrates the potential for constraining parameterizations of kinetic effects by combining 17O-excess, d-excess, and single isotopologue measurements of atmospheric water vapor. This could specifically be important when improving parameterization of Arctic cloud physics in GCMs. As illustrated by Cesana and Chepfer [2012], CMIP5 models cannot correctly simulate the seasonal cycle of low Arctic clouds. This is critical owing to the net heating of the surface associated with Arctic low clouds [Engström et al., 2014], an effect clearly illustrated by the low level clouds contributing to melt on 98% of the Greenland Ice Sheet surface during the Atmospheric river event in July 2012 [Bennartz et al., 2013].
6.6. Paleoclimate
Many paleoclimate proxies depend, in one way or another, on the isotopic composition of precipitation. Interpretation of paleoclimate archives depends on understanding the full suite of processes that govern the isotopic composition of precipitation. Studies of present-day water vapor and its isotopologues can provide important context for interpreting such records that is difficult with studies of precipitation alone. In this section, we review some of the ways that that the measurement and simulation of water vapor isotopic composition have been used to improve our understanding of paleoclimate proxies.
6.6.1. Polar
Beginning in the 1960s, ice core isotope records drilled in Greenland and Antarctic have provided unprecedened insight into the variability of the climate system, ranging from the last millennia e.g [Vinther et al., 2010] to the last ≈800,000 years [e.g., Jouzel et al., 2007]. The reconstruction of the past climate has relied more or less on present day empirical relationships between the temperature and the isotopic composition in the ice [e.g., Dahl-Jensen et al., 2013].
Ice core signals are also influenced by changes in precipitation seasonality and regional circulation patterns [Sturm et al., 2010]. Isotopically-equipped GCMs have been an important tool for quantifying these influences. Using the GISS II GCM, but with the addition of moisture source tagging from Koster et al. [1992], Charles et al. [1994] showed that in addition to temperature, changes in atmospheric circulation between present-day and LGM could also induce an isotopic response. Over Greenland, for example, they found that the relative contribution of high δ18O moisture from the Atlantic increased under LGM conditions, which offset the decrease in δ18O due to colder temperatures.
Following White et al. [1997] analysis of different factors influencing ice core δl8O at Summit, Werner et al. [2000] used model simulations to show that lower δ18O values were associated with a positive North Atlantic Oscillation (NAO) phase, emphasizing that precipitation isotope variability at a given site is influenced by regional climate patterns and not just local temperature.
One important paleoclimate application of isotopically-equipped GCMs was to resolve the difference between Greenland LGM temperatures reconstructed from boreholes and from a classical, spatially calibrated δ18O thermometer, which indicated temperatures 10K warmer than from boreholes. Using ECHAM-4, Werner et al. [2000] found that a more zonal winter flow under LGM conditions reduced the relative contribution of winter precipitation over Greenland, leading to a ‘warmer’, more summer like signal in the ice core. Using the fully-coupled GISS ModelE simulations, LeGrande and Schmidt [2009] examined the isotopic response to external changes in orbital parameters, greenhouse gas composition and land ice coverage at 1000-year time-slice intervals during the Holocene. They found that lower Greenland precipitation δ18O due to colder temperatures was offset by the presence of the Laurentide ice sheet, which directed moisture arriving from the Pacific southward, and increasing the relative contribution of local, North Atlantic moisture undergoing less isotopic depletion.
At a higher temporal resolution, snow falling on top of the ice sheets has been collected on event and sub-event time-scales in order to quantitatively understand the relationship between the climate state and the isotopic composition [Fujita and Abe, 2006; Grootes and Stuiver, 1997; Steen-Larsen et al., 2011]. Owing to the intermittency of the precipitation events, quantifying the climate fingerprint in the snow isotopic composition is difficult. However, measuring the isotopic composition of the intermediate product of the hydrological cycle (the water vapor) instead of the end product (the precipitation), offers the possibility of improving the constraints on the hydrological processes making up the ice core isotope records. Cryogenic samples collected with 12h resolution showed that the variability in the water vapor isotopic composition on synoptic time scales was comparable to the magnitude of the inter-seasonal cycle in the snow pack and during snowfall events the water vapor isotopic composition would follow the isotopic composition of the snow [Grootes and Stuiver, 1997; Steen-Larsen et al., 2011]. In general it was found that the water vapor was in isotopic equilibrium with the snow surface. With the availability of commercial water vapor isotope analyzers in recent years it became possible to measure with high accuracy and precision the water vapor isotopic composition on hourly times scales. Steen-Larsen et al. [2013] presented the first continuous record of water vapor isotope observations from the polar regions. They documented a strong diurnal cycle and gradient in the near surface water vapor isotopic composition above the ice sheet. This diurnal cycle was interpreted in terms of interactions between water vapor in the atmospheric boundary layer and the snow surface. Indeed it was shown by Steen-Larsen et al. [2014b] that in between precipitation events, the snow surface isotopic composition would follow the synoptically driven variation in the atmospheric water vapor isotopic composition. This conclusion questions the normal assumption that the ice core isotope signal is governed by the precipitation isotope signal. The exact mechanism governing the transfer of the atmospheric water vapor isotope signal to the snow surface isotopes is still not understood; however, it is hypothesized that snow metamorphosis causes the snow grains to take up the interstitial water vapor, which is continuously replaced by the synoptic driven atmospheric water vapor, thereby transferring the atmospheric water vapor isotopic composition into the snow isotope signal [Steen-Larsen et al., 2014b]. Solving how the ice core isotope signal is related to the climate offers the possibility of reconstructing more than just the temperature. Indeed, it was shown using δ15N gas isotope measurements that the isotope-temperature relationship was neither stable in time nor in space e.g., [Kindler et al., 2014; Guillevic et al., 2013].
6.6.2. Tropics
In the tropics, the isotopic composition of precipitation can be archived in ice cores [Thompson et al., 2000], speleothems [McDermott, 2004], shelly fossils [Eagle et al., 2013], cellulose [McCarroll and Loader, 2004], leaf waxes [Tierney et al., 2008] or ground waters [Gasse, 2000].
Water isotopic records in the tropics were first interpreted in terms of temperature [Thompson et al., 1989, 1998]. This interpretation was inspired by studies from polar ice cores [Jouzel, 2003]. The similarity between the isotopic signals recorded in all tropical records suggest that a global-scale feature is recorded, which supports this interpretation. For example, all tropical ice cores records show lower δ values at the Last Glacial Maximum [Thompson et al., 2000]. In addition, the amplification of temperature changes with altitude may explain why the strongest signals are recorded in high altitude archives [Poulsen and Jeffery, 2011].
In contrast, more recent studies have interpreted tropical isotopic records as precipitation proxies [Vuille et al., 2003; Hoffmann et al., 2003]. This interpretation is inspired by the fact that at the spatial, seasonal, intra-seasonal and inter-annual time scales, precipitation δ18O is anti-correlated with the precipitation amount.
Over the Asian Monsoon region, LeGrande and Schmidt [2009] used coupled AOGCM simulations to attribute changes in the precipitation δ18O to the strength of moisture export out of the tropics. In East Africa, coupled simulations have also been useful in interpreting paleoisotopic archives in terms of shifting moisture sources [Lewis et al., 2010; Tierney et al., 2011b]. Over longer time scales, Caley et al. [2014] used intermediate-complexity modeling simulations to separate ice-sheet coverage and orbital changes on precipitation δ18O over the Asian Monsoon region, also nothing that strength of the precipitation amount effect weakens moving away from the Tibetan Plateau.
At lower latitudes, isotopic signatures of the El Nino-Southern Oscillation (ENSO) were simulated over South America by Vuille and Werner [2005] and across the tropics more generally by Brown et al. [2006] and Tindall et al. [2009]. The isotopic signature of the Indian Ocean Zonal Mode over East Africa was identified by Vuille et al. [2005a]. The influence of the strength of the Asian Monsoon on δ18O values over the Tibetan Plateau was examined by Vuille et al. [2005b].
Unlike studies focusing on precipitation, measurements of water vapor isotopic composition provide continuous records, giving access to processes occurring between precipitating events and providing a more comprehensive context for the interpretation of proxy records. The global coverage provided by satellite measurements allows for the interpretation of isotopic variations along the complete air mass trajectory to proxy sites. Using water vapor measurements by TES, Samuels-Crow et al. [2014b] and He et al. [2015] analyzed how the isotopic signal is modified along trajectories towards sites of paleoclimatic interest in the Andes and in the Himalayas respectively. Both highlighted the key role of deep convection upstream of proxy sites.
The main limitation of these studies is that even if we understand perfectly well what controls the isotopic composition at the intra-seasonal, seasonal and inter-annual time scales for the present-day climatic state, this does not ensure that we understand the controls on isotopic variations on much longer time scales, e.g., glacial/interglacial time scales. Such studies would thus benefit from being combined with paleoclimatic modeling studies.
Due to diffusive exchange through the plan stomata, the isotopic composition of water vapor has a direct impact on the composition of plant tissues [Dongmann et al., 1974], and thus on the composition of cellulose and leaf wax archives [Sachse et al., 2009], although this has largely been ignored so far. Therefore, understanding the isotopic composition of water vapor is crucial for the interpretation of these proxies.
7. Perspectives and opportunities
As suggested by Dessler and Sherwood [2003] and Sayres et al. [2010], any complete model of water vapor mixing ratio should also explain the isotopic composition of the water vapor. A model may balance the effects of moistening, drying and transport to predict the correct humidity, but an isotopic constraint can help to determine if it is doing so for the wrong reasons and, subsequently, help to identify compensating errors. Until recently, there have been too few measurements to constrain models in this way, but this has changed with the significant increases in the availability of ground, aircraft and space-based measurements of water vapor isotopologues described in Section 3. We argue that these isotopic measurements have become mature enough to be more widely used to understand the atmospheric branch of the hydrological cycle in general.
For example, models of the controls on water vapor mixing ratios [e.g., Pierrehumbert et al., 2006; Sherwood et al., 2010], particularly in the subtropics [Galewsky et al., 2005], are an important framework for understanding a key uncertainty in climate sensitivity, and will benefit from additional isotopic analysis as described in Section 6.2.1. The controls on stratospheric water vapor are critical to understanding Earth’s radiation balance [Forster and Shine, 2002; Kirk-Davidoff et al., 1999], but remain uncertain [Fueglistaler et al., 2005; Holton and Gettleman, 2001]. The full wealth of satellite retrievals of HDO in the UTLS is starting to be applied to idealized budgets of stratospheric water vapor as described in sections 6.2.3 and 6.2.4, furthering the earlier work of Moyer et al. [1996] for which far less data was available. Other than Eichinger et al. [2015a], little work has been done to that end with full-complexity climate models, as proposed by Schmidt et al. [2005].
Similarly, isotopic constraints have shown early promise in better separating processes contributing to convective organization as described in sections 6.3, but this line of inquiry also remains in its infancy. As described in Section 6.1.2, there is also value in incorporating near-surface isotopic measurements for partitioning evaporation and transpiration over the land surface. These ideas extend more generally to improved characterization of the terrestrial water and carbon cycles, especially given the advent of global satellite measurements of biomass, XCO2, and plant fluorescence measurements that provide direct constraints on carbon cycling [Saatchi et al., 2013; Frankenberg et al., 2011; Crisp et al., 2004] and are directly linked to transpiration and its effect on regional hydrology.
As described in section 5.2, GCMs will benefit from the out-of-sample comparisons that isotopic data provide, particularly in understanding how unresolved moist processes contribute to the spread in future climate states [Sherwood et al., 2014] and also in interpreting paleoclimate archives as in Lee et al. [2012b]. Such studies would benefit from more advanced model inter-comparisons of isotopically-enabled GCMs. In particular, isotopic behavior at the daily scale can be informative on the model representation of convective processes. An inter-comparison beyond SWING2 that includes higher frequency outputs would be very valuable.
Another axis of research involves testing model behavior against past climatic variations. Given the importance of isotopic archives, an inter-comparison that includes paleoclimatic simulations, such as an isotopic version of PMIP3, would be needed. More generally, including water isotopes in at least some of the simulations performed for CMIP6 would open great opportunities, both for the evaluation of moist processes in the present-day climate and for paleoclimatic applications. Furthermore, most model-driven paleo proxy analyses that have been done have focused on one type of proxy at a time, which limits the inferences that can be made about large-scale climate changes. Recent efforts such as LeGrande and Schmidt [2009] to combine different types of proxies, in their case ice-cores and speleothems, and the more recent multiproxy analysis from the last millennium of Hakim et al. [2016] are promising steps. Further work in this direction will benefit from observational syntheses of multiple proxies, for example the combined analysis of speleothem, ice core and groundwater δ18O across all seven continents of Jasechko et al. [2015]. Proxy system models [Evans et al., 2013; Dee et al., 2015] provide a means with which to estimate proxy-specific δ18O responses to different forcings using climate models, which we expect will become the predominant approach to paleo-archive interpretation in the near future.
A hierarchy of isotopic models are now available from idealized models to General Circulation Models and cloud resolving models. The understanding of the various controls on water vapor composition should benefit from using this hierarchy of models, as has the understanding of cloud and convective processes [Randall et al., 2003]. In particular, idealized modeling, general circulation modeling and cloud resolving modeling should help fill the gap between simple theoretical frameworks and the complexity of the real world. Idealized modeling studies, such as those presented in Bolot et al. [2013] and Blossey et al. [2010] can link the basic processes of equilibrium and kinetic fractionation to fundamental atmospheric processes like convection and cloud microphysics. In addition, laboratory studies can now take advantage of the flexibility offered by laser absorption instruments to improve our understanding of kinetic processes [e.g., Lamb et al., 2015]. Such experiments have the potential to expand the palette of processes that can be used to interpret water vapor isotopic measurements.
All of these efforts will benefit from more, and more systematically organized, isotopic measurements. Despite the rapid increase in the use of these data for investigating the water cycle, many of these new water vapor isotopic data sets were created opportunistically from measurements intended for other Earth Science research objectives. A better synergy between different kinds of measurements will help address questions in a more comprehensive way. For example, the study of cloud processes would benefit from collocated satellite measurements of water vapor, water vapor isotopic composition and 3-dimensional cloud properties. The quantification of convective transport processes would benefit from the synergy between measurements of humidity, water vapor isotopes and chemical tracers such as ozone or CO. Satellite retrievals of water vapor isotopes would benefit from considering the spectral requirements for high quality measurements alongside other trace gases at the mission design stage. Since space-based observations are very cost-intensive, international cooperation or the involvement of international organizations is indispensable. EUMETSAT’s commitment to operate MetOp/IASI and follow-up instruments in the context of EPS-SG (EUMETSAT Polar System - Second Generation), offers a unique possibility: all these spectra can be used for retrieving free tropospheric {q, δD} pairs on global scale, each day and from 2007 to at least 2030. The prospect of using remote sensing isotope observations for model evaluation and tuning warrants the development of more sophisticated retrieval simulators, which exist for modern cloud retrievals [Bodas-Salcedo et al., 2014], but not for isotopic composition (or trace gases in general).
Progress in measuring and will increase the scope for improving our understanding of the processes that govern atmospheric water vapor with deuterium excess and 17O excess as additional, second order constraints. Most long-term in-situ measurement sites are in the Northern Hemisphere. There is clearly a research opportunity in expanding such measurements into the tropics and the Southern Hemisphere, especially into Africa, Australia, Indonesia, and Antarctica. Some efforts along these lines are already underway, but an expanded presence of in-situ measurements in the southern hemisphere would help constrain a variety of important processes including ENSO and the Madden-Julian Oscillation.
The network of in-situ measurements has provided a remarkably high frequency and high precision record of water vapor isotopic composition, but these instruments do not yet follow the same standardization protocols, nor is there any straightforward way to access the data to explore global or regional phenomena or inter-compare datasets. We suggest that the community may benefit from the development of a cooperative network along the lines of AERONET (for Sun photometry measurements) or NDACC (for the measurement of atmospheric trace gases) in which there are established standards for instrumentation, calibration, data processing, and data distribution. Such a network need not maintain heavy investments in instrumentation or infrastructure, but would provide a unified framework for emerging in-situ datasets.
Acknowledgments
This work partially supported by NSF-AGS award 1158582 to JG and NASA Energy and Water Cycle Grant NNH13ZDA001N to RF (PI A. LeGrande). MS is supported by the European Research Council under the European Community’s Seventh Framework Programme (FP7/2007-2013) / ERC Grant agreement number 256961. All of the data presented in this paper were obtained from the cited references.
Footnotes
Publisher's Disclaimer: This article has been accepted for publication and undergone full peer review but has not been through the copyediting, typesetting, pagination and proofreading process, which may lead to differences between this version and the Version of Record. Please cite this article as doi:10.1002/2015RG000512
8. * References
- Aemisegger F, Pfahl S, Sodemann H, Lehner I, Seneviratne SI, and Wernli H (2013), Deuterium excess as a proxy for continental moisture recycling and plant transpiration, Atmospheric Chemistry and Physics Discussions, 13 (11), 29,721–29,784. [Google Scholar]
- Albrecht B, Betts A, Schubert W, and Cox S (1979), Model of the Thermodynamic Structure of the Trade-Wind Boundary Layer: Part I. Theoretical Formulation and Sensitivity Tests, Journal of the Atmospheric Sciences. [Google Scholar]
- Angert A, Lee J-E, and Yakir D (2008), Seasonal variations in the isotopic composition of near-surface water vapor in the eastern Mediterranean, Tellus B, 60 (4), 674–684. [Google Scholar]
- Araguás-Araguás L, Froehlich K, and Rozanski K (2000), Deuterium and oxygen-18 isotope composition of precipitation and atmospheric moisture, Hydrological Processes, 14 (8), 1341–1355. [Google Scholar]
- Baer DS, Paul JB, Gupta M, and O’Keefe A (2002), Sensitive absorption measurements in the near-infrared region using off-axis integrated cavity output spectroscopy, Applied Physics B, 75, 261–265. [Google Scholar]
- Bailey A, Toohey D, and Noone D (2013), Characterizing moisture exchange between the Hawaiian convective boundary layer and free troposphere using stable isotopes in water, Journal of Geophysical Research, 118, 8208–8221. [Google Scholar]
- Bailey A, Noone D, Berkelhammer M, Steen-Larsen HC, and Sato P (2015a), The stability and calibration of water vapor isotope ratio measurements during long-term deployments, Atmospheric Measurement Techniques Discussions, 8 (5), 5425–5466. [Google Scholar]
- Bailey A, Nusbaumer J, and Noone D (2015b), Precipitation efficiency derived from isotope ratios in water vapor distinguishes dynamical and microphysical influences on subtropical atmospheric constituents, Journal of Geophysical Research: Atmospheres, doi: 10.1002/2015JD023403, 2015JD023403. [DOI] [Google Scholar]
- Barkan E, and Luz B (2005), High precision measurements of O-17/O-16 and O-18/O-16 ratios in H2O, Rapid Communications In Mass Spectrometry, 19 (24), 3737–3742. [DOI] [PubMed] [Google Scholar]
- Barkan E, and Luz B (2007), Diffusivity fractionations of (H2O)-O-16/(H2O)-O-17 and (H2O)-O-16/(H2O)-O-18 in air and their implications for isotope hydrology, Rapid Communications In Mass Spectrometry, 21 (18), 2999–3005. [DOI] [PubMed] [Google Scholar]
- Barnes CJ, and Allison GB (1988), Tracing of Water-Movement in the Unsaturated Zone Using Stable Isotopes of Hydrogen and Oxygen, Journal of Hydrology, 100 (1–3), 143–176. [Google Scholar]
- Barthlott S, Schneider M, Hase F, Blumenstock T, Kiel M, Dubravica D, García OE, Sepúlveda E, Mengistu Tsidu G, Takele Kenea S, Grutter M, Plaza EF, Stremme W, Strong K, Weaver D, Palm M, Warneke T, Notholt J, Mahieu E, Servais C, Jones N, Griffith DWT, Smale D, and Robinson J (2016), Tropospheric water vapor isotopologue data (HÔ, Hl,8O and HD16O) as obtained from ndacc/ftir solar absorption spectra, Earth System Science Data Discussions, 2016, 1–25, doi: 10.5194/essd-2016-9. [DOI] [Google Scholar]
- Bastrikov V, and Steen-Larsen HC (2014), Continuous measurements of atmospheric water vapor isotopes in Western Siberia (Kourovka), Atmospheric Measurement Techniques, 7 (6), 1763–1776, doi: 10.5194/amt-7-1763-2014. [DOI] [Google Scholar]
- Bechtold P, Redelsperger JL, Beau I, Blackburn M, Brinkop S, Grandper JY, Grant A, Gregory D, Guichard F, How C, and Ioannidou E (2000), A GCSS model intercomparison for a tropical squall line observed during toga-coare. II: Intercomparison of single-column models and a cloud-resolving model, Quarterly Journal of the Royal Meteorological Society, 126 (564), 865–888. [Google Scholar]
- Benedict JJ, and Randall DA (2007), Observed characteristics of the MJO relative to maximum rainfall, Journal of the Atmospheric Sciences, 64 (7), 2332–2354. [Google Scholar]
- Benetti M, Reverdin G, Pierre C, Merlivat L, Risi C, Steen Larsen HC, and Vimeux F (2014), Deuterium excess in marine water vapor: Dependency on relative humidity and surface wind speed during evaporation, Journal Of Geophysical Research-Atmospheres, 119 (2), 584–593. [Google Scholar]
- Benetti M, Aloisi G, Reverdin G, Risi C, and Sèze G (2015), Importance of boundary layer mixing for the isotopic composition of surface vapor over the subtropical North Atlantic Ocean, Journal Of Geophysical Research-Atmospheres, 120 (6), 2190–2209. [Google Scholar]
- Bennartz R, Shupe MD, Turner DD, Walden VP, Steffen K, Cox CJ, Kulie MS, Miller NB, and Pettersen C (2013), July 2012 Greenland melt extent enhanced by low-level liquid clouds, Nature, 496 (7443), 83–86. [DOI] [PubMed] [Google Scholar]
- Berkelhammer M, Risi C, Kurita N, and Noone DC (2012), The moisture source sequence for the Madden-Julian Oscillation as derived from satellite retrievals of HDO and H2O, Journal of Geophysical Research: Atmospheres, 117 (D3). [Google Scholar]
- Berkelhammer M, Hu J, Bailey A, Noone DC, Still CJ, Barnard H, Gochis D, Hsiao GS, Rahn T, and Turnipseed A (2013), The nocturnal water cycle in an open-canopy forest, Journal of Geophysical Research: Atmospheres, 118 (17), 10,225–10,242, doi: 10.1002/jgrd.50701. [DOI] [Google Scholar]
- Berman ESF, Levin NE, Landais A, Li S, and Owano T (2013), Measurement of δ 18O, δ 17O, and 17O-excess in Water by Off-Axis Integrated Cavity Output Spectroscopy and Isotope Ratio Mass Spectrometry, Analytical Chemistry, 85 (21), 10,392–10,398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bintanja R, and Selten FM (2014), Future increases in Arctic precipitation linked to local evaporation and sea-ice retreat, Nature, 509 (7501), 479–482. [DOI] [PubMed] [Google Scholar]
- Blossey P, Kuang Z, and Romps DM (2010), Isotopic composition of water in the tropical tropopause layer in cloud-resolving simulations of an idealized tropical circulation, Journal of Geophysical Research, 115 (D24309,). [Google Scholar]
- Bodas-Salcedo A, Williams KD, Ringer MA, Beau I, Cole JNS, Dufresne JL, Koshiro T, Stevens B, Wang Z, and Yokohata T (2014), Origins of the Solar Radiation Biases over the Southern Ocean in CFMIP2 Models, Journal of Climate, 27 (1), 41–56. [Google Scholar]
- Boesch H, Deutscher NM, Warneke T, Byckling K, Cogan AJ, Griffith DWT, Notholt J, Parker RJ, and Wang Z (2013), HDO/H2O ratio retrievals from gosat, Atmospheric Measurement Techniques, 6 (3), 599–612, doi: 10.5194/amt-6-599-2013. [DOI] [Google Scholar]
- Bolot M, Legras B, and Moyer EJ (2013), Modelling and interpreting the isotopic composition of water vapor in convective updrafts, Atmospheric Chemistry and Physics, 13, 7903–7935. [Google Scholar]
- Bonne JL, Masson-Delmotte V, Cattani O, Delmotte M, Risi C, Sodemann H, and Steen-Larsen HC (2014), The isotopic composition of water vapor and precipitation in Ivittuut, southern Greenland, Atmospheric Chemistry and Physics, 14 (9), 4419–4439. [Google Scholar]
- Bonne JL, Steen Larsen HC, Risi C, Werner M, Sodemann H, Lacour JL, Fettweis X, Cesana G, Delmotte M, Cattani O, Vallelonga P, Kjær HA, Clerbaux C, Sveinbjörnsdóttir ÁE, and Masson Delmotte V (2015), The summer 2012 Greenland heat wave: In situ and remote sensing observations of water vapor isotopic composition during an atmospheric river event, Journal Of Geophysical Research-Atmospheres, 120 (7), 2970–2989. [Google Scholar]
- Bony S, and Dufresne JL (2005), Marine boundary layer clouds at the heart of tropical cloud feedback uncertainties in climate models, Geophysical Research Letters, 32 (20). [Google Scholar]
- Bony S, and Emanuel KA (2005), On the role of moist processes in tropical intraseasonal variability: Cloud-radiation and moisture-convection feedbacks, Journal of the Atmospheric Sciences, 62 (8), 2770–2789. [Google Scholar]
- Bony S, Risi C, and Vimeux F (2008), Influence of Convective Processes on Isotopic Composition of Precipitation (Oxygen 18 and Deuterium of precipitation and water-vapor in the tropics:1. Radiative-convective equilibrium and Tropical Ocean–Global Atmosphere–Coupled Ocean-Atmosphere Response Experiment (TOGA-COARE) simulations, Journal of Geophysical Research, 113 (D19305). [Google Scholar]
- Bosilovich MG, and Schubert SD (2002), Water vapor tracers as diagnostics of the regional hydrologic cycle, Journal Of Hydrometeorology, 3 (2), 149–165. [Google Scholar]
- Bowman KP, and Carrie GD (2002), The mean-meridional transport circulation of the troposphere in an idealized GCM, Journal of the Atmospheric Sciences, 59, 1502–1514. [Google Scholar]
- Bowman KW, Rodgers CD, Kulawik SS, Worden J, Sarkissian E, Osterman G, Steck T, Lou M, Eldering A, Shephard M, Worden H, Lampel M, Clough S, Brown P, Rinsland C, Gunson M, and Beer R (2006), Tropospheric emission spectrometer: retrieval method and error analysis, Geoscience and Remote Sensing, IEEE Transactions on, 44 (5), 1297–1307. [Google Scholar]
- Braud I, Biron P, Bariac T, Richard P, Canale L, Gaudet JP, and Vauclin M (2009a), Isotopic composition of bare soil evaporated water vapor. Part I: RUBIC IV experimental setup and results, Journal of Hydrology, 369 (1–2), 1–16. [Google Scholar]
- Braud I, Bariac T, Biron P, and Vauclin M (2009b), Isotopic composition of bare soil evaporated water vapor. Part II: Modeling of RUBIC IV experimental results, Journal of Hydrology, 369 (1–2), 17–29. [Google Scholar]
- Brennan CE, Weaver AJ, Eby M, and Meissner KJ (2012), Modelling Oxygen Isotopes in the University of Victoria Earth System Climate Model for Pre-industrial and Last Glacial Maximum Conditions, Atmosphere-Ocean, 50 (4), 447–465. [Google Scholar]
- Brenninkmeijer CAM, Crutzen P, Boumard F, Dauer T, Dix B, Ebinghaus R, Filippi D, Fischer H, Franke H, Frieβ U, Heintzenberg J, Helleis F, Hermann M, Kock HH, Koeppel C, Lelieveld J, Leuenberger M, Martinsson BG, Miemczyk S, Moret HP, Nguyen HN, Nyfeler P, Oram D, O’Sullivan D, Penkett S, Platt U, Pupek M, Ramonet M, Randa B, Reichelt M, Rhee TS, Rohwer J, Rosenfeld K, Scharffe D, Schlager H, Schumann U, Slemr F, Sprung D, Stock P, Thaler R, Valentino F, van Velthoven P, Waibel A, Wandel A, Waschitschek K, Wiedensohler A, Xueref-Remy I, Zahn A, Zech U, and Ziereis H (2007), Civil aircraft for the regular investigation of the atmosphere based on an instrumented container: The new caribic system, Atmospheric Chemistry and Physics, 7 (18), 4953–4976, doi: 10.5194/acp-7-4953-2007. [DOI] [Google Scholar]
- Brown D, Worden J, and Noone D (2008a), Comparison of atmospheric hydrology over convective continental regions using water vapor isotope measurements from space, Journal of Geophysical Research, 113 (D15), D15,124. [Google Scholar]
- Brown D, Worden J, and Noone D (2008b), Comparison of atmospheric hydrology over convective continental regions using water vapor isotope measurements from space, Journal of Geophysical Research-Atmospheres, 113 (D15). [Google Scholar]
- Brown J, Simmonds I, and Noone D (2006), Modeling delta O-18 in tropical precipitation and the surface ocean for present-day climate, Journal Of Geophysical Research-Atmospheres, 111 (D5). [Google Scholar]
- Brubaker KL, Entekhabi D, and Eagleson PS (1994), Atmospheric water vapor transport and continental hydrology over the Americas, Journal of Hydrology, 155 (3–4), 407–428. [Google Scholar]
- Brunel J-P, Walker GR, and Kennett-Smith AK (1995), Field validation of isotopic procedures for determining sources of water used by plants in a semi-arid environment, Journal of Hydrology, 167 (1–4), 351–368. [Google Scholar]
- Brutsaert W (1965), A model for evaporation as a molecular diffusion process into a turbulent atmosphere, Journal of Geophysical Research: Atmospheres, 70 (20), 5017–5024. [Google Scholar]
- Brutsaert W (1975), A theory for local evaporation (or heat transfer) from rough and smooth surfaces at ground level, Water Resources Research, 11 (4), 543–550. [Google Scholar]
- Budyko MI (1974), Climate and Life, Academic Press. [Google Scholar]
- Burde GI, Zangvil A, and Lamb PJ (1996), Estimating the role of local evaporation in precipitation for a two-dimensional region, Journal of Climate, 9 (6), 1328–1338. [Google Scholar]
- Butchart N (2014), The Brewer-Dobson circulation, Reviews of Geophysics, 52 (2), 157–184. [Google Scholar]
- Caley T, Roche DM, Waelbroeck C, and Michel E (2014), Oxygen stable isotopes during the Last Glacial Maximum climate: perspectives from data-model (iLOVECLIM) comparison, Climate Of The Past, 10 (6), 1939–1955. [Google Scholar]
- Cappa C, Hendricks M, and DePaolo D (2003), Isotopic fractionation of water during evaporation, Journal of Geophysical Research. [Google Scholar]
- Casado M, Cauquoin A, Landais A, Israel D, Orsi A, Pangui E, Landsberg J, Kerstel E, Prie F, and Doussin J-F (2016), Experimental determination and theoretical framework of kinetic fractionation at the water vapor-ice interface at low temperature, Geochimica Et Cosmochimica Acta, 174, 54–69. [Google Scholar]
- Cau P, Methven J, and Hoskins B (2007), Origins of dry air in the tropics and subtropics, Journal of Climate, 20 (2745–2759). [Google Scholar]
- Cesana G, and Chepfer H (2012), How well do climate models simulate cloud vertical structure? A comparison between CALIPSO-GOCCP satellite observations and CMIP5 models, Geophysical Research Letters, 39 (20). [Google Scholar]
- Charles CD, Rind DV, Jouzel J, and Koster RD (1994), Glacial-interglacial changes in moisture sources for Greenland: Influences on the ice core record of climate, Science. [DOI] [PubMed] [Google Scholar]
- Chen P (1995), Isentropic cross-tropopause mass exchange in the extratropics, Journal of Geophysical Research: Atmospheres, 100 (D8), 16,661–16,673. [Google Scholar]
- Christner E (2015), MesSungen von wasserisotopologen von der planetaren grenzschicht bis zur oberen troposphre zur untersuchung des hydrologischen kreislaufs, dissertation, karlsruhe institute of technology (kit), germany, Ph.D. thesis. [Google Scholar]
- Ciais P (1994), Deuterium and Oxygen-18 in Precipitation - Isotopic Model, Including Mixed Cloud Processes, Journal Of Geophysical Research-Atmospheres, 99 (D8), 16,793–16,803. [Google Scholar]
- Clark ID, and Fritz P (1997), Environmental isotopes in hydrogeology, Lewis Publishers. [Google Scholar]
- Coffey MT, Hannigan JW, and Goldman A (2006), Observations of upper tropospheric/lower stratospheric water vapor and its isotopes, Journal Of Geophysical Research-Atmospheres, 111 (D14), D14,313. [Google Scholar]
- Cole JE, Rind D, Webb RS, Jouzel J, and Healy R (1999), Climatic controls on interannual variability of precipitation delta O-18: Simulated influence of temperature, precipitation amount, and vapor source region, Journal Of Geophysical Research-Atmospheres, 104 (D12), 14,223–14,235. [Google Scholar]
- Conroy JL, Cobb KM, and Noone D (2013), Comparison of precipitation isotope variability across the tropical Pacific in observations and SWING2 model simulations, Journal Of Geophysical Research-Atmospheres, 118 (11), 5867–5892. [Google Scholar]
- Couvreux F, Hourdin F, and Rio C (2010), Resolved Versus Parametrized Boundary-Layer Plumes. Part I: A Parametrization-Oriented Conditional Sampling in Large-Eddy Simulations, Boundary-Layer Meteorology, 134 (3), 441–458. [Google Scholar]
- Craig H (1961), Isotopic Variations in Meteoric Waters, Science, 133 (346), 1702–1703. [DOI] [PubMed] [Google Scholar]
- Craig H, and Gordon LI (1965), Deuterium and oxygen-18 variations in the ocean and the marine atmosphere, in Stable Isotopes in Oceanographic Studies and Paleotemperatures, edited by Tongiorgi E, Spoleto. [Google Scholar]
- Crisp D, Atlas RM, Bréon FM, Brown LR, Burrows JP, Ciais P, Connor BJ, Doney SC, Fung IY, Jacob DJ, Miller CE, O’Brien D, Pawson S, Randerson JT, Rayner P, Salawitch RJ, Sander SP, Sen B, Stephens GL, Tans PP, Toon GC, Wennberg PO, Wofsy SC, Yung YL, Kuang Z, Chudasama B, Sprague G, Weiss B, Pollock R, Kenyon D, and Schroll S (2004), The Orbiting Carbon Observatory (OCO) mission, Advances in Space Research, 34 (4), 700–709. [Google Scholar]
- Crosson ER, Ricci KN, and Richman BA (), Stable isotope ratios using cavity ring- down spectroscopy: determination of 13C/12C for carbon dioxide in human breath, Analytical Chemistry,74,2003–2007. [DOI] [PubMed] [Google Scholar]
- Dahl-Jensen D, Albert MR, Aldahan A, Azuma N, Balslev-Clausen D, Baumgartner M, Berggren AM, Bigler M, Binder T, Blunier T, Bourgeois JC, Brook EJ, Buchardt SL, Buizert C, Capron E, Chappellaz J, Chung J, Clausen HB, Cvijanovic I, Davies SM, Ditlevsen P, Eicher O, Fischer H, Fisher DA, Fleet LG, Gfeller G, Gkinis V, Gogineni S, Goto-Azuma K, Grinsted A, Gudlaugsdottir H, Guillevic M, Hansen SB, Hansson M, Hirabayashi M, Hong S, Hur SD, Huybrechts P, Hvidberg CS, Iizuka Y, Jenk T, Johnsen SJ, Jones TR, Jouzel J, Karlsson NB, Kawamura K, Keegan K, Kettner E, Kipfstuhl S, Kjaer HA, Koutnik M, Kuramoto T, Koehler P, Laepple T, Landais A, Langen PL, Larsen LB, Leuenberger D, Leuenberger M, Leuschen C, Li J, Lipenkov V, Martinerie P, Maselli OJ, Masson-Delmotte V, McConnell JR, Miller H, Mini O, Miyamoto A, Montagnat-Rentier M, Mulvaney R, Muscheler R, Orsi AJ, Paden J, Panton C, Pattyn F, Petit JR, Pol K, Popp T, Possnert G, Prié F, Prokopiou M, Quiquet A, Rasmussen SO, Raynaud D, Ren J, Reutenauer C, Ritz C, Röckmann T, Rosen JL, Rubino M, Rybak O, Samyn D, Sapart CJ, Schilt A, Schmidt AMZ, Schwander J, Schuepbach S, Seierstad I, Severinghaus JP, Sheldon S, Simonsen SB, Sjolte J, Solgaard AM, Sowers T, Sperlich P, Steen-Larsen HC, Steffen K, Steffensen JP, Steinhage D, Stocker TF, Stowasser C, Sturevik AS, Sturges WT, Sveinbjornsdottir A, Svensson A, Tison JL, Uetake J, Vallelonga P, van de Wal RSW, van der Wel G, Vaughn BH, Vinther B, Waddington E, Wegner A, Weikusat I, White JWC, Wilhelms F, Winstrup M, Witrant E, Wolff EW, Xiao C, Zheng J, and Community N (2013), Eemian interglacial reconstructed from a Greenland folded ice core, Nature, 493 (7433), 489–494. [DOI] [PubMed] [Google Scholar]
- Dansgaard W (1954), The O18-abundance in fresh water, Geochimica Et Cosmochimica Acta, 6 (5–6), 241–260. [Google Scholar]
- Dansgaard W (1964), Stable isotopes in precipitation, Tellus, 16 (4), 436–468. [Google Scholar]
- Dee S, Noone D, Buenning N, Emile-Geay J, and Zhou Y (2015), SPEEDY-IER: A fast atmospheric GCM with water isotope physics, Journal Of Geophysical Research-Atmospheres, 120 (1), 73–91. [Google Scholar]
- Del Genio AD, Chen Y, Kim D, and Yao M-S (2012), The MJO Transition from Shallow to Deep Convection in CloudSat/CALIPSO Data and GISS GCM Simulations, Journal of Climate, 25 (11), 3755–3770. [Google Scholar]
- Delattre H, Vallet-Coulomb C, and Sonzogni C (2015), Deuterium excess in atmospheric water vapor of a Mediterranean coastal wetland: regional versus local signatures, Atmospheric Chemistry and Physics Discussions, 15 (2), 1703–1746. [Google Scholar]
- DeMott CA, Klingaman NP, and Woolnough SJ (2015), Atmosphere-ocean coupled processes in the Madden-Julian oscillation, Rev. Geophys, 53 (4), 1099–1154. [Google Scholar]
- Dessler A, and Sherwood S (2003), A model of HDO in the tropical tropopause layer, Atmospheric Chemistry and Physics, 3, 4489–4501. [Google Scholar]
- Dessler AE, Weinstock EM, Hintsa EJ, Anderson JG, Webster CR, MAY RD, ELKINS JW, and DUTTON GS (1994), An Examination of the Total Hydrogen Budget of the Lower Stratosphere, Geophysical Research Letters, 21 (23), 2563–2566. [Google Scholar]
- Dessler AE, Hanisco TF, and Fueglistaler S (2007), Effects of convective ice lofting on H2O and HDO in the tropical tropopause layer, Journal Of Geophysical Research-Atmospheres, 112 (D18), D18,309. [Google Scholar]
- Dirmeyer PA, and Brubaker KL (1999), Contrasting evaporative moisture sources during the drought of 1988 and the flood of 1993, Journal Of Geophysical Research-Atmospheres, 104 (D16), 19,383–19,397. [Google Scholar]
- Dirmeyer PA, and Brubaker KL (2007), Characterization of the global hydrologic cycle from a back-trajectory analysis of atmospheric water vapor, Journal Of Hydrometeorology, 8 (1), 20–37. [Google Scholar]
- Dirmeyer PA, Schlosser CA, and Brubaker KL (2009), Precipitation, Recycling, and Land Memory: An Integrated Analysis, Journal Of Hydrometeorology, 10 (1), 278–288. [Google Scholar]
- Divine DV, Sjolte J, Isaksson E, Meijer HAJ, van de Wal RSW, Martma T, Pohjola V, Sturm C, and Godtliebsen F (2011), Modelling the regional climate and isotopic composition of Svalbard precipitation using REMOiso: a comparison with available GNIP and ice core data, Hydrological Processes, 25 (24), 3748–3759. [Google Scholar]
- Dongmann DG, Nürnberg HW, Förstel H, and Wagener K (1974), On the enrichment of H2 18O in the leaves of transpiring plants, Radiation and Environmental Biophysics, 11 (1), 41–52. [DOI] [PubMed] [Google Scholar]
- Draxler RR, and Hess GD (1998), An overview of the HYSPLIT 4 modelling system for trajectories, Australian Meteorological Magazine. [Google Scholar]
- Dyroff C, Fütterer D, and Zahn A (2010), Compact diode-laser spectrometer isowat for highly sensitive airborne measurements of water-isotope ratios, Appl. Phys. B, 98, 537–548, doi: 10.1007/s00340-009-3775-6. [DOI] [Google Scholar]
- Dyroff C, Sanati S, Christner E, Zahn A, Balzer M, Bouquet H, McManus JB, González-Ramos Y, and Schneider M (2015), Airborne in situ vertical profiling of hdo / h216o in the subtropical troposphere during the musica remote sensing validation campaign, Atmospheric Measurement Techniques, 8 (5), 2037–2049, doi: 10.5194/amt-8-2037-2015. [DOI] [Google Scholar]
- Eagle RA, Risi C, Mitchell JL, Eiler JM, Seibt U, Neelin JD, Li G, and Tripati AK (2013), High regional climate sensitivity over continental China constrained by glacial-recent changes in temperature and the hydrological cycle, Proceedings of the National Academy of Sciences, 110 (22), 8813–8818. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ehhalt D (1973), Vertical Profiles of HTO, HDO, and H2O in the Troposphere, NCAR Technical Note, NCAR-TN/STR-100.
- Ehhalt DH (1971), Vertical profiles and transport of HTO in the troposphere, Journal of Geophysical Research: Atmospheres, 76 (30), 7351–7367. [Google Scholar]
- Ehhalt DH, Rohrer F, and Fried A (2005), Vertical profiles of hdo/H2O in the troposphere, Journal of Geophysical Research: Atmospheres, 110 (D13), n/a-n/a, doi: 10.1029/2004JD005569, d13301. [DOI] [Google Scholar]
- Eichinger R, Joeckel P, Brinkop S, Werner M, and Lossow S (2015a), Simulation of the isotopic composition of stratospheric water vapor - Part 1: Description and evaluation of the EMAC model, Atmospheric Chemistry and Physics, 15 (10), 5537–5555. [Google Scholar]
- Eichinger R, Joeckel P, and Lossow S (2015b), Simulation of the isotopic composition of stratospheric water vapor - Part 2: Investigation of HDO/H2O variations, Atmospheric Chemistry and Physics, 15 (12), 7003–7015. [Google Scholar]
- Ellehøj MD, Steen-Larsen HC, Johnsen SJ, and Madsen MB (2013), Ice-vapor equilibrium fractionation factor of hydrogen and oxygen isotopes: Experimental investigations and implications for stable water isotope studies, Rapid Communications In Mass Spectrometry, 27 (19), 2149–2158. [DOI] [PubMed] [Google Scholar]
- Eltahir E, and Bras RL (1996), Precipitation recycling, Reviews of Geophysics, 34 (3), 367–378. [Google Scholar]
- Engström A, Karlsson J, and Svensson G (2014), The Importance of Representing Mixed-Phase Clouds for Simulating Distinctive Atmospheric States in the Arctic*, dx.doi, 27 (1), 265–272. [Google Scholar]
- Epstein S, and Mayeda T (1953), Variation of O18 content of waters from natural sources, Geochimica Et Cosmochimica Acta, 4 (5), 213–224. [Google Scholar]
- Evans MN, Tolwinski-Ward SE, Thompson DM, and Anchukaitis KJ (2013), Applications of proxy system modeling in high resolution paleoclimatology, Quaternary Science Reviews, 76, 16–28. [Google Scholar]
- Field RD, Jones DBA, and Brown DP (2010), Effects of postcondensation exchange on the isotopic composition of water in the atmosphere, Journal of Geophysical Research: Atmospheres, 115 (D24), D24,305. [Google Scholar]
- Field RD, Risi C, Schmidt GA, Worden J, Voulgarakis A, LeGrande AN, Sobel AH, and Healy RJ (2012), A Tropospheric Emission Spectrometer HDO/H2O retrieval simulator for climate models, Atmospheric Chemistry and Physics, 12 (21), 10,485–10,504. [Google Scholar]
- Field RD, Kim D, LeGrande AN, Worden J, Kelley M, and Schmidt GA (2014), Evaluating climate model performance in the tropics with retrievals of water isotopic composition from Aura TES, Geophysical Research Letters, 41 (16), 6030–6036. [Google Scholar]
- Flanagan LB, and Ehleringer JR (1991), Stable Isotope Composition of Stem and Leaf Water - Applications to the Study of Plant Water-Use, Functional Ecology, 5 (2), 270–277. [Google Scholar]
- Forster P, and Shine KP (2002), Assessing the climate impact of trends in stratospheric water vapor, Geophysical Research Letters, 29 (6). [Google Scholar]
- Frankenberg C, Yoshimura K, Warneke T, Aben I, Butz A, Deutscher N, Griffith D, Hase F, Notholt J, Schneider M, Schrijver H, and Rockmann T (2009), Dynamic Processes Governing Lower-Tropospheric HDO/H2O Ratios as Observed from Space and Ground, Science, 325 (5946), 1374–1377. [DOI] [PubMed] [Google Scholar]
- Frankenberg C, Fisher JB, Worden J, Badgley G, Saatchi SS, Lee J-E, Toon GC, Butz A, Jung M, Kuze A, and Yokota T (2011), New global observations of the terrestrial carbon cycle from GOSAT: Patterns of plant fluorescence with gross primary productivity, Geophysical Research Letters, 38 (17). [Google Scholar]
- Frankenberg C, Wunch D, Toon G, Risi C, Scheepmaker R, Lee JE, Wennberg P, and Worden J (2013), Water vapor isotopologue retrievals from high-resolution GOSAT shortwave infrared spectra, Atmospheric Measurement Techniques, 6 (2), 263–274. [Google Scholar]
- Franz P, and Röckmann T (2005), High-precision isotope measurements of (H2O)-O-16, (H2O)-O-17, (H2O)-O-18, and the Delta O-17-anomaly of water vapor in the southern lowermost stratosphere, Atmospheric Chemistry and Physics, 5, 2949–2959. [Google Scholar]
- Fudeyasu H, Ichiyanagi K, Sugimoto A, Yoshimura K, Ueta A, Yamanaka MD, and Ozawa K (2008), Isotope ratios of precipitation and water vapor observed in Typhoon Shanshan, Journal Of Geophysical Research-Atmospheres, 113 (D12). [Google Scholar]
- Fueglistaler S, Bonazzola M, Haynes P, and Peter T (2005), Stratospheric water vapor predicted from the Lagrangian temperature history of air entering the stratosphere in the tropics, Journal Of Geophysical Research-Atmospheres, 110 (D8), D08,107. [Google Scholar]
- Fujita K, and Abe O (2006), Stable isotopes in daily precipitation at Dome Fuji, East Antarctica, Geophysical Research Letters, 33 (18). [Google Scholar]
- Galewsky J (2009), Orographic precipitation isotopic ratios in stratified atmospheric flows: Implications for paleoelevation studies, Geology, 37 (9), 791–794. [Google Scholar]
- Galewsky J (2015), Constraining Supersaturation and Transport Processes in a South American Cold-Air Outbreak Using Stable Isotopologues of Water Vapor, Journal of the Atmospheric Sciences, 72 (5), 2055–2069. [Google Scholar]
- Galewsky J, and Hurley JV (2010), An advection-condensation model for subtropical water vapor isotopic ratios, Journal of Geophysical Research: Atmospheres, 115 (D16). [Google Scholar]
- Galewsky J, and Samuels-Crow K (2014), Water vapor isotopic composition of a stratospheric air intrusion: Measurements from the Chajnantor Plateau, Chile, Journal Of Geophysical Research-Atmospheres, 119 (16), 9679–9691. [Google Scholar]
- Galewsky J, and Samuels-Crow K (2015), Summertime Moisture Transport to the Southern South American Altiplano: Constraints from In Situ Measurements of Water Vapor Isotopic Composition, Journal of Climate, 28 (7), 2635–2649. [Google Scholar]
- Galewsky J, Sobel A, and Held I (2005), Diagnosis of Subtropical Humidity Dynamics Using Tracers of Last Saturation, Journal of the Atmospheric Sciences, 62, 3353–3367. [Google Scholar]
- Galewsky J, Strong M, and Sharp ZD (2007), Measurements of water vapor D/H ratios from Mauna Kea, Hawaii, and implications for subtropical humidity dynamics, Geophysical Research Letters, 34 (22), L22,808. [Google Scholar]
- Galewsky J, Rella C, Sharp Z, Samuels K, and Ward D (2011), Surface measurements of upper tropospheric water vapor isotopic composition on the Chajnantor Plateau, Chile, Geophysical Research Letters, 38 (17). [Google Scholar]
- Galewsky J, and Rabanus D (2016), A Stochastic Model for Diagnosing Subtropical Humidity Dynamics with Stable Isotopologues of Water Vapor, Journal of the Atmospheric Sciences, 73 (4), 1741–1753. [Google Scholar]
- Gao J, Masson-Delmotte V, Yao T, Tian L, Risi C, and Hoffmann G (2011), Precipitation Water Stable Isotopes in the South Tibetan Plateau: Observations and Modeling, Journal of Climate, 24 (13), 3161–3178. [Google Scholar]
- Gasse F (2000), Hydrological changes in the African tropics since the Last Glacial Maximum, Quaternary Science Reviews, 19 (1–5), 189–211. [Google Scholar]
- Gat J (1996), Oxygen and hydrogen isotopes in the hydrologic cycle, Annual Review Of Earth And Planetary Sciences, 24, 225–262. [Google Scholar]
- Gat J, Klein B, Kushnir Y, Roether W, Wernli H, Yam R, and Shemesh A (2003), Isotope composition of air moisture over the Mediterranean Sea: an index of the air-sea interaction pattern, Tellus B, 55 (5), 953–965. [Google Scholar]
- Gat JR (2008), The isotopic composition of evaporating waters - review of the historical evolution leading up to the Craig-Gordon model, Isotopes in Environmental and Health Studies, 44 (1), 5–9. [DOI] [PubMed] [Google Scholar]
- Gat JR, and Matsui E (1991), Atmospheric Water-Balance in the Amazon Basin - an Isotopic Evapotranspiration Model, Journal Of Geophysical Research-Atmospheres, 96 (D7), 13,179–13,188. [Google Scholar]
- Gedzelman S, and Arnold R (1994), Modeling the isotopic composition of precipitation, Journal of Geophysical Research. [Google Scholar]
- Gedzelman SD, and Lawrence JR (1990), The Isotopic Composition of Precipitation From 2 Extratropical Cyclones, Mon Wea. Rev, 118 (2), 495–509. [Google Scholar]
- Genty D, Labuhn I, Hoffmann G, Danis PA, Mestre O, Bourges F, Wainer K, Massault M, Van Exter S, Regnier E, Orengo P, Falourd S, and Minster B (2014), Rainfall and cave water isotopic relationships in two South-France sites, Geochimica Et Cosmochimica Acta, 131, 323–343. [Google Scholar]
- Gettelman A and Hoor P and Pan LL and Randel WJ and Hegglin MI and Birner T (2011), The extratropical upper troposphere and lower stratosphere, Reviews of Geophysics, 49 (3). [Google Scholar]
- Gimeno L, Drumond A, Nieto R, Trigo RM, and Stohl A (2010), On the origin of continental precipitation, Geophysical Research Letters, 37 (13), n/a-n/a. [Google Scholar]
- Gimeno L, Stohl A, Trigo RM, Dominguez F, Yoshimura K, Yu L, Drumond A, Maria Duran-Quesada A, and Nieto R (2012), Oceanic and Terrestrial Sources of Continental Precipitation, Reviews of Geophysics, 50 (4). [Google Scholar]
- Goessling HF, and Reick CH (2011), What do moisture recycling estimates tell us? Exploring the extreme case of non-evaporating continents, EPIC3Hydrology and Earth System Sciences, COPERNICUS GESELLSCHAFT MBH, 15, pp. 3217–3235, ISSN: 1027–5606, 15 (10), 3217–3235. [Google Scholar]
- Gong CL, and Eltahir E (1996), Sources of moisture for rainfall in west Africa, Water Resources Research, 32 (10), 3115–3121. [Google Scholar]
- González Y, Schneider M, Dyroff C, Rodríguez S, Christner E, García OE, Cuevas E, Bustos JJ, Ramos R, Guirado-Fuentes C, Barthlott S, Wiegele A, and Sepúlveda E (2016), Detecting moisture transport pathways to the subtropical north atlantic free troposphere using paired H2O-dd in situ measurements, Atmospheric Chemistry and Physics, 16 (7), 4251–4269, doi: 10.5194/acp-16-4251-2016. [DOI] [Google Scholar]
- Good SP, Soderberg K, Wang L, and Caylor KK (2012), Uncertainties in the assessment of the isotopic composition of surface fluxes: A direct comparison of techniques using laserbased water vapor isotope analyzers., Journal of Geophysical Research, 117, D15. [Google Scholar]
- Griffis TJ (2013), Tracing the flow of carbon dioxide and water vapor between the biosphere and atmosphere: A review of optical isotope techniques and their application, Agricultural and Forest Meteorology, 174, 85–109. [Google Scholar]
- Grootes PM, and Stuiver M (1997), Oxygen 18/16 variability in Greenland snow and ice with 10(−3)- to 10(5)-year time resolution, Journal of Geophysical Research: Oceans …, 102 (C12), 26,455–26,470. [Google Scholar]
- Gryazin V, Risi C, Kurita N, Worden J, Frankenberg C, Bastrikov V, Gribanov K, and Stukova O (2014), To what extent could water isotopic measurements help us understand model biases in the water cycle over Western Siberia, Atmospheric Chemistry and Physics, 14 (18), 9807–9830. [Google Scholar]
- Guillevic M, Bazin L, Landais A, Kindler P, Orsi A, Masson-Delmotte V, Blunier T, Buchardt SL, Capron E, Leuenberger M, Martinerie P, Prié F, and Vinther BM (2013), Spatial gradients of temperature, accumulation and delta O-18-ice in Greenland over a series of Dansgaard-Oeschger events, Climate Of The Past, 9 (3), 1029–1051. [Google Scholar]
- Gunson MR, Abbas MM, Abrams MC, Allen M, Brown LR, Brown TL, Chang AY, Goldman A, Irion FW, Lowes LL, Mahieu E, Manney GL, Michelsen HA, Newchurch MJ, Rinsland CP, Salawitch RJ, Stiller GP, Toon GC, Yung YL, and Zander R (1996), The Atmospheric Trace Molecule Spectroscopy (ATMOS) Experiment: Deployment on the ATLAS space shuttle missions, Geophysical Research Letters, 23 (17), 2333–2336. [Google Scholar]
- Gurney KR, Law RM, Denning AS, Rayner PJ, Baker D, Bousquet P, Bruhwiler L, Chen Y-H, Ciais P, Fan S, Fung IY, Gloor M, Heimann M, Higuchi K, John J, Maki T, Maksyutov S, Masarie K, Peylin P, Prather M, Pak BC, Randerson J, Sarmiento J, Taguchi S, Takahashi T, and Yuen C-W (2002), Towards robust regional estimates of CO2 sources and sinks using atmospheric transport models, Nature, 415 (6872), 626–630. [DOI] [PubMed] [Google Scholar]
- Hakim GJ, Geay JE, Steig EJ, Noone D, Anderson DM, Tardif R, Steiger N, and Perkins WA (2016), The Last Millennium Climate Reanalysis Project: Framework and First Results, Journal of Geophysical Research: Atmospheres, 121. [Google Scholar]
- Han L-F, Groening M, Aggarwal P, and Helliker BR (2006), Reliable determination of oxygen and hydrogen isotope ratios in atmospheric water vapor adsorbed on 3A molecular sieve, Rapid Communications In Mass Spectrometry, 20 (23), 3612–3618. [DOI] [PubMed] [Google Scholar]
- Hanisco TF, Moyer EJ, Weinstock EM, St Clair JM, Sayres DS, Smith JB, Lockwood R, Anderson JG, Dessler AE, Keutsch FN, Spackman JR, Read WG, and Bui TP (2007), Observations of deep convective influence on stratospheric water vapor and its isotopic composition, Geophysical Research Letters, 34 (4). [Google Scholar]
- Hannigan JW, Coffey MT, and Goldman A (2009), Semiautonomous FTS Observation System for Remote Sensing of Stratospheric and Tropospheric Gases, Journal of Atmospheric and Oceanic Technology, 26 (9), 1814–1828. [Google Scholar]
- He Y, Risi C, Gao J, Masson Delmotte V, Yao T, Lai C-T, Ding Y, Worden J, Frankenberg C, Chepfer H, and Cesana G (2015), Impact of atmospheric convection on south Tibet summer precipitation isotopologue composition using a combination of in-situ measurements, satellite data, and atmospheric general circulation modeling, Journal Of Geophysical Research-Atmospheres, 120 (9), 3852–3871. [Google Scholar]
- Held I, and Soden B (2000), Water vapor feedback and global warming, Annual Review Of Energy And The Environment, 25, 441–475. [Google Scholar]
- Helliker BR, Roden JS, Cook C, and Ehleringer JR (2002), A rapid and precise method for sampling and determining the oxygen isotope ratio of atmospheric water vapor, Rapid Communications In Mass Spectrometry, 16 (10), 929–932. [DOI] [PubMed] [Google Scholar]
- Helsen M, Van de Wal R, Van den Broeke M, Kerstel E, Masson-Delmotte V, Meijer H, Reijmer C, and Scheele M (2004), Modelling the isotopic composition of snow using backward trajectories: a particular precipitation event in Dronning Maud Land, Antarctica, Annals of Glaciology, pp. 293–299, 2015JD023403. [Google Scholar]
- Helsen MM, van de Wal RSW, van den Broeke MR, Masson-Delmotte V, Meijer HAJ, Scheele MP, and Werner M (2006), Modeling the isotopic composition of Antarctic snow using backward trajectories: Simulation of snow pit records, Journal Of Geophysical Research-Atmospheres, 111 (D15). [Google Scholar]
- Hendricks MB, DePaolo DJ, and Cohen RC (2000), Space and time variation of delta 18 O and deltaD in precipitation: Can paleotemperature be estimated from ice cores?, Global Biogeochemical Cycles, 14 (3), 851–861. [Google Scholar]
- Herbin H, Hurtmans D, Clerbaux C, Clarisse L, and Coheur PF (2009), (H2O)-O-16 and HDO measurements with IASI/MetOp, Atmospheric Chemistry and Physics, 9 (24), 9433–9447. [Google Scholar]
- Herman RL, Cherry JE, Young J, Welker JM, Noone D, Kulawik SS, and Worden J (2014), Aircraft validation of Aura Tropospheric Emission Spectrometer retrievals of HDO / H2O, Atmospheric Measurement Techniques, 7 (9), 3127–3138. [Google Scholar]
- Hoffmann G, Werner M, and Heimann M (1998), Water isotope module of the ECHAM atmospheric general circulation model: A study on timescales from days to several years, Journal Of Geophysical Research-Atmospheres, 103 (D14), 16,871–16,896. [Google Scholar]
- Hoffmann G, Ramirez E, Taupin JD, Francou B, Ribstein P, Delmas R, Dürr H, Gallaire R, Simões J, Stievenard M, and Werner M (2003), Coherent isotope history of Andean ice cores over the last century, Geophysical Research Letters, 30 (4), 1179. [Google Scholar]
- Holton J, and Gettleman A (2001), Horizontal transport and dehydration in the stratosphere, Geophysical Review Letters, 28, 2799–2802. [Google Scholar]
- Horita J, Rozanski K, and Cohen S (2008), Isotope effects in the evaporation of water: a status report of the Craig–Gordon model, Isotopes in Environmental and …. [DOI] [PubMed] [Google Scholar]
- Hourdin F, Grandpeix J-Y, Rio C, Bony S, Jam A, Cheruy F, Rochetin N, Fairhead L, Idelkadi A, Musat I, Dufresne J-L, Lahellec A, Lefebvre M-P, and Roehrig R (2013), LMDZ5B: the atmospheric component of the IPSL climate model with revisited parameterizations for clouds and convection, Climate Dynamics, 40 (9–10), 2193–2222. [Google Scholar]
- Hung M-P, Lin J-L, Wang W, Kim D, Shinoda T, and Weaver SJ (2013), MJO and Convectively Coupled Equatorial Waves Simulated by CMIP5 Climate Models, Journal of Climate, 26 (17), 6185–6214. [Google Scholar]
- Hurley JV, and Galewsky J (2010), A last-saturation diagnosis of subtropical water vapor response to global warming, Geophysical Research Letters, 37 (6). [Google Scholar]
- Hurley JV, Galewsky J, Worden J, and Noone D (2012), A test of the advection-condensation model for subtropical water vapor using stable isotopologue observations from Mauna Loa Observatory, Hawaii, J. Geophys. Res, 117 (D19). [Google Scholar]
- Insel N, Poulsen CJ, Sturm C, and Ehlers TA (2013), Climate controls on Andean precipitation delta O-18 interannual variability, Journal Of Geophysical Research-Atmospheres, 118 (17), 9721–9742. [Google Scholar]
- Iannone RQ, Kassi S, Jost H-J, Chenevier M, Romanini D, Meijer HA, Dhaniyala S, Snels M, and Kerstel ER (2009), Development and airborne operation of a compact water isotope ratio infrared spectrometer, Isotopes in Environmental and Health Studies, 45 (4), 303–320, doi: 10.1080/10256010903172715. [DOI] [PubMed] [Google Scholar]
- Jasechko Scott, Sharp Zachary D., Gibson John J., Birks S. Jean, Yi Yi, and Fawcett Peter J. (2013), Terrestrial water fluxes dominated by transpiration, Nature, 496, 347–350. [DOI] [PubMed] [Google Scholar]
- Jasechko S, Lechler A, Pausata FSR, Fawcett PJ, Gleeson T, Cendon DI, Galewsky J, LeGrande AN, Risi C, Sharp ZD, Welker JM, Werner M, and Yoshimura K (2015), Late-glacial to late-Holocene shifts in global precipitation delta O-18, Climate Of The Past, 11 (10), 1375–1393. [Google Scholar]
- Jiang Z, Jones DBA, Worden HM, Deeter MN, Henze DK, Worden J, Bowman KW, Brenninkmeijer CAM, and Schuck TJ (2013), Impact of model errors in convective transport on CO source estimates inferred from MOPITT CO retrievals, Journal Of Geophysical Research-Atmospheres, 118 (4), 2073–2083. [Google Scholar]
- Johnsen SJ, Dansgaard W, and White JWC (1989), The origin of Arctic precipitation under present and glacial conditions, Tellus Series B-Chemical and Physical Meteorology, 41 (4), 452–468. [Google Scholar]
- Johnson DG, Jucks KW, Traub WA, and Chance KV (2001a), Isotopic composition of stratospheric water vapor: Measurements and photochemistry, Journal Of Geophysical Research-Atmospheres, 106 (D11), 12,211–12,217. [Google Scholar]
- Johnson DG, Jucks KW, Traub WA, and Chance KV (2001b), Isotopic composition of stratospheric water vapor: Implications for transport, Journal Of Geophysical Research-Atmospheres, 106 (D11), 12,219–12,226. [Google Scholar]
- Johnson L, Sharp Z, and Galewsky J (2011), Hydrogen isotope correction for laser instrument measurement bias at low water vapor concentration using conventional isotope analyses: application to measurements from Mauna Loa Observatory, Hawaii, Rapid Communications In Mass Spectrometry, 25, 608–616. [DOI] [PubMed] [Google Scholar]
- Jones A, Thomson D, Hort M, and Devenish B (2007), The U.K. Met Office’s Next-Generation Atmospheric Dispersion Model, NAME III, in Air Pollution Modeling and Its Application XVII, pp. 580–589. [Google Scholar]
- Jones DBA, Bowman KW, Palmer PI, Worden JR, Jacob DJ, Hoffman RN, Bey I, and Yantosca RM (2003), Potential of observations from the Tropospheric Emission Spectrometer to constrain continental sources of carbon monoxide, Journal of Geophysical Research: Atmospheres, 108 (D24). [Google Scholar]
- Joussaume S, and Jouzel J (1993), Paleoclimatic Tracers - an Investigation Using an Atmospheric General-Circulation Model Under Ice-Age Conditions .2. Water Isotopes, J. Geophys. Res, 98 (D2), 2807–2830. [Google Scholar]
- Joussaume S, Sadourny R, and Jouzel J (1984a), A General-Circulation Model of Water Isotope Cycles in the Atmosphere, Nature, 311 (5981), 24–29. [Google Scholar]
- Joussaume S, Sadourny R, and Jouzel J (1984b), A general circulation model of water isotope cycles in the atmosphere, Nature, 311 (5981), 24–29. [Google Scholar]
- Jouzel J (1986), ISOTOPES IN CLOUD PHYSICS: MULTIPHASE AND MULTISTAGE CONDENSATION PROCESSES, in The Terrestrial Environment, B, pp. 61–112, Elsevier. [Google Scholar]
- Jouzel J (1979), Global Climatic Interpretation of the Deuterium-Oxygen-18 Relationship for Precipitation, Journal of Geophysical Research: Oceans, 84 (NC8), 5029–5033. [Google Scholar]
- Jouzel J (2003), Water Stable Isotopes: Atmospheric Composition and Applications in Polar Ice Core Studies, in Treatise on Geochemistry, Volume., Elsevier. [Google Scholar]
- Jouzel J, and Koster RD (1996), A reconsideration of the initial conditions used for stable water isotope models, Journal Of Geophysical Research-Atmospheres, 101 (D17), 22,933–22,938. [Google Scholar]
- Jouzel J, and Merlivat L (1984), Deuterium and oxygen 18 in precipitation: modeling of the isotopic effects during snow formation, Journal of Geophysical Research, 89 (D7), 11,749–11,757. [Google Scholar]
- Jouzel J, Russell GL, Suozzo RJ, Koster RD, White JWC, and Broecker WS (1987), Simulations of the HDO and H2 18O atmospheric cycles using the NASA GISS general circulation model: The seasonal cycle for present-day conditions, Journal of Geophysical Research: Atmospheres, 92 (D12), 14,739–14,760. [Google Scholar]
- Jouzel J, Koster RD, Suozzo RJ, and Russell GL (1994), Stable Water Isotope Behavior During the Last Glacial Maximum - a General-Circulation Model Analysis, Journal Of Geophysical Research-Atmospheres, 99 (D12), 25,791–25,801. [Google Scholar]
- Jouzel J, Hoffmann G, Koster RD, and Masson V (2000), Water isotopes in precipitation: data/model comparison for present-day and past climates, Quaternary Science Reviews, 19 (1–5), 363–379. [Google Scholar]
- Jouzel J, Masson-Delmotte V, Cattani O, Dreyfus G, Falourd S, Hoffmann G, Minster B, Nouet J, Barnola JM, Chappellaz J, Fischer H, Gallet JC, Johnsen S, Leuenberger M, Loulergue L, Luethi D, Oerter H, Parrenin F, Raisbeck G, Raynaud D, Schilt A, Schwander J, Selmo E, Souchez R, Spahni R, Stauffer B, Steffensen JP, Stenni B, Stocker TF, Tison JL, Werner M, and Wolff EW (2007), Orbital and millennial Antarctic climate variability over the past 800,000 years, Science, 317 (5839), 793–796. [DOI] [PubMed] [Google Scholar]
- Keeling CD (1961), The concentration and isotopic abundances of carbon dioxide in rural and marine air, Geochimica Et Cosmochimica Acta. [Google Scholar]
- Kerstel ERT, Iannone RQ, Chenevier M, Kassi S, Jost HJ, and Romanini D (2006), A water isotope (H-2, O-17, and O-18) spectrometer based on optical feedback cavity-enhanced absorption for in-situ airborne applications, Applied Physics B-Lasers and Optics, 85 (2–3), 397–406. [Google Scholar]
- Khairoutdinov MF, and Randall DA (2003), Cloud Resolving Modeling of the ARM Summer 1997 IOP: Model Formulation, Results, Uncertainties, and Sensitivities, , 60 (4), 607–625. [DOI] [Google Scholar]
- Kim D, Sobel AH, Del Genio AD, Chen Y, Camargo SJ, Yao M-S, Kelley M, and Nazarenko L (2012), The Tropical Subseasonal Variability Simulated in the NASA GISS General Circulation Model, Journal of Climate, 25 (13), 4641–4659. [Google Scholar]
- Kindler P, Guillevic M, Baumgartner M, Schwander J, Landais A, and Leuenberger M (2014), Temperature reconstruction from 10 to 120 kyr b2k from the NGRIP ice core, Climate Of The Past, 10 (2), 887–902. [Google Scholar]
- Kirk-Davidoff DB, Hintsa EJ, Anderson JG, and Keith DW (1999), The effect of climate change on ozone depletion through changes in stratospheric water vapor, Nature, 402 (6760), 399–401. [Google Scholar]
- Knutti R, and Sedlacek J (2013), Robustness and uncertainties in the new CMIP5 climate model projections, Nature Climate Change, 3 (4), 369–373. [Google Scholar]
- Kopec BG, Lauder AM, Posmentier ES, and Feng X (2014), The diel cycle of water vapor in west Greenland, Journal Of Geophysical Research-Atmospheres, 119 (15), 9386–9399. [Google Scholar]
- Koster R, Jouzel J, Suozzo R, Russell G, Broecker W, Rind D, and Eagleson P (1986), Global sources of local precipitation as determined by the Nasa/Giss GCM, Geophysical Research Letters, 13 (2), 121–124. [Google Scholar]
- Koster RD, Jouzel J, Suozzo RJ, and Russell GL (1992), Origin of July Antarctic Precipitation and Its Influence on Deuterium Content - a Gcm Analysis, Climate Dynamics, 7(4), 195–203. [Google Scholar]
- Kuang Z, Toon GC, Wennberg PO, and Yung YL (2003), Measured HDO/H2O ratios across the tropical tropopause, Geophysical Research Letters, 30 (7), 1372. [Google Scholar]
- Kurita N (2011), Origin of Arctic water vapor during the ice-growth season, Geophysical Research Letters, 38 (2). [Google Scholar]
- Kurita N (2013), Water isotopic variability in response to mesoscale convective system over the tropical ocean, Journal Of Geophysical Research-Atmospheres, 118 (18), 10,376–10,390. [Google Scholar]
- Kurita N, Noone D, Risi C, Schmidt GA, Yamada H, and Yoneyama K (2011), Intraseasonal isotopic variation associated with the Madden-Julian Oscillation, Journal of Geophysical Research: Atmospheres, 116 (D24). [Google Scholar]
- Kurita N, Newman BD, Araguas-Araguas LJ, and Aggarwal P (2012), Evaluation of continuous water vapor dd and d18o measurements by off-axis integrated cavity output spectroscopy, Atmospheric Measurement Techniques, 5 (8), 2069–2080, doi: 10.5194/amt-5-2069-2012. [DOI] [Google Scholar]
- Kurita N, Fujiyoshi Y, Nakayama T, Matsumi Y, and Kitagawa H (2015), East asian monsoon controls on the inter-annual variability in precipitation isotope ratio in japan, Climate of the Past, 11 (2), 339–353, doi: 10.5194/cp-11-339-2015. [DOI] [Google Scholar]
- Labuhn I, Daux V, Pierre M, Stievenard M, Girardclos O, Feron A, Genty D, Masson Delmotte V, and Mestre O (2014), Tree age, site and climate controls on tree ring cellulose delta O-18: A case study on oak trees from south-western France, Dendrochronologia, 32 (1), 78–89. [Google Scholar]
- Lacour J-L (2015), Estimations du profil du rapport isotopique deltaD de la vapeur d?eau dans la troposphre partir de spectres mesurs dans l?infrarouge thermique par le sondeur IASI : Mthodologie d?inversion et analyses des premires distributions spatiales. , Ph.D. thesis, Universit Libre de Bruxelles. [Google Scholar]
- Lacour JL, Risi C, Clarisse L, and Bony S (2012), Mid-tropospheric δD observations from IASI/MetOp at high spatial and temporal resolution, Atmospheric Physics and Chemistry, 12, 10,817–10,832. [Google Scholar]
- Lai C-T, and Ehleringer JR (2010), Deuterium excess reveals diurnal sources of water vapor in forest air, Oecologia, 165 (1), 213–223. [DOI] [PubMed] [Google Scholar]
- Lai C-T, Rambo J, Welp-Smith L, Bible K, and Hollinger D (2014), Comparing stable water isotope variation in atmospheric moisture observed over coastal water and forests, AGU Fall Meeting, Dec 15–19, PP31D–1162. [Google Scholar]
- Lamb K, Clouser B, Bolot M, Sarkozy L, Ebert V, Saathoff H, Möhler O, and Moyer E (2015), Laboratory measurements of HDO/H2O isotopic fractionation during ice deposition in simulated cirrus clouds, Arxiv. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Landais A, Barkan E, Yakir D, and Luz B (2006), The triple isotopic composition of oxygen in leaf water, Geochimica Et Cosmochimica Acta, 70 (16), 4105–4115. [Google Scholar]
- Landais A, Barkan E, and Luz B (2008), Record of delta O-18 and O-17-excess in ice from Vostok Antarctica during the last 150,000 years, Geophysical Research Letters, 35 (2). [Google Scholar]
- Landais A, Steen-Larsen HC, Guillevic M, Masson-Delmotte V, Vinther B, and Winkler R (2012), Triple isotopic composition of oxygen in surface snow and water vapor at NEEM (Greenland), Geochimica Et Cosmochimica Acta, 77, 304–316. [Google Scholar]
- Landsberg J, Romanini D, and Kerstel E (2014), Very high finesse optical-feedback cavity-enhanced absorption spectrometer for low concentration water vapor isotope analyses, Optics Letters, 39 (7), 1795–1798. [DOI] [PubMed] [Google Scholar]
- Langmuir I, and Langmuir DB (1927), The effect of monomolecular films on the evaporation of ether solutions, Journal of Physical Chemistry, 31 (11), 1719–1731. [Google Scholar]
- Lawrence J, and Gedzelman S (1996), Low stable isotope ratios of tropical cyclone rains, Geophysical Research Letters. [Google Scholar]
- Lawrence J, Gedzelman S, Gamache J, and Black M (2002), Stable Isotope Ratios: Hurricane Olivia, Journal Of Atmospheric Chemistry. [Google Scholar]
- Lawrence JR, and Gedzelman SD (2003), Tropical ice core isotopes: Do they reflect changes in storm activity?, Geophysical Research Letters, 30 (2). [Google Scholar]
- Lawrence JR, Gedzelman SD, Dexheimer D, Cho HK, Carrie GD, Gasparini R, Anderson CR, Bowman KP, and Biggerstaff MI (2004), Stable isotopic composition of water vapor in the tropics, Journal Of Geophysical Research-Atmospheres, 109 (D6). [Google Scholar]
- Lee X, Sargent S, and Smith R (2005), In situ measurement of the water vapor 18O/16O isotope ratio for atmospheric and ecological applications, Journal of Atmospheric and Oceanic Technology, 22 (5), 555–565. [Google Scholar]
- Lee J-E, and Fung I (2008), “Amount effect” of water isotopes and quantitative analysis of post-condensation processes, Hydrological Processes, 22 (1), 1–8. [Google Scholar]
- Lee J-E, Fung I, DePaolo DJ, and Henning CC (2007a), Analysis of the global distribution of water isotopes using the NCAR atmospheric general circulation model, Journal Of Geophysical Research-Atmospheres, 112 (D16). [Google Scholar]
- Lee J-E, Pierrehumbert R, Swann A, and Lintner BR (2009a), Sensitivity of stable water isotopic values to convective parameterization schemes, Geophysical Research Letters, 36 (23), L23,801. [Google Scholar]
- Lee J-E, Johnson K, and Fung I (2009b), Precipitation over South America during the Last Glacial Maximum: An analysis of the “amount effect” with a water isotope-enabled general circulation model, Geophysical Research Letters, 36 (19), L19,701. [Google Scholar]
- Lee J-E, Risi C, Fung I, Worden J, Scheepmaker RA, Lintner B, and Frankenberg C (2012a), Asian monsoon hydrometeorology from TES and SCIAMACHY water vapor isotope measurements and LMDZ simulations: Implications for speleothem climate record interpretation, Journal Of Geophysical Research-Atmospheres, 117 (D15). [Google Scholar]
- Lee J-E, Risi C, Fung I, Worden J, Scheepmaker RA, Lintner B, and Frankenberg C (2012b), Asian monsoon hydrometeorology from TES and SCIAMACHY water vapor isotope measurements and LMDZ simulations: Implications for speleothem climate record interpretation, Journal of Geophysical Research: Atmospheres, 117 (D15), D15,112. [Google Scholar]
- Lee X, Sargent S, Smith R, and Tanner B (2005), In situ measurement of the water vapor 18o/16o isotope ratio for atmospheric and ecological applications, Journal of Atmospheric and Oceanic Technology, 22 (5), 555565. [Google Scholar]
- Lee X, Smith R, and Williams J (2006), Water vapor 18 o/ 16 o isotope ratio in surface air in new england, usa, Tellus B, 58 (4). [Google Scholar]
- Lee X, Kim K, and Smith R (2007b), Temporal variations of the 18O/16O signal of the whole-canopy transpiration in a temperate forest, Global Biogeochemical Cycles, 21 (3). [Google Scholar]
- Lee X, Huang J, and Patton EG (2012c), A Large-Eddy Simulation Study of Water vapor and Carbon Dioxide Isotopes in the Atmospheric Boundary Layer, Boundary-Layer Meteorology, 145 (1), 229–248. [Google Scholar]
- LeGrande AN, and Schmidt GA (2009), Sources of Holocene variability of oxygen isotopes in paleoclimate archives, Climate Of The Past, 5 (3), 441–455. [Google Scholar]
- Lekshmy PR, Midhun M, Ramesh R, and Jani RA (2014), 18O depletion in monsoon rain relates to large scale organized convection rather than the amount of rainfall, Scientific reports, 4, 5661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewis SC, LeGrande AN, Kelley M, and Schmidt GA (2010), Water vapor source impacts on oxygen isotope variability in tropical precipitation during Heinrich events, Climate Of The Past. [Google Scholar]
- Lin J-L, Kiladis GN, Mapes BE, Weickmann KM, Sperber KR, Lin W, Wheeler MC, Schubert SD, Del Genio A, Donner LJ, Emori S, Gueremy J-F, Hourdin F, Rasch PJ, Roeckner E, and Scinocca JF (2006), Tropical intraseasonal variability in 14 IPCC AR4 climate models. Part I: Convective signals, Journal of Climate, 19 (12), 2665–2690. [Google Scholar]
- Lin Y, Clayton RN, Huang L, Nakamura N, and Lyons JR (2013), Oxygen isotope anomaly observed in water vapor from Alert, Canada and the implication for the stratosphere, Proceedings of the National Academy of Sciences, 110 (39), 15,608–15,613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lossow S, Steinwagner J, Urban J, Dupuy E, Boone CD, Kellmann S, Linden A, Kiefer M, Grabowski U, Glatthor N, Hoepfner M, Röckmann T, Murtagh DP, Walker KA, Bernath PF, von Clarmann T, and Stiller GP (2011), Comparison of HDO measurements from Envisat/MIPAS with observations by Odin/SMR and SCISAT/ACE-FTS, Atmospheric Measurement Techniques, 4 (9), 1855–1874. [Google Scholar]
- Madden RA, and Julian PR (1971), Detection of a 40–50 Day Oscillation in the Zonal Wind in the Tropical Pacific, Journal of the Atmospheric Sciences, 28 (5), 702–708. [Google Scholar]
- Madden RA, and Julian PR (1972), Description of Global-Scale Circulation Cells in the Tropics with a 40–50 Day Period, Journal of the Atmospheric Sciences, 29 (6), 1109–1123. [Google Scholar]
- Mathieu R, and Bariac T (1996), A numerical model for the simulation of stable isotope profiles in drying soils, Journal Of Geophysical Research-Atmospheres, 101 (D7), 12,685–12,696. [Google Scholar]
- Mauritsen T, Stevens B, Roeckner E, Crueger T, Esch M, Giorgetta M, Haak H, Jungclaus J, Klocke D, Matei D, Mikolajewicz U, Notz D, Pincus R, Schmidt H, and Tomassini L (2012), Tuning the climate of a global model, Journal of Advances in Modeling Earth Systems, 4 (3). [Google Scholar]
- McCarroll D, and Loader NJ (2004), Stable isotopes in tree rings, Quaternary Science Reviews, 23 (7–8), 771–801. [Google Scholar]
- McDermott F (2004), Palaeo-climate reconstruction from stable isotope variations in speleothems: a review, Quaternary Science Reviews, 23 (7–8), 901–918. [Google Scholar]
- McIntyre ME, and Palmer TN (1983), Breaking planetary waves in the stratosphere, Nature, 305, 593–600. [Google Scholar]
- Meehl GA, Covey C, Delworth T, Latif M, McAvaney B, Mitchell JFB, Stouffer RJ, and Taylor KE (2007), The WCRP CMIP3 multimodel dataset - A new era in climate change research, Bulletin Of The American Meteorological Society, 88 (9), 1383–+. [Google Scholar]
- Merlivat L (1978), Molecular Diffusivities of (H2O)-O-1 6 Hd16o, and (H2O)-O-18 in Gases, Journal of Chemical Physics, 69 (6), 2864–2871. [Google Scholar]
- Merlivat L, and Coantic M (1975), Study of mass transfer at the air-water interface by an isotopic method, J. Geophys. Res, 80 (24), 3455–3464. [Google Scholar]
- Merlivat L, and Jouzel J (1979), Global climatic interpretation of the deuterium-oxygen 18 relationship for precipitation, Journal of Geophysical Research: Oceans, 84 (C8), 5029–5033, doi: 10.1029/JC084iC08p05029. [DOI] [Google Scholar]
- Merlivat L, and Nief G (1967), Fractionnement isotopique lors des changements d’etat solide-vapeur et liquide-vapeur de l’eau à des températures inférieures à 0o C, Tellus Series A-Dynamic Meteorology And Oceanography, XIX, 122–127. [Google Scholar]
- Miller MF (2013), Oxygen isotope anomaly not present in water vapor from Alert, Canada, Proceedings of the National Academy of Sciences, 110 (48), E4567–E4567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moore M, Kuang Z, and Blossey PN (2014), A moisture budget perspective of the amount effect, Geophysical Research Letters, 41 (4), 1329–1335. [Google Scholar]
- Moreira M, Sternberg L, Martinelli L, Victoria R, Barbosa E, Bonates LA, and Nepstad D (1997), Contribution of transpiration to forest ambient vapor based on isotopic measurements, Global Change Biology, 3 (5), 439–450. [Google Scholar]
- Moyer E, Irion F, Yung Y, and Gunson M (1996), ATMOS stratospheric deuterated water and implications for troposphere-stratosphere transport, Geophysical Research Letters, 23 (17), 2385–2388. [Google Scholar]
- Nassar R, Bernath PF, Boone CD, Gettelman A, McLeod SD, and Rinsland CP (2007), Variability in HDO/H2O abundance ratios in the tropical tropopause layer, Journal of Geophysical Research: Atmospheres, 112 (D21), D21,305. [Google Scholar]
- Noone D (2012), Pairing Measurements of the Water Vapor Isotope Ratio with Humidity to Deduce Atmospheric Moistening and Dehydration in the Tropical Midtroposphere, Journal of Climate, 25, 4476–4494. [Google Scholar]
- Noone D, and Simmonds I (2002), Associations between delta O-18 of water and climate parameters in a simulation of atmospheric circulation for 1979–95, Journal of Climate, 15 (22), 3150–3169. [Google Scholar]
- Noone D, and Sturm C (2010), Comprehensive Dynamical Models of Global and Regional Water Isotope Distributions, in Isoscapes, pp. 195–219, Springer; Netherlands, Dordrecht. [Google Scholar]
- Noone D, Galewsky J, Sharp ZD, and Worden J (2011), Properties of air mass mixing and humidity in the subtropics from measurements of the D/H isotope ratio of water vapor at the Mauna Loa Observatory, Journal of Geophysical Research, 116 (D33113). [Google Scholar]
- Noone D, Risi C, and Bailey A (2012), Determining water sources in the boundary layer from tall tower profiles of water vapor and surface water isotope ratios after a snowstorm in Colorado, Atmos. Chem. Phys, 13, 1607–1623. [Google Scholar]
- Notholt J, Toon GC, Fueglistaler S, Wennberg PO, Irion FW, McCarthy M, Scharringhausen M, Rhee TS, Kleinboehl A, and Velazco V (2010), Trend in ice moistening the stratosphere - constraints from isotope data of water and methane, Atmospheric Chemistry and Physics, 10 (1), 201–207. [Google Scholar]
- Numaguti A (1999), Origin and recycling processes of precipitating water over the Eurasian continent: Experiments using an atmospheric general circulation model, Journal Of Geophysical Research-Atmospheres, 104 (D2), 1957–1972. [Google Scholar]
- Okazaki A, Satoh Y, Tremoy G, Vimeux F, Scheepmaker R, and Yoshimura K (2015), Interannual variability of isotopic composition in water vapor over western africa and its relationship to enso, Atmospheric Chemistry and Physics, 15 (6), 3193–3204, doi: 10.5194/acp-15-3193-2015. [DOI] [Google Scholar]
- Patton EG, Sullivan PP, and Moeng C-H (2005), The Influence of Idealized Heterogeneity on Wet and Dry Planetary Boundary Layers Coupled to the Land Surface, dx.doi, 62 (7), 2078–2097. [Google Scholar]
- Pausata F, Battisti DS, Nisancioglu KH, and Bitz CM (2011), Chinese stalagmite [delta] 18O controlled by changes in the Indian monsoon during a simulated Heinrich event, Nature Geoscience, 4 (7), 474–480. [Google Scholar]
- Payne VH, Noone D, Dudhia A, Piccolo C, and Grainger RG (2007), Global satellite measurements of HDO and implications for understanding the transport of water vapor into the stratosphere, Quarterly Journal of the Royal Meteorological Society, 133 (627), 1459–1471. [Google Scholar]
- Pfahl S, and Wernli H (2008), Air parcel trajectory analysis of stable isotopes in water vapor in the eastern Mediterranean, Journal of Geophysical Research: Atmospheres, 113 (D20), D20,104. [Google Scholar]
- Pfahl S, Wernli H, and Yoshimura K (2012), The isotopic composition of precipitation from a winter storm - a case study with the limited-area model COSMOiso, Atmospheric Chemistry and Physics, 12 (3), 1629–1648. [Google Scholar]
- Pierrehumbert R, Brogniez H, and Roca R (2006), On the relative humidity of the atmosphere, The Global Circulation of the Atmosphere. [Google Scholar]
- Postel G, and Hitchman M (1999), A climatology of Rossby wave breaking along the subtropical tropopause, Journal of the Atmospheric Sciences, 56 (3), 359–373. [Google Scholar]
- Poulsen CJ, and Jeffery ML (2011), Climate change imprinting on stable isotopic compositions of high-elevation meteoric water cloaks past surface elevations of major orogens, Geology, 39 (6), 595–598. [Google Scholar]
- Rambo J, Lai C-T, Farlin J, Schroeder M, and Bible K (2011), On-Site Calibration for High Precision Measurements of Water Vapor Isotope Ratios Using Off-Axis Cavity-Enhanced Absorption Spectroscopy, Journal of Atmospheric and Oceanic Technology, 28 (11), 1448–1457. [Google Scholar]
- Randall D, Krueger S, Bretherton C, Curry J, Duynkerke P, Moncrieff M, Ryan B, Starr D, Miller M, Rossow W, Tselioudis G, and Wielicki B (2003), Confronting models with data - The GEWEX cloud systems study, Bulletin Of The American Meteorological Society, 84 (4), 455–469. [Google Scholar]
- Randall DA, Xu KM, and Somerville R (1996), Single-column models and cloud ensemble models as links between observations and climate models, Journal of …. [Google Scholar]
- Randel WJ, Moyer E, Park M, Jensen E, Bernath P, Walker K, and Boone C (2012), Global variations of HDO and HDO/H2O ratios in the upper troposphere and lower stratosphere derived from ACE-FTS satellite measurements, Journal Of Geophysical Research-Atmospheres, 117 (D6). [Google Scholar]
- Redelsperger JL, and Lafore J-P (1988), A Three-Dimensional Simulation of a Tropical Squall Line: Convective Organization and Thermodynamic Vertical Transport, Journal of the Atmospheric Sciences, 45 (8), 1334–1356. [Google Scholar]
- Reijmer H, van den Broeke R, and Scheele MP (2002), Air parcel trajectories and snowfall related to five deep drilling locations in Antarctica based on the ERA-15 dataset, Journal of Climate, 15 (14), 1957–1968. [Google Scholar]
- Rhines A, and Huybers PJ (2014), Sea Ice and Dynamical Controls on Preindustrial and Last Glacial Maximum Accumulation in Central Greenland, Journal of Climate, 27 (23), 8902–8917. [Google Scholar]
- Ridal M (2002), Isotopic ratios of water vapor and methane in the stratosphere: Comparison between ATMOS measurements and a one-dimensional model, Journal Of Geophysical Research-Atmospheres, 107 (D16). [Google Scholar]
- Rideal EK (1925), The influence of thin surface films on the evaporation of water, Journal of Physical Chemistry, 29 (12), 1585–1588. [Google Scholar]
- Rio C, Hourdin F, and Grandpeix JY (2009), Shifting the diurnal cycle of parameterized deep convection over land, Geophysical Research …, 36 (L07809). [Google Scholar]
- Risi C, Bony S, and Vimeux F (2008a), Influence of convective processes on the isotopic composition (delta 18 O and deltaD) of precipitation and water vapor in the tropics:2. Physical interpretation of the amount effect, Journal of Geophysical Research, 113 (D19306). [Google Scholar]
- Risi C, Bony S, Vimeux F, Descroix L, Ibrahim B, Lebreton E, Mamadou I, and Sultan B (2008b), What controls the isotopic composition of the African monsoon precipitation? Insights from event-based precipitation collected during the 2006 AMMA field campaign, Geophysical Research Letters, 35 (24). [Google Scholar]
- Risi C, Bony S, Vimeux F, Frankenberg C, Noone D, and Worden J (2010a), Understanding the Sahelian water budget through the isotopic composition of water vapor and precipitation, Journal Of Geophysical Research-Atmospheres, 115 (D24). [Google Scholar]
- Risi C, Bony S, Vimeux F, Chong M, and Descroix L (2010b), Evolution of the stable water isotopic composition of the rain sampled along Sahelian squall lines, Quarterly Journal of the Royal Meteorological Society, 136 (S1), 227–242. [Google Scholar]
- Risi C, Bony S, Vimeux F, and Jouzel J (2010c), Water-stable isotopes in the LMDZ4 general circulation model: Model evaluation for present-day and past climates and applications to climatic interpretations of tropical isotopic records, Journal of Geophysical Research: Atmospheres, 115 (D12), D12,118. [Google Scholar]
- Risi C, Noone D, Worden J, Frankenberg C, Stiller G, Kiefer M, Funke B, Walker K, Bernath P, Schneider M, Wunch D, Sherlock V, Deutscher N, Griffith D, Wennberg PO, Strong K, Smale D, Mahieu E, Barthlott S, Hase F, Garcia O, Notholt J, Warneke T, Toon G, Sayres D, Bony S, Lee J, Brown D, Uemura R, and Sturm C (2012a), Process-evaluation of tropospheric humidity simulated by general circulation models using water vapor isotopologues: 1. Comparison between models and observations, Journal Of Geophysical Research-Atmospheres, 117 (D5). [Google Scholar]
- Risi C, Noone D, Worden J, Frankenberg C, Stiller G, Kiefer M, Funke B, Walker K, Bernath P, Schneider M, Bony S, Lee J, Brown D, and Sturm C (2012b), Process-evaluation of tropospheric humidity simulated by general circulation models using water vapor isotopic observations: 2. Using isotopic diagnostics to understand the mid and upper tropospheric moist bias in the tropics and subtropics, Journal of Geophysical Research: Atmospheres, 117 (D5), D05,304. [Google Scholar]
- Risi C, Noone D, Frankenberg C, and Worden J (2013), Role of continental recycling in intraseasonal variations of continental moisture as deduced from model simulations and water vapor isotopic measurements, Water Resources Research, 49 (7), 4136–4156. [Google Scholar]
- Roche D, Paillard D, and Cortijo E (2004), Constraints on the duration and freshwater release of Heinrich event 4 through isotope modelling, Nature, 432 (7015), 379–382. [DOI] [PubMed] [Google Scholar]
- Roche DM (2013), delta O-18 water isotope in the iLOVECLIM model (version 1.0) - Part 1: Implementation and verification, Geoscientific Model Development, 6 (5), 1481–1491. [Google Scholar]
- Rodgers CD (2000), Inverse methods for atmospheric sounding: theory and practice, World Scientific, Singapore. [Google Scholar]
- Rokotyan NV, Zakharov VI, Gribanov KG, Schneider M, Bréon F-M, Jouzel J, Imasu R, Werner M, Butzin M, Petri C, Warneke T, and Notholt J (2014), A posteriori calculation of d18o and dd in atmospheric water vapor from ground-based near-infrared ftir retrievals of h216o, h218o, and hd16o, Atmospheric Measurement Techniques, 7 (8), 2567–2580, doi: 10.5194/amt-7-2567-2014. [DOI] [Google Scholar]
- Rosenlof KH, Oltmans SJ, Kley D, Russell JM, Chiou EW, Chu WP, Johnson DG, Kelly KK, Michelsen HA, Nedoluha GE, Remsberg EE, Toon GC, and McCormick MP (2001), Stratospheric water vapor increases over the past half-century, Geophysical Research Letters, 28 (7), 1195–1198. [Google Scholar]
- Rozanski K, ARAGUASARAGUAS L, and Gonfiantini R (1992), Relation Between Long-Term Trends of O-18 Isotope Composition of Precipitation and Climate, Science, 258 (5084), 981–985. [DOI] [PubMed] [Google Scholar]
- Rozanski K, Araguás-Araguás L, and Gonfantini R (1993), Isotopic patterns in modern global precipitation, in Climate Change in Continental Isotopic records. [Google Scholar]
- Saatchi S, Asefi-Najafabady S, Malhi Y, Aragao LEOC, Anderson LO, Myneni RB, and Nemani R (2013), Persistent effects of a severe drought on Amazonian forest canopy, Proceedings of the National Academy of Sciences, 110 (2), 565–570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sachse D, Kahmen A, and Gleixner G (2009), Significant seasonal variation in the hydrogen isotopic composition of leaf-wax lipids for two deciduous tree ecosystems (Fagus sylvativa and Acerpseudoplatanus), Organic Geochemistry, 40 (6), 732–742. [Google Scholar]
- Salamalikis V, Argiriou A, and Dotsika E (2015), Stable isotopic composition of atmospheric water vapor in patras, greece: A concentration weighted trajectory approach, Atmospheric Research, 152, 93–104, doi: 10.1016/j.atmosres.2014.02.021, atmospheric Processes in the Mediterranean. [DOI] [Google Scholar]
- Salati E, Dall’Olio A, Matsui E, and Gat JR (1979), Recycling of Water in the Amazon Basin - Isotopic Study, Water Resources Research, 15 (5), 1250–1258. [Google Scholar]
- Saleska SR, Shorter JH, Herndon S, Jimnez R, Barry McManus J, William Munger J, Nelson DD and Zahniser MS (2006), What are the instrumentation requirements for measuring the isotopic composition of net ecosystem exchange of CO2 using eddy covariance methods?, Isotopes in Environmental and Health Studies, 42 (2), 115–133. [DOI] [PubMed] [Google Scholar]
- Samuels-Crow KE, Galewsky J, Sharp ZD, and Dennis KJ (2014a), Deuterium excess in subtropical free troposphere water vapor: Continuous measurements from the Chajnantor Plateau, northern Chile, Geophysical Research Letters, 41 (23), 8652–8659. [Google Scholar]
- Samuels-Crow KE, Galewsky J, Hardy DR, Sharp ZD, Worden J, and Braun C (2014b), Upwind convective influences on the isotopic composition of atmospheric water vapor over the tropical Andes, Journal Of Geophysical Research-Atmospheres, doi 10.1002/2014JD021487. [DOI] [Google Scholar]
- Sayres DS, Moyer EJ, Hanisco TF, St Clair JM, Keutsch FN, O’Brien A, Allen NT, Lapson L, Demusz JN, Rivero M, Martin T, Greenberg M, Tuozzolo C, Engel GS, Kroll JH, Paul JB, and Anderson JG (2009), A new cavity based absorption instrument for detection of water isotopologues in the upper troposphere and lower stratosphere, Review of Scientific Instruments, 80 (4). [DOI] [PubMed] [Google Scholar]
- Sayres DS, Pfister L, Hanisco TF, Moyer EJ, Smith JB, St Clair JM, OBrien AS, Witinski MF, Legg M, and Anderson JG (2010), Influence of convection on the water isotopic composition of the tropical tropopause layer and tropical stratosphere, Journal of Geophysical Research: Atmospheres, 115 (D10), D00J20. [Google Scholar]
- Scheele MP, Siegmund P, and van velthoven PFJ (1996), Sensitivity of trajectories to data resolution and its dependence on the starting point: In or outside a tropopause fold, Meteorological Applications, 3 (3), 267–273. [Google Scholar]
- Scheepmaker RA, Frankenberg C, Deutscher NM, Schneider M, Barthlott S, Blumenstock T, Garcia OE, Hase F, Jones N, Mahieu E, Notholt J, Velazco V, Landgraf J, and Aben I (2015), Validation of sciamachy hdo/h2o measurements using the tccon and ndacc-musica networks, Atmospheric Measurement Techniques, 8 (4), 1799–1818, doi: 10.5194/amt-8-1799-2015. [DOI] [Google Scholar]
- Scherer JJ, Paul JB, OKeefe A, and Saykally RJ (1997), Cavity ringdown laser absorption spectroscopy: History, development, and application to pulsed molecular beams, Chemical Reviews, 97 (1), 25–51. [DOI] [PubMed] [Google Scholar]
- Schmidt GA, Hoffmann G, Shindell DT, and Hu YY (2005), Modeling atmospheric stable water isotopes and the potential for constraining cloud processes and stratosphere-troposphere water exchange, Journal Of Geophysical Research-Atmospheres, 110 (D21). [Google Scholar]
- Schmidt GA, LeGrande AN, and Hoffmann G (2007), Water isotope expressions of intrinsic and forced variability in a coupled ocean-atmosphere model, Journal Of Geophysical Research-Atmospheres, 112 (D10). [Google Scholar]
- Schmidt M, Maseyk K, Lett C, Biron P, Richard P, Bariac T, and Seibt U (2010), Concentration effects on laser-based del O-18 and del H-2 measurements and implications for the calibration of vapor measurements with liquid standards, Rapid Communications In Mass Spectrometry, 24 (24), 3553–3561. [DOI] [PubMed] [Google Scholar]
- Schneider M, Hase F, and Blumenstock T (2006a), Ground-based remote sensing of HDO/H2O ratio profiles: introduction and validation of an innovative retrieval approach, Atmospheric Chemistry and Physics, 6, 4705–4722. [Google Scholar]
- Schneider T, O’Gorman PA, and Levine XJ (2010), Water Vapor and the Dynamics of Climate Changes, Reviews of Geophysics, 48 (3). [Google Scholar]
- Schneider M, and Hase F (2011), Optimal estimation of tropospheric h2o and δd with iasi/metop, Atmos. Chem. Phys, 11, 11,207–11,220, doi: 10.5194/acp-11-11207-2011. [DOI] [Google Scholar]
- Schneider M, Barthlott S, Hase F, Gonzalez Y, Yoshimura K, Garcia OE, Sepulveda E, Gomez-Pelaez A, Gisi M, Kohlhepp R, Dohe S, Blumenstock T, Wiegele A, Christner E, Strong K, Weaver D, Palm M, Deutscher NM, Warneke T, Notholt J, Lejeune B, Demoulin P, Jones N, Griffith DWT, Smale D, and Robinson J (2012), Ground-based remote sensing of tropospheric water vapor isotopologues within the project MUSICA, Atmospheric Measurement Techniques, 5, 3007–3027. [Google Scholar]
- Schneider M, Wiegele A, Barthlott S, González Y, Christner E, Dyroff C, García OE, Hase F, Blumenstock T, Sepúlveda E, Mengistu Tsidu G, Takele Kenea S, Rodríguez S, and Andrey J (2016), Accomplishments of the MUSICA project to provide accurate, long-term, global and high-resolution observations of tropospheric H2O, δD pairs - a review, Atmospheric Measurement Techniques, 2016, 2845–2875, doi: 10.5194/amt-9-2845-2016. [DOI] [Google Scholar]
- Schoenemann SW, Schauer AJ, and Steig EJ (2013), Measurement of SLAP2 and GISP δ17O and proposed VSMOW-SLAP normalization for δ17O and 17Oexcess, Rapid Communications In Mass Spectrometry, 27 (5), 582–590. [DOI] [PubMed] [Google Scholar]
- Sharp Z (2006), Principles of stable isotope geochemistry, Prentice Hall. [Google Scholar]
- Sharp ZD, Atudorei V, and Durakiewicz T (2001), A rapid method for determination of hydrogen and oxygen isotope ratios from water and hydrous minerals, Chemical Geology, 178 (1–4), 197–210. [Google Scholar]
- Sherwood S, and Dessler A (2000), On the control of stratospheric humidity, Geophysical Research Letters, 27 (16), 2513–2516. [Google Scholar]
- Sherwood SC, Roca R, Weckwerth TM, and Andronova NG (2010), Tropospheric Water Vapor, Convection, and Climate, Reviews of Geophysics, 48 (2). [Google Scholar]
- Sherwood SC, Bony S, and Dufresne J-L (2014), Spread in model climate sensitivity traced to atmospheric convective mixing, Nature, 505 (7481), 37–42. [DOI] [PubMed] [Google Scholar]
- Sjolte J, Hoffmann G, Johnsen SJ, Vinther BM, Masson-Delmotte V, and Sturm C (2011), Modeling the water isotopes in Greenland precipitation 1959–2001 with the meso-scale model REMO-iso, Journal Of Geophysical Research-Atmospheres, 116 (D18). [Google Scholar]
- Smith JA, Ackerman AS, Jensen EJ, and Toon OB (2006), Role of deep convection in establishing the isotopic composition of water vapor in the tropical transition layer, Geophysical Research Letters, 33 (6), L06,812. [Google Scholar]
- Sodemann H, Masson-Delmotte V, Schwierz C, Vinther BM, and Wernli H (2008), Interannual variability of Greenland winter precipitation sources: 2. Effects of North Atlantic Oscillation variability on stable isotopes in precipitation, Journal of Geophysical Research: Atmospheres, 113 (D12). [Google Scholar]
- St Clair JM, Hanisco TF, Weinstock EM, Moyer EJ, Sayres DS, Keutsch FN, Kroll JH, Demusz JN, Allen NT, Smith JB, Spackman JR, and Anderson JG (2008), A new photolysis laser-induced fluorescence instrument for the detection of H(2)O and HDO in the lower stratosphere, Review of Scientific Instruments, 79 (6). [DOI] [PubMed] [Google Scholar]
- Steen-Larsen HC, Masson-Delmotte V, Sjolte J, Johnsen SJ, Vinther BM, Bréon FM, Clausen HB, Dahl-Jensen D, Falourd S, Fettweis X, Gallee H, Jouzel J, Kageyama M, Lerche H, Minster B, Picard G, Punge HJ, Risi C, Salas D, Schwander J, Steffen K, Sveinbjoernsdottir AE, Svensson A, and White J (2011), Understanding the climatic signal in the water stable isotope records from the NEEM shallow firn/ice cores in northwest Greenland, Journal Of Geophysical Research-Atmospheres, 116 (D6). [Google Scholar]
- Steen-Larsen HC, Johnsen SJ, Masson-Delmotte V, Stenni B, Risi C, Sodemann H, Balslev-Clausen D, Blunier T, Dahl-Jensen D, Ellehøj MD, Falourd S, Grindsted A, Gkinis V, Popp T, Sheldon S, Simonsen SB, Sjolte J, Steffensen JP, Sperlich P, Sveinbjörnsdóttir AE, Vinther BM, and White JWC (2013), Continuous monitoring of summer surface water vapor isotopic composition above the Greenland Ice Sheet, Atmospheric Chemistry and Physics, 13 (9), 4815–4828. [Google Scholar]
- Steen-Larsen HC, Sveinbjörnsdóttir AE, Peters AJ, Masson-Delmotte V, Guishard MP, Hsiao G, Noone D, Warren JK, and White JWC (2014a), Climatic controls on water vapor deuterium excess in the marine boundary layer of the North Atlantic based on 500 days of in-situ, continuous measurements, Atmospheric Chemistry and Physics, 14 (15), 7741–7756. [Google Scholar]
- Steen-Larsen HC, Masson-Delmotte V, Hirabayashi M, Winkler R, Satow K, Prié F, Bayou N, Brun E, Cuffey KM, Dahl-Jensen D, Dumont M, Guillevic M, Kipfstuhl S, Landais A, Popp T, Risi C, Steffen K, Stenni B, and Sveinbjörnsdóttir AE (2014b), What controls the isotopic composition of Greenland surface snow?, Climate Of The Past, 10 (1), 377–392. [Google Scholar]
- Steen-Larsen HC, Sveinbjörnsdóttir AE, Jonsson T, Ritter F, Bonne JL, Masson-Delmotte V, Sodemann H, Blunier T, Dahl-Jensen D, and Vinther BM (2015), Moisture sources and synoptic to seasonal variability of North Atlantic water vapor isotopic composition, Journal Of Geophysical Research-Atmospheres. [Google Scholar]
- Steig EJ, Gkinis V, Schauer AJ, Schoenemann SW, Samek K, Hoffnagle J, Dennis KJ, and Tan SM (2014), Calibrated high-precision ¡sup¿17¡/sup¿O-excess measurements using cavity ring-down spectroscopy with laser-current-tuned cavity resonance, Atmospheric Measurement Techniques, 7 (8), 2421–2435. [Google Scholar]
- Steinwagner J, Milz M, Clarmann T. v., Glatthor N, Grabowski U, Höpfner M, Stiller GP, and Röckmann T (2007), HDO measurements with MIPAS, Atmospheric Chemistry and Physics, 7 (10), 2601–2615. [Google Scholar]
- Steinwagner J, Fueglistaler S, Stiller G, von Clarmann T, Kiefer M, Borsboom P-P, van Delden A, and Rockmann T (2010), Tropical dehydration processes constrained by the seasonality of stratospheric deuterated water, Nature Geoscience, 3 (4), 262–266. [Google Scholar]
- Stevens DE, and Bretherton S (1996), A Forward-in-Time Advection Scheme and Adaptive Multilevel Flow Solver for Nearly Incompressible Atmospheric Flow, Journal of Computational Physics, 129 (2), 284–295. [Google Scholar]
- Stewart MK (1975), Stable Isotope Fractionation Due to Evaporation and Isotopic-Exchange of Falling Waterdrops - Applications to Atmospheric Processes and Evaporation of Lakes, J. Geophys. Res, 80 (9), 1133–1146. [Google Scholar]
- Stohl A, Hittenberger M, and Wotawa G (1998), Validation of the lagrangian particle dispersion model FLEXPART against large-scale tracer experiment data, Atmospheric Environment, 32 (24), 4245–4264. [Google Scholar]
- Stohl A, Forster C, Frank A, Seibert P, and Wotawa G (2005), Technical note: The Lagrangian particle dispersion model FLEXPART version 6.2, Atmospheric Chemistry and Physics, 5, 2461–2474. [Google Scholar]
- Stowasser C, Buizert C, Gkinis V, Chappellaz J, Schuepbach S, Bigler M, Fain X, Sperlich P, Baumgartner M, Schilt A, and Blunier T (2012), Continuous measurements of methane mixing ratios from ice cores, Atmospheric Measurement Techniques, 5 (5), 999–1013. [Google Scholar]
- Strong M, Sharp ZD, and Gutzler DS (2007), Diagnosing moisture transport using D/H ratios of water vapor, Geophysical Research Letters, 34 (3), L03,404. [Google Scholar]
- Sturm C, Hoffmann G, and Langmann B (2007a), Simulation of the stable water isotopes in precipitation over South America: Comparing regional to global circulation models, Journal of Climate, 20 (15), 3730–3750. [Google Scholar]
- Sturm C, Vimeux F, and Krinner G (2007b), Intraseasonal variability in South America recorded in stable water isotopes, Journal Of Geophysical Research-Atmospheres, 112 (D20). [Google Scholar]
- Sturm C, Zhang Q, and Noone D (2010), An introduction to stable water isotopes in climate models: benefits of forward proxy modelling for paleoclimatology, Climate Of The Past, 6 (1), 115–129. [Google Scholar]
- Sturm K, Hoffmann G, Langmann B, and Stichler W (2005), Simulation of delta O-18 in precipitation by the regional circulation model REMOiso, Hydrological Processes, 19 (17), 3425–3444. [Google Scholar]
- Sturm P, Eugster W, and Knohl A (2012), Eddy covariance measurements of CO 2 isotopologues with a quantum cascade laser absorption spectrometer., Agricultural and Forest Meteorology, 152, 73–82. [Google Scholar]
- Sutanto SJ, Hoffmann G, Scheepmaker RA, Worden J, Houweling S, Yoshimura K, Aben I, and Röckmann T (2015), Global-scale remote sensing of water isotopologues in the troposphere: representation of first-order isotope effects, Atmospheric Measurement Techniques, 8 (3), 999–1019. [Google Scholar]
- Taupin J-D, and Gallaire R (1998), Variabilit isotopique I’chelle infra-vnement de quelques pisodes pluvieux dans la rgion de Niamey, Niger, C.R. Acad. des Sciences, 326, 493–498. [Google Scholar]
- Taylor CB (1972), The vertical variations of isotopic compositions of tropospheric water vapor over continental Europe and their relationship to tropospheric structure, Lower Hutt, New Zealand. [Google Scholar]
- Thompson L, Mosley-Thompson E, and Henderson K (2000), Ice-core palaeoclimate records in tropical South America since the Last Glacial Maximum, Journal Of Quaternary Science, 15 (4), 377–394. [Google Scholar]
- Thompson LG, Mosely Thompson E, Davis ME, BOLZAN JF, DAI J, Yao T, GUNDESTRUP N, Wu X, KLEIN L, and Xie Z (1989), Holocene Late Pleistocene Climatic Ice Core Records From Qinghai-Tibetan Plateau, Science, 246 (4929), 474–477. [DOI] [PubMed] [Google Scholar]
- Thompson LG, Davis ME, Mosley-Thompson E, Sowers TA, Henderson KA, Zagorodnov VS, Lin P-N, Mikhalenko VN, Campen RK, BOLZAN JF, Cole-Dai J, and Francou B (1998), A 25,000-year tropical climate history from Bolivian ice cores, Science, 282 (5395), 1858–1864. [DOI] [PubMed] [Google Scholar]
- Tian L, Masson-Delmotte V, Stievenard M, Yao T, and Jouzel J (2001), Tibetan Plateau summer monsoon northward extent revealed by measurements of water stable isotopes, Journal Of Geophysical Research-Atmospheres, 106 (D22), 28,081–28,088. [Google Scholar]
- Tierney JE, Russell JM, Huang Y, Damste JSS, Hopmans EC, and Cohen AS (2008), Northern hemisphere controls on tropical southeast African climate during the past 60,000 years, Science, 322 (5899), 252–255. [DOI] [PubMed] [Google Scholar]
- Tierney JE, Russell JM, Sinninghe Damsté JS, Huang Y, and Verschuren D (2011a), Late Quaternary behavior of the East African monsoon and the importance of the Congo Air Boundary, Quaternary Science Reviews, 30 (7–8), 798–807. [Google Scholar]
- Tierney JE, Lewis SC, Cook BI, and LeGrande AN (2011b), Model, proxy and isotopic perspectives on the East African Humid Period, Earth and Planetary …. [Google Scholar]
- Tindall JC, Valdes PJ, and Sime LC (2009), Stable water isotopes in HadCM3: Isotopic signature of El Nino Southern Oscillation and the tropical amount effect, Journal Of Geophysical Research-Atmospheres, 114 (D4). [Google Scholar]
- Tremoy G, Vimeux F, Mayaki S, Souley I, Cattani O, Risi C, Favreau G, and Oi M (2012), A 1-year long delta O-18 record of water vapor in Niamey (Niger) reveals insightful atmospheric processes at different timescales, Geophysical Research Letters, 39 (8). [Google Scholar]
- Tremoy G, Vimeux F, Soumana S, Souley I, Risi C, Favreau G, and Oi M (2014), Clustering mesoscale convective systems with laser-based water vapor delta O-18 monitoring in Niamey (Niger), Journal Of Geophysical Research-Atmospheres, 119 (9), 5079–5103. [Google Scholar]
- Trenberth KE (1999), Atmospheric moisture recycling: Role of advection and local evaporation, Journal of Climate, 12 (5), 1368–1381. [Google Scholar]
- Uemura R, Matsui Y, Yoshimura K, Motoyama H, and Yoshida N (2008), Evidence of deuterium excess in water vapor as an indicator of ocean surface conditions, Journal Of Geophysical Research-Atmospheres, 113 (D19). [Google Scholar]
- Uemura R, Barkan E, Abe O, and Luz B (2010), Triple isotope composition of oxygen in atmospheric water vapor, Geophysical Research Letters, 37 (4). [Google Scholar]
- van der Ent RJ, Savenije HHG, Schaefli B, and Steele Dunne SC (2010), Origin and fate of atmospheric moisture over continents, Water Resources Research, 46 (9), n/a–n/a. [Google Scholar]
- Vimeux F, Gallaire R, Bony S, Hoffmann G, and CHIANG J (2005), What are the climate controls on δD in precipitation in the Zongo Valley (Bolivia)? Implications for the Illimani ice core interpretation, Earth and Planetary Science Letters, 240 (2), 205–220. [Google Scholar]
- Vimeux F, Tremoy G, Risi C, and Gallaire R (2011), A strong control of the South American SeeSaw on the intra-seasonal variability of the isotopic composition of precipitation in the Bolivian Andes, Earth and Planetary Science Letters, 307 (1–2), 47–58. [Google Scholar]
- Vinther BM, Jones PD, Briffa KR, Clausen HB, Andersen KK, Dahl-Jensen D, and Johnsen SJ (2010), Climatic signals in multiple highly resolved stable isotope records from Greenland, Quaternary Science Reviews, 29 (3–4), 522–538. [Google Scholar]
- Vuille M, and Werner M (2005), Stable isotopes in precipitation recording South American summer monsoon and ENSO variability: observations and model results, Climate Dynamics, 25 (4), 401–413. [Google Scholar]
- Vuille M, Bradley RS, Werner M, Healy R, and Keimig F (2003), Modeling δ18O in precipitation over the tropical Americas: 1. Interannual variability and climatic controls, Journal of Geophysical Research: Atmospheres, 108 (D6), 4174. [Google Scholar]
- Vuille M, Werner M, Bradley RS, Chan RY, and Keimig F (2005a), Stable isotopes in east African precipitation record Indian ocean zonal mode, Geophysical Research Letters, 32 (21). [Google Scholar]
- Vuille M, Werner M, Bradley RS, and Keimig F (2005b), Stable isotopes in precipitation in the Asian monsoon region, Journal Of Geophysical Research-Atmospheres, 110 (D23). [Google Scholar]
- Walker G, Brunel J-P, Dighton J, Holland K, Leaney F, McEwan K, Mensforth L, Thorburn P, and Walker C (2001), The Use of Stable Isotopes of Water for Determining Sources of Water for Plant Transpiration, in Stable Isotope Techniques in the Study of Biological Processes and Functioning of Ecosystems, pp. 57–89, Springer Netherlands, Dordrecht. [Google Scholar]
- Washburn EW, and Smith ER (1934), The isotopic fractionation of water by physiological processes, Science, 79 (2043), 188–189. [DOI] [PubMed] [Google Scholar]
- Waugh D (2005), Impact of potential vorticity intrusions on subtropical upper tropospheric humidity, Journal Of Geophysical Research-Atmospheres, 110 (D11), D11,305. [Google Scholar]
- Webster C, and Heymsfield A (2003), Water Isotope Ratios D/H, 18O/16O, 17O/16O in and out of Clouds Map Dehydration Pathways, Science, 302 (5651), 1742–1745. [DOI] [PubMed] [Google Scholar]
- Wei Z, Yoshimura K, Okazaki A, Ono K, Kim W, Yokoi M, and Lai C-T (Submitted), Understanding the variability of water isotopologues in near-surface atmospheric moisture observed over a rice paddy in Tsukuba, Japan., Journal of Hydrology, 533, 91–102. [Google Scholar]
- Welp LR, Lee X, Griffis TJ, Wen X-F, Xiao W, Li S, Sun X, Hu Z, Val Martin M, and Huang J (2012), A meta-analysis of water vapor deuterium-excess in the midlatitude atmospheric surface layer, Global Biogeochemical Cycles, 26 (3), GB3021. [Google Scholar]
- Wen X-F, Zhang SC, Sun XM, Yu GR, and Lee X (2010), Water vapor and precipitation isotope ratios in Beijing, China, Journal of Geophysical Research: Atmospheres, 115 (D1), D01,103. [Google Scholar]
- Werner M, Mikolajewicz U, Heimann M, and Hoffmann G (2000), Borehole versus isotope temperatures on Greenland: Seasonality does matter, Geophysical Research Letters, 27 (5), 723–726. [Google Scholar]
- Werner M, Heimann M, and Hoffmann G (2001), Isotopic composition and origin of polar precipitation in present and glacial climate simulations, Tellus Series B-Chemical and Physical Meteorology, 53 (1), 53–71. [Google Scholar]
- Werner M, Langebroek PM, Carlsen T, Herold M, and Lohmann G (2011), Stable water isotopes in the ECHAM5 general circulation model: Toward high-resolution isotope modeling on a global scale, Journal Of Geophysical Research-Atmospheres, 116 (D15). [Google Scholar]
- Wernli H, and Davies HC (1997), A Lagrangian-based analysis of extratropical cyclones .1. The method and some applications, Quarterly Journal of the Royal Meteorological Society, 123 (538), 467–489. [Google Scholar]
- White J, Barlow LK, Fisher D, Grootes P, Jouzel J, Johnsen SJ, Stuiver M, and Clausen H (1997), The climate signal in the stable isotopes of snow from Summit, Greenland: Results of comparisons with modern climate observations, Journal of Geophysical Research: Oceans, 102 (C12), 26,425–26,439. [Google Scholar]
- Wiegele A, Schneider M, Hase F, Barthlott S, García OE, Sepúlveda E, González Y, Blumenstock T, Raffalski U, Gisi M, and Kohlhepp R (2014), The musica metop/iasi h2o and dd products: characterisation and long-term comparison to ndacc/ftir data, Atmospheric Measurement Techniques, 7, 2719–2732, doi: 10.5194/amt-7-2719-2014. [DOI] [Google Scholar]
- Williams DG, Cable W, Hultine K, Hoedjes J, Yepez EA, Simonneaux V, Er-Raki S, Boulet G, de Bruin H, Chehbouni A, Hartogensis OK, and Timouk F (2004), Evapotranspiration components determined by stable isotope, sap flow and eddy covariance techniques, Agricultural and Forest Meteorology, 125 (3–4), 241–258. [Google Scholar]
- Wilson JD, and Sawford BL (1996), Review of Lagrangian stochastic models for trajectories in the turbulent atmosphere, Boundary-Layer Meteorology, 78 (1–2), 191–210. [Google Scholar]
- Winkler R, Landais A, Risi C, Baroni M, Ekaykin A, Jouzel J, Petit JR, Prie F, Minster B, and Falourd S (2013), Interannual variation of water isotopologues at Vostok indicates a contribution from stratospheric water vapor, Proceedings of the National Academy of Sciences, 110 (44), 17,674–17,679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winnick Matthew J., Chamberlain C. Page, Caves Jeremy K., and Welker Jeffrey M. (2014), Quantifying the isotopic ‘continental effect’, Earth and Planetary Science Letters, 406, 123–133. [Google Scholar]
- Worden J, Bowman K, Noone D, Beer R, Clough S, Eldering A, Fisher B, Goldman A, Gunson M, Herman R, Kulawik SS, Lampel M, Luo M, Osterman G, Rinsland C, Rodgers C, Sander S, Shephard M, and Worden H (2006), Tropospheric Emission Spectrometer observations of the tropospheric HDO/H2O ratio: Estimation approach and characterization, Journal of Geophysical Research: Atmospheres, 111 (D16), D16,309. [Google Scholar]
- Worden J, Noone D, Bowman K, and Beer R (2007), Importance of rain evaporation and continental convection in the tropical water cycle, Nature, 445, 528–532. [DOI] [PubMed] [Google Scholar]
- Worden J, Kulawik S, Frankenberg C, Payne V, Bowman K, Cady-Peirara K, Wecht K, Lee JE, and Noone D (2012), Profiles of CH4, HDO, H2O, and N2O with improved lower tropospheric vertical resolution from Aura TES radiances, Atmospheric Measurement Techniques, 5 (2), 397–411. [Google Scholar]
- Wright JS, Sobel AH, and Schmidt GA (2009), Influence of condensate evaporation on water vapor and its stable isotopes in a GCM, Geophysical Research Letters, 36 (12). [Google Scholar]
- Wright JS, Sobel A, and Galewsky J (2010), Diagnosis of Zonal Mean Relative Humidity Changes in a Warmer Climate, Journal of Climate, 23 (17), 4556–4569. [Google Scholar]
- Yepez EA, Williams DG, Scott RL, and Lin GH (2003), Partitioning overstory and understory evapotranspiration in a semiarid savanna woodland from the isotopic composition of water vapor, Agricultural and Forest Meteorology, 119 (1–2), 53–68. [Google Scholar]
- Yoneyama K, and Parsons D (1999), A proposed mechanism for the intrusion of dry air into the Tropical Western Pacific region, Journal of the Atmospheric Sciences, 56 (11), 1524–1546. [Google Scholar]
- Yoshimura K, OKI T, OHTE N, and KANAE S (2004), Colored Moisture Analysis Estimates of Variations in 1998 Asian Monsoon Water Sources, Journal of the Meteorological Society of Japan, 82 (5), 1315–1329. [Google Scholar]
- Yoshimura K, Kanamitsu M, and Dettinger M (2010), Regional downscaling for stable water isotopes: A case study of an atmospheric river event, Journal Of Geophysical Research-Atmospheres, 115 (D18). [Google Scholar]
- Yoshimura K, Miyoshi T, and Kanamitsu M (2014), Observation system simulation experiments using water vapor isotope information, Journal Of Geophysical Research-Atmospheres, 119 (13). [Google Scholar]
- Yu W, Tian L, Ma Y, Xu B, and Qu D (2015), Simultaneous monitoring of stable oxygen isotope composition in water vapor and precipitation over the central Tibetan Plateau, Atmospheric Chemistry and Physics Discussions, 15 (10), 14,445–14,472. [Google Scholar]
- Zahn A (2001), Constraints on 2-way transport across the Arctic tropopause based on O-3, stratospheric tracer (SF6) ages, and water vapor isotope (D, T) tracers, Journal Of Atmospheric Chemistry, 39 (3), 303–325. [Google Scholar]
- Zahn A, Barth V, Pfeilsticker K, and Platt U (1998), Deuterium, oxygen-18, and tritium as tracers for water vapor transport in the lower stratosphere and tropopause region, Journal Of Atmospheric Chemistry, 30 (1), 25–47. [Google Scholar]
- Zahn A, Franz P, Bechtel C, Grooss JU, and Roeckmann T (2006), Modelling the budget of middle atmospheric water vapor isotopes, Atmospheric Chemistry and Physics, 6, 2073–2090. [Google Scholar]
- Zakharov VI, Imasu R, Gribanov KG, Hoffmann G, and Jouzel J (2004), Latitudinal distribution of the deuterium to hydrogen ratio in the atmospheric water vapor retrieved from IMG/ADEOS data, Geophysical Research Letters, 31 (12), L12,104. [Google Scholar]
- Zhang C (2005), Madden-Julian Oscillation, Reviews of Geophysics, 43 (2), RG2003. [DOI] [PMC free article] [PubMed] [Google Scholar]