Highlights
-
•
Social distancing index Pd was developed on basis of exhaled droplet distribution and transmission.
-
•
The perfect-mixing-based Wells-Riley model was modified by introducing the social distancing index Pd and ventilation effectiveness Ez.
-
•
The safe social distance is recommended as 1.6–3.0 m considering aerosol transmission of exhaled large droplets from talking.
-
•
The modified model used one actual pandemic case to calibrate the infectious dose and verified by a number of other existing cases.
-
•
Projections using the validated model illustrated the efficacy of social distancing and influence factors on required ventilation rate.
Keywords: COVID-19, Social distance, Ventilation, Infection probability, Wells-Riley model
Abstract
Social distancing and ventilation were emphasized broadly to control the ongoing pandemic COVID-19 in confined spaces. Rationales behind these two strategies, however, were debated, especially regarding quantitative recommendations. The answers to “what is the safe distance” and “what is sufficient ventilation” are crucial to the upcoming reopening of businesses and schools, but rely on many medical, biological, and engineering factors. This study introduced two new indices into the popular while perfect-mixing-based Wells-Riley model for predicting airborne virus related infection probability – the underlying reasons for keeping adequate social distance and space ventilation. The distance index Pd can be obtained by theoretical analysis on droplet distribution and transmission from human respiration activities, and the ventilation index Ez represents the system-dependent air distribution efficiency in a space. The study indicated that 1.6−3.0 m (5.2–9.8 ft) is the safe social distance when considering aerosol transmission of exhaled large droplets from talking, while the distance can be up to 8.2 m (26 ft) if taking into account of all droplets under calm air environment. Because of unknown dose response to COVID-19, the model used one actual pandemic case to calibrate the infectious dose (quantum of infection), which was then verified by a number of other existing cases with short exposure time (hours). Projections using the validated model for a variety of scenarios including transportation vehicles and building spaces illustrated that (1) increasing social distance (e.g., halving occupancy density) can significantly reduce the infection rate (20–40 %) during the first 30 min even under current ventilation practices; (2) minimum ventilation or fresh air requirement should vary with distancing condition, exposure time, and effectiveness of air distribution systems.
1. Introduction
The outbreak of novel coronavirus disease 2019 (COVID-19) rapidly spread over 215 countries, areas or territories, impacting every aspect of human life. As of May 1, 2020, more than 3,272,200 cases of COVID-19 had been confirmed, including over 230,100 reported deaths (WHO, 2020b). Similar to all respiratory infectious diseases, the ongoing COVID-19 pandemic warns that close contact should be avoided on account of virus transmission via droplet and airborne routes by respiratory activities (CDC, 2020a; CIDRAP, 2020; Peng, Xu, & Li, 2020; Radio, 2020; S, M.A., K, S., K, & A., 2020; Ta-Chih, Hsiao-Chi, & Stephen, 2020; WHO, 2020a). The virus spreads through respiratory droplets produced when an infected person coughs, sneezes, or talks (CDC, 2020a). Social distancing, also called “physical distancing”, means keeping space between anyone and others outside of their homes. Many countries (Richard & Horizon, 2020), such as Australia (Australian Government, D.o.H., 2020a, 2020b), Italy (Giordano, Blanchini, & Bruno, 2020), England(Liverpool, 2020), and America (Prevention, 2019, 2020) have implemented restrictions on social activities; and researchers (Aderibigbe, 2020; Ashwin & Shantal, 2020; CMAJ, 2020; Ginger, Jay, Benoit, & Eric, 2020; Mahase, 2020; Morawska, Lidia, & Junji, 2020; Muddasani, Housholder, Fleischer, B, & A., 2020; Qazi, Javaria, & Khulla, 2020; Setti, Auid-Orcid, Passarini, & Auid-Orcid, 2020; Zhang, Litvinova, & Liang, 2020) suggested increasing social distance to alleviate the spread of COVID-19. Some studies recommended (CDC, 2020b) that at least 2 m (6 feet) (about 2 arm’s length) should be kept from others, while others believed that 6 feet or 2 m may not be adequate during this COVID-19 outbreak (Setti et al., 2020).
Social distancing avoids the direct contacts among people and also reduces the potential cross-transmission of virus-carrying droplets from human respiration – two primary mechanisms for respiratory infection. A few studies can be found in literature exploring droplet transmission trajectories through human respiratory behaviors including talking, eating, coughing, and sneezing. Some studies believed the number of pathogens of respiratory infectious diseases to be associated with droplet size, where large droplets were the main objects carrying microorganisms generated from the infected person (Christian, Loutfy, & McDonald, 2004; Julia, RN, & MN, 1996; Mangili & Gendreau, 2005; Wells, 1934). Other studies suspected that small droplets/particles in the form of nucleus may disperse much farther (called “airborne”). It was broadly debated regarding “how far can respiratory droplets transfer” and “what is the safe social distance”. The question is indeed complicated because it not only concerns momentum transmission, but also relates to mass exchange with surrounding air such as by evaporation. It becomes more sophisticated when medical and biological factors are considered (e.g., infectious dose) along with the engineering factors. The critical size of large droplets is a function of many physical parameters, including ambient air temperature, relative humidity, velocity, etc. Evaporation effect should be taken into account to predict precise transmission distance of droplets by human respiration.
Social distancing also tightly interacts with ventilation, both amount (rate) and effectiveness. Indoor ventilation is highly associated with the risk of respiratory infectious disease (Nielsen, Winther, & Buus, 2008; WHO, 2009; Yang, Sekhar, & Cheong, 2015). Adequate ventilation (rate) is mandatory to reduce the risk of infection, such as for SARS (Jiang, Zhao, & Li, 2009), in confined spaces, especially in public transportations, large/open offices, stores, restaurants, and so on. It is thus critical to investigate the relationships among social distance, minimum ventilation rate, and probability of infection (PI), in order to control the PI to be less than the control target such as 2 %.
This study introduced two new indices into the popular while perfect-mixing-based Wells-Riley (WR) model to quantify the impacts from social distance and ventilation effectiveness to the PI. The distance index Pd (%) was obtained by theoretical analysis on droplet distribution and transmission during talking; and expressed in the form of droplet disperse distance fitted from experimental data. The ventilation index Ez represents the system-dependent air distribution efficiency in a space, as illustrated in the ASHRAE standard. This study calibrated the infective quantum q in the WR model using one real pandemic case and verified the modified model by comparing predicted and actual infection rates for other existing cases. The study further projected the PI for a variety of confined environments with different occupancy densities. Ventilation rate and effectiveness were varied and tested to achieve the targeted 2% infection rate with extended indoor time in different spaces.
2. Methods
2.1. Distribution and transmission model of exhaled droplets
Quite a few studies have investigated the number and size of droplets of saliva and other secretions from respiratory activities (Duguid, 1945; Fennelly, Martyny, Kayte, Fulton, & Ian, 2004; Hamburger & Robertson, 1948; Jennison & M.W, 1942; Loudon & Roberts, 1967; Papineni & Rosenthal, 1997). The actual size distribution of droplets depends on many parameters such as the exhaled air velocity, the viscosity of the fluid, and the flow path (i.e., through nose, mouth, or both) (Barker et al., 2001). This study analyzed the statistics and distributions of droplets in both size and number during normal talking using field experimental data (Xie, Li, & Sun, 2009).
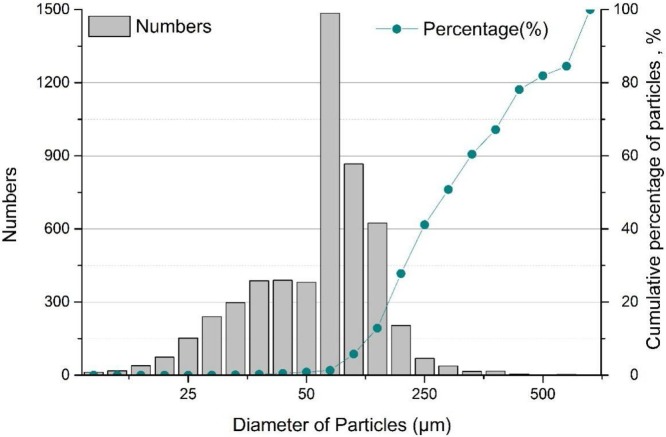
Several classical theoretical models and field measurement data were reviewed. One systematical laboratory study was chose to analyze the distributions of exhaled droplets during talking activity (Xie et al., 2009), which were consistent with previous studies (Loudon & Roberts, 1967; Xie et al., 2009). Experimental studies in literature mostly counted the spread droplet sizes and numbers, and some visualized trajectories, but did not provide quantitative distance tests and correlations. Fig. 1 shows the analyzed distribution of sizes, numbers and cumulative probabilities of respiratory droplets when subjects were talking. There were about 5,318 droplets during this talking activity and the diameters ranged from 0 to 1500 μm. Among these, the droplets with diameter of 50−75 μm account for the largest percentage of the total emission, about 28 %. Droplets with diameter below 10 μm and above 500 μm only accounted for 0.5 % and 0.1 %, respectively.
Fig. 1.
Sizes, numbers and cumulative mass percentages of respiratory droplets (Xie et al., 2009).
The transmission distances of droplets can be calculated and analyzed based on their characteristics of size and number. To simplify the falling and evaporation analysis of the droplets, the study firstly hypothesized a single free-falling particle following the Stokes Law to obtain the falling velocity vt (m/s) by balancing the drag force, gravity and buoyancy (Robinson, James, & Rodrigo, 2016), as seen in Eqs. (1) and (2).
| (1) |
where, is the dynamic viscosity of airflow (Pa·s), is the radius of particle (m), ρ is the particle density (kg/m3) and ρ’ is the density of flow medium (air, kg/m3), g is the gravitational acceleration (m/s2). When Re<2, in the Stokes zone, the particle terminal falling velocity, falling time, and horizontal travel distance can be obtained, respectively:
| (2) |
| (3) |
| (4) |
The initial height (H) of this particle was set as 1.5 m, which is the typical height of standing person mouth, and the falling time t (s) can be calculated by Eq. (3). The horizontal transmission distance d can be attained with a given initial velocity u0 (m/s) multiplying with the falling time t (Eq. (4)). Most particles can reach the terminal velocity quickly (compared to the total falling time) and then fall under this constant speed. In this analysis, the initial temperature of the respiratory droplets was set at 33 °C (Hoppe, 1981), and the air temperature was at 20 °C (Wells, 1934). The average u0 for talking was 5 m/s (Xie, Li, & Chwang, 2007).
When evaporation is considered, the droplet size alters during the falling and transmission, and thus the transmitted distance also changes. Eq. (5) is often used to determine the evaporation time te (ms) during an actual water droplet falling, where D 0 (μm) is the initial diameter of a droplet and λ (μm2/ms) is the evaporation factor that is almost constant (Lui & Zhai, 2007) under typical room conditions
| (5) |
The actual trajectory, therefore, is related to the droplet size D that is varying with t during the falling process. Eq. (6) represents the corrected falling velocity vt (m/s) with consideration of evaporation. The falling time t can be recalculated using the integral Eq. (7), where H is the vertical transmission distance of 1.5 m. The final horizontal transmission distance was then obtained by using Eq. (4).
| (6) |
| (7) |
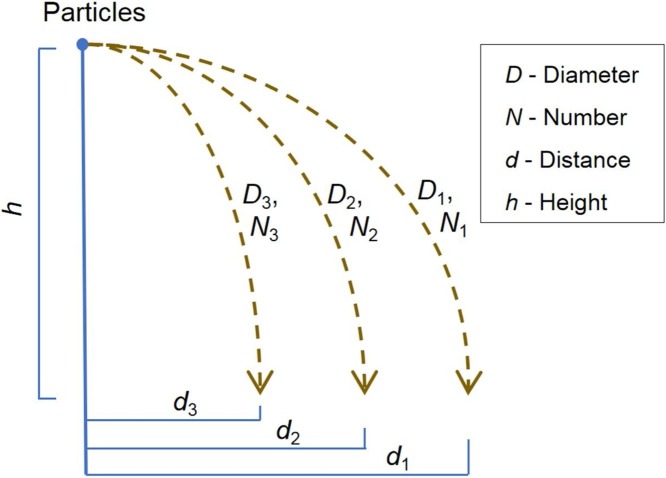
For the particles of different sizes (i.e., different masses), Eqs. (8) and (9) present the mass percentages of different transmission distances, with the assumption of three particle sizes as demonstration (Fig. 2 ). The percentage of transmission distance varies from 0 %, when beyond the maximum distance d 1, to 100 %, when below the minimum distance d 3. The same theoretical analysis process can be applied to the cases with actual droplet distributions from experiments.
| (8) |
| (9) |
where M (mg) is the total mass of the droplets, Mi (i = 1,2,3) is the mass of the droplets with the diameter of Di (μm), Ni (i = 1,2,3) is the number of droplets with Di, di (i = 1,2,3, m) is the horizontal transmission distance of droplets with Di.
Fig. 2.
Transmissions of particles with different sizes.
2.2. Role of social distance and development of social distance index Pd
This study built the relationship between the statistical probability of droplets in different sizes and their transmission distances based on the analysis of distribution and transmission of the experimental exhaled droplets. The social distance index Pd (%) is expressed as a function of distance d (m), where Pd is a cumulative percentage or probability (Eq. (9)) and its upper limit is 100 %. Principally, Pd increases with decrease of transmission distance that is negatively related to droplet size.
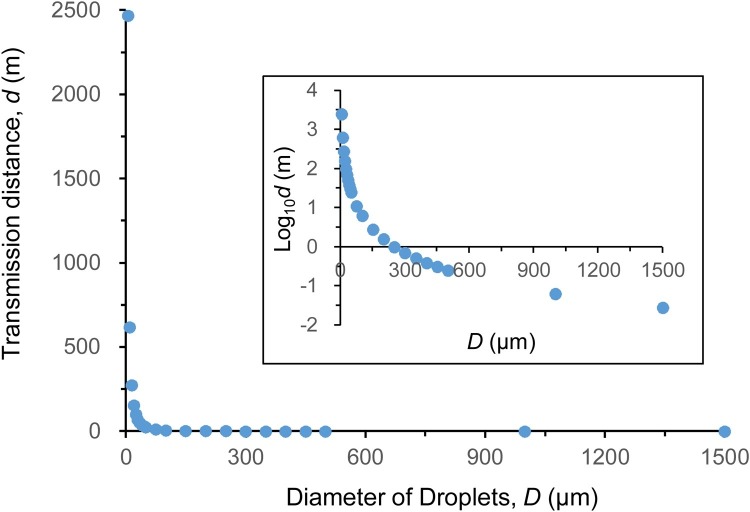
The study then calculated the transmission distance d according to Eqs. (1), (2), (3), (4), as seen in Fig. 3 . Analytically, the particle with diameter of 5 μm could spread up to 2500 m, and the larger the particles the shorter the transmission distance. For the droplets with diameter of above 1000 μm, the distance was close to 0 m.
Fig. 3.
The transmission distance of droplets with different sizes.
The evaporation effect of droplets during the transmission was not considered in the calculation of transmission distance shown in Fig. 3. As described earlier, changes in droplet size due to evaporation are calculated with Eq. (5). It was found that 92 μm was the critical diameter to distinguish the droplet final location. It resulted in a complete evaporation of the droplets with small sizes (D<92 μm) into the air before they landed on the ground. These evaporated droplets turned into droplet nucleus and stayed in the air for a longer time. However, because of the low mass percentage of droplets with these smaller sizes and inconclusive conclusions on airborne nature and risk impacts of COVID-19, this study focused on those larger droplets, which would land on ground before the full evaporation.
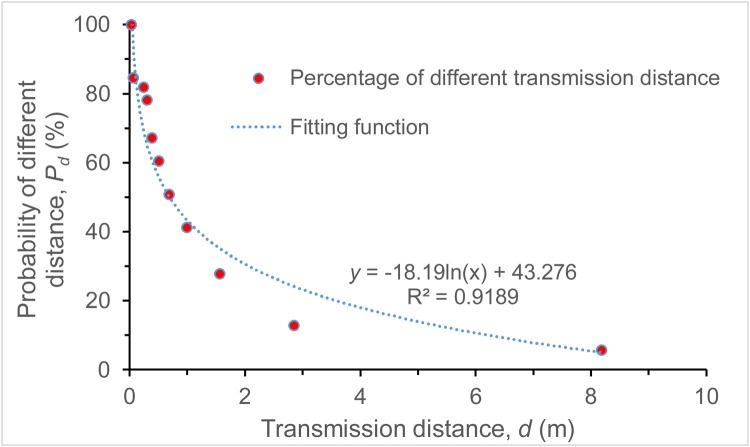
Under the influence of evaporation, the initial trajectory of a droplet altered, where the transmission distance would be longer than before owing to the gradual reduction of droplet size. The final horizontal transmission distance of droplets after evaporation should be recalculated using Eqs. (6) and (7). The relationship of this distance and the exposure mass percentage (probability) based on droplet distribution was then obtained by curve fitting, as seen in Fig. 4 . The social distance index Pd is expressed as a function of distance, as shown in Eq. (10), where the R2 = 0.9189.
| (10) |
Fig. 4.
The relationship between droplet transmission distance and its exposure probability.
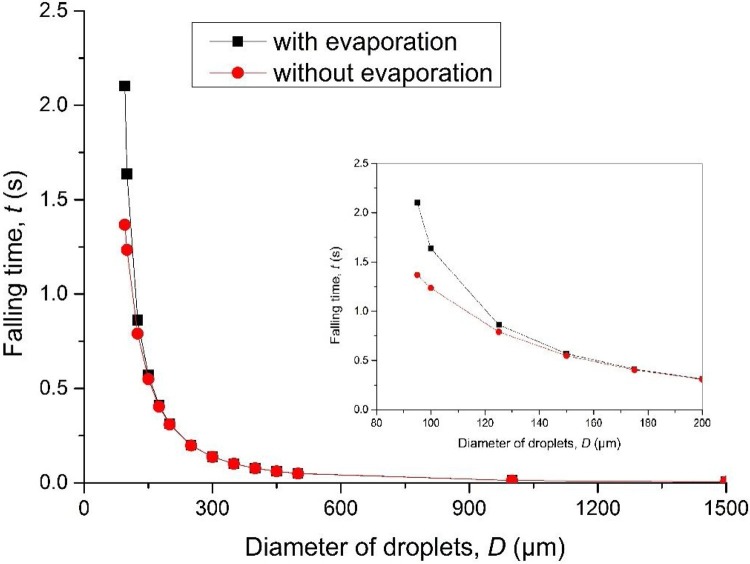
Fig. 5 compares the falling time of droplets of different sizes with and without evaporation. The difference of the falling time with and without evaporation was found among the droplets with the diameter of 100−200 μm. The disparity decreases with the increase of droplet size, and there is almost no difference when the diameter is above 150 μm. Small droplets are more affected by evaporation, but the probability of social distance Pd depends more on the droplets with large diameters. Eq. (10), hence, can be used with reasonable accuracy.
Fig. 5.
The falling time of droplets of different sizes with and without evaporation.
2.3. Ventilation factor - air distribution effectiveness EZ
For a confined space or zone, different ventilation systems or modes may bring different air distribution patterns and thus efficiencies. Among all of the air distribution configurations, ceiling supply of cool air and ceiling supply of warm air with floor return are often taken as the base cases for air distribution evaluation, respectively, with assignment 1.0 of ventilation factor in ASHRAE 62.1 (ASHRAE, 2019). This value is called air distribution effectiveness Ez and it ranges from 0.5, where makeup supply outlet is located less than half the length of the space from the exhaust, return, or both, to 1.5 with stratified air distribution systems or personalized ventilation system, as summarized in Table 1 . In the outbreak of respiratory diseases such as COVID-19, this ventilation factor is particularly important for the assessment of effective ventilation in confined spaces. Computational fluid dynamics (CFD) techniques can be used to simulate individual cases and obtain more accurate and case-specific Ez.
Table 1.
Zone air distribution effectiveness(ASHRAE, 2019).
| Air Distribution Configuration | Ez |
|---|---|
| Well-Mixed Air Distribution Systems | |
| Ceiling supply of cool air | 1.0 |
| Ceiling supply of warm air and floor return | 1.0 |
| Ceiling supply of warm air 15 F (8℃) or more above space temperature and ceiling return | 0.8 |
| Ceiling supply of warm air less than 15 F (8℃) above average space temperature where the supply air-jet velocity is less than 150 fpm(0.8 m/s) within 4.5 ft (1.4 m) of the floor and ceiling return | 0.8 |
| Ceiling supply of warm air less than 15 F(8℃) above average space temperature where the supply air-jet velocity is equal to or greater than 150 fpm(0.8 m/s) within 4.5 ft (1.4 m) of the floor and ceiling return | 1.0 |
| Floor supply of warm air and floor return | 1.0 |
| Floor supply of warm air and ceiling return | 0.7 |
| Makeup supply outlet located more than half the length of the space from the exhaust, return, or both | 0.8 |
| Makeup supply outlet located less than half the length of the space from the exhaust, return, or both | 0.5 |
| Stratified Air Distribution Systems (Section 6.2.1.2.1) | |
| Floor supply of cool air where the vertical throw is greater than or equal to 60 fpm (0.25 m/s) at a height of 4.5 ft (1.4 m) above the floor and ceiling return at a height less than or equal to 18 ft (5.5 m) above the floor | 1.05 |
| Floor supply of cool air where the vertical throw is less than or equal to 60 fpm (0.25 m/s) at a height of 4.5 ft (1.4 m) above the floor and ceiling return at a height less than or equal to 18 ft (5.5 m) above the floor | 1.2 |
| Floor supply of cool air where the vertical throw is less than or equal to 60 fpm (0.25 m/s) at a height of 4.5 ft (1.4 m) above the floor and ceiling return at a height greater than 18 ft (5.5 m) above the floor | 1.5 |
| Personalized Ventilation Systems(Section 6.2.1.2.2) | |
| Personalized air at a height of 4.5 ft (1.4 m) above the floor combined with ceiling supply of cool air and ceiling return | 1.40 |
| Personalized air at a height of 4.5 ft (1.4 m) above the floor combined with ceiling supply of warm air and ceiling return | 1.40 |
| Personalized air at a height of 4.5 ft (1.4 m) above the floor combined with a stratified air distribution system with nonaspirating floor supply devices and ceiling return | 1.20 |
| Personalized air at a height of 4.5 ft (1.4 m) above the floor combined with a stratified air distribution system with aspirating floor supply devices and ceiling return | 1.50 |
3. Modified Wells – Riley model
The Wells-Riley model is one of the most classic and popular models to predict the infection risk (Riley, Murphy, & Riley, 1978; Wells, 1955), as shown in Eq. (11).
| (11) |
where PI is the probability of infection (risk), C is the number of cases to develop infection, S is the number of susceptible, I is the number of source patients (infector), p is the pulmonary ventilation rate of each susceptible individual (m3/s) (p = 0.3 m3/h when people sits or conducts light indoor activities (Duan, Zhao, & Wang, 2013)), Q is the room ventilation rate (m3/s); q is the quantum generation rate produced by one infector (quantum/s), and t is the exposure time (s). The original Wells–Riley model considered the ventilation rate as the only influencing factor to the infection risk, by assuming the space is well-mixed.
The quantum q is tightly related to specific respiratory infectious diseases, as well as vulnerability of susceptible group in study. Since there is no uniform and broadly accepted value of q for COVID-19 in worldwide, one way to identify q is to perform a reverse calculation based on actual cases, where the other factors were known or could be determined. After several trial calculations, this study found that the q value varies largely in different spaces with different population densities and ventilation systems.
Two important indices described above, Pd and Ez, were thus introduced into the Wells-Riley model, as presented in Eq. (12).
| (12) |
The study firstly attempted to calibrate the q value in the model by using one real pandemic case with other known parameters, and then verified this modified model with other existing cases. The study then applied this modified model to predict the infection risk of COVID-19 in a variety of confined scenarios with different occupation densities, and to investigate the required minimum ventilation rate for these spaces to achieve the targeted 2% infection probability.
4. Calibration and verification of the modified model
This study has collected critical data from several actual pandemic cases. The relevant parameters of these cases were listed in Table 2 . Antibody tests from Stanford University (Nature, 2020) conducted in Santa Clara County, California, suggested that coronavirus infection rate may be 2.5–4.2 % vastly exceeding official counts. Preliminary findings from the tests in Hoosiers, Indiana, also showed a general population prevalence of about 2.8 % of the state’s population (INDIANA UNIVERSITY, 2020). According to these findings, the bus in Hunan-1 was chosen as a representative case in terms of the initial infection rate (2.17 %), the stay duration, and the occupant number. The infective quantum q in the modified model was subsequently calibrated by this case.
Table 2.
Parameters of actual pandemic cases for model calibration and verification.
| Case | Duration of stay | Ventilation rate with clean air m3/(h∙p) | Infected person | Percentage of infection | Number of infector | Total people, N | Initial infection rate, B | Social distance, d (m) | Distance index, Pd (%) | Ventilation index, Ez | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Calibration | Bus in Hunan-1, China | 2 h | 23.91 | 8 | 18.0 % | 1 | 46 | 2.17 % | 1.05 | 42.4 % | 1 |
| Verification | Bus in Hunan-2, China | 1 h | 28 | 3 | 25.0 % | 1 | 12 | 8.33 % | 1.30 | 38.5 % | 1 |
| Bus in Ningbo, China | 4 h | 20 | 25 | 36.7 % | 1 | 68 | 1.47 % | 0.70 | 49.8 % | 1 | |
| Airplane in Iran | 6.5 h | 28.1 | 37 | 11.9 % | 5 | 311 | 1.61 % | 0.88 | 45.6 % | 1 | |
The distance between two passengers on this bus was estimated to be 1.05 m based on the design regulation (GB 9673-1996 1996) and the actual occupancy rate against the seat design; and the Pd value on this bus was calculated to be 42.4 %. The air distribution on the bus was set as ceiling supply and floor return according to the bus design standard, and the ventilation effectiveness index Ez was 1.0. The ventilation rate (clean air) was obtained according to the actual situation in references (Jian, Ming, & Bo, 2000; Tang, Ke, & Gong, 2011). As a result, with the known percentage of infection (18 %) after 2 -h travel/exposure time, the value of q was calculated to be 0.238, where the unit of q was quantum/s. The q value was then kept as a constant to project the infection probability and the required ventilation rate for similar confined spaces. The related exposure parameters for all these cases, including d, Pd, Ez, were analyzed and calculated.
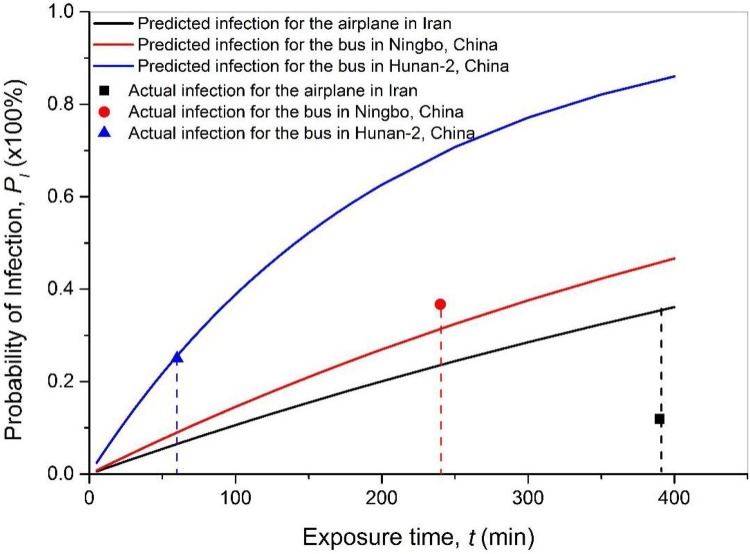
Fig. 6 shows the infection probability projected by the modified model with their own input parameters, compared against the actual infection probability in Table 2. The comparison reveals a reasonable accuracy of the model prediction for most actual cases. The lowest deviation of the prediction from the actual value was 2.2 %. The model presents a good capability for predicting the infection risk. However, I varied randomly from case to case, which lead to significant uncertainly in the predicted infection probability due to the limited sampling cases. This study attempted to explore the sensitivity of PI to the variable initial infection by introducing the initial infection rate B (=I/N, where N is the total number of passengers/occupants). The modified model can be expressed as Eq. (13).
| (13) |
Fig. 6.
The predicted and actual probability of infection in existing cases.
Table 2 shows that the initial infection rate B varies from 1.47 % to 8.33 %, so the sample standard deviation (root-mean-square error) of B is 3.3 % and the T-score of these samples is 36 %. The projection range of PI can be estimated by introducing ±3.3 % uncertainty of initial B into the Eq. (13). The uncertainty range of PI due to B, for the bus in Hunan-2, China after 60 min exposure, the bus in Ningbo, China after 4 h exposure, and the airplane in Iran after 6.5 h exposure was 3.8–33.8 %, 0–70.6 % and 0–73.7 %, respectively. The deviations of the predictions from the actual values in the three verification cases were within the error range. Attributed to the scarce sample size in this study (and the high randomness of B in individual cases), the uncertainty range of projected PI may seem large. But modeling the trend of infection using average B in general population by Eq. (3) can produce reasonable and meaningful outcomes. Upon the findings from the existing antibody tests, this study applied the estimated population infection rate 2.8 % as the initial infection rate B in the model to project the infection probability in the following case analysis.
Due to the fact that many other influential factors may likely involve in disease transmission in long-term exposure, such as wider activity spaces and more chances for direct body and surface contacts, this study would consider that this model is more appropriate for predicting infection risks in confined spaces with relative shorter exposure time (in hours), such as for public transportation, classroom, office, store, and restaurant.
5. Applications and implications of the modified model
This study utilized the modified model to predict the infection risks in typical confined spaces, including bus, air cabin, subway, high-speed train, classroom, office, and restaurant. The associated parameters and designed ventilation rate (required minimum fresh air rate, m3/h∙p) were determined according to respective standards as listed in Table 3 . The research calculated the distance index Pd using Eq. (10) with both the actual social distance and the double social distance (where the occupancy ratio is 50 %). The ventilation effectiveness Ez was set as 0.8–1.0 in accordance with specific air distribution forms.
Table 3.
Parameters of typical confined space scenarios.
| Scenario | Number of seats | Length (m) | Width (m) | Social distance, d (m) | Distance index, Pd | Pd with 50% occupancy ratio | Ventilation rate with clean air, Q/N(m3/h∙p) | Air distribution form | Ventilation index, Ez | |
|---|---|---|---|---|---|---|---|---|---|---|
| Long bus (GB9673-1996, 1996GB9673-, 1996GB9673-1996, 1996) | 69 | 13.7 | 2.55 | 0.72 | 49.3 % | 36.7 % | 20 | Ceiling supply, floor return | 1 | 0.025 (0.018) |
| Air cabin (GB9673-1996, 1996GB9673-, 1996GB9673-1996, 1996) | 350 | – | – | 0.78 | 48.0 % | 35.2 % | 25 | Ceiling supply, floor return | 1 | 0.019 (0.014) |
| Public bus (GB9673-1996, 1996GB9673-, 1996GB9673-1996, 1996) | 75 | 8.5 | 2.5 | 0.35 | 62.2 % | 49.6 % | 15 | Ceiling supply, ceiling return | 0.8 | 0.052 (0.041) |
| Subway (GB50157—2003, 2013GB50157—, 2013GB50157—2003, 2013) | 200 | 22 | 3 | 0.57 | 53.4 % | 40.8 % | 20 | Ceiling supply, ceiling return | 0.8 | 0.033 (0.026) |
| High-speed train (TB10621-2009, 2009TB10621-, 2009TB10621-2009, 2009) | 85 | 25 | 3.3 | 0.99 | 43.5 % | 30.9 % | 20 | Ceiling supply, floor return | 1 | 0.022 (0.015) |
| Office (GB50189-2005 2005GB50189—, 2005GB50189-2005 2005; JGJ/T67-2006 2006JGJ/T67-, 2019JGJ/T67-2006 2006; Mu, Yan, & Qian, 2017) | 10 | – | – | 2.00 | 30.7 % | 18.1 % | 30 | Ceiling supply, floor return | 1 | 0.010 (0.006) |
| Classroom (GB99-86, 2012; Y., J. Y.J., 2019) | 50 | – | – | 1.05 | 42.4 % | 29.8 % | 14 | Ceiling supply, floor return | 1 | 0.030 (0.021) |
| Restaurant (JG64-89, 1900) | 90 | – | – | 1.05 | 42.4 % | 29.8 % | 20 | Ceiling supply, ceiling return | 0.8 | 0.027 (0.019) |
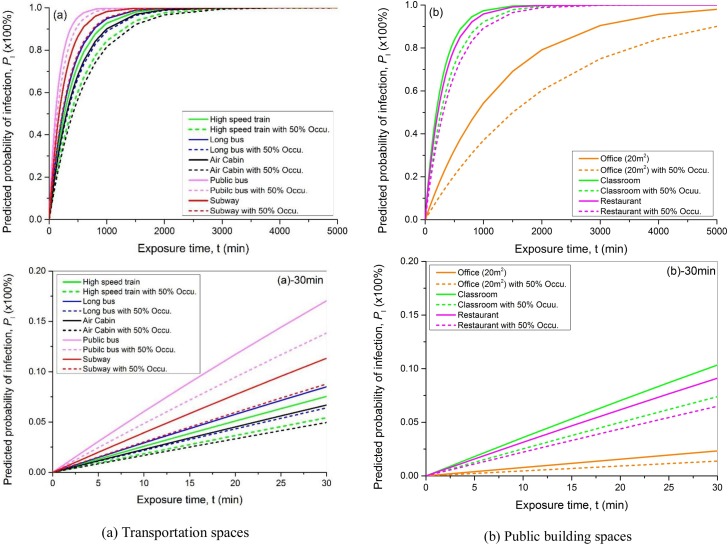
Fig. 7 shows the predicted probability of infection due to COVID-19 in representative confined environments with 100 % and 50 % occupancy ratio. All the infection probability eventually approached to 1 (100 %) with long enough exposure time. The results illustrate that the risk of infection in public bus was the highest among all the public transportation vehicles. This is consistent with the actual situation due to the lower air distribution effectiveness, lower fresh air rate, and higher occupancy density. The risk in aircraft cabin was the lowest, where the combined index of distance and ventilation Pd/(Ez∙Q/N) was the smallest. It should be noted that this finding was based on the required minimum ventilation rate for each application. The total ventilation rate (including both fresh air and cleaned recirculated air) for land transportation could be much more than aircraft (that is more restricted), which might reduce the infection risk.
Fig. 7.
Predicted probability of infection for different scenarios.
By reducing the occupancy ratio by 50 %, the infection risk could be decreased effectively during the same exposure time period with the same ventilation. For most of the tested transportations, the infection probability at the end of the first 30 min can be reduced by 18.8–28.2 %, while in confined building spaces, the reduction can be 28.6–40.6 %. Table 4 listed the projected infection probability for staying in various spaces with 100 % and 50 % occupancy ratio. The occupying/exposure time was determined by experienced estimation. For instance, people spend the most and least continuous time, respectively, in office (4 h) and commuter bus/subway (30 min). As anticipated, infection risk assuredly increases with the exposure time, but is also greatly affected by ventilation and social distancing. For example, staying on a high-speed train for 3 h produces a higher PI than staying in an office for 4 h. Reducing the occupancy density by 50 % can reduce the infected risk by 9.1 % for high-speed train and 9.6 % for office, while the reduction of PI on public bus and subway is, respectively, 3.2 % and 2.5 % after 30-minute time duration. It was noted that the infection probability varied linearly with time during the first 30-minutes exposure in all of the studied spaces.
Table 4.
Projected infection probability with 100 % and 50 % occupancy density in different spaces with their representative exposure times.
| Scenarios | Long bus | Air cabin | Public bus | Subway | High-speed train | Office | Classroom | Restaurant |
|---|---|---|---|---|---|---|---|---|
| Stay/exposure time | 2 h | 2.5h | 30 min | 30 min | 3 h | 4 h | 45 min | 1.5h |
| PI with 100 % occu. | 29.9 % | 29.3 % | 17.0 % | 11.3 % | 37.5 % | 25.6 % | 15.1 % | 24.9 % |
| PI with 50 % occu. | 23.2 % | 22.4 % | 13.8 % | 8.8 % | 28.4 % | 16.0 % | 10.9 % | 18.2 % |
Further analysis illustrates that the infection risk shows a clear linear dependence to the exposure time, respectively, during the first 200 min (about 3.3 h) for the long bus, 240 min (4 h) for the air cabin, 110 min (1.8 h) for the public bus, 140 min (2.3 h) for the subway, 240 min (4 h) for the high speed train, 360 min (6 h) for the office, 120 min (2 h) for the classroom, and 180 min (3 h). In other words, during these time periods, the infection risk increases linearly with occupying time. People usually spend more time inside buildings and transportations than outside, therefore social distancing (occupancy ratio) and ventilation play an important role in controlling the outbreak of COVID-19.
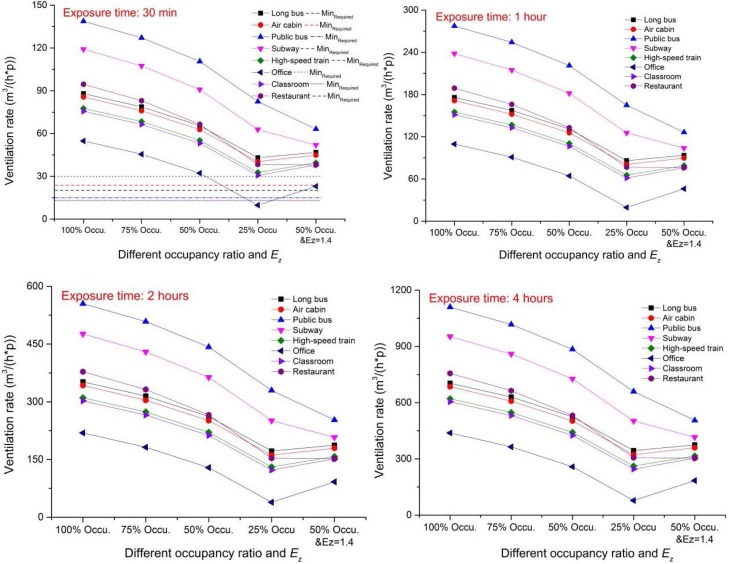
Although social distancing is effective in reducing the risk of infection, to control the PI to a lower level (for example, 2 %) requires adequate ventilation rate to dilute the contaminants from infectors. Social distancing can impact the required ventilation rate. Fig. 8 shows the requested minimum ventilation rate in order to achieve the targeted infection probability goal of 2 % in typical spaces with different occupancy densities (100 %, 75 %, 50 % and 25 %). The Ez values were derived from Table 3, representing the conventional design conditions. As a higher air distribution effectiveness may correspond to a less ventilation rate need, an occupancy ratio of 50 % with a higher Ez of 1.4 (for personalized ventilation) was also tested and compared. As expected, the requested minimum ventilation rate increases proportionally with the length of exposure time. Increasing social distance (i.e., reducing the occupancy ratio) can significantly reduce the required ventilation rate. For instance, for office, the required ventilation rate can be reduced by more than four fifth when the occupancy ratio reduced to 25 % at the first 30-minute exposure. For public bus with the highest infection risk, the required ventilation rate can be reduced by 40 %. Under the scenarios of 25–50 % occupancy ratio or 50 % occupancy ratio with a higher Ez of 1.4, the required ventilation rate for office was even below the conventional minimum fresh air (30 m3/(h∙p)) requirement in the standard. For all transportations and other public buildings, the standard-required minimum fresh air flow rate is not enough to achieve the set risk mitigation goal (PI < 2 %), even with lower occupancy ratio and higher ventilation effectiveness. The sole practical approach is to increase the ventilation rate. Fig. 8 also shows that with a 4 -h exposure time in office, the required ventilation rate decreased from 438.2 m3/(h∙p) to 77.8 m3/(h∙p) (about 82 % reduction) to achieve the same infection probability target of <2%, when the occupancy ratio was reduced to 25 %. Increasing the ventilation effectiveness to a higher level (i.e., with personalized ventilation at Ez = 1.4) also had a great impact on the required ventilation rate, especially for restaurant, public bus and subway, where the required ventilation rates with 50 % occupancy ratio were even lower than those with 25 % occupancy ratio and Ez = 1. In this situation, the required minimum ventilation rate during the first 30 min exposure in most of the studied spaces was lower than 50 m3/(h∙p) – a ventilation rate that can be achieved by most current ventilation systems without major renovation.
Fig. 8.
The requested ventilation rate for controlling the low infected probability.
6. Discussion
The projected probability of infection (PI) demonstrates that social distancing and ventilation play an important role in preventing the risk of COVID-19 outbreak. The minimum safe distance for regular social activities (e.g., breathing and talking) was 1.6−3 m (5.2–9.8 ft), while the maximum transmission distance could be up to 8.2 m (26 ft) and its probability was 5%. These findings also explain that extended social distancing can effectively mitigate the risk of infection.
A number of studies have articulated that the COVID-19 virus is airborne (Morawska et al., 2020; Q, Y., W, N., Z, & W., 2020; Setti et al., 2020). Respiratory droplets evaporate and their diameters thus become small enough to suspend in the air in the form of droplet nucleus. The nucleus can stay in the air for a long time, and if they carry the virus, they will undoubtedly jeopardize the susceptible population. However, the mechanism of airborne transmission and infection is complex and need further investigation. Owing to the low percentage of quality and number of small droplets, which might evaporate into the air and become nucleus before their deposition, this study focused on the primary risk through the droplet route as defined by WHO and US CDC. The convection flow around human body is also an important factor impacting the droplets transmission (Liu, Li, & Nielsen, 2017; Yang, Yang, & Zhao, 2016), but to simplify the transmission model, this factor was not taken into account. Besides, the risk from physical/surface contact is still unclear and not included in this study. It is necessary and valuable to propose a comprehensive scheme that can evaluate the risk from all possible routes.
A number of studies have suggested the social distance based on the exhaled droplets transmission. A 1 m (3 feet) seperation was suggested for public activities to prevent the virus spreading carried by larged droplets in previous studies (WHO, 2014). However, studies demonstrated that 1 m is not enough for infection controlling. They proposed that 2−6 m is the safe distance because >0.1 mm droplets may evaporate or fall to a surface within 2 m, depending on size, air humidity and temperature, but droplets can reach distances as far as 6 m away when coughing or sneezing with spray velocity up to 10−50 m/s (Bjørn & Nielsen, 2002; Xie et al., 2007). With the outbreaking of COVID-19, a study reported that droplets can travel up to eight meters (23–27 feet) in the case of a sneeze, which means even small droplets may spread throughout a room (Bourouiba, 2020). These statements are based on the CFD simulation or laboratory tests. This study attempeted to analyze the droplets falling and transmission in theoretically by considering the gravity, friction, buoyancy lift and the evaporation simultaneously. Instead of displaying the transmission distance for droplets with different sizes seperately, this study built the relationship of transmission distance with the expoure probability based on mass stastistics. It reveals the risk of virus spreading by droplets of different sizes.
The calibration of the modified Wells-Riley model provided a practical infective quantum q (0.238, quantum/s) for COVID-19 based on statistics and very limited case studies. Findings from verification on real cases indicated that the modified model with introduction of distance and ventilation indices (Pd and Ez) had a reasonable accuracy of prediction. Based on a limited number of real cases, the lowest deviation of the prediction from the actual value was 2.2 %, and the deviations of the projected PIs for the verification cases were within the uncertainty range. The case used to calibrate the model had an initial infection rate (2.17 %) that was close to the announced population infection rate (2.8 %) from the antibody tests.
The sensitivity studies show that 20–40 % reduction of infection risk would occur at the first 30 min of occupancy if the occupancy rate was reduced by 50 % in confined spaces. This reconfirms the efficacy of social distancing on mitigating infection risks. The combination of proper social distance and high ventilation effectiveness can significantly reduce the required minimum ventilation rate to the range that can be achieved by current mechanical systems. As a result, increasing social distance combined with high ventilation effectiveness should be considered as two effective manners to deliver ventilation and prevent COVID-19 cross-infection.
There are several limitations of this study. This study has several limitations. First, the modified model was developed in the case of virus transmission by droplet. In fact, direct contact has been confirmed as another significant path to spread virus. Besides, the droplet nuclei is also considered as a potential carrier of respiratory virus. Secondly, the initial infection probability for calibration was hypothesized as 2.8 % synthesizing the antibody test results and one real vehicle case in this study, which may bring the deviation of the projected infection probability and related required minimum ventilation rate. Thirdly, social distance in practical condition is unknown and the average value based on the space area and passengers’ number was hypothesized and employed. This estimation method may present its limitation for spaces with strong population mobility or irregular space shape in practice.
7. Conclusion
This paper developed and introduces two critical indices – social distance probability Pd and ventilation effectiveness Ez – into the Wells-Riley model to predict the infection probability of COVID-19. These two indices provide the quantitative evaluation of impacts of social distancing and ventilation effectiveness on respiratory disease infection risk. The study calibrated the infective quantum q in the model using one actual pandemic case and verified the modified model with other existing cases, which showed the reasonable accuracy of the model prediction for confined spaces. The projected infection probability in typical indoor environments using this modified model illustrated that social distancing had a great positive impact on decreasing both the infection risk and the required minimum ventilation rate so as to achieve the targeted infection probability. This study presents a promising prediction model for airborne virus in confined spaces that can quantify the influences of occupancy density, ventilation, and exposure time on infection probability.
Declaration of Competing Interest
The authors declare that no potential conflicts of interest with respect to the research, authorship and/or publication of this article.
Acknowledgement
The first author would like to thank the support of the National Natural Science Foundation of China [grant numbers 51708347].
References
- Aderibigbe A. ADEYINKA ADERIBIGBE; 2020. COVID-19: Social Distance, a work in progress intransportation. [Google Scholar]
- ASHRAE . 2019. ANSI/ASHRAE standrad 62.1-2019. [Google Scholar]
- Ashwin V., Shantal E. Social distancing in covid-19: what are the mental health implications? BMJ. 2020:369. doi: 10.1136/bmj.m1379. [DOI] [PubMed] [Google Scholar]
- Australian Government, D.o.H . 2020. Social distancing for coronavirus (COVID-19) [Google Scholar]
- Australian Government, D.o.H . 2020. Social distancing guidance. [Google Scholar]
- Barker J., Stevens D., Bloomfield S.F. Spread and prevention of some common viral infections in community facilities and domestic homes. J. Appl. Microbiol. 2001;91(1):7–21. doi: 10.1046/j.1365-2672.2001.01364.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bjørn E., Nielsen P.V. Dispersal of exhaled air and personal exposure in displacement ventilated rooms. Indoor Air. 2002;12:147–164. doi: 10.1034/j.1600-0668.2002.08126.x. [DOI] [PubMed] [Google Scholar]
- Bourouiba L. Turbulent gas clouds and respiratory pathogen emissions potential implications for reducing transmission of COVID-19. JAMA. 2020;323(18):1837–1838. doi: 10.1001/jama.2020.4756. [DOI] [PubMed] [Google Scholar]
- CDC . 2020. Centers for disease control - “How COVD-19 spreads.https://www.cdc.gov/oronavirus/209-110ncov/prevent-getting-sick/how-covid-spreads [Google Scholar]
- CDC . Centers for Disease Control and Prevention; 2020. Social distancing, quarantine, and isolation. [Google Scholar]
- Christian M.D., Loutfy M., McDonald L.C. Possible SARS coronavirus transmission during cardiopulmonary resuscitation. Emerging Infectious Diseases. 2004;10(2):287–293. doi: 10.3201/eid1002.030700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- CIDRAP . 2020. Unmasked: Experts explain necessary respiratory protection for COVID-19. [Google Scholar]
- CMAJ . CMAJ; 2020. How long will social distancing take to work? Experts weigh in on Canada’s COVID-19 response. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duan X., Zhao X., Wang B. China Environmental Science Press; Beijing: 2013. Exposure factors handbook of Chinese population (adults) (In Chinese) [Google Scholar]
- Duguid J. The numbers and the sites of origin of the droplets expelled during expiratory activities. Edinburgh Medical Journal. 1945;52(11):385–401. [PMC free article] [PubMed] [Google Scholar]
- Fennelly K.P., Martyny J., Kayte E., Fulton K., Ian M. Cough-generated aerosols of Mycobacterium tuberculosis: A new method to study infectiousness. American Journal of Respiratory and Critical Care Medicine. 2004;169(5):604–609. doi: 10.1164/rccm.200308-1101OC. [DOI] [PubMed] [Google Scholar]
- GB50157—2003 . China Building Industry Press; 2013. Code for design of metro. [Google Scholar]
- GB50189—2005 . China Building Industry Press; 2005. Design standard for energy efficiency of public buildings. [Google Scholar]
- GB9673-1996 . 1996. Hygienic standard for public means of transportation. General administration of quality supervision, inspection and quarantine of the People’s Republic of China. [Google Scholar]
- GB99-86 . Guangming Daily Press; 2012. Code for design of school. [Google Scholar]
- Ginger E., Jay F., Benoit H., Eric J. Wiley Online Library; 2020. Action at a distance: Geriatric research during a pandemic. [DOI] [Google Scholar]
- Giordano G., Blanchini F., Bruno R. Modelling the COVID-19 epidemic and implementation of population- wide interventions in Italy. Nature Medicine. 2020 doi: 10.1038/s41591-020-0883-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamburger M., Robertson O. Expulsion of group a hemolytic streptococci in droplets and droplet nuclei by sneezing, coughing and talking. The American Journal of Medicine. 1948;4(5):690–701. doi: 10.1016/s0002-9343(48)90392-1. [DOI] [PubMed] [Google Scholar]
- Hoppe P. Temperatures of expired air under varying climatic conditions. International Journal of Biometeorology. 1981;25(2):127–132. doi: 10.1007/BF02184460. [DOI] [PubMed] [Google Scholar]
- INDIANA UNIVERSITY . 2020. IU, ISDH release preliminary findings about impact of COVID-19 in Indiana.https://news.iu.edu/stories/2020/05/iupui/releases/13-preliminary-findings-impact-covid-19-indiana-coronavirus.html [Google Scholar]
- Jennison, M.W . 1942. American association of advanced science. Washington DC, 106. [Google Scholar]
- JG64-89 . China Building Industry Press; 1900. Standard for design of dietetic buildings. [Google Scholar]
- JGJ/T67-2019 . China Building Industry Press; 2019. Design code for office building. [Google Scholar]
- Jian M., Ming Q., Bo F. Energy Loss and Improvement of bus ventilation system. Energy Conservation. 2000:19–21. [Google Scholar]
- Jiang Y., Zhao B., Li X. Investigating a safe ventilation rate for the prevention of indoor SARS transmission: An attempt based on a simulation approach. Building Simulation. 2009;2(4):281–289. doi: 10.1007/s12273-009-9325-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Julia S., R.N, M.N Guidelines for isolation precautions in hospitals hospital infection control advisory committee. American Journal of Infection Control. 1996;24(1):24–31. [PubMed] [Google Scholar]
- Liu L., Li Y., Nielsen P. Short-range airborne transmission of expiratory droplets between two people. Indoor Air. 2017;27(2):452–462. doi: 10.1111/ina.12314. [DOI] [PubMed] [Google Scholar]
- Liverpool L. 2020. Coronavirus: What is social distancing and how do you do it?. [Google Scholar]
- Loudon R., Roberts R. Relation between the airborne diameters of respiratory droplets and the diameter of the stains left after recovery. Nature. 1967;213(5071):95–96. [Google Scholar]
- Lui X., Zhai Z. Identification of appropriate CFD models for simulating aerosol particle and droplet indoor transport. Indoor and Built Environment. 2007;16(4):322–330. [Google Scholar]
- Mahase E. Covid-19: UK starts social distancing after new model points to 260 000 potential deaths. BMJ. 2020 doi: 10.1136/bmj.m1089. [DOI] [PubMed] [Google Scholar]
- Mangili A., Gendreau M. Transmission of infectious diseases during commercial air travel. Lancet. 2005;365(9463):989–996. doi: 10.1016/S0140-6736(05)71089-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morawska, Lidia C., Junji Airborne transmission of SARS-CoV-2: The world should face the reality. Environment International. 2020;139 doi: 10.1016/j.envint.2020.105730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mu X., Yan X., Qian W. 2017. Simulation analysis of different air distribution in an air-conditioned office; pp. 60–64. [Google Scholar]
- Muddasani S., Housholder A., Fleischer, B, A An assessment of United States dermatology practices during the COVID-19 outbreak. The Journal of Dermatological Treatment. 2020:1–3. doi: 10.1080/09546634.2020.1750556. [DOI] [PubMed] [Google Scholar]
- Nature . 2020. Antibody tests suggest that coronavirus infections vastly exceed official counts.https://www.nature.com/articles/d41586-020-01095-0 [DOI] [PubMed] [Google Scholar]
- Nielsen P.V., Winther F.V., Buus M. Contaminant flow in the microenvironment between people under different ventilation conditions. ASHRAE Transactions. 2008;114:632–640. [Google Scholar]
- Papineni R., Rosenthal F. The size distribution of droplets in the exhaled breath of healthy human subjects. Journal of Aerosol Medicine-deposition Clearance and Effects in The Lung. 1997;10(2):105–116. doi: 10.1089/jam.1997.10.105. [DOI] [PubMed] [Google Scholar]
- Peng X., Xu X., Li Y. 2020. Transmission routes of 2019-nCoV and controls in dental practice; p. 9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prevention, C.f.D.C.a . 2019. Preventing transmission of infectious agents in healthcare settings. [Google Scholar]
- Prevention, C.f.D.C.a . 2020. Social distancing for tribal communities with local COVID-19 transmission. [Google Scholar]
- Q, Y, W, N, Z, W . 2020. Can novel coronavirus spread by aerosol? Ecological environment monitoring of the three gorges; pp. 1–5. [Google Scholar]
- Qazi A., Javaria N., Khulla Analyzing situational awareness through public opinion to predict adoption of social distancing amid pandemic COVID-19. Journal of Medical Virology. 2020;n/a(10) doi: 10.1002/jmv.25840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Radio N.P. 2020. WHO reviews ‘current’ evidence on coronavirus transmission through air.https://www.npr.org/2020/2003/2028/823292062/who-reviews-available-evidence-on-coronavirus-transmission-through-air [Google Scholar]
- Richard G., Horizon . 2020. Covid-19: Social distancing will help health authorities deal with coronavirus, says epidemiologist.https://medicalxpress.com/news/2020-2003-covid-social-distancing-health-authorities.html [Google Scholar]
- Riley E., Murphy G., Riley R. Airborne spread of measles in a suburban elementary school. American Journal of Epidemiology. 1978;107(5):421–432. doi: 10.1093/oxfordjournals.aje.a112560. [DOI] [PubMed] [Google Scholar]
- Robinson, James C., Rodrigo . Cambridge University Press; 2016. The three-dimensional Navier-Stokes equations: Classical theory Cambridge studies in advanced mathematics; pp. 484–486. [DOI] [Google Scholar]
- S, M.A, K, S, K, A . 2020. COVID-19 infection: Origin, transmission, and characteristics of human coronaviruses; pp. 91–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Setti L., Auid-Orcid, Passarini F., Auid-Orcid . Vol. 17. 2020. (Airborne transmission route of COVID-19: Why 2 meters/6 feet of inter-personal distance could not be enough). (8) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ta-Chih H., Hsiao-Chi C., Stephen M. COVID-19: An aerosol’s point of view from expiration to transmission to viral-mechanism. Aerosol and Air Quality Research. 2020;20:905–910. [Google Scholar]
- Tang W., Ke R., Gong Z. Testing, investigation and improvement on air quality in air-conditioning bus of Wuhan. Refrigeration Air Conditioning & Electric Power Machinery. 2011;32(138) 85–87, 138. [Google Scholar]
- TB10621-2009 . China Railway Publishing House; 2009. Code for design of high speed railway. [Google Scholar]
- Wells W. On air-borne infection*: Study II. Droplets and droplet nuclei. American Journal of Epidemiology. 1934;20(3):611–618. [Google Scholar]
- Wells W. Harvard University Press; Cambridge, MA: 1955. Airborne contagion and air hygiene. An ecological study of droplet infections. [Google Scholar]
- WHO . World Health Organization; 2014. Infection prevention and control of epidemic-and pandemic-prone acute respiratory infections in health care. [PubMed] [Google Scholar]
- WHO . World Health Organization; 2009. Natural ventilation for infection control in health-care settings. [PubMed] [Google Scholar]
- WHO . 2020. Modes of transmission of virus causing COVID-19: Implications for IPC precaution recommendations.https://www.who.int/news-room/commentaries/detail/modes-of-transmission-of-virus-causing-covid-19-implications-for-ipc-precaution-recommendations [Google Scholar]
- WHO . 2020. WHO. Coronavirus disease (COVID-19) outbreak situation.https://www.who.int/emergencies/diseases/novel-coronavirus-2019 [Google Scholar]
- Xie X., Li Y., Sun H. Exhaled droplets due to talking and coughing. Journal of the Royal Society, Interface. 2009:704–714. doi: 10.1098/rsif.2009.0388.focus. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie X., Li Y., Chwang A. How far droplets can move in indoor environments--revisiting the Wells evaporation-falling curve. Indoor Air. 2007;17(3):211–225. doi: 10.1111/j.1600-0668.2007.00469.x. [DOI] [PubMed] [Google Scholar]
- Y., J, Y.J Influence of air distribution in classroom on carbon dioxide concentration distribution. Contamination Control & Air-Conditioning Technology. 2019:42–44. [Google Scholar]
- Yang C., Yang X., Zhao B. Person to person droplets transmission characteristics in unidirectional ventilated protective isolation room: The impact of initial droplet size. Building Simulation. 2016;9(5) doi: 10.1007/s12273-016-0290-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J., Sekhar S., Cheong K. Performance evaluation of a novel personalized ventilation–personalized exhaust system for airborne infection control. Indoor Air. 2015;25(2):176–187. doi: 10.1111/ina.12127. [DOI] [PubMed] [Google Scholar]
- Zhang J., Litvinova M., Liang Y. Changes in contact patterns shape the dynamics of the COVID-19 outbreak in China. Science. 2020 doi: 10.1126/science.abb8001. [DOI] [PMC free article] [PubMed] [Google Scholar]