Abstract
Seagrass form the basis for critically important marine ecosystems. Previously, we implemented a deep convolutional neural network (CNN) model to detect seagrass in multispectral satellite images of three coastal habitats in northern Florida. However, a deep CNN model trained at one location usually does not generalize to other locations due to data distribution shifts. In this paper, we developed a semi-supervised domain adaptation method to generalize a trained deep CNN model to other locations for seagrass detection. First, we utilized a generative adversarial network loss to align marginal data distribution between source domain and target domain using unlabeled data from both data domains. Second, we used a few labelled samples from the target domain to align class specific data distributions between the two domains, based on the contrastive semantic alignment loss. We achieved the best results in 28 out of 36 scenarios as compared to other state-of-the-art domain adaptation methods.
Keywords: Deep convolutional neural network, Seagrass detection, Domain adaptation
Introduction
Seagrasses create critically important marine ecosystems that provide food to marine animals and humans, stabilize the sea bottom, and absorb carbon dioxide from the environment. Seagrass can be found in coastal areas all over the world [1]. Previous assessments of seagrass distributions from remotely sensed imagery have mostly been performed manually by domain experts [2], although various automated classification methods are now being explored [3]. Our previous work showed that deep convolutional neural network (CNN) models can effectively detect seagrass in multispectral images if the models were trained with enough labelled data [4, 5].
Deep CNN models usually require a large number of labelled training data to achieve competitive results. For seagrass quantification, these labelled data are obtained by in situ observations that are time consuming and labor intensive. Consequently, it can be difficult to collect enough labeled data to train a separate model for each location. However, a well-trained deep CNN model at one location may fail at another location if seagrass density distribution shifts from source domain to target domain. This happens due to the change of appearance/distribution of seagrass from one location to another. Our previous models degraded if directly applied to different locations for seagrass detection [4, 5].
For seagrass detection, we usually have a large amount of unlabeled data for a given new location and it is possible to obtain limited labeled data by domain experts. In this study, we propose a novel domain adaptation approach that uses both unlabeled data and a few labeled samples to learn an effective classifier for new locations. First, we utilized an unsupervised adversarial domain adaptation approach to adapt target domain representation to mimic source domain representation so that the classifier trained in source domain may work in target domain. In the unsupervised domain adaption step, we do not use any labeled samples from the target domain to solve the domain adaptation problem. Second, we utilized a supervised approach with the contrastive semantic alignment loss to learn domain invariant representations between source and target domains. The first step aligns marginal distribution between domains and the second step aligns class specific distributions using a few labeled samples from target domain. The contrastive semantic alignment loss consists of semantic alignment and separation losses. Here, the semantic alignment loss keeps the same class samples from different domains as close as possible. The class separation loss tries to put different class samples from different domains as far as possible. The proposed domain adaptation approach optimizes target domain embedding function to create a simple classifier that can work effectively in the target domain.
Contributions of our proposed approach are:
A novel approach that uses both unlabeled and a few labeled samples in the target domain to learn a domain invariant embedding for domain adaptation. It can utilize a large amount of unlabeled data for efficient training.
To the best of our knowledge, this is the first attempt and successful system that can generalize deep CNN models for seagrass detection from one location to another.
The paper is structured as follows: Section 2 discusses the relevant literature. Sections 3 and 4 describe the proposed method and experimental setup. Sections 5 and 6 present results and discussions, respectively, and Sect. 7 summarizes conclusions.
Related Work
Seagrass Distributions Mapping
Automated systems to map seagrass distribution in multispectral satellite images have been developed. Traganos et al. proposed a support vector machine (SVM) approach to map the Mediterranean seagrass distribution in Greece utilizing Sentinel-2 satellite imagery [6, 7]. Lions et al. utilized field survey data and multi-spectral image data from the QuickBird satellite for seagrass mapping in shallow coastal water [8]. Different data sources including Landsat [9], IKONOS [10–12], Quickbird [13] and WorldView-2 satellite image sensors [4, 5, 14–16], and different machine learning models such as decision trees, naive Bayes, SVMs [9], maximum likelihood [10, 11, 15, 16] and deep capsule network [4, 5] have been utilized for effective seagrass distribution mapping. However, no model can be directly applied to new locations successfully without adaptation.
Deep Learning
Deep learning models are a subset of machine learning methods which were inspired to mimic mammal’s vision system. A typical deep learning model consists of multiple layers of feature extraction processing units named as “neurons”. During training, these neurons learn to extract useful features from data to perform classification or regression. Deep learning has been successfully applied in image classification [17, 18], image segmentation [19], image super-resolution [20–22], hyperspectral images[23], object detection [24], speech recognition [25], audio classification [26], computer-aided medical diagnosis [27, 28], medical imaging [29, 30] and cybersecurity [31–33]. Among different deep learning models, deep CNN is the most popular model and more details are provided in a comprehensive survey by Alom et al [34]. A deep CNN model scans input image using a set of trained filters to search for matched patterns contained in the filters. Each layer in the deep CNN model contains a number of trained filters. A layer close to input searches for simple patterns such as edges with different orientations and layers adjacent to output try to match more class-specific patterns to conduct classification. This hierarchy feature extraction mechanism is key to the success of CNN. Popular deep vision CNN models include AlexNet [17], VGG-net [35], Resnet [18], Dense-net [36] and inceptionV3 [37]. Deep CNN has also been applied for seagrass detection in our previous studies [4, 5]. Deep learning models include feature extraction in the optimization loop and achieve state-of-the-art performances in many applications [34]. However, one challenge of deep learning models is they require large training data to achieve competitive performances, making adaptation of deep learning models between domains difficult.
Domain Adaptation
Domain adaptation techniques can be applied if there are not enough labeled data available to train a deep learning model from scratch in a new domain. In domain adaptation, a model in source domain is first trained using available large training dataset. A domain adaptation method is then applied to adapt the trained model to a new domain (named as target domain) w/o a few labeled samples from the target domain. Tzeng et. al proposed an unsupervised domain adaptation method that used the adversarial loss to match source and target domain distributions [38]. Motiian et. al proposed a semi-supervised approach for domain adaptation which used the Siamese architecture for domain adaptation [39]. This model learned an embedding function for source and target data where the two domains were semantically aligned and different classes were maximally separated.
Proposed Model
System Diagram
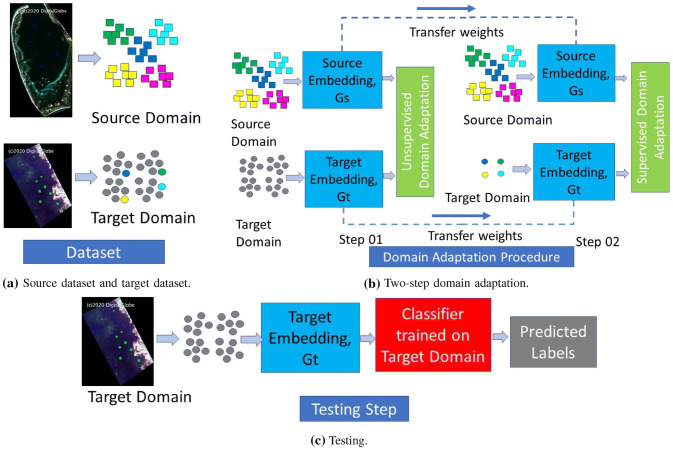
The diagram of the proposed domain adaptation method for seagrass detection is shown in Fig. 1. There are enough labelled data in the source domain to train a deep CNN model for seagrass detection, while only a few labelled samples in target domain as shown in Fig. 1a. The trained CNN model contains multiple convolutional layers for feature extraction and a fully connected layer for classification. These convolutional layers essentially learn an embedding function, and the fully connected layer takes its outputs for classification. Our proposed system uses two steps to adapt the embedding function trained in source domain to target domain as shown in Fig. 1b. In the first step, the proposed model uses unlabeled samples from both domains to modify the target embedding function while keeping the source embedding fixed, so that the outputs from both embedding functions have a similar distribution. In the second step, the proposed model pair labelled samples from source domain and a few labelled samples from target domain were used to align class specific distributions among both domains. Once the target embedding function is adapted, a simple classifier can be trained using the few labelled samples from the target domain to perform seagrass detection on the remaining target domain (Fig. 1c).
Fig. 1.
Diagram of the proposed domain adaptation model for seagrass detection. a Datasets from both domains where colored samples are labelled, while gray samples are unlabelled. b Unsupervised adversarial adaptation and supervised contrastive semantic alignment between target and source domains. c The adapted model used for seagrass detection in target domain
Model Architecture
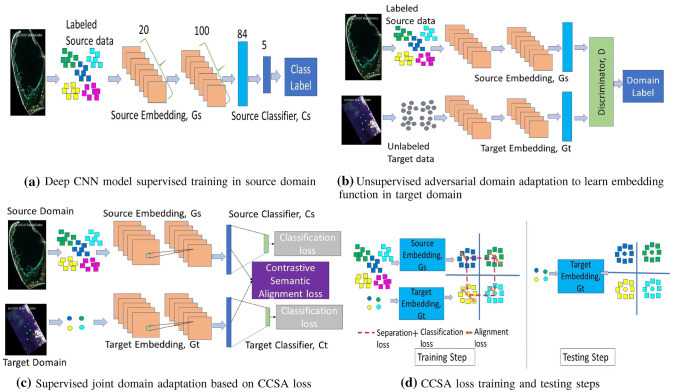
Figure 2 shows the domain adaptation procedures of the proposed method. We first train a deep CNN model in the source domain with labeled data (Fig. 2a), where the CNN model learns an embedding function, , named as source embedding function, and a simple classifier, , for seagrass detection. In the target domain (Fig. 2b), we first use unlabeled data samples from both domains to adapt the target embedding function with a genarative adversarial network (GAN) loss such that the discriminator cannot tell which domain an embedding comes from. This step will align marginal data distributions and of the source and target domains. In Fig. 2c, we utilize a few labeled samples from target domain with a classification and a contrastive semantic alignment loss to further adapt the target embedding function such that the class specific data distributions and from the two domains are aligned after embedding. Figure 2d illustrates the training and testing steps for class specific alignment. We will detail each of the steps in the following subsections.
Fig. 2.
Proposed semi-supervised domain adaption procedure
Deep CNN Model Training in Source Domain
Let and denote source and target domain datasets, and we assume that there are limited amount of labeled samples available in target domain. A source domain deep CNN model is trained with the following classification loss (Fig. 2a),
| 1 |
where is a classifier to be trained, E denotes the expectation function, and l denotes any related loss functions.
A classifier, f, can be modeled as two functions as , where G is the embedding function from the input image X to embedding space and C is the function for predicting the class label from the embedding space. So and denote the deep CNN model in source domain and target domain, respectively.
Adversarial Discriminative Domain Adaptation
By following the idea in Tzeng et al. [38], we utilize the GAN loss to adapt the embedding function in source domain to target domain. It is assumed that we have source image with label from source domain distribution , and image from target domain where we do not have any label information. This unsupervised domain adaptation step tries to learn a target embedding function based on and unlabeled data from both domains. and D in Fig. 2b are trained by MinMax optimization with the GAN loss ,
| 2 |
where D is the discriminator used in the GAN model [40] and works as a classifier trained by the cross-entropy loss. The source domain samples are labeled as ‘1’ and target domain samples labeled as ‘0’. The discriminator, D, distinguishes whether a sample belongs to source domain or target domain. The target embedding function modifies its parameters using following generator loss,
| 3 |
This is similar to the standard GAN loss where modifies its weights to mimic source domain sample embeddings to fool the discriminator, D. During training, we keep fixed while changing .
Classification and Contrastive Semantic Alignment
If there is a distribution shift between source and target domains, the source deep CNN model will not perform well in the target domain. We utilize a few labeled samples in the target domain and some labeled samples in the source domain to jointly adapt and using the classification loss and the contrastive semantic alignment (CCSA) loss proposed by Motiian et al. [39] as shown in Fig. 2c),
Classification Loss
We define the classification loss as
| 4 |
This loss function is minimized in the source domain and target domain, respectively, with the selected labeled samples from corresponding domain. This step will separate samples from different classes in both source and target domains, respectively.
Contrastive Semantic Alignment (CSA) Loss
To align class specific embedding between source and target domains, we use the CSA loss to jointly adapt and . The CSA loss in target domain contains two components and can be described as
| 5 |
where is the semantic alignment loss and is a class separation loss. is computed as,
| 6 |
where is the number of class label, and are conditional random variables. d is a distance metric between the distribution of and . This semantic alignment loss tries to map source domain and target domain data samples as close as possible if they carry the same class label. However, there is no guarantee that samples from different domains with different labels will be mapped as far as possible in the embedding space. To overcome this challenge, the class separation loss is computed as
| 7 |
where k is a similarity matrix which adds a penalty when the distribution of and are close to each other. This encourages samples with different labels from different domains to be mapped as far as possible in the embedding space. Figure 2d shows the working mechanism of the CSA loss.
During training, the semantic alignment loss (orange arrows) keeps the same class samples from different domains as close as possible. The class separation loss (red dashed line) tries to put different class samples from different domains as far as possible. The classification loss (blue solid line) ensures high classification accuracy in the embedding space. During testing, we use the trained target mapping function to put the unseen target samples into domain invariant space. The overall classification and contrastive semantic alignment loss becomes
| 8 |
Equations (5)–(8) are used to optimize . A similar set of equations are used to optimize such that both embedding functions are jointly adapted.
We paired each labeled sample in target domain with randomly selected labeled and unlabeled samples in source domain to compute the loss in Eq. (8), where d(, ) in Eq. (6) is Euclidean distance in the embedded space and k(, ) in Eq. (7) is a similarity measure defined between samples.
Loss Function Computation
The semantic alignment loss and class separation loss are defined as distance or similarity between distributions. It is not easy to estimate conditional distribution for each class given just a few labelled samples in target domain. Following the method described in [39], we compute the semantic alignment loss as
| 9 |
where are all paired labelled samples in source and target domains. Each labelled sample in target domain is paired with many selected labelled samples of the same class in source domain such that . It helps a single labeled target sample to be paired with many source labelled samples and force target labelled samples to be mapped as close as possible to the same class samples in source domain. The class separation loss is calculated as
| 10 |
where a and b denote class labels and . Each labelled sample in target domain is paired with many labelled samples from different classes in source domain. The distance measure, d(, ), is defined as Euclidean distance in the embedded space,
| 11 |
The similarity measure, k(, ), is calculated as
| 12 |
Here we use the Frobenius norm and m is the margin that specifies the separability in the embedding space. The combination of and is also known as contrastive loss as defined in [39]. Note that we use the CCSA loss to jointly optimize and .
Experiment Setup
Datasets
We validated the proposed model on three multispectral images captured by the WorldView-2 satellite at three locations in Florida coastal area: Saint Joseph Bay (SJB), Keeton Beach (KB) and Saint George Sound (SGS). Each image has eight bands (Coastal Blue, Blue, Green, Yellow, Red, Red Edge, NIR-1 and NIR-2) with spatial resolution of 2 meters. An experienced domain expert (co-author of this paper) labelled some regions for five classes in each image: seagrass, sea, sand, land, and inter tidal as shown as green, blue, cyan, yellow and magenta in Fig. 3. Figure 3d–f shows classification results by a physics model [41]. In this study, we trained a deep CNN model at one location and utilize the proposed domain adaptation model to generalize the model to other locations for seagrass detection.
Fig. 3.

WorldView2 mutlispectral images collected in Florida at a SJB b KB and c SGS. Labelled region colormap: seagrass green, sea blue, sand cyan, land yellow and intertidal magenta. Physics model [41] classification results are shown in d SJB e KB and f SGS
WorldView-2 Atmospheric Correction
We performed atmospheric correction in the three WorldView-2 satellite multispectral images by matching the images with in situ measurements collected at 22 stations across the images on the same day by a survey boat. At each station, the following measurements were obtained by two spectroradiometer systems in tandem:
: downwelling spectral irradiance above the sea surface (395 to 795 nm, 2.5 nm bandwidth),
: upwelling spectral radiance 0.65 m beneath the sea surface where represents wavelength [HTSRB, Satlantic Instr.],
and : upwelling irradiance and radiance 0.21 m beneath the sea surface [HyperPro, Satlantic Instr.].
With these measurements, we calculated the following attributes:
- Spectral upwelling diffuse attenuation coefficient,
where z was the difference in depth between the sensors placed at 0.65 m and 0.21 m.13 Upwelling radiance just beneath the air–water interface was calculated using to propagate to the surface using Beers Law [42].
Remote sensing reflectance was computed as .
We then reduced the spectral resolution of the field measurements to match the spectral bands of the WorldView-2 image based on the published spectral response functions (www.digitalglobe.com). Finally, we performed a linear regression between the 22 in situ measurements to their corresponding WorldView-2 spectra at the same location and created the gain and offset for each band to effectively remove atmospheric signals from the image.
Data Analysis
We compared the spectral signatures of each class in the multispectral WorldView-2 images taken at different locations. To better visualize the high-dimensional spectral information, we utilized the t-distributed stochastic neighbor embedding (t-SNE) algorithm [43] to compress high-dimensional data to 2 dimensions.
k-Fold Cross-validation (CV) for Seagrass Detection
At each of the three locations, we performed cross-validation for seagrass detection in the labeled regions. The experimental results gave us performance upper limits for domain adaptation. In k-fold CV, we split data into k parts and kept one part for testing and the remaining parts for training. We repeated this experiment k times such that each part was tested once.
Domain Adaptation Between Different Locations
In the domain adaptation experiments, each image was used as source image to train a deep CNN model and it was then adapted to other two locations guided by a few labeled samples from the new locations.
Models for Comparison
Source-Only
The source-only model used source domain samples to train a deep CNN model and the model was then directly applied to new locations for seagrass detection.
ADDA
Adversarial discriminative domain adaptation (ADDA) [38] adapts the embedding function in the source domain to the target domain based on the GAN loss (Sect. 3.4) with all unlabeled samples in new locations, which was then combined with the classifier trained in source domain to detect seagrass at the new locations.
Source + Target
We trained a deep CNN model in the source domain and used a few labeled data samples from the target domain to fine-tune the model. This is a baseline model for transfer learning.
CCSA
This model used the contrastive semantic alignment loss and classification loss to learn the embedding function and classification layers [39]. We used two separate embedding functions that were jointly optimized for source and target domains (Sect. 3.5).
Proposed Model
We first used the GAN loss to adapt the embedding function trained in the source domain. Then the CCSA loss together with a few labeled samples from target domain was utilized to further adapt the model to new locations as detailed in Sect. 3.5.
Results
Data Analysis
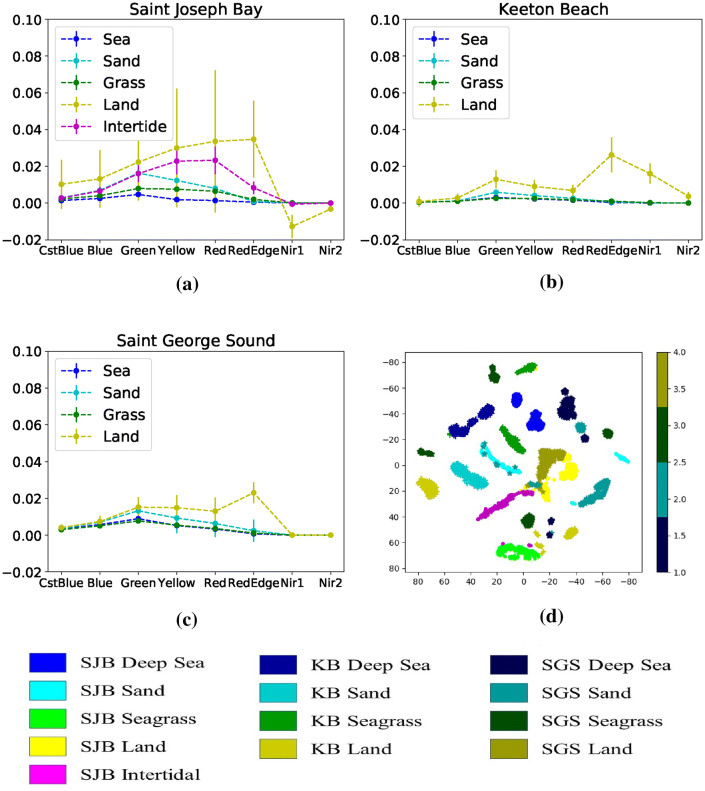
Figure 4 shows atmospherically corrected means and standard deviations of the eight WorldView-2 multispectral bands in the labelled regions at the three locations. Land had the highest mean spectral magnitude as it is located above water. Intertidal class is located between sand and land on spectral magnitude. These classes were followed by sand, seagrass and sea in spectral magnitude.
Fig. 4.
Atmospherically corrected spectral signature, means and standard deviations in mutlispectral WorldView-2 images for different classes shown at a SJB b KB and c SGS. X-axis represents different bands, and Y-axis represents spectral intensity mean and standard deviation. dt-SNE plotting of all three locations for different classes. Green, blue, cyan, yellow and magenta are used to represent seagrass, sea, sand, land and intertidal classes. For the t-SNE plotting, the bright shade, dark shade and shade between these two are used to represent SJB, SGS and KB samples, respectively. For seagrass class, we used three different green shades to represent three different locations, e.g.: green, dark green and bright green. Similarly, three shades of yellow, blue, cyan to represent land, sea, and sand classes
It is also observed that spectral signatures of the same class at different locations have different shapes, indicating that there are distribution shifts among locations. In Fig. 4d, we show t-SNE representations for samples from all the three locations. We use green, blue, cyan, yellow and magenta to represent seagrass, sea, sand, land and intertidal classes. We use three shades to represent three different locations: the most bright shade, most dark shade and shade between this two to represent SJB, SGS and KB samples, respectively (Fig. 4d). Note that there are significant distribution shifts among different locations in different classes.
Hyper-Parameter Determination
Deep CNN models take a patch from the multispectral image to predict a class label for the central pixel of the patch. A large patch may cause over-smoothing and requires higher computation power, whereas a too small patch may degrade the performance. After some trial and error, we found that a patch size produced the best results in the threefold CV experiment. Other parameters were determined in the same way and are listed below.
Embedding Functions and , in CNN Models
Both contain two convolutional layers followed by a flatten layer. The first layer had 20 filters with a size of 2 * 2 * 8, and the second layer had 100 filters with a size of 4 * 4 * 20. All layers used ReLu activation function.
Classifiers and , in CNN Models
Both contained a fully connected layer with 84 hidden units, and the output layer had 5 units with SoftMax activation function for classification.
Source and Target Data Pairing
400 labeled samples from each class in source domain were randomly selected to pair with the few labeled samples in target domain to compute the loss function described in Sect. 3.5.
Training Parameter Settings
We trained the source CNN models 50 epochs with a batch size of 128. We trained the unsupervised adversarial domain adaptation step 300 epochs and the CCSA step 240 epochs in all experimentals.
Learning Rate
We used 0.0002 as the learning rate in all experiments. No dropout layer was used.
Cross-validation
Table 1 shows threefold CV results at the three locations to find upper limits of domain adaption. We achieved 99.99% accuracy at SJB, 99.98% at KB and 99.71% at SGS, respectively. The low variances indicate that the results are very reliable.
Table 1.
Threefold cross-validation results at SJB, KB and SGS
| Fold no. | SJB (%) | KB (%) | SGS (%) |
|---|---|---|---|
| 1st Fold | 99.99 | 99.98 | 99.83 |
| 2nd Fold | 99.99 | 99.98 | 99.66 |
| 3rd Fold | 99.99 | 99.97 | 99.64 |
| Mean | 99.99 ± 0.00 | 99.98 ± 0.01 | 99.71 ± 0.10 |
Domain Adaptation
We conducted six domain adaptation experiments for the three WorldView-2 satellite images as KB SJB, SJB KB, SGS SJB, SJB SGS, SGS KB and KB SGS. Comparison of our proposed model with previous models and results is shown in Table 2. For each domain adaptation experiment, we implemented 6 scenarios including 1 to 5-shot and 10-shot cases (n-shot stands for having n labeled samples from each class). One “shot” means one labeled sample per class in target domain is used to adapt the model. Each scenario was performed three times with randomly selected labelled samples from target domain, and means and standard deviations are shown in Table 2. The proposed method achieved the best results in 28 out of 36 scenarios in Table 2. In the 10-shot domain adaptation scenario, the proposed method approached to model upper limits (3-fold CV performances). The second best model is the Source+Target (f.t.) that achieved the best results in 4 out of 36 scenarios in Table 2.
Table 2.
Classification results in target domain by different methods (All numbers are in %)
| Numb of shots | Tasks | SJB KB | KB SJB | SJB SGS | SGS SJB | KB SGS | SGS KB |
|---|---|---|---|---|---|---|---|
| N/A | Source Only (Baseline) | 34.75 | 45.00 | 25.08 | 74.04 | 15.91 | 64.14 |
| N/A | ADDA | 35.76 | 42.20 | 67.80 | 35.39 | 78.69 | 99.43 |
| 1-shot | Source+Target (f.t.) | 79.98 ± 15.05 | |||||
| CCSA | |||||||
| Proposed Model | 98.84 ± 0.29 | 86.12 ± 3.55 | 80.23 ± 3.04 | 93.32 ± 1.75 | 99.35 ± 0.09 | ||
| 2-shot | Source+Target ((f.t.) | ||||||
| CCSA | 90.79 ± 1.68 | ||||||
| Proposed Model | 99.30 ± 0.14 | 91.72 ± 5.88 | 89.65 ± 6.85 | 91.55 ± 6.98 | 99.45 ± 0.08 | ||
| 3-shot | Source+Target (f.t.) | ||||||
| CCSA | 90.84 ± 8.39 | ||||||
| Proposed Model | 99.32 ± 0.72 | 94.28 ± 1.90 | 92.22 ± 4.68 | 95.20 ± 1.23 | 99.42 ± 0.07 | ||
| 4-shot | Source+Target (f.t.) | ||||||
| CCSA | 90.93 ± 8.31 | ||||||
| Proposed Model | 99.44 ± 0.46 | 96.31 ± 2.04 | 96.84 ± 1.76 | 92.38 ± 6.83 | 99.38 ± 0.12 | ||
| 5-shot | Source+Target (f.t.) | 99.88 ± 0.07 | 98.20 ± 1.11 | ||||
| CCSA | 91.01 ± 8.14 | ||||||
| Proposed Model | 91.01 ± 8.00 | 96.27 ± 1.43 | 93.93 ± 4.67 | 99.47 ± 0.12 | |||
| 10-shot | Source+Target (f.t.) | 99.57 ± 0.67 | |||||
| CCSA | 98.73 ± 0.58 | ||||||
| Proposed Model | 99.09 ± 0.05 | 98.38 ± 0.87 | 98.33 ± 0.63 | 99.59 ± 0.32 | |||
| N/A | 3-fold CV |
t-SNE Plotting
We demonstrate how the proposed model maps samples from different domains to the embedding space by utilizing the t-SNE algorithm with the following procedure:
Compress the original samples from source and target domains (200 = 5*5*8 dimensions) to 2 dimensions using the t-SNE algorithm (before adaptation),
Feed original samples from source and target domains to the embedding functions, and , respectively, to obtain new representations in the embedding space,
Compress the new representations to 2 dimensions using the t-SNE algorithm (after adaptation),
Plot the compressed data samples on 2D plane using different colors for different classes. Use blue, cyan, green, yellow and magenta colors to represent sea, sand, seagrass, land and intertidal class. Utilize two different shades of same color to denote target and source samples
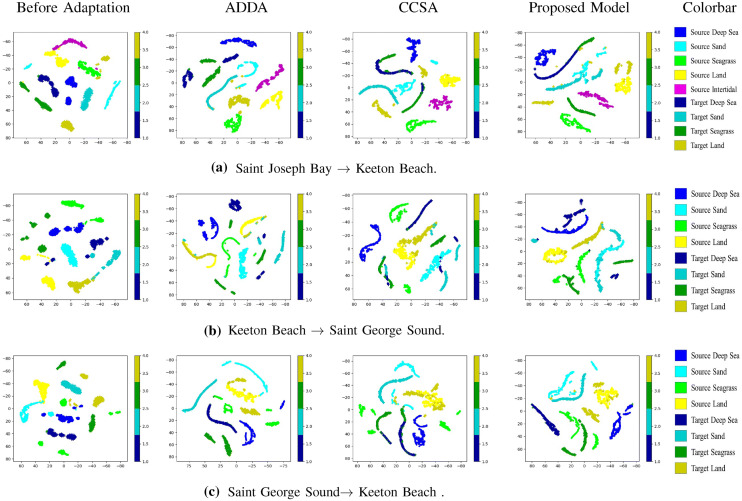
t-SNE results are shown in Fig. 5 for three domain adaptation scenarios: SJB KB, KB SGS and SGS KB. We used 400 samples in each class, respectively, from source and target domains. The proposed model achieved better embedding for sea and seagrass classes as compared to CCSA model in the scenario of SJB KB as shown in Fig. 5a. In Fig. 5b, c, similar trends are observed for KB SGS and SGS KB cases. The CCSA model incorrectly mapped seagrass samples closer to sea samples and sand samples in the embedding space. Unsupervised domain adaptation method was performed poorly in all the cases as shown in Fig. 5.
Fig. 5.
t-SNE plots in embedding space after 1-shot domain adaptation in target domain. a SJB KB b KB SGS and c SGS KB. Green, blue, cyan, yellow and magenta are used to represent seagrass, sea, sand, land and intertidal, respectively. The most bright shade and the most dark shade are used to represent source and target domain samples, respectively
Ablation Study
Our proposed model contained two loss functions: semantic contrastive alignment loss and GAN loss. If we remove the GAN loss from the proposed model and just use semantic contrastive alignment loss for domain adaptation, the model would be equivalent to the CCSA model. If we remove the contrastive semantic alignment loss from the proposed model, then it will be equivalent to the unsupervised ADDA model. Our proposed model also used joint optimization for the source embedding function, , and the target embedding function, , in the supervised domain adaption step. We investigated the three components in the ablation study for KB SGS and results are shown in Table 3. Note that ADDA does not require labelled samples from target domain, so only one scenario was performed. The proposed model with all the three components achieved the best results.
Table 3.
Ablation study of the proposed method
| Shots | Methods | KB SGS (%) |
|---|---|---|
| ADDA | 78.69 | |
| 1-shot | CCSA | |
| Proposed Model w/o Joint Optimization | ||
| Proposed Model | 93.32 ± 1.75 | |
| 2-shot | CCSA | |
| Proposed Model w/o Joint Optimization | ||
| Proposed Model | 91.55 ± 6.98 | |
| 3-shot | CCSA | |
| Proposed Model w/o Joint Optimization | ||
| Proposed Model | 95.20 ± 1.23 | |
| 4-shot | CCSA | |
| Proposed Model w/o Joint Optimization | ||
| Proposed Model | 92.38 ± 6.83 | |
| 5-shot | CCSA | |
| Proposed Model w/o Joint Optimization | ||
| Proposed Model | 93.93 ± 4.67 |
Classification Maps
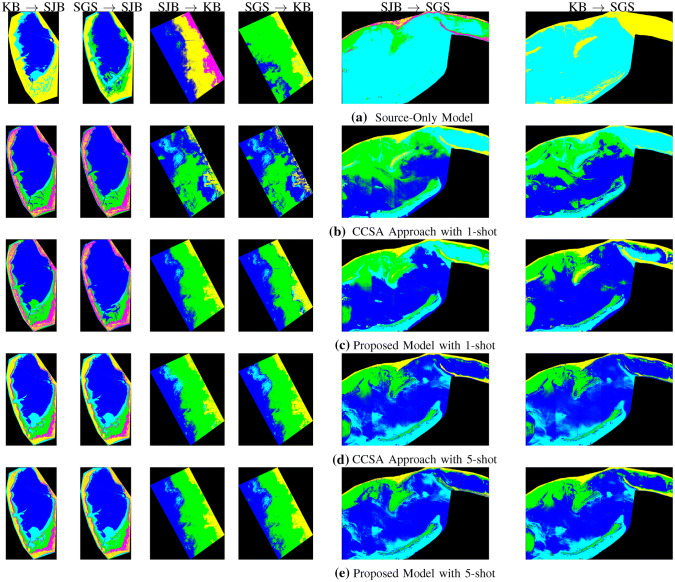
The classification maps produced by our proposed model, CCSA approach, and baseline model are shown in Fig. 6. The first row of Fig. 6 represents the base line classification maps where we directly applied classification models trained in source domains to classify target domain images without performing any adaptation. The baseline model performed poorly as compared to the physics model as shown in Fig. 3. Second and fourth rows of Fig. 6 represent classification maps produced by CCSA model with 1-shot (Fig. 6b) and 5-shot (Fig. 6d), respectively. In this step, we used only contrastive semantic alignment loss to perform domain adaptation task. The third and the last row in Fig. 6 represents classification results by the proposed model with 5-shot. We used both the GAN loss and the contrastive semantic alignment loss for domain adaptation. The proposed model with 5-shot produced good classification results as compared to the physics model as shown in Fig. 3. Note that the classification maps shown here are for visualization purpose only as the physics model has 10% error [41].
Fig. 6.
End-to-end classification maps produced by domain adaptation based on a source model b CCSA model with 1-shot c proposed model with 1-shot d CCSA model with 5-shot and e proposed model with 5-shot
Discussion
Our proposed approach produced the best results for 28 out of 36 domain adaptation experimental scenarios as shown in Table 2. For KB SGS and SGS KB, our proposed method won all the scenarios. For SJB KB, our model achieved 98.84% accuracy using just one labelled sample from target domain and it is much better than CCSA (71.26%), ADDA (35.76%) and Source+Target (f.t.) (84.78%). For KB SGS, our proposed model with one labelled sample from target domain achieved an accuracy of 93.32% as compared to CCSA (72.49%), ADDA (78.69%) and Source+Target (f.t.) (63.39%). Similar trends can also be found in SGS KB in all the 1-shot domain adaptation cases except SJB SGS, where all the methods achieved similar results. On average, our proposed method won by a large margin.
As we utilizing more labeled samples from the target domain, the proposed method can still provide better domain adaptation, winning four or five out of the six experimental scenarios with 2-shot up to 10-shot cases. On average, however, the winning margin decreased as more labeled samples were used for adaptation. For the 10-shot scenario, CCSA and the proposed method achieved similar results and the results were close to the threefold CV results, indicating that adding more labeled samples from target domain did not provide more benefits.
For most of the scenarios, standard deviations of the proposed method were much smaller than these of other methods. Our method first utilized a large number of unlabeled samples in both domains to perform domain adaptation. We then used a few labeled samples from target domain to semantically align class specific distribution in the embedding space. The first step of the method aligned marginal distribution based upon a large number of unlabeled data and worked as a regularizer for the subsequent semantic alignment. Therefore, the proposed method can provide more stable performances.
Figure 5 shows t-SNE plots for data samples or embeddings in source and target domains before and after domain adaptation. Before adaptation, we can see that data distributions in source domain and target domain are not aligned. ADDA aligned distributions between the source and target domains, but there is no guarantee that the same class samples from different domains will be mapped closer in the embedding space. With the guidance of labelled samples, CCSA and the proposed model can do a better semantic alignment: same class samples from different domains can be mapped closer, and the proposed method can do a better job as compared to CCSA.
We only performed the KB SGS case study for ablation as shown in Table 3. All three components in the proposed model are important. With joint optimization, the proposed model became much more stable and achieved much smaller standard deviation in performances for all the scenarios. With more labeled samples from target domain, CCSA can perform much better than ADDA.
As compared to the physics model classification maps in Fig. 3d–f, the classification maps produced by the proposed model with 5-shots were much better than those from the direct source domain model as shown in Fig. 6a. Classification maps produced by CCSA with 5-shot (Fig. 6d) are good. However, those produced by CCSA with 1-shot (Fig. 6b) are much worse. Note that the physics model results have 10% error [41] and the classification maps are shown for visualization purpose only. For accurate quantitative assessment of these models, please see results in Table 2 where the accuracy was computed in the labeled regions.
Conclusion
Automatic seagrass detection systems in multispectral images are important tools for seagrass monitoring. Labelling atmospherically corrected multispectral images is labor intensive and time consuming. We developed a semi-supervised domain adaptation method for deep CNN models for seagrass detection. The proposed model first used unlabelled samples in both domains to adapt source domain model to target domain based on the GAN loss. Then it utilized contrastive semantic loss with a few labelled samples from target domain to further adapt the model. In addition, the source model and target model were jointly optimized in the second step. We evaluated the proposed model in three atmospherically corrected WorldView-2 multispectral images taken in Florida and achieved the best results among 28 out of 36 experimental scenarios. Future work will evaluate the proposed model with other image detection methods across broader regional areas such as the southeastern USA.
Acknowledgements
This work was supported by the NASA Ocean Biology and Biogeochemistry Program NRA #NNH16ZDA001N and augmented by the NASA Commercial Data Buy. This article has been reviewed by the Center for Environmental Measurement and Modeling and approved for publication. Mention of trade names or commercial products does not constitute endorsement or recommendation for use by the US Government. The views expressed in this article are those of the authors and do not necessarily reflect the views or policies of the U.S. EPA.
Contributor Information
Kazi Aminul Islam, Email: kisla001@odu.edu.
Victoria Hill, Email: VHill@odu.edu.
Blake Schaeffer, Email: Schaeffer.Blake@epa.gov.
Richard Zimmerman, Email: RZimmerm@odu.edu.
Jiang Li, Email: JLi@odu.edu.
References
- 1.Cullen-Unsworth L, Jones BL, Lilley R, Unsworth RK (2018) Secret gardens under the sea: What are seagrass meadows and why are they important? Frontiers for Young Minds 6(2)
- 2.Moniruzzaman M, Islam S, Lavery P, Bennamoun M, Lam CP (2019) Imaging and classification techniques for seagrass mapping and monitoring: a comprehensive survey. arXiv:1902.11114
- 3.Su L, Huang Y. Seagrass resource assessment using worldview-2 imagery in the redfish bay, Texas. J Mar Sci Eng. 2019;7(4):98. doi: 10.3390/jmse7040098. [DOI] [Google Scholar]
- 4.Islam KA, Perez D, Hill V, Schaeffer B, Zimmerman R, Li J (2018) Seagrass detection in coastal water through deep capsule networks. In: Chinese conference on pattern recognition and computer vision (PRCV). Springer, pp 320–331
- 5.Perez D, Islam K, Hill V, Zimmerman R, Schaeffer B, Li J (2018) Deepcoast: quantifying seagrass distribution in coastal water through deep capsule networks. In: Chinese conference on pattern recognition and computer vision (PRCV). Springer, pp 404–416
- 6.Traganos D, Reinartz P. Mapping mediterranean seagrasses with sentinel-2 imagery. Mar Pollut Bull. 2018;134:197–209. doi: 10.1016/j.marpolbul.2017.06.075. [DOI] [PubMed] [Google Scholar]
- 7.Traganos D, Cerra D, Reinartz P. Cubesat-derived detection of seagrasses using planet imagery following unmixing-based denoising: is small the next big? Amsterdam: International Archives of the Photogrammetry; 2017. p. 42. [Google Scholar]
- 8.Lyons M, Phinn S, Roelfsema C. Integrating quickbird multi-spectral satellite and field data: mapping bathymetry, seagrass cover, seagrass species and change in moreton bay, australia in 2004 and 2007. Remote Sens. 2011;3(1):42–64. doi: 10.3390/rs3010042. [DOI] [Google Scholar]
- 9.Li F, Xiao B (2011) Aquatic vegetation mapping based on remote sensing imagery: an application to honghu lake. In: 2011 International conference on remote sensing, environment and transportation engineering. IEEE, pp 4832–4836
- 10.Hochberg EJ, Andréfouët S, Tyler MR. Sea surface correction of high spatial resolution ikonos images to improve bottom mapping in near-shore environments. IEEE Trans Geosci Remote Sens. 2003;41(7):1724–1729. doi: 10.1109/TGRS.2003.815408. [DOI] [Google Scholar]
- 11.Mishra DR, Narumalani S, Rundquist D, Lawson M. High-resolution ocean color remote sensing of benthic habitats: a case study at the roatan island, honduras. IEEE Trans Geosci Remote Sens. 2005;43(7):1592–1604. doi: 10.1109/TGRS.2005.847790. [DOI] [Google Scholar]
- 12.Fornes A, Basterretxea G, Orfila A, Jordi A, Álvarez A, Tintoré J. Mapping posidonia oceanica from ikonos. ISPRS J Photogram Remote Sens. 2006;60(5):315–322. doi: 10.1016/j.isprsjprs.2006.04.002. [DOI] [Google Scholar]
- 13.Yang D, Yang Y, Yang C, Zhao J, Sun Z. Detection of seagrass in optical shallow water with quickbird in the Xincun bay, Hainan province, China. IET Image Proc. 2011;5(5):363–368. doi: 10.1049/iet-ipr.2009.0392. [DOI] [Google Scholar]
- 14.Cerdeira-Estrada S, Heege T, Kolb M, Ohlendorf S, Uribe A, Müller A, Garza R, Ressl R, Aguirre R, Mari N et al (2012) Benthic habitat and bathymetry mapping of shallow waters in Puerto Morelos reefs using remote sensing with a physics based data processing. In: 2012 IEEE international geoscience and remote sensing symposium. IEEE, pp 4383–4386
- 15.Eugenio F, Marcello J, Martin J. High-resolution maps of bathymetry and benthic habitats in shallow-water environments using multispectral remote sensing imagery”. IEEE Trans Geosci Remote Sens. 2015;53(7):3539–3549. doi: 10.1109/TGRS.2014.2377300. [DOI] [Google Scholar]
- 16.Marcello J, Eugenio F, Marqués F, Martín J (2015) Precise classification of coastal benthic habitats using high resolution worldview-2 imagery. In: 2015 IEEE international geoscience and remote sensing symposium (IGARSS). IEEE, pp 2307–2310
- 17.Krizhevsky A, Sutskever I, Hinton GE (2012) Imagenet classification with deep convolutional neural networks. In: Advances in neural information processing systems, pp 1097–1105
- 18.He K, Zhang X, Ren S, Sun J (2016) Deep residual learning for image recognition. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp 770–778
- 19.Ronneberger O, Fischer P, Brox T (2015) U-net: convolutional networks for biomedical image segmentation. In: International conference on medical image computing and computer-assisted intervention. Springer, pp 234–241
- 20.Dong C, Loy CC, He K, Tang X. Image super-resolution using deep convolutional networks. IEEE Trans Pattern Anal Mach Intell. 2015;38(2):295–307. doi: 10.1109/TPAMI.2015.2439281. [DOI] [PubMed] [Google Scholar]
- 21.Dai T, Cai J, Zhang Y, Xia S.-T, Zhang L (2019) Second-order attention network for single image super-resolution. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp 11065–11074
- 22.Wang X, Yu K, Wu S, Gu J, Liu Y, Dong C, Qiao Y, Change Loy C (2018) Esrgan: enhanced super-resolution generative adversarial networks. In: Proceedings of the European conference on computer vision (ECCV), pp 0–0
- 23.Hu W, Huang Y, Wei L, Zhang F, Li H (2015) Deep convolutional neural networks for hyperspectral image classification. J Sens 2015
- 24.Liu Y, Wang Y, Wang S, Liang T, Zhao Q, Tang Z, Ling H (2019) Cbnet: a novel composite backbone network architecture for object detection. arXiv:1909.03625 [DOI] [PubMed]
- 25.Hinton G, Deng L, Yu D, Dahl G, Mohamed A-R, Jaitly N, Senior A, Vanhoucke V, Nguyen P, Kingsbury B, et al. Deep neural networks for acoustic modeling in speech recognition. IEEE Signal Process Mag. 2012;29(6):82–97. doi: 10.1109/MSP.2012.2205597. [DOI] [Google Scholar]
- 26.Hershey S, Chaudhuri S, Ellis DP, Gemmeke JF, Jansen A, Moore RC, Plakal M, Platt D, Saurous RA, Seybold B et al (2017) CNN architectures for large-scale audio classification. In: 2017 IEEE international conference on acoustics, speech and signal processing (ICASSP). IEEE, pp 131–135
- 27.Islam KA, Perez D, Li J (2018) A transfer learning approach for the 2018 FEMH voice data challenge. In: 2018 IEEE international conference on big data (big data). IEEE, pp 5252–5257
- 28.Banerjee D, Islam K, Mei G, Xiao L, Zhang G, Xu R, Ji S, Li J (2017) A deep transfer learning approach for improved post-traumatic stress disorder diagnosis. In: 2017 IEEE international conference on data mining (ICDM). IEEE, pp 11–20
- 29.Li F, Tran L, Thung K, Ji S, Shen D, Li J. A robust deep model for improved classification of AD/MCI patients. IEEE J Biomed Health Inf. 2015;19(5):1610–1616. doi: 10.1109/JBHI.2015.2429556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Li F, Tran L, Thung K, Ji S, Shen D, Li J (2014) Robust deep learning for improved classification of AD/MCI patients. In: International Workshop on Machine Learning in Medical Imaging. Springer, Cham, pp 240–247
- 31.Ning R, Wang C, Xin C, Li J, Wu H (2018) Deepmag: sniffing mobile apps in magnetic field through deep convolutional neural networks. In: IEEE conference on pervasive computing and communication (PerCom). IEEE, pp 1–10
- 32.Ning R, Wang C, Xin C, Li J, Wu H. Deepmag+: sniffing mobile apps in magnetic field through deep learning. Pervas Mobile Comput. 2020;61:101106. doi: 10.1016/j.pmcj.2019.101106. [DOI] [Google Scholar]
- 33.Chowdhury M, Hammond F, Konowicz G, Li J, Xin C, Wu H (2017) A few-shot deep learning approach for improved intrusion detection. In: 2017 IEEE 8th annual ubiquitous computing, electronics and mobile communication conference (UEMCON). IEEE, pp 456–462
- 34.Alom MZ, Taha TM, Yakopcic C, Westberg S, Sidike P, Nasrin MS, Hasan M, Van Essen BC, Awwal AA, Asari VK. A state-of-the-art survey on deep learning theory and architectures. Electronics. 2019;8(3):292. doi: 10.3390/electronics8030292. [DOI] [Google Scholar]
- 35.Simonyan K, Zisserman A (2014) Very deep convolutional networks for large-scale image recognition. arXiv:1409.1556
- 36.Huang G, Liu Z, Van Der Maaten L, Weinberger KQ (2017) Densely connected convolutional networks. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp 4700–4708
- 37.Szegedy C, Vanhoucke V, Ioffe S, Shlens J, Wojna Z (2016) Rethinking the inception architecture for computer vision. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp 2818–2826
- 38.Tzeng E, Hoffman J, Saenko K, Darrell T (2017) Adversarial discriminative domain adaptation. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp 7167–7176
- 39.Motiian S, Piccirilli M, Adjeroh DA, Doretto G (2017) Unified deep supervised domain adaptation and generalization. In: Proceedings of the IEEE international conference on computer vision, pp 5715–5725
- 40.Goodfellow I, Pouget-Abadie J, Mirza M, Xu B, Warde-Farley D, Ozair S, Courville A, Bengio Y (2014) Generative adversarial nets. In: Advances in neural information processing systems. pp 2672–2680
- 41.Hill VJ, Zimmerman RC, Bissett WP, Dierssen H, Kohler DD. Evaluating light availability, seagrass biomass, and productivity using hyperspectral airborne remote sensing in Saint Joseph’s Bay, Florida. Estuaries Coasts. 2014;37(6):1467–1489. doi: 10.1007/s12237-013-9764-3. [DOI] [Google Scholar]
- 42.Kirk J. Light and photosynthesis in the sea. Cambridge: Cambridge University Press; 1994. [Google Scholar]
- 43.Maaten LVD, Hinton G. Visualizing data using t-sne. J Mach Learn Res. 2008;9:2579–2605. [Google Scholar]