Inter-Individual Variability in Trajectories of Functional Limitations by Race/Gender

Abstract

Objective

Several theories emphasize that systematic interindividual divergence is a key feature of cohort aging and evidence for accumulative social inequality over the life course. While many have documented widening health gaps with age between subgroups, such divergence is only one aspect of the broader social inequality based on race and gender. This article examines patterns of interindividual variability in trajectories of functional limitations within each race/gender.

Methods

Using data from the Health and Retirement Study (HRS)’s HRS cohort (born 1931–1941), I estimate growth curves of functional limitations with Level 2 heteroscedasticity, allowing interindividual variability to differ across 4 groups: white men, black men, white women, and black women. I examine race/gender differences in the age-based pattern of interindividual variability using an interquartile range of estimated individual trajectories.

Results

Black men, white women, and black women have greater interindividual variability in functional limitations than do white men. Interindividual variability increases systematically with age at similar rates for all groups but black women.

Discussion

Functional limitations become more heterogeneous with age for the entire cohort and for white men, white women, and black men. Future research should identify life-course processes that generate the race and gender patterning of interindividual variability in late-life health.

Theoretical perspectives in gerontology have for some time emphasized that cohort aging is characterized by systematic interindividual divergence, as a result of accumulative social inequality over the life course (Crystal & Shea, 1990; Dannefer, 1987; Ferraro & Shippee, 2009; O’Rand, 1996). Health is a key domain of aging and within gerontology, a body of research on minority health and health disparities have linked age-health correlates to intra-cohort inequalities, particularly those by race/ethnicity (Brown, O’Rand, & Adkins, 2012; Ferraro & Farmer, 1996; Fuller-Thomson, Nuru-Jeter, Minkler, & Guralnik, 2009; Geronimus, Hicken, Keene, & Bound, 2006; Haas & Rohlfsen, 2010; Kelley-Moore & Ferraro, 2004; Kim & Miech, 2009; Liang, Xu, Bennett, Ye, & Quiñones, 2010; Liao, McGee, Cao, & Cooper, 1999; Maddox & Clark, 1992; Mendes de Leon, Barnes, Bienias, Skarupski, & Evans, 2005; Shuey & Willson, 2008; Taylor, 2008; Thorpe et al., 2011; Yao & Robert, 2008) and gender (Doblhammer & Hoffmann, 2010; Ferraro & Nuriddin, 2006; Laditka & Laditka, 2002; Liang et al., 2008; Yang & Lee 2009).

Evident from this literature is the ubiquitous health and disability gap between blacks and whites and between men and women during later life, which reveals how social inequalities reflect serious challenges for racial/ethnic minorities and women to age well. Some have even found widening gaps between these subpopulations over time (Brown et al., 2012; Geronimus et al., 2006; Shuey & Willson, 2008; Taylor, 2008; Thorpe et al., 2011; Yao & Robert, 2008), lending support to the notion that accumulative life-course processes contribute to increasing health inequality as cohorts age. Together these studies provide some of the most compelling evidence of the socially produced pattern in individuals’ aging experiences.

An overlooked limitation is that prior studies have largely relied on comparing average differences between subgroups defined by race/ethnicity and gender as the gold-standard approach. This is typically done by comparing group means across age strata in cross-sectional studies (e.g., Geronimus et al., 2006), or by comparing average trajectories of subgroups (e.g., Brown et al., 2012; Kelley-Moore & Ferraro, 2004; Shuey & Willson, 2008) as permitted by the explosion of multi-wave panel data in the last decade (Alwin, Hofer, & McCammon, 2006; George, 2009; Yang, 2011). It is anticipated that findings from these comparisons—subgroup divergence, convergence, neither or both—ought to explain whether health heterogeneity was driven by various life-course processes, such as cumulative dis/advantage, weathering, persistent inequality, and age-as-leveler, either individually or in some combination (Ferraro, 2011; Ferraro & Farmer, 1996).

Yet the overarching question of whether intra-cohort inequality increases systematically with age, as originally posited in Merton’s (1968) formulation of the Matthew Effect, or more formally in cumulative dis/advantage theory (Crystal & Shea, 1990; Dannefer, 1987), can be approached with a number of empirical measures, in addition to decomposing population mean into subgroup differences (DiPrete & Eirich, 2006). This is readily seen in the long tradition of using Gini coefficients (Crystal & Waehrer, 1996; Treas & Walther, 1978), variances (Rosenbaum, 1975), person-based biography (Laub & Sampson, 2003), and models of state dependence (Heckman, 1981) to describe interindividual differentiation in other areas of study. In studies of population health and aging, however, these measures have not been widely implemented, with the valuable exception of Maddox and Douglass’s (1974) seminal study of change in variance in psychosocial and physiological indicators. If it is true that intra-cohort inequality increases systematically with age due to complex mechanisms of social allocation, one might expect that average health differences between subgroups was only one aspect of the social inequality produced by race- and gender-based opportunity structure, and that other measures of heterogeneity could help reveal additional social regularities in health and aging.

Thus, average differences by race/gender in long-term health dynamics are actually a special case of the broader question regarding differential aging—how is variability within a cohort regulated by social factors over its collective life course? This article further explicates differential aging, focusing on the largely unchartered territory of interindividual variability in late-life functional health within subgroups defined by race/gender. This is important for several reasons. First, in a longitudinal analysis of within-individual change, one must take into account that race- and gender-based structural influence on health is mediated by the immediate social contexts, such as individuals’ everyday experience with economic adversities and marginalization. Since health trajectories over time reflect numerous interactions between the social contexts and the human body, long-term health dynamics are inevitably heterogeneous for the entire cohort. In this case, causal prediction can be difficult and shifting the focus to mechanisms that potentially regulate heterogeneity is necessary. Specifically, one may hypothesize that the socially advantaged (e.g., white men) is a more homogeneous group with respect to long-term functional health, as they encounter fewer adversities, have less exposure to health risk and can recover quickly and completely from incident morbidity. In contrast, socially disadvantaged individuals (e.g., black women) experience repeated adversities and more (re)occurrence of health problems due to a lack of resources, quality care, and structural support, thereby displaying instability and more heterogeneity in health dynamics.

Second, interindividual divergence is key evidence for cumulative dis/advantage, but most studies have only examined such divergence indirectly by looking at intergroup divergence. There are notable exceptions to this, such as Warner and Brown’s (2011) examination of how race and gender intersect and Brown, Richardson, Hargrove, and Thomas’s (2016) stratification of each race/ethnicity by education. These studies show that even within each group, individuals’ aging experiences are still differentiated based on other factors. Going forward, a direct examination of interindividual variability in functional health as a defining and systemic feature of cohort aging is warranted.

Finally, interindividual variability with each race/gender raises many questions about subgroup comparisons. Does each subgroup’s mean trajectory accurately characterize the health dynamics in individuals of the same race/gender? Are the residual variances around the subgroup mean merely random noise or socially organized? Might a group have a faster rate of health differentiation over the life course? Documenting interindividual variability within each race/gender can help explain the contradictory findings in previous research about whether race/gender-based disparities amplify, diminish, or persist as cohorts age.

Continuing the long tradition of focusing on aged heterogeneity in gerontology (Bass, Kutza, & Torres-Gil, 1989; Daatland & Biggs, 2006; Dannefer, 1988; Ferraro, Kemp, & Williams, 2017; Kelley-Moore & Lin, 2011; Maddox & Douglass, 1974; Neugarten, 1983; Stone, Lin, Dannefer, & Kelley-Moore, 2017), this article seeks to extend the line of inquiry in life course health inequalities to incorporate patterns of heterogeneity between individuals of the same race/gender. Taking advantage of more than 20 years of panel data from a national dataset, the analysis addresses two research questions: first, does interindividual variability in trajectories of functional limitations increase systematically with age for a birth cohort? Second, does the age-based pattern of interindividual variability differ by race/gender?

Method

Data and Sample

Data come from the Health and Retirement Study (HRS), a panel study of a nationally representative sample of noninstitutionalized adults aged 50 and older interviewed biennially since 1992 (W1). To provide a more precise documentation of intra-cohort inequality, the current study is a single cohort analysis of individuals from the HRS cohort (born 1931–1941). The first two waves of data are excluded due to measurement inconsistencies in functional limitations. After excluding proxy interviews and listwise deleting missing values in study variables, the analysis is further limited to individuals with at least two observation points over the panel to allow a meaningful calculation of variability in rates of change in functional limitations.

While it would be extremely valuable to include respondents of Hispanic origin that the HRS has oversampled, the available sample sizes for Hispanic men and women from the HRS cohort do not meet the statistical threshold for detecting differences in variability in trajectories. Higher rates of lost-to-follow-up in Hispanic older adults make it especially difficult to detect a meaningful trend in variability beyond age 65, which is the focal point of the current study. The final analytic sample is therefore limited to non-Hispanic white and non-Hispanic black men and women (n = 7,131), who have contributed 48,000 observations over the 1996–2014 panel from ages 55 to 83.

Measures

Functional limitations are measured as the sum score of 11 limitations related to mobility, strength, and upper- and lower-body activities (e.g., walking several blocks, getting up from the seated position, lifting or carrying 10 pounds) for each of which respondents indicate whether they have no difficulties (=0), some difficulties (=1), or a lot of difficulties (=2) performing the task. Age is measured in years and calculated from each individual’s birth year. Based on the respondents’ self-reported race/ethnicity and gender, four mutually exclusive dichotomized variables are coded for white men (=1, else = 0), black men (=1, else = 0), white women (=1, else = 0), and black women (=1, else = 0). Covariates include education (in years), individual earnings (ln-transformed), nonhousing financial assets (ln-transformed), married (=1, else = 0), currently working (=1, else = 0), obese (=1, else = 0; defined as a body mass index of 30 or greater), ever smoked (=1, else = 0), and comorbidity (number of chronic conditions ever had; range [0–7]). The sampling unit of the HRS is a household and both persons in a married couple are included in the study as long as they are otherwise eligible (Health & Retirement Study, 2008). A dichotomized variable indicating respondents from married couples (=1, else = 0) is included as a covariate. In multivariate analysis, age is centered at 55, the minimum age observed in the current analytic sample. Education, earnings, and assets are centered at respective means to optimize estimation.

Panel Attrition

More than one-quarter of the respondents died during the survey period. Of all deaths, 134 cases occurred before W3, and the vast majority (1,946 cases) occurred from W3 to W12. Preliminary analysis suggests that deaths are more likely in black men, in Supplemental Security Income or Social Security disability insurance recipients, and in those who had a hospital stay in the past 2 years. Since the pattern of mortality selection is the same before W3 and between W3 and W12, one hazard-rate selection instrument (λ) is calculated based on identified patterns of mortal attrition during the entire panel (Heckman, 1979) and included in all models as a covariate to correct estimates for selectivity. Attrition due to nonresponse does not significantly bias model estimates, and as a result, only panel mortal attrition is adjusted.

Models and Analytic Strategies

Growth curve model

I begin by estimating age-based growth curves using a multilevel mixed-effects model:

$${\displaystyle \begin{array}{l}{\displaystyle {\mathrm{y}}_{\mathrm{t}\mathrm{i}}={\displaystyle \stackrel{}{{\displaystyle \stackrel{\mathrm{f}\mathrm{i}\mathrm{x}\mathrm{e}\mathrm{d}-\mathrm{e}\mathrm{f}\mathrm{f}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{s}}{{\displaystyle \overbrace{{\mathrm{\beta }}_0+{\mathrm{\beta }}_1\mathrm{A}\mathrm{g}\mathrm{e}+{\displaystyle \sum _{\mathrm{p}}}{\mathrm{\beta }}_{\mathrm{p}}{\mathrm{X}}_{\mathrm{p}\mathrm{t}\mathrm{i}}+{\displaystyle \sum _{\mathrm{q}}}{\mathrm{\beta }}_{\mathrm{q}}{\mathrm{Z}}_{\mathrm{q}\mathrm{i}}}}}}}}+{\displaystyle \stackrel{\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{o}\mathrm{m}-\mathrm{e}\mathrm{f}\mathrm{f}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{s}}{{\displaystyle \overbrace{{\mathrm{\zeta }}_{0\mathrm{i}}+{\mathrm{\zeta }}_{1\mathrm{i}}\mathrm{A}\mathrm{g}\mathrm{e}+{\epsilon }_{\mathrm{t}\mathrm{i}}}}}}}\end{array}}$$

where $y_{\mathrm{t}\mathrm{i}}$ is the value of functional limitations for respondent i at time t. Fixed-effects terms include the intercept, ${\mathrm{\beta }}_0$, slope of the trajectory indexed by age, ${\mathrm{\beta }}_1$, and vectors of time-varying and time-invariant covariates, ${\mathrm{X}}_{\mathrm{p}\mathrm{t}\mathrm{i}}$ and ${\mathrm{Z}}_{\mathrm{q}\mathrm{i}}$. The random effect terms include Level 1 residual, ${\epsilon }_{\mathrm{t}\mathrm{i}}$, and Level 2 random intercept, ${\mathrm{\zeta }}_{0\mathrm{i}}$, and random slope, ${\mathrm{\zeta }}_{1\mathrm{i}}\mathrm{A}\mathrm{g}\mathrm{e}$. The estimated variances of the Level 2 terms, ${\mathrm{\psi }}_{00}$ and ${\mathrm{\psi }}_{11}$, summarize how much the individual trajectories deviate from the population mean trajectory. For example, if the estimated variance of the random intercept is 4, the individual trajectory can have an intercept that is greater than or less than the population mean by 2 units in functional limitations. Similarly, if the estimated variance of the random slope is 0.09, the individual trajectory can be steeper or less steep than the population mean trajectory by 0.3 units.

I estimate an unstructured residual covariance matrix of the random effects, allowing the intercepts and the slopes of the individual trajectories to freely covary. The estimated covariance suggests the extent of correlation between the random intercepts at time 0 (age 55 in current analysis) and the random slopes. If the covariance estimate is positive, it suggests a tendency for individual trajectories that are higher up at age 55 to have a greater rate of increase. A negative covariance estimate suggests a tendency for individual trajectories that are higher up at age 55 to have a slower rate of change.

It is important to note that the covariance estimate in itself does not provide sufficient evidence for interindividual divergence or convergence at the population level. This is primarily because the total amount of interindividual variability and its age patterning depend on all random-effects components at Level 2, not just the covariance. Moreover, the covariance estimate is influenced by where time 0 is placed, which is arbitrary. Changing time 0 would effectively change the value of the intercepts, leading to a different covariance estimate while the shape and relative positions of these trajectories remain the same. For these reasons, the current study examines interindividual variability and its age and race/gender patterning with two strategies: (a) modeling Level 2 heteroscedasticity and (b) calculating interquartile range (IQR) of estimated individual trajectories.

Growth curve model with level 2 heteroscedasticity by subgroups

To test whether interindividual variability differs by race/gender, I model Level 2 heteroscedasticity, allowing the random intercept variance, ${\mathrm{\psi }}_{00}$, and random slope variance, ${\mathrm{\psi }}_{11}$, to differ by race/gender, with parameters ${\mathrm{\psi }}_{00}^{(\mathrm{W}\mathrm{M})}$ and ${\mathrm{\psi }}_{11}^{(\mathrm{W}\mathrm{M})}$for white men, ${\mathrm{\psi }}_{00}^{(\mathrm{B}\mathrm{M})}$ and ${\mathrm{\psi }}_{11}^{(\mathrm{B}\mathrm{M})}$ for black men, ${\mathrm{\psi }}_{00}^{(\mathrm{W}\mathrm{W})}$ and ${\mathrm{\psi }}_{11}^{(\mathrm{W}\mathrm{W})}$ for white women, and ${\mathrm{\psi }}_{00}^{(\mathrm{B}\mathrm{W})}$ and ${\mathrm{\psi }}_{11}^{(\mathrm{B}\mathrm{W})}$ for black women. This is done by specifying different random effects for each race/gender group, expanding the base growth curve model as:

$${\displaystyle \begin{array}{l}{\displaystyle y_{ti}={\displaystyle \stackrel{\mathrm{f}\mathrm{i}\mathrm{x}\mathrm{e}\mathrm{d}-\mathrm{e}\mathrm{f}\mathrm{f}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{s}}{{\displaystyle \overbrace{{\mathrm{\beta }}_0+{\mathrm{\beta }}_1\mathrm{A}\mathrm{g}\mathrm{e}+{\displaystyle \sum _{\mathrm{p}}}{\mathrm{\beta }}_{\mathrm{p}}{\mathrm{X}}_{\mathrm{p}\mathrm{t}\mathrm{i}}+{\displaystyle \sum _{\mathrm{q}}}{\mathrm{\beta }}_{\mathrm{q}}{\mathrm{Z}}_{\mathrm{q}\mathrm{i}}}}}}+}\end{array}}$$

$${\displaystyle \begin{array}{l}{\displaystyle {\displaystyle \stackrel{\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{o}\mathrm{m}-\mathrm{e}\mathrm{f}\mathrm{f}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{s}}{{\displaystyle \overbrace{\begin{array}{ll}& {\displaystyle ({\mathrm{\zeta }}_{2\mathrm{i}}+{\mathrm{\zeta }}_{3\mathrm{i}}\mathrm{A}\mathrm{g}\mathrm{e})\mathrm{W}{\mathrm{M}}_{\mathrm{i}}+({\mathrm{\zeta }}_{4\mathrm{i}}+{\mathrm{\zeta }}_{5\mathrm{i}}\mathrm{A}\mathrm{g}\mathrm{e})\mathrm{W}{\mathrm{W}}_{\mathrm{i}}}\\ & {\displaystyle +({\mathrm{\zeta }}_{6\mathrm{i}}+{\mathrm{\zeta }}_{7\mathrm{i}}\mathrm{A}\mathrm{g}\mathrm{e})\mathrm{B}{\mathrm{M}}_{\mathrm{i}}+({\mathrm{\zeta }}_{8\mathrm{i}}+{\mathrm{\zeta }}_{9\mathrm{i}}\mathrm{A}\mathrm{g}\mathrm{e})\mathrm{B}{\mathrm{W}}_{\mathrm{i}}+{\epsilon }_{\mathrm{t}\mathrm{i}}}\end{array}}}}}}\end{array}}$$

This model also estimates an unstructured variance matrix. I perform a likelihood ratio test to compare the Level 2 heteroscedastic model with the base model that has constrained the unstructured random-effects variance matrix to be equal across race/gender (i.e., homoscedastic at Level 2). If the likelihood ratio test rejects the null ${\text{H}}_0:\text{} \text{ }\psi \text{}{}_{00}^{(\text{WM})}=\text{ }\psi \text{}{}_{00}^{(\text{WW})}=\text{ }{\psi }_{00}^{(\text{BM})}=\text{}{\psi }_{00}^{(\text{BW})},\text{ }{\psi }_{11}^{(\text{WM})}=\text{ } \text{}\psi \text{}{}_{11}^{(\text{WW})}=\text{}\psi \text{}{}_{11}^{(\text{BM})}=\text{}\psi \text{}{\text{}}_{11}^{(\text{BW})},\text{ } \text{}{\psi }_{10}^{(\text{WM})}=\text{} \text{}\psi {\text{}}_{10}^{(\text{WW})}=\text{} \text{}{\psi }_{10}^{(\text{BM})}=\text{}\psi \text{}{\text{}}_{10}^{(\text{BW})}$ it indicates that the variances in random intercept and random slope vary by race/gender, thereby suggesting race/gender patterning in interindividual variability in trajectories of functional limitations.

Interquartile range of estimated individual trajectories

A useful way to understand the variability implied by the model is to examine how spread out the estimated individual trajectories are. I obtain the fitted estimates from the growth curve model, which are linear prediction of the fixed portion plus contributions based on predictors of the random-effects. Based on these values, I calculate, at each age, individual trajectory estimates that are at the 75th percentile and the 25th percentile, respectively, to define an IQR within which the middle 50% of the individual trajectories fall. IQR is preferred to standard deviations as the measure of dispersion because in the current analysis the distributions of estimates are right-skewed across ages for all race/gender groups.

Analysis plan

First, I estimate an age-based trajectory of functional limitations using the total sample of black and white men and women, controlling for covariates. Although functional limitations are measured in intervals and have a slightly right-skewed distribution (1.37), this model assumes normality because the underlying concept of physical function has a censored normal distribution (Long, 1997). Interaction terms of race/gender groups and age parameters are specified to represent differences in initial level and rate of change by age for each group (white men as reference). Preliminary analysis comparing linear, quadratic, cubic, and quartic parameterizations of age indicates that a model with linear and quadratic age parameters has the optimal fit. This specification is thus retained in the final analysis. This base model assumes homoscedasticity at Level 2, that is, constant variance for all subgroups by race/gender.

Next, I allow the Level 2 variance to differ by race/gender. A likelihood ratio test compares this model to the base model and determines if specifying heteroscedastic variance over race/gender groups at Level 2 improves model fit. Fitted estimates of the individual trajectories are extracted from the better-fitting growth curve model and used to calculate IQR of estimated individual trajectories at each age. The calculation is limited to ages 55–81 for both black men and black women due to the sparsity of data (<30 data points) over age 81 in these two groups. IQR is then regressed on age for each race/gender to examine race/gender differences in age-based patterns of interindividual variability in trajectories of functional limitations. In the preliminary analysis, linear, quadratic, cubic, and quartic functions of age are tested for each race/gender group, and a linear specification is preferred for all race/gender groups based on model root-mean-square error (RMSE).

Results

Sample Characteristics by Race/Gender

Table 1 presents descriptive statistics of study variables at baseline (first observation in the current analytic sample) by race/gender. The average level of functional limitations at baseline is 2.32 for the total sample, and all race/gender groups are significantly different from one another in baseline functional limitations: white men have the lowest level of functional limitations (1.65), followed by black men (2.22) and white women (2.60); black women have the highest level of functional limitations (3.62). There is considerable variation in baseline functional limitations for all race/gender groups, as indicated by the corresponding standard deviations ranging from 2.50 to 3.73.

Table 1.

Means and Standard Deviations (in Parentheses) of Baseline Study Variables

	Total (n = 7,131)	White men (n = 2,720)	Black men (n = 513)	White women (n = 3,126)	Black women (n = 772)	Subgroup differences
Functional limitations	2.32 (3.05)	1.65 (2.50)	2.22 (3.14)	2.60 (3.13)	3.62 (3.73)	WM < BM < WW < BW
Age (in years)	60.71 (4.04)	60.68 (4.08)	61.47 (4.56)	60.62 (3.88)	60.67 (4.06)	BM > WM = WW = BW
Education (in years)	12.59 (2.75)	13.07 (2.87)	11.08 (3.31)	12.65 (2.34)	11.67 (2.89)	WM > WW > BW > BM
Earnings (ln)	5.41 (5.01)	6.28 (5.08)	5.38 (5.04)	4.74 (4.86)	5.06 (4.86)	WM > BM = WW = BW
Assets (ln)	14.35 (0.22)	14.38 (0.24)	14.27 (0.14)	14.36 (0.22)	14.25 (0.06)	WM > WW > BM = BW
Married	.70	.81	.62	.70	.40	WM > WW > BM > BW
Currently working	.56	.67	.57	.49	.48	WM > BM > WW = BW
Ever smoked	.63	.73	.72	.55	.53	WM = BM > WW = BW
Obese	.27	.25	.33	.24	.42	WM = WW < BM < BW
Comorbidity	2.57 (1.38)	2.58 (1.39)	2.61 (1.38)	2.49 (1.37)	2.87 (1.30)	WM = BM = WW < BW
Couple respondent	.74	.85	.69	.73	.43	WM > WW > BM > BW
Died W3–W12	.27	.30	.40	.23	.29	BM > WM > BW > WW

Note. The baseline is a first observation point. Differences in means by race/gender tested using chi-squared test or t-test (unequal variances) where appropriate (α = .05). WM = white men; BM = black men; WW = white women; BW = black women.

The average age is 61 years old at baseline for all groups. Black men are slightly older (61.47) than the other three race/gender groups. Of all race/gender, white men have the highest level of education, individual earnings, and financial assets. White women have more education and assets than black men and women, but are not significantly different from these two groups in earnings. Black men have less education but more assets than black women. Overall black women are the most disadvantaged with regards to socioeconomic status. At baseline, the percent of married individuals is higher in whites than in blacks, and the percent of individuals who are currently working is higher in men than in women. Women are less likely to have ever smoked than men, but within each gender, there is no racial difference in smoking. Black women have the highest rate of obesity (42%) and the highest level of comorbidity (2.87) whereas black men have the highest rate of death during the panel (40%).

Interindividual Variability in Trajectories of Functional Limitations

Table 2 presents two age-based growth curve models with and without specifying Level 2 heteroscedasticity over race/gender groups. Model 1 is the base model with estimates for the effect of race/gender on trajectories of functional limitations, controlling for covariates. The average level of functional limitations for white men at age 55 is −.6640 (p < .05), with a linear decrease of .0181 (p < .05) and a quadratic acceleration of .0036 (p < .05) per year of age. This means that, on average, white men do not have any functional limitation at age 55 and their limitations increase very modestly over time. Black men do not differ from white men in the initial level of functional limitations, but acquire limitations more rapidly, as indicated by a greater quadratic rate of change (b = 0.0021, p < .05). Compared with white men, white women have significantly higher initial level of functional limitations (b = 0.7287, p < .001) and faster linear increase (b = 0.0274, p < .05). Black women have a significantly higher initial level of functional limitations (b = 1.3399, p < .001) but do not differ from white men in rates of change. Socioeconomic status, marital and working status, ever smoked, obesity, and comorbidity are all associated with functional limitations in expected directions.

Table 2.

Trajectories of Functional Limitations: Black and White Adults Aged 55 and Older, HRS Cohort, Health & Retirement Study 1996–2014

	Model 1			Model 2
		Growth rate			Growth rate
Fixed effects	Intercept	Age(= Age − 55)	Age2	Intercept	Age(= Age − 55)	Age2
	−.6640*** (.1759)	−.0181 (.0098)	.0036*** (.0003)	−.4009* (.1685)	−.0225* (.0092)	−.0038** (.0003)
Black men	.2459 (.2086)	−.0449 (.0266)	.0021* (.0010)	.1759(.2166)	−.0380 (.0274)	.0021* (.0010)
White women	.7287*** (.1073)	.0274* (.0131)	−.0004 (.0005)	.6798*** (.1023)	−.0334** (.0128)	−.0005 (.0005)
Black women	1.3399*** (.1093)	.0053 (.0212)	.0004 (.0008)	1.2871*** (.1940)	.0139 (.0228)	.0001 (.0008)
Education (=Education – 12)	−.1716*** (.0108)			−.1720*** (.0105)
Earnings (ln; mean-centered)	−.0134*** (.0028)			−.0130*** (.0028)
Assets (ln; mean-centered)	−.2637*** (.0513)			−.2630*** (.0506)
Married	−.1694* (.0663)			−.1696** (.0658)
Working	−.3725*** (.0602)			−.3712*** (.0273)
Ever smoked	.3193*** (.0602)			.3284*** (.0306)
Obese	.3327*** (.0307)			.3284*** (.0306)
Comorbidity	.7076*** (.0221)			.6670*** (.0216)
Couple respondent	.0589 (.0662)			.0526 (.0658)
Panel attrition (λ)	.9280*** (.2061)			.7722*** (.2005)
Random effects
Variance (intercept)	7.3450	[6.9971, 7.7103]		White men	4.8901	[4.4832, 5.3339]
Variance (age)	0.0226	[0.0213, 0.0240]		0.0163	[0.0147, 0.0181]
Cov (intercept, age)	−0.2263	[−0.2453, −0.2073]			−0.1380	[−0.1610, −0.1149]
Variance (intercept)				Black men	8.8982	[7.3698, 10.7437]
Variance (age)				0.0314	[0.0248, 0.0397]
Cov (intercept, age)					−0.2771	[−0.3743, −0.1800]
Variance (intercept)				White women	7.8805	[7.3509, 8.4481]
Variance (age)				0.0234	[0.0215, 0.0255]
Cov (intercept, age)					−0.2346	[−0.2630, −0.2062]
Variance (intercept)				Black women	13.3642	[11.7091, 15.2532]
Variance (age)				0.0439	[0.0373, 0.0516]
Cov (intercept, age)					−0.5302	[−0.6299, −0.4305]
Variance (residual)	2.1815	[2.1486, 2.2149]		2.1760		[2.1432, 2.2094]
Log likelihood	−100029.1			−99897.7
BIC	200338.5			200172.7

Note. n = 7,131 individuals, 48,000 observations; maximum likelihood estimates; Gaussian linked used due to censored normal distribution of the outcome; Coefficients with standard errors (in parentheses) reported for fixed effects and coefficients with 95% confidence intervals [in brackets] reported for random effects; BIC = Bayesian information criterion; linear, quadratic, cubic, and quartic functions of age tested and quadratic specification selected based on BIC.

*p < .05. **p < .01. ***p < .001.

Estimates of the variance in random intercept and random slope in Model 1 indicate unexplained interindividual variability in trajectories of functional limitations, even after predictors are accounted for in the fixed-effects equation. All estimates are sizable, and statistically significant as indicated by the corresponding 95% confidence intervals (CI). A typical individual trajectory’s intercept can differ from the population mean by 2.7 (=$\sqrt{7.345}$) units. This suggests that while the cohort on average has no functional limitation, a sizable portion of the individuals can have a lot of difficulty in performing one functional task or some difficulty in performing two functional tasks. Some individuals can have a rate of change by age that is faster or slower than the population mean by a factor of .15 (=$\sqrt{.0226}$). For an observation window spanning 28 years, this could result in a difference of 4 units in functional limitations. The estimated covariance between the random intercepts and the random slopes is statistically significant and negative, suggesting that individual trajectories with greater intercepts at age 55 tend to have a slower rate of change.

Interindividual Variability: Age-Based Patterns and Race/Gender Variations

Model 1 suggests a considerable amount of residual variability between individuals in trajectories of functional limitations. The next step is to examine whether such variability varies by race/gender. Model 2 includes separate random intercept and random slope covariance matrices for each race/gender. Model 2 has a larger log likelihood of −99839.2 and a smaller Bayesian Information Criterion (BIC) of 200172.7 than Model 1 (log likelihood = −100029.1, BIC = 200338.5). A likelihood ratio test comparing goodness of fit of Models 1 and 2 yields a ${\mathrm{\chi }}^2$ statistic of 379.8 for 9 degrees of freedom, which is statistically significant at .001 level. This suggests that specifying Level 2 heteroscedasticity improves model fit and that interindividual variability in trajectories of functional limitations indeed varies by race and gender.

As shown in Model 2, of all four groups, white men have the smallest variance in both intercepts (${\widehat{\psi }}_{00}^{(\mathrm{W}\mathrm{M})}$ = 4.8901, 95% CI [4.4832, 5.3339]) and slope (${\widehat{\psi }}_{11}^{(\mathrm{W}\mathrm{M})}$ = .0163, 95% CI [0.0147, 0181]). Black men and white women are not significantly different from one another with respect to estimated variance of the intercept (${\widehat{\psi }}_{00}^{(\mathrm{B}\mathrm{M})}$ = 8.8982, 95% CI [7.3698, 10.7437]; ${\widehat{\psi }}_{00}^{(\mathrm{W}\mathrm{W})}$ = 7.8805, 95% CI [7.3509, 8.4481]) and that of the slope (${\widehat{\psi }}_{11}^{(\mathrm{B}\mathrm{M})}$ = 0.0314, 95% CI [0.0248, 0.0397]; ${\widehat{\psi }}_{11}^{(\mathrm{W}\mathrm{W})}$ = 0.0234, 95% CI [0.0215, 0.0255]). Both, however, have greater variances in intercept and slope compared with white men. Black women have the greatest variance in intercept (${\widehat{\psi }}_{00}^{(\mathrm{B}\mathrm{W})}$ = 13.3643, 95% CI [11.7091, 15.2532]). They also have a variance in slope (${\widehat{\psi }}_{11}^{(\mathrm{B}\mathrm{W})}$ = 0.0439, 95% CI [0.0373, 0.0516] that is greater than that for white men and white women but is not significantly different from that of black men. For all race/gender groups, the model yields an estimated covariance that is statistically significant and negative. This suggests that individual trajectories with greater intercepts at age 55 tend to have a slower rate of change. This correlation between intercepts at age 55 and slopes is smallest in white men and largest in black women. Black men and white women do no significant differ from each other in estimated covariance.

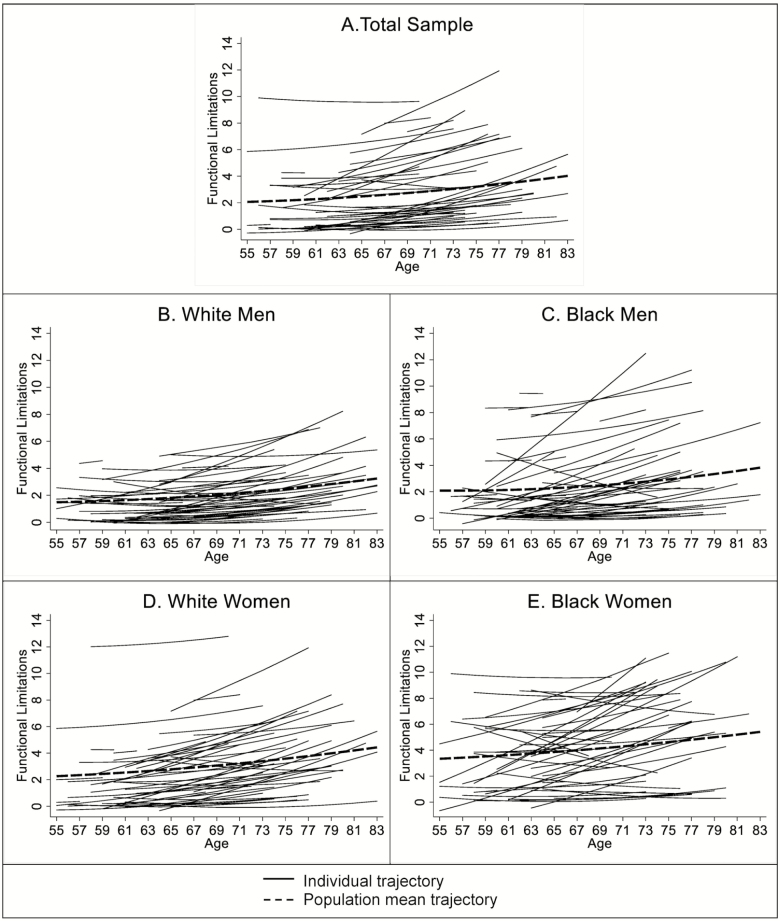
To provide a visual representation of interindividual variability, a random sample of estimated individual trajectories (n = 50) for the entire cohort and for each race/gender is plotted along with the estimated population mean trajectory for that group in Figure 1. For the entire cohort, there is substantial intervariability in trajectories of functional limitations, and the individual trajectories are not normally distributed around the population mean trajectory (Panel A, Figure 1). Panel B in Figure 1 shows that the vast majority of white men have low levels of functional limitations and a very modest rate of increase with age. The individual trajectories are also closely distributed around the group mean with a typical deviation of no more than 2 units. Compared with white men, there are greater variability white women’s trajectories (Panel D, Figure 1). For black men, a number of individual trajectories have low levels of functional limitations and stay stable across ages (Panel C, Figure 1). They are virtually indistinguishable from those of white men. There is, however, a group of black men with higher initial level and faster rate of increase in functional limitations, thereby skewing the group mean trajectory upward. For black women, the individual trajectories are much more spread out around the group mean trajectory, with substantial heterogeneity in initial level, as well as the direction and rate of change with age (Panel E, Figure 1).

Figure 1.

Mean trajectory and random sample of estimated individual trajectories (n = 50) by race/gender. Note. Trajectories calculated based on fixed and random effects estimates in Model 2, Table 2. Parametric smoothing applied.

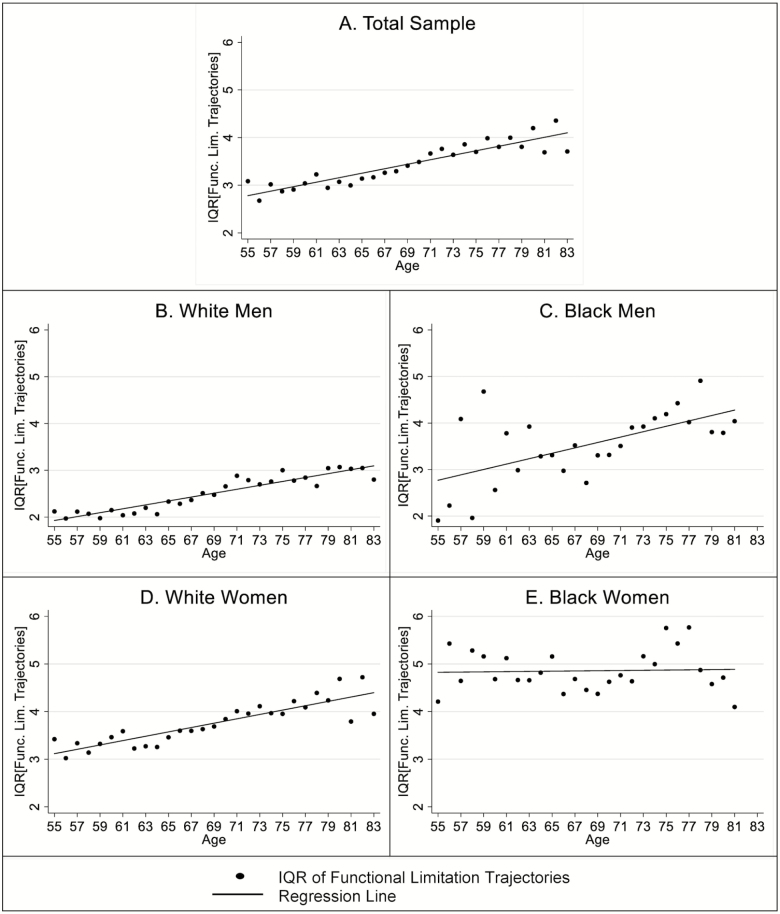
A cursory inspection of Figure 1 also suggests that except for black women, all groups exhibit a general pattern of increasing variability with age. Table 3 empirically examines age-based patterns of interindividual variability, measured by IQR of estimated individual trajectories for each race/gender. Age is a significant predictor of IQR for all race/gender groups except for black women. For white men, IQR increases by .0417 per year of increase in age (p < .01). Similarly, IQR increases by .0580 (p < .001) and .0457 (p < .001) per year for black men and white men, respectively. Such an age-based pattern could result in a 40%–60% increase in IQR over the entire observation window from age 55 to 83. Figure 2 presents the age-based pattern of IQR of estimated individual trajectories by race/gender. For the total sample, variability in functional limitations increases systematically with age (Panel A, Figure 2). White men (Panel B, Figure 2) and white women (Panel D, Figure 2) show a steady linear increase in IQR with age. For black men, there is a general trend toward increasing variability with age, although the data points are more spread out around the regression line, especially between age 55 and 65 (Panel C, Figure 2). For black women, IQR is quite large across ages with no apparent age patterning (Panel E, Figure 2).

Table 3.

Interquartile Range (IQR) of Estimated Individual Trajectories Regressed on Age by Race/Gender

	Total (n = 29)	White men (n = 29)	Black men (n = 27)	White women (n = 29)	Black women (n = 27)
Intercept	2.7803*** (.0645)	1.9276*** (.0502)	2.7700*** (.2362)	3.1164*** (.0796)	4.8248*** (.1649)
Age	.0471*** (.0040)	.0417*** (.0031)	.0580*** (.0156)	.0457*** (.0049)	.0024 (.0109)
F Sig.	141.84***	183.84***	13.84***	87.73***	.05
Adj-R2	.83	.87	.33	.76	−.04
RMSE	.18	.14	.63	.22	.44

Note. Calculation of IQR limited to ages 55–81 for black men and black women due to the sparsity of data (<30 data points) over age 81. Linear, quadratic, cubic, and quartic age functions tested for the total sample and for each race/gender and best-fitting model selected based on RMSE. Coefficients with standard errors (in parentheses) reported.

***p < .001.

Figure 2.

Age-based pattern of interquartile range in trajectories of functional limitations by race/gender.

Discussion

In the 1988 volume, Varieties of Aging, George Maddox and Powell Lawton (1988) assembled the first comprehensive set of thoughts on the heterogeneous nature of aging. The scope of this volume spanned many substantive areas, and yet focused “precisely on the neglected documentation and explanation of heterogeneity of how people grow older within a society (p. ix).” As Dannefer (1988) noted in the first chapter of this volume, at that time, the primary challenge to addressing aged heterogeneity was the lack of longitudinal data on individual trajectories. In the 30 years since, great methodological advances have been made, allowing researchers to examine average differences between groups in health trajectories. This article has sought to more fully explicate differential aging by examining interindividual variability within each race/gender, taking advantage of the unique analytic opportunity afforded by multilevel mixed-effects models.

The key findings are three-fold. First, even after adjusting for covariates, there is substantial interindividual variability left unexplained in trajectories of functional limitations within each race/gender, highlighting the complexity of life-course differentiation. Second, there is a tendency towards increasing interindividual variability with advancing age for the entire HRS cohort, and for each subgroup of white men, black men, and white women in this cohort. Not only do subgroups diverge, individuals of the same race/gender also become more dissimilar from one another as they age. Third, there are race/gender differences in both the magnitude and the age-based patterns of interindividual variability. Black men, white women, and black women have greater interindividual variability in functional limitations than do white men. Interindividual variability increases with age linearly at similar rates for all groups but black women.

Overall, the findings show robust evidence of interindividual divergence with age, consistent with cumulative dis/advantage theory. As one of the key frameworks in studies of health and aging, cumulative dis/advantage has stimulated numerous empirical work characterizing race/ethnicity and gender disparities in late life. Yet findings from this body of work are mixed, providing limited support to the theory or its competing hypotheses. Subgroup differences in health have been found to increase (Shuey & Willson, 2008; Taylor 2008), remain constant (Ferraro & Farmer, 1996; Kelley-Moore & Ferraro, 2004), or even shift from divergence to convergence over the life course (Brown et al., 2012; Warner & Brown 2011). Based on my results, the mixed findings in prior literature may be due to interindividual variability within each race/gender group. For example, the fixed-effects estimates suggest persistent inequality between black women and white men—black women as a group exceed white men in the intercept of the trajectory by a factor of 1.3 and the slopes are not significantly different. However, the random-effect estimates suggest that among black women, a typical individual trajectory’s intercept could deviate from the group average by a factor of 3.7, and the slope could deviate by a factor of 0.2. Since the group mean trajectory does not adequately summarize the data for black women, researchers may have overestimated the disability gap between these two groups. Moreover, inter-individual variability increases with age among white men, thereby increasing the amount of overlap in physical function between white men and black women over time. At upper ages, the mean trajectory does not characterize the health dynamics well for either white men or black women, raising questions about the substantive validity of using these group mean trajectories to establish empirical support for persistent inequality.

I found a somewhat stratified pattern of life course health differentiation in black men. Most individual trajectories of black men are very similar to those of white men. There are, however, a group of black men with higher initial levels of functional limitations and faster rates of functional deterioration with age. There are two possible explanations to this pattern. First, the current analysis includes a number of covariates. While robust, they provide limited accounts of the race- and gender-based opportunity structure. Future research should include other measures to help explain inter-individual variability in black men’s health. Second, due to its limitation of the scope, the current study does not focus on specifying how life course processes generate inter-individual variability in black men. While the fundamental cause of life course differentiation is the same for all persons, there are race- and gender-specific predictors of and pathways leading to poor health outcomes in each subpopulation. One example is that education may intersect with race and gender (Cummings & Jackson, 2008; Farmer & Ferraro, 2005; Hinze, Lin, & Andersson, 2012), with blacks receiving less health benefit from education relative to whites. In particular, Brown and colleagues’ (2016) analysis demonstrates that racial inequality is greater at higher levels of education over the life course, suggesting a differing effect of education specific to black men. The HRS cohort as a whole benefited from public investment and desegregation in education, but not every black man in this cohort have received the same degree of health return from these changes, and some still have the same access to economic resources and medical care, despite higher educational attainment (Oliver & Shapiro, 2006). Future search should explore potential interactions between race/gender and other social factors and characterize pathways that are specific to the cohort and the race/gender group under study.

“Left-censoring” is observed in all race/gender, and is most prominent in black women. The HRS sample is age-truncated at 51, and at the baseline of the current analysis, age 55, there is already substantial interindividual variability in functional limitations, especially among black women. This means that life-course processes that generate such health heterogeneity have largely played out before older adulthood. Consistent with previous studies that reported weathering (Geronimus et al., 2006) and accelerated disablement (Warner & Brown, 2011), my findings also suggest more rapid differentiation in black women. Future studies should address the “left-side” selection mechanisms, especially for black women, whereby the effect of socioeconomic status being most influential and consequential in mid-life rather than in late-life. Study designs with observation window spanning over the entire adult life course and models that analytically account for selectivity before the observation window can help chart the life paths of black women.

This study has two limitations. First, as discussed above, an analysis of variability where the individual trajectories are arrayed by age calls for more statistical power, especially at upper ages and as a result, this study is unable to include Hispanic men and women. However, there is preliminary evidence that Mexican American men and women are more heterogeneous in self-rated health relative to whites (Brown et al., 2016) and that Hispanic older adults have greater fluctuations in functional status over time (Lin & Kelley-Moore, 2017). Studies that document interindividual variability in Hispanics, and in each Hispanic origin groups, would greatly improve our understanding of how health inequality develops over the life course and are urgently needed to complement findings from the current study. Second, the current analysis may have underestimated interindividual variability due to two methodological issues—panel attrition and a floor effect in measuring functional limitations. The models adjust for panel mortal attrition bias, but cannot possibly remove all selectivity in the data. Because selective mortality reduces variability, more so for the socially disadvantaged, the actual extent of interindividual variability may be even greater. When measuring functional limitations, individuals without any limitations are censored at zero. Although the models account for the underlying censored distribution of physical function with a Gaussian link, the floor effect in the measurement can still to some extent reduce variability among individuals without limitations, which is a heterogeneous group in terms of physical health.

The limitations notwithstanding, this study provides a direct look of differential aging over the life course for black and white men and women in the HRS cohort. Future studies should continue to characterize interindividual variability in health and aging outcomes within defined subpopulations, to further explore the as-yet uninvestigated mechanisms that give rise to systematic social differentials during later life.

Conflict of Interest

None reported.