Highlights
-
•
Establish an adjusted design framework for optimal paths for public transport users considering their preferences at the requested time of travel.
-
•
Devise a novel lexicographical comparison methodology with a just noticeable difference (JND) consideration that captures human perception elements combined with preferences over different PT attributes.
-
•
Establish the theorem for the comparison method to satisfy the axiom of transitivity and develop a sorting algorithm and prove its correctness.
-
•
Case study using simulation on the Copenhagen PT network and the results of the case study imply a favorable potential for real-life applications.
Keywords: Personalization, Public transport planning, Route guidance
Abstract
The use of smartphone applications (apps) to acquire real time and readily available journey planning information is becoming instinctive behavior by public transport (PT) users. Through the apps, a passenger not only seeks a path from origin to destination, but a satisfactory path that caters to the passenger’s preferences at the desired time of travel. Essentially, apps attempt to provide a means of personalized PT service. As the implications of the Covid-19 pandemic take form and infiltrate human and environmental interactions, passenger preference personalization will likely include avoiding risks of infection or contagious contact. The personal preferences are enabled by multiple attributes associated with alternative PT routes. For instance, preferences can be connected to attributes of time, cost, and convenience.
This work establishes a personalized PT service, as an adjustment to current design frameworks, by integrating user app experience with operators’ data sources and operations modeling. The work proceeds to focus on its key component: the personalized route guidance methodology. In addition to using the existing shortest path or k-weighted shortest path method, this study develops a novel, lexicographical shortest path method, considering a just noticeable difference (JND). The method adopts lexicographical ordering to capture passenger preferences for different PT attributes following Ernst Weber’s law of human perception threshold. However, a direct application of Weber’s law violates the axiom of transitivity required for an implementable algorithm, and thus, a revised method is developed with proven algorithms for ranking different paths. The differences between the three route-guidance methods and the effects of the JND perception threshold on the order of the alternative PT routes are demonstrated with an example.
The developments were examined in a case study by simulation on the Copenhagen PT network. The results show that using the JND method reduces the value/cost of the most important attributes. Identical robust results are attained when JND parameters are not specified and default values are used. The latter may apply for the future with a mixture of specified and default preference input values. Finally, the computation time indicates a favorable potential for real-life applications. It is believed that the consideration of human threshold perception will encourage decision makers to establish new criteria to comply with this.
1. Introduction
With changes in awareness and perception of social distance, evolving from the Covid-19 pandemic, people are likely to be more inclined to changing their habits and thinking paradigms and to accepting a new era of personalized public transport (PT) mobility. In most major cities around the world, PT plays a key role. The development of smartphones has enabled making real time, easily accessible journey planning information an integral part of the PT system (Ceder, 2016). Simultaneously, smartphones and other devices provide information contributing to big data. Thus, as each passenger has specific preferences when undertaking a trip, s/he can send them to the operator via apps so as to improve travel experiences. This illustrates the duality of PT information: (a) informing big data centers which help passenger mobility planning and real-time adjustments, and (b) personalizing passenger preferences using optimal route guidance methodology. Whereas (a) and (b) are inseparable from the use and purpose of the same information, the objective of this study is to develop a methodology adjusting current design frameworks, considering (a) integrated with a new modeling of (b).
1.1. Passenger preferences
Beyond the basic mechanics of planning and paying for a journey, PT passengers are likely to have preferences for certain features of a journey, including modal and route choices, likely to influence their travel decisions. A number of factors have been found to affect passenger choices, such as the quality of a PT service, connectivity, fare cost, accessibility, and distance (Kingham et al., 2001, Galdames et al., 2011, Frappier et al., 2018, te Morschea et al., 2019). Each passenger might personalize requirements accordingly (Bian and Liu, 2019, Liao et al., 2019), so that these factors would play a major role in determining PT route choices (Grison et al., 2017). Moreover, passenger choices could then be adapted by preferences changing with time of day, mood, parallel plan and schedule adjustments, family considerations, etc. Indeed, a user has unique requirements for every trip. Thus, a well-designed smartphone app should enable passenger interaction with operators for sending preferences and receiving information accordingly. Increased attention has been given by the industry and researchers to informative and to some extent personalized smartphone apps in recent years, and this continues (Ludwig et al., 2009, Arentze, 2013; Shaheen et al., 2016, Campigotto et al., 2016).
Generally speaking, as per Chorus (2012), there are two perspectives to the benefits of personalized smartphone apps: (i) services remember and learn from passenger choice profiles and allow predicting passenger mobility and issuing context-sensitive personal advice (Lathia et al., 2013, Bouhana et al., 2013, Arentze, 2013), and (ii) services prioritize passenger preferences over other attributes (Peng and Huang, 2000, Zografos et al., 2009, Chorus et al., 2009). This study will construct an adjusted framework to capture both perspectives, proposing that perspective (i) be addressed by a big data center, wherein various data sources are stored and utilized to predict passengers’ travel behavior and to assist operators in making realtime operational decisions, and perspective (ii), the core of this study, be addressed by developing a personalized route guidance methodology considering passenger preferences.
In comparison with previous studies, our novel developments include:
(1) Devising a path comparison methodology which captures passenger preferences with respect to various PT attributes. In comparison with existing literature (Peng and Huang, 2000, Zografos et al., 2009, Chorus et al., 2009, Ludwig et al., 2009, Arentze, 2013, Nuzzolo et al., 2014), this study considers the order of passenger preferences that could be specified via an app, instead of using weighting parameters. The difference between the two methods is demonstrated using an illustrative example.
We propose that a personalized PT route guidance app should provide a set of ordered paths considering passenger preferences for different PT attributes, in contrast with most existing apps where path order is determined by only one PT attribute, such as travel time. In a study of online shopping systems (Kumar and Benbasat, 2006), recommendations are shown to affect customer choices. By analogy, we believe recommendations related to a route guidance app, i.e., ordered paths, would affect passengers’ route choice. Thus, the order of the paths must be based on different PT attributes rather than a single one. We attain that by adopting the lexicographical ordering approach to determine the set of paths by their order, aligned with passenger preference for certain PT attributes as per a personalized route-recommendation app. The lexicographic ordering method is an appropriate methodology for multicriteria decision analysis. It is well suited to hierarchical consideration of conflicting objectives (Ehrgott, 2005). Applying lexicographic ordering to the multicriteria pathfinding problem can be traced to Martins (1984), where a label setting algorithm was developed to find nondominated paths. Martins’s method is as an extension of the Dijkstra algorithm in the sense that it extends the min operator in Dijkstra algorithm to a lexicographic min operator. Martins’ method was further extended by Gandibleux et al. (2006) to handle bottleneck type criteria. Pulido et al. (2014) developed a label-setting algorithm to find optimal paths satisfying a set of lexicographic goals or minimizing deviation from goals if these cannot be fully satisfied. Another approach to solving the multicriteria pathfinding problem is to develop an aggregate function for converting multiple labels to a single label. Different aggregation functions have been proposed and examined in the literature (Tung and Chew, 1992, Iori et al., 2010, Paixão and Santos, 2013). The algorithm developed in this study is in line with the Martins' method and can be viewed as an extension of the Dijkstra algorithm. In the field of transport behavioral modeling, the application of the lexicographic ordering approach is very limited. To the best of our knowledge, only Karaliopoulos et al. (2017) noticed that lexicographic heuristics are a fast and frugal heuristic approach recognized by behavioral sciences such as psychology and biology and adapted it to model travelers' car-search behavior.
(2) Capturing elements of human perception combined with preferences for various PT attributes. Weber’s law, an established psychophysical phenomenon, is initially incorporated into a route guidance methodology. In short, Weber’s law states that when comparing two stimuli, a person is not likely to perceive any difference between them when the ratio of the difference is small. Modeling by this concept allows us to examine and understand a specific cognitive limitation of human behavior. To a certain extent, this law is similar to the framework of bounded rationality recognized by Nobel laureate economist, Simon (1955). In comparison with prevailing literature on bounded rationality by transport-related modeling (Zhang, 2011, Guo and Liu, 2011, Wu et al., 2013, Szeto et al., 2015, Di and Liu, 2016), this study focuses on the application of public transport service and does not solve equilibrium choice behavior for a set of options.
(3) Proposing a revised comparison method in the spirit of Weber’s law by establishing a theorem to satisfy the axiom of transitivity in developing an algorithm for the shortest path of prioritizing preferences, including a proof of its correctness. Generally speaking, the proposed pathfinding algorithm belongs to the class of multicriteria shortest path problems initiated by Hansen, 1980, Martins, 1984. Most existing studies use either a weighting function to convert multiple criteria into a single criterion (Modesti and Sciomachen, 1998, Horváth and Kis, 2018) or find the set of non-dominated Pareto paths (Martins, 1984, Guerriero and Musmanno, 2001, Disser et al., 2008, Androutsopoulos and Zografos, 2009, Reinhardt and Pisinger, 2011, Chen et al., 2013; Delling et al., 2014, Ambrosino and Sciomachen, 2014, Shi et al., 2017). In comparison with previously developed methods in the literature, the novelty of our method is to consider human perception as an important element in evaluating different options. The absence of this novel consideration from existing multicriteria shortest path methods makes its comparison with an available benchmark algorithm impossible. More importantly, the main objective of this study is, for the first time, to establish a solid and comprehensive framework of personalized PT services in addition to developing an efficient solution algorithm.
Basically, this study first presents a structural framework for future app personalization. Secondly, a novel route guidance methodology is developed prioritizing passenger preferences combined with elements of human perception above various PT attributes. The proposed methodology is compared with the k-weighted shortest path and shortest path methods to demonstrate the advantage of the novel approach in providing improved personalized routes in future apps.
1.2. Design framework
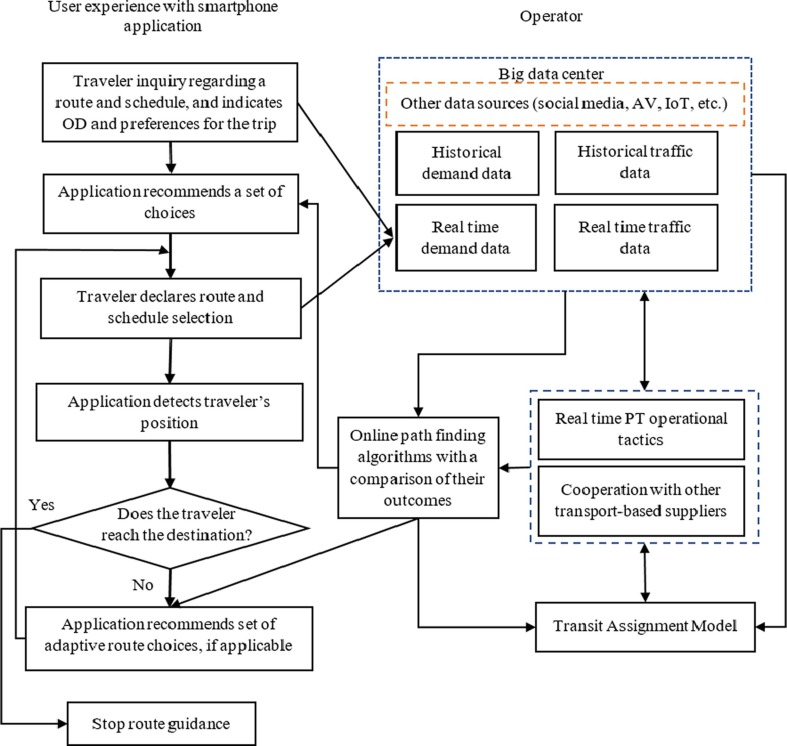
Fig. 1 depicts an adjustment to current design frameworks, such that the general scheme of the figure is already part of PT operation in most developed countries but without the use of a prudent, personalized, online pathfinding algorithm. Fig. 1, comprised of two parts, refers to the left side to the user experience with a smartphone app, and on the right side to operator data.
-
(1)
User experience: For the use of a personalized PT guidance app, a passenger first sets up a trip destination, along with preferences associated with various PT attributes for the trip. The passenger, then, declares the selection of a route and a schedule. During the trip, the app detects the passenger’s location and, if applicable, recommends a set of alternative route choices adapted to realtime circumstances. Passenger preferences and route choice data can be stored in the big data center given passenger consent.
-
(2)
Operator: The big data center stores both real time and historical data, including smartcard and traffic count data. In addition, it is suggested that other emerging data sources be incorporated from social networks (Xiao and Lo, 2016), special events (Calabrese et al., 2010), Internet of Things (IoT) (Handte et al., 2016), autonomous vehicles (AV), etc. These data will assist the operator in determining real time PT operational tactics. Notably, for further performance improvements, collaboration with other transport-related providers, such as shared autonomous vehicles, bike-sharing, on-demand transit, etc., is recommended. This will facilitate a seamless, multimodal travel experience and pave the way to mobility as a service.
Fig. 1.
Design framework.
Acknowledgement is warranted for personalized PT systems proposed by Arentze, 2013, Nuzzolo et al., 2014, and Campigotto et al. (2016). Comparatively speaking, their works focus more on the user side while our proposed framework incorporates the perspectives of both the user and the operator.
2. Route guidance methodology
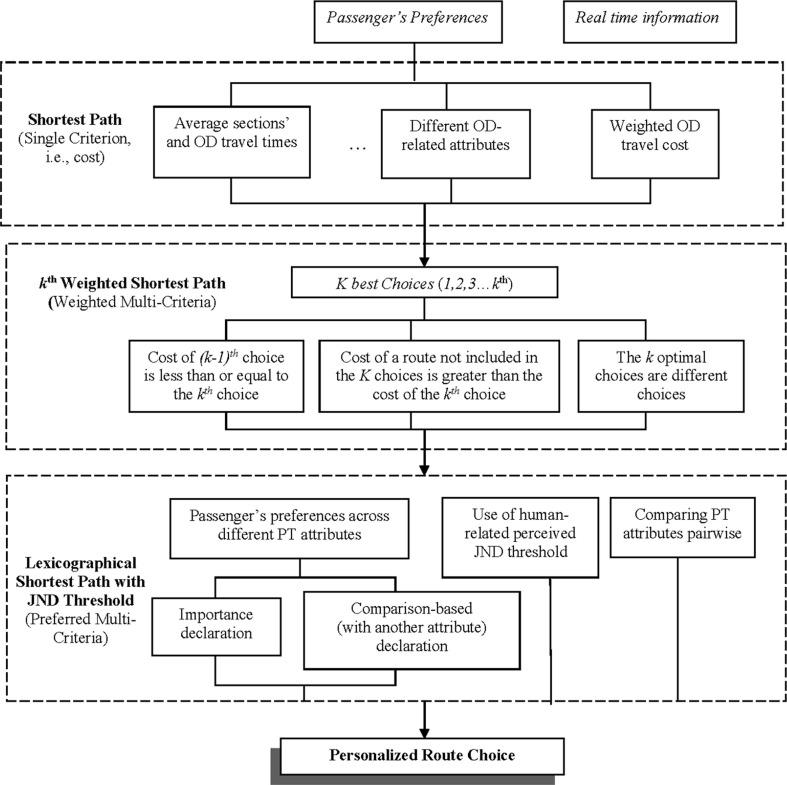
No doubt that the path recommended for a passenger is important because it affects the passenger’s route choice and results in different travel experiences. If the passenger is satisfied with the route suggested and experiences a pleasant journey, it improves the attractiveness and image of the PT service. This section discusses three path recommendation methods: the shortest path, k-weighted shortest path, and lexicographical ordering using JND threshold. The overview of these three methods is shown in Fig. 2 .
Fig. 2.
Three methods for path recommendation.
The basic methodology for recommending a path is the shortest path method. This method finds the best route based on one of the passenger’s preferences, e.g., travel time or an OD related attribute. The merit is its computational efficiency based on well-developed shortest path algorithms in practice. It is suitable for a passenger who is only interested in one attribute, such as time or fare. However, because this approach only recommends one path, it is highly possible that different passengers would receive the same recommendation, implying that the personalization level is low, and could induce congestion in PT vehicles if all passengers follow the same suggestion.
We found a few avenues to overcome the demerits of the shortest path method. First, is the use of the k-weighted shortest path method that provides a set of paths sorted by weighted cost. That is, the use of weighted cost to search and order paths by incorporating the effects of various PT attributes on passengers’ route choice. Generally speaking, the values of weighting parameters could be input by the passengers, using default values or predicted via advanced machine learning algorithms (i.e., Arentze, 2013, Campigotto et al., 2016). Because of the freedom of setting weighting parameters, across the time of day and day of the week, different passengers could obtain different paths catering to their preferences. This feature indeed achieves a certain degree of personalization. However, the set and order of paths considered and recommended are sensitive to the values of the weighting parameters; if the parameters are not well-calibrated, the path order may not reflect passenger preference order, as is shown below in the example in Section 4. A good personalized route guidance app should, on the one hand, provide satisfactory personalized results, but, on the other hand, minimize passenger effort in inserting input parameters. In addition, using the weighted cost path method implicitly requires that all of the PT attributes be converted to monetary values. In this respect, we note that although such a requirement is generally acceptable in practice and research, there are still investigations and discussions on valuing the PT attributes, such as passenger walking, waiting, and transfer times.
Nonetheless, for personalized consideration, it is most important to understand and consider human factors in modeling and analysis. Both the shortest path and k-weighted shortest path methods do not really take human factors into account. Therefore, our second avenue to overcome the demerits of the shortest path method is to propose a lexicographical ordering method with a just noticeable difference (JND) threshold. This method relies on passenger declaration of the importance of the different PT attributes and on a parameter that captures human perception as it is explicated below in Section 2.2. In the following subsection, we first list the key notations used throughout this paper and, then, elaborate on the proposed methodology mathematically.
2.1. Notations
| Set of PT routes, stops, arcs, and PT attributes | |
| Set of PT lines leaving node i | |
| P | Set of passenger’s preferences for all of the PT attributes |
| Set of acceptable candidate choices between nodes o and d | |
| Set of ordered PT attributes between nodes o and d using PT line l | |
| The value of the mth PT attribute between nodes o and d using PT line l | |
| Just noticeable difference (JND) threshold value associated with PT attribute m (Weber’s JND) | |
| Personal maximum/minimum acceptable value of the mth PT attribute |
2.2. Lexicographical ordering using JND threshold
The proposed new route guidance methodology is comprised of three components: (1) elimination of choices that are unacceptable to the passenger; (2) selection only of choices noticeable to the passenger; and (3) sorting the noticeable choices using lexicographical ordering method. These components are explained in this section.
2.2.1. Personal maximum or minimum acceptable value of an attribute
A passenger, naturally, can have preferences over a given set of PT attributes. Besides, a passenger would be able to set up a maximum or minimum acceptable value on certain PT attributes. For example, (i) a tired passenger who prefers waiting to walking may set a 20-minute wait limit to avoid being late; (ii) a slightly disabled passenger for whom having a seat constitutes the minimum comfort level sought. Existing apps, like Google Maps, limited to the travel time attribute, can set up this feature. For other attributes, the passenger needs to check and compare them manually. We envision that in the future, a highly personalized app will allow for a passenger to input an acceptable value for each PT attribute associated with a requested trip unless accepting default values. Moreover, the comparison should be completed automatically by the app instead of bothering the passenger. To attain this function, we determine a candidate set of paths, , as follows:
| (1) |
Eq. (1) states that the use of PT line l is contained in candidate choice set , if each of its attributes agrees with the personal max acceptable value.
2.2.2. Just noticeable difference (JND)
Following the determination of the candidate set of paths, we model passenger behavior in the process of deciding the order of these paths. Personalized decisions are naturally affected by human perception elements. Thus, in making a route choice, the differences between available PT routes must be perceived. This perception-based component leads us to the field of experimental psychology (psychophysics). That is, if the travel time of one route is 100 min and the travel time of the compared route is 103 min, the question arises of whether these three-minute differences are noticeable to the user. In other words, what is the range of non-perception minutes for the travel time of 100 min? Is it [95,105], or [90,110], or something else?
For this perception-based component, we use the difference threshold definition of JND highlighted by Ernst Weber’s law (Baird and Noma, 1978, Laming, 2008, Chowdhury et al., 2015). Weber’s law states that when two stimuli are compared with each other, rather than simply perceiving the difference between the magnitudes of stimuli being compared, human beings perceive the ratio of difference. Mathematically, it is formulated as
| (2) |
where ΔU is the change required for an individual to just notice a difference in the magnitude of an attribute, and U is the current stimulus’s (attribute’s) magnitude. As the value of the constant decreases, the perceptual sensitivity certainly improves.
In the field of transportation, the JND literature is limited. Shi et al. (2011) examined car following distances in driver behavior using JND with the adoption of 0.3 as the constant for drivers’ perception of change in headway. In Chowdhury et al. (2015), the JND is adopted to capture the minimum travel time and cost savings, invoking the willingness of PT users’ to take routes with transfers.
This work considers Weber’s law using as the JND threshold value associated with PT attribute m. Hence, the comparison between the personalized choices will consider the same if it is not perceived; i.e., the analysis will be looking at
| (3) |
where is the best (most attractive) value of the attribute m among the choices and may be presented in %.
2.2.3. Lexicographical ordering method
To incorporate the JND threshold value into the path comparison procedure, we propose using the lexicographical ordering method. The lexicographical ordering method is a method for multicriteria optimization problems when different objectives are considered in a hierarchical manner. This method is adopted because (a) the path recommendation problem is intrinsically a multicriteria optimization problem; (b) it fits our assumption that passengers have preferences for different PT attributes; (c) it could simplify the passenger’s input on the smartphone app, i.e., a passenger can either declare a PT attribute is “extremely important“ (=E), ”very important“ (=V), ”important“ (=I), or ”less important“ (=L), or simply indicate a preference for a comparison, i.e., “travel fare is more important than travel time.”
2.2.4. Formulation and algorithms
Instead of using an aggregated weighted cost like the k-weighted shortest path method, the lexicographical ordering method compares each PT attribute pairwise. Accordingly, we use an ordered set, , to represent various PT attributes given passenger preference P, where P is a set of preferences of all attributes. Mathematically, is defined by
| (4) |
The set also represents passengers’ preferences for different PT attributes, i.e., is the most important attribute and is the least important one. Meanwhile, denotes the scalar value of attribute m rather than a monetary value or a weighted value to reduce the number of parameters to be calibrated.
Suppose that at node o there are two candidate options leading to destination d, i.e., using PT lines l and l’. We say that option l is better than option l’ if the following holds:
| (5) |
Eq. (5a) states that the value of option l’ is larger (less desirable) than that of l’s for the q th attribute. Eq. (5b) states that for the k th attribute among the first q-1 attributes the difference of values between options l and l’ are within the JND threshold, meaning that a passenger does not notice the difference. It is worth noting that the min operator could be replaced by a max operator whenever applicable; for instance, if the attribute is getting points (similar to credit points with airlines), then, naturally, one wants to maximize it.
In Eq. (5), the symbol “” is used to denote a strictly preferred relationship; that is, indicates that the passenger prefers option l over . In Eq. (5a) if no q exists to suit the equation, it means that passengers are indifferent to the differences between the two options l and (“~”). Mathematically speaking
| (6) |
We integrate Eqs. (5), (6), and use symbol “” to denote a weak preferred l over l’ by
| (7) |
That is, option l is better or equal to option l′, where means both are true or either is true, and means indifference. In addition, it is necessary to differentiate the symbols “” (i.e., ) and “” (i.e,.). The former denotes a preferred relationship and the latter compares between the attribute’s order indexes. As is mentioned above under Eq. (6) the smaller the order index is, the more important the attribute is.
Intuitively, the comparison between lines l and using Eq. (5) can be clarified as follows: after determination of the set of acceptable choices, expressed by Eq. (3), we compare the choices of the acceptable set and look into each attribute according to the passenger’s preference order. Suppose that two choices, the use of PT line l or , are compared. Then, according to the methodology developed:
-
a.
If the values of the k th attribute of the two options are not noticeable to the passenger, then the passenger is indifferent to the two choices, and we proceed to the comparison of the next attribute, expressed by Eq. (5b).
-
b.
If the difference between the two options, for the q th attribute, is noticeable, then the passenger considers the best one of the two as a better choice, as expressed by Eq. (5a).
The following example is used as an explanatory device of Eq. (5). Consider three attributes: travel time, fare, and waiting time. A passenger ranks travel time as the most important attribute, followed by fare and waiting time. For simplicity, it is assumed that both options A and B are acceptable to the passenger. The data and computation procedures for the comparison are given in Table 1 .
Table 1.
Comparison based on Eq. (5).
| (a) Compare A and B | ||||||
|---|---|---|---|---|---|---|
| Ordered attributes m | Option A | Option B | Noticeable difference | |||
| Travel time (very important) | 11.5 min | 10 min | 20% | 1.5 min | 2 min | No: 1.5 min < 2.0 min |
| Waiting time (important) | 5 min | 10 min | 20% | 5 min | 1 min | Yes: 5 min > 1 min |
| Fare (least important) | $ 5 | $ 4 | 10% | $ 1 | $ 0.4 | Yes: $1 > $0.4 |
| (b) Compare B and C | ||||||
|---|---|---|---|---|---|---|
| Ordered Attributesm | Option B | Option C | Noticeable difference | |||
| Travel time (very important) | 10 min | 9 min | 20% | 1 min | 1.8 min | No: 1 min < 1.8 min |
| Waiting time (important) | 10 min | 9 min | 20% | 1 min | 1.8 min | No: 1 min < 1.8 min |
| Fare (least important) | $ 4 | $ 5 | 10% | $ 1 | $ 0.4 | Yes: $ 1 > $ 0.4 |
| (c) Compare A and C | ||||||
|---|---|---|---|---|---|---|
| Ordered Attributesm | Option A | Option C | Noticeable difference | |||
| Travel time (very important) | 11.5 min | 9 min | 20% | 2.5 min | 1.8 min | Yes: 2.5 min > 1.8 min |
| Waiting time (important) | 5 min | 9 min | 20% | 4 min | 1 min | Yes: 4 min > 1 min |
| Fare (least important) | $ 5 | $ 5 | 10% | $ 0 | $1 | No: $ 0 < $1 |
From Table 1 (a) we conclude that option A is better than B, i.e., . The last column of this table shows that the passenger does not perceive the difference of 1.5 min between the travel times, or in other words, it is less than the JND threshold value. Then, the difference of the waiting time is noticed, thus making option A a better choice. We note that the difference of the fare is also noticed (better for B than for A), but the waiting time is more important than the fare. Therefore, the conclusion drawn is that option A is better than B.
However, the personalized attribute-based option selection process above may not satisfy the axiom of transitivity, which requires that if and , then . This can be proven by the following two continuations of Table 1 using a third option, C.
From Table 1 (b) and Table 1 (c), it is concluded that and , respectively. Thus, we show here that the process of using Weber’s law violates the axiom of transitivity.
The axiom of transitivity is crucial because of the need to ensure a robust and consistent methodology. Our framework is established on the assumption that the passenger is rational, has preferences over different PT attributes, and can arrange different PT attributes by order of importance. This rationalism calls for maintaining the axiom of transitivity, and for setting the personalized preferences within a feasible and rational framework. Realistically, the input of preferences is boundless, and some users may input anything they want (also for their own amusement). This may violate the axiom of transitivity and thus must be checked and adjusted.
To amend this axiom violation possibility, we propose a revised comparison equation: to use the minimum value of attributes across all options as the reference point and define a noticeable threshold as the product of that minimum value and the Weber’s JND parameter. We shall call this the adjusted JND. Mathematically, it is as follows:
| (8) |
Eq. (8a) states that if option l is better than option , then there exists a q th attribute such that its value of is larger (less desirable) than that of l, and the difference between this value and the minimum attribute’s value across all feasible (acceptable) PT lines/routes is noticeable (crosses the JND threshold). Eq. (8b) states that for the k th attribute among the first q-1 attributes being more important than the q th attribute, the difference between its value and the minimum attribute’s value across all feasible lines is not noticeable (does not cross the JND threshold) for both l and . Similar to Eq. (5), the min operator could also be replaced by a max operator. In addition, we can rigorously define the indifference between optional lines, and the weak preferred line conditions based on Eqs. (6), (7).
Theorem 1
The comparison method based on Eq. (8) satisfies the axiom of transitivity.
Proof
See Appendix A.
Based on the theorem, we can obtain the following corollaries.
Corollary 1
If path A is better than path B because of attribute q (with a noticeable difference), the qth attribute values of paths B and C are not equal, and path B is better than path C because of attribute , then attribute is more important than attribute q or equally as important as attribute q.
Proof
See Appendix A.
Corollary 1 implies that for a given passenger’s choice between pairwise alternatives, we can deduce the passenger’s preference.
Corollary 2
In continuation of corollary 1; given because of the qth attribute and because of the attribute.
-
(a)
If , then (if attribute q is more important, then A is better than B);
-
(b)
If , then (if attribute is more important, then B is better than A).
Proof
See Appendix A.
Corollary 2 can be viewed as the counterpart of corollary 1. It indicates that for a given passenger’s pairwise alternatives and a partial preference, we can deduce the passenger’s preferences with regards to all options. A partial preference means that we only need to know the importance of and attributes, rather than all of the PT attributes.
The example from Table 1 has undergone changes in Table 2 to elaborate the comparison using Eq. (8) and to demonstrate that the results are in compliance with the axiom of transitivity.
Table 2.
Comparison based on Eq. (8).
| (a) The minimum value and JND threshold for each attribute | ||||||
|---|---|---|---|---|---|---|
| Ordered attributes m | Option A | Option B | Option C | |||
| Travel time (very important) | 11.5 min | 10 min | 9 min | 9 min | 20% | 1.8 min |
| Waiting time (important) | 5 min | 10 min | 9 min | 5 min | 20% | 1.0 min |
| Fare (least important) | $ 5 | $ 4 | $ 5 | $ 4 | 10% | $ 0.4 |
| (b) Compare A and B* | |||||
|---|---|---|---|---|---|
| Ordered attributes m | Option A | Option B | Compare with | Noticeable difference | |
| Travel time (very important) | 11.5 min | 10 min | A: (11.5–9) = 2.5 min B: (10–9) =1.0 min |
A: 2.5 >1.8 min B: 1.0 < 1.8 min |
A: Yes B: No |
| Waiting time (important) | 5 min | 10 min | A: (5–5) = 0 min B: (10–5) = 5 min |
A: 0 < 1.0 min B: 5 >1.0 min |
A: No B: Yes |
| Fare (least important) | $ 5 | $ 4 | A: (5–4) = $ 1 B: (4–4) =$ 0 |
A: $1 > $ 0.4 B: $ 0 < $ 0.4 |
A: Yes B: No |
| (c) Compare B and C** | |||||
|---|---|---|---|---|---|
| Ordered attributes m | Option B | Option C | Compare with | Noticeable difference | |
| Travel time (very important) | 10 min | 9 min | B: (10–9) = 1.0 min C: (9–9) = 0 min |
B: 1.0 < 1.8 min C: 0 < 1.8 min |
B: No C: No |
| Waiting time (important) | 10 min | 9 min | B: (10–5) = 5 min C: (9–5) = 4 min |
B: 5 > 1.0 min C: 4 >1.0 min |
B: Yes C: Yes |
| Fare (least important) | $ 4 | $ 5 | B: (4–4) = $ 0 C: (5–4) =$ 1 |
B: $1 > $ 0.4 C: $ 0 < $ 0.4 |
B: Yes C: No |
| (d) Compare A and C*** | |||||
|---|---|---|---|---|---|
| Ordered attributes m | Option A | Option C | Compare with | Noticeable difference | |
| Travel time (very important) | 11.5 min | 9 min | A: (11.5–9) = 2.5 min C: (9–9) = 0 min |
A: 2.5 >1.8 min C: 0 < 1.8 min |
A: Yes C: No |
| Waiting time (important) | 5 min | 9 min | A: (5–5) = 0 min C: (9–5) = 4 min |
A: 0 < 1.0 min C: 4 >1.0 min |
A: No C: Yes |
| Fare (least important) | $ 5 | $ 5 | A: (5–4) = $ 1 C: (5–4) =$ 1 |
A: $1 > $ 0.4 C: $ 0 < $ 0.4 |
A: Yes C: No |
It is concluded from the table that because of noticed difference between travel times (and the least is noticed for B).
It is concluded from the table that because of noticed difference between waiting times (and the least is noted for C).
It is concluded from the table that because of noticed differences between travel times (and the least is noted for C).
The three comparisons above follow the constructed Eq. (8) to assure agreement with the axiom of transitivity. This implies that if and , then . It is also observed that because of the waiting time and because of the travel time. This confirms corollary 1 to show that travel time is a more important attribute than waiting time.
Corollary 1 and corollary 2 imply that the perceived importance of the attributes always complies with the axiom of transitivity. These corollaries pave the way for us to develop a generalized sorting algorithm considering the order of importance and the JND threshold. The algorithm is as follows (for simplicity, the superscript “od” is omitted).
Algorithm 1:
Lexicographical ordering method using JND threshold (JND sorting algorithm)
| Input: | Set of acceptable options , and attributes associated with each option |
| Output: | Set of sorted options: |
| Procedure: | |
| 0: | // Initialization |
| 1: | Fori = 1 to m // Compare from the most important to the least important attributes |
| 2: | // Generate the noticeable set of (line) options |
| 3: | // Sort in ascending order based on the value of the ith attribute |
| 4: | // Insert into set |
| 5: | // Update the remaining choice set to be sorted. |
| 6: | If : |
| 7: | break // Stop if all the options have been added to the ordered set |
Theorem 2
The JND sorting algorithm is correct.
Proof
See Appendix B.
Remarks on the above JND sorting algorithm: (i) in Line 3 of the above procedure, when two or more (line) options of set have an equal value of the i th attribute, we need to further compare from the (i + 1)th to the m th attributes of these options until the preference is detected; (ii) in Line 4, the insert of at the beginning of is done because of the options in being better than the options determined previously; (iii) the JND sorting algorithm applies when the set of options is given; this set represents the scenario after enumerating all paths following the sorting of paths to satisfy passenger’s preference; and (iv) the complexity of the algorithm involves also the complexity of the sorting algorithm of step 3; in our simulation case studies, we use the genetic sort algorithm in C++ standard library with the worst-case complexity known to be .
The preceding comparison and ordering method rely on knowing all options a priori (see Table 2 (a)). This may not be efficient for large network applications because of the required path enumeration and storage. Thus, it would be more promising to apply the dynamic programming technique to develop a shortest path or k-shortest lexicographical ordering path algorithm based on the proposed comparison method. However, two issues are observed in the development of the shortest path algorithm. First, some PT attributes are not link-additive, such as zone-based fare or points from airlines, which we leave for a future study. Second, the options at a node cannot be known a priori in the label setting/correcting step of the shortest path algorithm. This step compares the existing best option and a new option and chooses the better one. Nonetheless, thanks to the fact that the shortest path algorithm only requires keeping the best option, the axiom of transitivity holds and can be utilized. This is formally stated as the following corollary:
Corollary 3
In continuation of corollaries 1 and 2; if with respect to options and with respect to options , then .
Proof
See Appendix A.
Corollary 3 states that the axiom of transitivity holds when augmenting the set of options, meaning that determining the best option does not require knowing all the options in advance. Thus, the set of options can be gradually updated. Corollary 3 allows for developing a multicriteria shortest path as follows.
Algorithm 2:
Shortest path for lexicographical ordering method with JND threshold
| Input: | Set of attributes , Set of nodes , Set of arcs |
| Attributes associated with each edge: . Source node: s | |
| Output: | Shortest path from s to all nodes |
| Procedure: | |
| 0: | , // Initialize label at source node // Initialize labels at other nodes |
| 1: | // Initialize the queue of nodes to be scanned |
| 3. | While |
| 2: | Select in // Popup a node from the queue |
| 3: | For each neighbor node , such that // Select a neighbor node |
| 4: | For q = 1 to m |
| 5: | If |
| 6: | //Update the minimum label |
| 7: | |
| 8: | End if |
| 9: | End for |
| 10: | If |
| 11: | // Update the best option label |
| 12: | // Add node to the queue |
| 13: | End if |
| 14: | End for |
| 15: | // Remove scanned node |
| 16: | End while |
Remarks on the algorithm above for the shortest path of ordering preferences: (1) The label associated with every node and arc is a vector of attributes. Accordingly, the “+” in Lines 10 and 11 represents vector addition. (2) We create another label for each node in comparison with the ordinary shortest path algorithm. This label is required to store the minimum value of each attribute and add another loop, Lines 4–9, to update the minimum attribute label. (3) We compare the preference relationship “” under Line 5.
We note that Algorithm 2 does not address the personal max/min acceptable value feature. For incorporating it, one needs to solve a constrained shortest path problem, known to be NP-complete (i.e., Handler and Zang, 1980, Lorenz and Raz, 2001; Dumitrescu and Boland, 2001). In our study, we adopt the k-shortest path approach to eliminate unacceptable choice, in which the k-shortest lexicographical ordered paths with JND threshold based on Yen’s k-shortest path algorithm (Yen, 1971) are generated first, and the routes that violate the boundary constraints are eliminated after generating the k-shortest lexicographical ordered paths.
3. Illustrative example
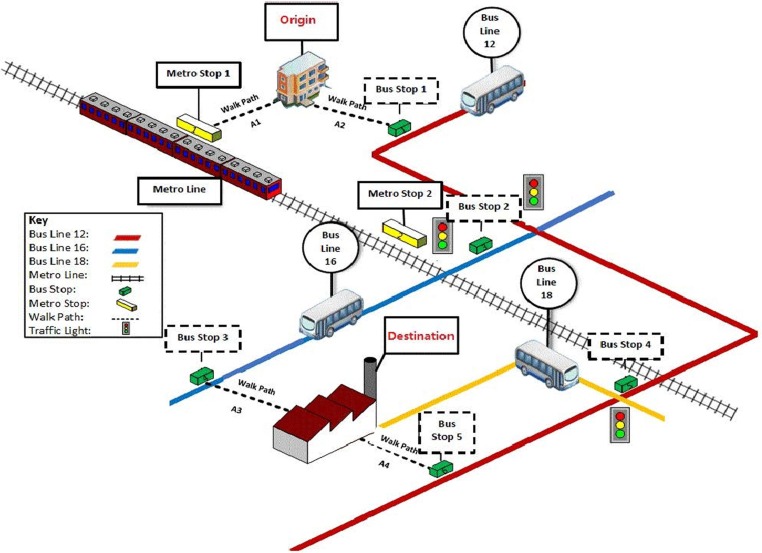
A schematic map of the illustrative example appears in Fig. 3 . It contains a small PT network comprised of walking, use of bus and metro lines, and making transfers. There are assumed to be two passengers, A and B, departing from the origin to the destination shown in Fig. 3. The two passengers naturally have different preferences.
Fig. 3.
Schematic map of an illustrative example.
3.1. Data and assumptions
The notations, data, and assumptions of the example are shown in Table 3 . Three groups of PT attributes are considered: time-related, fare-related, and comfort-related. The group of time-related attributes may include travel time, waiting time, walking time, transfer time, elevator time (if any), etc. The group of fare-related attributes may include fare of the trip, fare of a special app (if any), special service fare (if any), etc. The group of comfort-related attributes (for example, on a scale of 0–5, where 0 = no comfort at all, and 5 = excellent comfort) may include waiting comfort, riding comfort, transfer comfort, etc. It is worth noting that the PT attributes can be treated by individual attributes, and not by groups, as is demonstrated in the examples of Table 1, Table 2. With the use of the three groups of PT attributes, we illustrate, in the following problem example, the differences among the three path recommendation methods.
Table 3.
Input for the schematic map example of Fig. 3.
| (a) Notations used for the example | ||
|---|---|---|
| WPi = Walk path i | BLi = Bus line i | BSi = Bus stop i |
| MSi = Metro stop i | M = Metro | (…) = Element in the parenthesis is a PT transfer point |
|
(b) Routing data | ||||
|---|---|---|---|---|
| Option | Routing | Total fare ($)* | Travel time (min)** | Comfort level*** |
| 1 | WPA1 - MS1 - M - (MS2/BS2) - BL16 – BS3 - WPA3 | 12 | 70 | 3 |
| 2 | WPA2 - BS1 - BL12 – BS5 -WPA4 | 8 | 96 | 4 |
| 3 | WPA2 - BS1 - BL12 - (BS4) - BL18 | 10 | 75 | 4 |
| 4 | WPA2 - BS1 -BL12 - (BS2) - BL16 – BS3- WPA3 | 15 | 105 | 2 |
|
(c) Passenger’s preferences and weights (all weights sum up to 1.0) | ||||
|---|---|---|---|---|
| Preference |
Passenger A |
Passenger B |
||
| Attribute | Weight | Attribute | Weight | |
| Most important | Fare related | 0.60 | Time related | 0.60 |
| Moderately important | Time related | 0.30 | Comfort related | 0.30 |
| Least important | Comfort related | 0.10 | Fare related | 0.10 |
|
(d) Passenger’s preference and input of JND threshold (by percentage) and max/min acceptable values | ||||
|---|---|---|---|---|
| Preference |
Passenger A |
|||
| Attribute | Acceptable value | |||
| Most important | Fare related | 10% | $0.8 | $15 |
| Moderately important | Time related | 30% | 21.0 min | 120 min |
| Least important | Comfort related | 40% | 0.8 | 1 |
|
Preference |
Passenger B |
|||
|
Attribute |
|
|
Acceptable value |
|
| Most important | Time related | 10% | 7.0 min | 100 min |
| Moderately important | Comfort related | 20% | 0.4 | 3 |
| Least important | Fare related | 30% | $2.4 | $20 |
of all fare related attributes;
of all time-related attributes;
of all comfort-related attributes.
3.2. Clarifications and results
To ensure clarity, the following are a few comments on the example:
-
(1)
For the small network, all paths are enumerated and compared with subsequent outcomes.
-
(2)
BS2 is linked with MS2, BL12 and BL16.
-
(3)
Passenger A could represent a student, thus placing a high weight on the fare related attributes, expressed in the example as total fare. In addition, because of being sensitive to pocket dollars, the JND threshold of the total fare for Passenger A is low (it is an input based perceived value).
-
(4)
Passenger B could represent a passenger in a hurry, thus placing a high weight on time-related attributes, expressed in the example by travel time. Also, because of being pressed for time the JND travel time threshold for Passenger B is low (it is an input based perceived value).
-
(5)
Travel time (in minutes) contains all of the time-related attributes: walking, waiting and riding times.
-
(6)
Total fare (in dollars) contains the riding fare and any other fare required for using the PT service.
-
(7)
The hypothetical path comfort levels are set for illustration purposes. They are ranged from 0 (least comfort) and 5 (maximum comfort) and refers to the overall comfort of walking, waiting, riding and making transfers with each option. The JND threshold of comfort, expressed by percentage, refers to the 0–5 scale. Accordingly, 20% means that the passenger does not perceive the difference between two adjacent comfort levels, but a difference of two comfort levels is noticeable. For example, the comfort level for walking flat on asphalt is 4, for a low uphill gradient is 3, and for a semi-moderated uphill gradient is 2.
-
(8)
To obtain the k-weighted shortest path, other than setting the weighting parameters, it also requires inputting the parameters that convert the attributes’ value to monetary value so that the values are additive. In the example, it is set that the value of time is $0.2 per minute and the value of comfort is $(-1) per one unit of the comfort scale. The value of comfort is a negative value since it is set that the higher the comfort level, the lower the travel cost. In practice, both parameters can be based on either a survey or a fixed input monetary value from the passenger.
Subsequent to these clarifications, we present the results of the example in Table 4 .
Table 4.
Results of recommended paths per method used.
| Path recommendation method | For passenger A | For passenger B |
|---|---|---|
| Shortest path method* | Option 3 | Option 3 |
| Shortest path based on the most important attribute | Option 2 | Option 1 |
| k-weighted shortest path method | Option 3 2 1 4 | Option 1 3 2 4 |
| Lexicographical order with JND | Option 2 3 1 4 | Option 3 1 2 |
The shortest path of total travel cost.
Let us elaborate on the results of Table 4. The use of the shortest path method is straightforward because it is based only on the minimum travel cost across all paths. Thus, for both Passengers A and B it will be Option 3, because of the travel cost of Option 1 (see Table 3 (b)) is 12 + 0.2*70 + 3*(−1) = $23, and of Options 2, 3, and 4 are $23.2, $21 and $34, respectively. If the shortest path determination is based on the most important attribute, Options 2 and 1 are recommended for passengers A and B, respectively. Essentially, this case is equivalent to the lexicographical order method without the consideration of JND, or to the weighted shortest path method with a weight set up to 1 for the most important attribute.
For the k-weighted shortest path method we consider the weights of Table 3 (c), the value of travel time and comfort to be $0.2 and $(−1) as per comment (vii) above, and the attributes’ values in Table 3 (b). For example, for path Option 1 for Passenger B the weighted travel cost is 0.1*12 + 0.6*0.2*70 + 0.3*(−1) *3 = $8.7, and for Options 2, 3, 4 the costs are $11.12, $8.8, and $13.5, respectively. Thus, for Passenger B Option 1 3 2 4.
For the method using lexicographical order with JND, we use the information of Table 3 (d) and of the attributes’ values from Table 3 (b). For passenger B the travel time of path Option 4 is more than the passenger’s max acceptable value (105 min > 100 min) and thus this option is eliminated. Then, we first consider the most important time-related attribute and look at its minimum value plus the adjusted JND threshold. That is, (70 + 7)1 mins to find out that path Options 1 and 3 are perceived as the same (75 < 77 min, thus the difference is not noticeable) and better than Option 2. Secondly, because Options 1 and 3 are perceived as the same, we look at the moderately important comfort-related attribute to find that Option 3 is better than Option 1, where the difference of comfort units is greater than the adjusted JND threshold (1 > 0.4). Thus, Option 3 1 2. We find a similar situation to be the case for Passenger A.
3.3. Interpretation
A few characteristics of the illustrated example are noteworthy, including explanations of the results shown in Table 4, as follows: (1) The shortest path method finds only one path based on the total travel cost, while the k-weighted shortest path and the JND methods recommend a set of paths; (2) The k-weighted shortest path and the JND methods recommend different path sets for Passengers A and B. This demonstrates that our method could provide personalized path information for different passengers; (3) For passenger B (a passenger in a hurry), the k-weighted shortest path ranks path Option 1 as the best, and the JND method ranks path Option 3 as the best; however, for the most important time-related attribute both options are perceived identically because of being inside the range of the JND threshold. The JND method, in this case, shows its advantage by allowing the next important comfort related attribute to determine the preference of Passenger B; (4) For Passenger A (a student) using the k-weighted shortest path method, we find that the difference between path Options 2 and 3 is small ($10.16 for Option 2 and $10.10 for Option 3); however, for the JND method path Option 2 is clearly the preferred one from the perspective of the most important preference (fare related). This observation demonstrates some of the differences between the two methods.
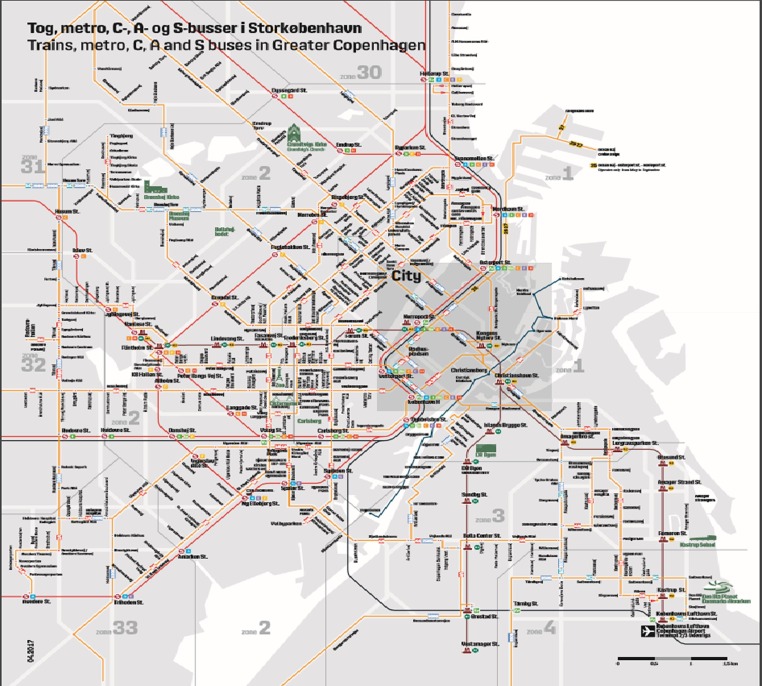
4. Case study
4.1. Comparison between different route guidance methods
The methodology developed was tested on the Copenhagen network shown in Fig. 4 (a). The Greater Copenhagen Area is divided into 99 zones. The network studied contains Copenhagen’s zones 1, 2, 3, and half of 4, covering most of central Copenhagen, involving 278 PT lines and 397 stops. The experiments were conducted based on the following: A1) Three attributes – travel time (TT), waiting time (WT), and the number of transfers (TR). WT for each line is approximated by the inverse of its frequency (Ceder, 2016). To incorporate the TR in computing the weighted travel time, one transfer is set to be equivalent to 5 min, based on the finding in Guo and Wilson (2011), which states that one transfer is comparable to around 4.9 min in in-vehicle travel time. Meanwhile, the transit network is coded using the route section network representation. The route section network representation was developed by de Cea and Fernández (1993) for solving the transit assignment problem (Szeto et al., 2011, Szeto et al., 2013, Szeto and Jiang, 2014b, Jiang and Szeto, 2016). In this network, a link is created to connect a pair of nodes where there is direct service between the two nodes. As a result, the number of transfers is link additive and equal to the number of traversed links minus 1. A2) A total of 1000 passengers was simulated based on Copenhagen’s OD data. A3) For each passenger, the JND values of TT and WT were randomly generated between 0.2 and 0.4. The JND value of TR is set to be 1, meaning that as long as the number of transfers is changed, the difference would be noticed. The upper and lower bounds of the JND were set based on the finding in Chowdhury et al. (2015), which states that the JND of travel time is at least 25%, or 33%, depending on the type of interchange. A4) To generate weights for the three attributes, we start with generating passenger preferences. For the three attributes considered, there are six possible preference orders: TT ≻ WT ≻ TR, TT ≻ TR ≻ WT, WT ≻ TT ≻ TR, WT ≻ TR ≻ TT, TR ≻ WT ≻ TT, and TR ≻ TT ≻ WT. One preference order from the six possibilities is randomly selected. Then, we generate the weight associated with the most important attribute between 0.5 and 0.7, the second most important attribute between 0.2 and 0.4, and the least important attribute between 0.001 and 0.1. Afterwards, the weights are normalized to ensure that their sum equals 1. As a result, a clear preference among the three attributes that can be distinguished by weights is shown for all simulated passengers. Meanwhile, in the default setting, it is assumed that the probability of selecting TT and WT as the most important attribute is higher than that of selecting TR. This represents travelers for whom travel time and/or waiting time is more important than transfer time. The effect of passenger preference distribution is demonstrated in the case study. A5) The simulated 1000 passengers are the source of the demand considered, and the JND and weights represent passengers’ actual preferences. A6) For analyzing and comparing results from the three different methods, we assume that a passenger selects only the first recommended path. Then we compare the three PT attributes of the first path recommended by each of the three methods to evaluate whether or not this passenger can benefit by each of the recommended paths and to what extent.
Fig. 4.
Copenhagen network.
Based on the above setting, we found the shortest travel time path, k-weighted shortest path (we set k = 1 according to A6)), and the lexicographical shortest path with the JND threshold. The program was coded in C++ and run on a personal laptop with Intel(R) Xeon (R) CPU E5-2697 v2 @2.30 GHz.
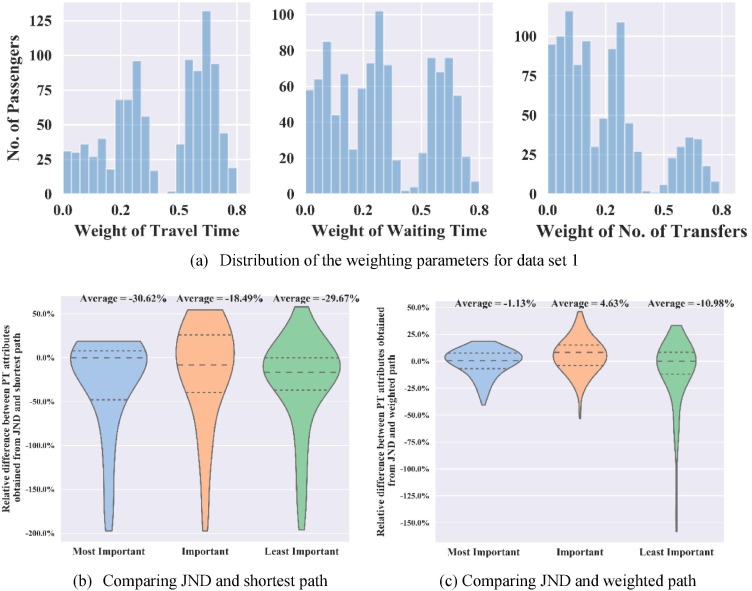
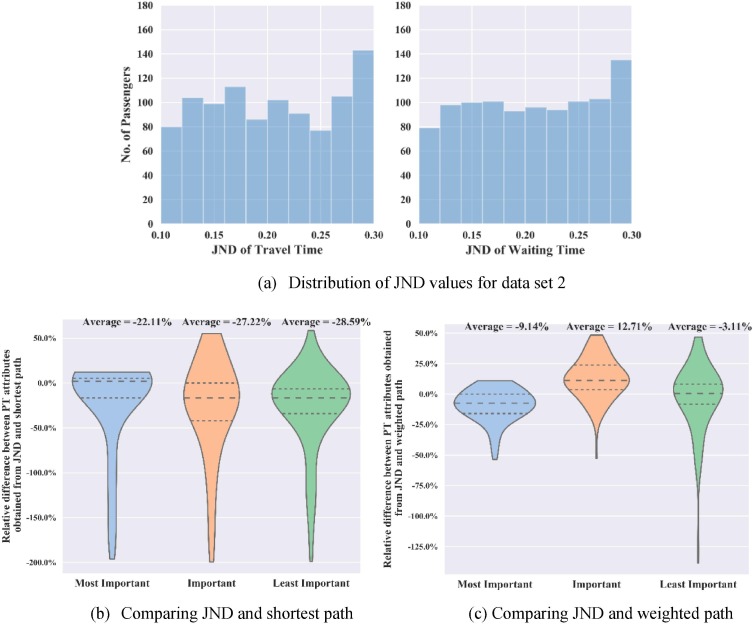
To examine the preference for the proposed methodology, three simulated data sets, depicted in Table 5 , are generated. The sets are created such that the comparison between the results obtained from the default set and set 1 will demonstrate the effect of passenger preference, while the comparison between the default set and set 2 will illustrate the effect of the JND values.
Table 5.
Three simulated data sets.
| Generated weighting parameters | Generated JND values | |
|---|---|---|
| Default | See A4) | See A3) |
| Set 1 | All six possible preference orders have the same probability to be selected | See A3) |
| Set 2 | See A4) | The JND values are generated between 0.1 and 0.3 |
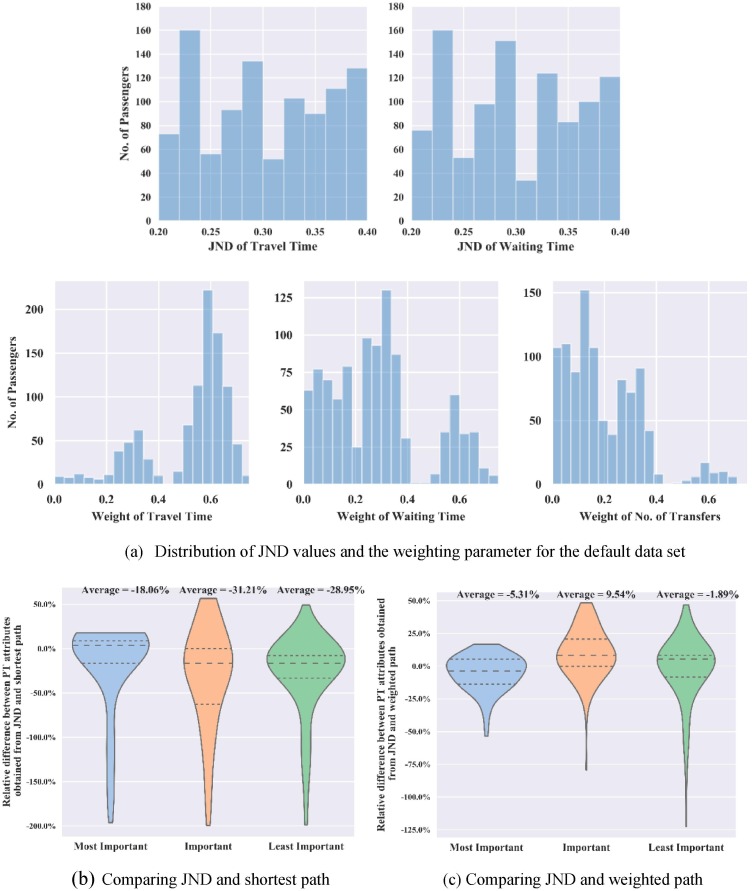
The results obtained from the three data sets are plotted in Fig. 5, Fig. 6, Fig. 7 , respectively. Each figure contains three subplots, namely, (a), (b), and (c). Plot (a) is the descriptive distribution of the JND and/or weighting parameters. Plots (b) and (c) illustrate how the changes of the three attributes vary when comparing the JND method, the two methods of the shortest path, and the k-weighted path.
Fig. 5.
Results of comparing different route guidance methods using default data set.
Fig. 6.
Results of comparing different route guidance methods using data set 1.
Fig. 7.
Results of comparing different route guidance methods using data set 2.
In Fig. 5 (a), both distributions of weighting parameters and JND are presented. In Fig. 6 (a), only the distribution of weighting parameters is presented because the JND values are the same as those in the default data set shown in Fig. 5 (a). In Fig. 7 (a), only the distribution of the JND values are presented for TT and WT because the JND value of TR is set as 1.
Plot (b) in the three figures compares the JND and the shortest path method. A positive percentage means that the value of the JND method attribute is greater than that obtained by the shortest path method. It is shown that all average relative difference2 values are negative in Fig. 5, Fig. 6, Fig. 7. Thus, it is concluded that the JND method is better than the shortest path method in reducing the average values of all three attributes across all three simulated data sets.
The comparison of the JND and the k-weighted shortest path method is represented in plot (c) of Fig. 5, Fig. 6, Fig. 7. Generally speaking, the results of all three data sets show that the JND method is better than the other methods in reducing the value/cost of the most important PT attribute and of the least important attribute, with a tradeoff of increasing the value/cost of the second most important attribute. It is impossible for the JND method to find a different path from the path of the weighted path method, and which has reduced value/cost for all attributes. If such a path exists, it should be identified by the weighted path method.
Nonetheless, we need to recall that the incentive for developing the proposed JND method is that when travelers' preferences are placed above various PT attributes, the proposed method recommends a path according to ordered preferences. From this perspective, the results demonstrate that the value/cost of the most important attribute value, on average, will always be reduced.
In comparing Fig. 5 (c) with Fig. 6 (c), a reduction or improvement in the average relative change is observed. For instance, in Fig. 5 (c), the reduction in the most important attribute is −5.31% compared with −1.13% in Fig. 6 (c). In comparing Fig. 5 (c) with Fig. 7 (c), it is found that the reduction or improvement in the average relative changes increases, meaning that the more sensitive the passengers are to the attributes’ change, the larger the discrepancy is between the two methods. In general, the results demonstrate that both the JND values and distribution of passenger preferences affect the performance of the proposed JND method.
Other than the difference between the methodologies, the reasoning behind the distributions shown in the figure can be explicitly ascribed to the data, such that (i) existing randomness generates the parameters of the weights and of the JND threshold values, and (ii) those different variations of the attributes appear across different PT services; for example, between an express bus service with TT = 10 min and WT = 60 min and a regular bus service with TT = 20 min and WT = 30 min. Such differences also warrant activating route guidance tools to provide special attention to the preferred PT attribute. From a PT operation perspective, these large differences of TT and WT can provide input into the design of different paths. These considerations, with evolving personalization, may have an impact on PT network design models for both ordinary and automated PT services – and whether or not multiple PT routes are designed, with each route catering to a passenger class defined by particular preferences.
Another noteworthy point is that the simulation study could incorporate the user selection process, however, this requires establishing a transit assignment model consistent with the proposed route guidance methodology, considering both users’ personalized requests and JND values. This warrants further study.
4.2. Effects of using default values
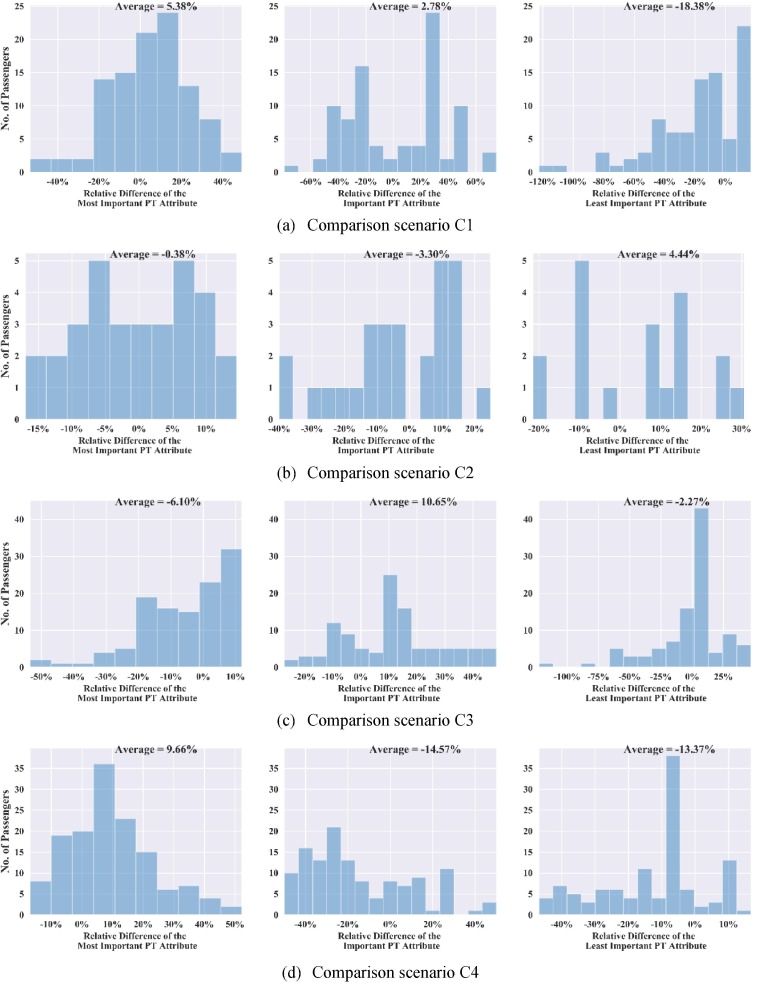
A fundamental assumption of the methodology is that users’ preferences and JND values are known. Nonetheless, there may be situations in which this information is inaccessible, whether that reflects lack of user time to provide the information, lack of awareness of the information, or objection to providing it. In such cases, default values will be used. To illustrate the performance using default values, four comparison scenarios are devised and listed in Table 6 . In the experiment, the default JND and weight values shown in Fig. 5 (a) are considered as users’ actual preference data. The results of the four comparison scenarios are presented in Fig. 8 .
Table 6.
Comparison scenarios.
| Comparison scenario | Description |
|---|---|
| C1 | Use the weighted path method. Compare the results of the case where the weighting parameters are known with the case using default weighting parameters. The default weights for the three attributes are set as: most important = 0.6, important = 0.3, least important = 0.1 |
| C2 | Use the proposed JND method. Compare the results of the case where the JND are known with the case using default JND values. The default JND for the three attributes are all set as 0.3. |
| C3 | Cross comparison. Compare the results from the JND method using default JND values, with the results from the weighted path using known weights. |
| C4 | Cross comparison. Compare the results from the weighted path method using default weights with the results from the JND method using known JND values |
Fig. 8.
Results of comparisons listed in Table 6.
In comparison scenario C1, it is assumed that the actual passenger preferred path is determined based on the weighted path method, but we do not know the weights; thus, this comparison shows the gap between using real and default weight values. A positive percentage means that the value of the attribute using default value is greater (inferior) than the real weight. Fig. 8 (a) shows that both the most important and important attributes become worse, and the opposite is only the case for the least important attribute.
In C2, it is assumed that passengers’ actual preferred path is determined by the JND method, but we do not know the JND values. Thus, this comparison illustrates the gap between using real and default JND values. Fig. 8 (b) shows that only the average value of the least important attribute increases. Comparison scenario C3 is devised to represent the scenario whereby passengers select a preferred path based on the weighted path method, but the app recommends routes using the JND method with default JND values. The results in Fig. 8 (c) show that both the values of the most important and least important attributes are reduced, with a tradeoff of increased value for the important attribute. Lastly, C4 represents the scenario of passengers selecting the preferred path based on the JND method, while the app recommends routes using the weighted path method with a default weight. Fig. 8 (d) shows that the value of the most important attribute increases by almost 10%, while the values of the important and least important attributes are reduced significantly.
The comparison studies fail to provide strong evidence for drawing a universal conclusion regarding the selection of the best path recommendation method because their results also depend on the setting of the default parameters and simulated data. Nevertheless, the results support one purpose of this study for recommending paths with respect to passenger prioritized preferences. From this perspective, it is safe to conclude that the JND method is better than the weighted path method, because when using the JND method with default values, the average value of passengers’ most important attributes is reduced, given that the increment in another one or two attributes is inevitable, due to the tradeoff among them. Below, we provide a numerical example to illustrate one scenario in which the default JND method is better than the weighted method. Notably, due to randomness in the simulated data, the scenario described in the following hypothetical example may not always occur, yet it illustrates why the default JND method is preferred.
Consider two paths connecting one passenger’s OD with the passenger’s true weights for TT = 0.7, WT = 0.2, TR = 0.1, and that TT is the most important attribute with WT as a secondary important attribute.
Path 1: TT = 10, WT = 14, TR = 0, and
Path 2: TT = 13.5, WT = 6, TR = 0
Consequently, Path 1 is the preferred path, because of 10*0.7 + 14*0.2 = 9.8 < 13.5*0.7 + 6*0.2 = 10.65. However, without knowing the passenger’s weightings and by setting up default values for TT = 0.6, WT = 0.3, and TR = 0.1 with a default value of JND = 0.3, we obtain a result preferring Path 2 because 10*0.6 + 14*0.3 = 10.2 > 13.5*0.6 + 6*0.3 = 9.9. Then, if using the default JND value, Path 1 is again preferred because of the difference between the values of the very important attribute, TT for the two paths which is greater than the default JND threshold value: (13.5–10)/10 > 0.3. Therefore, the difference in the most important attribute for the two paths is noticeable, and Path 1, with its lower TT value is recommended.
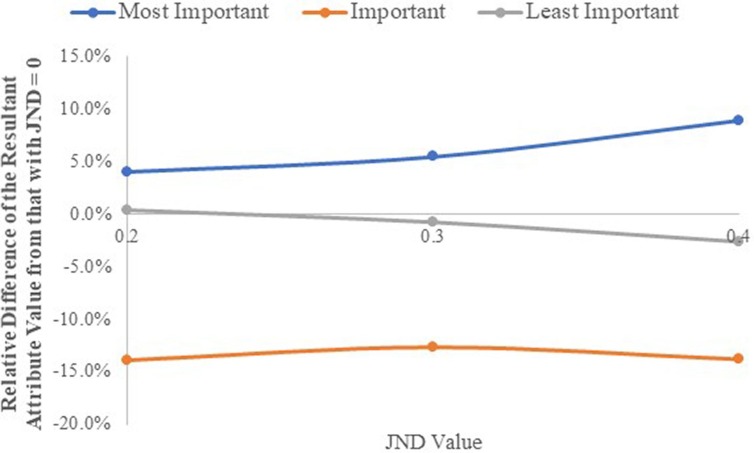
4.3. Effects of different JND values
The last part of the case study assesses the outcome of using different JND threshold values. To accomplish this, we first obtain the baseline results by setting all JND values to zero, where the proposed method is reduced to the traditional lexicographic ordering method without considering JND value. Secondly, we vary its values between 0.2 to 0.4. Fig. 9 illustrates the relative difference of the two attributes w.r.t. the baseline results of JND = 0. Fig. 9 demonstrates that the larger the JND values (passengers are less sensitive to possible changes and feel the same within this threshold range), the higher the values of the most important attribute, compensated by important and least important attributes. The reason for this result is that by using a larger JND value, the route that yields a slightly higher value for the most important attribute, but with a lower value for the important attribute, will be recommended. The following example further demonstrates this.
Fig. 9.
Effect of different JND values.
Consider three paths connecting one passenger’s OD pair with TT as the most important attribute, as follows.
Path 1: TT = 10, WT = 15, TR = 1
Path 2: TT = 11, WT = 13, TR = 1 and
Path 3: TT = 13, WT = 10, TR = 1
For JND = 0, Path 1 is preferred by having the lowest TT. For JND = 0.2, Paths 1 and 2 are indifferent to TT, because of the JND’s value, but Path 2 has a lower WT, thus Path 2 is preferred. For JND = 0.3, all three paths are indifferent to TT, but Path 3 is preferred having the lowest WT. However, the relative differences using JND = 0.2 (compared with to JND = 0) are computed by (11–10)/10 = 10% for TT, and by (13–15)/15 = −13% for WT. For JND = 0.3, the relative differences (compared with to JND = 0) are (13–10)/10 = 30% for TT, and (10–15)/15 = –33% for WT. This example shows that by increasing JND values, relative differences for the most important attribute could increase with a decrease in the important attribute. This is only an example of one passenger. Fig. 9 is obtained using the average values from all passengers, where it is also possible that some passengers will choose WT or TR as the most important attribute to them.
4.4. Effects of no. of attributes on the computation time
Finally, the computation times under the different numbers of attributes are reported in Table 7 . The computation time is the average time of the 1000 simulated passengers. In general, the computation time increases with the number of attributes considered. For the weighted path method, the increment in the computation time is linear with respect to the number of attributes. For the proposed JND method, the computation time is longer than for the weighted path method due to the added complexity in comparing multiple attributes and finding the minimum value of each attribute among all options (see Algorithm 2).
Table 7.
Computation time under different numbers of PT attributes.
| Computation time (seconds) |
||
|---|---|---|
| No. of attributes | Weighted path method | Proposed JND method |
| 1 | 0.129 | 0.205 |
| 2 | 0.150 | 0.254 |
| 3 | 0.175 | 0.315 |
5. Conclusion
In the conclusion of this work, it would be remiss not to mention the unforeseeable implications of the Covid-19 pandemic for future mobility. Presumably, more controllable automation of public transport (PT) vehicles will evolve, with a greater prospects for changing human habits and thinking paradigms. In view of the imminent era of personalized PT mobility, this work provides the setting for an adjusted design framework to create the modeling required for a personalized PT service. The framework integrates PT operators’ planning and operation components, with users’ experiences gathered using smartphone technologies. This work focuses on the key element of the adjusted design framework: the personalized route guidance methodology. Explication of three different route guidance methods is offered and they are compared - the classical shortest path method, a k-weighted shortest path method, and a novel lexicographical ordering shortest path method with a just noticeable difference (JND) consideration. The JND based method is based on Ernst Weber’s Law of the Human Perception Threshold. This work discovers that a straightforward application of Weber’s Law does not satisfy the axiom of transitivity required for an implementable algorithm, and thus a revised method was developed and proved for its correctness. A small network example illustrates the differences between the three methods. In addition, a large simulation study of the PT network of Copenhagen is conducted.
This work shows that the consideration of the human threshold based on human perception elements will encourage decision makers to establish new criteria that will comply with this perception-based component. In post Covid-19 pandemic times, important attributes for a traveler may also include minimization of the risk of becoming infected or any other risks. This is a significant channel by which decision makers may alter their policies, adjusting them in accordance with the development of new advanced technologies coming to ease and optimize future urban mobility. Moreover, this work opens a new arena for public transport researchers and planners with the use of smartphone apps for acquiring real time and readily available journey planning information. Future research includes, but will not be limited to:
-
(i)
conducting empirical studies to examine the impact of the recommendations on passenger route choice. The method proposed in this study is based on the hypothesis that the order of the recommended paths affects passenger route choice behavior. A similar hypothesis has been verified in the context of online shopping recommendations (Kumar and Benbasat, 2006).
-
(ii)
conducting empirical studies for calibrating the parameters used in this work, especially human perception parameters.
-
(iii)
continuing theoretical research using the rational choice theory for adjusting unintentional passenger input.
-
(iv)
connecting the pathfinding method to PT network design models for both ordinary and automated PT services and extending existing transit/traffic assignment models (Hamdouch et al., 2014, Jiang et al., 2016, Jiang and Szeto, 2016, Szeto et al., 2011, Szeto and Jiang, 2014a, Tang et al., 2020) to capture the effects of personalization and human perception.
-
(v)
developing an online algorithm and capturing the uncertainty and reliability of different PT attributes following, for example, Chen et al., 2016, Khani, 2019, Xing and Zhou, 2011, Xu et al., 2012, Yang and Zhou, 2017, and Zhang and Khani (2019).
-
(vi)
extending and applying the proposed methodology to solve other multicriteria pathfinding problems in a traffic network , multimodal transport network or emergency network Hadas and Ceder (1996).
CRediT authorship contribution statement
Avishai (Avi) Ceder: Conceptualization, Methodology, Validation, Formal analysis, Writing - original draft, Writing - review & editing. Yu Jiang: Methodology, Software, Validation, Writing - original draft, Writing - review & editing, Formal analysis, Visualization.
Acknowledgments
This work is partly funded by the Innovation Fund Denmark (IFD) under File No. 4109-00005. This research has been supported by the National Natural Science Foundation of China (NSFC) (Project No. 71701030 and 71971038)
Footnotes
When computing the relative changes in the number of transfers, the difference in the number of transfers is converted to minutes by multiplying 5 min per transfer (see A1). Then the results are normalized by dividing by 60 min.
Contributor Information
Avishai (Avi) Ceder, Email: ceder@technion.ac.il.
Yu Jiang, Email: yujiang@dtu.dk.
Appendix A.
A.1. Proof of Theorem 1
For clarity, we use A, B, C to denote three options and we omit the superscript od. Therefore, proving Theorem 1 is equivalent to proving that if and , then . Because of space limitations, we only present the proof of transitivity with respect to the strict preference relationship, i.e., if and , then .
First, given and , we have
| (A.1) |
| (A.2) |
We consider the following scenarios:
a)
It is easy to deduce from (A.1a) and (A.2a) that and , thus .
b)
Eqs. (A.1a) and (A.2a) imply that
| (A.3) |
Meanshile, when , Eq. (A.2b) can be written as
| (A.4) |
Eq. (A.4) indicates two cases that we need to consider:
Case 1) Eq. (A.4a) holds, i.e., , ; by combing it with Eq. (A.1b) we can easily obtain .
Case 2) Eq. (A.4b) holds, i.e., ; that is, , indicating that should be equal to when , i.e., . This implies that there exists a value such that and . This contradicts the prerequisite of the considered scenario b, i.e., . Therefore, we say that case 2) is invalided under the considered scenario b.
By combing Eq. (A.3) with the results from Case 1), we conclude that .
c)
In such a case, Eq. (A.1b) implies
| (A.5) |
Eq. (A.5a) implies that or . By combing this with Eq. (A.2a), we can derive that
| (A.6) |
Meanwhile, by eliminating from (A.5), we have
| (A.7) |
Similar to the analysis of scenario b, we consider two cases:
Case 1) ; combing this with the first equation of Eq. (A.2b) and the prerequisite of this scenario, i.e., , we have
| (A.8) |
Case 2) and , . This indicates that there exists a value , such that and , meaning that C could dominate B. This contradicts Eq. (A.2), requiring that B should dominate C. Therefore, we conclude that Case 2) is an invalid/impossible case.
By combing Eq. (A.6) and the analysis of Case 1), and Eq. (A.8), we conclude that .
d)
In such a case, Eq. (A.2b) indicates,
| (A.9) |
Similarly, two cases are considered,
-
1)
If . This contradicts equation (A.1a)
-
2)
If .
Meanwhile, Eqs. (A.4), (A.5) also hold, and thus, we can conclude . Combining scenarios a) - d), we conlucde that if and , then . □
A.2. Proof of corollary 1
This corollary is a direct conclusion from scenarios a) - d) in the proof of Theorem 1. □
A.3. Proof of corollary 2
Given and , Eq. (A.2) and the following Eq. (A.10) hold.
| (A.10) |
When , Eq. (A.2b) indicates
| (A.11) |
Meanwhile, Eq. (A.10a) states that . Thus .
According to Eqs. (A.10b) and (A.11), we have
| (A.12) |
Therefore, we can prove corollary 2 (a), i.e., . Similarly, we can prove corollary 2 (b). □
A.4. Proof of corollary 3
Proof: Due to space limitations, the proof is not presented here. In short, we follow the procedure for the proof of Theorem 1 and consider two cases: and .
Appendix B.
This appendix proves Theorem 2.
-
1)
If : the algorithm reduces to a simple sorting algorithm, which is addressed by line 2.
-
2)
When , we compare the sorted set generated at and
When , we obtain .
When , we obtain .
Given Theorem 1, the axiom of transitivity, we only need to prove that . In other words, the worst option generated at is better than the best option at . According to line 2 of the algorithm, we know
| (B.1) |
| (B.2) |
Thus, it is concluded that
| (B.3) |
This completes the proof. □
References
- Ambrosino D., Sciomachen A. An algorithmic framework for computing shortest routes in urban multimodal networks with different criteria. Procedia-Social Behav. Sci. 2014;108:139–152. [Google Scholar]
- Androutsopoulos K.N., Zografos K.G. Solving the multi-criteria time-dependent routing and scheduling problem in a multimodal fixed scheduled network. Eur. J. Oper. Res. 2009;192(1):18–28. [Google Scholar]
- Arentze T.A. Adaptive personalized travel information systems: A Bayesian method to learn users' personal preferences in multimodal transport networks. IEEE Trans. Intell. Transp. Syst. 2013;14(4):1957–1966. [Google Scholar]
- Baird J.C., Noma E.J. John Wiley & Sons; 1978. Fundamentals of Scaling and Psychophysics. [Google Scholar]
- Bian Z., Liu X. Mechanism design for first-mile ridesharing based on personalized requirements part I: Theoretical analysis in generalized scenarios. Transp. Res. Part B: Methodol. 2019;120:147–171. [Google Scholar]
- Bouhana A., Fekih A., Abed M., Chabchoub H. An integrated case-based reasoning approach for personalized itinerary search in multimodal transportation systems. Transp. Res. Part C. 2013;31:30–50. [Google Scholar]
- Calabrese F., Pereira F.C., Di Lorenzo G., Liang L., Ratti C. The geography of taste: Analyzing cell-phone mobility and social events. Pervasive Comput. 2010;6030:22–37. [Google Scholar]
- Campigotto P., Rudloff C., Leodolter M., Bauer D. Personalized and situation-aware multimodal route recommendations: the FAVOUR algorithm. IEEE Trans. Intell. Transp. Syst. 2016;18(1):92–102. [Google Scholar]
- Ceder A. second ed. CRC Press; Boca Raton, USA: 2016. Public Transit Planning and Operation: Modeling, Practice and Behavior. [Google Scholar]
- Chen B.Y., Lam W.H., Sumalee A., Li Q., Shao H., Fang Z. Finding reliable shortest paths in road networks under uncertainty. Netw. Spatial Econ. 2013;13(2):123–148. [Google Scholar]
- Chen B.Y., Li Q., Lam W.H.K. Finding the k reliable shortest paths under travel time uncertainty. Transp. Res. Part B. 2016;94:189–203. [Google Scholar]
- Chorus C.G. Travel information: time to drop the labels? IEEE Trans. Intell. Transp. Syst. 2012;13(3):1235–1242. [Google Scholar]
- Chorus C.G., Arentze T.A., Timmermans H.J. Traveler compliance with advice: A Bayesian utilitarian perspective. Transp. Res. Part E. 2009;45(3):486–500. [Google Scholar]
- Chowdhury S., Ceder A., Schwalger B. The effects of travel time and cost savings on urban commuters’ perception of public transport routes involving transfers. J. Transp. Geogr. 2015;43:151–159. [Google Scholar]
- Delling D., Pajor T., Werneck R.F. Round-based public transit routing. Transp. Sci. 2014;49(3):591–604. [Google Scholar]
- de Cea J., Fernández E. Transit assignment for congested public transport-systems: an equilibrium model. Transportation Science. 1993;27(2):133–147. [Google Scholar]
- Di X., Liu H.X. Boundedly rational route choice behavior: A review of models and methodologies. Transp. Res. Part B. 2016;85:142–179. [Google Scholar]
- Disser Y., Müller-Hannemann M., Schnee M. International Workshop on Experimental and Efficient Algorithms. Springer; Berlin, Heidelberg: 2008. Multi-criteria shortest paths in time-dependent train networks; pp. 347–361. [Google Scholar]
- Dumitrescu I., Boland N. Algorithms for the weight constrained shortest path problem. Int. Trans. Oper. Res. 2001;8(1):15–29. [Google Scholar]
- Ehrgott M. Springer Science & Business Media; 2005. Multicriteria Optimization. [Google Scholar]
- Frappier A., Morency C., Tre'panier M. Measuring the quality and diversity of transit alternatives. Transp. Policy. 2018;61:51–59. [Google Scholar]
- Galdames C., Tudela A., Carrasco J.A. Exploring the role of psychological factors in mode choice models by a latent variables approach. Transp. Res. Rec. 2011;2230:68–74. [Google Scholar]
- Gandibleux, X., Beugnies, F., Randriamasy, S., 2006. Martins' algorithm revisited for multi-objective shortest path problems with a MaxMin cost function. 4OR, 4(1), 47–59.
- Grison E., Burkhardt J.M., Gyselinck V. How do users choose their routes in public transport? The effect of individual profile and contextual factors. Transp. Res. Part F. 2017;51:24–37. [Google Scholar]
- Guerriero F., Musmanno R. Label correcting methods to solve multicriteria shortest path problems. J. Optim. Theory Appl. 2001;111(3):589–613. [Google Scholar]
- Guo X., Liu H.X. Bounded rationality and irreversible network change. Transp. Res. Part B. 2011;45(10):1606–1618. [Google Scholar]
- Guo Z., Wilson N.H. Assessing the cost of transfer inconvenience in public transport systems: A case study of the London Underground. Transp. Res. Part A: Policy Practice. 2011;45(2):91–104. [Google Scholar]
- Hadas Y., Ceder A. Shortest path of emergency vehicles under uncertain urban traffic conditions. Transp. Res. Rec. 1996;1560:34–39. [Google Scholar]
- Hamdouch Y., Szeto W.Y., Jiang Y. A new schedule-based transit assignment model with travel strategies and supply uncertainties. Transp. Res. Part B. 2014;67:35–67. [Google Scholar]
- Handler G.Y., Zang I. A dual algorithm for the constrained shortest path problem. Networks. 1980;10(4):293–309. [Google Scholar]
- Handte M., Foell S., Wagner S., Kortuem G., Marrón P.J. An internet-of-things enabled connected navigation system for urban bus riders. IEEE Internet Things J. 2016;3(5):735–744. [Google Scholar]
- Hansen P. Multiple criteria decision making theory and application. Springer; Berlin, Heidelberg: 1980. Bicriterion path problems; pp. 109–127. [Google Scholar]
- Horváth M., Kis T. Multi-criteria approximation schemes for the resource constrained shortest path problem. Optimization Lett. 2018;12(3):475–483. [Google Scholar]
- Iori M., Martello S., Pretolani D. An aggregate label setting policy for the multi-objective shortest path problem. Eur. J. Oper. Res. 2010;207(3):1489–1496. [Google Scholar]
- Jiang Y., Szeto W.Y. Reliability-based stochastic transit assignment: Formulations and capacity paradox. Transp. Res. Part B. 2016;93:181–206. [Google Scholar]
- Jiang Y., Szeto W.Y., Long J., Han K. Multi-class dynamic traffic assignment with physical queues: intersection-movement-based formulation and paradox. Transportmetrica A: Transport Sci. 2016;12(10):878–908. [Google Scholar]
- Karaliopoulos M., Katsikopoulos K., Lambrinos L. Bounded rationality can make parking search more efficient: The power of lexicographic heuristics. Transp. Res. Part B. 2017;101:28–50. [Google Scholar]
- Khani A. An online shortest path algorithm for reliable routing in schedule-based transit networks considering transfer failure probability. Transp. Res. Part B. 2019;126:549–564. [Google Scholar]
- Kingham S., Dickinson J., Copsey S. Travelling to work: Will people move out of their cars. Transp. Policy. 2001;8(2):151–160. [Google Scholar]
- Kumar N., Benbasat I. Research note: the influence of recommendations and consumer reviews on evaluations of websites. Information Systems Research. 2006;17(4):425–439. [Google Scholar]
- Laming, D.R.J., 2008. Weber’s law, in “Inside psychology: A science over 50 years”, Rabbit. P. (Ed.), Oxford University Press.
- Lathia N., Smith C., Froehlich J., Capra L. Individuals among commuters: Building personalised transport information services from fare collection systems. Pervasive Mob. Comput. 2013;9(5):643–664. [Google Scholar]
- Liao F., Molin E., Timmermans H., van Wee B. Consumer preferences for business models in electric vehicle adoption. Transp. Policy. 2019;73:12–24. [Google Scholar]
- Lorenz D.H., Raz D. A simple efficient approximation scheme for the restricted shortest path problem. Oper. Res. Lett. 2001;28(5):213–219. [Google Scholar]
- Ludwig B., Zenker B., Schrader J. International Conference on Intelligent Interactive Assistance and Mobile Multimedia Computing. Springer; Berlin, Heidelberg: 2009. Recommendation of personalized routes with public transport connections; pp. 97–107. [Google Scholar]
- Martins E.Q.V. On a multicriteria shortest path problem. Eur. J. Oper. Res. 1984;16(2):236–245. [Google Scholar]
- Modesti P., Sciomachen A. A utility measure for finding multiobjective shortest paths in urban multimodal transportation networks. Eur. J. Oper. Res. 1998;111(3):495–508. [Google Scholar]
- Nuzzolo A., Crisalli U., Comi A., Rosati L. An advanced traveller advisory tool based on individual preferences. Procedia-Social Behav. Sci. 2014;160:539–547. [Google Scholar]
- Paixão, J.M., Santos, J.L., 2013. Labeling methods for the general case of the multi-objective shortest path problem–a computational study. In Computational Intelligence and Decision Making (pp. 489–502). Springer, Dordrecht.
- Peng Z.R., Huang R. Design and development of interactive trip planning for web-based transit information systems. Transp. Res. Part C. 2000;8(1):409–425. [Google Scholar]
- Pulido F.J., Mandow L., de la Cruz J.L.P. Multiobjective shortest path problems with lexicographic goal-based preferences. Eur. J. Oper. Res. 2014;239(1):89–101. [Google Scholar]
- Reinhardt L.B., Pisinger D. Multi-objective and multi-constrained non-additive shortest path problems. Comput. Oper. Res. 2011;38(3):605–616. [Google Scholar]
- Shaheen, S., Martin, E., Cohen, A., Musunuri, A., Bhattacharyya, A., 2016. Mobile Apps and Transportation: A Review of Smartphone Apps and a Study of User Response to Multimodal Traveler Information. Final report, ITS of UC Berkeley, California Department of Transportation (Caltrans), October.
- Shi W., Wei Y.F., Li X.L. A safety distance design model based on just noticeable difference. J. Transport. Syst. Eng. Inform. Technol. 2011;11(2):33–38. [Google Scholar]
- Shi N., Zhou S., Wang F., Tao Y., Liu L. The multi-criteria constrained shortest path problem. Transp. Res. Part E. 2017;101:13–29. [Google Scholar]
- Simon H.A. A behavioral model of rational choice. Q. J. Econ. 1955;69(1):99–118. [Google Scholar]
- Szeto W.Y., Solayappan M., Jiang Y. Reliability-based transit assignment for congested stochastic transit networks. Comput.-Aided Civ. Infrastruct. Eng. 2011;26(4):311–326. [Google Scholar]
- Szeto W.Y., Jiang Y., Wong K.I., Solayappan M. Reliability-based stochastic transit assignment with capacity constraints: Formulation and solution method. Transp. Res. Part C. 2013;35:286–304. [Google Scholar]
- Szeto W.Y., Jiang Yu, Sumalee A. A cell‐based model for multi‐class doubly stochastic dynamic traffic assignment. Comput.‐Aided Civ. Infrastruct. Eng. 2011;26(8):595–611. doi: 10.1111/j.1467-8667.2011.00717.x. In this issue. [DOI] [Google Scholar]
- Szeto W.Y., Jiang Y. Transit route and frequency design: Bi-level modeling and hybrid artificial bee colony algorithm approach. Transp. Res. Part B. 2014;67:235–263. [Google Scholar]
- Szeto W.Y., Jiang Y. Transit assignment: Approach-based formulation, extragradient method, and paradox. Transp. Res. Part B. 2014;62:51–76. [Google Scholar]
- Szeto, W.Y., Wang, Y., Han, K., 2015. Bounded rationality in dynamic traffic assignment. In Bounded rational choice behaviour: Applications in transport. Emerald Group Publishing Limited.
- Tang, Yili, Jiang, Yu, Yang, Hai, Nielsen, Otto Anker, 2020. Modeling and optimizing a fare incentive strategy to manage queuing and crowding in mass transit systems . Modeling and optimizing a fare incentive strategy to manage queuing and crowding in mass transit systems 138, 247–267. 10.1016/j.trb.2020.05.006 (In this issue). [DOI]
- te Morschea W., Puellob L.L.P., Geursb K.T. Potential uptake of adaptive transport services: An exploration of service attributes and attitudes. Transp. Policy. 2019;84:1–11. [Google Scholar]
- Tung C.T., Chew K.L. A multicriteria Pareto-optimal path algorithm. Eur. J. Oper. Res. 1992;62(2):203–209. [Google Scholar]
- Wu J., Sun H., Wang D.Z., Zhong M., Han L., Gao Z. Bounded-rationality based day-to-day evolution model for travel behavior analysis of urban railway network. Transp. Res. Part C. 2013;31:73–82. [Google Scholar]
- Xiao Y., Lo H.K. Day-to-day departure time modeling under social network influence. Transp. Res. Part B. 2016;92:54–72. [Google Scholar]
- Xing T., Zhou X. Finding the most reliable path with and without link travel time correlation: A Lagrangian substitution based approach. Transp. Res. Part B. 2011;45(10):1660–1679. [Google Scholar]
- Xu W., He S., Song R., Chaudhry S.S. Finding the K shortest path in a schedule-based transit network. Comput. Oper. Res. 2012;39:1812–1826. [Google Scholar]
- Yang L., Zhou X. Optimizing on-time arrival probability and percentile travel time for elementary path finding in time-dependent transportation networks: Linear mixed integer programming reformulations. Transp. Res. Part B: Methodol. 2017;96:68–91. [Google Scholar]
- Yen J.Y. Finding the k shortest loopless paths in a network. Manage. Sci. 1971;17(11):712–716. [Google Scholar]
- Zhang L. Behavioral foundation of route choice and traffic assignment: Comparison of principles of user equilibrium traffic assignment under different behavioral assumptions. Transp. Res. Rec. 2011;2254(1):1–10. [Google Scholar]
- Zhang Y., Khani A. An algorithm for reliable shortest path problem with travel time correlations. Transp. Res. Part B. 2019;121:92–113. [Google Scholar]
- Zografos K.G., Androutsopoulos K.N., Spitadakis V. Design and assessment of an online passenger information system for integrated multimodal trip planning. IEEE Trans. Intell. Transp. Syst. 2009;10(2):311–323. [Google Scholar]