Abstract
Purpose
Accurate and timely diagnosis of breast cancer is extremely important because of its high incidence and high morbidity. Early diagnosis of breast cancer through screening can improve overall prognosis. Currently, biopsy remains as the gold standard for tumor pathological confirmation. Development of diagnostic imaging techniques for rapid and accurate characterization of breast lesions is required. We aim to evaluate the usefulness of texture-derivate features of QUS spectral parametric images for non-invasive characterization of breast lesions.
Methods
QUS Spectroscopy was used to determine parametric images of mid-band fit (MBF), spectral slope (SS), spectral intercept (SI), average scatterer diameter (ASD), and average acoustic concentration (AAC) in 204 patients with suspicious breast lesions. Subsequently, texture analysis techniques were used to generate texture maps from parametric images to quantify heterogeneities of QUS parametric images. Further, a second-pass texture analysis was applied to obtain texture-derivate features. QUS parameters, texture-parameters and texture-derivate parameters were determined from both tumor core and a 5-mm tumor margin and were used in comparison to histopathological analysis in order to develop a diagnostic model for classifying breast lesions as either benign or malignant. Both leave-one-out and hold-out cross-validations were used to evaluate the performance of the diagnostic model. Three standard classification algorithms including a linear discriminant analysis (LDA), k-nearest neighbors (KNN), and support vector machines-radial basis function (SVM-RBF) were evaluated.
Results
Core and margin information using the SVM-RBF attained the best classification performance of 90% sensitivity, 92% specificity, 91% accuracy, and 0.93 AUC utilizing QUS parameters and their texture derivatives, evaluated using leave-one-out cross-validation. Implementation of hold-out cross-validation using combination of both core and margin information and SVM-RBF achieved average accuracy and AUC of 88% and 0.92, respectively.
Conclusions
QUS-based framework and derivative texture methods enable accurate classification of breast lesions. Evaluation of the proposed technique on a large cohort using hold-out cross-validation demonstrates its robustness and its generalization.
Introduction
Breast cancer is the most common type of cancers diagnosed in women and is also the second leading cause of cancer morbidity among women [1]. In 2015, there were 242,476 new cases of female breast cancer in the United States [3]. Furthermore, in that same year 41,523 women died of breast cancer in the United States [3]. Early detection of breast cancer results in an improved overall prognosis as better treatments can be provided to patients with disease detected at an earlier stage. In order to achieve this goal, accurate and precise diagnostic techniques are required.
Breast cancer screening typically initiates with mammography, followed by standard ultrasound imaging (B-mode imaging), dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) as needed, followed by core-needle biopsy as necessitated [6]. Lesion detection using x-ray mammography is prone to false negative lesion detection for dense breasts [3]. Biopsy remains as the gold standard for confirming tumor pathological status and for characterizing tumor grade [4]. Nevertheless, biopsy is an invasive procedure that is associated with pain and a hypothetical increased risk of tumor cell migration. Furthermore, there is a trend of increasingly performing unnecessary biopsies due to the low specificity of ultrasound B-mode images [5] and MRI [6]. DCE-MRI may increase the specificity of breast cancer detection [7]. Still, DCE-MRI is not always available for rapid diagnosis because of the longer wait time associated with MR imaging as compared to ultrasound and mammography. The development of imaging techniques that can perform rapid and accurate characterization of breast lesions is very valuable for early detection of breast cancer and triaging patients in a screening workflow [6].
Previous studies have utilized sonographic features of ultrasound B-mode images to characterize breast lesions [34,35,41]. However, ultrasound B-mode images are qualitative in nature and do not provide quantitative microstructural information of tissues [6]. Additionally, they are instrument- and operator-dependent. To address these limitations, Quantitative Ultrasound (QUS) spectroscopy has been introduced. QUS Spectroscopy techniques analyze raw radiofrequency signal prior to envelope detection, logarithmic compression, and post-processing to form ultrasound B-mode images. These methods extract quantitative intrinsic acoustic properties of tissue microstructures and compensate for operator and instrument-dependent effects such as beamforming through normalization procedure [2]. The effect of intervening tissue layers is also considered through an attenuation correction of the normalized power spectrum (NPS). QUS Spectral parameters that include mid-band fit (MBF), spectral slope (SS), and 0-MHz spectral intercept (SI) are derived from linear parametrization of the attenuation-corrected normalized power spectrum. These parameters measure tissue microstructure features that include scattering power, size and shape of acoustic scatterers, and concentration of scatterers [6,9]. Fitting of theoretical backscattering models to the measured backscatter coefficient (BSC) obtained from the normalized power spectrum allows estimation of two other parameters: average scattering diameter (ASD) and average acoustic concentration (AAC). The AAC is defined as the product of number density of scatterers and the square of the acoustic impedance difference between the scatterers and the background medium [6].
QUS Techniques have demonstrated capabilities in multiple domains including the evaluation of tumor responses to cancer therapies in pre-clinical and clinical settings [7,8,9,10,13], the differentiation of various types of tissue such as prostate, liver, and retina [14,16,17,18,19,20], the determination of blood-clot and various intravascular plaque components [21,22,23], the detection of tumor deposits in ex-vivo lymph nodes [24], and the differentiation of normal versus cancerous thyroid tissues on preclinical animal tumor models [25]. In relation to breast cancer, earlier pre-clinical studies have demonstrated QUS capabilities for differentiating spontaneously occurring mammary fibroadenomas (benign lesions) and mammary carcinomas (malignant lesions), and for differentiating different types of mammary cancers: carcinoma and sarcoma [26,27]. QUS techniques have also been used to differentiate breast tumors from the surrounding normal tissues in locally advanced breast cancer (LABC) [4]. Therefore, QUS parametric imaging reflecting the size of acoustic scatterers can potentially be used for the characterization of breast lesions.
Tumor micro-environment, physiology and metabolism exhibit heterogeneities that offer diagnostic and prognostic values in cancer characterization [42,43,44,46,48]. Different imaging modalities have elucidated the spatially heterogeneous tumor characteristics. These include MRI [51], positron emission tomography (PET) [53,52], computerized tomography (CT) [15,47], and diffuse optical spectroscopy (DOS) [45]. Texture analysis techniques can quantify objectively such heterogeneities [49]. In the benign versus malignant characterization, texture analysis methods have been applied to ultrasound B-mode images [28,37,39,50]. The rationale for this is that benign and malignant lesions often exhibit homogeneous and heterogeneous textures, respectively [6]. Texture analysis methods measure spatial alterations of gray level transitions in B-mode images, providing distinctive characteristics for this application [6]. However, as ultrasound B-mode images are operator- and instrument-dependent, the quantitative texture measures do not represent independent intrinsic properties of the tumor. Texture analysis of QUS parametric images mitigates this limitation. Normalization of QUS parameters removes instrument-dependent effects such that the resultant textural measures represent independent intrinsic properties of the tumor.
This study builds from an earlier study [6] by significant expansion of the cohort. In addition, the feature space utilized here is expanded through the inclusion of texture and texture-derivate features. Texture-derivate features were obtained through a second-pass texture analysis to determine textural features from texture-encoded QUS parametric maps, determined originally from QUS parametric images. Subsequently, in this study we also applied, for the first time, texture and texture-derivate analyses utilizing peri-tumoral tissue in the characterization of breast lesions. Such QUS-based texture analysis of tumor margins has demonstrated capabilities in the a priori prediction of response and survival in locally advanced breast cancer patients undergoing neoadjuvant chemotherapy [33]. Margin information is potentially useful for characterizing breast lesions. Benign tumors have well-defined margins. On the other hand, malignant tumors are typically characterized by margins that are not clearly-defined and associated with irregular patterns of growth.
In this study, core and margin analyses were combined in order to develop a diagnostic model for non-invasive characterization of breast lesions as either benign or malignant. In order to develop a highly accurate and precise diagnostic model, three standard classification algorithms in the field of machine learning that include linear discriminant analysis (LDA), nearest neighbors (KNN), and support vector machines-radial basis function (SVM-RBF) were evaluated. We compared the performance of the developed diagnostic model using both leave-one-out (LOO) and hold-out cross-validation techniques. The latter is important to demonstrate the generalizability of the diagnostic model to independent test set that was not used for model development. We evaluated the classifier performance using the receiver operating characteristics (ROC) analysis to obtain metrics of sensitivity, specificity, accuracy, area under the receiver operating characteristic curve (AUC), positive predictive value (PPV), and negative predictive value (NPV).
Our results indicate that QUS spectral parametric imaging, along with texture and texture-derivate analyses, have high potentials for rapid, accurate, and non-invasive characterization of breast lesions. Evaluation of the proposed approach on a larger cohort utilizing proper cross-validation technique demonstrates the generalizability of the framework.
Methods
Study protocol & data acquisition
The study was conducted based on institutional-research-ethics board approval (Sunnybrook Health Sciences Center). Radiofrequency data were collected from 204 patients (99 benign and 105 malignant) with suspicious breast lesions at the Rapid Diagnostic Unit (RDU) of Louise Temerty Breast Cancer Center at Sunnybrook Health Sciences Center, Toronto, Ontario, Canada after obtaining informed consent. The inclusion criterion of the patients is sonographically identified breast lesions after the mass has been identified previously on clinical and or mammographical examinations. The ground truth for identification of benign versus malignant breast lesions was obtained from clinical reports that include results from MR images and biopsy specimens. An experienced sonographer acquired data using a Sonix Touch system (Ultrasonix, Vancouver, Canada) that was equipped with a linear array transducer (L14-5/60W). The transducer operates at a central frequency of 6.5 MHz and bandwidth of 3–8 MHz. The radiologist who performed the scan was not blinded to the presence of a tumor. The objective of the study is to demonstrate that QUS can objectively discriminate benign vs malignant breast tumors through extraction of acoustic properties of tissue microstructure (“acoustic signatures”) that are distinct between benign and malignant lesions as has been shown by histopathological analysis [11]. Therefore, the knowledge of the precise location of the lesion is required.
QUS analysis include multiple imaging slices across the three-dimensional tumor acquired using panoramic (PAN) scan. These images were acquired at about 5-mm intervals across the tumor volume. These are essentially B-mode scan (two-dimensional imaging) with an additional feature of saving the beam-formed ultrasound RF data. RF data were digitized using 40 MHz sampling frequency. Data acquisition was performed along 512 scan lines, corresponding to 6 cm lateral field-of-view (FOV) and 4 cm imaging depth. The focal depth was set at the mid-line of the tumor. The field of views were fixed to include the tumor, whether it is benign or malignant, prior to off-line QUS spectral analysis.
Contouring of the tumor regions of interest (ROI) was performed manually on US B-mode images based on the readings of a radiologist with familiarity to breast ultrasound interpretation. QUS spectral, texture and texture-derivate analyses were performed on selected ROIs covering the tumor core and the 5-mm tumor margin. Tumor margin is an extension of the tumor from the core up to a 5-mm maximum distance to the surrounding area (peri-tumoral region). 5-mm margin was chosen as it gives best prediction results for response and survival in LABC patients undergoing neoadjuvant chemotherapy [33].
Feature extraction: linear regression & acoustic form-factor parameters
QUS Spectral analysis was performed over ROIs that include the core and the 5-mm margin. We used sliding window technique with a 2-mm by 2-mm kernel to create parametric images of QUS parameters. The size of the window was chosen to include enough number of acoustic wavelengths for reliable spectral estimation, while preserving image texture. A 94% window overlap was used between adjacent windows both axially and laterally.
We used a Hanning gating function along the range direction on individual RF scan lines within the window for spectral analysis. RF Spectra were estimated using the Fast Fourier Transform (FFT). Several independent adjacent RF signals within the window were used to obtain an averaged power spectrum that better represent the true power spectrum of the sample. We acquired the normalized power spectrum using a reference phantom technique [2,9]. The reference phantom was composed of 5–30 μm glass beads embedded in a homogeneous medium of oil droplets that were sunk in gelatin. The measured attenuation coefficient and speed of sound of the phantom were 0.786 dB/cm/MHz and 1540 m/s, respectively (University of Wisconsin, Department of Medical Physics, Madison, WI, USA). Attenuation compensation was performed to correct for ultrasound attenuation from propagation through intervening tissues. We performed a two-layer (intervening tissue and tumor) attenuation correction using the total attenuation estimation [30]. The attenuation coefficient estimate (ACE) of the tumor was estimated using a spectral difference method by calculating the rate of change in the spectral power magnitude with depth (over the tumor region) and frequency relative to the reference phantom [31]. We used the assumed attenuation coefficient of 1 dB/cm/MHz for the overlying breast tissues [32,40]. Linear regression analysis on the attenuation-corrected normalized power spectrum resulted in mid-band fit (MBF), spectral slope (SS), and 0-MHz spectral intercept (SI) spectral parameters. Subsequently, the measured backscatter coefficient can be estimated via [9]
| (1) |
where Sm(f) and Sr(f) are the RF spectra from the sample and the reference phantom, respectively. Parameters αm and αr are the attenuation functions from the sample and the reference phantom, respectively. Parameter R is the distance from the transducer face to the proximal side of the ROI window, and ∆z is the window length. Theoretical backscatter coefficient using spherical Gaussian form factor model σtheor(f) was fitted to the measured backscatter coefficient, from which average scattering diameter aeff and average acoustic concentration nz parameters can be estimated [9,12]. The theoretical backscatter coefficient is expressed as [9,12]:
| (2) |
where and cl is the speed of sound. F(f, aeff) is the form factor that describes the frequency-dependent backscatter coefficient. These analyses resulted in parametric images of mid-band fit, spectral slope, spectral intercept, average scatterers diameter, and average acoustic concentration. Mean-values from these parametric images were obtained and subsequently used as features for classification.
Feature extraction: texture, texture-derivate, & image quality analysis
We performed texture analysis using the Gray-level Co-Occurrence Matrix (GLCM) method to quantify intra-and peri-tumor heterogeneities. The GLCM realizes second-order statistical analysis by studying the spatial relationship between neighboring pixels in an image [49]. The full range of gray levels in each parametric image was linearly scaled into 16 discrete gray levels. Symmetric GLCM matrices were created from each parametric image at inter-pixel distances: 1, 2, 3, 4, 5 pixels and at four angular directions: 0°, 45°, 90°, and 135°. From these GLCM matrices, we extracted GLCM features that include contrast, correlation, energy, and homogeneity:
| (3) |
| (4) |
| (5) |
| (6) |
In Eqs. (3), (4), (5), (6), the p(i, j) is the probability of having neighboring pixels of intensities i and j in the image, and Ng denotes the number of gray levels. The μ and σ are the mean and standard deviation for row i or column j of the GLCM matrix. Textural features are subsequently averaged over distances and angular directions. Textural measures were assumed to be reflected in these averaged values [49]. Contrast quantifies local gray level variations in an image. Smoother image produces a lower contrast, while coarser image results in a higher contrast. Correlation represents linear correlation between neighboring pixels. Energy measures textural uniformity in an image. Homogeneity quantifies the incidence of pixel pairs of different intensities [6].
Texture-derivate analysis was subsequently applied to the parametric images. In contrast with the previous texture analysis approach that produces averaged texture measures, texture-derivate analysis works through creation of intermediary texture-encoded maps using sliding window analysis with a 15-pixel by 15-pixel window. Each pixel in these maps represents quantification of local textures across the window. A second pass texture analysis was subsequently performed on these maps, resulting in texture-derivate features.
As our analyses include the core and the 5-mm margin, we also defined image quality metrics: core-to-margin ratio (CMR) and core-to-margin contrast ratio (CMCR) that compare pixel intensities between these two regions [33]:
| (7) |
| (8) |
CMR compares the level of desired signal to the background noise [33]. CMCR is like CMR but also considers bias in an image [33].
Feature selection & classification
Mean-value, texture, and texture-derivate features were estimated from each scan plane and averaged over all scan planes. These weighted averaged measures were subsequently used for classification. We performed statistical analysis to demonstrate the presence of discriminating features for building a diagnostic model. In order to determine which statistical tests to use, a Shapiro-Wilk normality test was performed on each feature to decide if it followed a normal distribution [54]. For a normally distributed feature, an unpaired t-test was used. Otherwise, a non-parametric Mann-Whitney U Test (two-sided, 95% confidence) was utilized. Feature selection was performed using forward sequential-feature-selection (SFS) to look for best combination of features that contribute to the diagnostic model. We used leave-one-out and hold-out cross-validations for assessing the performance of the diagnostic model. In leave-one-out cross-validation, the classification model is trained using all observations except one. The left-out observation is used for testing the developed model [54]. The process is repeated until all observations are left out for testing at least once [54]. The trained classifier performance was assessed based on F1-Score (the harmonic average of precision and sensitivity). A hybrid biomarker that consists of 11 features was used to classify breast lesions as either benign or malignant. This was chosen to limit classification bias [39]. Our previous studies used leave-one-out cross-validation for assessing the diagnostic/response predictive model performance [6,33]. Leave-one-out cross-validation is more appropriate when the data size is relatively small. The reason is that the number of observations is too small for random partitioning of the data into training and test sets. As the number of observations increases, hold-out cross-validation is more relevant for assessing the performance of the diagnostic model to an independent test set that was not used in model development [36]. This is a necessary step towards generalizing our diagnostic model Therefore, we have also implemented hold out cross-validation that randomly separates the data into a 70% train set (n = 143) and a 30% test set (n = 61). Model development was performed on the train set, while performance evaluation was performed on the unseen test set. As the partitioning is a random process, we repeat the step ten times and average the classification metrics of sensitivity, specificity, accuracy, AUC, PPV, and NPV.
In order to develop a highly accurate and precise diagnostic model, three standard computational algorithms: LDA, KNN, and SVM-RBF were evaluated. LDA projects multi-dimensional feature space into a feature space that maximizes the ratio of between-class to within-class variance [33]. Linear classifier works best for linearly separable data [33]. KNN classification algorithm used k = 1, 3, 5 nearest neighbors. The KNN is an instance-based learning algorithm that predicts class association of a test point in the feature space based on most of the points neighboring the test point and the distance between those points to the test point [33]. SVM-RBF performs nonlinear mapping of the input data into higher-dimensional space where the data are supposed to have better distribution, before selecting an optimal hyperplane that maximizes the margin between the two classes [33,54]. Class association of the test data is predicted based on which side of the gap they fall on [33]. We used Gaussian radial basis function as the kernel function. The model parameters for SVM-RBF are the soft margin parameter C and the free parameter γ. We used a grid search method to optimize these parameters.
Classification using either the core or the margin information utilized a total of 105 features. These include 5 mean-value, 20 texture, and 80 texture-derivate features from five parametric images. On the other hand, classification using both the core and the margin information used a total of 220 features comprising of 105 features from the core, 105 features from the margin, and 10 image quality features.
Results
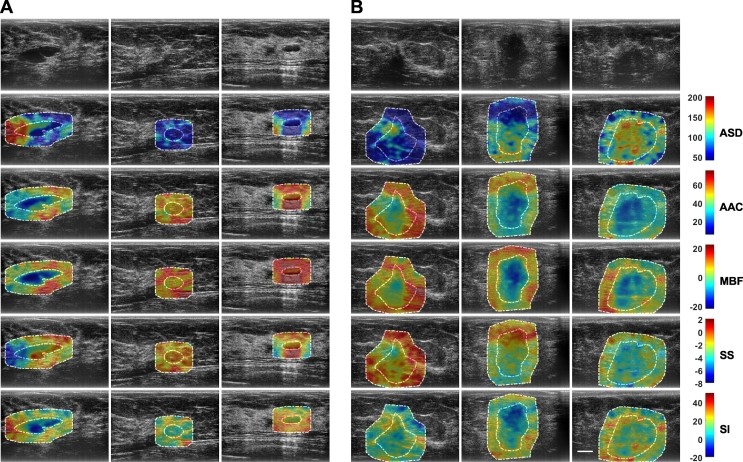
Ultrasound B-mode images and RF data were obtained from 204 patients in this study. Patients were aged 20 to 89 and 99 had benign masses and 105 had malignant masses in the research group. The sizes of the tumors are 1.6 ± 0.9cm and 3.2 ± 1.9 cm (mean value and standard deviation) for benign and malignant lesions, respectively. Fig. 1 shows representative ultrasound B-mode and parametric images of average scattering diameter, average acoustic concentration, mid-band fit, spectral slope, and spectral intercept from both benign and malignant groups with three different lesions in each group. The representative benign lesions in Fig. 1 were diagnosed as predominantly fibroadenomas (n = 50) and cysts/complicated cysts (n = 22). The malignant lesions were diagnosed as invasive ductal carcinoma (IDC) (n = 84), invasive mammary carcinoma (n = 7), and invasive lobular carcinoma (ILC) (n = 5), respectively. Mean-value, texture, and texture-derivate features determined from these parametric images were evaluated as imaging biomarkers associated with benign and malignant lesions. In the B-mode images, benign lesions appeared with better defined borders and less spiculated. In QUS parametric images, benign lesions demonstrated less heterogeneity than in the malignant lesions.
Fig. 1.
Representative ultrasound B-mode and QUS parametric images of ASD, AAC, MBF, SS, and SI from A benign (left three columns) and B malignant (right three columns) breast lesions. The colorbar range is 160 μm for ASD, 70 dB/cm3 for AAC, 44 dB for MBF, 10 dB/MHz for SS, and 70 dB for SI. The scale bar represents 1 cm. This corresponds to the full field-of-view of 4 cm axially and 6 cm laterally. The benign breast lesions were diagnosed as fibroadenomas and complicated a cyst. The malignant lesions were diagnosed as invasive ductal carcinoma (IDC), invasive mammary carcinoma, and invasive lobular carcinoma (ILC), respectively. From these parametric images, mean-value and texture features were extracted as imaging bio-markers for the characterization of breast lesions.
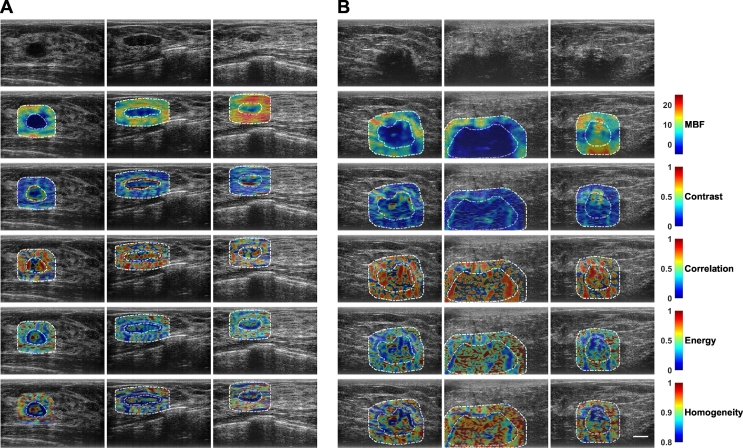
Texture analyses were used to analyze heterogeneities in breast lesions and surrounding tissues. Representative parametric overlays of textures (parametric texture images) are presented in Fig. 2. These images were used for further textural assessment. Specifically, from each of these texture images, four texture-derivate features were further determined and used for the classification of breast lesions.
Fig. 2.
Representative ultrasound B-mode images, primary mid-band fit parametric images, and texture-based parametric maps determined from mid-band fit parametric images from A benign and B malignant lesion groups. Texture images were obtained through application of sliding window analysis, resulting in contrast, correlation, energy, and homogeneity maps of mid-band fit. From each of these texture images, four texture-derivate features were calculated and subsequently used as potential imaging biomarkers to classify breast lesions as either benign or malignant. The scale bar represents 1 cm. This corresponds to the full field-of-view of 4 cm axially and 6 cm laterally.
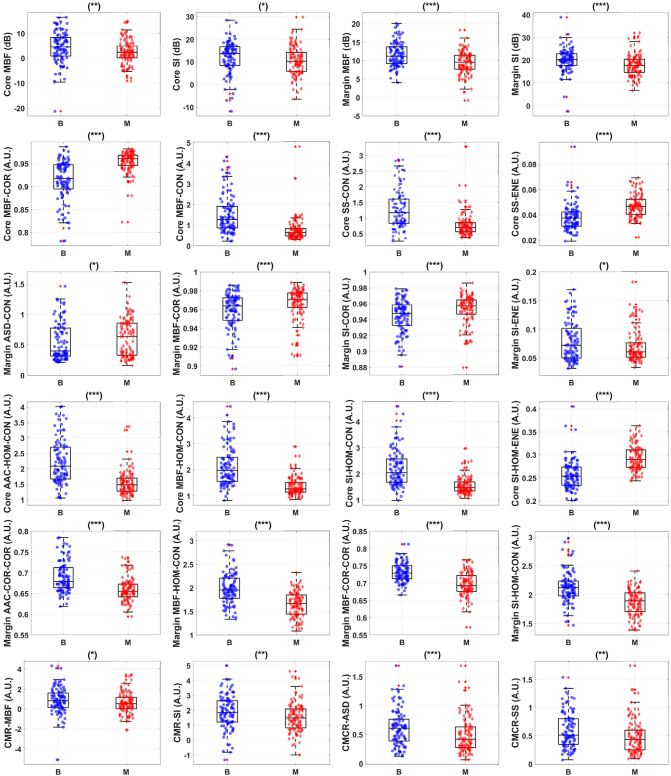
Fig. 3 presents representative box plots of mean-value, texture, texture-derivate, and image quality features that demonstrate statistical significant differences between benign and malignant breast lesions. The bottom and top edges of the box represent the 25th and 75th percentiles, respectively. The central mark in each box indicates the median. The whiskers represent 1.5 times the interquartile range. Five mean-value, 25 texture, 165 texture-derivate, and 4 image quality features demonstrated statistical significant differences (p < 0.05) between the two lesions types (benign versus malignant). Features were further subclassified based on their degree of statistical significance. Statistical significant (p < 0.05), highly significant (p < 0.01), and extremely significant (p < 0.001) features are indicated with (∗), (∗∗), and (∗∗∗) respectively. Among the mean-value parameters from the core, mid-band fit, spectral intercept, and average acoustic concentration showed statistical significant difference (p < 0.05). The mid-band fit, spectral intercept, and average acoustic concentration from the core are 4.4 ± 0.6 dB versus 2.4 ± 0.5 dB, 12.1 ± 0.7 dB versus 10.5 ± 0.6 dB, and 47.0 ± 1.2 dB/cm3 versus 44.0 ± 0.8 dB/cm3 for benign and malignant lesions, respectively. Among the mean-value parameters from the margin, mid-band fit and spectral intercept showed statistical significant difference (p < 0.05). The mid-band fit and spectral intercept from the margin are 11.3 ± 0.4 dB versus 9.3 ± 0.3 dB and 20.2 ± 0.5 dB versus 17.6 ± 0.5 dB for benign and malignant lesions, respectively.
Fig. 3.
Representative box and scatter plots of features that demonstrate statistical significant difference (p-values <0.05) between benign ('B') and malignant ('M') lesion groups. The first row shows mean-values features from both tumor core and tumor margin. The second row depicts textural features from tumor core that provide the most discriminative power. The third row shows textural features from tumor margin. The fourth row shows texture-derivate features from tumor core. The fifth row shows texture-derivate features from tumor margin. The last row depicts image quality parameters. There is a total of 220 features from tumor core and 5-mm margin, including 10 image quality features, available for feature selection. Among these features, 5 mean-values, 25 textural, 167 texture-derivate, and 4 image quality features demonstrate statistical significant difference between the two lesions. Statistical significant, highly significant (p < 0.01), and extremely significant (p < 0.001) are shown with (*), (**), and (***) respectively.
Mean-values, texture and texture-derivate (texture of texture) features were examined and feature selection for the purposes of classification was determined. The number of features was limited to 1/20 to prevent overfitting of data. Table 1 tabulates optimum features that contributed to a hybrid biomarker that best separated benign from malignant lesions. Although a maximum combination of 11 features was selected, the hybrid biomarkers that provided the best classification accuracy can result from a fewer combination of features. For instance, the peak core classification performance was obtained from a combination of 8 features: MBF-COR-ENE, SS-HOM-CON, ASD-HOM-COR, SI-HOM, ASD-CON-HOM, MBF-ENE-HOM, SI-HOM-ENE, and SS-HOM-ENE. Texture-derivate features dominated as discriminative features that resulted in the best hybrid biomarkers which separated patients into whether they had benign or malignant features.
Table 1.
Optimum features set for classification using tumor core, 5-mm tumor margin, and combination of both core and 5-mm margin information with SVM-RBF using leave-one-out cross-validation. A maximum of 11 features was selected for classification. Features were selected using forward SFS with leave-one-out cross-validation and F1-score metric. Texture-derivate features, for example Core – MBF-COR-ENE: energy of correlation image of mid-band fit parametric image of core ROI, were the dominant features that contributed to hybrid biomarkers that best separate the two lesion types.
| Core classification | 5-mm margin classification | Core and margin classification |
|---|---|---|
| Core MBF-COR-ENE | Margin MBF-COR-COR | Core MBF-COR-ENE |
| Core SS-HOM-CON | Margin AAC-CON-CON | Core SS-HOM-CON |
| Core ASD-HOM-COR | Margin ASD-ENE-HOM | Core MBF-COR-COR |
| Core SI-HOM | Margin MBF-HOM-COR | Core ASD-CON-CON |
| Core ASD-CON-HOM | Margin MBF-CON-CON | Margin SS-HOM-HOM |
| Core MBF-ENE-HOM | Margin AAC-COR-CON | Core AAC-CON-COR |
| Core SI-HOM-ENE | Margin AAC-CON-COR | Core SS-COR-HOM |
| Core SS-HOM-ENE | Margin MBF-HOM | Core AAC-HOM |
| Margin SI-COR-CON | ||
| Margin AAC-COR-COR |
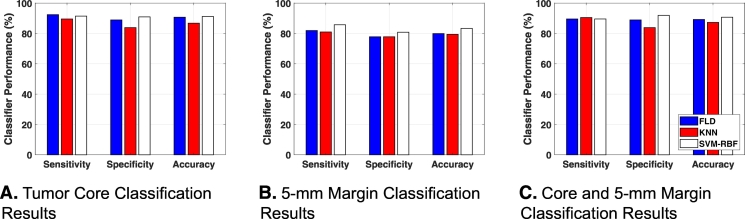
Different classifiers were compared in order to select the one with the best performance. Fig. 4 shows bar plots of the classification performance of three different classification algorithms using tumor core, tumor margin, and a combination of core and margin information. Tumor core information alone resulted in a high classification performance of more than 90% accuracy with LDA and SVM-RBF classifiers. Table 2A, Table 2B present classification performance using tumor core information from different classification algorithms with leave-one-out and hold-out cross-validations, respectively. Tumor margin information alone resulted in less classification performance compared to core classification. Using margin information, the best classification performance was obtained using SVM-RBF, with 83% accuracy and 0.87 AUC. Table 3A, Table 3B present classification performance using margin information from different classification algorithms with leave-one-out and hold-out cross-validations, respectively. The combination of both core and margin information resulted in a best classification performance of 91% accuracy and 0.93 AUC with SVM-RBF, compared to using core and margin information individually. Tables 4A and 4B present classification performance using core and margin information from different classification algorithms with leave-one-out and hold-out cross-validations, respectively. We observed that using hold out cross-validation, the classification performance decreases compared to leave-one-out cross-validation. This result is not unexpected as random partitioning of the data into training and test sets can result in variations in classification performance as the data used to develop the model are not the same each time. Nevertheless, combination of both core and margin analyses still obtained the best result of 88% accuracy and 0.92 AUC. This was achieved using SVM-RBF classification algorithm. As seen from Table 2B, Table 3B, Table 4B, SVM-RBF proves to be more robust to random partitioning of the data compared to linear discriminant analysis and nearest neighbors classification algorithms.
Fig. 4.
Benign versus malignant classification results from different classification algorithms using A tumor core, B 5-mm tumor margin, and C both core and 5-mm margin information utilizing leave-one-out cross-validation. Using tumor core information, both LDA and SVM-RBF produce accuracy of 91%. Using 5-mm tumor margin information, SVM-RBF provides the highest classification accuracy of 83%. Combination of tumor core and 5-mm tumor margin results in accuracies of 89% (LDA), 87% (KNN), and 91% (SVM-RBF).
Table 2A.
Core classification results using leave-one-out cross-validation. Classification performance of different classification algorithms using tumor core information. Core classification results in accuracy greater than 90% that is achieved using LDA and SVM-RBF. Interestingly, LDA achieved good classification performance, indicating linearly separable data.
| Classifier | Sensitivity | Specificity | Accuracy | AUC | PPV | NPV |
|---|---|---|---|---|---|---|
| LDA | 92% | 89% | 91% | 0.91 | 90% | 92% |
| KNN | 90% | 84% | 87% | 0.90 | 85% | 88% |
| SVM-RBF | 91% | 91% | 91% | 0.92 | 91% | 91% |
Table 2B.
Core classification results using hold out cross-validation. Classification performance of different classification algorithms using tumor core information. Core classification results in the best accuracy of 88% and AUC of 0.91 using SVM-RBF classification algorithm. Nonlinear classification algorithm in SVM-RBF is more robust to random data partitioning compared to linear and instance-based classification algorithms.
| Classifier | Sensitivity | Specificity | Accuracy | AUC | PPV | NPV |
|---|---|---|---|---|---|---|
| LDA | 85% | 82% | 83% | 0.88 | 83% | 84% |
| KNN | 80% | 74% | 77% | 0.81 | 78% | 77% |
| SVM-RBF | 92% | 83% | 88% | 0.91 | 86% | 91% |
Table 3A.
Margin classification results using leave-one-out cross-validation. Classification performance of different classification algorithms using 5-mm margin information. SVM-RBF results in a peak performance of 83% accuracy and 0.87 AUC.
| Classifier | Sensitivity | Specificity | Accuracy | AUC | PPV | NPV |
|---|---|---|---|---|---|---|
| LDA | 82% | 78% | 80% | 0.82 | 80% | 80% |
| KNN | 81% | 78% | 79% | 0.82 | 79% | 79% |
| SVM-RBF | 86% | 81% | 83% | 0.87 | 82% | 84% |
Table 3B.
Margin classification results using hold out cross-validation. Classification performance of different classification algorithms using 5-mm margin information. SVM-RBF results in a peak performance of 82% accuracy and 0.87 AUC. Nonlinear classification algorithm in SVM-RBF is more robust to random data partitioning compared to linear and instance-based classification algorithms.
| Classifier | Sensitivity | Specificity | Accuracy | AUC | PPV | NPV |
|---|---|---|---|---|---|---|
| LDA | 77% | 69% | 73% | 0.77 | 73% | 74% |
| KNN | 71% | 63% | 67% | 0.67 | 67% | 67% |
| SVM-RBF | 87% | 77% | 82% | 0.87 | 80% | 85% |
Table 4A.
Core and margin classification results with leave-one-out cross-validation. Classification performance of different classification algorithms using both tumor core and tumor margin information. SVM-RBF achieved the best classification performance of 91% accuracy and 0.93 AUC.
| Classifier | Sensitivity | Specificity | Accuracy | AUC | PPV | NPV |
|---|---|---|---|---|---|---|
| LDA | 90% | 89% | 89% | 0.91 | 90% | 89% |
| KNN | 90% | 84% | 87% | 0.89 | 86% | 89% |
| SVM-RBF | 90% | 92% | 91% | 0.93 | 92% | 89% |
Table 4B.
Core and margin classification Results with hold out cross-validation. Classification performance of different classification algorithms using both tumor core and tumor margin information. SVM-RBF achieved the best classification performance of 88% accuracy and 0.92 AUC.
| Classifier | Sensitivity | Specificity | Accuracy | AUC | PPV | NPV |
|---|---|---|---|---|---|---|
| LDA | 85% | 75% | 80% | 0.86 | 78% | 84% |
| KNN | 82% | 76% | 80% | 0.83 | 79% | 80% |
| SVM-RBF | 90% | 86% | 88% | 0.92 | 87% | 89% |
Discussion & conclusion
In this study, the utility of mean-value, texture, and texture-derivate features of QUS parametric images for non-invasive characterization of breast lesions is demonstrated. To our knowledge, this is the first study that explores on using texture-derivate features for such a characterization. In addition to analyzing texture and texture-derivate features from tumor core, the analysis here was expanded to include peri-tumoural tissue (5-mm margin extending from the core). This study builds upon an earlier [6] through a significant expansion of the number of patients. In the previous study, there were 78 patients with suspicious breast lesions (46 benign and 32 malignant cases). In the current study, newer techniques are applied on a larger cohort of patients consisting of 204 patients with suspicious breast lesions (99 benign and 105 malignant cases). In addition, appropriate cross-validation technique was implemented to demonstrate the generalizability of the developed diagnostic model to independent test sets that were not used in model development. Here, a hybrid vector of biomarkers developed through forward sequential feature selection achieved a sensitivity of 90%, a specificity of 92%, an accuracy of 91%, and an AUC of 0.93.
In the previous study, mean-values of MBF, SI, and AAC did not indicate any statistical significant difference between the two lesions [6]. In this study, however, mean-values of MBF, SI, and AAC from the core and the 5-mm margin demonstrated statistical significant difference (p < 0.05) between the two lesion types. This is likely due to the size of the increased cohort. In particular, it was observed that the MBF, SI, and AAC of malignant lesions are lower than those of benign lesions. This observation is consistent with the observation from an earlier study [4] where the QUS parameters of cancerous breast tissues were lower than those of normal breast tissues. Furthermore, this observation was also consistent with sonographic features of ultrasound B-mode images of breast lesions where malignant lesions often exhibited markedly hypoechoic appearance in comparison with benign lesions [34]. The MBF and SI parameters represent tissue features that includes scatterer size, shape, number, organization, and their elastic properties [8]. These properties are distinct between benign and malignant lesions as have been shown from histopathological analysis [11]. Benign lesions are characterized by more regular arrangement of cells [11]. On the other hand, malignant lesions are characterized by cellularity-rich cells with tendency to form cell clusters [11].
Since average-based parameters only characterize lesions using mean-values, the information regarding tumor heterogeneity is lost. Texture and texture-derivate features of QUS parametric images quantify lesion heterogeneities that includes variations in size, density, and distribution of acoustic scatterers. These biomarkers can potentially characterize tissue micro-structures and provide better separation between different histological tissue types compared to averaged mean-values parameters. Among textural features, 25 biomarkers showed statistical significant differences (p < 0.05) and 21 biomarkers showed statistically extremely significant differences (p < 0.001) between the two lesion types. In addition, a second pass texture analysis was applied to the parametric images, for the first time, resulting in analysis of texture images that represent local textural variations of QUS parametric images. From these texture images, texture-derivate features (texture of texture) were subsequently determined. Texture-derivate features can potentially provide even better separation between benign and malignant lesions. Among the texture-derivate features, 167 biomarkers demonstrated statistical significant differences (p < 0.05), 141 biomarkers demonstrated statistically highly significant differences (p < 0.01), and 110 biomarkers demonstrated statistically extremely significant differences (p < 0.001) between the two lesion groups. Analysis of QUS parameters and textures from the core and the 5-mm margin allows us to obtain image quality features including CMR and CMCR that were also used in the classification. We considered these features, for the first time, as potential biomarkers for characterizing breast lesions. CMR and CMCR have been used for the a priori prediction of response and survival in patients with locally advanced breast cancer undergoing neoadjuvant chemotherapy [33]. The CMR of MBF and SI parametric images, along with the CMCR of ASD and SS parametric images, demonstrated statistical significant differences (p < 0.05) between benign and malignant breast lesions.
In this study, we also observed that benign lesions are smaller than malignant lesions with mean values and standard deviations of 1.6 ± 0.9cm and 3.2 ± 1.9cm, respectively. The difference is statistically significant (p < 0.05). This observation is consistent with the findings of Stavros et al. [34]. In that study, they found that benign lesions are most associated with a maximum diameter of 1.5 cm or less, while malignant lesions are most associated with a maximum diameter of 1.5 cm or more [34]. Although this difference is present, Stavros et al. concluded that maximum diameter of the lesion is an indeterminate sonographic characteristic or feature [34]. Size alone is not enough for definitive discrimination of benign versus malignant breast lesions. QUS spectroscopy that extracts independent intrinsic distribution of acoustic properties can provide discriminating features that better separate the two groups. In addition, texture and derivative texture method allow quantification of intra- and peri-tumoral heterogeneities, resulting in more contrasting features.
Nearly all the selected features for hybrid biomarkers were texture-derivate features. This is not unexpected because statistical significant analysis using Mann-Whitney U Test showed that 110 texture-derivate features demonstrated statistically extremely significant differences (p < 0.001). Combinations of these strongly discriminating features resulted in hybrid biomarkers that best separated benign from malignant breast lesions. Core information alone was able to accurately classify breast lesions with 91% sensitivity, 91% specificity, 91% accuracy, and a 0.92 AUC. This was obtained using a SVM-RBF classification algorithm. On the other hand, margin-only information resulted in a best classification performance of 83% accuracy and a AUC of 0.87. This was also obtained using a SVM-RBF classifier. Among the classification algorithms assessed, KNN analysis yielded the lowest performance for margin-based classification. For core-based classification, the three classification algorithms performed comparably. Using LDA and SVM-RBF, core information alone was able to separate benign and malignant lesions with more than a 90% accuracy. The combination of core and margin information demonstrated a best classification performance of 90% sensitivity, 92% specificity, 91% accuracy, and 0.93 AUC using SVM-RBF algorithm.
As a necessary step towards generalizing the proposed QUS-based framework and novel derivative texture method for non-invasive characterization of breast lesions, we also implemented hold-out cross-validation in order to assess the performance of the diagnostic model. The classification performance using hold-out cross-validation showed a slight decrease compared to that obtained using leave-one-out cross-validation. This result is not unexpected as random partitioning of the data into training and test sets can result in variations of the trained decision boundary, ultimately affecting the diagnostic model's performance. Nevertheless, combination of both core and margin information for classification using SVM-RBF still achieved average accuracy and AUC of 88% and 0.92, respectively. Core information alone achieved the best average accuracy and AUC of 88% and 0.91, respectively using SVM-RBF. On the other hand, margin information alone attained the best accuracy and AUC of 82% and 0.87, respectively using SVM-RBF. Non-linear classification algorithm in SVM-RBF proves to be more robust to random data partitioning compared to linear and instance-based classification algorithms.
Previously, ultrasound B-mode images and the texture analysis of these images have been explored to perform noninvasive characterization of breast lesions [38]. The use of sonography for the characterization of breast lesions achieved 98% sensitivity, 68% specificity, and 73% accuracy from 750 patients with breast lesions (625 benign and 125 malignant) [34]. Further, analysis of envelope statistics of ultrasound B-mode images using Nakagami imaging achieved 92% sensitivity, 72% specificity, and 82% accuracy in characterizing 100 patients with breast lesions (50 benign and 50 malignant) [29]. Texture analysis of ultrasound B-mode images has been utilized for breast lesion characterization [28]. In that study, application of GLCM-based texture analysis on envelope-based images resulted in a classification performance of 70% sensitivity, 77% specificity, and 74% accuracy. Further work involving the application of advanced machine learning techniques in artificial neural network on ultrasound B-mode images of breast lesions resulted in a better classification performance of 92% sensitivity, 91% specificity, and 91% accuracy [35]. In this work, the combination of several single biomarkers was able to classify breast lesions with a peak classification performance of 90% sensitivity, 92% specificity, and 91% accuracy, and a AUC of 0.93. This was achieved with imaging biomarkers from the combination of the core and the 5-mm margin using a SVM-RBF classification algorithm. QUS-Based techniques, along with texture and texture-derivate analyses, provided an improved classification performance for the characterization of breast lesions compared to past work utilizing ultrasound B-mode images. This result can be attributed to the fact that QUS techniques measure independent intrinsic acoustic and mechanical properties of tissue microstructure that are distinct between benign and more structurally disorganized malignant lesions. Furthermore, QUS spectral analysis offers system-and operator-independent measurements of tissue properties through a normalization procedure. In the work here, the classification of breast lesions using these imaging biomarkers resulted in a more robust classification algorithm. Additionally, QUS does not use ionizing radiation and does not need the administration of exogenous contrast agents. These advantages of QUS spectroscopy over other imaging modalities including mammography, standard ultrasound B-mode, and contrast-enhanced MRI make it an ideal tool for rapid breast cancer diagnosis in clinical settings.
QUS offers rapid breast cancer diagnosis because the acquisition time of raw radiofrequency data for spectral analysis is the same with that of B-mode imaging. From the ultrasound imaging system perspective, QUS acquisition uses B-mode imaging sequence. Although data evaluation takes way much longer (depending on the size of the tumor and the size of the tumor margin), this is due to the way our spectral analysis routines are written and not a limitation of the QUS framework. Our codes implemented sequential processing as opposed to parallel processing. In the former, for a given ROI, the computation process goes through each point in the ROI, taking 2 mm by 2 mm window, once at a time. After the process for a window finishes, the process resumes to the next point in the 2D ROI. On the other hand, parallel processing allows for computation of many kernels (functions) simultaneously. In this way, each time, many kernels are deployed to process 2 mm by 2 mm regions within the ROI. This potentially results in speed-up in data processing and allows real-time QUS analysis. This can be achieved through implementation of QUS using graphical processing unit (GPU) computing.
A possible concern is the accuracy of the attenuation correction method used here. QUS spectroscopy extracts acoustic properties through estimation of average power spectra from the sample, after normalization procedure and attenuation compensation. The spectral difference method was used to estimate the local attenuation coefficient of the tumor. Labyed et al. [30] concluded that the optimal kernel/window sizes and ROI lengths for attenuation correction using clinical array transducer with the spectral difference method are kernels than contain 5 wavelengths or more and ROIs that contain 35 wavelengths or more. Window/kernel that contain 5 wavelengths or more can capture all spectral contents of the RF signal [30]. In addition, ROIs that contain 35 wavelengths or more axially resulted in mean and standard deviation of the ACE that are less than 15% and 10%, respectively [30]. In this study, a 2 mm by 2 mm window/kernel was used with typical ROI sizes of 16 mm (taking the mean size of the benign lesions) plus an additional of 10 mm for a 5-mm tumor rim analysis, resulting in effective ROIs of at least 26 mm. For a 6.5 MHz center frequency, the wavelength is 0.24 mm, such that the window/kernel here contains 8 wavelengths (greater than 5 wavelengths for optimal ACE estimation) and the ROIs contain 108 wavelengths or more (greater than 35 wavelengths as prescribed by Labyed et al. for optimal ACE estimation [30]).
In summary, the rapid and accurate characterization of breast lesions is an essential component of breast cancer diagnosis that can affect prognosis by providing better therapeutic options for patients with disease detected at an earlier stage. QUS parametric imaging, along with texture and texture-derivate analysis, can be a working non-invasive technique for breast lesions characterization. Our work demonstrated the robustness of QUS-based framework and texture analysis for larger patient populations with suspicious breast lesions. Implementation of hold-out cross-validation demonstrates the generalizability of the developed diagnostic model to unseen test sets. This work provides a foundation for the use of quantitative ultrasound in the characterization and differentiation of breast lesions.
Authors' individual contributions
Laurentius O. Osapoetra: Conceptualization, Formal analysis, Investigation, Methodology, Software, Project administration, Supervision, Validation, Visualization, Roles/Writing – original draft, Writing – review & editing.
Lakshmanan Sannachi: Conceptualization, Methodology, Validation, Software, Writing – review & editing.
Daniel DiCenzo: Data curation.
Karina Quiaoit: Data curation.
Kashuf Fatima: Data curation.
Gregory J. Czarnota: Conceptualization, Methodology, Formal analysis, Funding acquisitions, Resources, Supervision, Validation, Visualization, Writing – review & editing.
Declaration of competing interest
The authors declare no potential conflicts of interest.
Acknowledgements
This Research was supported by Natural Sciences and Engineering Research Council of Canada (NSERC), Canadian Institutes for Health Research (CIHR), the Hecht Foundation, and the Terry Fox Foundation.
Appendix A. Patient characteristics
Table 5.
Benign patient characteristics. Lesion size refers to the longest dimension of the tumor.
| Patient number | Age | Type | Size (cm) |
|---|---|---|---|
| 1 | 46 | Fibroadenoma | 1.8 |
| 2 | 39 | Fibroadenoma | 1.1 |
| 3 | 43 | Fibroadenoma | 1.0 |
| 4 | 40 | Lactating adenoma | 2.3 |
| 5 | 21 | Cyst | 0.8 |
| 6 | 42 | Fibroadenomatoid changes | 1.2 |
| 7 | 52 | Cyst | 2.6 |
| 8 | 34 | Fibroadenoma | 0.8 |
| 9 | 39 | Benign nodule | 1.2 |
| 10 | 62 | Fibroadenoma | 1.1 |
| 11 | 58 | Seroma | 5.6 |
| 12 | 39 | Fibroadenoma | 1.1 |
| 13 | 51 | Fibroadenoma | 2.3 |
| 14 | 60 | Cyst | 0.6 |
| 15 | 54 | Fibroadenoma | 1.0 |
| 16 | 67 | Cyst | 0.8 |
| 17 | 53 | Cyst | 0.6 |
| 18 | 31 | Fibroadenoma | 1.3 |
| 19 | 44 | Fibroadenoma | 1.5 |
| 20 | 66 | Cyst | 0.7 |
| 21 | 45 | Fibroadenoma | 0.4 |
| 22 | 33 | Fibroadenoma | 1.3 |
| 23 | 43 | Adenosis & fibrosis | 1.0 |
| 24 | 44 | Cyst | 0.8 |
| 25 | 50 | Fibroadenoma | 0.3 |
| 26 | 27 | Fibroadenoma | 1.4 |
| 27 | 38 | Fibroadenoma | 0.7 |
| 28 | 45 | Cyst | 0.7 |
| 29 | 62 | Fibroadenoma | 1.5 |
| 30 | 72 | Cyst | 0.5 |
| 31 | 53 | Benign nodule | 3.1 |
| 32 | 46 | Fibroadenoma | 2.9 |
| 33 | 63 | Apocrine metaplasia & usual ductal hyperplasia | 0.9 |
| 34 | 38 | Fibroadenoma | 1.9 |
| 35 | 31 | Fibroadenoma | 2.7 |
| 36 | 49 | Fibroadenoma | 1.0 |
| 37 | 39 | Fibroadenoma | 1.2 |
| 38 | 57 | Benign nodule | 0.9 |
| 39 | 61 | Fibroadenoma | 1.8 |
| 40 | 57 | Fibrosis | 1.6 |
| 41 | 41 | Fibroadenoma | 2.7 |
| 42 | 33 | Scar/fibrosis | 2.6 |
| 43 | 89 | Seroma | 0.7 |
| 44 | 29 | Fibroadenoma | 0.8 |
| 45 | 33 | Fibroadenoma | 1.5 |
| 46 | 59 | Apocrine metaplasia + PASH + stromal fibrosis | 1.0 |
| 47 | 47 | Fibroadenoma | 1.4 |
| 48 | 44 | PASH | 3.0 |
| 49 | 50 | Cyst | 0.8 |
| 50 | 56 | Benign nodule | 3.6 |
| 51 | 36 | Fibroadenoma | 1.2 |
| 52 | 46 | Fibroadenoma | 0.7 |
| 53 | 54 | Fibroadenoma | 0.8 |
| 54 | 25 | Fibroadenoma | 1.7 |
| 55 | 51 | Fibroadenoma | 1.0 |
| 56 | 56 | Cyst/fibroadenoma | 0.6 |
| 57 | 26 | Fibroadenoma | 2.3 |
| 58 | 49 | Benign nodule | 2.7 |
| 59 | 39 | Fibroadenoma | 1.7 |
| 60 | 32 | Benign lipoma | 3.9 |
| 61 | 20 | Fibroadenoma | 3.8 |
| 62 | 75 | Cyst | 1.4 |
| 63 | 53 | Cyst | 2.0 |
| 64 | 26 | Fibroadenoma | 2.1 |
| 65 | 44 | Fibroadenoma | 2.3 |
| 66 | 37 | Fibroadenoma | 0.8 |
| 67 | 45 | Fibroadenoma | 1.6 |
| 68 | 48 | Cyst | 2.2 |
| 69 | 53 | Cyst | 1.7 |
| 70 | 52 | Fibroadenoma | 1.1 |
| 71 | 47 | Cyst | 1.2 |
| 72 | 48 | Cyst | 1.6 |
| 73 | 63 | Cyst | 0.5 |
| 74 | 23 | Fibroadenoma | 1.6 |
| 75 | 52 | Benign nodule | 1.1 |
| 76 | 46 | Fibroadenoma | 1.6 |
| 77 | 43 | Fibroadenoma | 1.6 |
| 78 | 61 | Fibroadenoma | 0.9 |
| 79 | 43 | Cyst | 2.0 |
| 80 | 37 | Fibroadenoma | 2.7 |
| 81 | 51 | PASH | 2.4 |
| 82 | 44 | Fibroadenoma | 1.0 |
| 83 | 30 | Fibroadenoma | 2.9 |
| 84 | 53 | Cluster of cysts | 1.3 |
| 85 | 74 | Cyst | 1.4 |
| 86 | 39 | Radial scar | 0.5 |
| 87 | 40 | Fibroadenomatoid changes | 2.5 |
| 88 | 62 | Benign nodule | 1.3 |
| 89 | 45 | Cyst | 1.0 |
| 90 | 48 | Benign nodule | 1.6 |
| 91 | 49 | Benign nodule | 1.1 |
| 92 | 50 | Benign nodule | 1.4 |
| 93 | 43 | Fibroadenoma | 1.2 |
| 94 | 71 | Cyst | 0.9 |
| 95 | 57 | PASH | 1.3 |
| 96 | 45 | Fibroadenoma | 1.1 |
| 97 | 45 | Benign nodule | 2.5 |
| 98 | 47 | Fibroadenoma | 0.7 |
| 99 | 33 | Fibroadenoma | 1.7 |
Table 6.
Malignant patient characteristics. Lesion size refers to the longest dimension of the tumor. ER is estrogen receptor, PR is progesterone receptor, HER2 is human epithelial growth factor receptor 2. Lesion size refers to the longest dimension of the tumor. IDC stands for invasive ductal carcinoma. ILC stands for invasive lobular carcinoma. DCIS stands for ductal carcinoma in situ, IMC stands for invasive mammary carcinoma.
| Patient Number | Age | Type | Size (cm) | Tumor Grade | ER | PR | HER2 |
|---|---|---|---|---|---|---|---|
| 1 | 72 | IDC | 3.3 | II | + | − | − |
| 2 | 83 | ILC | 1.0 | II | + | + | − |
| 3 | 41 | IDC | 4.3 | II/III | − | − | − |
| 4 | 51 | IDC | 2.1 | II | + | + | + |
| 5 | 58 | IDC | 3.8 | II/III | + | − | + |
| 6 | 83 | IDC | 7.7 | II/III | + | − | + |
| 7 | 51 | IDC | 3.8 | III | + | + | − |
| 8 | 43 | IDC | 7.0 | III | − | − | − |
| 9 | 61 | IDC | 2.2 | III | − | − | − |
| 10 | 42 | IDC | 5.7 | II/III | + | + | − |
| 11 | 60 | IDC | 1.5 | III | + | + | + |
| 12 | 42 | IDC | 2.4 | II/III | + | + | − |
| 13 | 47 | IDC | 0.7 | I | + | + | − |
| 14 | 42 | IDC | 2.1 | III | + | + | − |
| 15 | 66 | IDC | 3.8 | II | + | + | − |
| 16 | 51 | IDC | 9.6 | II/III | + | + | + |
| 17 | 53 | Invasive carcinoma | 3.5 | II/III | − | − | − |
| 18 | 69 | IDC | 0.7 | II | + | + | − |
| 19 | 45 | IDC | 3.5 | II/III | + | + | + |
| 20 | 48 | IDC | 2.2 | III | − | − | − |
| 21 | 61 | IDC | 2.0 | III | + | + | + |
| 22 | 77 | ILC | 1.5 | N/A | + | − | − |
| 23 | 63 | DCIS | 1.3 | III | + | + | − |
| 24 | 41 | IDC | 1.5 | III | + | + | − |
| 25 | 64 | IDC | 1.2 | II | + | + | − |
| 26 | 44 | IDC/ILC | 0.9 | II | + | + | − |
| 27 | 50 | IDC | 4.2 | II | + | + | + |
| 28 | 61 | Invasive adenocarcinoma | 2.1 | II | − | − | − |
| 29 | 73 | IDC | 2.0 | II | + | + | − |
| 30 | 71 | ILC | 4.0 | II | + | + | + |
| 31 | 70 | IDC | 8.0 | I | + | + | − |
| 32 | 79 | IDC | 1.8 | II | + | + | + |
| 33 | 51 | Invasive tubular carcinoma | 1.8 | I | + | + | − |
| 34 | 43 | IDC | 1.5 | II | + | + | + |
| 35 | 70 | IDC | 1.7 | I/II | + | + | − |
| 36 | 56 | IDC | 5.0 | II | + | + | − |
| 37 | 47 | IDC | 2.6 | III | + | + | + |
| 38 | 63 | IDC | 8.6 | II | + | + | − |
| 39 | 52 | IDC | 3.1 | II/III | − | − | − |
| 40 | 54 | IDC | 2.3 | III | − | − | − |
| 41 | 68 | IDC | 2.2 | II | + | + | + |
| 42 | 49 | IDC | 2.5 | II/III | − | − | − |
| 43 | 49 | IDC | 2.6 | II | + | + | + |
| 44 | 60 | IDC | 6.0 | III | − | − | + |
| 45 | 57 | IDC | 3.3 | III | − | − | + |
| 46 | 57 | IDC | 2.1 | N/A | + | − | + |
| 47 | 67 | IDC | 2.5 | III | + | + | − |
| 48 | 55 | IDC | 3.2 | III | − | − | + |
| 49 | 45 | IDC | 2.6 | II | + | + | − |
| 50 | 45 | Invasive metaplastic carcinoma | 3.3 | N/A | − | − | − |
| 51 | 55 | IDC | 2.9 | II | + | + | − |
| 52 | 64 | Malignant neoplasm | 3.3 | N/A | − | − | − |
| 53 | 42 | IDC | 2.1 | III | + | + | + |
| 54 | 38 | IDC | 1.9 | III | − | − | + |
| 55 | 72 | IMC | 5.8 | III | − | − | − |
| 56 | 36 | IDC | 2.3 | II | + | + | + |
| 57 | 27 | IDC | 1.5 | II | + | + | + |
| 58 | 36 | IDC | N/A | II | + | + | − |
| 59 | 35 | DCIS | 1.6 | N/A | − | − | + |
| 60 | 69 | ILC | 6.2 | II | + | + | − |
| 61 | 81 | IMC | 2.9 | I | + | + | − |
| 62 | 38 | IMC | 1.5 | II | + | + | − |
| 63 | 50 | IDC | 5.7 | III | + | + | + |
| 64 | 67 | IDC | N/A | I,II,III | + | + | − |
| 65 | 63 | IDC | 0.6 | II | + | + | − |
| 66 | 53 | IDC | 5.2 | III | + | + | − |
| 67 | 64 | IDC | 3.7 | III | + | − | − |
| 68 | 54 | IDC | 5.0 | II | + | + | − |
| 69 | 81 | IDC | 3.8 | III | − | − | − |
| 70 | 55 | IMC | 3.4 | III | − | − | − |
| 71 | 31 | IDC | 4.6 | II | + | + | − |
| 72 | 34 | IDC | 4.0 | III | + | + | − |
| 73 | 46 | IMC | 8.0 | N/A | + | − | + |
| 74 | 53 | IDC | 4.8 | II | + | + | − |
| 75 | 67 | IDC | N/A | II | + | + | − |
| 76 | 51 | IMC | 1.9 | II | + | + | − |
| 77 | 67 | IDC | 1.6 | III | − | − | − |
| 78 | 77 | ILC | 5.0 | III | − | − | − |
| 79 | 47 | Locally-advanced carcinoma | N/A | III | + | − | − |
| 80 | 34 | IDC | 1.9 | III | − | − | − |
| 81 | 51 | IDC | 1.9 | III | − | − | − |
| 82 | 47 | IDC | N/A | III | − | − | + |
| 83 | 37 | IDC | 3.0 | II | + | + | − |
| 84 | 49 | IDC | 5.8 | III | − | − | − |
| 85 | 42 | IDC | 3.1 | N/A | − | − | + |
| 86 | 42 | IDC | 8.5 | III | + | − | − |
| 87 | 66 | IDC | 1.7 | N/A | − | − | + |
| 88 | 50 | IDC | 3.7 | I-II | + | + | − |
| 89 | 68 | IMC | 2.5 | II | + | − | − |
| 90 | 35 | IDC | 4.4 | II | + | + | + |
| 91 | 67 | IDC | 2.3 | II | + | − | − |
| 92 | 43 | IDC | 5.3 | III | − | − | + |
| 93 | 60 | IDC | 2.4 | II | + | − | − |
| 94 | 49 | IDC | 1.8 | III | + | + | − |
| 95 | 50 | IDC | 4.1 | II | + | + | + |
| 96 | 51 | IDC | 3.3 | III | + | + | − |
| 97 | 49 | IDC | 2.2 | II | + | + | − |
| 98 | 72 | IDC | 1.8 | III | + | + | + |
| 99 | 41 | IDC | 3.2 | III | + | + | + |
| 100 | 51 | IDC | 2.7 | III | − | − | + |
| 101 | 63 | IDC | 3.7 | III | − | − | − |
| 102 | 49 | IDC | 2.5 | N/A | + | + | − |
| 103 | 63 | IDC | 1.3 | III | + | + | − |
| 104 | 85 | IDC | 1.3 | N/A | N/A | N/A | N/A |
| 105 | 40 | IDC | N/A | N/A | N/A | N/A | N/A |
References
- 1.Siegel Cancer statistics, 2016, CA. Cancer J. Clin. 2016;66:730. [Google Scholar]
- 2.Yao Backscatter coefficient measurements using a reference phantom to extract depth-dependent instrumentation factors. Ultrason. Imaging. 1990;12:58–70. doi: 10.1177/016173469001200105. [DOI] [PubMed] [Google Scholar]
- 3.https://gis.cdc.gov/Cancer/USCS/DataViz.html
- 4.Tadayyon Quantitative ultrasound characterization of locally-advanced breast cancer by estimation of its scatterer properties. Med. Phys. 2014;41(1):129031–1290312. doi: 10.1118/1.4852875. [DOI] [PubMed] [Google Scholar]
- 5.Oelze and Mamou . vol. 63. 2016. Review of Quantitative Ultrasound: Envelope Statistics and Backscatter Coefficient Imaging and Contributions to Diagnostic Ultrasound; pp. 336–351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Sadeghi-Naini Breast-lesion characterization using textural features of quantitative ultrasound parametric maps. Sci. Rep. 2017;7(13638):1–10. doi: 10.1038/s41598-017-13977-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bhooshan Cancerous breast lesions on dynamic contrast-enhanced MR images: computerized characterization for image-based prognostic markers. Radiology. 2010;254(3):680–690. doi: 10.1148/radiol.09090838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Sadeghi-Naini Quantitative ultrasound evaluation of tumour cell death response in locally-advanced breast cancer patients receiving chemotherapy. Clin. Cancer Res. 2013;19(8):2163–2174. doi: 10.1158/1078-0432.CCR-12-2965. [DOI] [PubMed] [Google Scholar]
- 9.Sannachi Non-invasive evaluation of breast cancer response to chemotherapy using quantitative ultrasonic backscatter parameters. Med. Image Anal. 2014;20(1):224–236. doi: 10.1016/j.media.2014.11.009. [DOI] [PubMed] [Google Scholar]
- 10.Sadeghi-Naini Imaging innovations for cancer therapy response monitoring. Imaging Med. 2012;4(3):311–327. [Google Scholar]
- 11.Lakhani . International Agency for Research on Cancer; 2012. WHO Classification of Tumours of the Breast. [Google Scholar]
- 12.Insana and Hall Parametric ultrasound imaging from backscatter coefficient measurements: image formation and interpretation. Ultrason. Imaging. 1990;vol. 12:245–267. doi: 10.1177/016173469001200402. [DOI] [PubMed] [Google Scholar]
- 13.Sadeghi-Naini Early prediction of therapy responses and outcomes in breast cancer patients using quantitative ultrasound spectral texture. Oncotarget. 2014;5(11):3497–3511. doi: 10.18632/oncotarget.1950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Feleppa Three-dimensional ultrasound analyses of the prostate. Mol. Urol. 2000;4(3):133–139. discussion 141. 40. [PubMed] [Google Scholar]
- 15.Vaidya Combined PET/CT image characteristics for radiotherapy tumour response in lung cancer. Radiother. Oncol. 2012;102(2):239–245. doi: 10.1016/j.radonc.2011.10.014. [DOI] [PubMed] [Google Scholar]
- 16.Feleppa Typing of prostate tissue by ultrasonic spectrum analysis. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 1996;43(4):609–619. [Google Scholar]
- 17.Lizzi Ultrasonic spectrum analysis for tissue assays and therapy evaluation. Int. J. Imaging Syst. Technol. 1997;8:3–10. [Google Scholar]
- 18.Feleppa Quantitative ultrasound in cancer imaging. Semin. Oncol. 2011;38:136–150. doi: 10.1053/j.seminoncol.2010.11.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Balaji Role of advanced 2 and 3-dimensional ultrasound for detecting prostate cancer. J. Urol. 2002;168(6):2422–2425. doi: 10.1016/S0022-5347(05)64159-6. [DOI] [PubMed] [Google Scholar]
- 20.Feleppa Ultrasonic tissue-type imaging of the prostate: implications for biopsy and treatment guidance. Cancer Biomark. 2008;4:201–212. doi: 10.3233/cbm-2008-44-504. [DOI] [PubMed] [Google Scholar]
- 21.Sigel Ultrasonic tissue characterization of blood clots. Surg. Clin. North Am. 1990;70(1):13–29. doi: 10.1016/s0039-6109(16)45030-9. [DOI] [PubMed] [Google Scholar]
- 22.Noritomi Carotid plaque typing by multiple-parameter ultrasonic tissue characterization. Ultrasound Med. Biol. 1997;23(5):643–650. doi: 10.1016/s0301-5629(97)00013-6. [DOI] [PubMed] [Google Scholar]
- 23.Knig and Klauss Virtual histology. Heart. 2007;93:977–982. doi: 10.1136/hrt.2007.116384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Mamou Three-dimensional high-frequency backscatter and envelope quantification of cancerous human lymph nodes. Ultrasound Med. Biol. 2011;37(3):345–357. doi: 10.1016/j.ultrasmedbio.2010.11.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Lavarello Characterization of thyroid cancer in mouse models using high-frequency quantitative ultrasound techniques. Ultrasound Med. Biol. 2013;39(19) doi: 10.1016/j.ultrasmedbio.2013.07.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Oelze Differentiation and characterization of rat mammary fibroadenomas and 4T1 mouse carcinomas using quantitative ultrasound imaging. IEEE Trans. Med. Imaging. 2004;23(6):764–771. doi: 10.1109/tmi.2004.826953. [DOI] [PubMed] [Google Scholar]
- 27.Oelze and Zachary Examination of cancer in mouse models using high-frequency quantitative ultrasound. Ultrasound Med. Biol. 2006;32(11):1639–1648. doi: 10.1016/j.ultrasmedbio.2006.05.006. [DOI] [PubMed] [Google Scholar]
- 28.Gomez Analysis of co-occurrence texture statistics as a function of gray-level quantization for classifying breast ultrasound. IEEE Tran. Med. Imaging. 2012;31(10):1889–1899. doi: 10.1109/TMI.2012.2206398. [DOI] [PubMed] [Google Scholar]
- 29.Tsui Po-Hsiang. Ultrasound nakagami imaging: a strategy to visualize the scatterers properties of benign and malignant breast tumours. IEEE J. Sel. Topics Quantum Electron. 2010;36(2):209–217. doi: 10.1016/j.ultrasmedbio.2009.10.006. [DOI] [PubMed] [Google Scholar]
- 30.Labyed Estimate of the attenuation coefficient using a clinical array transducer for the detection of cervical ripening in human pregnancy. Ultrasonics. 2011;51:34–39. doi: 10.1016/j.ultras.2010.05.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Labyed and Bigelow Estimating the total ultrasound attenuation along the propagation path by using a reference phantom. J. Acoust. Soc. Am. 2010;128(5):3232–3238. doi: 10.1121/1.3483739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Duric Development of ultrasound tomography for breast imaging: technical assessment. Med. Phys. 2005;32(5):1375–1386. doi: 10.1118/1.1897463. [DOI] [PubMed] [Google Scholar]
- 33.Tadayyon A priori prediction of neoadjuvant chemotherapy response and survival in breast cancer patients using quantitative ultrasound. Nat. Sci. Rep. 2017;7(45733) doi: 10.1038/srep45733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Stavros Solid breast nodules: use of sonography to distinguish between benign and malignant lesions. Radiology. 1995;196(1):123–134. doi: 10.1148/radiology.196.1.7784555. [DOI] [PubMed] [Google Scholar]
- 35.Joo Segyeong. Computer-aided diagnosis of solid breast nodules: use of an artificial neural network based on multiple sonographic features. IEEE Trans. On Med. Imaging. 2004;23(10):1292–1300. doi: 10.1109/TMI.2004.834617. [DOI] [PubMed] [Google Scholar]
- 36.Park and Han Methodologic guide for evaluating clinical performance and effect of artificial intelligence technology for medical diagnosis and prediction. Radiology. 2018;286(3) doi: 10.1148/radiol.2017171920. [DOI] [PubMed] [Google Scholar]
- 37.Liao Y.-Y. Classification of scattering media within benign and malignant breast tumours based on ultrasound texture-feature based and nakagami-parameter images. Med. Phys. 2011;38(4):2198–2207. doi: 10.1118/1.3566064. [DOI] [PubMed] [Google Scholar]
- 38.Cheng Automated breast cancer detection and classification using ultrasound images: a survey pattern recognition. Pattern Recogn. 2010;43:299–317. [Google Scholar]
- 39.Garra Improving the distinction between benign and malignant breast lesions: the value of sonographic texture analysis. Ultrason. Imaging. 1993;15(4):267–285. doi: 10.1177/016173469301500401. [DOI] [PubMed] [Google Scholar]
- 40.Berger Global breast attenuation: control group and benign breast diseases. Ultrason. Imaging. 1990;12(1):47–57. doi: 10.1177/016173469001200104. [DOI] [PubMed] [Google Scholar]
- 41.Chen Chung-Ming. Breast lesions on sonograms: computer-aided diagnosis with nearly setting independent features and artificial neural networks. Radiology. 2003;226(2):504–514. doi: 10.1148/radiol.2262011843. [DOI] [PubMed] [Google Scholar]
- 42.O'Connor Imaging intratumour heterogeneity: role in therapy response, resistance, and clinical outcome. Clin. Cancer Res. 2015;21:249–257. doi: 10.1158/1078-0432.CCR-14-0990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Polyak Heterogeneity in breast cancer. J. Clin. Invest. 2011;121(10):3786–3788. doi: 10.1172/JCI60534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Heindl Mapping spatial heterogeneity in the tumour microenvironment: a new era for digital pathology. Lab. Investig. 2015;95:377–384. doi: 10.1038/labinvest.2014.155. [DOI] [PubMed] [Google Scholar]
- 45.Sadeghi-Naini Early detection of chemotherapy-refractory patients by monitoring textural alterations in diffuse optical spectroscopic images. Med. Phys. 2015;42(11):6130–6146. doi: 10.1118/1.4931603. [DOI] [PubMed] [Google Scholar]
- 46.Sengupta and Pratx Imaging metabolic heterogeneity in cancer. Mol. Cancer. 2016;15(4):1–12. doi: 10.1186/s12943-015-0481-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Goh Assessment of response to tyrosine kinase inhibitors in metastatic renal cell cancer: CT texture as a predictive biomarker. Radiology. 2011;261(1):165–171. doi: 10.1148/radiol.11110264. [DOI] [PubMed] [Google Scholar]
- 48.Davnall Assessment of tumour heterogeneity: an emerging imaging tool for clinical practice? Insights Imaging. 2012;3(6):573–589. doi: 10.1007/s13244-012-0196-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Haralick Textural features for image classification. IEEE Trans. Syst. Man. Cybern. 1973;(6):610–621. [Google Scholar]
- 50.Alvarenga Complexity curve and grey level co-occurrence matrix in the texture evaluation of breast tumour on ultrasound images. Med. Phys. 2007;34(2):379–387. doi: 10.1118/1.2401039. [DOI] [PubMed] [Google Scholar]
- 51.Ahmed Texture analysis in assessment and prediction of chemotherapy response in breast cancer. J. Magn. Reson. Imaging. 2013;38:89–101. doi: 10.1002/jmri.23971. [DOI] [PubMed] [Google Scholar]
- 52.Tan Spatial-temporal [18F]FDG-PET features for predicting pathologic response of esophageal cancer to neoadjuvant chemoradiation therapy. Int. J. Radiat. Oncol. Biol. Phys. 2013;85(5):1375–1382. doi: 10.1016/j.ijrobp.2012.10.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Chicklore Quantifying tumour heterogeneity in 18F-FDG PET/CT imaging by texture analysis. Eur. J. Nucl. Med. Mol. Imaging. 2013;40(1):133–140. doi: 10.1007/s00259-012-2247-0. [DOI] [PubMed] [Google Scholar]
- 54.Sannachi Breast cancer treatment response monitoring using quantitative ultrasound and texture analysis: comparative analysis of computational models. Transl. Oncol. 2019;12(10):1271–1281. doi: 10.1016/j.tranon.2019.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]