A Study on Herd Immunity of COVID-19 in South Korea: Using a Stochastic Economic-Epidemiological Model

Abstract

Vaccination is an effective measure to control the diffusion of infectious disease such as COVID-19. This paper analyzes the basic reproduction number in South Korea which enables us to identify a necessary level of vaccine stockpile to achieve herd immunity. An susceptible-infected-susceptible model is adopted that allows a stochastic diffusion. The result shows that the basic reproduction number of South Korea is approximately 2 which is substantially lower than those of the other regions. The herd immunity calculated from economic-epidemiological model suggests that at least 62% of the susceptible population be vaccinated when COVID-19 vaccine becomes available.

Introduction

Although COVID-19 virus is still ongoing in South Korea, the number of new infected cases has been substantially reduced since the mid April. The diffusion rate of the virus has been suppressed as a result of the various measures and efforts, e.g. the policy to keep social distancing among others. However, because the possibility of second or third wave of COVID-19 cannot be ruled out, it is necessary to study the level of herd immunity of COVID-19.

This short paper attempts to examine the herd immunity of COVID-19 using an economic-epidemiological model. The model allows us to calculate the basic reproduction number, $R_0$, which is an essential indicator to understand the infective power of the virus. The herd immunity calculated by means of $R_0$ provides a useful information on the scale of vaccine stockpile, if there is any vaccine that will be available in the near future. In addition, the paper confirms the importance of the social distancing rule in curbing the spread of the virus.

We start with an epidemiological model to analyze the herd immunity of COVID-19 in South Korea. The model to be presented in the paper is based on SIS (Susceptible-Infected-Susceptible) in which the population is distinguished into two compartments: susceptible S and infected I. An alternative compartment model is SIR (Susceptible-Infected-Recovered) that allows the full immunity once recovered from a disease.

Which model is suitable for COVID-19 depends on whether the population can obtain immunity to the disease. As discussed in Bokharaie (2020), it is somewhat premature to say which is the suitable one for analyzing COVID-19. Nevertheless, we adopt an SIS model in this study since there is no convincing evidence which shows the sheer possibility of permanent immunity from COVID-19 illness. For example, the growing number of reinfection cases in South Korea are reported: as of May 12, 429 reinfected cases among 10,936 first infection. Similarly, (Bethune and Korinek 2020) analyze an SIS model to examine the effects of containment strategy to eradicate COVID-19.

The model is largely based on Park (2016) that develops an approach to analyzing the stochastic diffusion of the disease. This model can be regarded as an extension of conventional epidemiological model by considering economic benefit and cost of vaccination. The paper is structured as follows: Sect. 2 provides a stochastic SIS combined with real option approach. Section 3 provides a numerical illustration focusing on COVID-19 case in Korea. Summary is presented in Sect. 4.

Model

The total population is denoted by N(t) that is normalized to 1. The population can be susceptible or infected with S(t) or I(t) so that $S(t)+I(t)=1$. The dynamics of susceptible and infected groups are

$$\begin{array}{cc}\hfill dS=& -\beta ISdt+\gamma Idt+{\sigma }_{S}d{w}_S,\hfill \end{array}$$ 1

$$\begin{array}{cc}\hfill dI=& \beta ISdt-\gamma Idt-mIdt+{\sigma }_{I}d{w}_I.\hfill \end{array}$$ 2

where Eq. (1) and Eq. (2) describe the evolution of susceptible and infected group, respectively. $\beta$ denotes a force of infection and $\gamma$ is the recovery rate from the disease. The mortality rate is given by m. The increment of the standard Wiener process is $w_i$ that is characterized by $E\left(d,w_i\right)=0$, $Var\left(d,w_i\right)=dt$ with volatility parameter ${\sigma }_i$. From $S=1-I,$ Eq. (2) is transformed to

$$\begin{array}{c}\hfill dI=I\left(\alpha ,-,\beta ,I\right)dt+\sigma Idw\end{array}$$ 3

where $\alpha =\beta -\gamma -m$ implies the force of infection. Note that Eq. (3) is a stochastic version of the logistic function. The epidemiological literature defines the basic reproduction number as $R_0=\beta /\left(\gamma ,+,m\right)$ to measure the average number of secondary infections from the primary infection. The herd immunity threshold (HIT) is calculated by $H_0=1-1/R_0$. We compare $H_0$ with $H_0^{\ast }$ that is calculated from economic-epidemiological model.

When V(I) denotes an option value for the vaccination, the Ito’s lemma yields

$$\begin{array}{c}\hfill \frac{1}{2}{\sigma }^2{I}^2{V}^{″}\left(I\right)+\alpha I\left(1,-,\frac{\beta }{\alpha },I\right)V^{\prime }\left(I\right)-\rho V\left(I\right)=0\end{array}$$ 4

where $\rho$ is the discount rate. Using the boundary condition ${lim}_{I\to 0}V\left(I\right)=0,$ the solution to Eq. (4) is

$$\begin{array}{c}\hfill V\left(I\right)=A\mathrm{\Phi }\left(I\right)I^a\end{array}$$ 5

where $\mathrm{\Phi }\left(I\right)=1+{\sum }_{i=1}^{\infty }\frac{{(2a)}_i}{{(b)}_i}\frac{{\left(\frac{\beta I}{{\sigma }^2}\right)}^i}{i!}$, $a=0.5-\alpha /{\sigma }^2+\sqrt{{\left(0.5,-,\alpha ,/,{\sigma }^2\right)}^2+2\rho /{\sigma }^2}$ and $b=2\alpha /{\sigma }^2+2a$ (Park 2016). Note that A is the option constant term that will be determined later using the boundary conditions and ${\left(·\right)}_i$ denotes Pochhammer symbols for the rising factorial.

The instantaneous benefit from vaccinating COVID-19 is $wgv\left(1,-,I\right)$ when w,  g and v denote the vaccine effective rate,  unit benefit and vaccination rate, respectively. We assume that the cost of vaccination is $c{v}^2\left(1,-,I\right)$ when c is the unit cost of the vaccination. Then, the instantaneous net benefit from the mass vaccination is

$$\begin{array}{c}\hfill wgv\left(1,-,I\right)-c{v}^2\left(1,-,I\right).\end{array}$$ 6

An optimal vaccination rate $v^{\ast }=wg/2c$ is substituted back to Eq. (6) to obtain $\left(1,-,I\right)w^2{g}^2/4c.$ The optimal threshold $I^{\ast }$ for the impulsive vaccination and the option constant term A are solved using the following value-matching and smooth-pasting conditions:

$$\begin{array}{cc}\hfill A\mathrm{\Phi }\left(I\right)I^a=& \left(1,-,I\right)w^2{g}^2/4c,\hfill \end{array}$$ 7

$$\begin{array}{cc}\hfill aA\mathrm{\Phi }\left(I\right)I^{a-1}+A{I}^a{\mathrm{\Phi }}^{\prime }\left(I\right)=& -w^2{g}^2/4c.\hfill \end{array}$$ 8

The herd immunity from economic-epidemiological model is calculated by $H_0^{\ast }=v^{\ast }\left(1,-,I^{\ast }\right)$ and it will be compared with the conventional herd immunity $H_0=1-1/R_0$.

An application to COVID-19

COVID-19 case in Korea is analyzed by using the data from Jan.20 of the first outbreak in South Korea to May.12. Among the total 10,936 confirmed cases, 258 death and 429 reinfection cases were reported while the rest of the infected were cured. The initial development of COVID-19 was somewhat slow with the infection spots that can be effectively isolated. It seemed that the disease was under control until the clustered infection cases soon came out particularly in Daegu City and a religion group. Since then, Korea CDC has performed strict monitoring and quarantine policy targeting the people with suspected contact. The measure includes the mobile phone tracking, phone-interview and home-visit tracking as well as self-report of the people to agency. The policy to keep social distancing became effective from the early March.

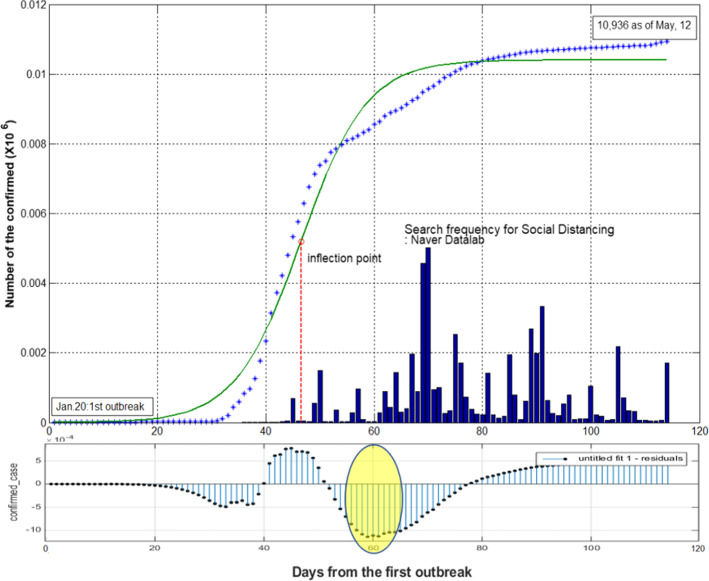
Figure 1 shows the number of confirmed COVID-19 cases (blue asterisk) following a logistic pattern. The estimation of non-linear least squares for the logistic function provides a best fitting curve with SSE: 2.855e-05, R${}^2$=0.9882, adj-R${}^2$=0.9881 and RMSE: 0.0005049. The fitted curve provides $K=0.01028$ with (0.01015, 0.01042) for 95% confidence interval. This let us to identify the date of inflection: the 46th date from the first outbreak. Note that this inflection point is corresponding to the maximum sustainable yield at the literature on biological resource. The recovery rate $\gamma$ and the mortality rate are 0.9372 and 0.0236, respectively by using the numbers of confirmed, death and reinfection. The basic reproduction number $R_0$ is $\beta /\left(\gamma ,+,m\right)=2.0270$ with (2.0237, 2.2083) for 95% confidence interval.

Fig. 1.

Logistic estimation and effects of social distancing

This basic reproduction number is less than the pooled global estimate of $R_0$ (3.38±1.40) as reported in the meta-analysis of Alimohamadi et al. (2020) but greater than the estimate of $R_0$ of Hwang et al. (2020) that excludes the clustered infection cases from Shincheongji religion group. D’Arienz and Coniglio (2020) find that $R_0$ values associated with the Italian outbreak may range from 2.43 to 3.10. Zhao et al. (2020) report that the mean estimate of $R_0$ ranges from 2.24 to 3.58 with an 8-fold to 2-fold increase in the reporting rate. Liu et al. (2020) report that region-specific $R_0$ of China: 2.26 at Wuhan and 6.29 at Hubei Province. A median $R_0$ of China is estimated to be 5.7 in Sanche et al. (2020). We calculate HIT $H_0$ of South Korea by using $H_0=1-1/R_0$. The result is $H_0=$0.51 which suggests that the vaccine stockpile cover at least 51% of the susceptible population.

Figure 1 also shows the search frequency of a keyword ’social distancing’ (blue-colored bar). The search frequency data from NAVER Datalab that is the most popular platform company in South Korea works as a proxy indicator to reflect a degree of public awareness on social distancing. The figure in the lower bottom shows the residual errors from the fitted curve and the realized confirmed cases. It appears that the largest residual is recorded 2 weeks after the first spike of the frequency. Note that the incubation period of COVID-19 virus is approximately 2 weeks. Hence, this finding proves the importance of the policy to keep social distancing.

In the next, we apply the economic-epidemiological model to calculate $H_0^{\ast }$ by solving Eq. (7) and Eq. (8). The vaccine effectiveness rate is assumed to be $w=0.5$ due to the vaccine data not yet available. As to the vaccine benefit that is the forgone cost of illness, we use an average cost based on the severe inpatient cares: The per capita cost of Category 20 Respiratory Illness and General Illness are 30 million KRW and 1.35 million KRW, respectively (NHIS 2017). The numerical analysis provides $H_0^{\ast }=0.6232$, implying that at least 62% of the susceptible group needs to be vaccinated to achieve the herd immunity. Figure 2 illustrates the sensitivity analysis of $H_0^{\ast }$ with respect to the vaccine cost and benefit: the herd immunity is positively (negatively) correlated to the vaccine benefit (cost) (Table 1).

Fig. 2.

Sensitivity analysis of $H^{\ast }$

Table 1.

Basic Reproduction Numbers and HIT of South Korea COVID-19

Basic Reprod. No. $R_0$	H.I. $H_0$	H.I. $H_0^{\ast }$
$2.{0270}^{\ast }$	0.5066	0.6232

*95% confidence interval: 2.0237, 2.2083

$\beta ,\sigma ,\gamma ,m=1.9475,,0.1665,0.9372,0.0236$

Summary

This paper presented an SIS model that is coupled with economic factors to determine the optimal vaccine stockpile. Two herd immunity concepts were compared to provide the optimal stockpile level of COVID-19 vaccine. Our finding is that $H_0^{\ast }$ of economic-epidemiological model requires relatively larger stockpile for COVID-19 vaccine compared to the stockpile level calculated from $H_0$ of conventional epidemiological model. The result also confirmed the social distancing rule as an effective measure to curb the diffusion of the disease. One of future research could include social network analysis with interacting agents under contagious disease environment.