COSMO: A dynamic programming algorithm for multicriteria codon optimization

Abstract

Codon optimization in protein-coding sequences (CDSs) is a widely used technique to promote the heterologous expression of target genes. In codon optimization, a combinatorial space of nucleotide sequences that code a given amino acid sequence and take into account user-prescribed forbidden sequence motifs is explored to optimize multiple criteria. Although evolutionary algorithms have been used to tackle such complex codon optimization problems, evolutionary codon optimization tools do not provide guarantees to find the optimal solutions for these multicriteria codon optimization problems.

We have developed a novel multicriteria dynamic programming algorithm, COSMO. By using this algorithm, we can obtain all Pareto-optimal solutions for the multiple features of CDS, which include codon usage, codon context, and the number of hidden stop codons. User-prescribed forbidden sequence motifs are rigorously excluded from the Pareto-optimal solutions. To accelerate CDS design by COSMO, we introduced constraints that reduce the number of Pareto-optimal solutions to be processed in a branch-and-bound manner. We benchmarked COSMO for run-time and the number of generated solutions by adapting selected human genes to yeast codon usage frequencies, and found that the constraints effectively reduce the run-time. In addition to the benchmarking of COSMO, a multi-objective genetic algorithm (MOGA) for CDS design was also benchmarked for the same two aspects and their performances were compared. In this comparison, (i) MOGA identified significantly fewer Pareto-optimal solutions than COSMO, and (ii) the MOGA solutions did not achieve the same mean hypervolume values as those provided by COSMO. These results suggest that generating the whole set of the Pareto-optimal solutions of the codon optimization problems is a difficult task for MOGA.

1. Introduction

Protein-coding regions of messenger RNAs have nucleotide-level redundancy by virtue of synonymous codons coding for the same amino acid. In general, the frequencies of synonymous codons are not equally distributed, but biased due to evolutionary pressure. This bias, which varies in accordance with species, is called codon bias [1]. Since a codon usage frequency different from that of a host organism may cause an undesirable inefficiency of protein synthesis, codon optimization has become a routinely utilized computational design tool for heterologously expressing non-endogenous genes in host organisms. In addition, it has been reported that codon pair usage, which is also referred to as codon context, has species-specific bias [2] and that these biases may affect the efficiency of protein production [3], [4], [5]. Recently, a computational resource providing codon pair usage data has also been developed [6]. Furthermore, while optimal codons correspond to abundant tRNAs that promote efficient expression of the protein products, it is known that non-optimal codons are also important to ensure that protein structure and function are maintained: e.g. non-optimal codons have been shown to play an important role in co-transcriptional protein folding, circadian rhythms and mRNA decay [7], [8]. Thus, elucidating the effect of codon usage and codon pair usage on translation efficiency is fundamental to improving the outcomes of synthetic biology [1].

To date, several tools that can be used for codon optimization have been proposed (for a review, see [9]). Since multiple features (including codon usage frequency, codon context, and sequence motif) of protein-coding sequence (CDS) may simultaneously affect protein expression, codon optimization could be viewed as a multi-objective optimization problem in which the solution space should be explored in an effort to find Pareto-optimal solutions [10]. In this context, multi-objective evolutionary algorithms have been proposed and utilized to design coding sequences under multiple criteria [11], [12], [13]. Although these multi-objective evolutionary approaches provide useful design results with reasonable computational costs, these heuristic algorithms do not guarantee to output optimal solutions.

In addition to these heuristics, methods that use exact approaches have also been applied to codon optimization. Condon and Thachuk [14] developed a dynamic programming (DP) algorithm designed to obtain optimal solutions for CDS design problems in which both the codon usage frequency score, codon adaptation index (CAI) [15], and the numbers of forbidden and desired sequence motifs are taken into account by introducing a priority based order for these objective functions (OFs). CCTool is another DP implementation for codon optimization, which optimizes the codon context of a coding sequence [16]. These DP algorithms are based on a single-objective optimization framework and are not designed to output Pareto-optimal solutions for problems with multiple criteria. In the present study, we propose a novel DP algorithm, COSMO (Codon Optimization Strategy with Multiple Objectives), for solving multicriteria codon optimization problems. This algorithm is deterministic and guarantees that all Pareto-optimal solutions are obtained. The OFs that can be optimized using COSMO include CAI, codon pair bias (CPB), and the number of specified short sequence motifs such as off-frame hidden stop codons (HSC). Forbidden sequence motifs, such as restriction sites and polynucleotide tracts, can also be specified and eliminated from the final solutions via the sequence constraint functions implemented in COSMO. Efficiency and applicability of the proposed DP algorithm are demonstrated by the adaptation of human CDSs to yeast codon frequencies in the results and discussion section. In this performance demonstration, benchmarking for the number of Pareto-optimal solutions and run-time is performed to compare the design performance of COSMO and that of a standard multi-objective genetic algorithm.

2. Methods

Let us denote the input amino acid sequence as $A=a_1,a_2,\dots ,a_L$, where $a_i$ is the i-th amino acid and L is the length of the amino acid sequence. A sequence of codons for A is defined as $C=c_1,c_2,\dots ,c_L$ with $c_i\in \lambda (a_i)$, where $\lambda (a_i)$ is the set of codons coding for amino acid $a_i$. Since a single codon is a nucleotide triplet, the nucleotide sequence S corresponding to C is expressed as $S=s_1,s_2,\dots ,s_{3L}$, where $s_i\in \{\mathrm{A},\mathrm{C},\mathrm{G},\mathrm{U}\}$.

The multicriteria codon optimization problem is formulated as follows:

$$\left(\begin{array}{cc}\mathrm{Maximize}{F}_i(C),\hfill & i=1,2,\dots ,n\text{;}\hfill \\ \mathrm{subject}\mathrm{to}\hfill & C\in \mathrm{\Phi },\hfill \end{array}\right\}$$ (1)

where $F_i(C)$ is the i-th objective function value for a sequence of codons, C; $\mathrm{\Phi }$ is the feasible decision space. This feasible decision space is composed of possible sequences of codons that code for the input amino acid sequence and do not have any forbidden motifs.

COSMO also allows for the minimization of OFs which can be performed by replacing the phrase “Maximize” in the Eq. (1) with “Minimize”.

Since, in general, there are trade-offs between the features expressed by the OFs, the aim of the present algorithm is to obtain Pareto-optimal solutions for a given amino acid sequence, OFs, and forbidden sequence motifs. In multicriteria optimization, if we maximize the OF values, the set of all Pareto-optimal solutions is defined as follows: $\{\mathit{x}\in \mathit{\varphi }\mid \nexists \mathit{y}\in \mathit{\varphi },\mathit{y}\mathrm{dominates}\mathit{x}\}$, where “$\mathit{y}\mathrm{dominates}\mathit{x}$” ($\mathit{x},\mathit{y}\in {\mathbb{R}}^m$ and m is a natural number) means that $\forall i{y}_i⩾x_i\mathrm{\Lambda }\exists i{y}_i\ne x_i$, and $\mathit{\varphi }$ is a feasible objective space [10]. In other words, the set of all Pareto-optimal solutions is the set of all “non-dominated” solutions in $\mathit{\varphi }$.

Using this notation, the set of all Pareto-optimal CDSs for the multicriteria codon optimization problem is expressed as $\{C\in \mathrm{\Phi }\mid \nexists B\in \mathrm{\Phi },\mathit{F}(B\left)\mathrm{dominates}\mathit{F}\right(C\left)\right\}$, where $\mathit{F}(C)=(F_1(C),F_2(C),\dots ,F_n(C))$.

Let a set of multiple features be denoted by a score vector $\mathit{v}\in {\mathbb{R}}^n$ where $v_i$ contains the value corresponding to the i-th OF. Throughout the present paper, the terms score vector and solution are used interchangeably. To describe the recurrence relation of the DP algorithm, we define the vmax operator as follows:

Definition 1

vmax operator gives the non-dominated score vectors of given sets: ${\mathrm{vmax}}_i{\mathit{V}}_i=\mathcal{N}({\cup }_i{\mathit{V}}_i)$, where $\mathcal{N}(\mathit{V})$ indicates the set of all non-dominated score vectors in a set of score vectors $\mathit{V}$.

2.1. Objective and score functions

The score vector function $\mathit{\tau }(c_h,\dots ,c_i)$ is a function of a partial codon sequence $c_h,\dots ,c_i$ $(1⩽h⩽i⩽L)$. Each score function [$\log (w^{\mathrm{CAI}}(c_i)),\mathrm{CPS}(c_{i-1},c_i)$, or $\mathrm{hsc}(c_{i-1},c_i)$] is an element of $\mathit{\tau }$ (the details of these score functions are described below). Users can select OFs from the score functions of CAI, CPB, and HSC, where the lengths of the argument codon sequence are $K_{\mathrm{CAI}}$ = 1, $K_{\mathrm{CPB}}$ = 2, and $K_{\mathrm{HSC}}$ = 2, respectively. If $i-h+1<K_{\eta }$ (i.e. when the partial codon sequence is too short), the corresponding score is set to zero, where $\eta$ indicates an OF type; if $i-h+1⩾K_{\eta }$ (i.e. when the partial codon sequence is long enough), the prefix $c_h,\dots ,c_{i-K_{\eta }}$ is ignored, so that the corresponding score is calculated for $c_{i-K_{\eta }+1},\dots ,c_i$.

Codon adaptation index (CAI): CAI is a measure for quantifying the use of “fitted” codons in given genes [15]. For each amino acid, the “fitted” codon is the most-frequently used codon. Since the fitted codons are thought to reflect corresponding tRNA expression levels, it is believed that the fitted codons are preferentially used in highly expressed genes. Usually, CAI is computed based on the codon frequencies in a set of (highly expressed) host genes.

Given a sequence C of codons coding for an amino acid sequence A, CAI is defined as follows:

$$\mathrm{CAI}(C)={\left({\displaystyle \prod _{i=1}^L}{w}^{\mathrm{CAI}}(c_i)\right)}^{1/L},$$ (2)

$$w^{\mathrm{CAI}}(c_i)=\frac{f(c_i)}{{\displaystyle \underset{c\in \lambda (a_i)}{\max }}f(c)},$$ (3)

where L is the length of the amino acid sequence, $w^{\mathrm{CAI}}(c)$ is the relative adaptiveness of codon c, and $f(c)$ indicates the frequency of codon c in a given set of genes (e.g. highly expressed genes) [15], [17]. In the recurrence computation, logarithm of $w^{\mathrm{CAI}}$ is used as an element of the score vector function $\tau$.

Codon pair bias (CPB): CPB is the log-odds ratio for how frequently each codon pair is observed compared with the expected value:

$$\mathrm{CPB}(C)=\frac{1}{L-1}{\displaystyle \sum _{i=2}^L}\mathrm{CPS}(c_{i-1},c_i),$$ (4)

$$\mathrm{CPS}(c_{i-1},c_i)=\log \frac{f(c_{i-1},c_i)}{\frac{f(c_{i-1})f(c_i)}{f(a_{i-1})f(a_i)}f(a_{i-1},a_i)},$$ (5)

where $\mathrm{CPS}(c_{i-1},c_i)$ ($1<i⩽L$) is the codon pair score of a codon pair $c_{i-1},c_i\text{; }f(c_{i-1},c_i),f\left(a_i\right)$, and $f(a_{i-1},a_i)$ are a codon pair frequency, an amino acid frequency, and an amino acid pair frequency, respectively [16]. CPB was proposed in the context of codon deoptimization for virus attenuation [18]. The previously described single-objective DP, CCTool, also uses CPB as the OF for codon context optimization [16]. To our knowledge, experimental reports on the coding sequences designed using CPB are relatively rare outside of its application in virus attenuation studies. For computer scientists, CPB is an interesting variable for multicriteria optimization, since there can be a trade-off between CAI and CPB.

Hidden stop codons (HSC): Hidden stop codons are expected to prevent erroneous translational frameshift by facilitating early termination [19]. The number of out-of-frame stop codons is expressed as follows:

$$\mathrm{HSC}(C)={\displaystyle \sum _{i=2}^L}\mathrm{hsc}(c_{i-1},c_i),$$ (6)

$$\mathrm{hsc}(c_{i-1},c_i)={\displaystyle \sum _{\sigma \in {\sigma }^{\mathrm{stop}}}}{\displaystyle \sum _{j=1,2}}{I}_{\mathrm{end}}^{\sigma ,j}(c_{i-1},c_i),$$ (7)

where ${\sigma }^{\mathrm{stop}}$ is a set of stop codons. We can easily incorporate the number of other sequence motifs that span continuous multiple codons (e.g. CpG dinucleotide frequency) into our OFs and maximize/minimize that in a similar way. The definition of $I_{\mathrm{end}}^{\sigma ,j}$ is described in Eq. (9).

2.2. Dynamic programming algorithm for multicriteria codon optimization

In order to take into account the nucleotide sequences, such as codon pairs and forbidden sequence motifs, that span continuous multiple codons in our DP, we introduce the parameter $k=\max (K_{\mathrm{score}},K_{\mathrm{motif}})$ [14]. The $K_{\mathrm{score}}$ is the minimum amino acid length necessary to compute the score vector functions. This parameter is determined by considering the user-specified OFs. Each score function has a codon sequence as an argument, and the maximum length of the argument codon sequences is used as $K_{\mathrm{score}}$. $K_{\mathrm{motif}}$ is the parameter for forbidden sequence motifs. It is calculated as $K_{\mathrm{motif}}={\max }_{\sigma \in M}K(\sigma )$, where M is a set of forbidden nucleotide sequence motifs, and

$$K\left(\sigma \right)=\left\{\begin{array}{cc}\lceil \left|\sigma \right|/3\rceil ,\hfill & \mathrm{if}\left|\sigma \right|\mathrm{mod}3=1,\hfill \\ \lceil \left|\sigma \right|/3\rceil +1,\hfill & \mathrm{otherwise}\text{.}\hfill \end{array}\right)$$ (8)

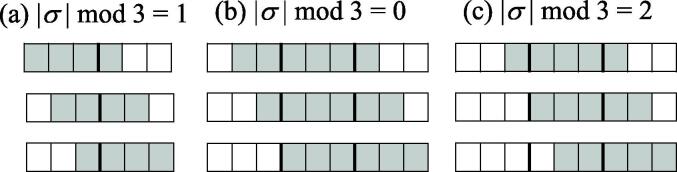
Examples of the three situations for forbidden motifs are shown in Fig. 1.

Fig. 1.

Schematic illustration of the three situations considered in Eq. (8). Bold lines represent boundaries between adjacent codons. (a), (b), and (c) are examples of $|\sigma |$ = 4 [$K(\sigma )$ = 2], $|\sigma |$ = 6 [$K(\sigma )$ = 3], and $|\sigma |$ = 5 [$K(\sigma )$ = 3], respectively. From top to bottom, examples for j = 1, j = 2, and j = 3 are shown. Gray boxes indicate the nucleotides of a forbidden motif.

To rigorously exclude user-specified forbidden nucleotide sequence motifs from the designed coding sequences, the following indicator functions are defined and utilized during the recurrence computation:

$$\begin{gathered} I_{\mathrm{end}}^{\sigma ,j}\left(i\right)=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}{s}_{3i-2-\left|\sigma \right|+j},\dots ,s_{3i-3+j}=\sigma ,\hfill \\ 0,\hfill & \mathrm{otherwise}\text{.}\hfill \end{array}\right) \\ {N}_{\mathrm{end}}^{\sigma }\left(i\right)=\sum _{j=\left\{1,2,3\right\}}{I}_{\mathrm{end}}^{\sigma ,j}\left(i\right), \end{gathered}$$ (9)

where i is an amino acid position; $I_{\mathrm{end}}^{\sigma ,j}(i)$ indicates whether the codon sequence $c_{i-k+1},\dots ,c_i$ has the nucleotide sequence motif $\sigma$ ending at the j-th nucleotide position of the $c_i$ or not, where $j\in \{1,2,3\}$. $N_{\mathrm{end}}^{\sigma }(i)$ is the frequency of the forbidden motif $\sigma$ that ends within the codon $c_i$.

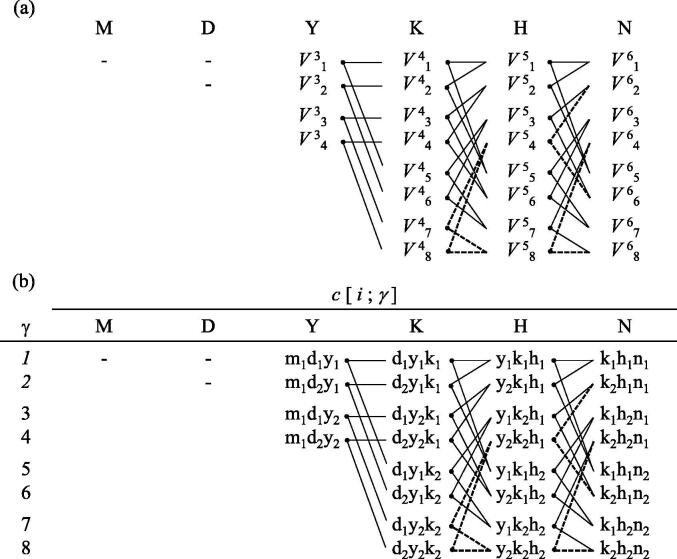
For an amino acid position i, let ${\mathit{V}}_{\gamma }^i$ be the set of all Pareto-optimal score vectors for a conditional subproblem of $a_1,a_2,\dots ,a_i$ $(k⩽i⩽L)$, where the condition is that the 3’ end of the coding sequence of length k is $c[i\text{;}\gamma ]$, where $\gamma$ is an integer variable (a codon assignment index) that specifies the suffix of the coding sequence of the $a_1,a_2,\dots ,a_i$; since the suffix is a sequence of codons with a length of k amino acids, $c[i\text{;}\gamma ]$ = $c_{i-k+1},\dots ,c_i$. Examples of $c[i\text{;}\gamma ]$ are shown in Fig. 2.

Fig. 2.

An example of the dynamic programming recurrence. (a) The relationships between the dynamic programming matrix elements. (b) The suffixes, $c[i\text{;}\gamma ]$, of the coding sequences corresponding to the matrix elements shown in (a); e.g. $c[5\text{;}3]={\mathrm{y}}_1{\mathrm{k}}_2{\mathrm{h}}_1$. Capital letters (M, D, Y, K, H, and N) indicate amino acid codes, and their corresponding non-capital letters are codons: e.g. Y is tyrosine; ${\mathrm{y}}_1$ and ${\mathrm{y}}_2$ represent UAU and UAC, respectively. Each solid line indicates which matrix element (a set of score vectors) is used as the argument of each vmax operation. Dashed lines indicate the matrix elements that are skipped in the vmax operations due to the occurrence of a forbidden sequence motif C AAG CA (${\mathrm{y}}_2{\mathrm{k}}_2{\mathrm{h}}_1$ = UAC AAG CAU and ${\mathrm{y}}_2{\mathrm{k}}_2{\mathrm{h}}_2$ = UAC AAG CAC). This is an example of k = 3.

The recurrence relation of our multicriteria CDS design is as described below. The base case ($i=k$) is as follows:

$${\mathit{V}}_{\gamma }^k=\left\{\begin{array}{cc}\varnothing ,\hfill & \mathrm{if}\exists \sigma \in M,{\displaystyle \sum _{j=1}^k}{N}_{\mathrm{end}}^{\sigma }(j)\ne 0,\hfill \\ {\displaystyle \sum _{j=1}^k}\mathit{\tau }(c_1,\dots c_j),\hfill & \mathrm{otherwise},\hfill \end{array}\right)$$ (10)

where $1⩽\gamma ⩽{\gamma }_k^{\max },{\gamma }_k^{\max }$ is the maximum codon assignment index value of the amino acid position k, and $\mathit{\tau }(c_1,\dots ,c_j)$ is the score vector function of $c_1,\dots ,c_j$. For $i>k$,

$${\mathit{V}}_{\gamma }^i=\left\{\begin{array}{c}\varnothing ,if\exists \sigma \in M,N_{end}^{\sigma }\left(i\right)\ne 0,\hfill \\ vma{x}_{\theta \mid suf[i-1\text{;}\theta ]=pre\left[i\text{;}\gamma \right]}\left\{\mathit{\tau }\right(c\left[i\text{;}\gamma \right])+\mathit{v}\mid \mathit{v}\in {\mathit{V}}_{\theta }^{i-1}\},otherwise,\hfill \end{array}\right)$$ (11)

where $\mathrm{suf}[i-1\text{;}\theta ]$ is the suffix of the $c[i-1\text{;}\theta ]$ with a length of $k-1$ amino acids, and $\mathrm{pre}[i\text{;}\gamma ]$ is the prefix of $c[i\text{;}\gamma ]$ with a length of $k-1$ amino acids; this condition guarantees that $c[i\text{;}\gamma ]$ and $c[i-1\text{;}\theta ]$ share the same codon sequence with a length of $k-1$.

Finally, the Pareto optimal solutions of the overall problem is given by

$${\mathit{V}}^L={\mathrm{vmax}}_{1⩽\gamma ⩽{\gamma }_L^{\max }}{\mathit{V}}_{\gamma }^L\text{.}$$ (12)

If the $c[i\text{;}\gamma ]$ has a forbidden sequence motif that ends within the amino acid position i, the coding sequences including the $c[i\text{;}\gamma ]$ are infeasible, therefore we assign $\varnothing$ to such a ${\mathit{V}}_{\gamma }^i$ and it is not considered in the subsequent DP steps. This branch-and-bound procedure guarantees that no forbidden sequence motif is included in the coding sequences in the decision space $\mathrm{\Phi }$. An example of this is shown in Fig. 2.

The procedure of our dynamic programming is summarized as follows:

Algorithm 1: (Step 1) Initialize ${\mathit{V}}_{\gamma }^k(1⩽\gamma ⩽{\gamma }_k^{\max })$ using Eq. (10); the amino acid position indicator i is set to $k+1$. (Step 2) Compute ${\mathit{V}}_{\gamma }^i(1⩽\gamma ⩽{\gamma }_i^{\max })$ for $a_1,\dots ,a_i$ with Eq. (11); during this computation, a pointer to the original score vector of position $i-1$ is assigned to each $\mathit{v}\in {\mathit{V}}_{\gamma }^i$; if $i<L$, increment i and go to Step 2. (Step 3) After completing the sets ${\mathit{V}}_{\gamma }^L(1⩽\gamma ⩽{\gamma }_L^{\max })$, we obtain all Pareto-optimal solutions ${\mathit{V}}^L$ of the whole amino acid sequence A using Eq. (12); the finally-designed sequences of codons can be constructed through the backtracking starting from each score vector in ${\mathit{V}}^L$ with the pointers assigned to the score vectors during the recurrence computation.

Since the score vector element is computed by summing the $\log (w^{\mathrm{CAI}})$ values in Eqs. (10), (11), the OF value for CAI is obtained as $F_{\mathrm{CAI}}\left(C\right)=\exp {\left(v_{\mathrm{CAI}}^L\right)}^{1/L}$, where $v_{\mathrm{CAI}}^L$ is an element of a score vector ${\mathit{v}}^L\in {\mathit{V}}^L$. The OF value for CPB is obtained as $F_{\mathrm{CPB}}\left(C\right)=v_{\mathrm{CPB}}^L/(1-L)$, where $v_{\mathrm{CPB}}^L$ is an element of ${\mathit{v}}^L$. The OF value for HSC $F_{\mathrm{HSC}}\left(C\right)$ is $v_{\mathrm{HSC}}^L$, which is an element of ${\mathit{v}}^L$.

2.2.1. Merging sets of non-dominated score vectors

The vmax operation used in the recurrence computation merges sets of non-dominated score vectors to obtain the non-dominated vectors in their union. This merging is done by repeatedly merging two sets (e.g. when ${\mathit{V}}_1,{\mathit{V}}_2$ and ${\mathit{V}}_3$ are merged, first ${\mathit{V}}_1$ and ${\mathit{V}}_2$ are merged, then its result [i.e. non-dominated solutions in ${\mathit{V}}_1\cup {\mathit{V}}_2$] and ${\mathit{V}}_3$ are merged). To compute the non-dominated vectors for given sets of score vectors, we use an $O(K)$ algorithm for the problems with two objective functions, where K is the total number of solutions. The $O(K)$ algorithm is based on the algorithm described in the “Maxima” section of [20].

To simplify the explanation, we assume no duplicated score vectors are included in the two lists of score vectors to be merged (duplicated score vectors can be allowed by slightly modifying the following procedure). First, we sort the union of the two lists each of which contains score vectors that are pre-sorted in descending order of OF1 values (if the OF1 values tie, the corresponding score vectors are sorted in descending order of OF2 values). By using the pre-sorted lists, this sorting is done in linear time with respect to the number of elements in the lists. Then, we set the OF2 value of the score vector at the head of the sorted list of the union to ymax, and scan the sorted list from the head. During the scanning, every time we meet a score vector with an OF2 value that is lower than or equal to ymax, we delete the score vector from the sorted list; otherwise, we update ymax by the new OF2 value. After finishing the scanning, we obtain a set of non-dominated score vectors that are sorted in descending order of OF1 value. An example of the merge algorithm is shown in Fig. 3.

Fig. 3.

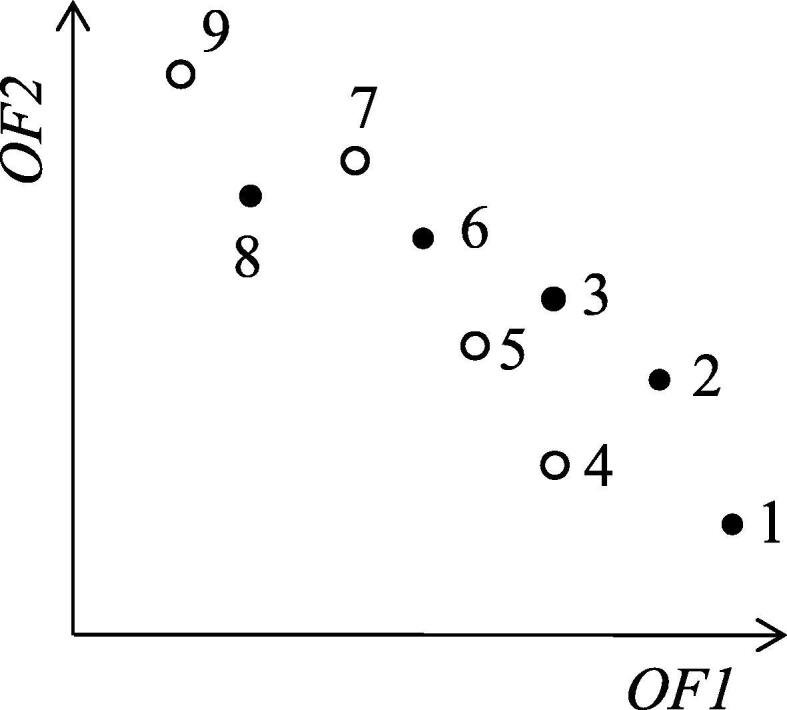
An example for the $O(K)$ merge algorithm. Solid circles indicate the score vectors of list 1, and open circles are those of list 2. The numbers indicate the order in the sorted list of the union of the two lists. We sequentially delete dominated solutions during scanning of the sorted list. In this example, by scanning score vectors 1 to 9, we remove score vectors 4, 5, and 8.

2.3. Correctness of the dynamic programming algorithm

As shown in the paper of the structural RNA alignment by multicriteria DP [21], the correctness of the multicriteria DP is shown by proving (i) deletion of dominated intermediate solutions during the recurrence computation does not delete any Pareto-optimal solutions, and (ii) all feasible intermediate solutions are considered by the recursion. These factors guarantee that all Pareto-optimal solutions of the overall problem are generated by the multicriteria DP algorithm.

Theorem 1

Algorithm 1 produces all Pareto-optimal protein-coding sequences in the feasible decision space for a given amino acid sequence A, score vector function (OFs) $\mathit{\tau }$, and a set of forbidden sequence motifs M.

Proof

(i) As shown in the first case of the proof of Theorem 2 in [21], multicriteria DP algorithms in which the solutions are generated by adding a score vector to each solution of the corresponding subproblems satisfy the monotonicity (if a solution $\alpha$ dominates a solution $\beta$ in a subproblem, $\alpha +s$ dominates $\beta +s$ in a larger problem, where s is a score vector). As can be seen from Eq. (11), the multicriteria codon optimization algorithm satisfies the monotonicity ($\mathit{\tau }$ is added to each $\mathit{v}$). In the multicriteria DP that satisfies the monotonicity, addition of any score vector to a dominated solution in a subproblem never produces Pareto-optimal solutions in larger problems. Therefore, deletion of dominated solutions in each subproblem does not affect the Pareto-optimal solutions of the overall problem.

(ii) Let us consider a recursion equation derived by replacing the vmax operator in Eq. (11) by union. If we assume that each ${\mathit{V}}^{i-1}$ in Eq. (11) contains all feasible solutions of the corresponding subproblem, this replaced recursion gives all feasible solutions of a subproblem (here we call it subproblem A) based on all feasible solutions of all subproblems that share the partial codon sequence with subproblem A and that are located just before subproblem A in terms of amino acid position. All infeasible solutions (those that violate the forbidden sequence motifs) are detected and deleted by checking the $N_{\mathrm{end}}^{\sigma }$ in Eqs. (10), (11).

Since the monotonicity holds as proved in (i), it is sufficient to keep the Pareto-optimal solutions of each subproblem in $\mathit{V}$ during the recurrence computation. Hence Eq. (11) considers all feasible solutions and gives all Pareto-optimal solutions of each subproblem. □

2.4. Constraints

To reduce the computational costs by focusing on the solutions satisfying given constraints, we developed a pruning technique. To prune the states in the recurrence computation, we compute the upper bound of each state. For each $\mathit{v}\in {\mathit{V}}_{\gamma }^i$, elements $U_{\eta }$ of the upper bound score vector are computed as

$$U_{\mathrm{CAI}}=\exp {(v_{\mathrm{CAI}}+v_{\mathrm{CAI}}^{\ast }(a_{i+1},\dots ,a_L))}^{1/L},$$ (13)

$$U_{\mathrm{CPB}}=(1/(L-1))(v_{\mathrm{CPB}}+v_{\mathrm{CPB}}^{\ast }(a_i,\dots ,a_L)),$$ (14)

$$U_{\mathrm{HSC}}=v_{\mathrm{HSC}}+v_{\mathrm{HSC}}^{\ast }(a_i,\dots ,a_L),$$ (15)

where $\eta$ indicates an OF type, and $v_{\eta }$ is an element of $\mathit{v}\text{; }{v}_{\eta }^{\ast }(a_{i+1},\dots ,a_L)$ is the maximal score of $\eta$ for an amino acid sequence $a_{i+1},\dots ,a_L$. The maximal score $v_{\mathrm{CAI}}^{\ast }(a_{i+1},\dots ,a_L)$ is ${\sum }_{j=i+1}^L\log 1=0$. The maximal score, $v_{\mathrm{CPB}}^{\ast }(a_i,\dots ,a_L)={\max }_{c_i}{v}_i^{\ast }(c_i)$, of CPB is computed by using a simple recursion $v_j^{\ast }(c_j)={\max }_{c_{j+1}}{v}_{j+1}^{\ast }(c_{j+1})+\mathrm{CPS}(c_j,c_{j+1})$ from $j=L-1$ to $j=i$, where the base case is $v_L^{\ast }(c_L)=0$ for any codon assignment $c_L$. The maximal score of HSC can also be computed in a similar manner. These maximal score values can be accessed in $O(1)$ time during the recurrence computation in Algorithm 1 by using the arrays storing the precomputed maximal score values. If the upper bound value is lower than a user-predefined lower bound (i.e. when the upper bound value does not satisfy a user-predefined constraint), the state is pruned. This is because designed CDSs through such a state are no longer the solutions that have a score value higher than or equal to the lower bound. Schematic illustration of the constraints is shown in Fig. 4. A similar pruning technique based on dominance has been utilized in the DP for bicriteria pairwise sequence alignment [22].

Fig. 4.

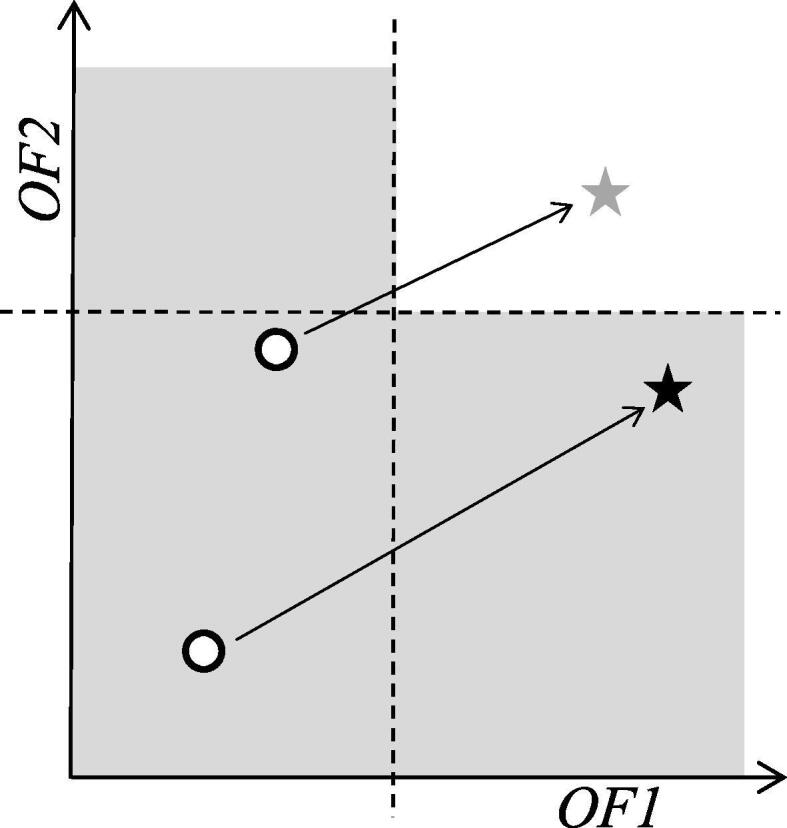
Schematic illustration of the constraints. Here we consider maximization of two OFs as an example. The user-prescribed constraints (i.e. lower bounds) for the OFs are denoted by dashed lines. In this figure, open circles represent intermediate solutions of the DP recurrence computation, black and gray stars are the corresponding upper bounds (this correspondence is indicated by the arrows). The black star indicates the upper bound of the pruned solution; the gray one is not pruned.

2.5. Complexity

The time ($O(L)$) and space ($O(L)$) complexities of unicriterion DP codon optimization have already been analyzed in [14], where the parameter corresponding to the parameter k of the present study is treated as a constant. By (i) replacing the max operation in the unicriterion DP codon optimization by the merge algorithm for two sets of non-dominated score vectors, (ii) treating k as a constant, and (iii) assuming that the largest set ${\mathit{V}}_{\gamma }^i$ has K elements, the bicriteria codon optimization algorithm requires $O(\mathit{LK})$ in both the time and space complexities, where the merging of the non-dominated solutions is performed at every amino acid position.

Multicriteria codon optimization with three or more OFs requires higher complexities than bicriteria optimization since the merge algorithm for three or more OFs has higher computational complexities than the linear complexities of the merge algorithm for bicriteria optimization (e.g. the merge algorithm for three or more OFs in [20] has $O(K{\log }^{n-2}K)$ time complexity, where n is the number of OFs).

2.6. Availability

The codon optimization software and the benchmark dataset are available at the COSMO website ( http://rna.eit.hirosaki-u.ac.jp/cosmo). In addition, we provide two utility Python scripts. (i) A utility script (distNearestParetoSol.py) computes the Euclidean distance between an input CDS sequence and each Pareto-optimal solution in normalized objective space, then outputs the nearest distance; this Python script is useful to examine how distant the input CDS is from the Pareto-optimal solutions. (ii) Another utility script (gc-filter.py) computes the Euclidean distance between the ideal point and each Pareto-optimal solution in normalized objective space (compromise programming approach [10]), where the ideal point is the vector composed of ideal OF values (maximum or minimum OF values in all Pareto-optimal solutions); e.g. if all OFs are maximized, maximum OF values are the ideal OF values. For a user who needs a small number of selected Pareto-optimal solutions, this Python script gives user-specified number of selected Pareto-optimal solutions nearest to the ideal point.

3. Results and discussion

We evaluated the CDS design performance of COSMO by creating a set of adapted sequences from distantly related species (human and yeast). To do this we constructed a dataset of amino acid sequences randomly taken from the human genes available in the UniProtKB/Swiss-Prot database [23]. The benchmark dataset contains 50 amino acid sequences ranging from 80 to 495 amino acids in length.

We designed Pareto-optimal CDSs for the dataset under various settings with respect to forbidden sequence motifs (with or without forbidden sequence motifs), constraints (with or without constraints), and combinations of OFs. In the present study, we performed bicriteria codon optimization, where three combinations (CAI&CPB, CAI&HSC, and CPB&HSC) of OFs were tested. Codon and codon pair frequencies were calculated based on the 5,887 yeast genes taken from the Saccharomyces Genome Database (SGD) [24]. These codon and codon pair frequencies were used to compute the CAI and CPB values. As the forbidden sequence motifs, we specified GACGTC (AatII restriction enzyme recognition motif), AAAAA, CCCCC, GGGGG, and UUUUU in the present benchmarking.

As an example of the CDS design by COSMO, all Pareto-optimal solutions for an amino acid sequence (004_sp_Q6UWN8_ISK6_HUMAN in the dataset) with a length of 81 residues are shown in Fig. 5. In this bicriteria design (CAI and CPB were maximized), 473 Pareto-optimal CDSs were obtained. As can be seen from this example, COSMO usually outputs a large number of Pareto-optimal solutions even when applied to relatively short amino acid sequences.

Fig. 5.

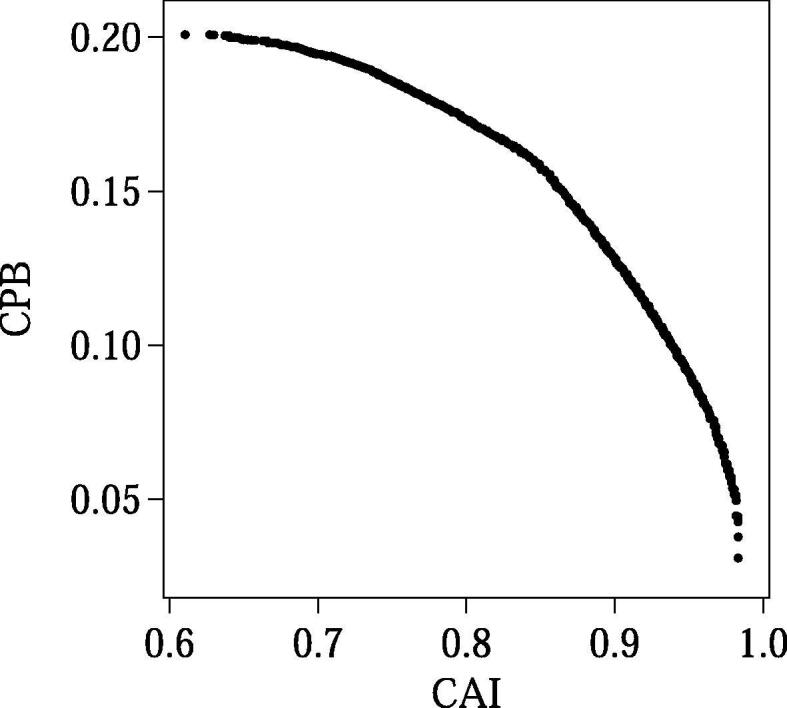
An example (an amino acid sequence with a length of 81 residues) of the Pareto-optimal solutions computed by COSMO. Solid circles indicate the OF values of the designed CDSs.

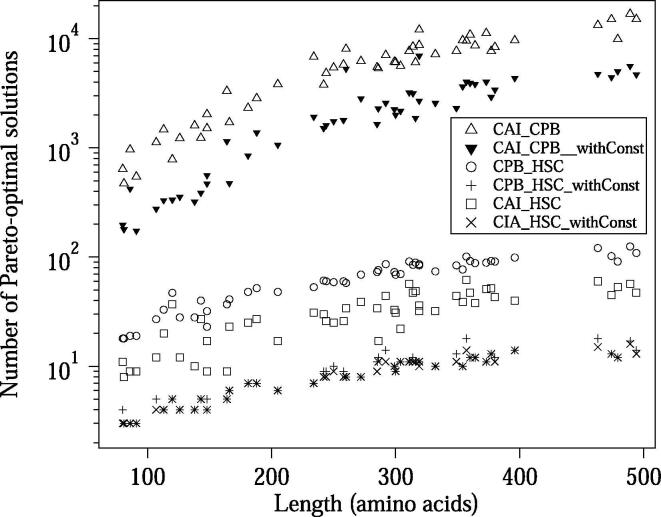
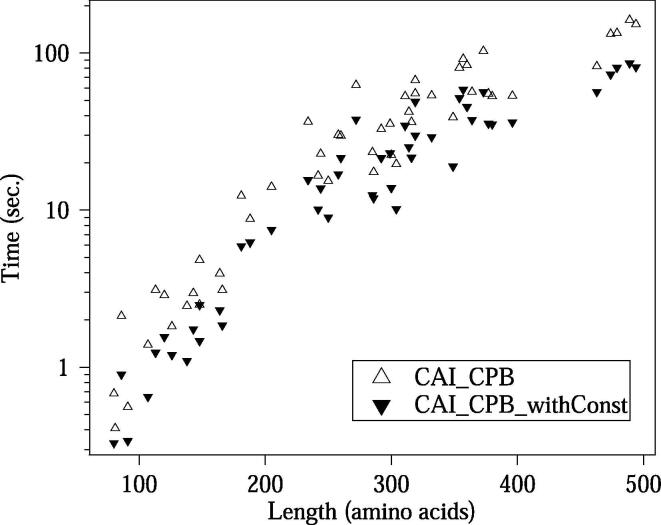
Fig. 6 shows the amino acid length dependencies of the number of Pareto-optimal solutions obtained for the benchmark dataset. We designed CDSs by maximizing two of the three OFs: CAI, CPB, and HSC. It should be noted that, in the case of the designs using CAI&HSC or CPB&HSC, we avoid computing solutions with identical OF values during the recurrence computation, since the occurrences of such solutions drastically raise the number of Pareto-optimal solutions in some cases; leading to the increased run-time and memory usage. This non-redundant processing is available by applying the -d option in COSMO. The run-times for the designs optimizing CAI&CPB are shown in Fig. 7. We performed these benchmarking analyses using a PC with Intel(R) Xeon(R) CPU E5-2699 v4 (2.20 GHz) and 115 GBytes of memory. The run-time for each design optimizing CAI&HSC or CPB&HSC took less than two seconds (data not shown); this fast computation is due to the small number of Pareto-optimal solutions generated when applying the -d option.

Fig. 6.

Design results for the benchmark dataset. Each marker corresponds to an amino acid sequence. The number of Pareto-optimal solutions designed with or without constraints is shown. The design results for CAI&HSC and CPB&HSC were computed using the -d option. If we do not use the -d option, the numbers will drastically increase.

Fig. 7.

The run-time for the designs with and without constraints for the benchmark dataset, where CAI and CPB are maximized. Each marker indicates an amino acid sequence. The designs optimizing CAI&HSC or CPB&HSC with the -d option took less than two seconds (data not shown). If we do not use the -d option, the run-times will drastically increase.

In COSMO, the OF constraints can be used to reduce the number of Pareto-optimal solutions in the output; this leads to reduced computational costs. We tested the performance of the constraints that specify the lower bound of each OF value. If the constraints are applied, COSMO outputs only the Pareto-optimal solutions higher than or equal to the lower bounds. Here we used 0.9 $\times$ range + (the minimum value) as the constraints for each OF, where range = (the OF value obtained by the weighted-sum method in COSMO with uniform weights) − (the minimum OF value). Introducing a cutoff for the Pareto-optimal solutions with OF values lower than these lower bounds makes sense, since we are interested in solutions with higher OF values when maximizing the OFs. These constraints successfully decreased the number of intermediate solutions in the recurrence computation and reduced the run-time. In Fig. 6, Fig. 7, the number of Pareto-optimal solutions and the run-time are shown, respectively, for the designs with and without the constraints. When we performed the bicriteria design for CAI&CPB, CAI&HSC and CPB&HSC, on average, the run-times of the designs with the constraints were 1.76, 1.25, and 2.21 times faster than the designs without the constraints, respectively.

If we do not specify forbidden sequence motifs, the run-time may be shorter, since the number of DP matrix elements, ${\mathit{V}}_{\gamma }^i$, for each amino acid position (at most k = 2) are smaller than those ($k>2$) with long forbidden motifs. On average, the run-time for designs specifying the forbidden motifs was three to four times longer than those without forbidden motifs.

To date, evolutionary algorithms for CDS design with multiple OFs have been proposed and used to design synthetic CDSs. The advantage of COSMO over these evolutionary design algorithms is the optimality of the solutions. To demonstrate the accuracy of the solutions computed by COSMO, we compared the design performance of COSMO and that of a multi-objective genetic algorithm (MOGA). For this performance comparison, we adopt one of the standard MOGA, Non-dominated Sorting Genetic Algorithm-II (NSGA-II) [25]. Our implementation of the NSGA-II for CDS design has the standard structure (initialization, and iteration between evaluation and reproduction) of the genetic algorithm, where one mutation operator and a one-point crossover operator are applied in the reproduction step. In the mutation and crossover operators, whenever the forbidden sequence motifs are found, these motifs are randomly mutated. No duplicated solutions are allowed in one population. The OFs and forbidden sequence motifs used in MOGA were identical to those used in the COSMO benchmarking.

To date, various measures for evaluating the quality of non-dominated solutions have been proposed. In the present study, we evaluated the quality of a set of designed CDSs using the hypervolume indicator (HV) [26], which is one of the standard measures for comparing multi-objective optimization methods. HV is a measure for the volume of the union of hypercubes: ${\cup }_{i=1}^{N_{\mathrm{sol}}}{\mathrm{\Delta }}_i$, where $N_{\mathrm{sol}}$ is the number of solutions in the set of non-dominated solutions, and ${\mathrm{\Delta }}_i$ is the hypercube of solution i; the hypercube $\mathrm{\Delta }=\{\mathit{x}\in {\mathrm{ℝ}}^n\mid 0⩽x_j⩽{\widehat{v}}_j(j=1,\dots ,n\left)\right\}$ is defined by normalized score vector values, ${\widehat{v}}_j$, of each non-dominated solution and a reference point (the origin) in the normalized objective space, where n is the number of OFs. To balance the contributions of the OFs to HV values, we computed the HV values after normalizing the OF values in such a way that the minimum and maximum OF values in each dimension are normalized to zero and one, respectively. A higher HV value indicates a better set of CDS designs.

To determine appropriate values for the parameter set (a mutation probability $p_{\mathrm{m}}$ and a crossover probability $P_{\mathrm{cr}}$) of the MOGA, we performed a grid search with five amino acid sequences, which have diverse sequence lengths, selected from the benchmark dataset. In the mutation operator, each codon is mutated with a probability of $p_{\mathrm{m}}$. We searched all combinations of $p_{\mathrm{m}}=\{0.001,0.005,0.01,0.05,0.1\}$ and $P_{\mathrm{cr}}=\{0,1/3,0.5,2/3,1\}$. In our MOGA, either the mutation or the crossover is applied to generate each child solution in the reproduction step, where $P_{\mathrm{cr}}$ and $P_{\mathrm{mut}}=(1-P_{\mathrm{cr}})$ give the probabilities that determine which one is applied. As a result, ($p_{\mathrm{m}},P_{\mathrm{cr}}$) = (0.005, 1/3) gave the best mean HV value, where five different initial random numbers were utilized for each parameter set. These appropriate parameter values were used in the subsequent benchmark tests.

Table 1 shows the mean run-times for COSMO and MOGA. For CAI&HSC and CPB&HSC, COSMO generates the Pareto-optimal solutions more quickly than MOGA generates designed CDSs. In these designs, duplicated solutions were eliminated using the -d option in COSMO; this reduction in output solutions drastically saved computational costs. In addition to these two cases, another bicriteria design (CAI&CPB) showed that COSMO generated the Pareto-optimal solutions more efficiently than MOGA.

Table 1.

Comparison of mean run-times in seconds between COSMO and MOGA. These were measured on a PC with Intel(R) Xeon(R) CPU E5-2699 v4 (2.20 GHz) and 115 GBytes of memory. In the designs optimizing CAI&HSC or CPB&HSC, the results of COSMO were obtained with the -d option. If we do not utilize the -d option, the run-times will drastically increase.

OFs	COSMO	MOGA
		50	100	200	500	1000
CAI&CPB	40.5	3.9	8.1	17.5	61.0	201.3
CAI&HSC	0.4	3.5	6.6	15.8	61.8	231.3
CPB&HSC	0.3	4.0	7.3	17.9	62.2	216.9

Table 2 shows how many Pareto-optimal solutions generated by COSMO were designed by MOGA; in Table 2, only the CAI&CPB results are shown, as solutions with duplicated score vectors were deleted for both CAI&HSC and CPB&HSC using -d in COSMO. In addition, the mean values for HV are shown in Table 3. MOGA was applied using a population size of 50, 100, 200, 500, and 1000; and an iteration number of 1000.

Table 2.

Rates (%) of the number of Pareto-optimal solutions recovered by MOGA for various population sizes. Mean values for fifty amino acid sequences in the benchmarking dataset are shown.

OFs	MOGA
	50	100	200	500	1000
CAI&CPB	0.2	1.1	3.4	9.9	20.1

Table 3.

Mean HV values of COSMO and MOGA obtained for the benchmark dataset. For those of MOGA, mean HV values for a population size of 50, 100, 200, 500, and 1000 are shown. The values in bold are the best ones. HV(COSMO) $⩾$HV(MOGA) holds in each input amino acid sequence.

OFs	COSMO	MOGA
		50	100	200	500	1000
CAI&CPB	0.91	0.83	0.85	0.86	0.87	0.88
CAI&HSC	0.97	0.94	0.95	0.95	0.96	0.96
CPB&HSC	0.94	0.87	0.88	0.90	0.91	0.92

COSMO outperformed MOGA in almost all aspects of this benchmarking; in particular, the solutions obtained by MOGA did not achieve the complete set of Pareto-optimal solutions. This is partially due to the limited population sizes (from 50 to 1000) used in the MOGA analysis. COSMO can output many more solutions if adequate RAM is available.

COSMO is based on DP, which provides optimal solutions in an efficient manner. The disadvantage of our algorithm is the less flexibility in terms of the choice of OFs; e.g. it is difficult to deal with a global quantity such as the target GC content of a whole sequence. If the user is interested in design problems that can be addressed within the DP, COSMO is the most reliable tool. If this is not the case, evolutionary design algorithms are the most practical choice. For example, if the user wants to optimize a CDS cluster composed of the same proteins, Tandem Designer [13] is suitable for this purpose, since such CDS designs use OF values containing global quantities (e.g. the minimum value of a normalized Hamming distance among all CDS pairs). RNA secondary structure is not optimized in the current version of COSMO. The addition of this type of computation would make COSMO more applicable in more complex CDS problems.

Using the current implementation of COSMO, we can optimize CAI, CPB, and HSC. In literature, the tRNA adaptation index (tAI) [27] has also been proposed as an OF for codon optimization [9]. In addition, dinucleotide counts, including the number of CpG motifs, are also of interest when optimizing CDSs; it has been reported that CG and UA motifs are underrepresented in humans [28], and viruses are weakened by increasing CG or UA nucleotide frequencies in viral genes [29].

In [30], it has been reported that homopolymer codons, which cause frameshifts during translation, have a tendency to be followed by hidden stop codons. Instead of optimizing the total number of hidden stop codons for a whole coding sequence, such position-specific optimization may be useful in enhancing protein expression.

4. Conclusion

We have developed a novel algorithm, COSMO, for obtaining Pareto-optimal solutions for multicriteria CDS design problems, where CAI, CPB, HSC, and forbidden sequence motifs are rigorously taken into account. To efficiently design CDSs, we proposed the application of a constraint technique that prunes the intermediate solutions based on both lower and upper bounds during computation via dynamic programming recurrence. In our benchmark tests, we found that this pruning successfully reduced the run-time of the multicriteria designs.

To evaluate the differences between the Pareto-optimal solutions obtained using COSMO and the non-dominated solutions generated by MOGA, we compared CDSs designed using both approaches. We found that the rates of Pareto-optimal solution recovery by MOGA were far less than the perfect value (100 %). In addition, we found that COSMO efficiently computed sets of Pareto-optimal solutions with higher HV values than MOGA. These results suggest that MOGA may have difficulty in identifying all of the Pareto-optimal CDS solutions. This benchmark test was performed purely in silico. To test these CDS optimization tools more rigorously, it is necessary to compare the performance of these CDSs in vitro/vivo.

Our method provides an exact approach for designing optimal CDSs in terms of multiple OFs, constraints and forbidden sequence motifs. For this reason, COSMO provides superior solutions for CDS design problems within the scope of the settings available in COSMO, while evolutionary design methods have no guarantee of obtaining the Pareto-optimal CDSs for these complex multicriteria design problems. The current version of COSMO is capable of only bicriteria or weighted-sum unicriterion designs; in order to perform optimization with three or more OFs, it is necessary to implement a merge algorithm for three or more OFs.

Funding

This research was partially supported by the Project Focused on Developing Key Technology for Discovering and Manufacturing Drugs for Next-Generation Treatment and Diagnosis from the Japan Agency for Medical Research and Development (AMED).

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.