The k-index is introduced to replace the h-index to evaluate better the scientific excellence of individuals

Abstract

The best possible methods are needed to evaluate the scientific excellence of individuals and research groups in order to award positions and distribute research grants with higher efficiency. It is shown here that for the symmetrical distribution of citations of an individual the currently used h-index is approximately half of the square root of the total number of citations, according to the rule of Hirsch. It is also shown that deviations from this “ideal” h-index are common and they are due to deviations in the citation distributions of different individuals. However, those deviations are not characteristic for the scientific excellence of an individual and therefore they lead only to confusion in scientific evaluation. Therefore the h-index is suggested here to be replaced by the k-index. The k-index of an individual is calculated from his/her all independent citations as self-citations cannot be considered as an indication of the excellence of any paper or its authors (the citation is independent if there is no overlap in the lists of authors of the citing and the cited paper). The k-index takes into account only partial citations for each author of multi-authored papers. In ideal case the shares of the authors in a paper are published in the same paper similarly as shares of the inventors are published in patents. If not, the share of each co-author is taken equal to the inverse of the number of authors of the given paper. The k-index of an individual is defined as the square root from the sum of his/her independent partial citations. The value of the k-index is dependent on the databank used for the citations and on the time of the measurement. If scientists of similar age working in similar fields are compared using the same databank, their personal scientific excellence will be proportional to their k-index. When the k-index is divided by the number of active scientific years, a correction can be made for different ages of different applicants. In average, the k-index has similar values, but a wider range compared to the h-index. More importantly the k-index is not biased by this or that type of citation distribution of an individual, not biased by the self-citations and not biased by the results of the co-authors. The squares of k-indexes of smaller units are additive, and so the k-index is extended to journals, publishing houses, departments, institutions, countries, continents and to the mankind.

h-index; Citation distribution; Self-citations; Multi-authored papers; k-index; Education; Evaluation in education; Information science; Information management; Social policy

1. Introduction

Since the elegant h-index introduced by Hirsch (2005), it has been modelled and widely discussed in the literature in thousands of papers (see for example Bornmann and Danie, 2005; Glänzel et al., 2006; Waltman and van Eck, 2012; Bormann and Leyersdorff, 2018; Aksnes et al., 2019; Leydesdorff et al., 2019), including the original author himself (Hirsch 2010, 2019). Herewith, its properties are discussed focusing on the question whether it contains any meaningful additional information compared to the total number of citations. Further, independent vs self-citations and the role of co-authors are discussed. Finally, the new k-index is defined to characterize better the true personal scientific excellence of an individual. The new k-index is also extended to journals, publishing houses, departments, institutions, countries, continents and even to mankind. As will be shown it is easy to do so as the square of the k-index is additive, while the h-index does not have this helpful property.

Before going into details let us make some general remarks. The first remark is that a single parameter to characterize the scientific excellence of an individual is indeed needed to improve our policies in difficult personal decisions (positions, grants, awards, etc), even if all of us agree that none of us can be described by a single parameter. There are several single parameters widely used in the past, such as the number of papers, the number of citations, the average number of citations per published paper, etc…. When the h-index was introduced by Hirsch, it received a very positive acceptance because it seemed to combine in one complex parameter at least two things: the number of published papers and the number of citations (and so also a kind of an average number of citations per paper). However, at a closer look it turns out that all of us have a much higher number of papers than our h-index, so the h-index is only a very weak function of the number of papers (Sandström and van den Besselaar, 2016). In fact, the h-index is mostly a function of the total number of citations. However, the majority of our citations are simply neglected when the h-index is calculated and the h-index is altered by the type of citation distribution of the author, which holds no information on his/her scientific excellence. All these properties of the h-index lead to lots of discussions in the literature, including this paper.

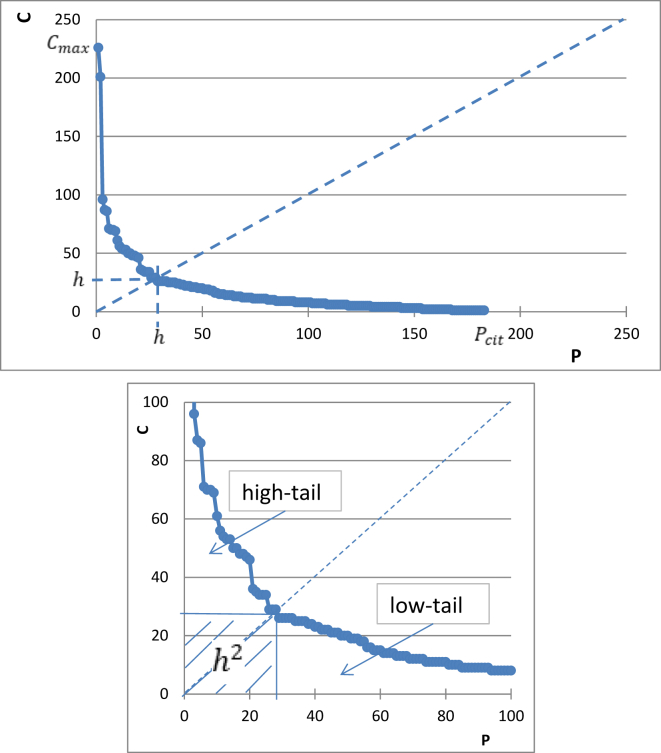
Our goal is to identify a new single parameter that is better in characterizing the scientific excellence of an individual compared to the h-index. This parameter should be calculable by a computer algorithm using scientific databases without looking into scientific details of the researcher. Thus, one can use only the scientific output of the author (the number of his or her papers with the number of authors) and the echo from peers (the number of citations gained by those papers). Each individual in each moment of time, according to each databank is characterized by his or her citation profile (see Figure 1 as an example). At the first look, such graphs are similar for all of us, but at the second look they are different in many details. Our task is to boil down the complex information shown in Figure 1 to one single parameter. It will be shown here that we can do it better than it was done by the h-index and its many alternatives.

Figure 1.

The citation profile of the author (9 January 2019, Google Scholar, all citations, including self-citations). The bottom figure is an enlarged part of the top figure.

2. On the properties of the h-index

The h-index of an individual is the maximum number of papers of this individual, which all have at least the same number of citations. Thus, the h-index is a positive integer number which becomes h = 1 when the individual gains his/her first citation. With time the h-index keeps its constant value, but time to time it increases by sudden integer jumps. As different scientific databases cover different parts of the scientific literature, the h-index is also database-dependent. Thus, the correct expression of the h-index is when the individual, the moment in time and the source/database are all specified. For example, the h-index of the author on 9 January 2019 is h = 28, according to Google Scholar (see Figure 1). This value has been the same for a couple of months and it is expected to have the same value for some more months to go. It is estimated that there are about 10⁴ other researchers world-wide with the same h-index.

In Figure 1 a citation profile of an author is shown as an example, in two different magnifications. Behind Figure 1 there is a table in which all papers are listed in order of their decreasing citations, showing the number of citations obtained by each paper (P is the number of papers starting from P = 1 and C is the number of citations received by a paper). Data points in Figure 1 can be characterized by the following values: C_max = 226 (the maximum number of citations received by the most cited paper of P = 1), P_cit = 182 (the number of papers that received at least one citation, which is 78.8 % of all papers for this author visible in the same database), C_tot = 3,183 (the total number of citations, which is the integral under the curve in Figure 1), h = 28 (the h-index as defined above), C_high = 1,018 (the number of citations in the high-tail of Figure 1), C_low = 1,381 (the number of citations in the low-tail of Figure 1). Based on Figure 1, the following balance of citations can be written:

$$C_{tot}=h^2·\left(1+k_{high}+k_{low}\right)$$ (1)

where $k_{high}\equiv C_{high}/h^2$ and $k_{low}\equiv C_{low}/h^2$. These values are connected to the empirical coefficient a introduced by Hirsch (2005) in his Eq. (1):

$$a=1+k_{high}+k_{low}$$ (2)

As follows from Eq. (2), the theoretical lowest limit of parameter a = 1, which is the case if k_high = k_low = 0 (such a case probably does not exist in reality, at least for h-indexes above 5). As found empirically by Hirsch (2005), the value of parameter a is in the range between 3 and 5 for the majority of the authors. From the above given data the characteristic values of the 182 data points shown in Figure 1 are: k_high = 1.30, k_low = 1.76, a = 4.06, the latter value positioned almost in the middle of the possible interval given by Hirsch. From combining Eqs. (1) and (2) the h-index can be written as:

$$h=\sqrt{\frac{C_{tot}}{a}}$$ (3)

Substituting the actual value of C_tot = 3,183 from Figure 1 and the average value of a = 4 after Hirsch (2005) into Eq. (3), $h\cong 28.2$ is obtained, being quite similar to the actual value of h = 28. This success of Eq. (3) is due to the fact that Figure 1 is relatively symmetrical, i.e. $C_{max}\cong P_{cit}$ (226 vs 182) and $C_{high}\cong C_{low}$ (1,018 vs 1,381). However, it should be mentioned that if the whole interval of possible values after Hirsch is applied (a = 3 … 5), then the following interval of rounded values is obtained from Eq. (3): h = 25 … 33. From this example we can conclude that the h-index is primarily determined by the total number of citations via Eq. (3), while parameter a has a secondary influence on its value.

This finding is further confirmed in Table 1 and Figure 2, where all the data of all those 64 employees of the university of the author are shown, who have their public personal profiles at Google Scholar, indicate our university as their affiliation, have at least 100 citations, at least 10 cited papers and at least h = 5. The 64 people in Figure 2 cover different fields of science, mostly engineering, but also sociology, economy, mathematics, chemistry, physics, medicine, materials science and earth sciences. Only 5 individuals (8 %) have their unique h-indexes, the other 59 individuals (92 %) have other fellow scientists with the same h-index (see Table 2). This is because the h-indexes of the 64 individuals span in the range of only 5–28 (average 2.66 individuals per h-digit).

Table 1.

Characteristic scientiometric values for 64 individuals of the University of Miskolc taken from their public personal Google Scholar profiles on 9^th January 2019 (only individuals with at least C_tot = 100, P_cit = 10 and h = 5 are considered).

Ctot	Initials	Pcit	Cmax	h	a	k
104	TE	20	12	7	2.12	6.4
106	BA	14	18	7	2.16	6.7
115	BT	27	15	6	3.19	8.3
119	AKN	18	20	6	3.31	6.9
130	FJ	33	22	5	5.20	5.3
133	SHK	14	69	5	5.32	6.4
133	SGA	26	22	6	3.69	7.2
134	LJ	30	31	5	5.36	7.0
136	TAN	29	50	5	5.44	7.7
143	CG	12	48	5	5.72	5.4
160	VD	20	23	8	2.50	5.7
162	SS	32	30	6	4.50	6.9
166	VFM	21	31	8	2.59	8.5
168	LA	22	45	7	3.43	6.5
179	KG1	29	56	7	3.65	13.2
189	CB	20	33	8	2.95	7.4
193	BP1	16	145	5	7.72	7.7
196	KL	56	145	7	4.00	9.8
219	PB	29	65	8	3.42	4.4
221	BP2	17	69	6	6.14	8.0
231	VJ	53	18	7	4.71	4.4
238	VG	37	29	10	2.38	10.6
240	MG	38	26	10	2.40	8.1
241	KF	42	38	9	2.98	7.9
254	HA	22	56	8	3.97	12.3
281	SP	39	53	9	3.47	8.4
300	BVG	66	25	9	3.70	10.7
306	NZ	26	45	10	3.06	5.5
310	ZN	23	23	7	6.33	7.6
311	SNP	43	38	11	2.57	9.6
322	TT1	17	107	11	2.66	5.1
385	FB	30	72	13	2.28	8.0
393	DI	47	157	9	4.85	13.4
411	GAL	63	49	9	5.07	10,4
443	MV	44	126	7	9.04	10.2
450	SAK	35	65	12	3.13	11.5
463	PI	54	41	13	2.74	8.1
465	OT	39	110	8	7.27	11.1
466	BLV	40	84	12	3.24	12.9
468	GA	26	110	8	7.31	11.1
492	TT2	33	75	11	4.07	10.0
509	TM	49	103	10	5.09	17.7
522	JI	40	67	13	3.09	15.6
524	LG1	33	148	11	5.24	8.7
561	PAB	33	148	11	4.64	11.6
564	KT	42	72	16	2.20	12.1
570	TG	41	150	11	4.71	18.1
587	DA	81	42	15	2.61	15.2
614	GZ	50	31	11	5.07	12.1
656	SM	46	65	15	2.92	11.9
669	DEV	31	199	11	5.53	12.9
781	DM	72	110	15	3.47	12.8
943	KL	62	200	15	4.19	25.0
1011	RA	100	145	13	5.98	17.3
1062	KJ	123	76	18	3.28	14.8
1083	RM	82	125	16	4.23	16.9
1311	JK	115	155	17	4.54	16.7
1463	FI	74	480	17	5.06	8,8
1518	KS	125	97	20	3.80	19.3
1669	MP	105	120	22	3.45	20.4
1683	VBT	110	104	23	3.18	19.3
1688	BS	154	208	21	3.83	23.0
1800	LG2	72	584	22	3.88	15.2
3176	KG2	180	226	28	4.05	41.1

Figure 2.

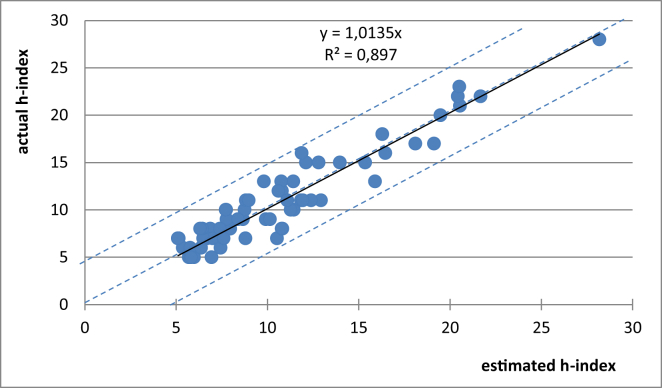
The correlation between the actual h-index and the estimated h-index calculated by Eq. (3) using the average parameter value of Hirsch a = 4 for all the scientists (64 individuals) of the University of Miskolc (Hungary), who have a public personal profile at Google Scholars (and indicate this university as their affiliation) and have their total number of citations at least 100, the number of their cited papers at least 10 and their h-index at least 5. Taken from Google Scholars on 9 January, 2019. The highest point corresponds to Figure 1.

Table 2.

The frequency of different h-values in Table 1.

h-index	frequency within the 64 individuals
5	6
6	5
7	8
8	7
9	5
10	4
11	7
12	2
13	3
15	4
16	2
17	2
18	1
20	1
21	1
22	2
23	1
28	1

As follows from Figure 2, Eq. (3) with the average parameter of Hirsch (a = 4) reproduces the actual h-indexes of these 64 random individuals with $R^2\cong 0.9$ and with a coefficient between the actual and the estimated h-index values being close to 1.0. Thus, the primary information hidden in the h-index is the total number of citations, as follows from Eq. (3). However, the total range of parameter a for the 64 points shown in Figure 2 is found as: 2.1 … 9.0, with only 31 of the 64 points (48 %) appearing within the interval of Hirsch (a = 3.0 … 5.0). The best (but still very weak) correlation is found for parameter a as function of the ratio of C_max/P_cit (see Figure 3). As follows from Figure 3, increasing the ratio of C_max/P_cit the role of high-tail citations increases, leading to some increase in the value of parameter k_high and also in parameter a. It is also supported by the fact that the majority of points with a-value below 3 are found at low C_max/P_cit values. The weak trend line in Figure 3 indicates that individuals with C_max/P_cit larger than 5 are expected to have their a-parameter larger than 5. This is actually true for 4 points out of the total 6 points positioned in this interval of Figure 3.

Figure 3.

Parameter a as function of the ratio of C_max/P_cit for the same 64 individuals as in Figure 2.

The increasing trend in Figure 3 is further confirmed if authors with extra highly cited papers are considered. One of the examples is J.E. Hirsch who obtained his C_max = 8,289 during the last 13 years for his seminal paper (Hirsch, 2005), while he has normal values of P_cit = 267 and h = 67 (9 Jan 2019, Google Scholar). As a result, his C_max/P_cit = 31, and therefore his parameter a = 6.19 (larger than 5, as expected). The high value of his a-parameter is mostly due to the extremely high value of his parameter k_high = 4.24. Even more extreme is the case of KS Novoselov, characterized by the following parameters (Google Scholar, 9 January 2019): C_tot = 241,705; C_max = 44,839; P_cit = 350; h = 127. As a result, his C_max/P_cit = 128, and therefore his parameter a = 15 (larger than 5, as expected). From here and from other similar data (see Table 3) one can conclude that scientists with some extremely highly cited papers generally have a higher value of their a-parameter and thus, according to Eq. (3), their h-index is lower for the same number of total citations. This follows from the definition of the h-index, as citations above the value of h are simply cut off. In other words authors with some extremely highly cited papers are punished by the h-index for their extreme single success stories compared to other authors with the same total number of citations but without single success stories. This is one of the artifacts caused by the h-index.

Table 3.

Data for some highly cited researchers (Google Scholar, 9 January 2019).

Ctot	Initials	Pcit	Cmax	h	a	k
28,752	JE Hirsch	267	8,279	67	6.19	156
54,218	L Lovasz	420	4,558	97	5.65	172
123,684	A Einstein	200	17,433	112	9.69	303
241,705	KS Novoselov	350	44,839	127	15.0	227

Let us now compare different individuals based on their data given in Table 1. The 64 individuals make 64∗63/2 = 2,016 possible couples. For 1614 of them (80.0 %) it is clear without applying the h-index, who is more excellent (A is more excellent than B if A has higher C_max and also higher P_cit compared to B). Within this class of couples 90.2 % are predicted correctly by the h-index, for 4.3 % of them the h-index cannot make a difference between A and B and for 5.5 % of them the h-index predicts the opposite (i.e. B is wrongly shown more excellent than A). These later cases are mostly due to considerably higher a-parameter values of A compared to B, and as follows from Eq. (3), in this case B is preferred by the h-index. One example from Table 1: MV (P_cit = 44, C_tot = 443, a = 9.0, h = 7) vs FB (P_cit = 30, C_tot = 385, a = 2.3, h = 13). So, MV with more cited papers and higher number of citations compared to FB seems to lag behind considerably if the h-index is applied (7 vs 13).

For 402 of the total 2016 couples of Table 1 (20.0 %) it is not clear who is more excellent if A and B are compared, as a larger C_tot value of A is compensated by a larger P_cit of B or vice versa. In the majority of cases in this sub-group (61.2 %) the h-index predicts the same result as follows from the larger total number of citations, while in the minority of cases (24.6 %) the h-index predicts the same result as follows from the larger number of cited papers (in 14.2 % of cases the h-indexes of the two individuals are the same).

Summarizing:

• -although in 0.800∗90.2 = 72.2 % of all cases the h-index correctly predicts who is more scientifically excellent, but the same information is also received from the higher total number of citations or from the higher number of cited papers, so in these cases the h-index does not provide any new information,
• -in 20.0 % of cases it is not clear who is more excellent based on a total number of citations and the number of cited papers, so whatever the h-index predicts, it cannot be logically confirmed. Even in this sub-group the h-index makes the same prediction in the majority of cases as one can do based on a higher total number of citations.
• -in 0.800∗9.8 = 7.8 % of all cases although the winner is obvious from point of view of the total number of citations and the number of cited papers, the h-index wrongly predicts equal values (3.4 %) or even the opposite (4.4 %).

Based on the above we can say that when the h-index provides a clearly correct prediction, then this prediction is the same as follows from the total number of citations and the number of cited papers. When the total number of citations and the number of cited papers lead to controversial results, then in the majority of cases the predictions of the h-index are the same as follows from the larger number of citations. Thus we can conclude that the predictions of the h-index are mostly determined by the total number of citations. In some cases the h-index predicts wrong results (if the right result is that A has a higher scientific excellence if he/she has higher scores in both the total number of citations and number of cited papers). This is mostly due to different citation distributions of different individuals. However, the latter is not connected with the scientific excellence of individuals. Thus, the h-index should be replaced by a better index. Now, let us consider different details to construct the new index.

3. On the total number of citations vs a part of all citations

The new index will be based on the total number of citations. This is because although the h-index is mostly based on the same parameter but it is biased by the citation distribution. The total number of citations is preferred to the total number of papers as any successful scientific activity is measured in efficient communication between the scientists. The measure of a novel scientific results of a researcher efficiently communicated to fellow scientists is the number of independent citations gained by the given researcher.

Now, let us first consider why one should neglect (as it is done by the h-index) the high-tail of the citation distribution of Figure 1, i.e. the citations above the h-level? The present author has no good answer for this. In other words there is no sense and value in neglecting the high tail of citations if a scientific excellence is measured. It should be mentioned that the g-index (Egghe, 2006) and the e-index (Zhang, 2009) were actually introduced to tackle the same problem.

Now, let us consider why one should neglect (as it is done by the h-index) the low-tail of the citation distribution of Figure 1, i.e. the citations obtained by papers having citations below the h-level? The present author has no good answer for this question, either. Moreover, it is believed that it is more difficult to obtain the first citation of a never-cited and half-forgotten paper compared to the next citation of a highly cited paper. This is because it is easy to find and cite a highly cited paper, but it is much more difficult to find and cite an almost forgotten paper. Thus, low-tail citations should be valued and not ignored.

In summary it is suggested here to value all citations of a researcher equally. However, it is not simply suggested here returning to the same old parameter “total number of citations”, it is rather suggested doing it in a new and better way.

4. On the independent citations vs self-citations

Definition: a citation is considered independent, if there is no single overlap in the lists of authors of the citing and cited papers. All other citations are considered self-citations.

Self-citations in relation to the h-index were discussed before by Aksnes (2003), Schreiber (2007) and Engquist and Frommen (2008). Counting citations of a given paper provides us information on the excellence of the paper only, if self-citations are excluded. It does not mean that there is anything wrong about self-citations. It just means that one should not consider a given paper excellent only because one or more authors of the same paper cite it. Therefore, it is suggested here to count only independent citations to measure the scientific excellence of individuals. This view is supported further by the recent paper by Seeber et al. (2019), who showed that some authors deliberately increase their self-citations to look better when evaluated. Moreover, co-authorship can further inflate self-citations, as was shown by Glänzel et al. (2006).

5. On the number of authors of the cited paper

It is a known fact that the larger is the number of authors of a paper, the larger number of citations it gains. This is one of the reasons why the number of authors per paper increases in time, not necessarily within the ethical limits. This is also one of the reasons why one should tackle the multi-author problem if a scientific excellence of an individual is of interest. The same problem was discussed before by Burrell and Rousseau (1995), Oppenheim (1998), Egghe (2008), Schreiber (2008), Leydesdorff and Opthof (2010), Wan et al. (2007), Bouyssou and Marchant (2016), and others.

When several people write a joint paper, they share the work, the responsibility and in rare cases even the shame for it, so they should also share the fame for it, i.e. the citations obtained by the paper. If a paper published by 10 authors obtained 100 citations, it means that at an average, each author obtained 10 citations. If we pretend that each of them obtained 100 citations, then we end up with total 10∗100 = 1,000 citations, which do not exist. This becomes especially problematic if we later calculate the citations of institutions by adding the citations obtained by their employees.

Although the later problem can be avoided with some care, it is simply not fair to compare authors publishing by themselves or in small groups with authors publishing in large groups if the scientific excellence of an individual is a question. For me the author of a single-authored paper with 100 independent citations seems more excellent than one of the authors of a 10-authored paper with the same 100 independent citations.

In ideal world co-authors should publish in their papers their shares in a way that the sum of all shares equal 1, similarly with patents in which the shares of the co-inventors are published. In patents it is done so because those shares are about potential (big) cash. However, the number of citations (or h-index today) is potentially also about (big) cash, as they lead to well-paid positions and grants (see Diamond, 1985). That is why the only fair way to deal with multi-authored papers is to take into account only partial citations, partial meaning the part belonging to an individual co-author.

Summarizing: the total number of citations should be divided within the co-authors of the paper. Each individual should have his/her partial number of citations such that the sum of all partial citations equals the total number of citations. Partial citations are calculated as a share of the given co-author multiplied by the total number of citations gained by the paper. The shares (= fractions of 1) can be calculated in two ways. In the best way the shares of each co-author are published in the paper (Sauermann and Haeussler, 2017). If such shares are not published in the paper, then one should suppose equal shares for each co-author, being equal to the inverse of the number of authors of the paper. This latter method is called fractional counting of citations, see Burrell and Rousseau (1995), Oppenheim (1998), Egghe (2008), Leydesdorff and Opthof (2010), Bouyssou and Marchant (2016).

Let us note that some authors in scientometrics (see for example Lange, 2001; Liu and Fang, 2012) try to guess who had a larger or smaller share in the paper, based on the place of different authors in the author list, or by preferring the corresponding author. The present author feels that we should not guess about any information which could be given by the authors if wished. Partly, because it is a cultural question who is the first author and who is the last author. If the authors have un-equal shares, let them publish those shares in the paper. The present author has never met any editor who denied publishing this information. Just the opposite: some time ago some editors wanted to publish this information, but this initiative died out as authors of multi-authored papers did not wish to provide this information. There is no other reason I can find behind this behavior that i). the authors had equal shares, or ii). the authors hope to get the whole cake, each of them (this is a naive and childish behavior, but unfortunately it seems to work). In both cases we should do as suggested above.

6. The k-index of individuals

Now, let us introduce the k-index, being more characteristic for the scientific excellence of the individual compared to the h-index. The k-index is designed to have in average a similar value as the h-index. Therefore the k-index is calculated as the square root of citations (compare with Eq. (3)), but without the ill-defined parameter a of Eq. (3). Definition: the k-index of an individual is the square root from the sum of his/her independent, partial citations:

$$k_i=\sqrt{\sum _j{p}_j·C_j}$$ (4a)

where k_i is the k-index of an individual i, j is the serial number of a paper of individual i, p_j is the author-share of the individual i in paper j (it should be given in the paper or if not, it is the inverse of the number of authors in the given paper), C_j is the number of independent citations of paper j of individual i (the citation is independent if there is no overlap in the authors list of the citing and cited papers). If scientists of similar age working in similar fields are compared using the same databank for their citations, then their personal scientific excellence will be proportional to their k-index. If the share of the authorship in each paper is estimated as the inverse of the number of authors, Eq. (4a) is re-written as:

$$k_i=\sqrt{\sum _j\frac{C_j}{N_j}}$$ (4b)

where N_j is the number of authors in paper j of the individual i. Compared with the h-index the k-index of the same individual will be:

• -somewhat lower as self-citations are excluded in the k-index,
• -somewhat lower as only partial citations are taken into account in the k-index,
• -somewhat higher, as the ill-defined a-parameter (being larger than 1) of Eq. (3) is eliminated from the definition of the k-index.

Due to the above factors the k-index can be equal, smaller or higher compared to the h-index of the same individual. As follows from Figure 4, the k-index calculated by Eq. (4b) has a similar value to the h-index, as an average. The k-index will not be an integer number rather it will increase a bit with each new citation. It will be especially motivating for young researchers who might worry about the long constant periods of their h-index. The maximum possible value of a k-index of an individual is calculated as:

$$k_{i,max}=\sqrt{C_{tot}}$$ (4c)

Figure 4.

The dependence of the k-index on the h-index for the same 64 individuals shown in Table 1.

Eq. (4c) follows from Eq. (4b), if all citations of the individual are independent citations and if all papers of the individual are single-authored papers (N_j = 1). As follows from the comparison of Eqs (3) and (4c), the maximum possible k-index of an individual is always larger than his/her h-index, as parameter a of Eq. (3) is always larger than 1. As the largest number of total citations is around a million, then (as follows from Eq .(4c)), the k-index will only in rare cases go above 1,000. Let me mention that the h-index of an individual is above 100 only in rare cases. The fact that the k-index has a wider range compared to the range of the h-index is especially obvious for highly cited researchers (see Table 3), at least if they publish in not very large author groups. This wider range of the values of the k-index helps to distinguish better between individuals compared to the possibilities of the h-index. But more importantly the k-index is not biased by this or that type of citation distribution of the individuals, not biased by the self-citations and not biased by the results of the co-authors.

Sometimes individuals of different ages should be compared, being important especially for relatively young researchers. For example, some grants for young researchers are offered in Hungary who already have their PhD degree but are not elder than 45. This means that often young researchers of age 30 vs age 44 should be compared. In this case the pure k-index as defined by Eqs (4a) and (4b) might be misleading as the k-index is a cumulative quantity (similar to the h-index). In this case the yearly average values should be compared (denoted as $k_i^{\ast }$), calculated for the scientifically active period, defined as:

$$k_i^{\ast }\equiv \frac{k_i}{A_i-A_o}$$ (4d)

where A_i (years) is the age of the person i, while A_o (years) is the age when the scientific carrier is usually started, marked by the publication of the first paper. The latter value is function of time and place (culture), but an indicative value of A_o = 24 years can be recommended. Further, A_o can be tuned to take into account empty scientific periods due to maternity leave (two years per child can be added to the standard value of A_o = 24 for females and 1 year per child can be added for males). Thus, the effective value of A_o might be different for different participants in the same competition. For a single male with no children A_o = 24 years seems to be correct, but for a mother of three children A_o = 30 years should be applied in the same competition (as a rule, mothers of three children having a PhD degree are considerably elder than 30). Let us note that the value of A_o in Eq. (4d) should be tuned such that mathematical uncertainty (division by zero) is excluded for all participants.

7. On other k-indexes

It was shown before by Braun et al. (2006) that the h-index can be also used to evaluate the scientific excellence of journals. This can also be done with the k-index. Definition: the k-index of a journal is the square root from the sum of all, independent citations gained by the papers published in the given journal. Mathematically:

$$k_J=\sqrt{\sum _j{C}_j}$$ (5a)

where k_J is the k-index of a journal, j is the serial number of a paper published in that journal, C_j is the number of independent citations obtained by this paper j (independent means there is no overlap between the lists of authors of the citing and the cited papers). If journals of similar age, with similar total number of published papers working in similar fields are compared using the same databank, then their scientific excellence will be proportional to their k-index.

Now, let us define the k-index of publishing houses (societies) and let us denote this value as k_P. Suppose the publishing house (society) has journals with their serial number J and with their individual k-indexes denoted as k_J. Then, the k-index of the publishing house (society) can be calculated as:

$$k_P=\sqrt{\sum _J{k}_J^2}$$ (5b)

As follows from Eq. (5b), the k-index of a publishing house (society) can be simply found from the k-indexes of their journals, while such a simple hierarchical relationship is not valid for the h-index.

It was shown before by Molinary and Molinary (2008) that the h-index can be also used to evaluate the scientific excellence of institutions. This can also be done with the k-index. However, the k-index is hierarchical, so the k-index of any larger unit can be easily found from the k-indexes of the individuals or the k-indexes of smaller units, as the square of the k-indexes is additive (see also Eq. (5b) above).

Let us first define the k-index of a smallest organizational unit, called here department and let us denote its k-index as k_D. Suppose the department has employees with their serial number i and with their individual k-indexes denoted as k_i. Then, the k-index of the department can be calculated as:

$$k_D=\sqrt{\sum _i{k}_i^2}$$ (6)

Care should be taken to take into account in Eq. (6) all the current and past employees of the department. If an employee spent only part of his/her carrier in the given department, then only a portion of his/her k-index should be taken into account in Eq. (6), corresponding to his/her published papers while being the employee of the given Department. Now, let us define the k-index of a larger organizational unit, called here institution and let us denote its k-index as k_I. Suppose the institution has several departments with their serial number D and with their own k-indexes denoted as k_D. Then, the k-index of the institution can be calculated as:

$$k_I=\sqrt{\sum _D{k}_D^2}$$ (7)

Care should be taken to take into account in Eq. (7) all the current and past departments of the institution. If a department spent only part of its lifetime in the given institution, then only the corresponding portion of its k-index should be taken into account in Eq. (7). Now, let us define the k-index of a country, and let us denote its k-index as k_C. The country has many institutions with their serial number I and with their own k-indexes denoted as k_I. Then, the k-index of the country can be calculated as:

$$k_C=\sqrt{\sum _I{k}_I^2}$$ (8)

Care should be taken to take into account in Eq. (8) all the current and past institutions of the country. Now, let us define the k-index of a continent, and let us denote its k-index as k_T. The k-index of a continent can be calculated from the k-indexes of all countries in the given continent k_T as:

$$k_T=\sqrt{\sum _C{k}_C^2}$$ (9)

Care should be taken to take into account in Eq. (9) all the current and past countries. Now, let us define the k-index of mankind, and let us denote its k-index as k_M. The k-index of mankind can be calculated from the k-indexes of the continents as:

$$k_M=\sqrt{\sum _T{k}_T^2}$$ (10)

It should be noted that at present time there is no ET civilization known to compare the k_M parameter with, so for the time being k_M has only a symbolic meaning.

8. Discussion

Before showing some specific examples let us write a simplified equation for the simplified calculation of the k-index of an individual i, written by Eq. (4b):

$$k_i=\sqrt{\frac{k_{ind,i}·C_{tot,i}}{N_{av,i}}}$$ (11)

where C_tot,i is the total number of citations gained by individual i, k_ind,i is the ratio of his/her independent citations to his/her total number of citations (its value is between 0 and 1), N_av,i is the weighted average number of authors in the cited papers of the given author (this value is usually larger than 1). Eq. (11) is true for the case when the shares of the authors in each paper are found as the inverse of the number of authors in those papers.

The present author (KG2 in Table 1) has 3,183 total citations, but his number of independent citations is only 2,582, so his k_ind.i = 0.811 (meaning that 81.1 % of all his citations are independent, while 18.9 % of all his citations are self-citations at least from the point of view of one of the co-authors of his papers). His individual k-index calculated by Eq. (4b) appeared to be k_i = 41.1, which is higher than his h-index (= 28, see Table 1). Substituting these values into Eq. (11), the weighted average number of authors in his papers follows as: N_av,i = 1.53. This is similar (but not the same) as the actual average number of authors in his papers (not weighed).

As the average value of parameter a in Eq. (3) is around 4, we can claim that for individuals with the average number of authors in their papers not exceeding 4, their k-index will be usually larger than their h-index, especially if the ratio of their self-citations is not too high. On the other hand, for individuals publishing in large groups of co-authors and/or working with high ratio of self-citations, their k-index will be lower compared to their h-index. This is because the k-index is designed to express the scientific excellence of individuals, separated from the effect of their co-authors. The authors publishing in large groups should not consider the k-index as a “punishment”. They should realize that this is a fair way of comparison of their results with those who publish in small groups or by themselves. Their pain connected with their lower k-index compared to their higher h-index should be partly released by the fact that the k-index is inversely proportional not to the average number of the authors in their papers, rather to the square root of this quantity.

In the last column of Table 1 the k-indexes of all the 64 individuals considered in Table 1 are calculated by Eq. (4b) based on the same databank (Google Scholar) and the same time (9 January, 2019). The two indexes are compared in Figure 4. One can see that the slope of k as function of h is close to 1.0 for 64 independent points, so the average of the h-index of Hirsch is almost the same as the average of our new k-index (this was our purpose). This is because the average of $k_{ind,i}/N_{av,i}$ of Eq. (11) is close to 4, similarly as the average value of coefficient a of Eq. (3).

On the other hand, a large scatter of data points can be seen in Figure 4, mostly because individuals with similar numbers of their citations differ in their citation distributions, in the ratios of their self-citations and in the average number of their co-authors, which all make their h-index and their k-index quite different (this was also our purpose, otherwise the k-index would carry the same information as the h-index). For example, at h = 10, the values of the k-index are in the interval between 5 and 18. This is a considerable difference, which makes the k-index based conclusions often quite different from the h-index based conclusions. Let us present it on the above example, comparing MV with FB of Table 1. According to the h-index FB (h = 13) seemed to be much better than MV (h = 7). However, according the k-index the opposite result is obtained: MV is judged better (k = 10.2) than FB (k = 8.0). The judgement based on the k-index is in better agreement with the higher number of cited papers and citations of MV (P_cit = 44, C_tot = 443) compared to FB (P_cit = 30, C_tot = 385). Thus, the k-index seems to perform better compared to the h-index. However, let us note that this is only because MV and FB have similar ratios of their $k_{ind,i}/N_{av,i}$ values. As follows from Eq. (11), if this ratio was much lower for MV compared to FB, then MV would have a lower k-index compared to FB despite his/her higher P_cit and C_tot values.

There would be no sense introducing the k-index instead of the h-index if their predictions were the same in the majority of cases. However, as follows from Table 1, this is not the case, especially if couples to be compared do not differ from each other more than twice in their total number of citations. For example, FB is in the middle of Table 1 with his C_tot = 385. In the range of C_tot = 192 … 770 there are 36 individuals. For 2/3 of them the h-index based prediction is opposite to the k-index based prediction, and the two predictions coincide only in 1/3 of cases. Thus, we can claim that although both the h-index and the k-index are based on the total number of citations, and in average the h-index has a similar value to k-index, their predictions differ significantly.

In Figure 5 the time dependences of the h-index and the k-index of the author are compared. Both graphs have strange incubation periods before 1998. This is because the early scientific career of the author (1984–1989) was interrupted by political events in Hungary (1989) and his scientific career was re-started again only in 1994. The k-index is higher compared to the h-index in Figure 5 mostly because the present author usually publishes himself or in relatively small groups (see Eq. (11) and N_av,i = 1.53 estimated above). Take note on the differences in the details in the two lines of Figure 5. Neglecting the incubation period, the time dependence of the k-index is smooth, reflecting the smooth scientific activity of the author during the last 25 years. On the other hand, a 3-years plateau is observed in his h-index at h = 10 (between 2005 and 2007), which has no reason behind except the random and uncontrollable distribution of the citations. If the author was evaluated by his stagnant h-index in early 2008, he could gain a negative remark mentioning that his h-index had been the same for 3 years, probably meaning his low recent scientific activity. As follows from the trend of the same h-index since 2008 it would have been a misleading conclusion. This misleading conclusion is another artifact caused by the h-index and has nothing to do with the activity or with the scientific excellence of the author in that period. Such an artifact is absent in the time dependence of the k-index, proving its superiority compared to the h-index. The time dependence of the k-index shows only some acceleration of the values, which are expected to slow down in the coming decades, due to reasons of aging of both the author and his papers.

Figure 5.

The time dependence of the h-index and the k-index of the present author (h = 25 is shown instead of 28 of Table 1 in this graph as the data are calculated from independent citations). Note a strange 3-year plateau in the h-index at h = 10 (between 2005-2007), while the time-dependence of the k-index is a smooth function of time.

9. Conclusions

It was shown that the h-index is mostly determined by the total number of citations. It is also shown that the deviations of the h-index from half of the square root of the total number of citations do not hold any additional value to judge the scientific excellence of an individual, compared to the total number of citations, it leads only to confusion. Therefore the h-index should be replaced by a better index. Such an index is suggested here as a k-index.

The k-index of an individual is based on all citations of the individual. The k-index uses only independent citations, as self-citations cannot be considered as an indication of the excellence of any paper or its authors. The k-index takes into account only partial citations for each author of a multi-authored paper, the sum of those partials being equal the total number of citations. In ideal case the shares of the authors are published in the paper similarly as shares of the inventors are published in patents. If not, the share of each co-author is taken equal to the inverse of the number of co-authors. The partial number of citations for the given author of the given paper is calculated as the share of the given author in the given paper multiplied by the total number of citations gained by the paper.

The k-index of an individual is defined as the square root from the sum of his/her independent partial citations (see Eqs. (4a), (4b), (4c)). If scientists of similar age working in similar fields are compared using the same databank for their citations, then their personal scientific excellence will be proportional to their k-index. The k-index can also be divided by the number of active scientific years (see Eq. (4d)), being especially important in comparing young scientists of different ages and different family background (with or without children).

The average values of the h-index and that for the k-index for the randomly selected group of scientists is almost the same. However, the range of the k-index for highly cited people is larger compared to the range of the h-index (see Table 3), as the h-index cuts off most of the citations of highly cited papers. Moreover, the h-index is an integer number, while the k-index is usually not an integer. All this makes the k-index more suitable to compare individuals than the h-index. More importantly the k-index is not biased by this or that type of citation distribution of an individual, not biased by the self-citations and not biased by the results of the co-authors. However, similar to the h-index, the k-index is cumulative and is dependent on the databank used for the citations and on the moment of the assessment.

The k-index of a journal is defined as the square root from the sum of independent citations gained by papers published in the given journal (see Eq. (5a)). If journals of similar age, similar total number of published papers working in similar fields are compared using the same databank, then their scientific excellence will be proportional to their k-index.

The k-index is hierarchical (the squares of the k-indexes are additive), so the k-index of a publication house (society) can be easily calculated from the k-indexes of its journals, the k-index of a department can be easily calculated from the k-indexes of its employees, the k-index of the institute can be easily calculated from the k-indexes of its departments, the k-index of the country can be easily calculated from the k-indexes of its institutions, the k-index of a continent can be easily calculated from the k-indexes of its countries and the k-index of mankind can be easily calculated from the k-indexes of the continents (see Eqs (5b), (6), (7), (8), (9), (10), (11)). The h-index does not have this helpful hierarchical property. So, although all the above summarized h-indexes can be defined and calculated, their calculation takes much more effort compared to their k-index analogues.

Declarations

Author contribution statement

George Kaptay: Analyzed and interpreted the data; Wrote the paper.

Funding statement

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Competing interest statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.