Abstract
Endolysosomal compartments maintain cellular fitness by clearing dysfunctional organelles and proteins from cells. Modulation of their activity offers therapeutic opportunities. Quantification of cargo delivery to and/or accumulation within endolysosomes is instrumental for characterizing lysosome-driven pathways at the molecular level and monitoring consequences of genetic or environmental modifications. Here we introduce LysoQuant, a deep learning approach for segmentation and classification of fluorescence images capturing cargo delivery within endolysosomes for clearance. LysoQuant is trained for unbiased and rapid recognition with human-level accuracy, and the pipeline informs on a series of quantitative parameters such as endolysosome number, size, shape, position within cells, and occupancy, which report on activity of lysosome-driven pathways. In our selected examples, LysoQuant successfully determines the magnitude of mechanistically distinct catabolic pathways that ensure lysosomal clearance of a model organelle, the endoplasmic reticulum, and of a model protein, polymerogenic ATZ. It does so with accuracy and velocity compatible with those of high-throughput analyses.
INTRODUCTION
Lysosomes (hereafter endolysosomes, EL) have for long time been considered static organelles ensuring degradation and recycling of cellular wastes. However, they are all but static and their activity, intracellular distribution, and number, as well as their capacity to welcome cargo, are regulated by various signaling pathways and cellular needs (Huotari and Helenius, 2011; Bright et al., 2016; Ballabio and Bonifacino, 2019). By clearing damaged organelles and proteins from cells, they make a substantial contribution to tissue and organ homeostasis. Cumulating knowledge expands the number of diseases directly and indirectly linked to their dysfunction, from rare lysosomal storage disorders (Marques and Saftig, 2019) to more frequent cancers, metabolic and neurodegenerative diseases (Fraldi et al., 2016; Kimmelman and White, 2017; Gilleron et al., 2019). Quantitative approaches to monitoring the magnitude of the delivery to EL of proteins or organelles to be removed from cells or the accumulation of unprocessed material within their lumina are expected to contribute to understanding of the mechanistic details of lysosomal-driven pathways and may find application for diagnostic and therapeutic purposes.
Here, we used confocal laser scanning microscopy (CLSM) to monitor delivery and/or luminal accumulation of cargo within LAMP1- or RAB7-positive EL. As cargo, we selected a model organelle (the endoplasmic reticulum [ER]) and a model disease-causing aberrant gene product (the polymerogenic ATZ variant of the secretory protein α1-antitrypsin), since their lysosomal turnover has clear connection with human diseases (Marciniak et al., 2016; Bergmann et al., 2017; Hubner and Dikic, 2019). As such, the catabolic pathways under quantitative investigation were recov-ER-phagy, which ensures lysosomal removal of excess ER during resolution of ER stresses (Fumagalli, Noack, Bergmann, Presmanes, et al., 2016; Loi et al., 2019), ER-to-lysosome-associated degradation (ERLAD) (Fregno and Molinari, 2019) that removes proteasome-resistant misfolded proteins from cells by delivering ER portions containing them to the EL (Forrester, De Leonibus, Grumati, Fasana, et al., 2019, Fregno, Fasana, et al., 2018) as well as conditions that mimic starvation-induced, FAM134B-driven ER-phagy (Khaminets, Heinrich, et al., 2015, Liang, Lingeman, et al., 2020). Quantitative analyses of CLSM images were first performed with classic segmentation algorithms, which rely on a set of manually defined features and the training of machine learning. Despite careful optimization, these tended to fail with objects of heterogeneous signal intensity and morphology (Kan, 2017), as EL in mammalian cells are. The performance of machine learning approaches remained well below human accuracy, for example, when the quantification tasks had to distinguish empty EL from EL capturing select material to be cleared from cells, such as an organelle (e.g., the ER) or a disease-causing polypeptide. We therefore turned to deep learning (DL), a set of machine learning techniques that involves neural networks with many layers of abstraction (LeCun et al., 2015). Supervised DL methods are computational models that extract relevant features from sets of human-defined training data and increasingly adapt with multiple iterations to perform a specific task (Marx, 2019). DL has been applied to many cellular image analysis tasks (Moen et al., 2019) and the application of DL techniques to morphometric studies of subcellular structures (in our study organelles, organelle portions and protein aggregates) is sought after (Moen et al., 2019).
Among the neural network architectures, U-Net has been used for detection and segmentation of medical and light microscopy images (Ronneberger et al., 2015; Falk et al., 2019). U-net is especially useful due to its training ability with limited annotated data sets (Van Valen et al., 2016; Bulten et al., 2019; Nguyen et al., 2019; Oktay and Gurses, 2019; van der Heyden et al., 2019; Zhuang et al., 2019). Additionally, U-Net automatically finds the representation of an image, which optimizes the segmentation performances through the use of the typical architecture of a convolutional network on subsequent abstraction levels, while adding an up-sampling path that increases network optimization by propagating context information to higher resolution layers (Ronneberger et al., 2015). In this study, we developed a novel DL approach to perform detection and segmentation of endolysosomal degradative compartments. For this, we constructed a dataset of images fully annotated manually by operators and built an optimized neural network architecture based on U-Net. We then integrated this DL framework into an ImageJ plugin, which we provide, to streamline the segmentation and analysis tasks. We challenged the neural network architecture for its capacity to quantitatively assess three catabolic pathways with proven involvement in maintenance of cellular homeostasis and proteostasis (recov-ER-phagy, ERLAD and ER-phagy). We evaluated the network performance with different metrics: Intersection over Union (IoU), Receiver Operating Characteristic (ROC) curve, and F1 scores for segmentation and detection tasks (Sokolova and Lapalme, 2009; Moen et al., 2019). LysoQuant determined the magnitude of recov-ER-phagy, ERLAD, and ER-phagy and the consequences of gene editing inactivating crucial regulatory elements of the pathways. It did so with high accuracy and provided information on a series of parameters such as number, size, shape, and position of empty and loaded EL that are instrumental to understanding the pathways under investigation and the consequences of their modulation in the finest detail. Its analytic speed makes LysoQuant useful for high-content screening.
RESULTS
Manual detection of endolysosomes
Ectopic expression of the ER-phagy receptor SEC62 in mouse embryonic fibroblasts (MEF) triggers delivery of ER portions within LAMP1-positive EL for clearance (Fumagalli, Noack, Bergmann, Presmanes, et al., 2016; Loi et al., 2019). SEC62-labeled ER portions accumulate within EL upon inhibition of lysosomal activity with bafilomycin A1 (BafA1) (Klionsky et al., 2016). We reasoned that this is a paradigmatic experiment to set up an approach that performs automated, image-based, quantitative analyses of EL features and function.
We first established a gold standard of EL detection accuracy in confocal laser scanning microscopy (CSLM) by asking three operators to manually annotate 1170 LAMP1-positive EL from 10 cells (in four biological replicates). We generated a lab consensus image, defined as the pixelwise regions annotated by at least two out of three operators. We then calculated the average IoU for each operator. Here, we were interested in segmentation differences between single operators, so we quantified the performance in drawing all EL irrespective of their content. This resulted in an average IoU of 0.850 ± 0.040 or a relative standard error of 12.9 ± 3.2%.
Automatized detection of endolysozymes: available approaches
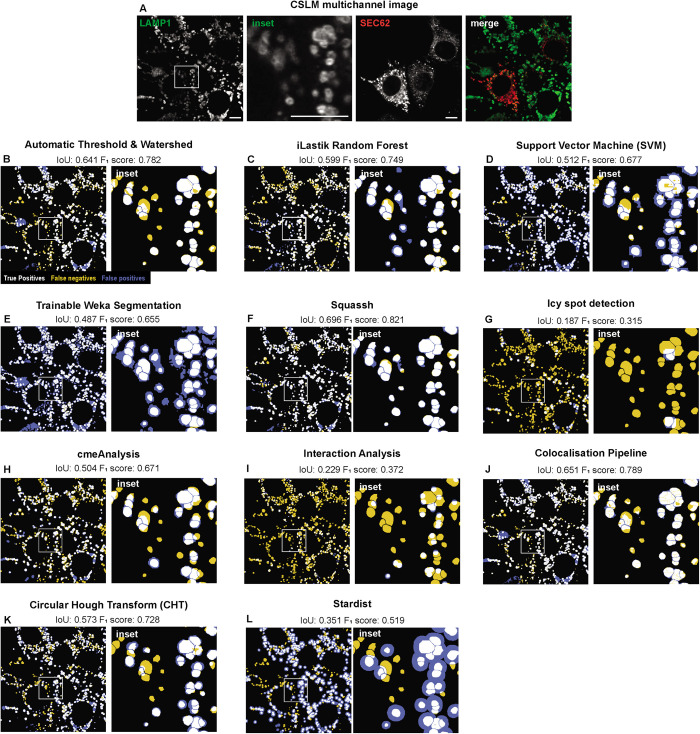
Next, we assessed the capacity of available image analysis approaches to faithfully recognize individual EL dispersed in the mammalian cells’ cytosol. EL are revealed in CSLM with antibodies to the endogenous surface protein LAMP1 (Figure 1A, green and its inset). Their size, the intensity of their surface signal, their intracellular distribution, and the distance between individual EL vary within a cell and among different cells (Figure 1A, inset). Thus, automatized analyses aiming at establishing the number of EL (detection task) and defining their shape (segmentation task) often fail when applied to biological samples. For example, common standard image analysis approaches that rely on automatic threshold with IsoData algorithm followed by watershed segmentation (Soille and Vincent, 1990; IoU 0.641, F1 score 0.782. Figure 1B, Supplemental Figure 1B), machine learning approaches such as iLastik Random Forest (Berg et al., 2019; IoU 0.599, F1 score 0.749. Figure 1C, Supplemental Figure 1C), Support Vector Machine (Sommer et al., 2011; IoU 0.512, F1 score 0.677. Figure 1D, Supplemental Figure 1D), Trainable Weka Segmentation (Arganda-Carreras et al., 2017; IoU 0.487, F1 score 0.655. Figure 1E, Supplemental Figure 1E), but also state-of-the-art algorithms previously developed for quantifying endosomes, such as Squassh (Helmuth et al., 2009; IoU 0.696, F1 score 0.821. Figure 1F, Supplemental Figure 1F), Icy spot plugin detection (de Chaumont et al., 2012; IoU 0.187, F1 score 0.315. Figure 1G, Supplemental Figure 1G), cmeAnalysis (Aguet et al., 2013; IoU 0.504, F1 score 0.671. Figure 1H, Supplemental Figure 1H) and object-based colocalization algorithms, such as the Interaction Analysis plugin (Helmuth et al., 2010; IoU 0.229, F1 score 0.372. Figure 1I, Supplemental Figure 1I) or the Colocalisation Pipeline plugin (Woodcroft et al., 2009; IoU 0.651, F1 score 0.789. Figure 1J, Supplemental Figure 1J), fail to satisfactorily distinguish individual EL if these are located in close proximity to each other. The Circular Hough Transform (IoU 0.573, F1 score 0.728. Figure 1K, Supplemental Figure 1K; Atherton and Kerbyson, 1999), when applied to detect circular bright (EL membrane) or circular dark regions (EL lumen), fails to detect EL in samples with heterogeneous intensity of their surface signal and to segment their shape (Figure 1K, Supplemental Figure 1K, inset). Finally, the application of Stardist star-convex polygons, which involves the training of a deep learning network (Schmidt, Weigert, et al., 2018; Weigert et al., 2020), correctly recognizes the positions of most of the individual EL with strong membrane signals but fails to recognize those with low intensity (IoU 0.351, F1 score 0.719. Figure 1L, Supplemental Figure 1L). Stardist also exaggerates EL size, resulting in poor shape definition, which would prevent the recognition of differences in shape factors and the overlapping of EL boundaries when in close proximity.
FIGURE 1:
Standard segmentation approaches. (A) CLSM image where LAMP1 decorates the limiting membrane of EL and its inset. (B) Automatic IsoData thresholding followed by watershed segmentation; (C) random forest machine learning with iLastik; (D) Support Vector Machine (SVM); (E) trainable Weka segmentation; (F) Squassh region competition segmentation; (G) Icy spot detection plugin; (H) cmeAnalysis; (I) Interaction Analysis ImageJ plugin; (J) Colocalisation Pipeline ImageJ plugin; (K) circular Hough transform (CHT); (L) Stardist star-convex polygons ImageJ plugin. In all images, true positives are in white, false negatives in yellow, and false positives in blue with respect to manual segmentation. F1 score for segmentation and Intersection over Union (IoU) are indicated.
The unsatisfactory results obtained with the approaches presented above prove the need for more reliable and accurate methods for rapid, automatic segmentation and quantification of EL shape and activity.
Detection and classification of endolysosomes: LysoQuant workflow
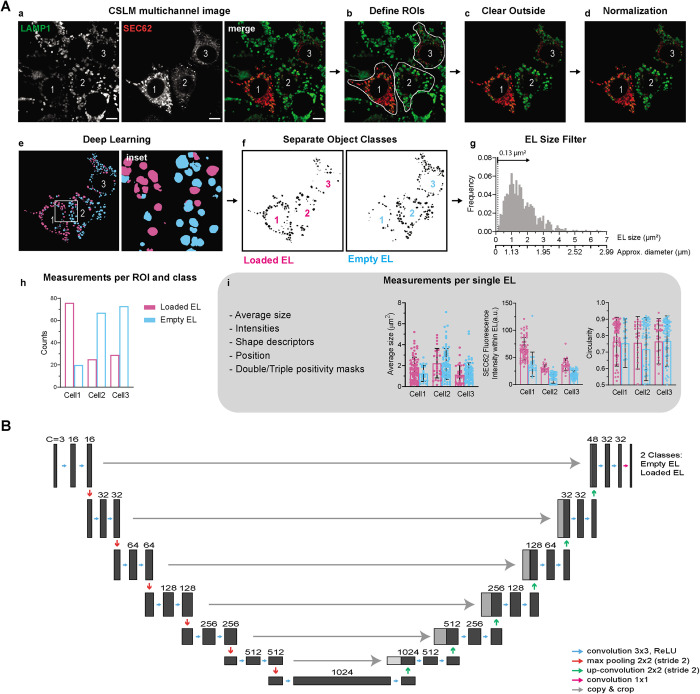
To tackle the weaknesses of these approaches in identifying and offer quantitative information on number, size, and other properties of cellular EL, we developed a supervised DL approach that we named LysoQuant. We anticipate here the analysis workflow initially established on the same cells analyzed in Figure 1, while leaving the details of the DL architecture and performance to the next sections. The image shows eight cells, where the EL have been labeled with an antibody to endogenous LAMP1 (Figures 1A and 2Aa). Three cells express variable levels of ectopic SEC62, which is labeled with an antibody to the HA epitope at the SEC62’s C-terminus. Cell 1 produces high, and cells 2 and 3 low levels of SEC62 (Figure 2Aa, SEC62). After drawing multiple regions of interest (ROIs), each delimiting one of the three cells to be analyzed (Figure 2Ab), we select channels corresponding to LAMP1-immunoreactivity (green) to visualize individual EL and to HA-immunoreactivity to show ectopically expressed SEC62 (red). All signal outside the ROIs is cleared (Figure 2Ac). The image is then normalized with min and max in the range [0, 1] (Falk et al., 2019; Figure 2Ad), linearly brought to a pixel size of 0.025 µm, and sent to the U-Net DL framework (either local or remote) for segmentation to generate a 16-bit image. Pixels corresponding to empty and loaded EL (defined as not containing or containing SEC62, respectively) take values 1 and 2, respectively (Figure 2A, e and f). In Figure 2Ae (and the inset), empty EL are colored in cyan and loaded EL in magenta. Given the optical sectioning properties of confocal microscopy, quantification relies on a good choice of the acquisition focal plane, where most of the EL are luminally cut. For this reason, we added an area threshold step corresponding to our minimum annotated EL size. To set this, we plotted a histogram of all annotated sizes from training images and set the filter threshold to the minimum value of this dataset (EL area larger than 0.13 µm2, Figure 2Ag, corresponding to an approximate EL diameter of 0.4 µm). This threshold is configurable.
FIGURE 2:
Analysis workflow and deep learning architecture. (A) Analysis workflow. (a) Multichannel CLSM image. LAMP1 decorates the limiting membrane of EL. SEC62 stains the cargo. (b) Cells to be analyzed are identified as regions of interest (ROIs). (c) Signal outside ROIs is cleared and image is converted to RGB color image. (d) This RGB is then normalized in the range [0, 1] and rescaled to a pixel size of 0.025 µm. (e, f) Image is segmented into two classes: empty (cyan) and loaded EL (magenta). Classes are filtered for a configurable minimum size, which in our case was equal to the minimum of all annotated EL (dotted line, n = 1573). Diameter scale was also added as a reference. (g–i) Total number of EL for each class and each ROI is listed with a configurable number of individual EL parameters (e.g., average size, fluorescence intensity, circularity). (B) Deep learning architecture is a seven–resolution level 2D U-net fully convolutional network with 16 base feature channels that takes RGB images as input. Green channel shows the EL structure, red channel the protein or the ER subdomain delivered within EL.
For each of the previously defined ROIs, the software identifies the segmented objects and quantifies total numbers for each class (Figure 2Ah). This workflow has been implemented in an ImageJ plugin that performs all the steps described above. Segmentation is instrumental for the assessment of morphological measurements for each EL, which include average size, shape descriptors such as circularity, position, and fluorescence intensity corresponding to cargo load, within EL (Figure 2Ai). Furthermore, and instrumental in analyzing more complex phenotypes, sequential quantification for multiple protein markers on the same cell and simple Boolean algebra between segmentation masks can be used to identify multiple positivity combinations.
Insufficient performance of a five-level neural network
Deep learning segmentation with U-Net architecture was first implemented with a 2D five-level and 64-feature-channel fully convolutional neural network (Falk et al., 2019). We trained this network with confocal images of 10 single cells, in which two operators fully annotated, at pixel level, 1573 individual EL and defined if they were empty or loaded with select cargo (organelle portions or misfolded proteins). Training data were augmented with random rotations, elastic deformations, and smooth intensity curve transformation (Falk et al., 2019). To prevent model overfitting due to data leakage (Riley, 2019), we acquired and manually annotated two separate image sets for training and test, so that validation was always occurring on unseen data (Jones, 2019).
Low signal-to-noise ratio, size, and position with respect to the acquisition plane may hamper recognition of individual EL. To minimize this, two operators verified the annotated images before the learning process and confronted them with the output segmentations after a learning test in order to spot and correct inaccurate or missing regions. Also, the pixel size can determine the accuracy of manual annotation. To provide consistency in this phase, we linearly scaled all training images to a pixel size of 0.025 µm. Segmented images were then linearly downscaled to the original pixel size for comparison with original images. We anticipate that these steps greatly improved the segmentation ability of the network and did not introduce any noticeable artifact in the final segmented image (Figure 3).
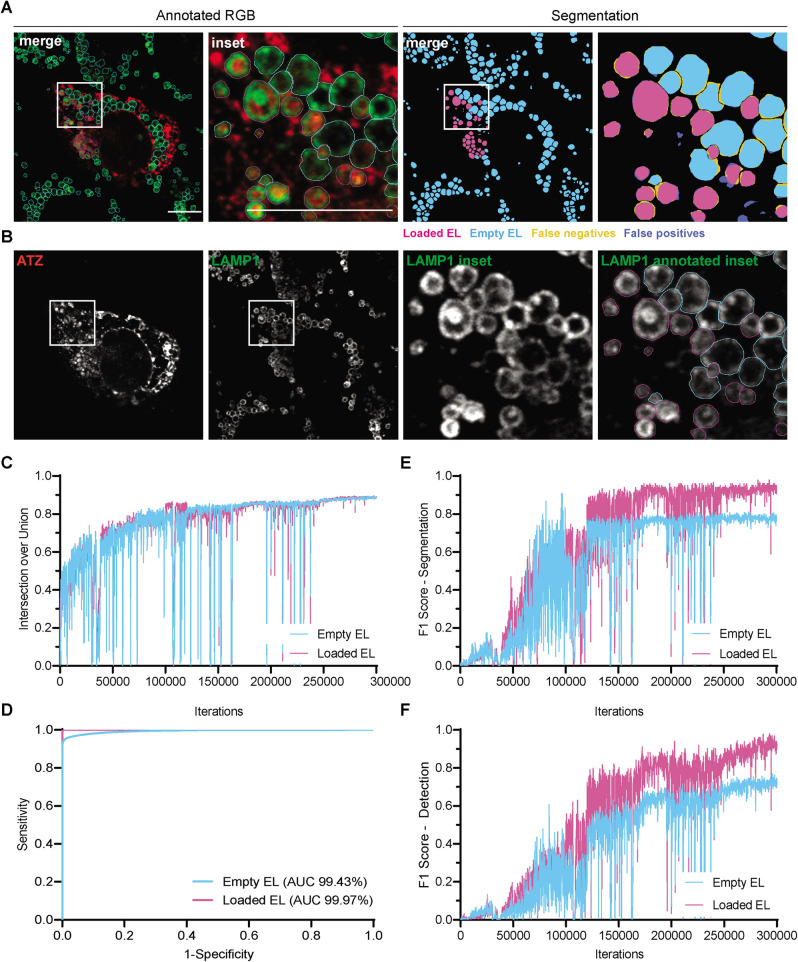
FIGURE 3:
Computational performance of the machine learning architecture. (A) Fully annotated and segmented image of wild-type mouse embryonic fibroblasts (MEF) transfected with ATZ-HA (red). LAMP1-positive EL are stained in green. The annotated RGB and its inset show empty EL (cyan ROIs) and ATZ-loaded EL (magenta ROIs). The segmented image and its inset show empty EL (cyan) and ATZ-loaded EL (magenta). False positives (not annotated but segmented) are in blue. False negatives,(annotated but not segmented) are in yellow. (B) Single channels of input image, inset of LAMP1 channel, and its overlay with annotated ROIs. Scale bars 10 µm. Computational performance is evaluated with different metrics. After 3 × 105 iterations, (C) IoU is 0.881 ± 0.012 and 0.877 ± 0.014 for empty and cargo-loaded EL classes, respectively (average ± SD of three validation images). (D) ROC curves for both classes show AUCs of 99.43% and 99.47% for empty and loaded EL, respectively. (E) F1 scores for segmentation task 0.752 ± 0.134 and 0.814 ± 0.100, respectively. (F) F1 scores for detection task 0.777 ± 0.136 and 0.790 ± 0.055, respectively.
To evaluate the network performance, we first assessed the IoU, as a measure of the area overlap, between the automatically segmented EL and human-annotated EL. Both upon transfer learning from previously published 2D U-Net network weights (Falk et al., 2019) and if trained from scratch (Supplemental Figure 2), after 60,000 iterations, the network reached a plateau corresponding to IoUs of 0.722 ± 0.176 and 0.686 ± 0.093 for empty and cargo-loaded EL, respectively (Supplemental Figure 2B; metrics expressed as average ± SD of three test images). These values are in the range of those delivered by Squassh (Figure 1F) and the Colocalisation pipeline (Figure 1J), the best performers amongst the algorithms tested in Figure 1, which were not suited for our quantitative analyses because they failed to properly distinguish individual EL (both tests one-sample Student’s t test, p > 0.05) and were much worse than the IoU of 0.850 ± 0.040 for manual segmentation (Student’s t-test, p < 0.05 and p < 0.001 for empty and loaded EL classes, respectively). The neural network showed good performance in avoiding false classifications of empty vs. loaded EL by drawing the receiver operating characteristic (ROC) curve and calculating its area under curve (AUC; Sokolova and Lapalme, 2009) as 98.40% and 99.83% for empty and cargo-loaded EL, respectively (Supplemental Figure 2C). However, assessment of the F1 score (a value in the range [0, 1] expressing the harmonic mean between precision, the algorithm ability to avoid false positives, and recall, the ability to avoid false negatives) highlighted insufficient performance of the neural network (F1 scores for segmentation 0.361 ± 0.211 and 0.404 ± 0.215 for empty and cargo-loaded EL, respectively; F1 scores for detection 0.323 ± 0.104 and 0.370 ± 0.132, respectively, Supplemental Figure 2, D and E). In this case, the performance of the neural network was worse than those of Squassh and Colocalisation Pipeline (one sample Student’s t test, p < 0.05). The low IoU values with respect to manual segmentation, plus the low F1 values, reveal that the performances of the 2D five-level and 64-feature channels network is below human accuracy. We anticipate that the limiting factor is the network architecture.
Setting-up LysoQuant, a seven-level fully convolutional neural network
To improve segmentation accuracy, we increased the neural network depth to seven levels with 16 base features (Figure 2B). As for the five-level neural network, the training data were augmented with random rotations, elastic deformations, and smooth intensity curve transformation (Falk et al., 2019). To accelerate the learning process, we initially ran the iterations with a learning rate of 1 × 10–4, and then switched in the last 50,000 steps to 5 × 10–5 for refinement (Figure 3, A and B, shows an output example with inset and comparison with manual annotation, Figure 3, C–F the performance evolution over training iterations). After a total of 3 × 105 iterations, the resulting trained network provided IoUs of 0.881 ± 0.012 and 0.877 ± 0.014 for empty and cargo-loaded EL classes, respectively (Figure 3C, average ± SD of three validation images), which fall within the manual annotation accuracy (IoU of 0.850 ± 0.040 as reported above, Student’s t test, p > 0.05), thus validating the performance of LysoQuant and largely surpassing the performance of Squassh and the Colocalisation Pipeline (one-sample Student’s t test, p < 0.01). F1 scores for segmentation (0.752 ± 0.134 and 0.814 ± 0.100, respectively) and for the detection task (0.777 ± 0.136 and 0.790 ± 0.055, respectively; Figure 3, E and F) were in line with those of Squassh and the Colocalisation Pipeline. LysoQuant achieved AUC values of 99.43% and 99.47% for empty and cargo-loaded EL, respectively (Figure 3D).
All in all, the seven-level architecture globally improved the performance of the network, as confirmed by the close correspondence of segmented images with manual annotation, and performed significantly better than other tested approaches. Thus, LysoQuant provides accurate, efficient, and scalable classification and segmentation of lysosomal-driven pathways in living cells.
Testing LysoQuant on biological, lysosomal-driven pathways
recov-ER-phagy.
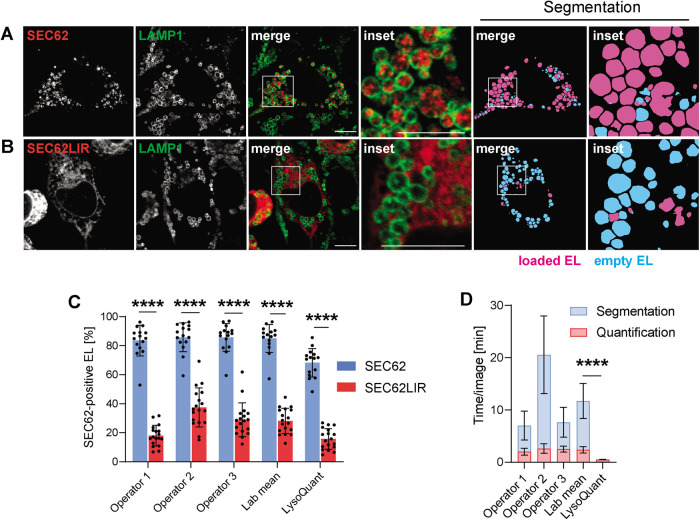
To challenge the consistency of our automated analysis, we applied LysoQuant to quantitatively assess recov-ER-phagy, an ER turnover pathway that cells activate to recover from acute ER stress (Fregno and Molinari, 2018). Recov-ER-phagy relies on ER fragmentation and formation of ER-derived vesicles displaying the ER-resident LC3-binding protein SEC62 at the limiting membrane. These are eventually engulfed by RAB7/LAMP1-positive EL in microER-phagy pathways relying on intervention of the ESCRT-III machinery (Fumagalli, Noack, Bergmann, Presmanes, et al., 2016; Loi et al., 2019). Recov-ER-phagy is faithfully recapitulated in MEF ectopically expressing SEC62 (Fumagalli, Noack, Bergmann, Presmanes, et al., 2016; Loi et al., 2019). On inhibition of lysosomal activity with BafA1, ER portions decorated with SEC62 (Figure 4A, red signal) accumulate within LAMP1-positive EL (Figure 4A, green circles). As a negative control, cells were transfected with a plasmid for expression of SEC62LIR, where the LC3-interacting motif in the cytosolic domain of SEC62 (-FEMI-) has been replaced by an -AAAA- tetrapeptide (Fumagalli, Noack, Bergmann, Presmanes, et al., 2016; Loi et al., 2019). This abolishes the association of SEC62 with LC3 and substantially reduces ER delivery within EL (Fumagalli et al., 2016; Loi et al., 2019; Figure 4B, inset, where the green EL do not contain the red ER).
FIGURE 4:
Mimicking ER delivery within EL during recov-ER-phagy. (A) CLSM shows MEF transfected transiently with SEC62-HA and (B) with SEC62LIR-HA, subsequently segmented and quantified with LysoQuant. (C) Quantification of the same set of images by three different operators (with the Lab mean) and by LysoQuant to establish the fraction of EL containing SEC62-labeled ER in both SEC62- and SEC62LIR-expressing MEF cells. (D) Same as C to compare the time required for manual and LysoQuant-operated detection and segmentation tasks.
We analyzed 15 cells expressing ectopic SEC62 and 18 cells expressing ectopic SEC62LIR. The images were segmented into SEC62-positive and SEC62-negative EL (magenta and cyan, respectively, in Figure 4, A and B, Segmentation). Three different operators and LysoQuant were then asked to establish the occupancy of EL with ER portions in cells expressing active (SEC62) or inactive (SEC62LIR) forms of the ER phagy receptor. In cells expressing ectopic SEC62, the three operators reported an EL occupancy of 85 ± 9% (Figure 4C, blue column, Lab mean), which substantially decreases to 28 ± 8% in cells expressing ectopic SEC62LIR (Figure 4C, red column, Lab mean). LysoQuant revealed an EL occupancy of 68 ± 9% (Figure 4C, blue column, LysoQuant), which substantially decreases to 15 ± 7% in cells expressing ectopic SEC62LIR (Figure 4C, red column, LysoQuant).
If compared with the operators, LysoQuant has two major advantages: 1) the variety of information that it can offer in addition to EL occupancy, which includes, for example the size, shape, and intracellular distribution of the EL (Figure 2Ai); 2) the much reduced time to complete the analyses. In our setup, where an analysis computer is remotely connected to a Caffe U-Net framework, LysoQuant completes analysis of each image in 0.53 ± 0.04 min (Figure 4D) by informing on size, shape, occupancy, intensity of the surface and of the luminal signal, and intracellular distribution of the EL. The average time for operators, who can only inform on number and occupancy of individual EL, is highly variable and about 30-fold higher (14.10 ± 3.42 min, Lab mean, Figure 4D). The gain in time and in accuracy offered by LysoQuant is expected to increase substantially when large numbers of cells are counted, when operators’ performance will inevitably decrease due to fatigue, and in high-throughput screenings. In fact, the time required by Lysoquant corresponds to 0.008 CPU hours/image, which is consistent with the rate required for high-throughput studies (Carpenter et al., 2006).
To test whether the segmentation output was dependent on the confocal acquisition settings, we acquired the same set of cells with different pixel sizes and compared the quantification output. Variations up to twofold in pixel size had no significant effect on the measured occupancy and total EL number (one-way ANOVA, N = 5 cells; Supplemental Figure 3, A and B), while the analysis speed in the same pixel size range increased from 0.58 ± 0.05 min to 1.45 ± 0.04 min (Supplemental Figure 3C). Interestingly, this makes it possible to optimize the acquisition settings by taking larger fields of view with a relatively small increase in analysis time, helping to reduce both acquisition times and potential cell selection bias.
Thus, LysoQuant performs fast and accurate classification of EL, enabling clear, unbiased discrimination of two different phenotypes associated with functional and impaired recov-ER-phagy, respectively. LysoQuant achieves segmentation of EL with operator-like accuracy within a fraction of the time required for manual annotation. It offers additional information concerning size, geometrical parameters, and distribution and intensities of single EL to further dissect unclear or particular phenotypes and to perform high-throughput microscopy studies.
ERLAD.
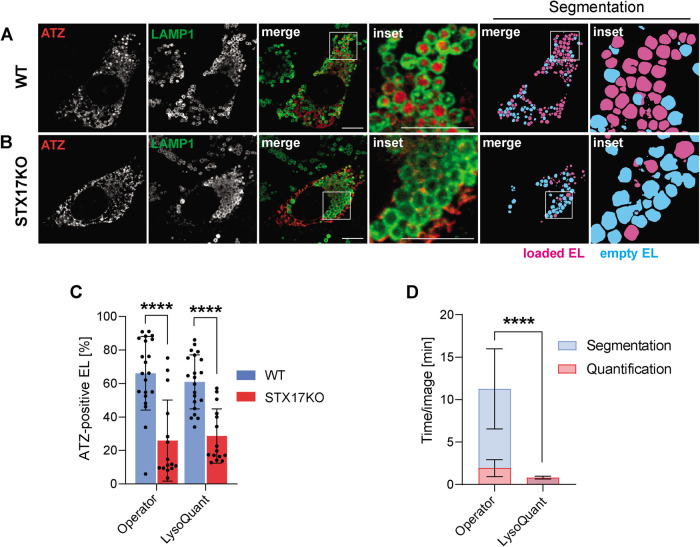
We next challenged LysoQuant to acquire quantitative information on another biological pathway, the ERLAD pathway devised by mammalian cells to remove misfolded proteins that cannot be degraded by cytosolic proteasomes. These are segregated in ER subdomains that are eventually shed from the bulk ER and are delivered to EL for clearance (Fregno and Molinari, 2019). The polymerogenic Z variant of alpha1-antitrypsin (ATZ) is a classical ERLAD substrate (Fregno, Fasana, et al., 2018), and defective degradation of ATZ polymers results in clinically significant hepatotoxicity, which is the major inherited cause of pediatric liver disease and transplantation (Sharp et al., 1969; Eriksson et al., 1986; Wu et al., 1994; Hidvegi et al., 2010; Perlmutter, 2011; Roussel et al., 2011; Marciniak et al., 2016). Lysosomal delivery of ATZ polymers relies on the ER-phagy receptor FAM134B, on the LC3 lipidation machinery and on fusion of ER-derived vesicles containing ATZ with LAMP1-positive EL, which depends on the SNARE complex STX17/VAMP8 (Fregno, Fasana, et al., 2018; Fregno and Molinari, 2019). To evaluate the performance of LysoQuant and to compare it with manual operations, we monitored ATZ delivery to EL in 21 wild-type MEF (Figure 5A, WT) and in 15 MEF that we generated by CRISPR/Cas9 gene editing to delete STX17 (Figure 5B, STX17KO). This case is particularly challenging for automatized quantification because in WT cells exposed to BafA1 to inactivate hydrolytic enzymes, the cargo under investigation (ATZ) accumulates within EL (LysoQuant must identify these as “loaded EL”). In cells lacking STX17, ATZ remains in vesicles that dock at the cytosolic face of the EL membrane (Fregno, Fasana, et al., 2018), which requires an accurate quantification of the EL membrane for a correct result. As reported above for recov-ER-phagy, LysoQuant correctly reported on the drastic reduction of ATZ delivery within EL upon deletion of STX17 (Figure 5C). In particular, it was able to classify LAMP1-positive EL displaying ATZ docked at their membrane correctly (Figure 5B and Fregno, Fasana, et al., 2018) as empty EL. It did so, with high accuracy and about 20× faster than manual operators (Figure 5D, 0.81 ± 0.16 min/image vs. 13.18 ± 4.82). Note that this operation could not have been performed without accurate segmentation of individual EL.
FIGURE 5:
Quantification of misfolded protein delivery to lysosomes. (A) CLSM shows delivery of ATZ within LAMP1-positive EL in wild-type MEF. (B) Same as A in STX17KO MEF. (C) Quantification of ATZ delivery within EL in both wild-type and STX17KO MEF. (D) Time required for manual and LysoQuant-operated detection and segmentation tasks.
Mimicking starvation-induced ER-phagy in a different cellular model.
To further prove the versatility of LysoQuant, quantification of lysosomal activity was also performed in human embryonic kidney 293 (HEK293) cells, which are characterized by smaller size than the MEF used so far and are less adherent to surfaces. We labeled the EL with ectopically expressed GFP-RAB7 (another difference from the experiments described so far, where EL were identified with antibodies to endogenous LAMP1). ER delivery within EL was induced upon ectopic expression of FAM134 to mimic starvation-induced ER-phagy (Khaminets, Heinrich, et al., 2015; Liang, Lingeman, et al., 2020).
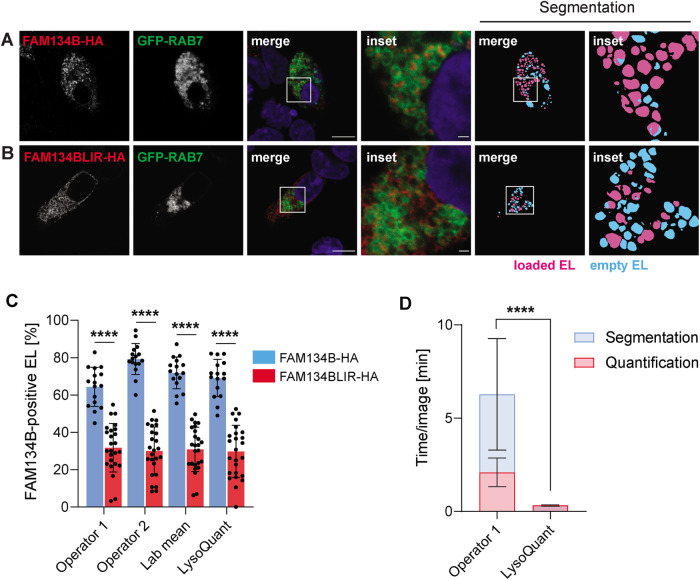
Here, we analyzed 16 HEK293 cells expressing ectopic FAM134B and 25 HEK293 cells expressing ectopic FAM134BLIR, which is inactive in driving ER fragments within EL (Khaminets, Heinrich, et al., 2015; Liang, Lingeman, et al., 2020). The confocal images were segmented to reveal FAM134-positive and FAM134B-negative EL (magenta and cyan, respectively, in Figure 6, A and B, segmentation). In HEK293 cells expressing ectopic FAM134B, two operators independently established an EL occupancy ranging between 65% and 78% (average value 72 ± 9%, Figure 6C, blue column, lab mean). The occupancy dropped to 31 ± 12% in HEK293 cells expressing the inactive FAM134BLIR (Figure 6C, red column, lab mean). LysoQuant established values of 69 ± 10% (Figure 6C, blue column, LysoQuant) in HEK293 cells expressing ectopic FAM134B and of 30 ± 14% in HEK293 cells expressing the inactive FAM134BLIR (Figure 6C, red column, LysoQuant). In this case as well, LysoQuant, with 0.32 ± 0.04 min per image, was much faster than the operators (4.18 ± 3.08 min per cell, Figure 6D). Thus, LysoQuant maintains high performance even in quantifying lysosomal-driven pathways in small and poorly adherent cells that were a suboptimal choice to perform imaging analyses.
FIGURE 6:
Quantification of ER remodeling in HEK293 cells. (A) CLSM showing HEK293 cotransfected transiently with the late endosomal/lysosomal marker GFP-Rab7 and FAM134-HA. (B) Same as A in cells transfected for expression of FAM134BLIR-HA. Nuclei are shown to identify transfected and nontransfected HEK293 cells. (C) Same as 4C to quantify ER delivery within GFP-RAB7-positive EL in cells expressing FAM134B and FAM134BLIR, respectively. (D) Same as 4D.
DISCUSSION
Quantitative analysis of biological samples is time-consuming when it is about collecting a statistically significant number of cells and conditions and minimizing operator errors that are inherent to manual operations (Grams, 1998). Here, we report on a deep learning-based approach, LysoQuant, that quantifies and segments CSLM images capturing lysosomal delivery of subcellular entities such as organelles and proteins. Direct comparison with classic machine learning approaches clearly shows the superiority of LysoQuant, which was trained to evaluate images rapidly with human-level performance (Figures 1–3). LysoQuant performance was validated on quantification of catabolic pathways that maintain cellular homeostasis and proteostasis by ensuring lysosomal clearance of excess ER during recovery from ER stress (Figure 4), by removing ER portions containing aberrant, disease-causing gene products (Figure 5), and under conditions that mimic starvation-induced ER-phagy (Figure 6). It goes without saying that LysoQuant, tested here in MEF and HEK293 cells, is applicable to all adherent cell lines. Here, we used endogenous and ectopically expressed protein markers to monitor and quantify lysosomal properties (size, number, distribution, occupancy, shape) and delivery of the ER or of misfolded, disease-causing polypeptides within EL for clearance. However, LysoQuant is certainly applicable to quantitative investigation of biological processes involving other organelles and subcellular structures, if high-quality confocal images and appropriate tools to fluorescently label actors in the pathway under investigation are available. Moreover, with appropriate training, this approach is applicable to images obtained with other techniques, such as superresolution or electron microscopy.
Praise for standardization in deep learning methods in biology has recently emerged (Jones, 2019). Indeed, quantitative image analyses are very suitable tasks for DL approaches because of the large number of variables (pixels) and the clear definition of the classified objects. Given the ability of U-Net to work with a limited set of images, at first, we approached the problem of the training dataset size by adding a training and validation image in sequential steps until maximal performance. Imbalances in the number of data points (in this case, EL) between classes can lead to misleading accuracy values (Moen et al., 2019). Though U-Net balances classes through the use of a loss-weighting function, we choose training images to globally have a similar number of EL in both classes. Data leakage was avoided in our case by training the network with a different dataset than the datasets used for measuring the metrics and phenotypical validation.
A point of attention has been raised also on so-called “adversarial images,” i.e. slight alterations in images that may fool a proper recognition (Serre, 2019). Confocal images of cells with varying levels of intensity have inherently different signal-to-noise ratios, and even in cells with low levels of expression and higher acquisition noise, we did not detect alteration in the segmentation accuracy.
Looking forward, LysoQuant’s automatic segmentation with human-level performance and much faster operations will be instrumental in increasing the number of images analyzed and will thus enable the identification of subtler phenotypes. The reported analysis time per image makes LysoQuant applicable to high-throughput studies, rivaling other reported high-throughput analysis techniques in speed (Collinet et al., 2010; Aguet et al., 2013; Rizk et al., 2014).
MATERIALS AND METHODS
Antibodies, expression plasmids, cell lines, and inhibitors
Commercial antibodies used to perform our studies were the following: HA (Sigma) and LAMP1 (DSHB). Alexa Fluor conjugated secondary antibodies (Invitrogen, Jackson Immunoresearch, Thermo Fisher) were used for immunofluorescence (IF) analysis. Plasmids encoding SEC62, ATZ, and FAM134B were subcloned in a pcDNA3.1 vector and a C-terminus hemagglutinin (HA) tag was added. SEC62LIR was generated by site-directed mutagenesis of the LIR motif by replacing the -FEMI- residues with -AAAA-. These plasmids and GFP-Rab7 are described in Fumagalli, Noack, Bergmann, Presmanes, et al. (2016). FAM134B-HA and FAM134BLIR-HA (DDFELL to AAAAAA) expression plasmids were purchased from GenScript. MEF STX17KO were generated in our lab using CRISPR-Cas9 technology as described in Fregno, Fasana, et al. (2018). BafA1 was administered to MEF for 12 h at the final concentration of 50 nM and to HEK293 for 6 h at 100 nM.
Cell culture and transient transfection
MEF and HEK293 cells were grown at 37°C and 5% CO2 in DMEM supplemented with 10% FCS. Transient transfections were performed using JetPrime transfection reagent (PolyPlus) according to the manufacturer’s instructions. Twenty-four hours after transfection and after a 12-h treatment with BafA1, MEF cells were fixed to perform IF. HEK293 cells were treated for 6 h with 100 nM BafA1 24 h after transfection and then fixed for IF.
Confocal laser scanning microscopy
Either 1.5 × 105 MEF or 3 × 105 HEK293 were seeded on alcian blue–covered (MEF) or uncoated (HEK293) glass coverslips in a 12-well plate, transfected, and exposed to BafA1 as specified above. After two washes with phosphate-buffered saline (PBS) supplemented with calcium and magnesium (PBS++), they were fixed with 3.7% paraformaldehyde at room temperature for 20 min, washed three times with PBS++, and incubated for 15 min with a permeabilization solution (PS) composed of 0.05% saponin, 10% goat serum, 10 mM HEPES, and 15 mM glycine for intracellular staining at room temperature. The cells were then incubated with the aforementioned antibodies diluted 1:100 (HA) and 1:50 (LAMP1) in PS for 90 min at room temperature. They were washed three times (5 min each) using PS and subsequently incubated with Alexa Fluor–conjugated secondary antibodies diluted 1:300 in PS for 30 min at room temperature. After three washes with PS and deionized water, coverslips were mounted using Vectashield (Vector Laboratories) supplemented with 40,6-diamidino-2-phenylindole (DAPI). Confocal images were acquired using a Leica TCS SP5 microscope with a 63.0 × 1.40 OIL UV objective. FIJI ImageJ was used for image analysis and processing. These protocols are explained in more detail in (Fumagalli, Noack, Bergmann, Presmanes, et al., 2016; Fregno, Fasana, et al., 2018).
Manual annotation accuracy
Three operators manually annotated 10 cells from four different experiments for a total of 1170 EL. These ROIs were used to create annotation masks where annotated regions took the value 1 and background regions 0. Masks from the three operators where then summed to get images in the range [0, 3]. Lab consensus was defined as regions higher or equal to 2, that is, pixelwise regions that were drawn by at least two out of three operators. We then computed the intersection and union masks and calculated the IoU. For the relative standard error, we calculated the difference mask between the lab consensus mask and each operator and measured the area of the lab consensus and differences. From these values we then calculated variance, standard error, and relative error for each cell. All image processing was performed in Fiji/ImageJ.
Classic and machine-learning segmentation
Automatic thresholding was performed comparing all the thresholding algorithms available in ImageJ (Supplemental Figure 4). Results were then compared with manual segmentation to evaluate F1 scores for segmentation and Intersection over Union, choosing the algorithm closest to ground truth.
Trainable Weka Segmentation was performed with Random Forest, a widely adopted algorithm for image and data classification in the Fast Random Forest implementation provided with the plugin (Schroff et al., 2008; Glory-Afshar et al., 2010; Liang et al., 2016). Training was performed with the LAMP1 channels of the same dataset used for deep learning training and the same annotations used for deep learning. After balancing the classes, we selected all available features and performed the training.
Random forest segmentation was also performed with iLastik version 1.3.3rc2. Training was performed with the LAMP1 channels of the same dataset used for deep learning training and the same annotations. As classification algorithm, we used the VIGRA Parallel Random Forest algorithm. Features were selected with an automatic feature selection method based on the default algorithm (Jakulin, 2005).
Support Vector Machine was performed with the Weka LibSVM library (Fan et al., 2005) and the Trainable Weka Segmentation ImageJ plugin. Training was performed with the LAMP1 channels of the same dataset used for deep learning training and the same annotations used for deep learning. After balancing the classes, we selected all available features and performed the training.
The circular Hough transform was performed with MATLAB R2019a by recognizing bright regions on dark background. We extrapolated the range of sizes from the sizes of the annotated data as shown in the histogram in Figure 2Ag. Processing the images with a background subtraction in this case did not improve the results, due to the high signal-to-noise ratio of the original images. We performed the analysis with Two Stage and Phase code methods. Two parameters can be controlled, sensitivity and edge recognition factors. These values have the range [0,1]. We then selected the image with the lowest values of errors, evaluated as false negatives and false positives. To assess this, we scanned both parameters with a step size of 0.1 and evaluated the F1 score and Intersection over Union for each condition. We then chose the parameters corresponding to the best F1 score and IoU (Supplemental Table 1).
Squassh segmentation was performed following the method previously described (Rizk et al., 2014) on the LAMP1 channel. After background subtraction with a rolling ball radius of 10 pixels, segmentation was performed with subpixel accuracy, Automatic local intensity estimation and PSF model were derived from the acquisition settings. Regions below two pixels in size were excluded.
Icy spot detection plugin segmentation was performed on the LAMP1 channel with the UnDecimated Wavelet Transform detector, recognizing bright spots on a dark background with spot scales 2, 3 and 4.
CmeAnalysis was performed on MATLAB R2019a on the LAMP1 channel, with wavelength and camera pixel size estimated from the acquisition settings.
The Stardist convolutional neural network was trained from the same training dataset used for the deep learning techniques presented in this paper, with the stardist Docker container, based tensorflow/tensorflow:1.13.2-gpu-py3-jupyter, Ubuntu 18.04 with CUDA 10.0 and Python 3.6.8 (github: mpicbg-csbd/stardist). Labels were imported from the annotations masks generated for the DL computations described in the results. After normalization, eight images were randomly selected for training and two for model validation. The network was set with 32 rays, one channel, and a 2 × 2 grid. The model was trained for 400 epochs. We then calculated the threshold optimization factors for this training (probability threshold: 0.4, NMS threshold: 0.5) and exported the Tensorflow model to the Stardist Fiji plugin, with which we performed the segmentation.
Interaction analysis segmentation was performed with radius size ranging from three to seven pixels, cutoff of 0.001. Percentile values were tested in a range from 0.3 to 0.9.
Colocalisation Pipeline was performed with a watershed tolerance of 5, threshold 1, and a local autothreshold method.
ImageJ plugin and deep learning computations
The ImageJ plugin takes as an input a CSLM image (Figure 2Aa), the ROIs of the selected cells (Figure 2Ab), and the channels to analyze. It then performs the conversion to RGB, clears the signal outside the selected ROIs (Figure 2Ac), and calls the U-Net plugin, which normalizes the image (Figure 2Ad) and performs segmentation with the specified weight file. The segmented image (Figure 2Ae) is then recalled by the plugin and for each class (Figure 2Af) the objects above the minimum size (Figure 2Ag) are quantified (Figure 2A, h and i) through the use of the Analyze Particles class. Deep learning computations were performed on a single graphical processing unit (GPU, nVidia GTX 1080 with 8GB of VRAM). The Caffe framework was patched with U-Net version 99bd99_20190109 and compiled on a Linux CentOS remote server with cuda 8.1 and cudNN 7.1.
Statistical analysis
Statistical analysis was performed using GraphPad Prism 8 software. An unpaired two-tailed t test, ordinary one-way ANOVA with Tukey’s multiple comparisons test, or two-way ANOVA with Sidak’s multiple comparisons test was used to assess statistical significance. A p-value corresponding to 0.05 or less was considered statistically significant. All values are expressed as average ± SD unless otherwise stated.
Data availability
All data needed to evaluate the conclusions in the paper are present in the paper and/or in the Supplemental Information. The described plugin, the training network, and the model are available on the github platform (https://github.com/irb-imagingfacility/lysoquant) and through the ImageJ update site. Training datasets of the experiments will be available on request. Additional data related to this paper may be requested from the authors.
Supplementary Material
Acknowledgments
We thank A. Cavalli for providing access to computing resources. M. Loi, I. Fregno, E. Fasana, and T. Soldà are acknowledged for manual quantification of the data, and all the members of Molinari’s lab for discussions and critical reading of the manuscript. M.M. is supported by the AlphaONE Foundation, the Foundation for Research on Neurodegenerative Diseases, the Swiss National Science Foundation, and the Comel and Gelu Foundations.
Abbreviations used:
- ATZ
polymerogenic Z variant of protein α1-antitrypsin
- AUC
area under curve
- BafA1
bafilomycin A1
- CSLM
confocal laser scanning microscopy
- DL
deep learning
- EL
endolysosomes
- ER
endoplasmic reticulum
- ERLAD
ER-to-lysosome-associated degradation
- GPU
graphical processing unit
- IoU
intersection over union
- MEF
mouse embrionic fibroblasts
- PSF
point spread function
- ROC Curve
receiver operating characteristic curve
- ROI
region of interest
Footnotes
This article was published online ahead of print in MBoC in Press (http://www.molbiolcell.org/cgi/doi/10.1091/mbc.E20-04-0269) on May 13, 2020.
REFERENCES
Boldface names denote co–first authors.
- Aguet F, Antonescu CN, Mettlen M, Schmid SL, Danuser G. (2013). Advances in analysis of low signal-to-noise images link dynamin and AP2 to the functions of an endocytic checkpoint. Dev Cell , 279–291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arganda-Carreras I, Kaynig V, Rueden C, Eliceiri KW, Schindelin J, Cardona A, Sebastian Seung H. (2017). Trainable Weka segmentation: a machine learning tool for microscopy pixel classification. Bioinformatics , 2424–2426. [DOI] [PubMed] [Google Scholar]
- Atherton TJ, Kerbyson DJ. (1999). Size invariant circle detection. Image Vision Comput , 795–803. [Google Scholar]
- Ballabio A, Bonifacino JS. (2019). Lysosomes as dynamic regulators of cell and organismal homeostasis. Nat Rev Mol Cell Biol. [DOI] [PubMed] [Google Scholar]
- Berg S, Kutra D, Kroeger T, Straehle CN, Kausler BX, Haubold C, Schiegg M, Ales J, Beier T, Rudy M, et al. (2019). iLastik: interactive machine learning for (bio)image analysis. Nat Methods , 1226–1232. [DOI] [PubMed] [Google Scholar]
- Bergmann TJ, Fumagalli F, Loi M, Molinari M. (2017). Role of SEC62 in ER maintenance: a link with ER stress tolerance in SEC62-overexpressing tumors? Mol Cell Oncol , e1264351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bright NA, Davis LJ, Luzio JP. (2016). Endolysosomes are the principal intracellular sites of acid hydrolase activity. Curr Biol , 2233–2245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bulten W, Bandi P, Hoven J, van de Loo R, Lotz J, Weiss N, van der Laak J, van Ginneken B, Hulsbergen-van de Kaa C, Litjens G. (2019). Epithelium segmentation using deep learning in H&E-stained prostate specimens with immunohistochemistry as reference standard. Sci Rep-Uk , 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carpenter AE, Jones TR, Lamprecht MR, Clarke C, Kang IH, Friman O, Guertin DA, Chang JH, Lindquist RA, Moffat J, et al. (2006). CellProfiler: image analysis software for identifying and quantifying cell phenotypes. Genome Biol , R100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collinet C, Stoter M, Bradshaw CR, Samusik N, Rink JC, Kenski D, Habermann B, Buchholz F, Henschel R, Mueller MS, et al. (2010). Systems survey of endocytosis by multiparametric image analysis. Nature , 243–249. [DOI] [PubMed] [Google Scholar]
- de Chaumont F, Dallongeville S, Chenouard N, Herve N, Pop S, Provoost T, Meas-Yedid V, Pankajakshan P, Lecomte T, Le Montagner Y, et al. (2012). Icy: an open bioimage informatics platform for extended reproducible research. Nat Methods , 690–696. [DOI] [PubMed] [Google Scholar]
- Eriksson S, Carlson J, Velez R. (1986). Risk of cirrhosis and primary liver-cancer in alpha-1-antitrypsin deficiency. N Engl J Med , 736–739. [DOI] [PubMed] [Google Scholar]
- Falk T, Mai D, Bensch R, Cicek O, Abdulkadir A, Marrakchi Y, Bohm A, Deubner J, Jackel Z, Seiwald K, et al. (2019). U-Net: deep learning for cell counting, detection, and morphometry. Nat Methods , 67–70. [DOI] [PubMed] [Google Scholar]
- Fan R-E, Chen P-H, Lin C-J. (2005). Working set selection using second order information for training SVM. J Mach Learn Res , 1889–1918. [Google Scholar]
- Forrester A, De Leonibus C, Grumati P, Fasana E, Piemontese M, Staiano L, Fregno I, Raimondi A, Marazza A, Bruno G, et al. (2019). A selective ER-phagy exerts procollagen quality control via a Calnexin-FAM134B complex. EMBO J , e99847. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fraldi A, Klein AD, Medina DL, Settembre C. (2016). Brain disorders due to lysosomal dysfunction. Annu Rev Neurosci , 277–295. [DOI] [PubMed] [Google Scholar]
- Fregno I, Fasana E, Bergmann TJ, Raimondi A, Loi M, Solda T, Galli C, D’Antuono R, Morone D, Danieli A, et al. (2018). ER-to-lysosome-associated degradation of proteasome-resistant ATZ polymers occurs via receptor-mediated vesicular transport. EMBO J , e99259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fregno I, Molinari M. (2018). Endoplasmic reticulum turnover: ER-phagy and other flavors in selective and non-selective ER clearance. F1000Res , 454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fregno I, Molinari M. (2019). Proteasomal and lysosomal clearance of faulty secretory proteins: ER-associated degradation (ERAD) and ER-to-lysosome-associated degradation (ERLAD) pathways. Crit Rev Biochem Mol Biol , 153–163. [DOI] [PubMed] [Google Scholar]
- Fumagalli F, Noack J, Bergmann TJ, Presmanes EC, Pisoni GB, Fasana E, Fregno I, Galli C, Loi M, Soldà T, et al. (2016). Translocon component Sec62 acts in endoplasmic reticulum turnover during stress recovery. Nat Cell Biol , 1173–1184. [DOI] [PubMed] [Google Scholar]
- Gilleron J, Gerdes JM, Zeigerer A. (2019). Metabolic regulation through the endosomal system. Traffic , 552–570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glory-Afshar E, Osuna-Highley E, Granger B, Murphy RF. (2010). A graphical model to determine the subcellular protein location in artificial tissues. Proc IEEE Int Symp Biomed Imaging , 1037–1040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grams T. (1998). Operator errors and their causes. Lect Notes Comput Sc , 89–99. [Google Scholar]
- Helmuth JA, Burckhardt CJ, Greber UF, Sbalzarini IF. (2009). Shape reconstruction of subcellular structures from live cell fluorescence microscopy images. J Struct Biol , 1–10. [DOI] [PubMed] [Google Scholar]
- Helmuth JA, Paul G, Sbalzarini IF. (2010). Beyond co-localization: inferring spatial interactions between sub-cellular structures from microscopy images. BMC Bioinformatics , 372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hidvegi T, Ewing M, Hale P, Dippold C, Beckett C, Kemp C, Maurice N, Mukherjee A, Goldbach C, Watkins S, et al. (2010). An autophagy-enhancing drug promotes degradation of mutant alpha 1-antitrypsin Z and reduces hepatic fibrosis. Science , 229–232. [DOI] [PubMed] [Google Scholar]
- Hubner CA, Dikic I. (2019). ER-phagy and human diseases. Cell Death Differ. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huotari J, Helenius A. (2011). Endosome maturation. EMBO J , 3481–3500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jakulin A. (2005). Machine Learning Based on Attribute Interactions. Ljubljana, Slovenia: University of Ljubljana. [Google Scholar]
- Jones DT. (2019). Setting the standards for machine learning in biology. Nat Rev Mol Cell Biol , 659–660. [DOI] [PubMed] [Google Scholar]
- Kan A. (2017). Machine learning applications in cell image analysis. Immunol Cell Biol , 525–530. [DOI] [PubMed] [Google Scholar]
- Khaminets A, Heinrich T, Mari M, Grumati P, Huebner AK, Akutsu M, Liebmann L, Stolz A, Nietzsche S, Koch N, et al. (2015). Regulation of endoplasmic reticulum turnover by selective autophagy. Nature , 354–358. [DOI] [PubMed] [Google Scholar]
- Kimmelman AC, White E. (2017). Autophagy and tumor metabolism. Cell Metab , 1037–1043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klionsky DJ, Abdelmohsen K, Abe A, Abedin MJ, Abeliovich H, Arozena AA, Adachi H, Adams CM, Adams PD, Adeli K, et al. (2016). Guidelines for the use and interpretation of assays for monitoring autophagy (3rd edition). Autophagy , 1–222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- LeCun Y, Bengio Y, Hinton G. (2015). Deep learning. Nature , 436–444. [DOI] [PubMed] [Google Scholar]
- Liang C, Li Y, Luo J. (2016). A novel method to detect functional microRNA regulatory modules by bicliques mMerging. IEEE/ACM Trans Comput Biol Bioinform , 549–556. [DOI] [PubMed] [Google Scholar]
- Liang JR, Lingeman E, Luong T, Ahmed S, Muhar M, Nguyen T, Olzmann JA, Corn JE. (2020). A genome-wide ER-phagy screen highlights key roles of mitochondrial metabolism and ER-resident UFMylation. Cell , 1160–1177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loi M, Raimondi A, Morone D, Molinari M. (2019). ESCRT-III-driven piecemeal micro-ER-phagy remodels the ER during recovery from ER stress. Nat Commun , 5058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marciniak SJ, Ordonez A, Dickens JA, Chambers JE, Patel V, Dominicus CS, Malzer E. (2016). New concepts in alpha-1 antitrypsin deficiency disease mechanisms. Ann Am Thorac Soc (Suppl 4), 289–296. [DOI] [PubMed] [Google Scholar]
- Marques ARA, Saftig P. (2019). Lysosomal storage disorders—challenges, concepts and avenues for therapy: beyond rare diseases. J Cell Sci : jcs221739. [DOI] [PubMed] [Google Scholar]
- Marx V. (2019). Machine learning, practically speaking. Nat Methods , 463–467. [DOI] [PubMed] [Google Scholar]
- Moen E, Bannon D, Kudo T, Graf W, Covert M, Van Valen D. (2019). Deep learning for cellular image analysis. Nat Methods , 1233–1246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nguyen D, Uhlmann V, Planchette AL, Marchand PJ, Van De Ville D, Lasser T, Radenovic A. (2019). Supervised learning to quantify amyloidosis in whole brains of an Alzheimer’s disease mouse model acquired with optical projection tomography. Biomed Opt Express , 3041–3060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oktay AB, Gurses A. (2019). Automatic detection, localization and segmentation of nano-particles with deep learning in microscopy images. Micron , 113–119. [DOI] [PubMed] [Google Scholar]
- Perlmutter DH. (2011). Alpha-1-antitrypsin deficiency: importance of proteasomal and autophagic degradative pathways in disposal of liver disease-associated protein aggregates. Annu Rev Med , 333–345. [DOI] [PubMed] [Google Scholar]
- Riley P. (2019). Three pitfalls to avoid in machine learning. Nature , 27–29. [DOI] [PubMed] [Google Scholar]
- Rizk A, Paul G, Incardona P, Bugarski M, Mansouri M, Niemann A, Ziegler U, Berger P, Sbalzarini IF. (2014). Segmentation and quantification of subcellular structures in fluorescence microscopy images using Squassh. Nat Protoc , 586–596. [DOI] [PubMed] [Google Scholar]
- Ronneberger O, Fischer P, Brox T. (2015). U-Net: convolutional networks for biomedical image segmentation. Med Image Comput Comput Assist Interv , 234–241. [Google Scholar]
- Roussel BD, Irving JA, Ekeowa UI, Belorgey D, Haq I, Ordonez A, Kruppa AJ, Duvoix A, Rashid ST, Crowther DC, et al. (2011). Unravelling the twists and turns of the serpinopathies. Febs J , 3859–3867. [DOI] [PubMed] [Google Scholar]
- Schmidt U, Weigert M, Broaddus C, Myers G. (2018). Cell detection with star-convex polygons. In: International Conference on Medical Image Computing and Computer-Assisted Intervention (MICCAI), Grenada, Spain. [Google Scholar]
- Schroff F, Criminisi A, Zisserman A. (2008). Object Class Segmentation using Random Forests. BMVA Press. [Google Scholar]
- Serre T. (2019). Deep learning: the good, the bad, and the ugly. Annu Rev Vis Sci , 399–426. [DOI] [PubMed] [Google Scholar]
- Sharp HL, Bridges RA, Krivit W, Freier EF. (1969). Cirrhosis associated with alpha-1-antitrypsin deficiency—a previously unrecognized inherited disorder. J Lab Clin Med , 934–939. [PubMed] [Google Scholar]
- Soille P, Vincent LM. (1990). Determining watersheds in digital pictures via flooding simulations. Proceedings , 1240–1250. [Google Scholar]
- Sokolova M, Lapalme G. (2009). A systematic analysis of performance measures for classification tasks. Inform Process Manag , 427–437. [Google Scholar]
- Sommer C, Straehle C, Köthe U, Hamprecht FA. (2011). ILASTIK: interactive learning and segmentation toolkit. IEEE Int Symp Biomed Imaging: From Nano to Macro 230–233. [Google Scholar]
- van der Heyden B, Wohlfahrt P, Eekers DBP, Richter C, Terhaag K, Troost EGC, Verhaegen F. (2019). Dual-energy CT for automatic organs-at-risk segmentation in brain-tumor patients using a multi-atlas and deep-learning approach. Sci Rep-UK 9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Valen DA, Kudo T, Lane KM, Macklin DN, Quach NT, DeFelice MM, Maayan I, Tanouchi Y, Ashley EA, Covert MW. (2016). Deep learning automates the quantitative analysis of individual cells in live-cell imaging experiments. PLoS Comput Biol , e1005177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weigert M, Schmidt U, Haase R, Sugawara K, Myers G. (2020). Star-convex polyhedra for 3D object detection and segmentation in microscopy. In: The IEEE Winter Conference on Applications of Computer Vision (WACV), Snowmass Village, CO. [Google Scholar]
- Woodcroft BJ, Hammond L, Stow JL, Hamilton NA. (2009). Automated organelle-based colocalization in whole-cell imaging. Cytometry A , 941–950. [DOI] [PubMed] [Google Scholar]
- Wu Y, Whitman I, Molmenti E, Moore K, Hippenmeyer P, Perlmutter DH. (1994). A lag in intracellular degradation of mutant alpha 1-antitrypsin correlates with the liver disease phenotype in homozygous PiZZ alpha 1-antitrypsin deficiency. Proc Natl Acad Sci USA , 9014–9018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhuang Z, Li N, Joseph Raj AN, Mahesh VGV, Qiu S. (2019). An RDAU-NET model for lesion segmentation in breast ultrasound images. PLoS One , e0221535. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data needed to evaluate the conclusions in the paper are present in the paper and/or in the Supplemental Information. The described plugin, the training network, and the model are available on the github platform (https://github.com/irb-imagingfacility/lysoquant) and through the ImageJ update site. Training datasets of the experiments will be available on request. Additional data related to this paper may be requested from the authors.