Spatial heterogeneity of the cytosol revealed by machine learning-based 3D particle tracking

Abstract

The spatial structure and physical properties of the cytosol are not well understood. Measurements of the material state of the cytosol are challenging due to its spatial and temporal heterogeneity. Recent development of genetically encoded multimeric nanoparticles (GEMs) has opened up study of the cytosol at the length scales of multiprotein complexes (20–60 nm). We developed an image analysis pipeline for 3D imaging of GEMs in the context of large, multinucleate fungi where there is evidence of functional compartmentalization of the cytosol for both the nuclear division cycle and branching. We applied a neural network to track particles in 3D and then created quantitative visualizations of spatially varying diffusivity. Using this pipeline to analyze spatial diffusivity patterns, we found that there is substantial variability in the properties of the cytosol. We detected zones where GEMs display especially low diffusivity at hyphal tips and near some nuclei, showing that the physical state of the cytosol varies spatially within a single cell. Additionally, we observed significant cell-to-cell variability in the average diffusivity of GEMs. Thus, the physical properties of the cytosol vary substantially in time and space and can be a source of heterogeneity within individual cells and across populations.

INTRODUCTION

The nature of the cytosol has been speculated about since the first glimpses of cells in primitive microscopes, yet the cytosolic environment experienced by macromolecules across different length scales remains elusive today. In 1899, E.B. Wilson expanded on the possible explanations for the meshwork appearance of the cytosol and described it as an emulsion in which multiple liquids of different chemical and physical properties coexist (Wilson, 1899). With electron microscopy, it became clear that the cytoskeleton, endomembrane systems, and protein translation machinery can generate a crowded landscape in the cytosol. Furthermore, substantial molecular crowding within the cytosol has been predicted due to the high concentration of macromolecules. Measurements of colloid osmotic pressure have been used to argue for a less crowded picture of the cytosol at the length scale of single proteins (<10 nm) due to the potential for many macromolecules to exist in higher-order complexes (Mitchison, 2019). It is not well understood to what degree the motion of macromolecular complexes on the scale of ∼10–100 nm is impacted by crowding, or how crowding may impact the formation of biomolecular condensates within cells. Thus, the structure of the cytosol across length scales and the effect that this has on biochemistry are still a highly debated topic in cell biology.

Molecular crowding can alter the material properties of the cytosol, which in turn influences the thermal, entropic fluctuations of molecular species within, such as Brownian motion of small molecules. Crowding may therefore have a critical influence on cell function, as molecular motion directly affects a broad range of physiological processes (Bressloff and Newby, 2013). For example, the diffusion of signaling molecules could be much slower within crowded regions of the cytosol delaying the downstream response in those regions. Conversely, some reactions may be potentiated by crowding through entropic depletion attraction effects, which favor molecular interactions (Zhou et al., 2008) and molecular condensation (Delarue et al., 2018). Additionally, it has been shown that glucose starvation can lead to a drastic reduction in mobility of molecules in the cytosol, indicating that cells may be able to tune their cytosolic material properties as a survival mechanism (Joyner et al., 2016; Munder et al., 2016). These impacts of cytosolic crowding are not limited to eukaryotes but have also been seen in bacterial cells (Parry et al., 2014; Gray et al., 2019).

The effect of crowding on particle motion is particularly relevant for large, multinucleate cells, where distinct functional territories emerge within the cytosol. In certain multinucleate fungi, including Ashbya gossypii, nuclei that reside in a common cytosol divide asynchronously, indicating that proteins that control the division cycle do not diffuse uniformly. Our previous work showed that this asynchrony is in part due to the assembly of RNAs and proteins important for the cell cycle into liquidlike condensates in the vicinity of nuclei (Lee et al., 2013, 2015; Zhang et al., 2015; Langdon et al., 2018). Multiple studies of liquid–liquid phase separation (Boeynaems et al., 2018; Delarue et al., 2018; Langdon and Gladfelter, 2018; Alberti et al., 2019) showed that phase separation can be enhanced by crowding, and we speculated that spatial heterogeneity in crowding can influence where biomolecular condensates form.

The best-established methods for evaluating molecular crowding involve particle tracking of passive particles of known sizes that are introduced into cells in a noninvasive manner. Based on the observed position-time series tracks, local properties of the medium such as crowding, confinement, viscosity, and elasticity can be estimated. Applications of particle tracking to measure cytosolic properties in a living cell have been limited due to challenges in creating ideal probes, rapid 3D imaging, and tracking. The recent development of genetically encoded multimeric nanoparticles (GEMs) has greatly facilitated the measurement of material properties of the cytosol (Delarue et al., 2018). Two types of GEMs have been described, each at a well-defined diameter of 20 and 40 nm and icosahedral shape. Introduction of a single gene leads to self-assembly of GEMs in any cell. They are an improvement over previous probes such as the μNS system which lacked a stereotypical assembly stoichiometry, size, and shape (Parry et al. 2014; Munder et al., 2016). As the proteins that make up the structure of GEMs are from separate kingdoms than Ashbya, it is unlikely that they will be subject to specific chemical interactions within the Ashbya cytosol. Recently, GEMs were used to show that changes in ribosome concentration had a substantial impact on molecular crowding and altered diffusivity in the cytosol. The specific 20 and 40 nm size of GEMs was critical for detecting the changes in porosity of the cytosol at the mesoscale length-scale relevant to macromolecular complexes (Delarue et al., 2018).

The goal of this work was to spatially resolve cytosolic properties within cellular volumes, which require 3D particle tracking. There are multiple challenges for 3D particle tracking in live cells using probes based on biological fluorophores. Compared to synthetic nanoparticles, GEMs have lower signal output that, when expressed in Ashbya and imaged rapidly in 3D, degrades over time due to photobleaching, leading to low and temporally decaying signal-to-noise ratio (SNR) conditions. To tackle these challenges, we developed an image processing pipeline that begins with a recently designed neural network-based particle tracker (Newby et al., 2018), which is highly automated and was shown to perform well in low SNR conditions. Neural networks have recently made several breakthroughs in microscopy image analysis, including cell tracking (Moen et al., 2019). Expanding on the neural network-based particle tracking software, we built an analysis pipeline that constructs a polygonal mesh of the cell surface so that our measurements can be correlated with cellular structures.

Here, we analyze mobility of 40-nm GEM particles within the morphologically complex and large cells of the multinucleate fungus Ashbya to study the spatial heterogeneity of the cytosol at this length scale. We find substantial variability in the apparent crowding of the cytosol both within a single cell and between different cells. Furthermore, we find that biomolecular condensates are more likely to form at hyphal tips and in the vicinity of nuclei, regions where we also detected more pronounced apparent crowding. This work provides evidence that the fundamental structure of the cytosol may be an underappreciated source of cell-to-cell variation in populations, which has far-reaching implications for diverse cell processes. This study also provides a technical platform for the spatial analysis of 3D particle tracking data within cells.

RESULTS

Native and artificial condensates localize in the vicinity of nuclei and at hyphal tips

How cells control the location of liquidlike compartments formed through phase separation is not well understood. There could be specific molecular determinants that nucleate condensates and/or their positions could be driven by physiochemical parameters such as crowding or pH. The RNA-binding protein Whi3 forms liquidlike condensates in the vicinity of nuclei and hyphal tips in Ashbya cells to localize transcripts for the cell cycle and cell polarity (Figure 1, A and B) (Lee et al., 2013, 2015; Zhang et al., 2015; Langdon et al., 2018). We wondered if the physical properties of the cytosol in these areas generally promote phase separation, potentially through molecular crowding. In this case, we would predict that phase separation of other biomolecules would also occur in the same areas where Whi3 condensates are formed.

FIGURE 1:

Native and exogenous condensates are nonrandomly localized. (A) Part of a large, multinucleate Ashbya cell. Ashbya grows in branched filaments called hyphae, each containing many nuclei residing in a common cytosol. Cells are made up of multiple hyphae and grow exclusively at regions called tips. Nuclei are labeled with HHF1-GFP. (B) Condensates comprised of endogenously expressed RNA-binding protein Whi3 localize near nuclei and at hyphal tips. (C) Exogenous synthetic phase-separating proteins are also largely located in the vicinity of nuclei and hyphal tips; 41.3% of hyphal tips had a condensate present within 1 μm of the tip apex, measured from the center of the condensate (N > 100 tips). In regions >1 μm from a tip, 72.5% of condensates were within 1 μm of a nucleus, measured from the center of the condensate to the edge of the nearest nucleus (N > 100 condensates).

To test this, we expressed an exogenous synthetic phase separating system made up of multivalent protein interaction domains, coexpressed from a single plasmid developed by Emmanual Levy’s lab (Heidenreich et al., 2020). We were surprised to see that these exogenous proteins also condensed in the regions around nuclei and at hyphal tips (Figure 1C). These condensates span a range of sizes with many much larger than Whi3 condensates; 41.3% of hyphal tips had an artificial condensate with center within 1 μm of the tip apex (N > 100 tips). Hyphae tend to be multiple orders of magnitude longer than these 1-μm tip regions, suggesting that they are not located here from random chance. In the rest of the hyphae (regions >1 μm from a tip), 72.5% of the artificial condensates were located within 1 μm of the edge of a nucleus (N > 100 condensates), despite the fact that an estimated 39% of the cytosol resides within 1 μm of nuclei (see Materials and Methods). This suggests that the cytosol around nuclei and at tips where Whi3 normally condenses is also able to promote the formation of artificially engineered condensates. Thus, there may be general features in these areas that promote phase separation. These observations motivated us to examine the physical properties of the cytosol near nuclei and at hyphal tips through 3D particle tracking of GEMs.

Development of a pipeline for cytosolic particle tracking analysis

To test the hypothesis that there are spatial inhomogeneities in the cytosol of Ashbya cells, we tracked 40-nm GEMs throughout the 3D space of the cytosol to measure its physical properties. As the tracked motion of nanoparticles can report local crowding, we used the measured diffusivity as a readout for the state of the cytosol at the 40-nm length scale. We attempted to film smaller 20-nm GEMs, but these were too dim when expressed in these cells, making it impossible to film fast enough in 3D to accurately track. Therefore we restricted our focus to the brighter 40-nm GEMs, which we will refer to simply as GEMs throughout the manuscript.

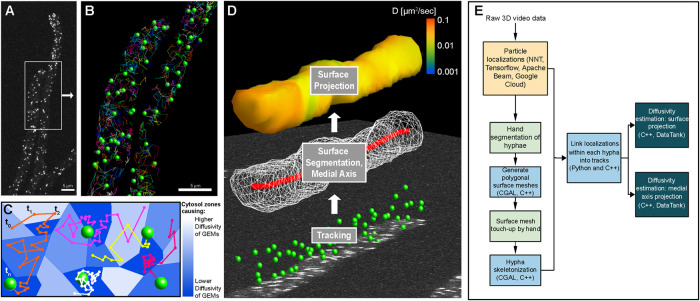
There are multiple challenges for particle tracking in live cells, including acquisition, storage, and automated analysis of 3D video sets. The 3D videos can be exceptionally large datasets; a single video can range from ∼10 to 100 GB and potentially much larger given the current rapid development in the 3D microscopy space. We implemented our pipeline within Google Cloud to take advantage of their data storage facilities and its full array of high-performance computing services that are designed for high-throughput data processing. The ultimate purpose of the analysis pipeline is extraction of spatiotemporal information of diffusivity in the context of cell architecture (see Figure 2, C and D).

FIGURE 2:

Particle tracking and cellular geometry analysis pipeline. (A) A representative max projection of GEMs imaged within Ashbya. (B) Green spheres show location of GEMs from the region in A that were localized for this frame and linked to at least one other time point. Any GEMs visible in A that are not shown in B are likely due to an inability to link in time, rather than a missed localization. Multicolored lines show the tracks for the entirety of the video. (C) Schematic of a heterogeneous cytosol, where local material properties, and resultant diffusivity of GEMs, change throughout space as represented by the blue tessellation. Hypothetical GEMs tracks through time are shown as colored lines as in B. Due to the small 40 nm size of GEMs, they have high mobility and individual particles can explore a relatively large region of the cytosol over the course of 3D imaging. Due to this, we use only the frame-to-frame displacements of GEMs to create a map of spatially varying diffusivity within the cytosol. (D) A diagram representing the flow of the analysis pipeline, starting with particle tracking on image data (bottom panel, green spheres), followed by surface segmentation (middle panel, white wireframe of the polygonal surface mesh), and computation of the medial axis (red curve). A representative surface projection of diffusivity is shown for the final step (top panel, heat map). (E) A diagram showing the general organization and steps of the particle tracking analysis pipeline.

The traditional approach of measuring diffusivity from tracked particles is through mean square displacement (MSD) analysis of particle tracks. The applicability of this approach assumes that particles experience spatially uniform fluid properties and unconfined motion. The small size of GEMs and their resulting high mobility over the timescales of 3D imaging mean that particles are routinely observed to move between regions having large differences in diffusivity (see Figure 2C). The standard MSD approach would effectively average the spatial variability experienced by the particle throughout the observed track, as a single diffusivity value is calculated from a full track. Additionally, GEMs within the Ashbya cytosol are confined within the tubelike interior of hyphae, which have diameters generally less than 5 μm (see Figure 2A). MSD estimates use particle displacements over timescales large enough to be significantly affected by confinement due to the cell boundary. This is particularly relevant for 3D particle tracking, as the z-stack acquisition rate is lower than the 2D video frame rate.

These considerations, combined with the main purpose of our pipeline to map and quantify spatial heterogeneity with respect to specific intracellular structures, call for a different approach to measuring spatially varying diffusivity within the cytosol of Ashbya cells. Variable diffusion is defined here as being governed by Fick’s law of diffusion which states that the particle concentration flux points in the opposite direction of the concentration gradient, with the diffusion coefficient dependent on location (for more details, see the Materials and Methods section on spatially varying diffusion). Instead of analyzing the entire trajectory of a particle, which could contain information about multiple spatial regions with differing amounts of crowding, we use the Maximum Likelihood estimator for diffusivity to analyze frame-to-frame particle displacements to get a local estimate of diffusivity. As a result, the diffusivity estimates can be spatially resolved and are more resistant to the effects of confinement (see the Materials and Methods section Boundary effects on particle tracking). As with any parameter estimation from data, fewer observations imply more uncertainty in the estimate. Therefore, it is then necessary to combine our individual diffusivity estimates into groups to get a reasonably accurate estimate of diffusivity within a given spatial region. To accomplish this, we perform spatiotemporal averaging using a kernel-regression estimator (KRE), which can be thought of as grouping particle displacements that are close to one another spatially and temporally. Length scale and timescale parameters control how far apart in space and time to group observations (see Materials and Methods section on KRE). Tuning of these parameters was done by testing our pipeline on synthetic videos (described below). Parameters were set to be small enough to get sufficient spatial and temporal resolution and large enough that a sufficient number of observations are grouped together for an accurate estimate.

Particle tracking with machine learning

To spatially analyze diffusivity, we implemented a new processing pipeline built on a recently developed automatic particle tracking algorithm (Newby et al., 2018). The neural network tracker (NNT) employs machine learning methods to accurately localize particle centers from 3D image data. After localization, particle positions are ‘linked’ into tracks (see Figure 2B). Linking algorithms generally have at least one parameter that fixes the maximum allowable step size between localizations. Because particle mobility varied strongly in space, some regions required small step sizes while others much larger. To adaptively and automatically link a wide range of particle step sizes, we employed a machine learning method based on the Expectation-Maximization algorithm (Rabiner and Juang, 1986).

The localizations were first linked assuming a spatially constant diffusivity. The linked tracks were then used to obtain a preliminary estimate of spatially varying diffusivity using a 3D KRE estimator. We used this preliminary estimate (replacing the spatially constant diffusivity) to link a new set of tracks, which were used to obtain a better estimate of the spatially varying diffusivity. This process was repeated, with each iteration yielding progressively better results. We found that after 12 iterations we achieved sufficient convergence (see accuracy indicated in Figure 3). Additional iterations made virtually no change to the estimates. These methods would ordinarily be computationally expensive to perform on a full set of localizations from a 3D video. By segmenting localizations by hyphae, we were able to link only those that shared the same cytosolic space, as two particles can be close in terms of three dimensional distance but be in different hyphae. The subdivided localizations were also used to compute the cellular geometry for each hypha.

FIGURE 3:

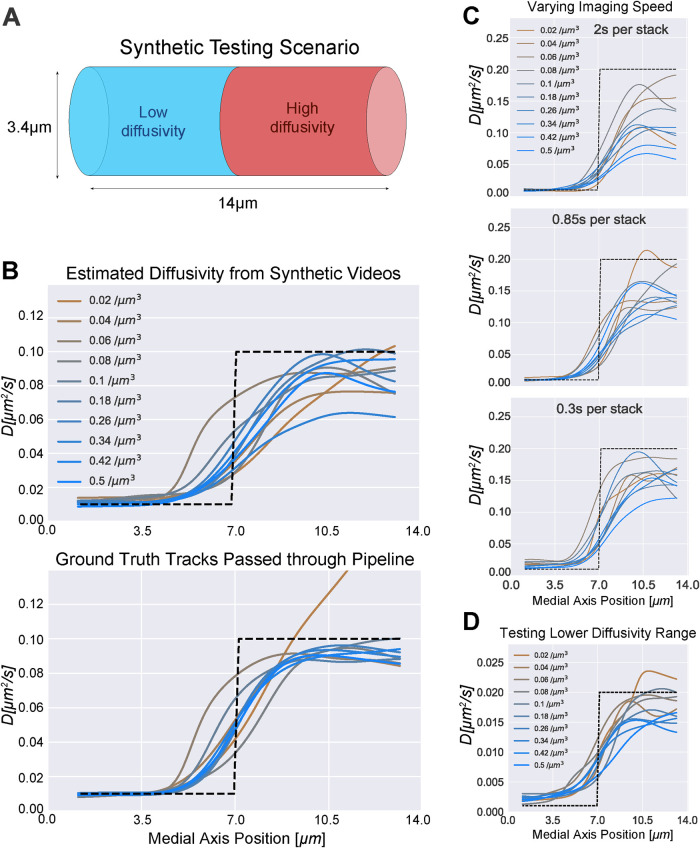
Synthetic testing shows accuracy across a range of diffusivities and imaging speeds. (A) Diagram illustrating the cylindrical domain used to generate synthetic testing videos. The cylinder represents a small segment of a hypha where there is a sharp jump in diffusivity. The diameter was chosen to match the experimental z-stack distance. The purpose of the test is to quantitatively measure the ability of the pipeline to simultaneously measure low and high diffusivity adjacent within a hypha. The plots in B–D contain testing results from medial axis diffusivity projections because all quantification in Figure 4, C–F and Figure 5, B, C, E, and F was performed on the medial axis curves. (B) Top: results of analysis of simulations in which hyphae containing GEM-like particles were created to closely mimic our real data. Half the field was comprised of low diffusivity (0.01 μm² s⁻¹) particles and half high diffusivity (0.1 μm² s⁻¹), shown as a dotted black line. The z-stack acquisition rate was set at 0.85 s per stack. The videos were then passed through the full analysis pipeline. A curve representing the average diffusivity moving along the medial axis is plotted for each simulation. Each curve shows results from simulations with a different density of particles. Bottom: the diffusivity estimated from passing ground truth tracks through the analysis pipeline (bypassing the particle tracking stage). This removes error due to particle tracking and shows purely error due to sample size and spatial averaging. (C) Diffusivity estimates obtained by processing synthetic videos of varying imaging speeds through the full pipeline. For reference, the GEMs videos were imaged 0.92 s per stack on average, and GEMs particle density varied around 0.05–0.15 μm⁻³. (D) Diffusivity estimates from particle tracks obtained by processing synthetic videos of a lower diffusivity range through the full pipeline. The z-stack acquisition rate was set at 0.85 s per stack.

Estimating diffusivity relative to cell surfaces and cell geometry

Even with high quality automated tracking software, the end result is a collection of space-time series tracks without the context of surrounding cellular structures. Without this information, we cannot say how a particular particle’s motion relates to the cell structure, or whether it should be combined with or compared with nearby observations. To address this challenge, we used the particle observations to reconstruct the cell surfaces (Figure 2D) of Ashbya, which form highly branched mycelial structures (see Figure 1). Using the open-source software library CGAL, we used the cell surfaces to compute a medial axis curve that traverses the midline along the interior of the cell surface, which includes the graph structure of branches (Figure 2D). After obtaining particle localizations, we used the set of 3D points to segment individual hyphae within a given video. The grouped points were then used to construct polygonal meshes of the cell surfaces. The resulting surfaces were used to compute an approximate medial axis curve, also using the CGAL library (Figure 2D, middle). Additional details are included in Materials and Methods.

As discussed previously, we used KRE and exponential time averaging to compute spatiotemporal estimates of diffusivity (see the Materials and Methods section KRE with exponential time averaging for precise definitions). We use two geometric projections for these estimates: a medial axis projection and a surface projection. In each, observations of particle movement are grouped together based on their location. For example, in the medial axis projection, we group observations by their closest point on the medial axis. The medial axis projection assumes that the cytosol is approximately radially symmetric around a given medial axis point and that its properties change only along the length of each hypha. The surface projection assumes that cytosolic properties might vary depending on the radial direction but not on the radial distance from the medial axis. The medial axis curves have fewer points than the surfaces, which means the medial axis projection has reduced sampling error compared with the surface projection because, on average, more observations are grouped together compared with the surface projections.

The surface projections allow us to visualize a heat map of the diffusivity overlaid on the surfaces using the 3D-capable interactive data visualization software DataTank (see Figure 2D, top; Figure 4A; and Supplemental Videos S1 and S2) (Adalsteinsson, 2002–2020). While the surface meshes contain more 3D information than the medial axial projections, they also have more uncertainty due to lower sample size. The particle tracking observations are more spread out on the surface than they are on the medial axis. We found both methods to be useful for characterizing the variability in diffusivity over the full dataset. Due to the positioning of nuclei being fairly evenly spaced along the medial axis (see Figure 1A), and the tip regions being easily defined as end portions of the medial axis, the medial axis projection was chosen for quantifying these regions. Surface projections were used as a visualization tool, as well as a method of putting the medial axis projections into context.

FIGURE 4:

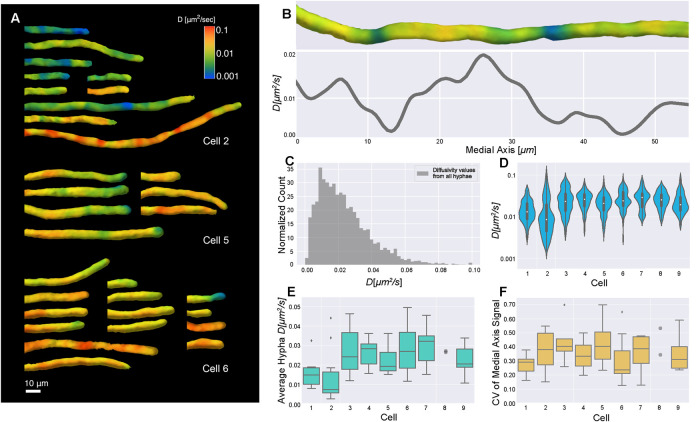
Diffusivity varies within hyphae and between cells. (A) Surface diffusivity projections from three cells in the analysis. Note that segmented hyphae were manually aligned for visualization. (B) Diffusivity surface projection (top) and corresponding medial axis projection (line plot) for a representative hypha. The surface projection and medial axis plot were lined up by matching the positions of the end points; however, as the surface projection is shown on the surface of a 3D shape and the medial axis plot contains averaged values along a line, they were impossible to perfectly match up. (C) Histogram of all medial axis diffusivity values from every hypha, normalized so the area of the histogram is 1 by dividing count/(number of observations * bin width) to get a probability density. Nine cells were imaged with 63 hyphae in total, each containing many nuclei and local environments. In a uninucleate context, this would be equivalent to hundreds to a thousand cells in terms of biomass per nucleus. Average diffusivity is 0.02 ± 0.02 (SD) μm² s⁻¹ and n = 8558 for medial axis diffusivity values from all hyphae, coming from a total 2148 μm of medial axis. The diffusivity value at each medial axis point comes from a cytosolic volume of 2 μm³ on average. Each diffusivity value is weighted by the volume that it was estimated from. (D) Violin plots show the log-scaled distribution of the medial axis diffusivity values from all hyphae for each cell, indicating overall cell–cell variability. When we compared these distributions to each other, about half were significantly different (see Table 1). The number of medial axis diffusivity values per cell ranges from 374 to 1702. (E) Box plots show the average of each hypha’s medial axis signal, indicating hypha-to-hypha variability of average diffusivity within each cell. Each cell had seven hyphae on average. Outliers are shown as diamonds. Any cell with less than five hyphae has all data points shown as gray circles. (F) Box plots show CV for each hypha’s medial axis signal. Each CV provides a measure of the variability of diffusivity along the medial axis in a given hypha.

Movie S1.

Download video file ^{(32.8MB, mov)}

Max projection of GEMs in an Ashbya cell. 3D GEM localizations are visualized as green spheres above the max projection, and surface projected diffusivity estimates are shown above those.

Movie S2.

Download video file ^{(13.5MB, mov)}

Max projection, localizations, and surface projected diffusivity estimates for a single hypha. Lower diffusivity at the hyphal tip as well as heterogeneity of diffusivity within the hypha can be seen.

Testing inference accuracy using synthetic videos

To test the accuracy of the pipeline, we generated synthetic videos of simulated particles moving within a cylindrical hypha (see Figure 3A). The 3D synthetic videos were generated using a custom Python script that simulated particle trajectories and computed corresponding images that were carefully constructed to closely mimic the video conditions we observed, including noise, 3D particle PSFs, stochastic motion between z-stack slices, and random background intensity within the hypha (additional details are in the Materials and Methods section on pipeline testing). All particles moved by simulated Brownian motion with spatially variable diffusivity consistent with Fickian diffusion. Particle diffusion in each half of the hypha was set to a different value (up to 0.2 μm²/s).

For the initial test in Figure 3B, a set of 10 videos with a range of particle densities was generated to test the accuracy of the medial axis diffusivity estimates. The synthetic videos were fully processed through the particle tracker and the subsequent pipeline (see Supplemental Video S3). Medial axis projections of the test data are shown in Figure 3B, top. Error in the absolute measurement of diffusivity was partially due to missing observations and linking errors at the initial particle tracking stage. For comparison, we also used ground-truth particle tracks (simulating perfect tracking by bypassing the initial particle tracking step) to isolate the subsequent pipeline error from particle tracking error (see Figure 3B, bottom). Error in the diffusivity estimates using the ground truth tracks was due to sample size and spatial averaging. This can be seen in the lowest density conditions (brown curves) where even the ground-truth tracks result in increased variability because of the low number of observations.

Additional synthetic video test sets were generated to assess performance over a range of imaging speeds and diffusivities (see Figure 3, C and D) with similar results. Faster imaging speed improved the accuracy of high diffusivity, while accuracy at low diffusivity was slightly reduced for the fastest imaging speed (0.3 s per stack) due to simulated localization error. To ensure that we can simultaneously measure very small differences and very large differences, automatically, with the same linker, we varied the range of diffusivities in an additional test set. In Figure 3D, we show a 10× reduction of diffusivities, compared with Figure 3C. Overall, we were able to accurately estimate diffusivities between 0.001 and 0.2 μm²/s. Lower diffusivities may be possible but were not tested or observed in our experiments. We underestimate high diffusivity values due to time lost imaging through z, but this is a trade-off to enable 3D tracking. We expect the accuracy to improve and better estimates of high diffusivity to emerge in the future as faster 3D imaging techniques are developed.

The measured diffusivities were able to capture the relative change in diffusivity within the synthetic hyphae with sufficient spatial resolution to distinguish each region, which was the primary goal of the pipeline. Importantly, the measurements maintained consistent performance over a wide range of particle densities at the SNR conditions observed in real videos. In summary, these simulations gave us confidence that the pipeline is able to track 3D particles of the intensity and density seen in the data we collected from live cells.

Diffusivity varies within and between cells

We next analyzed Ashbya cells expressing 40-nm GEMs (Delarue et al., 2018) using the described pipeline. Figure 4 shows spatially and temporally averaged diffusivity estimates through the first 50 frames, around 40 s into imaging, as diffusivity estimates have converged by this time and photobleaching is still negligible. We found that average GEM diffusivity was 0.02 ± 0.02 (SD) μm²/s (Figure 4C), slower than previously reported for the same particles in the budding yeast Saccharomyces cerevisiae (Delarue et al., 2018). Our diffusivity is underestimated due to the limitations of 3D imaging rate, but direct comparisons between the species in identical imaging conditions also show that diffusivity in Ashbya is ∼2-fold slower than S. cerevisiae (G.P. Brittingham, personal communication). Notably, we found substantial spatial variability in diffusivity, both within individual hyphae and between cells, which are made up of many individual hyphae connected by a common cytosol (Figure 4, A–F).

In Figure 4A, we show three representative montages of cell surface projections of GEMs diffusivity, demonstrating that cells show varying degrees of heterogeneity within hyphae. The diffusivity within single hyphae (e.g., Figure 4B showing a representative medial axis projection) was observed to range roughly over 0.01–0.1 μm²/s overall. Given the testing we performed on the pipeline, our measurements likely underestimate the total range of diffusivities somewhat. Nevertheless, it is the relative variability that is of primary interest. In terms of spatial resolution, we were able to detect significant changes in diffusivity over distances as small as 1 μm. The resolution is limited by the need to spatially average the diffusivity. Decreasing the length scale of averaging results in noisier estimates because fewer observations are grouped together.

In Figure 4C, we show a histogram of measured medial axis diffusivities, weighted by volume, of the combined dataset. To get a picture of the cell-to-cell variability, the global histogram can be compared with violin plots in Figure 4D, which show diffusivity distributions grouped by cell. As each cell contains many hyphae that each have multitudes of nuclei and corresponding microenvironments within them, aggregating in this manner could cause us to miss local differences. Therefore, to further quantify the cell-to-cell, intracell, and intrahyphae variability, we computed the average diffusivity per hypha, and the coefficient of variation (CV) of each medial axis signal, defined as the SD divided by the mean (Figure 4, E and F), respectively. Hyphal diffusivity averages varied considerably both within the same cell and between cells. The distributions of CVs show that some cells (e.g., cell 5) exhibited much more intrahyphal heterogeneity of diffusivity than others (e.g., cell 1). These analyses indicate that there is substantial spatial variation in crowding as measured by GEM diffusivity both within a single cytosol and between individual cells.

Diffusivity is correlated with nuclear position and cell cycle

With the observation of spatially heterogeneous diffusivity, we next asked how the variability is organized relative to cellular structures such as nuclei and hyphal tips (see Figure 5, A and D). Videos of cells with both GEMs and a fluorescently tagged component of the spindle pole body (SPB), which is embedded in the nuclear envelope, were collected to localize nuclei in different stages of the cell division cycle in relation to diffusivity estimates. To correlate our diffusivity estimates with the position of nuclei, we projected the SPB locations to their nearest medial axis point. As nuclei in Ashbya move relatively slowly (Alberti-Segui et al., 2001), the nuclei-localized diffusivity values are representative of the local environment around nuclei and unlikely to be impacted by the motion of the neighboring nucleus.

FIGURE 5:

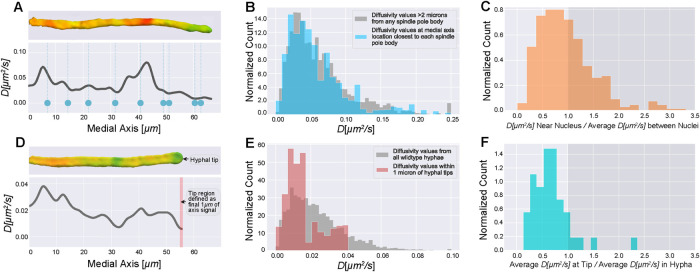
Diffusivity estimates relative to cell landmarks. (A) Single hypha diffusivity surface projection and corresponding medial axis projection. Blue dots show medial axis locations of nuclei within the hypha. Nuclei were imaged first in a single z-stack, followed immediately by 3D imaging of GEMs; 353 nuclei were localized within 59 total hyphae from four cells by fluorescently tagging a component of the SPB. (B) Blue histogram shows diffusivity values near nuclei, as determined by mapping each SPB to its nearest medial axis point and extracting the diffusivity value there. The diffusivity value at each medial axis point comes from a cytosolic volume of 2 μm³ on average. Each diffusivity value is weighted by the volume that it was estimated from. The gray histogram shows medial axis diffusivity values that are more than 2 μm from any SPB. As nuclei are 2 μm in diameter on average, and we only have the SPB marked, these values give diffusivity in the regions between nuclei. Note that we observed a slightly higher range in estimated diffusivities in this strain compared with wild type. For the gray histogram, n = 4457 for medial axis diffusivity values more than 2 μm from any SPB, coming from a combined 1194 μm of medial axis. For the blue histogram, n = 353 medial axis values from nuclei locations. (C) For each of the 353 nuclei, we calculated the ratio of diffusivity near nuclei to average diffusivity of regions between nuclei. (D) Single hypha diffusivity surface projection and corresponding medial axis projection, with the red bar highlighting the tip region which we have defined to be the last 1 μm of the medial axis diffusivity curve. For these measurements, 41 hyphal tips were analyzed across nine cells from the large dataset used for analysis in Figure 4. (E) Diffusivity values from all hyphae compared with diffusivity values within the tip region. The gray histogram is from Figure 4C. For the red histogram, n = 226 medial axis diffusivity values from 41 tip regions. (F) For each of the 41 hypha with tips analyzed, we calculated the ratio of average diffusivity in the tip region to average hyphal diffusivity. All histograms normalized to have area of 1 by dividing count/(number of observations * bin width) to get a probability density.

Initially, we noticed that some of the low diffusivity regions in the surface projections appeared to be in the vicinity of nuclei. To assess if there was indeed a systematic association between slower than average diffusing GEMs and nuclei, we compared the distribution of GEMs’ diffusivities at the medial axis point closest to each SPB to the medial axis values from the spaces in between nuclei. Any deviation of the former distribution, if statistically significant, would suggest heterogeneity of the physical properties of cytosol around nuclei. Surprisingly, as Figure 5B shows, both distributions are nearly identical (up to sampling error); however, this is comparing nuclear regions to the whole distribution of diffusivity values rather than comparing regions within a single cell which, given cell-to-cell variability, could be masking local differences. Therefore, for each nuclei, we computed the ratio of (diffusivity at the medial axis point closest to nucleus)/(the average diffusivity between nuclei in that hypha), a more local comparison of relative crowding differences (Figure 5C). The distribution of these ratios was compared with a baseline distribution: the ratio of (diffusivity at each medial axis point between nuclei)/(the average diffusivity between nuclei in that hypha), of which 55.8% of ratios were <1. For all nuclei, 59.2% of ratios were <1, a slight (and not statistically significant compared with baseline, p < 0.16, see Table 2 and the Materials and Methods section Statistics) tendency for diffusivity to be locally lower near nuclei. Because the SPB is a reporter of the cell cycle stage of a given nucleus, we also checked if there was any connection between the cell cycle stage and the local diffusivity that might be masked when the data are aggregated for all cell cycle stages. For nuclei in G1 and M, 53.7 and 50.0% of ratios were <1, respectively. For nuclei in S/G2, 69.0% of ratios were <1, a moderate increase above baseline (and statistically significant, p < 0.03, see Table 2 and Materials and Methods), indicating a cell cycle-dependent change in local cytosolic crowding.

TABLE 2:

Statistics from Figure 5, C and F.

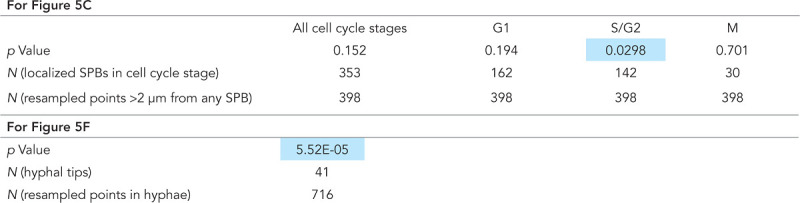Statistics from Figure 5, C and F. For statistics relevant to Figure 5C, p values are shown from two- sample KS tests comparing the distribution of ratios: (D at each SPB)/(average D in regions >2 μm from any SPB) with the distribution of ratios: (D at each medial axis point >2 μm from any SPB)/(average D in regions >2 μm from any SPB). Blue highlights p < 0.05. Medial axis points >2 μm from any SPB were resampled (with replacement) with N equal to the length of medial axis in those regions/3 μm to ensure independent observations. p Values are the average of 1000 runs. For statistics relevant to Figure 5F, p values are from two-sample KS tests comparing the distribution of ratios: (average D at each tip)/(average D in hypha) with the distribution of ratios: (D at each medial axis point)/(average D in hypha). The first ratio was resampled with N equal to the number of tips and the second as described above to ensure independent observations. p Values shown are again the average of 1000 runs.

It is possible that boundary effects from the nuclear membrane could account for some of the observed relative reduction of diffusivity. However, based on our synthetic testing, we estimate that boundary effects might account for a ∼1–2% reduction. In our simulations we tested a completely solid wall barrier (each hyphal segment had solid barriers at both ends, see Figure 3A) and observed a ∼5% relative reduction at high diffusivity (recall that boundary effects are more significant at higher diffusivity; see Materials and Methods). Most cytosolic regions we measured had lower diffusivity than was used in testing. Moreover, a nucleus would typically form only a partial barrier. A nucleus with radius 1 μm within a hypha of radius 2 μm would occupy (at most) 25% of the cross-sectional area of the hypha. It is therefore unlikely that the presence of a nuclear boundary could fully explain the effect we measured for nuclei in S/G2. Overall, these results suggest a moderate correlation between nuclei and lower diffusivity compared with the hypha average, specifically for nuclei in S/G2.

Hyphal tips are more crowded than other regions of the cell

In Ashbya, cell growth occurs exclusively at the hyphal tips, which are known to be sites of enriched actin assembly and liquid–liquid phase separation (see Figure 1). To quantitatively compare the diffusivity at tips to the overall average, we defined the tip region to be the last 1 μm of the medial axis curve (see Figure 5D). Overall, diffusivities at hyphal tips were lower than those measured throughout the full volume of cytosol (see Figure 5E). Looking within individual hyphae, we observed that a majority of hyphal tips (∼90%) had lower diffusivity relative to the average within their hypha (see Figure 5F). Note that the observed difference was also statistically significant, p < 10⁻⁴, see Table 2 and Materials and Methods. We suspect a small fraction (∼10%) of tips have higher diffusivity because they are not actively growing, and the organization of cytosol may depend on the local growth rate. Note that the reduction we observed at tips is substantially higher than could be accounted for by boundary effects based on our simulations (for more details, see the Materials and Methods section Boundary effects on particle tracing).

DISCUSSION

A major frontier in cell biology is to map the structure of the cytosol to understand how cells may use and react to its different physical states. Although differences in organization can have profound influences on a molecule’s ability to localize to distinct sites in a cell and interact with particular partners or substrates, little is known about how cells actively control the crowding of their cytosol to tune molecular diffusion. Here we find significant variations in the diffusivity of GEM particles within a continuous cytosol and between genetically identical cells indicating that cytosolic organization can be highly heterogeneous. This finding is important because it indicates that a potentially underappreciated source of regulation and noise in biological systems can arise from the physical structure of the cytosol.

As we observed self-assembly of artificial condensates near nuclei and at hyphal tips, our main goal was to correlate cytosolic heterogeneity with the positions of these relevant cellular structures. Compared to their individual hyphal averages, approximately 90% of hyphal tips were found to have lower diffusivity. Tips are known to be sites of actin dynamics, enrichment of ribosomes, and liquid–liquid phase separation which all may contribute to local crowding. Taken together, our results suggest a link between crowding and low diffusivity at hyphal tips and a more modest association between diffusivity at nuclei that is most pronounced in the S/G2 phase of the cell cycle. This period is associated with growth and could reflect enhanced ribosome density locally as it is known that the amount of local cytosol per nucleus increases through progression of the nuclear division cycle (Anderson et al., 2013).

Why do we not see a more substantial correlation between nuclear areas and low diffusivity zones? It is possible that in this area phase separation is more driven by specific molecules that nucleate condensates or chemical cues that are not detected here. Additionally, there could be a small volume of crowding surrounding nuclei that is a minor fraction of the total local volume of cytosol, making it hard to distinguish by volume averaging estimates. It is also possible that changes in cytosolic properties near nuclei are too small to be detected by our current analysis or are not accessible to the GEMs due to small pore sizes.

This work shows substantial heterogeneity in the motion of 40 nm-GEMs in a single cell. What is the source of this variation in motion? The initial characterization of GEMs supported that they are not interacting substantially with native proteins, indicating that they should display Brownian motion when the cytosol porosity is larger than 40 nm (Delarue et al., 2018). We therefore infer that low diffusivity zones are an indication of crowding rather than elastic effects from GEMs interacting with subcellular structures.

How do low diffusivity zones arise and persist? We observed significantly lower than average diffusivity within regions as small as 1 μm, and smaller regions may be beyond our ability to resolve without further improvement in the particle tracking methods used here. These regions were relatively stable and often persisted over the full duration of the video (∼1–2 min). There are several possibilities for what might be causing low diffusivity regions, including crowding by large macromolecules and liquidlike condensates. If untethered, large macromolecules and condensates would diffuse and eventually spread out evenly throughout the cytosol, which would eliminate any heterogeneities. However, for large enough macromolecules, mixing could take a sufficiently long time that crowded regions could persist on the timescale of minutes or longer, consistent with our findings. Moreover, it is possible that some low diffusivity areas are GEMs reporting from within condensates. The interior of RNA liquid condensates has been measured to have substantially higher viscosity than the bulk average we observed within the cytosol (Zhang et al., 2015). Cytoskeletal networks would also be capable of restricting molecular mobility. However, it is unclear if such polymeric structures within fungal cells have pore size sufficiently small to affect diffusion of molecules smaller than 50 nm, as the actin and microtubule networks are far less dense than in animal cells.

Looking forward with respect to our analysis pipeline, it could, with small modifications, be applied to virtually any cell shape. Segmenting filamentous fungal cells proved challenging to automate, so time was lost manually doing this. For traditional cells, the manual segmentation step in the pipeline could be replaced with something automated, which would speed up the process. The rest of the pipeline, including particle tracking, averaging, and surface projections, is not shape dependent. Medial axis projections may be relevant for cells of narrower shape; however, the surface projections are likely to be more informative for nonfilamentous cells.

Substantial improvements in particle tracking are on the horizon, such as improved tracking methods, diffusivity estimation, and microscope and camera hardware. A recent study claims to achieve accurate diffusivity estimates and Hurst exponents from short tracks using neural network-based regression (Granik et al., 2019), which could allow for less KRE averaging and finer spatial resolution with the same quantity of tracking data. Using light sheet microscopy would reduce photobleaching and allow for longer videos. Currently, imaging speed for 3D microscopy with standard piezoelectric stepping is slower than the frame rate of a typical camera, and many groups are working to eliminate this bottleneck (Abrahamsson et al., 2013; Voleti et al., 2019). Higher acquisition speeds will generally further improve the quality of all tracking inferences, will enable tracking of smaller rapidly diffusing probes, and will allow for acquisition of thicker volumes. These improvements, combined with the engineering of different sized probes with different chemical features, will bring substantial insights into how cells control and use cytosolic organization.

MATERIALS AND METHODS

Plasmid and strain construction

Plasmid expressing exogenous phase-separating peptides were gifted from the Emmanual Levy lab, modified to have a selectable marker for Ashbya expression and transformed under standard conditions to generate strain AG893 (Wendland et al., 2000). For nuclear visualization in Figure 1A, strain AG275 was used. Whi3-tomato strains (AG834) were generated by transforming the plasmid AGB 050 into the wild-type Ashbya strain (AG416). For pPfV-Sapphire GEMs::GEN strains, we transformed the plasmid AGB 910 (pPfV-Sapphire GEMs under control of the ScHIS3 promoter) into Ashbya wild type (AG416) and cells expressing Tub4-mCherry (AG270.1) via electroporation and selection on Ashbya full media (AFM)+G418 plates. This generated strains AG837(WT) and AG908(Tub4).

Cell culture and microscope setup

Ashbya cells AG837(WT) and AG908(Tub4) expressing the 40-nm GEM plasmid were grown under selection of G418 (150 µg/ml) in 10 ml AFM in a 125-ml baffled flask shaking at 30°C for 16 h. Cultures were transferred to 15-ml conical tubes (VWR) and spun at 300 rpm for 2 min. Cells were then washed with 2× low fluorescence media, spun again, and placed on a gel-pad embedded in a depression slide comprised of 2× low fluorescence media and 1% agarose. Slides were sealed with valap and imaged on a spinning disk confocal microscope (Nikon Ti-Eclipse with a Yokogawa CSU-X spinning disk module and PI P-736.ZR2S triggered piezo stage) using a 100× 1.49 NA oil immersion objective and sCMOS 95% QE camera (Photometrics prime 95B). The 3D time lapses of GEMs were acquired using triggered 488-nm lasers at 100% power for 1–2 min with a z-stack volume of 3.2 μm (0.2 μm per slice) and 40 ms exposure per image. The average time to image through a volume was 0.92 s, with 200 ms on average spent resetting the piezo. For cells expressing Tub4-mCherry, nuclei were imaged prior to GEMs with a single, equivalent z-stack using a 561-nm laser at 40% power with 200 ms exposure. Cells expressing exogenous phase-separating peptides were grown and prepared for imaging under the same selection and conditions as cells expressing GEMs. These slides were then imaged using a 60× 1.49 NA oil immersion objective over a z-stack volume of 3.2 μm (0.2 μm per slice) using a 561-nm laser at 100% power with 400 ms exposure. Cells with Whi3-tomato tag were also grown and prepared in the same way, and imaged over a z-stack volume of 3.2 μm using a 561-nm laser at 80% power with a 200 ms exposure.

Analysis of exogenous phase-separating condensates

The locations of the exogenous condensates relative to hyphal tips and nuclei were measured manually in ImageJ from max projections. Condensates were counted as being at a hyphal tip if the center of the condensate was within 1 μm of the tip apex. If the condensate was so large that it obstructed the view of the tip apex, it was scored as being at the tip. All visible tips (138) within four cells were scored. Nuclei could be seen as holes in the cytosolic background, and condensates were counted as being near a nuclei if their center was within 1 μm of the edge of the nearest nuclei. Forty-three hyphae across four cells were analyzed, chosen based on visibility of nuclear holes; 102 droplets within these hyphae were scored. The cytosolic area within 1 μm of nuclei can be estimated as a 1-μm thick shell surrounding a circle of radius 1 μm. Assuming nuclei are spaced 4.3 μm apart (Anderson et al., 2013) within a rectangular hypha of width 4 μm, 39% of the cytosolic area is within these shells.

Statistics

Due to the KRE spatial averaging (see the Materials and Methods section KRE with exponential time averaging) used to generate the medial axis diffusivity estimates, the diffusivity value at each medial axis point is not necessarily independent from its immediate neighbors. Based on our synthetic testing (see the Materials and Methods section Pipeline testing with stochastic particle simulations and synthetic videos), the KRE averaging smooths the diffusivity estimates over a ∼3-μm section of the medial axis. In other words, diffusivity estimates spaced farther than 3 μm apart were approximately uncorrelated (from the KRE smoothing). For statistically comparing the distributions in Figure 4D, we therefore applied bootstrapping (random resampling with replacement) to each distribution with the number of samples, N, set to the total length of all medial axis segments in that cell divided by 3 μm. We performed pairwise comparisons over the collection of bootstrapped sample sets with a two-sample Kolmogorov–Smirnov (KS) test, resulting in a p value for each pairwise comparison. We repeated this procedure 1000 times, each time using independent bootstrap samples, to get a set of averaged p value for each pair of datasets, as shown in Table 1.

TABLE 1:

Statistics from Figure 4D.

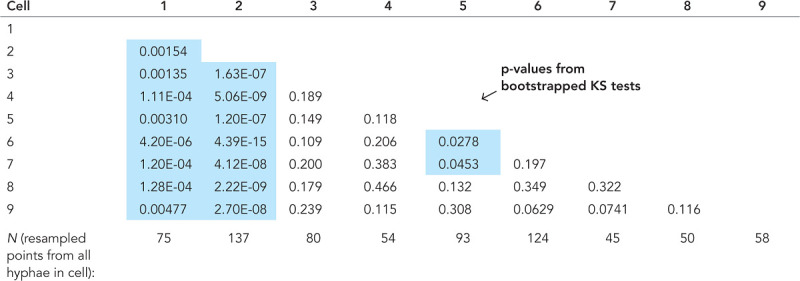Statistics from Figure 4D. Matrix of p values from two-sample KS tests, with blue highlighting p < 0.05. As each GEM displacement substantially contributes to the surrounding 3 μm of medial axis due to the spatial averaging, the distributions of all medial axis points were resampled (with replacement) with N equal to the total length of cell’s medial axis/3 μm to ensure independent observations. Each cell’s resampled distribution was then compared with all other cells, and this process was repeated 1000 times to get an average p value.

For Figure 5C, for all nuclei combined (as well as split up by cell cycle stage), we sought to compare the distribution of ratios: (D at each SPB)/(average D in regions >2 μm from any SPB) with the distribution of ratios: (D at each medial axis point >2 μm from any SPB)/(average D in regions >2 μm from any SPB). As nuclei tend to be spaced 5 μm apart, we assumed that each data point in the first ratio was independent. We applied the reasoning described above to the second ratio and resampled it (with replacement) with N as the total number of 3-μm medial axis segments in regions > 2μm from any SPB. A two-sample KS test was then applied to these two distributions, and this was then repeated 1000 times to get an average p value, shown in Table 2. This was done for all of the nuclei combined and then for nuclei subdivided by cell cycle stage.

For Figure 5F, we compared the distribution of ratios: (average D at each tip)/(average D in hypha) with the distribution of ratios: (D at each medial axis point)/(average D in hypha). The distribution of the first ratio was resampled (with replacement) with N equal to the number of tips and the second with N equal to the number of 3-μm medial axis segments in all of the analyzed hyphae. A two-sample KS was again applied and this procedure was repeated 1000 times to get an average p value.

Tracking analysis pipeline

The GEMs video dataset is comprised of two subsets: WT+GEMs (AG837) and tub4-mCherry+GEMs (AG908). The main purpose of the analysis pipeline is to track GEMs and use the tracks to infer properties of the cytosol, namely, spatiotemporally varying GEMs concentration and diffusivity. The analysis pipeline is comprised of custom software (written in Python and C++), combined with a number of open source software libraries. In Figure 2E, we show the basic steps in the pipeline.

The first step performs particle tracking on all videos using the NNT. The NNT uses map reduce-style methods (Apache Beam) together with cloud computing resources from Google Cloud (Dataflow) to batch process our large datasets and large file sizes.

The second stage of the pipeline computes an accurate reconstruction of the cell surface and a coordinate system representing the cell geometry. Because of the branched morphology of the cells, multiple branches often lay side by side, making it difficult to group GEM localizations belonging to a specific hypha. To compute the GEM concentration, we also needed to estimate the local volume of the cell interior, which required some means of determining whether a given point was inside or outside the cell and which hypha it belonged to.

Once we fully constructed cell geometries for each hypha segment, we used it to group GEM localizations by hypha segment. We then linked the grouped GEM localizations through time into paths or tracks. This ensured that a given particle path would not jump from one hypha segment to another.

Google Cloud image processing

We built our pipeline to use the Google Cloud Dataflow service, which is an implementation of Apache Beam. The challenges for batch processing large image datasets are 1) processing images through hardware without exceeding the memory capacity and 2) delivering large quantities of data in storage to distributed CPUs over a network. Convolutional neural networks are particularly challenging because they require large amounts of memory, many times the file size of the image being processed. Dataflow uses one or more “workers” or virtual machines (an independent computational unit comprised of a CPU, memory, and storage) to read image data from Google Cloud Storage and process it through the neural network pipeline. The main benefit of using Dataflow is that the service automatically scales the number of workers based on the size of the job. In our case, the size of the job was primarily determined by the quantity of image data, which could range from ∼10 GB to several terabytes.

We designed our pipeline to break up large videos into manageable blocks of fixed size, predetermined to be sufficiently small that they could be processed through the neural network without overloading the memory available to a single worker. The image blocks were “padded” to include overlapping regions of the image to eliminate artifacts at the edges of each block. The image blocks were then distributed to the available workers, which sequentially processed each block through the neural network. After neural network processing, particle localizations were identified. At this stage, the size of a localization dataset was orders of magnitude less than the image data, which allowed all of the localizations from a single video to be combined together for further processing without overloading the memory available to a single worker.

Uploading the videos to cloud storage was the slowest step. Upload of large datasets over a high-speed connection can take hours to days to complete. Google Cloud provides command-line utilities to efficiently and quickly upload files using multiple threads and compression. The uploads are resumable in case of disruption or network dropouts. Downloading the results (in our case, the set of particle localizations for each video) is fast and essentially instantaneous over most high-speed connections.

Processing time did not scale linearly with the amount of data. The pipeline was designed with large datasets in mind and was relatively less efficient for smaller datasets. On average, small datasets took at least 1 h to process, while larger datasets (as large as 1–2 terabytes) took roughly 5–10 h to process.

The cost of running videos through the Dataflow pipeline was surprisingly low, though it required an initial investment of time for development of the pipeline. The cost of using Google Cloud computing resources is based on the duration of time the resources are used (e.g., CPUs per hour). Dataflow only uses the computational resources for as long as they are needed and automatically shuts down workers when finished. Our pipeline used as many as 1000 workers for large datasets. A rough estimate for our pipeline was $0.15 (US) per gigabyte of image data (uncompressed).

Hypha geometry estimation

After the videos were tracked, we used the tracking data to generate a surface mesh and the medial axis curve (including branch points) extending down the length of each hypha. All of the particle localizations (particle positions), were grouped within each video. The resulting point set was used to generate a polygonal surface mesh of each hypha. Because it was exceedingly difficult to automatically segment each hypha (particularly when two hyphae lay alongside one another), hand segmentation and hand touch-ups of the surfaces meshes were performed. Only the nonoverlapping portions of hyphae were segmented, with all included hyphae containing or being near to a hyphal tip. These were the only steps in the pipeline that required interactive processing; the remaining steps were fully automated.

The surface meshes were initially constructed using tools from the Computational Geometry Algorithms Library (CGAL). First, a 3D Delaunay triangulation was computed for each hypha segment, which resulted in a convex solid comprised of many connected tetrahedra. The cell surface was then computed using the CGAL 3D Alpha Shapes package. The resulting surface mesh was usually quite rough and ill conditioned for the downstream steps of the pipeline. The CGAL Triangulated Surface Mesh Simplification package was used to resample and smooth the surface mesh. In some cases, topological imperfections could not be removed automatically (a known problem in constructing surface meshes from random point collections). We typically saw one to two small spots on approximately one out of every 10 hypha segments that required hand corrections. We repaired these surfaces meshes using Meshmixer.

The medial axis for each hypha segment was computed using the CGAL Triangulated Surface Mesh Skeletonization package (Tagliasacchi et al., 2012). This package required a well-formatted surface mesh, free of holes and topological imperfections. An approximation of the medial axis was obtained, a connected graph of points, which extends along the center of each hypha, connected at branch points. A secondary product of the mesh skeletonization procedure was a mapping from a given medial axis point to surface points. Each medial axis point was connected to zero or more surface points such that each surface point is connected to exactly one medial axis point.

This data structure was used to determine if a given point was inside or outside a given hyphal segment. We also used this mapping to project a given point within a hyphal segment to the closest medial axis point. This allowed us to generate estimates of diffusivity along each hypha medial axis. We also obtained estimates of concentration and diffusivity on the cell surfaces by mapping a given interior point to the nearest surface point.

Using polygonal surface mesh and medial axis to sort points inside a given hypha segment

We used the surface mesh and the medial axis curve to efficiently determine if a given point was inside or outside a hyphal segment. While this is trivial to compute for closed convex regions, hypha segments are almost never convex. They are, however, locally convex. Let the medial axis be given by 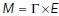, where 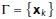is the set of nodes and 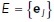is the set of edges linking each node. As described above, we also have a mapping from medial axis points to local surrounding surface points. Let 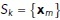be the set of surface points connected to the medial axis point .

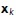Given an input point x to test, the method proceeds as follows. First, the closest medial axis point 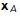to the test point x is computed. This step can be done quickly by brute force as there are a relatively small number of medial axis points. Second, we search the set of surface points connected to 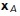for the closest local surface point 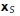. These are given by

Then, we say that the test point x is inside the hypha segment if

where 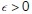is a small parameter that pads the estimate so that points that are very close to the surface are not mistakenly excluded. The parameter 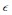can be thought of as the uncertainty in the estimated surface position. In pixel coordinates, we used 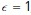, which works out to be approximately 100 nm.

KRE with exponential time averaging

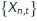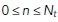Spatiotemporal estimates of diffusivity were computed using a kernel-regression estimator (KRE). This can be thought of as a “smooth histogram.” Let the set of particle positions at time t be given by , for , where 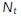is the total number of particles at time t. A Gaussian centered at each observation with a predetermined length scale parameter 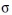(∼6 μm for surface projections and ∼12 μm for medial axis projections) are summed together. For the first stage in computing estimates (prior to time averaging), we define

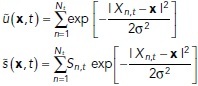where 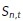is the contribution to the estimate from a single observation, centered at 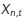. For diffusivity, the standard maximum likelihood estimator for a track in d = 1,2,3 dimensions is given by

where 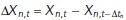is a particle displacement (or increment) and 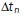is the time step between observations within the track, which is an integer multiple of the average interstack time interval of the video (the linker can skip over missing observations).

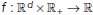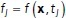The next step is to apply exponential time averaging to the result. For a given function , let , for 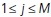, where 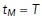is the max time. Then, the final time-averaged estimates are defined by

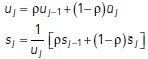where 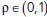. We can relate ρ to a physical timescale with 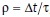, where 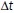is the average interstack time interval of the video and 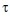is a parameter that determines the time-scale of averaging. We used timescales of 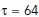and 192 s for exponential averaging of surface projections and medial axis projections, respectively.

Radius estimation and filtering large particles

We observed a small number (compared with GEMs) of fluorescent particles with larger radii than GEMs within some hyphae. Their origin could not be determined. The distribution of these larger particles was random, though possibly elevated somewhat near tips. They moved randomly, diffusively, or possibly subdiffusively, with mobility substantially lower than GEMs. To reduce their potential influence on our measurements of heterogeneous diffusivity of GEMs, we estimated the PSF radius and peak intensity of all particle localizations by regression of the local surrounding image patch to a Gaussian profile.

The filter was more accurate when applied to tracks instead of individual localizations. Averaging the PSF radius and peak intensity over all localizations within a track mitigated the influence of noise. We applied basic linking (assuming constant diffusivity for filtering) to the localizations to obtain a set of tracks specifically for filtering. The tracks used in the primary analysis were computed during a later step. After linking, we averaged the radius over each track to get the average PSF radius (r) and the peak intensity 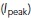. We filtered those tracks that had at least four observations and satisfied at least of one of the following two conditions

These criteria were chosen heuristically to achieve a balance between filtering as many large particles as possible while minimizing the number of true GEMs mistakenly filtered out. Due to this trade-off, a small fraction of the larger particles was tracked. However, their contribution to the overall observed heterogeneity was minimal.

Within the wild-type set, over half of the hyphae had no larger particles visible, and 90% of the hyphae had <5% of their localizations coming from the larger particles. All hyphae in the analysis had <10% of their total localizations coming from large particles. Hyphal tips were only included in the analysis if they did not have large particles within last 3 μm of the hypha. The larger particles were infrequent in the Tub4-Cherry set, accounting for <1% of localizations.

Motion model used to define spatially varying diffusion

The notion of a spatially varying diffusivity assumes an underlying particle motion model. We assumed that diffusion is governed by the so-called Fickian model, which is consistent with Fick’s Law of diffusion

The corresponding motion model (a stochastic differential equation) is described in a below section. A large (approaching infinite) number of independent particles moving by the stochastic motion model will give rise to a particle concentration 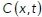that satisfies the above equation. This model was chosen because it preserves detailed balance and is consistent with a thermodynamic equilibrium. Note that we do not assume that the system is at thermodynamic equilibrium, since the living cell is certainly far from equilibrium. The model assumes that at steady state, the concentration of particles will be uniform throughout the accessible volume of the cell. Any concentration gradients that exist would require an energy-consuming “pump” to maintain. It is possible to maintain concentration differences of a given chemical species across the interface of phase-separated liquids, provided that there is a chemical potential difference between the two liquids. We assume that GEMs are sufficiently inert that they do not interact with any cellular components that would establish such an effective pumping mechanism. Note that we do not assume that the GEMs concentration is uniform within any particular observation. The thermodynamic consistency is simply the criteria we use to select the motion model. Other models of spatially variable diffusion, such as Ito or Stratonovich diffusion, do not give rise to uniform steady state concentrations (Schnitzer, 1993).

Pipeline testing with stochastic particle simulations and synthetic videos

To test the particle tracking pipeline, we generated synthetic videos of particle diffusing in a cylindrical domain with reflecting boundaries. The cylindrical domain was used to mimic a small section of a hypha, 14 μm long and 3.4 μm in diameter (see Figure 3A); 3.4 μm was chosen for the diameter to match the total z-step distance of the experimental videos.

Videos were comprised of a time series of 50 z-stacks with an average acquisition time of 0.85 s per stack. Each z-stack had 17 slices with separation of 0.2 μm. Each image slice contained 128 × 128 pixels with a pixel size of 0.11 μm. Videos were generated with Gaussian noise (with mean intensity 100 and SD 5), slowly varying background intensity (mimicking nonspecific fluorescence within the hypha), and a small ∼3 pixel radius Gaussian PSF (with max intensity above background of 34) for each particle (see Supplemental Video S3).

Movie S3.

Download video file ^{(15.6MB, mov)}

An example of a testing video as described in Figure 3A. Max projection of simulated Brownian motion shown, with localizations as green spheres, and surface projected diffusivity estimates above.

The diffusivity was changed at the midpoint of the hypha so that the left half had a lower diffusivity than the right half. Five video sets, each containing 10 videos, were generated with different diffusivity values for the left and right halves of the cylinder. We varied the total number of diffusing particles for each video within a given video set.

Stochastic particle simulations

Particle simulations of Brownian motion with spatially varying diffusivity (under the Fickian interpretation) were performed using a time-stepping method. We assumed independent particle motion so that there were no interactions between particles. Let be the position of a track at time t. The simulation scheme is given by

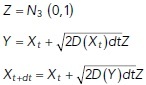where 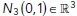is a vector of numerically generated, independent, normal random variables with mean zero and unit variance. The simulation time step was 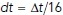(i.e., there were 16 simulation time steps between each z-stack of the simulated video). Reflection at cylinder boundaries was done using the method of ballistic reflection, which preserves detailed balance.

Note that the motion model appears “anticipatory” (meaning that steps depend on future motion), but it can be formulated as the motion of a nonanticipatory particle in a potential D(x), with the corresponding Ito SDE,

where dW is a 3D Wiener process (Gardiner 2009).

Boundary effects on particle tracking

The tubelike hyphal geometry restricts 3D Brownian motion to a quasi-1D closed domain. Using a 3D diffusivity maximum likelihood estimator, the apparent diffusivity from purely 1D Brownian motion would be 4× lower than unbounded 3D Brownian motion. We were able to reduce this potential effect by ignoring the z-position in our diffusivity estimates, which reduced the maximum possible boundary effect from a 4× reduction to a 2× reduction. Boundary effects should begin to affect diffusivity estimates (reducing the estimated diffusivity by up to 2× its actual value) once the average width of a hypha is about the same distance as a typical GEMs displacement during one video frame. In the synthetic testing, we observed ∼10% reduction in estimated diffusivity when the true diffusivity was 0.2 μm²/s. At hyphal tips, there is another boundary restricting motion, and we again observed an underestimation effect at high diffusivities (∼15% at 0.2 μm²/s, with ∼5% due to the presence of the boundary). As expected, this effect was negligible for lower diffusivities.

Figures

Plots were generated using the open-source Python packages, Matplotlib and Seaborn. Images were generated using the open-source application ImageJ and Nikon’s proprietary Elements. Three-dimensional surface projections and supplemental videos were generated using the proprietary application DataTank. Adobe Photoshop and Illustrator were used to compile the main figures together.

Surface projection videos

Three videos were generated to illustrate the spatio-temporal surface projection estimates. Supplemental Video S1 shows the max projection of GEMs in an Ashbya cell; 3D GEM localizations are visualized as green spheres above the max projection, and surface-projected diffusivity estimates are shown above those. Supplemental Video S2 shows the max projection, localizations, and surface-projected diffusivity estimates for a single hypha. Lower diffusivity at the hyphal tip as well as heterogeneity of diffusivity within the hypha can be seen. Supplemental Video S3 shows an example of a testing video as described in Figure 3A. Max projection of simulated Brownian motion is shown, with localizations as green spheres and surface-projected diffusivity estimates above.

Code availability

Data analysis and figure generation code is available at https://github.com/newby-jay/AshbyaTracking.

Abbreviations used:

AFM

Ashbya full media

CGAL

Computational Geometry Algorithms Library

CV

coefficient of variation

GEM

genetically encoded multimeric nanoparticle

KRE

kernel regression estimation

KS

Kolmogorov–Smirnov

MSD

mean square displacement

NNT

neural network tracker

SNR

signal-to-noise ratio

SPB

spindle pole body.