Abstract
When seeded in fibrous gels, pairs of cells or cell aggregates can induce bands of deformed gel, extending to surprisingly long distances in the intercellular medium. The formation of bands has been previously shown and studied in collagen systems. In this study, we strive to further our understanding of this fundamental mechanical mechanism in fibrin, a key element in wound healing and angiogenesis processes. We embedded fibroblast cells in 3D fibrin gels, and monitored band formation by real-time confocal microscopy. Quantitative dynamic analysis of band formation revealed a gradual increase in fiber density and alignment between pairs of cells. Such intercellular bands extended into a large-scale network of mechanically connected cells, in which the connected cells exhibited a more spread morphology than the isolated cells. Moreover, computational modeling demonstrated that the direction of cell-induced force triggering band formation can be applied in a wide range of angles relative to a neighboring cell. Our findings indicate that long-range mechanical coupling between cells is an important mechanism in regulating multicellular processes in reconstituted fibrin gels. As such, it should motivate exploration of this mechanism in studies in vivo, in wound healing or angiogenesis, in which fibrin is contracted by fibroblast cells.
INTRODUCTION
While cell–cell signaling by biochemical means is well studied, biomechanical forces and their contribution to cell-to-cell communication is less understood. Under physiological conditions, cells are often surrounded by an extracellular matrix (ECM), a fibrous network which acts as a scaffold, providing structural support to cells composing the tissue and upon which biochemical and biomechanical signals can be conducted (Frantz et al., 2010; Burla et al., 2019). Cells constantly apply contractile forces on the ECM, which are imperative to their function, such as for migration (Gjorevski et al., 2015) and division (Lesman et al., 2014).
The fibers of the ECM display unique nonlinear elastic properties, including strain stiffening under tension (Gentleman et al., 2003; van der Rijt et al., 2006; Piechocka et al., 2010; Wen and Janmey, 2013; Steinwachs et al., 2016) and microbuckling under compression (Gentleman et al., 2003; Conti and MacKintosh, 2009; Munster et al., 2013; Xu and Safran, 2015, 2017; Goren et al., 2020). This nonlinearity allows for cell-applied forces to propagate from the cell far into the matrix, and for cells to mechanically sense distant neighbors (Vader et al., 2009) or rigid boundaries (Rudnicki et al., 2013). Cells cultured on linear-elastic substrates demonstrate a shorter range of force propagation and more limited ability to sense their neighbors (Reinhart-King et al., 2008). Such cell forces can lead to dramatic densification and alignment of the ECM fibers extending between neighboring cell clusters (Stopak and Harris, 1982; Korff and Augustin, 1999; Vader et al., 2009) or between single cells in fibrous matrices (Reinhart-King et al., 2008; Piotrowski-Daspit et al., 2017; Sopher et al., 2018; Gomez et al., 2019; Mann et al., 2019), forming structures that were previously referred to as “tracks” (Ban et al., 2018), “lines” (Shi et al., 2014), “tethers” (Notbohm et al., 2015a), “bundles” (Stopak and Harris, 1982; Vader et al., 2009; Winer et al., 2009; Kim et al., 2017; Reinhardt and Gooch, 2018), or “bands” in the ECM (Stopak and Harris, 1982). Such bands of increased fiber density and directionality can mechanically couple distant cells, and regulate the biological activity of the affiliated cells, including orienting cells toward each other (Vader et al., 2009), directing capillary sprouting (Korff and Augustin, 1999) and facilitating invasion of cancer cells (Shi et al., 2014). Moreover, the anisotropic and dense character of the bands may facilitate cell-to-cell communication by introducing stiffness gradients, which can be sensed by a durotaxis mechanism (Kim et al., 2017) or by topological alignment guidance (Gjorevski et al., 2015). Such matrix bands may also support mechanical–biochemical feedback interactions between cells by facilitating rapid transport of molecules secreted by the coupled cells (Gomez et al., 2019; Jung et al., 2020).
In vivo, the ECM of each tissue varies according to location and function, in terms of its protein content, structure, and mechanics. Most studies on mechanical ECM remodeling, and specifically on ECM band connection between cells, have been performed almost exclusively in collagen gels, the major protein of the ECM in tissues (Korff and Augustin, 1999; Vader et al., 2009; Shi et al., 2014; Kim et al., 2017; Ban et al., 2018; Reinhardt and Gooch, 2018). Notable works include that of Kim et al., who demonstrated that collagen tracks are generated by breast cancer cells, and that the track formation mechanism is associated with plastic and irreversible deformation of the fibers (Kim et al., 2017). In the context of multicellular cultures, Shi et al. demonstrated that collagen tracks can be generated by mammary acini cultured in collagen gels, and facilitate the invasion of the coupled acini (Shi et al., 2014).
In addition to collagen gels, fibrin, an extracellular biopolymer that is secreted during blood clotting and wound healing and supports angiogenesis, forms key biological matrices. Following injury, fibrinogen is cleaved by thrombin, resulting in the formation of a branched fibrin gel into which fibroblasts migrate to start the healing process and eventually contract the wound (Smithmyer et al., 2014). The in vitro model of fibroblast cells grown in fibrin gels is a well-established model of wound healing (Smithmyer et al., 2014). Also, fibrin was associated with long-range propagation of cellular forces and mechanosensing abilities. For example, Jansen and colleagues demonstrated that fibroblast cells actively contract and stiffen the fibrin matrix around them, causing global stiffening of the gel (Jansen et al., 2013). Winer et al. demonstrated that the cells stiffen the fibrin over a long distance, affecting neighboring cells hundreds of microns away, manifested by their adoption of a mutual orientation (Winer et al., 2009). Rudnicki et al. demonstrated increased cell spread as cells distant rigid boundary (Rudnicki et al., 2013).
Because fibroblast cells deform, align, and stiffen fibrin gels, already within the first hours after seeding, we expect that the band formation phenomenon will be significant in the case of fibrin, and may play an important role in cellular communication. Experimental evidence of band formation between cells in fibrin gels has been presented in our previous works (Notbohm et al., 2015a; Sopher et al., 2018; Gomez et al., 2019; Mann et al., 2019). However, in-depth characterization of these bands over time and their possible impact on cellular behavior has yet to be investigated. Understanding the phenomenon of matrix densification and alignment that leads to band formation, in fibrin and other types of ECM, can enhance our overall comprehension of wound healing (Evans et al., 2013), fibrosis (Li et al., 2007), and tumorigenesis (Paszek et al., 2005; Shi et al., 2014). It may also enable directed morphogenesis in cell and tissue engineering efforts.
In this study, we utilized a model system comprised of fibroblast cells fully embedded in 3D fibrin gels. We quantitatively analyze how cell-induced forces deform the fibrin matrix and allow for separated cells to be mechanically coupled by the aligned and dense fibers of the matrix. The influence of mechanical coupling between cells on cell morphology is further examined.
RESULTS
Fibroblast cells embedded in fibrin gels form band coupling between neighboring cells
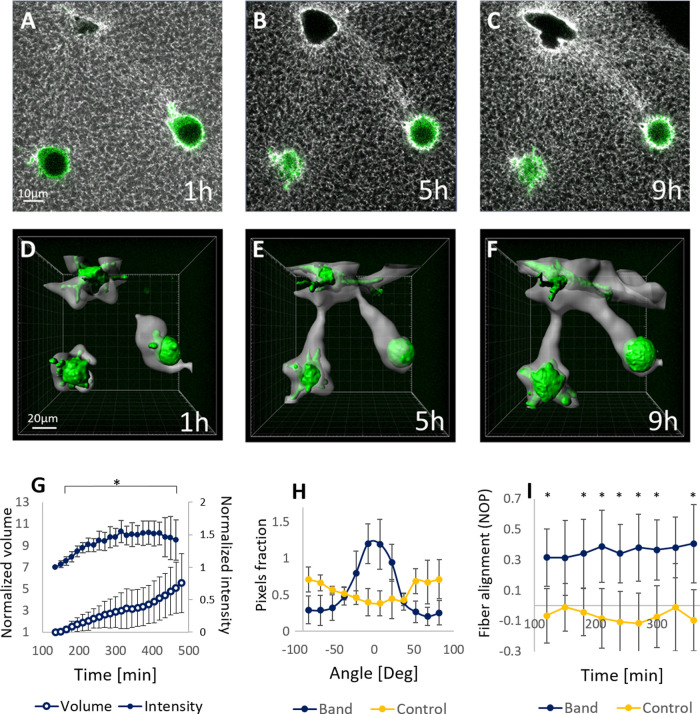
We study the ability of fibroblast cells, fully embedded in 3D fibrin gels, to propagate deformations in the fibrous matrix that result in long-range mechanical coupling of cell pairs. We embedded 3T3 cells expressing actin–green fluorescent protein (GFP) in fluorescently labeled fibrin gels, at a sparse cell density that accounted for cell–cell distances of several to tens of the cell size (see Materials and Methods). Using real-time confocal microscopy, cells and their surrounding fibrous environment were imaged for over 6 h, from cell seeding and fibrin polymerization. During this period, the fibrous area between cell pairs often became locally dense and aligned, resulting in the formation of visible “bands” bridging the cells (Figure 1, A–C). Band formation was systematically and quantitatively evaluated based on the bright fluorescence intensity originating from the densified bands versus the unremolded matrix, which allowed for 3D rendering of the band structure (Figure 1, D–F). Within 6 h, the fluorescence intensity of the bands, a reflection of fiber density, increased by about 1.5-fold, and band volume by about 5-fold, relative to the initial analyzed time point (Figure 1G). The intensity of fibrin outside the band was not significantly lower than the background level, indicating that the accumulation of fibrin in the band is not only coming from the local surrounding of the band but also from a more global region of the gel (Supplemental Figure S1).
FIGURE 1:
Band formation over time. (A–C) Fibroblast cells (actin-GFP, green) seeded in fluorescently labeled fibrin gels (gray) were imaged using a confocal microscope. Shown are images captured at 1, 5, and 9 h after cell seeding, with visible areas of increased density and alignment between the cells. (D–F) Cell isosurfaces (green) and the detected band regions (gray). (G) Normalized band volume and intensity over time. Normalization is relative to the first time point of the analysis. Significant differences were obtained from the fourth time point relative to the first time point, for both the normalized volume and the intensity (indicated by *). Values represent the mean ± standard deviation (SD) of five cell pairs. (H) The orientation of fibrin fibers in the band at 3 h postseeding (blue), in comparison to a control area far from the cells (yellow). The angle was calculated relative to the direction between the cell bodies. (I) Measurement of the nematic order parameter (NOP) over time in the band area and a control area far from the cells. The values represent the mean ± SD of three cell pairs for each condition. * represents p values of t test analysis <0.05. Videos corresponding to this figure are provided in the Supplemental Information.
Also, the fibers comprising the band gradually aligned over time, as reflected by increasing peaks in the fiber angle histograms as time progressed, whereas areas farther away from the cells displayed no clear directionality (Figure 1H). The nematic order parameter (NOP), an average measure of alignment, indicated a high level of alignment in the bands, which gradually increased from ∼0.3 to ∼0.4 within approximately 8 h, and was significantly higher than regions distant from cells, which remained relatively isotropic (NOP = ±0.1; Figure 1I).
The formation of bands between cells was not limited to individual cell pairs, and extended to large-scale networks of mechanically coupled cells (Figure 2, A and B). The average distance between the coupled pairs increased from 60 ± 23 µm at 2 h to 249 ± 154 µm at 6 h, indicating that more remotely separated cells become coupled at later times (Figure 2C). In addition, the average number of bands per cell gradually increased over time, from 0.4 ± 0.7 at 2 h to 1.9 ± 1.6 at 6 h (Figure 2D), indicating that the network of mechanically connected cells grows and expands over time. In addition, the coupled cells often sprouted protrusions along the general direction of the band (∼83%), and in more limited cases (∼17%) bands were formed between rounded cells without any protrusions (Figure 2E).
FIGURE 2:
Large-scale network of mechanically coupled cells. Fibroblast-embedded gels were fixated at 0, 2, 4, and 6 h after seeding and then imaged. (A) The cells deformed the matrix, creating a network of band connections at 6 h. (B) Identification of bands and cells by isosurface analysis. Several bands are indicated with arrows. (C) Analysis of band length, and (D) number of bands per cell. Over time, cells reached out to a larger number of more distant cells. The average values of band length and bands per cell were calculated and the histogram of distribution is displayed for each time point. (E) Presence of cellular protrusions in the band area (indicated by parallel lines). At the time of band formation, –5% of all coupled cells were rounded without any protrusions, ∼12% had protrusions facing away from the band, ∼40% had sprouted protrusions from one cell in the band area, and ∼43% had protrusions originating from both cells (n = 42 paired cells). * represents p values of t test analysis <0.05, and ** represents p values of chi-square analysis <0.005.
Mechanical characterization of the bands
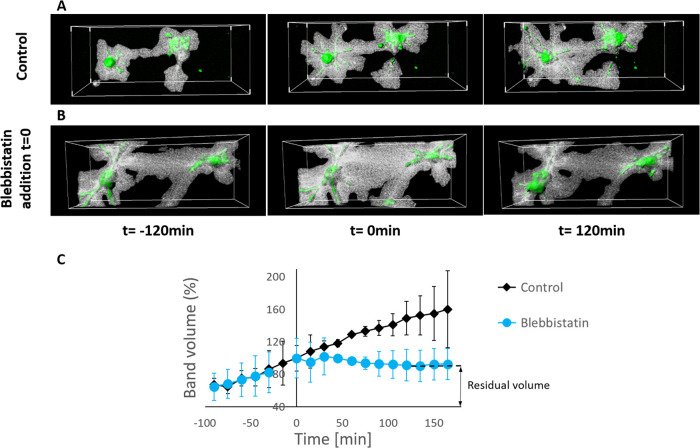
To demonstrate that the bands form due to active cellular contractility, gels were treated with blebbistatin, a myosin II inhibitor, added at the time of gel formation (Figure 3). In the presence of blebbistatin (Figure 3), cells were generally less spread out, and matrix deformation was significantly reduced, without any indication of bands between cells. We thus concluded that cellular actin–myosin contractility is the driving force behind band formation.
FIGURE 3:
The effect of myosin II inhibition on the ability of cells to generate bands. Cells embedded in fibrin untreated gels (A) and in the presence of blebbistatin (B), imaged 5 h after seeding. Blebbistatin was added immediately after gel polymerization. (A) In untreated gels, the matrix underwent dramatic deformation and many of the cell pairs generated bands with their neighbors, as can be seen in the zoom-in image in C. (D) Blebbistatin significantly reduced gel deformation and formation of bands. * represents p values of t test analysis <0.05. The values represent the mean ± SD of 30 gel locations.
The cellular gels were also treated with blebbistatin after bands had already formed, at 4.5 h from seeding. This allowed us to observe how the bands respond to force inhibition, and to characterize the elastic and plastic deformation of the bands. When blebbistatin was added (indicated as t = 0 in Figure 4), band volume gradually declined by approximately 40% in the first hour from addition of blebbistatin (Figure 4), as opposed to the increased band volume seen in untreated control samples (Figures 4, A and C, and 1G). The fact that band volume decreased by only 40% indicates that a large portion of the band deformed plastically and irreversibly (∼60%), causing permanent deformation in the matrix.
FIGURE 4:
Band plasticity. Confocal stacks of fibroblast cells (actin-GFP, green) and the fluorescently labeled fibrin gel in the band (gray), in (A) untreated control gels, and (B) gels treated with blebbistatin added at 3.5 h postseeding (indicated by t = 0 min). (C) Quantification of band volume before and after treatment with blebbistatin. In control gels, bands between cells increased in volume over time. In gels treated with blebbistatin, bands increased in volume until t = 0 (addition of blebbistatin), and then their volume declined until reaching a plateau, approximately 1 h after blebbistatin was added. Band volume is normalized to its volume at t = 0. Note that in the first time point of the analysis, band volume is already evident. The relative amount of the residual volume indicates plasticity of bands. A significant difference was observed between blebbistatin-treated and untreated samples at times >15 min from the addition of blebbistatin. Before the addition of blebbistatin, there was no significant difference between control and blebbistatin groups (times <0). The values represent the mean ± SD of 20 cell pairs for each condition.
In 3D matrices, it is known that contractile forces and deformation of the surrounding matrix are mainly generated by cellular protrusions, which can branch into daughter protrusions that regulate force application (Giri et al., 2013). To examine the role of protrusion branching on band formation, gels were treated with CK636, an inhibitor of ARP2/3 complex, which is known to regulate protrusion branching in 3D settings (Giri et al., 2013). As expected, ARP2/3 inhibition reduced protrusion branching by 40%, with almost no effect on the number of protrusions (Figure 5). In parallel, ARP2/3 inhibition led to an approximate 60% reduction in the number of bands per cell (Figure 5D), indicating that protrusion branching is involved in band formation by cells.
FIGURE 5:
The effect of ARP2/3 inhibition on protrusion branching and band formation. Fibroblast cells (actin-GFP, green) were embedded in untreated fibrin gels (A) or treated with CK636, an inhibitor of ARP2/3, immediately after gel polymerization (B). The highly deformed matrix is indicated in gray isosurface. Two examples of cells from untreated and ARP2/3-inhibited gels are shown; white arrows indicate protrusion branching (C). Inhibition of ARP2/3 did not affect the average number of protrusions per cell, but decreased the number of protrusion branching per cell by ∼40% compared with cells in untreated gels. The number of bands per cell was reduced by about 60% in gels treated with ARP2/3 compared with cells in untreated gels (D). A statistically significant difference was observed between the number of protrusion branching and bands per cell, in comparison to control untreated samples. The values represent the mean ± SD of 100–200 analyzed cells. ** represents p values of chi-square analysis <0.005.
Effect of cell force directionality on band formation
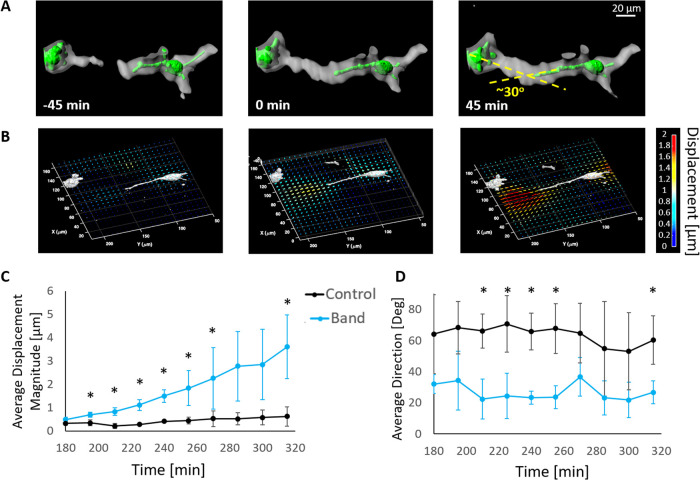
In most of the developed bands, the interacting cells grow at least one protrusion along the general direction of the band (>80%; Figure 2E). For example, in the situation shown in Figure 6A, a band extends from the tip of the long protrusion to the neighboring rounded cell. The protrusion direction is approximately 30° relative to the band direction, that is, the axis that connects the protrusion tip and the center of the rounded cell. We thus speculated that there is a “permitted” range of angles in which the cells apply forces that will result in band connection with their neighbor. We thus measured the 3D displacements of the matrix induced by two interacting cells using traction force microscopy, which allowed us to resolve the direction of cell-induced force and its relative orientation to the nearby cell. To measure 3D matrix displacements, the speckle pattern of fluorescently labeled gel fibers was subjected to digital volume correlation (DVC) analysis (Figure 6B; Lesman et al., 2014; Notbohm et al., 2015a,b). These results suggest that matrix displacements in the area between cells gradually increased as the band developed and were higher than for noninteracting cells (Figure 6C). The resultant displacement direction, which informs on the direction of force, was found to be within an angle interval of 10–40° relative to the neighboring cell (Figure 6D). In the case of noninteracting cells, the direction of force spanned a broader angular range, without a clear directionality toward the other cell (Figure 6D). The variability in the separate DVC experiments is provided in Supplemental Figure S2, indicating that controls do not have a preferred direction with higher variability than for bands. These results motivate the hypothesis that bands can be formed when the angle of applied force is below 40° relative to the other cell. This hypothesis is next examined using a computational model.
FIGURE 6:
3D matrix displacements during band formation. (A) Cell isosurface (green) and band regions (gray) over time, with indication of the angle between cell protrusion and the neighboring cell. (B) Quiver plots of matrix displacements, for the same cell pair and designated time points shown in A. The traction force applied on the matrix was primarily originated from the tip of cell protrusion in the rough direction of the neighboring cell. (C) Matrix displacements increased over time as the band formed (blue) and were considerably higher than between cell pairs that did not form a band (black). Time is from cell seeding. (D) The direction of the resultant displacement relative to the neighboring cell, as a function of time. The values represent the mean ± SD of three analyzed cell pairs for each condition. * represents p values of t test analysis <0.05.
To better understand the effect of force direction on band formation, we developed a computational finite element model. In our simplified model, we simulated a point force acting on a 2D fibrous network at various angles (0–90°) relative to a fixed circular cell (Figure 7A). The point force mimics a force exerted by a long, slender cellular protrusion, as was often observed in the biological experiments. The fixed circular cell represents a passive cell that is not applying force but resists the deformation around it. We consider increased fiber density and alignment in the area between the point force and the circular cell (indicated by a rectangle in Figure 7A) to inform on the potential to form a band. We found that application of a point force increased the alignment of fibers (NOP; Figure 7B) in the area of interest, in an angle-dependent manner. Fiber alignment was highest—approximately four times higher than the undeformed matrix—when the point force was applied in the angular range of about 0–30° with significant differences between NOP values at angles 0–50° relative to the undeformed state. At angles higher than 30°, the alignment gradually declined, until reaching the value of undeformed fibers at a 90° angle. Fiber density was found to be less dependent on the angle of the applied force, with moderately higher values at angles of 0–30°. The increase in density measured in the model was around 7% in relation to the undeformed state, which is in line with the average ∼4% change in intensity measured between respective time points in the biological experiments (Figure 1G). The fact that both fiber alignment and densification were most significant in the angle range of ∼0–30° may explain the tendency of cells to develop bands in a similar range of angles in the biological experiments.
FIGURE 7:
Computational modeling of a point force applied at various angles relative to a nearby cell. A point force applied at a distance of 2.5 cell radii and at various angles relative to a fixed, rounded “carved” cell in a 2D fibrous network (A). Fiber alignment (NOP, B) and densification (C) were measured in the area between the point force and the cell (white rectangles in A), and normalized to a control, undeformed network. A statistically significant difference was observed between NOP values in angles 0–50° relative to the undeformed state, with p values of t test analysis <0.05 (indicated by *). All values represent the mean ± SD of six different randomized networks.
Relation between cell morphology and band coupling
As described in Figure 2, the formation of bands established a large-scale network of mechanically coupled cells. In such networks, we distinguish between the population of mechanically coupled (purple cells, Figure 8A) and mechanically isolated cells (green cells, Figure 8A). To study the possible biological impact of bands on the connected cells, the morphology of mechanically coupled cells was compared with that of mechanically isolated cells, at 0, 2, 4, and 6 h from seeding. Most cells started off (t = 0) rounded and uncoupled. The percentage of coupled cells increased gradually from 0 at t = 0, to ∼50% at 2 h and ∼70% at 4 h. At 6 h from seeding, almost all cells (∼90%) were a part of the coupled network (Figure 8B). In general, the coupled cells spread more, became more elongated, and had more protrusions over time, as compared with the isolated cells, which mainly remained rounded. This was evident by the larger volume (Figure 8C), longer cell axis (Figure 8D), and more major protrusions (Figure 8E) of the coupled cells. Interestingly, the differences in the morphological features at 2 h were relatively small, but increased at later time points, suggesting causality between band coupling and cell morphology (Figure 8, B–E). A key question is whether the spread morphology of the coupled cells is driven by natural heterogeneity in cell population, or related to the fact that these cells were mechanically coupled. To gain more insights into this aspect, we performed experiments in which cells were seeded at a lower density (2000 cells/gel compared with the regular 8000 cells/gel; (Supplemental Figure S3). In the sparse situation, the mechanical interaction was lessened, and most cells (>95%) were isolated, without band connection to their neighbors. The morphology of these isolated cells was relatively rounded, similar to the isolated cells in the dense situation, but significantly different than the coupled spread cells. This suggests that the spread morphology of the coupled cells in the dense population is a result of the mechanical band connections.
FIGURE 8:
Relation between cell morphology and band coupling. Fibroblast cells were embedded in fibrin gels and fixated at 0, 2, 4, and 6 h postseeding, and large mm-scale 3D volumes were imaged by confocal microscopy. (A) The cell population was divided into mechanically coupled cells (via bands; cells in purple) and mechanically isolated cells (green). The matrix and bands are not shown in the images. At t = 0, all cells were categorized as isolated because matrix remodeling was minor. Over time, cells became coupled, forming vast networks of mechanically coupled cells. (B) The percentage of coupled cells increased over time, until, at 6 h, almost all cells were mechanically connected. To compare the mechanically coupled and isolated cells, various cell morphology parameters were evaluated including cell volume (C), elongation (D), and protrusions (E). Significant differences were observed between all groups indicated by asterisks. All values represent the mean ± SD of 140–250 analyzed cells. * represents p values of t test analysis <0.05, and ** represents p values of chi-square analysis <0.005.
DISCUSSION
In this study, we demonstrated that contractile forces generated by fibroblast cells embedded in fibrin gels lead to significant densification and alignment of the fibrous matrix between cell pairs. We refer to such remodeled structures in the matrix as “bands.” The formation of bands resulted in cell–cell mechanical coupling over a distance much larger than the size of the cell, typically 50–200 μm. The bands developed and matured over time and extended into a large-scale network of mechanically coupled cells. Cells that were part of the connected network were more spread out and elongated, with more sprouted protrusions than cells that were not part of the network (i.e., isolated), suggesting a relation between the presence of bands and cellular behavior. Experiments with low density of cells, in which the mechanical coupling is lessened, provide evidence that the spread morphology of the coupled cells is not coincidental and driven by the natural heterogeneity in cell population but related to the fact that these cells were mechanically coupled to neighboring cells. This is under the assumption that biochemical signaling is similar in the sparse and dense populations, and not driving the observed differences. These findings are relevant for understanding the role of fibrin contraction by cells and the formation of long-range matrix connections in guiding multicellular processes. It should motivate future studies to explore whether similar fibrin “bands” form in vivo and studying their role in wound healing and angiogenesis processes. For example, band coupling between fibroblast cells could facilitate coordination of wound contraction for better tissue repair.
Although the literature about long-range matrix connections and their importance has been well described in collagen systems, the role of band connections in fibrin gels, a matrix relevant to different physiological scenarios, including wound healing and angiogenesis, is much less understood. In accordance with previous studies that used collagen gels (Vader et al., 2009; Kim et al., 2017; Sopher et al., 2018), the 3D structure of fibrin bands was determined by the strong fluorescence intensity associated with the densified band volume. We focus here on fully embedded cells in the 3D fibrin matrix, in which bands could form along the three spatial directions and provided quantitative analysis of 3D volume of bands, whereas previous studies typically cultured cells on top of the gel surface and analyzed 2D band features (Shi et al., 2014; Ban et al., 2018). We also quantitatively analyzed the large-scale formation of the connected network, which revealed its expansion over time, with increased number of bands and their length over time. We note that observation of bands typically started after more than 1 h from seeding, and at that time some bands already matured to some level. We were not able to image and analyze the bands earlier as it took time until the gel was ready for imaging in the microscope. Also, we note that in our system of fibroblast-embedded fibrin gels, in the first 6 h from seeding, cell migration was rare (cells started to migrate at longer times after degrading their local matrix). Therefore, we do not suspect that the increase in band length over time is because cells migrated away from their partners, but because cells reached out to more distant partners forming new longer bands.
To verify that the formation of bands was due to cell-generated forces, a myosin II inhibitor was added to the cellular gels immediately after gel polymerization. This led to complete prevention of bands, indicating that cell forces drive band formation. It also indicates that the early remodeling of bands (manifested by the apparent fiber alignment already at the first 2 h from seeding) is due to active cell forces and not related to gel polymerization processes (e.g., fibers polymerize more extensively between cell pairs). The effect of myosin II inhibition is in accordance with previous studies in fibrin demonstrating that myosin II is essential for gel deformation, and for formation of band/bundles in collagen gels (Kim et al., 2017).
When inhibiting cellular forces after the bands had already formed (at 3.5 h from seeding), most of the band volume did not dissipate, leaving about 90% residual volume, which indicates a high degree of plasticity. Similar irreversible deformation was previously identified in collagen gels (Kim et al., 2017; Ban et al., 2018), which was ascribed to sliding and merging (new cross-links) events of collagen fibers, as well as sliding of the fibrils composing a single fiber, which resulted in permanent lengthening of the fiber (Kim et al., 2017). In that regard, the time of inhibiting cell contractility might be an important factor in establishing plasticity. We inhibited myosin II after 3.5 h from seeding, while in Ban et al. (2018) cell contractility was inhibited after 10–17 h from cell seeding. In both cases, plasticity was clearly evident but comparing the level of plasticity is difficult due to differences in experimental settings and ways of analysis. That being said, it was previously demonstrated that the dwell time of force application can greatly influence the plasticity of the band (Kim et al., 2017).
Plasticity in fibrin was documented before, with similar mechanisms as in collagen gels, including the sliding of protofibrils (subunits) within a single fiber, as well as the formation of transient cross-links arising due to the affinity between the fibers in proximity (Litvinov and Weisel, 2017; Burla et al., 2019). Also, the formation of new cohesive cross-links between fibers was recently described in experiments of stretched fibrin gels (Britton et al., 2019). Because fibers inside the band become denser over time and are more likely to contact each other, new cross-linking (merging) events can be generated, resulting in plastic deformation of the bands. Noteworthy is the 1-h relaxation time that it takes for the band volume to reach a steady state after blebbistatin addition (Figure 4C). This 1-h relaxation may be a result of two contributing factors: the viscoelasticity of the material and the time it takes for blebbistatin to diffuse into the gel from the surrounding medium.
In 3D gels, cells typically exhibit long and slender protrusions that grow in various orientations in the 3D space (Rhee et al., 2007; Khetan et al., 2013; Polackwich et al., 2013; Notbohm et al., 2015b; Malandrino et al., 2019). The cellular forces on the matrix are mainly applied at the tip of the cellular protrusions (Legant et al., 2009; Khetan et al., 2013; Notbohm et al., 2015a). To determine the effect of the orientation of cell-induced force relative to a neighboring cell on band formation, a computational model was developed. The computational model was based on a randomly rendered network of fibers that strain stiffen in tension and buckle in compression; phenomena which occur in fibrin, and other biological gels, and which have been shown to be important in displacement propagation and remodeling of fibers between cells (Sopher et al., 2018). The model results indicate that band formation was promoted when the direction of force was under 30° relative to the other cell, which can explain the angle range of 10–40° measured in the experiments of traction force microscopy. The increased alignment and densification in the band area is likely facilitated by the nonlinear properties of the fibers, and particularly their buckling mechanism. Our previous computational work by Sopher et al. (Sopher et al., 2018) demonstrated that nonlinear fiber networks in comparison to linear networks enhance the density and alignment of fibers in the band area between two simulated contractile cells. Previous computational models of cell–cell interactions in fibrous networks have examined the effect of various parameters on the long-range interaction of contractile cells, including cell–cell distance and magnitude of cell contraction (Sopher et al., 2018), cell anisotropic shape, network geometry, and nonlinear mechanics (Abhilash et al., 2014; Wang et al., 2014; Humphries et al., 2017; Sopher et al., 2018). Here, we provide new insights into the effect of cell–cell orientation on the establishment of mechanical communication.
We note that not all cell pairs formed a band connection, and that the process was highly heterogenetic, with different time of band initiation. We suggest that the heterogeneity in the band-forming process is mainly a consequence of the variations in the relative orientations between cell protrusions, and in the magnitudes of cell contractile activity. Random pulls of the cells on the matrix, in different directions, can lead to the formation of bands, if the direction of the applied force is within an allowable angle interval relative to the neighboring cell, as predicted by our computational model. The formation of bands between cells can potentially initiate a positive feedback loop in which the spread morphology of cells and maturation of bands intensify each other. The bands can encourage cell spreading and protrusion infiltration into the band areas by durotaxis (by stiffness gradients) or topographical guidance (by the aligned fibers; Shi et al., 2014). In parallel, the growing cellular protrusions generate mechanical forces that can encourage more band maturation (Polackwich et al., 2013; Notbohm et al., 2015b; Malandrino et al., 2019).
The formation of areas with increased fiber densification between contractile elements in biological systems seems to occur at different scales and systems. Here we observed this in fibrin-reconstituted ECM networks between cells, but it can also be seen in higher scales, between cell clusters in fibrous collagen ECM (Stopak and Harris, 1982; Shi et al., 2014), as well as in smaller scales, between myosin motors in actin fibers (Ideses et al., 2013; Murrell and Gardel, 2014).
In processes in vivo, similar matrix “bands” have been mainly observed in collagen ECM. For example, tumor cells were observed to interact and follow bundles of aligned collagen fibers as they attempt to cross the basement membrane of blood vessels (Conklin et al., 2013; Han et al., 2016). Such ECM deformation was suggested to increase intravasation, promoting cancer cell breakage into the basement membrane before entering the circulation. In liver fibrosis, “fibrosis tracks” composed of aligned collagen fibers were detected extending between islands of liver cells, facilitating migration of myofibroblasts and vascular cells (Wells, 2013; Desai et al., 2016). To the best of our knowledge, the formation of “bands” in fibrin in vivo, during wound healing or angiogenesis, has yet to be described. Our study in reconstituted fibrin gels should motivate such in vivo exploration.
MATERIALS AND METHODS
Biological experiments
Cells culture.
Swiss 3T3 fibroblasts stably transfected with GFP-actin (obtained as gifts from S. Fraser, University of Southern California, Los Angeles, CA) were cultured in DMEM supplemented with 10% fetal bovine serum, nonessential amino acids, sodium pyruvate, l-glutamine, 100 units/ml penicillin, 100 µg/ml streptomycin, and 100 µg/ml neomycin, in a 37°C humid incubator.
3D fibrin gel preparation.
Actin-GFP 3T3 fibroblast cells (8 × 103 cells) were mixed with 10 µl of a 20 U/ml thrombin solution (Omrix Biopharmaceuticals). Then, 10 µl of a 10 mg/ml fluorescently labeled fibrinogen (Omrix Biopharmaceuticals) suspension was placed on a no. 1.5 coverslip in a 35-mm dish (MatTek Corporation) and mixed gently with cell-thrombin suspension. The resulting fibrin gel was placed in the incubator for 20 min to polymerize, after which, warm medium was added to cover the gel. The fibrin gels had an approximate shape of half a sphere, attached to the bottom surface of a coverslip, with a gel height of approximately 2–3 mm.
Fibrin gel labeling.
Alexa Fluor 546 carboxylic acid, succinimidyl ester (Invitrogen) was mixed with fibrinogen solution in a 7.5:1 M ratio for 1 h at room temperature and then filtered through a HiTrap desalting column (GE Healthcare) packed with Sephadex G-25 resin, to separate the unreacted dye. The labeled fibrinogen was then mixed with thrombin and cells, as described above, to create labeled, cell-loaded fibrin gels.
Time-lapse microscopy.
Pairs of cells were imaged with a Zeiss 880 confocal microscope, equipped with a 40× NA = 1.1 water immersion lens (Zeiss) and a 30-mW argon laser (wavelengths 488 and 514 nm). Throughout imaging, cells were maintained in a 37°C 5% CO2 incubation chamber. Confocal z-stacks were acquired every 15 min.
Image analysis
Band analysis.
Bands were identified using the Imaris image analysis software (version 8.4.1; Bitplane). The “surface” tool was used as a method of edge detection to separate areas of increased fiber intensity. First, a background subtraction option was used in Imaris. Then, a threshold was manually selected to capture voxels that after background subtraction displayed intensity higher than 2.44 [AU]. These voxels were defined as part of the band, and were ∼150% more intense than the unremolded areas far from cells. Imaging parameters and the edge detection threshold were both kept constant throughout all analyses. All voxels with fluorescence intensities above the threshold were marked by the isosurface, and used for the deformed matrix volume analysis. Band volume and the average intensity originating from the band were then extrapolated.
Fiber orientation of bands.
Orientation distribution of the fibrous matrix between cell pairs was conducted based on 2D images, using ImageJ (National Institutes of Health, Bethesda, MD) with the ImageJ plug-in, OrientationJ (Puspoki et al., 2016). From these measurements, the NOP in the region between the cell pairs and in a control region, far from the cells, were extrapolated. NOP is given by (Vader et al., 2009; Puspoki et al., 2016; Sopher et al., 2018; Gomez et al., 2019; Goren et al., 2020) NOP = <cos(2θ)>, with θ measured relative to the direction between the two cells. NOP ranges from −1 to 1, where a value of 0 corresponds to an isotropic network, a value of 1 corresponds to a network with fully aligned fibers along the strain direction, and a value of −1 corresponds to a network of transversely aligned fibers.
Band length measurement.
Gels were fixated at 2, 4, and 6 h postseeding and large 3D sections of approximately 1.2 mm × 1.2 mm × 0.14 mm were imaged by 3D confocal microscopy; two macro gels were analyzed at each time point. The images were then analyzed for identification of bands by the cell isosurface analysis, based on the procedure detailed under “Band” in the Materials and Methods section. Cell pairs with bands between them were manually identified, and the number of bands per cell at each time point was counted. Band length was calculated as the distance between cell pairs that had bands between them. More than 50 cells were analyzed for each time point.
Protrusion direction analysis
Time-lapse experiments were conducted on cells embedded in gels. The cells were imaged every 15 min, from 2 h up to 6 h postseeding. In total, 55 cells from two separate experiments were analyzed. Bands were identified and cell pairs with bands between them were manually examined to determine the number of cell protrusions and their orientation at the time of band formation.
Experiments with blebbistatin
To examine the effect of myosin II inhibition on band formation or maintenance, fibrin gels were treated with blebbistatin (Sigma-Aldrich, Israel). Gels were polymerized as described above and the medium was replaced with DMEM containing 83 µM blebbistatin, either immediately after polymerization or 3.5 h postseeding.
Experiments with CK636
To examine the effect of ARP2/3 inhibition on band formation, fibrin gels were treated with CK636 (Sigma-Aldrich, Israel). Gels were polymerized as described above and the medium was replaced with DMEM containing 100 µM CK636, immediately after gel polymerization.
Cell morphological parameters
Cell isosurface was identified using the surface tool of the Imaris image analysis software. To exclude detected objects that were not cells, objects smaller than one-tenth of the average cell volume were filtered out. Then, the morphological parameters, including the number of cells, cells volume, and cell elongation, were extracted by Imaris.
Measurement of matrix displacements
To compute matrix displacements, images of the fluorescently labeled matrix were used as a speckle pattern for a DVC algorithm, implemented in MATLAB (MathWorks), as previously described by Lesman and Notbohm et al. (Lesman et al., 2014; Notbohm et al., 2015b). Displacements were computed over time relative to the initial unremolded state as a reference. Displacement magnitudes and direction were calculated for areas in between cell pairs.
Statistics
All statistical tests were performed with excel or MATLAB. The chi-square test was used to compare noncontinuous variables (bands per cell and protrusions per cell). We use the following convention in the figures to indicate the level of significance: * represents p values of t test analysis <0.05, and ** represents p values of chi-square analysis <0.005.
Computational model
Numerical methods.
MATLAB was used to create the network geometry and architecture, and the finite element software Abaqus/CAE 2017 (Dassault Systèmes Simulia) was used to model the network mechanics and perform the simulations. The software’s implicit static solver was used in all simulations.
Network construction
To establish the network for our model system, we started by randomly inserting nodes in a two-dimensional circular domain. Pairs of nodes were then connected by single fibers generated following a minimum cost algorithm, as described in our recent publication (Goren et al., 2020). The generated networks are isotropic and homogeneous at the scale of the cell. The cell is modeled as a circular void region, where elements were removed from the network. Several new nodes are then created at the cell edge that intersects with the network.
Mechanical and geometrical network properties
Each individual fiber was modeled as a one-dimensional truss element, subjected to uniaxial tension or compression. In part of the simulations, we also modeled the fibers as beams, which are elements that resist perpendicular forces and transfer moments, and we show that truss and beam elements support similar effects and conclusions (Supplemental Figure S4). The nonlinear fibers are characterized by an elastic modulus which is 10 times smaller at compressive strains exceeding 2%, and increases exponentially under tensile strains exceeding 2%. This mechanical behavior is largely based on computational models described in our previous studies (Sopher et al., 2018; Goren et al., 2020). Nodes were modeled as freely rotating hinges (i.e., neglecting the rotational resistance of cross-linkers). The network connectivity is around eight.
Simulation setup
A point force (mimicking a pull by a cell protrusion) was applied by translating a group of four nodes by 0.75 cell radii in a range of directions and at a distance of 2.5 cell radii relatively to a fixed circular cell (void area). The nodes comprising the cell edge were kept fixed as well as the outer edge of the network. To quantify fiber alignment, we used the NOP, as defined under “Fiber orientation of bands,” with the fiber orientation measured with respect to the line that connects the cell’s center and the group of nodes that were translated. The NOP was calculated throughout the area of interest, which was a rectangle of one cell diameter width and a length of the distance between the lower cell’s edge and the group of nodes. Of note, the size of this area remained the same for the entire range of the pulling directions, before and after the pulling was applied. To quantify fiber densification, the total length of the fiber segments located within the area of interest was calculated. The response of three separate randomly rendered networks was used to reduce the effect of the network geometry on the obtained results. For the alignment analysis, positive and negative angles were averaged as well, so overall six repetitions were averaged together.
Supplementary Material
Acknowledgments
We would like to thank Oren Tchaicheeyan for developing the algorithm to quantify fiber density in the computational model, as well as with the support of the DVC analysis. We would also like to thank Noga Kalish for the help with Imaris analysis of some of the experiments.
This project was supported by the Israel Science Foundation (1474/16), the Israel Science Foundation - Israeli Centers for Research Excellence (1902/12), and the Zimin Institute for Engineering Solutions Advancing Better Lives.
Abbreviations used:
- DVC
digital volume correlation
- ECM
extracellular matrix
- GFP
green fluorescent protein
- NOP
nematic order parameter
- SD
standard deviation.
Footnotes
This article was published online ahead of print in MBoC in Press (http://www.molbiolcell.org/cgi/doi/10.1091/mbc.E20-01-0079) on May 6, 2020.
REFERENCES
- Abhilash AS, Baker BM, Trappmann B, Chen CS, Shenoy VB. (2014). Remodeling of fibrous extracellular matrices by contractile cells: predictions from discrete fiber network simulations. Biophys J , 1829–1840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ban E, Franklin JM, Nam S, Smith LR, Wang HL, Wells RG, Chaudhuri O, Liphardt JT, Shenoy VB. (2018). Mechanisms of plastic deformation in collagen networks induced by cellular forces. Biophys J , 450–461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Britton S, Kim O, Pancaldi F, Xu ZL, Litvinov RI, Weisel JW, Alber M. (2019). Contribution of nascent cohesive fiber-fiber interactions to the non-linear elasticity of fibrin networks under tensile load. Acta Biomater , 514–523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burla F, Tauber J, Dussi S, van Der Gucht J, Koenderink GH. (2019). Stress management in composite biopolymer networks. Nat Phys , 549–553. [Google Scholar]
- Conklin MW, Eickhoff JC, Riching KM, Pehlke CA, Eliceiri KW, Provenzano PP, Friedl A, Keely PJ. (2013). Aligned collagen is a prognostic signature for survival in human breast carcinoma. Am J Pathol , 1221–1232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conti E, MacKintosh FC. (2009). Cross-linked networks of stiff filaments exhibit negative normal stress. Phys Rev Lett , 088102. [DOI] [PubMed] [Google Scholar]
- Desai SS, Tung JC, Zhou VX, Grenert JP, Malato Y, Rezvani M, Espanol-Suner R, Willenbring H, Weaver VM, Chang TT. (2016). Physiological ranges of natrix rigidity modulate primary mouse hepatocyte function in part through hepatocyte nuclear factor 4 alpha. Hepatology , 261–275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evans ND, Oreffo ROC, Healy E, Thurner PJ, Man YH. (2013). Epithelial mechanobiology, skin wound healing, and the stem cell niche. J Mech Behav Biomed , 397–409. [DOI] [PubMed] [Google Scholar]
- Frantz C, Stewart KM, Weaver VM. (2010). The extracellular matrix at a glance. J Cell Sci , 4195–4200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gentleman E, Lay AN, Dickerson DA, Nauman EA, Livesay GA, Dee KC. (2003). Mechanical characterization of collagen fibers and scaffolds for tissue engineering. Biomaterials , 3805–3813. [DOI] [PubMed] [Google Scholar]
- Giri A, Bajpai S, Trenton N, Jayatilaka H, Longmore GD, Wirtz D. (2013). The Arp2/3 complex mediates multigeneration dendritic protrusions for efficient 3-dimensional cancer cell migration. FASEB J , 4089–4099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gjorevski N, Piotrowski AS, Varner VD, Nelson CM. (2015). Dynamic tensile forces drive collective cell migration through three-dimensional extracellular matrices. Sci Rep-Uk , 11458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gomez D, Natan S, Shokef Y, Lesman A. (2019). Mechanical interaction between cells facilitates molecular transport. Adv Biosyst , 1900192. [DOI] [PubMed] [Google Scholar]
- Goren S, Koren Y, Xu X, Lesman A. (2020). Elastic anisotropy governs the range of cell-induced displacements. Biophys J , 1152–1164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han WJ, Chen SH, Yuan W, Fan QH, Tian JX, Wang XC, Chen LQ, Zhang XX, Wei WL, Liu RC, et al. (2016). Oriented collagen fibers direct tumor cell intravasation. Proc Natl Acad Sci USA , 11208–11213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Humphries DL, Grogan JA, Gaffney EA. (2017). Mechanical cell-cell communication in fibrous networks: the importance of network geometry. Bull Math Biol , 498–524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ideses Y, Sonn-Segev A, Roichman Y, Bernheim-Groswasser A. (2013). Myosin II does it all: assembly, remodeling, and disassembly of actin networks are governed by myosin II activity. Soft Matter , 7127–7137. [Google Scholar]
- Jansen KA, Bacabac RG, Piechocka IK, Koenderink GH. (2013). Cells actively stiffen fibrin networks by generating contractile stress. Biophys J , 2240–2251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jung W-H, Yam N, Chen C-C, Elawad K, Hu B, Chen Y. (2020). Force-dependent extracellular matrix remodeling by early-stage cancer cells alters diffusion and induces carcinoma-associated fibroblasts. Biomaterials , 119747. [DOI] [PubMed] [Google Scholar]
- Khetan S, Guvendiren M, Legant WR, Cohen DM, Chen CS, Burdick JA. (2013). Degradation-mediated cellular traction directs stem cell fate in covalently crosslinked three-dimensional hydrogels. Nat Mater , 458–465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim J, Feng J, Jones CAR, Mao X, Sander LM, Levine H, Sun B. (2017). Stress-induced plasticity of dynamic collagen networks. Nat Commun , 842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Korff T, Augustin HG. (1999). Tensional forces in fibrillar extracellular matrices control directional capillary sprouting. J Cell Sci , 3249–3258. [DOI] [PubMed] [Google Scholar]
- Legant WR, Pathak A, Yang MT, Deshpande VS, McMeeking RM, Chen CS. (2009). Microfabricated tissue gauges to measure and manipulate forces from 3D microtissues. Proc Natl Acad Sci USA , 10097–10102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lesman A, Notbohm J, Tirrel DA, Ravichandran G. (2014). Contractile forces regulate cell division in three-dimensional environments. J Cell Biol , 155–162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li ZD, Dranoff JA, Chan EP, Uemura M, Sevigny J, Wells RG. (2007). Transforming growth factor-beta and substrate stiffness regulate portal fibroblast activation in culture. Hepatology , 1246–1256. [DOI] [PubMed] [Google Scholar]
- Litvinov RI, Weisel JW. (2017). Fibrin mechanical properties and their structural origins. Matrix Biol , 110–123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malandrino A, Trepat X, Kamm RD, Mak M. (2019). Dynamic filopodial forces induce accumulation, damage, and plastic remodeling of 3D extracellular matrices. Plos Comput Biol , e1006684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mann A, Sopher RS, Goren S, Shelah O, Tchaicheeyan O, Lesman A. (2019). Force chains in cell–cell mechanical communication. J R Soc Interface , 20190348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Munster S, Jawerth LM, Leslie BA, Weitz JI, Fabry B, Weitz DA. (2013). Strain history dependence of the nonlinear stress response of fibrin and collagen networks. Proc Natl Acad Sci USA , 12197–12202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murrell M, Gardel ML. (2014). Actomyosin sliding is attenuated in contractile biomimetic cortices. Mol Biol Cell , 1845–1853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Notbohm J, Lesman A, Rosakis P, Tirrell DA, Ravichandran G. (2015a). Microbuckling of fibrin provides a mechanism for cell mechanosensing. J R Soc Interface , 20150320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Notbohm J, Lesman A, Tirrell DA, Ravichandran G. (2015b). Quantifying cell-induced matrix deformation in three dimensions based on imaging matrix fibers. Integr Biol-Uk , 1186–1195. [DOI] [PubMed] [Google Scholar]
- Paszek MJ, Zahir N, Johnson KR, Lakins JN, Rozenberg GI, Gefen A, Reinhart-King CA, Margulies SS, Dembo M, Boettiger D, et al. (2005). Tensional homeostasis and the malignant phenotype. Cancer Cell , 241–254. [DOI] [PubMed] [Google Scholar]
- Piechocka IK, Bacabac RG, Potters M, MacKintosh FC, Koenderink GH. (2010). Structural hierarchy governs fibrin gel mechanics. Biophys J , 2281–2289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piotrowski-Daspit AS, Nerger BA, Wolf AE, Sundaresan S, Nelson CM. (2017). Dynamics of tissue-induced alignment of fibrous extracellular matrix. Biophys J , 702–713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Polackwich RJ, Koch D, Arevalo R, Miermont AM, Jee KJ, Lazar J, Urbach J, Mueller SC, McAllister RG. (2013). A novel 3D fibril force assay implicates Src in tumor cell force generation in collagen networks. PLoS One , e58138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Püspoki Z, Storath M, Sage D, Unser M. (2016). Transforms and operators for directional bioimage analysis: a survey. Adv Anat Embryol Cell Biol , 69–93. [DOI] [PubMed] [Google Scholar]
- Reinhardt JW, Gooch KJ. (2018). An agent-based discrete collagen fiber network model of dynamic traction force-induced remodeling. J Biomech Eng , 1–13. [DOI] [PubMed] [Google Scholar]
- Reinhart-King CA, Dembo M, Hammer DA. (2008). Cell-cell mechanical communication through compliant substrates. Biophys J , 6044–6051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rhee S, Jiang H, Ho CH, Grinnell F. (2007). Microtubule function in fibroblast spreading is modulated according to the tension state of cell-matrix interactions. Proc Natl Acad Sci USA , 5425–5430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rudnicki MS, Cirka HA, Aghvami M, Sander EA, Wen Q, Billiar KL. (2013). Nonlinear strain stiffening is not sufficient to explain how far cells can feel on fibrous protein gels. Biophys J , 11–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi QM, Ghosh RP, Engelke H, Rycroft CH, Cassereau L, Sethian JA, Weaver VM, Liphardt JT. (2014). Rapid disorganization of mechanically interacting systems of mammary acini. Proc Natl Acad Sci USA , 658–663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smithmyer ME, Sawicki LA, Kloxin AM. (2014). Hydrogel scaffolds as in vitro models to study fibroblast activation in wound healing and disease. Biomater Sci , 634–650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sopher RS, Tokash H, Natan S, Sharabi M, Shelah O, Tchaicheeyan O, Lesman A. (2018). Nonlinear elasticity of the ECM fibers facilitates efficient intercellular communication. Biophys J , 1357–1370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steinwachs J, Metzner C, Skodzek K, Lang N, Thievessen I, Mark C, Munster S, Aifantis KE, Fabry B. (2016). Three-dimensional force microscopy of cells in biopolymer networks. Nat Methods , 171–176. [DOI] [PubMed] [Google Scholar]
- Stopak D, Harris AK. (1982). Connective-tissue morphogenesis by fibroblast traction: I. Tissue-culture observations. Dev Biol , 383–398. [DOI] [PubMed] [Google Scholar]
- Vader D, Kabla A, Weitz D, Mahadevan L. (2009). Strain-induced alignment in collagen gels. PLoS One , e5902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van der Rijt JAJ, van der Werf KO, Bennink ML, Dijkstra PJ, Feijen J. (2006). Micromechanical testing of individual collagen fibrils. Macromol Biosci , 697–702. [DOI] [PubMed] [Google Scholar]
- Wang HL, Abhilash AS, Chen CS, Wells RG, Shenoy VB. (2014). Long-range force transmission in fibrous matrices enabled by tension-driven alignment of fibers. Biophys J , 2592–2603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wells RG (2013). Tissue mechanics and fibrosis. Biochim Biophys Acta , 884–890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wen Q, Janmey PA. (2013). Effects of non-linearity on cell-ECM interactions. Exp Cell Res , 2481–2489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winer JP, Oake S, Janmey PA. (2009). Non-linear elasticity of extracellular matrices enables contractile cells to communicate local position and orientation. PLoS One , e6382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu XP, Safran SA. (2015). Nonlinearities of biopolymer gels increase the range of force transmission. Phys Rev E , 032728. [DOI] [PubMed] [Google Scholar]
- Xu XP, Safran SA. (2017). Compressive elasticity of polydisperse biopolymer gels. Phys Rev E , 052415. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.