Automated Measurement of Lumbar Lordosis on Radiographs Using Machine Learning and Computer Vision

Abstract

Study Design:

Cross sectional database study.

Objective:

To develop a fully automated artificial intelligence and computer vision pipeline for assisted evaluation of lumbar lordosis.

Methods:

Lateral lumbar radiographs were used to develop a segmentation neural network (n = 629). After synthetic augmentation, 70% of these radiographs were used for network training, while the remaining 30% were used for hyperparameter optimization. A computer vision algorithm was deployed on the segmented radiographs to calculate lumbar lordosis angles. A test set of radiographs was used to evaluate the validity of the entire pipeline (n = 151).

Results:

The U-Net segmentation achieved a test dataset dice score of 0.821, an area under the receiver operating curve of 0.914, and an accuracy of 0.862. The computer vision algorithm identified the L1 and S1 vertebrae on 84.1% of the test set with an average speed of 0.14 seconds/radiograph. From the 151 test set radiographs, 50 were randomly chosen for surgeon measurement. When compared with those measurements, our algorithm achieved a mean absolute error of 8.055° and a median absolute error of 6.965° (not statistically significant, P > .05).

Conclusion:

This study is the first to use artificial intelligence and computer vision in a combined pipeline to rapidly measure a sagittal spinopelvic parameter without prior manual surgeon input. The pipeline measures angles with no statistically significant differences from manual measurements by surgeons. This pipeline offers clinical utility in an assistive capacity, and future work should focus on improving segmentation network performance.

Introduction

Spinal alignment is increasingly being recognized as a key, quantitative assessment of spinal health, and is associated with various spinal disorders such as adolescent idiopathic scoliosis, adult spinal deformity, and degenerative spondylolisthesis.^1-4 Malalignment, and the resulting compensatory response to maintain upright posture, places additional strain on key spinal, pelvic, and lower extremity structures that can cause arthritis and pain.^5,6 Restoring proper alignment in the coronal and sagittal plane is therefore essential for improving biomechanical efficiency and preventing further progression of disease.^5,7,8 In clinical practice, preoperative radiographic assessment of spinal alignment is conducted by measuring key angles and distances using various landmarks and comparing them with established alignment targets.^3,6

Poor sagittal alignment in particular has recently been associated with negative health-related quality of life (HRQoL).^2,9 Sagittal alignment is characterized by 5 key radiographic parameters: cervical lordosis (CL), thoracic kyphosis (TK), pelvic incidence minus lumbar lordosis (PI-LL), sagittal vertical axis (SVA), and pelvic tilt (PT).^3,6 While surgeons require these manually acquired radiographic measurements for presurgical planning, the process is both time-consuming and prone to rater-dependent error.^10,11 Furthermore, previous studies have demonstrated significant differences between standing and supine angle measurements.^4,12 Intraoperative surgical measurements better reflect postoperative sagittal balance because rigid fixation from instrumentation can prevent the passive corrections in spinopelvic parameters that occur in the supine position.¹³ Therefore, the development of automated tools for making rapid, intraoperative calculation of sagittal parameters may be useful for proper evaluation of alignment correction and to improve surgical decision making.

Machine learning, deep learning in particular, is being deployed on medical data to triage patients, automate preoperative planning, and predict outcomes for surgeons.^14-16 Within the field of orthopedics, segmentation using neural networks is a particularly promising technique for automatically identifying bony structures in medical images. Spurred by advances in computer vision techniques, multiple groups have attempted to apply artificial intelligence and other computational methods on radiographs to combat the numerous sources of variability inherent to radiographic angle measurement. While many studies have attempted coronal Cobb angle calculations, they required a large amount of a priori annotation by physicians on the input radiographs. This level of input may help reduce variability but has little intraoperative value and precludes robust spinal curvature assessment at scale.^17,18 Other groups attempted to work directly on unannotated radiographs to identify landmarks but did not measure any sagittal angles.^19,20

The purpose of this study was to develop a novel fully automated machine learning pipeline that reliably measures lumbar lordosis (LL) from radiographic images. Our methods do not require any a priori feature engineering or landmark identification. We report a combined segmentation and computer vision pipeline to measure lumbar lordosis in 0.14 seconds with potential perioperative value.

Materials and Methods

Materials

A total of 780 radiographs were collected from patients who received a lateral lumbar X-ray at our orthopedics department over a 1-year period. All radiographs were standardized and taken by an X-ray technician with the patient standing neutral weightbearing. Only 1 radiograph was selected for each patient to reduce potential bias of training the model on multiple X-rays from a single patient. Any patients with prior spine surgery or spine instrumentation were excluded. Standing lateral X-rays were used because they are higher quality and better standardized than intraoperative X-rays, increasing the probability of successfully training the model. Binary masks were generated by manually annotating every vertebral body in each radiograph using Photoshop (Adobe Systems, San Jose, CA) (Figure 1). This study was approved by our institutional review board.

Figure 1.

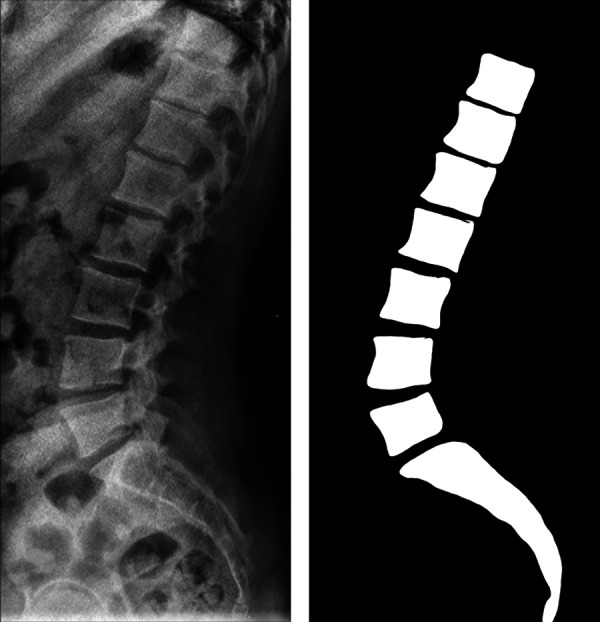
Example of a raw radiograph and its corresponding manually generated binary mask.

Model Training and Optimization

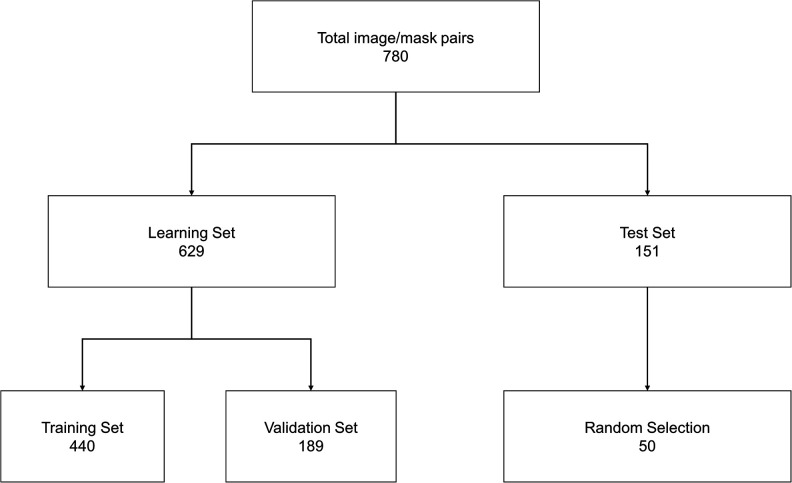
Radiographs were preprocessed using adaptive histogram equalization to improve contrast and normalize signal intensity.²¹ The dataset was split into 629 learning images (80% of total data) and 151 test images (20% of total data) for future performance testing. The learning data was then synthetically augmented using a custom script to 12 580 images and further split into 70% training and 30% validation data (Figure 2). The augmentations included flipping, randomly rotating, and randomly cropping the radiographs to incorporate natural variations inherent to clinical radiographs into the training dataset.

Figure 2.

Overview of data workflow for training and testing the U-Net. Augmentation involved flips, random rotations, and random zooms. Each dataset was randomized prior to splitting.

We utilized U-Net, a well-established convolutional neural net (CNN) architecture for segmentation, to generate bone segmentations of the radiographs by optimizing dice similarity coefficient (DSC) loss.^22,23 DSC is a standard metric for evaluating the accuracy of segmentations by comparing the overlap between CNN generated segmentations and manually generated masks. While a loss function defined by a simple pixel accuracy may be more intuitive, the DSC outperforms these more naive approaches for segmentation based problems.²³ The final model was trained using batch size of 20 on a NVIDIA GeForce GTX 1080-TI GPU for 200 epochs over 24.4 hours.

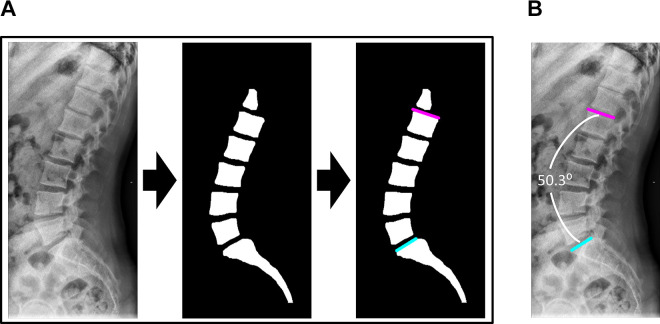
Beginning with raw radiographs, the algorithm first segments the image. Then, it automatically identifies the L1 and S1 vertebra from the segmentation and approximates their superior endplates to calculate the LL angle (Figure 3). Failure to properly identify L1 and S1 was treated as an algorithm failure, and no Cobb angle was measured for these cases. The algorithm was written using Python (version 3.5) and Keras (version 2.2.0).^24,25

Figure 3.

Overview of algorithm workflow for automatic lumbar lordosis angle calculation. (A) The raw radiograph is captured and preprocessed. Bony segmentation is generated from the raw radiograph with the trained U-Net. The L1 and S1 slopes are identified from the segmented image with a computer vision algorithm. (B) Overlay of the L1 and S1 slopes on the raw radiograph demonstrates proper slope placement and accurate angle estimation.

Statistical Analysis

The segmentation performance was evaluated using DSC and the area under the receiver operating characteristic curve (AUC). The algorithm-generated angles were compared to manual angle measurements from a chief resident (JK), spine fellow (SL), and attending surgeon (SKC) on 50 randomly selected radiographs from the test dataset using Welch’s 2-sample t test. Each surgeon measured every radiograph twice over a 2-week period to evaluate intra- and interrater reliability using interrater correlation coefficient (ICC) with a 2-way random effects model.²⁶ Measurements from surgeon 3 (SKC) were used as the gold standard for comparison. All statistical analysis was performed with R (version 3.4.4).²⁷

Results

Automatic Segmentation of Vertebral Bodies

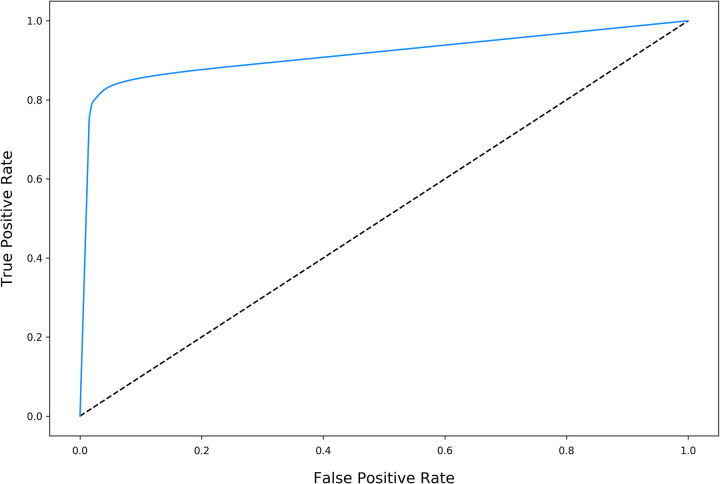
The final U-Net achieved a training DSC of 0.966 and validation DSC of 0.923 with an overall training time of approximately 24.4 hours. The U-Net performed well on segmenting the test dataset, with a test DSC of 0.821, AUC of 0.914, and accuracy of 0.862 (Figure 4).

Figure 4.

Receiver operating characteristic (ROC) of the U-Net for the test dataset. The overall test area under the ROC curve (AUC) was 0.914 and the overall test accuracy was 0.862. The dotted line denotes AUC = 0.50.

Calculation of Lumbar Lordosis Angle From Segmentations

The algorithm measured LL Cobb angles for 127 of the 151 radiographs in the test dataset, an overall success rate of 84.1%, with an average speed of 0.14 seconds/radiograph. From the 151-image test set, 50 radiographs were randomly chosen for surgeon measurement. On comparison, the algorithm succeeded in measuring angles for 42 images, a success rate of 84%.

Manual measurements among the surgeons demonstrated excellent intra- and interrater reliability, consistent with previous studies evaluating the surgeon reliability of radiographic spine angle measurements, with an overall ICC of 0.958 (95% CI: 0.931-0.976).^10,11,28-30 The intrarater correlation coefficients (IaCC) for surgeons 1, 2, and 3 were 0.933 (95% CI: 0.878-0.963), 0.984 (95% CI: 0.970-0.991), and 0.970 (95% CI: 0.945-0.984), respectively. The algorithm had higher variability in the mean absolute difference (MAD) from gold standard measurements, with a standard deviation of 12.989°, compared with 3.232° and 3.152° for surgeons 1 and 2 (JK, LS), respectively (Table 1). However, the algorithm still achieved good accuracy, with an overall mean absolute angle difference of 8.055 degrees and was not statistically different from the gold standard measurements (P = .372). Compared with the gold standard measurements, the algorithm was even more accurate with a median absolute angle difference of 6.965°, and this was also not statistically different (P = .161).

Table 1.

Absolute Angle Difference Performance Metrics.

Operator	Minimum	Q1	Median	Mean	Q3	Maximum	SD	P a
Relative to gold standard (deg)
Algorithm	0.668	3.810	6.965	13.441	21.857	50.528	12.989	0.161
Surgeon 1	0.300	1.762	4.050	4.474	6.650	14.000	3.232	0.224
Surgeon 2	0.100	1.375	3.050	3.529	4.825	18.400	3.152	0.460
Relative to overall surgeon average (deg)
Algorithm	0.187	3.815	8.055	13.069	19.834	54.395	13.126	0.372

^a P values computed using Welch’s 2-sample t test.

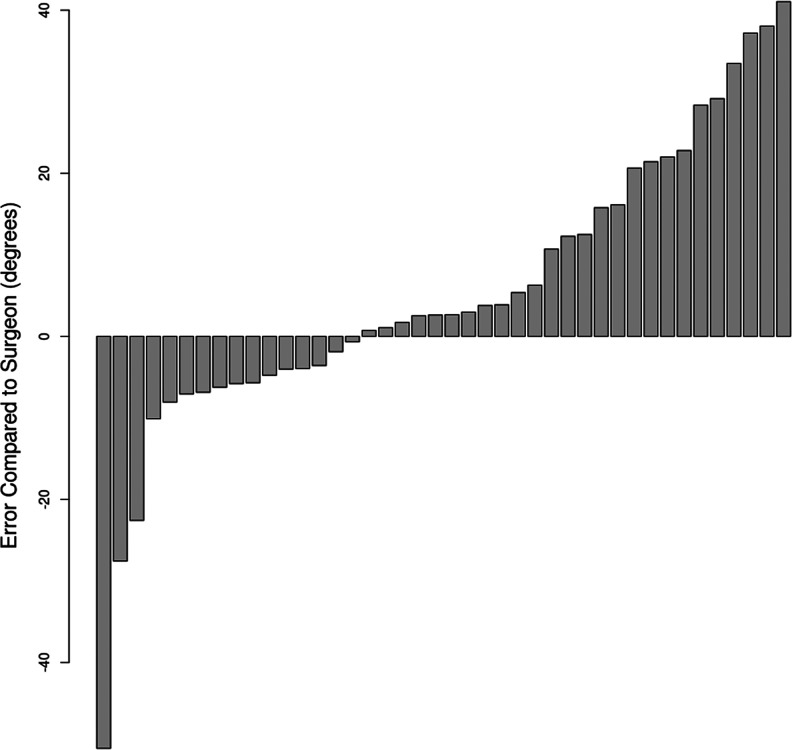
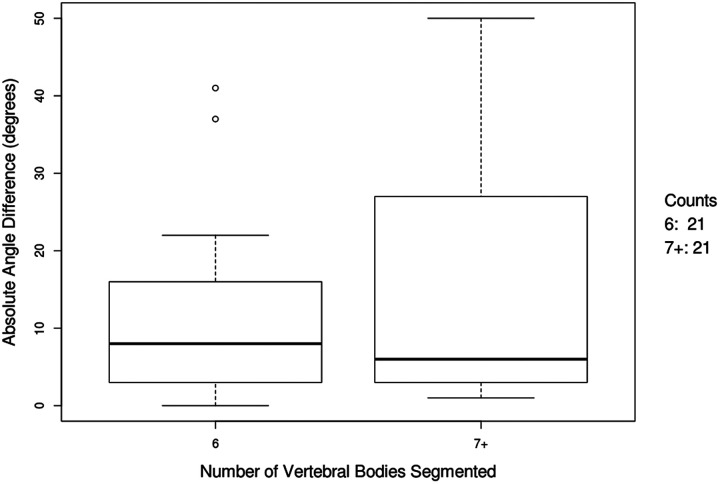
The sorted bar plot of the raw angle differences between the algorithm and gold standard measurements demonstrated higher rates of overestimation than underestimation (Figure 5). A subpopulation analysis revealed much lower variation in absolute angle difference in the images with 6 compared with 7 or more segmented vertebral bodies (Figure 6).

Figure 5.

Sorted bar plot of predicted angle error compared to the gold standard measurements (n = 42). The algorithm overestimated in 26 radiographs and underestimated in 16 radiographs.

Figure 6.

Box-whisker plot of absolute angle difference for radiographs with 6 and 7+ vertebral bodies segmented.

Discussion

Accurate measurement of radiographic parameters is essential for proper assessment of sagittal alignment and surgical planning.^31,32 The present study demonstrates the first fully automated system for the assessment of sagittal alignment on routine lumbar imaging. The pipeline in this study demonstrates strong segmentation quality (assessed by DSC) and accurate spinopelvic measurement when compared with 3 orthopedic surgeons.

While the advent of digital radiographs and computer-assisted measurement software have simplified the process of acquiring those parameters, they still require extensive manual input from the surgeon—increasing surgeon demand and introducing potential for interrater variability.^28,30,33 Previous work on automatic extraction of spinal parameters focused mostly on computed tomography and magnetic resonance data, as they contain higher-resolution data with less noise and allow for 3-dimensional reconstruction.^34-37 These imaging modalities allow for high-fidelity segmentations and measurement of additional parameters such as apical vertebral rotation but are not routinely used for monitoring or intraoperative imaging due to exposure to radiation and high price, limiting their clinical utility.^38-40 Therefore, this study aimed to evaluate the effectiveness of a fully automated, rapid LL Cobb angle measuring algorithm on lateral lumbar radiographs.

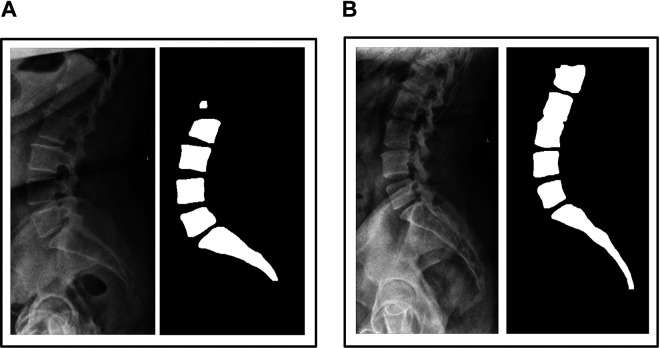
Previous groups have utilized machine learning models such as faster region-based convolutional neural networks (faster R-CNN) as well as traditional computer vision techniques to automatically localize the spine on radiographs.^17,41-44 However, many of these studies were limited by small sample sizes, due to a lack of widely available source of labeled data, and utilized single vertebra-level segmentation—increasing complexity of the model and thus potential for error.^17,41 One systematic review of Cobb angle measurement also noted that all previous Cobb angle computerized approaches, even ones that were deemed “automatic,” require landmark identification or another user input to generate each measurement, reducing scalability.⁴⁵ Recent work by Al Arif, et al⁴⁶ demonstrated how a high-performance cervical vertebra segmentation algorithm that achieved an average DSC of 0.944 suffered decreases in performance to a DSC of 0.840 when integrated to a fully automatic workflow due to accumulation of error in the multimodel pipeline.⁴⁶ In comparison, our model segmented the entire radiograph at once and still achieved a similar test DSC of 0.852 on lateral lumbar radiographs, which contains additional physiological radiopaque artifacts such as bowel gas and panniculus that increases segmentation difficulty. Most of the algorithm failures were due to segmentation of too few vertebral bodies (<5 lumbar + 1 sacrum) or due to the missegmentation of separate vertebral bodies as a single, fused body (Figure 7). The importance of segmentation quality on performance was also demonstrated in our subpopulation analysis (Figure 6), where the variability in absolute angle difference was much higher in the radiographs with higher than expected number of segmented vertebral bodies (7+ vs 6).

Figure 7.

Examples of U-Net segmentation failures. (A) Image and corresponding segmentation characterized by L1 segmentation failure. (B) Image and corresponding segmentation characterized by fused L2 and L3 vertebrae.

Segmentation allows the algorithm to determine where the vertebral bodies are located in a radiograph, just as spinal surgeons identify the vertebral bodies before identifying the end plates to use for measurement. While this may seem like a trivial task, the large variability in posture and vertebral shape as well as the presence of various radiopaque artifacts make this a difficult problem using traditional computer vision techniques. Computer vision algorithms exhibit robust performance on visual tasks and are largely insensitive to a lack of training data, but they tend to fail on images with high complexity such as radiographs. Deep learning algorithms and CNNs, on the other hand, can tolerate higher complexity but require training on massive datasets in order to identify refined features. While the size of our dataset is significantly larger than those reported in other spine segmentation studies, training a neural network to directly predict the angle from raw radiographs would require an unreasonably large dataset. Segmentation networks are therefore necessary to reduce the complexity of the input image so that robust computer vision algorithms can be utilized. Further improving the robustness of segmentation will therefore be essential for improving the performance of future algorithms, as the computer vision techniques rely on the algorithm-generated segmentation to determine which landmarks to use for measurement.

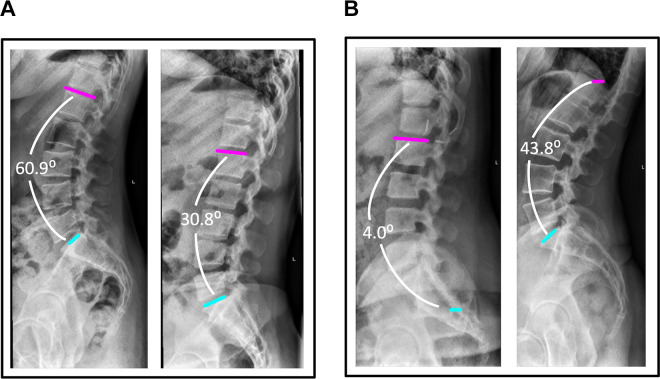
Our overall median absolute angle difference of 8.055° is larger than the error margins from surgeons (Table 1). While the t test showed that the algorithm measurements were not significantly different from surgeon measurements, demonstrating good accuracy, the standard deviation was much higher for the algorithm, demonstrating lower precision. Considering the lower precision relative to surgeon measurement, this algorithm may find perioperative clinical utility in an assistive capacity. We envision the algorithm could be integrated into manual tools for digital radiograph measurement to provide a visualized default measurement suggestion similar to that seen in Figure 8. The surgeon could then adjust the interactive measurement visualization tools as needed from the automatically generated starting point, reducing surgeon input compared to fully manual measurement. Even in cases of inaccurate measurement suggestion, the algorithm often still often succeeds in locating one of the necessary end plates (Figure 8b). Thus, deployment of this algorithm could provide clinical utility despite its lower precision by providing a bridge between manual measurement and fully automated measurement. Before fully automating the measurement of PI − LL with clinically acceptable error, consideration should be made to achieve absolute error and standard deviation that are sufficiently small to avoid affecting management. While there have been attempts at automating the measurement of Cobb angles in adolescent idiopathic scoliosis,^17,47,48 there is an unfortunate lack of literature on automating the measurement of other radiographic parameters such as pelvic incidence and sagittal alignment that are important for grading and surgical planning.⁴⁹ Further work in providing near real-time measurements from radiographs may increase the utility of these measurements in the outpatient as well as pre-, intra-, and postoperative settings, leading to improved screening and/or surgical outcomes.

Figure 8.

Computer-generated visualizations of end plate location and angle measurement for accurate and inaccurate algorithm measurements. (A) Accurate algorithm measurements corresponding to gold standard measurements of 61.1° (left) and 32.8° (right). (B) Inaccurate algorithm measurements corresponding to gold standard measurements of 37.7° (left) and 66.4° (right).

This study has several limitations. The first limitation is that radiographs with any implants were excluded. This exclusion criteria simplified the process of generating masks, which allowed us to create a large enough database for robust training, optimization, and testing. However, it limits the utility of our tool in the setting of postoperative follow up or revision, as a U-Net trained solely on radiographs without implants is most likely to include the highly radiopaque implant in the segmentation. A large number of image/mask pairs with advanced augmentation techniques may be necessary to account for the high variability in the types of implants used and the levels at which they are placed.⁴⁶ Another limitation is that all the radiographic data originated from a single hospital system, which may not reflect the differences in X-ray machines and acquisition techniques used in other institutions that could introduce additional artifacts to the radiographs. Additionally, this study did not stratify the radiographs by severity of ASD, which has been shown to increase the MAD for LL Cobb angle between human observers.¹¹ Severe deformities in the vertebral bodies that are not included in the training data may affect the quality of the segmentation, decreasing the performance of the algorithm. Finally, our comparison analysis excluded radiographs that the algorithms failed to identify the L1 and S1 vertebra on. This may have biased our analysis, as we do not know how the algorithm would have performed on them if the segmentation quality was higher.

Conclusion

This is the first published fully automatic algorithm that measures the LL Cobb angle using lateral lumbar radiographs. Deep learning, in combination with computer vision, is a promising tool in automating the measurement of various radiographic parameters. Our algorithm accurately measures the LL Cobb angle and is not statistically different from manual measurements made by surgeons, suggesting potential clinical utility in an assistive capacity. As techniques in bone segmentation and computer vision improve over time, these types of tools may prove useful in preoperative and intraoperative surgical decision making. Future work should focus on improving the quality of segmentation to increase the reliability of measurements. We envision this to be possible with multilabel segmentation nets that incorporate the femoral heads, which would allow us to calculate important measurements such as pelvic tilt, pelvic incidence, and PI − LL.