Abstract
Anatomical evidence shows that our visual field is initially split along the vertical midline and contralaterally projected to different hemispheres. It remains unclear at which processing stage the split information converges. In the current study, we applied the Double Filtering by Frequency (DFF) theory (Ivry & Robertson, 1998) to modeling the visual field split; the theory assumes a right-hemisphere/low-frequency bias. We compared three cognitive architectures with different timings of convergence and examined their cognitive plausibility to account for the left-side bias effect in face perception observed in human data. We show that the early convergence model failed to show the left-side bias effect. The modeling, hence, suggests that the convergence may take place at an intermediate or late stage, at least after information has been extracted/encoded separately in the two hemispheres, a fact that is often overlooked in computational modeling of cognitive processes. Comparative anatomical data suggest that this separate encoding process that results in differential frequency biases in the two hemispheres may be engaged from V1 up to the level of area V3a and V4v, and converge at least after the lateral occipital region. The left-side bias effect in our model was also observed in Greeble recognition; the modeling, hence, also provides testable predictions about whether the left-side bias effect may also be observed in (expertise-level) object recognition.
INTRODUCTION
Because of the partial decussation of optic nerves, our visual system is initially vertically split and the two visual hemifields are initially contralaterally projected to different hemispheres. The representations of the two visual hemifields have to converge at a certain stage. Nevertheless, it remains unclear where and when this convergence takes place. Neurophysiological studies of macaque monkeys suggest that the projection to the primary visual cortex of primates is completely crossed, with little or no measurable activity from the ipsilateral visual hemifield (e.g., Tootell, Switkes, Silverman, & Hamilton, 1988). However, it also has been shown that the primate visual system is organized as a set of hierarchically connected regions and the receptive field sizes of the neurons increase by a factor of about 2.5 at each succeeding stage (Rolls, 2000). In other words, in lower visual areas, input from the ipsilateral visual hemifield may occur near the retinotopic representation of the vertical meridian, whereas in the higher visual areas, the neurons may have a large receptive field that receives bilateral input, and retinotopy is no longer demonstrated.
The findings from functional magnetic resonance imaging (fMRI) examinations of the human visual cortex are, in general, consistent with the neurophysiological studies of monkeys. There has been converging evidence showing that neurons in lower visual areas, such as V1 to V4, have retinotopic receptive fields, whereas higher visual areas, such as MT and the lateral occipital region, have large and bilateral receptive fields that are poorly retinotopic (e.g., Tootell et al., 1997; Sereno et al., 1995; Sereno, McDonald, & Allman, 1994). Tootell, Mendola, Hadjikhani, Liu, and Dale (1998) explicitly conducted an fMRI examination of the representation of the ipsilateral visual field in the human visual cortex. They showed that, in most of the visual cortex, the amplitude of the activity due to input from the ipsilateral visual hemifield (i.e., activation from the other hemisphere after the initial contralateral projection) was not as high as the activity from the initial contralateral projection. In addition, in areas that show significant contralateral retinotopy, such as areas V1, V2, and V3, there was consistent and significant decrease in activity (i.e., inhibition) during ipsilateral stimulus presentation. This weak ipsilateral activity extends continuously but nonuniformly into different areas, consistent with previous neurophysiological studies with monkeys (e.g., Cusick, Gould, & Kaas, 1984; Van Essen, Newsome, & Bixby, 1982). In particular, Tootell et al. (1998) reported that the areas anterior to V3a and V4v, which are the most anterior retinotopic areas, show significantly greater ipsilateral activity compared with adjacent lower visual areas.
In summary, the anatomical data suggest that the influence from the ipsilateral activity may be a continuous but nonuniform process throughout the visual cortex, but there does not seem to be a precise location of the convergence of the initially split visual input. If there is, indeed, a convergence location, it may be the areas anterior to V3a and V4v due to the abrupt increase of ipsilateral activity. However, it remains unclear what kind of processes are engaged before the convergence. In addition, the initial trajectory of visual activation flow is a fast and widespread sweep and continues through iterations of feedback loops for further processing in the sensory area (Foxe & Simpson, 2002); hence, it is unclear yet to what extent the visual split influences human cognition. In other words, does this initial split have any functional significance?
Evidence from visual word recognition supports a functional split. The general finding is that the two hemispheres have contralateral influence on responses driven by the left and right halves of the stimuli, which are initially projected to different visual hemifields (e.g., Hsiao, Shillcock, & Lavidor, 2006; Hsiao & Shillcock, 2005a; Lavidor & Walsh, 2003, 2004; Lavidor, Ellis, Shillcock, & Bland, 2001). There is also evidence from face recognition supporting a functional split. For example, a left-side bias effect has been frequently reported in face perception. The classical experiment is to ask participants to judge the similarity between a face and chimeric faces made from the two left halves (left chimeric face) or the two right halves (right chimeric face) of the original face (from the viewer’s perspective; Figure 1). The results show that the left chimeric face is usually judged more similar to the original face than the right chimeric face, especially for highly familiar faces (Brady, Campbell, & Flaherty, 2005; Bruce & Young, 1998). Consistent with this result, other studies have argued for a right-hemisphere (RH) bias in face perception (e.g., Rossion, Joyce, Cottrell, & Tarr, 2003). Nevertheless, it remains unclear how far the split effect extends. In visual word recognition, Hsiao and Shillcock (2005a) showed that this split effect can reach far enough to interact with sex differences in brain laterality for phonological processing, suggesting that the split reaches far enough to influence high-level cognition. The question is at which processing stage does the information start to converge in order to show the effects of the functional split?
Figure 1.
Left chimeric, original, and right chimeric faces (images are taken from Bruce & Young, 1998, p. 234; reproduced with permission of Oxford University Press).
In order to address the splitting effects observed in visual word recognition, Shillcock and Monaghan (2001) proposed a split fovea model (Figure 2) and showed that some psychological phenomena in visual word recognition can be better accounted for by the split architecture, such as exterior letter effects in English word recognition and eye fixation behavior in reading English (Shillcock, Ellison, & Monaghan, 2000). Hsiao and Shillcock (2005b) further showed that the split and nonsplit architectures (i.e., the split fovea model and the intermediate convergence model shown in Figure 2) in modeling Chinese character recognition exhibited qualitatively different processing, and the results were able to account for the sex differences in naming Chinese characters in human data.
Figure 2.
Architectures of different models.
Our final motivation comes from studies of neurocomputational models of face identification. Dailey and Cottrell (1999) found, consistent with human studies (Schyns & Oliva, 1999; Costen, Parker, & Craw, 1996), that a neural network with a bias toward low spatial frequencies (LSFs) generalized to new images of the same person much better than a network biased toward high spatial frequencies (HSF). This result suggests that if there is a spatial frequency bias in the two hemispheres, the one biased toward LSF should identify faces better, and dominate the other.
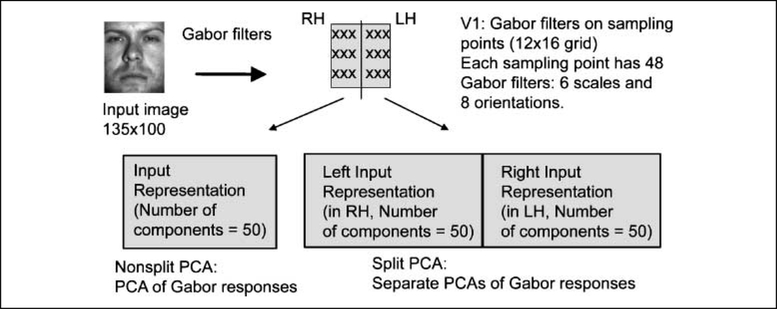
In the current study, we apply the split fovea model to face and object recognition. In contrast to previous models in visual word recognition, which act on a relatively abstract level of representation (i.e., localist representation of letters or stroke patterns), we incorporate several known aspects of visual anatomy and its computation into the modeling, in order to examine the timing of convergence in terms of processing stages along the hierarchical visual system. We use Gabor responses over the input image to simulate neural responses of complex cells in the early visual system (Lades et al., 1993). We then reduce the dimension of this perceptual representation with Principal Component Analysis (PCA), which has been argued to be a biologically plausible linear compression technique (Sanger, 1989; cf. Dailey, Cottrell, Padgett, & Ralph, 2002); this is the visual input shown in Figure 2. With this level of abstraction, convergence of the initial split may happen at three different stages: early, after Gabor filters in the early visual system (i.e., at the input layer); intermediate, after information extraction through PCA (i.e., at the hidden layer); and late, at the output layer (Figure 2). In the early convergence model, the left and right Gabor filters are processed as a whole through PCA (i.e., nonsplit input representation; Figure 3). In the intermediate convergence model, PCA is applied separately to the left and right Gabor filters and the convergence is at the hidden layer. In the late convergence model, in addition to the split input layer, the hidden layer is also split, and the information converges at the output layer. According to this categorization, the split fovea and nonsplit models, proposed first by Shillcock and Monaghan (2001), can be considered as late and intermediate convergence models, respectively.1 Here we conduct a more general comparison between these three architectures and examine their performance and cognitive plausibility.
Figure 3.
Nonsplit and split visual input representations.
In order to account for various psychological phenomena involving hemispheric differences, Ivry and Robertson (1998) proposed a Double Filtering by Frequency (DFF) theory. The theory argues that information coming into the brain goes through two frequency filtering stages. The first stage involves attentional selection of task-relevant frequency information, and at the second stage, the two hemispheres have asymmetric filtering processing: The left hemisphere (LH) amplifies high-frequency information (i.e., a high-pass filter), whereas the RH amplifies low-frequency information (i.e., a low-pass filter). The split architectures introduced here enable us to apply the DFF theory to modeling face and object recognition.
There has been an ongoing debate regarding whether the brain processes faces differently from objects. Evidence for this argument comes from studies showing that the fusiform face area (FFA) in the brain selectively responds to face stimuli (e.g., McKone & Kanwisher, 2005), whereas other studies have suggested that several phenomena that were thought to be unique to face recognition may be due to expertise (e.g., Gauthier, Tarr, Anderson, Skudlarski, & Gore, 1999). Thus, the left-side bias effect observed in face perception may be due to a designated face processor located in the RH, or the reliance on LSF processing in the RH (according to the DFF theory), once the expertise is acquired. In the following sections, we will first examine whether the DFF theory is able to account for the left-side bias effect in face perception. A positive result will suggest that the RH reliance in face processing is due to the low-frequency bias in the RH. We will then examine the cognitive plausibility of the models with different timings of convergence in accounting for the left-side bias effect in face perception. We will also examine whether the left-side bias effect can be obtained in expert object recognition in the models with different timings of convergence. The objects under examination are Greebles, a novel class of objects that have been frequently used in studies of object recognition and perceptual expertise (e.g., Gauthier et al., 1999). The results will provide testable predictions regarding whether faces and objects are processed differently in the brain.
METHODS
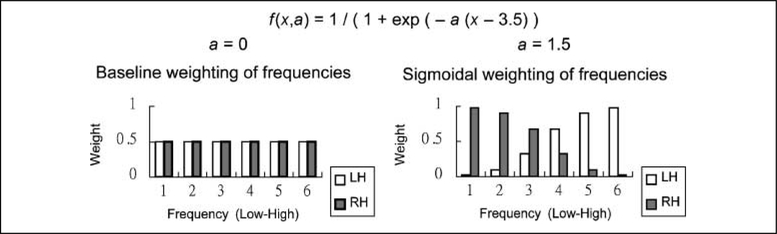
To simulate responses of complex cells in the early visual system, the input image (135 × 100 pixels) was first filtered with a rigid grid (16 × 12) of overlapping 2-D Gabor filters (Daugman, 1985) in quadrature pairs at six scales and eight orientations (Figure 3). The six scales corresponded to 2 to 64 (i.e., 21 to 26) cycles per face. Given the width of the image (100 pixels), this frequency range, hence, can be considered as the task-relevant frequency range (the seventh scale would have 128 cycles per face, and thus, one cycle would cover smaller than one pixel). Hence, the first stage of the DFF is implemented by simply giving this input to all of our models. The paired Gabor responses were combined to obtain Gabor magnitudes. In the nonsplit input representation, this 9216 (16 × 12 Gabor filters × 6 scales × 8 orientations) element perceptual representation was compressed into a 50-element representation with PCA. In the split input representation, the face was split into left and right halves, and each had 16 × 6 Gabor filters (4608 elements). The perceptual representation of each half was compressed into a 50-element representation (hence, in total there were 100 elements).2 After PCA, each principal component was z-scored to equalize the contribution of each component in the models. In the three models, the early convergence model had a nonsplit input representation, whereas both the intermediate and late convergence models had a split input representation. In order to equalize their computational power, the hidden layer of the early and the intermediate convergence models had 20 units, and each of the two hidden layers of the late convergence model had 10 units; in the intermediate convergence model, half of the connections from the input layer to the hidden layer were randomly selected and removed. Hence, the three models had exactly the same number of hidden units and weighted connections. To implement the second stage of the DFF theory, we gated the spatial frequencies by scaling the Gabor filter responses using a sigmoidal weighting function (Figure 4). This process biased the Gabor responses on the left half face (RH) to LSF and those on the right half face (LH) to HSF. We also conducted a separate baseline simulation in which no such frequency bias was applied; more specifically, the weighting function had a uniform distribution and the LH and the RH received the same amount of information in all frequency scales (Figure 4).
Figure 4.
Sigmoidal weighting functions: unbiased (a = 0) and biased conditions (a = 1.5).
In short, we tried to bring the model architecture as close to the visual anatomy as possible. The Gabor filters correspond to V1; the PCA can be thought of as analogous to the information extraction/encoding process up to the lateral occipital region, for instance, the occipital face area in face recognition (Gauthier et al., 2000), which has been argued to be related to structural representation of faces (Rossion et al., 2003); the hidden layer of the network has been associated with the fusiform area (e.g., FFA; Tong, Joyce, & Cottrell, 2008). Finally, the output layer has a unit for each individual subject. We examined the three models’ cognitive plausibility in addressing the left-side bias effect in face perception with two face identification tasks. In order to examine whether the effect generalizes to expert object recognition, we also conducted a Greeble identification task (we describe the details of each task in the following section, together with the results). In each task, we ran each model 80 times and analyzed its behavior with analysis of variance after a 100-epoch training (their performance on the training set all reached 100% accuracy). The training algorithm was discrete back propagation through time (Rumelhart, Hinton & Williams, 1986), with a learning rate of 0.1. Performance was analyzed at the end of seven time steps (cf. Hsiao & Shillcock, 2005b; Shillcock & Monaghan, 2001).3 The independent variables were architecture (early, intermediate, and late convergence) and frequency bias (unbiased vs. biased). The dependent variables were accuracy and size of left-side bias effect. To examine the size of left-side bias effect, we took output node activation for a particular individual as a measure of similarity between the chimeric face and the original face. After training, we presented the networks with left and right chimeric faces using test set images. The size of left-side bias effect was measured as the difference between the activation of the output node for the original face when the left chimeric face was presented and when the right chimeric face was presented (note that output activation ranged from 0 to 1). For each simulation, the materials comprised images of 30 different individuals (so there are 30 output nodes; see the following sections for simulation details). Two datasets were created for training and testing, and the order was counterbalanced across the simulation runs. In order to eliminate any bias effect due to the baseline difference between the two sides of the images, in half of the simulation runs, the mirror images of the original images were used.
RESULTS
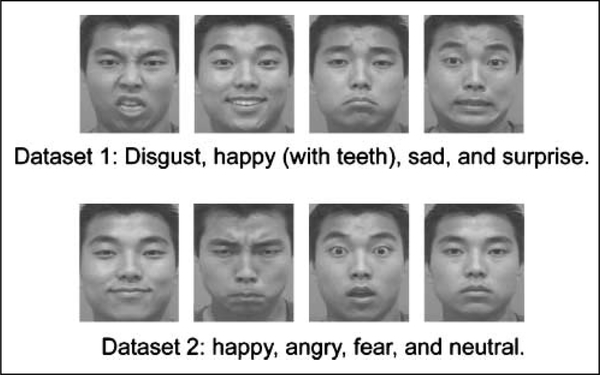
In our first experiment, we trained the network to identify 30 individuals whose images varied in facial expression (thus their expressions were noise with respect to the identity classification; Figure 5). We used two datasets of the 30 individuals, with four expressions in each dataset, for a total of 120 training and 120 test images. These images were taken from CAlifornia Facial Expressions dataset (CAFÉ; Dailey, Cottrell, & Reilly, 2001). The generalization accuracy results showed a significant interaction between architecture and frequency bias [F(2, 474) = 8.513, p < .001; Figure 6A]. In general, biased spatial frequency hurt performance [F(1, 474) = 33.254, p ≪ .001], and the later the convergence, the bigger the effect. As for the left-side bias effect for chimeric faces, there was a main effect of architecture [F(2, 474) = 141.457, p ≪ .001], a main effect of frequency bias [F(1, 474) = 709.651, p ≪ .001], and a significant interaction between architecture and frequency bias [F(2, 474) = 144.386, p ≪ .001; Figure 6B]. None of the models had a left-side bias effect in the unbiased frequency condition. In the biased frequency condition, there was a significant left-side bias effect in the late [F(1, 158) = 596.068, p ≪ .001] and intermediate convergence models [F(1, 158) = 520.160, p ≪ .001]. In contrast, the early convergence model did not have the left-side bias effect [F(1, 158) = 3.861, ns]. This suggests that in the biased condition, converging at an early stage (i.e., nonsplit representation) may still extract balanced low- and high-frequency information for recognition, whereas converging at a later stage (i.e., split representation) allows more low-frequency information from the left half face to the hidden layer, and consequently, brings about the left-side bias effect.4
Figure 5.
Face images for facial expression recognition.
Figure 6.
(A) Performance and (B) left-side bias effect in the three models. Error bars show standard errors (*p < .01; **p < .001; ***p < .0001).
In order to reconfirm the left-side bias effects we obtained, we conducted another simulation of face identification, using multiple lighting conditions as the variability factor across images of the same person. We selected face images from the Yale face database (Georghiades, Belhumeur, & Kriegman, 2001) with a light source moving from right to left. Each individual had eight different lighting conditions (Figure 7); the lighting conditions in the training and test datasets had the same azimuths but different altitudes. The results showed that the late convergence model performed the worst [F(2, 474) = 158.918, p ≪ .001], and performance in the unbiased frequency condition was better than the biased frequency condition [F(1, 474) = 172.075, p ≪ .001; Figure 8A]. As for the left-side bias effect for chimeric faces, there was a main effect of architecture [F(2, 474) = 233.286, p ≪ .001], a main effect of frequency bias [F(1, 474) = 369.360, p ≪ .001], and a significant interaction between architecture and frequency bias [F(2, 474) = 242.055, p ≪ .001; Figure 8B]. The frequency bias again significantly induced the left-side bias effect in the late [F(1, 158) = 231.353, p ≪ .001] and intermediate convergence models [F(1, 158) = 524.643, p ≪ .001]; the early convergence model failed to show the left-side bias effect; in fact, it exhibited a slight right-side bias effect [F(1, 158) = 86.509, p ≪ .001]. The results hence confirmed again that the intermediate and late convergence models had a strong left-side bias effect, and the early convergence model was not able to exhibit the left-side bias effect in human data.
Figure 7.
Face images for training. From left to right, the azimuths are: −60, −35, −20, −10, +10, +20, +35, and +60. Altitudes range from −20 to 20.
Figure 8.
(A) Performance of the three models. (B) Left-side bias effect in the three models. Error bars show standard errors (***p < .0001).
We turned to see whether similar effects can be obtained in Greeble recognition. Because objects such as Greebles do not have expressions, we were only able to replicate the lighting experiment with them. Our previous work suggests that once a network becomes a Greeble expert, it behaves analogously to a face expert (Tong et al., 2008). Hence, we examined the networks’ performance on recognizing Greebles under different lighting changes. We considered the sun as the major source of light in nature, and its azimuth increases during a day and its altitude first increases and then decreases from midday. In each of the two datasets created, each Greeble had eight images under the eight different lighting conditions shown in Figure 9.
Figure 9.
A Greeble, facing south, under the sun in San Francisco, California (latitude, longitude: 27.618, 122.373) and Ketchikan, Alaska (55.342, 131.647), from 9 am to 4 pm.
The first set was Greebles under the San Francisco sun, and the other was the same Greebles in Ketchikan. Hence, in the two datasets, the sun positions had different azimuths and altitudes. The accuracy results showed that there was a main effect of frequency bias [F(1, 474) = 94.089, p ≪ .001]: Performance in the unbiased frequency condition was better than the biased frequency condition (Figure 10A). As for the left-side bias effect for chimeric Greebles, there was a main effect of architecture [F(2, 474) = 100.768, p ≪ .001], a main effect of frequency bias [F(1, 474) = 13.891, p < .001], and an interaction between architecture and frequency bias [F(2, 474) = 178.707, p ≪ .001; Figure 10B]. Similar to the previous simulation with faces, the frequency bias significantly induced the left-side bias effect in the late [F(1, 158) = 25.279, p ≪ .001] and intermediate convergence models [F(1, 158) = 202.184, p ≪ .001]; the early convergence model did not have the left-side bias effect; it exhibited right-side bias instead [F(1, 158) = 173.858, p ≪ .001]. The results thus predict that the left-side bias effect may also exist in Greeble experts.
Figure 10.
(A) Performance of the three models. (B) Left-side bias effect in the three models. Error bars show standard errors (***p < .0001).
DISCUSSION
In the current study, we explored split architecture in modeling face and object recognition in order to examine the timing of convergence of the visual field split; more specifically, we aimed to examine at which processing stage the representations of the two visual hemifields converge. We tried to bring the model architecture and computation as close to known aspects of visual anatomy and computation as possible, and applied the DFF theory to simulate the fundamental hemispheric processing differences: For the input representation, we first selected a task-relevant frequency range, and then biased the information coming into the RH (i.e., left half of the input) to low frequency and that coming into the LH (i.e., right half of the input) to high frequency through a sigmoidal weighting function. We then compared performance and cognitive plausibility of three cognitive architectures with different timings of convergence. We showed that, in this computational exploration, the combination of the spatial frequency bias and the splitting of information processing between left and right is sufficient to show the left-side bias effect, but neither alone can show the effect. This is consistent with the observation that there is an LSF bias in face identification, both in humans and computational models (Dailey & Cottrell, 1999; Schyns & Oliva, 1999). This is reflected in the higher activation of the identity unit when the model’s RH receives the same side of the face it was trained upon, compared with when it does not.
The failure of the early convergence model in exhibiting the left-side bias effect suggests that the initially split visual input may converge at an intermediate or late stage, after some information extraction/encoding has been applied separately in each hemisphere. This result is consistent with several behavioral studies showing that each hemisphere seems to have a dominant influence on the processing of the visual information presented in the visual hemifield to which it has direct access, for both centrally presented stimuli (e.g., Hsiao et al., 2006; Brady et al., 2005; Lavidor & Walsh, 2004) and unilaterally presented stimuli (e.g., right visual field/LH advantage in English word recognition; see Brysbaert & d’Ydewalle, 1990; Bryden & Rainey, 1963). Recent electrophysiological studies of face and visual word recognition also support this claim: An early ERP component N170 is modulated by contralateral features of the stimulus, whereas late components that respond to task-dependent information (e.g., P300 for face categorization and N350 for word naming) are usually bilaterally distributed (see, e.g., Hsiao, Shillcock, & Lee, 2007; Schyns, Petro, & Smith, 2007; Smith, Gosselin, & Schyns, 2004). The anatomical findings suggest that the abrupt increase of ipsilateral activity in the areas anterior to area V3a and V4v (Tootell et al., 1998) may be the locus of the convergence. Thus, from area V1 up to the level of areas V3a and V4v, the information from the two visual hemifields may go through different encoding processes separately in different hemispheres and converge at least after the lateral occipital region. This claim is consistent with the findings from fMRI adaptation studies that the lateral occipital region (and also the inferior temporal region, such as the FFA) has position-invariant properties in object recognition (e.g., Large, Kuchinad, Aldcroft, Culham, & Vilis, 2006; Grill-Spector et al., 1999; Malach, Grill-Spector, Kushnir, Edelman, & Itzchak, 1998).5 It is also consistent with the observation from psychophysical studies that hemispheric differences in perception (as a function of spatial frequencies) must result from processes taking place beyond the sensory level (Sergent, 1982) because studies examining grating detection did not report a hemispheric difference in contrast sensibility or visible persistence (Fendrich & Gazzaniga, 1990; Peterzell, Harvey, & Hardyck, 1989; Di Lollo, 1981; Rijsdijk, Kroon, & Van der Wildt, 1980). In other words, the two hemispheres may receive the same type of information at the sensory level; it is the encoding processes beyond the sensory level that results in the observed hemispheric differences in perception. The current split modeling thus allows us to infer possible functions and computations in different areas along the hierarchical visual system through comparing the modeling data with behavioral, anatomical, and psychophysical data.
The results from modeling Greeble recognition also showed a left-side bias effect in both the intermediate and late convergence models, but not in the early convergence model. In human data, the left-side bias effect has never been shown in recognition tasks other than faces, hence, has been considered a face-specific effect. However, it may also be due to our expertise in face processing (cf. Gauthier et al., 1999). The modeling result, hence, provides a testable prediction about whether a left-side bias effect can also be observed in object recognition once expertise is acquired.
Although it is beyond the scope of the current examination, the current study also brings about a theoretical question: Why would such a visual field split and differential frequency bias exist in the brain? The current simulations seem to suggest that frequency biases deteriorate performance and may be suboptimal. Nevertheless, the advantage of the split and the frequency biases may be observed when the system (i.e., the brain) has to deal with tasks with different frequency requirements; for example, word recognition may rely more on high-frequency information processing, in contrast with LSF information for face recognition. Thus, the design of differential frequency biases in the two hemispheres may be optimal given that the brain has limited computational resources. These issues require further examination.
The models we propose here unavoidably involve abstraction and assumptions about the underlying neural complexity, but they, nevertheless, address the issue under examination here and convey an important message to the research in computational modeling of cognitive processes. The study provides a computational explanation of the cognitive implausibility of the early convergence model, which has been the most typical model for face/object/word recognition in the literature (e.g., Dailey & Cottrell, 1999; Harm & Seidenberg, 1999; Riesenhuber & Poggio, 1999). The fact that the initial split has a functional significance has been overlooked in most computational models of cognitive processes; the current study shows that this fact does have significant impact on how modeling is able to explain and predict human behavior. Brysbaert (2004) takes city planning with a wide river running through the city center as an analogy with the representation of the visual field split in the brain—no matter how many bridges and tunnels are built, the communication across the river is always going to be more effortful than the communication within each half of the city. Thus, by analogy with city planning, it is reasonable to hypothesize that interhemispheric transfer in the brain is reduced in favor of intrahemispheric communication. The current modeling result is consistent with this view: The two halves of the representation go through separate encoding processes in the two hemispheres before the convergence.
“No city planner can afford to overlook the presence of a wide river in a city,” as pointed out by Brysbaert (2004), not until we understand how the brain has solved the problem of the visual field split and the division of labor between the two hemispheres are we able to have a complete understanding about the recognition of visual stimuli. Researchers should now consider the influence of the split architecture in the brain on our perception and cognition.
Acknowledgments
We thank the NIH (grant MH57075 to G. W. Cottrell), the James S. McDonnell Foundation (Perceptual Expertise Network, I. Gauthier, PI), and the NSF (grant SBE-0542013 to the Temporal Dynamics of Learning Center, G. W. Cottrell, PI). We also thank the editor, Chad Marsolek, and an anonymous referee for helpful comments.
Footnotes
The late convergence model differs from the split fovea model in that it does not have interconnections between the two hidden layers. We removed these interconnections here for comparison reasons; in separate simulations, we found that adding these interconnections did not change the effects we reported here.
Although the split and nonsplit representation had different number of dimensions in the input layer, they both contained information from the first 50 principal components. This equalizes the information contained in each representation better than increasing the number of dimensions in the nonsplit representation to match that of the split representation. In fact, with 100 components, the nonsplit model performs worse.
Although the networks do not have recurrent connections, we used discrete back propagation through time to be consistent with the split fovea model (Shillcock & Monaghan, 2001), which has recurrent connections between the two hidden layers. We found that adding these interconnections did not change the effects we reported here.
The only difference between the early and intermediate convergence models was the input representation (nonsplit vs. split). In a separate simulation, we used a simple perception (i.e., the hidden layer was removed) to examine the baseline behavior between the two representations, and the split representation, indeed, had a left-side bias effect, whereas the nonsplit representation did not; This effect was consistent across the three simulations we reported here.
Note that Large et al.’s (2006) study showed that the position invariance effect (i.e., the adaptation effect) in the lateral occipital region is greater within a hemifield than between hemifields, whereas the FFA does not have this property, although both the FFA and the lateral occipital region have a preference for stimuli in the contralateral versus ipsilateral visual hemifield.
REFERENCES
- Brady N, Campbell M, & Flaherty M (2005). Perceptual asymmetries are preserved in memory for highly familiar faces of self and friend. Brain and Cognition, 58, 334–342. [DOI] [PubMed] [Google Scholar]
- Bruce V, & Young A (1998). In the eye of the beholder: The science of face perception. New York: Oxford University Press. [Google Scholar]
- Bryden MP, & Rainey CA (1963). Left-right differences in tachistoscopic recognition. Journal of Experimental Psychology, 66, 568–571. [DOI] [PubMed] [Google Scholar]
- Brysbaert M (2004). The importance of interhemispheric transfer for foveal vision: A factor that has been overlooked in theories of visual word recognition and object perception. Brain and Language, 88, 259–267. [DOI] [PubMed] [Google Scholar]
- Brysbaert M, & d’Ydewalle G (1990). Tachistoscopic presentation of verbal stimuli for assessing cerebral dominance: Reliability data and some practical recommendations. Neuropsychologia, 28, 443–455. [DOI] [PubMed] [Google Scholar]
- Costen NP, Parker DM, & Craw I (1996). Effects of high-pass and low-pass spatial filtering on face identification. Perception & Psychophysics, 58, 602–612. [DOI] [PubMed] [Google Scholar]
- Cusick CG, Gould HJ III, & Kaas JH (1984). Interhemispheric connections of visual cortex of owl monkeys (Aotus trivirgatus), marmosets (Callithrix jacchus), and galagos (Galago crassicaudatus). Journal of Comparative Neurology, 230, 311–336. [DOI] [PubMed] [Google Scholar]
- Dailey MN, & Cottrell GW (1999). Organization of face and object recognition in modular neural networks. Neural Networks, 12, 1053–1074. [DOI] [PubMed] [Google Scholar]
- Dailey MN, Cottrell GW, Padgett C, & Ralph A (2002). EMPATH: A neural network that categorizes facial expressions. Journal of Cognitive Neuroscience, 14, 1158–1173. [DOI] [PubMed] [Google Scholar]
- Dailey MN, Cottrell GW, & Reilly J (2001). California Facial Expressions (CAFE). www.cs.ucsd.edu/users/gary/CAFE/ Accessed on 10 January 2005.
- Daugman JG (1985). Uncertainty relation for resolution in space, spatial frequency, and orientation optimized by two-dimensional visual cortical filters. Journal of the Optical Society of America A, 2, 1160–1169. [DOI] [PubMed] [Google Scholar]
- Di Lollo V (1981). Hemispheric symmetry in visible persistence. Perception & Psychophysics, 11, 139–142. [DOI] [PubMed] [Google Scholar]
- Fendrich R, & Gazzaniga M (1990). Hemispheric processing of spatial frequencies in two commissurotomy patients. Neuropsychologia, 28, 657–663. [DOI] [PubMed] [Google Scholar]
- Foxe JJ, & Simpson GV (2002). Flow of activation from V1 to frontal cortex in humans: A framework for defining “early” visual processing. Experimental Brain Research, 142, 139–150. [DOI] [PubMed] [Google Scholar]
- Gauthier I, Tarr MJ, Anderson AW, Skudlarski P, & Gore JC (1999). Activation of the middle fusiform “face area” increases with expertise in recognizing novel objects. Nature Neuroscience, 2, 568–573. [DOI] [PubMed] [Google Scholar]
- Gauthier I, Tarr MJ, Moylan J, Skudlarski P, Gore JC, & Anderson AW (2000). The fusiform “face area” is part of a network that processes faces at the individual level. Journal of Cognitive Neuroscience 12 495–504. [DOI] [PubMed] [Google Scholar]
- Georghiades AS, Belhumeur PN, & Kriegman DJ (2001). From few to many: Illumination cone models for face recognition under variable lighting and pose. IEEE Transactions on Pattern Analysis and Machine Intelligence, 6, 643–660. [Google Scholar]
- Grill-Spector K, Kushnir T, Edelman S, Avidan G, Itzchak Y, & Malach R (1999). Differential processing of objects under various viewing conditions in the human lateral occipital complex. Neuron, 24, 187–203. [DOI] [PubMed] [Google Scholar]
- Harm MW, & Seidenberg MS (1999). Phonology, reading acquisition, and dyslexia: Insights from connectionist models. Psychological Review, 106, 491–528. [DOI] [PubMed] [Google Scholar]
- Hsiao JH, & Shillcock R (2005a). Foveal splitting causes differential processing of Chinese orthography in the male and female brain. Cognitive Brain Research, 25, 531–536. [DOI] [PubMed] [Google Scholar]
- Hsiao JH, & Shillcock R (2005b). Differences of split and non-split architectures emerged from modelling Chinese character pronunciation. Proceedings of the Twenty Seventh Annual Conference of the Cognitive Science Society (pp. 989–994). Mahwah, NJ: Erlbaum. [Google Scholar]
- Hsiao JH, Shillcock R, & Lavidor M (2006). A TMS examination of semantic radical combinability effects in Chinese character recognition. Brain Research, 1078, 159–167. [DOI] [PubMed] [Google Scholar]
- Hsiao JH, Shillcock R, & Lee C (2007). Neural correlates of foveal splitting in reading: Evidence from an ERP study of Chinese character recognition. Neuropsychologia, 45, 1280–1292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ivry R, & Robertson LC (1998). The two sides of perception. Cambridge, MA: MIT Press. [Google Scholar]
- Lades M, Vorbruggen JC, Buhmann J, Lange J, von der Malsburg C, Wurtz RP, et al. (1993). Distortion invariant object recognition in the dynamic link architecture. IEEE Transactions on Computers, 42, 300–311. [Google Scholar]
- Large M-E, Kuchinad A, Aldcroft A, Culham J, & Vilis T (2006). Visual field representation in the lateral occipital complex. Journal of Vision, 6, 539a. [Google Scholar]
- Lavidor M, Ellis AW, Shillcock R, & Bland T (2001). Evaluating a split processing model of visual word recognition: Effects of word length. Cognitive Brain Research, 12, 265–272. [DOI] [PubMed] [Google Scholar]
- Lavidor M, & Walsh V (2003). A magnetic stimulation examination of orthographic neighbourhood effects in visual word recognition. Journal of Cognitive Neuroscience, 15, 354–363. [DOI] [PubMed] [Google Scholar]
- Lavidor M, & Walsh V (2004). The nature of foveal representation. Nature Reviews Neuroscience, 5, 729–735. [DOI] [PubMed] [Google Scholar]
- Malach R, Grill-Spector K, Kushnir T, Edelman GM, & Itzchak Y (1998). Rapid shape adaptation reveals position and size invariance in the object-related lateral occipital (LO) complex. Neuroimage, 7, S43. [Google Scholar]
- McKone E, & Kanwisher N (2005). Does the human brain process objects of expertise like faces? A review of the evidence In Dehaene S, Duhamel JR, Hauser M, & Rizzolatti (Eds.), From monkey brain to human brain. Cambridge, MA: MIT Press. [Google Scholar]
- Peterzell DH, Harvey LO Jr., & Hardyck CD (1989). Spatial frequencies and the cerebral hemispheres: Contrast sensitivity, visible persistence, and letter classification. Perception & Psychophysics, 46, 433–455. [DOI] [PubMed] [Google Scholar]
- Riesenhuber M, & Poggio T (1999). Hierarchical models of object recognition in cortex. Nature Neuroscience 2 1019–1025. [DOI] [PubMed] [Google Scholar]
- Rijsdijk JP, Kroon JN, & Van der Wildt GJ (1980). Contrast sensitivity as a function of position on retina. Vision Research, 20, 235–241. [DOI] [PubMed] [Google Scholar]
- Rolls ET (2000). Functions of the primate temporal lobe cortical visual areas in invariant visual object and face recognition. Neuron 27 205–218. [DOI] [PubMed] [Google Scholar]
- Rossion B, Caldara R, Seghier M, Schuller A-M, Lazeyras F, & Mayer E (2003). A network of occipito-temporal face-sensitive areas besides the right middle fusiform gyrus is necessary for normal face processing. Brain 126 2381–2395. [DOI] [PubMed] [Google Scholar]
- Rossion B, Joyce CA, Cottrell GW, & Tarr MJ (2003). Early lateralization and orientation tuning for face, word, and object processing in the visual cortex. Neuroimage 20 1609–1624. [DOI] [PubMed] [Google Scholar]
- Rumelhart DE, Hinton GE, & Williams RJ (1986). Learning representations by back-propagating errors. Nature, 323, 533–536. [Google Scholar]
- Sanger T (1989). An optimality principle for unsupervised learning In Touretzky D (Ed.), Advances in neural information processing systems (Vol. 1, pp. 11–19). San Mateo, CA: Morgan Kaufmann. [Google Scholar]
- Schyns PG, & Oliva A (1999). Dr. Angry and Mr. Smile: When categorization flexibly modifies the perception of faces in rapid visual presentations. Cognition, 69, 243–265. [DOI] [PubMed] [Google Scholar]
- Schyns PG, Petro LC, & Smith ML (2007). Dynamics of visual information integration in the brain for categorizing facial expressions. Current Biology, 17, 1580–1585. [DOI] [PubMed] [Google Scholar]
- Sereno MI, Dale AM, Reppas JB, Kwong KK, Belliveau JW, Brady TJ, et al. (1995). Borders of multiple visual areas in humans revealed by functional magnetic resonance imaging. Science, 268, 889–893. [DOI] [PubMed] [Google Scholar]
- Sereno MI, McDonald CT, & Allman JM (1994). Analysis of retinotopic maps in extrastriate cortex. Cerebral Cortex, 4, 601–620. [DOI] [PubMed] [Google Scholar]
- Sergent J (1982). The cerebral balance of power: Confrontation or cooperation? Journal of Experimental Psychology: Human Perception and Performance, 8, 253–272. [DOI] [PubMed] [Google Scholar]
- Shillcock R, Ellison TM, & Monaghan P (2000). Eye-fixation behavior, lexical storage, and visual word recognition in a split processing model. Psychological Review, 107, 824–851. [DOI] [PubMed] [Google Scholar]
- Shillcock RC, & Monaghan P (2001). The computational exploration of visual word recognition in a split model. Neural Computation, 13, 1171–1198. [DOI] [PubMed] [Google Scholar]
- Smith ML, Gosselin F, & Schyns PG (2004). Receptive fields for flexible face categorizations. Psychological Science, 15, 753–761. [DOI] [PubMed] [Google Scholar]
- Tong MH, Joyce CA, & Cottrell GW (2008). Why is the fusiform face area recruited for novel categories of expertise?: A neurocomputational investigation. Brain Research, 1202, 14–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tootell RB, Switkes E, Silverman MS, & Hamilton SL (1988). Functional anatomy of macaque striate cortex: II. Retinotopic organization. Journal of Neuroscience 8 1531–1568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tootell RBH, Mendola JD, Hadjikhani NK, Ledden PJ, Liu AK, Reppas JB, et al. (1997). Functional analysis of V3A and related areas in human visual cortex. Journal of Neuroscience, 17, 7060–7078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tootell RBH, Mendola JD, Hadjikhani NK, Liu AK, & Dale AM (1998). The representation of the ipsilateral visual field in human cerebral cortex. Proceedings of the National Academy of Sciences, U.S.A, 95, 818–824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Essen DC, Newsome WT, & Bixby JL (1982). The pattern of interhemispheric connections and its relationship to extrastriate visual areas in the macaque monkey. Journal of Neuroscience 2 265–283. [DOI] [PMC free article] [PubMed] [Google Scholar]