Curvature and Torsion of Protein Main Chain as Local Order Parameters of Protein Unfolding

Abstract

Thermal protein unfolding resembles a global (two-state) phase transition. At the local scale, protein unfolding is, however, heterogeneous and probe dependent. Here, we consider local order parameters defined by the local curvature and torsion of the protein main chain. Because chemical shifts (CS) measured by NMR spectroscopy is extremely sensitive to the local atomic environment, CS has served as a local probe of thermal unfolding of proteins by varying the position of the atomic isotope along the amino-acid sequence. The variation of the CS of each C^α atom along the sequence as a function of the temperature defines a local heat-induced denaturation curve. We demonstrate that these local heat-induced denaturation curves mirror the local protein nativeness defined by the free-energy landscape of the local curvature and torsion of the protein main chain described by the C^α-C^α virtual bonds. Comparison between molecular dynamics simulations and CS data of the gpW protein demonstrates that some local native states defined by the local curvature and torsion of the main chain, mainly located in secondary structures, are coupled to each other whereas others, mainly located in flexible protein segments, are not. Consequently, CS of some residues are faithful reporters of global protein unfolding, with heat-induced denaturation curves similar to the average global one, whereas other residues remain silent about the protein unfolded state. For these latter, the local deformation of the protein main chain, characterized by its local curvature and torsion, is not cooperatively coupled to global unfolding.

Graphical Abstract

Introduction

By analogy with the solid/liquid first-order phase transition, protein folding/unfolding is often described by a global order parameter, as for example the fraction of native-like contacts or the root-mean-square-deviation between the unfolded structure relative to the folded one. The protein heat-induced denaturation curve, i.e. the variation of the global order parameter as a function of the temperature, represents a global measure of the unfolding transition. For most of the proteins, this global heat-induced denaturation curve can be formally described by a simple two-state (folded/unfolded) statistical model. Agreement with a two-state model does not imply, however, that the macromolecule does not unfold through a number of intermediate states. Intermediates states are expected as macromolecules are nanosized. Hence, the global denaturation curve hides the heterogeneity of protein unfolding. There is, therefore, a considerable interest to investigate protein unfolding at a local state, by defining a local order parameter measuring the local protein folded state or the local protein nativeness. Measure of the local nativeness as a function of the temperature defines a local heat-induced denaturation curve which is the purpose of the present study.

Local nativeness is not uniquely defined and is probe dependent ¹. From a theoretical point of view, the concept of protein local nativeness backs to the early statistical models of the helix-coil transition where each residue occurs in only two local states ². In a previous work, we defined the local nativeness of a protein from the free-energy landscape of coarse-grained angles (CGA) built on the sole Cartesian coordinates of the C^α atoms ³. These local nativeness-based CGA were successfully included in an Ising type-model to describe unfolding of the model gpW protein ³. The CGA fully characterized the protein fold ⁴. Assuming a constant virtual bond length between C^α atoms of successive residues, a chain of N amino-acids is fully characterized by N-3 CGA: the torsion angles γ_n, built from the positions of $C_{n-1}^{\alpha },C_n^{\alpha },C_{n+1}^{\alpha }$ and $C_{n+2}^{\alpha }$; and the bond angles θ_n, built from $C_{n-1}^{\alpha },C_n^{\alpha },C_{n+1}^{\alpha }$, with n=2 to N-2. These CGA were used successfully to describe large conformational changes and are part of coarse-grained models of proteins. The CGA have clear geometrical meanings: they are respectively the discrete version of the local curvature (θ_n) and the local torsion (γ_n) of the chain formed by the successive C^α-C^α virtual bonds ⁵. From a mathematical point of view, the local curvature and torsion fully describe the structure of a string. The CGA have also an advantage over more popular Ramachandran angles. Indeed, the C^α coordinates represent a complete representation of the protein main chain: the structure of the main chain can be rebuilt correctly from the CGA internal coordinates and the average C^α-C^α bond distance ⁶. On the contrary, the main chain structure rebuilt from the Ramachandran angles (ϕ, ψ) and the average bond distances of the protein backbone deviates significantly from the experimental structure ⁶. Hence, statistical properties of the proteins deposited in the PDB, as the variation of the gyration radius of the proteins as a function of the polymer length, are not reproduced if the structures are rebuilt from the (ϕ, ψ) coordinates. On the opposite, the power-law dependence of the gyration radius of the ensemble of proteins deposited in the PDB as a function of the chain length is accurately reproduced if the structures are rebuilt from the sole (θ,γ) coordinates ⁶. In conclusion, the (ϕ, ψ) angles do not form a complete set of local order parameters whereas (θ,γ) do.

In the present work, we demonstrate that the local nativeness built on CGA can be measured experimentally by measuring the variation of the NMR chemical shift (CS) of C^α atoms as function of temperature. NMR CS are extensively used to probe atom-scale structures of proteins in solution in their native state and under the influence of an external perturbation (temperature, pH, pressure, ligand) ^7–13. For example, CS of ¹H, ¹⁵N and ¹³C atomic probes have provided valuable and very detailed information on the thermal folding/unfolding of proteins in recent years ¹²,¹⁴. While it is certain that the CS variation of atom as a function of an external parameter renders modifications of the chemical neighborhood of a nuclei, the precise nature and the spatial scope of these modifications are not trivial. Deciphering the relation between local information recorded along the amino-acid sequence of a protein, such as the CS, and the global conformation of a protein in protein folding/unfolding ^12,14 is challenging. The CS are scalar functions of multiple structural variables, so a heat-induced variation of the CS may be associated with local and global motions of different kinds. Moreover, global unfolding of a protein may have no effect on the CS in a particular region of the polymer chain.

The fundamental questions we addressed here are: (i) how the local heat-induced denaturation curves measured by the variation of the CS as function of the temperature can provide an information on the global unfolding of a protein; (ii) how the CS local heat-induced denaturation curves may be related to the local curvature and torsion of the protein main chain defined by the CGA? In short, can we define the local nativeness built on the CGA experimentally? To answer these questions, we defined the local native state of a residue within the molecule and quantified the relation between the protein local nativeness of each residue and the CS of its ¹³C^α atom as well as the cooperativity of the local native states in folding/unfolding, using all-atom molecular dynamics (MD) simulations of the fast downhill folder gpW ¹⁵, ¹⁶. Previous studies have shown that all-atom MD simulations with current force fields can reproduce the folding of medium size proteins, and are valuable tools to examine the relation between local structural fluctuations and global unfolding ¹⁷.

The choice of the downhill folder gpW is motivated by the recent measures of CS of 180 atomic probes of gpW as functions of temperature ¹⁴. The CSs exhibit jumps near the melting temperature, leading the authors to interpret the CS curves as local heat-induced denaturation curves ¹⁴. For gpW, both the qualitative behavior of the CS and the weak cooperativity of its folding/unfolding transition ¹⁸ are reproduced by all-atom MD ¹⁴. Therefore, we examined the relation between local structural fluctuations and global unfolding by simulating the thermal unfolding of gpW ¹⁵,¹⁶ between 280 K and 380 K using all-atom MD, and predicted the CS of each ¹³C^α atom along the amino-acid sequence as a function of temperature using the SHIFTX2 software ¹⁹ (see Material and Methods). Comparison between CS denaturation curves and the local nativeness defined from the CGA permit us to (i) demonstrate that the CGA nativeness, which reflects the local curvature and torsion of the main chain, may be quantified experimentally; and (ii) to identify why some CS are silent on global unfolding of a protein and others are faithful reporters of global conformational changes.

Material and methods

The protein gpW is a 62 amino-acid polypeptide featuring a folded structure consisting of two α-helices (residues 4–19, 40–54) on top of a β hairpin (residues 23–28 and 31–36) (PDB ID:2L6Q) ^15,16. In a previous work ³, we performed all-atom MD simulations of gpW in explicit solvent [TIP3P water model ²⁰] at a pressure of 1 bar and at 18 different temperatures between 300 K and 500 K using the GROMACS ²¹ and the amber99sb-ildn force field ²². The atom coordinates were saved every ps from each MD trajectory and for each snapshot, the CS of all ¹³C^α of gpW were computed from these coordinates using SHIFTX2 predictor ¹⁹. The correlation coefficient between the chemical shifts of ¹³C^α predicted by SHIFTX2 and the chemical shifts experimentally measured attains 0.9959 with RMS errors of 1.1159 ppm at standard pH and temperature. The program is expected to be less accurate at higher temperatures (in the unfolding state). As chemical shift is extremely sensitive to small coordinate displacements, another source of error is the inaccuracy of the current force-fields used in MD simulations, which limits the quantitative agreement between simulated chemical shifts based on MD trajectories and the experimentally observed ones.

The temperatures in the present main text are actually rescaled temperatures compared to the temperature parameters used in the MD simulations. In GROMACS parameters, the temperature used T_GRO covers the range [300 K, 500 K]. It is known that the temperatures in the MD force fields simulations are not the actual temperatures. As in Ref. ¹⁴, we used NMR experimental data as a standard to define a more accurate temperature range to compare to experiments. The temperature range was transformed so that the <δ_i>(T) curves become similar to the experimental curves. The observed global unfolding temperature, measured in the NMR study of gpW and to which we compare our simulations, is 330K¹⁴. Comparisons between experimental and simulated signals for the CS of C^α atoms are shown and discussed in Results and Discussion section and Supporting Information. We retain the following temperature transformation: T = 0.5×T_GRO + 130. Proceeding this way, the actual temperature range discussed in the main text and corresponding to our simulations is [280K-380K] and the unfolding temperature is similar to the one observed in Ref. 14.

The range of variation of the measured CS were reduced to the range [0,1] by an isometric transformation and then averaged over the sequence to produce a global parameter.

Results and Discussion

CGA free-energy landscapes

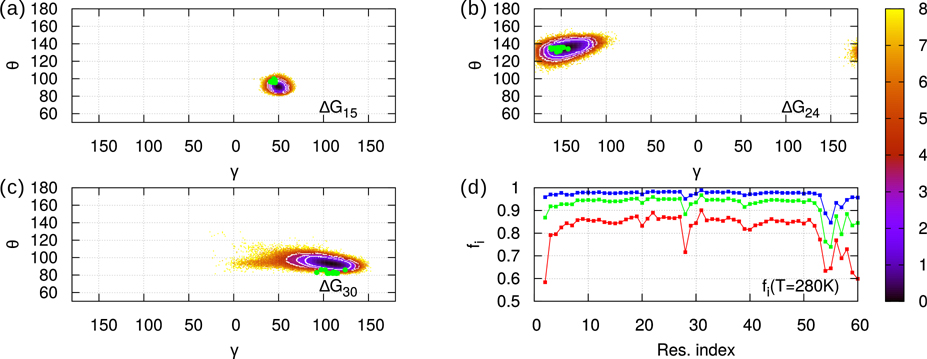
At each temperature, gpW explores a great variety of conformations whose statistical weights are represented by the free-energy landscapes (FEL): ΔG(γ_i,θ_i) = −RT ln[P(γ_i,θ_i)], where P(γ_i,θ_i) is the two-dimensional probability density of the CGAs computed from the MD trajectories ³, and T and R are the absolute temperature and the gas constant, respectively. Typical FELs are represented in Fig. 1 for i=15, 24 and 30 (panels a, b and c) at T=280K. As explained in the Material and Methods section, all temperatures of the MD simulations reported here are rescaled temperatures (T=280K corresponds to T_GRO=300K in the GROMACS software). The most probable values of the CGA angles appear as dark wells in Fig. 1. While at T=280K the exploration of (γ_i,θ_i) angles does not extend much (see Fig. S1–S3 for all FELs at 280K), at T>330K (unfolding temperature) the FELs cover most of the range available to (γ_i,θ_i), featuring several wells (see Fig. S4–S6 for all FELs at 355K). Secondary structures at 280K (native state) correspond to well-defined area in the (γ_i,θ_i) FELs (Figs. S1–S3). The α-helix area is narrow and centred around (γ=50°, θ=90°). For β−sheets, the CGAs comprise the area −180°< γ <−120°, 100°< θ <150° and appear alternatively along the sequence centered at γ =−180° and at γ =−120°, reflecting the alternative geometry of the backbone in β strands. The values of (γ_i,θ_i) angles computed from the experimental structure (PDB ID: 2L6Q) ¹⁶ are marked as green dots on the 280K landscapes in Fig. 1 (panels a, b and c) and in Figs. S1–S3. Correspondence between experimental points and most stable values in MD (black areas) is qualitatively verified.

Figure 1:

Panels a-c: Free-energy landscapes ΔG(γ_i,θ_i) = -RT ln(P(γ_i,θ_i)/P_max) for i=15 (a), i=24 (b), i=30 (c). Probability distribution function P(γ_i,θ_i) is sampled from 750 ns MD trajectories at T=280K. The native areas corresponding to the three values of the cut-off H (see text) are the concentric white circles (inner for 2RT, outer for 4RT). Green dots mark the twenty experimental values of the angles extracted from the 2L6Q PDB. Panel d: f_i (T=280K) curves for three different values of the cut-off H: H=2RT (red), 3RT (green), 4RT (blue). Values of f_i range from i=2,…,60.

Local and global nativeness from CGA

Since (γ_i,θ_i) angles describe the conformation of the main chain formed by the residues i-1 to i+2, we want to characterize the native state of gpW at local scale using these angles. We define a local two-state model as follows. The local native state of the main chain in the neighbourhood of the ith residue is defined as an ensemble of (γ_i,θ_i) values, micro-states, representing the predominant conformation at T=280K. We sort the angles by increasing ΔG(γ_i,θ_i). Low-values of ΔG(γ_i,θ_i) correspond to the local native state; high-values belong to the local unfolded state for the pair of CGAs (γ_i,θ_i). The separation between native and unfolded micro-states is defined by a ΔG cut-off whose value H determines the area (white circles in Fig. 1 a, b and c) that contains (γ_i,θ_i) values of the native state. In other words, the ensemble of values of (γ_i,θ_i) for which ΔG(γ_i,θ_i) < ΔG_min(γ_i,θ_i) + H defines the local native state of ith residue. The value of H determines the local nativeness of the protein defined as the fraction f_i of native state for (γ_i,θ_i): $f_i\equiv {\sum }_{\mathrm{\Delta }G({\gamma }_i,{\theta }_i)<H}P({\gamma }_i,{\theta }_i)$. The local nativeness f_i is represented as a function of the amino-acid sequence in Fig. 1 d for different values of H at 280 K. At 280K selecting H=2RT gives f_i>80%, H=3RT f_i>90%, and H=4RT f_i>95% (Fig. 1 d). All these values of H, give the same qualitative variation of f_i along the sequence (Fig. 1 d). In the following, we choose H=4RT (Fig. 1 d) as a good compromise between a high value of f_i and a small native area in the FEL at 280 K.

The lowest values of f_i are found outside helices and sheets, near loops or terminal parts of gpW. They are flexible parts of the main chain for which the (γ_i,θ_i) angles have a large set of values and for which the local native state has a large entropic contribution. The local nativeness f_i is expected to converge to a non-zero finite value at high temperature (Fig. S7). Indeed, at temperatures much larger than the unfolding temperature, the probability to be locally in a non-native state converges to the ratio between the number of micro-states in the unfolded area of the local FEL (θ,γ) to the number of micro-states in the restricted area (ΔG < H) of the native state (Fig. S7).

The global nativeness of the protein ⟨f_i⟩ is calculated at each temperature by averaging the local nativeness f_i over all pair of CGAs. The variation ⟨f_i⟩ as a function of the temperature compares very well with the variation of the global nativeness computed from the average variation of the CS measured as a function of the temperature ³. Application of a two-state model to the global unfolding denaturation curve ⟨f_i⟩(T) is meaningless as intermediate states are significantly populated in the thermal unfolding of gpW between the fully native and fully unfolded states as expected for a downhill folder and shown in Ref. ³.

Average CS associated with local native and unfolded states

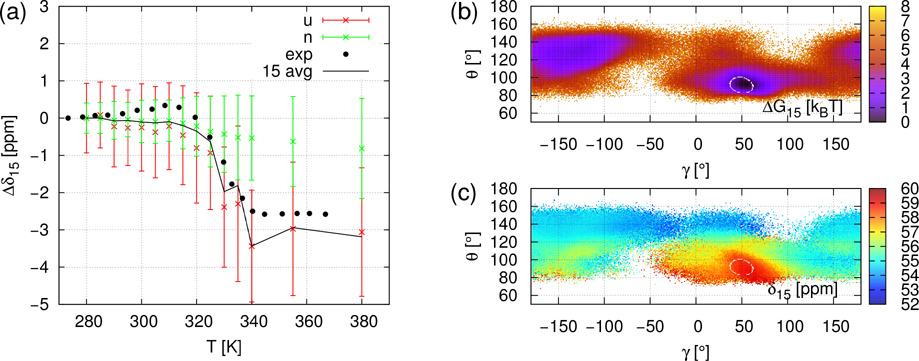
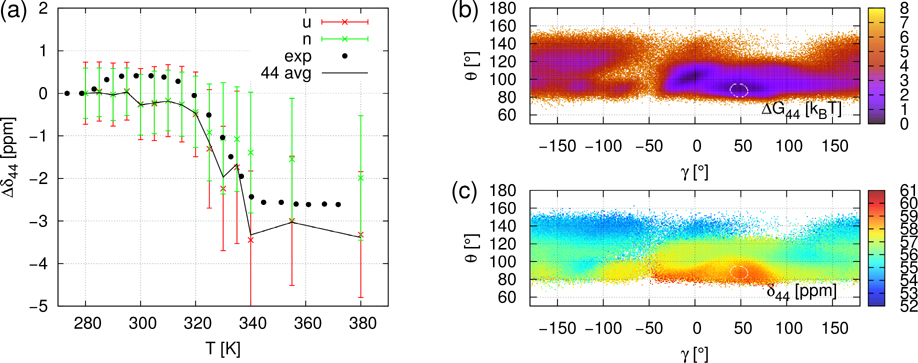
CS of all ¹³C^α of gpW were computed using SHIFTX2 predictor ¹⁹ from the C^α atom coordinates extracted from the MD trajectories at each ps. The chemical shift of the i-th C^α is denoted by δ_i. The δ_i(t,T) refer to the timeseries of chemical shift for the simulation at temperature T. In order to remove the offset induced by ShiftX2 and to compare with experimental data, we express the computed and measured chemical shifts as the difference between the average CS at the temperature T and at 280 K; i.e., ⟨Δδ_i⟩(T) = ⟨δ_i(T)⟩ − ⟨δ_i(280K)⟩. It is worth noting that the simulated values ⟨Δδ_i⟩(T) are the time average of δ_i(t,T) over 750 ns (duration of MD trajectories) while the measured values ⟨Δδ_i⟩(T) ¹⁴ reflect an average over a much larger ensemble of protein conformations and on a much larger time-scale than in the MD simulations. Typical ⟨Δδ_i⟩(T) curves are illustrated in panel a of Figs 2, 3 and 4 for i=21 (β-strand 1), for i=15 (α-helix 1), and i=44 (α-helix 2), respectively. All ⟨Δδ_i⟩(T) curves for i=2 to 60, similar to the panels a of Figs. 2–4, are represented in Figures S8–S10. No fit of the simulated data on the experimental ones was attempted, except for a rescaling of the MD temperature on the experimental one (see Material and Methods). Panels b and c of Figs 2, 3 and 4 represent respectively the local free-energy landscape and chemical shifts landscape for the residues i=21, i=15 and i=44 and are discussed in section “Local unfolding through chemical shift landscapes δ_i(γ_i,θ_i)”.

Figure 2:

Panel a: NMR CS of C^α₂₁: ⟨Δδ₂₁⟩(T) = ⟨δ₂₁⟩(T) − ⟨δ₂₁⟩(280K). Black dots are the experimental values and black lines are the average values of ⟨Δδ₂₁⟩ computed from MD+ShiftX2. Green and red crosses are average values of ⟨Δδ₂₁⟩ computed from MD+ShiftX2 for the snapshots belonging to the native ensemble N and unfolded ensemble U, respectively (see text). The errorbars are ⟨Δδ₂₁⟩ ± σ(⟨Δδ₂₁⟩) signals where σ are the computed standard deviations. Panel b: Free-energy landscape ΔG(γ₂₁,θ₂₁) at T=355K, the color bar unit is RT. Panel c: Map of ⟨δ₂₁⟩ of C^α₂₁ as a function of the CGA γ₂₁ and θ₂₁ at T=355K. The color bar unit is ppm. The value of ⟨δ₂₁⟩ is computed from MD+SHIFTX2 by averaging the CS over the snapshots with the same values of γ₂₁ and θ₂₁.

Figure 3:

Same as Figure 2 (Panels a-c) for NMR CS of C^α₁₅: ⟨Δδ₁₅⟩(T) = ⟨δ₁₅⟩(T) − ⟨δ₁₅⟩(280K).

Figure 4:

Same as Figure 2 (Panels a-c) for NMR CS of C^α₄₄: ⟨Δδ₄₄⟩(T) = ⟨δ₄₄⟩(T) − ⟨δ₄₄⟩(280K).

Noticeable disagreements between simulations and experimental data are observed for a few residues which are outside of the secondary structures or at their C-terminus (see Figs. S8–S10), namely at i=18–21 (C-terminus of the α-helix), i=27, 28 (C-terminus of the β-strand), i=30 (turn), and i=55–60 (disordered C-terminus). In the secondary structures, only for i=46 is there a significant disagreement between simulated and experimental data (Fig. S10). For all residues for which the disagreement is large, the simulated ⟨Δδ_i⟩(T) are constant while the experimental signals increase gradually or by multiple small steps as shown for the typical example of i=21 in Fig. 2. The reason for the deviation between theory and experiment for these residues might be either the very short duration of the MD simulations (750 ns) to capture these flexible local conformational states or a failure of SHIFTX2 to predict the CS in such flexible regions. However, for most of the residues, ⟨Δδ_i⟩(T) jumps occurring around the transition temperature (T~330K) are rather well reproduced by ⟨Δδ_i⟩(T) extracted from the present simulations (MD+SHIFTX2) (Figs. S8–S10). This is illustrated for example for i=15 (α-helix 1), and i=44 (α-helix 2) in Figs 3 and 4, respectively.

Is the jump in the simulated curve ⟨Δδ_i⟩(T) characteristic of the local unfolding measured by the local nativeness f_i? To answer this question, we defined the binary time series s_i(t) = {1 IF (γ_i,θ_i)(t) is native | 0 ELSE} for all MD trajectories and for each pair of CGA, i=2,…,60. The snapshots with s_i = 1 define the ensemble N of local native structures and those with s_i = 0 the complementary ensemble U of the local unfolded structures, in the vicinity of residue i; i.e., for the ith CGA. The time average of the CS ⟨Δδ_i⟩(T) and its variance σ(⟨Δδ_i(T)⟩) were computed separately for the ensembles of MD snapshots N and U. The variance reflects the exploration of the ensemble of the micro-states of the N and U ensembles as a function of time. In Figs. 2–4 and S8–S10, in addition to the values ⟨Δδ_i⟩(T) computed and measured ¹⁴, we also considered the simulated ⟨Δδ_i,N⟩(T) and ⟨Δδ_i,U⟩(T). The ensembles N and U cannot be separated in experiments as the measured CS are averages of the CS of local unfolded U and native N micro-states at a given temperature.

In a perfect local two-state model, ⟨Δδ_i,N⟩(T) should be rigorously constant which is not exactly the case (Fig. S8–S10) as shown for typical examples in Figs. 2–4 (i=21, 15 and 44). The variation of ⟨Δδ_i,N⟩(T) reflects the fact that the CS does not only depend on (γ_i,θ_i) but also on other hidden degrees of freedom (side-chain conformations and other CGA (γ_j,θ_j)_j≠i). However, the amplitude of the native CS interval ⟨Δδ_i,N⟩(T) ± σ(⟨Δδ_i,N⟩) remains less than 1 ppm between 280 and 380 K. This states the limit of resolution of the N state in the present local two-state model.

Even in a perfect local two-state model, we do not expect ⟨Δδ_i,U⟩(T) to be constant, except for residues which do not have a well-defined native state; i.e., residues in disordered regions of the main chain, where all micro-states (γ_i,θ_i) are explored even at low temperature (280 K). For residues in secondary structures, the number of micro-states involved in the average of the unfolded local state increases with the temperature and so as ⟨Δδ_i,U⟩(T). Below the transition temperature, unfolded micro-states represent the outskirt of the local native state defined by the cut-off value of H and, hence, ⟨Δδ_i,U⟩(T) is not really statistically relevant. Above the unfolding transition T>330K, the protein explores a large enough number of unfolded micro-states and ⟨Δδ_i,U⟩(T) is rather constant. However, the separation between the N and U ensembles is successful for most C^α for which the overlap of the intervals of the N and U ensembles is limited. This is achieved when ⟨Δδ_i,N⟩ is at the edge or out of the ⟨Δδ_i,U⟩ ± σ(⟨Δδ_i,U⟩) interval.

Assuming that the separation between the N and U ensembles is correct and that ⟨Δδ_i,N⟩ and ⟨Δδ_i,U⟩ do not vary with temperature, we have ⟨Δδ_i⟩(T) = f_i(T) ⟨Δδ_i,N⟩ + (1−f_i(T)) ⟨Δδ_i,U⟩. We consider that the averages are constant as soon as the amplitude of their variations is less than 1 ppm. Then the jump of ⟨Δδ_i⟩(T) observed at the folding temperature (≅ 330 K) (Fig. 4) is due to the change of the relative populations of N and U ensembles which reflects the local unfolding transition.

The exhaustive interpretation of the plots should treat each value of i separately. In summary, three cases emerge in the analysis of ⟨Δδ_i,U⟩(T) and ⟨Δδ_i,N⟩(T) curves.

A / Fig. 2a. ⟨Δδ_i,N⟩ and ⟨Δδ_i,U⟩ are constant over the entire range of temperature but they are not separated: ⟨Δδ_i,N⟩ ∈ [⟨Δδ_i,U⟩ ± σ(⟨Δδ_i,U⟩)]. No jump of ⟨Δδ_i⟩(T) is observed. ¹³C^α NMR remains mute though the local unfolding has happened. Experimental signals with a jump inferior to 1 ppm enter this case. In panel b, we can see that a large part of the free energy landscape of (γ₂₁,θ₂₁) is of similar stability. The most probable value (black) is distributed among a very large area, indicating that there is no actual stable unique conformation.

B / Fig. 3a. ⟨Δδ_i,N⟩ is constant over the entire range of temperature. In addition, ⟨Δδ_i,U⟩ is constant above the unfolding transition temperature (below the unfolding temperature δ_i,U is not statistically relevant as discussed above) and the separation between ⟨Δδ_i,N⟩ and ⟨Δδ_i,U⟩ is large enough as their variances overlap by less than 1 ppm. In this case, the ⟨Δδ_i⟩(T) jump fully renders the (γ_i,θ_i) transition. As shown in Fig. 3b, when gpW is globally unfolded, the statistical exploration of (γ₁₅,θ₁₅) features several potential wells and fast scanning of unstable values. The stability of the native area (α-helix, γ=50°, θ=90°) is still noticeable. The β-sheet area (−180°< γ <−120°, 100°< θ <150°) is also significantly explored.

C / Fig. 4a. ⟨Δδ_i,N⟩ and ⟨Δδ_i,U⟩ are separated but ⟨Δδ_i,N⟩ is not constant. The variation of ⟨Δδ_i,N⟩ is due to another structural change different from the local unfolding transition of (γ_i,θ_i). As a consequence, the jump of δ_i is not only due to the local unfolding but also because of other factors. This case essentially occurs for residues located in helices. In the last section, we will study the dependence of ⟨Δδ_44,N⟩ on (γ_j,θ_j), j≠44 to see if the neighbouring residues influence ⟨Δδ_44,N⟩(T). In panel b, at T=355K, the free-energy landscape ΔG(γ₄₄,θ₄₄) features the quite persistent stability of the native α-helix region. Another region with a potential well is located at (γ=0°, θ=100°). The rest of the landscape, representing much of the partition function, has uniform low stability, picturing the fast scan of unstable values.

Local unfolding through chemical shift landscapes δ_i(γ_i,θ_i)

Ensemble averaging is now performed on structures of similar (γ_i,θ_i) values extracted from the (γ_i,θ_i)(t) timeseries recorded from the MD trajectories for i=2,…,60. We focus on the 355K MD trajectory as at this temperature the protein explores the full (γ_i,θ_i) landscape (see panel b of Figs. 2–4). For i=2,…,60, 1°×1° bins are defined in the (γ_i,θ_i) interval [−180°,180°]×[60°,180°]. Inside all bins, we computed the time average ⟨δ_i⟩ (γ_i,θ_i) by selecting only the frames where the value of (γ_i,θ_i) was accepted in the bin. We plotted these values as a coloured surface. Results are shown for i=21, 15 and 44 in panel c of Figs. 2–4. CS landscapes for i=2,…,60 at T=355K are displayed in Figs. S11–S13.

The repartition of values shows that the variation of ⟨δ_i⟩(γ_i,θ_i) always has an amplitude of 1 ppm at least. It confirms that ⟨δ_i⟩ (γ_i,θ_i) is sensible to the CGA (γ_i,θ_i), and that molecular MD analyzed with ShiftX2 renders this sensibility. Varying i=2,…,60, the ⟨δ_i⟩(γ_i,θ_i) distribution is quite similar, except for a global δ-offset. The highest values of chemical shift are typically found around the α-helix region (γ=50°, θ=90°). On the contrary ⟨δ_i⟩(γ_i,θ_i) is the lowest when θ_i ≥ 120°, and it takes variable intermediate values for θ_i ≤ 120° and outside of the helical zone. Therefore, the smallest values were observed for β-sheets.

The ⟨δ_i⟩ (γ_i,θ_i) landscapes enable us to interpret the values of ⟨δ_i,N⟩ and ⟨δ_i,U⟩ at T=355K. Indeed ⟨δ_i,N⟩ and ⟨δ_i,U⟩ are the average of ⟨δ_i⟩ (γ_i,θ_i) values over respectively native and unfolded regions. Figures 2–4 allow us to make a link between ⟨δ_i⟩ (γ_i,θ_i) landscapes on one side (panel c, where the native region is drawn as a white circle), and the separation of ⟨δ_i,N⟩(355K) and ⟨δ_i,U⟩ (355K) on the other side (panel a).

For i=15 (Fig. 3c) and 44 (Fig. 4c) the native region is the small α-helix area. Values of ⟨δ_i,N⟩ (355K) are respectively 59 and 60 ppm. For i=15 (Fig. 3c), highest values go to the α-helix area ⟨δ₁₅⟩~59 ppm and ⟨δ₁₅⟩ globally decreases as θ increases. The lowest values ⟨δ₁₅⟩~53ppm correspond to non-structured conformations. The angles of the β-sheet area (−180°< γ <−120°, 100°< θ <150°) encompass two-component intermediate values (55 and 56 ppm). Therefore, the native NMR signal is clearly demarcated from non-native ⟨δ₁₅⟩(γ₁₅,θ₁₅) values. For i=44 (Fig. 4c), ⟨δ₄₄⟩ is globally decreasing as θ increases. The highest value corresponds to the native α-helix area ⟨δ₄₄⟩~59 ppm. The lowest values, δ₄₄~54 ppm, appear when θ >130°. The rest of the non-native areas have intermediate δ values. So the ⟨δ₄₄⟩ (γ₄₄,θ₄₄) landscape at T=355K shows that native and non-native states can be distinguished by chemical shift. In conclusion, the native states are near the maxima in both landscapes (i=15 and 44), so averaging over the unfolded domain necessarily results in much lower values of ⟨δ_i,U⟩, well separated from ⟨δ_i,N⟩.

On the contrary, for i=21 (Fig. 2c), the native region (similar to β-sheet) is large and encompasses both high and low values of ⟨δ₂₁⟩ (γ₂₁,θ₂₁), resulting in ⟨δ_21N⟩~56 ppm. Values of δ₂₁ span over only 2 ppm overall (from 55 to 57 ppm). From this small range, the native area of (γ₂₁,θ₂₁) includes two steps of δ values, at 55 and 56 ppm. The highest value is only found in the α-helix region, whose statistical weight is low. Averaging over the non-native region does not produce a much different value of ⟨δ_21,U⟩ compared to ⟨δ_21,N⟩. Only the well-explored α-helix region slightly pulls ⟨δ_21,U⟩ up. But all in all, the location of the native region in the CS landscape explains why the difference does not exceed 0.5 ppm, as shown in Fig 2a.

We generalize this analysis shown for three typical cases in Figs. 2–4 to all i=2,…,60 (see Figs. S11–S13). If the chemical shift landscape ⟨δ_i⟩(γ_i,θ_i) has the extrema in the native region, then ⟨δ_i,U⟩ and ⟨δ_i,N⟩ are separated. This is a necessary condition in order to render (γ_i,θ_i) unfolding in ¹³C^α NMR as shown by the comparison between Figs. S8–S10 and Figs. S11–S13.

Neighboring (γ_j,θ_j) free energy landscapes associated with extreme values of δ_i(γ_i,θ_i)

In the analysis of ⟨Δδ_i,U⟩(T) and ⟨Δδ_i,N⟩(T) curves, we highlighted the case where ⟨Δδ_i,N⟩(T) varies significantly during unfolding. This evolution is mainly encountered in helices and indicates the action of structural parameters other than (γ_i,θ_i).

We took i=44, as an example of the evolution of ⟨Δδ_i,N⟩(T) as a function of the temperature. The decrease of ⟨Δδ_44,N⟩(T) above the unfolding temperature is accompanied by an increase of σ[⟨Δδ_44,N⟩] such as at high temperature, the value of ⟨Δδ₄₄⟩(280K) is still reached in the ⟨Δδ_44,N⟩±σ(⟨Δδ_44,N⟩) interval. To understand this behavior of the CS, we selected snapshots contributing to a given range of δ_i and studied the structural properties of this ensemble. The δ_i criterion was |Δδ₄₄|<0.5 ppm, which corresponds to values near δ_44,N(280K). We chose to study the 355K trajectory for the same reason as before. All snapshots, which have Δδ₄₄ meeting the criterion |Δδ₄₄|<0.5 ppm, form an ensemble that we call the restricted trajectory. The number of snapshots in this ensemble is between 60000 and 70000 depending on the initial conditions of the MD trajectories.

The CGA (γ₄₄,θ₄₄) belongs to the α₂-helix, which encompasses the CGA (γ₄₀,θ₄₀) to (γ₅₁,θ₅₁). The free-energy landscapes ΔG(γ_j,θ_j) were computed from both all the snapshots of the MD trajectory and from the snapshots of the restricted MD trajectory. They are shown for j=44 to 47 in Fig. 5 and for the other CGAs of the α₂-helix in Figs. S14 and S15.

Figure 5:

Free-energy landscapes of neighbor residues of i=44. The color bar unit is RT. Top landscapes were computed on the full 355K trajectory. Bottom landscapes were computed by selecting only frames where |Δδ₄₄|<0.5 ppm. For all values of j, the free-energy landscape of the restricted trajectory occupies less extensive area of (γ_j,θ_j) compared to the full trajectory landscape, and tends towards majority occupation of the native (γ_j,θ_j) area. The effect is less pronounced on j=47. This behavior of neighboring residues indicates the influence of non-local (γ_j,θ_j) angles on δ_i evolution.

Results show that the free-energy landscapes displayed on Fig. 5 are different when the values of δ₄₄ are restricted. In the free-energy landscape of j=44 for the restricted trajectory, as expected, only the native region is explored. For j=45 and 46, landscapes of the restricted ensemble mostly feature the native area and remnants of the wide γ<0° area. On the restricted landscape of j=47, only a small area at γ=100° is missing and the γ<0° area is quite well explored.

Small differences between the restricted and unrestricted trajectories can also be spotted in the j=42 landscape (see Fig. S14). Overall, the free-energy landscapes for the restricted ensemble show that Δδ₄₄ is likely to be close to 0 when the neighboring residues tend to be in native conformation, in addition to j=44 itself.

As a conclusion, the jump observed in case C (δ₄₄ and others) is not only caused by the unfolding of local backbone angles but also reflects the denaturation of more distant residues. It is noteworthy that this case essentially happens in α-helix regions, unfolding of which is strongly cooperative. Therefore, ¹³C^α NMR is a probe for the unfolding of groups of cooperative residues of gpW in α-helix.

Conclusions

Starting from MD simulations, we defined local native and non-native states regarding (γ_i,θ_i) angles exploration. A (γ_i,θ_i) local conformation has to meet the following condition to be considered as a native state: ΔG(γ_i,θ_i)<4RT. The corresponding (γ_i,θ_i) areas match experimental values of angles in the native state and represent more than 95 % of the conformations explored by the protein in the 280K MD trajectory.

The ShiftX2 calculations performed on the simulated trajectories produced ¹³C^α CS that vary realistically with temperature when compared to experimental points. For each position i in the amino-acid sequence (i=2 to N-2), we used local nativeness definition and MD data to average the CS of residue i independently over local native (N) and non-native (U) states. The results showed to what extent the CS variation as function of the temperature reflects the local unfolding of (γ_i,θ_i). We established two conditions for this interpretation to be possible: (i) δ_i,N must be approximately constant with temperature, (ii) δ_i,N and δ_i,U must be separated by more than 1 ppm. Neglecting variations less than 1 ppm, a part of gpW residues met the above conditions. The corresponding δ_i(T) curves can be read as (γ_i,θ_i) local heat-induced denaturation curves. Because the CGA represent the discrete version of the local curvature and torsion of a curve, the local nativeness of the protein measured by the δ_i mirrors these local order parameters.

For certain residues δ_i,N and δ_i,U were mixed up, resulting in non-jumping signals. The CS landscapes δ_i(γ_i,θ_i) were built at 355K to understand the separation of δ_i,N and δ_i,U. Non-jumping signals are caused by the fact that δ_i(γ_i,θ_i) takes non extremal values in the native state. Taking extrema values of δ_i in native conformation is a necessary condition for the (γ_i,θ_i) unfolding to be reflected in NMR.

For other residues, δ_i,N(T) is jumping with a significant amplitude during unfolding, implying that a structural change different of (γ_i,θ_i) was reflected by δ_i. We demonstrated the non-local influence of neighbouring (γ_j,θ_j), j≠i, for the special case of i=44. The same analysis could be conducted for other values of i showing non-constant δ_i,N(T).

The last two phenomena, which we described as deviations from an ideal case, are particular combinations of influences. A δ_i,N(T) is actually never strictly constant. But given our limited statistics we were forced to neglect variations under a certain threshold. When there is no jump, non-local unfolding events oppose the influence of (γ_i,θ_i) unfolding on δ_i. This tells us that very local backbone angles (γ_i,θ_i) outclass neither the neighbouring ones nor maybe other close structural angles. On the contrary, the non-local structural changes may enhance the effect of (γ_i,θ_i) unfolding on δ_i, as we demonstrated for i=44. In turn, this enhancement involves simultaneous structural similarity of the neighbouring residues, which means that the unfolding is strongly cooperative near the i-th residue. High amplitude jumps in α-helices correspond to the concerted unfolding of several residues of the helix.

In summary, we demonstrated that local heat-induced denaturation curves, built from the local curvature and torsion of the protein main chain, are comparable to the heat-induced denaturation curve of the ¹³C^α chemical shift for most of the residues, for which the chemical shifts of non-local native states and local native states are not overlapping in the high temperature limit. In other cases, the ¹³C^α chemical shift is blind and no information about the local unfolding can be inferred from its measurement. MD simulations allowed to separate the local native and non-native states and to explain the qualitative behavior of local heat-induced denaturation curves and its possible departure from the global heat-induced denaturation curve which is dominated by cooperative local unfolding.