Abstract
Thermal protein unfolding resembles a global (two-state) phase transition. At the local scale, protein unfolding is, however, heterogeneous and probe dependent. Here, we consider local order parameters defined by the local curvature and torsion of the protein main chain. Because chemical shifts (CS) measured by NMR spectroscopy is extremely sensitive to the local atomic environment, CS has served as a local probe of thermal unfolding of proteins by varying the position of the atomic isotope along the amino-acid sequence. The variation of the CS of each Cα atom along the sequence as a function of the temperature defines a local heat-induced denaturation curve. We demonstrate that these local heat-induced denaturation curves mirror the local protein nativeness defined by the free-energy landscape of the local curvature and torsion of the protein main chain described by the Cα-Cα virtual bonds. Comparison between molecular dynamics simulations and CS data of the gpW protein demonstrates that some local native states defined by the local curvature and torsion of the main chain, mainly located in secondary structures, are coupled to each other whereas others, mainly located in flexible protein segments, are not. Consequently, CS of some residues are faithful reporters of global protein unfolding, with heat-induced denaturation curves similar to the average global one, whereas other residues remain silent about the protein unfolded state. For these latter, the local deformation of the protein main chain, characterized by its local curvature and torsion, is not cooperatively coupled to global unfolding.
Graphical Abstract
Introduction
By analogy with the solid/liquid first-order phase transition, protein folding/unfolding is often described by a global order parameter, as for example the fraction of native-like contacts or the root-mean-square-deviation between the unfolded structure relative to the folded one. The protein heat-induced denaturation curve, i.e. the variation of the global order parameter as a function of the temperature, represents a global measure of the unfolding transition. For most of the proteins, this global heat-induced denaturation curve can be formally described by a simple two-state (folded/unfolded) statistical model. Agreement with a two-state model does not imply, however, that the macromolecule does not unfold through a number of intermediate states. Intermediates states are expected as macromolecules are nanosized. Hence, the global denaturation curve hides the heterogeneity of protein unfolding. There is, therefore, a considerable interest to investigate protein unfolding at a local state, by defining a local order parameter measuring the local protein folded state or the local protein nativeness. Measure of the local nativeness as a function of the temperature defines a local heat-induced denaturation curve which is the purpose of the present study.
Local nativeness is not uniquely defined and is probe dependent 1. From a theoretical point of view, the concept of protein local nativeness backs to the early statistical models of the helix-coil transition where each residue occurs in only two local states 2. In a previous work, we defined the local nativeness of a protein from the free-energy landscape of coarse-grained angles (CGA) built on the sole Cartesian coordinates of the Cα atoms 3. These local nativeness-based CGA were successfully included in an Ising type-model to describe unfolding of the model gpW protein 3. The CGA fully characterized the protein fold 4. Assuming a constant virtual bond length between Cα atoms of successive residues, a chain of N amino-acids is fully characterized by N-3 CGA: the torsion angles γn, built from the positions of and ; and the bond angles θn, built from , with n=2 to N-2. These CGA were used successfully to describe large conformational changes and are part of coarse-grained models of proteins. The CGA have clear geometrical meanings: they are respectively the discrete version of the local curvature (θn) and the local torsion (γn) of the chain formed by the successive Cα-Cα virtual bonds 5. From a mathematical point of view, the local curvature and torsion fully describe the structure of a string. The CGA have also an advantage over more popular Ramachandran angles. Indeed, the Cα coordinates represent a complete representation of the protein main chain: the structure of the main chain can be rebuilt correctly from the CGA internal coordinates and the average Cα-Cα bond distance 6. On the contrary, the main chain structure rebuilt from the Ramachandran angles (ϕ, ψ) and the average bond distances of the protein backbone deviates significantly from the experimental structure 6. Hence, statistical properties of the proteins deposited in the PDB, as the variation of the gyration radius of the proteins as a function of the polymer length, are not reproduced if the structures are rebuilt from the (ϕ, ψ) coordinates. On the opposite, the power-law dependence of the gyration radius of the ensemble of proteins deposited in the PDB as a function of the chain length is accurately reproduced if the structures are rebuilt from the sole (θ,γ) coordinates 6. In conclusion, the (ϕ, ψ) angles do not form a complete set of local order parameters whereas (θ,γ) do.
In the present work, we demonstrate that the local nativeness built on CGA can be measured experimentally by measuring the variation of the NMR chemical shift (CS) of Cα atoms as function of temperature. NMR CS are extensively used to probe atom-scale structures of proteins in solution in their native state and under the influence of an external perturbation (temperature, pH, pressure, ligand) 7–13. For example, CS of 1H, 15N and 13C atomic probes have provided valuable and very detailed information on the thermal folding/unfolding of proteins in recent years 12,14. While it is certain that the CS variation of atom as a function of an external parameter renders modifications of the chemical neighborhood of a nuclei, the precise nature and the spatial scope of these modifications are not trivial. Deciphering the relation between local information recorded along the amino-acid sequence of a protein, such as the CS, and the global conformation of a protein in protein folding/unfolding 12,14 is challenging. The CS are scalar functions of multiple structural variables, so a heat-induced variation of the CS may be associated with local and global motions of different kinds. Moreover, global unfolding of a protein may have no effect on the CS in a particular region of the polymer chain.
The fundamental questions we addressed here are: (i) how the local heat-induced denaturation curves measured by the variation of the CS as function of the temperature can provide an information on the global unfolding of a protein; (ii) how the CS local heat-induced denaturation curves may be related to the local curvature and torsion of the protein main chain defined by the CGA? In short, can we define the local nativeness built on the CGA experimentally? To answer these questions, we defined the local native state of a residue within the molecule and quantified the relation between the protein local nativeness of each residue and the CS of its 13Cα atom as well as the cooperativity of the local native states in folding/unfolding, using all-atom molecular dynamics (MD) simulations of the fast downhill folder gpW 15, 16. Previous studies have shown that all-atom MD simulations with current force fields can reproduce the folding of medium size proteins, and are valuable tools to examine the relation between local structural fluctuations and global unfolding 17.
The choice of the downhill folder gpW is motivated by the recent measures of CS of 180 atomic probes of gpW as functions of temperature 14. The CSs exhibit jumps near the melting temperature, leading the authors to interpret the CS curves as local heat-induced denaturation curves 14. For gpW, both the qualitative behavior of the CS and the weak cooperativity of its folding/unfolding transition 18 are reproduced by all-atom MD 14. Therefore, we examined the relation between local structural fluctuations and global unfolding by simulating the thermal unfolding of gpW 15,16 between 280 K and 380 K using all-atom MD, and predicted the CS of each 13Cα atom along the amino-acid sequence as a function of temperature using the SHIFTX2 software 19 (see Material and Methods). Comparison between CS denaturation curves and the local nativeness defined from the CGA permit us to (i) demonstrate that the CGA nativeness, which reflects the local curvature and torsion of the main chain, may be quantified experimentally; and (ii) to identify why some CS are silent on global unfolding of a protein and others are faithful reporters of global conformational changes.
Material and methods
The protein gpW is a 62 amino-acid polypeptide featuring a folded structure consisting of two α-helices (residues 4–19, 40–54) on top of a β hairpin (residues 23–28 and 31–36) (PDB ID:2L6Q) 15,16. In a previous work 3, we performed all-atom MD simulations of gpW in explicit solvent [TIP3P water model 20] at a pressure of 1 bar and at 18 different temperatures between 300 K and 500 K using the GROMACS 21 and the amber99sb-ildn force field 22. The atom coordinates were saved every ps from each MD trajectory and for each snapshot, the CS of all 13Cα of gpW were computed from these coordinates using SHIFTX2 predictor 19. The correlation coefficient between the chemical shifts of 13Cα predicted by SHIFTX2 and the chemical shifts experimentally measured attains 0.9959 with RMS errors of 1.1159 ppm at standard pH and temperature. The program is expected to be less accurate at higher temperatures (in the unfolding state). As chemical shift is extremely sensitive to small coordinate displacements, another source of error is the inaccuracy of the current force-fields used in MD simulations, which limits the quantitative agreement between simulated chemical shifts based on MD trajectories and the experimentally observed ones.
The temperatures in the present main text are actually rescaled temperatures compared to the temperature parameters used in the MD simulations. In GROMACS parameters, the temperature used TGRO covers the range [300 K, 500 K]. It is known that the temperatures in the MD force fields simulations are not the actual temperatures. As in Ref. 14, we used NMR experimental data as a standard to define a more accurate temperature range to compare to experiments. The temperature range was transformed so that the <δi>(T) curves become similar to the experimental curves. The observed global unfolding temperature, measured in the NMR study of gpW and to which we compare our simulations, is 330K14. Comparisons between experimental and simulated signals for the CS of Cα atoms are shown and discussed in Results and Discussion section and Supporting Information. We retain the following temperature transformation: T = 0.5×TGRO + 130. Proceeding this way, the actual temperature range discussed in the main text and corresponding to our simulations is [280K-380K] and the unfolding temperature is similar to the one observed in Ref. 14.
The range of variation of the measured CS were reduced to the range [0,1] by an isometric transformation and then averaged over the sequence to produce a global parameter.
Results and Discussion
CGA free-energy landscapes
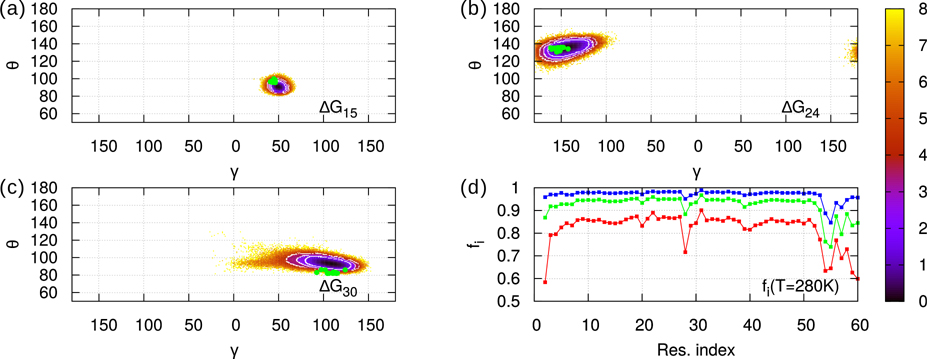
At each temperature, gpW explores a great variety of conformations whose statistical weights are represented by the free-energy landscapes (FEL): ΔG(γi,θi) = −RT ln[P(γi,θi)], where P(γi,θi) is the two-dimensional probability density of the CGAs computed from the MD trajectories 3, and T and R are the absolute temperature and the gas constant, respectively. Typical FELs are represented in Fig. 1 for i=15, 24 and 30 (panels a, b and c) at T=280K. As explained in the Material and Methods section, all temperatures of the MD simulations reported here are rescaled temperatures (T=280K corresponds to TGRO=300K in the GROMACS software). The most probable values of the CGA angles appear as dark wells in Fig. 1. While at T=280K the exploration of (γi,θi) angles does not extend much (see Fig. S1–S3 for all FELs at 280K), at T>330K (unfolding temperature) the FELs cover most of the range available to (γi,θi), featuring several wells (see Fig. S4–S6 for all FELs at 355K). Secondary structures at 280K (native state) correspond to well-defined area in the (γi,θi) FELs (Figs. S1–S3). The α-helix area is narrow and centred around (γ=50°, θ=90°). For β−sheets, the CGAs comprise the area −180°< γ <−120°, 100°< θ <150° and appear alternatively along the sequence centered at γ =−180° and at γ =−120°, reflecting the alternative geometry of the backbone in β strands. The values of (γi,θi) angles computed from the experimental structure (PDB ID: 2L6Q) 16 are marked as green dots on the 280K landscapes in Fig. 1 (panels a, b and c) and in Figs. S1–S3. Correspondence between experimental points and most stable values in MD (black areas) is qualitatively verified.
Figure 1:
Panels a-c: Free-energy landscapes ΔG(γi,θi) = -RT ln(P(γi,θi)/Pmax) for i=15 (a), i=24 (b), i=30 (c). Probability distribution function P(γi,θi) is sampled from 750 ns MD trajectories at T=280K. The native areas corresponding to the three values of the cut-off H (see text) are the concentric white circles (inner for 2RT, outer for 4RT). Green dots mark the twenty experimental values of the angles extracted from the 2L6Q PDB. Panel d: fi (T=280K) curves for three different values of the cut-off H: H=2RT (red), 3RT (green), 4RT (blue). Values of fi range from i=2,…,60.
Local and global nativeness from CGA
Since (γi,θi) angles describe the conformation of the main chain formed by the residues i-1 to i+2, we want to characterize the native state of gpW at local scale using these angles. We define a local two-state model as follows. The local native state of the main chain in the neighbourhood of the ith residue is defined as an ensemble of (γi,θi) values, micro-states, representing the predominant conformation at T=280K. We sort the angles by increasing ΔG(γi,θi). Low-values of ΔG(γi,θi) correspond to the local native state; high-values belong to the local unfolded state for the pair of CGAs (γi,θi). The separation between native and unfolded micro-states is defined by a ΔG cut-off whose value H determines the area (white circles in Fig. 1 a, b and c) that contains (γi,θi) values of the native state. In other words, the ensemble of values of (γi,θi) for which ΔG(γi,θi) < ΔGmin(γi,θi) + H defines the local native state of ith residue. The value of H determines the local nativeness of the protein defined as the fraction fi of native state for (γi,θi): . The local nativeness fi is represented as a function of the amino-acid sequence in Fig. 1 d for different values of H at 280 K. At 280K selecting H=2RT gives fi>80%, H=3RT fi>90%, and H=4RT fi>95% (Fig. 1 d). All these values of H, give the same qualitative variation of fi along the sequence (Fig. 1 d). In the following, we choose H=4RT (Fig. 1 d) as a good compromise between a high value of fi and a small native area in the FEL at 280 K.
The lowest values of fi are found outside helices and sheets, near loops or terminal parts of gpW. They are flexible parts of the main chain for which the (γi,θi) angles have a large set of values and for which the local native state has a large entropic contribution. The local nativeness fi is expected to converge to a non-zero finite value at high temperature (Fig. S7). Indeed, at temperatures much larger than the unfolding temperature, the probability to be locally in a non-native state converges to the ratio between the number of micro-states in the unfolded area of the local FEL (θ,γ) to the number of micro-states in the restricted area (ΔG < H) of the native state (Fig. S7).
The global nativeness of the protein ⟨fi⟩ is calculated at each temperature by averaging the local nativeness fi over all pair of CGAs. The variation ⟨fi⟩ as a function of the temperature compares very well with the variation of the global nativeness computed from the average variation of the CS measured as a function of the temperature 3. Application of a two-state model to the global unfolding denaturation curve ⟨fi⟩(T) is meaningless as intermediate states are significantly populated in the thermal unfolding of gpW between the fully native and fully unfolded states as expected for a downhill folder and shown in Ref. 3.
Average CS associated with local native and unfolded states
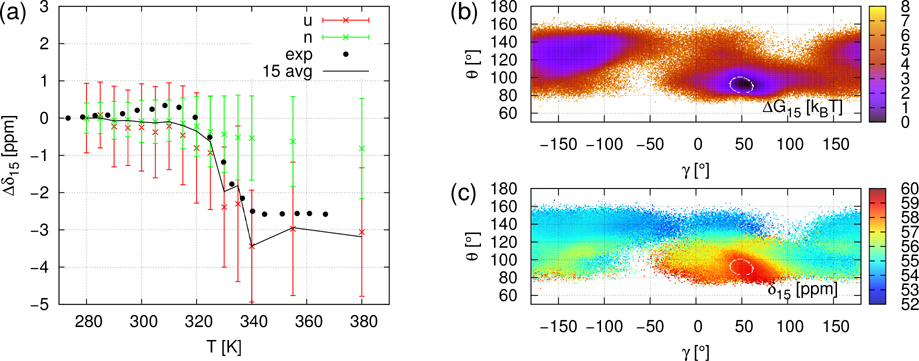
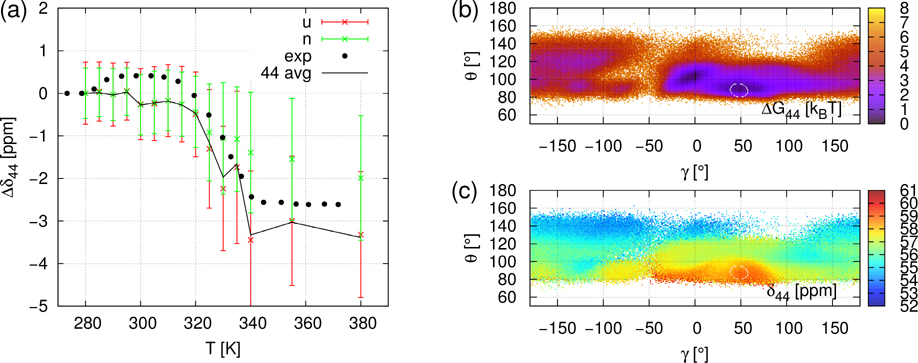
CS of all 13Cα of gpW were computed using SHIFTX2 predictor 19 from the Cα atom coordinates extracted from the MD trajectories at each ps. The chemical shift of the i-th Cα is denoted by δi. The δi(t,T) refer to the timeseries of chemical shift for the simulation at temperature T. In order to remove the offset induced by ShiftX2 and to compare with experimental data, we express the computed and measured chemical shifts as the difference between the average CS at the temperature T and at 280 K; i.e., ⟨Δδi⟩(T) = ⟨δi(T)⟩ − ⟨δi(280K)⟩. It is worth noting that the simulated values ⟨Δδi⟩(T) are the time average of δi(t,T) over 750 ns (duration of MD trajectories) while the measured values ⟨Δδi⟩(T) 14 reflect an average over a much larger ensemble of protein conformations and on a much larger time-scale than in the MD simulations. Typical ⟨Δδi⟩(T) curves are illustrated in panel a of Figs 2, 3 and 4 for i=21 (β-strand 1), for i=15 (α-helix 1), and i=44 (α-helix 2), respectively. All ⟨Δδi⟩(T) curves for i=2 to 60, similar to the panels a of Figs. 2–4, are represented in Figures S8–S10. No fit of the simulated data on the experimental ones was attempted, except for a rescaling of the MD temperature on the experimental one (see Material and Methods). Panels b and c of Figs 2, 3 and 4 represent respectively the local free-energy landscape and chemical shifts landscape for the residues i=21, i=15 and i=44 and are discussed in section “Local unfolding through chemical shift landscapes δi(γi,θi)”.
Figure 2:
Panel a: NMR CS of Cα21: ⟨Δδ21⟩(T) = ⟨δ21⟩(T) − ⟨δ21⟩(280K). Black dots are the experimental values and black lines are the average values of ⟨Δδ21⟩ computed from MD+ShiftX2. Green and red crosses are average values of ⟨Δδ21⟩ computed from MD+ShiftX2 for the snapshots belonging to the native ensemble N and unfolded ensemble U, respectively (see text). The errorbars are ⟨Δδ21⟩ ± σ(⟨Δδ21⟩) signals where σ are the computed standard deviations. Panel b: Free-energy landscape ΔG(γ21,θ21) at T=355K, the color bar unit is RT. Panel c: Map of ⟨δ21⟩ of Cα21 as a function of the CGA γ21 and θ21 at T=355K. The color bar unit is ppm. The value of ⟨δ21⟩ is computed from MD+SHIFTX2 by averaging the CS over the snapshots with the same values of γ21 and θ21.
Figure 3:
Same as Figure 2 (Panels a-c) for NMR CS of Cα15: ⟨Δδ15⟩(T) = ⟨δ15⟩(T) − ⟨δ15⟩(280K).
Figure 4:
Same as Figure 2 (Panels a-c) for NMR CS of Cα44: ⟨Δδ44⟩(T) = ⟨δ44⟩(T) − ⟨δ44⟩(280K).
Noticeable disagreements between simulations and experimental data are observed for a few residues which are outside of the secondary structures or at their C-terminus (see Figs. S8–S10), namely at i=18–21 (C-terminus of the α-helix), i=27, 28 (C-terminus of the β-strand), i=30 (turn), and i=55–60 (disordered C-terminus). In the secondary structures, only for i=46 is there a significant disagreement between simulated and experimental data (Fig. S10). For all residues for which the disagreement is large, the simulated ⟨Δδi⟩(T) are constant while the experimental signals increase gradually or by multiple small steps as shown for the typical example of i=21 in Fig. 2. The reason for the deviation between theory and experiment for these residues might be either the very short duration of the MD simulations (750 ns) to capture these flexible local conformational states or a failure of SHIFTX2 to predict the CS in such flexible regions. However, for most of the residues, ⟨Δδi⟩(T) jumps occurring around the transition temperature (T~330K) are rather well reproduced by ⟨Δδi⟩(T) extracted from the present simulations (MD+SHIFTX2) (Figs. S8–S10). This is illustrated for example for i=15 (α-helix 1), and i=44 (α-helix 2) in Figs 3 and 4, respectively.
Is the jump in the simulated curve ⟨Δδi⟩(T) characteristic of the local unfolding measured by the local nativeness fi? To answer this question, we defined the binary time series si(t) = {1 IF (γi,θi)(t) is native | 0 ELSE} for all MD trajectories and for each pair of CGA, i=2,…,60. The snapshots with si = 1 define the ensemble N of local native structures and those with si = 0 the complementary ensemble U of the local unfolded structures, in the vicinity of residue i; i.e., for the ith CGA. The time average of the CS ⟨Δδi⟩(T) and its variance σ(⟨Δδi(T)⟩) were computed separately for the ensembles of MD snapshots N and U. The variance reflects the exploration of the ensemble of the micro-states of the N and U ensembles as a function of time. In Figs. 2–4 and S8–S10, in addition to the values ⟨Δδi⟩(T) computed and measured 14, we also considered the simulated ⟨Δδi,N⟩(T) and ⟨Δδi,U⟩(T). The ensembles N and U cannot be separated in experiments as the measured CS are averages of the CS of local unfolded U and native N micro-states at a given temperature.
In a perfect local two-state model, ⟨Δδi,N⟩(T) should be rigorously constant which is not exactly the case (Fig. S8–S10) as shown for typical examples in Figs. 2–4 (i=21, 15 and 44). The variation of ⟨Δδi,N⟩(T) reflects the fact that the CS does not only depend on (γi,θi) but also on other hidden degrees of freedom (side-chain conformations and other CGA (γj,θj)j≠i). However, the amplitude of the native CS interval ⟨Δδi,N⟩(T) ± σ(⟨Δδi,N⟩) remains less than 1 ppm between 280 and 380 K. This states the limit of resolution of the N state in the present local two-state model.
Even in a perfect local two-state model, we do not expect ⟨Δδi,U⟩(T) to be constant, except for residues which do not have a well-defined native state; i.e., residues in disordered regions of the main chain, where all micro-states (γi,θi) are explored even at low temperature (280 K). For residues in secondary structures, the number of micro-states involved in the average of the unfolded local state increases with the temperature and so as ⟨Δδi,U⟩(T). Below the transition temperature, unfolded micro-states represent the outskirt of the local native state defined by the cut-off value of H and, hence, ⟨Δδi,U⟩(T) is not really statistically relevant. Above the unfolding transition T>330K, the protein explores a large enough number of unfolded micro-states and ⟨Δδi,U⟩(T) is rather constant. However, the separation between the N and U ensembles is successful for most Cα for which the overlap of the intervals of the N and U ensembles is limited. This is achieved when ⟨Δδi,N⟩ is at the edge or out of the ⟨Δδi,U⟩ ± σ(⟨Δδi,U⟩) interval.
Assuming that the separation between the N and U ensembles is correct and that ⟨Δδi,N⟩ and ⟨Δδi,U⟩ do not vary with temperature, we have ⟨Δδi⟩(T) = fi(T) ⟨Δδi,N⟩ + (1−fi(T)) ⟨Δδi,U⟩. We consider that the averages are constant as soon as the amplitude of their variations is less than 1 ppm. Then the jump of ⟨Δδi⟩(T) observed at the folding temperature (≅ 330 K) (Fig. 4) is due to the change of the relative populations of N and U ensembles which reflects the local unfolding transition.
The exhaustive interpretation of the plots should treat each value of i separately. In summary, three cases emerge in the analysis of ⟨Δδi,U⟩(T) and ⟨Δδi,N⟩(T) curves.
A / Fig. 2a. ⟨Δδi,N⟩ and ⟨Δδi,U⟩ are constant over the entire range of temperature but they are not separated: ⟨Δδi,N⟩ ∈ [⟨Δδi,U⟩ ± σ(⟨Δδi,U⟩)]. No jump of ⟨Δδi⟩(T) is observed. 13Cα NMR remains mute though the local unfolding has happened. Experimental signals with a jump inferior to 1 ppm enter this case. In panel b, we can see that a large part of the free energy landscape of (γ21,θ21) is of similar stability. The most probable value (black) is distributed among a very large area, indicating that there is no actual stable unique conformation.
B / Fig. 3a. ⟨Δδi,N⟩ is constant over the entire range of temperature. In addition, ⟨Δδi,U⟩ is constant above the unfolding transition temperature (below the unfolding temperature δi,U is not statistically relevant as discussed above) and the separation between ⟨Δδi,N⟩ and ⟨Δδi,U⟩ is large enough as their variances overlap by less than 1 ppm. In this case, the ⟨Δδi⟩(T) jump fully renders the (γi,θi) transition. As shown in Fig. 3b, when gpW is globally unfolded, the statistical exploration of (γ15,θ15) features several potential wells and fast scanning of unstable values. The stability of the native area (α-helix, γ=50°, θ=90°) is still noticeable. The β-sheet area (−180°< γ <−120°, 100°< θ <150°) is also significantly explored.
C / Fig. 4a. ⟨Δδi,N⟩ and ⟨Δδi,U⟩ are separated but ⟨Δδi,N⟩ is not constant. The variation of ⟨Δδi,N⟩ is due to another structural change different from the local unfolding transition of (γi,θi). As a consequence, the jump of δi is not only due to the local unfolding but also because of other factors. This case essentially occurs for residues located in helices. In the last section, we will study the dependence of ⟨Δδ44,N⟩ on (γj,θj), j≠44 to see if the neighbouring residues influence ⟨Δδ44,N⟩(T). In panel b, at T=355K, the free-energy landscape ΔG(γ44,θ44) features the quite persistent stability of the native α-helix region. Another region with a potential well is located at (γ=0°, θ=100°). The rest of the landscape, representing much of the partition function, has uniform low stability, picturing the fast scan of unstable values.
Local unfolding through chemical shift landscapes δi(γi,θi)
Ensemble averaging is now performed on structures of similar (γi,θi) values extracted from the (γi,θi)(t) timeseries recorded from the MD trajectories for i=2,…,60. We focus on the 355K MD trajectory as at this temperature the protein explores the full (γi,θi) landscape (see panel b of Figs. 2–4). For i=2,…,60, 1°×1° bins are defined in the (γi,θi) interval [−180°,180°]×[60°,180°]. Inside all bins, we computed the time average ⟨δi⟩ (γi,θi) by selecting only the frames where the value of (γi,θi) was accepted in the bin. We plotted these values as a coloured surface. Results are shown for i=21, 15 and 44 in panel c of Figs. 2–4. CS landscapes for i=2,…,60 at T=355K are displayed in Figs. S11–S13.
The repartition of values shows that the variation of ⟨δi⟩(γi,θi) always has an amplitude of 1 ppm at least. It confirms that ⟨δi⟩ (γi,θi) is sensible to the CGA (γi,θi), and that molecular MD analyzed with ShiftX2 renders this sensibility. Varying i=2,…,60, the ⟨δi⟩(γi,θi) distribution is quite similar, except for a global δ-offset. The highest values of chemical shift are typically found around the α-helix region (γ=50°, θ=90°). On the contrary ⟨δi⟩(γi,θi) is the lowest when θi ≥ 120°, and it takes variable intermediate values for θi ≤ 120° and outside of the helical zone. Therefore, the smallest values were observed for β-sheets.
The ⟨δi⟩ (γi,θi) landscapes enable us to interpret the values of ⟨δi,N⟩ and ⟨δi,U⟩ at T=355K. Indeed ⟨δi,N⟩ and ⟨δi,U⟩ are the average of ⟨δi⟩ (γi,θi) values over respectively native and unfolded regions. Figures 2–4 allow us to make a link between ⟨δi⟩ (γi,θi) landscapes on one side (panel c, where the native region is drawn as a white circle), and the separation of ⟨δi,N⟩(355K) and ⟨δi,U⟩ (355K) on the other side (panel a).
For i=15 (Fig. 3c) and 44 (Fig. 4c) the native region is the small α-helix area. Values of ⟨δi,N⟩ (355K) are respectively 59 and 60 ppm. For i=15 (Fig. 3c), highest values go to the α-helix area ⟨δ15⟩~59 ppm and ⟨δ15⟩ globally decreases as θ increases. The lowest values ⟨δ15⟩~53ppm correspond to non-structured conformations. The angles of the β-sheet area (−180°< γ <−120°, 100°< θ <150°) encompass two-component intermediate values (55 and 56 ppm). Therefore, the native NMR signal is clearly demarcated from non-native ⟨δ15⟩(γ15,θ15) values. For i=44 (Fig. 4c), ⟨δ44⟩ is globally decreasing as θ increases. The highest value corresponds to the native α-helix area ⟨δ44⟩~59 ppm. The lowest values, δ44~54 ppm, appear when θ >130°. The rest of the non-native areas have intermediate δ values. So the ⟨δ44⟩ (γ44,θ44) landscape at T=355K shows that native and non-native states can be distinguished by chemical shift. In conclusion, the native states are near the maxima in both landscapes (i=15 and 44), so averaging over the unfolded domain necessarily results in much lower values of ⟨δi,U⟩, well separated from ⟨δi,N⟩.
On the contrary, for i=21 (Fig. 2c), the native region (similar to β-sheet) is large and encompasses both high and low values of ⟨δ21⟩ (γ21,θ21), resulting in ⟨δ21N⟩~56 ppm. Values of δ21 span over only 2 ppm overall (from 55 to 57 ppm). From this small range, the native area of (γ21,θ21) includes two steps of δ values, at 55 and 56 ppm. The highest value is only found in the α-helix region, whose statistical weight is low. Averaging over the non-native region does not produce a much different value of ⟨δ21,U⟩ compared to ⟨δ21,N⟩. Only the well-explored α-helix region slightly pulls ⟨δ21,U⟩ up. But all in all, the location of the native region in the CS landscape explains why the difference does not exceed 0.5 ppm, as shown in Fig 2a.
We generalize this analysis shown for three typical cases in Figs. 2–4 to all i=2,…,60 (see Figs. S11–S13). If the chemical shift landscape ⟨δi⟩(γi,θi) has the extrema in the native region, then ⟨δi,U⟩ and ⟨δi,N⟩ are separated. This is a necessary condition in order to render (γi,θi) unfolding in 13Cα NMR as shown by the comparison between Figs. S8–S10 and Figs. S11–S13.
Neighboring (γj,θj) free energy landscapes associated with extreme values of δi(γi,θi)
In the analysis of ⟨Δδi,U⟩(T) and ⟨Δδi,N⟩(T) curves, we highlighted the case where ⟨Δδi,N⟩(T) varies significantly during unfolding. This evolution is mainly encountered in helices and indicates the action of structural parameters other than (γi,θi).
We took i=44, as an example of the evolution of ⟨Δδi,N⟩(T) as a function of the temperature. The decrease of ⟨Δδ44,N⟩(T) above the unfolding temperature is accompanied by an increase of σ[⟨Δδ44,N⟩] such as at high temperature, the value of ⟨Δδ44⟩(280K) is still reached in the ⟨Δδ44,N⟩±σ(⟨Δδ44,N⟩) interval. To understand this behavior of the CS, we selected snapshots contributing to a given range of δi and studied the structural properties of this ensemble. The δi criterion was |Δδ44|<0.5 ppm, which corresponds to values near δ44,N(280K). We chose to study the 355K trajectory for the same reason as before. All snapshots, which have Δδ44 meeting the criterion |Δδ44|<0.5 ppm, form an ensemble that we call the restricted trajectory. The number of snapshots in this ensemble is between 60000 and 70000 depending on the initial conditions of the MD trajectories.
The CGA (γ44,θ44) belongs to the α2-helix, which encompasses the CGA (γ40,θ40) to (γ51,θ51). The free-energy landscapes ΔG(γj,θj) were computed from both all the snapshots of the MD trajectory and from the snapshots of the restricted MD trajectory. They are shown for j=44 to 47 in Fig. 5 and for the other CGAs of the α2-helix in Figs. S14 and S15.
Figure 5:
Free-energy landscapes of neighbor residues of i=44. The color bar unit is RT. Top landscapes were computed on the full 355K trajectory. Bottom landscapes were computed by selecting only frames where |Δδ44|<0.5 ppm. For all values of j, the free-energy landscape of the restricted trajectory occupies less extensive area of (γj,θj) compared to the full trajectory landscape, and tends towards majority occupation of the native (γj,θj) area. The effect is less pronounced on j=47. This behavior of neighboring residues indicates the influence of non-local (γj,θj) angles on δi evolution.
Results show that the free-energy landscapes displayed on Fig. 5 are different when the values of δ44 are restricted. In the free-energy landscape of j=44 for the restricted trajectory, as expected, only the native region is explored. For j=45 and 46, landscapes of the restricted ensemble mostly feature the native area and remnants of the wide γ<0° area. On the restricted landscape of j=47, only a small area at γ=100° is missing and the γ<0° area is quite well explored.
Small differences between the restricted and unrestricted trajectories can also be spotted in the j=42 landscape (see Fig. S14). Overall, the free-energy landscapes for the restricted ensemble show that Δδ44 is likely to be close to 0 when the neighboring residues tend to be in native conformation, in addition to j=44 itself.
As a conclusion, the jump observed in case C (δ44 and others) is not only caused by the unfolding of local backbone angles but also reflects the denaturation of more distant residues. It is noteworthy that this case essentially happens in α-helix regions, unfolding of which is strongly cooperative. Therefore, 13Cα NMR is a probe for the unfolding of groups of cooperative residues of gpW in α-helix.
Conclusions
Starting from MD simulations, we defined local native and non-native states regarding (γi,θi) angles exploration. A (γi,θi) local conformation has to meet the following condition to be considered as a native state: ΔG(γi,θi)<4RT. The corresponding (γi,θi) areas match experimental values of angles in the native state and represent more than 95 % of the conformations explored by the protein in the 280K MD trajectory.
The ShiftX2 calculations performed on the simulated trajectories produced 13Cα CS that vary realistically with temperature when compared to experimental points. For each position i in the amino-acid sequence (i=2 to N-2), we used local nativeness definition and MD data to average the CS of residue i independently over local native (N) and non-native (U) states. The results showed to what extent the CS variation as function of the temperature reflects the local unfolding of (γi,θi). We established two conditions for this interpretation to be possible: (i) δi,N must be approximately constant with temperature, (ii) δi,N and δi,U must be separated by more than 1 ppm. Neglecting variations less than 1 ppm, a part of gpW residues met the above conditions. The corresponding δi(T) curves can be read as (γi,θi) local heat-induced denaturation curves. Because the CGA represent the discrete version of the local curvature and torsion of a curve, the local nativeness of the protein measured by the δi mirrors these local order parameters.
For certain residues δi,N and δi,U were mixed up, resulting in non-jumping signals. The CS landscapes δi(γi,θi) were built at 355K to understand the separation of δi,N and δi,U. Non-jumping signals are caused by the fact that δi(γi,θi) takes non extremal values in the native state. Taking extrema values of δi in native conformation is a necessary condition for the (γi,θi) unfolding to be reflected in NMR.
For other residues, δi,N(T) is jumping with a significant amplitude during unfolding, implying that a structural change different of (γi,θi) was reflected by δi. We demonstrated the non-local influence of neighbouring (γj,θj), j≠i, for the special case of i=44. The same analysis could be conducted for other values of i showing non-constant δi,N(T).
The last two phenomena, which we described as deviations from an ideal case, are particular combinations of influences. A δi,N(T) is actually never strictly constant. But given our limited statistics we were forced to neglect variations under a certain threshold. When there is no jump, non-local unfolding events oppose the influence of (γi,θi) unfolding on δi. This tells us that very local backbone angles (γi,θi) outclass neither the neighbouring ones nor maybe other close structural angles. On the contrary, the non-local structural changes may enhance the effect of (γi,θi) unfolding on δi, as we demonstrated for i=44. In turn, this enhancement involves simultaneous structural similarity of the neighbouring residues, which means that the unfolding is strongly cooperative near the i-th residue. High amplitude jumps in α-helices correspond to the concerted unfolding of several residues of the helix.
In summary, we demonstrated that local heat-induced denaturation curves, built from the local curvature and torsion of the protein main chain, are comparable to the heat-induced denaturation curve of the 13Cα chemical shift for most of the residues, for which the chemical shifts of non-local native states and local native states are not overlapping in the high temperature limit. In other cases, the 13Cα chemical shift is blind and no information about the local unfolding can be inferred from its measurement. MD simulations allowed to separate the local native and non-native states and to explain the qualitative behavior of local heat-induced denaturation curves and its possible departure from the global heat-induced denaturation curve which is dominated by cooperative local unfolding.
Supplementary Material
Acknowledgments
The calculations were performed using HPC resources from DSI-CCuB (Centre de Calcul de l’Université de Bourgogne). This work is supported by a grant from the National Institutes of Health grant no. R01GM14312 and by a grant from the Air Force Office of Scientific Research as part of a joint program with the Directorate for Engineering of the National Science Foundation, Emerging Frontiers and Multidisciplinary Office grant no. FA9550-17-1-0047. The authors acknowledge support from the Bourgogne Franche-Comté Graduate School EUR-EIPHI (17-EURE-0002).
Footnotes
Supporting Information
The Supporting Information is available free of charge at the https://pubs.acs.org
Supporting figures of CGA free-energy landscapes, local nativeness, NMR signals, CS landscapes.
References
- (1).Sukenik S; Pogorelov TV; Gruebele M Can Local Probes Go Global? A Joint Experiment–Simulation Analysis of Λ6–85 Folding. J. Phys. Chem. Lett 2016, 7, 1960–1965. [DOI] [PubMed] [Google Scholar]
- (2).Lifson S; Roig A On the Theory of Helix—Coil Transition in Polypeptides. J. Chem. Phys. 1961, 34, 1963–1974. [Google Scholar]
- (3).Grassein P; Delarue P; Scheraga HA; Maisuradze GG; Senet P Statistical Model To Decipher Protein Folding/Unfolding at a Local Scale. J. Phys. Chem. B 2018, 122, 3540–3549. [DOI] [PubMed] [Google Scholar]
- (4).Nishikawa K; Momany FA; Scheraga HA Low-Energy Structures of Two Dipeptides and Their Relationship to Bend Conformations. Macromolecules 1974, 7, 797–806. [DOI] [PubMed] [Google Scholar]
- (5).Rackovsky S; Scheraga HA Differential Geometry and Polymer Conformation. 1. Comparison of Protein Conformations. Macromolecules 1978, 11, 1168–1174. [Google Scholar]
- (6).Hinsen K; Hu S; Kneller GR; Niemi AJ A Comparison of Reduced Coordinate Sets for Describing Protein Structure. J. Chem. Phys 2013, 139, 124115. [DOI] [PubMed] [Google Scholar]
- (7).Wüthrich K The Way to NMR Structures of Proteins. Nat. Struct. Biol 2001, 8, 923–925. [DOI] [PubMed] [Google Scholar]
- (8).Grzesiek S; Bax A Amino Acid Type Determination in the Sequential Assignment Procedure of Uniformly 13C/15N-Enriched Proteins. J. Biomol. NMR 1993, 3, 185–204. [DOI] [PubMed] [Google Scholar]
- (9).Clore G; Gronenborn A Structures of Larger Proteins in Solution: Three- and Four-Dimensional Heteronuclear NMR Spectroscopy. Science 1991, 252, 1390–1399. [DOI] [PubMed] [Google Scholar]
- (10).Nielsen G; Schwalbe H Protein NMR Spectroscopy: Hydrogen Bonds under Pressure. Nat. Chem 2012, 4, 693–695. [DOI] [PubMed] [Google Scholar]
- (11).Garcia-Mira MM Experimental Identification of Downhill Protein Folding. Science 2002, 298, 2191–2195. [DOI] [PubMed] [Google Scholar]
- (12).Sadqi M; Fushman D; Muñoz V Atom-by-Atom Analysis of Global Downhill Protein Folding. Nature 2006, 442, 317–321. [DOI] [PubMed] [Google Scholar]
- (13).Neudecker P; Robustelli P; Cavalli A; Walsh P; Lundstrom P; Zarrine-Afsar A; Sharpe S; Vendruscolo M; Kay LE Structure of an Intermediate State in Protein Folding and Aggregation. Science 2012, 336, 362–366. [DOI] [PubMed] [Google Scholar]
- (14).Sborgi L; Verma A; Piana S; Lindorff-Larsen K; Cerminara M; Santiveri CM; Shaw DE; de Alba E; Muñoz V Interaction Networks in Protein Folding via Atomic-Resolution Experiments and Long-Time-Scale Molecular Dynamics Simulations. J. Am. Chem. Soc 2015, 137, 6506–6516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (15).Fung A; Li P; Godoy-Ruiz R; Sanchez-Ruiz JM; Muñoz V Expanding the Realm of Ultrafast Protein Folding: GpW, a Midsize Natural Single-Domain with Α+β Topology That Folds Downhill. J. Am. Chem. Soc 2008, 130, 7489–7495. [DOI] [PubMed] [Google Scholar]
- (16).Sborgi L; Verma A; Muñoz V; Alba E. de. Revisiting the NMR Structure of the Ultrafast Downhill Folding Protein GpW from Bacteriophage λ. PLOS ONE 2011, 6, e26409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (17).Lindorff-Larsen K; Piana S; Dror RO; Shaw DE How Fast-Folding Proteins Fold. Science 2011, 334, 517–520. [DOI] [PubMed] [Google Scholar]
- (18).Muñoz V; Campos LA; Sadqi M Limited Cooperativity in Protein Folding. Curr. Opin. Struct. Biol 2016, 36 (Supplement C), 58–66. [DOI] [PubMed] [Google Scholar]
- (19).Han B; Liu Y; Ginzinger SW; Wishart DS SHIFTX2: Significantly Improved Protein Chemical Shift Prediction. J. Biomol. NMR 2011, 50, 43–57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (20).Jorgensen WL; Chandrasekhar J; Madura JD; Impey RW; Klein ML Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys 1983, 79, 926–935. [Google Scholar]
- (21).Hess B; Kutzner C; van der Spoel D; Lindahl E GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J. Chem. Theory Comput 2008, 4 (3), 435–447. [DOI] [PubMed] [Google Scholar]
- (22).Lindorff‐Larsen K; Piana S; Palmo K; Maragakis P; Klepeis JL; Dror RO; Shaw DE Improved Side-Chain Torsion Potentials for the Amber Ff99SB Protein Force Field. Proteins: Struct., Funct., Bioinf 2010, 78, 1950–1958. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.