Highlights
-
•
Developed deep learning methods to forecast the COVID19 spread.
-
•
Five deep learning models have been compared for COVID-19 forecasting.
-
•
Time-series COVID19 data from Italy, Spain, France, China, the USA, and Australia are used.
-
•
Results demonstrate the potential of deep learning models to forecast COVID19 data.
-
•
Results show the superior performance of the Variational AutoEncoder model.
Keywords: Data-driven, Deep learning, COVID-19, Forecasting, Gated recurrent units, Long short-term memory, Recurrent neural network, Variational autoencoder
Abstract
The novel coronavirus (COVID-19) has significantly spread over the world and comes up with new challenges to the research community. Although governments imposing numerous containment and social distancing measures, the need for the healthcare systems has dramatically increased and the effective management of infected patients becomes a challenging problem for hospitals. Thus, accurate short-term forecasting of the number of new contaminated and recovered cases is crucial for optimizing the available resources and arresting or slowing down the progression of such diseases. Recently, deep learning models demonstrated important improvements when handling time-series data in different applications. This paper presents a comparative study of five deep learning methods to forecast the number of new cases and recovered cases. Specifically, simple Recurrent Neural Network (RNN), Long short-term memory (LSTM), Bidirectional LSTM (BiLSTM), Gated recurrent units (GRUs) and Variational AutoEncoder (VAE) algorithms have been applied for global forecasting of COVID-19 cases based on a small volume of data. This study is based on daily confirmed and recovered cases collected from six countries namely Italy, Spain, France, China, USA, and Australia. Results demonstrate the promising potential of the deep learning model in forecasting COVID-19 cases and highlight the superior performance of the VAE compared to the other algorithms.
1. Introduction
At the end of 2019, a new coronavirus called Corona-virus Disease 2019 (COVID-19) has appeared in Wuhan city in China. Recently, the COVID-19 is flagged out a pandemic by the World Health Organization on March 11th, after over-passing 118,000 cases in over 110 countries at that time. This disease has exponentially spread over all the world and highly impacted healthcare systems in many countries, such as Italy, Spain, France, and the United States. In fact, increased demand for healthcare generated large flows of patients leads to hospital bed shortages and strain situations in hospitals. Accurately modeling and forecasting the spread of confirmed and recovered COVID-19 cases is vital to understand and help decision-makers to slowdown or arrest its spreading [1], [2], [3].
Today, COVID-19 pandemic is one of the most serious problems confronting our modern world because of its highly negatively affects public health [4]. Its impact is noticeable on sensitive populations, including the elderly and peoples with chronic diseases, such as asthmatics. Therefore, it becomes a multidisciplinary issue that involves both the epidemiological experts, pharmaceutical industry, specialists in modeling diagnosis systems, and local authorities. This paper is within the framework of modeling and forecasting of COVID-19 time-series data.
With the appearance and spreading of COVID-19, a big challenge of researches has been witnessed in several science domains around the world to slowdown or arrest the increasing trends of the spread of this disease. Thereby, to understand and manage this epidemic, various modeling, estimation, and forecasting approaches are introduced. For instance, several mathematical models are applied to estimate and forecast the evolution of confirmed infected cases [5], [6]. In susceptible exposed infectious recovered model (SEIR) models, the flows of people are categorized in four states according to the states of individuals: S (Susceptible), E (Exposed), I (Infected), and R (Remove) [7]. Very recently, in [8], a method based generalized SEIR model has been developed by incorporating quarantined and recovery states to predict and analyze the COVID-19 epidemic. In [9], both of SEIR and SIR models are applied to model the predictions and representing the confirmed cases data information. It has been shown that the SIR model outperforms the SEIR model in terms of Akaike Information Criteria (AIC). In [10], [11], another extended SIR version has been developed by introducing the number of reported and unreported cases in the prediction of the number of the reported cumulative cases. In [12], the SIR model is extended on the euclidean network to enhance the prediction quality of confirmed cases and illustrate the key role of the spatial factor in the epidemic propagation. In [13] three phenomenological models namely generalized logistic growth model (GLM), Richards growth model, and sub-epidemic wave model are proposed for short term forecasting of the number of confirmed cases. Specifically, the GLM model is used to capture the sub-exponential growth dynamics, the Richards model handles the deviation between the symmetric logistic curve, and the sub-epidemic wave model is introduced for the complex trajectories. Other studies have investigated using different models for understanding the epidemic spread. In [7], Logistic, Bertalanffy, and Gompertz models have been applied to fit and analyze epidemic predictions. The logistic model showed better prediction performance compared to the two other considered models. However, the major limitations of these three models are their restricted applicability only on some outbreak stages and with the availability of enough data. To alleviate this shortcoming, in [14], generalized versions are proposed by including additional parameters on the previous models. These improved versions permit to increase the analysis features as the documentation of the four epidemic phases (early stage, fast-growth phase, slow growth phase, and outbreak ends) and the identification of the high risk in estimated confirmed cases. In [15], a discrete-time stochastic model is developed to describe the dynamic of the epidemic spread. This model demonstrated the capacity to capture the epidemiological status [15]. Other studies applied time-series methods, such as Auto-Regressive Integrated Moving Average (ARIMA) to forecast the number of confirmed cases [16]. In [17], a traditional ARIMA modeling and Exponential Smoothing methods have applied to analyze and forecast the trends of the COVID-19 outbreak in India. In [18], the ARIMA model, which is suitable in describing short-term autocorrelation in time series data, is applied to forecast registered and recovered COVID-19 cases after sixty-day lock-down in Italy. Various previous studies based on traditional time series forecasting models have been explored to forecast future COVID cases in China and a few other countries, see [19], [20], [21].
Accurate forecasting of the number of COVID-19 cases is becoming the backbone to facilitate the use of the available resources in hospitals and improve management strategies to optimally manage infected patients. Recently, machine learning and deep learning have emerged as a promising field of research in a wide range of applications, both in academia and industry [1], [22]. In [23], four supervised machine learning algorithms namely linear regression, LASSO regression, Exponential Smoothing (ES), and Support Vector Machine (SVM) have been applied to predict COVID-19 Future. It has been shown that ES outperformed other models in predicting the number of newly contaminated cases, the number of recoveries, and the number of deaths. This is mainly due to the capacity of ES in handling time-series data by including information from past data in the prediction process. The study in [24] showed that Machine Learning and cloud computing provided promise solutions in improving the prediction of the growth of the epidemic proactively. In [25], a deep learning approach based on Long short-term memory (LSTM) is investigated in the forecasting of COVID-19 transmission in Canada, Italy, and the USA. Results showed the LSTM achieved good forecasting performance due to its capacity in handling time-dependent datasets. In [26], a stacked auto-encoder model is introduced to fit the dynamical propagation of the epidemic and real-time forecasting of confirmed cases in China. In [27] a shallow Long short-term memory is proposed to predict the risk category, trend, and weather data are used as input for the prediction. See, for instance [28] for more details about intelligent computing-based research for COVID-19.
Still within the deep learning techniques, this paper is aimed at presenting a comparative study between the five most advanced data-driven forecasting methods in forecasting COVID 19 cases. Here, the forecasting is performed for two the number of confirmed cases and the number of the recovered cases with the forecasting horizon of 17 days. Essentially, five deep learning models namely simple Recurrent Neural Network (RNN), Long short-term memory (LSTM), Bidirectional LSTM (BiLSTM), Variational Auto Encoder (VAE) and Gated recurrent units (GRUs) are applied and compared to forecast the time series of the number of new affected COVID 19 cases and recovered cases. These models have many attractive features, such as handling temporal dependencies in time series data, distribution-free learning models, and their flexibility in modeling nonlinear features. To the best of our knowledge, the VAE model has not been investigated before for COVID-19 forecasting. The deep learning models have been evaluated on the publically available COVID-19 patient stats dataset provided by Johns Hopkins recorded from the starting of COVID-19 till June 17, 2020. Data from five highly impacted countries are considered in this study: Italy, Spain, France, the USA, China, and Australie.
Section 2 provides a brief presentation of the simple RNN, GRU, LSTM, BiLSTM and VAE modeling and how they can be employed in forecasting. Section 3 presents the involved COVID-19 dataset and discusses the models fitting results and comparisons. Lastly, conclusions are drawn in Section 4.
2. Materials and methods
2.1. Deep learning models
Deep learning techniques demonstrated important performance improvements in different applications in the literature. This section is devoted to briefly describe the basic principle of six deep learning models that will be used later for COVID-19 time-series forecasting namely RNN, LSTM, Bi-LSTM, GRU, and VAE.
2.1.1. Recurrent neural networks
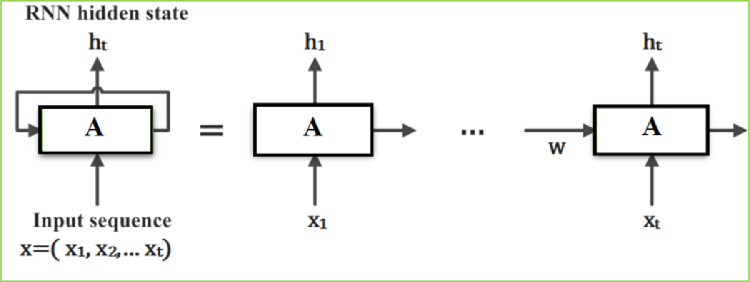
Regular feedforward neural networks have been widely used with success in numerous fields. In such networks, data flow transformations are passed via hidden layers in one direction where the output is influenced only with the current situation. However, these neural networks possess less memory and are not suitable for modeling data sequencing, and time dependencies in historical data. To bypass this limitation, recurrent neural networks (RNNs) have been developed to handle time-dependent learning problems [29]. The basic essence in RNNs is to consider the influence of past information for generating the output. To this end, cells represented by gates influencing the output using historical observations are included to generate the output. Fig. 1 displays a schematic illustration of RNNs. Indeed, a chunk of a neural network, A, looks at some input xt and provides a value ht. Essentially, RNNs are efficient for learning temporal information [30]. In RNN, a hidden state ht can be computed for a given an input sequence as:
where φ is a non-linear function. The recurrent hidden state is updated as follows
| (1) |
where g is a hyperbolic tangent function (tanh ).
Fig. 1.
Schematic presentation of RNN.
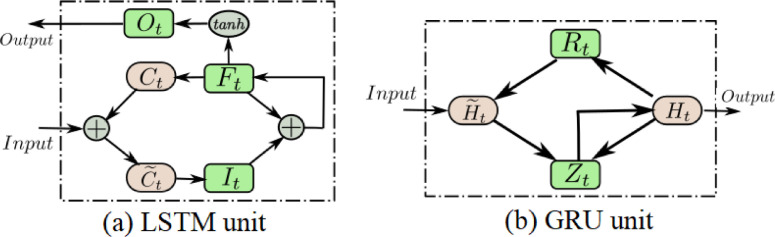
There are two powerful RNN models that are efficient for time-dependent in time-series data namely: LSTM and GRU. These deep learning models have shown considerable success in modeling and forecasting compared to the classical time series models and traditional networks have demonstrated that they can reach good results in many application domains with time series [31], [32]. The basic architectures of LSTM and GRU models are illustrated in Fig. 2 (a-b).
Fig. 2.
Basic structure of LSTM and GRU models. (a) It, Ft, and Ot represent the three LSTM gates (input, forget and output gates respectively), C and represent the candidate memory cells and memory cell content. (b) Rt and Zt are reset gate and update gates respectively, Ht and are the candidate hidden state and hidden state respectively.
2.1.2. LSTM models
LSTM is a sophisticated gated memory unit designed to mitigate the vanishing gradient problems limiting the efficiency of a simple RNN [29]. More specifically, in the case of the significant time step, the gradient becomes too small or large, which results in a vanishing gradient problem. This problem appears during the training, where the optimizer backpropagates and makes the procedure run, while the weights almost do not change at all. Essentially, LSTM possesses three gates controlling the information flow termed input, forge, and output gates. Basically, these gates are formed simply with logistic functions of weighted sums; the weights can be obtained during training by backpropagation. The cell state is managed via the input gate and the forget gate. The output is generated from the output gate or the hidden state, which represents the memory directed for use. This mechanism allows the network memorizing for a long time which is missed the conventional single RNNS. Of course, The desirable characteristics of LSTM are their extended capacity to capture long-term dependencies and great ability to handle time-series data. Given the input time-series Xt, and the number of hidden units as h, the gates have the following equations:
-
•
Input Gate:
-
•
Forget Gate:
-
•
Output Gate:
-
•
Intermediate Cell State:
-
•
Cell State (next memory input)
-
•
New State:
where
-
•
Wxi, Wxf, Wxo and Whc, Whf, Who refer respectively to the weight parameters and bi, bf, bo denote bias parameters.
-
•
Wxc, Whc denote weight parameters, bc is bias parameter, o refer to the element-wise multiplication. The estimation of Ct depends on the output information’s from memory cells () and the current time step .
2.1.3. Bidirectional LSTM
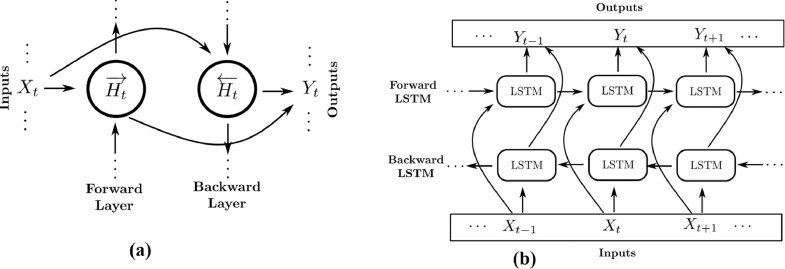
A bi-directional LSTM (BiLSTM) is an enhanced version of the LSTM algorithm. As discussed above, in the LSTM, the current state can only be reconstructed according to the backward context. However, the forward context also presents a relationship with the actual state, which is not considered in the LSTM model. To deal with this handicap and for more accuracy in state reconstruction, the bidirectional LSTM (BiLSTM) algorithm has been introduced by merging the desirable features of the bidirectional RNN [33] with those of the LSTM [34]. This has been done by combining two hidden states, which allow the information to come from the backward layer as well as from the forward layer.
Fig. 3 (a) presents the bidirectional RNN architecture. Wherein, the forward, backward and output sequences are given as following:
-
•
Forward hidden:
-
•
Backward hidden:
-
•
Output :
where is the sigmoid function application, which considered as LSTM unit in the BiLSTM architecture (Fig. 3(b)).
Fig. 3.
Schematic representation of (a) Bidirectional RNN structure and (b) Bidirectional LSTM architecture.
The BiLSTM is helpful for situations requiring context input. It has been widely used in classification, especially in text classification [35], sentiment classification [36] and speech classification and recognition [37]. In addition, the Bi-LSTMs are used in PM2.5 concentration prediction [38], and Load forecasting [39].
2.1.4. GRU models
GRU is basically an alternative LSTM version that is proposed in [40] for improving the LSTM performance and reduce the number of LSTM parameters and make its design less complicated. In GRU, the input gate and forget gate from the LSTM model have been merged in only one gate called update gate (Fig. 2). There only two gates in GRU, update and reset gates, instead of three gates in LSTM. The proposition of the reset and update gates concepts are among the new benefits brought by GRUs models. This latter, offer a new assessment method that allows the calculation of hidden states in RNN models. The GRU enhanced the LSTM structure through the coupling of the input and forget gates of the LSTM by the update gate and using the output gate as a reset gate. The update gate provides the quantity of previously kept memory and the reset gate ensures the combination way between actual (new inputs) and previous memory. The mathematical relationships between the various GRU components are given by:
-
•
Update gate:
-
•
Reset gate:
-
•
Cell state:
-
•
New state:
where
-
•
Wxr, Wxz and Whr are weight parameters and br, bz are bias parameters.
-
•
Wxh, Whh are weight parameters and bh is a bias parameter. For a given time step t, the current update gate Zt is used to combine the previous hidden state and current candidate hidden state .
2.1.5. Variational autoencoders
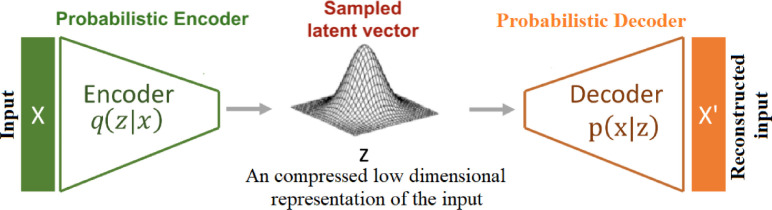
The variational autoencoders (VAE) belong to generative models that use learned approximate inference and could be constructed based on gradient-based techniques [41], [42]. Variational in this context refers to the variational inference method used in statistics. Basically, the VAE is considered as an autoencoder whose training is regularised to bypass the overfitting problem and establish a latent space with suitable properties enabling the generative process. Fig. 4 illustrates a basic schematic representation of the architecture of a VAE. Similar to a traditional autoencoder, a VAE contains both an encoder and a decoder. The training of a VAE is done by minimizing the reconstruction error of the encoded-decoded data and the original input data. At first, the VAE encodes the input data, X as distribution, q(z|x) via the latent space. Then, a sample, z ~ q(z|x), is generated from the code distribution. Finally, the sampled point is decoded p(x|z) and the reconstruction error is calculated and backpropagated through the network.
Fig. 4.
Schematic representation of Variational Autoencoders architecture.
The key insight behind VAE is to minimize the loss function, during the training stage. The loss function contains in addition to reconstruction term (on the output layer) that tries making the encoding-decoding process as efficient as possible, a regularisation term (on the latent layer) that regularizes the structure of the latent space by ensuring that the distributions obtained from the encoder closer to a specified distribution which is usually chosen Gaussian distribution.
| (2) |
The term is the reconstruction loss, helps the decoder learning the reconstruction of the data. Inadequate reconstruction will lead to a large cost in the loss function. On the other hand, the regularization term is represented as the Kulback-Leibler divergence (KL) between the encoder’s distribution, q(z|x) and a prior of the latent variable z, |p(z). The KLD quantifies the loss when using q to represent p. In other words, in the training step, the minimization of the loss function is done to ensure the regularization of the latent space and consist of two terms, the first term penalizes reconstruction error while the second term encourages the learned distribution q(z|x) to be close to the true prior distribution p(z), resulting on a regular latent space z and more suitable for sampling new observation using z ~ p(x|z), such as new images or music generation.
Due to its simplicity, flexibility, and easy to implement, the VAE framework has been extended to other model architectures. For instance, one sophisticated extension of VAE is the deep recurrent attention writer (DRAW) [43]. Specifically, DRAW is performed by combining a recurrent encoder and recurrent decoder and an attention mechanism [43]. Also, VAE has been extended for generating sequences by introducing variational RNNs that use a recurrent encoder and decoder within the VAE framework [44].
2.2. Evaluation metrics
The NN-based forecasting models were evaluated using the following indexes: Root Mean Square Error (RMSE), mean absolute percentage error (MAPE), mean absolute error (MAE), explained variance (EV), and Root Mean Squared Log Error (RMSLE).
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
where yt are the actual values, are the corresponding estimated values, and n is the number of measurements. Here, we use the RMSLE indicator because it is widely used for evaluating model quality in regression problems and as a score indicator in many data science challenges. Basically, it is similar to RMSE but calculated at the logarithmic scale. The benefit of using RMSLE as the statistical indicator is that its great robustness to outliers. Lower RMSE, MAE, or MAPE values and EV closer to 1 represent more accurate forecasting performances. Furthermore, we shall investigate the distribution of forecasting errors via histograms.
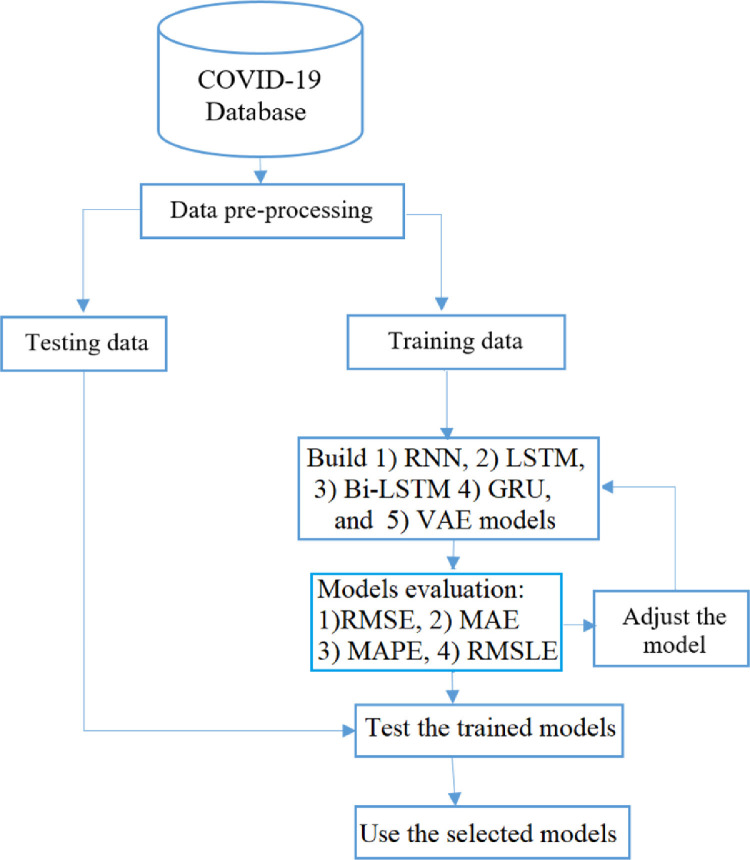
2.3. Deep learning-based COVID-19 forecasting
This study proposes a deep-learning framework for COVID-19 time-series forecasting. Five deep learning models have been applied to forecast daily conrmed and recovered cases. The general framework of the forecasting proposed strategies is illustrated in Fig. 5 . The COVID-19 forecasting has been done two main stages: training and testing. In the first stage, the raw data is preprocessed and standardized and then it is used to construct the deep learning model. The values of parameters of deep learning models are selected such that the loss function is minimized during the training. Here, Adam optimizer is used for this purpose. After that, in the testing stage, the previously constructed models with the selected parameters are used to forecast the number of COVID cases. The accuracy of the model will be verified by comparing the measured data with real data via different statistical indicators including RMSE, MAE, MAPE, and RMSLE.
Fig. 5.
Conceptual framework of the proposed forecasting methods.
The key underlying idea of this study is to investigate the capacity of the deep learning models RNN, LSTM, BiLSTM, GRU and VAE in forecasting the number of COVID-19 cases in the presence of a limited sized dataset.
3. Results and discussion
3.1. Data description
The COVID-19 disease has been reported by the WHO in around 210 countries and territories worldwide. In particular, many countries of Europe and North America suffer from a large COVID-19 outbreak. The role of large air traffic between Asia, North America, and Europe has significantly facilitated the propagation of COVID-19 from its origin to the other infected countries; person-to-person spread was subsequently reported among close contacts of returned travelers. The main objective of the herein study is aimed at the COVID 19 forecasting and prediction of the epidemic spreading. This study is based on daily figures of confirmed and recovered cases collected from six highly impacted countries namely Italy, Spain, Italy, China, the USA, and Australia. The considered datasets are gathered from the starting of COVID-19 for the respective countries (22 January 2020) till June 17th, 2020. These datasets are made publically by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University
(https://github.com/CSSEGISandData /COVID-19 accessed on 17/06/2020).
3.2. Data analysis and modeling
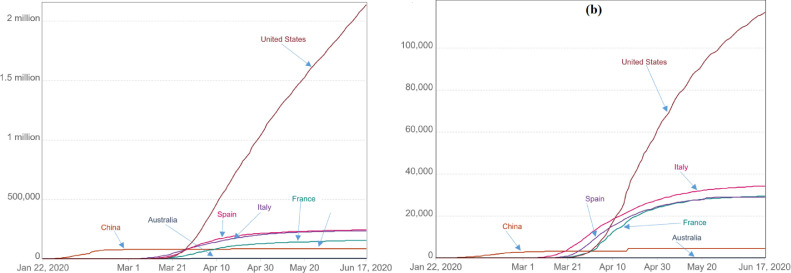
The first step to getting a better understanding of the COVID-19 data, the daily contaminated cases with the COVID-19 since its appearance until June 17, 2020, is displayed in Fig. 6 . It can be seen that this disease exponentially increased since its appearance and reached a high number of confirmed cases of 8349950, recovered cases 4073955, and deaths 448959. Due to the limited testing, the number of total cases is expected to be higher than the number of cases. The total number of U.S. coronavirus (COVID-19) deaths as of June 17, 2020, reaches 117,717 deaths, which is the United States the most affected country by this epidemic (Fig. 6). As shown in Fig. 6 Italy, Spain, and France are most affected European countries by the COVID-19, which shows a high growth with very quickly epidemic propagation with a high number of deaths that exceeds the threshold of 20,000 deaths. At the same time, it presents a considerable number of recovered persons. With the same pace as the previous European countries, recently, the United States American has presented a high increase of confirmed affected persons with less number of recovered and deaths. Australia is a country that has a considerable number of virus infections. However, compared with other countries it presents a remarkable number of recovered persons with the fewest deaths cases.
Fig. 6.
(a) Total confirmed contaminated COVID-19 cases and (b) COVID-19 deaths in Italy, Spain, France, USA, China, and Australia.
Table 1 gives a summary of each univariate time series used in this study. Here, the asymmetry and flatness of the traffic distribution are checked via the skewness and kurtosis statistics, respectively. Generally speaking, kurtosis with a value 3 is an indicator of Gaussian distribution. A kurtosis with a value 3 is an indicator of more peaked distribution than the Gaussian distribution and kurtosis less than 3 characterizes distributions that are flatter than Gaussian distribution. Moreover, the skewness statistic is computed to checking the asymmetry of the data distribution around the sample mean. Importantly, we recognize a skewed distribution to the left side by a skewness with a negative value and a distribution skewed to the right side by positive skewness. More information related to the location and spread of the dataset can be extracted using the other statistics including the standard deviation and quartiles. We can conclude from Table 1 that the confirmed and covered COVID-19 datasets are non-Gaussian distributed with positive support and exhibit a wide range of standard deviations.
Table 1.
Summary of the considered COVID-19 datasets.
| Min | Max | STD | Q-0.25 | Q-0.5 | Q-0.75 | Skew | Kurtosis | |
|---|---|---|---|---|---|---|---|---|
| Conf-Italy | 0 | 237,828 | 98930.476 | 771.5 | 126,790 | 220,515 | -0.035 | 1.247 |
| Reco-Italy | 0 | 179,455 | 62803.598 | 45.5 | 21405.5 | 107,813 | 0.772 | 2.025 |
| Conf-Spain | 0 | 244,683 | 104976.13 | 23.5 | 128,907 | 227,733 | -0.009 | 1.177 |
| Reco-Spain | 0 | 150,376 | 64187.728 | 2 | 36149.5 | 138059.5 | 0.348 | 1.364 |
| Conf-France | 0 | 189,906 | 81621.764 | 47.5 | 69541.5 | 175,730 | 0.101 | 1.170 |
| Reco-France | 0 | 70,223 | 27876.933 | 11 | 15810.5 | 56,093 | 0.349 | 1.400 |
| Conf-China | 548 | 84,458 | 23640.122 | 78,764 | 82572.5 | 84014.5 | -2.146 | 6.081 |
| Reco-China | 28 | 79,510 | 30217.499 | 34629.5 | 77076.5 | 79,210 | -1.038 | 2.338 |
| Conf-Australia | 0 | 7391 | 3257.1966 | 15 | 5618.5 | 6975 | -0.185 | 1.144 |
| Reco-Australia | 0 | 6877 | 2965.836 | 11 | 729 | 6241.5 | 0.344 | 1.243 |
| Conf-USA | 1 | 2,163,290 | 747576.74 | 20 | 351559.5 | 1,363,938 | 0.588 | 1.796 |
| Reco-USA | 0 | 592,191 | 184097.64 | 6.5 | 16,050 | 231,510 | 1.206 | 3.034 |
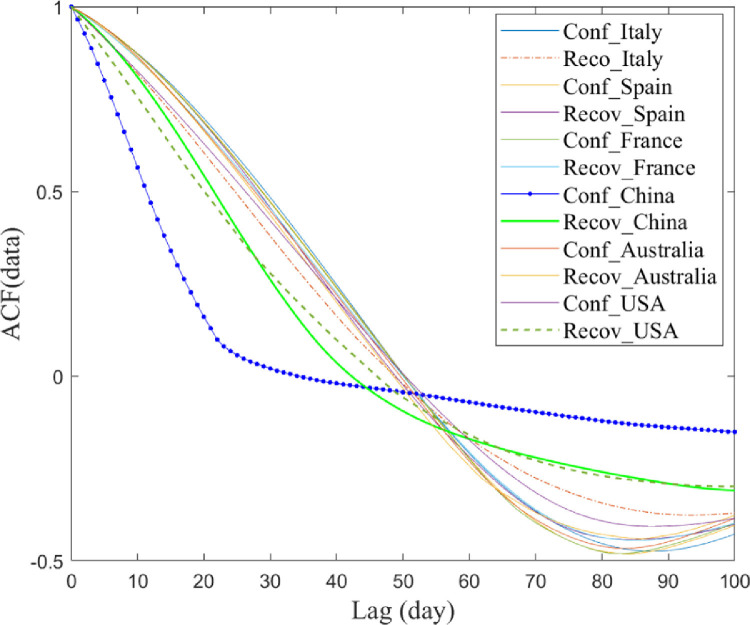
To verify the nonstationary and time-dependent behavior of COVID-19 time series data, the autocorrelation function (ACF) of confirmed and recovered daily cases is computed for each considered country (Fig. 7 ). Essentially, ACF is a time-domain metric that is able to quantify the stochastic process memory. Generally, for a signal, xt, the ACF is expressed as,
| (8) |
Fig. 7.
ACF of confirmed and covered COVID-19 time-series datasets in the considered countries.
Fig. 7 indicates the presence of relatively short-term autocorrelation in the studied COVID-19 time series data. Also, it can be observed the high similarity between the ACFs from the majority of data except the data recorded from the USA and Australia. This may be explained by the high spread of COVID-19 in the USA compared to the other countries and also low spread in Australia compared to the other high impacted countries (Italy, Spain, Italy, and China).
Five deep learning models will be used to handle the COVID-19 time-series datasets. It should be noted that the gated architectures RNN, LSTM, BiLSTM, GRU and VAE, owing to its data-driven approaches, are assumption-free regarding the underlying distribution of data. Also, they are very efficient in extracting relevant information from time-dependent data.
3.3. Forecasting results
This section will compare the forecasting performances of several neural networks time series forecasting models namely RNN, GRU, LSTM, BiLSTM and VAE. In this study, we focus on the univariate time-series data of daily conrmed and recovered cases from six considered countries Italy, Spain, France, the USA, China, and Australia. First, each model is trained with the training measurements. Then, we forecast each variable using the trained models for the unseen testing dataset. The training data consist of univariate time series data of confirmed and recovered cases from January 22, 2020, through May 31, 2020. Here, the challenge in this study is to investigate the performance of these five deep learning models in the presence of relatively small data. Parameters of the constructed RNN, LSTM, BiLSTM, GRU, and VAE models based on training datasets are presented in Table 2 .
Table 2.
Parameter settings of the studied approaches.
| Models | Parameter | Value |
|---|---|---|
| Visible units | 05 | |
| Latent dimension | 16 | |
| VAE | Learning rate | 0.0005 |
| Training epochs | 1000 | |
| Layers | 02 | |
| RNN | Learning rate | 0.0005 |
| Timestep | 05 | |
| Features | 01 | |
| Hidden units | 16 | |
| Training epochs | 1000 | |
| GRU | Learning rate | 0.0005 |
| Timestep | 05 | |
| Features | 01 | |
| Hidden units | 16 | |
| Training epochs | 1000 | |
| LSTM | Learning rate | 0.0005 |
| Timestep | 05 | |
| Features | 01 | |
| Hidden units | 16 | |
| Training epochs | 1000 | |
| BiLSTM | Learning rate | 0.0005 |
| Timestep | 05 | |
| Features | 01 | |
| Hidden units | 16 | |
| Training epochs | 1000 |
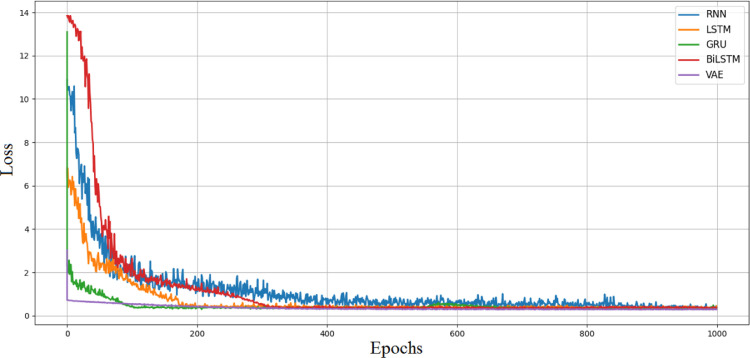
Fig. 8 displays the evolutions the loss function as a function of the number of epochs in RNN, LSTM, Bi-LSTM, GRU, and VAE during the training stage. It can be seen that the three models (RNN, LSTM, and GRU) converge very quickly and the RNN is relatively faster than the other models followed by GRU. This is mainly due to the fact that the RNN is a simple model and the GRU use directly all hidden states without control, and presents fewer computational parameters compared to LSTM, Bi-LSTM and VAE.
Fig. 8.
Convergence of the loss function of RNN, LSTM, Bi-LSTM, GRU, and VAE models during training stage.
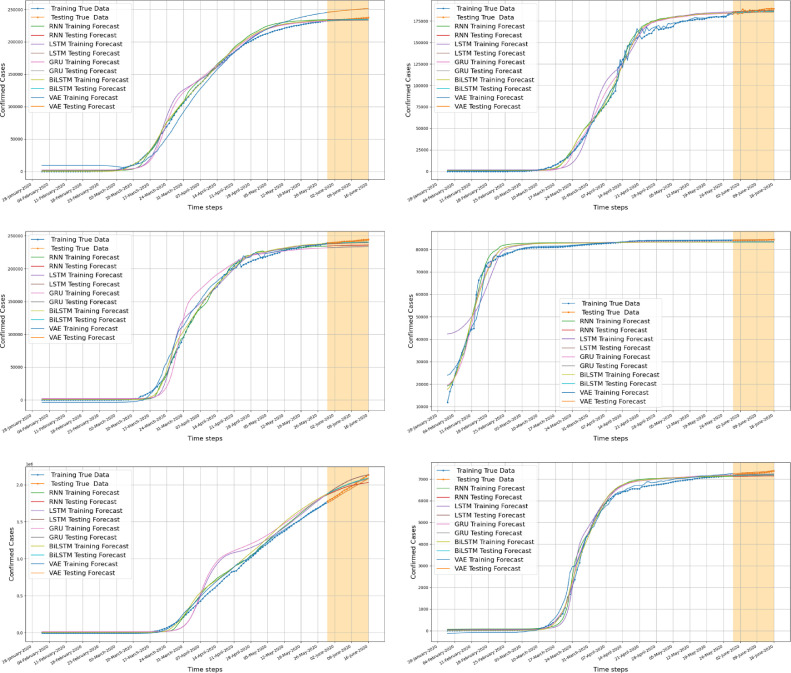
3.4. Forecasting new contaminated cases
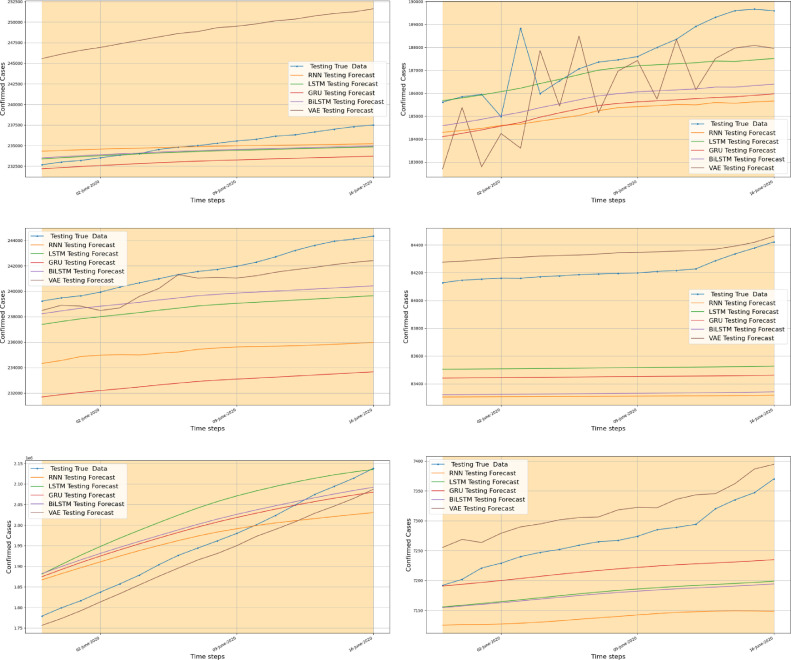
Now, the forecasting quality of the previously designed models will be verified using unseen testing data. The testing data consists of confirmed and recovered COVID-19 cases recorded in the six considered countries from 1st June to 17th June 2020. Fig. 9 (a–f) shows the forecasting results of the confirmed COVID-19 cases on the six consider countries using the five deep learning models. These models show good forecasting performance in the testing stage. To more clearly compare the forecasting results, Fig. 10 illustrates the measured and forecasted confirmed cases COVID19 using RNN, LSTM, BiLSTM, GRU, and VAE based only on the testing data of 17 days. As it can be observed in Fig. 10, the method VAE provides better forecasting of COVID-19 confirmed cases in comparison to the other considered models for almost all considered countries except in Italy. To assess quantitatively the performances of the five forecasting methods in one-ahead forecasting of new confirmed cases the metrics MAE, RMSE, MAPE, EV, and RMSLE values have been computed based on the testing measurements for each country and summarized in Table 3 . It can be easily seen that the VAE model outperformed the other models by providing good forecasting performance with lower RMSE, MAE, MAPE and RMSLE, and EV values colorer to 1 explaining most of the variance in the data, for all data countries except Italy. For illustration, the VAE model achieved MAPE values of 5.90%, 2.19%, 1.88%, 0.128%, 0.236%, and 2.04% for COVID-19 data form Italy, Spain, France, China, Australia, and the USA, respectively. It should be noted that this is the first time that the VAE model is applied for COVID-19 time series forecasting. Moreover, results show that the VAE method for forecasting new COVID-19 confirmed cases has superior performance. For Italy data, It is not obvious to tell which model is absolutely better on the basis of the RMSE, MAE, MAPE, and EV values. Indeed, the VAE model possesses a desirable feature that permits to track the trend of COVID-19 (Fig. 10) and explain the most variability in the data (i.e., EV=0.951 for Italy), however, it is penalized by larger RMSE compared to the other models. Thus, the efficiency of the VAE model for COVID-19 forecasting is promising and manifested. This fact is maybe due to the capacity of the VAE in dealing with small data compared to the other recurrent models (RNN, LSTM, Bi-LSTM, and GRU) which may need more lengthy data to extract relevant variability in time series data. On the other hand, RNN and its improved versions LSTM, BiLSTM, and GRU provide relatively moderate forecasting performance in terms of the evaluation metrics (RMSE, RMSE, MAPE, and RMSEL) and perform very poorly in terms of explained variance. This may be explained by the lack of a good amount of training data needed to capture the COVID-19 data dynamics.
Fig. 9.
Real and forecasted confirmed COVID19 cases using RNN, LSTM, BiLSTM, GRU and VAE (training and testing dataset) for (a) Italy, (b) France, (c) Spain, (d) China, (e) USA and (f) Australia. The orange band represent the forecast horizon.
Fig. 10.
Measured and forecasted confirmed COVID19 cases from 14 April to 21 April 2020 using RNN, LSTM, BiLSTM, GRU and VAE for (a) Italy, (b) France, (c) Spain, (d) China, (e) USA and (f) Australia.
Table 3.
Validation Metrics for confirmed cases COVID19 forecasting using RNN, LSTM, BiLSTM, GRU,and VAE models.
| Country | Model | RMSE | MAE | MAPE | EV | RMSLE |
|---|---|---|---|---|---|---|
| Italy | RNN | 1,070,474 | 1,062,061 | 4519 | 0201 | 00022 |
| GRU | 113,775 | 1,130,957 | 4813 | 0314 | 00025 | |
| LSTM | 1,054,089 | 1,046,257 | 4452 | 0267 | 00021 | |
| BiLSTM | 1,041,374 | 1,033,467 | 4398 | 0269 | 00021 | |
| VAE | 1,386,225 | 1,385,829 | 5901 | 0951 | 00033 | |
| Spain | RNN | 1,683,011 | 167,719 | 6944 | 0272 | 00052 |
| GRU | 1,795,678 | 1,791,683 | 7419 | 0467 | 0006 | |
| LSTM | 1,254,449 | 1,247,959 | 5166 | 0396 | 00028 | |
| BiLSTM | 1,194,711 | 1,187,629 | 4916 | 0372 | 00026 | |
| VAE | 5,315,748 | 5,288,172 | 2,19 | 0891 | 00005 | |
| France | RNN | 1,287,786 | 1,279,681 | 6827 | 0224 | 00051 |
| GRU | 1,204,139 | 1,196,438 | 6383 | 0311 | 00044 | |
| LSTM | 1,085,008 | 1,075,795 | 5738 | 0258 | 00036 | |
| BiLSTM | 1,168,893 | 1,160,923 | 6193 | 0308 | 00041 | |
| VAE | 3,688,083 | 3,522,353 | 1,88 | 0554 | 00004 | |
| China | RNN | 1,252,034 | 1,250,442 | 1485 | 0095 | 00002 |
| GRU | 1,085,698 | 1,083,975 | 1287 | 0151 | 00002 | |
| LSTM | 101,482 | 1,013,002 | 1203 | 0163 | 00001 | |
| BiLSTM | 1,205,955 | 1,204,413 | 1,43 | 0156 | 00002 | |
| VAE | 11,103 | 107,873 | 0128 | 0843 | 0 | |
| Australia | RNN | 39,928 | 397,443 | 5,47 | 0279 | 00032 |
| GRU | 295,978 | 293,738 | 4042 | 0349 | 00017 | |
| LSTM | 327,123 | 325,203 | 4476 | 0383 | 00021 | |
| BiLSTM | 335,033 | 333,098 | 4584 | 0363 | 00022 | |
| VAE | 18,732 | 17,186 | 0236 | 0952 | 0 | |
| USA | RNN | 5,227,287 | 5,136,497 | 26,373 | 0208 | 00967 |
| GRU | 4,369,108 | 4,240,145 | 21,697 | 0066 | 00635 | |
| LSTM | 1,129,183 | 1,123,909 | 58,008 | 0 | 07589 | |
| BiLSTM | 4,330,228 | 4,194,141 | 21,451 | 0024 | 00621 | |
| VAE | 4,079,244 | 3,976,682 | 2,04 | 0993 | 00004 |
3.5. Forecasting new recovered cases
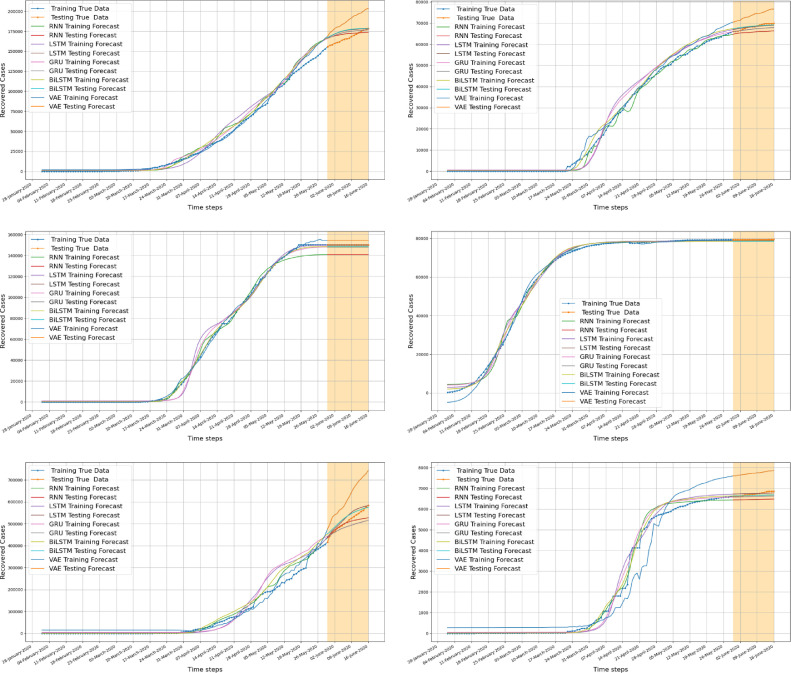
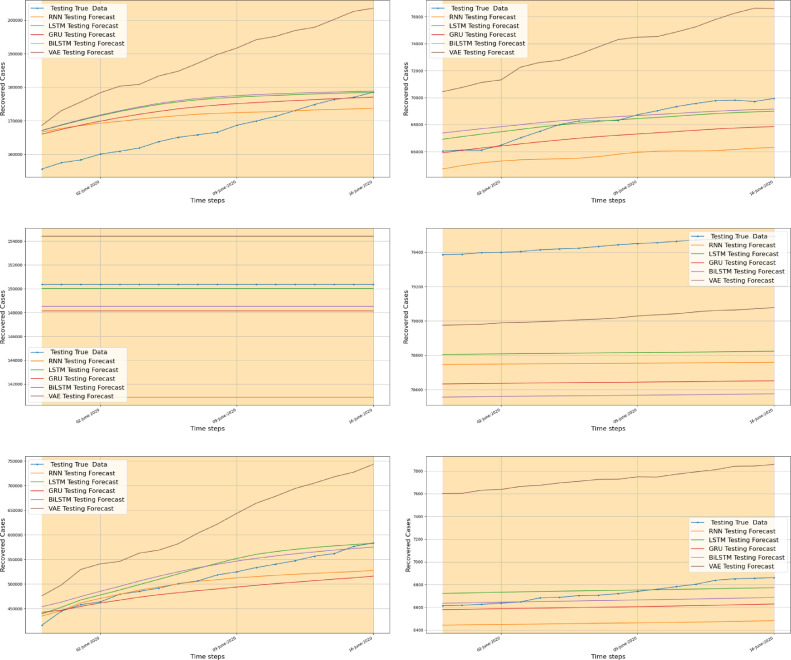
As for the new confirmed cases, we applied the five deep learning models to forecast the newly recovered cases. Fig. 11 displays the forecasting results of the recovered COVID-19 cases on the six considered countries using RNN, LSTM, BiLSTM, GRU, and VAE based forecasting models. The forecasting results of the RNN, LSTM, BiLSTM, GRU, and VAE based models follow the overall trend of the recorded recovered COVID-19 cases, indicating that the NN-based models can capture the time-dependent in the recovered COVID-19 data. Fig. 12 presents the forecasted recovered cases using RNN, LSTM, BiLSTM, GRU, and VAE models with the actual data from June 1st to June 17, 2020. These algorithms provide promising forecasting of the number of recovered cases in the six considered countries. This fact is due to their high capability to model non-linear and time-dependent data. Furthermore, the results reveal the potential in using deep learning models even in the presence of small data. Similar conclusions hold true for forecasting recovered COVID-19 time-series data, where the VAE again performs better among all the other models.
Fig. 11.
Real and forecasted recovered COVID19 cases using RNN, LSTM, BiLSTM, GRU and VAE models (training and testing dataset) for (a) Italy, (b) France, (c) Spain, (d) China, (e) USA and (f) Australia.
Fig. 12.
Measured and forecasted recovered COVID19 cases from 14 April to 21 April 2020 using RNN, LSTM, BiLSTM, GRU and VAE for (a) Italy, (b) France, (c) Spain, (d) China, (e) USA and (f) Australia.
The performance of RNN, LSTM, BiLSTM, GRU, and VAE models in terms of MAE, RMSE, MAPE, EV, and RMSLE when applied to the recovered COVID-19 data from six countries are summarized in Table 4 . The results confirmed the superiority of the VAE models compared to the other models (Table 4). The VAE can capture almost all variability in data and provide more accurate forecasting in comparison to the other RNN-based models. All other models perform moderate forecasting performance in terms of RMSE, MAE, MAPE, and RMSLE and show poor performance in terms of explained variance. This is maybe due to their need for more data in the training to capture the dynamics of COVID-19. The worst model is RNN because of its simplicity and followed by its extended versions of LSTM, Bi-LSTM, and GRU models.
Table 4.
Validation Metrics for recovered cases COVID19 forecasting.
| Country | Model | RMSE | MAE | MAPE | EV | RMSLE |
|---|---|---|---|---|---|---|
| Italy | RNN | 4,006,731 | 3,950,381 | 23,734 | 0103 | 00754 |
| GRU | 3,892,321 | 382,867 | 22,989 | 0017 | 00705 | |
| LSTM | 3,887,027 | 3,822,325 | 22,949 | 0002 | 00703 | |
| BiLSTM | 3,886,682 | 3,821,869 | 22,946 | 0 | 00702 | |
| VAE | 2,273,616 | 2,250,268 | 13,537 | 0789 | 00163 | |
| Spain | RNN | 9,460,326 | 9,460,326 | 6291 | 1 | 00042 |
| GRU | 2,221,248 | 2,221,248 | 1477 | 1 | 00002 | |
| LSTM | 368,623 | 368,623 | 0245 | 1 | 0 | |
| BiLSTM | 1,850,373 | 1,850,373 | 1,23 | 1 | 00002 | |
| VAE | 4,022,143 | 4,022,143 | 2675 | 1 | 00007 | |
| France | RNN | 100,203 | 9,943,735 | 14,594 | 0229 | 00253 |
| GRU | 8,467,965 | 8,380,523 | 12,294 | 0257 | 00176 | |
| LSTM | 7,880,727 | 7,771,507 | 11,395 | 0138 | 0015 | |
| BiLSTM | 785,049 | 773,904 | 11,347 | 0124 | 00149 | |
| VAE | 3,946,933 | 3,898,492 | 5,72 | 0808 | 00031 | |
| China | RNN | 856,465 | 855,913 | 1078 | 0,2 | 00001 |
| GRU | 957,498 | 957,048 | 1205 | 0269 | 00001 | |
| LSTM | 784,579 | 784,043 | 0987 | 0287 | 00001 | |
| BiLSTM | 1,031,264 | 103,086 | 1298 | 0295 | 00002 | |
| VAE | 415,008 | 414,998 | 0522 | 0993 | 0 | |
| Australia | RNN | 630,847 | 626,654 | 9,32 | 0213 | 00097 |
| GRU | 48,319 | 477,924 | 7105 | 0245 | 00055 | |
| LSTM | 35,956 | 35,174 | 5225 | 0,17 | 0003 | |
| BiLSTM | 429,146 | 423,132 | 6289 | 0235 | 00043 | |
| VAE | 972,236 | 972,169 | 1448 | 0,98 | 00183 | |
| USA | RNN | 2,301,648 | 2,256,944 | 44,603 | 0114 | 03612 |
| GRU | 2,252,458 | 220,556 | 43,556 | 0091 | 03399 | |
| LSTM | 2,227,272 | 2,175,034 | 42,894 | 0 | 0329 | |
| BiLSTM | 2,227,271 | 2,175,034 | 42,894 | 0 | 0329 | |
| VAE | 1,194,272 | 1,139,793 | 22,338 | 0447 | 0042 |
Overall, this study provided a comparison between deep learning models in forecasting the number of confirmed and recovered COVID-19 cases recorded from six different countries. This work highlights the potential of RNN, LSTM, BiLSTM, GRU, and VAE methods to be used for forecasting COVID-19 cases, even when applied to small COVID-19 training data sets. Essentially, these deep learning models are able to capture time-variant properties and relevant patterns of past data and forecast the future tendency of COVID-19 time-series data. The forecasting results show the superiority of the VAE model by achieving higher accuracy compared to the other models for one-step forecasting. This can be attributed to the great capacity of the VAE in capturing process nonlinearity and dealing with small times series data. Compared to the other herein forecasting models, the VAE presents the advantage of the lower dimensionality because of using reduced hidden units number. This last permits the extraction of the discriminative features. Generally speaking, there is no obvious answer here that one of them is better than the other, but for this application, the VAE model outperforms the other herein forecasting approaches used for the COVID-19 prediction.
4. Conclusion
The COVID-19 pandemic is exponentially spreading over the world, and the healthcare systems in some high impacted countries, such as Italy, Spain, France, and the United States are already overcrowded. Accurately forecasting the number of confirmed and recovered cases provides pertinent information to governments and decision-makers about the expected situation and the needed measures to impose. Also, forecasting information can be useful for motivating the wider public to consider the imposed measures for down slowing the spread of this virus. In this study, NN-based models including RNN, LSTM, BiLSTM, GRU, and VAE have been applied to the real-time forecasts of the daily confirmed and recovered COVID-19 cases in six different countries. This choice is highly motivated by the extended capacity of deep learning models in capturing process nonlinearity and their flexibility in modeling time-dependent data. Seventeen days-ahead forecasts are provided based on historical data of 148 days since January 22, 2020, for six countries namely Italy, Spain, France, China, USA, and Australia. The performance of each model has been verified in terms of RMSE, MAE, MAPE, EV and RMSLE. Results demonstrate that the VAE achieved better forecasting performance in comparison to all other models.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgment
This work was supported by funding from King Abdullah University of Science and Technology (KAUST), Office of Sponsored Research (OSR) under Award No: OSR-2019-CRG7-3800.
References
- 1.Velásquez R.M.A., Lara J.V.M. Forecast and evaluation of COVID-19 spreading in USA with reduced-space gaussian process regression. Chaos Solitons Fractals. 2020:109924. doi: 10.1016/j.chaos.2020.109924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Yousaf M., Zahir S., Riaz M., Hussain S.M., Shah K. Statistical analysis of forecasting COVID-19 for upcoming month in Pakistan. Chaos Solitons Fractals. 2020:109926. doi: 10.1016/j.chaos.2020.109926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ribeiro M.H.D.M., da Silva R.G., Mariani V.C., dos Santos Coelho L. Short-term forecasting COVID-19 cumulative confirmed cases: perspectives for Brazil. Chaos Solitons Fractals. 2020:109853. doi: 10.1016/j.chaos.2020.109853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Toğaçar M., Ergen B., Cömert Z. COVID-19 detection using deep learning models to exploit social mimic optimization and structured chest x-ray images using fuzzy color and stacking approaches. Comput Biol Med. 2020:103805. doi: 10.1016/j.compbiomed.2020.103805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Benvenuto D., Giovanetti M., Vassallo L., Angeletti S., Ciccozzi M. Application of the ARIMA model on the COVID-2019 epidemic dataset. Data Brief. 2020:105340. doi: 10.1016/j.dib.2020.105340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ceylan Z. Estimation of COVID-19 prevalence in Italy, Spain, and France. Sci Total Environ. 2020:138817. doi: 10.1016/j.scitotenv.2020.138817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Jia L., Li K., Jiang Y., Guo X., zhao T.. Prediction and analysis of coronavirus disease 2019. 2020. arXiv:2003.05447.
- 8.Peng L., Yang W., Zhang D., Zhuge C., Hong L.. Epidemic analysis of COVID-19 in China by dynamical modeling. arXiv:2002065632020;.
- 9.Roosa K., Lee Y., Luo R., Kirpich A., Rothenberg R., Hyman J. Real-time forecasts of the COVID-19 epidemic in China from february 5th to february 24th, 2020. Infect Dis Modell. 2020;5:256–263. doi: 10.1016/j.idm.2020.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Liu Z., magal p., Seydi O., Webb G. Understanding unreported cases in the COVID-19 epidemic outbreak in Wuhan, China, and the importance of major public health interventions. Biology. 2020;9(50) doi: 10.3390/biology9030050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.LiuZhihua and magal, pierre and Seydi, Ousmane and Webb, Glenn Predicting the cumulative number of cases for the COVID-19 epidemic in China from early data. medRxiv. 2020 doi: 10.1101/2020.03.11.20034314. [DOI] [PubMed] [Google Scholar]
- 12.Biswas K., Khaleque A., Sen P.. COVID-19 spread: reproduction of data and prediction using a sir model on euclidean network. 2020. arXiv:2003.07063.
- 13.Roosa K., Lee Y., Luo R., Kirpich A., Rothenberg R., Hyman J.M. Short-term forecasts of the COVID-19 epidemic in Guangdong and Zhejiang, China: february 13–23, 2020. J Clin Med. 2020;9(2):1–15. doi: 10.3390/jcm9020596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wu K., Darcet D., Wang Q., Sornette D.. Generalized logistic growth modeling of the COVID-19 outbreak in 29 provinces in China and in the rest of the world. 2020a. arXiv:2003.05681. [DOI] [PMC free article] [PubMed]
- 15.Sha He L.R., Sanyi T. A discrete stochastic model of the COVID-19 outbreak: forecast and control. Math Biosci Eng. 2020;17(4):2792–2804. doi: 10.3934/mbe.2020153. [DOI] [PubMed] [Google Scholar]
- 16.Dehesh T., Mardani-Fard H., Dehesh P. Forecasting of COVID-19 confirmed cases in different countries with ARIMA models. medRxiv. 2020 doi: 10.1101/2020.03.13.20035345. [DOI] [Google Scholar]
- 17.Gupta R., Pal S.K. Trend analysis and forecasting of COVID-19 outbreak in India. medRxiv. 2020 [Google Scholar]
- 18.Chintalapudi N., Battineni G., Amenta F. COVID-19 disease outbreak forecasting of registered and recovered cases after sixty day lockdown in Italy: a data driven model approach. J Microbiol Immunol Infect. 2020 doi: 10.1016/j.jmii.2020.04.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kucharski A.J., Russell T.W., Diamond C., Liu Y., Edmunds J., Funk S. Early dynamics of transmission and control of COVID-19: a mathematical modelling study. Lancet Infect Dis. 2020 doi: 10.1016/S1473-3099(20)30144-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Wu J.T., Leung K., Leung G.M. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: a modelling study. Lancet. 2020;395(10225):689–697. doi: 10.1016/S0140-6736(20)30260-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Zhuang Z., Zhao S., Lin Q., Cao P., Lou Y., Yang L. Preliminary estimation of the novel coronavirus disease (COVID-19) cases in iran: a modelling analysis based on overseas cases and air travel data. Int J Infect Dis. 2020;94:29–31. doi: 10.1016/j.ijid.2020.03.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kırbaş İ., Sözen A., Tuncer A.D., Kazancıoğlu F.Ş. Comperative analysis and forecasting of COVID-19 cases in various European countries with ARIMA, NARNN and LSTM approaches. Chaos Solitons Fractals. 2020:110015. doi: 10.1016/j.chaos.2020.110015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Rustam F., Reshi A.A., Mehmood A., Ullah S., On B., Aslam W. IEEE Access. 2020. COVID-19 future forecasting using supervised machine learning models. [Google Scholar]
- 24.Tuli S., Tuli S., Tuli R., Gill S.S. Predicting the growth and trend of COVID-19 pandemic using machine learning and cloud computing. Internet Things. 2020:100222. doi: 10.1016/j.iot.2020.100222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Chimmula V.K.R., Zhang L. Time series forecasting of COVID-19 transmission in canada using LSTM networks. Chaos Solitons Fractals. 2020:109864. doi: 10.1016/j.chaos.2020.109864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Hu Z., Ge Q., Li S., Jin L., Xiong M.. Artificial intelligence forecasting of COVID-19 in China. 2020. arXiv:2002.07112. [DOI] [PMC free article] [PubMed]
- 27.Pal R., Sekh A.A., Kar S., Prasad D.K.. Neural network based country wise risk prediction of COVID-19. 2020. arXiv:2004.00959.
- 28.rekha Hanumanthu S. Role of intelligent computing in COVID-19 prognosis: a state-of-the-art review. Chaos Solitons Fractals. 2020:109947. doi: 10.1016/j.chaos.2020.109947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Hochreiter S., Schmidhuber J. Long short-term memory. Neural Comput. 1997;9(8):1735–1780. doi: 10.1162/neco.1997.9.8.1735. [DOI] [PubMed] [Google Scholar]
- 30.Oksuz I., Cruz G., Clough J., Bustin A., Fuin N., Botnar R.M. 2019 IEEE 16th International symposium on biomedical imaging (ISBI 2019) IEEE; 2019. Magnetic resonance fingerprinting using recurrent neural networks; pp. 1537–1540. [Google Scholar]
- 31.Ashour A.S., El-Attar A., Dey N., El-Kader H.A., El-Naby M.M.A. Long short term memory based patient-dependent model for FOG detection in Parkinson’s disease. Pattern Recognit Lett. 2020;131:23–29. [Google Scholar]
- 32.Harrou F., Kadri F., Sun Y. Advanced statistical modeling, forecasting, and fault detection in renewable energy systems. IntechOpen; 2020. Forecasting of photovoltaic solar power production using LSTM approach. [Google Scholar]
- 33.Schuster M., Paliwal K.K. Bidirectional recurrent neural networks. IEEE Trans Signal Process. 1997;45(11):2673–2681. [Google Scholar]
- 34.Graves A., Schmidhuber J. Framewise phoneme classification with bidirectional LSTM and other neural network architectures. Neural Netw. 2005;18(5–6):602–610. doi: 10.1016/j.neunet.2005.06.042. [DOI] [PubMed] [Google Scholar]
- 35.Liu Z.-x., Zhang D.-g., Luo G.-z., Lian M., Liu B. A new method of emotional analysis based on CNN–BiLSTM hybrid neural network. Cluster Comput. 2020:1–13. [Google Scholar]
- 36.Sharfuddin A.A., Tihami M.N., Islam M.S. 2018 International conference on bangla speech and language processing (ICBSLP) IEEE; 2018. A deep recurrent neural network with BiLSTM model for sentiment classification; pp. 1–4. [Google Scholar]
- 37.Graves A., Jaitly N., Mohamed A.-r. 2013 IEEE workshop on automatic speech recognition and understanding. IEEE; 2013. Hybrid speech recognition with deep bidirectional LSTM; pp. 273–278. [Google Scholar]
- 38.Zhang B., Zhang H., Zhao G., Lian J. Constructing a PM2.5 concentration prediction model by combining auto-encoder with Bi-LSTM neural networks. Environ Modell Softw. 2020;124:104600. [Google Scholar]
- 39.Wang S., Wang X., Wang S., Wang D. Bi-directional long short-term memory method based on attention mechanism and rolling update for short-term load forecasting. Int J Electr Power Energy Syst. 2019;109:470–479. [Google Scholar]
- 40.Cho K., Van Merriënboer B., Gulcehre C., Bahdanau D., Bougares F., Schwenk H. 2014. Learning phrase representations using RNN encoder-decoder for statistical machine translation. [Google Scholar]; arXiv:14061078.
- 41.Kingma D.P. 2013. Fast gradient-based inference with continuous latent variable models in auxiliary form. [Google Scholar]; arXiv preprint arXiv:13060733.
- 42.Rezende D.J., Mohamed S., Wierstra D. 2014. Stochastic backpropagation and approximate inference in deep generative models. [Google Scholar]; arXiv preprint arXiv:14014082.
- 43.Gregor K., Danihelka I., Graves A., Rezende D.J., Wierstra D. 2015. Draw: a recurrent neural network for image generation. [Google Scholar]; arXiv preprint arXiv:150204623.
- 44.Chung J., Kastner K., Dinh L., Goel K., Courville A.C., Bengio Y. Advances in neural information processing systems. 2015. A recurrent latent variable model for sequential data; pp. 2980–2988. [Google Scholar]