Calibration of low-cost particulate matter sensors: model development for a multi-city epidemiological study

Abstract

Low-cost air monitoring sensors are an appealing tool for assessing pollutants in environmental studies. Portable low-cost sensors hold promise to expand temporal and spatial coverage of air quality information. However, researchers have reported challenges in these sensors’ operational quality. We evaluated the performance characteristics of two widely used sensors, the Plantower PMS A003 and Shinyei PPD₄₂NS, for measuring fine particulate matter compared to reference methods, and developed regional calibration models for the Los Angeles, Chicago, New York, Baltimore, Minneapolis-St. Paul, Winston-Salem and Seattle metropolitan areas. Duplicate Plantower PMS A003 sensors demonstrated a high level of precision (averaged Pearson’s r=0.99), and compared with regulatory instruments, showed good accuracy (cross-validated R²=0.96, RMSE=1.15 µg/m³ for daily averaged PM_2.5 estimates in the Seattle region). Shinyei PPD₄₂NS sensor results had lower precision (Pearson’s r=0.84) and accuracy (cross-validated R²=0.40, RMSE=4.49 µg/m³). Region-specific Plantower PMS A003 models, calibrated with regulatory instruments and adjusted for temperature and relative humidity, demonstrated acceptable performance metrics for daily average measurements in the other six regions (R²=0.74–0.95, RMSE=2.46–0.84 µg/m³). Applying the Seattle model to the other regions resulted in decreased performance (R²=0.67–0.84, RMSE=3.41-1.67 µg/m³), likely due to differences in meteorological conditions and particle sources. We describe an approach to metropolitan region-specific calibration models for low-cost sensors that can be used with caution for exposure measurement in epidemiological studies.

1. Introduction

Exposure to air pollution, including fine particulate matter (PM_2.5), is a well-established risk factor for a variety of adverse health effects including cardiovascular and respiratory impacts (EPA, 2012; Brunekreef & Holgate, 2002; EPA, 2018; Pope et al., 2002). Low-cost sensors are a promising tool for environmental studies assessing air pollution exposure (Jerrett, et al., 2017, Mead et al., 2013; Morawska et al., 2018; Zheng et al., 2018). These less expensive, portable sensors have potentially major advantages for research: a) investigators can deploy more sensors to increase spatial coverage; b) sensors are potentially easier to use, maintain, and require less energy and space to operate and; c) they can be easily deployed in a variety of locations (and moved from one location to another). Low-cost sensors have been proposed to stand alone or to be adjuncts to the existing federal air quality monitoring regulatory network that measure air pollution concentrations (Borrego et al., 2015, US EPA, 2013). However, optical particle sensors have demonstrated challenges that can include accuracy, reliability, repeatability and calibration (Castell et al., 2017; Clements et al., 2017). Several studies that examine specific individual sensors in laboratory environments report accuracy variation in pollutant concentrations among light scattering sensors (Austin et al., 2015; Manikonda et al., 2016). Other investigators have reported that low-cost sensors are sensitive to changes in temperature and humidity, particle composition, or particle size (Gao et al., 2015; Holstius et al., 2014; Kelly et al., 2017; Zheng et al., 2018). Recent evaluations of 39 low-cost particle monitors conducted by the South Coast Air Quality Management District’s AQ-SPEC program, using both exposure chamber and field site experiments comparing low-cost monitors and regulatory reference method instruments, found that performance varies considerably among manufacturers and models (SCAQMD AQ-SPEC, 2019).

In this study, we combined data from two monitoring campaigns used to measure PM_2.5 to: 1) evaluate the performance characteristics of two types of low-cost particle sensors; 2) develop regional calibration models that incorporate temperature and relative humidity; and 3) evaluate whether a region-specific model can be applied to other regions. We aimed to develop models we could use to develop exposure estimates in epidemiological analyses.

2. Methods

2.1. Contributing Studies and Monitoring Strategies

Air quality monitoring data were collected for the “Air Pollution, the Aging Brain and Alzheimer’s Disease” (ACT-AP) study, an ancillary study to the Adult Changes in Thought (ACT) study, and “The Multi-Ethnic Study of Atherosclerosis Air Pollution Study” (MESA Air), an ancillary study to the MESA study (ACT-AP, 2019; Kaufman et al., 2012; MESA Air, 2019).

The objective of ACT-AP is to determine whether there are adverse effects of chronic air pollution exposure on the aging brain and the risk of Alzheimer’s disease (AD). Low-cost monitoring at approximately 100 participant and volunteer homes in two seasons will be used in the development of spatio-temporal air pollution models. Predictions from these models will be averaged over chronic exposure windows. All low-cost monitors were co-located periodically with regulatory sites throughout the monitoring period.

MESA Air assessed the relation between the subclinical cardiovascular outcomes over a 10-year period and long-term individual level residential exposure to ambient air pollution) in six metropolitan areas: Baltimore, MD; Chicago, IL; Winston-Salem, NC; Los Angeles, CA; New York City, NY; and Minneapolis-St. Paul, MN. (Kaufman et al. 2012). A supplemental monitoring study to MESA Air was initiated in 2017 to support spatio-temporal models on a daily scale in order to assess relationships with acute outcomes. Between spring 2017 and winter 2019, MESA Air deployed low-cost monitors at four to seven locations per city with half co-located with local regulatory monitoring sites. The duration of each co-located low cost sensor’s monitoring period per study is presented in supplemental materials (SM; see Figure S1).

2.2. Monitor Characteristics

Low-cost monitors (LCMs) for both the ACT-AP and MESA studies were designed and assembled at the University of Washington. Each LCM contained identical pairs of two types of PM_2.5 sensors (described below) and sensors for relative humidity, temperature, and four gases (not presented here). Additional components included thermostatically controlled heating, a fan, a memory card, a modem, and a microcontroller running custom firmware for sampling, saving, and transmitting sensor data. Data were transmitted to a secure server every five minutes.

PM sensors were selected for this study primarily based on cost (≤$25/sensor), ease of use, preliminary quality testing, availability of multiple bin sizes, suitability for outdoor urban settings, and real-time response. Both selected PM sensors use a light scattering method (Morawska et al., 2018). The Shinyei PPD₄₂NS (Shinyei Corp, 2010) uses a mass scattering technique (MST). The Plantower PMS A003 is a laser based optical particle counter (OPC) (Plantower, 2016). The Shinyei PPD₄₂NS sensor routes air through a sensing chamber that consists of a light emitting diode and photo-diode detector that measures the near-forward scattering properties of particles in the air stream. A resistive heater located at the bottom inlet of the light chamber helps move air convectively through the sensing zone. The resulting electric signal, filtered through an amplification circuitry produces a raw signal (lo-pulse occupancy) which is proportional to particle count concentration (Holstius et al., 2014). Shinyei PPD₄₂NS sensors have shown relatively high precision and correlation with reference instruments but also high inter-sensor variability (Austin et al., 2015; Gao et al., 2015). The laser-based Plantower PMS A003 sensor derives the size and number of particles from the scatter pattern of the laser using Mie theory; these are then converted to an estimate of mass concentration by the manufacturer using pre-determined shape and density assumptions. The Plantower PMS A003 model provided counts of particles ranging in optical diameter from 0.3 to 10 micrometers. Different monitors that employ Plantower sensors have demonstrated high precision and correlation with reference instruments in field and laboratory experiments (Levy et al., 2018; SCAQMD AQ-SPEC, 2019), however some (e.g., the PurpleAir) use a different Plantower model than the PMS A003.

2.3. Co-location with Air Quality System (AQS) Monitors

EPA’s Air Quality System (AQS) network reports air quality data for PM_2.5 and other pollutants collected by EPA, state, local, and tribal air pollution control agencies. PM_2.5 is measured and monitored using three categorizations of methods: the Federal Reference Method (FRM); the Federal Equivalent Methods (FEMs), including the tapered element oscillating microbalance (TEOM) and beta attenuation monitor (Met-One BAM); and other non-FRM/FEM methods (US EPA, 2016b, US EPA, 2017). FRM is a formal EPA reference method that collects a 24-hour integrated sample (12:00 AM to 11:59 PM) of particles on a filter, weighs the mass in a low humidity environment, and divides by the air volume drawn across the filter. A FEM can be any measurement method that demonstrates equivalent results to the FRM method in accordance with the EPA regulations. Unlike filter-based FRM measurements, most FEMs semi-continuously produce data in real time. Some FEMs (e.g., TEOM) collect particles using a pendulum system consisting of a filter attached to an oscillating glass element; as the mass on the filter increases, the fundamental frequency of the pendulum decreases. Several TEOM models have a filter dynamic measurement system that is used to account for both nonvolatile and volatile PM components. Other FEMs (e.g., BAM) measure the absorption of beta radiation by particles collected on a filter tape. Data from FEM monitors are used for regulatory enforcement purposes.

Although most new TEOM and BAM instruments have been EPA-designated as a PM_2.5 FEM, some older semi-continuous TEOM or BAM monitors are still operating at NYC, Chicago, and Winston-Salem sites but are not approved by EPA as equivalent to FRM. The data from semi-continuous monitors is not used for regulatory enforcement purposes. Due to the unavailability of the EPA-designated FEM monitoring data in these locations, we included measures from the six TEOM or BAM non-regulatory monitors (NRMs) in our study. For simplicity, we refer collectively to data from TEOM and BAM NRMs as “FEM” regardless of the EPA classification (relevant sites are marked in Table 1).

Table 1:

Summary of co-location AQS sites

Regions	Stations	Site ID	Setting	PM2.5 refa	PM2.5 FEM including NRMd
				FRM (Frequency)	TEOMb	BAMc
Seattle Metropolitan Areas	Duwamish	PSCA1	Urban Center and Industrial		+	+
	Beacon Hill	PSCA3	Suburban	+ (1 in 3 days)	+
	10th & Weller	PSCA6	Urban			+
	Tacoma: South L	PSCA4	Suburban	+ (Daily)	+	+
	Kent	PSCA2	Suburban		+
	Marysville	PSCA5	Suburban		+
Los Angeles	Los Angeles Main St	L001	Urban Center	+ (Daily)		+
	Mira Loma	L(R)002	Urban	+ (Daily)		+
	Long Beach Near Road	L005	Urban	+ (Daily)		+
Baltimore	Essex	B003	Suburban	+ (1 in 6 days)
	Oldtown	B009	Urban Center	+ (Daily)		+
	Howard NR	B010	Near-road/Urban			+
	Padonia	B011	Suburban	+ (1 in 6/12 days)		+
Chicago	ComEd/Lawndale	C004	Urban Center	+ (1 in 6 days)		+*
	Northbrook	C008	Suburban	+ (1 in 3 days)		+
	SchillerPark	C009	(next to O’Hare)	+ (1 in 3 days)
New York City	IS52	N001	Urban	+ (1 in 3 days)	+
	NYBG	N003	Urban	+ (1 in 3 days)
	CCNY	N004	Urban		+*
	PS19	N005	Urban	+ (1 in 3 days)	+*
	Division	N006	Urban	+ (1 in 3 days)	+*
Minneapolis/St. Paul	Ramsey Health Center	S001	Urban Center	+ (1 in 3 days)
	Minneapolis Near Road	S005	Near Road/Urban			+
	Harding	S006	Suburban	+ (1 in 3 days)		+
Winston - Salem	Hattie	W001	Small city	+ (1 in 3 days)	+*
	Clemmons	W002	Suburban		+*

^a- Federal reference method (FRM) provided by EPA

^b- The tapered element oscillating microbalance (TEOM) is a federal equivalent method (FEM) that measures PM_2.5 mass concentrations. A filter dynamic measurement system is used to account for both nonvolatile and volatile PM components.

^c- The beta attenuation monitor (Met-One BAM) is a FEM that evaluates PM_2.5 mass on a filter tape based on the attenuation of beta radiation, minimizing loss of semi-volatile PM components.

^d- NRM - non-regulatory monitors;

^(*)Indicates NRMs whose method code is not classified by EPA as FEM. In present study NRMs were grouped into “FEM” category.

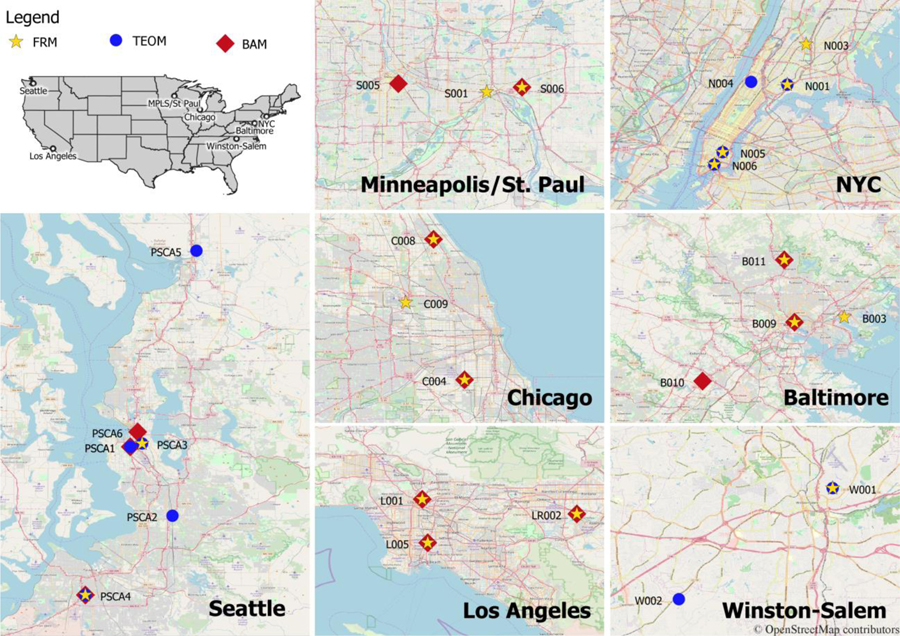
During 2017-2018, all 80 LCMs between the two above mentioned studies were co-located at regulatory stations in the AQS network in seven U.S. metropolitan regions: the Seattle metropolitan area, Baltimore, Los Angeles, Chicago, New York City, Minneapolis-Saint Paul area and Winston-Salem (see Figure 1). Criteria for selecting reference stations for sensor’s deployment included: proximity to ACT-AP and MESA Air participants’ homes; availability of instruments measuring PM_2.5; physical space for the LCMs at the regulatory station; and cooperation of site personnel.

Figure 1:

Map of regions covered by the ACT-AP and MESA Air studies with the locations of PM_2.5 reference sites.

Table 1 lists the regulatory stations included in our study, along with their location, setting, and method(s) of PM_2.5 measurement (see Figure 1 for maps of AQS sites). Data from regulatory sites were obtained from the “Air Quality System” EPA web server and Puget Sound Clean Air Agency (PSCAA) website (PSCAA, 2018; US EPA, 2018).

For the period of 2017-2018, several LCMs were relocated from one regulatory station to another. Due to the specific study goals, MESA sensors were often monitored continuously at one site for a long period, while most ACT sensors were frequently moved from site to site. For the ACT study and Baltimore subset of the MESA study, participant and community volunteer locations were monitored as well. These non-regulatory site data are outside the scope of this paper, and will not be presented further. The monitoring periods for each LCM is demonstrated in SM Section, Figure S1.

2.4. Sensor Quality Assurance and Data Monitoring

An automated weekly report was generated to flag specific data quality issues. We examined data completeness, concentration variability, correlation of duplicate sensors within a LCM, and network correlation with nearby monitors.

Five Plantower PMS A003 broken sensors were detected and replaced during March 2017 through December 2018. Several broken sensors consistently produced unreasonably high PM_2.5 values (sometimes a hundred times higher than the expected PM_2.5 average compared to a second sensor from the same box or for reported season and location). Other Plantower PMS A003 broken sensors were identified when one sensor of the identical pairs stopped sending monitoring data for particles, whereas the second sensor was still reporting.

We also examined Plantower PMS A003 sensors for drift. To determine if the sensor output drifted during the study period, Plantower PMS A003 sensors’ calculated PM_2.5 mass concentration data that were co-located for a long time period (>1 year) were binned by reference concentration (2.5 µm/m³ intervals) and then examined against reference data over time. No significant drift was found.

2.5. Analytical Methods and Modeling Decisions

Calibration models were developed using data from March 2017 through December 2018. LCMs recorded and reported measurements on a 5-minute time scale; these were averaged to the daily (12:00 AM to 11:59 PM) time scale to compare with reference data (either daily or hourly averaged to daily). Descriptive analyses that were performed at the early stage of examination included data completeness and exploration of operating ranges and variation that might affect sensor’s reading. These analyses addressed the influence of factors such as meteorological conditions, regional differences, and comparisons with different reference instruments. Multivariate linear regression calibration models were developed for each study region. The Seattle model was applied to measurements from the other regions to evaluate the generalizability of predictions from a single calibration model across regions.

2.5.1. Sensor Exclusion Criteria

Data from malfunctioning sensors were excluded from data analysis. We also excluded the first 8 hours of data after each deployment of the LCMs because occasional spikes of PM_2.5 concentrations were observed as the sensors warmed up.

The completeness in the collected data among all monitors that were deployed during March 2017 through December 2018 was 85.6%. The percent of completeness was estimated using observed “sensor-days” of all Plantower PMS A003 sensors’ data (i.e. duplicated sensors within the same monitor box were counted individually) divided by expected number of “sensor-days”. The percent of missing data among Plantower PMS A003 sensors was 14.4% due to following reasons: broken sensor/no data were recorded; clock related errors (no valid time variable); removal of the first 8 hours of deployment (see Section 2.5.1); failure in box operation (e.g. unplugged); and failure to transmit data. The percent of data completeness per sensor was on average 84.2% with a median of 94.7%. During the quality control screening, an additional 2.1% of remaining sensors’ data were excluded from the analysis due to broken or malfunctioning sensors as described above. After all the exclusion stages, approximately 84% of the expected data were useable (although only the subset of data co-located at reference sites is used to fit calibration models).

Outlier concentrations were observed on July 4^th and 5^th (recreational fires and fireworks) and in the Seattle metropolitan area during August 2018 (wildfire season). We excluded these data to prevent our models from being highly influenced by unusual occurrences. In the SM, we present results from a model in the Seattle region that includes these time periods (see Table S1). After exclusions were made, we also required 75% completeness of the measures when averaging sensor data to the hourly or daily scales.

Among 80 sensors that were deployed, data from 8 MESA sensors are not included in the analyses because they were not co-located at PM_2.5 regulatory stations during the time period selected for the data analysis, were co-located for less than a day, or were only co-located when the sensors were broken or malfunctioning.

2.5.2. Model Input Considerations

The calibration models incorporated the following decisions.

a). Duplicate Sensors

Each LCM included two of each type of PM_2.5 sensor (see Section 2.2). Paired measurements for each sensor type were averaged when possible. Single measurements were included otherwise.

b). Regulatory Station Instruments and Available Time Scales

For calibration purposes, we used data at co-location sites from days where both LCM and regulatory station data were available. FRM monitors provide 24-hour integrated measurement daily or once every three or six days. TEOM and BAM instruments provide hourly measurements that were averaged up to daily values. Both TEOM and BAM measures were available at the PSCA1 and PSCA4 sites in Seattle. At these sites, only the TEOM measure was used. The differences in reference instruments, including substitution of FEM data for FRM data in model fitting and evaluation, and a comparison of models fit on the hourly scale versus the daily scale are presented in the supplement (see SM Section, Table S2 and Table S3 respectively).

c). Temperature and Relative Humidity

Our models adjusted for temperature and relative humidity (RH), as measured by the sensors in the LCMs, to account for the known sensitivity of these sensors to changes in meteorological conditions (Casstell, 2017). Prior studies suggest a non-linear relationship between particle concentrations that are monitored by low-cost sensors and relative humidity (Chakrabarti et al., 2004; Di Antonio et al., 2018; Jayaratne et al., 2018). Jayaratne et al. (2018) demonstrated that an exponential increase in PM_2.5 concentrations was observed at 50% RH using the Shinyei PPD₄₂NS and at 75% RH using Plantower PMS1003. We tested both linear and non-linear RH adjustments (in models already adjusting for PM instrument measures and temperature splines). Our analysis showed similar to slightly worse model performance when correcting for RH with non-linear terms compared to a linear adjustment. Based on these results, we used a linear correction of RH for the calibration models.

d). Plantower PMS A003 Raw Sensor Data Readings

Plantower sensors provide two types of output values: 1) the count of particles per 0.1 L of air in each of the various bin sizes that represent particles with diameter beyond a specified size in µm (available count size bins: >0.3, >0.5, >1.0, >2.5, >5.0 and >10.0 µm) and 2) a device-generated calculated mass concentration estimate (µg/m³) for three size fractions (1.0, 2.5 and 10 µm) (Plantower, 2016).

The calibration models can be developed using the standard size-resolved counts or mass concentrations. For the transformation from size-resolved counts that are measured by particle sensors to mass concentrations, most researchers use the manufacturer’s device-generated algorithm for the sensor (Castell et al., 2017; Clements et al., 2017; Crilley et al., 2018; Northcross et al., 2013). The manufacturer’s algorithm for the correction factor (C) incorporates assumptions about potentially varying properties (e.g., density and shape) of the particles observed, but information on these assumptions and properties is not available. In our preliminary analyses, we evaluated both types of values (counts and mass) and transformations thereof (e.g. higher order terms, and natural log). We found that linear adjustment for bin counts provided the best results. We excluded the >10 µm bin from final models since it should primarily contain coarse particles.

e). Sensor Evaluation: Plantower PMS A003 vs. Shinyei PPD₄₂NS

We developed separate models for Plantower PMS A003 and Shinyei PPD₄₂NS PM_2.5 mass measurements in the Seattle metropolitan area. Sensors’ precision was evaluated comparing the daily averaged PM_2.5 mass measures from duplicate sensors within a box for each sensor type. The description of the form of the models and the results from model comparisons between the sensors for evaluation of the relative accuracy levels for the two sensors types are provided in Figure 2b and in the SM section, Equation S1.

2.5.3. Modeling Approach and Statistical Implementation

For our analysis, we used data from the total of 72 co-located LCMs in different regions and focused on region-specific calibration models for each sensor type (see Section 2.5.1). This allows calibration models tailored to regions with specific particle sources and to better adjust for factors such as meteorological conditions.

We considered several calibration models for each study region to understand how regulatory instrument differences, regional factors, and other modeling choices influence calibration models. We evaluated staged regression models based on cross-validated metrics as well as residual plots, in order to find a set of predictor variables that provided appropriate adjustment for sensor and environmental factors

We developed region-specific models with just FRM data and with FRM data combined with FEM data. In addition to these two region-specific models, we consider “out-of-region” predictions made with the Seattle model to evaluate the generalizability of calibration models across regions.

a). Region-Specific Daily FRM Models

We fit region-specific models using Plantower PMS A003 data on the daily time scale for each of the seven regions with FRM PM_2.5 measurements (µg/m³) as the outcome variable. These models included the count of particles per 0.1 L of air in each of the various bin sizes predictors (µm), linear adjustment for RH, and temperature adjustment with B-splines (knots at 40, 55, 70 and 85 degrees Fahrenheit). Each region had the same model form:

$$\begin{gathered} Y_i={\beta }_0+{\beta }_1*P{l}_{0.3,i}+{\beta }_2*P{l}_{0.5,i}+{\beta }_3*P{l}_{1,i}+{\beta }_4*P{l}_{2.5,i}+{\beta }_5*P{l}_{5,i}+{\beta }_6*R{H}_i \\ \hspace{0.17em}\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{1em}+{\beta }_7*S_1\left(Tem{p}_i\right)+{\beta }_8*S_2\left(Tem{p}_i\right)+{\beta }_9*S_3\left(Tem{p}_i\right)+{\beta }_{10}*S_4\left(Tem{p}_i\right) \\ \hspace{0.17em}\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{1em}+{\beta }_{11}*S_5\left(Tem{p}_i\right)+{ϵ}_i \end{gathered}$$ (1)

for i = 1, 2, … n. Here, Y_i = i^th observation of the FRM PM_2.5 (µg/m³) measurement, β₀:β₁₁ = regression coefficients, Pl_k,i = Plantower bin count for bin size k=0.3, 0.5, 1, 2.5, 5 µm, RH_i = relative humidity, S_k (Temp_i) for k=1, …, 5 = basis functions of the temperature splines, and ε_i = random error. The temperature and relative humidity values that were entered into the models are raw measures of low-cost monitor.

b). Region-Specific Combined FRM & FEM Models

We also developed models that combined FRM with daily averaged FEM data for each region in order to leverage a greater number of available days and locations. These models were of the same form as the region-specific daily FRM models (see Section 2.5.3(a)). Sensitivity analyses explored comparability of models that included different methods, since FEM measurements are noisier than FRM measurements.

c). Application of the Seattle Metropolitan Model to Other Regions

Out-of-region predictions using the combined FRM & FEM Seattle metropolitan model (see Section 2.5.3(b)) were generated for each region in order to explore the portability of a calibration model across regions.

2.5.4. Model Validation

We evaluated the daily FRM and combined FRM & FEM models with two different cross-validation structures: 10-fold (based on time) and “leave-one-site-out” (LOSO). Model performance was evaluated with cross-validated summary measures (root mean squared error (RMSE) and R²), as well as with residual plots. The 10-fold cross-validation approach randomly partitions weeks of monitoring with co-located LCM and FRM data into 10 folds. Typically, 10-fold methods partition data based on individual observations, but using data from adjacent days to both fit and evaluate models could result in overly optimistic performance statistics. We intended to minimize the effects of temporal correlation on our evaluation metrics by disallowing data from the same calendar week to be used to both train and test the models. In LOSO validation, predictions are made for one site with a model using data from all other sites in the region. This approach most closely mimics our intended use of the calibration model: predicting concentrations at locations without reference instruments. Since Winston-Salem has only one FRM site, the LOSO analysis could not be performed there.

A “leave-all-but-one-site-out” (LABOSO) cross-validation design was also performed to assess the generalizability of calibration models based on data from a single site. Models developed using data from a single site were used to predict observations from the remaining sites.

All statistical analyses were conducted in R version 3.6.0.

3. Results:

3.1. Site Descriptive Characteristics

Table 2 summarizes the co-location of the LCMs with regulatory sites. Certain regulatory sites had the same monitor co-located for a long period of time, and other sites had monitors rotated more frequently. The PSCA3 (Beacon Hill) site in Seattle often had many LCMs co-located at the same time. The highest average concentrations of PM_2.5 during 2017-2018 were observed in the LA sites (12.4-13.7 µg/m³) along with the highest average temperatures (66–67°F). The largest observed difference in average PM_2.5 concentrations across sites was observed in the Seattle metropolitan region (5.6 – 9.3 µg/m³).

Table 2:

Co-located monitors across regions in the period of 2017-2018

Region	Site IDs	No. Monitors Ever Co-located	Co-location Days with FRM Referencea	Co-location Days with TEOM/BAM Referencea	PM2.5 Concentration (µg/m3) Mean (SD)b,c	Average Temperature (°F) Mean (SD)b,d	Average RH% Mean (SD)b,d
Seattle metropolitan	PSCA1e	24	---	223 (580)	9.3 (6.2)*	59 (7)	70 (12)
	PSCA2	15	---	522 (738)	6.1 (6.4)*	57 (10)	74 (14)
	PSCA3	52	166 (856)	510 (2320)	5.6 (3.6)	53 (8)	76 (12)
	PSCA4	1	480 (480)	533 (533)	8.3 (8.0)	51 (11)	84 (14)
	PSCA5	2	---	439 (439)	7.4 (6.7)*	53 (11)	82 (13)
	PSCA6	1	---	480 (480)	8.9 (6.8)*	58 (8)	72 (10)
LA	L001	7	536 (539)	554 (563)	12.4 (6.4)	67 (7)	64 (13)
	L(R)002	1	359 (359)	363 (363)	13.7 (9.0)	66 (8)	58 (14)
	L005	1	495 (495)	501 (501)	12.7 (8.7)	66 (5)	66 (12)
Baltimore	B003	2	131 (131)	---	7.9 (4.3)	60 (12)	67 (15)
	B009	11	352 (857)	541 (1254)	8.2 (4.3)	63 (12)	66 (16)
	B010	2	---	590 (590)	8.9 (3.8)*	60 (13)	74 (16)
	B011e	2	27 (44)	294 (463)	7.0 (3.7)	59 (14)	64 (18)
Chicago	C004	6	100 (101)	598 (605)	8.5 (4.3)	57 (14)	66 (13)
	C008	1	168 (168)	490 (490)	7.9 (4.2)	55 (14)	68 (14)
	C009	1	195 (195)	---	10.7 (5.0)	56 (14)	64 (13)
NYC	N001	6	218 (218)	366 (370)	7.5 (3.9)	59 (13)	65 (15)
	N003	6	219 (221)	---	8.0 (4.3)	58 (13)	69 (16)
	N004	1	---	617 (617)	8.1 (3.3)*	57 (13)	65 (16)
	N005	1	54 (54)	231 (231)	8.8 (4.2)	60 (13)	64 (16)
	N006	2	206 (206)	612 (613)	9.2 (4.0)	59 (13)	66 (15)
Minneapolis/St. Paul	S001	1	169 (169)	---	8.1 (4.3)	57 (15)	59 (14)
	S005	5	---	195 (197)	7.0 (3.4)*	60 (12)	70 (13)
	S006e	1	68 (68)	200 (200)	6.5 (3.5)	63 (9)	68 (13)
Winston - Salem	W001	5	174 (174)	270 (278)	7.7 (3.4)	64 (11)	73 (15)
	W002	1	---	265 (265)	8.2 (3.1)*	62 (10)	78 (14)

Notes:

^a- These columns reports unique days (monitor-days) when both LCM data and regulatory station reference data are available. The days presented in the FRM and TEOM/BAM columns overlap considerably, since a day with FRM & FEM reference data will add to both columns.

^b- The average concentration/temperature/RH values were averaged across daily observations at the site when both LCM and agency reference data were available, and thus depend on co-location schedule which may differ across sites.

^c- Mean and standard deviation PM_2.5 concentrations are calculated using FRM measurements when available. If FRM measurements are not available, then TEOM or BAM measurements are used.

^(*)- The average is from FEM monitors.

^d- The average temperature/RH values were estimated based on the low-cost sensors measurements. Values were calibrated with reference temperature/RH data from the PSCA3 Seattle site in order to present recognizable units.

^e- Most monitors were co-located and monitored during 2017-2018. Monitors at sites PSCA1 and S006 were deployed and monitored only during 2017 while monitors at site B011 were only deployed during 2018.

3.2. Comparison of Reference Instruments

Table 3 presents the Pearson correlation between FEM and FRM reference instruments at all sites where both types of instruments are available. The correlations of FRM with BAM are high at most sites, with only Chicago Lawndale (C004) having considerably lower correlation (r=o.78, RMSE=4.23 µg/m³). Reference stations with TEOM showed a somewhat lower correlation with FRM at the NYC sites (r=0.84–0.88, RMSE=2.14-2.62 µg/m³) compared to Winston-Salem and Seattle metropolitan regions (r=0.95–0.99, RMSE=0.71-1.82 µg/m³). The results justify the use of FRM data whenever possible, but the generally good correlation tend to support the incorporation of FEM data into the models in cases where FEM monitoring instruments have greater temporal and/or spatial coverage than FRM instruments.

Table 3:

The correlation between BAM/TEOM and FRM PM_2.5 daily averaged measurements by site

Region	Site ID	Days with BAM	FRM-BAM Pearson’s r	BAM RMSE	Days with TEOM	FRM-TEOM Pearson’s r	TEOM RMSE
Seattle	PSCA3	---	---	---	149	0.99	0.71
Metropolitan	PSCA4	309	0.98	2.44	385	0.98	1.82
LA	L001	532	0.96	4.86	---	---	---
	L(R)002	337	0.97	3.21	---	---	---
	L005	457	0.97	3.07	---	---	---
Baltimore	B009	345	0.93	1.68	---	---	---
	B011	25	0.94	1.34	---	---	---
Chicago	C004*	91	0.78	4.23	---	---	---
	C008	149	0.93	1.76	---	---	---
NYC	N001	---	---	---	115	0.88	2.62
	N005*	---	---	---	53	0.84	2.50
	N006*	---	---	---	188	0.87	2.14
Minneapolis/St. Paul	S006	66	0.98	0.81	---	---	---
Winston-Salem	W001*	---	---	---	76	0.95	1.10

Note:

^(*)Indicates sites with NRMs (TEOM/BAM) whose method code is not classified by EPA as FEM. In present study NRMs were grouped into “FEM” category

3.3. Sensor Precision and Accuracy

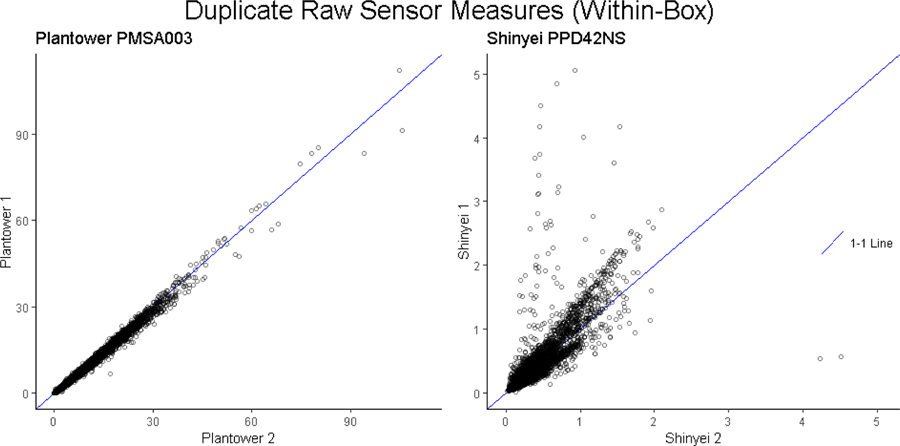
Plots comparing the calculated daily average PM_2.5 measures from duplicate Plantower PMS A003 sensors within a box and daily averaged raw sensor readings from duplicate Shinyei PPD₄₂NS are provided in Figure 2a. After removing invalid data, the PM_2.5 manufacturer-calculated mass measurements from all duplicate Plantower PMS A003 sensors within a box had a mean Pearson correlation of r=0.998, (min r=0.987 and max r=1), compared to all Shinyei PPD₄₂NS sensors’ raw readings average correlation of r=0.853, min r=0.053, max r= 0.997). Some Shinyei PPD₄₂NS sensors demonstrated a strikingly poor correlation between duplicate sensors within a monitor. In addition to having weaker precision, the quality control was more difficult with Shinyei PPD₄₂NS sensors, as it was harder to distinguish concentration-related spikes from the large amounts of sensor noise. For this reason, during our quality control procedures we removed all data above a particular threshold that was defined during preliminary analysis (raw measurement hourly averages above 10, which is almost certainly an incorrect raw measurement). We also removed data if either of the two paired sensors had a value 10 times greater than the other.

Figure 2a:

Correlation between duplicate sensors within a box

Note: Plantower PMS A003 measures are the manufacturer calculated daily averaged PM_2.5 mass; Shinyei PPD₄₂NS measures are daily averaged raw sensor readings (low pulse occupancy). Data from all regions are included.

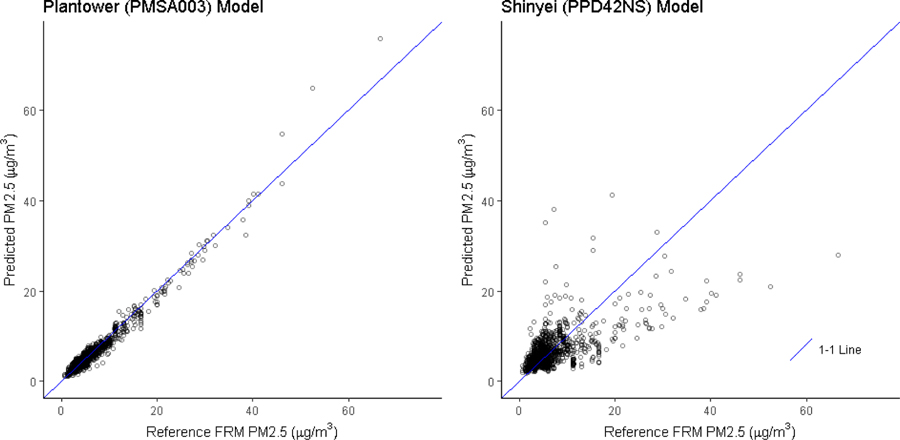
Comparison of calibration models developed using calculated PM_2.5 mass measures with each sensor type fit with Seattle combined FRM & FEM data demonstrated that the Plantower PMS A003 sensors performed better than Shinyei PPD₄₂NS sensors. The results for this analysis are given in Figure 2b. According to the results of precision and accuracy evaluation of both sensors, our primary analysis that follows is limited to use of Plantower PMS A003 data.

Figure 2b:

Relationship of Plantower PMS A003 and Shinyei PPD₄₂NS PM_2.5 daily scale model predictions with PM_2.5 FRM measurements in the Seattle metropolitan areas.

Note: Both models were evaluated against the subset of 1308 FRM monitor-days in Seattle with both Plantower PMS A003 and Shinyei PPD₄₂NS data.

3.4. Model Evaluation

3.4.1. Region Specific FRM Daily Models

In Table 4, we present calibration model performance summaries in each of the seven study regions adjusted for temperature and RH. The coefficient estimates for the region-specific models are also presented in the supplement (see Figure S2 and Tables S4a and S4b)). The region-specific models fit with FRM data have strong performance metrics with 10-fold cross-validation (R²=0.80–0.97; RMSE=0.84-2.26 µg/m³). The LOSO measures are less strong (R²=0.72-0.94; RMSE=1.09-2.54 µg/m³), most notably for Seattle. However, this difference is not surprising with low numbers of sites (such as two sites in the Seattle metropolis).

Table 4:

Performance of calibration models for Plantower PMS A003 low-cost sensors in each region, evaluated with regulatory FRM monitoring sites

Region	FRM Daily Modela,b				Combined FRM & FEM Daily Modela,c				Seattle Combined FRM & FEM Modela,d
	Sitese,f	Obs. (wks)g,h	LOSO RMSE (R2)	10-fold RMSE (R2)	Sitese	Obs. (wks)g, i	LOSO RMSE (R2)	10-fold RMSE (R2)	RMSE (R2)
Seattle Metropolitan	2	1336 (84)	2.13 (0.86)	1.02 (0.97)	6	5010 (88)	1.27 (0.95)	1.15 (0.96)	---
LA	3	1393 (80)	2.54 (0.90)	2.26 (0.92)	3	1432 (80)	2.55 (0.90)	2.27 (0.92)	3.41 (0.83)
Baltimore	3	1032 (90)	1.09 (0.94)	1.00 (0.95)	4	2377 (92)	1.73 (0.85)	1.37 (0.90)	1.80 (0.84)
Chicago*	3	464 (91)	2.49 (0.72)	2.10 (0.80)	3	1256 (91)	3.06 (0.62)	2.46 (0.74)	2.76 (0.67)
NYC*	4	699 (96)	1.83 (0.80)	1.67 (0.84)	5	2029 (96)	1.88 (0.79)	1.81 (0.81)	1.69 (0.83)
Minneapolis/St. Paul	2	237 (77)	1.62 (0.85)	1.13 (0.92)	3	555 (77)	1.38 (0.89)	1.22 (0.91)	1.94 (0.78)
Winston-Salem*	1	174 (78)	---	0.84 (0.94)	2	598 (78)	---	1.04 (0.90)	1.67 (0.79)

Notes:

^a–All models are only evaluated against FRM data, regardless of what data are used to fit the models.

^b– Models based on average PM_2.5 Plantower PMS A003 measures against available FRM daily data.

^c– Models based on average PM_2.5 Plantower PMS A003 measures against FRM daily data when available with daily averaged TEOM or BAM measurements when FRM measurements are not available.

^d– Models based on average PM_2.5 Plantower PMS A003 measures in Seattle against combined daily FRM & FEM daily averaged measurements. The model was fit with 5010 monitor-days at 6 Seattle sites over 88 weeks (1336 FRM, 3243 TEOM, 431 BAM) and then used to make predictions in other regions.

^e– Number of sites used to fit the model. With the LOSO cross-validation method, each model is actually fit with one fewer site than the total number of sites listed.

^f– Since we evaluate against FRM data, this is the number of sites that all models are evaluated against.

^g– Total number of observations, in monitor-days, and unique weeks used to fit the models. The 10-fold CV models are actually fit with on average 90% of the total monitor-days, and each LOSO CV model is fit with on average (#sites-1)/(#sites)*100% of the total monitor-days.

^h– Since we evaluate against FRM data, these are the number of observations and unique weeks used to evaluate predictions. The unique weeks with FRM data were also what were randomly partitioned to create the 10-fold cross-validation folds.

ⁱ– The number of FEM monitor-days incorporated into the model can be calculated by taking this column and subtracting the monitor-days used for the FRM model. The additional FEM observations are used to fit models, but evaluation is only done with FRM data. Since the 10-fold CV folds are based on the unique weeks with FRM data, this means that when regions have additional weeks with FEM data and no FRM data, these weeks will contribute to each 10-fold CV model fit, but the weeks will never be used in model evaluation.

^(*)Indicates that for these regions FEM includes data from NRMs whose method code is not classified by EPA as FEM. In present study NRMs were grouped into “FEM” category.

The FRM daily results for Chicago show lower R² and higher RMSE compared to other regions (10-fold cross-validation R²=0.80; RMSE=2.10 µg/m³ and LOSO R²=0.72; RMSE=2.49 µg/m³). The LA model has high RMSE and R² (10-fold cross-validation: RMSE=2.26 µg/m³, R²=0.92; LOSO: RMSE=2.54 µg/m³, R²=0.90). At the same time, LA has the highest average concentrations of any region (see Table 2).

By incorporating FEM reference data, we increased the number of observations and, in some metropolitan regions, the number of sites available to fit the model (Table 4). The most data were added to the Seattle metropolitan model, which dropped the LOSO RMSE from 2.13 to 1.27 µg/m³. However, the 10-fold cross-validation RMSE increases slightly from 1.02 to 1.15 µg/m³. The decrease seen with the LOSO measures in Seattle is reasonable since with only two FRM sites, each model is based on a single site, whereas with six combined FRM and FEM sites, each model is fit with five sites. We see a similar result in Minneapolis-St Paul, which also has two FRM sites. Otherwise, we observe slightly weaker summary measures when FEM data are included in the models. This may be partially attributable to weaker correlations of FRM to FEM reference methods shown in Section 3.2. It also could be due to differences in the sites, as additional FEM sites and times were used for fitting the models but only FRM data were used for evaluation.

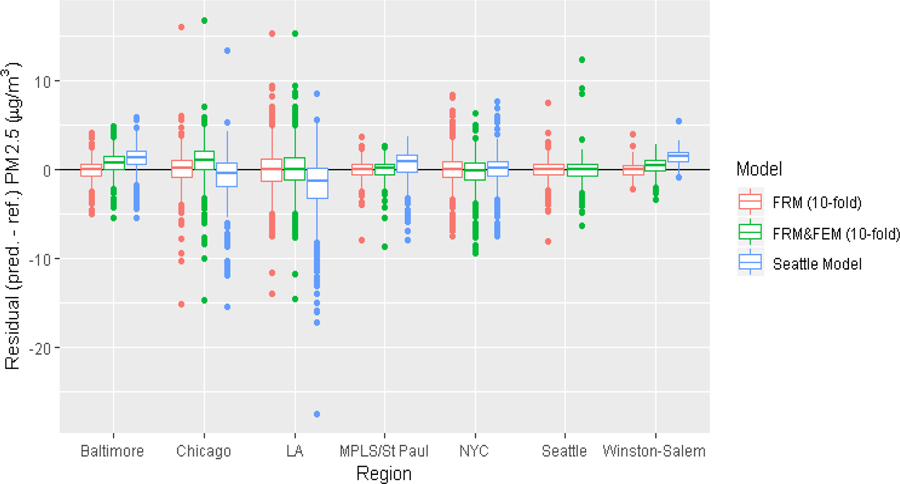
3.4.2. Application of Seattle Metropolitan Model to Other Regions

In most metropolitan regions, we find the Seattle metropolitan combined FRM & FEM model predictions to be weaker than those made with the region-specific models (see Table 4). The Seattle metropolitan model is less successful in LA compared to the LA region specific model (R²=0.83, RMSE=3.41 µg/m³ and R²=0.90–0.92, RMSE=2.26-2.55 µg/m³ respectively), where the Seattle model predictions are consistently lower than the reference concentrations (see Figure 3). We see similarly systematic differences in the Seattle metropolitan model predictions in Winston-Salem, where concentrations are consistently overestimated, and in Chicago, where low concentrations are overestimated, and high concentrations are underestimated (Figure 3). The best results of the Seattle metropolitan model are observed in NYC (R²=0.83, RMSE=1.69 µg/m³, Table 4), which is comparable to the NYC region-specific models (R²=0.79–0.84, RMSE=1.67-1.88 µg/m³, Table 4).

Figure 3:

The comparison of distributions of calibration model residuals between different types of models in each region.

Note: Figure shows boxplots of model residuals from the FRM daily model (10-fold cross-validation), FRM & FEM daily model (10-fold cross-validation), and Seattle out-of-region model. The models were evaluated against FRM PM_2.5 monitoring sites;

3.4.3. The Impact of Temperature and Relative Humidity

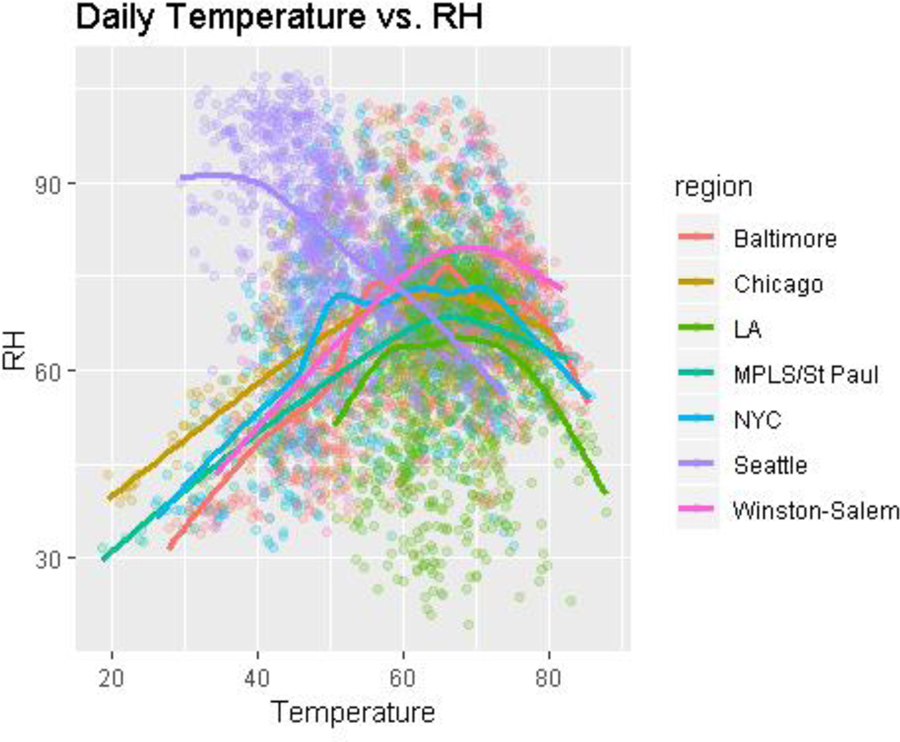
The distributions of temperature and RH across different study regions are presented in Figure 4. We observe that Chicago, NYC, Minneapolis-St. Paul, Winston-Salem and Baltimore have similar temperature/RH distributions, with the lowest RH values at high and low ends of the temperature levels, and highest RH measurements inside the temperature range of about 60–70°F. In LA, the trend is similar but restricted to temperatures above 50°F. The Seattle metropolitan region shows a different pattern, with a fairly linear inverse relationship between temperature and RH.

Figure 4:

Correlation between daily averaged temperature (°F) and RH measures within low-cost monitors across different regions

Note: low-cost sensors readings of temperature and RH were calibrated with reference temperature/RH data from Seattle, Beacon Hill site in order to present standard units.

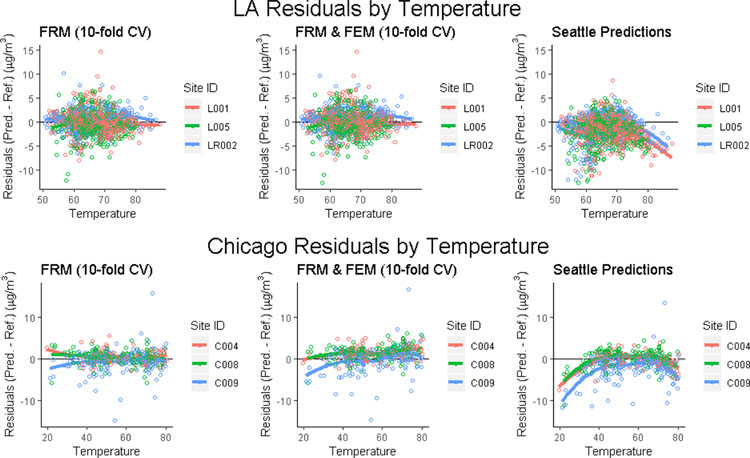
Differences in environmental conditions across regions contribute to differences between regional models and to poor predictive performance of the Seattle model in other regions. For example, residual plots of predicted concentrations show poor performance at high temperatures in LA, while the LA regional models are noticeably better at high temperatures (Figure 5). Similarly, poor performance of the Seattle model is observed in Chicago at high and low temperatures, compared to the Chicago-specific models.

Figure 5:

Residuals by temperature (°F) from different calibration models in LA and Chicago.

Note: low-cost sensors readings of temperature were calibrated with reference temperature data from Seattle, Beacon Hill site in order to present standard units.

4. Discussion

This analysis demonstrates the performance of two co-located low-cost sensors deployed in seven metropolitan regions of the United States, and describes approaches to calibrating results for potential use in environmental epidemiological studies. We fit region-specific calibration models using FRM data as the outcome, or FRM data supplemented with daily averaged FEM data, along with adjustment for temperature and humidity measures. We found that good calibration models were feasible with the Plantower PMS A003 sensor only. We also tested the generalizability of the Seattle calibration model to other metropolitan regions, and found that climatological differences between regions limit its transferability.

Our models were built based on time series data from different regions to cover temporal, seasonal, and spatial variations that are considered in every environmental study. When building the calibration models, we compared different reference instruments available at co-located sites and used two cross-validation designs.

In order to approach our study goal we chose to derive the calibration models fully empirically, as documentation was not available to determine that the size bin techniques for this optical measurement approach are fully validated or whether the cut-points provided by the sensor were applicable or accurate under the conditions in which we deployed our sensors. According to the product data manual for Plantower PMS A003 strengths (2016), each size cut-off “bin” is: “…the number of particles with diameter beyond [size] µm in 0.1 L of air”, with cut-offs at 0.3 µm, 0.5 µm, 1 µm, 2.5, 5 µm, 10 µm. No other specifications are provided. As with other optical measurement methods, we anticipate there is error associated with the cut-point of each bin, and are biases due to the fact that the particle mix we measured differed from the particle mix used by the manufacturer in their calibration method. We also suspect that the Plantower PMS A003 instrument measures some particle sizes more efficiently than other, in particular some optical sensors are less sensitive to particles below 1 µm in diameter. Therefore, using exploratory analyses we developed best fitted calibration models for PM_2.5 which we described in Table 4. However, we recognize that such models could be developed in different ways. Therefore, we have tested other model specifications with different transformations of the Plantower PMS A003 sensor counts and different sets of included bin sizes. We developed daily averaged regional calibration models using differences of the original Plantower PMS A003 count output in various size bins (which represent particles [size]µm and above), in order to define variables for the Plantower PMS A003 count size bins (0.3 to 0.5 µm), (0.5 to 1 µm), (1 to 2.5 µm). This allowed us to minimize the potential correlation effect between count size bins inside the model and to exclude counts of particles that are larger than 2.5 µm for a theoretically better comparison with federal instruments (EPA 2001). In order to account for particles that are equal or larger than 2.5 µm but less than 10 µm, we included two additional variables: (2.5 to 5 µm) and (5 to 10 µm) count size bins differences into separate models. The results in Table S5 (see SM Section) suggest that the best performing models are those which adjust for raw Plantower PMS A003 count size bins or those which adjust for differences of the Plantower PMS A003 count size bins but including particles larger than 2.5 µm (especially the model including particles in optical diameter up to 10 µm). The models are not very different, but we observed slightly better predictive performance in the original model which uses all of the available count size bin data (except 10 µm bin) from the device. The contribution of larger than 2.5 µm size bins to the PM_2.5 mass prediction estimate might be explained by size misclassification and by the particular source of PM_2.5 emissions (the sensor may respond differently to particles with varying optical properties apart from size).The results of our analysis are consistent with other studies involving Plantower PMS A003 and Shinyei PPD₄₂NS PM_2.5 low-cost sensors at co-located stations. Zheng et al. (2018) demonstrated an excellent precision between Plantower PMS A003 sensors and high accuracy after applying an appropriate calibration model that adjusted for meteorological parameters. Holstius et al. (2014) found the Shinyei PPD₄₂NS data were more challenging to screen for data quality, and showed poorer accuracy and weaker performance of calibration models, though findings by Gao et al. (2015) differed. The calibrated Shinyei sensors evaluated by Holstius et al. in California, US, explained about 72% of variation in daily averaged PM_2.5. Gao et al. deployed Shinyei PPD₄₂NS sensors in a Chinese urban environment with higher PM_2.5 concentrations and was able to explain more of the variability (R²>0.80). The differences in these reported results for calibration models are potentially due to the Shinyei’s PPD₄₂NS higher limit of detection and noisier response, which would limit their utility in lower pollution settings.

Our results are also concordant with prior findings that low-cost sensor performance results vary across regions and are influenced by conditions such as temperature, RH, size and composition of particulate matter, and co-pollutants (Castell et al., 2017, Gao et al., 2015; Holstius et al., 2014; Kelly et al., 2017, Levy et al., 2018; Mukherjee et al., 2017, Shi et al., 2017, Zheng et al., 2018). For instance, Figure S2 in SM section shows the estimated differences in the fitted model coefficient values across metropolitan regions. Furthermore, model residuals varied by site across the Seattle metropolitan region (see SM Section, Figure S3). Residuals at industry-impacted or near-road sites (Duwamish (PSCA1) and 10^th & Weller (PSCA6), respectively) were noisier than at other sites. These stations’ differences might be explained by different particle compositions (Zheng et al., 2018) or by size distribution. For example, diesel exhaust particles less than 0.3 micrometers in size would be included in the reference mass measurement but not in the light scattering sensed by these low-cost sensors. Particle density has also been observed to vary within and between cities, likely explaining variations in the relationship between OPC measured particle count and FRM mass measurements (Hasheminassab et al., 2014; Zhu et al., 2004).

Calibration was necessary to produce accurate measures of PM_2.5 from both types of low-cost sensors. Uncalibrated Plantower PMS A003 PM_2.5 mass calculations were fairly well correlated with co-located FRM measures, but not on the 1-to-1 line and sometimes non-linear (see SM Section, Figure S4). This aligns with our finding that relatively simple calibration models provided good calibration of the Plantower PMS A003 sensors. The observed non-linearity in the plots also highlights limitations in the manufacturer’s algorithm to convert particle counts to mass. Even though the calculated mass is based on a scientifically-motivated algorithm that should account for shape and density of the observed particles (usually by using a fixed value for these parameters), in practice we found that the flexibility of an empirical area-specific adjustment of the separate particle count bins resulted in the best model performance. In smaller calibration datasets, there will be a higher risk of overfitting, and the calculated mass may be a more appropriate choice.

Study design choices play an important role in calibration model development and success. We had access to diverse reference monitoring locations where we were able to co-locate monitors over an approximately two year period. This allowed us to observe monitor performance in various environmental conditions. Other studies have evaluated similar low-cost monitors under laboratory or natural conditions in the field (Austin et al., 2015; Holstius et al., 2014; SCAQMD AQ-SPEC, 2019), but were limited to a single co-location site, single regions, or short monitoring periods. Therefore, calibration models based on a single co-located reference sensor have often been applied to data from different sites within a region, to which the models may not generalize. Our results suggest that low-cost sensors should be calibrated to reference monitors that are sited in environmental conditions that are as similar as possible to the novel monitoring locations. Our LABOSO results, which are presented in supplemental Table S6, indicate that this is especially important when calibration models rely on co-location at a single site. Models from single sites do not necessarily generalize well, and overfitting becomes more of a concern. Simpler model forms may perform better in cases with little data.

As a sensitivity analysis, we excluded certain regulatory sites from the Seattle model. Duwamish (PSCA1) data were excluded due to observed differences in the sites’ residuals (see SM Section, Figure S3) and because the industrial site is not representative of participant residential locations. We excluded Tacoma (PSCA4) site BAM data for observed differences with the co-located FRM data. We conducted an additional analysis using data from only the days where both FRM and FEM data were available, and substituted FEM data for FRM data in both model fitting and model evaluation (see SM Section, Table S7). We found that in Seattle, using FEM data for model evaluation led to slightly weaker RMSE and R² than evaluation with FRM data, but had little effect on model coefficients. These results suggest that the differences in Seattle model comparisons for different evaluation methods used in Table S3 are dominated by the site types used (e.g. whether the industrial Duwamish site is used for evaluation) and less impacted by the differences in reference instruments.

In the Seattle region, incorporating certain FEM data from additional sites into the evaluation improves the spatial variation and is more representative of the locations where predictions will be made for the ACT-AP study. However, evaluation with FEM data may not always be suitable due to the potential differences in data quality. In our study, we used measures from the six non-regulatory TEOM and BAM monitors due to the lack of the EPA-designated FEM monitors in some NYC, Chicago and Winston-Salem sites. For simplicity, we united a non-regulatory TEOM and BAM data into “FEM” group. However, the differences in sampling methods and data quality between FEM and non-regulatory instruments can be observed in FRM-BAM and FRM-TEOM low correlation results in NYC and Chicago sites compared to FRM-FEM correlation results in other regions (see Table 3). Such difference in quality of instruments might be one of a reasons for a lower performance of FRM and FEM regional models in NYC, Chicago and Winston-Salem compared to FRM only regional models at the same regions. Our results suggested that FEM data do not generally improve calibration models when FRM data are available, though often there is little difference between using only FRM vs. using both FRM and FEM (see e.g. Table 4). FRM data provided the most consistent evaluation method across regions, but this depends on data availability (see SM Section, Table S2). When there are already enough FRM data, including additional FEM data will likely not improve prediction accuracy. However, when there are little FRM data (i.e. sites and/or observations), additional FEM data may improve calibration models.

The choice of model evaluation criteria depends on the purpose of calibration. R² is highly influenced by the range of PM_2.5 concentrations and may be a good measure if the purpose of monitoring is to characterize variations in concentration over time. RMSE is an inherently interpretable quantity on the scale of the data and may be more relevant if one is more concerned with detecting small-scale spatial differences in concentrations (e.g. for long-term exposure predictions for subjects in cohort studies when accurately capturing spatial heterogeneity is more important). An appropriate cross-validation structure is also necessary. Roberts et al. (2017) in their study suggest choosing a strategic split of the data rather than random data splitting to account for temporal, spatial, hierarchical or phylogenetic dependencies in datasets. Barcelo-Ordinas et al. (2019) applies a cross-validation method that analyzes LCM ozone concentrations in different monitoring periods: in the short-term and in the long-term. They warn that short-term calibration using multiple linear regression might produce biases in the calculated long-term concentrations. Other researchers from Spain, prior to dividing the data into training and test sets for cross-validation technique, shuffled the data in order to randomly include high and low ozone concentrations in both training and test datasets (Ripoll et al., 2019). For the validation analysis of our PM_2.5 calibration models we used three different cross-validation structures: 10-fold (based on time), “leave-one-site-out” (LOSO) and a “leave-all-but-one-site-out” (LABOSO) cross-validation design (see Section 2.5.4). The 10-fold cross-validation approach randomly partitions weeks of monitoring with co-located LCM and FRM data into 10 folds. While using the 10-fold cross-validation approach, we tried to minimize the effects of temporal correlation on our evaluation metrics by disallowing data from the same calendar week to be used to both train and test models. A 10-fold cross-validation design with folds randomly selected on the week scale consistently produced higher R² and lower RMSE measures than a “leave-one-site-out” (LOSO) cross-validation design. For our purposes, we would prefer to use LOSO in settings with sufficient data from each of at least 3 reference sites. This most closely replicates prediction at non-monitored locations, which is the end goal of our studies. However, the 10-fold cross-validation design is more robust to the number of reference sites, and is preferred (or necessary) in settings with sufficient data from only 1-2 reference sites.

5. Conclusions

Calibration models developed based on Plantower PMS A003 particles counts incorporating temperature and humidity data, using daily FRM or FRM supplemented with FEM, performed well for Plantower PMS A003 sensors, especially with region-specific calibration. Investigators should develop calibration models using measurements from within the region where the model will be applied. The Seattle metropolitan calibration model could be applied to other regions under similar meteorological and environmental conditions, but region-specific calibration models based on the thoughtful selection of at least 3 reference sites are preferred. This study highlights the importance of deriving calibrations of low-cost sensors based on regional scale comparison to data from reference or equivalent measurement methods, and produces sufficient evidence to caution against using manufacturer provided general calibration factors. Calibrated Plantower PMS A003 PM_2.5 sensor data provide measurements of ambient PM_2.5 for exposure assessment which can be potentially used in environmental epidemiology studies.

HIGHLIGHTS.

Low-cost sensors for air pollutants such as particulate matter are of interest, are appealing to deploy in epidemiological studies, but have not been adequately studied for this use.

Different sensors have different performance characteristics.

With adequate calibration of results, and several important caveats, one commonly deployed sensor was found to produce measurements that are precise and reliable.

Calibration of the devices need to be performed with caution, as an approach which is effective in one region may not be effective in a different region.

Epidemiologists may find these devices useful for exposure assessment in epidemiological studies, but need to use caution in using the data, paying attention to data quality and calibration of measurements.