Abstract
Linearizability is the de facto correctness criterion for concurrent data type implementations. Violation of linearizability is witnessed by an error trace in which the outputs of individual operations do not match those of a sequential execution of the same operations. Extensive work has been done in discovering linearizability violations, but little work has been done in trying to provide useful hints to the programmer when a violation is discovered by a tester tool. In this paper, we propose an approach that identifies the root causes of linearizability errors in the form of code blocks whose atomicity is required to restore linearizability. The key insight of this paper is that the problem can be reduced to a simpler algorithmic problem of identifying minimal root causes of conflict serializability violation in an error trace combined with a heuristic for identifying which of these are more likely to be the true root cause of non-linearizability. We propose theoretical results outlining this reduction, and an algorithm to solve the simpler problem. We have implemented our approach and carried out several experiments on realistic concurrent data types demonstrating its efficiency.

Introduction
Efficient multithreaded programs typically rely on optimized implementations of common abstract data types (adts) like stacks, queues, sets, and maps [31], whose operations execute in parallel across processor cores to maximize performance [36]. Programming these concurrent objects correctly is tricky. Synchronization between operations must be minimized to reduce response time and increase throughput [23, 36]. Yet this minimal amount of synchronization must also be adequate to ensure that operations behave as if they were executed atomically, one after the other, so that client programs can rely on the (sequential) adt specification; this de-facto correctness criterion is known as linearizability [24]. These opposing requirements, along with the general challenge in reasoning about thread interleavings, make concurrent objects a ripe source of insidious programming errors [12, 15, 35].
Program properties like linearizability that are difficult to determine statically are typically substantiated by dynamic techniques like testing and runtime verification. While monitoring linearizability of an execution against an arbitrary adt specification requires exponential time in general [20], there exist several efficient approaches for dealing with this problem that led to practical tools, e.g., [3, 4, 13, 14, 16, 33, 39, 47]. Although these approaches are effective at identifying non-linearizable executions of a given object, they do not provide any hints or guidelines about the source of a non-linearizability error once one is found. If some sort of root-cause for non-linearizability can be identified, for example a minimal set of commands in the code that explain the error, then the usability of such testing tools will significantly increase for average programmers. Root-causing concurrency bugs in general is a difficult problem. It is easy enough to fix linearizability if one is willing to disregard or sacrifice performance measures, e.g., by enforcing coarse-grain atomic sections that span a whole method body. It is difficult to localize the problem to a degree that fixing it would not affect the otherwise correct behaviours of the adt. Simplifying techniques, such as equating root causes with some limited set of “bad” patterns, e.g., a non-atomic section formed of two accesses to the same shared variable [10, 28, 38] have been used to provide efficient coarse approximations for root cause identifications.
In this paper, we present an approach for identifying non-linearizability root-causes in a given execution, which equates root causes with optimal repairs that rule out the non-linearizable execution and as few linearizable executions as possible (from a set of linearizable executions given as input). Our approach can be extended to a set of executions and therefore in the limit identify the root cause of the non-linearizability of an adt as a whole. Sequential1 executions of a concurrent object are linearizable, and therefore, linearizability bugs can always be ruled out by introducing one atomic section per each method in the adt. Thus, focusing on atomic sections as repairs, there is a guarantee of existence of a repair in all scenarios. We emphasize the fact that our goal is to interpret such repairs as root-causes. Implementing these repairs in the context of a concrete concurrent object using synchronization primitives (eg., locks) is orthogonal and beyond the scope of this paper. Some solutions are proposed in [28, 29, 46].
As a first step, we investigate the problem of finding all optimal repairs in the form of sets of atomic sections that rule out a given (non-linearizable) execution. A repair is considered optimal when roughly, it allows a maximal number of interleavings. We identify a connection between this problem and conflict serializability
[37], an atomicity condition originally introduced in the context of database transactions. In the context of concurrent programs, given a decomposition of the program’s code into code blocks, an execution is conflict serializable if it is equivalent2 to an execution in which all code blocks are executed in a sequential non-interleaved fashion. A repair that rules out a non-linearizable execution 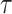 can be obtained using a decomposition of the set of events in
can be obtained using a decomposition of the set of events in  into a set of blocks that we call intervals, such that
into a set of blocks that we call intervals, such that 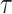 is not conflict serializable with respect to this decomposition. Each interval will correspond to an atomic section in the repair (obtained by mapping events in the execution to statements in the code). A naive approach to compute all optimal repairs would enumerate all decompositions into intervals and check conflict-serializabiliy with respect to each one of them. Such an approach would be inefficient because the number of possible decompositions is exponential in both the number of events in the execution and the number of threads. We show that this problem is actually polynomial time assuming a fixed number of threads. This is quite non-trivial and requires a careful examination of the cyclic dependencies in non conflict-serializable executions. Assuming a fixed number of threads is not an obstacle in practice since recent work shows that most linearizability bugs can be caught with client programs with two threads only
[12, 15].
is not conflict serializable with respect to this decomposition. Each interval will correspond to an atomic section in the repair (obtained by mapping events in the execution to statements in the code). A naive approach to compute all optimal repairs would enumerate all decompositions into intervals and check conflict-serializabiliy with respect to each one of them. Such an approach would be inefficient because the number of possible decompositions is exponential in both the number of events in the execution and the number of threads. We show that this problem is actually polynomial time assuming a fixed number of threads. This is quite non-trivial and requires a careful examination of the cyclic dependencies in non conflict-serializable executions. Assuming a fixed number of threads is not an obstacle in practice since recent work shows that most linearizability bugs can be caught with client programs with two threads only
[12, 15].
In general, there may exist multiple optimal repairs that rule out a non-linearizable execution. To identify which repairs are more likely to correspond to root-causes, we rely on a given set of linearizable executions. We rank the repairs depending on how many linearizable executions they disable, prioritizing those that exclude fewer linearizable executions. This is inspired by the hypothesis that cyclic memory accesses occurring in linearizable executions are harmless.
We evaluated this approach on several concurrent objects, which are variations of lock-based concurrent sets/maps from the Synchrobench repository [21]. We considered a set of non-linearizable implementations obtained by modifying the placement of the lock/unlock primitives, and applied a linearizability testing tool called Violat [14] to obtain client programs that admit non-linearizable executions. We applied our algorithms on the executions obtained by running these clients using Java Pathfinder [44]. Our results show that our approach is highly effective in identifying the precise root cause of linearizability violations since in every case, our tool precisely identifies the root cause of a violation that is discoverable by the client of the library used to produce the error traces.
Overview
Figure 1 lists a variation of a concurrent stack introduced by Afek et al. [1]. The values pushed into the stack are stored into an unbounded array items; a shared variable range keeps the index of the first unused position in items. The push method stores the input in the array and it increments range using a call to an atomic fetch and increment (F&I) primitive. This primitive returns the current value of range while also incrementing it at the same time. The pop method reads range and then traverses the array backwards starting from the predecessor of this position, until it finds a position storing a non-null value. It also nullifies all the array cells encountered during this traversal. If it reaches the bottom of the array without finding non-null values, it returns that the stack is empty.
Fig. 1.
A non-linearizable concurrent stack.
This concurrent stack is not linearizable as witnessed by the execution in Fig. 2. This is an execution of a client with three threads executing two push and two pop operations in total. The push in the first thread is interrupted by operations from the other two threads which makes both pop operations return the same value b. The execution is not linearizable because the value b was pushed only once and it cannot be returned by two different pop operations.
Fig. 2.

A client program of the concurrent stack of Fig. 1 and one of its non-linearizable executions illustrate as a sequence of read/write events.
The root-cause of this violation is the non-atomicity of the statements at lines 8 and 9 of pop, reading items[i] and updating it to null. The stack is linearizable when the two statements are executed atomically (see [1]).
Our goal is to identify such root-causes. We start with a non-linearizable execution like the one in Fig. 2. The first step is to compute all optimal repairs in the form of atomic sections that disable the non-linearizable execution. There are two such optimal repairs for the execution in Fig. 2: (1) an atomic section containing the statements at lines 8 and 9 in pop (representing the root-cause), and (2) an atomic section that includes the two statements in the push method.
These repairs disable the execution because each pair of statements is interleaved with conflicting3 memory accesses in that execution. This is illustrated by the boxes and the edges in Fig. 2 labeled by  : the boxes include these two pairs of statements and the edges emphasize the order between conflicting memory accesses. In Sect. 5, we formalize this by leveraging the notion of conflict serializability. The execution is not conflict-serializable assuming any decomposition of the code in Fig. 1 into a set of code blocks (transactions) such that one of them contains one of these two pairs. These repairs are optimal because they consist of a single atomic section of minimal size (with just two statements). We formalize a generic notion of optimality in Sect. 4 through the introduction of an order relation between repairs, defined as component-wise inclusion of atomic sections and compute the minimal repairs w.r.t. this order.
: the boxes include these two pairs of statements and the edges emphasize the order between conflicting memory accesses. In Sect. 5, we formalize this by leveraging the notion of conflict serializability. The execution is not conflict-serializable assuming any decomposition of the code in Fig. 1 into a set of code blocks (transactions) such that one of them contains one of these two pairs. These repairs are optimal because they consist of a single atomic section of minimal size (with just two statements). We formalize a generic notion of optimality in Sect. 4 through the introduction of an order relation between repairs, defined as component-wise inclusion of atomic sections and compute the minimal repairs w.r.t. this order.
At the end of the first phase, our approach produces a set of all such optimal (incomparable) repairs. To isolate one as the best candidate, we use a heuristic to rank the optimal repairs. The heuristic relies on the hypothesis that repairs which disable fewer linearizable executions are more likely to represent the best candidate for the true root-cause of a linearizability bug.
For instance, the client in Fig. 2 admits a linearizable execution where the first two threads are interleaved exactly as in Fig. 2 and where the pop in the third thread executes after the first two threads finished. This is linearizable because the pop in the third thread returns the value a written by the push in the first thread in items[1] (this is the first non-null array cell starting from the end). Focusing on the two optimal repairs mentioned above, enforcing only the atomic section in the push will disable this linearizable execution. The atomic section in the pop, which permits this execution, is ranked higher to indicate it as the more likely root-cause. This is the expected result for our example.
This ranking scheme can easily be extended to a set of linearizable executions. Given a set of linearizable executions, we rank optimal repairs by keeping track of how many of the linearizable executions each disables.
Preliminaries
We formalize executions of a concurrent object as sequences of events representing calling or returning from a method invocation (called operation), or an access (read or write) to a memory location. Then, we recall the notion of linearizability [24].
We fix arbitrary sets  and
and 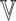 of method names and parameter/return values. We fix an arbitrary set
of method names and parameter/return values. We fix an arbitrary set 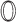 of operation identifiers, and for given sets
of operation identifiers, and for given sets 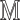 and
and 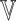 of methods and values, we fix the sets
of methods and values, we fix the sets 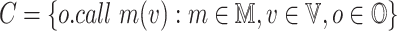 and
and  of call actions and return actions. Each call action
of call actions and return actions. Each call action  combines a method
combines a method 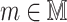 and value
and value 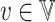 with an operation identifier
with an operation identifier
 . A return action
. A return action  combines an operation identifier
combines an operation identifier 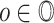 with a value
with a value  . Operation identifiers are used to pair call and return actions. Also, let
. Operation identifiers are used to pair call and return actions. Also, let 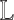 be a set of (shared) memory locations and
be a set of (shared) memory locations and 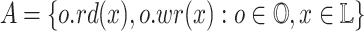 the set of read and write actions. The operation identifier of an action a is denoted by
the set of read and write actions. The operation identifier of an action a is denoted by 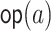 .
.
We fix an arbitrary set 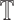 of thread ids. An event is a tuple
of thread ids. An event is a tuple 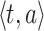 formed of a thread id
formed of a thread id  and an action
and an action 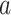 . A trace
. A trace
 is a sequence of events satisfying standard well-formedness properties, e.g., the projection of
is a sequence of events satisfying standard well-formedness properties, e.g., the projection of 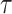 on events of the same thread is a concatenation of sequences formed of a call action, followed by read/write actions with the same operation identifier, and a return action. Also, we assume that every atomic section (block) is interpreted as an uninterrupted sequence of events that correspond to the instructions in that atomic section.
on events of the same thread is a concatenation of sequences formed of a call action, followed by read/write actions with the same operation identifier, and a return action. Also, we assume that every atomic section (block) is interpreted as an uninterrupted sequence of events that correspond to the instructions in that atomic section.
We define two relations over the events in a trace  : the program order relation
: the program order relation  relates any two events
relates any two events  and
and 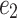 of the same thread such that
of the same thread such that 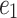 occurs before
occurs before 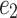 in
in  , and the conflict relation
, and the conflict relation  relates any two events
relates any two events 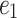 and
and  of different threads that access the same location, at least one of them being a write, such that
of different threads that access the same location, at least one of them being a write, such that 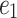 occurs before
occurs before 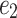 in
in 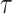 . We omit the subscript
. We omit the subscript 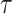 when the trace is understood from the context.
when the trace is understood from the context.
Two traces 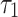 and
and 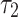 are called equivalent, denoted by
are called equivalent, denoted by  , when
, when 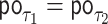 and
and  . They are called
. They are called 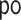 -equivalent when only
-equivalent when only  .
.
The projection of a trace  over call and return actions is called a history and denoted by
over call and return actions is called a history and denoted by 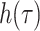 . A history is sequential when each call action c is immediately followed by a return action r with
. A history is sequential when each call action c is immediately followed by a return action r with  . A linearization of a history
. A linearization of a history 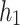 is a sequential history
is a sequential history 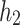 that is a permutation of
that is a permutation of  that preserves the order between return and call actions, i.e., a given return action occurs before a given call action in
that preserves the order between return and call actions, i.e., a given return action occurs before a given call action in 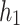 iff the same holds in
iff the same holds in 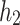 .
.
A library
 is a set of traces4. A trace
is a set of traces4. A trace 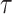 of a library
of a library 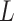 is linearizable if
is linearizable if  contains some sequential trace whose history is a linearization of
contains some sequential trace whose history is a linearization of 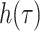 . A library is linearizable if all its traces are linearizable5. In the following, since linearizability is used as the main correctness criterion, a bug is a trace
. A library is linearizable if all its traces are linearizable5. In the following, since linearizability is used as the main correctness criterion, a bug is a trace 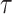 that is not linearizable.
that is not linearizable.
Linearizability Violations and Their Root Causes
Given a non-linearizable library, our goal is to identify the root cause of non-linearizability in the library code. Let us start by formally describing the state space of all such causes and state some properties of the space that will aid the understanding of our algorithm. First, our focus is on a specific category of causes, namely those that can be removed through the introduction of new atomic code blocks to the library code without any other code changes.
Definition 1 (Non-linearizability Root Cause)
For a non-linearizable library  , the root cause is formally identified by
, the root cause is formally identified by  , a set of atomic blocks
, a set of atomic blocks  such that
such that  is linearizable with the addition of blocks from
is linearizable with the addition of blocks from 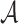 .
.
Observe that the set of atomic blocks identified in Definition 1 can conceptually be viewed as blocks of code whose non-atomicity is the root cause of non-linearizability and their introduction would repair the library. For the rest of this paper, we use the two terminologies interchangeably since for this specific class, the two notions perfectly coincide. The immediate question that comes to mind is whether Definition 1 is general enough. Observe that since linearizability is fundamentally an atomicity type property for individual methods in a library, if every single method of the library is declared atomic at the code level, then the library is trivially linearizable. The only valid executions of the library are the linear (sequential) executions in this case. Therefore,
Remark 1
Every non-linearizable library can be made linearizable by adding atomic code blocks in 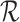 according to Definition 1.
according to Definition 1.
Since there always is a trivial repair, one is interested in finding a good one. The quality of a repair is contingent on the amount of parallelism that the addition of the corresponding atomic blocks removes from the executions of an arbitrary client of the library. Generally, it is understood that the fewer the number of introduced atomic blocks and the shorter their length, the more permissive they will be in terms of the parallel executions of a client of this library. This motivates a simple formal subsumption relationship between repairs of a bug. We say an atomic code block b subsumes another atomic code block  , denoted as
, denoted as  , if and only if
, if and only if 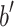 is contained within b.
is contained within b.
Definition 2 (Repair Subsumption)
A repair  subsumes another repair
subsumes another repair 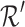 , we write
, we write  if and only if for all atomic blocks
if and only if for all atomic blocks  , there exists an atomic block
, there exists an atomic block 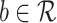 such that
such that  .
.
It is easy to see that  is a partial order, and combined with the finite set of all possible program repairs gives rise to the concept of a set of optimal repairs, namely those that do not subsume any other repair. It can be lifted to sets of repairs in the natural way:
is a partial order, and combined with the finite set of all possible program repairs gives rise to the concept of a set of optimal repairs, namely those that do not subsume any other repair. It can be lifted to sets of repairs in the natural way:  iff
iff  .
.
Remark 2
The set of traces of a library  with a repair
with a repair  is a superset of the set of traces of
is a superset of the set of traces of  with the repair
with the repair 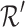 if
if  .
.
This means that an optimal repair identification according to Definition 2 should lead to an optimal amount of parallelism in the library repaired by forcing the corresponding code blocks to execute atomically. The goal of our algorithm is to identify such a set of optimal repairs.
Now, let us turn our attention to an algorithmic setup to solve this problem. The non-linearizability of a library  is witnessed by a non-empty set of non-linearizable traces T. These are the concrete erroneous traces of (a client of) the library, for which we intend to identify the repair.
is witnessed by a non-empty set of non-linearizable traces T. These are the concrete erroneous traces of (a client of) the library, for which we intend to identify the repair.
Note that if  is a non-linearizable trace, then all the traces
is a non-linearizable trace, then all the traces 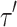 that are equivalent to
that are equivalent to  are also non-linearizable. Indeed, if
are also non-linearizable. Indeed, if 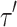 is equivalent to
is equivalent to  , then the values that are read in
, then the values that are read in  are the same as in
are the same as in  6, which implies that the return values in
6, which implies that the return values in  are the same as in
are the same as in  , and therefore,
, and therefore,  is non-linearizable when
is non-linearizable when  is.
is.
Consider a conceptual oracle, 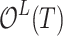 , that takes a set of non-linearizable traces of a library
, that takes a set of non-linearizable traces of a library  and produces the set of all optimal repairs
and produces the set of all optimal repairs 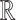 such that each
such that each  excludes all the traces that are equivalent to those in T. Then the following iterative algorithm produces
excludes all the traces that are equivalent to those in T. Then the following iterative algorithm produces  for a library
for a library  :
:
Let
 and
and  .
.- Check if
 with the addition of atomic blocks from
with the addition of atomic blocks from 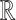 is linearizable:
is linearizable:- Yes? Return
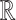 .
. - NO? Produce a set of non-linearizability witnesses
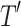 and let
and let 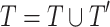 .
.
Call
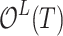 and update the set of repairs
and update the set of repairs 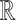 with the result.
with the result.Go to back to step 2.
Proposition 1
The above algorithm produces an optimal set of repairs 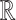 that make its input library linearizable.
that make its input library linearizable.
It is easy to see that if oracle 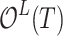 can be relied on to produce perfect results, then the algorithm satisfies a progress property in the sense that
can be relied on to produce perfect results, then the algorithm satisfies a progress property in the sense that 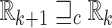 , where
, where  is the value of
is the value of  in the k-th iteration of the loop. Following Remark 1, this chain of increasingly stronger repairs is bounded by the specific repair in which every method of the library
in the k-th iteration of the loop. Following Remark 1, this chain of increasingly stronger repairs is bounded by the specific repair in which every method of the library 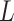 has to be declared atomic. Therefore, the algorithm converges. The assumption of optimality for
has to be declared atomic. Therefore, the algorithm converges. The assumption of optimality for 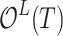 implies that on the iteration that the algorithm terminates, it will produce the optimal
implies that on the iteration that the algorithm terminates, it will produce the optimal 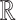 .
.
Note that in oracle  , the focus shifts from identifying the source of error for the entire library to identifying the source of error in a specific set of non-linearizability witnesses. First, we propose a solution for implementing
, the focus shifts from identifying the source of error for the entire library to identifying the source of error in a specific set of non-linearizability witnesses. First, we propose a solution for implementing 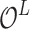 for a singleton set, i.e. precisely one error trace, and later argue why the solution easily generalizes to finitely many error traces.
for a singleton set, i.e. precisely one error trace, and later argue why the solution easily generalizes to finitely many error traces.
Repair Oracle Approximation
Given a trace 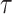 as a violation of linearizability, we wish to implement
as a violation of linearizability, we wish to implement 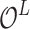 that takes a single trace
that takes a single trace 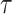 and proposes an optimal set of repairs for it.
and proposes an optimal set of repairs for it.
Observe that if every trace of 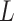 is conflict serializable
[37] (i.e., equivalent to a sequential trace), assuming method boundaries as transaction boundaries, then it is necessarily linearizable. Therefore, knowing that it is not linearizable, we can conclude that there exists some trace of
is conflict serializable
[37] (i.e., equivalent to a sequential trace), assuming method boundaries as transaction boundaries, then it is necessarily linearizable. Therefore, knowing that it is not linearizable, we can conclude that there exists some trace of  which is not serializable. Following the same line of reasoning, we can conclude that the error trace
which is not serializable. Following the same line of reasoning, we can conclude that the error trace  itself is not conflict serializable, for some choice of transaction boundaries. This observation is the basis of our solution for approximating repairs for non-linearizability through an oracle that is actively seeking to repair for non-serializability violations.
itself is not conflict serializable, for some choice of transaction boundaries. This observation is the basis of our solution for approximating repairs for non-linearizability through an oracle that is actively seeking to repair for non-serializability violations.
Definition 3 (Trace Eliminator)
For an error trace (a bug)  , a set of atomic blocks
, a set of atomic blocks 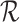 is called a trace eliminator if and only if every trace that is equivalent to
is called a trace eliminator if and only if every trace that is equivalent to  is not a trace of the new library with the addition of blocks from
is not a trace of the new library with the addition of blocks from  .
.
Any trace eliminator that removes 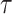 as a valid trace of a client of the library
as a valid trace of a client of the library  (and all the traces equivalent to
(and all the traces equivalent to  ), by amending the library for the conflict serializability violation, (indirectly) eliminates it as a witness to non-linearizability as well. Note that the universes of trace eliminators and non-linearizability repairs are the same set of objects, and therefore the subsumption relation
), by amending the library for the conflict serializability violation, (indirectly) eliminates it as a witness to non-linearizability as well. Note that the universes of trace eliminators and non-linearizability repairs are the same set of objects, and therefore the subsumption relation  is well defined for trace eliminators, and the concept of optimality is similarly defined. Moreover, Definition 3 is agnostic to linearizability and can be interchangeably used for serializability repairs.
is well defined for trace eliminators, and the concept of optimality is similarly defined. Moreover, Definition 3 is agnostic to linearizability and can be interchangeably used for serializability repairs.
Theorem 1
 is a trace eliminator for
is a trace eliminator for 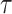 if and only if
if and only if  is not conflict serializable with transaction boundaries that subsume
is not conflict serializable with transaction boundaries that subsume  (statements that are not included in the atomic sections from
(statements that are not included in the atomic sections from  are assumed to form singleton transactions).
are assumed to form singleton transactions).
Proof
(Sketch) For the if direction, assume by contradiction that 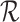 is not a trace eliminator for
is not a trace eliminator for 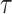 . This implies that there exists a trace
. This implies that there exists a trace 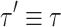 where the sequences of events corresponding to the atomic sections in
where the sequences of events corresponding to the atomic sections in 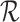 occur uninterrupted (not interleaved with other events). This is a direct contradiction to
occur uninterrupted (not interleaved with other events). This is a direct contradiction to  not being conflict serializable when transaction boundaries are defined precisely by the atomic sections in
not being conflict serializable when transaction boundaries are defined precisely by the atomic sections in 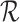 . For the only if direction, assume by contradiction that
. For the only if direction, assume by contradiction that 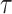 is conflict serializable. By definition, there is an equivalent trace
is conflict serializable. By definition, there is an equivalent trace  where the sequences of events corresponding to the atomic sections in
where the sequences of events corresponding to the atomic sections in 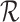 occur uninterrupted. Therefore, the library
occur uninterrupted. Therefore, the library 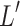 obtained by adding the atomic code blocks in
obtained by adding the atomic code blocks in 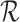 admits
admits 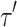 , which contradicts the fact that
, which contradicts the fact that  is a trace eliminator for
is a trace eliminator for 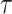 .
. 
The relationship between the set of trace eliminators for 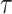 and
and 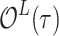 can be made precise. Since every trace eliminator is a linearizability repair by definition, but not necessarily an optimal one, we have:
can be made precise. Since every trace eliminator is a linearizability repair by definition, but not necessarily an optimal one, we have:
Proposition 2
Let  represent the optimal set of repairs that eliminate
represent the optimal set of repairs that eliminate  as a witness to non-linearizability and
as a witness to non-linearizability and 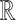 be the set of optimal trace eliminators for
be the set of optimal trace eliminators for 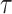 . We have
. We have 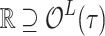 .
.
This is precisely why the set of trace eliminators safely overapproximates the set of linearizability repairs for a single trace. Note that Theorem 1 links any trace eliminator (a set of code blocks) to a collection of dynamic (runtime) transactions. It is fairly straightforward to see that given the latter as an input, the former can be inferred in a way that the dynamic transactions generated by the static code blocks are as close as possible to the input transaction boundaries, assuming no structural changes occur in the code. In Sect. 5, we discuss how an optimal set of dynamic transaction boundaries can be computed, which give rise to a set of optimal trace eliminators.
Generalization to Multiple Traces
If we have an implementation for an oracle  that takes a single trace and produces the set of optimal trace eliminators for it, then the following algorithm implements an oracle for
that takes a single trace and produces the set of optimal trace eliminators for it, then the following algorithm implements an oracle for 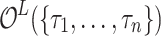 for any finite number of traces:
for any finite number of traces:
Let
 .
.For each
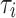 (
(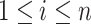 ): let
): let 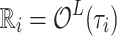 .
.Let
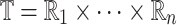 .
.For each
 : let
: let 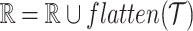 .
.For each
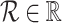 : if
: if 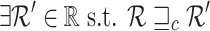 then
then 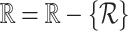 .
.
where  basically takes the union of repairs suggested by individual components of
basically takes the union of repairs suggested by individual components of  while merging any overlapping atomic blocks. Note that the ith component of
while merging any overlapping atomic blocks. Note that the ith component of  suggests an optimal trace eliminator for
suggests an optimal trace eliminator for  . If we want a tight combination of all such trace eliminators, we need the minimal set of atomic blocks that covers all atomic blocks suggested by each eliminator. Formally:
. If we want a tight combination of all such trace eliminators, we need the minimal set of atomic blocks that covers all atomic blocks suggested by each eliminator. Formally:
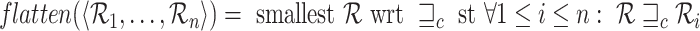 |
we can then conclude:
Theorem 2
If  produces the optimal set of trace eliminators for trace
produces the optimal set of trace eliminators for trace  , then the above algorithm correctly implements
, then the above algorithm correctly implements 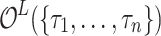 , that is, it produces the optimal set of repairs for the set of error traces
, that is, it produces the optimal set of repairs for the set of error traces 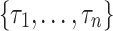 .
.
Conflict-Serializability Repairs
In this section, we investigate the theoretical properties of conflict serializability repairs to provide a set up for an algorithm that implements the oracle 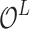 for a single input trace. The goal of this algorithm is to take a trace
for a single input trace. The goal of this algorithm is to take a trace 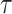 as an input and return the optimal trace eliminator for
as an input and return the optimal trace eliminator for 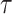 , under the assumption that
, under the assumption that  witnesses the violation of linearizability.
witnesses the violation of linearizability.
Repairs and Conflict Cycles
We start by introducing a few formal definitions and some theoretical connections that will give rise to an algorithm for identifying an optimal set of atomic blocks that can eliminate a trace  as a witness to violation of conflict serialiazability.
as a witness to violation of conflict serialiazability.
Definition 4 (Decompositions and Intervals)
A decomposition of a trace 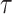 is an equivalence relation
is an equivalence relation  over its set of events such that:
over its set of events such that:
 relates only events of the same operation, i.e. if
relates only events of the same operation, i.e. if 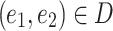 , then
, then  , and
, andthe equivalence classes of
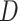 are continuous sequences of events of the same operation, i.e., if
are continuous sequences of events of the same operation, i.e., if 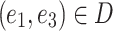 and
and 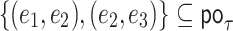 , then
, then 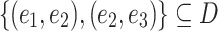
The equivalence classes of a decomposition  , denoted by
, denoted by  are called intervals.
are called intervals.
Observe that the relation  is well defined partial order over the universal all possible intervals (of all possible decompositions) of a trace
is well defined partial order over the universal all possible intervals (of all possible decompositions) of a trace  .
.
Definition 5 (Interval Graphs)
Given a trace 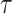 , and decomposition
, and decomposition  , an interval graph is defined as
, an interval graph is defined as 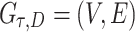 where the set of vertexes V is the set of intervals of
where the set of vertexes V is the set of intervals of  and the set of edges E is defined as follows
and the set of edges E is defined as follows
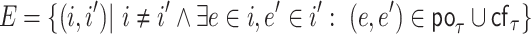 |
Since, by definition, each edge in the interval graph is induced by an edge from either relation 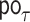 or
or 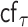 , but note both, we lift these relations over the sets of intervals in the natural way, that is:
, but note both, we lift these relations over the sets of intervals in the natural way, that is:
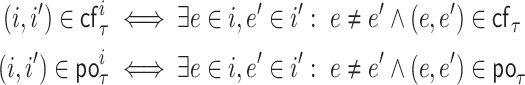 |
Given an interval graph edge 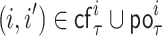 , let
, let
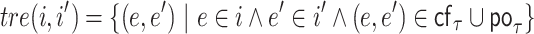 |
Figure 3 illustrates an interval graph. Node 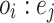 denotes an event
denotes an event  of operation
of operation 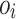 . Events of the same thread are aligned vertically. We draw only
. Events of the same thread are aligned vertically. We draw only 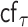 edges since the
edges since the  edges are implied by the vertical alignment of events. Non-singleton intervals of
edges are implied by the vertical alignment of events. Non-singleton intervals of 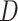 are
are  ,
, 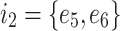 and
and 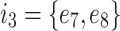 . Singleton intervals are identified by the corresponding event identifiers. Edges among interval nodes correspond to
. Singleton intervals are identified by the corresponding event identifiers. Edges among interval nodes correspond to 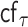 or
or  . For instance,
. For instance, 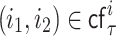 since
since  ,
, 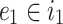 and
and  . As an example for the function
. As an example for the function 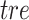 , we have
, we have 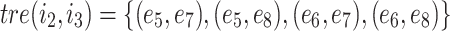 that consists of
that consists of  edges and
edges and 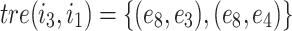 that consists of
that consists of 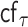 edges.
edges.
Fig. 3.

An interval graph.
For the degenerate decomposition in which each event is an interval of size one by itself, the interval graph collapses into a trace graph, denoted by 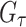 . Note that
. Note that  is acyclic since the relations
is acyclic since the relations 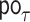 and
and  are consistent with the order between the events in
are consistent with the order between the events in  .
.
Intervals are closely related to the static notion of transactions and the induced transaction boundaries on traces. For example, in the decomposition in which the intervals coincide with the boundaries of transactions (e.g. method boundaries), it is straightforward to see that the interval graph becomes precisely the conflict graph
[19] widely known in the conflict serializability literature. It is a known fact that a trace is conflict serializable if and only if its conflict graph is acyclic
[37]. Since  is not conflict serializable with respect to the boundaries of methods from
is not conflict serializable with respect to the boundaries of methods from  , we know the interval graph with those boundaries is cyclic.
, we know the interval graph with those boundaries is cyclic.
With intervals set as single events, 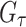 is acyclic, and with the intervals set at method boundaries, it is cyclic. The high level observation is that there exist a decomposition
is acyclic, and with the intervals set at method boundaries, it is cyclic. The high level observation is that there exist a decomposition  in the middle of this spectrum, so to speak, such that
in the middle of this spectrum, so to speak, such that 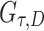 is cyclic, but
is cyclic, but  for any
for any 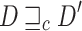 is acyclic. In the following we will formally argue why such a decomposition
is acyclic. In the following we will formally argue why such a decomposition  is at the centre of identification of serializability repairs.
is at the centre of identification of serializability repairs.
A cycle in a graph is simple if only one vertex is repeated more than once.
Definition 6 (Critical Segment Sets)
Let  be a decomposition such that the interval graph
be a decomposition such that the interval graph 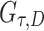 is cyclic and
is cyclic and 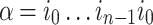 be a simple cycle. Define
be a simple cycle. Define
 |
where the set 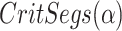 is the set of all critical segments sets of cycle
is the set of all critical segments sets of cycle 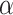 .
.
Note that each cycle may induce several different segment sets, determined by 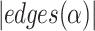 . More importantly, each segment set includes at least one critical segment.
. More importantly, each segment set includes at least one critical segment.
Lemma 1
For any 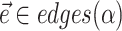 , we have
, we have 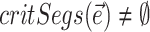 .
.
Example 1
In Fig. 3,  is a simple cycle. Included in
is a simple cycle. Included in 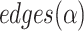 are the following three cycles and their corresponding segments:
are the following three cycles and their corresponding segments:
 |
The critical segments for these are 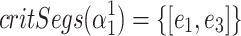 ,
, 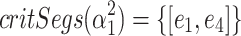 and
and  .
.
There is a direct connection between the notion of critical segment sets and conflict serializability repairs that the following lemma captures. A segment is called uninterrupted in a trace 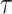 when all its events occur continuously one after another in
when all its events occur continuously one after another in 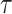 without an interruption from events of another interval.
without an interruption from events of another interval.
Lemma 2
Let 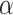 be a cycle in some interval graph
be a cycle in some interval graph 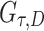 of trace
of trace 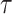 which is not conflict serializable wrt to the decomposition
which is not conflict serializable wrt to the decomposition 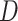 and
and 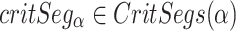 . There does not exist trace
. There does not exist trace  which is equivalent to
which is equivalent to  in which all segments from
in which all segments from 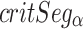 are uninterrupted in
are uninterrupted in 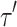 .
.
The immediate corollary of Lemma 2 is that if one ensures the atomicity of the segments of events in  by adding atomic blocks at the code level, then
by adding atomic blocks at the code level, then 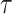 can no longer be an execution of the library. In other words, a set of such atomic code blocks is precisely a trace eliminator (Definition 3) for
can no longer be an execution of the library. In other words, a set of such atomic code blocks is precisely a trace eliminator (Definition 3) for  .
.
A Simple Algorithm
Lemma 2 and its corollary suggest a simple enumerative algorithm to discover the set of all trace eliminators for a buggy trace  .
.
Let
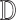 be the set of all decompositions of
be the set of all decompositions of 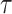 and
and  .
.- For each
 :
:- Let
 be the set of all simple cycles in
be the set of all simple cycles in 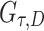 .
. - For each
 :
: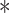 Let
Let  .
.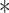
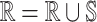
- For each
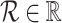 :
:- If
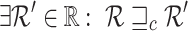 then
then 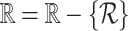 .
.
Theorem 3
The above algorithm produces the optimal set of trace eliminators for a buggy trace 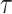 .
.
This theorem is non-trivial, because the set of cycles considered are limited to simple cycles and an argument is required for why no optimal solution is missed as the result of this limitation. An important point is that any optimal trace eliminator 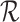 defines a decomposition
defines a decomposition 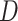 where the non-singleton intervals are precisely those defined by
where the non-singleton intervals are precisely those defined by  such that
such that 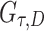 contains a simple cycle
contains a simple cycle 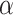 and the set of code blocks in
and the set of code blocks in 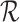 is a member of
is a member of  . Note that the algorithm may end up producing non-ideal solutions in the first loop, and the proof of Theorem 3 relies on the argument that all such solutions will be filtered out by a proper solution that guarantees to exist and subsume them.
. Note that the algorithm may end up producing non-ideal solutions in the first loop, and the proof of Theorem 3 relies on the argument that all such solutions will be filtered out by a proper solution that guarantees to exist and subsume them.
Example 2
The first loop of the above algorithm includes in 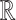 the trace eliminators induced by the critical segments mentioned in Example 1. After the last loop, however, only
the trace eliminators induced by the critical segments mentioned in Example 1. After the last loop, however, only 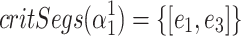 will remain in
will remain in 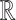 since the other two are subsumed by it.
since the other two are subsumed by it.
The algorithm is obviously very inefficient. There are two levels of enumeration: all decompositions and all cycles of each decomposition. Assuming that there are  events in an operation, then there are
events in an operation, then there are 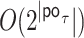 different decompositions for it. Assuming that there are
different decompositions for it. Assuming that there are 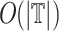 operations, we conclude that
operations, we conclude that 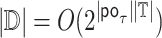 . There could be
. There could be 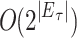 possible cycles for each decomposition where
possible cycles for each decomposition where 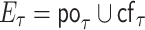 . Therefore, the first loop may generate
. Therefore, the first loop may generate 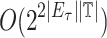 many repairs. The last loop iterates over
many repairs. The last loop iterates over  and each repair takes
and each repair takes 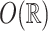 time. The algorithm operates in time
time. The algorithm operates in time  . It is exponential both in the size of threads set and the graph. There are many redundancies in the output of the first loop, however. These are exploited to propose an optimized version of this algorithm.
. It is exponential both in the size of threads set and the graph. There are many redundancies in the output of the first loop, however. These are exploited to propose an optimized version of this algorithm.
A Sound Optimization
Consider an arbitrary cycle  in the interval graph
in the interval graph  . If we want to trace the cycle
. If we want to trace the cycle 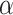 over the trace graph
over the trace graph 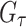 , we would potentially need additional edges that would let us go against the program order inside some intervals that appear on
, we would potentially need additional edges that would let us go against the program order inside some intervals that appear on 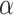 . Let us call the graph extended with such edges
. Let us call the graph extended with such edges  . Formally,
. Formally, 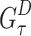 includes all the nodes and edges from a trace graph and incorporates additional edges between the events of each interval of
includes all the nodes and edges from a trace graph and incorporates additional edges between the events of each interval of  to turn it into a clique7 which is by definition a strongly connected and therefore accommodates the connectivity of any event of an interval to another event in it.
to turn it into a clique7 which is by definition a strongly connected and therefore accommodates the connectivity of any event of an interval to another event in it.
The converse also holds, that is, every simple cycle with at least one conflict edge in the 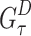 with the aforementioned additional edges corresponds to a cycle in the interval graph
with the aforementioned additional edges corresponds to a cycle in the interval graph  . Note that the inclusion of at least one conflict edge is essential, since every interval graph cycle always includes one such edge by default; since the program order relation is acyclic. Formally:
. Note that the inclusion of at least one conflict edge is essential, since every interval graph cycle always includes one such edge by default; since the program order relation is acyclic. Formally:
Lemma 3
For each simple cycle  of
of 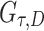 , there exists a simple cycle
, there exists a simple cycle  of
of 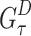 that contains at most two events from each interval in
that contains at most two events from each interval in 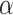 .
.
The above lemma can immediately be generalized. Consider the graph 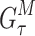 where M indicates the decomposition whose intervals coinciding with the library method boundaries. Since for any arbitrary decomposition
where M indicates the decomposition whose intervals coinciding with the library method boundaries. Since for any arbitrary decomposition 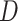 , we have
, we have 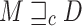 , we can conclude that
, we can conclude that 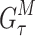 includes all possible additional edges that one may want to consider as part of a cycle in an arbitrary
includes all possible additional edges that one may want to consider as part of a cycle in an arbitrary  for an arbitrary decomposition
for an arbitrary decomposition  . Hence, the set of edges of
. Hence, the set of edges of 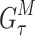 is a superset of the set of edges of all graphs
is a superset of the set of edges of all graphs 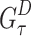 for all
for all  . This immediately implies that the set of cycles of
. This immediately implies that the set of cycles of 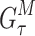 is the superset of the set of cycles of all such graphs. This fact, combined with Lemma 3 leads us to the new simplified algorithm below in place of the one in Sect. 5.2:
is the superset of the set of cycles of all such graphs. This fact, combined with Lemma 3 leads us to the new simplified algorithm below in place of the one in Sect. 5.2:
Let
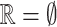 .
.Let
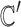 be the set of all simple cycles in
be the set of all simple cycles in 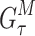 .
.- For each
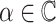 :
:- Let
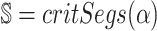 .
. 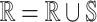
- For each
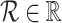 :
:- If
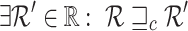 then
then 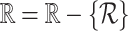 .
.
Note that we are slightly bending the definition of 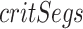 in the above algorithm, compared to the one given in Definition 6 since the input cycle there is formally a tuple, and here itis simply a list. The function is semantically the same, however and therefore we do not redefine it.
in the above algorithm, compared to the one given in Definition 6 since the input cycle there is formally a tuple, and here itis simply a list. The function is semantically the same, however and therefore we do not redefine it.
Observe that ever cycle of  corresponds to a cycle in some graph
corresponds to a cycle in some graph 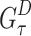 for some decomposition
for some decomposition 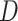 . This observation together with Lemma 3 and Theorem 3 implies the correctness of the above algorithm. Every cycle of every
. This observation together with Lemma 3 and Theorem 3 implies the correctness of the above algorithm. Every cycle of every  is covered by the algorithm, and conversely every cycle considered is valid.
is covered by the algorithm, and conversely every cycle considered is valid.
We can simplify the above algorithm one step further by further limiting the set of cycles  that need to be enumerated. In graph theory, a chord of a simple cycle is an edge connecting two vertices in the cycle which is not part the cycle.
that need to be enumerated. In graph theory, a chord of a simple cycle is an edge connecting two vertices in the cycle which is not part the cycle.
Theorem 4
The above algorithm produces the set of optimal trace eliminators for 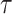 if
if  is limited to the set of simple chordless cycles of
is limited to the set of simple chordless cycles of 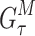 .
.
Theorem 4 makes a non-trivial and algorithmically subtle observation. Enumerating the set of all simple chordless cycles of 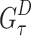 is a much simpler algorithmic problem to solve compared to the initial one from Sect. 5.2. Lemma 3 supports part of this argument since it ensures that all repairs explored in the algorithm from Sect. 5.2 are also explored by the above algorithm. For Theorem 4 to hold, one needs to additionally argue that the cycles of
is a much simpler algorithmic problem to solve compared to the initial one from Sect. 5.2. Lemma 3 supports part of this argument since it ensures that all repairs explored in the algorithm from Sect. 5.2 are also explored by the above algorithm. For Theorem 4 to hold, one needs to additionally argue that the cycles of 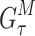 do not produce any junk, that is, each cycle’s critical segments correspond to a valid trace eliminator for
do not produce any junk, that is, each cycle’s critical segments correspond to a valid trace eliminator for  . Also, as for simple cycles,
. Also, as for simple cycles,  for a cycle
for a cycle 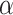 subsumes
subsumes 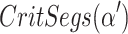 for any chordless cycle
for any chordless cycle 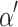 included in
included in  . In Sect. 6.1, we present an algorithm that solves the problem of enumerating all cycles in
. In Sect. 6.1, we present an algorithm that solves the problem of enumerating all cycles in  effectively.
effectively.
Repair List Generation
In this section, we first start by giving a detailed algorithm that produces the set of all optimal trace eliminators. These repairs suggest incomparable optimal ways of removing an erroneous trace from the library. We then present a novel heuristic that orders this set into a list such that the the ones ranked higher in the list are more likely to correspond to something that a human programmer would identify (amongst the entire set) as the ideal repair.
Optimal Repairs Enumeration Algorithm
In this section, we present an algorithm for enumerating all simple chordless cycles in 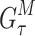 with at least one
with at least one 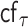 edge, prove its correctness, and formally analyze its time complexity. The algorithm is the following:
edge, prove its correctness, and formally analyze its time complexity. The algorithm is the following:
Let
 .
.- For each sequence
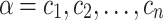 where
where 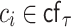 and
and 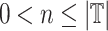 :
:- Let
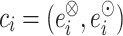 for all
for all 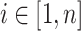 .
. - If
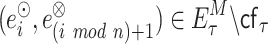 and
and 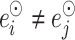 s.t.
s.t.  s.t.
s.t. 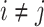 :
:
It enumerates all non-empty  sequences of length less than or equal to
sequences of length less than or equal to 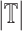 . If the sequence forms a valid simple cycle and visits each thread at most once (i.e. there are no two distinct conflict edges such that its end points are on the same thread), then it is added to the result set
. If the sequence forms a valid simple cycle and visits each thread at most once (i.e. there are no two distinct conflict edges such that its end points are on the same thread), then it is added to the result set  . Correctness of the algorithm relies on the following observation:
. Correctness of the algorithm relies on the following observation:
Lemma 4
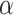 is a chordless cycle of
is a chordless cycle of 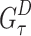 with at least one
with at least one  edge if and only if
edge if and only if 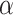 visits each thread at most once and it visits at least two threads.
visits each thread at most once and it visits at least two threads.
As a corollary of Lemma 4, we know that a chordless cycle could have at most 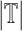 conflict edges. Otherwise, by the pigeon hole principle, at least two conflict edges end up in the same thread. Therefore, the algorithm can soundly enumerate only sequences of
conflict edges. Otherwise, by the pigeon hole principle, at least two conflict edges end up in the same thread. Therefore, the algorithm can soundly enumerate only sequences of  edges of length less than or equal to
edges of length less than or equal to 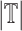 . Moreover, the choice of
. Moreover, the choice of  determines the rest of the edges in the cycle. Therefore, there are at most
determines the rest of the edges in the cycle. Therefore, there are at most  chordless cycles with at least one
chordless cycles with at least one 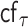 edge of a graph
edge of a graph 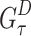 .
.
Note that, in general, the number of simple cycles can be exponential in the number of edges. This means that enumerating only chordless cycles reduces the size asymptotically. In other words, our proposed sound optimization of Sect. 5.3 is at the roof of the polynomial complexity results presented here.
Interestingly, this upper bound is not loose. There is a class of traces parametrized by 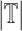 such that the number of chordless cycles with at least one
such that the number of chordless cycles with at least one  edge is
edge is 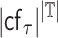 . Let
. Let 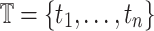 be the set of threads and
be the set of threads and 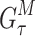 has k parallel conflict edges between
has k parallel conflict edges between 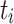 and
and 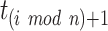 for all
for all 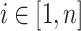 . Moreover, conflict edges that start from
. Moreover, conflict edges that start from 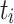 is above the conflict edges that end at
is above the conflict edges that end at 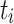 in terms of program order. This graph is depicted in Fig. 4. To form a cycle, one needs to pick one of k edges between
in terms of program order. This graph is depicted in Fig. 4. To form a cycle, one needs to pick one of k edges between 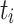 and
and 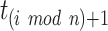 for all
for all 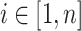 . So, there are
. So, there are 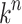 cycles. Since
cycles. Since 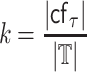 , there are
, there are  chordless cycles with a conflict edge. If we consider
chordless cycles with a conflict edge. If we consider 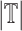 as a constant, there are
as a constant, there are 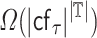 chordless cycles with at least one
chordless cycles with at least one 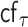 edge. We are finally ready to state the main complexity result:
edge. We are finally ready to state the main complexity result:
Fig. 4.
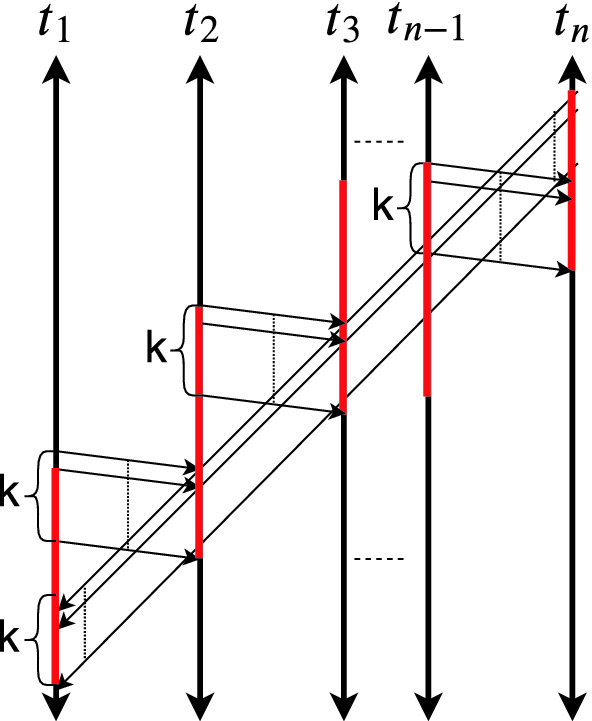
 with
with  chordless cycles. (Color figure online)
chordless cycles. (Color figure online)
Theorem 5
Above enumeration algorithm generates all chordless cycles with at least one 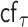 edge of
edge of  in
in  time.
time.
Proof
The loop enumerates all the 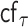 sequences of length at most
sequences of length at most 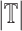 in
in  time. For each such sequence, it takes
time. For each such sequence, it takes 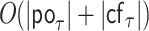 time to check whether this sequence forms a cycle (if each consecutive conflict edges are connected through a
time to check whether this sequence forms a cycle (if each consecutive conflict edges are connected through a 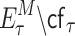 edge) and whether it visits a thread more than once. As a consequence, the above bound holds.
edge) and whether it visits a thread more than once. As a consequence, the above bound holds. 
Lastly, there may be as many optimal repairs as there are chordless cycles in 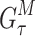 . Consider the class of traces depicted in Fig. 4. Each chordless cycle with at least one
. Consider the class of traces depicted in Fig. 4. Each chordless cycle with at least one 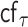 edge has exactly n critical segments (illustrated in red). Consider two distinct chordless cycles
edge has exactly n critical segments (illustrated in red). Consider two distinct chordless cycles 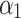 and
and 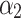 . There exists a thread
. There exists a thread 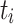 such that there is a different edge between
such that there is a different edge between 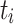 and
and 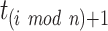 in
in 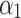 compared to
compared to 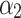 . Without loss of generality, assume that the corresponding edge of
. Without loss of generality, assume that the corresponding edge of  has source and destination events that appear before the source and destination events of the corresponding edge of
has source and destination events that appear before the source and destination events of the corresponding edge of  in program order (
in program order ( ). Then,
). Then, 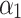 has a larger critical segment on
has a larger critical segment on 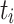 and smaller critical segment in
and smaller critical segment in 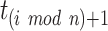 compared to
compared to 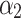 . Therefore, the neither critical segment subsumes the other. Therefore, each chordless cycle with at least one
. Therefore, the neither critical segment subsumes the other. Therefore, each chordless cycle with at least one 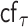 edge produces an optimal repair.
edge produces an optimal repair.
This implies that the bound presented in Theorem 5, namely 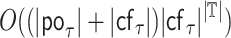 , applies any other algorithm that outputs all optimal repairs.
, applies any other algorithm that outputs all optimal repairs.
Ranking Optimal Repairs
We argued through the example in Sect. 2 and a formal statement in Sect. 4.1 that not every eliminator of a buggy trace 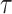 is an optimal root cause for non-linearizability. All that we know is that they are all optimal trace eliminators. As a heuristic to identify optimal linearizability repairs out of a set of trace eliminators, we rely on another input in the form of a set
is an optimal root cause for non-linearizability. All that we know is that they are all optimal trace eliminators. As a heuristic to identify optimal linearizability repairs out of a set of trace eliminators, we rely on another input in the form of a set 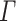 of linearizable executions, and rank trace eliminators depending on how many linearizable traces from
of linearizable executions, and rank trace eliminators depending on how many linearizable traces from 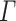 they disable, giving preference to trace eliminators that disable fewer ones. This heuristic relies on an experimental hypothesis that there are harmless cyclic dependencies that occur in linearizable executions.
they disable, giving preference to trace eliminators that disable fewer ones. This heuristic relies on an experimental hypothesis that there are harmless cyclic dependencies that occur in linearizable executions.
Given a buggy trace  , and a set
, and a set 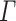 of linearizable traces, we use the following algorithm to rank trace eliminators for
of linearizable traces, we use the following algorithm to rank trace eliminators for  :
:
Let
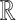 be the set of optimal trace eliminators for
be the set of optimal trace eliminators for 
- For each
 :
:- Let

Sort
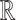 in ascending order depending on
in ascending order depending on 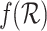 with
with  .
.
Since the above algorithm is heuristic in nature, there are no theoretical guarantees for the optimality of its results. For instance, its effectiveness depends on the set of linearizable traces 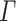 given as input. We discuss the empirical aspects of the underlying hypothesis in more detail in Sect. 7.
given as input. We discuss the empirical aspects of the underlying hypothesis in more detail in Sect. 7.
Experimental Evaluation
We demonstrate the efficacy of our approach for computing linearizability root-causes on several variations of lock-based concurrent sets/maps from the Synchrobench repository [21]. We consider three libraries from this repository: two linked-list set implementations, with coarse-grain and fine-grain locking, respectively, and a map implementation based on an AVL tree overlapping with two singly-linked lists, and fine-grain locking. We define three non-linearizable variations for each library by shrinking one atomic section only in the add method, only in the remove method, or an atomic section in each of these two methods. For each non-linearizable variation, we use Violat [14] to randomly sample three library clients that admit non-linearizable traces8. We use Java Pathfinder [44] to extract all traces of each client, up to partial-order reduction, partitioning them into linearizable and non-linearizable traces. Traces are extracted as sequences of call/return events and read/write accesses to explicit memory addresses, associated to line numbers in the source code of each of the API methods. The latter is important for being able to map critical segments (which refer to events in a trace) to atomic code blocks in the source code.
In Table 1, we list some quantitative data about our benchmarks, the clients, and the non-linearizable variations identified by the line numbers of the modified atomic sections (the original libraries can be found in the Synchrobench repository). For instance, the first variation of RWLockCoarseGrainedListIntSet is obtained by shrinking the atomic section in the add method between lines [26, 32/35] to [32, 32/35] (there are two line numbers for the end of the atomic section because it ends with an if conditional).
Table 1.
Benchmark data. Column Lib. shows the transformation on the atomic section(s) of the original library (we write atomic sections as pairs of line numbers in square brackets), Client shows the clients (we abbreviate the names of add, remove, and contains to a, r, and c, resp.), Non-lin. Out. shows an outcome (set of return values) witnessing for non-linearizability (true, false, and null are abbreviated to T, F, and N, resp.), # bugs and #valid give the number of non-linearizable and linearizable traces extracted using Java Pathfinder, respectively, # ev. and # conf. give the average number of events and conflict edges in these traces, Total(s) and Tr. Elim(s) give the clock time in seconds for applying our approach, the latter excluding the Java Pathfinder time for extracting traces.
For each non-linearizable trace  of a client C, we compute the set of optimal trace eliminators for
of a client C, we compute the set of optimal trace eliminators for 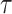 using the algorithm in Sect. 5.3 with the cycle enumeration described in Sect. 6.1. We then compute the ranking of these trace eliminators using as input the set of linearizable traces of C (the restriction to linearizable traces of the same client is only for convenience). Note that multiple trace eliminators can be ranked first since they disable exactly the same number of linearizable traces. Also, note that an optimal root-cause can disable a number of linearizable traces. This is true even for the ground truth repair (i.e. a repair that a human would identify trough manual inspection).
using the algorithm in Sect. 5.3 with the cycle enumeration described in Sect. 6.1. We then compute the ranking of these trace eliminators using as input the set of linearizable traces of C (the restriction to linearizable traces of the same client is only for convenience). Note that multiple trace eliminators can be ranked first since they disable exactly the same number of linearizable traces. Also, note that an optimal root-cause can disable a number of linearizable traces. This is true even for the ground truth repair (i.e. a repair that a human would identify trough manual inspection).
The results are presented in Table 2 and are self-explanatory. In the majority of cases, the first elements in this ranking are atomic sections which are precisely or very close to the expected results, i.e., atomic sections that belong to the original (error-free) version of the corresponding library. In some cases, the output of our approach is close, but not precisely the expected one. This is only due to the particular choice of the client used to generate the traces. In general, the quality of the produced repairs (compared to the ground truth) depends the types of behaviours of the library that the client exercises. However, if our tool ranks repair  first, in the context of a client C, then after repairing the library according to
first, in the context of a client C, then after repairing the library according to  the client C produces no linearizability violations.
the client C produces no linearizability violations.
Table 2.
Experimental data. Column #res gives the number of different results (sequences of trace eliminators) returned by our algorithm when applied on each of the non-linearizable traces of a client, and Tr. Elim. gives the first or the first two trace eliminators in the ranking obtained with our approach. For each trace eliminator we give the number of linearizable traces it disables (after  ).
).
The methods in the libraries OptimisticListSortedSetWaitFreeContains and LogicalOrderingAVL use optimistic concurrency, i.e., unbounded loops that restart when certain interferences are detected. This could potentially guide our heuristic in the wrong direction of giving the ground truth a lower rank. Indeed, a ground truth that concerns statements in the loop body could disable a large number of executions which only differ in the number of loop iterations. This, however, does not happen for small-size clients (like the ones used in our evaluation) since the number of invocations are bounded, which bounds the number of interferences and therefore the number of restarts.
Optimistic concurrency has the potential to mess with the heuristic, but this does not happen in small bounded clients as witnessed by our blah benchmark that does just fine.
To conclude, our empirical study demonstrates that given a good client (one that exercises the problems in the library properly), our approach is very effective in identifying the method at fault and the part of its code that is the root cause of the linearizability violation.
Related Work
Linearizability Violations. There is a large body of work on automatic detection of specific bugs such as data races, atomicity violations, e.g. [18, 40, 41, 45]. The focus of this paper is on linearizability errors. Wing and Gong [47] proposed an exponential-time monitoring algorithm for linearizability, which was later optimized by Lowe [33] and by Horn and Kroening [25]; neither avoided exponential-time asymptotic complexity. Burckhardt et al. [4] and Burnim et al. [5] implement exponential-time monitoring algorithms in their tools for testing of concurrent objects in .net and Java. Emmi and Enea [14, 15] introduce the tool Violat (used in our experiments) for checking linearizability of Java objects.
Concurrency Errors. There have been various techniques for fault localization, error explanation, counterexample minimization and bug summarization for sequential programs. We restrict our attention to relevant works for concurrent programs. More relevant to our work are those that try to extract simple explanations (i.e. root causes) from concurrent error traces. In [30], the authors focus on shortening counterexamples in message-passing programs to a set of “crucial events” that are both necessary and sufficient to reach the bug. In [27], the authors introduce a heuristic to simplify concurrent error traces by reducing the number of context-switches. Tools that attempt to minimize the number of context switches, such as SimTrace [26] and Tinertia [27], are orthogonal to the approach presented in this paper. To gain efficiency and robustness, some works rely on simple patterns of bugs for detection and a simple family of matching fixes to remove them, e.g., [10, 28, 29, 38]. Our work is set apart from these works by addressing linearizability (in contrast to simple atomicity violation patterns) as the correctness property of choice, and by being more systematic in the sense that it enumerates all trace eliminators for a given linearizability violation. We also present crisp results for the theoretical guarantees behind our approach and an analysis of the time complexity. Weeratunge et al. [46] use a set of good executions to derive an atomicity “specification”, i.e., pairs of accesses that are atomic, and then enforce it using locks.
There is large body of work on synchronization synthesis [2, 6–8, 11, 22, 34, 42, 43]. The approaches in [11, 42] are based on inferring synchronization by constructing and exploring the entire product graph or tableaux corresponding to a concurrent program. A different group of approaches infer synchronization incrementally from traces [43] or generalizations of bad traces [7, 8]. These techniques [7, 8, 43] also infer atomic sections but they do not focus on linearizability as the underlying correctness property but rather on assertion local violations. Several works investigate the problem of deriving an optimal lock placement given as input a program annotated with atomic sections, e.g., [9, 17, 48]. Afix [28] and ConcurrencySwapper [7] automatically fix concurrency-related errors. The latter uses error invariants to generalize a linear error trace to a partially ordered trace, which is then used to synthesize a fix.
Linearizability Repairs. Flint [32] is the only approach we know of that focuses on repairing non-linearizable libraries, but it has a very specific focus, namely fixing linearizability of composed map operations. It uses a different approach based on enumeration-based synthesis and it does not rely on concrete linearizability bugs.
Footnotes
An execution is called sequential when methods execute in isolation, one after another.
Two executions are equivalent if roughly, they are the same modulo reordering statements that do not access the same shared variable.
As usual, two memory accesses are conflicting when they access the same variable and at least one of them is a write.
Intuitively, this corresponds to running a concrete library under a most general client that makes an arbitrary number of invocations from an arbitrary number of threads.
Linearizability is typically defined with respect to a sequential ADT. Here, we take the simplifying assumption that the ADT is defined by the set of sequential histories of the library. This holds for all concurrent libraries that we are aware of.
We assume that program instructions are deterministic, which is usually the case.
A clique is a complete subgraph of a given graph.
These linearizability violations are quite rare. The frequencies reported by Violat in the context of a fixed client (when using standard testing) are in the order of 1/1000.
This work is supported in part by the European Research Council (ERC) under the EU’s Horizon 2020 research and innovation program (grant agreement No. 678177).
Contributor Information
Shuvendu K. Lahiri, Email: shuvendu.lahiri@microsoft.com
Chao Wang, Email: wang626@usc.edu.
Berk Çirisci, Email: cirisci@irif.fr.
Constantin Enea, Email: cenea@irif.fr.
Azadeh Farzan, Email: azadeh@cs.toronto.edu.
Suha Orhun Mutluergil, Email: mutluergil@irif.fr.
References
- 1.Afek Y, Gafni E, Morrison A. Common2 extended to stacks and unbounded concurrency. Distrib. Comput. 2007;20(4):239–252. doi: 10.1007/s00446-007-0023-3. [DOI] [Google Scholar]
- 2.Bloem, R., Hofferek, G., Könighofer, B., Könighofer, R., Ausserlechner, S., Spork, R.: Synthesis of synchronization using uninterpreted functions. In: Formal Methods in Computer-Aided Design, FMCAD 2014, Lausanne, Switzerland, 21–24 October 2014, pp. 35–42. IEEE (2014). 10.1109/FMCAD.2014.6987593
- 3.Bouajjani, A., Emmi, M., Enea, C., Hamza, J.: Tractable refinement checking for concurrent objects. In: Rajamani, S.K., Walker, D. (eds.) Proceedings of the 42nd Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2015, Mumbai, India, 15–17 January 2015, pp. 651–662. ACM (2015). 10.1145/2676726.2677002
- 4.Burckhardt, S., Dern, C., Musuvathi, M., Tan, R.: Line-up: a complete and automatic linearizability checker. In: Zorn, B.G., Aiken, A. (eds.) Proceedings of the 2010 ACM SIGPLAN Conference on Programming Language Design and Implementation, PLDI 2010, Toronto, Ontario, Canada, 5–10 June 2010, pp. 330–340. ACM (2010). 10.1145/1806596.1806634
- 5.Burnim, J., Necula, G.C., Sen, K.: Specifying and checking semantic atomicity for multithreaded programs. In: Gupta, R., Mowry, T.C. (eds.) Proceedings of the 16th International Conference on Architectural Support for Programming Languages and Operating Systems, ASPLOS 2011, Newport Beach, CA, USA, 5–11 March 2011, pp. 79–90. ACM (2011). 10.1145/1950365.1950377
- 6.Černý P, et al. From non-preemptive to preemptive scheduling using synchronization synthesis. In: Kroening D, Păsăreanu CS, et al., editors. Computer Aided Verification; Cham: Springer; 2015. pp. 180–197. [Google Scholar]
- 7.Černý P, Henzinger TA, Radhakrishna A, Ryzhyk L, Tarrach T. Efficient synthesis for concurrency by semantics-preserving transformations. In: Sharygina N, Veith H, editors. Computer Aided Verification; Heidelberg: Springer; 2013. pp. 951–967. [Google Scholar]
- 8.Černý P, Henzinger TA, Radhakrishna A, Ryzhyk L, Tarrach T. Regression-free synthesis for concurrency. In: Biere A, Bloem R, editors. Computer Aided Verification; Cham: Springer; 2014. pp. 568–584. [Google Scholar]
- 9.Cherem, S., Chilimbi, T.M., Gulwani, S.: Inferring locks for atomic sections. In: Gupta, R., Amarasinghe, S.P. (eds.) Proceedings of the ACM SIGPLAN 2008 Conference on Programming Language Design and Implementation, Tucson, AZ, USA, 7–13 June 2008, pp. 304–315. ACM (2008). 10.1145/1375581.1375619
- 10.Chew, L., Lie, D.: Kivati: fast detection and prevention of atomicity violations. In: Morin, C., Muller, G. (eds.) European Conference on Computer Systems, Proceedings of the 5th European Conference on Computer Systems, EuroSys 2010, Paris, France, 13–16 April 2010, pp. 307–320. ACM (2010). 10.1145/1755913.1755945
- 11.Clarke EM, Emerson EA. Design and synthesis of synchronization skeletons using branching time temporal logic. In: Grumberg O, Veith H, editors. 25 Years of Model Checking; Heidelberg: Springer; 2008. pp. 196–215. [Google Scholar]
- 12.Emmi, M., Enea, C.: Exposing non-atomic methods of concurrent objects. CoRR abs/1706.09305 (2017). http://arxiv.org/abs/1706.09305
- 13.Emmi, M., Enea, C.: Sound, complete, and tractable linearizability monitoring for concurrent collections. PACMPL 2(POPL), 25:1–25:27 (2018). 10.1145/3158113
- 14.Emmi M, Enea C. Violat: generating tests of observational refinement for concurrent objects. In: Dillig I, Tasiran S, editors. Computer Aided Verification; Cham: Springer; 2019. pp. 534–546. [Google Scholar]
- 15.Emmi, M., Enea, C.: Weak-consistency specification via visibility relaxation. PACMPL 3(POPL), 60:1–60:28 (2019). 10.1145/3290373
- 16.Emmi, M., Enea, C., Hamza, J.: Monitoring refinement via symbolic reasoning. In: Grove, D., Blackburn, S. (eds.) Proceedings of the 36th ACM SIGPLAN Conference on Programming Language Design and Implementation, Portland, OR, USA, 15–17 June 2015, pp. 260–269. ACM (2015). 10.1145/2737924.2737983
- 17.Emmi, M., Fischer, J.S., Jhala, R., Majumdar, R.: Lock allocation. In: Hofmann, M., Felleisen, M. (eds.) Proceedings of the 34th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2007, Nice, France, 17–19 January 2007, pp. 291–296. ACM (2007). 10.1145/1190216.1190260
- 18.Engler, D.R., Ashcraft, K.: Racerx: effective, static detection of race conditions and deadlocks. In: Scott, M.L., Peterson, L.L. (eds.) Proceedings of the 19th ACM Symposium on Operating Systems Principles 2003, SOSP 2003, Bolton Landing, NY, USA, 19–22 October 2003, pp. 237–252. ACM (2003). 10.1145/945445.945468
- 19.Farzan A, Madhusudan P. Monitoring atomicity in concurrent programs. In: Gupta A, Malik S, editors. Computer Aided Verification; Heidelberg: Springer; 2008. pp. 52–65. [Google Scholar]
- 20.Gibbons PB, Korach E. Testing shared memories. SIAM J. Comput. 1997;26(4):1208–1244. doi: 10.1137/S0097539794279614. [DOI] [Google Scholar]
- 21.Gramoli, V.: More than you ever wanted to know about synchronization: synchrobench, measuring the impact of the synchronization on concurrent algorithms. In: Cohen, A., Grove, D. (eds.) Proceedings of the 20th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming, PPoPP 2015, San Francisco, CA, USA, 7–11 February 2015, pp. 1–10. ACM (2015). 10.1145/2688500.2688501
- 22.Gupta, A., Henzinger, T.A., Radhakrishna, A., Samanta, R., Tarrach, T.: Succinct representation of concurrent trace sets. In: Rajamani, S.K., Walker, D. (eds.) Proceedings of the 42nd Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2015, Mumbai, India, 15–17 January 2015, pp. 433–444. ACM (2015). 10.1145/2676726.2677008
- 23.Herlihy M, Shavit N. The Art of Multiprocessor Programming. Burlington: Morgan Kaufmann; 2008. [Google Scholar]
- 24.Herlihy M, Wing JM. Linearizability: a correctness condition for concurrent objects. ACM Trans. Program. Lang. Syst. 1990;12(3):463–492. doi: 10.1145/78969.78972. [DOI] [Google Scholar]
- 25.Horn A, Kroening D. Faster linearizability checking via P-compositionality. In: Graf S, Viswanathan M, editors. Formal Techniques for Distributed Objects, Components, and Systems; Cham: Springer; 2015. pp. 50–65. [Google Scholar]
- 26.Huang J, Zhang C. An efficient static trace simplification technique for debugging concurrent programs. In: Yahav E, editor. Static Analysis; Heidelberg: Springer; 2011. pp. 163–179. [Google Scholar]
- 27.Jalbert, N., Sen, K.: A trace simplification technique for effective debugging of concurrent programs. In: Roman, G., van der Hoek, A. (eds.) Proceedings of the 18th ACM SIGSOFT International Symposium on Foundations of Software Engineering, 2010, Santa Fe, NM, USA, 7–11 November 2010, pp. 57–66. ACM (2010). 10.1145/1882291.1882302
- 28.Jin, G., Song, L., Zhang, W., Lu, S., Liblit, B.: Automated atomicity-violation fixing. In: Hall, M.W., Padua, D.A. (eds.) Proceedings of the 32nd ACM SIGPLAN Conference on Programming Language Design and Implementation, PLDI 2011, San Jose, CA, USA, 4–8 June 2011, pp. 389–400. ACM (2011). 10.1145/1993498.1993544
- 29.Jin, G., Zhang, W., Deng, D.: Automated concurrency-bug fixing. In: Thekkath, C., Vahdat, A. (eds.) 10th USENIX Symposium on Operating Systems Design and Implementation, OSDI 2012, Hollywood, CA, USA, 8–10 October 2012, pp. 221–236. USENIX Association (2012). https://www.usenix.org/conference/osdi12/technical-sessions/presentation/jin
- 30.Kashyap S, Garg VK. Producing short counterexamples using “crucial events”. In: Gupta A, Malik S, editors. Computer Aided Verification; Heidelberg: Springer; 2008. pp. 491–503. [Google Scholar]
- 31.Liskov B, Zilles SN. Programming with abstract data types. SIGPLAN Not. 1974;9(4):50–59. doi: 10.1145/942572.807045. [DOI] [Google Scholar]
- 32.Liu, P., Tripp, O., Zhang, X.: Flint: fixing linearizability violations. In: Black, A.P., Millstein, T.D. (eds.) Proceedings of the 2014 ACM International Conference on Object Oriented Programming Systems Languages & Applications, OOPSLA 2014, part of SPLASH 2014, Portland, OR, USA, 20–24 October 2014, pp. 543–560. ACM (2014). 10.1145/2660193.2660217
- 33.Lowe, G.: Testing for linearizability. Concurr. Comput.: Pract. Exper. 29(4) (2017). 10.1002/cpe.3928
- 34.Manna Z, Wolper P. Synthesis of communicating processes from temporal logic specifications. ACM Trans. Program. Lang. Syst. 1984;6(1):68–93. doi: 10.1145/357233.357237. [DOI] [Google Scholar]
- 35.Michael, M.M.: ABA prevention using single-word instructions. Technical report RC 23089, IBM Thomas J. Watson Research Center, January 2004
- 36.Moir, M., Shavit, N.: Concurrent data structures. In: Mehta, D.P., Sahni, S. (eds.) Handbook of Data Structures and Applications. Chapman and Hall/CRC (2004). 10.1201/9781420035179.ch47
- 37.Papadimitriou CH. The serializability of concurrent database updates. J. ACM. 1979;26(4):631–653. doi: 10.1145/322154.322158. [DOI] [Google Scholar]
- 38.Park, S., Lu, S., Zhou, Y.: Ctrigger: exposing atomicity violation bugs from their hiding places. In: Soffa, M.L., Irwin, M.J. (eds.) Proceedings of the 14th International Conference on Architectural Support for Programming Languages and Operating Systems, ASPLOS 2009, Washington, DC, USA, 7–11 March 2009, pp. 25–36. ACM (2009). 10.1145/1508244.1508249
- 39.Pradel, M., Gross, T.R.: Automatic testing of sequential and concurrent substitutability. In: Notkin, D., Cheng, B.H.C., Pohl, K. (eds.) 35th International Conference on Software Engineering, ICSE 2013, San Francisco, CA, USA, 18–26 May 2013, pp. 282–291. IEEE Computer Society (2013). 10.1109/ICSE.2013.6606574
- 40.Said M, Wang C, Yang Z, Sakallah K. Generating data race witnesses by an SMT-based analysis. In: Bobaru M, Havelund K, Holzmann GJ, Joshi R, editors. NASA Formal Methods; Heidelberg: Springer; 2011. pp. 313–327. [Google Scholar]
- 41.Savage S, Burrows M, Nelson G, Sobalvarro P, Anderson TE. Eraser: a dynamic data race detector for multithreaded programs. ACM Trans. Comput. Syst. 1997;15(4):391–411. doi: 10.1145/265924.265927. [DOI] [Google Scholar]
- 42.Vechev M, Yahav E, Yorsh G. Inferring synchronization under limited observability. In: Kowalewski S, Philippou A, editors. Tools and Algorithms for the Construction and Analysis of Systems; Heidelberg: Springer; 2009. pp. 139–154. [Google Scholar]
- 43.Vechev, M.T., Yahav, E., Yorsh, G.: Abstraction-guided synthesis of synchronization. In: Hermenegildo, M.V., Palsberg, J. (eds.) Proceedings of the 37th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2010, Madrid, Spain, 17–23 January 2010, pp. 327–338. ACM (2010). 10.1145/1706299.1706338
- 44.Visser, W., Pasareanu, C.S., Khurshid, S.: Test input generation with java pathfinder. In: Avrunin, G.S., Rothermel, G. (eds.) Proceedings of the ACM/SIGSOFT International Symposium on Software Testing and Analysis, ISSTA 2004, Boston, Massachusetts, USA, 11–14 July 2004, pp. 97–107. ACM (2004). 10.1145/1007512.1007526
- 45.Wang C, Limaye R, Ganai M, Gupta A. Trace-based symbolic analysis for atomicity violations. In: Esparza J, Majumdar R, editors. Tools and Algorithms for the Construction and Analysis of Systems; Heidelberg: Springer; 2010. pp. 328–342. [Google Scholar]
- 46.Weeratunge, D., Zhang, X., Jagannathan, S.: Accentuating the positive: atomicity inference and enforcement using correct executions. In: Lopes, C.V., Fisher, K. (eds.) Proceedings of the 26th Annual ACM SIGPLAN Conference on Object-Oriented Programming, Systems, Languages, and Applications, OOPSLA 2011, part of SPLASH 2011, Portland, OR, USA, 22–27 October 2011, pp. 19–34. ACM (2011). 10.1145/2048066.2048071
- 47.Wing JM, Gong C. Testing and verifying concurrent objects. J. Parallel Distrib. Comput. 1993;17(1–2):164–182. doi: 10.1006/jpdc.1993.1015. [DOI] [Google Scholar]
- 48.Zhang Y, Sreedhar VC, Zhu W, Sarkar V, Gao GR. Minimum lock assignment: a method for exploiting concurrency among critical sections. In: Amaral JN, editor. Languages and Compilers for Parallel Computing; Heidelberg: Springer; 2008. pp. 141–155. [Google Scholar]