Abstract
IC3 has been a leap forward in symbolic model checking. This paper proposes PrIC3 (pronounced pricy-three), a conservative extension of IC3 to symbolic model checking of MDPs. Our main focus is to develop the theory underlying PrIC3. Alongside, we present a first implementation of PrIC3 including the key ingredients from IC3 such as generalization, repushing, and propagation.

Introduction
IC3. Also known as property-directed reachability (PDR) [23], IC3 [13] is a symbolic approach for verifying finite transition systems (TSs) against safety properties like “bad states are unreachable”. It combines bounded model checking (BMC) [12] and inductive invariant generation. Put shortly, IC3 either proves that a set B of bad states is unreachable by finding a set of non-B states closed under reachability—called an inductive invariant—or refutes reachability of B by a counterexample path reaching B. Rather than unrolling the transition relation (as in BMC), IC3 attempts to incrementally strengthen the invariant “no state in B is reachable” into an inductive one. In addition, it applies aggressive abstraction to the explored state space, so-called generalization [36]. These aspects together with the enormous advances in modern SAT solvers have led to IC3 ’s success. IC3 has been extended [27, 38] and adapted to software verification [19, 44]. This paper develops a quantitative IC3 framework for probabilistic models.
MDPs. Markov decision processes (MDPs) extend TSs with discrete probabilistic choices. They are central in planning, AI as well as in modeling randomized distributed algorithms. A key question in verifying MDPs is quantitative reachability: “is the (maximal) probability to reach
B
at most
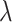 ?”. Quantitative reachability
[5, 6] reduces to solving linear programs (LPs). Various tools support MDP model checking, e.g., Prism
[43], Storm
[22], modest
[34], and EPMC
[31]. The LPs are mostly solved using (variants of) value iteration
[8, 28, 35, 51]. Symbolic BDD-based MDP model checking originated two decades ago
[4] and is rather successful.
?”. Quantitative reachability
[5, 6] reduces to solving linear programs (LPs). Various tools support MDP model checking, e.g., Prism
[43], Storm
[22], modest
[34], and EPMC
[31]. The LPs are mostly solved using (variants of) value iteration
[8, 28, 35, 51]. Symbolic BDD-based MDP model checking originated two decades ago
[4] and is rather successful.
Towards IC3 for MDPs. Despite the success of BDD-based symbolic methods in tools like Prism, IC3 has not penetrated probabilistic model checking yet. The success of IC3 and the importance of quantitative reachability in probabilistic model checking raises the question whether and how IC3 can be adapted—not just utilized—to reason about quantitative reachability in MDPs. This paper addresses the challenges of answering this question. It extends IC3 in several dimensions to overcome these hurdles, making PrIC3—to our knowledge—the first IC3 framework for quantitative reachability in MDPs1. Notably, PrIC3 is conservative: For a threshold  , PrIC3 solves the same qualitative problem and behaves (almost) the same as standard IC3. Our main contribution is developing the theory underlying PrIC3, which is accompanied by a proof-of-concept implementation.
, PrIC3 solves the same qualitative problem and behaves (almost) the same as standard IC3. Our main contribution is developing the theory underlying PrIC3, which is accompanied by a proof-of-concept implementation.
Challenge 1
(Leaving the Boolean domain).IC3 iteratively computes frames, which are over-approximations of sets of states that can reach B in a bounded number of steps. For MDPs, Boolean reachability becomes a quantitative reachability probability. This requires a shift: frames become real-valued functions rather than sets of states. Thus, there are infinitely many possible frames—even for finite-state MDPs—just as for infinite-state software
[19, 44] and hybrid systems
[54]. Additionally, whereas in TSs a state reachable within k steps remains reachable on increasing k, the reachability probability in MDPs may increase. This complicates ensuring termination of an IC3 algorithm for MDPs. 
Challenge 2
(Counterexamples
 single paths). For TSs, a single cycle-free path2 to B suffices to refute that “B
is not reachable”. This is not true in the probabilistic setting
[32]. Instead, proving that the probability of reaching B exceeds the threshold
single paths). For TSs, a single cycle-free path2 to B suffices to refute that “B
is not reachable”. This is not true in the probabilistic setting
[32]. Instead, proving that the probability of reaching B exceeds the threshold 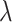 requires a set of possibly cyclic paths—e.g., represented as a sub-MDP
[15]—whose probability mass exceeds
requires a set of possibly cyclic paths—e.g., represented as a sub-MDP
[15]—whose probability mass exceeds 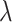 . Handling sets of paths as counterexamples in the context of IC3 is new.
. Handling sets of paths as counterexamples in the context of IC3 is new. 
Challenge 3
(Strengthening). This key IC3 technique intuitively turns a proof obligation of type (i) “state s is unreachable from the initial state 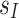 ” into type (ii) “s’s predecessors are unreachable from
” into type (ii) “s’s predecessors are unreachable from 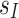 ”. A first issue is that in the quantitative setting, the standard characterization of reachability probabilities in MDPs (the Bellman equations) inherently reverses the direction of reasoning (cf. “reverse” IC3
[53]): Hence, strengthening turns (i) “s cannot reach
”. A first issue is that in the quantitative setting, the standard characterization of reachability probabilities in MDPs (the Bellman equations) inherently reverses the direction of reasoning (cf. “reverse” IC3
[53]): Hence, strengthening turns (i) “s cannot reach 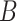 ” into (ii) “s’s successors cannot reach
” into (ii) “s’s successors cannot reach 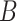 ”.
”.
A much more challenging issue, however, is that in the quantitative setting obligations of type (i) read “s is reachable with at most probability
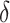 ”. However, the strengthened type (ii) obligation must then read: “the weighted sum over the reachability probabilities of the successors of
s is at most
”. However, the strengthened type (ii) obligation must then read: “the weighted sum over the reachability probabilities of the successors of
s is at most  ”. In general, there are infinitely many possible choices of subobligations for the successors of s in order to satisfy the original obligation, because—grossly simplified—there are infinitely many possibilities for a and b to satisfy weighted sums such as
”. In general, there are infinitely many possible choices of subobligations for the successors of s in order to satisfy the original obligation, because—grossly simplified—there are infinitely many possibilities for a and b to satisfy weighted sums such as 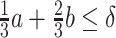 . While we only need one choice of subobligations, picking a good one is approximately as hard as solving the entire problem altogether. We hence require a heuristic, which is guided by a user-provided oracle.
. While we only need one choice of subobligations, picking a good one is approximately as hard as solving the entire problem altogether. We hence require a heuristic, which is guided by a user-provided oracle. 
Challenge 4
(Generalization). “One of the key components of IC3 is [inductive] generalization”
[13]. Generalization
[36] abstracts single states. It makes IC3 scale, but is not essential for correctness. To facilitate generalization, systems should be encoded symbolically, i.e., integer-valued program variables describe states. Frames thus map variables to probabilities. A first aspect is how to effectively present them to an SMT-solver. Conceptually, we use uninterpreted functions and universal quantifiers (encoding program behavior) together with linear real arithmetic to encode the weighted sums occurring when reasoning about probabilities. A second aspect is more fundamental: Abstractly, IC3 ’s generalization guesses an unreachable set of states. We, however, need to guess this set and a probability for each state. To be effective, these guesses should moreover eventually yield an inductive frame, which is often highly nonlinear. We propose three SMT-guided interpolation variants for guessing these maps. 
Structure of this Paper. We develop PrIC3 gradually: We explain the underlying rationale in Sect. 3. We also describe the core of PrIC3—called  —which resembles closely the main loop of standard IC3, but uses adapted frames and termination criteria (Challenge 1). In line with Challenge 3,
—which resembles closely the main loop of standard IC3, but uses adapted frames and termination criteria (Challenge 1). In line with Challenge 3,  is parameterized by a heuristic
is parameterized by a heuristic  which is applied whenever we need to select one out of infinitely many probabilities. No requirements on the quality of
which is applied whenever we need to select one out of infinitely many probabilities. No requirements on the quality of  are imposed.
are imposed.  is sound and always terminates: If it returns
is sound and always terminates: If it returns  , then the maximal reachability probability is bounded by
, then the maximal reachability probability is bounded by 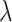 . Without additional assumptions about
. Without additional assumptions about 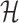 ,
,  is incomplete: on returning
is incomplete: on returning 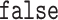 , it is unknown whether the returned subMDP is indeed a counterexample (Challenge 2). Section 4 details strengthening (Challenge 3). Section 5 presents a sound and complete algorithm
, it is unknown whether the returned subMDP is indeed a counterexample (Challenge 2). Section 4 details strengthening (Challenge 3). Section 5 presents a sound and complete algorithm  on top of
on top of  . Section 6 presents a prototype, discusses our chosen heuristics, and addresses Challenge 4. Section 7 shows some encouraging experiments, but also illustrates need for further progress.
. Section 6 presents a prototype, discusses our chosen heuristics, and addresses Challenge 4. Section 7 shows some encouraging experiments, but also illustrates need for further progress.
Related Work. Just like IC3 has been a symbiosis of different approaches, PrIC3 has been inspired by several existing techniques from the verification of probabilistic systems.
BMC. Adaptions of BMC to Markov chains (MCs) with a dedicated treatment of cycles have been pursued in [57]. The encoding in [24] annotates sub-formulae with probabilities. The integrated SAT solving process implicitly unrolls all paths leading to an exponential blow-up. In [52], this is circumvented by grouping paths, discretizing them, and using an encoding with quantifiers and bit-vectors, but without numerical values. Recently, [56] extends this idea to a PAC algorithm by purely propositional encodings and (approximate) model counting [17]. These approaches focus on MCs and are not mature yet.
Invariant Synthesis. Quantitative loop invariants are key in analyzing probabilistic programs whose operational semantics are (possibly infinite) MDPs [26]. A quantitative invariant I maps states to probabilities. I is shown to be an invariant by comparing I to the result of applying the MDP’s Bellman operator to I. Existing approaches for invariant synthesis are, e.g., based on weakest pre-expectations [33, 39, 40, 42, 46], template-based constraint solving [25], notions of martingales [3, 9, 16, 55], and solving recurrence relations [10]. All but the last technique require user guidance.
Abstraction. To combat state-space explosion, abstraction is often employed. CEGAR for MDPs [37] deals with explicit sets of paths as counterexamples. Game-based abstraction [30, 41] and partial exploration [14] exploit that not all paths have to be explored to prove bounds on reachability probabilities.
Statistical Methods and (deep) Reinforcement Learning. Finally, an avenue that avoids storing a (complete) model are simulation-based approaches (statistical model checking [2]) and variants of reinforcement learning, possibly with neural networks. For MDPs, these approaches yield weak statistical guarantees [20], but may provide good oracles.
Problem Statement
Our aim is to prove that the maximal probability of reaching a set
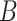 of bad states from the initial state
of bad states from the initial state 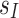 of a Markov decision process
of a Markov decision process
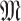 is at most some threshold
is at most some threshold 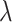 . Below, we give a formal description of our problem. We refer to
[7, 50] for a thorough introduction.
. Below, we give a formal description of our problem. We refer to
[7, 50] for a thorough introduction.
Definition 1
(MDPs). A Markov decision process (MDP) is a tuple  , where S is a finite set of states,
, where S is a finite set of states, 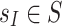 is the initial state,
is the initial state, 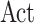 is a finite set of actions, and
is a finite set of actions, and 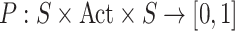 is a transition probability function. For state s, let
is a transition probability function. For state s, let 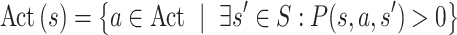 be the enabled actions at s. For all states
be the enabled actions at s. For all states  , we require
, we require  and
and 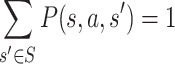 .
. 
For this paper, we fix an MDP 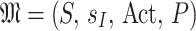 , a set of bad states
, a set of bad states
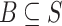 , and a threshold
, and a threshold  . The maximal3
(unbounded) reachability probability to eventually reach a state in
. The maximal3
(unbounded) reachability probability to eventually reach a state in 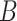 from a state s is denoted by
from a state s is denoted by  . We characterize
. We characterize 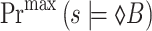 using the so-called Bellman operator. Let
using the so-called Bellman operator. Let  denote the set of functions from N to M. Anticipating IC3 terminology, we call a function
denote the set of functions from N to M. Anticipating IC3 terminology, we call a function 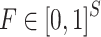 a frame. We denote by F[s] the evaluation of frame F for state s.
a frame. We denote by F[s] the evaluation of frame F for state s.
Definition 2
(Bellman Operator). For a set of actions 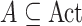 , we define the Bellman operator for
A as a frame transformer
, we define the Bellman operator for
A as a frame transformer  with
with
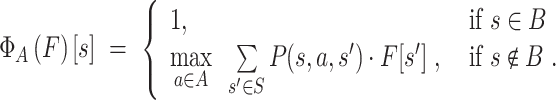 |
We write 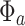 for
for 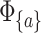 ,
,  for
for 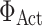 , and call
, and call 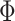 simply the Bellman operator.
simply the Bellman operator. 
For every state s, the maximal reachability probability 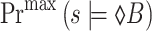 is then given by the least fixed point of the Bellman operator
is then given by the least fixed point of the Bellman operator 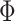 . That is,
. That is,
 |
where the underlying partial order on frames is a complete lattice with ordering
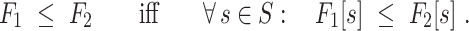 |
In terms of the Bellman operator, our formal problem statement reads as follows: 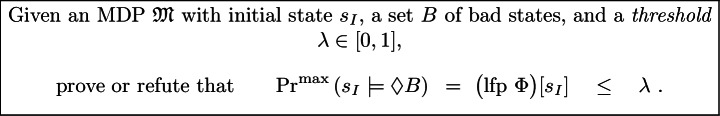 Whenever
Whenever 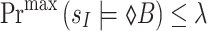 indeed holds, we say that the MDP
indeed holds, we say that the MDP  is safe (with respect to the set of bad states
is safe (with respect to the set of bad states  and threshold
and threshold  ); otherwise, we call it unsafe.
); otherwise, we call it unsafe.
Recovery Statement 1
For 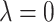 , our problem statement is equivalent to the qualitative reachability problem solved by (reverse) standard IC3, i.e, prove or refute that all bad states in
, our problem statement is equivalent to the qualitative reachability problem solved by (reverse) standard IC3, i.e, prove or refute that all bad states in 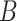 are unreachable from the initial state
are unreachable from the initial state 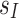 .
.
Example 1
The MDP 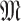 in Fig. 1 consists of 6 states with initial state
in Fig. 1 consists of 6 states with initial state 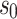 and bad states
and bad states 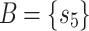 . In
. In 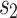 , actions a and b are enabled; in all other states, one unlabeled action is enabled. We have
, actions a and b are enabled; in all other states, one unlabeled action is enabled. We have  . Hence,
. Hence,  is safe for all thresholds
is safe for all thresholds 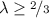 and unsafe for
and unsafe for  . In particular,
. In particular, 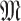 is unsafe for
is unsafe for 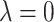 as
as  is reachable from
is reachable from 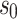 .
. 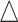
Fig. 1.
The MDP 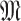 serving as a running example.
serving as a running example.
The Core PrIC3 Algorithm
The purpose of PrIC3 is to prove or refute that the maximal probability to reach a bad state in 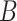 from the initial state
from the initial state 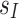 of the MDP
of the MDP 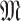 is at most
is at most  . In this section, we explain the rationale underlying PrIC3. Moreover, we describe the core of PrIC3—called
. In this section, we explain the rationale underlying PrIC3. Moreover, we describe the core of PrIC3—called  —which bears close resemblance to the main loop of standard IC3 for TSs.
—which bears close resemblance to the main loop of standard IC3 for TSs.
Because of the inherent direction of the Bellman operator, we build PrIC3 on reverse IC3 [53], cf. Challenge 3. Reversing constitutes a shift from reasoning along the direction initial-to-bad to bad-to-initial. While this shift is mostly inessential to the fundamentals underlying IC3, the reverse direction is unswayable in the probabilistic setting. Whenever we draw a connection to standard IC3, we thus generally mean reverse IC3.
Inductive Frames
IC3 for TSs operates on (qualitative) frames representing sets of states of the TS at hand. A frame F can hence be thought of as a mapping4 from states to 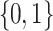 . In PrIC3 for MDPs, we need to move from a Boolean to a quantitative regime. Hence, a (quantitative) frame is a mapping from states to probabilities in [0, 1].
. In PrIC3 for MDPs, we need to move from a Boolean to a quantitative regime. Hence, a (quantitative) frame is a mapping from states to probabilities in [0, 1].
For a given TS, consider the frame transformer T that adds to a given input frame  all bad states in
all bad states in  and all predecessors of the states contained in
and all predecessors of the states contained in  . The rationale of standard (reverse) IC3 is to find a frame
. The rationale of standard (reverse) IC3 is to find a frame 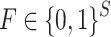 such that (i) the initial state
such that (i) the initial state  does not belong to F and (ii) applying T takes us down in the partial order on frames, i.e.,
does not belong to F and (ii) applying T takes us down in the partial order on frames, i.e.,
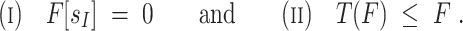 |
Intuitively, (i) postulates the hypothesis that  cannot reach
cannot reach  and (ii) expresses that F is closed under adding bad states and taking predecessors, thus affirming the hypothesis.
and (ii) expresses that F is closed under adding bad states and taking predecessors, thus affirming the hypothesis.
Analogously, the rationale of PrIC3 is to find a frame 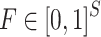 such that (i) F postulates that the probability of
such that (i) F postulates that the probability of 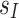 to reach
to reach 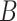 is at most the threshold
is at most the threshold 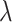 and (ii) applying the Bellman operator
and (ii) applying the Bellman operator 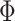 to F takes us down in the partial order on frames, i.e.,
to F takes us down in the partial order on frames, i.e.,
 |
Frames satisfying the above conditions are called inductive invariants in IC3. We adopt this terminology. By Park’s Lemma [48], which in our setting reads
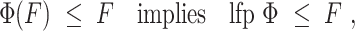 |
an inductive invariant F would indeed witness that 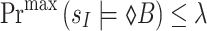 , because
, because
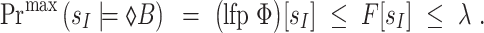 |
If no inductive invariant exists, then standard IC3 will find a counterexample: a path from the initial state  to a bad state in
to a bad state in  , which serves as a witness to refute. Analogously, PrIC3 will find a counterexample, but of a different kind: Since single paths are insufficient as counterexamples in the probabilistic realm (Challenge 2), PrIC3 will instead find a subsystem of states of the MDP witnessing
, which serves as a witness to refute. Analogously, PrIC3 will find a counterexample, but of a different kind: Since single paths are insufficient as counterexamples in the probabilistic realm (Challenge 2), PrIC3 will instead find a subsystem of states of the MDP witnessing  .
.
The PrIC3 Invariants
Analogously to standard IC3, PrIC3 aims to find the inductive invariant by maintaining a sequence of frames
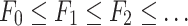 such that
such that  overapproximates the maximal probability of reaching B from s within at most i steps. This i-step-bounded reachability probability
overapproximates the maximal probability of reaching B from s within at most i steps. This i-step-bounded reachability probability
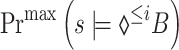 can be characterized using the Bellman operator:
can be characterized using the Bellman operator:  is the 0-step probability; it is 1 for every
is the 0-step probability; it is 1 for every  and 0 otherwise. For any
and 0 otherwise. For any  , we have
, we have
where  , the frame that maps every state to 0, is the least frame of the underlying complete lattice. For a finite MDP, the unbounded reachability probability is then given by the limit
, the frame that maps every state to 0, is the least frame of the underlying complete lattice. For a finite MDP, the unbounded reachability probability is then given by the limit
where  is a consequence of the well-known Kleene fixed point theorem
[45].
is a consequence of the well-known Kleene fixed point theorem
[45].
The sequence  maintained by PrIC3 should frame-wise overapproximate the increasing sequence
maintained by PrIC3 should frame-wise overapproximate the increasing sequence  . Pictorially:
. Pictorially: 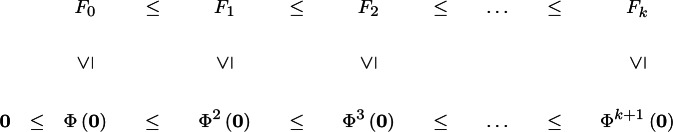 However, the sequence
However, the sequence 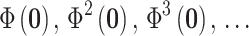 will never explicitly be known to PrIC3. Instead, PrIC3 will ensure the above frame-wise overapproximation property implicitly by enforcing the so-called PrIC3 invariants on the frame sequence
will never explicitly be known to PrIC3. Instead, PrIC3 will ensure the above frame-wise overapproximation property implicitly by enforcing the so-called PrIC3 invariants on the frame sequence  . Apart from allowing for a threshold
. Apart from allowing for a threshold 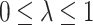 on the maximal reachability probability, these invariants coincide with the standard IC3 invariants (where
on the maximal reachability probability, these invariants coincide with the standard IC3 invariants (where 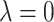 is fixed). Formally:
is fixed). Formally:
Definition 3
(
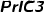 Invariants). Frames
Invariants). Frames  , for
, for 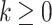 , satisfy the PrIC3 invariants, a fact we will denote by
, satisfy the PrIC3 invariants, a fact we will denote by 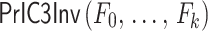 , if all of the following hold:
, if all of the following hold:
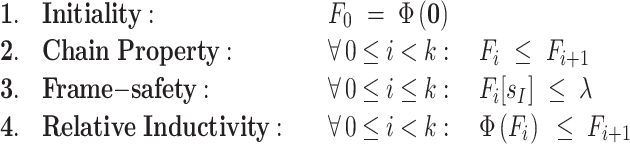 |
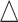
The PrIC3 invariants enforce the above picture: The chain property ensures 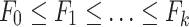 . We have
. We have 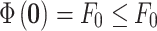 by initiality. Assuming
by initiality. Assuming  as induction hypothesis, monotonicity of
as induction hypothesis, monotonicity of 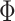 and relative inductivity imply
and relative inductivity imply 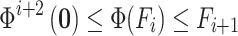 .
.
By overapproximating 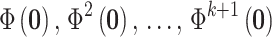 , the frames
, the frames 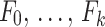 in effect bound the maximal step-bounded reachability probability of every state:
in effect bound the maximal step-bounded reachability probability of every state:
Lemma 1
Let frames 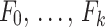 satisfy the PrIC3 invariants. Then
satisfy the PrIC3 invariants. Then
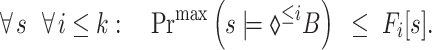 |
In particular, Lemma 1 together with frame-safety ensures that the maximal step-bounded reachability probability of the initial state
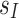 to reach
to reach  is at most the threshold
is at most the threshold 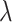 .
.
As for proving that the unbounded reachability probability is also at most  , it suffices to find two consecutive frames, say
, it suffices to find two consecutive frames, say 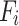 and
and  , that coincide:
, that coincide:
Lemma 2
Let frames 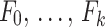 satisfy the PrIC3 invariants. Then
satisfy the PrIC3 invariants. Then
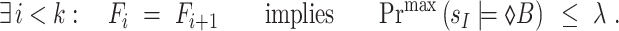 |
Proof
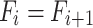 and relative inductivity yield
and relative inductivity yield  , rendering
, rendering  inductive. By Park’s lemma (cf. Sect. 3.1), we obtain
inductive. By Park’s lemma (cf. Sect. 3.1), we obtain 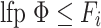 and—by frame-safety—conclude
and—by frame-safety—conclude
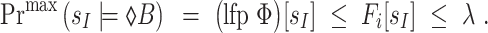 |

Operationalizing the PrIC3 Invariants for Proving Safety
Lemma 2 gives us a clear angle of attack for proving an MDP safe: Repeatedly add and refine frames approximating step-bounded reachability probabilities for more and more steps while enforcing the PrIC3 invariants (cf. Definition 3.2) until two consecutive frames coincide. Analogously to standard IC3, this approach is taken by the core loop
Analogously to standard IC3, this approach is taken by the core loop  depicted in Algorithm 1; differences to the main loop of IC3 (cf.
[23, Fig. 5]) are highlighted in
depicted in Algorithm 1; differences to the main loop of IC3 (cf.
[23, Fig. 5]) are highlighted in
 . A particular difference is that
. A particular difference is that  is parameterized by a heuristic
is parameterized by a heuristic  for finding suitable probabilities (see Challenge 3). Since the precise choice of
for finding suitable probabilities (see Challenge 3). Since the precise choice of  is irrelevant for the soundness of
is irrelevant for the soundness of  , we defer a detailed discussion of suitable heuristics to Sect. 4.
, we defer a detailed discussion of suitable heuristics to Sect. 4.
As input,  takes an MDP
takes an MDP  , a set
, a set 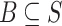 of bad states, and a threshold
of bad states, and a threshold 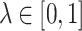 . Since the input is never changed, we assume it to be globally available, also to subroutines. As output,
. Since the input is never changed, we assume it to be globally available, also to subroutines. As output,  returns
returns 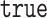 if two consecutive frames become equal. We hence say that
if two consecutive frames become equal. We hence say that  is sound if it only returns
is sound if it only returns  if
if  is safe.
is safe.
We will formalize soundness using Hoare triples. For precondition  , postcondition
, postcondition  , and program P, the triple
, and program P, the triple 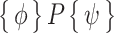 is valid (for partial correctness) if, whenever program P starts in a state satisfying precondition
is valid (for partial correctness) if, whenever program P starts in a state satisfying precondition 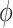 and terminates in some state
and terminates in some state 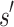 , then
, then 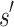 satisfies postcondition
satisfies postcondition 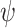 . Soundness of
. Soundness of  then means validity of the triple
then means validity of the triple
Let us briefly go through the individual steps of  in Algorithm 1 and convince ourselves that it is indeed sound. After that, we discuss why
in Algorithm 1 and convince ourselves that it is indeed sound. After that, we discuss why  terminates and what happens if it is unable to prove safety by finding two equal consecutive frames.
terminates and what happens if it is unable to prove safety by finding two equal consecutive frames.
How
 works. Recall that
works. Recall that  maintains a sequence of frames
maintains a sequence of frames 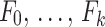 which is initialized in l. 1 with
which is initialized in l. 1 with 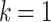 ,
, 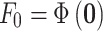 , and
, and  , where the frame
, where the frame  maps every state to 1. Every time upon entering the while-loop in terms l. 2, the initial segment
maps every state to 1. Every time upon entering the while-loop in terms l. 2, the initial segment 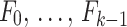 satisfies all PrIC3 invariants (cf. Definition 3), whereas the full sequence
satisfies all PrIC3 invariants (cf. Definition 3), whereas the full sequence  potentially violates frame-safety as it is possible that
potentially violates frame-safety as it is possible that 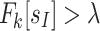 .
.
In l. 3, procedure  —detailed in Sect. 4—is called to restore all PrIC3 invariants on the entire frame sequence: It either returns
—detailed in Sect. 4—is called to restore all PrIC3 invariants on the entire frame sequence: It either returns  if successful or returns
if successful or returns  and a counterexample (in our case a subsystem of the MDP) if it was unable to do so. To ensure soundness of
and a counterexample (in our case a subsystem of the MDP) if it was unable to do so. To ensure soundness of  , it suffices that
, it suffices that  restores the PrIC3 invariants whenever it returns
restores the PrIC3 invariants whenever it returns  . Formally,
. Formally,  must meet the following specification:
must meet the following specification:
Definition 4
Procedure  is sound if the following Hoare triple is valid:
is sound if the following Hoare triple is valid:
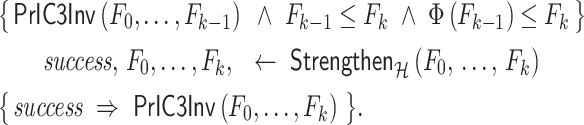 |
If  returns
returns  , then a new frame
, then a new frame  is created in l. 5. After that, the (now initial) segment
is created in l. 5. After that, the (now initial) segment  again satisfies all PrIC3 invariants, whereas the full sequence
again satisfies all PrIC3 invariants, whereas the full sequence 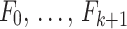 potentially violates frame-safety at
potentially violates frame-safety at  . Propagation (l. 6) aims to speed up termination by updating
. Propagation (l. 6) aims to speed up termination by updating 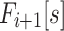 by
by 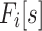 iff this does not violate relative inductivity. Consequently, the previously mentioned properties remain unchanged.
iff this does not violate relative inductivity. Consequently, the previously mentioned properties remain unchanged.
If  returns
returns 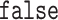 , the PrIC3 invariants—premises to Lemma 2 for witnessing safety—cannot be restored and
, the PrIC3 invariants—premises to Lemma 2 for witnessing safety—cannot be restored and  terminates returning
terminates returning  (l. 4). Returning
(l. 4). Returning 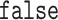 (also possible in l. 8) has by specification no affect on soundness of
(also possible in l. 8) has by specification no affect on soundness of  .
.
In l. 7, we check whether there exist two identical consecutive frames. If so, Lemma 2 yields that the MDP is safe; consequently,  returns
returns 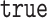 . Otherwise, we increment k and are in the same setting as upon entering the loop, now with an increased frame sequence;
. Otherwise, we increment k and are in the same setting as upon entering the loop, now with an increased frame sequence;  then performs another iteration. In summary, we obtain:
then performs another iteration. In summary, we obtain:
Theorem 1
(Soundness of
 ). If
). If 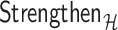 is sound and
is sound and  does not affect the PrIC3 invariants, then
does not affect the PrIC3 invariants, then  is sound, i.e., the following triple is valid:
is sound, i.e., the following triple is valid:
 Terminates for Unsafe MDPs. If the MDP is unsafe, then there exists a step-bound n, such that
Terminates for Unsafe MDPs. If the MDP is unsafe, then there exists a step-bound n, such that 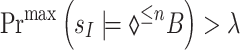 . Furthermore, any sound implementation of
. Furthermore, any sound implementation of  (cf. Definition 4) either immediately terminates
(cf. Definition 4) either immediately terminates  by returning
by returning 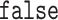 or restores the PrIC3 invariants for
or restores the PrIC3 invariants for  . If the former case never arises, then
. If the former case never arises, then 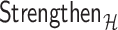 will eventually restore the PrIC3 invariants for a frame sequence of length
will eventually restore the PrIC3 invariants for a frame sequence of length  . By Lemma 1, we have
. By Lemma 1, we have 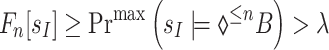 contradicting frame-safety.
contradicting frame-safety.
 Terminates for Safe MDPs. Standard IC3 terminates on safe finite TSs as there are only finitely many different frames, making every ascending chain of frames eventually stabilize. For us, frames map states to probabilities (Challenge 1), yielding infinitely many possible frames even for finite MDPs. Hence,
Terminates for Safe MDPs. Standard IC3 terminates on safe finite TSs as there are only finitely many different frames, making every ascending chain of frames eventually stabilize. For us, frames map states to probabilities (Challenge 1), yielding infinitely many possible frames even for finite MDPs. Hence, 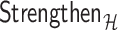 need not ever yield a stabilizing chain of frames. If it continuously fails to stabilize while repeatedly reasoning about the same set of states, we give up.
need not ever yield a stabilizing chain of frames. If it continuously fails to stabilize while repeatedly reasoning about the same set of states, we give up.  checks this by comparing the subsystem
checks this by comparing the subsystem 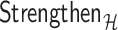 operates on with the one it operated on in the previous loop iteration (l. 8).
operates on with the one it operated on in the previous loop iteration (l. 8).
Theorem 2
If 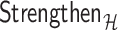 and Propagate terminate, then
and Propagate terminate, then  terminates.
terminates.
Recovery Statement 2
For qual. reachability (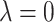 ),
),  never terminates in l. 8.
never terminates in l. 8.
 is Incomplete. Standard IC3 either proves safety or returns
is Incomplete. Standard IC3 either proves safety or returns  and a counterexample—a single path from the initial to a bad state. As single paths are insufficient as counterexamples in MDPs (Challenge 2),
and a counterexample—a single path from the initial to a bad state. As single paths are insufficient as counterexamples in MDPs (Challenge 2),  instead returns a subsystem of the MDP
instead returns a subsystem of the MDP  provided by
provided by  . However, as argued above, we cannot trust
. However, as argued above, we cannot trust  to provide a stabilizing chain of frames. Reporting
to provide a stabilizing chain of frames. Reporting 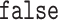 thus only means that the given MDP may be unsafe; the returned subsystem has to be analyzed further.
thus only means that the given MDP may be unsafe; the returned subsystem has to be analyzed further.
The full PrIC3 algorithm presented in Sect. 5 addresses this issue. Exploiting the subsystem returned by  , PrIC3 returns
, PrIC3 returns 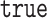 if the MDP is safe; otherwise, it returns
if the MDP is safe; otherwise, it returns 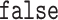 and provides a true counterexample witnessing that the MDP is unsafe.
and provides a true counterexample witnessing that the MDP is unsafe.
Example 2
We conclude this section with two example executions of  on a simplified version of the MDP in Fig. 1. Assume that action b has been removed. Then, for every state, exactly one action is enabled, i.e., we consider a Markov chain. Figure 2 depicts the frame sequences computed by
on a simplified version of the MDP in Fig. 1. Assume that action b has been removed. Then, for every state, exactly one action is enabled, i.e., we consider a Markov chain. Figure 2 depicts the frame sequences computed by  (for a reasonable
(for a reasonable 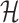 ) on that Markov chain for two thresholds:
) on that Markov chain for two thresholds: 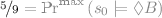 and
and  . In particular, notice that proving the coarser bound of
. In particular, notice that proving the coarser bound of
 requires fewer frames than proving the exact bound of
requires fewer frames than proving the exact bound of
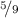 .
. 
Fig. 2.
Two runs of  on the Markov chain induced by selecting action a in Fig. 1. For every iteration, frames are recorded after invocation of
on the Markov chain induced by selecting action a in Fig. 1. For every iteration, frames are recorded after invocation of  .
.
Strengthening in 
When the main loop of  has created a new frame
has created a new frame  in its previous iteration, this frame may violate frame-safety (Definition 3.3) because of
in its previous iteration, this frame may violate frame-safety (Definition 3.3) because of  . The task of
. The task of 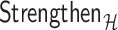 is to restore the PrIC3 invariants on all frames
is to restore the PrIC3 invariants on all frames 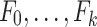 . To this end, our first obligation is to lower the value in frame
. To this end, our first obligation is to lower the value in frame  for state
for state 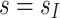 to
to 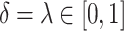 . We denote such an obligation by
. We denote such an obligation by  . Observe that implicitly
. Observe that implicitly 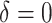 in the qualitative case, i.e., when proving unreachability. An obligation
in the qualitative case, i.e., when proving unreachability. An obligation 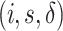 is resolved by updating the values assigned to state s in all frames
is resolved by updating the values assigned to state s in all frames
 to at most
to at most 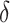 . That is, for all
. That is, for all 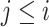 , we set
, we set 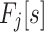 to the minimum of
to the minimum of  and the original value
and the original value  . Such an update affects neither initiality nor the chain property (Definitions 3.1, 3.2). It may, however, violate relative inductivity (Definition 3.4), i.e.,
. Such an update affects neither initiality nor the chain property (Definitions 3.1, 3.2). It may, however, violate relative inductivity (Definition 3.4), i.e., 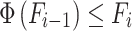 . Before resolving obligation
. Before resolving obligation 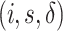 , we may thus have to further decrease some entries in
, we may thus have to further decrease some entries in 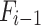 as well. Hence, resolving obligations may spawn additional obligations which have to be resolved first to maintain relative inductivity. In this section, we present a generic instance of
as well. Hence, resolving obligations may spawn additional obligations which have to be resolved first to maintain relative inductivity. In this section, we present a generic instance of  meeting its specification (Definition 4) and discuss its correctness.
meeting its specification (Definition 4) and discuss its correctness.
 by Example.
by Example.
 is given by the pseudo code in Algorithm 2; differences to standard IC3 (cf.
[23, Fig. 6]) are highlighted in
is given by the pseudo code in Algorithm 2; differences to standard IC3 (cf.
[23, Fig. 6]) are highlighted in
 . Intuitively,
. Intuitively,  attempts to recursively resolve all obligations until either both frame-safety and relative inductivity are restored for all frames or it detects a potential counterexample justifying why it is unable to do so. We first consider an execution where the latter does not arise:
attempts to recursively resolve all obligations until either both frame-safety and relative inductivity are restored for all frames or it detects a potential counterexample justifying why it is unable to do so. We first consider an execution where the latter does not arise: 
Example 3
We zoom in on Example 2: Prior to the second iteration, we have created the following three frames assigning values to the states 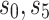 :
:
To keep track of unresolved obligations  ,
,  employs a priority queue Q which pops obligations with minimal frame index i first. Our first step is to ensure frame-safety of
employs a priority queue Q which pops obligations with minimal frame index i first. Our first step is to ensure frame-safety of  , i.e., alter
, i.e., alter  so that
so that 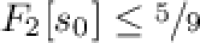 ; we thus initialize the queue Q with the initial obligation
; we thus initialize the queue Q with the initial obligation 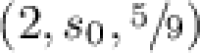 (l. 1). To do so, we check whether updating
(l. 1). To do so, we check whether updating 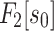 to
to  would invalidate relative inductivity (l. 6). This is indeed the case:
would invalidate relative inductivity (l. 6). This is indeed the case:
To restore relative inductivity, 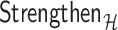 spawns one new obligation for each relevant successor of
spawns one new obligation for each relevant successor of 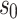 . These have to be resolved before retrying to resolve the old obligation.5
. These have to be resolved before retrying to resolve the old obligation.5
In contrast to standard IC3 , spawning obligations involves finding suitable probabilities
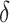 (l. 7). In our example this means we have to spawn two obligations
(l. 7). In our example this means we have to spawn two obligations  and
and 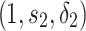 such that
such that 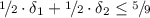 . There are infinitely many choices for
. There are infinitely many choices for 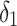 and
and  satisfying this inequality. Assume some heuristic
satisfying this inequality. Assume some heuristic 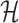 chooses
chooses 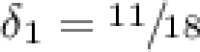 and
and 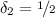 ; we push obligations
; we push obligations 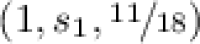 ,
, 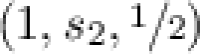 , and
, and 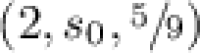 (ll. 8, 9). In the next iteration, we first pop obligation
(ll. 8, 9). In the next iteration, we first pop obligation 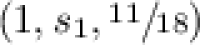 (l. 3) and find that it can be resolved without violating relative inductivity (l. 6). Hence, we set
(l. 3) and find that it can be resolved without violating relative inductivity (l. 6). Hence, we set 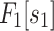 to
to  (l. 11); no new obligation is spawned. Obligation
(l. 11); no new obligation is spawned. Obligation 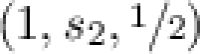 is resolved analogously; the updated frame is
is resolved analogously; the updated frame is  . Thereafter, our initial obligation
. Thereafter, our initial obligation  can be resolved; relative inductivity is restored for
can be resolved; relative inductivity is restored for 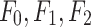 . Hence,
. Hence,  returns
returns  together with the updated frames.
together with the updated frames. 
 is Sound. Let us briefly discuss why Algorithm 2 meets the specification of a sound implemenation of
is Sound. Let us briefly discuss why Algorithm 2 meets the specification of a sound implemenation of  (Definition 4): First, we observe that Algorithm 2 alters the frames—and thus potentially invalidates the PrIC3 invariants—only in l. 11 by resolving an obligation
(Definition 4): First, we observe that Algorithm 2 alters the frames—and thus potentially invalidates the PrIC3 invariants—only in l. 11 by resolving an obligation 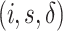 with
with 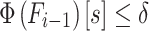 (due to the check in l. 6).
(due to the check in l. 6).
Let  denote the frame F in which F[s] is set to
denote the frame F in which F[s] is set to  , i.e.,
, i.e.,
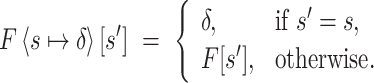 |
Indeed, resolving obligation  in l. 11 lowers the values assigned to state s to at most
in l. 11 lowers the values assigned to state s to at most 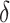 without invalidating the PrIC3 invariants:
without invalidating the PrIC3 invariants:
Lemma 3
Let 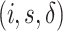 be an obligation and
be an obligation and 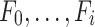 , for
, for 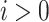 , be frames with
, be frames with 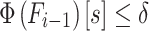 . Then
. Then 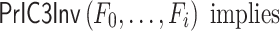
Crucially, the precondition of Definition 4 guarantees that all PrIC3 invariants except frame safety hold initially. Since these invariants are never invalidated due to Lemma 3, Algorithm 2 is a sound implementation of  if it restores frame safety whenever it returns
if it restores frame safety whenever it returns  , i.e., once it leaves the loop with an empty obligation queue Q (ll. 12–13). Now, an obligation
, i.e., once it leaves the loop with an empty obligation queue Q (ll. 12–13). Now, an obligation 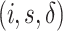 is only popped from Q in l. 3. As
is only popped from Q in l. 3. As 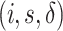 is added to Q upon reaching l. 9, the size of Q can only ever be reduced (without returning
is added to Q upon reaching l. 9, the size of Q can only ever be reduced (without returning  ) by resolving
) by resolving 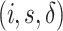 in l. 11. Hence, Algorithm 2 does not return
in l. 11. Hence, Algorithm 2 does not return  unless it restored frame safety by resolving, amongst all other obligations, the initial obligation
unless it restored frame safety by resolving, amongst all other obligations, the initial obligation 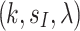 . Consequently:
. Consequently:
Lemma 4
Procedure  is sound, i.e., it satisfies the specification in Definition 4.
is sound, i.e., it satisfies the specification in Definition 4.
Theorem 3
Procedure  is sound, i.e., satisfies the specification in Theorem 1.
is sound, i.e., satisfies the specification in Theorem 1.
We remark that, analogously to standard IC3, resolving an obligation in l. 11 may be accompanied by generalization. That is, we attempt to update the values of multiple states at once. Generalization is, however, highly non-trivial in a probabilistic setting. We discuss three possible approaches to generalization in Sect. 6.2.
 Terminates. We now show that
Terminates. We now show that  as in Algorithm 2 terminates. The only scenario in which
as in Algorithm 2 terminates. The only scenario in which 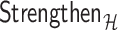 may not terminate is if it keeps spawning obligations in l. 9. Let us thus look closer at how obligations are spawned: Whenever we detect that resolving an obligation
may not terminate is if it keeps spawning obligations in l. 9. Let us thus look closer at how obligations are spawned: Whenever we detect that resolving an obligation  would violate relative inductivity for some action a (l. 6), we first need to update the values of the successor states
would violate relative inductivity for some action a (l. 6), we first need to update the values of the successor states 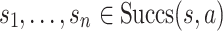 in frame
in frame  , i.e., we push the obligations
, i.e., we push the obligations  which have to be resolved first (ll. 7–9). It is noteworthy that, for a TS, a single action leads to a single successor state
which have to be resolved first (ll. 7–9). It is noteworthy that, for a TS, a single action leads to a single successor state 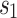 . Algorithm 2 employs a heuristic
. Algorithm 2 employs a heuristic 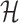 to determine the probabilities required for pushing obligations (l. 7). Assume for an obligation
to determine the probabilities required for pushing obligations (l. 7). Assume for an obligation 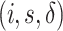 that the check in l. 6 yields
that the check in l. 6 yields  . Then
. Then  takes s, a,
takes s, a, 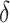 and reports some probability
and reports some probability  for every a-successor
for every a-successor  of s. However, an arbitrary heuristic of type
of s. However, an arbitrary heuristic of type 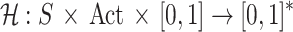 may lead to non-terminating behavior: If
may lead to non-terminating behavior: If 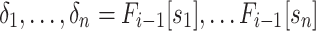 , then the heuristic has no effect. It is thus natural to require that an adequate heuristic
, then the heuristic has no effect. It is thus natural to require that an adequate heuristic  yields probabilities such that the check
yields probabilities such that the check 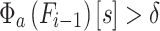 in l. 6 cannot succeed twice for the same obligation
in l. 6 cannot succeed twice for the same obligation
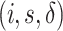 and same action a. Formally, this is guaranteed by the following:
and same action a. Formally, this is guaranteed by the following:
Definition 5
Heuristic  is adequate if the following triple is valid (for any frame F):
is adequate if the following triple is valid (for any frame F):
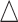
Details regarding our implementation of heuristic 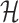 are found in Sect. 6.1.
are found in Sect. 6.1.
For an adequate heuristic, attempting to resolve an obligation 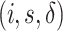 (ll. 3 – 11) either succeeds after spawning it at most
(ll. 3 – 11) either succeeds after spawning it at most  times or
times or  returns
returns 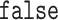 . By a similar argument, attempting to resolve an obligation
. By a similar argument, attempting to resolve an obligation 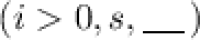 leads to at most
leads to at most  other obligations of the form
other obligations of the form 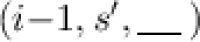 . Consequently, the total number of obligations spawned by Algorithm 2 is bounded. Since Algorithm 2 terminates if all obligations have been resolved (l. 12) and each of its loop iterations either returns
. Consequently, the total number of obligations spawned by Algorithm 2 is bounded. Since Algorithm 2 terminates if all obligations have been resolved (l. 12) and each of its loop iterations either returns  , spawns obligations, or resolves an obligation, we conclude:
, spawns obligations, or resolves an obligation, we conclude:
Lemma 5
 terminates for every adequate heuristic
terminates for every adequate heuristic 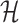 .
.
Recovery Statement 3
Let 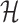 be adequate. Then for qualitative reachability (
be adequate. Then for qualitative reachability (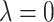 ), all obligations spawned by
), all obligations spawned by  as in Algorithm 2 are of the form (i, s, 0).
as in Algorithm 2 are of the form (i, s, 0).
 returns
returns
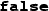 . There are two cases in which
. There are two cases in which  fails to restore the PrIC3 invariants and returns
fails to restore the PrIC3 invariants and returns 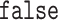 . The first case (the left disjunct of l. 4) is that we encounter an obligation for frame
. The first case (the left disjunct of l. 4) is that we encounter an obligation for frame  . Resolving such an obligation would inevitably violate initiality; analogously to standard IC3, we thus return
. Resolving such an obligation would inevitably violate initiality; analogously to standard IC3, we thus return 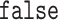 .
.
The second case (the right disjunct of l. 4) is that we encounter an obligation 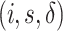 for a bad state
for a bad state 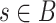 with a probability
with a probability 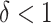 (though, obviously, all
(though, obviously, all  have probability
have probability  ). Resolving such an obligation would inevitably prevents us from restoring relative inductivity: If we updated
). Resolving such an obligation would inevitably prevents us from restoring relative inductivity: If we updated 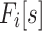 to
to 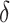 , we would have
, we would have  . Notice that, in contrast to standard IC3, this second case can occur in PrIC3:
. Notice that, in contrast to standard IC3, this second case can occur in PrIC3:
Example 4
Assume we have to resolve an obligation 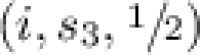 for the MDP in Fig. 1. This involves spawning obligations
for the MDP in Fig. 1. This involves spawning obligations  and
and  , where
, where 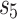 is a bad state, such that
is a bad state, such that 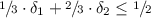 . Even for
. Even for 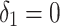 , this is only possible if
, this is only possible if 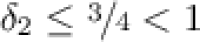 .
. 
 Cannot Prove Unsafety. If standard IC3 returns
Cannot Prove Unsafety. If standard IC3 returns 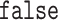 , it proves unsafety by constructing a counterexample, i.e., a single path from the initial state to a bad state. If PrIC3 returns
, it proves unsafety by constructing a counterexample, i.e., a single path from the initial state to a bad state. If PrIC3 returns  , there are two possible reasons: Either the MDP is indeed unsafe, or the heuristic
, there are two possible reasons: Either the MDP is indeed unsafe, or the heuristic  at some point selected probabilities in a way such that
at some point selected probabilities in a way such that  is unable to restore the
is unable to restore the  invariants (even though the MDP might in fact be safe).
invariants (even though the MDP might in fact be safe).  thus only returns a potential counterexample which either proves unsafety or indicates that our heuristic was inappropriate.
thus only returns a potential counterexample which either proves unsafety or indicates that our heuristic was inappropriate.
Counterexamples in our case consist of subsystems rather than a single path (see Challenge 2 and Sect. 5).  hence returns the set
hence returns the set  of all states that eventually appeared in the obligation queue. This set is a conservative approximation, and optimizations as in
[1] may be beneficial. Furthermore, in the qualitative case, our potential counterexample subsumes the counterexamples constructed by standard IC3:
of all states that eventually appeared in the obligation queue. This set is a conservative approximation, and optimizations as in
[1] may be beneficial. Furthermore, in the qualitative case, our potential counterexample subsumes the counterexamples constructed by standard IC3:
Recovery Statement 4
Let  be the adequate heuristic mapping every state to 0. For qual. reachability (
be the adequate heuristic mapping every state to 0. For qual. reachability ( ), if
), if  is returned by
is returned by  , then
, then  contains a path from the initial to a bad state.6
contains a path from the initial to a bad state.6
Dealing with Potential Counterexamples
Recall that our core algorithm  is incomplete for a fixed heuristic
is incomplete for a fixed heuristic  : It cannot give a conclusive answer whenever it finds a potential counterexample for two possible reasons: Either the heuristic
: It cannot give a conclusive answer whenever it finds a potential counterexample for two possible reasons: Either the heuristic  turned out to be inappropriate or the MDP is indeed unsafe. The idea to overcome the former is to call
turned out to be inappropriate or the MDP is indeed unsafe. The idea to overcome the former is to call  finitely often in an outer loop that generates new heuristics until we find an appropriate one: If
finitely often in an outer loop that generates new heuristics until we find an appropriate one: If  still does not report safety of the MDP, then it is indeed unsafe. We do not blindly generate new heuristics, but use the potential counterexamples returned by
still does not report safety of the MDP, then it is indeed unsafe. We do not blindly generate new heuristics, but use the potential counterexamples returned by  to refine the previous one.
to refine the previous one.
Let consider the procedure  in Algorithm 3 which wraps our core algorithm
in Algorithm 3 which wraps our core algorithm  in more detail: First, we create an oracle
in more detail: First, we create an oracle
 which (roughly) estimates the probability of reaching
which (roughly) estimates the probability of reaching  for every state. A perfect oracle would yield precise maximal reachability probabilites, i.e.,
for every state. A perfect oracle would yield precise maximal reachability probabilites, i.e., 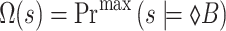 for every state s. We construct oracles by
for every state s. We construct oracles by
 (highlighted in
(highlighted in
 ). Examples of implementations of all user-supplied methods in Algorithm 3 are discussed in Sect. 7.
). Examples of implementations of all user-supplied methods in Algorithm 3 are discussed in Sect. 7.
Assuming the oracle is good, but not perfect, we construct an adequate heuristic  selecting probabilities based on the oracle7 for all successors of a given state: There are various options. The simplest is to pass-through the oracle values. A version that is more robust against noise in the oracle is discussed in Sect. 6. We then invoke
selecting probabilities based on the oracle7 for all successors of a given state: There are various options. The simplest is to pass-through the oracle values. A version that is more robust against noise in the oracle is discussed in Sect. 6. We then invoke  . If
. If  reports safety, the MDP is indeed safe by the soundness of
reports safety, the MDP is indeed safe by the soundness of  .
.
Check Refutation. If  does not report safety, it reports a subsystem that hints to a potential counterexample. Formally, this subsystem is a subMDP of states that were ‘visited’ during the invocation of
does not report safety, it reports a subsystem that hints to a potential counterexample. Formally, this subsystem is a subMDP of states that were ‘visited’ during the invocation of  .
.
Definition 6
(subMDP). Let 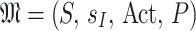 be an MDP and let
be an MDP and let 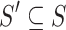 with
with 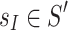 . We call
. We call  the subMDP induced by
the subMDP induced by
 and
and
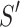 , where for all
, where for all  and all
and all  , we have
, we have 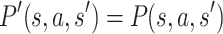 .
. 
A subMDP  may be substochastic where missing probability mass never reaches a bad state. Definition 1 is thus relaxed: For all states
may be substochastic where missing probability mass never reaches a bad state. Definition 1 is thus relaxed: For all states 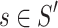 we require that
we require that 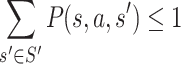 .If the subsystem is unsafe, we can conclude that the original MDP
.If the subsystem is unsafe, we can conclude that the original MDP  is also safe.
is also safe.
Lemma 6
If  is a subMDP of
is a subMDP of  and
and  is unsafe, then
is unsafe, then  is also unsafe.
is also unsafe.
The role of  is to establish whether the subsystem is indeed a true counterexample or a spurious one. Formally,
is to establish whether the subsystem is indeed a true counterexample or a spurious one. Formally, 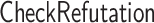 should ensure:
should ensure:
 |
Again,  is backward compatible in the sense that a single fixed heuristic is always sufficient when reasoning about reachability (
is backward compatible in the sense that a single fixed heuristic is always sufficient when reasoning about reachability (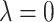 ).
).
Recovery Statement 5
For qualitative reachability (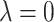 ) and the heuristic
) and the heuristic 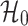 from Recovery Statement 4,
from Recovery Statement 4,  invokes its core
invokes its core  exactly once.
exactly once.
This statement is true, as  returns either
returns either  or a subsystem containing a path from the initial state to a bad state. In the latter case,
or a subsystem containing a path from the initial state to a bad state. In the latter case,  detects that the subsystem is indeed a counterexample which cannot be spurious in the qualitative setting.
detects that the subsystem is indeed a counterexample which cannot be spurious in the qualitative setting.
We remark that the procedure  invoked in l. 5 is a classical fallback; it runs an (alternative) model checking algorithm, e.g., solving the set of Bellman equations, for the subsystem. In the worst case, i.e., for
invoked in l. 5 is a classical fallback; it runs an (alternative) model checking algorithm, e.g., solving the set of Bellman equations, for the subsystem. In the worst case, i.e., for  , we thus solve exactly our problem statement. Empirically (Table 1) we observe that for reasonable oracles the procedure
, we thus solve exactly our problem statement. Empirically (Table 1) we observe that for reasonable oracles the procedure  is invoked on significantly smaller subMDPs. However, in the worst case the subMDP must include all paths of the original MDP, and then thus coincides.
is invoked on significantly smaller subMDPs. However, in the worst case the subMDP must include all paths of the original MDP, and then thus coincides.
Table 1.
Empirical results. Run times are in seconds; time out = 15 min.
| |S| | 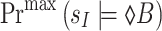 |
 |
w/o |  |
lin |  |
pol |  |
hyb |  |
Storm
|
Storm
|
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BRP |  |
0.035 | 0.1 | TO | – | TO | – | TO | – | TO | – | 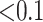 |
0.12 |
|
|
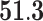 |
324 | 125.8 | 324 | TO | – | MO | – | 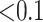 |
0.18 | |||
|
|
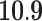 |
188 | 38.3 | 188 | TO | – | MO | – | 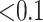 |
0.1 | |||
| ZeroConf | 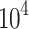 |
0.5 | 0.9 | TO | – | TO | – | 0.4 | 0 | 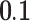 |
0 | 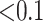 |
296.8 |
| 0.52 | TO | – | TO | – | 0.2 | 0 | 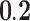 |
0 | 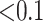 |
282.6 | |||
|
|
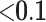 |
1 |  |
1 |  |
1 | 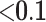 |
1 |  |
300.2 | |||
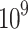 |
 |
0.9 | TO | – | TO | – | 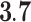 |
0 | MO | – | MO | TO | |
| 0.75 | TO | – | TO | – |  |
0 | MO | – | MO | TO | |||
| 0.52 | TO | – | TO | – | TO | – | TO | – | MO | TO | |||
|
|
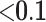 |
1 |  |
1 | 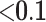 |
1 |  |
1 | MO | TO | |||
| Chain | 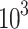 |
0.394 | 0.9 | 18.8 | 0 | 60.2 | 0 | 1.2 | 0 |  |
0 |  |
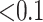 |
| 0.4 | 20.1 | 0 | 55.4 | 0 |  |
0 | TO | – |  |
 |
|||
|
|
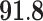 |
431 | 119.5 | 431 | TO | – | TO | – | 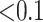 |
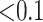 |
|||
|
|
 |
357 | 64.0 | 357 | TO | – | TO | – | 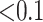 |
 |
|||
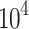 |
0.394 | 0.9 | TO | – | TO | – | 1.6 | 0 | 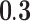 |
0 |  |
4.5 | |
| 0.4 | TO | – | TO | – | 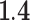 |
0 | TO | – | 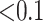 |
4.9 | |||
|
|
TO | – | TO | – | TO | – | TO | – |  |
4.9 | |||
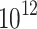 |
0.394 | 0.9 | TO | – | TO | – |  |
0 | MO | – | MO | TO | |
| 0.4 | TO | – | TO | – |  |
0 | MO | – | MO | TO | |||
| Double chain | 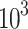 |
0.215 | 0.9 | 528.1 | 0 | 828.8 | 0 | 203.3 | 0 |  |
0 |  |
 |
| 0.3 | 588.4 | 0 | TO | – | 138.3 | 0 |  |
0 |  |
 |
|||
| 0.216 |  |
0 | TO | – | 765.8 | 0 | MO | – |  |
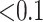 |
|||
|
|
TO | – | TO | – | TO | – | TO | – |  |
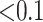 |
|||
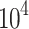 |
0.22 | 0.3 | TO | – | TO | – | 17.5 | 0 | 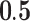 |
0 | 0.2 | 2.6 | |
| 0.24 | TO | – | TO | – |  |
0 | MO | – | 0.2 | 2.7 | |||
 |
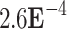 |
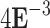 |
TO | – | TO | – | TO | – | MO | – | TO | TO | |
 |
TO | – | TO | – |  |
0 | MO | – | TO | TO |
Refine Oracle. Whenever we have neither proven the MDP safe nor unsafe, we refine the oracle to prevent generating the same subsystem in the next invocation of  . To ensure termination, oracles should only be refined finitely often. That is, we need some progress measure. The set
. To ensure termination, oracles should only be refined finitely often. That is, we need some progress measure. The set 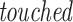 overapproximates all counterexamples encountered in some invocation of
overapproximates all counterexamples encountered in some invocation of  and we propose to use its size as the progress measure. While there are several possibilities to update
and we propose to use its size as the progress measure. While there are several possibilities to update 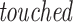 through the user-defined procedure
through the user-defined procedure
 (l. 6), every implementation should hence satisfy
(l. 6), every implementation should hence satisfy  . Consequently, after finitely many iterations, the oracle is refined with respect to all states. In this case, we may as well rely on solving the characteristic LP problem:
. Consequently, after finitely many iterations, the oracle is refined with respect to all states. In this case, we may as well rely on solving the characteristic LP problem:
Lemma 7
The algorithm  in Algorithm 3 is sound and complete if
in Algorithm 3 is sound and complete if  returns a perfect oracle
returns a perfect oracle 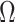 (with S is the set of all states).
(with S is the set of all states).
Weaker assumptions on 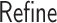 are possible, but are beyond the scope of this paper. Moreover, the above lemma does not rely on the abstract concept that heuristic
are possible, but are beyond the scope of this paper. Moreover, the above lemma does not rely on the abstract concept that heuristic  provides suitable probabilities after finitely many refinements.8
provides suitable probabilities after finitely many refinements.8
Practical PrIC3
So far, we gave a conceptual view on PrIC3, but now take a more practical stance. We detail important features of effective implementations of PrIC3 (based on our empirical evaluation). We first describe an implementation without generalization, and then provide a prototypical extension that allows for three variants of generalization.
A Concrete PrIC3 Instance Without Generalization
Input. We describe MDPs using the Prism guarded command language9, exemplified in Fig. 3. States are described by valuations to m (integer-valued) program variables 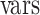 , and outgoing actions are described by commands of the form
, and outgoing actions are described by commands of the form
If a state satisfies guard, then the corresponding action with k branches exists; probabilities are given by probi, the successor states are described by updatei, see Fig. 3b.
Fig. 3.
Illustrative Prism-style probabilistic guarded command language example
Encoding. We encode frames as logical formulae. Updating frames then corresponds to adding conjuncts, and checking for relative inductivity is a satisfiability call. Our encoding is as follows: States are assignments to the program variables, i.e., 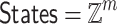 . We use various uninterpreted functions, to whom we give semantics using appropriate constraints. Frames10 are represented by uninterpreted functions
. We use various uninterpreted functions, to whom we give semantics using appropriate constraints. Frames10 are represented by uninterpreted functions  satisfying
satisfying  implies
implies 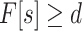 . Likewise, the Bellman operator is an uninterpreted function
. Likewise, the Bellman operator is an uninterpreted function 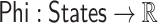 such that
such that 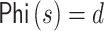 implies
implies 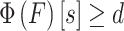 . Finally, we use
. Finally, we use 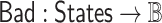 with
with  iff
iff 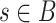 .
.
Among the appropriate constraints, we ensure that variables are within their range, bound the values for the frames, and enforce 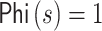 for
for 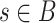 . We encode the guarded commands as exemplified by this encoding of the first command in Fig. 3:
. We encode the guarded commands as exemplified by this encoding of the first command in Fig. 3:
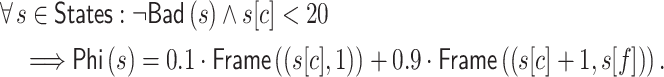 |
In our implementation, we optimize the encoding. We avoid the uninterpreted functions by applying an adapted Ackerman reduction. We avoid universal quantifiers, by first observing that we always ask whether a single state is not inductive, and then unfolding the guarded commands in the constraints that describe a frame. That encoding grows linear in the size of the maximal out-degree of the MDP, and is in the quantifier-free fragment of linear arithmetic (QFLRIA).
Heuristic. We select probabilities 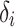 by solving the following optimization problem, with variables
by solving the following optimization problem, with variables  ,
, 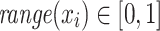 , for states
, for states 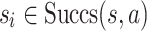 and oracle
and oracle  11.
11.
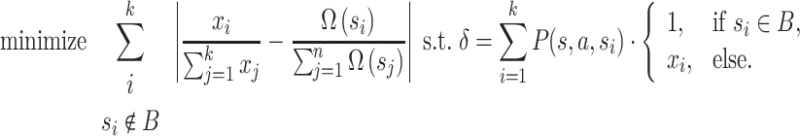 |
The constraint ensures that, if the values  correspond to the actual reachability probabilities from
correspond to the actual reachability probabilities from  , then the reachability from state s is exactly
, then the reachability from state s is exactly  . A constraint stating that
. A constraint stating that 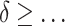 would also be sound, but we choose equality as it preserves room between the actual probability and the threshold we want to show. Finally, the objective function aims to preserve the ratio between the suggested probabilities.
would also be sound, but we choose equality as it preserves room between the actual probability and the threshold we want to show. Finally, the objective function aims to preserve the ratio between the suggested probabilities.
Repushing and Breaking Cycles.
Repushing
[23] is an essential ingredient of both standard IC3 and PrIC3. Intuitively, we avoid opening new frames and spawning obligations that can be deduced from current information. Since repushing generates further obligations in the current frame, its implementation requires that the detection of Zeno-behavior has to be moved from  into the
into the  procedure. Therefore, we track the histories of the obligations in the queue. Furthermore, once we detect a cycle we first try to adapt the heuristic
procedure. Therefore, we track the histories of the obligations in the queue. Furthermore, once we detect a cycle we first try to adapt the heuristic  locally to overcome this cyclic behavior instead of immediately giving up. This local adaption reduces the number of
locally to overcome this cyclic behavior instead of immediately giving up. This local adaption reduces the number of  invocations.
invocations.
Extended Queue. In contrast to standard IC3, the obligation queue might contain entries that vary only in their 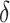 entry. In particular, if the MDP is not a tree, it may occur that the queue contains both
entry. In particular, if the MDP is not a tree, it may occur that the queue contains both 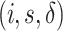 and
and  with
with 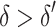 . Then,
. Then,  can be safely pruned from the queue. Similarly, after handling
can be safely pruned from the queue. Similarly, after handling 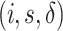 , if some fresh obligation
, if some fresh obligation 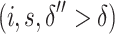 is pushed to the queue, it can be substituted with
is pushed to the queue, it can be substituted with 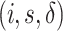 . To efficiently operationalize these observations, we keep an additional mapping which remains intact over multiple invocations of
. To efficiently operationalize these observations, we keep an additional mapping which remains intact over multiple invocations of 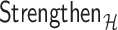 . We furthermore employed some optimizations for
. We furthermore employed some optimizations for 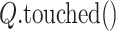 aiming to track potential counterexamples better. After refining the heuristic, one may want to reuse frames or the obligation queue, but empirically this leads to performance degradation as the values in the frames are inconsistent with behavior suggested by the heuristic.
aiming to track potential counterexamples better. After refining the heuristic, one may want to reuse frames or the obligation queue, but empirically this leads to performance degradation as the values in the frames are inconsistent with behavior suggested by the heuristic.
Concrete PrIC3 with Generalization
So far, frames are updated by changing single entries whenever we resolve obligations  , i.e., we add conjunctions of the form
, i.e., we add conjunctions of the form  . Equivalently, we may add a constraint
. Equivalently, we may add a constraint  with
with  and
and 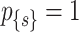 for all
for all 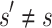 .
.
Generalization in IC3 aims to update a set 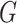 (including s) of states in a frame rather than a single one without invalidating relative inductivity. In our setting, we thus consider a function
(including s) of states in a frame rather than a single one without invalidating relative inductivity. In our setting, we thus consider a function 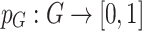 with
with 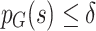 that assigns (possibly different) probabilities to all states in
that assigns (possibly different) probabilities to all states in 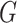 . Updating a frame then amounts to adding the constraint
. Updating a frame then amounts to adding the constraint
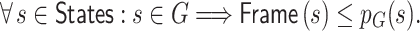 |
Standard IC3 generalizes by iteratively “dropping” a variable, say v. The set 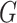 then consists of all states that do not differ from the fixed state s except for the value of v.12 We take the same approach by iteratively dropping program variables. Hence,
then consists of all states that do not differ from the fixed state s except for the value of v.12 We take the same approach by iteratively dropping program variables. Hence,  effectively becomes a mapping from the value s[v] to a probability. We experimented with four types of functions
effectively becomes a mapping from the value s[v] to a probability. We experimented with four types of functions  that we describe for Markov chains. The ideas are briefly outlined below; details are beyond the scope of this paper.
that we describe for Markov chains. The ideas are briefly outlined below; details are beyond the scope of this paper.
Constant
 . Setting all
. Setting all 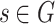 to
to 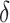 is straightforward but empirically not helpful.
is straightforward but empirically not helpful.
Linear Interpolation. We use a linear function  that interpolates two points. The first point
that interpolates two points. The first point 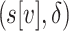 is obtained from the obligation
is obtained from the obligation 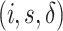 . For a second point, consider the following: Let
. For a second point, consider the following: Let 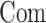 be the unique13 command active at state s. Among all states in
be the unique13 command active at state s. Among all states in 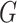 that are enabled in the guard of
that are enabled in the guard of  , we take the state
, we take the state 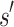 in which
in which 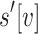 is maximal14. The second point for interpolation is then
is maximal14. The second point for interpolation is then 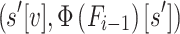 . If the relative inductivity fails for
. If the relative inductivity fails for  we do not generalize with
we do not generalize with 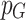 , but may attempt to find other functions.
, but may attempt to find other functions.
Polynomial Interpolation. Rather than linearly interpolating between two points, we may interpolate using more than two points. In order to properly fit these points, we can use a higher-degree polynomial. We select these points using counterexamples to generalization (CTGs): We start as above with linear interpolation. However, if 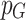 is not relative inductive, the SMT solver yields a model with state
is not relative inductive, the SMT solver yields a model with state 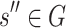 and probability
and probability 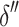 , with
, with 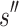 violating relative inductivity, i.e.,
violating relative inductivity, i.e., 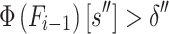 . We call
. We call  a CTG, and
a CTG, and  is then a further interpolation point, and we repeat.
is then a further interpolation point, and we repeat.
Technically, when generalizing using nonlinear constraints, we use real-valued arithmetic with a branch-and-bound-style approach to ensure integer values.
Hybrid Interpolation. In polynomial interpolation, we generate high-degree polynomials and add them to the encoding of the frame. In subsequent invocations, reasoning efficiency is drastically harmed by these high-degree polynomials. Instead, we soundly approximate 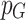 by a piecewise linear function, and use these constraints in the frame.
by a piecewise linear function, and use these constraints in the frame.
Experiments
We assess how PrIC3 may contribute to the state of the art in probabilistic model checking. We do some early empirical evaluation showing that PrIC3 is feasible. We see ample room for further improvements of the prototype.
Implementation. We implemented a prototype15 of PrIC3 based on Sect. 6.1 in Python. The input is represented using efficient data structures provided by the model checker Storm. We use an incremental instance of Z3 [47] for each frame, as suggested in [23]. A solver for each frame is important to reduce the time spent on pushing the large frame-encodings. The optimization problem in the heuristic is also solved using Z3. All previously discussed generalizations (none, linear, polynomial, hybrid) are supported.
Oracle and Refinement. We support the (pre)computation of four different types of oracles for the
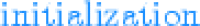 step in Algorithm 3: (1) A perfect oracle solving exactly the Bellman equations. Such an oracle is unrealistic, but interesting from a conceptual point. (2) Relative frequencies by recording all visited states during simulation. This idea is a naïve simplification of Q-learning. (3) Model checking with decision diagrams (DDs) and few value iterations. Often, a DD representation of a model can be computed fast, and the challenge is in executing sufficient value iterations. We investigate whether doing few value iterations yields a valuable oracle (and covers states close to bad states). (4) Solving a (pessimistic) LP from BFS partial exploration. States that are not expanded are assumed bad. Roughly, this yields oracles covering states close to the initial states.
step in Algorithm 3: (1) A perfect oracle solving exactly the Bellman equations. Such an oracle is unrealistic, but interesting from a conceptual point. (2) Relative frequencies by recording all visited states during simulation. This idea is a naïve simplification of Q-learning. (3) Model checking with decision diagrams (DDs) and few value iterations. Often, a DD representation of a model can be computed fast, and the challenge is in executing sufficient value iterations. We investigate whether doing few value iterations yields a valuable oracle (and covers states close to bad states). (4) Solving a (pessimistic) LP from BFS partial exploration. States that are not expanded are assumed bad. Roughly, this yields oracles covering states close to the initial states.
To implement
 (cf. Algorithm 3, l. 7), we create an LP for the subMDP induced by the touched states. For states whose successors are not in the touched states, we add a transition to B labeled with the oracle value as probability. The solution of the resulting LP updates the entries corresponding to the touched states.
(cf. Algorithm 3, l. 7), we create an LP for the subMDP induced by the touched states. For states whose successors are not in the touched states, we add a transition to B labeled with the oracle value as probability. The solution of the resulting LP updates the entries corresponding to the touched states.
For
 (cf. Algorithm 3, l. 6), we take the union of the subsystem and the touched states. If this does not change the set of touched states, we also add its successors.
(cf. Algorithm 3, l. 6), we take the union of the subsystem and the touched states. If this does not change the set of touched states, we also add its successors.
Setup. We evaluate the run time and memory consumption of our prototype of PrIC3. We choose a combination of models from the literature (BRP
[21], ZeroConf
[18]) and some structurally straightforward variants of grids (chain, double chain; see
[11, Appendix A]). Since our prototype lacks the sophisticated preprocessing applied by many state-of-the-art model checkers, it is more sensitive to the precise encoding of a model, e.g., the number of commands. To account for this, we generated new encodings for all models. All experiments were conducted on an single core of an Intel® Xeon® Platinum 8160 processor. We use a 15 min time-limit and report TO otherwise. Memory is limited to 8GB; we report MO if it is exceeded. Apart from the oracle, all parameters of our prototype remain fixed over all experiments. To give an impression of the run times, we compare our prototype with both the explicit (Storm ) and DD-based (Storm
) and DD-based (Storm ) engine of the model checker Storm 1.4, which compared favourably in QComp
[29].
) engine of the model checker Storm 1.4, which compared favourably in QComp
[29].
Results. In Table 1, we present the run times for various invocations of our prototype and Oracle 416. In particular, we give the model name and the number of (non-trivial) states in the particular instance, and the (estimated) actual probability to reach B. For each model, we consider multiple thresholds  . The next 8 columns report on the four variants of PrIC3 with varying generalization schemes. Besides the scheme with the run times, we report for each scheme the number of states of the largest (last) subsystem that
. The next 8 columns report on the four variants of PrIC3 with varying generalization schemes. Besides the scheme with the run times, we report for each scheme the number of states of the largest (last) subsystem that  in Algorithm 3, l. 5 was invoked upon (column |sub|). The last two columns report on the run times for Storm that we provide for comparison. In each row, we mark with
in Algorithm 3, l. 5 was invoked upon (column |sub|). The last two columns report on the run times for Storm that we provide for comparison. In each row, we mark with
 MDPs that are unsafe, i.e., PrIC3 refutes these MDPs for the given threshold
MDPs that are unsafe, i.e., PrIC3 refutes these MDPs for the given threshold 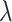 . We highlight the best configurations of PrIC3.
. We highlight the best configurations of PrIC3.
Discussion. Our experiments give a mixed picture on the performance of our implementation of PrIC3. On the one hand, Storm significantly outperforms PrIC3 on most models. On the other hand, PrIC3 is capable of reasoning about huge, yet simple, models with up to  states that Storm is unable to analyze within the time and memory limits. There is more empirical evidence that PrIC3 may complement the state-of-the-art:
states that Storm is unable to analyze within the time and memory limits. There is more empirical evidence that PrIC3 may complement the state-of-the-art:
First, the size of thresholds matters. Our benchmarks show that—at least without generalization—more “wiggle room” between the precise maximal reachability probability and the threshold generally leads to a better performance. PrIC3 may thus prove bounds for large models where a precise quantitative reachability analysis is out of scope.
Second, PrIC3enjoys the benefits of bounded model checking. In some cases, e.g., ZeroConf for  , PrIC3 refutes very fast as it does not need to build the whole model.
, PrIC3 refutes very fast as it does not need to build the whole model.
Third, if PrIC3 proves the safety of the system, it does so without relying on checking large subsystems in the  step.
step.
Fourth, generalization is crucial. Without generalization, PrIC3 is unable to prove safety for any of the considered models with more than  states. With generalization, however, it can prove safety for very large systems and thresholds close to the exact reachability probability. For example, it proved safety of the Chain benchmark with
states. With generalization, however, it can prove safety for very large systems and thresholds close to the exact reachability probability. For example, it proved safety of the Chain benchmark with 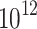 states for a threshold of 0.4 which differs from the exact reachability probability by 0.006.
states for a threshold of 0.4 which differs from the exact reachability probability by 0.006.
Fifth, there is no best generalization. There is no clear winner out of the considered generalization approaches. Linear generalization always performs worse than the other ones. In fact, it performs worse than no generalization at all. The hybrid approach, however, occasionally has the edge over the polynomial approach. This indicates that more research is required to find suitable generalizations.
In
[11, Appendix A], we also compare the additional three types of oracles (1–3). We observed that only few oracle refinements are needed to prove safety; for small models at most one refinement was sufficient. However, this does not hold if the given MDP is unsafe. DoubleChain with  , for example, and Oracle 2 requires 25 refinements.
, for example, and Oracle 2 requires 25 refinements.
Conclusion
We have presented PrIC3—the first truly probabilistic, yet conservative, extension of IC3 to quantitative reachability in MDPs. Our theoretical development is accompanied by a prototypical implementation and experiments. We believe there is ample space for improvements including an in-depth investigation of suitable oracles and generalizations.
Footnotes
Recently, (standard) IC3 for TSs was utilized in model checking Markov chains [49] to on-the-fly compute the states that cannot reach B.
In [38], tree-like counterexamples are used for non-linear predicate transformers in IC3.
Maximal with respect to all possible resolutions of nondeterminism in the MDP.
In IC3, frames are typically characterized by logical formulae. To understand IC3 ’s fundamental principle, however, we prefer to think of frames as functions in 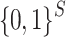 partially ordered by
partially ordered by  .
.
We assume that the set 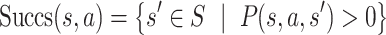 of relevant a-successors of state s is returned in some arbitrary, but fixed order.
of relevant a-successors of state s is returned in some arbitrary, but fixed order.
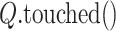 might be restricted to only contain this path by some simple adaptions.
might be restricted to only contain this path by some simple adaptions.
We thus assume that heuristic  invokes the oracle whenever it needs to guess some probability.
invokes the oracle whenever it needs to guess some probability.
One could of course now also create a heuristic that is trivial for a perfect oracle and invoke  with the heuristic for the perfect oracle, but there really is no benefit in doing so.
with the heuristic for the perfect oracle, but there really is no benefit in doing so.
Preprocessing ensures a single thread (module) and no deadlocks.
In each operation, we only consider a single frame.
If 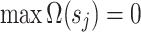 , we assume
, we assume 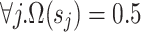 . If
. If 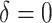 , we omit rescaling to allow
, we omit rescaling to allow  .
.
Formally, 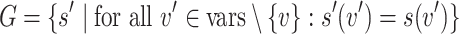 .
.
Recall that we have a Markov chain consisting of a single module.
This implicitly assumes that v is increased. Adaptions are possible.
The prototype is available open-source from https://github.com/moves-rwth/PrIC3.
We explore 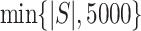 states using BFS and Storm.
states using BFS and Storm.
This work has been supported by the ERC Advanced Grant 787914 (FRAPPANT), NSF grants 1545126 (VeHICaL) and 1646208, the DARPA Assured Autonomy program, Berkeley Deep Drive, and by Toyota under the iCyPhy center.
Contributor Information
Shuvendu K. Lahiri, Email: shuvendu.lahiri@microsoft.com
Chao Wang, Email: wang626@usc.edu.
Kevin Batz, Email: kevin.batz@cs.rwth-aachen.de.
References
- 1.Ábrahám E, Becker B, Dehnert C, Jansen N, Katoen J-P, Wimmer R. Counterexample generation for discrete-time Markov models: an introductory survey. In: Bernardo M, Damiani F, Hähnle R, Johnsen EB, Schaefer I, editors. Formal Methods for Executable Software Models; Cham: Springer; 2014. pp. 65–121. [Google Scholar]
- 2.Agha G, Palmskog K. A survey of statistical model checking. ACM Trans. Model. Comput. Simul. 2018;28(1):6:1–6:39. doi: 10.1145/3158668. [DOI] [Google Scholar]
- 3.Agrawal, S., Chatterjee, K., Novotný, P.: Lexicographic ranking supermartingales: an efficient approach to termination of probabilistic programs. In: PACMPL 2(POPL), pp. 34:1–34:32 (2018)
- 4.de Alfaro L, Kwiatkowska M, Norman G, Parker D, Segala R. Symbolic model checking of probabilistic processes using MTBDDs and the kronecker representation. In: Graf S, Schwartzbach M, editors. Tools and Algorithms for the Construction and Analysis of Systems; Heidelberg: Springer; 2000. pp. 395–410. [Google Scholar]
- 5.Baier C, de Alfaro L, Forejt V, Kwiatkowska M. Handbook of Model Checking. Cham: Springer; 2018. Model checking probabilistic systems; pp. 963–999. [Google Scholar]
- 6.Baier C, Hermanns H, Katoen J-P. The 10,000 facets of MDP model checking. In: Steffen B, Woeginger G, editors. Computing and Software Science; Cham: Springer; 2019. pp. 420–451. [Google Scholar]
- 7.Baier C, Katoen J-P. Principles of Model Checking. Cambridge: MIT Press; 2008. [Google Scholar]
- 8.Baier C, Klein J, Leuschner L, Parker D, Wunderlich S. Ensuring the reliability of your model checker: interval iteration for markov decision processes. In: Majumdar R, Kunčak V, editors. Computer Aided Verification; Cham: Springer; 2017. pp. 160–180. [Google Scholar]
- 9.Barthe G, Espitau T, Ferrer Fioriti LM, Hsu J. Synthesizing probabilistic invariants via Doob’s decomposition. In: Chaudhuri S, Farzan A, editors. Computer Aided Verification; Cham: Springer; 2016. pp. 43–61. [Google Scholar]
- 10.Bartocci E, Kovács L, Stankovič M. Automatic generation of moment-based invariants for prob-solvable loops. In: Chen Y-F, Cheng C-H, Esparza J, editors. Automated Technology for Verification and Analysis; Cham: Springer; 2019. pp. 255–276. [Google Scholar]
- 11.Batz, K., Junges, S., Kaminski, B.L., Katoen, J.-P., Matheja, C., Schröer, P.: Pric3: Property directed reachability for MDPS. ArXiv e-prints (2020). https://arxiv.org/abs/2004.14835
- 12.Biere, A.: Bounded model checking, Handbook of Satisfiability. Frontiers in Artificial Intelligence and Applications, vol. 185, pp. 457–481. IOS Press (2009)
- 13.Bradley AR. SAT-based model checking without unrolling. In: Jhala R, Schmidt D, editors. Verification, Model Checking, and Abstract Interpretation; Heidelberg: Springer; 2011. pp. 70–87. [Google Scholar]
- 14.Brázdil T, Chatterjee K, Chmelík M, Forejt V, Křetínský J, Kwiatkowska M, Parker D, Ujma M. Verification of Markov decision processes using learning algorithms. In: Cassez F, Raskin J-F, editors. Automated Technology for Verification and Analysis; Cham: Springer; 2014. pp. 98–114. [Google Scholar]
- 15.Chadha R, Viswanathan M. A counterexample-guided abstraction-refinement framework for Markov decision processes. ACM Trans. Comput. Logist. 2010;12(1):1:1–1:49. [Google Scholar]
- 16.Chakarov A, Sankaranarayanan S. Probabilistic program analysis with martingales. In: Sharygina N, Veith H, editors. Computer Aided Verification; Heidelberg: Springer; 2013. pp. 511–526. [Google Scholar]
- 17.Chakraborty, S., Fried, D., Meel, K.S., Vardi, M.Y.: From weighted to unweighted model counting. In: IJCAI, pp. 689–695. AAAI Press (2015)
- 18.Cheshire S, Aboba B, Guttman E. Dynamic configuration of ipv4 link-local addresses. RFC. 2005;3927:1–33. [Google Scholar]
- 19.Cimatti A, Griggio A, Mover S, Tonetta S. Infinite-state invariant checking with IC3 and predicate abstraction. FMSD. 2016;49(3):190–218. [Google Scholar]
- 20.D’Argenio, P.R., Hartmanns, A., Sedwards, S.: Lightweight statistical model checking in nondeterministic continuous time. In: Margaria, T., Steffen, B. (eds.) ISoLA 2018. LNCS, vol. 11245, pp. 336–353. Springer, Cham (2018). 10.1007/978-3-030-03421-4_22
- 21.D’Argenio, P.R., Jeannet, B., Jensen, H.E., Larsen, K.G.: Reachability analysis of probabilistic systems by successive refinements. In: de Alfaro, L., Gilmore, S. (eds.) PAPM-PROBMIV 2001. LNCS, vol. 2165, pp. 39–56. Springer, Heidelberg (2001). 10.1007/3-540-44804-7_3
- 22.Dehnert C, Junges S, Katoen J-P, Volk M. A Storm is coming: a modern probabilistic model checker. In: Majumdar R, Kunčak V, editors. Computer Aided Verification; Cham: Springer; 2017. pp. 592–600. [Google Scholar]
- 23.Eén, N., Mishchenko, A., Brayton, R.K.: Efficient implementation of property directed reachability. In: FMCAD, pp. 125–134. FMCAD Inc. (2011)
- 24.Fränzle M, Hermanns H, Teige T. Stochastic satisfiability modulo theory: a novel technique for the analysis of probabilistic hybrid systems. In: Egerstedt M, Mishra B, editors. Hybrid Systems: Computation and Control; Heidelberg: Springer; 2008. pp. 172–186. [Google Scholar]
- 25.Gretz F, Katoen J-P, McIver A. Prinsys—On a Quest for Probabilistic Loop Invariants. In: Joshi K, Siegle M, Stoelinga M, D’Argenio PR, editors. Quantitative Evaluation of Systems; Heidelberg: Springer; 2013. pp. 193–208. [Google Scholar]
- 26.Gretz F, Katoen J-P, McIver A. Operational versus weakest pre-expectation semantics for the probabilistic guarded command language. Perform. Eval. 2014;73:110–132. doi: 10.1016/j.peva.2013.11.004. [DOI] [Google Scholar]
- 27.Gurfinkel, A., Ivrii, A.: Pushing to the top. In: FMCAD, pp. 65–72. IEEE (2015)
- 28.Haddad S, Monmege B. Interval iteration algorithm for MDPs and IMDPs. Theor. Comput. Sci. 2018;735:111–131. doi: 10.1016/j.tcs.2016.12.003. [DOI] [Google Scholar]
- 29.Hahn EM, Hartmanns A, Hensel C, Klauck M, Klein J, Křetínský J, Parker D, Quatmann T, Ruijters E, Steinmetz M. The 2019 comparison of tools for the analysis of quantitative formal models. In: Beyer D, Huisman M, Kordon F, Steffen B, editors. Tools and Algorithms for the Construction and Analysis of Systems; Cham: Springer; 2019. pp. 69–92. [Google Scholar]
- 30.Hahn EM, Hermanns H, Wachter B, Zhang L. PASS: abstraction refinement for infinite probabilistic models. In: Esparza J, Majumdar R, editors. Tools and Algorithms for the Construction and Analysis of Systems; Heidelberg: Springer; 2010. pp. 353–357. [Google Scholar]
- 31.Hahn EM, Li Y, Schewe S, Turrini A, Zhang L. iscasMc: a web-based probabilistic model checker. In: Jones C, Pihlajasaari P, Sun J, editors. FM 2014: Formal Methods; Cham: Springer; 2014. pp. 312–317. [Google Scholar]
- 32.Han T, Katoen J-P, Damman B. Counterexample generation in probabilistic model checking. IEEE Trans. Software Eng. 2009;35(2):241–257. doi: 10.1109/TSE.2009.5. [DOI] [Google Scholar]
- 33.Hark, M., Kaminski, B.L., Giesl, J., Katoen, J.-P.: Aiming low is harder: Induction for lower bounds in probabilistic program verification. In: PACMPL 4(POPL), 37:1–37:28 (2020)
- 34.Hartmanns A, Hermanns H. The modest toolset: an integrated environment for quantitative modelling and verification. In: Ábrahám E, Havelund K, editors. Tools and Algorithms for the Construction and Analysis of Systems; Heidelberg: Springer; 2014. pp. 593–598. [Google Scholar]
- 35.Hartmanns, A., Kaminski, B.L.: Optimistic value iteration. CAV. LNCS, Springer (2020). [to appear]
- 36.Hassan, Z., Bradley, A.R., Somenzi, F.: Better generalization in IC3. In: FMCAD, pp. 157–164. IEEE (2013)
- 37.Hermanns H, Wachter B, Zhang L. Probabilistic CEGAR. In: Gupta A, Malik S, editors. Computer Aided Verification; Heidelberg: Springer; 2008. pp. 162–175. [Google Scholar]
- 38.Hoder K, Bjørner N. Generalized property directed reachability. In: Cimatti A, Sebastiani R, editors. Theory and Applications of Satisfiability Testing – SAT 2012; Heidelberg: Springer; 2012. pp. 157–171. [Google Scholar]
- 39.Kaminski, B.L.: Advanced Weakest Precondition Calculi for Probabilistic Programs. Ph.D. thesis, RWTH Aachen University, Germany (2019). http://publications.rwth-aachen.de/record/755408/files/755408.pdf
- 40.Kaminski BL, Katoen J-P, Matheja C, Olmedo F. Weakest precondition reasoning for expected runtimes of randomized algorithms. J. ACM. 2018;65(5):30:1–30:68. doi: 10.1145/3208102. [DOI] [Google Scholar]
- 41.Kattenbelt M, Kwiatkowska MZ, Norman G, Parker D. A game-based abstraction-refinement framework for Markov decision processes. FMSD. 2010;36(3):246–280. [Google Scholar]
- 42.Kozen, D.: A probabilistic PDL. In: STOC, pp. 291–297. ACM (1983)
- 43.Kwiatkowska M, Norman G, Parker D. PRISM 4.0: verification of probabilistic real-time systems. In: Gopalakrishnan G, Qadeer S, editors. Computer Aided Verification; Heidelberg: Springer; 2011. pp. 585–591. [Google Scholar]
- 44.Lange, T., Neuhäußer, M.R., Noll, T., Katoen, J.-P.: IC3 software model checking. In: STTT, vol. 22, pp. 135–161 (2020)
- 45.Lassez JL, Nguyen VL, Sonenberg L. Fixed point theorems and semantics: a folk tale. Inf. Process. Lett. 1982;14(3):112–116. doi: 10.1016/0020-0190(82)90065-5. [DOI] [Google Scholar]
- 46.McIver A, Morgan C. Abstraction, Refinement and Proof for Probabilistic Systems. New York: Springer; 2005. [Google Scholar]
- 47.de Moura L, Bjørner N. Z3: an efficient SMT solver. In: Ramakrishnan CR, Rehof J, editors. Tools and Algorithms for the Construction and Analysis of Systems; Heidelberg: Springer; 2008. pp. 337–340. [Google Scholar]
- 48.Park D. Fixpoint induction and proofs of program properties. Machine intelligence. 1969;5:59–78. [Google Scholar]
- 49.Polgreen, E., Brain, M., Fränzle, M., Abate, A.: Verifying reachability properties in Markov chains via incremental induction. CoRR abs/1909.08017 (2019)
- 50.Puterman, M.L.: Markov Decision Processes: Discrete Stochastic Dynamic Programming. Wiley Series in Probability and Statistics, Wiley, Hoboken (1994)
- 51.Quatmann T, Katoen J-P. Sound value iteration. In: Chockler H, Weissenbacher G, editors. Computer Aided Verification; Cham: Springer; 2018. pp. 643–661. [Google Scholar]
- 52.Rabe MN, Wintersteiger CM, Kugler H, Yordanov B, Hamadi Y. Symbolic approximation of the bounded reachability probability in large Markov chains. In: Norman G, Sanders W, editors. Quantitative Evaluation of Systems; Cham: Springer; 2014. pp. 388–403. [Google Scholar]
- 53.Seufert, T., Scholl, C.: Sequential verification using reverse PDR. MBMV. pp. 79–90. Shaker Verlag (2017)
- 54.Suenaga K, Ishizawa T. Generalized property-directed reachability for hybrid systems. In: Beyer D, Zufferey D, editors. Verification, Model Checking, and Abstract Interpretation; Cham: Springer; 2020. pp. 293–313. [Google Scholar]
- 55.Takisaka T, Oyabu Y, Urabe N, Hasuo I. Ranking and repulsing supermartingales for reachability in probabilistic programs. In: Lahiri SK, Wang C, editors. Automated Technology for Verification and Analysis; Cham: Springer; 2018. pp. 476–493. [Google Scholar]
- 56.Vazquez-Chanlatte, M., Rabe, M.N., Seshia, S.A.: A model counter’s guide to probabilistic systems. CoRR abs/1903.09354 (2019)
- 57.Wimmer R, Braitling B, Becker B. Counterexample generation for discrete-time markov chains using bounded model checking. In: Jones ND, Müller-Olm M, editors. Verification, Model Checking, and Abstract Interpretation; Heidelberg: Springer; 2008. pp. 366–380. [Google Scholar]





