A homily on signal detection theory

Abstract

A lifetime ago, as an undergraduate, I joined a team that developed a new way of thinking about the sensitivity of sensory systems. My teammates were Wilson (Spike) Tanner and John Swets, both now deceased, and we were working at the University of Michigan. I also wish to thank J.C.R. Licklider, J. P. Egan, and Lloyd Jeffress who aided and encouraged that development. I am gratified that what came to be called signal-detection theory (SDT) was so widely accepted and its methods so widely adopted. However, I am somewhat disappointed about how SDT commonly is portrayed, and taught. My reasons are presented here.

I. INTRODUCTION

For a recent conference on signal detection theory, held at Northwestern University and sponsored by the Hugh Knowles Foundation, the cover on the program listing the participants contained a logo that has long been associated with signal detection theory, namely, two equal-variance Gaussian distributions separated by about one standard deviation (see Fig. 1).¹ My complaint is that similar logos have become the main message of the theory, rather than only one particular embodiment of it. Therefore, I composed this brief homily on the topic to illustrate what I believe is the critical contribution of this theory, the true gospel if you will. I will argue that, while the equal-variance Gaussian icon is commonly used, it is inappropriate for illustrating the essential contribution of the theory. Rather, we should be focusing on more general measurements of a signal's detectability and how those different measurements are related. I also must disclose that I had nothing to do with the advertisements for that conference nor, for that matter, the choice of the honoree.

FIG. 1.

Logo of two equal-variance Gaussian distributions printed on the cover of the program for the conference on signal detection theory sponsored by the Hugh Knowles Foundation.

II. NARRATIVE

In determining how human observers detect weak signals, historically, investigators often simply asked them whether they heard, saw, or sensed a given signal. Such responses were private evaluations, and there was no means of counting such actions as anything more than individual opinions. The responses did not indicate whether or not the signal was actually detected. The sensations produced by the stimuli were subjective; they were private or covert. The only objective fact was the observer's response on that particular trial.

The objective fact, a datum that we all can agree upon, is whether an observer says that he/she detects a signal or does not detect a signal. That leaves but one problem. What shall be done when the observer says he/she detects a signal when no signal had been presented? Historically, these responses were called false positives or false alarms, and the general advice to the observers was to avoid making such incorrect responses. To determine if, in fact, the observer was following these instructions, occasional “catch” trials were offered where no signal was presented with the hope that a correct response of “no detection” would occur.

An early and important contribution of signal detection theory was to suggest that not a few but many trials without signals should be presented. Accurately estimating both the proportion of affirmative responses (yes) on these no-signal trials (called false alarms), as well as the proportion of yes responses when the signal was actually presented (called hits), provides a much more useful data set than just estimating the yes responses on signal trials.

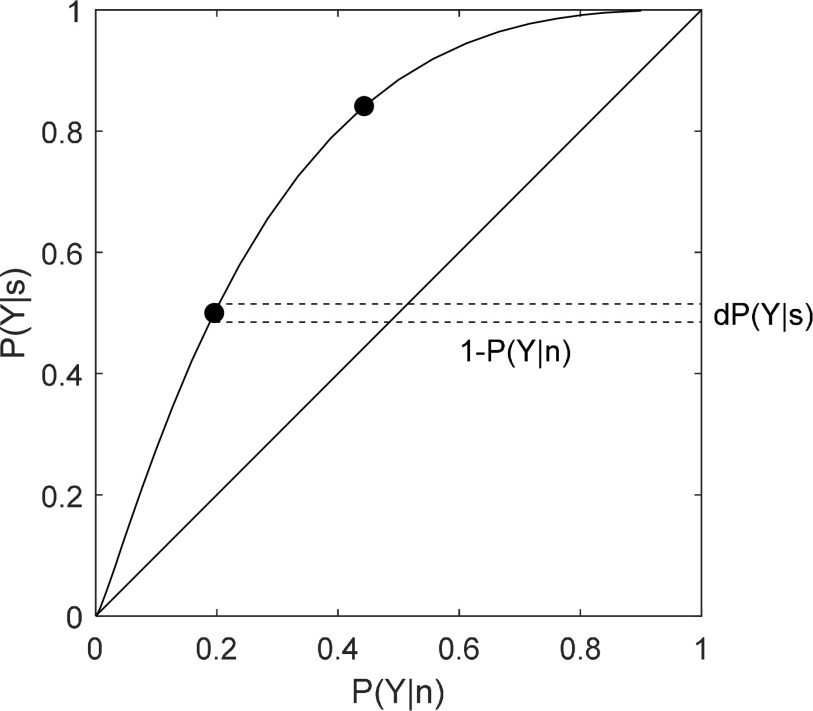
Suppose an observer's attitude was very conservative about saying when a signal was presented. Then, the probability of a hit will be low and the proportion of false alarms also will be low. If, on the other hand, the observers were very liberal about saying they detected a signal, then the proportion of hits will be high and the proportion of false alarms will also be high. An investigator can use inducements (say, by altering the total number of signals presented or providing financial incentives) to encourage an observer to say yes more or less often on different blocks of trials. In the parlance of signal detection theory, the observer has been induced to adopt different criteria for those subjective events that are accepted as a “signal.” The investigator next can use the pairs of hit rates and false-alarm rates obtained under these different inducements to construct a receiver operating characteristic (ROC) curve. The probability of a false alarm is plotted along the abscissa of a ROC curve, and the probability of a hit is plotted on the ordinate. If a signal were not detectable, then the two probabilities should be equal and would fall along the major diagonal of the ROC curve (the chance line). The area under that diagonal is 0.5 or simple chance performance. As the signal becomes more detectable, the hit rate exceeds the false-alarm rate and the curve encompasses a greater area. The area under the ROC curve is, thus, a measure of the signal's detectability. Figure 2 illustrates the pairs of points one might obtain for a moderately detectable signal. To understand this, it will be helpful to get a bit technical and explain how the theory handles these notions explicitly.

FIG. 2.

Example of a receiver operating characteristic (ROC) curve. The solid curve gives all possible pairs of theoretical hit and false-alarm probabilities, P(Y|s) and P(Y|n), respectively, for a given level of detectability. The solid symbols give two hypothetical outcomes corresponding to different inducements to report the presence of a signal. The diagonal line represents chance performance. The small area in the rectangle given by the dashed lines is used in the calculus to compute the area under the ROC curve, which corresponds to percent correct in the two-alternative forced-choice (2AFC) task.

Signal detection theory assumes that the covert sensory events occurring on signal and non-signal trials can be characterized by two different probability density functions. One such function is labeled the signal density function f_s(x) and the other is the non-signal density function f_n(x), where x is the magnitude of the covert sensory events aroused on different trials. Accordingly, the signal function lies to the right of the non-signal function because, on average, signal trials produce larger sensory events than do non-signal trials. Signal detection theory assumes that the observer establishes a criterion value C along the x dimension such that when the covert sensory events exceed C, the observer responds yes; otherwise, he/she responds no. Therefore, if a signal is present, the probability that the sample exceeds C yields the hit probability P(Y|s). If the non-signal event is presented and the sensory sample exceeds C, we have the false-alarm probability P(Y|n),

$$P\left(Y|s\right)={\int }_C^{\infty }{f}_s\left(x\right)dx,$$ (1)

$$P\left(Y|n\right)={\int }_C^{\infty }{f}_n\left(x\right)dx.$$ (2)

An important point here is that the way that the hit and false-alarm probabilities change with C (the shape of the ROC) depends on the forms of the underlying functions f_s and f_n. In signal detection theory, these functions are often drawn as equal-variance Gaussian distributions, but this is not a requirement of the theory; they can be any functions whatsoever. Indeed, the shape of the ROC curve can inform us about the underlying functions, which reflect an essential property of the underlying sensory/perceptual process.

Another detection procedure, advocated by many engineers, is called the A/B test. This procedure is also commonly called two-alternative forced-choice (2AFC), or in audition, it is called two-interval forced choice (2IFC). In this test, a pair of stimulus alternatives is presented in successive time intervals or in different spatial locations. The target (A) is presented in one interval (or location), the non-target (B) is presented in the other, and the observer is asked when (or where) the target appeared. The 2AFC test is, generally, regarded to be superior to single-interval (yes/no) tasks because the listener hears an example of the signal on every trial and is reminded of what the signal sounds like.

Signal detection theory can also describe the A/B or 2AFC test. Let us call the A alternative a signal event, and the B alternative is called a non-signal event. In the A/B task, what produces a correct response? The observer gets two samples, one from the signal alternative and one from the non-signal alternative. If the sample x_s from the signal distribution f_s, is greater than the sample x_n from the non-signal distribution f_n, then the observer will choose the correct interval or location and a correct response will occur. Or, to express it in integral terms,

$$P\left(C\right)=P\left(x_s>x_n\right)={\int }_{-\infty }^{\infty }{f}_s\left(x\right){\int }_{-\infty }^{x_s}{f}_n\left(y\right)dy\hspace{0.17em}dx.$$ (3)

The probability of being correct in the A/B or 2AFC test is simply that integral when summed for all possible values of x_s.

So, now we have two different ways of assessing the detectability of a signal. One is the yes/no method, in which we construct the ROC curve, and signal detectability is measured as the area under this curve. The other method is the A/B task, in which a signal is presented in only one of two observation intervals (locations), and the detectability of the signal is measured by the proportion of times the signal is correctly selected in a number of trials. To understand a remarkable fact of signal detection theory, we now will prove that the area under the ROC curve is equal to the probability of being correct in the A/B task.² Although well known, I believe the importance of this relationship has been overlooked in the intervening years.

Consider, first, how we usually calculate the area under a function, y = f(x). One method is to make approximations to that area by constructing vertical slices along the function. The area of each slice is equal to the slice's width, dx, times the height of the rectangle, f(x), at that value of x. Thus, the area of the small slice is simply dA = f(x)dx, which is the fundamental theorem of calculus. By making the slices smaller and smaller, that is, by making dx approach zero, we converge on the actual value of the area under the function f(x).

Let us now calculate the area under the ROC curve for the yes/no task using the same approximation method as above. To make things easier, let us imagine horizontal rather than vertical slices made along the ROC curve. The horizontal slices extend from the ROC curve to the right-hand border of Fig. 1 (see the dashed rectangle in Fig. 1). The length of the slice is equal to 1 − P(Y|n), the complement of the false-alarm probability at the hit probability, P(Y|s). Next, look carefully at Eq. (3). The second integral, the area of f_n(y)dy from minus infinity to x_s, is also just the complement of the false-alarm probability at that value of x_s, the criterion value for the hit probability. Now, we must describe the width of the slice shown in Fig. 2. For the moment, let us call that width dP(Y|s). That width is given by the difference between two probabilities, the value of P_u(Y|s) at the upper value of the slice minus the value of P_l(Y|s) at the lower value of the slice. As the slice becomes smaller and smaller, that difference approaches the value of the signal distribution function f_s(y). Again, we see from Eq. (3) that f_s(y) is the multiplier of the complement of the false-alarm term. So, the quantities used to calculate P(C) are exactly those used to approximate the area under the yes-no ROC curve. Using the same calculus arguments, the approximation becomes the exact value as the widths of the horizontal slices are made smaller and smaller. Hence, we have proved that the total area under the ROC curve is equal to the probability of being correct in the A/B task. One should also note that the proof does not make any assumption about the form of the functions f_s and f_n. They do not need to be Gaussian.

I should note here for extra credit that if in Eq. (3) the second integral is raised to the M − 1 power, we can find the probability of being correct in an M-alternative forced-choice task. The non-signal samples are all independent, and, thus, all M − 1 samples must be less than x_s and the joint probability is simply the probability P (raised to the M – 1st power). If we alter the original yes-no ROC curve by simply moving the false-alarm values to the right by raising their value to a power of M − 1, then the percent correct in the M-alternative task is simply the area under the altered ROC curve. Once more, we have predicted the behavior in one task from the behavior in another task. We also should note that this method is not equal to the erroneous “correction for chance” formula, sometimes used to predict the percentage of correct responses in a different M-alternative forced-choice task.

Finally, I should mention a third general measure of a signal's detectability, Kullback-Leibler divergence (D_KL), also known as information divergence or discriminable information. D_KL is the expected value of the log-likelihood ratio of f_s and f_n,

$$D_{\text{KL}}\left(f_s\parallel f_n\right)=E_{f_s}\hspace{0.17em}\text{ln}\hspace{0.17em}\left(\frac{f_s}{f_n}\right).$$ (4)

It is a measure of how two distribution functions differ and, if expressed as bits, is related to a number of important quantities in Shannon information theory (Kullback, 1959). Like our previous two measures, it is distribution free. Its value is in indexing optimal performance for the detection task when there is information that distinguishes the signal from the noise in the higher moments of the distributions beyond the mean. Note that our equal-variance Gaussian assumption would have us believe that the only information identifying the signal is a shift along the axis of the two distributions.³ Having a general measure of optimal performance can also be of tremendous value because it serves as a standard for identifying limits of observer sensitivity across a broad range of stimulus conditions and psychophysical tasks. Indeed, this approach has been central to signal detection theory from the outset and is treated in the theory of ideal observers.

III. CONCLUSION

The moral of this homily is that while individual perceptual experiences are covert subjective quantities, there are procedures that can convert them into completely objective data. Those data are as objective as any of the quantities used in the so-called hard sciences. The contribution of signal detection theory is to provide a means of understanding the structure of different detection tasks and generate predictions about how the quantities measured in each task should be related. The theory does assume the existence of distribution functions of sensory events, but these distributions need not be equal-variance nor Gaussian; that is just a simplifying assumption.