Background and Review of Cavity-Enhanced Spontaneous Parametric Down-Conversion

Abstract

Spontaneous parametric down-conversion (SPDC) in a nonlinear crystal has been a workhorse for the generation of entangled and correlated single-photon pairs used for quantum communications applications for nearly three decades. However, as a naturally broadband process, the ability of SPDC to interface with the very narrow energy transitions in atomic ensembles for implementing quantum memories, which are needed for quantum repeaters to extend the reach of quantum communications, was initially limited. To overcome this limitation, the process was enhanced by placing the nonlinear crystal inside a resonating cavity. This modified process has some important advantages, including narrowing the spectral linewidth of generated photons into brighter resonant modes of the cavity, and the ability to lock the desired mode of the cavity to the targeted transition frequency of the atomic ensemble. This paper presents an overview of the principle of cavity-enhanced SPDC, a review of works to date using this technique, and an example of one of these implementations.

1. Introduction

The process of spontaneous parametric down-conversion (SPDC) in a nonlinear crystal has been used for generating entangled photon pairs for quantum communications applications for almost three decades [1]. The process generates a pair of correlated photons, known as a “signal” photon and an “idler” photon, which are frequency down-converted from a single “pump” photon. Due to the phase-matching range within the crystal, the bandwidths of the signal and idler beams are relatively large (typically in the order of terahertz or a few nanometers) for common lengths of crystals [1–3]. However, for many quantum communication applications using atomic ensemble–based quantum memories (QM) [4, 5], a linewidth in the order of tens of megahertz or less is required to interface with the narrow atomic transitions that are used to store the quantum state. To achieve suitably narrow linewidths for use in QM, the nonlinear crystal may be placed inside a cavity that is resonating at the desired frequency. The effect of the cavity is to restrict the generation of signal and idler photons to the narrow linewidth resonant modes of the cavity. When both the signal and idler beams are resonating in the cavity, the scheme is referred to as doubly resonant. When only one of the generated beams is resonating in the cavity, the scheme is referred to as singly resonant. For the singly resonant scheme, although only one of the beams is resonating, both the signal and idler are restricted to narrow modes due to the conservation of energy in the SPDC process. This technique has matured significantly, and now is a good time to summarize the key spectral equations (Sec. 2) and experimental techniques and results to date (Sec. 3). Finally, we describe in more detail the implementation of a singly resonant cavity-enhanced SPDC (Sec. 4).

Following the cavity, the signal and idler photons are no longer distributed continuously over the phase-matched bandwidth, but they are instead squeezed into brighter modes as illustrated in Fig. 1a. The modes themselves are distributed over the phase-matched bandwidth of the nonlinear interaction (dashed lines in Fig. 1a). For singly resonant schemes, the brightness of the modes is increased by a factor of the cavity finesse, while for doubly resonant schemes, the brightness of the modes is increased by a factor of the square of the cavity finesse.

Fig. 1.

Simulation of (a) the spectral profiles of the generated beams from a single-pass SPDC (green), singly resonant oscillator (SRO) (orange), and doubly resonant oscillator (DRO) (blue); (b) singly resonant cross-correlation function; (c) doubly resonant cross-correlation function.

Terms: δυ_PM: phase-matching linewidth; δυ_mode: modal linewidth; Δν_fsr: free spectral range; τ₀: temporal linewidth; T_rt: round-trip time.

Since the cavity narrowed spectral modes are typically orders of magnitude narrower than the phase-matched linewidths, the frequency terms δν and Δν are commonly used to describe the cavity-based source’s linewidth and free-spectral range, respectively. In keeping with common notation, the relevant equations are introduced using the angular frequency notation (δω or Δω) and converted to the frequency (δν or Δν) and wavelength (δλ or Δλ) notation as suitable according to $\delta v=\frac{\delta \omega }{2\pi }$ and $\delta \lambda =\delta \omega \frac{{\lambda }^2}{2\pi c_0}$ or $\Delta v=\frac{\Delta \omega }{2\pi }$ and $\Delta \lambda =\Delta \omega \frac{{\lambda }^2}{2\pi c_0}$.

2. Spontaneous Parametric Down-Conversion

Spontaneous parametric down-conversion is a purely quantum mechanical phenomenon stemming from the spontaneous parametric amplification of vacuum thermal noise photons in a nonlinear medium pumped at a low enough power to avoid any stimulated photon generation. SPDC leads to the spontaneous generation of photons at the frequencies ω_S and ω_I following the destruction of a pump photon at frequency ω_p (where the subscripts S, I, and P refer to the signal, idler, and pump photon, respectively) when certain conditions are satisfied. These conditions stem from the conservation of energy and momentum in the conversion process and are often collectively referred to as phase-matching conditions. The conservation of energy in the SPDC process ensures that ω_p = ω_S + ω_I. Table 1 shows the power spectral function and second-order correlation function for the cases of a single pass, a singly-resonant cavity, and a doubly-resonant cavity. More details and parameter definitions are given later in this section.

Table 1.

Power spectral function (P_S/I) and second-order correlation function $\left[G_{S,I}^{(2)}(\tau )\right]$ for the cases of single-pass, singly-resonant (SRO) and doubly-resonant (DRO) cavities.

	PS/I	$G_{S,I}^{(2)}(\tau )$
Single Pass [3]	$\propto {\text{sinc}}^2\left(\pi \Delta v_{\mathit{\text{SPDC}}}{\tau }_o\right)$	$\propto \left|{\tau }_o\right|=\left|\frac{L_{cry}}{c_0}\left(n_I-n_s\right)\right|$
SRO [6]	$\propto \sum _{m=-\infty }^{\infty }\frac{{\text{sinc}}^2\left(m\Delta {\omega }_{fsr}\frac{{\tau }_o}{2}\right)}{{\left(\frac{{\alpha }_{cav}}{2}\right)}^2+{\left({\omega }_{s/I}-m\Delta {\omega }_{fsr}-\omega \right)}^2}$	$\propto \{\begin{array}{c}{e}^{-{\alpha }_{cav}\tau }{\left|\sum _{m=-\infty }^{\infty }\mathit{\text{sinc}}\left(m\Delta {\omega }_{fsr}\frac{{\tau }_o}{2}\right)e^{-\text{i}m\Delta {\omega }_{fsr}\left(\tau +\frac{{\tau }_o}{2}\right)}\right|}^2\\ 0\end{array}$ $\text{ for }\{\begin{array}{c}\tau +\frac{{\tau }_o}{2}\ge -\frac{\left|{\tau }_o\right|}{2}\\ \tau +\frac{{\tau }_o}{2}<-\frac{\left|{\tau }_o\right|}{2}\end{array}$
DRO [7]	$\propto {\omega }_S{\left|\sum _{m_{S/I}=-\infty }^{\infty }\frac{\sqrt{{\alpha }_{ca{v}_S}{\alpha }_{ca{v}_I}}\text{sinc}\left(\left(\omega -{\omega }_{S/I}\right)\frac{{\tau }_o}{2}\right)}{\left({\Omega }_S-i\left(\omega -{\omega }_S\right)\right)\left({\Omega }_I+i\left(\omega -{\omega }_S\right)\right)}\right|}^2$	$\propto \left|\frac{\sqrt{{\alpha }_{ca{v}_S}{\omega }_S{\alpha }_{ca{v}_I}{\omega }_I}}{{\Omega }_S+{\Omega }_I}\{\begin{array}{c}\frac{e^{-i{\Omega }_S\left(\tau -\frac{{\tau }_o}{2}\right)}\mathit{\text{sinc}}\left(\frac{i{\tau }_o}{2}{\Omega }_S\right)}{{\Omega }_S+{\Omega }_I}\\ \frac{e^{+i{\Omega }_I\left(\tau -\frac{{\tau }_o}{2}\right)}\mathit{\text{sinc}}\left(\frac{i{\tau }_o}{2}{\Omega }_I\right)}{{\Omega }_S+{\Omega }_I}\end{array}\right|$ $\text{ for }\{\begin{array}{l}\tau \ge \frac{{\tau }_o}{2}\hfill \\ \tau <\frac{{\tau }_o}{2}\hfill \end{array}$

2.1. Single-Pass SPDC

The SPDC spectral power function for the signal, P_S, and idler, P_I, from a crystal that is not inside a cavity is proportional to a sinc² function [8, 9]:

$$P_{S/I}\propto {\text{sinc}}^2\frac{\Delta k{L}_{cry}}{2}={\text{sinc}}^2\left(\delta {\omega }_{PM}\frac{{\tau }_o}{2}\right)={\text{sinc}}^2\left(\pi \delta v_{PM}{\tau }_o\right),$$ (1)

where δω_PM is the quasi-phase-matched (QPM) limited angular frequency width of the generated signal and idler photons; τ_o is the difference in transmission time of the signal and idler waves through a nonlinear crystal of length L_cry, and Δk is the wavevector mismatch over which conversion occurs. The full width at half maximum (FWHM) of δω_PM occurs at a power level of ${\text{sinc}}^2\left(\delta {\omega }_{PM}\frac{{\tau }_o}{2}\right)=\frac{1}{2}$, such that $\delta {\omega }_{PM}\frac{{\tau }_o}{2}=0.44\pi$, giving $\delta {\omega }_{PM}=\frac{0.88\pi }{{\tau }_o}$ with τ_o specifically given by ${\tau }_o=\frac{L_{cry}}{c_0}\left(n_I-n_S\right)$, where n_S and n_I are the refractive indices of the nonlinear crystal for the signal and idler frequencies, respectively. The linewidth of a single-pass SPDC is given by:

$$\delta v_{PM}=\frac{\delta {\omega }_{PM}}{2\pi }.$$ (2)

The second-order correlation function, $G_{S,I}^{(2)}(\tau )$, describes the coherence of the intensity of signal and idler photons measured at the times t and t + τ, where τ is the delay between the crystal exit times of the heralding and heralded photons. For a single-pass SPDC, the $G_{S,I}^{(2)}(\tau )$ function is zero outside a single peak of width |τ_o|, since the arrival time of a heralded photon can lag the heralding photon by at most $\tau \pm \frac{\left|{\tau }_o\right|}{2}$, representing the temporal delay in exiting the crystal due to the different group velocities of the signal and idler traversing the crystal. It should be noted that for different group velocities of the signal and idler through the crystal, as would be the case for nondegenerate (where the frequencies of the signal and idler are different) or type-II (where the polarizations of signal and idler are perpendicular) SPDC, the symmetry of the peak can be asymmetric.

2.2. SPDC Inside a Cavity

When the nonlinear interaction occurs inside a cavity, the cavity characteristics need to be considered. In this case, the SPDC phase-matching linewidth, δν_PM, forms an envelope that is composed of m modes separated by the free spectral range, Δν_fsr, of the cavity. The narrow mode linewidths, δν_mode, are determined by the length of the cavity and the losses from the cavity.

2.2.1. General Cavity Formulations

For a cavity, such as shown in Fig. 2, consisting of an input mirror, M_ip, with a reflection r_ip, and an output mirror, M_op, with a reflection r_op and with a crystal placed between the mirrors, the round-trip power loss, α_RT, includes the transmission through each of the end mirrors (t_ip = 1 − r_ip and t_op = 1 − r_op, for the input and output mirrors, respectively) and any other internal cavity losses, α_int, within the cavity. The power loss from the cavity during a round-trip is given as α_rt = 1 − [r_ipr_op(1 − 2α_int)], where α_int is doubled since these losses are incurred twice for a round trip. For the typical and targeted cases in which the losses are relatively low (α_RT ≤ 10 %), the cavity finesse can be approximated by $F\approx \frac{2\pi }{{\alpha }_{rt}}$ [10].

Fig. 2.

Symmetric Fabry-Perot cavity with a nonlinear crystal.

By considering only the transmission through the output mirror, another quantity, F₀, can be defined as $F_0\approx \frac{2\pi }{t_{op}}$ [11]. The quantity F₀ is the bounding limit of the finesse for the output power, since any other losses (such as t_ip or α_int) reduce the output power and the cavity finesse. The cavity length, L_rt, is defined here as the total effective round-trip distance of the cavity and is given by $L_{rt}=\frac{m\lambda }{\tilde{n}}=\frac{m}{\tilde{n}}\frac{2\pi c_0}{\omega }$, where $\omega =\frac{2\pi c_0}{\lambda }$, m is an integer representing the number of resonating modes (m = 0, ±1, ±2, ±3 …), and $\tilde{n}$ is the average refractive index inside of the cavity. The angular frequency of the mth mode is given as ${\omega }_m=\frac{m}{\tilde{n}}\frac{2\pi c_0}{L_{rt}}$. The angular frequency separation of the cavity modes is given by $\Delta {\omega }_{fsr}={\omega }_m-{\omega }_{m-1}=\frac{m}{\tilde{n}}\frac{2\pi c_0}{L_{rt}}-\left(\frac{m}{\tilde{n}}\frac{2\pi c_0}{L_{rt}}-\frac{1}{\tilde{n}}\frac{2\pi c_0}{L_{rt}}\right)=\frac{2\pi c_0}{\tilde{n}{L}_{rt}}$. The time taken to travel one round trip of the cavity is given from the distance over speed formula $T_{rt}=\frac{\tilde{n}{L}_{rt}}{c_0}=\frac{2\pi }{\Delta {\omega }_{fsr}}$, giving $\Delta {\omega }_{fsr}=\frac{2\pi }{T_{rt}}$. The rate at which photons are lost from the cavity, the cavity decay rate coefficient, α_cav, is given by the round-trip loss per round-trip time ${\alpha }_{cav}=\frac{{\alpha }_{rt}}{T_{rt}}=\frac{\Delta {\omega }_{fsr}}{F}$. The angular frequency width of the cavity mode is related to the cavity decay rate as δω_cav = α_cav. As photons exit the cavity, the energy inside the cavity, E_cavity, decays exponentially as a function of time and the decay rate $E_{\mathit{\text{cavity}}}\propto e^{-{\alpha }_{cav}t}$. The energy will drop to half $\left(e^{-{\alpha }_{cav}{\tau }_{cav}}=\frac{1}{2}\right)$ after the cavity coherence time, τ_cav, such that ${\alpha }_{cav}=\frac{\text{Ln}2}{{\tau }_{cav}}$. The linewidths of the cavity modes are:

$$\delta v_{cav}=\frac{\delta {\omega }_{cav}}{2\pi }=\frac{\text{Ln}2}{2\pi {\tau }_{cav}}.$$ (3)

The cavity free spectral range is given by:

$$\Delta v_{fsr}=\frac{\Delta {\omega }_{fsr}}{2\pi }=\frac{1}{T_{rt}}.$$ (4)

The linewidth and free spectral range of the cavity are related to its finesse by:

$$\delta v_{cav}=\frac{\delta v_{fsr}}{F}.$$ (5)

2.2.2. Singly Resonant (SRO) SPDC

In a singly resonant cavity, only the signal frequency is resonating inside the cavity, while the idler frequency is nonresonating, and its photon exits the cavity after the first pass. Following the theory presented in [6], the output power spectral function for both the signal and idler waves is given as:

$$P_{S/I}(\omega )\propto {\sum }_{m=-\infty }^{\infty }\frac{{\text{sinc}}^2\left(m\Delta {\omega }_{fsr}\frac{{\tau }_o}{2}\right)}{{\left(\frac{{\alpha }_{cav}}{2}\right)}^2+{\left({\omega }_{S/I}-m\Delta {\omega }_{fsr}-\omega \right)}^2}.$$ (6)

The numerator in Eq. (6) represents the SPDC phase-matching envelope corresponding to Eq. (1), while the denominator describes the generation of SPDC pairs being restricted to the cavity modes at ω_m = ω_S/I + m Δω_fsr. Even though only the signal is resonant in the cavity, the power spectral function consists of equally spaced modes for both the signal and idler due to the conservation of energy in the SPDC process, assuming a narrow pump. The angular frequency width of the signal and idler modes, $\delta {\omega }_{mode}^{SRO}$, from the singly resonant cavity is determined by the widths of the cavity modes according to $\delta {\omega }_{mode}^{SRO}=\delta {\omega }_{cav}={\alpha }_{cav}$. The linewidth is then $\delta v_{mode}^{SRO}=\frac{\delta {\omega }_{cav}}{2\pi }=\frac{{\alpha }_{cav}}{2\pi }$.

The overall brightness of the SRO is the same as the single-pass case; however, the brightness of any mode in an SRO is enhanced by at most a factor of the cavity finesse, F, compared to the same bandwidth at the same frequency from a single-pass SPDC. Photons lost inside the cavity through absorption or scattering or through the input mirror will reduce this enhancement by a factor of $\frac{F}{F_o}$ [11].

The $G_{S,I}^{(2)}(\tau )$ profile from an SRO will also be affected by the cavity. Although one photon will pass through the cavity without delay, the resonating photon will pass over and back between the mirrors and exit at some multiple of the round-trip time of the cavity [6]:

$$G_{S,I}^{(2)}(\tau )\propto \{\begin{array}{c}{e}^{-{\alpha }_{cav}\tau }{\left|{\sum }_{m=-\infty }^{\infty }\mathit{\text{sinc}}\left(m\Delta {\omega }_{fsr}\frac{{\tau }_o}{2}\right)e^{-\text{i}m\Delta {\omega }_{fsr}\left(\tau +\frac{{\tau }_o}{2}\right)}\right|}^2\\ 0\end{array}\begin{array}{l}\text{ for }\tau +\frac{{\tau }_o}{2}\ge -\frac{\left|{\tau }_o\right|}{2}\hfill \\ \text{ for }\tau +\frac{{\tau }_o}{2}<-\frac{\left|{\tau }_o\right|}{2}\hfill \end{array}.$$ (7)

Notwithstanding the temporal resolution of the detectors used in a real experiment, the $G_{S,I}^{(2)}(\tau )$ profile will then be a series of periodic peaks, each of the temporal width ∣τ_o∣ and separated by the round-trip time of the cavity, T_rt. The maxima of the successive periodic peaks follow the cavity decay rate, α_cav, and can be fitted to $G_{FIT}^{(2)}(\tau )\propto \{\begin{array}{r}\hfill e^{-{\alpha }_{cav}\tau }\text{ for }\tau \ge 0\\ \hfill 0\text{ for }\tau <0\end{array}$ (as shown in Fig. 1b). From this, the characteristics of the source at the single-photon level can be obtained, including the spectral linewidth and coherence time of the photons emitted. This is a very useful, since the characterization of the narrow spectral linewidth of single photons is beyond the capability of most unspecialized spectrometers.

2.2.3. Doubly Resonant (DRO) SPDC

For a doubly resonant cavity, both the signal and idler frequencies are resonant in the cavity. Maintaining the resonance of both the signal and idler frequencies typically requires additional design elements (such as a compensating crystal) inside the cavity to compensate for any phase differences due to different group velocities or polarizations for the signal and idler beams. Following the analysis presented in [7], the output power spectral function for the signal wave is given as:

$$P_S(\omega )\propto {\omega }_S{\left|{\sum }_{m_{\frac{S}{I}}=-\infty }^{\infty }\frac{\sqrt{{\alpha }_{ca{v}_S}{\alpha }_{ca{v}_I}}\text{sinc}\left(\left(\omega -{\omega }_{S/I}\right)\frac{{\tau }_o}{2}\right)}{\left({\Omega }_S-i\left(\omega -{\omega }_S\right)\right)\left({\Omega }_I+i\left(\omega -{\omega }_S\right)\right)}\right|}^2,$$ (8)

where ${\Omega }_{S/I}=\frac{{\alpha }_{ca{v}_{S/I}}}{2}+i\left(m_{S/I}\Delta {\omega }_{fs{r}_{S/I}}\right)$. A corresponding statement exists for the power spectral function for the idler wave, P_I(ω). Unlike the SRO, due to the dual resonance, the widths of the SPDC generated modes, $\delta {\omega }_{mod{e}_{S/I}}$, are narrower than the cavity damping rates, ${\alpha }_{ca{v}_{S/I}}$. For the case where ${\alpha }_{ca{v}_S}\approx {\alpha }_{ca{v}_I}$, the angular frequency width of the SPDC modes is given by $\delta {\omega }_{mode}^{DRO}\approx \sqrt{\sqrt{2}-1}{\alpha }_{cav}=0.64{\alpha }_{cav}$ [7]. The linewidth is then $\delta v_{mode}^{DRO}\approx 0.64\frac{{\alpha }_{cav}}{2\pi }$.

The total photon pair generation rate in a DRO is enhanced by a factor of the cavity finesse, F, compared to the single-pass case, and the brightness of any mode in a DRO is enhanced by at most a factor of the square of the cavity finesse, F², reduced by a factor of $\frac{F}{F_o}$ for any cavity losses not contributing to the output [11]. The $G_{S,I}^{(2)}(\tau )$ profile from a DRO is given by Ref. [7] as

$$G_{S,I}^{(2)}(\tau )\propto \left|\frac{\sqrt{{\alpha }_{ca{v}_S}{\omega }_S{\alpha }_{ca{v}_I{\omega }_I}}}{{\Omega }_S+{\Omega }_I}\{\begin{array}{c}\frac{e^{-i{\Omega }_S\left(\tau -\frac{{\tau }_0}{2}\right)}\mathit{\text{sinc}}\left(\frac{i{\tau }_0}{2}{\Omega }_S\right)}{{\Omega }_S+{\Omega }_I}\text{ for }\tau \ge \frac{{\tau }_0}{2}\\ \frac{e^{+i{\Omega }_I\left(\tau -\frac{{\tau }_0}{2}\right)}\mathit{\text{sinc}}\left(\frac{i{\tau }_0}{2}{\Omega }_I\right)}{{\Omega }_S+{\Omega }_I}\text{ for }\tau <\frac{{\tau }_0}{2}\end{array}\right|.$$ (9)

The $G_{S,I}^{(2)}(\tau )$ profile will then be a series of peaks, each of the temporal width ∣τ_o∣ and separated by the round-trip time of the cavity, T_rt. The maxima of the successive periodic peaks decay at a rate proportional to δν_S for τ ≥ 0 and δν_I for τ < 0 given by the fitting curve $G_{FIT}^{(2)}(\tau )\propto \{\begin{array}{cc}{e}^{-2\pi \delta v_S\tau }& \text{ for }\tau \ge 0\\ e^{2\pi \delta v_S\tau }& \text{for }\tau <0\end{array}$ (as shown in Fig. 1c). When the decay rates for the signal and idler are the same, the $G_{S,I}^{(2)}(\tau )$ fitting curve will be symmetrical. For the case where δν_S ≠ δν_I, the $G_{S,I}^{(2)}(\tau )$ fitting curve will not be symmetrical.

3. Review of Published Works

3.1. Theory Treatments

The role of cavities in generating optimally nonlasing squeezed states in a parametric amplifier inside a cavity operated just under the lasing threshold was modeled by Yurke [12] and Collett and Gardiner [13]. Later, Lu and Ou [14] and Hariharan and Sanders [15] applied these earlier theories to an optical parametric oscillator (OPO) operating far below threshold for the squeezing of spontaneously generated two-photon states into narrow modes and found that the earlier theories worked just as well, leading to equations describing the enhancement of the spontaneous generation within the narrow cavity modes. The results further showed that in order to ensure that the down-conversion process resulted in narrowband two-photon states, it was necessary for the spontaneous process, rather than a stimulated process, to dominate the generation of the photon pairs. To eliminate the stimulated process, it is necessary to operate the OPO device far below the lasing threshold condition. Zielińska and Mitchell [16] extended this theory for below threshold but otherwise arbitrary gain. Shapiro et al. [17] described the quantum signatures from SRO and DRO schemes, noting that overall enhancement of the SPDC generation rate occurs in the doubly resonant scheme only, although the brightness of modes in both schemes is increased due to the squeezing. Theoretical treatments for a singly resonant SPDC cavity by Herzog et al. [6] and a doubly resonant SPDC cavity by Scholz et al. [7] provided specific expressions for the single-photon spectral distributions and the signal-idler cross-correlation functions (restated in Sec. 2.2). Meanwhile, Jeronimo-Moreno et al. [18] provided a recipe for a singly resonant cavity achieving linewidths suitable for atomic interaction with a large enough modal separation for passive filtering of a single mode.

3.2. Experimental Implementations

There have been several implementations of cavity-narrowed SPDC since the early theory work. Generally, the SRO configurations are more stable and have greater tunability because only one of the generated photons must be resonant in the cavity. Designs to implement SROs vary depending on the wavelength of the outputs and the type of phase matching implemented. In type-0 or type-I phase matching, the signal and idler polarizations are the same, and in type-II phase matching (most common for generating entangled photon pairs), the signal and idler polarizations are perpendicular. The SPDC crystal will have different refractive indices for different wavelengths and polarizations of the signal and idler beams, resulting in different effective cavity lengths for the respective resonance conditions. In a degenerate, type-II source [19], the Fabre-Perot type cavity length was scanned to be resonant with either the signal or idler as the cavity length changed, resulting in narrowband modes separated by the free-spectral-range distance, with the single mode at exact degeneracy also being doubly resonant. For a cavity length that is fixed at the resonance condition of the signal wavelength for a degenerate type-II SPDC [17, 20], a polarization beamsplitter can be placed inside the cavity to remove the idler polarization and allow the signal polarization to remain inside the cavity. In the case where there is greatly nondegenerate generation in either type-0/type-I [21] or type-II [22] sources, the mirror coating can be designed to reflect the signal and transmit the idler wavelengths. In Refs. [19, 20], the output mirror was highly reflective for the pump wavelength, so as to double the interacting length of the crystal.

DRO configurations are more effective in generating bright sources of single photon pairs but have to overcome stability issues associated with keeping both the signal and idler beams in a resonance condition despite different parameters such as polarization or wavelength. In all cases for DROs, one of the mirrors is coated for high reflection for both the signal and idler wavelengths, while the output mirror is partially transmitting for both wavelengths. In some cases, the pump is also reflected by the output mirrors [19, 23, 24], so as to double the effective interaction length of the crystal, or by both mirrors [25–28], so as to also be resonant (a scheme referred to as triply resonant). Various engineering designs have been implemented to maintain the doubly (or triply) resonant condition. The simplest option for maintaining double resonance is to have degenerate type-I phase matching [11], although separating the signal and idler afterwards becomes an issue. To maintain double resonance in degenerate type-II phase matching, one or more compensating crystals of the same material (and therefore the same refractive index) and same total length as the periodically poled SPDC crystal can be placed inside the cavity [25, 28–30]. The compensating crystal will not be poled to generate any output but will be rotated at 90 degrees to partially reverse the difference in group velocities of the different polarizations in the SPDC crystal. This is limited, however, since the interaction length inside the SPDC crystal upon generation is not typically the full crystal, whereas the compensation occurs over the full length of the unpoled crystal. Alternatively, a polarization rotator can be placed inside the cavity to ensure that each beam’s polarization is opposite from one pass through the crystal to the next [17, 26]. In this way, the group velocity difference accumulated by the different polarizations passing through the crystal will be reversed after each round trip. In the case of a ring cavity, in which the beams pass through the crystal just once during a round trip, a half-wave-plate (HWP) can be used [26]. For a Fabry-Perot cavity, in which the beams pass through the cavity twice for each round trip, a quarter-wave-plate can be used [17]. Using two perpendicular type-I phase-matched crystals with degenerate signal and idler output has the advantage of automatically compensating for each other during each round trip [31]. For nondegenerate phase matching, maintaining the dual resonance becomes more complex. In [24, 32], for example, the dual resonance was maintained by fixing the cavity length to resonate the signal frequency and adjusting the pump to maintain the idler at a resonant frequency of the fixed cavity length.

The linewidths of cavity-narrowed SPDC are achieved with a combination of longer cavity lengths and/or high cavity finesses. As described earlier, the cavity parameters (length and finesse) influence the modal structure of the generated outputs. For a similar finesse, longer cavities will generate narrower modes than shorter cavities. The narrowest linewidth reported to date [26] was from an effective cavity length of approximately 2.5 m, which achieved a sub-megahertz linewidth (0.66 MHz) in a DRO configuration with a cavity finesse of approximately 180. In Ref. [32], a longer DRO cavity with an effective length of approximately 72 cm achieved a linewidth of approximately just 2 MHz with a cavity finesse of 200. On the other hand, a very short cavity (effective length of approximately just 4.5 cm) in [24] recently achieved very narrow linewidths (6.6 MHz) but required a very high finesse of 800. In most short cavity schemes [21, 25, 33], the large modal separation is a key objective to enable passive filtering. In Ref. [33], for example, a short effective cavity length of approximately 1 cm achieved a modal separation of almost 30 GHz, which can be matched to ultradense wavelength division multiplexers (U-DWDM). In Ref. [21], the short effective cavity length of under 7 cm, giving a modal separation of 4.5 GHz, enabled filtering to a few modes using a volume Bragg grating. Isolation of a single or few modes when there are small modal separations is typically implemented with additional cavity filtering [34, 35].

Only the photons in spectral modes that are matched to the wavelength and bandwidth of a suitable atomic or solid-state structure will be viable for quantum memory. In cavity systems, this is typically achieved by locking the cavity length to resonate a reference beam that matches the narrow atomic bandwidth. However, since the reference beam is typically in the milliwatt (mW) power range and co-aligned with the generated single-photon outputs, care must be taken to avoid the reference beam reaching the sensitive single-photon detector. This is frequently achieved by chopping the reference beam and only collecting the single photons that exit the cavity while the reference beam is blocked. Continuous operation can be implemented in the cases where the pump frequency is double the output frequency, and where the pump is used as a reference that can be removed upon exiting the cavity without effecting the outputs [20, 26, 27]. The most popular atomic structures are rubidium [24, 26, 30, 31, 36, 37] and cesium [21, 22, 24, 25, 27], although other quantum memory–compatible structures are sometimes used, such as praseodymium-doped [32, 38] or neodymium-doped [39] solids.

By far the most common cavity configuration uses physically independent mirrors, reflection and antireflection coated as appropriate, surrounding the SPDC crystal in either a bow-tie [22, 26, 30–32, 34, 40] or Fabry-Perot [19–21, 25, 27–29, 33] configuration. Some Fabre-Perot schemes use the end facets of the crystal itself as one [11, 24, 35] or both [23, 41, 42] of the reflecting surfaces to form the cavity. In Refs. [41, 42], the SPDC cavity was formed from a single-crystal waveguide, the engineering recipe for which was given in Ref. [43].

As a complete system, the number of photon pairs generated or available for applications is a key figure of merit. The brightness of the source is presented differently in various works, and care must be taken to fully understand the particular claim being made. Several works infer a “pair generation rate” from their results as a measure of the brightness of their source. Some works, on the other hand, report the number of photons in either arm—the “singles count rate”—to characterize their source. Another value that is common for characterizing the source brightness is the “coincidence count rate,” indicating the whole system performance. While most works fiber couple the generated photons, some emphasize the “fiber coupled rate” as a measure of brightness to indicate that the photons are captured and available for transmission. Therefore, although reported rates are typically stated for a certain pump power (mW), time (s), and bandwidth (Hz), they are often not directly comparable. In all works that state the pair generation rate or fiber coupled rate, the value given is inferred (corrected for losses and/or normalized for power, time, and bandwidth) from values measured later in the system. In the works that state either the singles count or coincidence count rates, the data may be reported as directly measured, corrected for losses (such as detector or coupling losses), and/or normalized from measured results (such as with different integration times, pump powers, or bandwidths used in the measurements). Regardless of the definition of brightness in sources, the effect of a cavity in enhancing the number of photon pairs generated and measured is clear. In SPDC without a cavity, the brightness has been very low (≪0.1 pairs [s mW MHz]⁻¹ pair generation rate before any filtering) [3, 44]. Even early implementations of cavity-enhanced SPDC saw significant improvements over single-pass implementations, and more recent implementations have achieved brightness levels that are viable for quantum applications.

In many quantum applications, single spectral-mode output is desirable. This can be achieved by postfiltering of the output resonant modes from many modes to a single mode [11, 22, 25, 34, 35, 42, 45, 46] or by taking advantage of a beating effect, in which signal and idler waves with different round-trip times are simultaneously resonant only in certain sets of modes called clusters [47]. Nondegenerate sources naturally have different round-trip times to achieve clustering [23, 24, 27, 32, 38, 41, 42], while degenerate sources have used fine tuning of the crystal angle [27] or additional birefringent elements [48] in the cavity to achieve clustering.

Table 2 lists the output characteristics of several experimental implementations of cavity-enhanced SPDC using a bulk or waveguide nonlinear crystal. The material, length, and conversion wavelengths of the nonlinear crystal are also shown. The pair generation, fiber coupled, singles count, or coincidence count rates are listed in the table according to how they are reported in the published work, and the reader is referred to these publications for more details on the extent of correction and inferences for the stated values. The sources that report a single-mode implementation are also indicated as SM in the δν_mode column. Note that although the complete system may emit a single mode, the cavity itself retains a free spectral range between cavity modes. Some alternative SPDC cavity configurations are not included in this table, such as microcavities [49] or Bragg-grating cavities [50].

Table 2.

A sample of experimental implementations of cavity-enhanced SPDC.

Year: Author(s) [Ref.]	δvmode (MHz)	Δvfsr (GHz)	DRO / SRO	Material / length (mm)	Conversion: λP/λS /λI (nm)	Pairs generated / singles counts / coincidence counts / pairs fiber coupled per specified bandwidth (Hz) at a specified pump power (mW):
1999: Ou and Lu [11]	44 (SM)	16	DRO	KNbO3/4	427/855/855	Measured singles counts of 1.2 × 106 s−1 in the peak mode (44 MHz) at 1 mW pump.
2002: Kuklewicz et al. [19]	30	5.6	SRO	KTiOPO4 (KTP)/10	532/1064/1064	Inferred pair generation of 1.7 × 106 s−1 in all modes in δvPM (320 GHz) at 0.1 mW pump.
	20	5.6	DRO
2004: Wang et al. [31]	18	0.54	DRO	KNbO3/20	430/860/860	Measured coincidences of 2.2 × 104 s−1 in all modes in δvPM (1.6 THz) at 1 mW pump.
2006: Kuklewicz et al. [29]	22	1.21	DRO	KTP/10	397.5/795/795	Inferred coincidences of 0.7 s−1 per megahertz of the peak mode at 1 mW pump.
2007: Neergaard - Nielsen et al. [34]	8 (SM)	0.37	DRO	KTP/10	430/860/860	Inferred pair generation of 2.15 × 105 s−1 in the peak mode (8 MHz) at 1.7 mW pump.
2007: Scholz et al. [20]	62	1.15	SRO	BiBO/20	447.3/894.6/894.6	Inferred pair generation of 1.6 × 104 s−1 in all modes in δvPM (4 THz) at 1 mW pump.
2008: Wolfgramm et al. [30]	7	0.49	DRO	KTP/20	397.5/795/795	Inferred coincidences of 70 s−1 per megahertz of the peak mode at 1 mW pump.
2008: Bao et al. [35]	9.6 (SM)	1.9	DRO	KTP/10	390/780/780	Inferred pair generation of 1.78 × 103 s−1 in the peak mode (9.6 MHz) at 27 mW pump.
2009: Scholz et al. [25]	2.7 (SM)	1.5	DRO	KTP/20	447/894.3/894.3	Measured singles counts of 1 × 103 s−1 in the peak mode (2.7 MHz) at 1 mW pump.
2009: Pomarico et al. [42]	117 (SM)	1.8	DRO	LN/3.6	780/1559.5/ 1561.5	Inferred pair fiber coupling of 17 s−1 per megahertz of the peak mode at 1 mW pump.
2010: Wang et al. [45]	21 (SM)	6	DRO	KTP/10	390/780/780	Inferred coincidences of 5.4 s−1 per megahertz of the peak mode at 1 mW pump.
2012: Chuu et al. [23]	8.3 (SM)	5.5	DRO	KTP/10	532/1063.5/ 1064.9	Inferred pair generation of 1.34 × 104 s−1 per megahertz of the peak mode at 1 mW pump.
2013: Fekete et al. [32]	2 (SM)	0.41	DRO	LN/20	426/606/1436	Inferred coincidences of 11 s−1 per megahertz of the peak mode at 1 mW pump.
2014: Monteiro et al. [33]	116	30	DRO	LN/1	780/1550/1550	Inferred coincidence of 134 s−1 per megahertz of the peak mode at 1 mW pump.
2014: Zhou et al. [28]	8	0.95	DRO	KTP/10	780/1550/1550	Inferred pair generation of 134 s−1 per megahertz of the peak mode at 1 mW pump.
2015: Leonard et al. [22]	7.2 (SM)	0.94	SRO	LiTaO3/30	352/854/1411	Inferred pair generation of 2.5 × 106 s−1 in the peak mode (7.2 MHz) at 300 mW pump.
2015: Slattery et al. [21]	48	4.5	SRO	LN/6	532/894.6/1312	Measured coincidence of 5 s−1 per megahertz of the peak mode at 1 mW pump.
2015: Luo et al. [41]	66 (SM)	5.3	DRO	LN/12.3	532/890/1320	Inferred pair generation of 3 × 104 s−1 per megahertz of the peak mode at 1 mW pump.
2016: Ahlrichs and Benson [27]	100 (SM)	2.5	DRO	KTP/20	447/894/894	Measured coincidences of 1.1 × 103 s−1 in the peak mode (100 MHz) at 1 mW pump.
2016: Tian et al. [46]	15 (SM)	1.5	DRO	KTP/10	397.5/795/795	Measured coincidences of 1.43 × 103 s−1 in the peak mode (15 MHz) at 32 mW pump.
2016: Reilander et al. [38]	3 (SM)	0.42	DRO	LN/20	426/606/1436	Inferred pair generation of 2.2 × 103 s−1 in the peak mode (3 MHz) at 1 mW pump.
2017: Rambach et al. [26, 51, 52]	0.43	0.12	DRO	KTP/25	397.5/795/795	Inferred coincidences of 4.4 × 103 s−1 per megahertz of the peak mode at 1 mW pump.
2017: Arenskotter et al. [36]	10 (SM)	—	DRO	KTP	427/854/854	Inferred pair fiber coupling of 9 × 104 s−1 in the peak mode (10 MHz) at 1 mW pump.
2018: Akat’ev et al. [39]	73	1.2	SRO	LN/20	532/867/1377	Inferred pair generation of 4 × 105 s−1 in all modes in δvPM (250 GHz) at 1 mW pump.
2018: Tsai and Chen [24]	6.7 (SM)	8	DRO	KTP/10	407/852/780	Inferred pair generation of 1.06 × 105 s−1 per megahertz of the peak mode at 1 mW pump.
2018: Moqanaki et al. [48]	10.9	1.57	DRO	KTP/30	426/852/852	Inferred pair generation of 4.7 × 104 s−1 in the peak mode (10.9 MHz) at 10 mW pump.
2018: Niizeki et al. [40]	2.4	0.53	DRO	LN/10	757/1514/1514	Inferred pair generation of 3.94 × 105 s−1 per megahertz of the peak mode at 1 mW pump.

4. Example Experimental Implementation of SRO

We implemented cavity-enhanced SPDC in a symmetrical Fabry-Perot singly resonant cavity with a 6 mm periodically poled lithium niobate (PPLN) crystal placed in the center. The setup, as shown in Fig. 3, is similar to that reported in Ref. [21] but with different cavity characteristics resulting in a narrower but slightly less bright source. The crystal was designed to convert a pump photon at 532 nm to a signal photon at 894.6 nm, corresponding to the cesium atom suitable for quantum memory, and an idler photon at 1312 nm, suitable for longer-distance fiber transmission. In this way, the source can act as an interface between quantum memory frequencies and telecommunications frequencies. The mirrors are coated to reflect only the signal wavelength, and the pump and idler wavelengths are transmitted on the first pass. The setup consists of three sections, including the atomic reference locking of the cavity, the cavity-narrowed SPDC, and the filtering and detection of the SPDC-generated photons from a small number of resonating modes.

Fig. 3.

Experimental setup, where LD: laser diode with wavelength indicated in subscript; PC: polarization controller for optimizing 532 nm pump into crystal; DBS: dichroic beamsplitter; M_ip/op: cavity input/output mirrors; SPDC: crystal for spontaneous parametric down-conversion of 532 nm to 1310 nm and 895 nm single photons; Lens: lenses for focusing pump and reference beams into center of crystal and cavity and for collimating output alter cavity; PDH: Pound–Drever–Hall module for stabilization of the reference beam and the cavity; Piezo: high-speed piezoelectric motor connected to one cavity mirror; VBG: volume Bragg grating for narrow band-pass filtering of 895 nm; Chopper: mechanical chopper for protecting single-photon detectors from strong reference beam; Up-Conversion: sum-frequency-generation (SFG) of 1310 nm photons to 710 nm photons with 1550 nm pump (not shown) and for narrow band-pass filtering of 1310 nm; Si-APD: silicon avalanche photodiode; TCSPC: time-correlated single-photon counter.

4.1. Cavity Finesse, Free Spectral Range, and Modal Linewidth

The Fabre-Perot cavity configuration is shown in Fig. 2. It consists of two concave mirrors, each with a radius of curvature of R_ip = R_op = 25 mm, separated by a physical distance of d_phy ≈ 49 mm [8]. A PPLN crystal of length L_cry = 6 mm is placed in the center of the cavity, and its ends are antireflection coated for the signal, idler, and pump wavelengths. The refractive indices for the signal and idler wavelengths in PPLN are n_S ≈ 2.166 and n_I ≈ 2.145, respectively. The transmission for the input and output mirrors is t_ip ≈ 0.5 % and t_op ≈ 5 %, respectively, for the resonating signal wavelength of 895 nm. The transmission is > 99.9 % in both mirrors for the pump and idler wavelengths. The internal losses of the cavity at the resonating signal wavelength are measured to be approximately 0.5 % per transmission through the crystal due to reflection and absorption in the crystal and scattering inside the cavity, so the total internal round-trip loss, 2α_int, is approximately 1 %. An estimate for the finesse is $F_{est}\approx \frac{2\pi }{t_{ip}+t_{op}+2{\alpha }_{int}}\approx \frac{2\pi }{0.065}\approx 97$. This estimate for the finesse does not account for other losses from the cavity, and the final measured finesse is lower. In addition to the transmission at the mirrors and the internal losses, other factors can reduce the finesse, including beam misalignment and cavity instability.

Having the nonlinear crystal in the optical path increases the round-trip time, T_rt, of the light in the cavity due to the higher refractive index of the crystal at the resonating wavelength. The refractive index of the crystal at the resonating signal wavelength (895 nm) is n_S ≈ 2.166. The round-trip time, $T_{RT}=\frac{\tilde{n}{L}_{RT}}{c_0}=\frac{n_{air}\ast 2\left(d_{phy}-L_{cry}\right)+n_S\ast 2L_{cry}}{c_0}$, is 0.38 ns, and the corresponding FSR of the cavity modes, $\Delta v_{fsr}=\frac{\Delta {\omega }_{fsr}}{2\pi }=\frac{1}{T_{rt}}$ [from Eq. (4)], is 2.6 GHz, while the estimated modal linewidth, $\delta V_{\mathit{\text{mode}}}=\frac{\Delta v_{fsr}}{F_{est}}$ [from Eq. (5)], is 27 MHz. The temporal width of the peaks, ${\tau }_o=\frac{L_{cry}}{c_0}\left(n_I-n_S\right)$, is 0.42 ps.

4.2. Geometry of Cavity and Stability Consideration

Inside the cavity, the resonating beam is repeatedly focused into the center of the crystal. The presence of the crystal affects the geometrical conditions for the focusing beams. With no crystal in the air-based cavity, the refractive index of the beam’s path is uniform and equal to 1, n = 1. A focusing beam achieves its narrowest waist, w₀, at the mirror’s effective focal distance, f_n=1. With a crystal (n > 1) in the beam’s path, the focusing light is diffracted so as to extend the physical focal distance, f_phy, of the beam further into the crystal. The effective distance is related to the physical distance by $d_{n=1}=d_{phy}-L_{cry}+\frac{L_{cry}}{n_{cry}}$.

For calculations relating to the cavity stability conditions and the focusing beam parameters, the effective distances (d_n=1) are used. For a focusing (curved) mirror, the effective focal length is half the mirror radius of curvature $f_{M_{n=1}}=\frac{R_M}{2}\to R_M=2f_{M_{n=1}}$. The minimum waist, w₀, located in the center of the cavity is given by $w_{\text{0}}=\sqrt[4]{\frac{\frac{d_{n=1}}{R_M}\left(1-\frac{d_{n=1}}{R_M}\right)\left(2-\frac{d_{n=1}}{R_M}\right){\text{w}}_{CF}}{1-\frac{d_{n=1}}{R_M}}}$, where $w_{CF}=\sqrt{\frac{\lambda R_M}{2\pi }}$ is the focused beam waist radius in a confocal symmetric $\left(d_{n=1}^{CF}=R_M\right)$ configuration [53]. The w_CF radius corresponds to the largest waist radius in the cavity stability region. A symmetrical (R_M = R_ip = R_op) Fabry-Perot cavity is stable while the condition 0 < d_n=1 < 2 R_M is satisfied. The mirror separation corresponding to a concentric symmetric cavity $\left(d_{n=1}^{CS}=2R_M\right)$ therefore gives the maximum mirror separation for a stable cavity. A stability polynomial, U, is a unitless parameter that is used to quantify the stability region of the cavity. The cavity remains stable while 0 < U < 1, where $U=1-2\frac{d_{n=1}}{R_M}+{\left(\frac{d_{n=1}}{R_M}\right)}^2$ [53]. Figure 4a shows the stability curves for symmetric cavities with mirrors R_M =25 mm, giving $d_{n=1}^{CS}=50$ mm. In our setup, the effective mirror separation is set to be slightly less than the concentric symmetric configuration in order to remain inside the stability region of the cavity (d_n=1 ≈ 46 mm as highlighted in Fig. 4a). This effective separation corresponds to the physical separation of d_phy ≈ 49 mm. The resulting minimum cavity waist radius, w₀, within the stability region as a function of the mirror separation is w₀ ≈ 45 μm as graphed in Fig. 4b. This is larger than the pump waist radius (according to [54]) for optimal interaction inside a bulk crystal, which is given by ${\text{w}}_{p_0}=\sqrt{\frac{L_{cry}{\lambda }_p}{2\pi \times 2.84}}$ where λ_p is the pump wavelength, and L_cry is the length of the nonlinear crystal. Therefore, a 532 nm pump waist radius of approximately $w_{p_0}=13$ μm provides an optimal interaction inside the 6 mm crystal. It is clear from Fig. 4b that the optimal pump waist radius would leave the cavity very close to the edge of the stability region (as indicated by the orange star in the figure). Although desirable, this is not a critical requirement, and therefore an experimental waist radius of slightly under 50 μm was chosen to satisfy the stability conditions rather than the optimal pump conditions. Additionally, the abundance of pump power available allows for some flexibility regarding optimal interaction efficiency.

Fig. 4.

(a) Stability parameter for the R_ip,op = 25 mm cavity as a function of the effective distance, showing stable region (solid line), unstable region (dashed line), and target distance (highlighted). (b) Radius of the focused beam waist for the R_ip,op = 25 mm cavity as a function of the effective distance between the mirrors. Since the optimal pump waist radius (w₀ = 13 μm, indicated by the orange star) for a 6 mm crystal (without consideration for the cavity) is close to the unstable region of the cavity, the actual experimental waist radius is larger (at just under 50 μm, indicated by a bold line). The inset shows the focused beam profile for the external cavity locking laser beam near 895 nm (empty black squares) and the SPDC pump beam at 532 nm (empty gray circles) as a function of distance from the focused point.

4.3. Atomic Reference and Cavity Locking

For quantum memory applications, the generated SPDC signal should be compatible with an atomic transition, both in terms of the frequency and the linewidth. In our case, the target atomic transition is a Doppler-free hyperfine line of the cesium atom. This is achieved in two steps. First, a tunable reference laser is locked to the target transition line, and second, the cavity length is locked to the optimal transmission of the reference laser through the cavity. In both steps, we use the Pound–Drever–Hall (PDH) technique to implement the lock [55].

Referring to Fig. 3, the reference laser, a distributed feedback (DFB) laser (Toptica Photonics: DL-100 pro¹) at 895 nm, is externally modulated at 5 MHz by a PDH module (Toptica Photonics: PDD). The 5 MHz modulation is set by the PDH module to operate the specific modulator at the laser head. Approximately 5 % of the power is syphoned to a vacuum compact absorption saturation spectroscopy cell (CoSy) filled with cesium gas (Toptica Photonics: CoSy:895). The remaining power is sent to the cavity. As the beam passes through the cesium cell, its frequency is scanned across the absorption lines (inset of Fig. 5a). After isolation of the target hyperfine transition (Fig. 5a, solid black line), the absorption signal is then fed back into the PDH module, where it is decoupled from the 5 MHz modulation to generate an error signal identifying the peak of the absorption signal line (Fig. 5a, solid gray line). The error signal is then sent to a proportional-integral-differential (PID) controller (Toptica Photonics: Digilock), where it generates a locking signal for the laser current controller. Figure 5b shows the reference laser locked to the peak absorption from the transition and the continuously correcting current control. The reference laser lock is stable for several hours.

Fig. 5.

(a) The targeted hyperfine absorption line (inverted, solid black, left axis) in the cesium atom and the error signal (solid blue, right axis) showing a peak at approximately 0.85 V. Inset: Doppler-broadening-free cesium D1 line with an arrow pointing to the hyperfine peak used for locking. (b) Locked laser at the hyperfine peak (solid black, left axis) at approximately 0.85 V and control signal (solid blue, right axis). Note: The oscillation of the control and error signals is due to aliasing between the oscilloscope sampling rate and the 5 MHz modulation signal from the PDD module.

Once the laser has been locked to the desired atomic transition, the cavity can be locked to the laser. The cavity length, controlled by a high-speed piezoelectric motor, is the scanning mechanism, and the peak transmission of the reference laser through the cavity is the mode to which the cavity length is locked. The reference laser is periodically blocked by a mechanical chopper to protect the sensitive single-photon detectors. The spokes on the chopper disk are aligned so that when the reference laser is transmitted through the cavity for locking, its strong signal is blocked from passing back through the chopper to the detectors. While the reference beam is blocked by a spoke from entering the cavity, the SPDC-generated photons are permitted back through the chopper between spokes to the single-photon detectors.

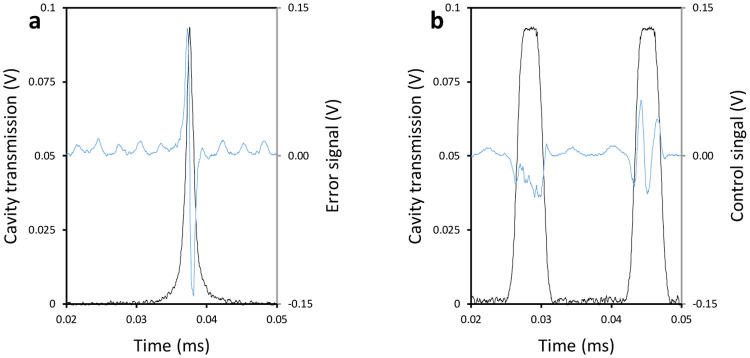
After focusing, alignment, and transmission through the cavity, 10 % of the reference beam is syphoned to a high-speed photodiode detector (Newport: 1601FS-AC). The electrical signal from the detector (including the modulation at 5 MHz) is sent to the PDH module to decouple the 5 MHz modulation and to generate an error signal identifying the peak of the transmission through the cavity. Figure 6a shows a single transmission peak and the corresponding error signal identifying the transmission peak. A second PID controller module processes the error signal and generates a control signal for a piezo amplifier (Physik Instrumente: E-505). Figure 6b shows the locked and chopped output corresponding to the peak transmission through the cavity and the continuously correcting control signal.

Fig. 6.

(a) Cavity transmission mode (solid black, left axis) with a peak at 0.09 V and the error signal (solid blue, right axis). (b) Locked cavity transmission (solid black, left axis) at 0.09 V (when the chopper is open) and piezoelectric motor control signal (solid blue, right axis).

It is important to have the cavity in a stable environment. Several factors need to be considered, including the mechanical stability of the opto-mechanics, as well as the temperature stability of the environment around the cavity and locally at the crystal. For that purpose, high-quality opto-mechanics with low thermal expansion coefficients are used in and around the cavity. The phase-matching temperature of the crystal is maintained to within 3 millikelvin (mK) using a high-quality temperature controller and a custom-built crystal mount. In addition, the area around the cavity is enclosed to prevent air circulation from affecting the temperature near the opto-mechanical components or the nonlinear crystal.

4.4. Measurement and Results

The pump and reference locking beam are combined using a dichroic beamsplitter and directed into the cavity through an achromatic lens. The SPDC pump power is set to 0.5 mW, measured at the entrance to the cavity. It remains close to 0.5 mW after exiting the cavity. A pinhole aperture is placed inside the cavity to help achieve co-alignment of the pump and reference locking beams. The 532 nm pump is focused onto the center of the crystal to generate an 894.6 nm signal and a 1312 nm idler.

After exiting the cavity, the generated signal and idler photons are transmitted back through the chopper and separated using a dichroic beamsplitter. The signal photons are filtered by a volume Bragg grating (VBG), the bandwidth of which is δν_VBG ≈ 37 GHz, and detected using a silicon avalanche photodiode (Si-APD). The idler photons are filtered and detected by an up-conversion detector based on sum-frequency-generation (SFG) with a bandwidth of δν_SFG ≈ 43 GHz [56]. This filtering reduces the number of modes to approximately 14 signal modes and 16 idler modes. Finally, the signal and idler detection events are sent to the time-correlated single-photon counter (TCSPC) for $G_{S,I}^{(2)}(\tau )$ coincidence measurement.

The coincidence counts are measured over an integration time of 300 s while the chopper is open to SPDC photons passing through, with the result shown in Fig. 7. The graph is fitted to the exponential decay $\left(G_{S,I}^{(2)}(\tau )\propto e^{-{\alpha }_{cav}t}=e^{-2\pi \delta v_{\mathit{\text{mode}}}\Delta \tau }\right)$, indicating a linewidth of δν_mode ≈ 28 MHz. This is close to the estimated value given earlier. Based on this measurement, the actual cavity finesse is approximately F ≈ 92. The temporal resolution of the detectors used, τ_det, is about 400 ps, which is far larger than the intrinsic temporal width |τ_o| of the $G_{S,I}^{(2)}(\tau )$ function peaks. Therefore, for shorter cavities in which the round-trip time is less than the detector resolution, these peaks will overlap, and the $G_{S,I}^{(2)}(\tau )$ profile will be measured as a continuous exponential decay.

Fig. 7.

(a) Coincidence counts during 300 seconds between signal and idler (through 37 GHz and 43 GHz filters, respectively) photons generated in the 6 mm PPLN crystal inside the cavity as a function of the signal and idler delay (orange). The ring-down is fitted (black) to an exponential decay $\left(e^{-2\pi \delta v_{\mathit{\text{mode}}}\Delta T}\right)$ with δν_mode ≈ 28 MHz. (b) Same data applied to an illustration showing the peaked structure if the peaks were temporally resolvable by the detector. The data are normalized, i.e., corrected for accidental coincidences and adjusted to have the first maxima at a zero delay. For the purpose of plotting, the illustration shows the temporally wider peaks than the actual width |τ_o| of 0.42 ps, separated by the round-trip time, T_rt, of 0.38 ns.

Following the cavity, the filtering reduces the number of detected modes from 384 (within the SPDC phase-matched bandwidth) to 16 (idler) and 14 (signal) modes. When the cavity is aligned to the fundamental spectral mode, the total detected count rates following the cavity are similar to the single-pass case through the same filters. For 1 mW of pump power, the single count rates through the filters without correcting for system losses were S_I = 2.5 × 10⁴ s⁻¹ idler photons and S_S = 2.6 × 10⁴ s⁻¹ signal photons. The number of coincidence events per second after subtracting accidental coincidences was approximately 1.8 × 10³ s⁻¹. Since there are 14 signal modes (each 28 MHz in width), the measured coincidence count rate is given by $R_{cc}=\frac{1.8\times {10}^3{(smW)}^{-1}}{14\times 28MHz}\approx 4.5{(\text{s}\text{mW}\text{MHz})}^{-1}$. This is brighter by a factor of approximately 90 over the same linewidth from the single-pass case, i.e., $R_{CC}^{PM}\approx 5\times {10}^{-2}{(\text{s}\text{mW}\text{MHz})}^{-1}$, which corresponds closely to the finesse of the cavity, as expected.

5. Conclusion

Cavity-enhanced SPDC has become a mature technique that can be used to achieve bright narrow linewidth modes of correlated and entangled photon pairs suitable for quantum memory applications. In this review, we provided an overview of the principles and a summary of the key spectral equations in both the singly and doubly resonant configurations. We presented a review of several experimental implementations, highlighting the key results and features of each implementation. We also described a more detailed example of the implementation of a singly resonant configuration, bringing attention to the geometrical and stability considerations.