Training set coherence and set size effects on concept generalization and recognition

Abstract

Building conceptual knowledge that generalizes to novel situations is a key function of human memory. Category-learning paradigms have long been used to understand the mechanisms of knowledge generalization. In the present study, we tested the conditions that promote formation of new concepts. Participants underwent one of six training conditions that differed in the number of examples per category (set size) and their relative similarity to the category average (set coherence). Performance metrics included rates of category learning, ability to generalize categories to new items of varying similarity to prototypes, and recognition memory for individual examples. In categorization, high set coherence led to faster learning and better generalization, while set size had little effect. Recognition did not differ reliably among conditions. We also tested the nature of memory representations used for categorization and recognition decisions using quantitative prototype and exemplar models fit to behavioral responses. Prototype models posit abstract category representations based on the category’s central tendency, whereas exemplar models posit that categories are represented by individual category members. Prototype strategy use during categorization increased with increasing set coherence, suggesting that coherent training sets facilitate extraction of commonalities within a category. We conclude that learning from a coherent set of examples is an efficient means of forming abstract knowledge that generalizes broadly.

Concept learning is a cognitive process in which individuals organize related pieces of information in memory by linking them to a shared label. Forming concept representations has been shown to broadly affect cognitive processing, including affecting perception of related information (Van Gulick & Gauthier, 2014), facilitating new learning (Murphy & Allopenna, 1994), and allowing for rapid decision-making (Koriat & Sorka, 2015; Rips, Shoben, & Smith, 1973). Further, category knowledge can affect processing across a variety of domains ranging from visual perception (Bornstein & Korda, 1984), to speech processing (Liberman, Harris, Hoffman, & Griffith, 1957), emotion recognition (Etcoff & Magee, 1992), and social biases (E. R. Smith & Zarate, 2011). One hallmark of category knowledge is the ability to classify never-before-seen examples – generalizing acquired knowledge to novel situations. While psychologists have long sought to understand the role of generalized knowledge in cognition (Bartlett, 1932), there are still open questions about what types of learning experiences best promote generalization and how generalization relates to memory for individual items.

A key finding from early studies of category learning was that subjects were better able to generalize when there was high variability among the training items compared to when training items were relatively coherent (Homa & Vosburgh, 1976; Posner & Keele, 1968). The benefit of training on sets in which individual items were atypical of the overall category was particularly apparent for generalization to items at the category boundary. These results suggested that exposing individuals to training sets with high variability among examples led to a greater understanding of the breadth of the category structure, making category knowledge robust and highly transferable. These studies, however, trained subjects to a performance criterion, such as a certain proportion correct on training exemplars. Because subjects trained on variable as opposed to coherent sets took significantly longer to reach such a criterion, the effect of training set coherence was confounded with the amount of training received (Hintzman, 1986). Others who equated the amount of training found quicker learning and better generalization following training on coherent sets of examples (Hintzman, 1984; Homa & Cultice, 1984; Peterson, Meagher, Herschel, & Gillie, 1973), although not always for items furthest from the category center (Peterson et al., 1973). Thus, training on coherent sets may be more efficient than training with variable examples in terms of the amount of training needed to achieve good generalization performance. However, training on coherent sets may make it more challenging to classify new items near category boundaries.

It is also possible that the coherence of training examples affects the nature of the representations underlying category knowledge, regardless of the effects on accuracy. There has been a long-standing debate about how categories are represented and the type of information accessed to make generalization judgments. Exemplar models posit that categories are represented by individual category members that have been encountered in the past, and that generalization involves classifying new items to the category with the greatest similarity to specific items stored in memory (Kruschke, 1992; Lamberts, 1994; Medin & Schaffer, 1978; Nosofsky, 1988; see Figure 1A for conceptual illustration). In contrast, prototype models posit that abstract category representations exist instead of (or in addition to) representations of individual items. These models propose that categories are represented by the central tendency across individual category members – an idealized category prototype that contains all the most typical features of category members (Homa & Little, 1985; Minda & Smith, 2002; Posner & Keele, 1968; Figure 1A for conceptual model illustration). Generalization involves comparison of new items to relevant category prototypes, with the new item assigned to the category with the most similar prototype (Hampton, 1995; Reed, 1972; Rosch & Mervis, 1975).

Figure 1.

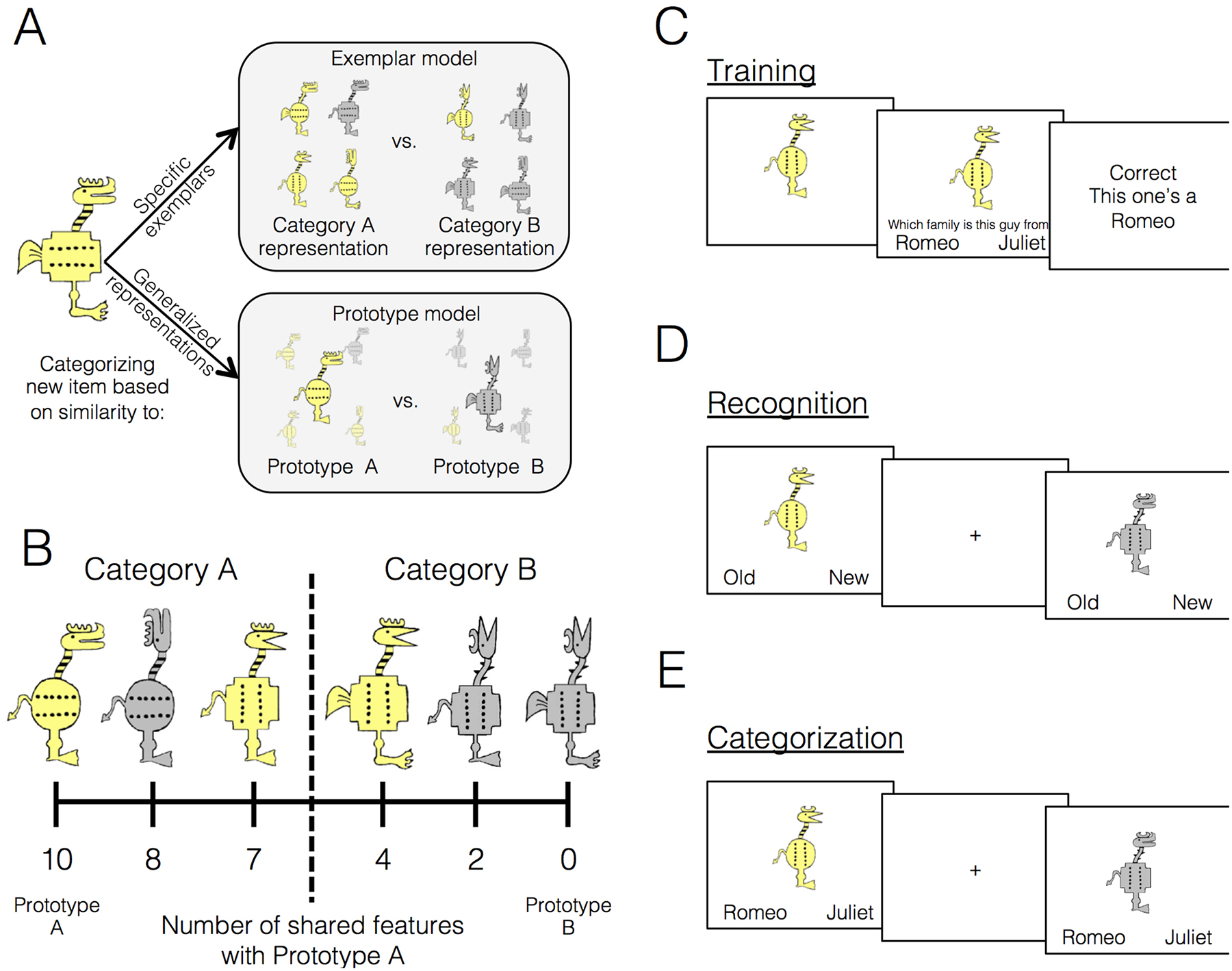
Category-learning task. A. Category representations and generalization to new items under the assumptions of the exemplar and prototype models. Exemplar: categories are represented as individual exemplars. New items are classified into the category with the most similar exemplars. Prototype: categories are represented by their central tendencies (prototypes). New items are classified into the category with the most similar prototype. B. Example stimuli. The leftmost stimulus is the prototype of category A and the rightmost stimulus is the prototype of category B, which shares no features with prototype A. Members of category A share more features with prototype A than prototype B and vice versa for members of category B. Stimulus coherence is computed by dividing the number of prototypical features by the total features (10) to compute the percentage of typical features. C. Participants underwent feedback-based training with one of six possible training sets that varied the size of the training set and the coherence of the examples. D. In recognition, participants were shown training (old) items and never seen category members and made old/new judgments. E. In categorization, participants were shown training (old) items and never seen category members and made categorization judgments without feedback.

Both classes of models often account for behavioral categorization responses well (exemplar meta-analysis: Nosofsky, 1988; prototype meta-analysis: J. D. Smith & Minda, 2000). Recent work has also identified brain regions whose signal tracks predictors generated from the exemplar model (Mack, Preston, & Love, 2013) and distinct regions tracking prototype model predictors (Bowman & Zeithamova, 2018). One possibility is that strong empirical support for each of these models emerges because individuals are capable of forming both types of representations under some circumstances (Medin, Altom, & Murphy, 1984). For example, training on more variable sets may promote formation of exemplar representations because category members are relatively distinct from one another, and distinctiveness often facilitates encoding of individual items (Konkle, Brady, Alvarez, & Oliva, 2010; Vokey & Read, 1992; Winograd, 1981). In contrast, the greater overlap between items within a category for coherent sets may promote extraction of common features (Hampton, 1979; Rosch & Mervis, 1975), leading to greater reliance on prototype representations.

In addition to training set coherence, there is also some evidence across past studies that the number of training examples affects the relative fit of prototype versus exemplar models. Studies finding support for the exemplar model have frequently trained participants to discriminate between categories using a small number of category examples (Blair & Homa, 2003; Lamberts, 1994; Medin & Schaffer, 1978; Palmeri & Nosofsky, 1995), whereas studies finding support for prototype models tend to use larger training sets (Homa, Sterling, & Trepel, 1981; Minda & Smith, 2001). This difference in representations may arise because encoding individual examples becomes more difficult as their number increases (Murdock, 1962), whereas the number of individual items may have less of an impact on prototype extraction.

One goal of the current study was to resolve conflicting claims regarding the benefits of coherence vs. variability of input on concept learning (Hintzman, 1984; Homa & Cultice, 1984; Homa & Vosburgh, 1976; Peterson et al., 1973; Posner & Keele, 1968). We predicted that training on more coherent training sets would facilitate extraction of abstract prototype information, leading to fast learning and better generalization. Demonstrating that coherence of category exemplars impacts the nature of the concept representation formed would also help resolve conflicting neuroimaging findings regarding the nature of concept representations in the brain (Bowman & Zeithamova, 2018; Mack et al., 2013). Second, small categories may be well suited to exemplar representations, but reliance on prototype representations may increase with larger set sizes because prototypes can economically represent categories when the number of items to individually encode becomes large (Minda & Smith, 2001). Thus, we hypothesized that prototype reliance may increase with larger set sizes. To test these hypotheses, participants were trained to discriminate between two categories using study sets varying in the coherence and the number of category examples. We then compared groups trained on different sets in terms of ease of learning (training accuracy), generalization success for new items, and the types of representations (exemplar, prototype) underlying generalization judgments.

The ability to remember specific details and the ability to generalize across experiences are typically studied in distinct lines of research. However, testing item memory for the same stimuli and in the same participants as categorization can provide new insights that can inform current theories of adaptive memory function. First, different generalization models make distinct predictions about the relationship between item memory and memory generalization. Exemplar accounts posit that both types of decisions are based on a single representation, making the prediction that the ability to recognize items and categorize them should be linked (Hintzman, 1984; Nosofsky, 1988). Theories that posit the existence of multiple memory representations differ in how they conceptualize the interactions between memory systems. Some assume that representations compete, leading to trade-off between memory for individual experiences and the ability to generalize (Poldrack & Packard, 2003; Zeithamova, Schlichting, & Preston, 2012). Alternatively, specific and generalized representations may be relatively independent of one another, with abstract representations forming alongside item specific ones (Brunec et al., 2018; Collin, Milivojevic, & Doeller, 2015; Schlichting, Mumford, & Preston, 2015; Schlichting, Zeithamova, & Preston, 2014). Recent studies have explicitly tested these predictions, but in a different generalization paradigm and with conflicting results (Banino, Koster, Hassabis, & Kumaran, 2016; Carpenter & Schacter, 2017, 2018).

Second, measuring performance and the type of representation relied on for recognition vs. categorization decisions can help us assess representational flexibility. In particular, while categorization decisions can be made successfully based on either exemplar or prototype representations, decisions such as old/new recognition require memory for individual experiences that are not maintained in the prototype representation. As such, stronger evidence of exemplar-based responding may emerge during recognition compared to categorization, which would demonstrate that participants can form multiple types of representations during learning to be flexibly utilized to inform distinct judgments. Thus, a secondary goal of the current study was to address these questions by including an old/new recognition task for training items and novel category examples. This allowed us to test how training category structure affects memory for individual items, how recognition relates to generalization, and to what degree participants can flexibly shift between different representations when making recognition as compared to categorization judgments. We hypothesized that less coherent category structures and small training sets would result in better recognition accuracy due to more distinctive encoding of individual items, indicating a trade-off between memory specificity and generalization.

Method

Participants

One hundred and seventy-six participants from the University of Oregon completed the experiment for course credit or monetary compensation. A total of thirteen participants were excluded for failure to complete the entire experiment (2), failing to respond on more than 30% of trials during either categorization or recognition (5), or only using one of the two responses during either the recognition or categorization phase (6), leaving data from 163 participants reported in all analyses (107 female, mean age = 19.34 years, SD age = 2.23 years, age range = 18–34 years). Participants were randomly assigned to one of six experimental conditions that differed in the stimulus set used during training. Condition names reflect the training set size (as exemplars per category) and training set coherence, measured as average exemplar typicality (the percent of features that an exemplar shares with a category prototype, see Materials). Table 1 lists demographic information separated by training condition. The training condition with a set size of 8 and an average of 75% typical features has twice the sample size because there were two versions of this condition (described below). As we found no differences between these versions in terms of rate of learning, final training accuracy, generalization accuracy, or recognition accuracy, we collapsed across them in all analyses. All participants completed written informed consent, and all procedures were approved by the University of Oregon’s Institutional Review Board.

Table 1.

Demographic information separated by training set

Training Set	n (n females)	Mean age (SD age, age range)
5 items: 60% typical	22 (14)	18.82 (1.56, 18–25)
6 items: 67% typical	25 (17)	18.64 (1.08, 18–21)
10 items: 70% typical	23 (16)	20.70 (4.18, 18–34)
7 items: 72% typical	23 (16)	19.30 (2.03, 18–27)
8 items: 75% typical	45 (28)	19.20 (1.14, 18–22)
5 items: 80% typical	25 (16)	19.52 (2.31, 18–28)

Materials

The complete stimulus set is freely available through the Open Science Framework (Bowman & Zeithamova, 2019; https://osf.io/8bph2) Stimuli consisted of cartoon animals that varied along 10 binary dimensions: color (yellow/grey), foot shape (clawed/webbed), leg size (thin/thick), body shape (squared/circular), tail shape (devil tail/feather tail), body dot orientation (vertical/horizontal), neck pattern (stripes/thorns), head shape (with beak/with horn), crown shape (crescent/comb), and head orientation (forward/up). One stimulus was chosen randomly for each subject from a set of four possible prototypes to be the prototype of category A. The stimulus that shared no features with the category A prototype served as the category B prototype. The two possible versions of each feature can be seen across the two prototypes shown on Figure 1B. Physical similarity between all stimuli was defined based on the number of shared features. Category A stimuli were those that shared more features with Prototype A than Prototype B. Category B stimuli were those that shared more features with Prototype B than Prototype A. Stimuli equidistant from the two prototypes were not used in the study. We refer to the percentage of features that an exemplar shares with its category prototype as its typicality (e.g., 8 out of 10 shared features = 80% typical). In contrast to research on natural categories, where the term typicality may refer to subjective typicality ratings, here it is used only as a descriptive term for the proportion of category-consistent features an item has.

Training sets.

Six training sets were created that varied in set size and set coherence. Set size was defined by the number of individual category exemplars from each category presented during training, with sets including 5, 6, 7, 8, or 10 items per category. Set coherence was defined by the average percentage of shared features between training stimuli and their respective prototypes. This meant that in more coherent training sets (compared to lower coherence training sets), there was also greater within-category similarity and smaller between-category similarity of the training items. This difference in training sets did not, however, extend to the category as a whole: the categories from which the training examples were selected were identical across groups, and the structure of the generalization items was the same for all subjects (see recognition and categorization sets below).

All training sets were constrained so that all individual features within a set were equally predictive of category membership. Furthermore, we avoided using the prototypes and items that differed from prototypes by only one feature in the training sets. Items equidistant (sharing 5 features with each prototype) were not used in any phase of the experiment. Thus, training items were limited to those that shared 6, 7 or 8 features with their respective prototypes, and each training item differed from all other training items by at least 2 features. We then aimed to generate as many training sets as possible that would satisfy the constraints on the number of training stimuli, equal predictivity of individual features, and the typicality of the training items included. The 60% typical condition consisted of only 60% typical items, the 80% typical condition consisted of only 80% typical items. All other training sets contained a combination of typicality levels. The average coherence values in the resulting sets were 60%, 67%, 70%, 72%, 75%, and 80% category-typical features. Table 1 lists the generated training sets, including set size and average coherence for each set. Appendix A includes training set structures for all conditions and a description of how these sets were generated. As noted above, we generated two sets with 8 items at 75% average typicality: one with 4 items that shared 8 features with the prototype and 4 items that shared 7 features with the prototype, and one with 6 items that shared 8 features with the prototype and 2 items shared 6 features. They were collapsed into a single condition in all reported analyses because their results did not differ. While our approach allowed us to test a wide variety of training sets, the constraints meant that set size and set coherence were not fully crossed. We thus employed multiple regression approach rather than factorial ANOVA when aiming to separate the effect of training set size and training set coherence on behavior.

Recognition and categorization sets.

In addition to old (training) items that differed based on the initial training condition, categorization and recognition tests included 42 new stimuli had the same structure across all conditions. Category prototypes themselves, which were not included in any training set, were included in both the recognition and categorization testing sets. In addition, there were 5 new test items at each distance from the category A prototype, excluding those equidistant. Stimuli with 6–9 prototypical A features were considered category A members, stimuli with 1–4 prototypical A features (thus 9–6 prototypical B features) were considered category B members. A different set of such stimuli was selected for recognition and generalization, randomly from all possible stimuli. Importantly, although category separability of training items differed across training sets, the category structure of generalization items was the same across all groups.

Procedure

Participants completed the three phases of the experiment in the following order: training, recognition, and categorization. Recognition always preceded categorization to minimize interference during recognition from new exemplars presented during the generalization phase.

In each trial of the feedback-based training (Figure 1C), an individual exemplar was presented on the screen and participants were instructed to decide which of two families (Romeo’s or Juliet’s) it belonged to. Participants were told that they would have to start by guessing, but that it was possible to learn to sort the items accurately over time. Each exemplar was presented for 2.5 seconds before the response options appeared on the screen. When the response options appeared, participants were asked to indicate their response with a keyboard press. Response timing was self-paced following the initial display period. Two seconds following the response, participants were told if their answer was correct or wrong, and to which family the stimulus belonged. Feedback appeared for 1.5 seconds. There were 8 blocks of training, with two repetitions of each exemplar in each block. Exemplars within a block were pseudorandomly ordered so that each was presented once in the first half and once in the second half of a block. For each half block, exemplars were pseudorandomly ordered so that no more than three exemplars from the same category were presented consecutively. This constraint served to reduce the likelihood that some subjects would by randomly assigned to have long blocks of items only from one category whereas other subjects would see the categories more intermixed, a factor that is known to affect category learning (Carvalho & Goldstone, 2014; Kang & Pashler, 2012).

Recognition (Figure 1D) immediately followed training. Individual exemplars were presented and participants judged if that exact exemplar had been presented during training (old) or had not been presented previously in the experiment (new). Each exemplar was presented on the screen for 4 seconds followed by an 8 second fixation period. No feedback was given. Categorization (Figure 1E) immediately followed recognition. Individual exemplars were presented and participants indicated which family they belong to. Each exemplar was presented on the screen for 4 seconds followed by an 8 second fixation period. No feedback was given. There were two blocks of each task, and stimuli were pseudorandomly ordered so that so that there were an equal number of items from each category in each block and that old items were distributed equally across the two blocks. In between individual training, recognition and categorization blocks, participants took self-paced breaks.

Statistical analyses

Of main interest in all phases was the effect of training set. Given the large number of conditions and to limit the number of statistical comparisons, we first evaluated the effect of training condition on behavior using an ANOVA with the training group as a between-subjects factor (6 levels). We followed up any significant effects of training group by computing a multiple regression analysis that included training set size and training set coherence as separate predictors to determine the degree to which the differences among groups were driven by each aspect of training. Most ANOVAs also included a within-subject manipulation relevant for the given phase and analysis (e.g., training block, test item typicality) as a within-subject factor, with Greenhouse-Geisser corrections for violations of the sphericity assumption applied as needed (denoted with ‘GG’). We followed up any significant within-subject effects with t-tests to quantify the strength and direction of differences between conditions. Bonferroni correction for multiple comparisons was applied when multiple independent statistical tests were computed, such as when conducting a separate t-test for each group or following an omnibus ANOVA with multiple pair-wise comparisons. The dependent variables and within-subject factors of interest for each task phase are described as follows.

Training accuracy.

Training accuracy was computed as the proportion of correct classifications for each block of training. Accuracy during the final block of training was compared to chance (proportion correct = 0.5 for two categories) to evaluate whether each training group acquired category knowledge by the end of training. To evaluate whether learning occurred during training and whether training set modulated acquisition of category knowledge, we computed a 6 (training group) × 8 (training block) mixed-factor ANOVA.

Categorization accuracy.

Overall accuracy was computed as the proportion of correct classifications. To determine if each group showed above-chance generalization, one-sample t-tests were computed for each group comparing accuracy for new items to theoretical chance (proportion correct = 0.5 for two categories). To test for an overall effect of training group on subsequent generalization to new items at varying levels of typicality, we computed a 6 (training group) × 5 (test item typicality: 6–10 prototypical features) mixed-factors ANOVA with classification accuracy only for new items as the dependent measure. To test whether training group affected subsequent categorization of old (training) items, we also computed a one-way ANOVA comparing categorization accuracy across groups.

Recognition accuracy.

Recognition accuracy was computed as the corrected hit rate [i.e., probability (‘old’ | old item) – probability (‘old’ | new item)]. This measure ensures that participants cannot reach low or high recognition scores simply due to a bias in responding “old” frequently or infrequently, making it a suitable measure for our situation of unbalanced number of old and new items in the test set. To determine if each group showed above-chance recognition performance, one-sample t-tests were computed in each training group comparing to chance = 0 (i.e., no differentiation between old and new items). To test whether training group affected subsequent recognition, we computed a one-way ANOVA comparing the six training groups in terms of their corrected hit rates. We were also interested in whether subjects were more likely to falsely recognize items closer to the prototypes and whether that effect was moderated by training group. We computed a 6 (training group) × 5 (test stimulus typicality: 6–10 prototypical features) mixed-factors ANOVA on the proportion of new items falsely endorsed as ‘old.’

Relationship between recognition and categorization.

To test for a relationship between memory for individual items and the ability to generalize category labels, we computed a multiple regression that included the hit and false alarm rates from recognition as predictors of categorization accuracy for new items. We were primarily interested in whether the false alarm rate was related to category generalization, given theoretical views postulating that false memories and generalization are flip sides of the same coin (Marsh, Cantor, & Brashier, 2015; Roediger et al., 1995; Varga, Gaugler, & Talarico, 2019). However, high false memory rates could be also driven by bias to respond “old”. We thus included both hit rate and false alarm rate in the regression, to ensure that any relationship was specific to the false alarm rate and not only the tendency to respond ‘old.’ We also included training set coherence and size as predictors to account for mean differences between groups.

Prototype and exemplar model fitting.

Prototype and exemplar models were fit to trialby-trial data in individual subjects separately for the recognition and categorization tests. We chose to fit separate parameters for each phase rather than jointly fitting categorization and recognition because we were interested in whether individuals might flexibly use different types of information when making different types of memory judgments. Further, there is evidence that items within a category can become less distinguishable from one another following learning (Goldstone, Lippa, & Shiffrin, 2001). We reasoned that the features that participants paid most attention to during categorization might be particular drivers of this effect and therefore not good candidates for recognition decisions that require subtle discrimination of previously encountered category members vs. not previously encountered category members. We thus allowed the models to return different attention and sensitivity parameters across phases. However, we also tested two alternative parameter fitting approaches for the attention weights: (1) using categorization-derived attention weights in fitting recognition data, and (2) fitting recognition and categorization responses of a given participant jointly. The sensitivity parameter was always allowed to vary between the categorization and recognition phases. All conclusions remain unchanged when using these alternative procedures.

The conceptual representations of the models are depicted in Figure 1A. Prototype models assume that categories are represented by their prototypes (i.e., the combination of typical category features from all training items in each category). Consistent with prior modeling literature (Maddox et al., 2011; Minda & Smith, 2001), similarity of each test stimulus to each prototype was computed, assuming that perceptual similarity is an exponential decay function of physical similarity. Assuming a non-linear mapping between physical and perceptual similarity is supported by prior findings (Shepard, 1957), and allows the prototype and exemplar models to make different predictions (otherwise the distance to the prototype is the same as the average distance to individual stimuli). In addition, we took into account potential differences in attention to individual features. Formally:

$$S_A(x)=\text{exp}\left[-c{\sum }_{i=1}^m{\left(w_i{|x_i-\mathit{\text{prot}}{o}_{Ai}|}^r\right)}^{1/r}\right]$$ (1)

where S_A(x) is the similarity of item x to category A, x_i represents the value of the item x on the i-th dimension of its m binary dimensions (m=10 in our study), proto_A is the prototype of category A, r is the distance metric (fixed at 1 for city-block metric for the binary-dimension stimuli), w is a vector with weights for each of the 10 stimulus features with weight values estimated from the data (fixed to sum to 1), and c is sensitivity (rate at which similarity declines with distance), also estimated from the data and constrained to be between 0–700.

Exemplar models assume that categories are represented by their exemplars, and that summed similarity across category exemplars drives exemplar-based decision-making. Formally (Nosofsky, 1987; Zaki, Nosofsky, Stanton, & Cohen, 2003), similarity of an item x to category A is computed as:

$$S_A(x)={\sum }_{y\in A}\text{exp}\left[-c{\sum }_{i=1}^m{\left(w_i{|x_i-y_i|}^r\right)}^{1/r}\right]$$ (2)

where y represents the individual training stimuli from category A, and the remaining notation and parameters as in Equation 1.

For categorization, for both models, the probability of assigning a stimulus x to category A is equal to the similarity to category A divided by the summed similarity to categories A and B, formally:

$$P(A|x)=\frac{S_A(x)}{S_A(x)+S_B(x)}$$ (3)

For recognition, for each model, similarity values were used to predict whether a participant will label an individual item as old or new by summing across the similarity across both categories (S_A(x) + S_B(x)) to determine an overall familiarity of item x (Nosofsky, 1988). The familiarity for each item is then compared to a threshold (k) that is estimated from the data. The probability of labeling stimulus x as old is equal to its summed similarity to both categories divided by the summed similarity plus the threshold, k (Nosofsky & Zaki, 1998), formally:

$$P(Old|x)=\frac{S_A(x)+S_B(x)}{S_A(x)+S_B(x)+k}$$ (4)

We note that for both categorization and recognition, we also fit a version of the exemplar model that includes an additional parameter, γ, which allows for more or less deterministic responding based on subjective similarity. Including this parameter did not affect the pattern of results.

For each trial, for each test (recognition, categorization) the probability of the participant’s response under the assumptions of each model was computed. An error metric (negative log-likelihood of the whole sequence of responses) was then computed for each model by summing the negative of log-transformed probabilities. This summed value was minimized by adjusting the threshold (for recognition only) and attention weights and sensitivity parameters (for both categorization and recognition) using standard maximum likelihood methods with the “fminsearch” function in MATLAB (Mathworks, Natick, MA). Parameters were optimized separately for each test (recognition/categorization), for each model (prototype/exemplar), and for each participant.

Determining participants’ strategies.

To label participants as exemplar-users or prototype-users, we tested whether the models fit reliably better than a random model and whether one model fit reliably better than the other using Monte Carlo simulations. We found a Monte Carlo approach more suitable than other metrics, such as AIC or BIC, for two reasons. First, we needed to determine whether either model fit better than chance. Penalization for free parameters (such as the attention weights) would be quite severe if using AIC/BIC approaches, given the 10-dimensional stimuli used here. Many participants with above chance accuracy would end up being classified as best fit by a random response model, indicating that such criteria are overly conservative. The second consideration is the choice between the prototype and the exemplar model (when they outperform chance). When two models have the same number of parameters (as the model versions used here), the model with better fit is traditionally considered the winner, no matter how small the difference. But small differences in the fit values may not be meaningful and the assumption that equal model fits can be equated with a fit difference of exactly zero may not be valid. For example, Monte Carlo simulations with randomly shuffled data (that both models should fit comparably poorly) showed that the exemplar model provided on average a slightly better fit to randomly shuffled categorization responses than the prototype model (mean exemplar advantage across subjects, M = 0.05, one-sample t(162) = 4.82, p < 0.001) whereas randomly shuffled recognition response were on average better fit by the prototype model (M = 0.13, one-sample t(162) = 3.50, p < 0.001). Thus, despite the comparable number of free parameters, one model may be slightly more flexible when fit to a specific set of stimuli, and the Monte Carlo approach is better equipped to account for such a bias than a simple fit comparison. However, to ensure that the results were robust with respect to the model selection procedure, we verified that all conclusions remained unchanged if we used AIC instead.

To generate the Monte Carlo null distribution, for each participant for each test, we randomly shuffled the stimuli associated with their series of responses. We chose to shuffle the stimuli in order to maintain the participant’s overall response bias and any temporal dependency between responses from one trial to the next. This procedure was repeated 1,000 times to generate a subject-specific null distribution of model fits for each model and for each test. We then compared the observed prototype and exemplar model fits to this null distribution to determine whether one or both models fit the participant’s data better than chance. This was determined by comparing the actually observed model fit to the null distribution of fits and testing whether the observed model fit appeared by chance with a frequency less than 5% (p < 0.05; one-tailed).

To determine whether one model fit reliably better than the other, we compared the observed difference in model fits to the null distribution of differences in model fits generated by the Monte Carlo simulation. One model was deemed a better fit than the other for a given test for a given participant when that difference score appeared by chance with a frequency less than 25% (75% probability that the model fit differences did not arise by chance, two-tailed test). Using this method, participants were labeled as prototype-users, exemplar-users, or having comparable fit for both strategies (“similar”). We chose this alpha level for labeling participants’ strategies as a compromise between a strict alpha level of 5%, which labeled many subjects as showing similar fits between the two models, and a no-alpha model selection approach, such as when AIC is used to select the winning model based on lower fit error value without addressing whether the fit value difference is reliably above chance. However, to ensure that our results were robust to the alpha level chosen, we verified that all conclusions remained the same with any of these thresholds (AIC metric without assessing difference reliability, Monte Carlo alpha = 5%, Monte Carlo alpha = 25%).

Within each phase (categorization, recognition), we tested whether each aspect of the training sets (coherence, size) affected the proportion of participants best fit by each model using a logistic regression. We also compared whether model fits differed across categorization and recognition, using McNemar’s test for paired nominal data.

Results

Training accuracy

See Figure 2 for training accuracy in each block separated by training group. We first tested whether accuracy in the final block of training was above chance (proportion correct = 0.5 for two categories) for each training group by computing separate one-sample t-tests using a Bonferroni corrected alpha-level of p < 0.0083 to account for the six separate tests. All groups were able to classify at above-chance levels by the end of training (see Table 2 for exact means and t-statistics).

Figure 2.

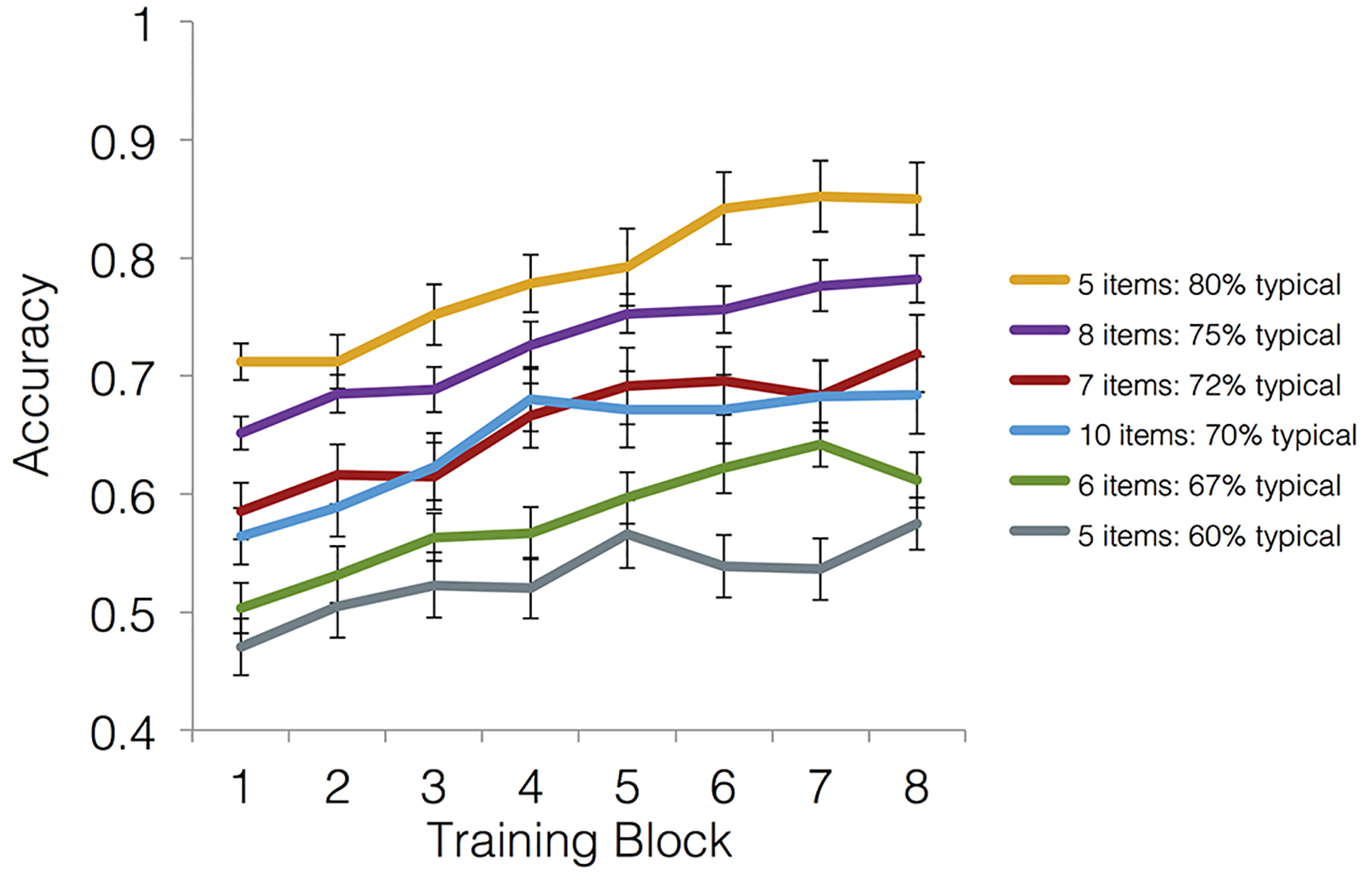
Training accuracy. Mean accuracy from each block of the training separated by training group. In the legend, the number of items corresponds to the set size manipulation and the percentages indicate the average percentage of typical features in the training set, corresponding to the set coherence manipulation. Error bars depict the standard error of the mean.

Table 2.

Accuracy in final training block separated by training set. T-statistics indicate comparison to chance performance.

Training Set	Mean	SD	t-statistic	p-value
5 items: 60% typical	0.58	0.10	3.37	0.002
6 items: 67% typical	0.61	0.12	4.79	<0.001
10 items: 70% typical	0.68	0.16	5.61	<0.001
7 items: 72% typical	0.72	0.11	9.94	<0.001
8 items: 75% typical	0.78	0.14	14.01	<0.001
5 items: 80% typical	0.85	0.15	11.46	<0.001

We tested whether training accuracy differed by training group and across training blocks by computing a training group x training block mixed-factors ANOVA. There was a significant main effect of group [F(5,157) = 30.47, p < 0.001, ${\eta }_p^2=0.49$], indicating that overall training scores differed among groups. There was a significant main effect of training block [F(5.42,850.89) = 34.86, p < 0.001, ${\eta }_p^2=0.18$, GG], indicating learning across time. The group x training block interaction was not significant [F(27.10, 850.89) = 0.73, p = 0.88, ${\eta }_p^2=0.02$, GG], indicating comparable improvement across blocks in all groups (Figure 2). To follow up on the main effect of group and test to what degree training set size and coherence drive group differences, we computed a multiple regression with training set size and coherence as predictors and accuracy in the final training block as the outcome. Training set coherence was a significant positive predictor of final training accuracy [ß = 0.57, t(160) = 8.65, p < 0.001], but the set size predictor was not significant [ß = −0.02, t(160) = −0.31, p = 0.76]. Thus, training on more typical sets led to better learning with no evidence that set size affected learning rates.

Categorization accuracy

Categorization accuracy for each group and for each level of test item typicality is presented in Figure 3. To test whether individuals in each group were able to generalize category knowledge at above-chance levels, we first submitted accuracy on all new items from each training group to one-sample t-tests comparing to theoretical chance (proportion correct = 0.5 for two categories) using a Bonferroni corrected alpha-level of p < 0.0083 to account for the six separate tests. Only the group trained with the least coherent set (5 items: 60% typical) did not generalize at significantly above-chance levels [t(21) = 1.47, p = 0.16, d = 0.31; all other t’s > 6, p’s < 0.001]. In fact, those trained on the least typical items did not even show above-chance classification of the items they were trained on [t(21) = 0.45, p = 0.66, d = 0.10]. This chance-level performance occurred despite this group being significantly above chance by the end of training.

Figure 3.

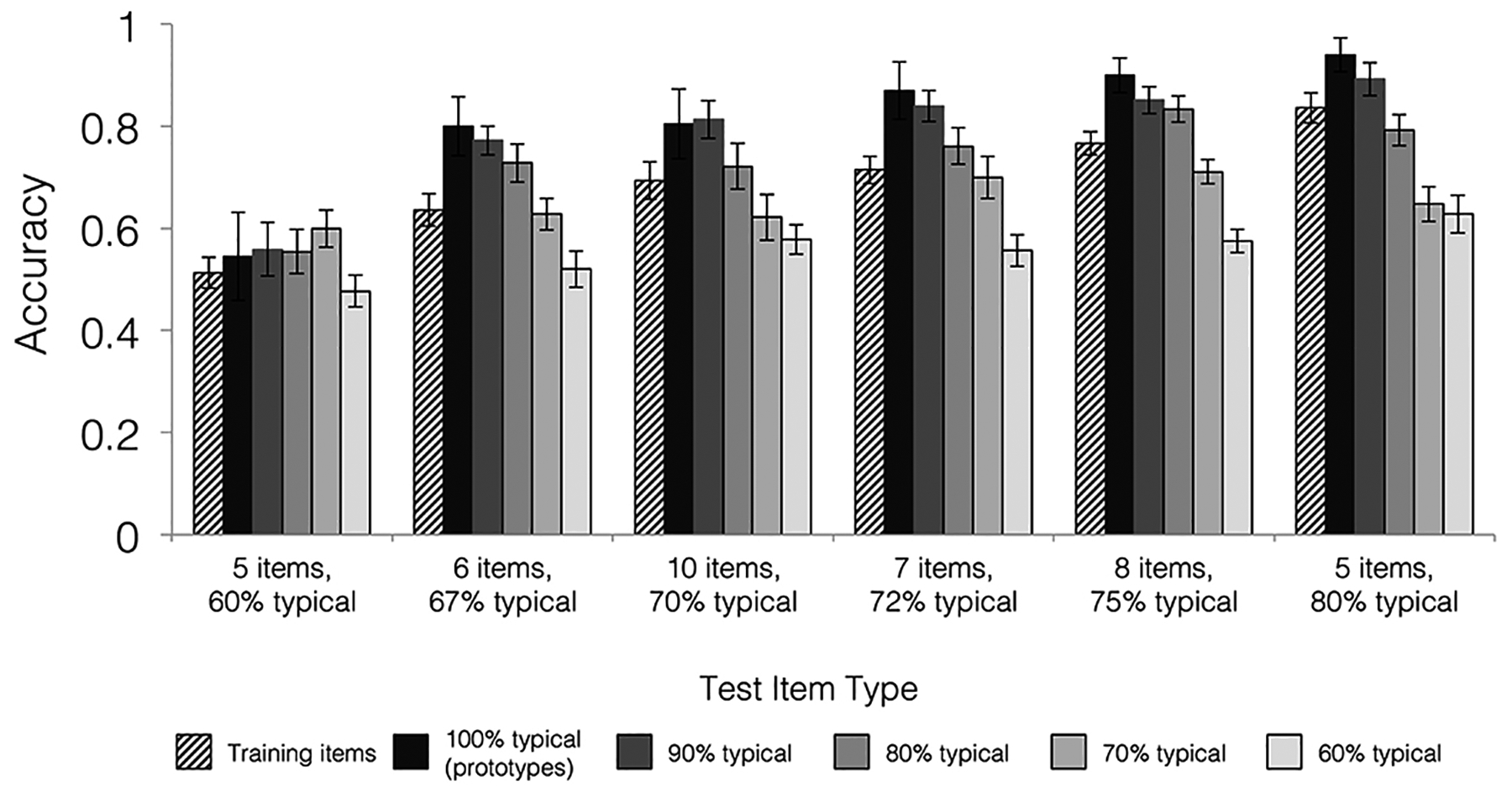
Categorization accuracy for each item type separated by training set. Training sets are organized with increasing coherence from left to right, with specific coherence levels indicated by the percentages on the x-axis. Training set size is indicated on the x-axis by the number of items per category. Accuracies on training (old) items re-presented during the categorization test are depicted with striped bars. Accuracies for new items (common across all groups) varying in their similarity to category prototypes are depicted with solid bars. Accuracies for prototypes are depicted in the darkest bars with increasingly lighter bars for new items sharing fewer features with the prototypes. Error bars depict standard error of the mean.

We next tested whether generalization accuracy differed across training groups. Test item typicality and the group x test item typicality interaction were also included to determine whether generalization to atypical items was especially low or especially high in any group. The 6 (training group) × 5 (test item typicality: 6–10 prototypical features) mixed factors ANOVA revealed a significant main effect of training group [F(5,157) = 10.03, p < 0.001, ${\eta }_p^2=0.24$], a significant main effect of test item typicality [F(3.17,498.21) = 62.26, p < 0.001, ${\eta }_p^2=0.28$, GG], and a significant training group x test item typicality interaction effect [F(15.86,498.21) = 2.41, p = 0.002, ${\eta }_p^2=0.07$, GG]. As apparent on Figure 3, the significant effect of test typicality was driven by a significant linear trend [F(1,157) = 150.16, p < 0.001, ${\eta }_p^2=0.49$], with accuracy increasing from the least typical to the most typical test items.

To follow-up on the significant test typicality by group interaction, we conducted one-way repeated-measured ANOVAs within each training group using a Bonferroni corrected alpha-level of p < 0.0083 to account for the six separate tests. The training group x test item typicality interaction was driven by all groups showing a significant linear effect of test item typicality [all F’s > 22, p’s < 0.001, ${\eta }_p^2’\text{s }>0.28$] except the 5 items: 60% typical group that did not show an effect of test item typicality [F(1,21) = 0.311, p = 0.58, ${\eta }_p^2=0.02$].

Given that the 5 items: 60% typical group performed at chance, we recomputed the mixed effects ANOVA with group and test typicality as factor after excluding this group. This allowed us to evaluate whether overall accuracy and the magnitude of the test item typicality effects differed among groups that did perform above chance. We found an even more pronounced main effect of test typicality [F(3.25, 442.15) = 76.97, p < 0.001, ${\eta }_p^2=0.36$, GG] that was well described as a linear trend [F(1,136) = 192.61, p < 0.001, ${\eta }_p^2=0.59$]. There was also a main effect of group [F(4,136) = 2.78, p = 0.03, ${\eta }_p^2=0.08$]. However, there was no group x test item typicality interaction [F(13.00,442.15) = 0.85, p = 0.61, ${\eta }_p^2=0.02$], indicating a comparable effect of test item typicality among all groups that performed above chance.

To follow up on the main effect of training group, we computed a multiple regression model including training set size and training set coherence as predictors of overall generalization accuracy. Training set coherence was a significant positive predictor of generalization accuracy [ß = 0.44, t(160) = 6.17, p < 0.001], but training set size did not significantly predict generalization [ß = 0.11, t(160) = 1.50, p = 0.14]. Thus, training on typical sets led to better categorization of new items with little effect of training set size. We were interested in whether the effect of training set coherence was consistent across all levels of test item typicality or if more coherent training sets only showed an advantage for test items closest to the prototypes. We repeated the above multiple regression using accuracy for each test item typicality as the dependent variable using a Bonferroni corrected alpha-level of p < 0.01 to account for the five separate tests. Training set coherence positively predicted accuracy at every level of test item typicality (all ß’s > .25, t’s > 3, p’s < 0.002) with the exception of 70% typical items where it did not reach significance [ß = 0.14, t(160) = 1.79, p = 0.075]. The training set size predictor never reached significance (all |ß’s| < .12, t’s < 1.6, p’s > .11). Thus, training on typical items was beneficial not only for generalization to other typical items, but also for generalization to atypical items near the category boundary.

To test whether training group also affected classification accuracy of old (training) items in the categorization test, we computed a one-way ANOVA comparing training groups. There was a significant effect of training group [F(5,157) = 13.41, p < 0.001, ${\eta }_p^2=0.30$] indicating that classification of training (old) examples differed among groups. A follow-up multiple regression that included set size and set coherence as predictors of classification of old items showed again set coherence as a significant positive predictor [ß = 0.54, t(160) = 8.08, p < 0.001], with no effect of set size [ß = 0.03, t(160) = 0.49, p = 0.62].

Recognition accuracy

Corrected hit rate.

Figure 4A depicts corrected hit rates separated by training group. To test whether individuals in each training group were able to discriminate between old and new category examples in a recognition task, we first submitted corrected hit rates [probability (‘old’ | old item) – probability (‘old’ | new item)] to one-sample t-tests comparing to theoretical chance = 0 using a Bonferroni corrected alpha-level of p < 0.0083 to account for the six separate tests. Two groups showed above-chance recognition performance: the 5 items: 60% and 6 items: 67% groups (t’s > 3.7, p’s < 0.002). The 8 items: 75% group showed recognition performance that was above-chance but did not survive correction for multiple comparisons [t(44) =2.38, p = 0.02]. Recognition performance in the other three groups did not differ reliably from chance (all t’s < 2, all p’s > 0.08). Although some groups showed significantly above-chance recognition and others did not, overall recognition rates did not differ significantly across training groups (one-way ANOVA F(5,157) = 1.40, p = 0.23, ${\eta }_p^2=0.04$).

Figure 4.

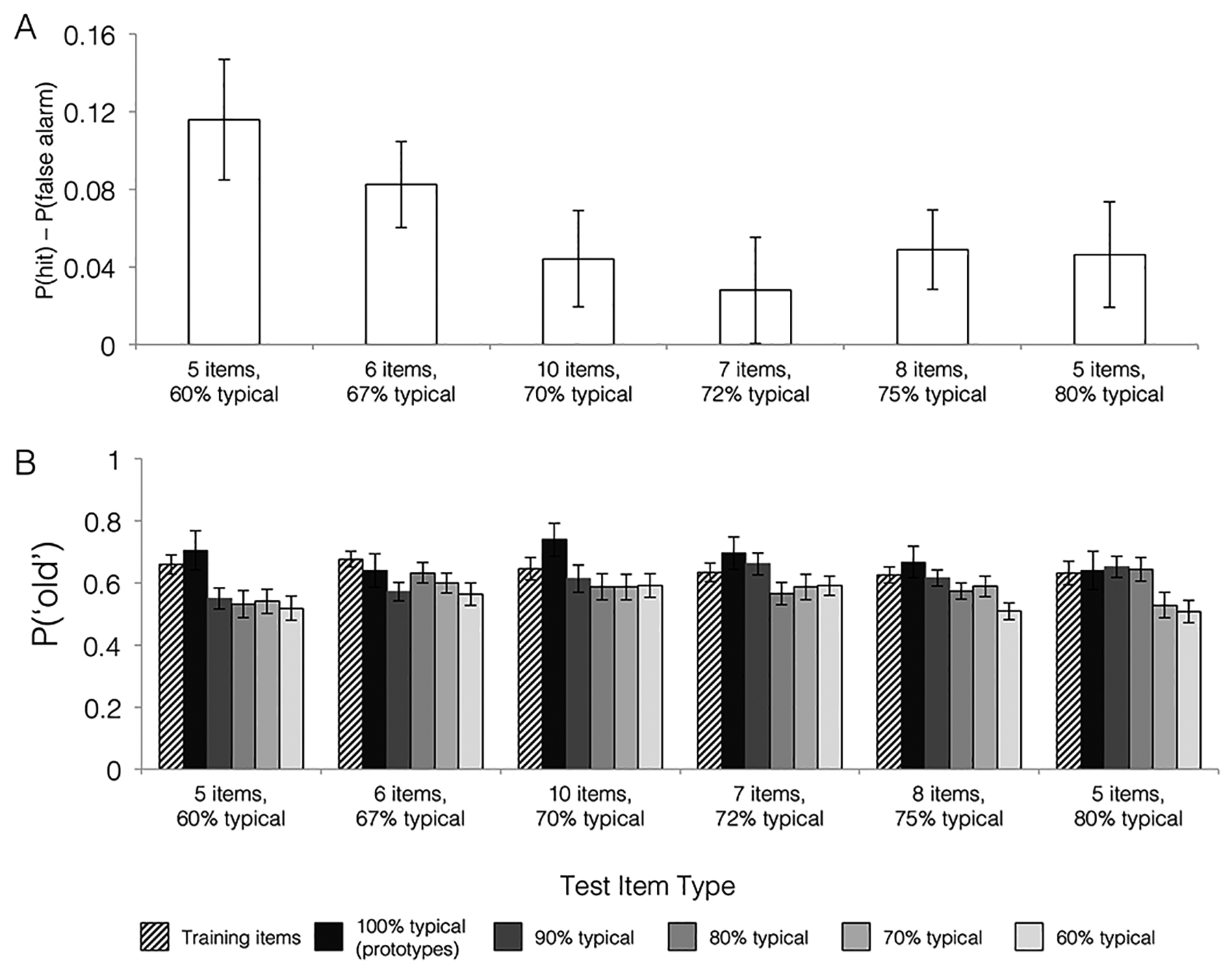
Recognition task. A. Overall recognition performance measured by corrected hit rates (hits – false alarms) B. Proportion of ‘old’ responses during recognition for items varying in their presentation history (old/training items v. all others/new items) and similarity to prototypes (60%–100% typical). Hit rates for training (old) items re-presented during the recognition test are depicted with striped bars. False alarm rates for new items varying in their similarity to category prototypes are depicted with solid bars. False alarm rates for prototypes are depicted in the darkest bars with increasingly lighter bars for new items sharing fewer features with the prototypes. Both graphs separate results by training group: coherence levels are indicated by the percentages on the x-axis, and training set size is indicated on the x-axis by the number of items per category. Error bars depict standard error of the mean.

Endorsement rates.

We were also interested in whether individuals were more likely to falsely recognize new items that were similar to category prototypes and whether that effect differed across training groups (Figure 4B). We computed a 6 (training group) × 5 (test item typicality) mixed factors ANOVA. The main effect of training group was not significant [F(5,157) = 0.53, p = 0.75, ${\eta }_p^2=0.02$] nor was the training group x test item typicality interaction [F(14.90,467.83) = 1.08, p = 0.38, ${\eta }_p^2=0.03$, GG]. There was a significant main effect of test item typicality [F(2.98,467.83) = 12.03, p < 0.001, ${\eta }_p^2=0.07$, GG], that was well described as a linear increase in false recognition for new items with increasing number of shared features with category prototypes [F(1,157) = 28.24, p < 0.001, ${\eta }_p^2=0.15$].

Relationship between recognition and category generalization

To test for a relationship between recognition and category generalization, we computed a multiple regression that included the hit and false alarm rates from recognition as predictors of generalization accuracy (categorization accuracy for new items). We also included training set coherence and set size as predictors to account for mean differences across groups. Results revealed a marginal relationship between the false alarm rate and generalization [ß = 0.17, t(158) = 1.89, p = 0.06] but not the hit rate [ß = 0.05, t(158) = 0.54, p = 0.59]. However, reliability of the hit rate measure was somewhat low (split-half Pearson’s r with Spearman-Brown correction = 0.43), and thus the lack of hit rate effect may be due to poor measure reliability. The reliability of false alarm rates was within an acceptable range (split-half Pearson’s r with Spearman-Brown correction = 0.67) and reliability of the generalization accuracy measure was good (split-half Pearson’s r with Spearman-Brown correction = 0.84). After accounting for recognition performance, the relationship between training set coherence and generalization accuracy remained significant [ß = 0.43, t(158) = 6.14, p > 0.001], and the effect of training set size remained non-significant [ß = 0.10, t(158) = 1.40, p = 0.16]. When we included interaction effects between the false alarm rate and each training set manipulation, neither reached significance [coherence ß = −0.36, t(156) = −0.36, p = 0.71; size ß = 0.43, t(156) = 0.98, p = 0.33].

Prototype and exemplar model fits

Categorization data model fits.

Figure 5 depicts raw model fits with the relative prototype vs. exemplar fit for each individual subject. Across the whole set, 57% (93 subjects) were better fit by the prototype model than the exemplar model, 23% (37 subjects) were best fit by the exemplar model, 3% (5 subjects) were similarly fit by both models, and 17% (28 subjects) had fits that did not differ from chance. Figure 6a depicts the proportion of subjects who were best fit by the prototype model, the exemplar model, those whose model fits did not differ significantly between the prototype and exemplar models (“similar”), and those with fits not above chance (“chance”) separated by training group. Table 3 presents raw fit values for prototype and exemplar models with subjects grouped by their best fitting model. Prototype and exemplar model fits were correlated with generalization accuracy to a similar degree (prototype r = −.83, p < .001, exemplar r = −.84, p < .001), with better accuracy associated with lower model error.

Figure 5.

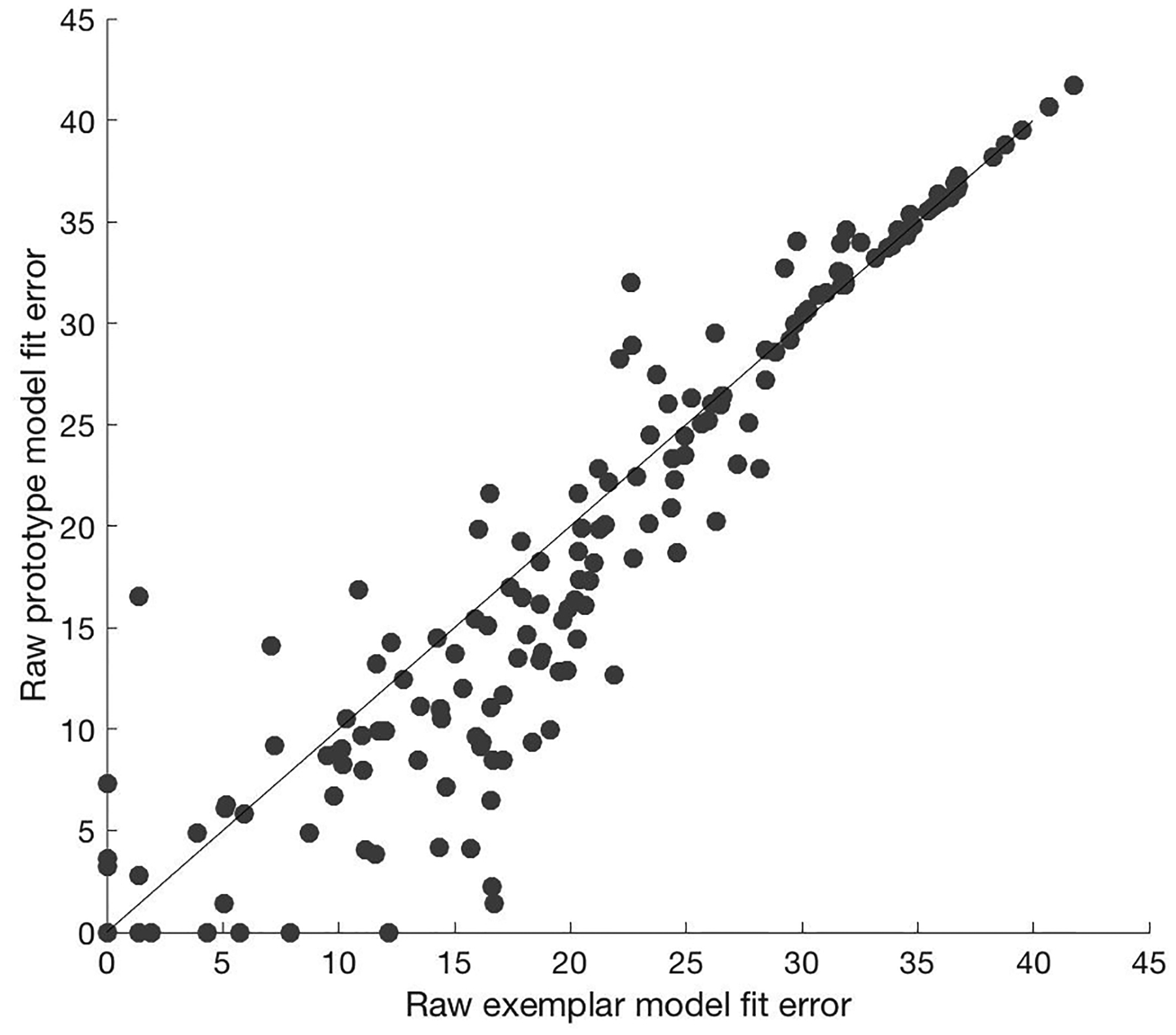
Raw model fit error for categorization data. Relative exemplar (x-axis) and prototype (y-axis) model fits for each subject in terms of negative log likelihood. Trend line represents equal exemplar and prototype model fit. Dots below the trend line represent subjects with smaller model error for the prototype model compared to the exemplar model. Dots above the trend line represent subjects with smaller model error for the exemplar model relative to the prototype model.

Figure 6.

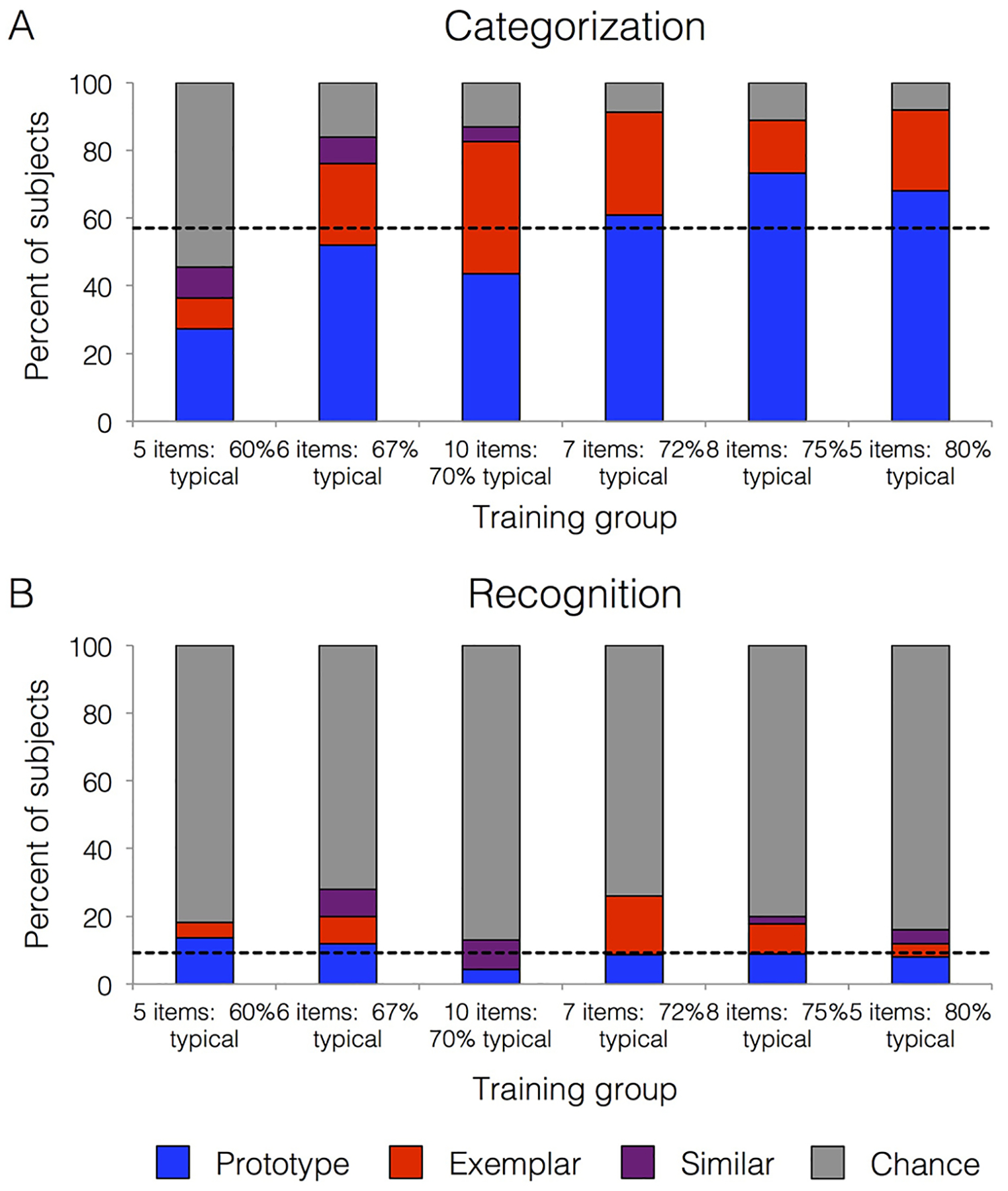
Model fits. A. Models fit to categorization data and B. recognition data. The percent of subjects better fit by the prototype than exemplar model is depicted in blue, the percent better fit by the exemplar than prototype model in red, the percent who were comparably fit by both models (‘similar’) in purple, and those whose fits did not differ from chance in grey. Both graphs separate results by training group: coherence levels are indicated by the percentages on the x-axis, and training set size is indicated on the x-axis by the number of items per category. The dashed lines depict the percent of subjects best fit by the prototype model across the entire group for each respective test.

Table 3.

Mean fit values for prototype and exemplar models with subjects grouped by their best fitting model. Standard deviation is listed in parentheses. Lower numbers mean better fit.

	Categorization		Recognition
	Prototype model	Exemplar model	Prototype model	Exemplar model
Prototype-users	13.61 (8.24)	17.48 (7.16)	23.33 (5.39)	28.24 (5.05)
Exemplar-users	20.05 (11.20)	17.10 (11.58)	23.70 (9.06)	18.12 (8.68)
Similar fits	29.93 (4.86)	29.55 (4.97)	24.72 (5.24)	24.31 (6.14)
Chance	35.18 (2.72)	34.88 (2.96)	28.39 (6.03)	28.02 (6.04)

To test whether each aspect of the training sets (set size, coherence) affected subsequent model fits, we used a logistic regression with training set size and coherence as predictors and the model fit status (best fit by the prototype model or not) as the outcome. Training set coherence was a significant predictor (ß = 0.99, SE = 0.29, p = 0.001) of prototype fit status, with greater training set coherence being associated with greater probability of adopting a prototype strategy. Set size did not predict prototype fit status (ß = 0.001, SE = 0.10, p = 0.99). The pattern of results was similar when we used an AIC metric to label participants as prototype users, exemplar users, and those not different from chance: set coherence, but not set size, predicted the proportion of prototype users in categorization.

Recognition data model fits.

Across the whole set, 9% (15 subjects) were better fit by the prototype model than the exemplar model, 7% (12 subjects) were best fit by the exemplar model, 4% (6 subjects) were similarly fit by both models, and 80% (130 subjects) had fits that did not differ from chance. The proportion of those classified as using a prototype strategy was reliably smaller during recognition than categorization (McNemar test for paired nominal data, X² (1) = 0.73, p < 0.001), reflecting lower utility of the prototype strategy for the recognition than categorization test. Figure 6b depicts the proportion of subject from each training group that were best fit by the prototype model, the exemplar model, similarly by both models, and those not differing from chance. A logistic regression showed that neither training set size nor training set coherence was reliably predictive of the proportion of prototype users in the recognition phase (p’s > 0.4). The pattern of results was similar when we used an AIC metric to label participants: training set did not affect the proportion of prototype users in recognition and the overall proportion of prototype users was smaller during recognition than during categorization.

Model parameters.

We were also interested in whether the parameters estimated from the prototype and exemplar models were similar across test phases or if instead there was evidence that participants used different information to make these two judgments. Table 4 presents mean parameter values for each model separately for categorization and recognition. We computed within-subject correlations of the attention weights estimated for each phase separately. We then Fisher-transformed the correlation coefficients and averaged them across participants. We did not find a significant relationship between phases in either model (mean exemplar Fischer’s z = 0.05, one-sample t(162) = 1.74, p = 0.08; prototype Fisher’s z = 0.03, one-sample t(162) = 1.01, p = 0.32). Additionally, we tested whether sensitivity parameters estimated in the two phases (one parameter per participant per phase) were related using an across-subjects correlation. We found no relationship between sensitivity estimates across phases for either the exemplar (r = −0.02, p = 0.73) or prototype model (r = −0.06, p = 0.43). This lack of a correlation between phases is in contrast to the similarity in the attention weight estimates for exemplar and prototype models within a phase (mean categorization Fisher’s z = 1.59, one-sample t(162) = 19.20, p < 0.001; recognition Fisher’s z = 0.38, one-sample t(162) = 9.40, p < 0.001), indicating that both models tended to identify the same features being attended to for a given phase and participant. Similarly, there was a reliable across-subject correlation between sensitivity parameters estimated from each model within each phase. The magnitude of this effect was large during categorization and small to medium during recognition (categorization r = 0.47, p < 0.001; recognition r = 0.17, p < 0.03). Thus, the lack of a correlation across phases was not simply due to poor reliability in estimating the parameters. Instead, there seem to be genuine differences between the phases that both models converge on.

Table 4.

Mean parameter estimates separated by model (prototype, exemplar) and phase (categorization, recognition)

Attention weights by dimension
	1	2	3	4	5	6	7	8	9	10	C	K
Categorization: Prototype	0.13 (0.20)	0.09 (0.15)	0.10 (0.18)	0.11 (0.18)	0.08 (0.14)	0.12 (0.17)	0.08 (0.13)	0.05 (0.10)	0.09 (0.17)	0.16 (0.20)	23.42 (57.11)	--
Categorization: Exemplar	0.14 (.26)	0.10 (0.20)	0.10 (0.23)	0.12 (0.24)	0.07 (0.18)	0.11 (0.23)	0.08 (0.19)	0.04 (0.11)	0.09 (0.21)	0.15 (0.25)	47.52 (90.66)	--
Recognition: Prototype	0.11 (0.20)	0.09 (0.19)	0.11 (0.20)	0.11 (0.19)	0.08 (0.14)	0.11 (0.19)	0.12 (0.21)	0.10 (0.20)	0.09 (0.18)	0.09 (0.17)	13.40 (8.52)	0.21 (0.22)
Recognition: Exemplar	0.12 (0.17)	0.09 (0.16)	0.11 (0.17)	0.11 (0.16)	0.08 (0.15)	0.16 (0.10)	0.11 (0.17)	0.11 (0.17)	0.08 (0.14)	0.08 (0.16)	59.11 (23.65)	0.59 (0.65)

The sensitivity parameter indexes how physical similarity to a given category representation relates to subjective similarity and thus response probabilities. Values closer to zero correspond to more uniform subjective similarity across levels of physical similarity and thus more flat relationship between physical similarity and response probabilities. Higher values mean a steeper similarity gradient and thus a stronger effect of physical similarity on responses. As such, we were interested in whether there were differences in model-estimated sensitivity across phases (categorization vs. recognition). We hypothesized greater exemplar model-estimated sensitivity during recognition than categorization and greater prototype model-estimated sensitivity during categorization than recognition. To test this idea, we computed a 2 (model: prototype, exemplar) × 2 (phase: categorization, recognition) repeated-measures ANOVA on estimates of the sensitivity (c) parameter. There was a significant main effect of model [F(1,162) = 114.03, p < 0.001, ${\eta }_{\text{p}}^2=0.41$] with higher overall sensitivity values for the exemplar compared to the prototype model (see Table 4). The main effect of phase was not significant [F(1,162) = 0.02, p = .88, ${\eta }_{\text{p}}^2<0.001$], but the model x phase interaction was significant [F(1,162) = 10.29, p = 0.002, ${\eta }_{\text{p}}^2=0.06$]. To determine the locus of the interaction, we compared the estimates from categorization and recognition using paired t-tests, one for the prototype model and one for the exemplar model. The interaction was driven by numerically higher prototype-related sensitivity estimates for categorization than recognition [t(162) = 2.19, p = 0.03] and numerically higher exemplar-related sensitivity estimates for recognition than categorization [t(162) = 1.57, p = 0.12], although neither pair-wise comparison reached a corrected threshold (p < 0.025). These findings provide some evidence that participants’ recognition judgments were less sensitive to physical similarity to prototypes compared to their categorization judgments, and vice-versa. There were no significant moderating effects of training version when we included it as a between-subjects factor (all F’s < 1.7, p’s > 0.15).

Discussion

In the present study, we tested how training on category structures that varied in their coherence and number of exemplars affected category learning, subsequent generalization, and category representations. As a secondary question, we were also interested in how category generalization related to memory for individual items and whether individuals flexibly used different representations to make categorization vs. recognition judgments. Subjects learned to classify novel cartoon stimuli into two categories, with the size and coherence of training sets differing across subjects. Afterward, subjects were tested on their ability to recognize individual exemplars presented during study and their ability to generalize the category labels to new examples. We compared groups in terms of accuracy and the fit of formal prototype and exemplar models. Results showed faster learning and better subsequent generalization from more coherent training sets. This advantage for more coherent training sets was apparent even for the least typical new items at test. Training on more coherent sets also led to greater reliance on prototype representations when making categorization judgments. These results suggest that learning from a coherent set of examples facilitates extraction of category prototypes, promoting category knowledge that generalizes even to items at category boundaries. Contrary to our predictions, there was little effect of training set size on accuracy during either the training phase or categorization test and no evidence that set size affected the reliance on prototype vs. exemplar representations. Training condition did not reliably affect the ability to recognize individual category members. Instead, we found a marginal trade-off between recognition and generalization across individuals and an overall reduction in the proportion of participants fit by either model in recognition compared to categorization. Together, these results suggest that forming abstract category representations facilitates later category generalization but may constrain individuals’ abilities to make other types of memory judgments.

Early studies of category learning provided conflicting results regarding whether learning from coherent or more variable examples better promotes generalization (Hintzman, 1984; Homa & Vosburgh, 1976; Peterson et al., 1973; Posner & Keele, 1968). The present study included a wide range of training set coherence levels and showed a clear effect on category learning and the ability to later generalize: better performance resulted from training on sets with higher coherence. Thus, prior advantages for high variability training sets likely resulted from training subjects to a performance criterion, which was necessarily more extensive in these difficult-to-learn category structures. When we equated the number of repetitions of each training item across sets varying in coherence, there was a clear advantage for training on more coherent sets, as expected from prior computational modeling of categorization (Hintzman, 1984, 1986). Critically, the advantage for more coherent training sets was not limited to generalization items closest to the prototype: training set coherence positively predicted classification even for generalization items sharing the fewest features with the prototypes. This finding is particularly novel because previous studies have suggested that training on less coherent stimuli may be especially beneficial for fostering a breadth of category knowledge (Dukes & Bevan, 1967; Perry, Samuelson, Malloy, & Schiffer, 2010; Peterson et al., 1973). However, it is consistent with prior work showing that it is sometimes easier to generalize a category after learning from easy discriminations compared to more difficult ones, even if the more difficult training better resembles the types of discriminations made during test (Edmunds, Wills, & Milton, 2019), and that repeated exposures to the same examples provides stability that facilitates broad knowledge (Carvalho, Chen, & Chen, 2019; Horst, Parsons, & Bryan, 2011). These findings (with matched variability across the two contrasting categories) also complement studies on category generalization under conditions where one of the contrasting categories has higher variability than the other (Cohen, Nosofsky, & Zaki, 2001; Rips, 1989; Stewart & Chater, 2002). In such a case, subjects are biased toward classifying items equidistant from the two categories into the more variable category. One possibility, consistent with our results, is that subjects in unequal variability tasks may have a poorer conception of what defines the more variable category compared to the more coherent category. Thus, subjects may treat this contrasting category task perhaps as a single category (A/non-A) task and assume that any questionable items must not belong to the coherent category (Rips, 1989).

We also found that training set coherence led to differences in the category representations underlying categorization judgments, as indexed by the relative fit of prototype versus exemplar models. Supporting our prediction, training on more coherent sets was associated with greater use of prototype representations during generalization. This finding is consistent with the idea that training on a coherent set of examples facilitates linking of common features across items within a category, promoting the formation of abstract memory representations. Prior work has shown that training individuals on which feature values are most typical of a given category prior to showing any specific category examples (e.g., most category A members are red, most category B members are blue) leads to a greater reliance on prototype representations compared to when individual examples are presented first (Medin et al., 1984). Our work complements this previous finding, showing that prototypical feature values can be made salient not only via explicit training on individual features, but also by increasing the coherence of training examples around the prototype.

Unlike set coherence, training set size did not reliably affect either category learning or generalization, suggesting that differences in set coherence were the primary driver of differences in learning and generalization of novel concepts. While some research has suggested that larger category sets are associated with better generalization (Goldman & Homa, 1977; Homa, Cross, Cornell, Goldman, & Shwartz, 1973; Homa et al., 1981), we found that differences in generalization were well accounted for by set coherence and that set size did not explain additional variability in generalization performance. While we predicted that increasing the number of examples would constrain individuals to the cognitive economy that prototype representations afford, we did not find evidence that set size affected subjects’ tendency to make categorization judgments based on prototype representations. This finding stands in contrast to previous work that compared across two levels of category set size (5 versus 15 examples) and found an overall prototype model advantage that was numerically stronger for larger set sizes (Minda & Smith, 2001). Here, comparing groups across a larger number of set sizes (5, 6, 7, 8 or 10 examples), we found that set size did not reliably predict prototype use. One possibility is that prototype use does not increase linearly with set size but rather there is a step-wise increase at a set size value larger than that included in the present study. Future studies with set sizes larger than 10 items per category can test this possibility. Alternatively, the effect of set size may differ across levels of set coherence. Because set size and set coherence were somewhat correlated in the present study, we were not able to test for interactions between these factors. Thus, further research is needed to better understand the circumstances in which training set size affects representations underlying categorization judgments.

By showing that the structure of training examples can affect the types of representations that individuals form or access, our behavioral findings help resolve some past contradictions regarding the nature of concept representations (Minda & Smith, 2002; Nosofsky, 1988). Among recent examples, Mack and colleagues (2013) used neuroimaging evidence to adjudicate between a prototype and an exemplar account of concept representation and found predominantly exemplar neural evidence. Training stimuli in that study were not coherently clustered around prototypes, which likely led to strong exemplar dominance in brain and behavior. In contrast, Bowman and Zeithamova (2018) used training exemplars that were more category-typical and found predominantly prototype correlates in brain and behavior. The prototype-tracking regions identified in Bowman and Zeithamova (2018) differed from the exemplar-tracking regions identified in Mack et al. (2013), suggesting that the representational flexibility apparent across studies may be possible because different representations form in distinct brain regions. Wutz and colleagues (2018) directly compared training on low vs. high variability sets in monkeys while recording from prefrontal cortex. They found that distinct prefrontal circuits and distinct oscillation frequencies were involved in learning to categorize low vs. high distortions of category prototypes. Thus, depending on the coherence of category examples, category information can be coded at different levels of abstraction, possibly supported by different brain regions.

Our findings that the training set structure affects the representations underlying later generalization is consistent with the broader literature showing multiple mechanisms underlying category knowledge (Ashby & Maddox, 2005; Seger & Miller, 2010). By showing the critical role of category coherence at training, we add to a body of work showing that features of the learning set and context can shift the extent to which individuals rely on one mechanism or another. For example, training manipulations such as observational versus feedback-based training (Shohamy et al., 2004), intentional versus incidental learning (Aizenstein et al., 2000; Reber, Gitelman, Parrish, & Mesulam, 2003), learning of single versus contrasting categories (Zeithamova, Maddox, & Schnyer, 2008), and learning of rule conforming items versus exceptions (Davis, Love, & Preston, 2012) have all been shown to engage different neural systems. Behavioral evidence shows that features of training can also affect category representations by highlight distinctive vs. characteristic features. For example, when training is interleaved such that items from opposing categories are presented in an intermixed fashion, individuals tend to better encode features that distinguish categories compared to when items from the same category are presented together and opposing categories are presented across separate blocks (Carvalho & Goldstone, 2014, 2017). Similarly, whether participants learn a single (A/non-A) or contrasting (A/B) categories and whether those categories are separable by a simple rule (rule-based) or require integration across multiple dimensions (information integration) can effect whether individuals tend to focus on similarity within the category vs. differences across opposing categories (Ell, Smith, Peralta, & Hélie, 2017; Hélie, Shamloo, & Ell, 2017, 2018). Adding to this work, the present study provides new evidence for flexibility in how individuals represent category information based on demands at the time of learning.

Unlike category learning and generalization, recognition accuracy measures and recognition model fits were much less affected by training conditions. Instead we found that recognition performance was not above chance in half of the training groups, with high rates of false alarms to category prototypes in most conditions. Such false alarms are a typical consequence of emphasizing commonalities among items during encoding (Arndt & Hirshman, 1998; Roediger et al., 1995). Supporting our hypothesis that individuals would be less likely to rely on prototypes when making recognition judgments, we found a smaller proportion of prototype users in recognition than in categorization. We also found lower sensitivity to prototype similarity for recognition compared to categorization judgments. In contrast, sensitivity to exemplar similarity was numerically greater during recognition compared to categorization. Because prototype representations discard details of individual category members that are critical for distinguishing between old and new items, they are much less useful for recognition than for categorization. However, while most prototype users shifted away from a prototype strategy, it seems that they had not formed another representation that could support recognition judgments and instead were best fit by a random model. This may indicate that participants did not develop an exemplar representation sufficient to support the fine-grained discrimination required for stimuli with so many overlapping features or that the exemplar representation posited here is in fact only one component of a more complex recognition memory system (Tulving, 1987; Yonelinas, 2002).

Finally, we evaluated the relationship between recognition of individual stimuli and category generalization success, testing the contrasting predictions of current theories of generalization. We found a marginally significant relationship between generalization success and rates of false alarms, indicating that better generalization was associated with lower memory specificity. This result runs contrary to the single system prediction that category generalization and recognition performance should be positively related because both depend on the same representation (Banino et al., 2016; Hintzman & Ludlam, 1980). However, because the effect was only marginally significant and recognition was poor overall, it does not clearly differentiate between the alternatives. A plausible interpretation is that encoding specific information vs. generalizing across related events are competing strategies, resulting in a trade-off between memory specificity and generalization (Knowlton & Squire, 1993; Marsh et al., 2015; Varga et al., 2019; Zeithamova et al., 2012). However, it is not possible to confidently reject the alternative that specific and generalized representations form in parallel and coexist rather than trade-off (Brunec et al., 2018; Collin et al., 2015; Schapiro, Turk-Browne, Botvinick, & Norman, 2017; Schlichting et al., 2015), but the formation of specific representation was especially difficult with the current stimuli. Thus, future studies are needed to more decisively determine the categorization-recognition relationship.

Understanding how to promote acquisition of generalizable knowledge is of interest across a number of domains, with particular interest in the role of coherence vs. variability in learning examples. For example, a key question in linguistics is how people learn spoken language from multiple speakers, each having their own speech production quirks that make learning experiences noisy (Bulgarelli & Weiss, 2019; Estes & Lew-Williams, 2015; Houston & Jusczyk, 2000; Kuhl, 1979). In education, the coherence of materials, such as textbooks (Kintsch, 1994) and multimedia presentations (Mayer & Fiorella, 2014), has been identified as a key factor in determining comprehension and retention. Our finding that learning from a coherent set of typical examples promoted abstraction and facilitated generalization to a wide variety of examples suggests that consistency rather than variability may be most beneficial to learning. Future research examining the generalizability of these findings to other kinds of materials would be helpful in determining their degree of applicability across domains. Our finding that typical examples are more likely to be represented in a joint summary representation (such as a prototype) may also relate to findings on different levels of generalization from typical vs. atypical category members. People infer that traits of typical members apply to the entire category but traits of atypical members apply narrowly (Rips, 1975). Fear responses conditioned from typical members are more likely to be generalized to other members of the same category than those learned from atypical members (Dunsmoor & Murphy, 2014). Thus, typical examples may be more likely to be represented jointly, which in turn may affect the degree to which new information learned about one category member is generalized to others in the same category.

Linking related information into categories is a key way that individuals organize their experiences to support future decision-making. In the present study, we showed that structuring information in a way that emphasizes commonalities among items facilitates acquisition of category knowledge and promotes generalization to a wide range of new items. Accompanying benefits to generalization performance, learning from more coherent sets of examples also promoted formation of abstract category representations indexed by formal model fits. Lastly, while reliance on abstract prototype representations was reduced when subjects made recognition as opposed to categorization judgments, this effect was driven by a failure of either model to explain response, suggesting that subjects did not form strong representations of individual category members. Together, these results suggest that learning from a coherent set of examples is an efficient means of forming abstract knowledge that is highly transferable.

Appendix A

For each participant, the prototype of category A was chosen by randomly selecting from one of four possible prototypes (Table 1). The prototype of category B was defined as the stimulus sharing no features with the prototype of category A. Tables 2–8 present structures of stimuli for each training group coded with respect to the first possible category A prototype (i.e., 1111111111, with 0000000000 serving as the category B prototype). For each training group, the authors pre-defined possible stimuli for the training sets. For each training group, an initial set was created that contained feature values for half of the total number of training stimuli (i.e., enough for one of the two categories). Feature values were selected to ensure that all dimensions were equally predictive of category membership. Three additional sets were created by shuffling which feature values were associated with each dimension. For example, in Table 2, each row represents a stimulus in a given set and the columns represent the ten dimensions. The feature values associated with Dimension 1 in Set 1 are associated with Dimension 8 in Set 2. A participant’s training set was created by randomly selecting two of these sets, recoding the first with regard to the category A prototype, and recoding the second with regard to the category B prototype, and combining them into a single training set with stimuli for both categories. Note: groups trained on sets presented in Tables 6 and 7 were collapsed for all analyses.

Table A1.

Possible category A prototypes

Dimension
1	2	3	4	5	6	7	8	9	10
1	1	1	1	1	1	1	1	1	1
0	0	0	0	0	1	1	1	1	1
1	1	0	0	1	1	0	0	1	1
0	1	1	1	0	0	0	1	0	0

Table A2.

Possible training stimuli for 5 items: 60% training group

Dimension
Set	1	2	3	4	5	6	7	8	9	10
1	1	0	0	1	0	1	0	1	1	1
1	1	1	1	0	1	0	0	1	0	1
1	0	1	1	1	0	1	1	0	0	1
1	0	1	0	0	1	1	1	1	1	0
1	1	0	1	1	1	0	1	0	1	0
2	0	1	1	1	0	0	1	1	1	0
2	0	0	0	0	1	1	1	1	1	1
2	1	0	1	1	1	0	1	0	0	1
2	1	1	0	1	0	1	0	0	1	1
2	1	1	1	0	1	1	0	1	0	0
3	1	1	0	0	0	1	1	1	0	1
3	0	0	0	1	1	1	1	0	1	1
3	1	0	1	0	1	0	1	1	1	0
3	0	1	1	1	1	1	0	1	0	0
3	1	1	1	1	0	0	0	0	1	1
4	0	1	0	0	1	1	1	1	0	1
4	1	1	1	0	0	1	0	1	1	0
4	1	0	1	1	1	0	1	1	0	0
4	1	0	0	1	1	1	0	0	1	1
4	0	1	1	1	0	0	1	0	1	1

Table A3.

Possible training stimuli for 6 items: 67% training group

Dimension
Set	1	2	3	4	5	6	7	8	9	10
1	1	1	0	0	1	1	1	1	1	1
1	0	0	1	1	1	1	1	1	1	1
1	1	1	0	1	0	0	0	1	1	1
1	0	1	1	1	0	1	1	0	0	1
1	1	0	1	1	1	0	1	0	1	0
1	1	1	1	0	1	1	0	1	0	0
2	1	0	1	1	1	1	1	1	0	1
2	1	1	0	1	1	1	0	1	1	1
2	0	0	1	1	1	1	1	0	1	0
2	1	1	1	0	0	1	0	0	1	1
2	0	1	0	1	0	0	1	1	1	1
2	1	1	1	0	1	0	1	1	0	0
3	1	1	1	0	1	0	1	1	1	1
3	1	1	1	1	0	1	0	1	1	1
3	1	1	0	0	1	1	1	1	0	0
3	0	0	1	1	1	1	0	1	1	0
3	1	0	0	1	0	1	1	0	1	1
3	0	1	1	1	1	0	1	0	0	1
4	1	1	1	0	1	1	1	0	1	1
4	1	1	1	1	1	0	1	1	0	1
4	0	1	1	1	0	1	0	0	1	1
4	1	0	1	1	1	1	0	1	0	0
4	1	0	0	1	0	0	1	1	1	1
4	0	1	0	0	1	1	1	1	1	0

Table A4.

Possible training stimuli for 10 items: 70% training group

Dimension
Set	1	2	3	4	5	6	7	8	9	10
1	1	0	1	1	1	1	1	0	1	1
1	1	1	0	1	0	1	1	1	1	1
1	1	1	1	1	1	0	1	1	1	0
1	1	1	1	1	0	0	0	1	1	1
1	0	1	1	1	1	1	1	1	0	0
1	0	1	1	0	1	1	0	1	1	1
1	1	0	1	1	0	1	1	1	0	1
1	1	1	0	0	1	1	0	0	1	1
1	1	0	0	1	1	0	1	1	0	1
1	0	1	1	0	1	1	1	0	1	0
2	1	1	0	1	1	1	1	1	0	1
2	1	0	1	1	1	1	1	0	1	1
2	1	1	1	1	0	1	1	1	1	0
2	1	1	1	0	1	0	1	1	1	0
2	0	1	1	1	1	1	0	1	1	0
2	1	1	1	0	1	0	0	1	1	1
2	0	1	0	1	1	1	1	0	1	1
2	1	1	0	1	0	1	1	0	0	1
2	1	0	1	0	0	0	1	1	1	1
2	0	0	1	1	1	1	0	1	0	1
3	1	1	0	1	1	1	1	1	0	1
3	1	1	1	1	0	1	1	1	1	0
3	1	1	1	0	0	1	1	1	1	1
3	0	1	1	1	1	1	1	1	0	0
3	1	0	1	1	1	1	0	0	1	1
3	1	0	1	0	1	1	0	1	1	1
3	1	0	1	1	1	0	1	1	0	1
3	1	1	0	1	0	1	1	0	1	0
3	0	1	1	0	1	0	1	0	1	1
3	0	1	0	1	1	0	0	1	1	1
4	0	1	1	1	1	1	0	1	1	1
4	0	1	0	1	1	1	1	1	1	1
4	1	1	0	1	0	1	1	1	1	1
4	1	0	1	1	0	0	1	1	1	1
4	1	1	1	0	1	1	1	1	0	0
4	1	1	0	1	1	1	1	0	0	1
4	1	0	1	0	1	1	1	0	1	1
4	1	1	1	1	0	0	0	1	1	0
4	0	0	1	1	1	1	1	0	1	0
4	1	1	1	0	1	0	0	1	0	1

Table A5.

Possible training stimuli for 7 items: 72% training group

Dimension
Set	1	2	3	4	5	6	7	8	9	10
1	1	1	0	0	1	1	1	1	1	1
1	0	0	1	1	1	1	1	1	1	1
1	1	1	1	1	1	1	0	0	1	1
1	1	1	1	1	0	0	1	1	1	1
1	1	1	0	1	1	0	1	1	0	0
1	1	0	1	1	0	1	0	1	0	1
1	0	1	1	0	1	1	1	0	1	0
2	1	1	0	1	0	1	1	1	1	1
2	1	1	1	1	1	1	0	1	1	0
2	1	1	1	1	1	0	1	1	0	1
2	0	1	1	1	1	1	1	0	1	1
2	1	0	1	0	1	1	0	0	1	1
2	0	1	1	0	0	0	1	1	1	1
2	1	0	0	1	1	1	1	1	0	0
3	0	1	1	1	0	1	1	1	1	1
3	1	1	1	0	1	1	1	1	1	0
3	1	0	1	1	1	1	1	1	0	1
3	1	1	0	1	1	1	0	1	1	1
3	1	1	1	0	1	0	0	0	1	1
3	1	0	0	1	0	1	1	0	1	1
3	0	1	1	1	1	0	1	1	0	0
4	1	0	1	0	1	1	1	1	1	1
4	1	1	1	1	1	1	0	0	1	1
4	1	1	1	1	0	1	1	1	0	1
4	0	1	0	1	1	1	1	1	1	1
4	1	0	0	1	1	0	1	1	1	0
4	0	1	1	1	0	1	1	0	1	0
4	1	1	1	0	1	0	0	1	0	1

Table A6.

Possible training stimuli for 8 items: 75% training group, 70% and 80% typical

Dimension
Set	1	2	3	4	5	6	7	8	9	10
1	1	1	0	1	1	1	1	1	1	0
1	1	1	0	1	1	1	1	1	0	1
1	1	1	1	1	0	1	1	1	1	0
1	0	1	1	1	1	1	0	1	1	1
1	1	0	1	0	1	0	1	1	1	1
1	1	0	1	1	1	1	1	0	0	1
1	0	1	1	0	0	1	1	1	1	1
1	1	1	1	1	1	0	0	0	1	1
2	1	1	1	0	1	1	1	0	1	1
2	1	1	1	1	0	0	1	1	1	1
2	1	1	1	1	1	0	1	1	0	1
2	0	1	1	1	1	1	1	1	1	0
2	0	1	1	1	0	1	1	1	0	1
2	1	1	0	0	1	1	0	1	1	1
2	1	0	1	1	1	1	0	0	1	1
2	1	0	0	1	1	1	1	1	1	0
3	1	1	1	1	1	0	1	1	1	0
3	1	0	1	1	1	1	1	1	1	0
3	1	1	0	1	1	1	1	1	0	1
3	1	1	1	1	0	1	0	1	1	1
3	0	1	1	1	0	1	1	0	1	1
3	1	1	0	0	1	1	0	1	1	1
3	1	1	1	0	1	1	1	0	0	1
3	0	0	1	1	1	0	1	1	1	1
4	0	1	1	1	0	1	1	1	1	1
4	1	1	1	1	1	1	0	1	1	0
4	1	1	1	0	1	1	1	1	1	0
4	1	1	1	1	0	1	0	1	1	1
4	1	0	1	1	1	0	1	0	1	1
4	0	1	1	1	1	0	1	1	0	1
4	1	0	0	1	1	1	1	1	0	1
4	1	1	0	0	1	1	1	0	1	1

Table A7.

Possible training stimuli for 8 items: 75% training group, 60% and 80% typical

Dimension
Set	1	2	3	4	5	6	7	8	9	10
1	0	1	1	1	1	1	0	1	1	1
1	1	0	1	1	1	1	0	1	1	1
1	1	1	0	1	1	1	1	0	1	1
1	1	1	1	0	1	1	1	0	1	1
1	1	0	1	1	0	1	1	1	1	1
1	0	1	1	1	1	0	1	1	1	1
1	1	1	1	0	1	0	1	1	0	0
1	1	1	0	1	0	1	1	1	0	0
2	1	1	0	1	1	1	1	1	1	0
2	1	1	1	1	1	1	0	1	1	0
2	1	1	1	1	0	1	1	0	1	1
2	1	1	1	1	1	1	1	0	0	1
2	0	1	1	1	1	1	0	1	1	1
2	1	1	0	0	1	1	1	1	1	1
2	1	0	1	0	1	0	1	1	0	1
2	0	0	1	1	0	0	1	1	1	1
3	1	1	0	1	1	0	1	1	1	1
3	0	1	0	1	1	1	1	1	1	1
3	1	1	1	0	1	1	1	1	1	0
3	1	1	1	0	1	1	1	0	1	1
3	0	1	1	1	1	1	0	1	1	1
3	1	1	1	1	0	0	1	1	1	1
3	1	0	1	1	0	1	1	0	0	1
3	1	0	1	1	1	1	0	1	0	0
4	0	1	0	1	1	1	1	1	1	1
4	0	1	1	1	1	1	1	1	1	0
4	1	1	1	1	1	1	1	0	0	1
4	1	0	1	1	1	1	1	0	1	1
4	1	1	1	1	0	1	1	1	1	0
4	1	1	0	1	1	1	0	1	1	1
4	1	0	1	0	1	0	0	1	1	1
4	1	1	1	0	0	0	1	1	0	1

Table A8.

Possible training stimuli for 5 items: 80% training group

Dimension
Set	1	2	3	4	5	6	7	8	9	10
1	1	0	1	1	1	0	1	1	1	1
1	0	1	1	1	1	1	1	1	0	1
1	1	1	1	0	1	1	1	1	1	0
1	1	1	1	1	1	1	0	0	1	1
1	1	1	0	1	0	1	1	1	1	1
2	0	1	1	1	1	1	1	0	1	1
2	1	1	0	1	1	1	0	1	1	1
2	1	1	1	1	1	0	1	1	0	1
2	1	0	1	1	0	1	1	1	1	1
2	1	1	1	0	1	1	1	1	1	0
3	1	1	1	0	1	0	1	1	1	1
3	1	0	1	1	1	1	1	1	0	1
3	1	1	1	1	1	1	0	0	1	1
3	1	1	1	1	0	1	1	1	1	0
3	0	1	0	1	1	1	1	1	1	1
4	1	0	1	1	1	1	1	1	0	1
4	1	1	0	1	0	1	1	1	1	1
4	1	1	1	1	1	0	1	1	1	0
4	1	1	1	0	1	1	1	0	1	1
4	0	1	1	1	1	1	0	1	1	1