Abstract
Objective:
There may be a need to perform dynamic skull aberration corrections during the non-invasive high-intensity transcranial treatment with magnetic resonance imaging (MRI) -guided focused ultrasound in order to accurately and rapidly restore the focus in the brain.
Methods:
This could possibly be accomplished by using an ultrasound-based correction method based on the skulls’ thickness resonance frequencies. The focus of a 500 kHz transducer was centered in the ex vivo human skull caps at different temperatures. The pulse-echoed signals reflected from the skulls were analyzed in the frequency domain to reveal the resonance frequencies for the phase shift calculation. The accuracy was compared to both hydrophone and computed tomography (CT) based analytical methods.
Results:
Around 73% of the measurements (n=784) were in the optimal constructive interference region, with a 15° decrease in the average phase error compared to the previous study. In the best implementation, it performed approximately the same or better than the CT based analytical method currently in clinical use. Linear correlation was found between the resonance frequencies or skull induced phase shifts and the skull temperature with an average rate of −0.4 kHz/°C and 2.6 deg/°C, respectively.
Conclusion:
The ultrasound based resonance method has shown the feasibility of detecting heating-induced changes of skull phase shift non-invasively and accurately.
Significance:
Since the technique can be made MRI compatible and integrated in the therapy arrays, it may enable temperature tracking and adaptive focusing during high-intensity transcranial ultrasound treatments, to prevent skull overheating and preserve the transcranial focusing integrity.
Keywords: phase shift, resonance frequency, noninvasive, computed tomography, transcranial ultrasound
I. Introduction
MAGNETIC resonance imaging guided focused ultrasound (MRIgFUS) thermal ablations have been increasingly employed and investigated in transcranial treatments for brain diseases and disorders, as a potential alternative to invasive interventions. Clinically, this technique has been studied and employed successfully in thermal ablation of small targets for essential tremor [1–3], brain tumors [4, 5], obsessive-compulsive disorder [6], chronic neuropathic pain [7, 8], and depression [9]. The essential tremor treatments have now received regulatory approvals from multiple regulatory agencies including U.S. Food and Drag Administration in 2016.
The clinical implementations of transcranial FUS techniques require the capability of accurate and precise targeting through an intact skull, which is challenging due to the inhomogeneity of the skull [10], resulting in a distorted focus in the brain [11]. As a result, different approaches have been proposed to correct such aberration, including the ultrasound imaging time-shift method [12–14], time-reversal mirror [15, 16], and catheter-inserted hydrophone based correction [17, 18]. These methods have shown the feasibility of improving the focusing quality, but an initial invasive implantation of a transducer is required. To achieve a noninvasive transcranial treatment, it was discovered that skull aberration correction can be accomplished by using skull density and thickness information obtained from pre-operative CT images [19] that made clinical brain treatments feasible. Several computer models that use the CT information have since been developed and shown to achieve trans-skull focusing [20, 21]. In addition, this CT information can also be used in the design of acoustic lenses with controlled thicknesses coupled with single element transducers for transcranial applications [22, 23].
With the CT based phase aberration correction, most of the tremor treatments among the clinical trials are successful. However, there are a number of patients where it is not possible to reach adequate temperatures for thermal ablation [24] as measured with MRI thermometry and others where the skull temperatures are so high that skull damage may be induced [25]. In addition, only the central targets are treatable due to excessive skull heating [25–27]. One of the reasons that limits the focal temperature elevation is the reduced heating efficiency at the higher output powers that is at least partly a result of focal widening [24]. There is evidence that this may be caused by speed of sound changes in the skull while its temperature is elevated nonuniformly [28–31]. MRI thermometry using the proton resonance frequency (PRF)-shift method [32] is often used to track the temperature elevation in the brain during sonication, however it is not sensitive to the temperature changes in the skull bone due to its low water density and fast signal decay. Therefore, there is a need to have a method that would allow either the skull temperature or its impact on the phase of the propagating ultrasound wave to be monitored.
A resonance method, based on measuring the materials’ thickness resonance frequencies [33, 34], has been proposed for the measurements of the phase shifts caused by the skull bones [35]. In that study, a wideband ultrasound transducer was used to emit an impulse, and the reflected acoustic signals from the skull within the lateral focal zone were recorded followed by the frequency spectra analysis to extract the resonance frequency of the skull bone. Although results showed that approximately 65% of the calculated phase shifts were within the region with optimal constructive interference quality defined by the Goodman criteria [36], the study lacks a comparison to the other noninvasive skull phase aberration correction methods [35]. In addition, the skull thickness was obtained via direct measurement with caliper or micrometer, which is not available in actual clinical applications. However, since this method may allow measurements of the skull properties during the sonication, we decided to further explore the accuracy of this method when combined with CT skull thickness measurement, to compare it with other noninvasive methods as well as to investigate its ability to track sound propagation through a skull bone while the temperature is rising [11]·
II. Materials And Methods
A. Skull Specimens
Four human ex vivo skull caps fixed in 10% buffered formalin were used in this study. The skulls were obtained through a research agreement with the Division of Anatomy of the University of Toronto with the approval from the Research Ethics Board of Sunnybrook Health Sciences Centre. Each skull was mounted in a polycarbonate frame and was rinsed with deionized water then degassed in degassed/deionized water under vacuum for at least two hours before the experiments. The four skull specimens had been imaged with a CT scanner previously as described in [37] in order to obtain the skull thickness information for the resonance method and the density information for the CT-based aberration correction. The voxel dimensions were 0.625 mm × 0.625 mm × 0.625 mm, and the image matrix was 512 × 512, with a total of 287-307 slices covering the skull caps.
B. Benchtop Experiments with Single Transducer
The experimental setup is shown in Fig. 1. A focused transducer (V389, Olympus, Center Valley, PA, USA) was used in this study, with a fundamental frequency at 0.5 MHz, aperture of 38.1 lmn, axial focal depth of 55 lmn, lateral and axial full-width-at-half-maximum of 6.8 ± 0.3 and 60.5 ± 0.2 lmn, respectively. A hydrophone was fabricated in-house with a lead zirconate titanate (PZT) tube in a diameter of 1 lmn and a height of 5 lmn. The hydrophone and transducer were 65 mm apart, mounted and co-registered by an in-house-fabricated C-shaped holder, whose movement was controlled by a 3-axis positioning system with 2-phase stepping motors (PK266-03B-P2, VEXTA®, Oriental Motor Co., Ltd., Taito-Ku, Tokyo, Japan), stepping motor controllers (Velmex Inc., East Bloomfield, NY, USA) and an encoder (Quadra-Chek 100, Heidenhain, Schaumburg, IL, USA). The skull specimen was inserted between the transducer and hydrophone. It was attached to a manual rotary positioner (Series 481-A, Newport, Irving, CA, USA) and a three-directional Cartesian positioning system (UniSlide® Assemblis Series A4000, Velmex Inc., East Bloomfield, NY, USA), which allowed the ultrasound incident angle to be adjusted. An oscilloscope (TDS 3012, Tektronix, Beaverton, OR, USA) was used to record the reflection (Fig. 1(a))/transmission (Fig. 1(b)) signals captured by the transducer and hydrophone, respectively. The focus of the transducer was centered within the skull bone. Since the axial focal size (~60.5 mm) is much larger than the skull thickness (~ 10 lmn), the wave within the skull can be treated as plane wave. The hydrophone was moved to at least four fiducial markers on the skull to measure the coordinates in the ultrasound space. The locations of the same markers in CT space were also recorded, and a transformation matrix from CT to ultrasound coordinate systems was calculated [38] to allow the skull CT to be registered to the ultrasound space. All measurements were conducted in a tank with rubber-lined walls filled with degassed and deionized water.
Fig. 1.
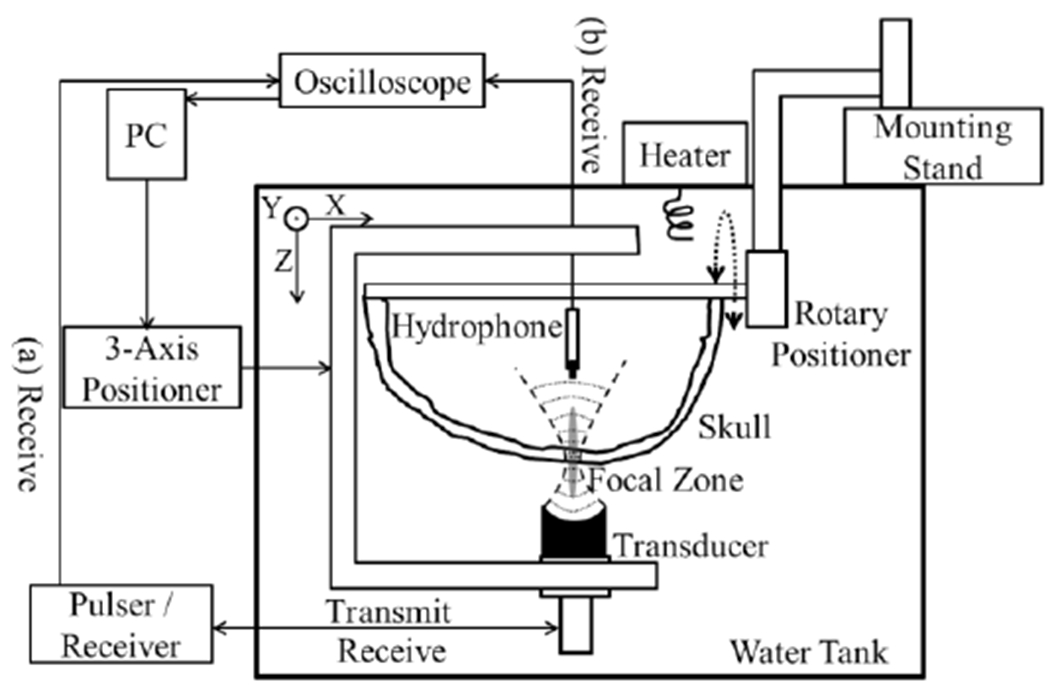
Experiental setup for (a) pulse-echo measurements based on the resonance method and (b) hydrophone measurements.
The configuration of the resonance method is shown in Fig. 1(a). A pulse was emitted through the transducer from a Pulser/Receiver (DPR300, JSR Ultrasonics, Pittsford, NY, USA). The signals reflected back from the skull within the lateral focal region were recorded by the transducer and eventually transferred to PC via Pulser/Receiver and oscilloscope. The pulse duration was 2.12 μs, generating a spatial-peak-temporal-peak (SPTP) pressure of approximately 0.37 MPa at the focus measured by a calibrated fiber-optic hydrophone (Precision Acoustics, Dorchester, Dorset, UK), resulting in the SPTP, spatial-peak-pulse-average (SPPA) and spatial-peak-temporal average acoustic intensity (SPTA) of 4.63, 0.37, and 7.8×10−5 W/cm2, respectively. With the low ISPPA and ISPTA value, no thermal or mechanical effects were expected in the skull or skin.
Second (Fig. 1(b)), the hydrophone method was applied by cross-correlating the time of flight of the pulsed signal received by the hydrophone with and without the presence of the skull. This technique has served as the gold-standard method to determine the skull phase aberration corrections in several studies [19, 21, 39–41]. All the waveforms were captured by the oscilloscope (sample size: 104, sampling frequency: 50 MHz) and transferred to the computer for further analysis with MATLAB™ (R2016b, Mathworks, Natick, MA, USA). Fig. 2(e) serves as an example of the signals received by the hydrophone before cross-correlation was performed. Due to the small surface area of the hydrophone, the transmission from the transducer to the hydrophone can be treated as a single acoustic path whereas reflection from the skull is affected by both lateral focal size and transducer aperture.
Fig. 2.
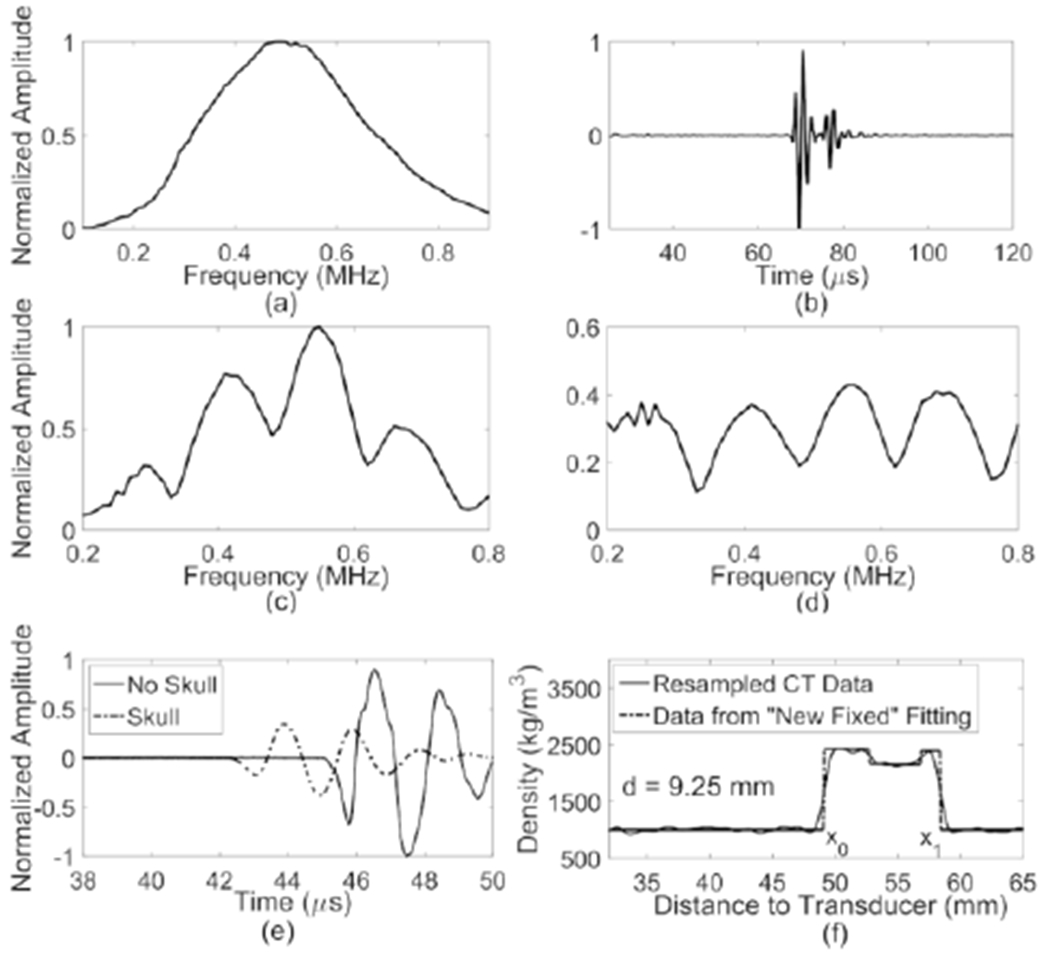
(a) Impulse response of the 500kHz transducer; (b) Measured radiofrequency (RF) signal reflected from the skull in time domain; (c) Frequency spectrum of the RF signal; (d) Frequency spectrum with deconvolution; (e) signals received by hydrophone without (solid line) and with the insertion (dashed line) of human skull cap; (f) density profile (solid line) resampled 100 times along a line passing through the skull and the corresponding optimized fitting from the “New Fixed” model (dashed line) to get the thickness of the skull cap (d = x1 – x0).
C. Temperature Dependence Of Skull Resonance Frequency
The temperature of the water was elevated and controlled by a heater (Thermomix® B, B. Braun Melsungen AG, Melsungen, Germany) from 25 °C to 42 °C with an increment of 3 °C. Each skull sample was submerged in the water at the targeted temperature for approximately 20 min to achieve thermal equilibrium. Both the resonance and hydrophone methods were employed to measure the phase shift of the ultrasonic wave induced by the skull at the selected skull locations.
D. Skull Induced Phase Shift Calculation By Resonance Method
The theory of the resonance method lias been explained in the following works [34, 42, 43]. In brief, the frequency spectra of the reflected signal from a broadband pulse in a lossy medium yield a result similar to the plane wave intensity-transmission coefficient:
| (1) |
where ρ, c, kb and d represent the density, speed of sound (SoS), wave number and thickness, respectively, and the subscript b and w denote the propagation mediums bone and water, respectively. From (1), it is evident that at frequencies such that kbd = nπ, total transmission occurs, which is shown as a decreased reflection from skull bone on the frequency spectra of the reflected signal. These frequency minima are the resonance frequencies of the bone layer and can be obtained by locating the zeros of the first derivatives with respect to frequency:
| (2) |
From (2), the SoS in bone can be calculated as
| (3) |
The time delay caused by the skull insertion can be represented as
| (4) |
which yields the equation of the phase difference caused by the skull:
| (5) |
where f represents the center frequency of the transducer, the SoS in the water, cw, is temperature dependent, and d is the thickness of the skull bone at the center of the lateral focal region obtained from CT images which will be explained in the next section.
After the signals echoed from the skull (Fig. 2(b)) were recorded, a Fourier transform was applied (Fig. 2(c)) followed by a deconvolution of the transducer’s impulse response (Fig. 2(d)). The impulse response (Fig. 2(a)) was measured separately by Fourier transforming the reflected pulsed signals from the water-air interface at a distance of the transducer’s focal depth. The local minima within the bandwidth of the transducer (0.2-0.8 MHz, above 25% of the maximum amplitude at the center frequency) were used to calculate the phase shift and an average was taken at each spot. The results were compared to the gold-standard hydrophone method, in which the waveforms were digitally filtered with a fourth order Butterworth bandpass fdter (0.1-1 MHz) and the change in the time of flight was calculated through cross-correlating the data with and without the skull (Fig. 2(e)).
E. Incident Angle Calculation And Skull Thickness Measurement From CT Data
To register the skull CT with the experimental space, a transformation matrix, solved with the method described by Horn [38], was applied to the CT data calculated from the positions of the landmarks in both of the CT and experimental coordinate systems. Registration accuracy was also tested by calculating the averaged distance between the experimental positions of the landmarks and the new positions transfonned from CT data. In our measurements, this registration error is 0.6 ± 0.4 lmn across all four skulls.
CT image intensity in Hounsfield units was converted to a density map following a linear relationship illustrated in Connor el al. [44]. Skull segmentation was performed in MATLAB™ by thresholding the density and thus only the voxels related to skull bones were shown. The incident angles of the ultrasonic impulses at the skulls were calculated by using the triangular-meshed skull surface data which were generated from CT segmentation following the procedure outlined in Jones el al. [45]. The incident ray represented by a vector from the center of the transducer to the location of the hydrophone was defined and discretized with a step size a quarter of the CT voxel resolution 0.625 lmn. The distance from every point along tliis ray to the centroid of every triangle on the meshed skull surfaces was calculated and the triangles with shortest distance were found. The incident angle to the skull surface at the closest triangle to the transducer center was determined.
The thickness of the skull was calculated from the CT data based on the “New Fixed” method introduced in Treece’s study [46]. The resolution of the CT image (0.625 mm) in this study is close to a quarter of the wavelength of the transducer center frequency (0.75 mm) in water, which means that one voxel difference may lead to an almost 90° phase changing (d′ = d – cw/4f substituted the d with d′ in (5) ). With the given resolution, it is necessary to interpolate the CT data and fit it with an optimized model in order to provide accurate skull thickness estimation. Two algorithms, “Half-Max” and “New Fixed”, described in Treece’s study [46] have been tested. “Half-Max” provided better thickness estimation on Sk2 and Sk4, while “New Fixed” was more accurate with thinner skulls (skull thicknesses are summarized in Table 1). This matched with the simulation in Treece’s study that the “Half-Max” method tends to overestimate the thickness of the cortical bone thinner than 2.2 lmn, especially with low CT resolution. Eventually, the “New fixed” technique lias been chosen to estimate the skull thicknesses in our study.
TABLE I.
Mean thickness, incident angles and the percentage of phase difference less than 45° and 20° of all the measured spots on skulls 1-4 (ntotal = 784).
| Incident Angle (°) | Percentage (%) of Phase Shift Difference | ||||||
|---|---|---|---|---|---|---|---|
| #Skull | Thickness (mm) | Outer Surface | Inner Surface | <45° | <20° | ||
| Resonance vs Hydrophone | CT-based vs Hydrophone | Resonance vs Hydrophone | CT-based vs Hydrophone | ||||
| Sk1 | 6.7 ± 0.6 | 5.5 ± 3.2 | 7.8 ± 4.5 | 67.4 | 59.1 | 36.2 | 22.8 |
| Sk2 | 7.0 ± 1.5 | 4.5 ±2.5 | 9.0 ± 5.6 | 86.1 | 76.2 | 45.0 | 31.1 |
| Sk3 | 5.3 ± 0.6 | 5.0 ± 2.8 | 9.1 ± 5.4 | 82.4 | 91.2 | 42.0 | 65.5 |
| Sk4 | 8.5 ± 0.9 | 5.5 ± 3.2 | 9.2 ± 4.4 | 67.9 | 81.8 | 34.5 | 32.5 |
| All 4 skulls | 74.0 | 74.5 | 38.5 | 35.1 | |||
| All 4 Skulls (incident angle < 5°) | 80.9 | 76.2 | 45.4 | 37.2 | |||
Assuming that the cortical layer is locally flat and of uniform thickness within the extent of the imaging system’s point spread function (PSF), and the cortical layer lie orthogonal to the CT imaging plane (i.e., out-of-plane PSF not taken into consideration), the density along the incident ray through the skull can be modeled as a convolution of the density with an in-plane PSF. The density y over distance x can be expressed as follows [46]:
| (6) |
where y0, y1, y2 are the density of water, cortical and trabecular bone, respectively, x0 and x1 are the locations of outer and inner skull surfaces, and H(x) is a step function. The in-plane PSF gi can be modeled as the follows:
| (7) |
where σ is the blur extension. By differentiating y(x) , convolving with gi(x) and integrating the result, the density variation over distance, yblur,r=0(x) can be modeled as
| (8) |
The CT data were resampled using spline-interpolation along the line in the image plane normal to the skull surface at 100 times the original CT samples (Fig. 2(f) solid line). These were later fitted with the model of (11) (Fig. 2(f) dashed line) in order to estimate the edges of the cortical layer (x0, x1). In the process of optimization, the density of water y0 was determined from the histogram of the CT images. y2 (the density of the trabecular bone) was left free for the model to discover due to the fact that its density varies at different locations. The in-plane extent of uncertainty σ was unconstrained and the cortical density yi was set within the range of [2000, 3000] kg/m3.
F. Skull Induced Phase Shift Calculation By CT-Based Analytical Method
An analytical method based on Clement’s study [11] was used to simulate the phase shift induced by the skull based on the CT-derived skull density, thickness and the orientation with respect to the transducer in the experimental setup, similar to the technique employed in Jones & Hynynen [47] for transcranial passive acoustic imaging. The longitudinal SoS in skull is density- and frequency-dependent achieved from a two dimensional spline-interpolation of the empirical data of SoS as a function of density under various frequencies [37]. The time of flight in skull bone was determined by calculating the longitudinal sound speed profde within the skull along the incident ray between the center of the transducer and the skull, neglecting both reflection and refraction effects. As a result, the time delay caused by the presence of the skull can be represented as the time-of-flight difference between the trans-skull and water-path cases:
| (13) |
where Dn is the length of the ray within the skull. The phase shift can then be calculated with (4).
III. Results
There were in total 784 locations measured on four ex vivo human skull caps (nSk1 = 276, nSk2 = 151, nSk3 = 148, nSk4 = 209). An example of the radiofrequency signal received and converted by the transducer from the reflected ultrasound on Sk2 is shown in Fig. 2(b), and the corresponding normalized frequency spectrum before and after deconvolution are displayed in Fig. 2(c & d). The SoS in skull bone can be calculated by measuring the locations of the minima and applying the frequency difference of the adjacent minima to (3).
The resonance method-calculated phase shifts were compared to the hydrophone method in Fig. 3(a). An absolute phase difference of 45° (dotted lines) was set as the boundaries based on the Goodman criterion of λ/8, which is a theoretically established cutoff indicating good focusing quality [36, 48]. It is demonstrated by the simulation that an absolute phase error of 45° results in a decrease of acoustic pressure approximately 10% [49]. The mean difference between the two modalities is 33° ± 26°. A histogram of the phase shift difference is shown in Fig. 3(b). In 72.9% of the 784 measurements the two modalities differed by less than 45°, and in 37.1% by less than 20°. By excluding the spots with incident angles on the outer surface larger than or equal to 5°, 80.4% of the 403 measured spots had a phase shift difference less than 45°, and 42.9% by less titan 20°, as shown in Fig. 3(c & d).
Fig. 3.
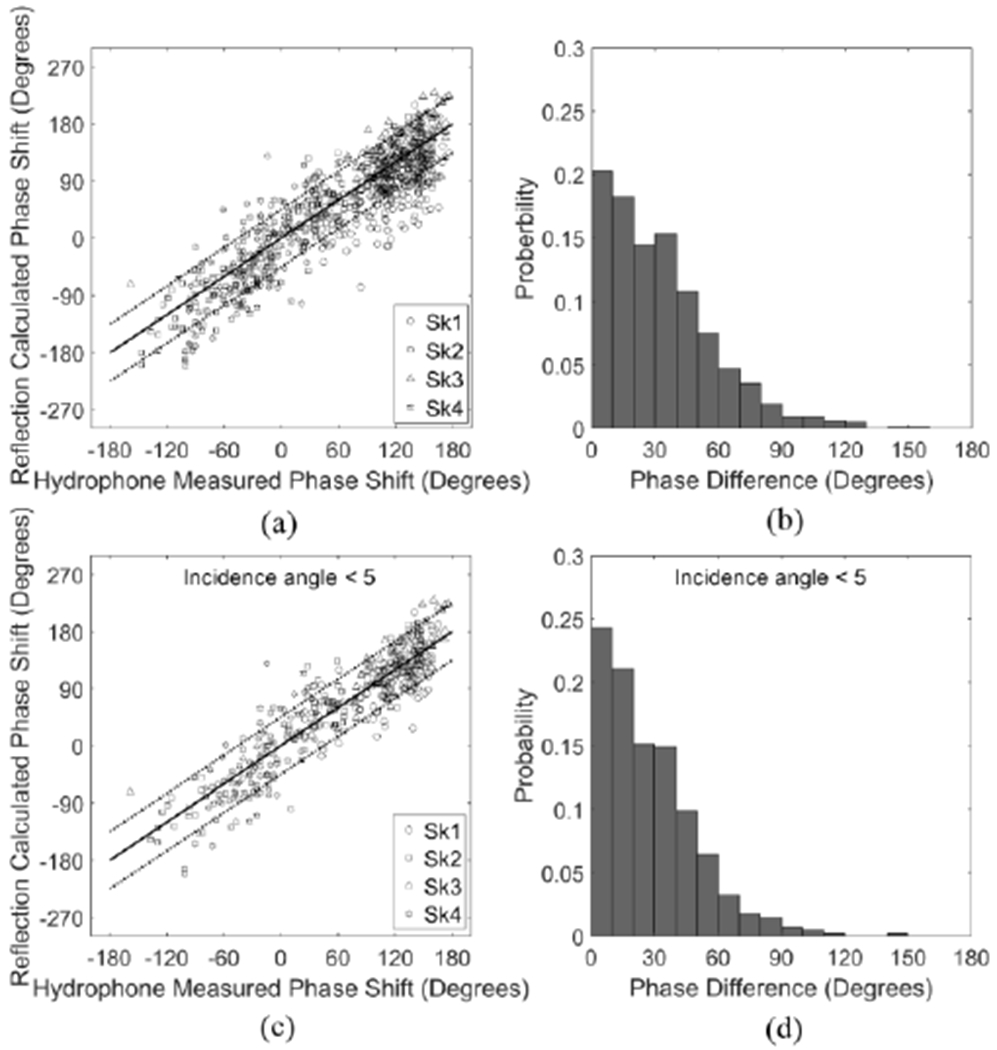
(a) Reflection-calculated phase shifts (°) based on resonance method as a function of hydrophone-measured phase shifts (°) and (b) histogram of the phase differences in skull caps Sk1-4. (c) Reflection-calculated phase shifts (°) as a function of hydrophone-measured phase shifts (°) and (d) histogram of the phase differences in skull caps Sk1-4, excluding the measured spots with incident angle ≥ 5°. Solid and dotted lines denote 0° and ± 45° in phase differences between the two modalities, respectively.
The phase shifts calculated from CT-based method with analytical model as a function of the hydrophone-measured phase shift are presented in Fig. 4(a & c). There is a systematic shift for the CT-based analytical method as it can be seen that most of the markers are within the region between 0 and - 45°. The mean difference between the two modalities is 31° ± 20°, which slightly drops to 29° ±19° when the spots with incident angles larger than 5° have been excluded. 74.5% of the measurements have a phase shift difference between the two methods of less than 45°, and 35.1% differed by less than 20° (Fig. 4(b & d)). Skull thicknesses, incident angles and the percentage of phase shift difference have been summarized in Table 1. The resonance method provides similar results as the CT-based analytical method in general, although the accuracy varies from skull to skull.
Fig. 4.
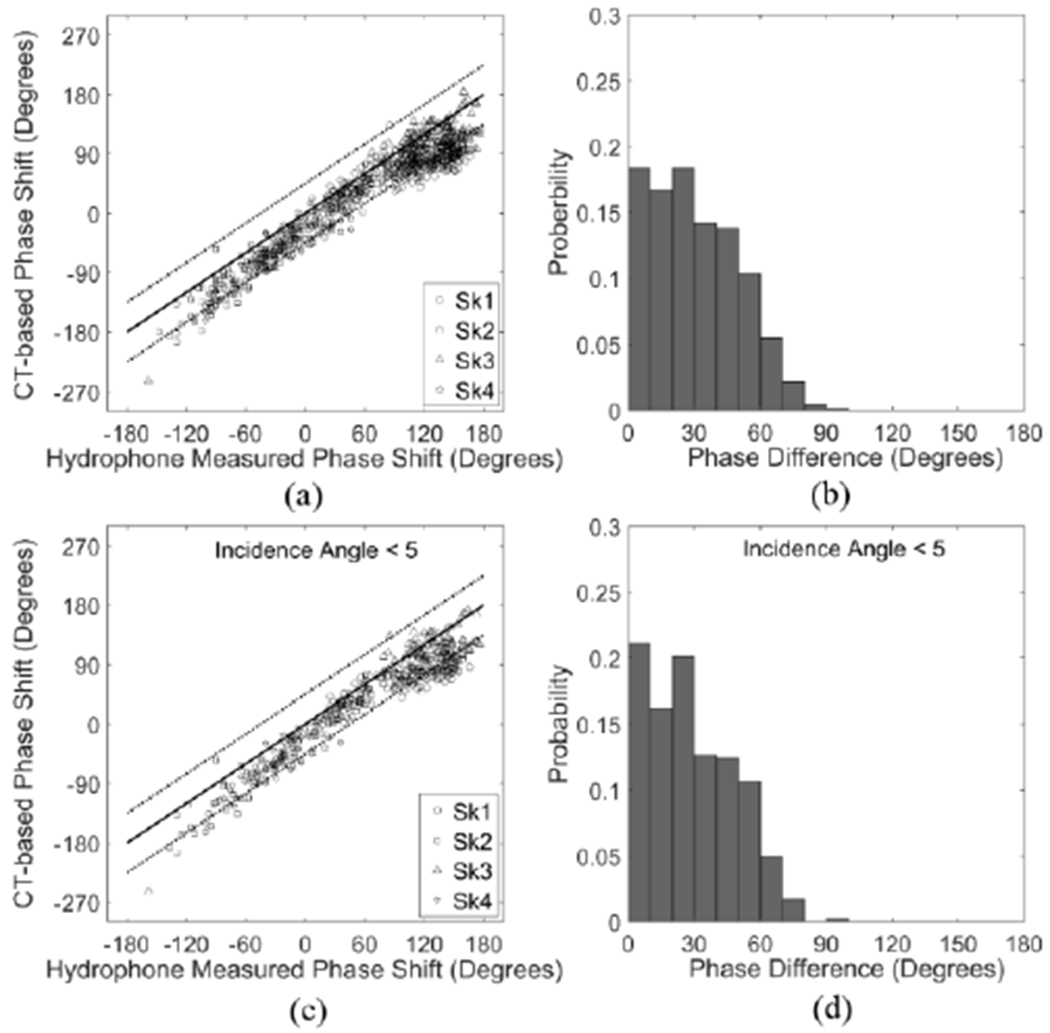
(a) CT-based phase shifts (°) as a function of hydrophone-measured phase shifts (°) and (b) histogram of the phase differences in skull caps Sk1-4. (c) CT-based phase shifts (°) as a function of hydrophone-measured phase shifts (°) and (d) histogram of the phase differences in skull caps Sk1-4, excluding the measured spots with incident angle ≥ 5°. Solid and dotted lines denote 0° and ± 45° in phase differences between the two modalities, respectively.
Additional information is revealed in Fig. 5, which shows the percent of measured points with a deviation smaller than a given phase angle difference from the three modalities. A sharp rise indicates good correlation between the resonance or CT-based method and the hydrophone method. Fig. 5(a) illustrates the overall comparison of resonance and CT-based methods relative to the hydrophone. Resonance method with incident angle less than 5° lias a slightly sharper rise than the CT-based one. Specific cases were displayed in Fig. 5(b). The measurements on each skull plotted in terms of this deviation illustrate better correlation on Sk2 & Sk3, with 86.1% and 82.4% differing by less than 45°, respectively, and 45.0% and 42.0% less than 20°, respectively, as opposed to an around 67% of the spots with deviation less than 45° and approximately 35% less than 20° on Ski and Sk4.
Fig. 5.
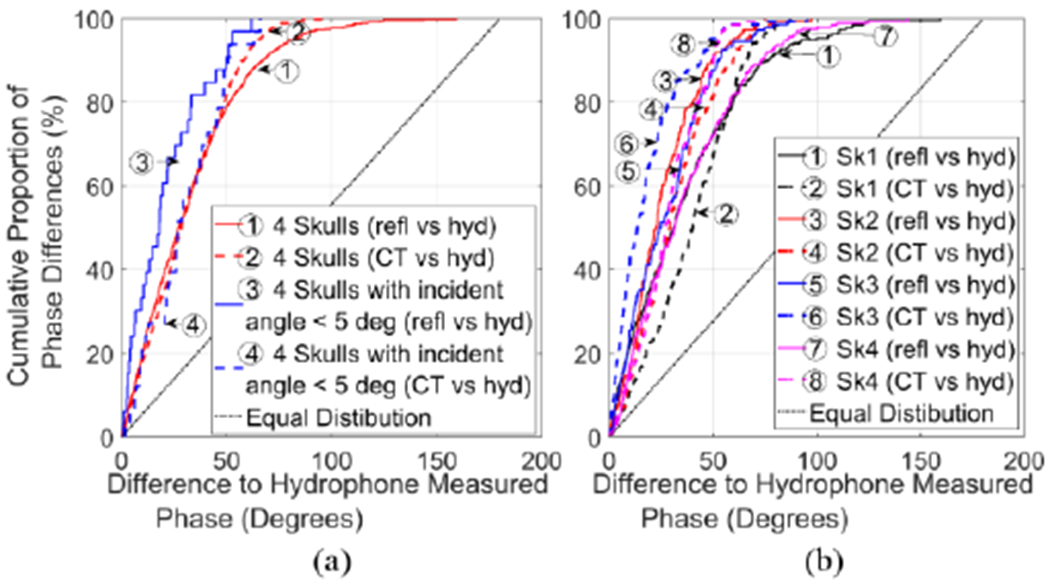
Cumulative proportion of the phase differences of the three modalities (solid line: resonance vs. hydrophone method; dashed line: CT-based correction vs. hydrophone method) for all the spots measured. (a).All 4 skulls were represented with red line, the case with incident angle less than 5° with blue line, and (b) skull 1-4 with black, red, blue, and magenta lines, correspondingly. Equal distribution was marked with dotted line. Ideally the graph would be a step function.
Comparison of the resonance/CT methods to the hydrophone method in tenns of the calculated average time delays induced by the skull and SoS in skull bones are shown in Fig. 6. SoS of resonance and hydrophone methods were calculated with (3) and (4), respectively. SoS of CT-based method was calculated via 2D interpolation as mentioned in the Method Section. It is illustrated that the resonance method produces an average time delay and SoS closer to the hydrophone method than the CT-based method by comparing their average values. An analysis of variance (ANOVA) test and a post-hoc paired samples test were performed on the data using SPSS® (SPSS for Windows, Version 15.0. Chicago, SPSS Inc.; 2006). Statistically significant differences were found between the hydrophone, resonance and CT methods. ANOVA tests of within-subjects effects showed that there were statistically significant differences between the means of time-delays (df = 2, F = 309.745, p-value < 0.001) and SoS (df = 2, F = 201.528, p-value < 0.001) from the three modalities. Tests of between-subjects effects also showed statistically significant differences between the four skull samples (time delay: df = 3, F = 85.977, p-value < 0.001; SoS: df = 3, F = 132.935, p-value < 0.001). Post-hoc paired tests with the data obtained from all 403 locations on the skulls illustrated statistically significant differences between the three modalities as well, except for Sk3 between the hydrophone and resonance methods.
Fig. 6.
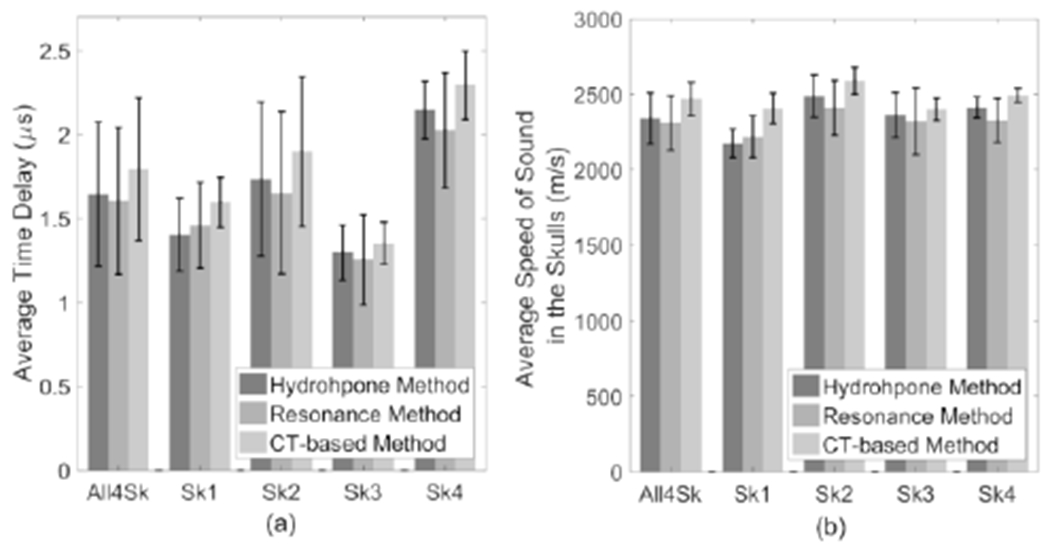
Comparison of (a) the average time delay and (b) speed of sound in skull bones calculated from hydrophone and resonance method (n = 403). “All4Sk” represents the average time delay and speed of sound for all 4 skulls.
The information of the skull phase shift difference between the resonance/CT methods and the hydrophone method allows an estimation of the reduction of transcranial peak acoustic pressure. In the case of a phase array with N elements, assuming the peak amplitudes with the hydrophone phase correction through each element are the same and all nonnalized to 1, the peak pressure amplitude at the focus will be reduced by a percentage [11]:
| (14) |
where ΔP is the pressure loss, P0 is the peak pressure at the focus with hydrophone method, ϕn is the absolute value of the phase error induced by the inaccurate prediction of the skull phase shift from the resonance/CT-based analytical methods. With the resonance method, there is a 6.7%, 4.4%, 5.6%, and 10.8% of peak pressure reduction, as opposed to a smaller pressure loss of 2.4%, 5.5%, 4.9%, and 3.5% with the CT method on the skulls Ski, Sk2, Sk3, and Sk4, correspondingly.
Measurements of the skull phase shift with temperature elevated from 25 °C to 42 °C were performed with both resonance and hydrophone methods. The mean change in phase from all 4 skull samples between room temperature and 42 °C as a function of temperature at 0.5 MHz has been shown in Fig. 7(a). The resonance method produced 2.65° of phase change per °C, slightly higher than 2.05° as given by the hydrophone method. The change of mean resonance frequencies of skulls is proportional to the variation of temperature with a negative coefficient, as illustrated in Fig. 7(b).
Fig. 7.
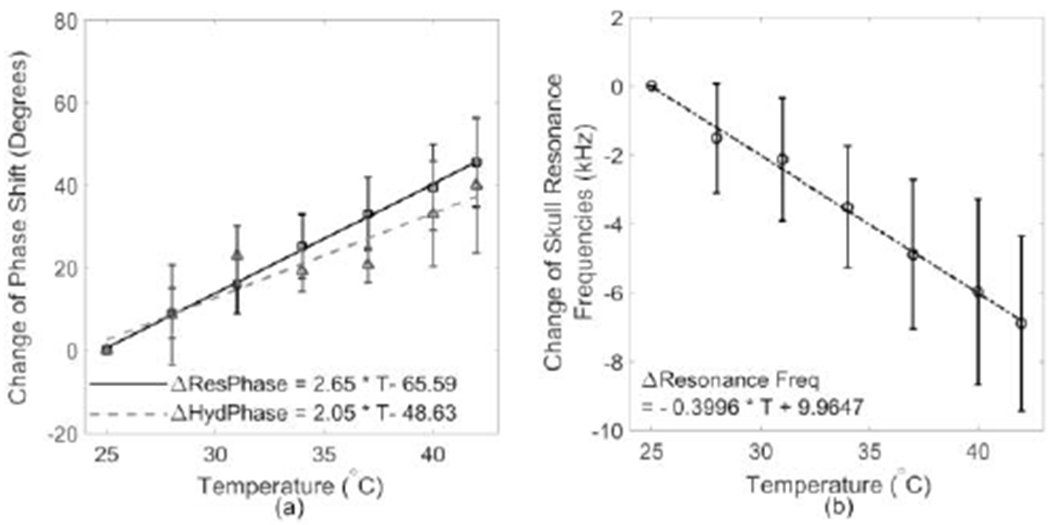
(a) a summary of the change of phase shift measured on all four skulls with resonance (solid line) and hydrophone methods (dashed line); (b) the change of skull resonant frequencies as a function of temperature.
The phase shift was measured at each spot with elevated temperature using both the resonance and hydrophone methods. No sharp decrease in the accuracy was observed during the temperature elevation. The mean accuracy across the 17 °C temperature difference is 78% ± 9% for all the measured points on the 4 skull specimen.
IV. Discussion
This study explored the factors that may improve the accuracy of the resonance method in determining the ultrasound phase shift induced by the skull bone as well as the feasibility of using the resonance method to detect the change of skull phase shift dynamically. The results show that approximately 73% and 37% of all measured points (ntotal = 784) deviate by less than 45° and 20°, respectively, when comparing the resonance method to the hydrophone one, which were increased from nearly 65% and 30% in the previous study [35]. The mean difference of the phase shifts between the two modalities is 30.5°, approximately 15° less than Aarnio’s study [35]. This decreased difference demonstrates a higher accuracy in phase aberration correction with the modified resonance method.
The improvement of accuracy may first of all come from the experimental configuration that the focus of the transducer was centered within the skull bone. It benefits from both a small field size and large aperture resulting in smaller measurement discrepancy in geometry interfering with skull and a higher signal-to-noise ratio (SNR), than the earlier study [43]. Secondly, the incident angle of the ultrasound burst plays an important role in the measurement accuracy. It has been shown that the frequency spectra deteriorated rapidly with an increasing incident angle [43, 50], which induced extra difficulties in detecting the resonance frequencies. By excluding the measured spots with incident angle ≥ 5°, about 80% of the measurements had a deviation of 45° or less. Comparing the SoS in skull predicted by the two modalities, the resonance method offered 2310 ± 180 m/s, approximately 1.3% lower than the mean sound speed 2340 ± 170 m/s given by the hydrophone method, as opposed to 5.8% higher in the previous study [35].
In addition, the choice of a lower frequency transducer also contributed to the improvement of the measurement accuracy from 65% (at 0.9 MHz) [35] to 73% (at 0.5 MHz), resulting from a lower attenuation rate at 0.5 MHz through skull [51] and an increased SNR. Furthermore, it is less impacted by the incident angle with lower frequency. However, there is a trade-off between the low center frequency and wide bandwidth. The narrow bandwidth brought in by the low frequency increases the difficulty of determining the resonance frequencies on thin skulls. The bandwidth of the 0.5 MHz transducer at 25% of the maximum amplitude is in the range of [0.2, 0.8] MHz, much narrower than the range [0.6, 1.74] MHz in the previous work [35], which made it difficult in measuring the resonance frequencies with thinner skulls Sk1 & Sk3.
The skull thickness calculated from the CT data is also critical to the accuracy and practicality of the method. Under the limited CT resolution, the “New Fixed” model provided a better estimation of the skull thickness. Otherwise, an overestimation of thickness may result in a systematic shift of the skull induced phase shifts.
Although the accuracy of the resonance method has been improved, there are still some outliers distributed out of the Goodman criteria region [36], as shown on Fig. 3(c). Several factors might cause the errors when using the resonance method. First, by comparing the “New Fixed” fitting in the skull thickness calculation to the CT density profiles along the ultrasound wave propagation paths at the locations with big errors, it was found that with the thick skulls the “New Fixed” method [46] sometimes failed to find the correct boundaries of the cortical bone, resulting in the inaccuracy of the calculated phase shifts. This phenomenon matches with Treece’s simulation that the “New Fixed” fitting tends to give a slightly bigger error compared to the true value when the cortical bone thickness is over 3.5 mm, but it is less sensitive to the cortical bone thickness overall compared to the other fitting methods. Additionally, the heterogeneity of the skull also introduced error into the calculation. By going through the CT slices adjacent to the outliers, it was found that at some locations the skull structure was not consistent within the focal region (lateral-FWHM: 6.8 ± 0.3 mm), where a sharp drop of the trabecular bone density was shown. Since the phase shift information given by the resonance method was a combination of multiple reflection paths, the big change in bone density may cause a big error, while compared to the hydrophone and CT-based analytical methods that are based on single path transmission with simplified skull structure. As a result, to further improve the accuracy of the resonance method, a transducer with a smaller lateral focus is preferable, in order to avoid the big variance from skull structure and to keep the assumption of flat skull surface valid. In the measurement with the hardware limitation, a strict target spot selection protocol should be developed, based on the SNR of the frequency spectra, the incident angles and the CT images at the targets and their surroundings. Spots may need to be excluded if small spikes were shown all over the resonance frequency spectra, which are signs of shear wave propagation due to large incident angles [35], no matter what incident angles given by the calculation. In addition, it may be beneficial to scan the targets as well as their surrounding area within the focal region and exclude the ones with inconsistent frequency spectra. It may be also helpful if the skull thickness and incident angle calculation are based on multiple paths in the simulation. Once the results vary a lot within the focal region, the target spot should be excluded. Last but not least, a CT scan with higher resolution will provide a clearer boundary of the cortical bones and thus a better fitting with the ‘New-fixed’ method in the thickness calculation.
A direct comparison of the resonance method to the other noninvasive method such as CT-based analytical model has been presented. In general, the resonance method offers a slightly better prediction of the skull phase shift as the CT-based analytical model in terms of the distribution of phase discrepancy compared to the gold-standard method, as demonstrated in Fig. 5(a). The pressure loss estimated via (14) from the resonance method is close to the CT analytical method overall. On Sk4 (the thickest skull in this study), the reduction from resonance method was three times higher. It may result from the skull thickness calculation fitted with the “New Fixed” model since it has slightly larger error in estimating thicker cortical layers [46]. The resonance-calculated phase shifts seem to be unbiasedly distributed along the main diagonal as presented in Fig. 3 (a & c), offering a better accuracy than the CT-based analytical method, in which a systematic shift can be seen in the phase lag as displayed in Fig. 4(a & c). Although spline-interpolation has been performed along the incident ray through skull, it might still be ambiguous to define the boundaries of the cortical bones limited by the low CT imaging resolution, which may result in an overestimation of the thickness and the time delays, similar to the results given by the ‘Half-Max’ method [46], and contribute to the systematic shift. In this study, the CT-based analytical model was chosen in the comparison due to its low computational load [47] in the same range as the resonance method. There are other CT-based simulation models [52, 53] that are also capable to offer a high pressure restoration through skull similar to the level achieved by the resonance method. For example, 3D finite differences code in the time domain (FDTD) was used to simulate ultrasound propagation through skull. 90% of the optimal pressure amplitude was restored with a 300-element array at 1 MHz through human skull [52]. A speed of sound model for a 3D finite difference time domain fluid simulation was optimized, with 14% reduction of acoustic pressure at 1 MHz [53]. A lower pressure loss is expected at 0.5 MHz with the CT based numerical models, but it may not be suitable for dynamic skull aberration correction due to the relatively long computational time (2 to 3 hours).
Adaptive focusing via dynamic skull aberration correction would be necessary in high-intensity transcranial therapeutic ultrasound treatments. Several techniques have been explored to perform dynamic phase corrections. For example, energy-based adaptive focusing was developed by using Magnetic Resonance Acoustic Radiation Force Imaging (MR-ARFI) to map tissue displacement induced by the radiation force of the focused ultrasound beam [54–56]. Adaptive focusing for transcranial ultrasound imaging has also been studied by using two identical linear phased arrays to measure skull bone attenuation and phase shifts with migrated spatiotemporal inverse filter [57–59]. In high intensity FUS transcranial treatments, the potential technique for adaptive focusing has to have the capability to capture the change of skull induced phase shift due to temperature elevation during the ramp of acoustic power. In clinical trials, a reduction of energy-temperature efficiency was observed during repeated high power sonications [24], and local skull bone changes were revealed in some patients potentially indicating thermal damage [25]. Previous simulation and in-vivo experiments investigated these phenomena and revealed the positive correlation between the acoustic power and the focal volume dispersion, which illustrated a de-phasing effect occurring as the skull was heated. Computer simulations further implied that a change in the SoS of the cranial bone due to the temperature elevation during the sonication was partially responsible for the widening of the focus. In addition, the increased skull bone attenuation was also demonstrated, resulting in the local thermal damage [24]. As a result, the model prediction with the initial temperature may no longer be accurate, leading to a distortion of the focusing pattern and thus the necessity of dynamic phase correction and adaptive focusing. With the improved accuracy and low computational load, the resonance method shows the potential to track the temperature change and to detect the adaptive phase shift change during the temperature elevation.
Previous work has shown that the change of skull phase shift measured with hydrophone as a function of temperature follows a linear fit with a slowly increasing rate of 0.29° of phase per °C, leading to a total phase shift change less than 14° when the temperature was elevated from 22 °C to 50 °C [11]. As a result, conclusions have been drawn that the increased temperature would not significantly affect the phase shift change and thus the phase shift measured at room temperature can be applied to the skull phase correction at body temperature. However, the temperature control was not performed in that study. Skull samples were heated in a separated water tank and were transferred into the experimental setup when temperature reached the set value. Heat diffusion would occur once skulls were placed in the water at room temperature thus decreasing the actual skull temperature in the measurement. In our study, modification has been made so that temperature control and skull phase shift measurements were performed in the same experimental setup. Both resonance (2.65°/°C) and hydrophone methods (2.05°/°C) were found to produce higher slopes than the previous study (Fig. 7(a)). Therefore, it is necessary to compensate the change of phase shift due to thermal deposition, since a 10 °C increase in high intensity ultrasound sonications leads to approximately 20° variation in phase and about 39% of the phase correction shifted out of the Goodman criteria region [36]. Secondly, it is shown that, in general, the resonance method provides a higher slop than the hydrophone method in Fig. 7(a). Resonance method relies on the impulse-echoed signals from multiple paths depending on the aperture of the transducer and its lateral focal size as shown in Fig. 1. Thus more variation in term of skull density and incident angles during the temperature elevation process was expected, as opposed to the hydrophone measurement based on single path transmission. Thirdly, it is found that the resonance method provides a linear fit to the phase shift dependency of temperature change in all of the skulls tested better than the hydrophone method. Last but not least, the accuracy of the resonance method in determining the skull phase shift during temperature elevation has been summarized as compared to the standard hydrophone method. No obvious trend of accuracy decreasing with an increase of temperature has been observed on the skull, and the averaged accuracy was able to be maintained at 78% ± 9% (n = 110). Therefore, the resonance method has shown the capability to not only determine the skull phase shift but also track its change under temperature elevation, which could be useful during therapy sonications. The skull heating has been shown to increase the focal spot size and decrease the heating efficiency of clinical brain treatments [24]. Thus, the method could be implemented to the therapy device and used intermittently during the sonication to monitor the skull heating noninvasively. These measurements could then be used to adjust the phases of the driving signals to compensate for the heating induced changes. With the formula given by the linear fitting on Fig. 7(b), 400 Hz decrease of resonance frequency correlates with approximately 1 °C increase. The trend indicates an inverse relationship between the speed of sound in the bone and the temperature, in agreement with the previous study [60].
The configuration of centering the focus within the skull bone not only minimizes the impact of the skull geometry, but also will be beneficial to the conformal phased array design proposed in the work [61]. Each of the concave transducers in this conformal helmet, with proper design, can naturally focus inside the skull bone with normal incidence so that planar transmission would occur in the skull bone and the brain would be in the far field of the transducer, in order to increase the transcranial transmission and the beam steering range. With such conformal array configuration, it would be naturally conducive to calculating the skull phase shift with the resonance method. Since the resonance method is sensitive to detect the phase shift change due to temperature elevation demonstrated by the linear relationships in Fig. 7, adaptive focusing may be achieved with the use of this conformal phased array design [61] to dynamically correct the distortions induced by the skull bone and update the phase correction for each element in the phased array during temperature elevation. By monitoring the change of the skull resonance frequencies, the coefficient describing the average change of resonance frequency per 1 °C (−0.4 kHz/°C) may be used as an empirical parameter in estimating the skull temperature. In clinical practice, the conformal array scaffolding is customized based on the specific patient’s CT information and constructed to fit the patient’s head, allowing the natural focus of the concave transducers being centered inside the skull [61]. Without using this conformal array design, it is still feasible to place the focal zone within the skull bone, if the single element concave transducer is replaced by a phased array such that the focus can be electronically steered into the skull bone. Without centering the focus in between the outer/inner surfaces of skull, lower SNR of the reflected signal is expected. However, the resonance method should still work as long as the size of the axial-FWHM is larger than the skull thickness.
V. Conclusion
In conclusion, this study demonstrates that the accuracy of resonance ultrasound method in determining skull phase shift can be improved by centering the focus within the skull bone and confining the incident angle. An increased accuracy of approximately 15% and a better estimation of speed of sound were achieved compared to the previous work. In addition, a comparison with CT-based analytical method has indicated similar or a higher accuracy of the resonance method and a closer estimation of speed of sound in skulls. Finally, the resonance method was able to reveal the change of resonance frequencies along with the temperature elevation, illustrating the potential for dynamic phase correction in order to achieve adaptive focusing during high-intensity transcranial FUS treatments. Skull temperature may also be monitored with this linear temperature dependency.
Acknowledgment
The authors would like to thank Dr. Ryan M. Jones and Dr. Meaghan A. O’Reilly for suggestions and discussions, Dr. Skyler Mooney and Dr. Dallan McMahon for statistical analysis, and Anthony Chau, Elektra Lindquist-Dakogiannis, Michelle Kim and Pablo Gonzalez for technical support.
This work is supported by the National Institute of Biomedical Imaging and Bioengineering of the National Institutes of Health (R01 EB003268), the Canadian Institutes for Health Research (FRN 119312), and the Canada Research Chair Program.
Contributor Information
Lulu Deng, Physical Sciences Platform, Sunnybrook Research Institute, Toronto, ON, Canada.
Alec Hughes, Physical Sciences Platform, Sunnybrook Research Institute and the Department of Medical Biophysics, University of Toronto, Toronto, ON, Canada.
Kullervo Hynynen, Physical Sciences Platform, Sunnybrook Research Institute, the Department of Medical Biophysics and also the Institute of Biomaterials & Biomedical Engineering, University of Toronto, Toronto, ON, Canada.
References
- [1].Elias WJ et al. (2013, August). A pilot study of focused ultrasound thalamotomy for essential tremor. N. Engl. J. Med [Online]. 369(7). pp. 640–648. Available: doi: 10.1056/NEJMoa1300962 [DOI] [PubMed] [Google Scholar]
- [2].Lipsman N et al. (2013, May). MR-guided focused ultrasound thalamotomy for essential tremor: a proof-of-concept study. Lancet Neurol. [Online]. 12(5). pp. 462–468. Available: doi: 10.1016/S1474-4422(13)70048-6 [DOI] [PubMed] [Google Scholar]
- [3].Elias WJ et al. (2016, August). A Randomized Trial of Focused Ultrasound Thalamotomy for Essential Tremor. N. Engl. J. Med [Online]. 375(8). pp. 730–739. Available: doi: 10.1056/NEJMoa1600159 [DOI] [PubMed] [Google Scholar]
- [4].McDannold N et al. (2010, February). Transcranial magnetic resonance imaging-guided focused ultrasound surgery of brain tumors: initial findings in 3 patients. Neurosurgery [Online]. 66(2). pp. 323–332. Available: doi: 10.1227/01.NEU.0000360379.95800.2F [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Coluccia D et al. (2014, October). First noninvasive thermal ablation of a brain tumor with MR-guided focused ultrasound. J. Ther. Ultrasound [Online]. 2(17). pp. 1–7 Available: doi: 10.1186/2050-5736-2-17 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Jung HH et al. (2015, October). Bilateral thermal capsulotomy with MR-guided focused ultrasound for patients with treatment-refractory obsessive-compulsive disorder: a proof-of-concept study. Mol Psychiatry [Online]. 20(10). pp. 1205–1211. Available: doi: 10.1038/mp.2014.154 [DOI] [PubMed] [Google Scholar]
- [7].Martin E et al. (2009, December). Uigh-intensity focused ultrasound for noninvasive functional neurosurgery. Ann. Neurol [Online]. 66(6). pp. 858–861. Available: doi: 10.1002/ana.21801 [DOI] [PubMed] [Google Scholar]
- [8].Jeanmonod D et al. (2012, January). Transcranial magnetic resonance imaging-guided focused ultrasound: noninvasive central lateral thalamotomy for chronic neuropathic pain. Neurosurg. Focus [Online]. 32(1):E1, pp. 1–11. Available: doi: 10.3171/2011.10.FOCUS11248 [DOI] [PubMed] [Google Scholar]
- [9].Kim M et al. (2018, January). Treatment of Major Depressive Disorder via Magnetic Resonance-Guided Focused Ultrasound Surgery. Biol. Psychiatry [Online]. 83(1). pp. e17–e18. Available: doi: 10.1016/j.biopsych.2017.05.008 [DOI] [PubMed] [Google Scholar]
- [10].Fry FJ and Barger JE. (1978, May). Acoustical properties of the human skull. J. Acoust. Soc. Am [Online]. 63(5). pp. 1576–1590. Available: doi: 10.1121/1.381852 [DOI] [PubMed] [Google Scholar]
- [11].Clement GT and Hynynen K. (2002, May). Correlation of ultrasound phase with physical skull properties. Ultrasound Med. Biol. [Online]. 28(5). pp. 617–624. Available: doi: 10.1016/s0301-5629(02)00503-3 [DOI] [PubMed] [Google Scholar]
- [12].Flax SW and O’Donnell M. (1988, November). Phase aberration correction using signals from point reflectors and diffuse scatterers: Basic principles. IEEE Trans. Ultason. Ferroelec. Freq. Contr [Online]. 35(6). pp. 758–767. Available: doi: 10.1109/58.9333 [DOI] [PubMed] [Google Scholar]
- [13].O’Donnell M and Flax SW. (1988, November). Phase aberration correction using signals from point reflectors and diffuse scatterers: Measurements. IEEE Trans. Ultrason. Ferroelec. Freq. Contr [Online]. 35(6). pp. 768–774. Available: doi: 10.1109/58.9334 [DOI] [PubMed] [Google Scholar]
- [14].Nocl L, Trahey GE, and Smith SW. (1989, January). Phase aberration correction in medical ultrasound using speckle brightness as a quality factor. J. Acoust. Soc. Am [Online]. 85(5). pp. 1819–1833. Available: doi: 10.1121/1.397889 [DOI] [PubMed] [Google Scholar]
- [15].Thomas JL and Fink MA. (1996, November). Ultrasonic beam focusing through tissue inhomogeneities with a time reversal mirror: application to transskull therapy. IEEE Trans. Ultrason. Ferroelectr. Freq. Contr [Online]. 43(6). pp. 1122–1129. Available: doi: 10.1109/58.542055 [DOI] [Google Scholar]
- [16].Tanter M, Thomas JL, and Fink M. (1998, May). Focusing and steering through absorbing and aberrating layers: application to ultrasonic propagation through the skull. J. Acoust. Soc. Am [Online]. 103(5). Pt 1, pp. 2403–2410. Available: doi: 10.1121/1.422759 [DOI] [PubMed] [Google Scholar]
- [17].Aubry etal JF. (2001. July). Optimal focusing by spatio-temporal inverse filter. II. Experiments. Application to focusing through absorbing and reverberating media. J. Acoust. Soc. Am [Online]. 110(1). pp. 48–58. Available: doi: 10.1121/1.1377052 [DOI] [PubMed] [Google Scholar]
- [18].Clement GT and Hynynen K. (2002, April). Micro-receiver guided transcranial beam steering. IEEE Trans. Ultrason. Ferroelectr. Freq. Contr [Online]. 49(4). pp 447–453. Available: doi: 10.1109/58.996562 [DOI] [PubMed] [Google Scholar]
- [19].Clement GT and Hynynen K. (2002, April). A non-invasive method for focusing ultrasound through the human skull. Phys. Med. Biol [Online].47(8), pp. 1219–1236. Available: doi: 10.1088/0031-9155/47/8/301 [DOI] [PubMed] [Google Scholar]
- [20].Aubry JF et al. (2003, January). Experimental demonstration of noninvasive transskull adaptive focusing based on prior computed tomography scans. J. Acoust. Soc. Am [Online]. 113(1). pp. 84–93. Available: doi: 10.1121/1.1529663 [DOI] [PubMed] [Google Scholar]
- [21].Jones RM, O’Reilly MA, and Hynynen K. (2015, July). Experimental demonstration of passive acoustic imaging in the human skull cavity using CT-based aberration corrections. Med. Phys [Online]. 42(7). pp. 4385–4400. Available: doi: 10.1118/1.4922677 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Maimbourg G et al. (2018, January). 3D-printed adaptive acoustic lens as adisruptive technology for transcranial ultrasound therapy using single-element transducers. Phys. Med. Biol [Online]. 63(2). pp. 025026. Available: doi: 10.1088/1361-6560/aaa037 [DOI] [PubMed] [Google Scholar]
- [23].Maimbourg G et al. (2019, March). Steering capabilities of an acoustic lens for transcranial therapy: numerical and experimental studies. IEEE Trans. Biomed. Eng Available: doi: 10.1109/TBME.2019.2907556 [DOI] [PubMed] [Google Scholar]
- [24].Hughes A et al. (2018, July). The reduction in treatment efficiency at high acoustic powers during MR-guided transcranial focused ultrasound thalamotomy for Essential Tremor. Med. Phys [Online]. 45(7). pp. 2925–2936. Available: doi: 10.1002/mp.12975 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Schwartz ML et al. (2018, May). Skull bone marrow injury caused by MR-guided focused ultrasound for cerebral functional procedures. J. Neurosurg [Online]. 130(3). pp. 758–762. Available: doi: 10.3171/2017.11.JNS17968 [DOI] [PubMed] [Google Scholar]
- [26].Connor CW and Hynynen K. (2014, October). Patterns of thermal deposition in the skull during transcranial focused ultrasound surgery. IEEE Trans. Biomed. Eng [Online]. 51(10). pp. 1693–706. Available: doi: 10.1109/TBME.2004.831516 [DOI] [PubMed] [Google Scholar]
- [27].Hynynen K et al. (2006, August). Pre-clinical testing of a phased array ultrasound system for MRI-guided noninvasive surgery of the brain--a primate study. Eur. J. Radiol [Online]. 59(2). pp. 149–156. Available: doi: 10.1016/j.ejrad.2006.04.007 [DOI] [PubMed] [Google Scholar]
- [28].McCarthy RN, Jeffcott LB, and McCartney RN. (1990. November). Ultrasound speed in equine cortical bone: effects of orientation, density, porosity and temperature. J. Biomech [Online]. 23(11). pp. 1139–43. Available: doi: 10.1016/0021-9290(90)90006-o [DOI] [PubMed] [Google Scholar]
- [29].Wear KA. (2000, March). Temperature dependence of ultrasonic attenuation in human calcaneus. Ultrasound Med. Biol [Online]. 26(3), pp. 469–472. Available: doi: 10.1016/s0301-5629(99)00135-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Nicholson PH and Bouxsein ML. (2002, November) Effect of temperature on ultrasonic properties of the calcaneus in situ. Osteoporos. Int [Online]. 13(11). pp. 888–892. Available: 10.1007/s001980200122 [DOI] [PubMed] [Google Scholar]
- [31].Pinton G et al. (2012, January). Attenuation, scattering, and absorption of ultrasound in the skull bone. Med. Phys [Online]. 39(1), pp. 299–307. Available: doi: 10.1118/1.3668316 [DOI] [PubMed] [Google Scholar]
- [32].Rieke V and Butts Pauly K. (2008, February). MR thermometry. J. Magn. Reson. Imaging [Online].27(2), pp. 376–390. Available: doi: 10.1002/jmri.21265 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Ohkawai H et al. (1983, July). In vivo measurement of thickness or of speed of sound in biological tissue structures. IEEE Trans. Sonics. Ultrason [Online]. 30(4). pp. 231–237. Available: doi: 10.1109/T-SU.1983.31413 [DOI] [Google Scholar]
- [34].Guyott CCH and Cawley P. (1988, February). The measurement of through thickness plate vibration using a pulsed ultrasound transducer. J. Acoust. Soc. Am [Online]. 83(2). pp. 623–631. Available: doi: 10.1121/1.396156 [DOI] [Google Scholar]
- [35].Aarnio J, Clement GT, and Hynynen K. (2005, June). A new ultrasound method for determining the acoustic phase shifts caused by the skull bone. Ultrasound Med. Biol [Online]. 31(6). pp. 771–780. Available: doi: 10.1016/j.ultrasmedbio.2005.01.019 [DOI] [PubMed] [Google Scholar]
- [36].Goodman JW, Introduction to Fourier Optics. McGraw-Hill, 1968 [Google Scholar]
- [37].Pichardo S, Sin VW, and Hynynen K. (2011, January). Multi-frequency characterization of the speed of sound and attenuation coefficient for longitudinal transmission of freshly excised human skulls. Phys. Med. Biol [Online]. 56(1). pp. 219–250. Available: doi: 10.1088/0031-9155/56/1/014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Horn BKP (1987, April). Closed-form solution of absolute orientation using unit quaternions. J. Opt. Soc. Am. A [Online]. 4(4). pp. 629–642. Available: doi: 10.1364/JOSAA.4.000629 [DOI] [Google Scholar]
- [39].Hynynen K and Sun J. (1999, May). Trans-skull ultrasound therapy: the feasibility of using image-derived skull thickness information to correct the phase distortion. IEEE Trans. Ultrason. Ferroelectr. Freq. Contr [Online]. 46(3). pp. 752–755. Available: doi: 10.1109/58.764862. [DOI] [PubMed] [Google Scholar]
- [40].Gateau J et al. (2010, January). Transcranial ultrasonic therapy based on time reversal of acoustically induced cavitation bubble signature. IEEE Trans. Biomed. Eng [Online]. 57(1). pp. 134–144. Available: doi: 10.1109/TBME.2009.2031816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Hertzberg Y et al. (2010, June). Ultrasound focusing using magnetic resonance acoustic radiation force imaging: application to ultrasound transcranial therapy. Med. Phys [Online]. 37(6). pp. 2934–2942. Available: doi: 10.1118/1.3395553 [DOI] [PubMed] [Google Scholar]
- [42].Kinsler LE et al. , “Reflection and transmission” in Fundamentals of Acoustics. 4th ed. New York: Wiley, 2000, ch. 6, sec. 1-5 pp. 149–160. [Google Scholar]
- [43].Aarnio J, Clement GT, and Hynynen K. (2004, September). Accuracy of the resonance ultrasound method in determination of the acoustic phase shifts in plastic and bone. IEEE Ultrason. Symp [Online]. pp. 1800–1803. Available: doi: 10.1109/ULTSYM.2004.1418177 [DOI] [Google Scholar]
- [44].Connor CW, Clement GT, and Hynynen K. (2002, November). A unified model for the speed of sound in cranial bone based on genetic algorithm optimization. Phys. Med. Biol [Online]. 47(22). pp. 3925–3944. Available: doi: 10.1088/0031-9155/47/22/302 [DOI] [PubMed] [Google Scholar]
- [45].Jones RM, O’Reilly MA, and Hynynen K. (2013, July). Transcranial passive acoustic mapping with hemispherical sparse arrays using CT-based skull-specific aberration corrections: a simulation study. Phys. Med. Biol [Online]. 58(14). pp. 4981–5005. Available: doi: 10.1088/0031-9155/58/14/4981 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Treece GM et al. (2010, June). High resolution cortical bone thickness measurement from clinical CT data. Med. Image Anal [Online]. 14(3). pp. 276–290. Available: doi: 10.1016/j.media.2010.01.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Jones RM and Hynynen K. (2016, January). Comparison of analytical and numerical approaches for CT-based aberration correction in transcranial passive acoustic imaging. Phys. Med. Biol [Online]. 61(1). pp. 23–36. Available: doi: 10.1088/0031-9155/61/1/23 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Pinton G et al. (2011, March). Effects of nonlinear ultrasound propagation on high intensity brain therapy. Med. Phys [Online] 38(3). pp. 1207–1216. Available: doi: 10.1118/1.3531553 [DOI] [PubMed] [Google Scholar]
- [49].Pulkkinen A. (2014). Simulation Methods in Transcranial Ultrasound Therapy. University of Eastern Finland, Thesis pp. 20 Available: http://epublications.uef.fi/pub/urn_isbn_978-952-61-1510-8/urn_isbn_978-952-61-1510-8.pdf [Google Scholar]
- [50].White PJ, Clement GT, and Hynynen K. (2006, July). Longitudinal and shear mode ultrasound propagation in human skull bone. Ultrasound Med. Biol [Online]. 32(7), pp. 1085–1096. Available: doi 10.1016/j.ultrasmedbio.2006.03.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Hynynen K and Sun J. (1999, May). Trans-skull ultrasound therapy: the feasibility of using image-derived skull thickness information to correct the phase distortion. IEEE Trans. Ultrason. Ferroelectr. Freq. Contr [Online]. 46(3), pp. 752–755. Available: doi: 10.1109/58.764862. [DOI] [PubMed] [Google Scholar]
- [52].Marquet F et al. (2009, May). Non-invasive transcranial ultrasound therapy based on a 3D CT scan: protocol validation and in vitro results. Phys. Med. Biol. [Online]. 54(9), pp. 2597–2613. Available: doi: 10.1088/0031-9155/54/9/001 [DOI] [PubMed] [Google Scholar]
- [53].Marsac L et al. (2017, September). Ex vivo optimisation of a heterogeneous speed of sound model of the human skull for non-invasive transcranial focused ultrasound at 1 MHz. Int. J. Hyperthermia [Online]. 33(6), pp. 635–645. Available: doi: 10.1080/02656736.2017.1295322 [DOI] [PubMed] [Google Scholar]
- [54].Herbert E et al. (2009, November). Energy-based adaptive focusing of waves: application to noninvasive aberration correction of ultrasonic wavefields. IEEE Trans. Ultrason. Ferroelectr. Freq. Control [Online]. 56(11), pp. 2388–2399. Available: doi: 10.1109/TUFFc.2009.1327 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Larrat B et al. (2010, August). MR-guided adaptive focusing of ultrasound. IEEE Trans. Ultrason. Ferroelectr. Freq. Control [Online]. 57(8), pp. 1734–1737. Available: doi: 10.1109/tuffc.2010.1612 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Marsac L et al. (2012, February). MR-guided adaptive focusing of therapeutic ultrasound beams in the human head. Med. Phys [Online]. 39(2), pp. 706–713. Available: doi: 10.1118/1.3678988 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57].Seip R, VanBaren P, and Ebbini ES. (1994, September). Dynamic focusing in ultrasound hyperthermia treatments using implantable hydrophone arrays. IEEE Trans. Ultrason. Ferroelec. Freq. Contr [Online]. 41(5), pp. 706–713. Available: doi: 10.1109/58.308507 [DOI] [PubMed] [Google Scholar]
- [58].Tanter M et al. (2001, July). Optimal focusing by spatio-temporal inverse filter. I. Basic principles. J. Acoust. Soc. Am [Online]. 110(1), pp. 37–47. Available: doi: 10.1121/1.1377051 [DOI] [PubMed] [Google Scholar]
- [59].Vignon F et al. (2006, November). Adaptive focusing for transcranial ultrasound imaging using dual arrays. J. Acoust. Soc. Am [Online]. 120(5), pp. 2737–2745. Available: doi: 10.1121/1.2354073 [DOI] [PubMed] [Google Scholar]
- [60].Bonfield W and Tully AE, (1982, January). Ultrasonic analysis of the Youngs modulus of cortical bone. J. Biomed. Eng [Online]. 4(1), pp. 23–27. Available: doi: 10.1016/0141-5425(82)90022-x [DOI] [PubMed] [Google Scholar]
- [61].Hughes A and Hynynen K. (2017, August). Design of patient-specific focused ultrasound arrays for non-invasive brain therapy with increased trans-skull transmission and steering range. Phys. Med. Biol [Online]. 62(17), pp. L9–L19. Available: doi: 10.1088/1361-6560/aa7cd5. [DOI] [PMC free article] [PubMed] [Google Scholar]


