ABSTRACT
Although strong evidence exists that certain activities can increase bone density and structure in people, it is unclear what specific mechanical factors govern the response. This is important because understanding the effect of mechanical signals on bone could contribute to more effective osteoporosis prevention methods and efficient clinical trial design. The degree to which strain rate and magnitude govern bone adaptation in humans has never been prospectively tested. Here, we studied the effects of a voluntary upper extremity compressive loading task in healthy adult women during a 12‐month prospective period. A total of 102 women age 21 to 40 years participated in one of two experiments: (i) low (n = 21) and high (n = 24) strain magnitude; or (ii) low (n = 21) and high (n = 20) strain rate. Control (n = 16) no intervention. Strains were assigned using subject‐specific finite element models. Load cycles were recorded digitally. The primary outcome was change in ultradistal radius integral bone mineral content (iBMC), assessed with QCT. Interim time points and secondary outcomes were assessed with high resolution pQCT (HRpQCT) at the distal radius. Sixty‐six participants completed the intervention, and interim data were analyzed for 77 participants. Likely related to improved compliance and higher received loading dose, both the low‐strain rate and high‐strain rate groups had significant 12‐month increases to ultradistal iBMC (change in control: −1.3 ± 2.7%, low strain rate: 2.7 ± 2.1%, high strain rate: 3.4 ± 2.2%), total iBMC, and other measures. “Loading dose” was positively related to 12‐month change in ultradistal iBMC, and interim changes to total BMD, cortical thickness, and inner trabecular BMD. Participants who gained the most bone completed, on average, 128 loading bouts of (mean strain) 575 με at 1878 με/s. We conclude that signals related to strain magnitude, rate, and number of loading bouts contribute to bone adaptation in healthy adult women, but only explain a small amount of variance in bone changes. © 2020 The Authors. Journal of Bone and Mineral Research published by American Society for Bone and Mineral Research.
Keywords: BIOMECHANICS, BONE MODELING AND REMODELING, BONE QCT/μCT, CLINICAL TRIALS, EXERCISE
Introduction
Exercise‐based interventions have long been considered a viable option for preserving and enhancing bone strength1 because bone adapts to best resist its habitual mechanical loading environment. Individuals who play sports and load with highly variable, off‐axis loads (eg, soccer, squash) have been observed to have better bone mechanical properties than those who do not.2, 3 Clinical trials have shown that high impact activities such as jumping and hopping can improve bone density in growing children4 and young adults5 and maintain bone density in older adults.6 However, although the evidence is strong that certain activities can increase bone density and structure in some individuals, it is not clear what specific mechanical factors govern the response. Furthermore, these factors interact with individual physiology to create a variable response, which is not well understood.
Animal in vivo loading models demonstrate that mechanical signals related to strain rate7, 8, 9 and magnitude10, 11 regulate bone adaptation. There is no consensus on which specific signal(s) osteocytes sense; evidence supports lacunar‐canalicular fluid flow,12, 13 flow of ions and the resulting electromagnetic signal,14 direct damage of osteocytes,15 microdamage of the surrounding bone that results in altered stress or strain16, 17 and other candidates.18 Regardless of the exact mechanism, all of these signals are closely related to (and driven by) mechanical strain. In vivo loading models have also established that, to elicit an adaptive response, the mechanical signal must be both dynamic and unaccustomed.19 Despite extensive animal literature, the degree to which mechanical strain magnitude and rate govern bone adaptation in humans has never been prospectively tested.
One major challenge is that bone strain is difficult to measure noninvasively. As a result, indirect measures, such as surveys for physical activity, which include weighting factors based on experimentally measured ground reaction force (GRF) and rate of GRF, have been proposed.20, 21 Others have proposed “bone loading” indices that are based on similar measures (e.g., accelerometry).22, 23 Although these can be helpful in identifying the types of activities that should theoretically elicit an osteogenic response, they do not account for individual differences in bone structure, which have a large influence on bone strain.24 Alternatively, validated subject‐specific finite element (FE) models can provide accurate estimates of bone strain25, 26, 27 when the proper boundary conditions (magnitude, direction, and locations of application) are known.
Our previously validated upper extremity loading model27 provides a well‐controlled framework to understand the degree to which strain magnitude and rate influence bone adaptation in people. In this model, an individual produces a compressive force through the radius by leaning onto the palm of the hand. Feedback is given using a scale or load cell, and individuals are given sound cues to assist in achieving a regular and consistent load/unload cycle. In a pilot group of 19 young adult women, we found that a mean energy equivalent strain of 734 ± 238 με applied 50 cycles per day, 3 days per week elicited modest increases in distal radius bone mineral content (BMC) and prevented seasonal loss of BMC observed in a control group.27 We also observed that high strain regions of the radius gained significantly more bone than low strain regions, suggesting that the local mechanical signals were, in part, driving the response.28 Although these results were promising, the study was limited in scope and duration.
Here, our purpose was to quantify the degree to which bone strain influences bone adaptation in the upper extremity of healthy adult women during a 12‐month prospective study period. Based on previous findings in humans27, 28 and small animals,8, 11, 29 we hypothesized that (i) bone accrual would be proportional to strain magnitude and strain rate, and (ii) structural changes would include increased cross‐sectional area and cortical thickness, and increased trabecular bone mass near the endosteal surface.
Subjects and Methods
Participant characteristics
Healthy women age 21 to 40 years were recruited from the community for this mechanistic randomized controlled trial (Clinical Trials: NCT04135196). This group is at peak bone mass,30, 31 and compared to men, have increased risk of osteoporosis later in life. An initial telephone interview of 497 potential participants was used to exclude individuals with self‐reported BMI outside the range 18 to 29 kg/m2, irregular menstrual cycles, no regular calcium intake, use of medications affecting bone health, history of radius fracture or injury to the nondominant shoulder or elbow, or regular participation (more than two times per month) in activities with high loads at the forearm (e.g., gymnastics, volleyball). These criteria were selected to reduce possible adverse events and exclude individuals who were unlikely to respond to, or achieve, the loading stimulus. After a positive telephone interview, 159 potential participants provided written informed consent to be screened with dual‐energy X‐ray absorptiometry (DXA) of the nondominant radius and measurement of circulating levels of 25‐hydroxyvitamin vitamin D and estradiol. Exclusion criteria were 25‐hydroxyvitamin D serum levels below 20 ng/mL, and DXA T‐score outside the range −2.5 to 1.0. In total, 102 participants were eligible after screening and opted to enroll in this institutionally approved study. All participants were recruited at a single site between December 2013 and June 2017 via social media, posters, email newsletters, and word of mouth at nearby universities, hospitals, and community events. The trial was conducted in accordance with Good Clinical Practice Guidelines. Compliance and adverse events data were reviewed annually with a study monitor.
Study design
This was a 12‐month, prospective, mechanistic randomized controlled trial that utilized a distal radius compressive loading intervention to investigate the effect of strain on bone adaptation. After meeting eligibility criteria from screening tests, participants were assigned into either control or one of two exercise arms that manipulated strain magnitude (experiment 1: low and high strain magnitude) or strain rate (experiment 2: low and high strain rate, detailed in Table 1). Group assignments were made by drawing slips of paper from an envelope (eg, low, high, control), and control participants were randomized during experiment 1. Participants were blinded to the study hypotheses and were not aware of the exercises or instructions given to groups other than their own. Based on pilot data27 and simulations that showed little benefit for loading more than 100 cycles in a single bout,32 exercise groups were instructed to apply 100 cycles of axial force (one bout), four times weekly, by leaning onto the palm of the hand. Although participants were given a goal of four bouts per week, our experimental goal was to achieve an average of three bouts per week (75% compliance), based on the positive response we previously observed with this frequency of loading. Loading was accomplished using a custom device, consisting of a uniaxial load cell (Standard Load Cells, Gujarat, India), data logger (DATAQ DI‐710; DATAQ Instruments, Inc. Akron, OH, U.S.A.), and light‐emitting diode (LED) indicators that lit up when the applied force was within ±10 N of the target value. To allow participants to get used to the intervention, reduce the possibility of wrist soreness, and give the investigative team time to assign subject‐specific forces, those in the exercise groups were assigned a nominal 200‐N target force magnitude for the first 3 months of loading. Thereafter, a subject‐specific target force was prescribed to achieve target strain parameters based on CT‐based FE models (described in Continuum FE modeling; Fig. 1 A).
Table 1.
Baseline Participant Characteristics and Loading Intervention by Group
| A. Baseline Participant Characteristics | ||||||
|---|---|---|---|---|---|---|
| Treatment group | Low strain magnitude (n = 21) | High strain magnitude (n = 24) | Low strain rate (n = 21) | High strain rate (n = 20) | Control (n = 16) | Total (n = 102) |
| Participant characteristics | ||||||
| Age (years), mean ± SD | 30.3 ± 5.5 | 29.3 ± 6.3 | 27.2 ± 5.1 | 27.1 ± 5.4 | 28.2 ± 5.3 | 28.4 ± 5.6 |
| Height (cm), mean ± SD | 165.8 ± 6.1 | 161.9 ± 6.1 | 165.0 ± 6.2 | 164.9 ± 5.7 | 167.3 ± 7.6 | 164.8 ± 6.4 |
| Body mass (kg), mean ± SD | 65.2 ± 8.8 | 61 ± 5.9 | 65.4 ± 9.8 | 65.4 ± 10.0 | 65 ± 8.9 | 64.3 ± 8.7 |
| Serum vitamin D (ng/mL), mean ± SD | 33.7 ± 9.9 | 31.5 ± 8.9 | 31.1 ± 12.2 | 29.1 ± 7.8 | 33.2 ± 7.5 | 31.7 ± 9.5 |
| DXA total forearm aBMD (g/cm2), mean ± SD | 0.586 ± 0.0 | 0.568 ± 0.03 | 0.576 ± 0.04 | 0.569 ± 0.04 | 0.570 ± 0.04 | 0.574 ± 0.04 |
| DXA total forearm T‐score, mean ± SD | 0.138 ± 0.8 | −0.187 ± 0.63 | 0.138 ± 0.76 | −0.175 ± 0.74 | −0.162 ± 0.67 | −0.087 ± 0.70 |
| Ethnicity, n (%) | ||||||
| Hispanic or Latino | 2 (10) | 5 (21) | 1 (5) | 2 (10) | 2 (13) | 12 (12) |
| Non‐hispanic | 19 (90) | 18 (75) | 20 (95) | 18 (90) | 14 (87) | 89 (87) |
| Not reported | 0 (0) | 1 (4) | 0 (0) | 0 (0) | 0 (0) | 1 (1) |
| Race, n (%) | ||||||
| African American | 0 (0) | 0 (0) | 0 (0) | 1 (5) | 0 (0) | 1 (1) |
| White | 16 (76) | 17 (71) | 16 (76) | 14 (70) | 13 (81) | 76 (75) |
| Asian | 3 (14) | 2 (8) | 4 (19) | 3 (15) | 0 (0) | 12 (12) |
| Pacific Islander | 0 (0) | 0 (0) | 0 (0) | 1 (5) | 0 (0) | 1 (1) |
| More than one race | 1 (5) | 2 (8) | 1 (5) | 1 (5) | 2 (13) | 7 (7) |
| Not reported | 1 (5) | 3 (13) | 0 (0) | 0 (0) | 1 (6) | 5 (5) |
| B. Loading Intervention by Group | ||||
|---|---|---|---|---|
| Prescribed loading | ||||
| Sessions, n | 208 | 208 | 208 | 208 |
| Ultradistal mean strain magnitude (με), mean ± SD | 490 ± 103 | 748 ± 143 | 632 ± 138 | 641 ± 157 |
| Strain rate (με/s), mean ± SD | 1485 ± 312 | 2267 ± 434 | 790 ± 173 | 6410 ± 1570 |
| Achieved loading | ||||
| Participants completing no loading, n | 2 | 4 | 6 | 4 |
| Sessions, mean ± SD | 126 ± 100 | 81 ± 76 | 70 ± 71 | 83 ± 115 |
| Ultradistal mean strain magnitude (με), mean ± SDa | 456 ± 125 | 572 ± 171 | 549 ± 147 | 552 ± 147 |
| Ultradistal median strain magnitude (με), mean ± SDa | 376 ± 86 | 468 ± 135 | 458 ± 113 | 447 ± 105 |
| Ultradistal maximum strain magnitude (με), mean ± SDa | 2074 ± 1199 | 2291 ± 775 | 2372 ± 883 | 2494 ± 1108 |
| Ultradistal mean strain rate (με/s), mean ± SDa | 1018 ± 604 | 1510 ± 1094 | 945 ± 499 | 1698 ± 1167 |
| StrainStim (με*s−1*Files*10−7), mean ± SD | 141 ± 193 | 118 ± 240 | 36 ± 73 | 78 ± 14 |
| Strain_MagRate (με2*s−1*Files*10−5), mean ± SD | 319 ± 353 | 428 ± 651 | 204 ± 255 | 407 ± 533 |
| Strain_Mag (με*Files*10−2), mean ± SD | 493 ± 435 | 463 ± 518 | 343 ± 364 | 413 ± 522 |
| Strain_Rate (με*s−1*Files*10−3), mean ± SD | 130 ± 135 | 141 ± 186 | 71 ± 90 | 156 ± 214 |
Strain magnitudes were assigned based on the maximum energy‐equivalent strain within the ultradistal region, as calculated by FE model. However, for loading dose calculations, the achieved mean energy‐equivalent strain was used, since it better represents the strain experienced within the region. Strain magnitude is calculated as energy equivalent strain, which is a positive scalar.
Calculations of Ultradistal Strain Magnitude and Strain Rate excluded participants who completed no loading. Number of Sessions and loading dose calculations include all participants randomized in each group.
Figure 1.
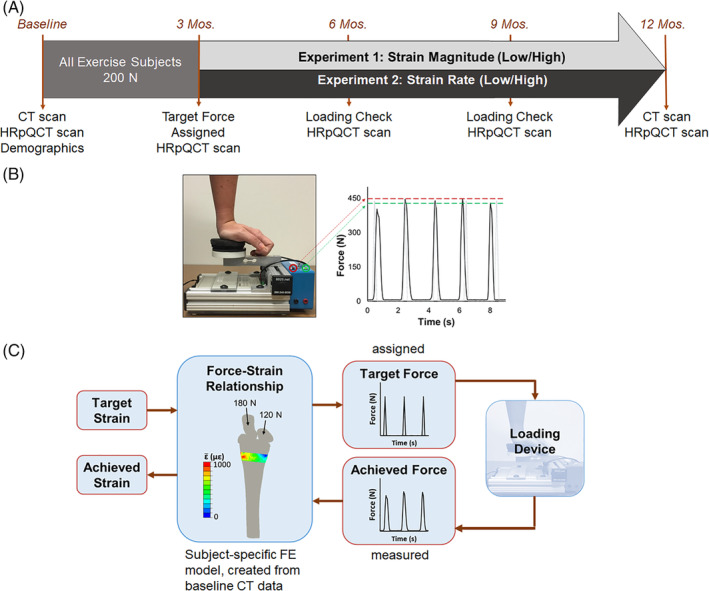
(A) Summary of the data collection timeline for participants assigned to exercise groups. (B) Loading device used to manipulate applied force magnitude via feedback lights (green set to target force minus 10 N, red to target force plus 10 N). Loading frequency was controlled using pre‐recorded auditory cues. The force versus time curve shows a representative load cell signal (black) versus ideal assigned loading stimulus (gray), with dashed lines indicating the forces at which feedback is given. (C) Linear FE model used to estimate energy equivalent strain in the transverse section matching the imaged site. The force‐strain relationship was used to assign each participant a target force and calculate the resulting strain from load cell recordings.
Because of considerations of participant safety, no participant was assigned a force larger than 450 N or what she could comfortably and consistently apply, even if the force required to achieve the target strain was larger than that. Partway through the study, in response to reports of wrist soreness from some participants, this upper limit was reduced to 350 N. Loading magnitude was controlled by adjusting LED indicators on the device, whereas loading rate and cycle period were controlled using verbal instructions (eg, “load slowly and evenly” versus “load as rapidly as possible”) and sound cues recorded on a portable voice recorder. Sound cues consisted of 100 beeps (long beeps for the slow rate group, short beeps for the fast rate group) occurring at 2‐s intervals. Compliance was monitored every 3 months using data logger recordings and log books maintained by participants (Fig. 1 B).
The primary outcome was 12‐month change in integral ultradistal radius bone mineral content and bone mineral density (iBMC and iBMD), as measured by quantitative CT analysis (QCT). Secondary outcomes included 12‐month changes in other regions, and microstructural measures with interim time points. A power analysis based on pilot data27 determined that 20 participants per group would have 80% power to detect a 12‐month change in BMC of 1.0 ± 1.1%. Part way through the experiment the randomization ratio was adjusted to oversample the loading groups (increasing the target enrollment by six participants) and to undersample the control group (reducing the target by four participants) going forward. This was to ensure that a sufficient number of participants had loading doses that were non‐zero, even if a subset of those assigned to a loading group were noncompliant.
Data collection
Demographic information and imaging data (CT, and high‐resolution peripheral QCT [HRpQCT]) were collected at baseline. Hand dominance was determined using the Edinburgh inventory.33 CT was collected at baseline and 12 months. HRpQCT was updated every 3 months during the study period.
HRpQCT
Changes in radius microstructure were assessed using HRpQCT (Xtreme CT I; Scanco Medical; Brüttisellen, Switzerland). Bilateral scans were acquired in a standard 9.02‐mm region consisting of 110 transverse slices (82 μm isotropic voxel size) beginning 9.5 mm proximal to the distal endplate. Structural changes were measured for the mutually overlapping region, using the manufacturer's 2D region‐matching algorithm. Total mean cross‐sectional area (CSA; mm2) and total volumetric bone mineral density (Tt.BMD; mg hydroxyapatite [HA]/cm3) were measured. Trabecular number (Tb.N; mm−1), thickness (Tb.Th; mm), and BMD (Tb.BMD; mgHA/cm3) were measured using the manufacturer's standard analysis protocol. The trabecular region was further divided into inner (central 60%; Tb.BMDinn) and outer regions (outer 40%; Tb.BMDmeta). Cortical vBMD (Ct.BMD; mgHA/cm3) and cortical thickness (Ct.Th; mm) were calculated using the dual‐threshold method.34, 35, 36 In our laboratory, the coefficient of variation (CV) for densitometric variables is <0.3%. The CVs of microstructural variables range from 0.4% to 4.7%. All HRpQCT analyses were blinded to group assignment.
Quantitative CT analysis
At baseline and 12 months, CT scans of the distal‐most 12 cm of each forearm were acquired (GE Brightspeed; GE Medical, Milwaukee, WI, USA; 120 kV, 180 mA, voxel size 234 μm × 234 μm × 625 μm). A calibration phantom (QRM, Moehrendorf, Germany) with known calcium HA equivalent concentrations was included in the field of view to relate CT attenuation (Hounsfield Units) to equivalent bone density (g/cm3).
Changes in bone macrostructure were quantified from CT data using Mimics v15.1 (Materialize, Leuven, Belgium). Follow‐up scans were registered to baseline using rigid image registration and the periosteal surface was defined using a 0.175‐g/cm3 density threshold.27 Based on methods previously established,37 we defined integral and endocortical compartments (denoted in QCT variable names with prefixes i and ec). Briefly, the integral compartment consisted of all voxels enclosed within the periosteal surface. The endocortical compartment was comprised of the subset of integral voxels located within 2.5 mm of the periosteal surface (including all cortical bone). For each compartment bone volume (BV; cm3), bone mineral content (BMC; g), and volumetric bone mineral density (BMD; g/cm3) were calculated. QCT parameters for the trabecular compartment were not analyzed. Instead, HRpQCT data were analyzed, which provided a greater level of detail. Using previously established methods,27 we also calculated compressive strength index (CSI; g2/cm4) and bending strength index (BSI, cm3). All parameters were calculated for total and ultradistal regions except for strength measures, which were only calculated for the ultradistal region. The total region extended 45 mm proximal from the subchondral plate and distally to the styloid tip; the ultradistal region extended 9.375 mm proximal from the subchondral plate. The CV for these QCT measures in our laboratory ranges from 0.7% to 2.3% for the ultradistal region; 0.3% to 0.6% for the total region; and 0.9% to 2.3% for strength indices. All QCT analyses were blinded to group assignment.
Continuum FE modeling
FE models were constructed from the QCT scans using methods validated with cadaveric mechanical testing.38 Models were used to simulate one cycle of axial loading to determine the subject‐specific force needed to achieve the desired target strain within the distal radius. We used energy‐equivalent strain as the measure of interest, because it provides a scalar value that has been related to bone adaptation.28, 39 Force values were assigned to each participant based on the maximum energy‐equivalent strain within the ultradistal region of the radius, as calculated using the continuum FE model for that participant. This value was used to adjust the custom loading device so that the LEDs would light up when that individual achieved her target strain. At all subsequent time points, data recorded from the load cell were applied to the FE model to calculate the actual mean strain within the region achieved by the participant, based on applied force (Fig. 1 C).
Load cell analysis
At each follow‐up visit, load cell recordings were analyzed using custom code in Matlab (MathWorks, Natick, MA, USA). The beginning, peak, and end of each loading waveform were identified using a custom algorithm, and the resulting frequency spectrum calculated using fast Fourier transform. Based on subject‐specific FE models, frequency data were used to calculate the loading stimulus using the relationship suggested by Turner.19
| (1) |
where E is the strain stimulus for the entire loading bout, f i is the frequency value for bin i, and ε i is the peak‐to‐peak energy‐equivalent strain magnitude of frequency component i. A cutoff of 5 Hz was selected, based on analysis of the load cell frequency content, which showed that over 95% of the signal power was <2 Hz. We also calculated peak‐to‐peak strain magnitude and average strain rate for the loading portion of each cycle for each participant and loading bout. Because voluntary loading produced variable and sometimes inconsistent loading signals, we evaluated several candidate measures of “loading dose,” which was intended to serve as an overall metric of mechanical loading, considering strain parameters and protocol compliance. We considered the following candidate measures of “loading dose”:
| (2) |
| (3) |
| (4) |
| (5) |
Statistical analysis
Descriptive statistics were calculated and data normality was assessed. Group demographics and loading dose received were compared using ANOVA and Bonferroni‐corrected post hoc t tests. The hypothesis that bone mass would increase proportionally to the applied strain magnitude (experiment 1) was tested in two ways. First, participants were analyzed by group using intention to treat (control versus low and high strain magnitude groups). For this analysis, the 12‐month change in ultradistal iBMC was analyzed as the primary dependent variable in a linear regression model with coefficients representing contrasts between each of the two experimental groups and the control group. The secondary outcome measures were also compared between groups using regression models based on the change scores at each of the time points (change from baseline). Similar analyses were performed to examine the effect of strain rate on bone (experiment 2).
In the second analysis, we considered “loading dose” achieved by each participant as a continuous variable, with the dose for control participants being zero. Because dose includes both magnitude and frequency components, all groups were combined into a single regression model with the 12‐month change in radius ultradistal iBMC as the primary outcome. The secondary outcome measures were also considered. To test the hypothesis that bone structural changes would include increased cross‐sectional area and cortical thickness, and increased endocortical density, these factors were treated as dependent variables in linear regression models, similar to the previous analyses. We assessed the F‐statistic of the overall regression, and the t statistic of each explanatory variable, considering α = 0.05 to be significant. As an exploratory post hoc analysis, participants were ranked by change in ultradistal iBMC, and then divided into tertiles (greatest, medium, and least gain in iBMC). To gain insight into what factors were associated with the greatest gains in ultradistal iBMC, participant demographics, baseline values, and metrics describing loading dose were compared between the tertiles using ANOVA. Where significant effects were observed, Bonferroni‐adjusted post hoc t tests were used to compare values between individual tertiles.
Results
Participant characteristics
A total of 102, women, age: 28 ± 6 years, height: 165 ± 6 cm, mass: 64 ± 9 kg were enrolled and randomized. Baseline characteristics are summarized in Table 1 and were not different between groups. Sixty‐six participants completed the study and were included in the 12‐month analysis. Seventy‐seven participants had some follow‐up data available and were included in our analyses of interim time points (Fig. 2). On average, participants assigned to one of the loading groups completed 85 ± 92 loading bouts in total (41% of the total prescribed number). However, the total number of loading bouts varied considerably, from 0 to 357. Strain magnitude and rate were significantly higher in the high versus low groups for experiments 1 and 2, respectively (p ≤ .03). However, the high strain magnitude and rate groups failed to achieve the prescribed target values. All measures of loading dose were significantly greater for loading groups than for controls (p ≤ .046; Table 1).
Figure 2.

Consort chart describing participant flow.
Adverse events
There were no serious adverse events. Temporary soreness of the loaded wrist was the most commonly reported adverse event (28% of participants; 29 reports). Two of these participants noted that this briefly affected their daily activities (did fewer chores or avoided exercises that weighted the hands), and one took ibuprofen. Eight participants reported soreness at other sites (elbow, shoulder, hand), which included aggravation of previous injuries (e.g., shoulder pain from an injury that was several years old) that they thought might be due to the intervention. All participants reported that soreness resolved within 3 to 14 days. Five participants reported that pain from previous injuries temporarily prevented them from completing the assigned loading, but did not believe this was caused or aggravated by the intervention. Radiology reports indicated no visible changes in wrist anatomy between initial and 12‐month visits. Lack of time or relocation were the most common reasons expressed for dropping out (22 participants).
Effect of strain on 12‐month change in bone mass and structure (QCT)
None of the regression models that included strain magnitude groups were significant for overall model fit, although the membership in the low strain magnitude group was associated with slight gains in ultradistal iBMC (p = .041), and consistent and significant increases in CSA, iBV and ecBV that indicated periosteal expansion (Table 2). Achieved strain magnitude was only 25% higher for the high versus low group, and the low magnitude group completed more loading sessions on average than the high magnitude group. Therefore, the favorable outcomes in the low group may be attributable to practical limitations of the assigned loading regimen. The groups in which strain rate was manipulated had greater 12‐month changes in QCT variables than those in which strain magnitude was manipulated (Fig. 3). In models comparing the low and high strain rate groups to the control group, both loading groups were significantly and positively associated with the increases to total and ultradistal iBMC, iBMD, ecBMC, and ecBMD. Fifty‐six percent (56%) and 52% of the variance in change to ultradistal and total iBMD, respectively, was explained by group membership of these participants (Table 3). Increases to ultradistal compressive and bending strength indices were significantly and positively associated with experiment 2 loading group membership.
Table 2.
Baseline of the Pooled Data, and Percent Change at 12 months in QCT Variables, by Group
| Variable | Total baseline (n = 66) | Control %ΔV5 (n = 13) | Low magnitude (n = 13) %ΔV5 | High magnitude %ΔV5 (n = 17) | Low rate %ΔV5 (n = 12) | High rate %ΔV5 (n = 11) |
|---|---|---|---|---|---|---|
| Ultradistal | ||||||
| iBV (cm3) | 3.84 ± 0.40 | −1.17 ± 2.51 | 0.75 ± 2.14 | −0.01 ± 2.23 | −0.29 ± 1.29 | 0.35 ± 1.86 |
| iBMC (g) | 0.91 ± 0.15 | −1.31 ± 2.68 | 0.46 ± 1.52 | −0.33 ± 2.03 | 2.73 ± 2.07 | 3.42 ± 2.21 |
| iBMD (g/cm3) | 0.24 ± 0.03 | −0.59 ± 2.08 | −0.23 ± 0.96 | −0.33 ± 1.19 | 3.03 ± 1.08 | 3.07 ± 1.46 |
| ecBV (cm3) | 1.99 ± 0.15 | −0.41 ± 1.49 | 0.89 ± 1.39 | 0.34 ± 1.58 | −0.01 ± 1.25 | 0.41 ± 1.46 |
| ecBMC (g) | 0.63 ± 0.18 | −0.19 ± 4.87 | 0.12 ± 2.46 | −0.10 ± 2.62 | 4.84 ± 3.64 | 4.45 ± 3.47 |
| ecBMD (g/cm3) | 0.31 ± 0.08 | 0.21 ± 4.52 | −0.74 ± 2.79 | −0.43 ± 2.59 | 4.85 ± 3.46 | 4.03 ± 3.30 |
| Total | ||||||
| iBV (cm3) | 12.96 ± 1.55 | −0.06 ± 0.47 | −0.25 ± 0.52 | −0.13 ± 0.45 | 0.16 ± 0.64 | 0.38 ± 0.41 |
| iBMC (g) | 5.10 ± 0.60 | −0.23 ± 1.20 | −0.45 ± 0.80 | −0.19 ± 0.78 | 1.97 ± 0.86 | 1.93 ± 0.75 |
| iBMD (g/cm3) | 0.39 ± 0.04 | −0.17 ± 1.14 | −0.19 ± 0.58 | −0.06 ± 0.78 | 1.81 ± 0.63 | 1.55 ± 0.86 |
| ecBV (cm3) | 8.24 ± 0.72 | 0.17 ± 0.71 | −0.07 ± 0.57 | 0.18 ± 0.44 | 0.45 ± 0.62 | 0.35 ± 0.64 |
| ecBMC (g) | 4.09 ± 0.55 | 0.15 ± 1.78 | −0.26 ± 1.11 | 0.00 ± 1.01 | 2.06 ± 1.40 | 1.72 ± 1.37 |
| ecBMD (g/cm3) | 0.50 ± 0.05 | −0.02 ± 1.28 | −0.20 ± 0.76 | −0.18 ± 0.98 | 1.60 ± 0.84 | 1.36 ± 0.83 |
| Ultradistal strength | ||||||
| CSA (cm2) | 4.15 ± 0.42 | −0.67 ± 1.67 | 0.65 ± 1.45 | 0.00 ± 1.48 | −0.26 ± 1.23 | 0.35 ± 1.75 |
| CSI (g2/cm4) | 0.24 ± 0.07 | −1.81 ± 4.40 | 0.18 ± 1.96 | −0.65 ± 2.85 | 5.90 ± 3.05 | 6.62 ± 3.26 |
| BSI (cm3) | 0.12 ± 0.03 | −0.59 ± 4.31 | 0.32 ± 1.90 | −0.29 ± 2.30 | 4.74 ± 2.44 | 4.81 ± 2.70 |
Data are shown as mean ± SD. Bold indicates significant regression coefficient representing contrast with control group for raw change. Baseline is for participants with follow‐up data available. %ΔV5 = percent change at visit 5.
Figure 3.
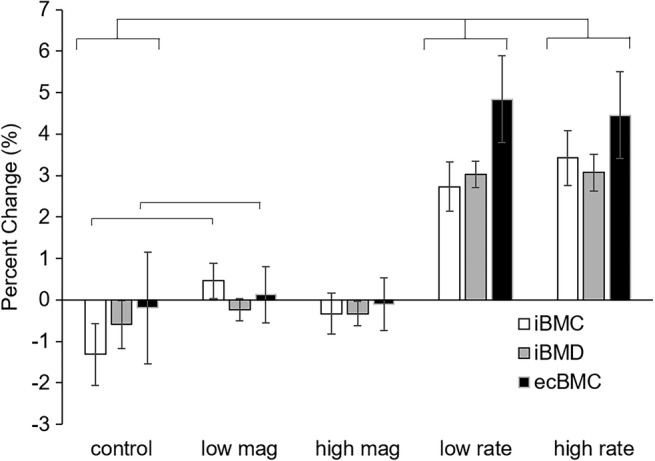
Twelve‐month changes in QCT‐derived primary outcome variables. Both the low‐rate and high‐rate groups had significant differences compared to the control group in all three variables.
Table 3.
Standardized Regression Coefficients for QCT, by Group and by Loading Dose
| Parameter | Model definition | R 2 | β1 | β2 |
|---|---|---|---|---|
| UD iBMC (g) | β1*Low1 + β2*High1 + ε | 0.101 | 0.374 | 0.221 |
| β1*Low2 + β2*High2 + ε | 0.438 | 0.599 | 0.678 | |
| β1*StrainStim+ε | 0.039 | 0.197 | ||
| β1*Strain_MagRate+ε | 0.117 | 0.342 | ||
| β1*Strain_Mag + ε | 0.124 | 0.352 | ||
| β1*Strain_Rate + ε | 0.102 | 0.320 | ||
| UD iBMD (g/cm3) | β1*Low1 + β2*High1 + ε | 0.009 | 0.091 | 0.101 |
| β1*Low2 + β2*High2 + ε | 0.563 | 0.739 | 0.716 | |
| β1*StrainStim+ε | 0.003 | 0.051 | ||
| β1*Strain_MagRate+ε | 0.041 | 0.203 | ||
| β1*Strain_Mag + ε | 0.045 | 0.212 | ||
| β1*Strain_Rate + ε | 0.044 | 0.209 | ||
| Total iBMC (g) | β1*Low1 + β2*High1 + ε | 0.019 | −0.119 | 0.028 |
| β1*Low2 + β2*High2 + ε | 0.545 | 0.743 | 0.687 | |
| β1*StrainStim+ε | 0.001 | −0.028 | ||
| β1*Strain_MagRate+ε | 0.008 | 0.091 | ||
| β1*Strain_Mag + ε | 0.011 | 0.106 | ||
| β1*Strain_Rate + ε | 0.012 | 0.109 | ||
| Total iBMD (g/cm3) | β1*Low1 + β2*High1 + ε | 0.005 | −0.018 | 0.059 |
| β1*Low2 + β2*High2 + ε | 0.520 | 0.756 | 0.627 | |
| β1*StrainStim+ε | 0.001 | 0.027 | ||
| β1*Strain_MagRate+ε | 0.023 | 0.153 | ||
| β1*Strain_Mag + ε | 0.036 | 0.189 | ||
| β1*Strain_Rate + ε | 0.012 | 0.166 |
Low1 and High1 indicate low and high strain magnitude groups from experiment 1. Low2 and High2 indicate low and high strain rate groups from experiment 2. Bold for R 2 indicates p < .05 for F‐test of overall model fit. Bold for β1 or β2 indicates p < .05 for t test of significance for coefficient.
In models examining the effects of loading dose on the changes to bone, ultradistal iBMC, iBV, and ecBV were all positively and consistently associated with measures of loading dose, especially Strain_MagRate (Fig. 4 A). However, in all cases, loading dose explained less than 15% of the variance in the change values. The StrainStim metric was not related to change in any variable.
Figure 4.

(A) Percent change in ultradistal iBMC versus Strain_MagRate. (B) Percent change in Tb.vBMDinn versus Strain_MagRate. Both plots represent 12‐month change for all participants with available data.
Effect of strain on 3‐month, 6‐month, 9‐month, and 12‐month bone microstructure (HRpQCT)
After 3 months, membership in the low and high magnitude loading groups explained up to 17% of the increases in Tt.BMD compared to the control group (Supplemental Table S1). Similarly, high loading rate was significantly associated with 3‐month increases to Tt.BMD, Ct.BMD, and Ct.Th (Supplemental Table S1). Strain_MagRate, Strain_Mag, and Strain_Rate were all significant predictors for the change in Tt.BMD and Ct.Th, although 12% or less of the variance in these measures was explained by loading dose.
At 6 months, none of the microstructural changes were different between groups. However, at 9 months, the low strain magnitude group was significantly and positively associated with increases to Tt.BMD, Tb.BMD, Tb.BMDinn, and Tb.BMDmeta (Fig. 5 A). Similarly, the high strain magnitude and low strain rate groups were positively associated with changes to Tb.BMDinn (Fig. 5 B). Strain_MagRate and Strain_Rate were positively associated with the increase to Tb.BMDinn in 9 months. These changes persisted at 12 months, with Strain_MagRate being associated with increases to Tb.BMD and Tb.BMDinn (Fig. 4 B).
Figure 5.

(A) Change in Tt.BMD and (B) Tb.vBMDinn from baseline versus time, per group. Significant group changes versus control group at specific time points are labeled with *. Error bars represent standard error.
Comparison between change in ultradistal iBMC tertile groups
Participant characteristics at baseline were not different between tertile groups (Table 4). Nearly all loading‐related variables were significantly different across the three tertiles. However, after Bonferroni adjustment for multiple comparisons, only the highest versus lowest tertiles were different.
Table 4.
Grouped by Change in Ultradistal iBMC Tertile
| Highest tertile | Middle tertile | Lowest tertile | p | |
|---|---|---|---|---|
| Demographics | ||||
| Age (years) | 27.7 ± 4.7 | 29.4 ± 5.8 | 29.3 ± 5.6 | .510 |
| Height (cm) | 166 ± 7 | 165 ± 6 | 165 ± 7 | .847 |
| Body mass (kg) | 64.9 ± 8.1 | 65.2 ± 9.2 | 63.7 ± 7.3 | .817 |
| Serum Vitamin D (ng/mL) | 30 ± 10 | 29 ± 7a | 36 ± 10b | .015 |
| Total forearm aBMD (g/cm2) | 0.59 ± 0.04 | 0.57 ± 0.04 | 0.58 ± 0.03 | .425 |
| Group membership (n; control/exercise) | 2/20 | 3/19 | 8/14 | – |
| Applied load | ||||
| Peak force (N) | 297 ± 103a | 230 ± 135 | 167 ± 139 | .005 |
| Loading rate (N/s) | 865 ± 586a | 540 ± 515 | 344 ± 407 | .010 |
| Number of bouts | 128 ± 85 | 96.8 ± 84 | 72 ± 87 | .098 |
| Peak strain (με) | 575 ± 246a | 490 ± 347 | 323 ± 283 | .020 |
| Strain rate (με/s) | 1878 ± 1428a | 1206 ± 1031 | 918 ± 1077 | .029 |
| StrainStim (με*s−1*bouts*10−7) | 208 ± 278 | 92.3 ± 119 | 121 ± 224 | .195 |
| Strain_MagRate (με2*s−1*bouts*10−5) | 799 ± 723a | 428 ± 531 | 249 ± 383 | .007 |
| Strain_Mag (με*bouts*10−2) | 847 ± 620a | 641 ± 639 | 382 ± 497 | .038 |
| Strain_Rate (με*s−1*bouts*10−3) | 280 ± 257a | 149 ± 165 | 105 ± 143 | .012 |
| Bone QCT values | ||||
| Baseline ultradistal iBMC | 0.949 ± 0.172 | 0.889 ± 0.141 | 0.881 ± 0.114 | .244 |
| Visit 5 change (mg) | 36 ± 13a b | 5 ± 7a | −17 ± 13b | <.001 |
| Visit 5 percent change (%) | 3.8 ± 1.3a b | 0.6 ± 0.7a | −2.0 ± 1.6b | <.001 |
Data are shown as mean ± SD. Values of p indicate significant between‐group differences. Bold values are significant. Symbols indicate significant Bonferroni‐adjusted post hoc comparisons between specific tertiles.
p < .05 versus lowest tertile after Bonferroni adjustment.
p < .05 versus middle tertile after Bonferroni adjustment.
Discussion
We conducted a randomized controlled trial to characterize the relationship between mechanical strain magnitude and rate and changes to bone in healthy adult women. We found that the application of mechanical strain produced small but significant changes to the ultradistal radius after 1 year. However, our first hypothesis, that bone accrual would be proportional to strain magnitude and strain rate, was not fully tested. The relatively small ranges of strain magnitude and rate achieved by experimental participants limits the ability to draw conclusions regarding their independent roles. This was further complicated by differences in compliance between groups. In light of this challenge, the analysis considering loading dose is potentially most informative. Loading dose includes a combination of strain magnitude, rate, and number of loading bouts, and reflects achieved loading without issues associated with participant compliance. In fact, aligned with the scientific premise of our first hypothesis, we observed a dose‐dependent relationship between measures of loading dose versus changes in iBMC and BMD across all participants.
Our second hypothesis, that structural changes would include increased cortical diameter and thickness, and increased trabecular bone mass near the endosteal surface, was only partly supported. This hypothesis was based on the structural mechanics principle that bone added near the cortical surface would result in the greatest gains in moment of inertia and structural resistance to bending. Endocortical BV, BMC, and BMD increased at 12 months, indicating bone apposition on both the periosteal and endosteal surfaces due to loading. At 3, 9, and 12 months, increases to overall density and trabecular density were observed with HRpQCT, and were dependent on loading dose. However, contrary to our expectation, the inner trabecular density (Tb.BMDinn) rather than more peripheral regions appeared to be primarily affected. During aging, trabecular structure is first lost from this region, and later from more peripheral regions,40 thus maximizing moment of inertia for a given quantity of bone. We previously reported age‐associated declines in Tb.BMDinn within a large subset of the participants measured here.41 It is possible that in our cohort of young, healthy women, trabecular microstructure in the more peripheral regions was already at its physiologic maximum, limiting the degree to which it might be improved. We observed Tb.BMDinn was lower than Tb.BMDmeta (Supplemental Table S1), suggesting that there was greater capacity to improve the inner region with anabolic physical activity.
We observed significant positive effects of loading on Tt.BMD, Tb.BMDinn, and Ct.BMD after 3 months. Interestingly, all participants were assigned the same loading magnitude (200 N) during this ramp‐up period, rather than a group‐specific strain. Compliance was also the best during the first 3 months. Therefore, it is not surprising that both low and high magnitude groups had increases in these variables, because they both received the same stimulus. Overall, this supports the notion that loads must be novel to elicit an osteogenic response.19 However, the ramp‐up period may have diminished the possible osteogenic response by stimulating cellular accommodation42 to initially lower loads. Furthermore, it diminished the between‐group differences in achieved strain. The improved response in the low magnitude group, who completed more loading bouts in total than other groups, also suggests that regular performance of exercise is as important as strain magnitude and rate. This is in agreement with studies in mice showing that separating loading cycles into multiple bouts is more osteogenic than a single bout with the same total number of cycles,29, 43 potentially due to desensitization of osteocytes.
We observed significant increases to bone mass in the strain rate experiment; however, both low and high strain rate groups demonstrated positive results and the regression coefficients were similar between groups. Although strain rates were significantly different between the high and low groups, participants in the high group fell far short of the target values. This may explain the similar response between groups. Surprisingly, in experiment 1 (strain magnitude) only the low strain magnitude group showed even slight increases in ultradistal iBMC after 12 months, with no observable changes in the high strain magnitude group. In fact, despite being given different target strains and strain rates, the different loading groups did not achieve the expected range of rates and magnitudes (Table 1). This, combined with varying participant compliance may partly explain these counterintuitive results. The analysis by tertile change in iBMC suggests that changes to bone are indeed associated with bone loading dose. Participants in the highest tertile also had had a nonsignificant trend toward higher baseline BMC, suggesting that perhaps these individuals simply had a greater physiologic capacity to respond to osteogenic stimuli. We did not observe any other obvious factors related to the change (e.g., vitamin D status) that might explain this, although our measurements did not include biomarkers related to bone metabolism. The degree to which strain magnitude can be manipulated is limited because of risk of secondary injury, although greater magnitudes are possible in the lower extremities. With vibration and other external assistance, it is possible to manipulate strain rate over a much wider range than strain magnitude.
In contrast to small animal in vivo loading models, which use a materials testing machine to generate a predictable and repeatable waveform, voluntarily applied forces are variable in terms of frequency content, even when the peak magnitude is guided through visual feedback, as in our study. Although many measures of bone loading dose have been proposed in the literature,19, 22, 23, 39 we found it impractical to implement any of them exactly as described by the authors. In addition to voluntarily produced loading signals being inconsistent, mechanical strain is nonuniform within a bone, both temporally and spatially; thus, no single strain value completely describes the strain occurring within a bone. It is not practical to place strain gauges on most bones, and even when such measures are obtained (e.g., Milgrom and colleagues(44) ), they only represent a small fraction of the bone surface. We previously observed that high‐strain regions in the distal radius experienced the greatest gains in BMC, suggesting local control of osteogenic response.28 Here, we examined several candidate versions of loading dose, based on load cell recordings and subject‐specific FE models. Each version included a combination of strain magnitude, frequency, and number of loading bouts. As a first attempt, we chose to examine a linear combination of the continuum strain produced within the analysis region in question (corresponding with the QCT or HRpQCT analysis region for those respective variables) and the total number of bouts achieved up to the time point in question. Although we observed significant associations between these measures and changes to bone, we found that at best, dose explained 12% of the variance in the change. It is possible that other formulations of loading dose that include exponential scaling factors, local strain rate, strain gradient, or other measures, may be more relevant.
The magnitude and nature of the changes we observed are similar to an earlier, 6‐month study using a similar loading protocol.27 In that set of 19 young women, control participants lost 1.7% ± 1.1% ultradistal iBMC, whereas those in the loading group had no change in iBMC, but significant increases in trabecular BMC (1.3% ± 2.8%). Here, we found a similar decrease in the control group iBMC (−1.3% ± 2.7%), and increases to BMC and BMD that were associated with loading dose. The present cohort differed from the previous study in several ways. First, present participants were generally older (28 versus 22 years old) and many had a history of pregnancy or lactation (although not within the 2 years preceding enrollment). The present group were assigned loading magnitudes based on strain within the ultradistal radius at the instant of peak force production. However, because of safety limits, many participants fell short of their target strains. Thus, although high strain magnitudes may have, in theory, elicited a greater osteogenic response, they were impractical or unsafe to implement. Similarly, participants in the low and high strain rate groups were given instruction sets designed to elicit significantly different strain rates. Although the rates were significantly different between groups, (low: 945 με/s, high: 1698 με/s, p = .02) the sample did not vary as widely as designed and the rates were substantially lower than those occurring during impact activities such as running.45 Both low and high strain rate groups experienced similar increases in bone. Forearm loading is a relatively constrained activity that produces both compression and bending within the distal radius,24 and the ability to voluntarily manipulate the strain signal was limited.
Our results suggest that, although compressive loading in general is osteogenic, it may not be necessary to generate extremely high strain magnitudes or rates to elicit a positive response in the upper extremity. Significant gains in BMC were associated with strain rates and magnitudes within the range of those measured experimentally during activities of daily living (less than or equal to ~1300 με)46 and can be achieved in a reasonable amount of time (100 loading cycles/bout, and an average of 128 loading bouts over a 12‐month period for the highest tertile group). This is reassuring, because although impact loads are osteogenic,3 high loading rates have also been linked to increased risk of bone stress injury.47 Although we did not systematically test the effect of loading cycles/bout, we based our target of 100 on: (i) feasibility and time to complete the intervention, about 3 min; and (ii) theoretical calculations of bone adaptation32, 39 that suggested a diminished osteogenic response with additional cycles. Others have shown that breaking loading bouts into multiple sessions,48, 49 inserting rest periods between cycles,43 and changing the number of cycles50 all can independently influence the osteogenic response in small animal loading models. An alternative loading regimen may have produced a greater response than what was observed here, although testing these parameters was not the focus of the present investigation.
This study had several important limitations. Only 66 of the 102 original participants completed all 12 months of the study, and the results may be biased toward those who did not drop out. However, the demographics and baseline data of individuals who dropped out were not different from those who completed the study. We adjusted the randomization ratio part‐way through enrollment to oversample the loading groups, which may have introduced other unknown biases. Due to the lower number of completers and lower precision, we were not powered to detect trabecular microstructural changes. However, we did observe significant changes to iBMC and Tb.BMD. The magnitude of the increases to iBMC due to the loading interventions, 1.2% across all participants, is not dissimilar to other treatment effects considered clinically relevant, and is well above (>4×) the CV for this measure. And, participants participating in experiment 2 had much larger increases (2.9% and 3.6% for iBMC, and 4.8 to 6.6% for strength indices), also several times greater than the CV. For comparison, a 3.3% increase in trochanter integral BMD over 36 months was observed in postmenopausal women given zoledronic acid,51 and it has been estimated that each 1% increase in peak bone mass imparts over 1 year of osteoporosis‐free life in the future.52 Although the present study examined the effects of strain magnitude and rate on bone adaptation, an underlying assumption is that the bone of each individual is already well adapted for her habitual activities; our analysis only considered the novel/added stimulus. Dominant (non‐loaded) forearm data were not included in the present analysis, but would provide an indication of the systemic versus local effects of loading. Although we collected physical activity data as part of this study, they were beyond the scope of the present analysis, but may potentially explain some of the variability in response to our intervention. Our results may not be generalizable to other populations, including postmenopausal women, those with low vitamin D, men, or specific clinical populations. Finally, more research is needed to determine the specific strain requirements to elicit clinically relevant changes to lower extremity bone, given the high habitual loading stimulus in these sites.
Although other clinical trials have investigated the efficacy of various types of exercise to for improving bone mass, this study is the first to systematically investigate the effect of mechanical strain rate and magnitude on bone adaptation in humans. The data presented here fill a critical translational gap, linking in vivo animal models to clinical trials, and may be useful for informing the design of future clinical interventions targeting bone health. In particular, our data show that in healthy adult women, the distal radius is capable of modest adaptation in response to mechanical strain, and that the adaptation is associated with measures of loading dose that include strain magnitude, rate, and number of loading bouts.
In conclusion, we conducted a randomized controlled trial to systematically investigate the effect of mechanical strain rate and magnitude on bone adaptation, using an in vivo upper extremity loading model in healthy adult women. We found that compressive loading of the forearm was osteogenic, with high and low strain rate groups having similar significant increases to bone mass. We observed that participants who gained the most bone had, on average, completed 128 compressive loading bouts, generating an average energy‐equivalent strain of 575 με at 1878 με/s within the distal radius, over a period of 12 months. Individuals with the greatest gains to bone mass were similar in demographics to those with the lowest gains to bone mass. We conclude that signals related to strain magnitude, strain rate, and number of loading bouts collectively contribute to bone adaptation in healthy adult women.
Disclosures
KLT reports grants and personal fees from National Institutes of Health, during the conduct of the study; non‐financial support from International Society of Biomechanics, grants from Merck, Inc, personal fees from National Science Foundation, outside the submitted work; MEM reports grants from National Science Foundation (DGE‐1106756),during the conduct of the study; All other authors declare no conflicts of interest.
Supporting information
Table S1 Mean (SD) of baseline and percent changes of HRpQCT measures during each visit (V1 at baseline through V5 at 12 months), by group.
Table S2. Mean (SD) loading parameters for loading groups considering all participants randomized in each group, and after removing participants who completed zero loading sessions.
Acknowledgments
This research was fully supported by NIAMS of the National Institutes of Health under award number R01AR063691.The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. This material is also based upon work supported by the National Science Foundation Graduate Research Fellowship Program under Grant No. DGE‐1106756. We thank Sabahat Ahmed for her organization and dedication as research coordinator, and Dr. Jane Marone for serving as our Independent Safety Monitor.
Authors' roles: Study conceived by KLT and designed by KLT with assistance from TJS. Data collection by MEM, KLT, JEJ, and TAB. Data analysis and interpretation: MEM, KLT, JEJ, TAB, ZW, TJS. Manuscript writing: KLT and MEM. Manuscript approval: MEM, KLT, JEJ, TAB, ZW, TJS.
Public clinical trial registration: http://clinicaltrials.gov/show/NCT04135196. A Prospective Study of Human Bone Adaptation Using a Novel in vivo Loading Model.
The peer review history for this article is available at https://publons.com/publon/10.1002/jbmr.3999.
References
- 1. Howe TE, Shea B, Dawson LJ, et al. Exercise for preventing and treating osteoporosis in postmenopausal women. Cochrane Database Syst Rev. 2011;7(7):CD000333. [DOI] [PubMed] [Google Scholar]
- 2. Weidauer L, Minett M, Negus C, et al. Odd‐impact loading results in increased cortical area and moments of inertia in collegiate athletes. Eur J Appl Physiol. 2014;114(7):1429–38. [DOI] [PubMed] [Google Scholar]
- 3. Martyn‐St James M, Carroll S. Effects of different impact exercise modalities on bone mineral density in premenopausal women: a meta‐analysis. J Bone Miner Metab. 2010;28(3):251–67. [DOI] [PubMed] [Google Scholar]
- 4. Kontulainen SA, Kannus PA, Pasanen ME, et al. Does previous participation in high‐impact training result in residual bone gain in growing girls? One year follow‐up of a 9‐month jumping intervention. Int J Sports Med. 2002;23(8):575–81. [DOI] [PubMed] [Google Scholar]
- 5. Bailey CA, Brooke‐Wavell K. Optimum frequency of exercise for bone health: randomised controlled trial of a high‐impact unilateral intervention. Bone. 2010;46(4):1043–9. [DOI] [PubMed] [Google Scholar]
- 6. Korpelainen R, Keinanen‐Kiukaanniemi S, Heikkinen J, Vaananen K, Korpelainen J. Effect of impact exercise on bone mineral density in elderly women with low BMD: a population‐based randomized controlled 30‐month intervention. Osteoporos Int. 2006;17(1):109–18. [DOI] [PubMed] [Google Scholar]
- 7. LaMothe JM, Hamilton NH, Zernicke RF. Strain rate influences periosteal adaptation in mature bone. Med Eng Phys. 2005;27(4):277–84. [DOI] [PubMed] [Google Scholar]
- 8. Mosley JR, Lanyon LE. Strain rate as a controlling influence on adaptive modeling in response to dynamic loading of the ulna in growing male rats. Bone. 1998;23(4):313–8. [DOI] [PubMed] [Google Scholar]
- 9. O'Connor JA, Lanyon LE, MacFie H. The influence of strain rate on adaptive bone remodelling. J Biomech. 1982;15(10):767–81. [DOI] [PubMed] [Google Scholar]
- 10. Mosley JR, March BM, Lynch J, Lanyon LE. Strain magnitude related changes in whole bone architecture in growing rats. Bone. 1997;20(3):191–8. [DOI] [PubMed] [Google Scholar]
- 11. Rubin CT, Lanyon LE. Regulation of bone mass by mechanical strain magnitude. Calcif Tissue Int. 1985;37(4):411–7. [DOI] [PubMed] [Google Scholar]
- 12. Donahue SW, Donahue HJ, Jacobs CR. Osteoblastic cells have refractory periods for fluid‐flow‐induced intracellular calcium oscillations for short bouts of flow and display multiple low‐magnitude oscillations during long‐term flow. J Biomech. 2003;36(1):35–43. [DOI] [PubMed] [Google Scholar]
- 13. Steck R, Niederer P, Knothe Tate ML. A finite difference model of load‐induced fluid displacements within bone under mechanical loading. Med Eng Phys. 2000;22(2):117–25. [DOI] [PubMed] [Google Scholar]
- 14. Kowalchuk RM, Pollack SR. Stress‐generated potentials in bone: effects of bone fluid composition and kinetics. J Orthop Res. 1993;11(6):874–83. [DOI] [PubMed] [Google Scholar]
- 15. Hazenberg JG, Freeley M, Foran E, Lee TC, Taylor D. Microdamage: a cell transducing mechanism based on ruptured osteocyte processes. J Biomech. 2006;39(11):2096–103. [DOI] [PubMed] [Google Scholar]
- 16. Burr DB, Martin RB, Schaffler MB, Radin EL. Bone remodeling in response to in vivo fatigue microdamage. J Biomech. 1985;18(3):189–200. [DOI] [PubMed] [Google Scholar]
- 17. Muir P, Sample SJ, Barrett JG, et al. Effect of fatigue loading and associated matrix microdamage on bone blood flow and interstitial fluid flow. Bone. 2007;40(4):948–56. [DOI] [PubMed] [Google Scholar]
- 18. Nguyen AM, Jacobs CR. Emerging role of primary cilia as mechanosensors in osteocytes. Bone. 2013;54(2):196–204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Turner CH. Three rules for bone adaptation to mechanical stimuli. Bone. 1998;23(5):399–407. [DOI] [PubMed] [Google Scholar]
- 20. Dolan SH, Williams DP, Ainsworth BE, Shaw JM. Development and reproducibility of the bone loading history questionnaire. Med Sci Sports Exerc. 2006;38(6):1121–31. [DOI] [PubMed] [Google Scholar]
- 21. Weeks BK, Beck BR. The BPAQ: a bone‐specific physical activity assessment instrument. Osteoporosis Int. 2008;19(11):1567–77. [DOI] [PubMed] [Google Scholar]
- 22. Ahola R, Korpelainen R, Vainionpaa A, Jamsa T. Daily impact score in long‐term acceleration measurements of exercise. J Biomech. 2010;43(10):1960–4. [DOI] [PubMed] [Google Scholar]
- 23. Turner CH, Robling AG. Designing exercise regimens to increase bone strength. Exerc Sport Sci Rev. 2003;31(1):45–50. [DOI] [PubMed] [Google Scholar]
- 24. Bhatia VA, Edwards WB, Troy KL. Predicting surface strains at the human distal radius during an in vivo loading task–finite element model validation and application. J Biomech. 2014;47(11):2759–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Gray HA, Taddei F, Zavatsky AB, Cristofolini L, Gill HS. Experimental validation of a finite element model of a human cadaveric tibia. J Biomech Eng. 2008;130(3):031016. [DOI] [PubMed] [Google Scholar]
- 26. Taddei F, Schileo E, Helgason B, Cristofolini L, Viceconti M. The material mapping strategy influences the accuracy of CT‐based finite element models of bones: an evaluation against experimental measurements. Med Eng Phys. 2007;29(9):973–9. [DOI] [PubMed] [Google Scholar]
- 27. Troy KL, Edwards WB, Bhatia VA, Bareither ML. In vivo loading model to examine bone adaptation in humans: a pilot study. J Orthop Res. 2013;31(9):1406–13. [DOI] [PubMed] [Google Scholar]
- 28. Bhatia VA, Edwards WB, Johnson JE, Troy KL. Short‐term bone formation is greatest within high strain regions of the human distal radius: a prospective pilot study. J Biomech Eng. 2015;137(1):011001. 10.1115/1.4028847. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Hsieh YF, Turner CH. Effects of loading frequency on mechanically induced bone formation. J Bone Min Res. 2001;16(5):918–24. [DOI] [PubMed] [Google Scholar]
- 30. Baxter‐Jones AD, Kontulainen SA, Faulkner RA, Bailey DA. A longitudinal study of the relationship of physical activity to bone mineral accrual from adolescence to young adulthood. Bone. 2008;43(6):1101–7. [DOI] [PubMed] [Google Scholar]
- 31. Henry YM, Fatayerji D, Eastell R. Attainment of peak bone mass at the lumbar spine, femoral neck and radius in men and women: relative contributions of bone size and volumetric bone mineral density. Osteoporosis Int. 2004;15(4):263–73. [DOI] [PubMed] [Google Scholar]
- 32. Bhatia VA, Edwards WB, Troy KL. Predicting bone adaptation at the human distal radius using cadaveric specimens and the daily strain stimulus theory. Proceedings of the 59th Annual Meeting of the Orthopaedic Research Society. San Antonio, TX: Orthopaedic Research Society; 2013. [Google Scholar]
- 33. Oldfield RC. The assessment and analysis of handedness: the Edinburgh inventory. Neuropsychologia. 1971;9(1):97–113. [DOI] [PubMed] [Google Scholar]
- 34. Buie HR, Campbell GM, Klinck RJ, MacNeil JA, Boyd SK. Automatic segmentation of cortical and trabecular compartments based on a dual threshold technique for in vivo micro‐CT bone analysis. Bone. 2007;41(4):505–15. [DOI] [PubMed] [Google Scholar]
- 35. Burghardt AJ, Buie HR, Laib A, Majumdar S, Boyd SK. Reproducibility of direct quantitative measures of cortical bone microarchitecture of the distal radius and tibia by HR‐pQCT. Bone. 2010;47(3):519–28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Burghardt AJ, Kazakia GJ, Link TM, Majumdar S. Automated simulation of areal bone mineral density assessment in the distal radius from high‐resolution peripheral quantitative computed tomography. Osteoporos Int. 2009;20(12):2017–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Edwards WB, Schnitzer TJ, Troy KL. Bone mineral and stiffness loss at the distal femur and proximal tibia in acute spinal cord injury. Osteoporosis Int. 2014;25(3):1005–15. [DOI] [PubMed] [Google Scholar]
- 38. Edwards WB, Troy KL. Finite element prediction of surface strain and fracture strength at the distal radius. Med Eng Phys. 2012;34(3):290–8. [DOI] [PubMed] [Google Scholar]
- 39. Mikic B, Carter DR. Bone strain gage data and theoretical models of functional adaptation. J Biomech. 1995;28(4):465–9. [DOI] [PubMed] [Google Scholar]
- 40. Sode M, Burghardt AJ, Kazakia GJ, Link TM, Majumdar S. Regional variations of gender‐specific and age‐related differences in trabecular bone structure of the distal radius and tibia. Bone. 2010;46(6):1652–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Mancuso M, Johnson J, Ahmed S, Butler T, Troy K. Distal radius microstructure and finite element bone strain are related to site‐specific mechanical loading and areal bone mineral density in premenopausal women. Bone Rep. 2018;8:187–94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Schriefer JL, Warden SJ, Saxon LK, Robling AG, Turner CH. Cellular accommodation and the response of bone to mechanical loading. J Biomech. 2005;38(9):1838–45. [DOI] [PubMed] [Google Scholar]
- 43. Srinivasan S, Weimer DA, Agans SC, Bain SD, Gross TS. Low‐magnitude mechanical loading becomes osteogenic when rest is inserted between each load cycle. J Bone Miner Res. 2002;17(9):1613–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Milgrom C, Burr DB, Finestone AS, Voloshin A. Understanding the etiology of the posteromedial tibial stress fracture. Bone. 2015;78:11–4. [DOI] [PubMed] [Google Scholar]
- 45. Milgrom C, Radeva‐Petrova DR, Finestone A, et al. The effect of muscle fatigue on in vivo tibial strains. J Biomech. 2007;40(4):845–50. [DOI] [PubMed] [Google Scholar]
- 46. Foldhazy Z, Arndt A, Milgrom C, Finestone A, Ekenman I. Exercise‐induced strain and strain rate in the distal radius. J Bone Joint Surg Br. 2005;87(2):261–6. [DOI] [PubMed] [Google Scholar]
- 47. Zadpoor AA, Nikooyan AA. The relationship between lower‐extremity stress fractures and the ground reaction force: a systematic review. Clin Biomech. 2011;26(1):23–8. [DOI] [PubMed] [Google Scholar]
- 48. Robling AG, Burr DB, Turner CH. Partitioning a daily mechanical stimulus into discrete loading bouts improves the osteogenic response to loading. J Bone Miner Res. 2000;15(8):1596–602. [DOI] [PubMed] [Google Scholar]
- 49. Robling AG, Burr DB, Turner CH. Recovery periods restore mechanosensitivity to dynamically loaded bone. J Exp Biol. 2001;204:3389–99. [DOI] [PubMed] [Google Scholar]
- 50. Umemura Y, Ishiko T, Yamauchi T, Kurono M, Mashiko S. Five jumps per day increase bone mass and breaking force in rats. J Bone Miner Res. 1997;12(9):1480–5. [DOI] [PubMed] [Google Scholar]
- 51. Eastell R, Lang T, Boonen S, et al. Effect of once‐yearly zoledronic acid on the spine and hip as measured by quantitative computed tomography: results of the HORIZON Pivotal Fracture Trial. Osteoporosis Int. 2010;21(7):1277–85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Hernandez CJ, Beaupre GS, Carter DR. A theoretical analysis of the relative influences of peak BMD, age‐related bone loss and menopause on the development of osteoporosis. Osteoporos Int. 2003;14(10):843–7. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Table S1 Mean (SD) of baseline and percent changes of HRpQCT measures during each visit (V1 at baseline through V5 at 12 months), by group.
Table S2. Mean (SD) loading parameters for loading groups considering all participants randomized in each group, and after removing participants who completed zero loading sessions.


