Abstract
This paper presents a comparative study on the energy, exergetic and thermo-economic performance of a novelty thermal power system integrated by a supercritical CO2 Brayton cycle, and a recuperative organic Rankine cycle (RORC) or a simple organic Rankine cycle (SORC). A thermodynamic model was developed applying the mass, energy and exergy balances to all the equipment, allowing to calculate the exergy destruction in the components. In addition, a sensitivity analysis allowed studying the effect of the primary turbine inlet temperature (TIT, PHIGH, rP and TC) on the net power generated, the thermal and exergy efficiency, and some thermo-economic indicators such as the payback period (PBP), the specific investment cost (SIC), and the levelized cost of energy (LCOE), when cyclohexane, acetone and toluene are used as working fluids in the bottoming organic Rankine cycle. The parametric study results show that cyclohexane is the organic fluid that presents the best thermo-economic performance, and the optimization with the PSO method conclude a 2308.91 USD/kWh in the SIC, 0.22 USD/kWh in the LCOE, and 9.89 year in the PBP for the RORC system. Therefore, to obtain technical and economic viability, and increase the industrial applications of these thermal systems, thermo-economic optimizations must be proposed to obtain lower values of the evaluated performance indicators.
Keywords: Energy, Mechanical engineering, Thermodynamics, Energy conservation, Gas turbine, Organic Rankine cycle, Supercritical CO2 Brayton cycle, Exergetic analysis, Energy analysis, Thermo-economic indicators, PSO optimization
Energy; Mechanical engineering; Thermodynamics; Energy conservation; Gas turbine; Organic Rankine cycle; Supercritical CO2 Brayton cycle; Exergetic analysis; Energy analysis; Thermo-economic indicators; PSO optimization.
1. Introduction
Energy demand has grown gradually in recent decades, and primary energy resources are limited, so it is necessary to establish other energy generation alternatives to help diversify the energy mix [1]. In addition to the problem of limited clean energy sources, the increased use of conventional methods of energy generation increases the amount of CO2 emitted into the atmosphere, which is the main cause of the greenhouse effect. Therefore, among the requirements that address the implementation of power generation systems is the reduction of CO2 emissions into the atmosphere to reduce the global warming potential [2]. In order to achieve a reduction in the consumption of primary energy resources and CO2 emissions, it has been proposed to increase the thermal efficiency of industrial power generation systems the use of organic Rankine cycle (ROC) as bottoming cycles, where the thermal source can be the exhaust gases from engines [3]. Among the various advantages of an ORC system is the high reliability and ease of maintenance that make it a cost-effective system in the process of converting waste heat into energy from various energy sources [4].
Furthermore, studies have shown that the ORC is a suitable bottoming cycle from other systems [5], due to its considerable cost-effectiveness ratio for energy conversion from a diversity of energy sources such as solar, exhaust gases of an internal combustion engine, biomass and Brayton supercritical CO2 (S-CO2) cycle [6]. According to the study conducted by Dostal et al. [7], with the implementation of a Brayton S-CO2 cycle, it is possible to achieve greater efficiency compared to the ORC when the turbine inlet temperature (TIT) is higher than 470 °C, but this has not been studied when the system is integrated with an ORC [8]. The energy generation through the S-CO2 Brayton cycle has a high potential in the fields of nuclear, chemical and renewable energy, because of its high efficiency and safety. Also, its easy implementation in power generation systems increases due to its easy acquisition, its economical cost and the capacity that this fluid has to resist high temperatures where heat sources can reach a range from 600 °C to 700 °C [9].
The Brayton S-CO2 system is considered a promising energy generation alternative because it has a high cycle performance at the identical turbine inlet temperature. Also, the compression reduction presented, the smaller devices required that make the system simpler, higher thermal capacity measured based on the specific heat produced at constant pressure [10]. In the same way, when a carbon dioxide energy conversion process is operating above its critical conditions, the fluid density is increased to achieve the benefit of a low volume/power ratio, i.e. the compression work performed in the compressor in the S-CO2 decreases significantly due to the change of the CO2 thermal properties, observing a compressibility factor of the fluid from 0.2 to 0.5 [11]. Therefore, its integration with an ORC cycle with low acquisition costs operating in optimal operating conditions could guarantee values of thermo-economic indicators such as the specific cost of investment, which enable its application in real operating conditions at an industrial level.
On the other hand, based on the economic results from Dostal and Hejzlar [12], the use of the S-CO2 cycle provides approximately savings of 15% compared to an equivalent helium cycle, and savings of 30% related to the indirect steam cycle [13]. In this study, an optimization approach of the system is proposed, but a thermo-economic variable that allows to connect the economic and thermodynamic variables of the system is not considered as an objective function. Furthermore, the performance of this thermal system is not evaluated when it is integrated with another bottoming cycle that improves its energy and exergy efficiency.
In the case of the organic Rankine cycle (ORC) system, Toffolo et al. [14] studied the economic performance that can be achieved through the optimal working fluid choice, and the establishing the best operational parameters that allow the correct configuration of the cycle to be chosen, by setting out numerous methods together, such as the thermodynamic optimization technique of the thermal system structure and operational parameters, that examines all potential configurations, design alternatives near the best objective function. This studied was limited only to the ORC cycle and they did not consider thermo-economic performance indicator as objective function. In this sense, the levelized energy cost, payback period and specific investment cost had been selected as objective function in a thermo-economic optimization of the ORC as bottoming cycle of a natural gas engine, where the RORC system increases the thermal efficiency by 9.29% respect to the SORC [15], but these studied had not been conducted when the ORC and RORC are proposed as bottoming cycles from S-CO2 cycle.
El-Emam et al. [16] show thermodynamic studies of an ORC based on the first and second thermodynamic laws, in which energy and exergetic efficiency values of 16.37% and 48.8% were obtained, for optimal operational conditions for the geothermal water rejection temperature ranging from 78.49 °C to 116.2 °C. However, the thermal system evaluated differs to the Brayton S-CO2-ORC thermal configurations proposed in the present study, so these results must be obtained for the comparative energy, and exergo-economic analysis under different organic working fluids.
The typical approach to improve the thermal systems is an exergy-based optimization method [15, 17], where the objective is to minimize the exergy destroyed through components of the thermal cycle. However, these types of objective variables do not consider economic criteria that allow generating favorable conditions with economic and energy savings that are attractive to industries worldwide. Related to ORC limited to bottoming cycle from industrial gas engine, these studies had been conducted highlighting the location of the main exergy destroyed in the system [18], and evaluating the potential environmental impact through a life cycle assessment [19]. Also, the main opportunities for improvement with the help of advance exergo-economic analysis had been evaluated [20], revealing promising results when this system will be evaluated integrated as bottoming cycle from a Brayton, and also optimized. In addition, parametric study of the integrated system considering the main operational variables are not widely reported in literature, where the monetary value is allocated to the exergy flow to calculate the cost of the exergetic inefficiency these systems [21].
In regards to the combination of gas turbine and ORC, the energy and exergy efficiencies, in addition to the total cost were considered as the three objective functions of the optimization problem [22], revealing a higher exergy destruction fraction in the combustion chamber, follow by the steam generator, and the gas turbine. Also, an exergo-economic factor of 10.59% for the thermal cycle was calculated, demonstrating that the cost related to exergy destruction is predominant respect to capital investment cost, and the purchase equipment cost must be considered in the performance optimization of the ORC system integrated to gas turbine.
The integration of a 260 kW ORC to a 453 MW gas turbine was evaluated only from an energy point of view increasing power generation by 1.65 MW [23]. In addition, the Brayton S-CO2 cycle was optimized using ORC as the bottoming cycle, which allowed for a 1.3% increase in thermal efficiency by increasing the organic fluid evaporation temperature [24]. However, this study was did not consider the thermo-economic performance indicators.
On the other hand, the layout of the system equipment has also been studied [25], where the ORC as a bottoming cycle was evaluated from the thermodynamic approach, concluding that the steam turbine could be of higher capacity, and thus improve the overall performance of the system by optimizing the heat exchangers configuration.
In addition, several authors have studied different ORC-based configurations with different organic fluids. Thus, the R1234ze presented better thermal performance than the other organic fluids in an ORC as a waste heat recovery system from the compressed air line of a Brayton S-CO2 [26]. However, the study does not consider an operational optimization of the thermal system involving economic criteria. Singh and Mishra [27] studied solar energy as the thermal source of the Brayton S-CO2-ORC system from five organic working fluids, but they did not consider a thermo-economic optimization to obtain the best operating conditions of the system.
These improvements obtained in different research allow reducing greenhouse gas emissions by integrating the prime mover to a bottoming ORC [28]. However, because of the heat source from the Brayton S-CO2 is typically high or medium grade [29], and the operational temperature is limited in the ORC, a thermal oil circuit is necessary to use.
Therefore, the main contribution of this study is to present the energy, exergy and thermo-economic study of an organic Rankine cycle, and recuperative organic Rankine cycle as bottoming cycle of a Brayton S-CO2-ORC configuration. A parametric study is presented to study the effect of high temperature and pressure of the Brayton, condenser temperature and pressure ratio on the combined power generated, the increase in the thermal efficiency of combined system, the decrease in the specific fuel consumption, the overall thermal efficiency, the ORC energy efficiency and the second law efficiency of the combined system.
Also, three different organic working fluids were studied in this research to quantify the effects of thermophysical fluid properties on the considered techno-economic performance indicators, and a thermo-economic optimization was applied by mean of the PSO method, selecting the specific investment cost as objective function.
2. Methodology
2.1. System description
In the proposed combined thermal system configuration, the energy is supplied from the Brayton S-CO2 cycle to the SORC through a thermal oil circuit, as shown in Figure 1. Two configurations in the ORC were considered as bottoming cycles, including a recuperator heat exchanger in RORC, and another similar system without the use of recuperator SORC.
Figure 1.
The physical structure of a Brayton S-CO2-SORC/RORC system.
In the Brayton S-CO2 cycle, the carbon dioxide enters to the primary turbine at a high temperature and pressure in the state (1 BC), follow to the heat source mainly at the superheater (2 BC). Then it is expanded to low pressure and temperature in the secondary turbine (3 BC). Subsequently, the carbon dioxide stream (4 BC) goes to the recuperator (Printed Circuit Heat Exchanger) to be reheated by the outlet flow from the compressor (7 BC). It enters to the recuperator to obtain the stream to received energy from the thermal source (8 BC). On the other hand, the flow (5 BC) yields energy to the thermal oil circuit (TOC) in the shell and tube heat exchanger, and in (6 BC) it enters to the compressor to continue the process.
After the thermal oil (Therminol 75) receives heat through the heat exchanger, in the stream (1 TOC) the oil flow transfer heat to the ORC working fluid through the evaporator, which is a Plate heat exchanger with three stages, where in the first the organic fluid is preheated by the thermal oil, then in the evaporation stage organic change to vapour saturated phase, and finally the superheating to obtain the fluid with the thermodynamic condition to produce energy in the turbine.
The RORC and the SORC are considered in this research as a bottoming cycle from the Brayton S-CO2. In the RORC, the organic fluid through in (1 ORC) flow to the ORC turbine achieving an expansion; then it is reheater in the recuperator through the stream (2 ORC) to obtain the thermodynamic state in (6 ORC). Before, the flow (3 ORC) at low pressure and temperature is condensing a heat exchanger integrated by two section, with the help of water at ambient pressure from (1 Wt) to (2 Wt). Finally, the fluid leaves the condenser (4 ORC) to enter Pump 2 and continue the process. The SORC operation is the same as the RORC, but it does not have a recuperator heat exchanger. In Figure 2 is shown the T-s diagram of the Brayton S-CO2-SORC/RORC.
Figure 2.
T-s diagram of the Brayton S-CO2-SORC and Brayton S-CO2-RORC.
2.2. Thermodynamic model
For each component k of the combined novelty system, the mass balance according to Eq. (1), the energy balance from the Eq. (2), and the exergy balance (Eq. (3)) were applied, from the thermal properties of the working fluid in the ORC, carbon dioxide in the Brayton S-CO2, and the Therminol 75 in the thermal oil circuit. In the ORC system were considered two configurations, the SORC and RORC operating with three organic working fluids under a steady-state condition.
| (1) |
| (2) |
where is the mass flow, h is the specific enthalpy. Likewise, and are the heat rate and power for each component k, while and represent the mass and energy inside the control volume. The net power of the Brayton cycle () is estimated by Eq. (3), the net power for the SORC and RORC is given by Eq. (4).
| (3) |
| (4) |
The specific physical exergy can be determined by Eq. (5) without taking into account the variation of kinetic and potential energy.
| (5) |
where is the reference enthalpy, and the reference entropy. The reference conditions considered to calculate these properties were , and .
Besides, the second law of thermodynamics was considered from the exergy balance (Equation 6) for every component of the integrated system.
| (6) |
where is the exergy destroyed, and is the specific exergy of a flow. Also, the exergy destruction fraction of each component () was calculated from the total exergy destroyed. The second thermodynamic law analysis for the thermal system was complemented with the exergetic efficiency () calculated from the Eq. (3), as a function of product exergy () and fuel exergy ) for the system or device.
| (7) |
The thermal efficiency of the Brayton S-CO2 system () can be calculated from Eq. (8), which is a function of the net power and heat supplied in the heater and reheater equipment.
| (8) |
The ORC thermal efficiency is determined from the Eq. (9), and measure the ratio between the net power and the energy supplied in the heat exchanger. Finally, the overall efficiency of the Brayton S-CO2-SORC cycle is a function of the net power and heat supplied from the thermal source and is calculated from Eq. (10).
| (9) |
| (10) |
The increase in thermal efficiency () of the combined Brayton S-CO2-ORC system compared to the Brayton S-CO2 cycle can be calculated from Eq. (11), which is due to the additional energy generated with the same heat supplied from the thermal source.
| (11) |
Therefore, the specific fuel consumption of the Brayton S-CO2 calculated from the Eq. (12), presents reduction respect to the specific fuel consumption of the combined Brayton S-CO2-ORC , which is estimated with the Eq. (13).
| (12) |
| (13) |
Thus, the decrease in specific fuel consumption () is calculated by mean of the Eq. (14), as follow.
| (14) |
2.3. Thermo-economic model
The thermo-economic modelling was carried out to combine the energy and exergetic analysis with the economic criteria required to propose a system with a good cost-efficiency ratio. The main objective of this approach is to calculate thermo-economic performance indicators from the cost per unit of exergy of each flow [30]. In addition, the cash flow of the project allowed to calculate some economic indicators, such as the PBP, and SIC. Besides, to determine the specific cost of exergy, the exergy flows of the stream are calculated, then the flows to the input and output for each equipment in the system are determined. Subsequently, cost balances are proposed for each component of the system, as shown in Education (15) [31].
| (15) |
where represents the costs associated with the power output from the component, and the thermal energy input to the component. The unit cost of each exergy flow (c) is calculated by Eq. (16).
| (16) |
The total cost rate () is calculated using Eq. (17), based on the cost of operation and maintenance for each k component (, and the cost of capital investment ().
| (17) |
The annual capital investment levelized for the k-component can be calculated using Eq. (18).
| (18) |
where CRF is the capital recovery factor and is calculated using Eq. (19), while τ is the annual operating hours of the system [31].
| (19) |
where is the rate of interest, and n is the lifetime of the proposed thermal system. In Table 1 are the equations required to determine for each system component.
Table 1.
Purchase equipment cost function used in the economic modeling.
On the other hand, the annual levelized maintenance and operating cost for each k component is determined by Eq. (20).
| (20) |
where represents the fixed operation, and associated variable for each k component, and its value is 0.06 [36]. The total unit product cost is considered as the object of study in the thermo-economic analyses and is calculated by means of Eq. (21) [32].
| (21) |
To developed the thermo-economic model, a 5% interest rate was considered [37, 38], a project lifetime of 20 years [16, 39], and the annual operating hours was 7446 h. On the other hand, for a thermo-economic analysis it was necessary to evaluate the purchase equipment costs, which are a function of thermodynamic variables, and the heat exchanger area. To calculate this area of each equipment, the overall heat transfer coefficient (), the log mean temperature difference , and the process heat transfer was used, as shown in Eq. (22). The heat exchangers considered were tube and shell [40], printed circuit board in the Brayton S-CO2 [41], and plate in both ORC configurations [42].
| (22) |
Among the thermo-economic performance parameters considered, the LCOE, SIC and PBP were considered. The LCOE refers to the electricity generation of each configuration, where it is possible to sustain the costs needed to invest, operate and maintain the thermal system, and it is calculated through the Eq. (23).
| (23) |
where is the initial investment cost, is the operational and maintenance cost, is the fuel cost, and is the insurance cost. Also, the SIC is calculated from the Eq. (24). It is an indicator of system cost-effectiveness as a function of the amount of energy generated (Wnet), and the total investment costs of the ORC system ().
| (24) |
In addition, the PBP indicator evaluates the profitability of the project, and measures the time required for the investment previously made in the thermal generation project to be paid, or the cash inflow of the economic resources from the project, and is calculated by means of the Eq. (25).
| (25) |
where i is the discount rate, and is the annual profitability cash flow in the lifetime.
2.4. PSO optimization
Particle Swarm Optimization (PSO) was created as an option for optimization and search. This is a multidimensional and evolutionary computer technique inspired by the behavior of insects in nature, much like a group of swarming bees looking for pollen, flying in a multidimensional space in search of a solution. Each member of the group searches in different areas, and they focus on areas with a higher probability of success. Swarm members learn from their experiences, and from the experiences of their peers [43]. This optimization has 5 main cases, which are presented in Figure 3.
Figure 3.
Flowchart for PSO algorithm.
The first step in implementing the PSO is to prepare the information. Here, position, speed and fitness values within the expected search ranges must be taken into account. After this, the values are evaluated in order to minimize the target function. As a next step, the values update the particles for the next iteration, and in the fourth step the SIC is updated for the next iteration of each particle according to Eq. (26).
| (26) |
In Eq. (26) is presented as the particle velocity in a time instant, the constants is a cognitive attraction parameter, which is given by the personal experience of each particle. And the parameter is the global attraction. The values of and are random numbers in an interval between 0 and 1. The value of is the most favorable position through which the particular has moved throughout its history, and is the most favorable position of the whole swarm. On the other hand, w is the value of inertia, which is a determining factor for the convergence of PSO optimization, and is used to control the search capacity of the swarm. The large inertial weights focus on speed updates, which allows a search in design spaces. The smaller inertial weights, on the other hand, focus on speed updates in regions close to the design space. For the present work, the PSO algorithm varies following Eq. (27) [44].
| (27) |
The position of the particle in the k + 1 iteration can be estimated using the new velocity in the 28 equation.
| (28) |
Finally, the parameters used in GA for the present investigation are enunciated through the Table 2.
Table 2.
Parameter PSO.
| Parameters | Value |
|---|---|
| Maximum iteration | 30 |
| Population size | 10-20-30-40 |
| Inertial factor, w | 0.4–0.9 |
| Cognitive parameter, c1 | 0.5–1.5 |
| Social parameter, c2 | 0.5–1.5 |
3. Results and discussions
3.1. Model validation
The RORC configuration model was validated using the results obtained in a geothermal application. For both investigations, the parameters presented in Table 3.
Table 3.
Operational condition used for model validation.
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| [%] | 95 | [°C] | 15 |
| [%] | 89 | Pinch Point [°C] | 10 |
| [°C] | 165 | [MPa] | 0.31 |
| [kg/s] | 84.36 | - | - |
The following considerations were taken into account in carrying out the comparative analysis of the RORC: Processes and subsystems in steady state, pressure losses in devices and pipes are negligible, in the dead state the reference temperature was 288 K. Table 4 shows the results obtained from the model proposed in this research. This table also presents the results available in the literature and the error obtained by the proposed model. This error allows to verify that in the three models there is a good fit of the results, compared to the results published in the reference geothermal application. For the case of isobutane as a working fluid, the percentage error in exergetic efficiency of 0.43% and 0.97% in the comparison with the works of R. S. El-Emam et al. [16] and V. Zare [45] respectively. On the other hand, the thermal efficiency reached an error of 0.49% and 1.86% with respect to the works of R. S. El-Emam et al. and V. Zare respectively. These results allow us to validate the model proposed for use in the evaluation of this configuration operating as a heat recovery system. It is important to highlight that, when validating the model for the RORC cycle, which is more complex than the simple ORC, the simple cycle can be taken as validated.
Table 4.
Validation of the RORC proposed model.
| Proposed model | 165 | 84.93 | 75.94 | 395.44 | 808.08 | 123.96 | 16.45 | 49.01 |
| R. S. El-Emam et al. [16] | 165 | 84.36 | 78.06 | 399.3 | 810.1 | 124.8 | 16.37 | 48.8 |
| Absolute error [%] | - | 0.68 | 2.72 | 0.97 | 0.25 | 0.67 | 0.49 | 0.43 |
| V. Zare [45] | 165 | 82.16 | 76.09 | 390.6 | 808.7 | 124.2 | 16.15 | 48.54 |
| Absolute error [%] | - | 3.37 | 0.20 | 1.24 | 0.08 | 0.19 | 1.86 | 0.97 |
As for the Brayton cycle, the validation was made considering the temperature of the heat exchanger and the pressure drop of it are insignificant, it was considered an adiabatic thermodynamic process in each mechanical component, the mechanical components were thermally isolated during the electrical production for each working condition. For the calculation of the system solution, a steady state condition was considered, and the pressure and temperature values were considered to reach the maximum and minimum value of the thermodynamics during the energy transfer process.
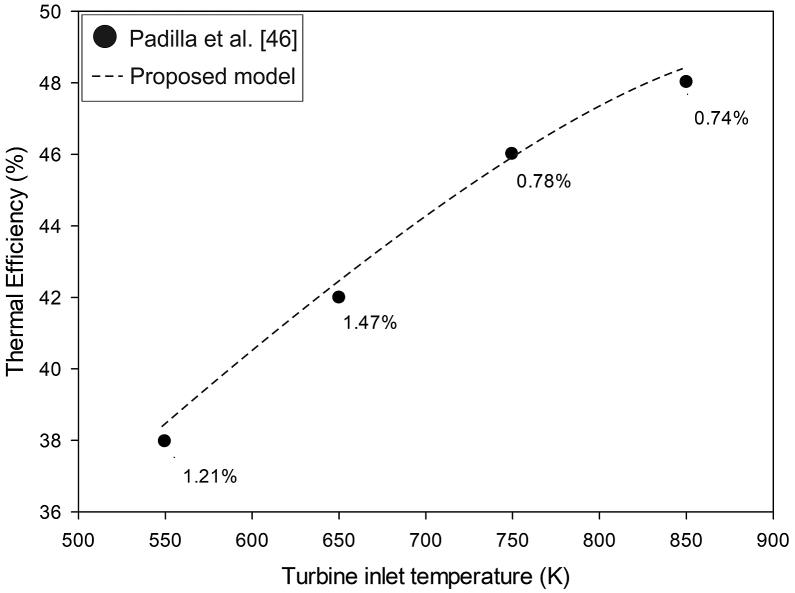
Based on these considerations, the validation was made based on the work carried out by Padilla et al [46], where an energy and exergetic analysis of a Brayton S-CO2 cycle was made with the application of concentrated solar technology, using Python 3.2 and REFPRO 9.1 to obtain the properties of the working fluid in critical conditions. The values used to validate the model are presented in Table 5.
Table 5.
Input values for the S-CO2 Brayton model validation.
| Turbine efficiency | Compressor Efficiency | Heat exchanger effectiveness | Turbine inlet temperature | Cycle high pressure | Minimum pinch point temperature | |
|---|---|---|---|---|---|---|
| Value | 93% | 89% | 95% | 500–800 °C | 25 MPa | 5 °C |
In evaluating these values taken from the work of Padilla et al, the thermal efficiency values were taken and compared. These values are presented in Figure 4 together with the error presented by the model proposed in this work, against the values obtained by the model used for the validation. The error obtained in the 4 points analyzed did not exceed 1.5%, which allows the validation of the model proposed for use in the proposed configuration.
Figure 4.
Validation of the S-CO2 Brayton proposed model.
3.2. Energy and exergy analysis
For the Brayton S-CO2 combined with the SORC and RORC system, the base operational conditions are shown in Table 6. The operational condition of the Brayton S-CO2 system was selected from the energy and exergy study conducted by Padilla et al. [46], and the operational based condition of the ORC and ROC form thermo-economic study developed by Valencia et al. [18], where the systems is proposed as a waste heat recovery system from a natural gas engine.
Table 6.
Base condition parameters for a combined Brayton S-CO2 -SORC/RORC.
| Configuration | Parameter | Value | Unit |
|---|---|---|---|
| SORC/RORC | Isentropic ORC turbine efficiency | 80 | % |
| SORC/RORC | Isentropic ORC pumps efficiency | 75 | % |
| SORC/RORC | Cooling water temperature (1 Wt–2 Wt) | 50 | °C |
| SORC/RORC | Condenser Pinch Point Temperature | 15 | °C |
| SORC/RORC | Pressure ratio pump 1 | 2.5 | |
| SORC/RORC | Evaporator Pinch Point temperature | 40 | °C |
| RORC | Recuperator effectiveness | 80 | % |
| SORC/RORC | Pressure ratio pump 2 | 20 | |
| Brayton S-CO2 | Turbine inlet temperature | 750 | °C |
| Brayton S-CO2 | Brayton Cycle High Pressure | 25 | MPa |
| Brayton S-CO2 | Efficiency Brayton Turbines | 93 | % |
| Brayton S-CO2 | Compressor Efficiency | 89 | % |
| Brayton S-CO2 | Effectiveness of the heat exchanger | 95 | % |
| Brayton S-CO2 | Minimum temperature of Pinch Point | 5 | °C |
| Brayton S-CO2 | Temperature low | 140 | °C |
The variation in the energy and exergy performance indicators of the system was studied considering the toluene, acetone and cyclohexane as working fluids in the RORC and SORC system. Therefore, Table 7 shows the values obtained for energy and exergy indicator in the base condition of the configurations considered. The thermodynamic properties for the case of the toluene as organic working fluid is presented in Appendix A, Table A1 (S-CO2-SORC) and Table A2 (S-CO2-RORC).
Table 7.
Thermodynamic properties of the RORC systems for each organic working fluid.
| S-CO2 – RORC |
S-CO2 – SORC |
|||||
|---|---|---|---|---|---|---|
| Toluene | Acetone | Cyclohexane | Toluene | Acetone | Cyclohexane | |
| [kW] | 24.74 | 25.64 | 27.46 | 22.62 | 25.28 | 23.65 |
| 120.04 | 120.94 | 122.76 | 117.91 | 120.57 | 118.94 | |
| [%] | 14.29 | 15.97 | 14.95 | 14.29 | 15.92 | 14.93 |
| [%] | 47.92 | 48.28 | 49.01 | 47.07 | 48.14 | 47.48 |
| [%] | 25.82 | 26.91 | 28.82 | 23.74 | 26.53 | 24.81 |
| [g/kWh] | 197.12 | 197.12 | 197.12 | 197.12 | 197.12 | 197.12 |
| [g/kWh] | 156.49 | 155.32 | 153.02 | 159.31 | 155.79 | 157.93 |
| [%] | 20.61 | 21.21 | 22.37 | 19.18 | 20.97 | 19.88 |
These results show better energetic and exergetic performance for the Brayton S-CO2-RORC. Thus, by using cyclohexane as the organic working fluid in the combined configuration, an increase in the energy efficiency of 28.82% is achieved with respect to the performance of the Brayton S-CO2 system, which implies a decrease in fuel consumption of 22.37%. Therefore, this fluid is suggested based on energy and exergy performance under the selected operational conditions. These results are in line with those obtained by Eveloy et al. [47], who studied a triple SOFC-Brayton-ORC to improve the energy generation, capacity and thermal efficiency using toluene as working fluid. The integrated Brayton S-CO2-SORC system increases the power generation capacity in relation to the Brayton base cycle considered, where an energy efficiency of approximately 48% was achieved, which represents in this case average improvements in the efficiency of 25% compared to the Brayton cycle. From the thermodynamic properties in each state for the Brayton S-CO2-RORC system using the acetone, toluene, and cyclohexane as the organic working fluids, energy and exergetic performance indicators were also calculated for each component, as shown in Table A3 in Appendix A, while the results for the Brayton S-CO2-SORC system are presented in Table A4.
According to the results, the highest heat transfer rate in the system is presented in the HTR (576 kW), with a heat transfer area of 15.66 m2. In comparison, the RHR (296.10 kW) demands a heat transfer area of 176.24 m2, which is reflected in a contribution of 47% on the total exergy destroyed in the system for working fluids studied. By evaluating the irreversibilities and exergy destruction in each component of the process, destroyed exergy of 36.66 kW was determined in the heat transfer process from the thermal source, being this combustion process the main irreversibility source of this system. The results showed that an increase in the power generated in the Brayton S-CO2 cycle, independent of the ORC system considered, decreases the exergy destruction of this component, which is mainly a consequence of an increase in the CO2 exergy entering to the expansion stage.
The exergetic efficiency is defined as the percentage of exergy supplied to the system transformed into useful work, and it was calculated at a TIT of 650 °C for each component of the Brayton S-CO2 system integrated to the ORC as shown in Figure 5. Thus, according to these results, a significant increase in exergetic efficiency is observed when using the RORC, especially in Pump 1 with toluene (1.63%) as shown in Figure 5a, and cyclohexane (3.28%) as shown in Figure 5c, while the increase with acetone was only 0.08% (see Figure 2b).
Figure 5.
Exergetic efficiency for the S-CO2-SORC and S-CO2-RORC components using different organic working fluids, a) Toluene, b) Acetone, and c) Cyclohexane.
The Brayton cycle turbines were the components with the highest exergetic efficiencies (97.71%) for the different organic fluids studied, and this is because the expansion does not develop in a single stage. However, the thermal oil pump (11) was the device with the lowest exergetic efficiency, with values of 11.03% for the acetone in the Brayton S-CO2-SORC system. This result is a consequence of the high pressure ratio presented in this equipment to circulate the thermal oil in the thermal coupling circuit. Thus, a proposal to increase the exergetic efficiency of the pump is to reduce the pressure ratio through an optimal thermo-hydraulic design of the evaporator and heat exchanger that reduces the pressure drop, like the multi-objective optimization proposed by Valencia et al. [42].
The percentage of exergy destruction per component for the two configurations is presented in Figure 6, where the impact of each of the three fluids on the percentage of exergy destruction is evaluated, allowing us to observe that the components with the greatest irreversibilities are the evaporator followed by the condenser for all configurations. In the Brayton S-CO2-RORC coupled system with toluene as working fluid, the evaporator is the component with the highest irreversibility, presenting 21.21%, followed by the percentage presented by this equipment for the Brayton S-CO2-SORC configuration with 20.31%.
Figure 6.
Exergy destruction fraction for the S-CO2-SORC and S-CO2-RORC using different organic working fluids, a-b) Cyclohexane, c-d) Toluene, and e-f) Acetone.
3.3. Parametric study
This section presents the results of the sensitivity analysis of both systems for the three organic fluids considered, by varying important parameters such as the high pressure in the Brayton cycle, the pressure ratio in the ORC and the condensation temperature in the ORC on energy parameters (combined net power generated, the increase in thermal efficiency respect to the Brayton S-CO2 system, the decrease in specific fuel consumption, the overall thermal efficiency, the ORC energy efficiency and the exergetic efficiency) and thermo-economic (LCOE, SIC, PBP).
-
•
Effect of Brayton turbine inlet temperature on the energy, exergy and thermo-economic performance indicators
For this case, three organic working fluids were pre-selected, in which it is possible to observe the behavior of the variability of the thermodynamic indicators (see Figure 7), using the combined Brayton S-CO2 with SORC and RORC under the operational conditions shown in Table 6. This case study was proposed to compare the energy and exergetic performance of the system, and identify an operational condition in the Brayton TIT where the cycle performance will be maximized, both from the thermodynamic, exergetic and economic approach.
Figure 7.
Performance of the Brayton S-CO2–SORC and RORC configuration for three working fluids, a) combined net power generated, b) the increase in thermal efficiency respect to the Brayton S-CO2 system, c) the decrease in specific fuel consumption, d) the overall thermal efficiency, e) ORC energy efficiency and f) the exergetic efficiency.
Likewise, toluene in the system with recuperator achieves about 37%, while without recuperator, the system reduces its efficiency by 28%. Therefore, it can be inferred that cyclohexane is the organic fluid that shows an effective thermal effect to be selected as a potential organic working fluid in this novelty configuration. Similarly, the combined Brayton S-CO2-RORC system is the best alternative compared to combined Brayton S-CO2-SORC without taking into account the organic fluid used. Also, this system achieves better values in the decrease in specific fuel consumption (30.21%) at 550 °C in the inlet turbine temperature with cyclohexane as shown on Figure 7c. This result could be explained by the addition of a recuperator heat exchanger to the system, while without the recuperator the higher rate of ΔBSFC (30.7%). was reflected using toluene as a working fluid, followed by cyclohexane (30.47%) and acetone (30.09%).
Considering the overall efficiency of the system () shown in Figure 7d, the use of cyclohexane in the combined Brayton S-CO2-RORC reaches the best performance at 800 °C, and 20.80% in the overall energy efficiency, while for the acetone was 20.82%, and for toluene a value of 20.83%. On the other hand, the combined Brayton S-CO2-SORC system at the same temperature, acetone achieved a higher overall energy efficiency of 20.82%, while cyclohexane and toluene achieved 20.84% in the overall energy efficiency. For the SORC system, the thermal efficiency () increases gradually for the three fluids in this case study (see Figure 7e) until the maximum threshold is reached for cyclohexane with a percentage of 0.27% at a TIT of 800 °C, followed by the Brayton S-CO2-RORC with 0.24% in the thermal efficiency using the acetone as a organic working fluid.
The exergetic efficiency () result is shown in Figure 7f, as the inlet turbine temperature increases an enhancement in the exergetic efficiency is observed, presenting a better behavior for cyclohexane with a 71.68% when the temperature has a value of 800 °C for the combined Brayton S-CO2-RORC, and the acetone for the Brayton S-CO2-SORC presented a better performance with respect to other fluids achieving 70.48%. Finally, as shown in Figure 7a with cyclohexane both with and without a recuperator, a higher net power of approximately 109.55 kW is achieved at the higher turbine inlet temperature. These results could be explained because in the proposed system, it was no considered two compression stages, nor an intercooler heat exchanger that would cool the CO2 between the compression stages, allowing to burn more fuel and generate more power. The limiting factor for the amount of heat supplied from the thermal source is the temperature of the hot CO2 generated by the combustion, because there are restrictions on the temperatures that the turbine blades and other parts of the turbine can withstand, as was reported in previous studies [46].
The fractions of exergy destroyed per component of the Brayton S-CO2-SORC and RORC cycle were calculated. These fractions at different inlet turbine temperature of the primary turbine (TIT) of the Brayton S-CO2 cycle are shown in Figure 8 for the toluene, acetone and cyclohexane. It can be seen that for all three fluids the exergy destruction fraction in the RORC system is higher than that presented by SORC in the following components: Pump 2, Turbine ORC, Recuperator ORC and Heat exchanger, while in the case of SORC the Condenser, Pump 1 and Evaporator exergy destruction are higher in relation to the RORC.
Figure 8.
Exergy destruction for components of the Brayton S-CO2-SORC system using a) Toluene, b) Acetone, c) Ciclohexane, and Brayton S-CO2-RORC system using d) Toluene, e) Acetone, and f) Ciclohexane.
The estimation of the percentage decrease of exergy destruction in the system integrated by the Brayton S-CO2 cycle with the RORC and SORC, was found that the system operating with both configurations the higher exergy destruction (85 kW) was presented for the heat exchanger. The total exergy destruction results for the SORC with toluene indicated that the heat exchanger and evaporator lead to a value greater than 31% of the total exergy destruction as shown in Figure 8a, where a 1.55% increase was obtained when increasing the temperature (TIT) from 600 °C to 700 °C, and a 0.71% in the increase changing the temperature from 700 °C to 750 °C. Also, for the case of the RORC system (see Figure 8d), which shows a considerable increase in total exergy destruction of 1.82% when the temperature change from 600 °C to 700 °C, and 0.76% from 700 °C to 750 °C. The results show that the largest fraction of exergy destruction fraction was evident at a temperature of 750 °C, where the RORC system achieves a 0.3% increase over the SORC.
For the case of the Brayton S-CO2 cycle, it is observed that as TIT increases the percentage of exergy destruction decreases gradually (see Figure 8c), taking into account that the largest fraction is presented in the Brayton recuperator (from 600 °C to 700 °C), and the reheater (700 °C–750 °C). The presented reduction on the exergy destruction for the Brayton S-CO2 cycle was 2% and 1.04% for the Brayton Recuperator and reheater, respectively. Also, it was evidenced the maximum exergy destruction for the Evaporator (7.99 kW), Heat Exchanger (7.8 kW) and the Brayton Recuperator (7.67 kW). This result can be explained because for the Brayton S-CO2 cycle with regeneration, and the thermal performance depends not only on the pressure ratio but also on the operating temperature ratio.
The heat exchanger and the ORC recuperator exceed 80% of the exergy destruction in the Brayton S-CO2- RORC system using the cyclohexane as organic working fluid (Figure 8f), in which a significant increase of 3.25% is appreciated when increasing the TIT temperature from 600 °C to 700 °C. Similarly, the increase in temperature from 700 °C to 750 °C led to an increase of 0.37% with a value of 32.4% of exergy destruction from the Brayton S-CO2- RORC system. It should be noted that there is a significant effect of the TIT on the total exergy losses for both systems, and the highest exergy losses are presented in the heat exchanger, contributing in the 50% of the total exergy destruction of the configuration.
The results of the thermo-economic indicators are presented in Figure 9, in which a decreasing behavior is observed in the LCOE and SIC for the two configurations as the TIT increases. The variation of this temperature from at the established operating conditions causes a considerable variation on the thermo-economic indicators for the Brayton S-CO2-SORC, as shown in Figures 9a–c. The LCOE value as shown in Figure 9a at a TIT of 550 °C using toluene and cyclohexane has 37.44% and 37.08% less than acetone, respectively. Besides, the SIC in this operational condition is evaluated at the same temperature showing that acetone has value 2.03% and 0.98% less than toluene, and cyclohexane, respectively. However, in the case of cyclohexane, the SIC decreased by 37.18% and LCOE by 37.44%, thus inferring that cyclohexane is a beneficial fluid over the Brayton S-CO2-SORC system from the thermo-economic point of view.
Figure 9.
Effect of Brayton turbine inlet temperature on the thermo-economic indicators: a, d) LCOE, b, e) SIC, and c, f) PBP.
The minimum value for the Brayton S-CO2-RORC was LCOE (0.2394 USD/kWh) as shown in Figure 9d, and PBP (10.37 years) using the cyclohexane at a temperature of 800 °C as shown in Figure 9f, being the most profitable configuration the Brayton S-CO2-RORC. The least profitable configuration according to the results, is the Brayton S-CO2-RORC. When acetone is considered as fluid, since the SIC values were ranging from 2438.04 USD/kWh and 3956.19 USD/kWh, with a payback period from 10.43 and 16.81 years and the highest LCOE of 0.3924 USD/kWh, therefore, these values are similar than the minimum LCOE obtained for most alternative and conventional generation systems, including wind energy with an LCOE of 0.30 USD/kWh [43].
However, acetone was the most thermally profitable fluid in the Brayton S-CO2-SORC system at 800 °C, presenting the minimum LCOE of 0.2281 USD/kWh and a SIC of 2308.51 USD/kWh with a PBP of 9.89 years. Also, the use of acetone and toluene organic fluid in the Brayton S-CO2-RORC system with decreased the SIC by 38.37% and 38.47%, respectively, but in the case of cyclohexane, the SIC decreased by 37.68% and LCOE by 37.92%, thus inferring that cyclohexane is a beneficial fluid over the Brayton S-CO2-RORC system. These results are due to the fact that by using a regenerator with an adequate heat transfer area a good energetic, exergetic and thermo-economic performance can be achieved; however, a larger heat transfer area also increases the pressure drop, which implies an exergy loss in the equipment, and therefore the thermo-economic performance of the regenerator by having high purchase equipment costs. Thus, thermo-economic optimizations should be considered that maximize system indicators such as LCOE, PBP, and SIC based on parameters such as the regenerator area, ORC pressure ratio and Brayton turbine inlet temperature. From the thermo-economic approach, the cost of the regenerator must be considered to know if it justifies the savings that will be obtained with its installation and use.
-
•
Effect of Brayton high pressure on the energy, exergy and thermo-economic performance indicators
Figure 10 shows the effect that high pressure has on the behavior of the Brayton S-CO2-SORC and Brayton S-CO2-RORC cycle, allowing us to see that the parameter with the greatest influence on the performance of the system is the net power. As the high working pressure increases, the system obtains an increase in the net power producing approximately a 5.5% increase between the operating pressures as shown in Figure 10a, for the different configurations with the variation of the three working fluids. Therefore, it can be analyzed that the working fluid with the highest net power generation is achieved by cyclohexane for the RORC configuration 28.1 kW, reaching these results with an operating pressure of 30 MPa.
Figure 10.
Performance of the Brayton S-CO2–SORC and RORC configuration for three working fluids, a) combined net power generated, b) the increase in thermal efficiency respect to the Brayton S-CO2 system, c) the decrease in specific fuel consumption, d) the overall thermal efficiency, e) ORC energy efficiency and f) the exergetic efficiency.
Figure 11 shows the economic performance of the evaluation parameters of the Brayton S-CO2 configurations coupled with the two SORC and RORC heat recovery systems. Due to the fact that the behavior of the two systems shows little significant difference with respect to the performance of the working fluids, a comparison is made between the economic indicators studied, obtaining that in the case of the LCOE there is an average difference of 0.0109 USD/kWh approximately between both systems for each one of the working fluids, allowing to determine that the Brayton S-CO2-SORC configuration presents a better minimization of this indicator with the increase of the operation parameters of the high pressure. In the case of the SIC indicator, the average performance difference between the fluids that presented the best minimization acetone for the SORC configuration and cyclohexane for the RORC configuration is approximately 126.2 USD/kWh, allowing to analyze that, due to the processes properties, the best profitability is obtained through the Brayton S-CO2-SORC system. On the other hand, the performance of the PBP in both configurations is determined by the initial investment of the systems, this parameter determines that the lower the initial investment and the operation parameters are adequate, the faster the return on investment will be, finding that the system coupled with a SORC configuration with the most critical operation parameters will have a better performance regarding the coupling of the system with RORC obtaining a difference of 0.55 years between the fluids with better performance.
-
•
Effect of Brayton Pressure ratio on the energy, exergy and thermo-economic performance indicators
Figure 11.
Effect of Brayton Pressure high on the thermo-economic indicators: a, d) LCOE, b, e) SIC, and c, f) PBP.
The evaluation of the effect of the pressure ratio on the behavior of the energy parameters of the two configurations studied is presented in Figure 12, where it can be seen that the fluid with the best results in the operating properties is cyclohexane for the Brayton S-CO2-RORC configuration. For the analysis of cyclohexane as a working fluid in the results obtained from the indicators, an increase in net power of 17.46% can be observed, as well as the increase that was observed for the case of the difference in thermal efficiency of 17.46%. In the evaluation of the performance of the fuel switching ratio for the two configurations the increase of this indicator is 13.55%. On the other hand, for the results obtained for the overall thermal efficiency the increase obtained is the same as the increase in the thermal efficiency of the ORC 17.46% compared to the increase obtained for the exergetic efficiency that was obtained of 4.51%. The above described allows analyzing that the optimized operation conditions for the best results of the studied indicators are presented when the high pressure is 30 MPa.
Figure 12.
Performance of the Brayton S-CO2–SORC and RORC configuration for three working fluids, a) combined net power generated, b) the increase in thermal efficiency respect to the Brayton S-CO2 system, c) the decrease in specific fuel consumption, d) the overall thermal efficiency, e) ORC energy efficiency and f) the exergetic efficiency.
Figure 13 shows the influence that pressure ratio has on the economic performance of the configurations studied, where it is identified that the working fluid that presents the best behavior for each system. In the case of the Brayton S-CO2-SORC configuration, the fluid that minimized all the economic indicators was acetone, presenting for the SIC an average of minimization below cyclohexane 0.49%, for the LCOE 0.47% and for the PBP 0.48%. On the other hand, cyclohexane is the fluid that presents the best economic performance in the Brayton S-CO2-RORC configuration, presenting a minimization of the SIC 2.71%, LCOE 2.73% and PBP 2.67% parameters with respect to acetone, which is the fluid with the best performance of the three fluids studied in this research for the Brayton S-CO2-RORC system.
-
•
Effect of Brayton temperature condenser on the energy, exergy and thermo-economic performance indicators
Figure 13.
Effect of Brayton pressure ratio on the thermo-economic indicators: a, d) LCOE, b, e) SIC, and c, f) PBP.
The influence of the operating temperature of the condenser on the performance of the two configurations studied is presented in Figure 14, where the results of better behavior are presented by the cyclohexane in the configuration of the Brayton S-CO2-RORC system. Due to the use of the temperature of the systems, the configuration that presents not so favorable results is the one of the Brayton S-CO2-SORC, where the behaviors of the acetone and toluene are the lowest values for the different evaluated energetic parameters, allowing to select by criterion of performance in the properties of operation to the cyclohexane, which when increasing the temperature of operation from 55 °C to 70 °C of the condenser presents an average increase of 3. 69% in net power, 3.71% for thermal efficiency, 8.4% for exergetic efficiency as shown in Figures 14a, e and f respectively.
Figure 14.
Performance of the Brayton S-CO2–SORC and RORC configuration for three working fluids, a) combined net power generated, b) the increase in thermal efficiency respect to the Brayton S-CO2 system, c) the decrease in specific fuel consumption, d) the overall thermal efficiency, e) ORC energy efficiency and f) the exergetic efficiency.
The effect that the operating temperature of the condenser has on the economic parameters evaluated for the two Brayton S-CO2-SORC and Brayton S-CO2-RORC configurations is presented in Figure 15, where cyclohexane as a working fluid presents the best performance in economic minimization for all operating parameters. Because the Brayton S-CO2-SORC configuration does not present a heat recovery equipment in the ORC cycle as the Brayton S-CO2-RORC configuration, as the operating temperature of the condenser increases, the SORC system is less efficient, obtaining as a result that instead of minimizing the economic parameters with the increase of the temperature, an increase of 0.051% for the LCOE, 0.053% for the SIC indicator and 0.059% for the PBP indicator is obtained. Otherwise, in the case of the Brayton S-CO2-RORC configuration, the minimization obtained obtains a decrease for the economic indicators 0.34% for the LCOE, 0.33% for the SIC indicator and 0.31% for the PBP indicator.
Figure 15.
Effect of Brayton Pressure high on the thermo-economic indicators: a, d) LCOE, b, e) SIC, and c, f) PBP.
3.4. Thermo-economic optimization
By means of a literature review, it was possible to observe that many objective functions can be used for the application of a techno-economic optimization of the Rankine cycle. Taking into account the works published by M.M. Hettiarachi et al. [48], in which the optimization of the total heat transfer area per unit of power (m2/kW) was proposed as well as J. Wang et al. [49] Similarly, Y. Feng and others [50] in their work proposed an optimization of the heat exchange surface only, taking into account the cost of the surface represents the major part of the cost of the system. Authors such as E. Cayer and others [51] and S. Quoilin and others [52], presented an optimization of the relative cost per unit of power (€/kW). Despite the proposals made with different approaches, it has not been possible to find information regarding which one is more relevant.
Rankine cycles represent an interesting option in the energy market. Despite this, the high cost in relation to the power obtained from them decreases the competitiveness against other energy sources, such as wind or solar energy in some conditions [53]. According to the above, the optimization of the specific investment cost of the plant.
The PSO algorithm has been considered to minimize the SIC in both configurations using cyclohexane as the working fluid. In this algorithm the values of the starting positions of the population were generated randomly within the search region. However, a study was carried out to determine the size of the population in this problem in order to obtain a good relationship between the computational cost and the convergence error. Figure 16 shows the response of the target SIC function for a number of particles 10, 20, 30 and 40, and a total of 30 generations, for the S-CO2-SORC system (Figure 16a), and the S-CO2-RORC system (Figure 16b).
Figure 16.
Variation of the SIC function with the number of generations and particles for: a) Brayton S-CO2-SORC, and b) Brayton S-CO2-RORC.
The results show that the increase in the number of particles implies an increase in computational time, but in both cases of the processes considered as minimization of the SIC, the same value is obtained at a number of generations of 30. Therefore, it is recommended to use in this type of problems smaller numbers of particular and to guarantee the convergence of the algorithm with a greater number of generations, without incurring in high computational times.
Figure 17 shows the temporal behavior of the decision variables selected to perform the optimization of the objective function in both systems, TIT (Figure 17a), PHIGH (Figure 17b), TC (Figure 17c), and rP (Figure 17d) for a population size of 10.
Figure 17.
Variation of decision variables using the SIC as objective function for the a) Turbine inlet temperature, b) high pressure in the Brayton cycle, c) condenser temperature, and d) pressure ratio.
The variation of the TIT generated by the minimization of the SIC is shown in Figure 17a, in it you can observe the behavior for the SORC. In the first generation it starts with a value of 680.31 °C and reaches its stability in the sixth generation, with a value of 800 °C. On the other hand, the RORC starts with a value of 3.85% less and it took one more generation to achieve stability at 800 °C. Figure 17b shows the behavior of the PHIGH, which starts with values of 25.52 MPa and 24.45 MPa for the SORC and RORC systems, respectively. The SORC shows an increasing behavior until the fifth generation, and then shows a decrease of 2.15% of the value reached in that initial increase, to then reach stability in the tenth generation. On the other hand, the behavior of the PHIGH for the RORC began with a decrease until the fifth generation, and then began an increase until reaching stability in the fifteenth generation with a value of 30 MPa. On the other hand, the Figure 17c shows the variation of TC with the optimization of the SIC, where a behavior related to the pressure ratio is shown (Figure 17d), because a higher condensation temperature implies a higher condensation pressure and a higher evaporation pressure of the organic fluid. Therefore, in the initial generations, an inverse behavior of these is observed, in order to obtain the highest power delivery within the restrictions proposed in the optimization problem.
By means of PSO optimization, new values of the decision variables were obtained, which are presented in the Table 8. These results are presented for the S-CO2-SORC system and the S-CO2-RORC system. The solutions found through PSO for the TIT variable in the S-CO2-RORC system for toluene showed a 6.66% variation with respect to the base case. On the other hand, the value of this variable for the S-CO2-SORC system showed the same variation. As for the behavior of the PHIGH, for both systems the variation after optimization reached 20%, increasing 5 MPa. In the same way, the rP presented the same percentage of increase for both systems, reaching 100% of variation in the increase of its value. Likewise, the last decision variable, the TC, presented an increase of 2.10% for the S-CO2-RORC system and an increase of 2.46% for the S-CO2-SORC. With these values, the decision variables led to the optimization of the objective function SIC, which went from 2613.13 USD/kWh to 2308.91 USD/kWh, for the case of the S-CO2-RORC system. For the S-CO2-SORC system, it went from 2515.67 USD/kWh to 2248.17 USD/kWh.
Table 8.
SIC optimization solution using the PSO algorithm.
| S-CO2 – RORC – Cyclohexane |
S-CO2 – SORC – Cyclohexane |
|||||
|---|---|---|---|---|---|---|
| Base case | Optimized | Absolute difference [%] | Base case | Optimized | Absolute difference [%] | |
| [°C] | 750 | 800 | 6.66 | 750 | 800 | 6.66 |
| [MPa] | 25 | 30 | 20 | 25 | 30 | 20 |
| [°C] | 65 | 67.67 | 2.10 | 65 | 66.06 | 2.46 |
| rP | 15 | 30 | 100 | 15 | 30 | 100 |
| [kW] | 27.46 | 36.31 | 32.19 | 23.65 | 29.68 | 25.54 |
| 122.75 | 148.73 | 21.16 | 118.93 | 142.11 | 19.49 | |
| [%] | 14.95 | 21.07 | 40.93 | 14.93 | 17.23 | 15.40 |
| [%] | 49.01 | 52.76 | 7.65 | 47.48 | 50.41 | 6.17 |
| [%] | 28.82 | 32.30 | 12.07 | 24.81 | 26.40 | 6.40 |
| [g/kWh] | 153.02 | 188.05 | 22.89 | 157.93 | 188.05 | 19.07 |
| [%] | 22.37 | 24.41 | 9.11 | 19.88 | 20.89 | 5.13 |
| LCOE [USD/kWh] | 0.26 | 0.22 | 15.38 | 0.24 | 0.22 | 8.33 |
| PBP [year] | 11.17 | 9.89 | 11.45 | 10.76 | 9.63 | 10.50 |
| SIC [USD/kWh] | 2613.13 | 2308.91 | 11.64 | 2515.67 | 2248.17 | 10.63 |
4. Conclusions
The energy, exergy, and thermo-economic study of two combined Brayton S-CO2-ORC configurations were conducted under different organic working fluids. The optimized performance obtained for the Brayton S-CO2-RORC through the thermo-economic optimization under the SIC as objective function were the combined power generated (29.68 kW), the increase in the thermal efficiency respect to the Brayton S-CO2 system (26.40%), the absolute decrease in the specific fuel consumption (20.89%), the overall thermal efficiency (63.72%), the ORC energy efficiency (17.23%), levelized energy cost (0.22 USD/kWh), and payback period of 9.63 years considering cyclohexane as the organic working fluid. Therefore, RORC is selected respect to SORC from an energetic point of view, while considering thermo-economic approach the SORC is appropriate.
From the parametric study, is concluded that the inlet turbine temperature is the most influential operational parameter of the Brayton S-CO2 energy and exergy performance. Thus, when this temperature was changed from 550 °C to 800 °C with cyclohexane, the thermal efficiency of the configurations was increased 21.32% (Brayton S-CO2-RORC), and 22.90% (Brayton S-CO2-SORC), while the exergy efficiency was increased from 67.14% to 71.68% (Brayton S-CO2-RORC), and 64.34%–69.58% (Brayton S-CO2-SORC).
The maximum exergy destruction was obtained in the Brayton S-CO2-SORC system with cyclohexane, mainly in the HE1 heat exchanger (16.5%) of the Brayton sub-system, and in the HE3 (14.86%) in the ORC, which reveal the largest opportunities of improvement in the heat exchanger design and rating. Also, the lowest exergetic efficiency was presented in the thermal oil pump, with values of 9.57% for the acetone in the Brayton S-CO2-SORC system. Therefore, a proposal to increase the exergetic efficiency of the pump is to reduce the pressure ratio by means of an optimal thermo-hydraulic design of the evaporator and heat exchanger that reduces the pressure drop.
From the thermo-economic indicator analysis, the economic profitability is higher for the Brayton S-CO2-SORC system with acetone as working fluid at 800 °C in the turbine inlet temperature, with a LCOE (0.2281 USD/kWh), SIC (2308.51 USD/kWh), and PBP (9.89 years). On the other hand, at the same temperature for the Brayton S-CO2-RORC system, it was determined that cyclohexane achieved greater profitability with an LCOE value of 0.2394 USD/kWh and a PBP of 10.37 years. These results are due to the lower costs involved in this configuration since in the Brayton S-CO2-RORC configuration the purchase equipment costs are higher due to the addition of the recuperator.
Declarations
Author contribution statement
Javier Cardenas Gutierrez: Conceived and designed the experiments; Analyzed and interpreted the data; Wrote the paper.
Guillermo Valencia Ochoa: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Wrote the paper.
Jorge Duarte-Forero: Conceived and designed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Funding statement
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Competing interest statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
Acknowledgements
The authors are grateful for the support received from the engineering faculty of the Universidad del Atlántico, and Universidad Francisco de Paula Santander.
Appendix A. Supplementary data
The following is the supplementary data related to this article:
Appendix A
References
- 1.Jouhara H., Sayegh M.A. Energy efficient thermal systems and processes. Therm. Sci. Eng. Prog. 2018;7(125–130):1–5. [Google Scholar]
- 2.Quoilin S., Van Den Broek M., Declaye S., Dewallef P., Lemort V. Techno-economic survey of organic rankine cycle (ORC) systems. Renew. Sustain. Energy Rev. 2013;22:168–186. [Google Scholar]
- 3.Wang E.H. Parametric analysis of a dual-loop ORC system for waste heat recovery of a diesel engine. Appl. Therm. Eng. 2014;67(1–2):168–178. [Google Scholar]
- 4.Bao J., Zhao L. A review of working fluid and expander selections for organic Rankine cycle. Renew. Sustain. Energy Rev. 2013;24:325–342. [Google Scholar]
- 5.Valencia G., Fontalvo A., Cárdenas Y., Duarte J., Isaza C. Energy and exergy analysis of different exhaust waste heat recovery systems for natural gas engine based on ORC. Energies. 2019;12(12) [Google Scholar]
- 6.Landelle A., Tauveron N., Haberschill P., Revellin R., Colasson S. Organic Rankine cycle design and performance comparison based on experimental database. Appl. Energy. 2017;204:1172–1187. [Google Scholar]
- 7.Dostal V., Driscoll M.J., Hejzlar P. Massachusetts Institute of Technology, Department of Nuclear Engineering; 2004. A Supercritical Carbon Dioxide Cycle for Next Generation Nuclear Reactors. [Google Scholar]
- 8.Suárez de la Fuente S., Roberge D., Greig A.R. “Safety and CO2 emissions: implications of using organic fluids in a ship’s waste heat recovery system. Mar. Pol. 2017;75:191–203. [Google Scholar]
- 9.Garg P., Kumar P., Srinivasan K. Supercritical carbon dioxide Brayton cycle for concentrated solar power. J. Supercrit. Fluids. 2013;76:54–60. [Google Scholar]
- 10.Sarkar J. Second law analysis of supercritical CO2 recompression Brayton cycle. Energy. 2009;34(9):1172–1178. [Google Scholar]
- 11.Liu Z., Liu Z., Yang X., Zhai H., Yang X. Advanced exergy and exergoeconomic analysis of a novel liquid carbon dioxide energy storage system. Energy Convers. Manag. 2020;205:112391. [Google Scholar]
- 12.Dostal V., Hejzlar P., Driscoll M.J. The supercritical carbon dioxide power cycle: comparison to other advanced power cycles. Nuclear technology. 2006;154(3):283–301. [Google Scholar]
- 13.Iverson B.D., Conboy T.M., Pasch J.J., Kruizenga A.M. Supercritical CO2 Brayton cycles for solar-thermal energy. Appl. Energy. 2013;111:957–970. [Google Scholar]
- 14.Toffolo A., Lazzaretto A., Manente G., Paci M. A multi-criteria approach for the optimal selection of working fluid and design parameters in Organic Rankine Cycle systems. Appl. Energy. 2014;121:219–232. [Google Scholar]
- 15.Valencia G., Peñaloza C., Forero J. Thermoeconomic optimization with PSO algorithm of waste heat recovery systems based on organic rankine cycle system for a natural gas engine. Energies. Oct. 2019;12:4165. [Google Scholar]
- 16.El-Emam R.S., Dincer I. Exergy and exergoeconomic analyses and optimization of geothermal organic Rankine cycle. Appl. Therm. Eng. 2013;59(1–2):435–444. [Google Scholar]
- 17.Valencia G., Peñaloza C., Forero J. Thermo-economic assessment of a gas microturbine-absorption chiller trigeneration system under different compressor inlet air temperatures. Energies. Dec. 2019;12:4643. [Google Scholar]
- 18.Valencia G., Duarte J., Isaza-Roldan C. Thermoeconomic analysis of different exhaust waste-heat recovery systems for natural gas engine based on ORC. Appl. Sci. 2019;9(19) [Google Scholar]
- 19.Ochoa G.V., Gutierrez J.C., Forero J.D. Exergy, economic, and life-cycle assessment of ORC system for waste heat recovery in a natural gas internal combustion engine. Resources. 2020;9(1) [Google Scholar]
- 20.Ochoa G.V., Rojas J.P., Forero J.D. Advance exergo-economic analysis of a waste heat recovery system using ORC for a bottoming natural gas engine. Energies. 2020;13(1):267. [Google Scholar]
- 21.Ochoa G., Peñaloza C., Rojas J. Thermoeconomic modelling and parametric study of a simple ORC for the recovery of waste heat in a 2 MW gas engine under different working fluids. Appl. Sci. Oct. 2019;9:4526. [Google Scholar]
- 22.Khaljani M., Khoshbakhti Saray R., Bahlouli K. Comprehensive analysis of energy, exergy and exergo-economic of cogeneration of heat and power in a combined gas turbine and organic Rankine cycle. Energy Convers. Manag. 2015;97:154–165. [Google Scholar]
- 23.Esquivel-Patiño G.G., Serna-González M., Nápoles-Rivera F. Thermal integration of natural gas combined cycle power plants with CO2 capture systems and organic Rankine cycles. Energy Convers. Manag. 2017;151:334–342. [Google Scholar]
- 24.Song J., Li X., Ren X., Gu C. Performance analysis and parametric optimization of supercritical carbon dioxide (S-CO2) cycle with bottoming Organic Rankine Cycle (ORC) Energy. 2018;143:406–416. [Google Scholar]
- 25.Katulić S., Čehil M., Schneider D.R. “Thermodynamic efficiency improvement of combined cycle power plant’s bottom cycle based on organic working fluids. Energy. 2018;147:36–50. [Google Scholar]
- 26.Shaaban S. Analysis of an integrated solar combined cycle with steam and organic Rankine cycles as bottoming cycles. Energy Convers. Manag. 2016;126:1003–1012. [Google Scholar]
- 27.Singh H., Mishra R.S. Performance analysis of solar parabolic trough collectors driven combined supercritical CO2 and organic Rankine cycle. Eng. Sci. Technol. – Int. J. 2018;21(3):451–464. [Google Scholar]
- 28.Ochoa G.V., Isaza-Roldan C., Forero J.D. A phenomenological base semi-physical thermodynamic model for the cylinder and exhaust manifold of a natural gas 2-megawatt four-stroke internal combustion engine. Heliyon. Oct. 2019;5(10) doi: 10.1016/j.heliyon.2019.e02700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Paanu T., Aho P., Ekman J.K., Saveljeff H., Niemi S. Vaasan yliopisto; 2015. Effect of the Exhaust Gas Side Fouling on the Performance of a Plate and Shell Type Heat Exchanger. [Google Scholar]
- 30.Zare V., Mahmoudi S.M.S., Yari M., Amidpour M. “Thermoeconomic analysis and optimization of an ammonia–water power/cooling cogeneration cycle. Energy. 2012;47(1):271–283. [Google Scholar]
- 31.Bejan A., Tsatsaronis G., Moran M.J. Willey; 1996. Optimization and thermal Design. [Google Scholar]
- 32.Zare V., Mahmoudi S.M.S., Yari M. “An exergoeconomic investigation of waste heat recovery from the Gas Turbine-Modular Helium Reactor (GT-MHR) employing an ammonia–water power/cooling cycle. Energy. 2013;61:397–409. [Google Scholar]
- 33.Ghaebi H., Amidpour M., Karimkashi S., Rezayan O. Energy, exergy and thermoeconomic analysis of a combined cooling, heating and power (CCHP) system with gas turbine prime mover. Int. J. Energy Res. 2011;35(8):697–709. [Google Scholar]
- 34.Guo-Yan Z., En W., Shan-Tung T. “Techno-economic study on compact heat exchangers. Int. J. Energy Res. 2008;32(12):1119–1127. [Google Scholar]
- 35.Nami H., Mahmoudi S.M.S., Nemati A. Exergy, economic and environmental impact assessment and optimization of a novel cogeneration system including a gas turbine, a supercritical CO2 and an organic Rankine cycle (GT-HRSG/SCO2) Appl. Therm. Eng. 2017;110:1315–1330. [Google Scholar]
- 36.Vieira L.S., Donatelli J.L., Cruz M.E. Mathematical exergoeconomic optimization of a complex cogeneration plant aided by a professional process simulator. Appl. Therm. Eng. 2006;26(5–6):654–662. [Google Scholar]
- 37.Tchanche B.F. 2010. Low-grade Heat Conversion into Power Using Small Scale Organic Rankine Cycles. Ph.D Thesis. [Google Scholar]
- 38.Han Z., Li P., Han X., Mei Z., Wang Z. Thermo-economic performance analysis of a regenerative superheating organic rankine cycle for waste heat recovery. Energies. 2017;10(10):1593. [Google Scholar]
- 39.Preißinger M., Brüggemann D. Thermoeconomic evaluation of modular organic Rankine cycles for waste heat recovery over a broad range of heat source temperatures and capacities. Energies. 2017;10(3):269. [Google Scholar]
- 40.Quinones L.G.O., Viana L.F.A., Ochoa G.E.V. Thermal design and rating of a shell and tube heat exchanger using a matlab® GUI. Indian J. Sci. Technol. 2017;10(25):1–9. [Google Scholar]
- 41.Jiang Y., Liese E., Zitney S.E., Bhattacharyya D. Design and dynamic modeling of printed circuit heat exchangers for supercritical carbon dioxide Brayton power cycles. Appl. Energy. 2018;231:1019–1032. [Google Scholar]
- 42.Valencia G., Núñez J., Duarte J. Multiobjective optimization of a plate heat exchanger in a waste heat recovery organic rankine cycle system for natural gas engines. Entropy. 2019;21(7) doi: 10.3390/e21070655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Kennedy J., Eberhart R. Vol. 4. 1995. Particle swarm optimization; pp. 1942–1948. (Proceedings of ICNN’95 - International Conference on Neural Networks). [Google Scholar]
- 44.V Rao R., Patel V.K. Thermodynamic optimization of cross flow plate-fin heat exchanger using a particle swarm optimization algorithm. Int. J. Therm. Sci. 2010;49(9):1712–1721. [Google Scholar]
- 45.Zare V. A comparative exergoeconomic analysis of different ORC configurations for binary geothermal power plants. Energy Convers. Manag. 2015;105:127–138. [Google Scholar]
- 46.Padilla R.V., Soo Too Y.C., Benito R., Stein W. Exergetic analysis of supercritical CO2 Brayton cycles integrated with solar central receivers. Appl. Energy. 2015;148:348–365. [Google Scholar]
- 47.Eveloy V., Karunkeyoon W., Rodgers P., Al Alili A. “Energy, exergy and economic analysis of an integrated solid oxide fuel cell–gas turbine–organic Rankine power generation system. Int. J. Hydrogen Energy. 2016;41(31):13843–13858. [Google Scholar]
- 48.Hettiarachchi H.D.M., Golubovic M., Worek W.M., Ikegami Y. Optimum design criteria for an organic Rankine cycle using low-temperature geothermal heat sources. Energy. 2007;32(9):1698–1706. [Google Scholar]
- 49.Ahmadi M.H. Thermodynamic analysis and optimization of a waste heat recovery system for proton exchange membrane fuel cell using transcritical carbon dioxide cycle and cold energy of liquefied natural gas. J. Nat. Gas Sci. Eng. 2016;34:428–438. [Google Scholar]
- 50.Feng Y., Zhang Y., Li B., Yang J., Shi Y. Sensitivity analysis and thermoeconomic comparison of ORCs (organic Rankine cycles) for low temperature waste heat recovery. Energy. 2015;82:664–677. [Google Scholar]
- 51.Cayer E., Galanis N., Nesreddine H. Parametric study and optimization of a transcritical power cycle using a low temperature source. Appl. Energy. 2010;87(4):1349–1357. [Google Scholar]
- 52.Quoilin S., Declaye S., Tchanche B.F., Lemort V. Thermo-economic optimization of waste heat recovery Organic Rankine Cycles. Appl. Therm. Eng. 2011;31(14–15):2885–2893. [Google Scholar]
- 53.Tocci L., Pal T., Pesmazoglou I., Franchetti B. Small scale organic rankine cycle (ORC): a techno-economic review. Energies. 2017;10(4):413. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix A