A note on the impact of late diagnosis on HIV/AIDS dynamics: a mathematical modelling approach

Abstract

Objectives:

The global incidence of HIV infection is not significantly decreasing, especially in sub-Saharan African countries. Though there is availability and accessibility of free HIV services, people are not being diagnosed early for HIV, and hence HIV-related mortality remains significantly high. We formulate a mathematical model for the spread of HIV using non linear ordinary differential equations in order to investigate the impact of late diagnosis of HIV on the spread of HIV.

Results:

The results suggest the need to encourage early initiation into HIV treatment as well as promoting HIV self-testing programs that enable more undiagnosed people to know their HIV status in order to curtail the continued spread of HIV.

Introduction

Antiretroviral therapy (ART) has successfully transformed human immunodeficiency virus (HIV) infection from a fatal to a manageable chronic disease [1]. Nonetheless, there remains critical factors to be addressed along with the roll out of effective ART regimens in order to eradicate HIV. We seek to investigate the impact of late diagnosis on the transmission dynamics of HIV. Mathematical modeling of HIV dynamics is quite advanced, see for instance the following works on HIV and the references therein [2–9].

We extend a more recent HIV/AIDS mathematical model developed by Omondi et al. [8] to investigate the impact of late diagnosis on the spread and control of HIV. In their work, Omondi et al. [8] proposed a five state deterministic compartmental model for the time evolution of population states to study the trend of HIV infection in Kenya. The model was premised on dividing the infected classes according to CD4⁺ T cell counts in the blood. For more information about the description of parameters and model analysis, readers are referred to Omondi et al. [8].

The paper is arranged as follows; in "Main text" section, we formulate and establish the basic properties of the model. The model is analysed for stability in this section. In "Results and discussion" section, we carry out some numerical simulations. Parameter estimation and numerical results are also presented in this section. The paper is concluded in "Conclusions" section.

Main text

The model

We propose a five state compartmental model for HIV that takes into account untimely initiation of HIV positive individuals into ART. The human population comprises classes; S(t), $I_1(t)$, $I_2(t)$, $I_{A1}(t)$ and $I_{A2}(t)$. The class S(t) represents the population at high risk of HIV infection. Upon acquiring HIV infection, susceptible individuals move to infection class which is divided into two stages according to CD4⁺ T cell count in the blood. The infectives class $I_1$ comprise of individuals with CD4⁺ T cell count $\ge 350$/μL. Individuals in class $I_1$ are assumed to be having a lower viral load and hence are considered to be the new infections. Individuals in class $I_1$ progress to the second stage of infection $I_2$ at a rate given by $\delta$. This class consists of individuals with CD4⁺ T cell count in the range $200-350$/μL. Individuals in this stage are assumed to be having high viral load. Individuals in class $I_1$ are initiated into ART treatment at a rate given by ${\sigma }_1$. In this paper, we develop a mathematical model that takes into account the effect of late initiation into ART treatment of HIV positive patients. We define initiation of HIV positive individuals in stage $I_2$ into ART treatment by the expression

$$\begin{array}{c}\hfill H\left(I_2\right)=\frac{{\sigma }_2{I}_2}{1+r{I}_2}.\end{array}$$ 1

Here, ${\sigma }_2$ represent the maximum treatment uptake per unit of time for individuals in class $I_2$ and r measures the extent of the effect of late initiation into ART treatment. Firstly, observe that for small $I_2$, $H(I_2)\approx {\sigma }_2{I}_2$. Secondly, observe that for large $I_2$, $H(I_2)\approx {\sigma }_2/r$. Finally, when $r=0$, we obtain $H(I_2)={\sigma }_2{I}_2$, which is the case considered in Omondi et al. [8]. Individuals in class $I_{A1}$ move to the class $I_{A2}$ through a deteriorative process at a rate given by ${\gamma }_1$ whereas individuals in class $I_{A2}$ move to the class $I_{A1}$ through an ameliorative process at a rate given by ${\gamma }_2$. In this model, we exclude the class of full blown AIDS patients as these are usually hospitalised and/or sexually inactive and hence their contribution to new HIV infections is negligible [8]. The total human population is thus given by

$$\begin{array}{c}\hfill N(t)=S(t)+I_1(t)+I_2(t)+I_{A1}(t)+I_{A2}(t).\end{array}$$

Susceptible humans are recruited into the system through births or immigration at a constant rate $\mathrm{\Lambda }$. Susceptible individuals acquire new HIV infections at a rate given by

$$\begin{array}{c}\hfill \lambda =\frac{{\beta }_1{I}_1+{\beta }_2{I}_2+{\beta }_3{I}_{A1}+{\beta }_4{I}_{A2}}{N}\end{array}$$ 2

where ${\beta }_1$, ${\beta }_2$, ${\beta }_3$ and ${\beta }_4$ denote the HIV transmission rates between susceptible individuals and infectious individuals. We assume that individuals in each compartment are indistinguishable and there is homogeneous mixing. Individuals in classes $I_2$ and $I_{A2}$ experience disease related death at rates given respectively by ${\omega }_1$ and ${\omega }_2$. The natural death rate of the general population is represented by $\mu$. The differential equations for the model are given as follows;

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle \frac{\mathit{dS}}{\mathit{dt}}}=\mathrm{\Lambda }-\lambda S-\mu S,\hfill \\ {\displaystyle \frac{d{I}_1}{\mathit{dt}}}=\lambda S-(\mu +\delta +{\sigma }_1)I_1,\hfill \\ {\displaystyle \frac{d{I}_2}{\mathit{dt}}}=\delta I_1-(\mu +{\omega }_1)I_2-H(I_2),\hfill \\ {\displaystyle \frac{d{I}_{A1}}{\mathit{dt}}}={\sigma }_1{I}_1-(\mu +{\gamma }_1)I_{A1}+{\gamma }_2{I}_{A2},\hfill \\ {\displaystyle \frac{d{I}_{A2}}{\mathit{dt}}}=H(I_2)-(\mu +{\gamma }_2+{\omega }_2)I_{A2}+{\gamma }_1{I}_{A1},\hfill \end{array}\right)\end{array}$$ 3

with the initial conditions:

$$\begin{array}{c}\hfill S(0)=S_0>0,I_1(0)=I_{10}\ge 0,I_2(0)=I_{20}\ge 0,I_{A1}(0)=I_{A10}\ge 0,I_{A2}(0)=I_{A20}\ge 0,\end{array}$$

where we assume that all the model parameters are positive.

Analysis of the model

Positivity of solutions

The following theorem (Theorem 1) entails that all the state variables remain non-negative and the solutions of system (3) with positive initial conditions will remain positive for all $t>0$.

Theorem 1

Given that the initial conditions of system (3) are$S(0)>0$, $I_1(0)>0$, $I_2(0)>0$, $I_{A1}(0)>0$and$I_{A2}(0)>0$. There exists$(S(t),I_1(t),I_2(t),I_{A1}(t),I_{A2}(t)):(0,\infty )\to (0,\infty )$which solve system (3).

For more details on the proof of Theorem 1, we refer the reader to [8].

Invariant region

The feasible region for system (3) is given by

$$\begin{array}{c}\hfill \mathrm{\Omega }=\left\{(S,I_1,I_2,I_{A1},I_{A2}),\in ,{\mathbb{R}}_{+}^5,|N\le ,\frac{\mathrm{\Lambda }}{\mu }\right\}.\end{array}$$ 4

Results to verify that the region $\mathrm{\Omega }$ is positively invariant with respect to system (3) can be obtained as given in [8].

Disease-free equilibrium and the basic reproduction number

The model has a disease-free equilibrium given by

$$\begin{array}{c}\hfill {\mathcal{D}}^f=\left(S^f,,,I_1^f,,,I_2^f,,,I_{A_1}^f,,,I_{A_2}^f\right)=\left(\frac{\mathrm{\Lambda }}{\mu },,,0,,,0,,,0,,,0\right),\end{array}$$

a scenario depicting a disease-free state in the community or society. The basic reproduction number ${\mathcal{R}}_0$ of the model, is defined herein as the average number of people infected by each HIV infected individual during his/her infectious period in a population of completely susceptible individuals. The determination of ${\mathcal{R}}_0$ is done using the next generation matrix approach [10]. It works out that, the basic reproduction number of system (3) is given by:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{R}}_0={\mathcal{R}}_{I_1}+{\mathcal{R}}_{I_2}+{\mathcal{R}}_{I_{A1}}+{\mathcal{R}}_{I_{A2}}\text{where}\hfill \\ {\mathcal{R}}_{I_1}={\displaystyle \frac{{\beta }_1}{h_1}},{\mathcal{R}}_{I_2}={\displaystyle \frac{{\beta }_2\delta }{h_1{h}_2}},{\mathcal{R}}_{I_{A1}}={\displaystyle \frac{{\beta }_3\left({\gamma }_2,\delta ,{\sigma }_2,+,h_2,h_4,{\sigma }_1\right)}{h_1{h}_2{h}_3{h}_4\left(1,-,\mathrm{\Phi }\right)}}\text{and}\hfill \\ {\mathcal{R}}_{I_{A2}}={\displaystyle \frac{{\beta }_4\left({\gamma }_1,h_2,{\sigma }_1,+,\delta ,h_3,{\sigma }_2\right)}{h_1{h}_2{h}_3{h}_4\left(1,-,\mathrm{\Phi }\right)}}\text{with}\mathrm{\Phi }={\displaystyle \frac{{\gamma }_1{\gamma }_2}{h_3{h}_4}},h_1=\mu +\delta +{\sigma }_1,\hfill \\ h_2=\mu +{\sigma }_2+{\omega }_1,h_3=\mu +{\gamma }_1\text{and}{h}_4=\mu +{\gamma }_2+{\omega }_2.\hfill \end{array}\right)\end{array}$$ 5

Here, the four sub-reproduction numbers ${\mathcal{R}}_{I_1}$, ${\mathcal{R}}_{I_2}$, ${\mathcal{R}}_{I_{A_1}}$ and ${\mathcal{R}}_{I_{A_2}}$ represent the contributions of individuals in compartments $I_1$, $I_2$, $I_{A_1}$ and $I_{A_2}$ on the spread of HIV infection respectively. We can clearly note that ${\mathcal{R}}_0$ is non-negative as $h_3{h}_4>{\gamma }_1{\gamma }_2$ which implies that $\mathrm{\Phi }<1$.

Local stability of the disease-free steady state

The following theorem follows from van den Driessche and Watmough [10] (Theorem 2).

Theorem 2

The disease-free equilibrium point${\mathcal{D}}^f$of model system equations (3) is locally asymptotically stable if${\mathcal{R}}_0<1$and is unstable if${\mathcal{R}}_0>1$.

Endemic equilibrium

The endemic equilibrium denoted by ${\mathcal{D}}^{\ast }=\left(S^{\ast },,,I_1^{\ast },,,I_2^{\ast },,,I_{A_1}^{\ast },,,I_{A_2}^{\ast }\right)$ satisfies

$$\begin{array}{c}\hfill \left\{\begin{array}{c}0=\mathrm{\Lambda }-{\lambda }^{\ast }{S}^{\ast }-\mu S^{\ast },\hfill \\ 0={\lambda }^{\ast }{S}^{\ast }-h_1{I}_1^{\ast },\hfill \\ 0=\delta I_1^{\ast }-(\mu +{\omega }_1)I_2^{\ast }-H(I_2^{\ast }),\hfill \\ 0={\sigma }_1{I}_1^{\ast }-(\mu +{\gamma }_1)I_{A1}^{\ast }+{\gamma }_2{I}_{A2}^{\ast },\hfill \\ 0=H(I_2^{\ast })-(\mu +{\gamma }_2+{\omega }_2)I_{A2}^{\ast }+{\gamma }_1{I}_{A1}^{\ast }.\hfill \end{array}\right)\end{array}$$ 6

From the first, third, fourth and fifth equation of (6), we have $S^{\ast },I_1^{\ast },I_{A_1}^{\ast },I_{A_2}^{\ast }$ expressed in terms of $I_2^{\ast }$ as follows

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{S}^{\ast }={\displaystyle \frac{\delta \mathrm{\Lambda }(I_2^{\ast }r+1)-h_1{I}_2^{\ast }\left(h_2,+,I_2^{\ast },r,\left(\mu ,+,{\omega }_1\right)\right)}{\delta \mu (I_2^{\ast }r+1)}},I_1^{\ast }={\displaystyle \frac{I_2^{\ast }\left(h_2,+,I_2^{\ast },r,\left(\mu ,+,{\omega }_1\right)\right)}{\delta +\delta I_2^{\ast }r}},\hfill \\ I_{A1}^{\ast }={\displaystyle \frac{I_2^{\ast }\left({\gamma }_2,\delta ,{\sigma }_2,+,h_4,{\sigma }_1,\left(h_2,+,I_2^{\ast },r,\left(\mu ,+,{\omega }_1\right)\right)\right)}{\delta \left(h_3,h_4,-,{\gamma }_1,{\gamma }_2\right)(I_2^{\ast }r+1)}}\text{and}{I}_{A2}^{\ast }={\displaystyle \frac{I_2^{\ast }\left(\delta ,h_3,{\sigma }_2,+,{\gamma }_1,{\sigma }_1,\left(h_2,+,I_2^{\ast },r,\left(\mu ,+,{\omega }_1\right)\right)\right)}{\delta \left(h_3,h_4,-,{\gamma }_1,{\gamma }_2\right)(I_2^{\ast }r+1)}}.\hfill \end{array}\right)\end{array}$$ 7

Substituting expressions (7) into the second equation of (6) leads to the following fourth order polynomial equation

$$\begin{array}{c}\hfill I_2^{\ast }\left({\xi }_3,I_2^{\ast 3},+,{\xi }_2,I_2^{\ast 2},+,{\xi }_1,I_2^{\ast },+,{\xi }_0\right)=0.\end{array}$$ 8

Solving (8) gives $I_2^{\ast }=0$ which corresponds to the disease-free equilibrium or

$$\begin{array}{c}\hfill {\xi }_3{I}_2^{\ast 3}+{\xi }_2{I}_2^{\ast 2}+{\xi }_1{I}_2^{\ast }+{\xi }_0=0,\end{array}$$ 9

where the coefficients ${\xi }_i$, $0\le i\le 3$ are given in (10).

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\xi }_0=\mu \delta h_1{h}_2{h}_3{h}_4\left(1,-,\mathrm{\Phi }\right)\left(1,-,{\mathcal{R}}_0\right),\hfill \\ {\xi }_1=h_1({\beta }_3{h}_2({\gamma }_2\delta {\sigma }_2+h_2{h}_4{\sigma }_1)-{\gamma }_1({\gamma }_2({\beta }_1{h}_2^2+\delta h_2({\beta }_2+\mu r)+\delta \mu r(\mu +{\omega }_1))\hfill \\ -{\beta }_4{h}_2^2{\sigma }_1)+h_3({\beta }_4\delta h_2{\sigma }_2+h_4({\beta }_1{h}_2^2+\delta h_2({\beta }_2+\mu r)+\delta \mu r(\mu +{\omega }_1))))\hfill \\ -\delta \mathrm{\Lambda }r({\beta }_3{\gamma }_2\delta {\sigma }_2-2{\beta }_2{\gamma }_1{\gamma }_2\delta +{\beta }_4{\gamma }_1\mu {\sigma }_1-{\beta }_1{\gamma }_1{\gamma }_2(h_2+\mu +{\omega }_1)+{\sigma }_1{\omega }_1({\beta }_4{\gamma }_1+{\beta }_3{h}_4)\hfill \\ +{\beta }_4{\gamma }_1{h}_2{\sigma }_1+h_3({\beta }_4\delta {\sigma }_2+h_4(2{\beta }_2\delta +{\beta }_1(h_2+\mu +{\omega }_1)))+{\beta }_3{h}_4{\sigma }_1(h_2+\mu )),\hfill \\ {\xi }_2=r(h_1({\beta }_3(\mu +{\omega }_1)({\gamma }_2\delta {\sigma }_2+2h_2{h}_4{\sigma }_1)+{\gamma }_1(2{\beta }_4{h}_2{\sigma }_1(\mu +{\omega }_1)-{\gamma }_2(h_2({\beta }_2\delta +2{\beta }_1(\mu +{\omega }_1))\hfill \\ +\delta (\mu +{\omega }_1)({\beta }_2+\mu r)))+h_3({\beta }_4\delta {\sigma }_2(\mu +{\omega }_1)+h_4(h_2({\beta }_2\delta +2{\beta }_1(\mu +{\omega }_1))+\delta (\mu +{\omega }_1)\hfill \\ \times ({\beta }_2+\mu ))))-\delta \mathrm{\Lambda }r({\gamma }_1({\beta }_4\mu {\sigma }_1-{\beta }_2{\gamma }_2\delta )-{\beta }_1{\gamma }_1{\gamma }_2(\mu +{\omega }_1)+{\sigma }_1{\omega }_1({\beta }_4{\gamma }_1+{\beta }_3{h}_4)\hfill \\ +h_3{h}_4({\beta }_2\delta +{\beta }_1(\mu +{\omega }_1))+{\beta }_3{h}_4\mu {\sigma }_1)),\hfill \\ {\xi }_3=r^2(\mu +{\omega }_1)h_1({\beta }_2\delta ({\omega }_2{h}_3+\mu ({\gamma }_1+{\gamma }_2+\mu ))+{\sigma }_1(\mu +{\omega }_1)({\beta }_3{h}_4+{\beta }_4{\gamma }_1)\hfill \\ +{\beta }_1(\mu +{\omega }_1)({\gamma }_1(\mu +{\omega }_2)+\mu h_4)).\hfill \end{array}\right)\end{array}$$ 10

We can clearly note that, ${\xi }_0>0\iff {\mathcal{R}}_0<1$ and ${\xi }_0<0\iff {\mathcal{R}}_0>1$. We now determine the number of possible positive real zeros of the polynomial (10) using the Descartes Rule of Signs. The possibilities can be presented as shown below. Here, the number of possible positive real zeros is denoted by $i^{\ast }$.

${\xi }_3>0$
${\xi }_2>0$					${\xi }_2<0$
${\xi }_1>0$			${\xi }_1<0$		${\xi }_1>0$		${\xi }_1<0$
${\xi }_0>0$		${\xi }_0<0$	${\xi }_0>0$	${\xi }_0<0$	${\xi }_0>0$	${\xi }_0<0$	${\xi }_0>0$	${\xi }_0<0$
$i^{\ast }$	0	1	2	1	2	3	2	1

Backward bifurcation

Theorem 4.1 proven in Castillo-Chavez and Song [11] will be useful. We show that system (3) undergoes a backward bifurcation. Let us make the following change of variables:

$S=x_1,I_1=x_2,I_2=x_3,I_{A1}=x_4,I_{A2}=x_5$, so that ${\displaystyle \text{N}=\sum _{n=1}^5{x}_n}$. We now use the vector notation $X={\left(x_1,,,x_2,,,x_3,,,x_4,,,x_5\right)}^T$. Then, system (3) can be written in the form

${\displaystyle \frac{\mathit{dX}}{\mathit{dt}}}=F(t,x(t))={\left(f_1,,,f_2,,,f_3,,,f_4,,,f_5\right)}^T$, where

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle \frac{d{x}_1}{\mathit{dt}}}=\mathrm{\Lambda }-{\displaystyle \frac{\left({\beta }_1,x_2,+,{\beta }_2,x_3,+,{\beta }_3,x_4,+,{\beta }_4,x_5\right)x_1}{N}}-\mu x_1=f_1,\hfill \\ {\displaystyle \frac{d{x}_2}{\mathit{dt}}}={\displaystyle \frac{\left({\beta }_1,x_2,+,{\beta }_2,x_3,+,{\beta }_3,x_4,+,{\beta }_4,x_5\right)x_1}{N}}-h_1{x}_2=f_2,\hfill \\ {\displaystyle \frac{d{x}_3}{\mathit{dt}}}=\delta x_2-(\mu +{\omega }_1)x_3-{\displaystyle \frac{{\sigma }_2{x}_3}{1+r{x}_3}}=f_3,\hfill \\ {\displaystyle \frac{d{x}_4}{\mathit{dt}}}={\sigma }_1{x}_2-h_3{x}_4+{\gamma }_2{x}_5=f_4,\hfill \\ {\displaystyle \frac{d{x}_5}{\mathit{dt}}}={\displaystyle \frac{{\sigma }_2{x}_3}{1+r{x}_3}}-h_4{x}_5+{\gamma }_1{x}_4=f_5.\hfill \end{array}\right)\end{array}$$ 11

We now define

$$\begin{array}{c}\hfill {\beta }_{i+1}={\theta }_i{\beta }_1,i=1,2,3\end{array}$$ 12

with ${\theta }_i=1$ signifying that the chance of acquiring HIV infection upon contact with individuals in class $x_2$ or upon contact with individuals in classes $x_3$, $x_4$ and $x_5$ is the same, ${\theta }_i\in (0,1)$ signifying a reduced chance of acquiring HIV infection upon contact with individuals in classes $x_3$, $x_4$ and $x_5$ as compared to individuals in class $x_2$, ${\theta }_i>1$ signifies an increased rate of acquiring HIV infection upon contact with individuals in classes $x_3$, $x_4$ and $x_5$ as compared to individuals in class $x_2$.

Let ${\beta }_1$ be the bifurcation parameter, ${\mathcal{R}}_0=1$ corresponds to

$$\begin{array}{c}\hfill {\beta }_1={\beta }_1^{\ast }=\frac{h_1{h}_2\left(h_3,h_4,-,{\gamma }_1,{\gamma }_2\right)}{{\gamma }_2\delta {\theta }_2{\sigma }_2-{\gamma }_1{\gamma }_2\delta {\theta }_1+{\gamma }_1{h}_2{\theta }_3{\sigma }_1-{\gamma }_1{\gamma }_2{h}_2+\delta h_3{\theta }_3{\sigma }_2+\delta h_3{\theta }_1{h}_4+h_2{\theta }_2{h}_4{\sigma }_1+h_2{h}_3{h}_4}.\end{array}$$ 13

The Jacobian matrix of model system (3) at ${\mathcal{D}}_f$ when ${\beta }_1={\beta }_1^{\ast }$ is given by

$$\begin{array}{c}\hfill J^{\ast }({\mathcal{D}}_f)=\left(\begin{array}{ccccc}-\mu & -{\beta }_1^{\ast }& -{\beta }_1^{\ast }{\theta }_1& -{\beta }_1^{\ast }{\theta }_2& -{\beta }_1^{\ast }{\theta }_3\\ 0& {\beta }_1^{\ast }-h_1& {\beta }_1^{\ast }{\theta }_1& {\beta }_1^{\ast }{\theta }_2& {\beta }_1^{\ast }{\theta }_3\\ 0& \delta & -h_2& 0& 0\\ 0& {\sigma }_1& 0& -h_3& {\gamma }_2\\ 0& 0& {\sigma }_2& {\gamma }_1& -h_4\end{array}\right)\end{array}$$

where $h_1$, $h_2$, $h_3$ and $h_4$ are defined as before.

Model system (11), with ${\beta }_1={\beta }_1^{\ast }$ has a simple eigenvalue, hence the center manifold theory can be used to analyse the dynamics of model system (3) near ${\beta }_1={\beta }_1^{\ast }$. It can be shown that $J^{\ast }({\mathcal{D}}^f)$, has a right eigenvector given by $w={(w_1,w_2,w_3,w_4,w_5)}^T$, where

$$\begin{array}{cc}\hfill w_1=& -h_1{h}_2{h}_3{h}_4\left(1,-,\mathrm{\Phi }\right),w_2=\mu h_2{h}_3{h}_4\left(1,-,\mathrm{\Phi }\right),w_3=\mu \delta h_3{h}_4\left(1,-,\mathrm{\Phi }\right),\hfill \\ \hfill w_4=& \mu \left({\gamma }_2,\delta ,{\sigma }_2,+,h_2,h_4,{\sigma }_1\right),w_5=\mu \left({\gamma }_1,h_2,{\sigma }_1,+,\delta ,h_3,{\sigma }_2\right).\hfill \end{array}$$

Here, we note that $w_1<0$ and $w_i>0,i=2,3,4,5$. Further, the left eigenvector of $J^{\ast }({\mathcal{D}}^f)$, associated with the zero eigenvalue at ${\beta }_1={\beta }_1^{\ast }$ is given by $v={(v_1,v_2,v_3,v_4,v_5)}^T$, where

$$\begin{array}{cc}\hfill v_1=& 0,\hfill \\ \hfill v_2=& {\gamma }_2\delta \left({\theta }_2,{\sigma }_2,-,{\gamma }_1,{\theta }_1\right)+h_2\left(-,{\gamma }_1,{\gamma }_2,+,{\sigma }_1,\left({\gamma }_1,{\theta }_3,+,h_4,{\theta }_2\right),+,h_3,h_4\right)+\delta h_3\left(h_4,{\theta }_1,+,{\theta }_3,{\sigma }_2\right),\hfill \\ \hfill v_3=& h_1\left({\gamma }_2,\left({\theta }_2,{\sigma }_2,-,{\gamma }_1,{\theta }_1\right),+,h_3,\left(h_4,{\theta }_1,+,{\theta }_3,{\sigma }_2\right)\right),\hfill \\ \hfill v_4=& h_1{h}_2\left({\gamma }_1,{\theta }_3,+,h_4,{\theta }_2\right),v_5=h_1{h}_2\left({\gamma }_2,{\theta }_2,+,h_3,{\theta }_3\right).\hfill \end{array}$$

Here, take note that $v_2>0$, $v_3>0$ accordingly as ${\sigma }_2{\theta }_2>{\gamma }_1{\theta }_1$ and $v_2<0$, $v_3<0$ accordingly as ${\sigma }_2{\theta }_2<{\gamma }_1{\theta }_1$. Also, $v_4>0$ and $v_5>0$.

The computations of a and b are necessary in order to apply Theorem 4.1 in Castillo-Chavez and Song [11]. For system (11), the associated non-zero partial derivatives of F at the disease-free equilibrium are given in (14).

$$\begin{array}{cc}\hfill \frac{{\partial }^2{f}_1}{\partial x_1^2}& =\frac{2{\beta }_1^{\ast }\mu }{\mathrm{\Lambda }},\frac{{\partial }^2{f}_1}{\partial x_2\partial x_3}=\frac{{\partial }^2{f}_1}{\partial x_3\partial x_2}=\frac{{\beta }_1^{\ast }{\theta }_1\mu }{\mathrm{\Lambda }}+\frac{{\beta }_1^{\ast }\mu }{\mathrm{\Lambda }},\hfill \\ \hfill \frac{{\partial }^2{f}_1}{\partial x_2\partial x_4}& =\frac{{\partial }^2{f}_1}{\partial x_4\partial x_2}=\frac{{\beta }_1^{\ast }{\theta }_2\mu }{\mathrm{\Lambda }}+\frac{{\beta }_1^{\ast }\mu }{\mathrm{\Lambda }},\frac{{\partial }^2{f}_1}{\partial x_2\partial x_5}=\frac{{\partial }^2{f}_1}{\partial x_5\partial x_2}=\frac{{\beta }_1^{\ast }{\theta }_3\mu }{\mathrm{\Lambda }}+\frac{{\beta }_1^{\ast }\mu }{\mathrm{\Lambda }},\hfill \\ \hfill \frac{{\partial }^2{f}_1}{\partial x_3^2}& =\frac{2{\beta }_1^{\ast }{\theta }_1\mu }{\mathrm{\Lambda }},\frac{{\partial }^2{f}_1}{\partial x_3\partial x_4}=\frac{{\partial }^2{f}_1}{\partial x_4\partial x_3}=\frac{{\beta }_1^{\ast }{\theta }_1\mu }{\mathrm{\Lambda }}+\frac{{\beta }_1^{\ast }{\theta }_2\mu }{\mathrm{\Lambda }},\hfill \\ \hfill \frac{{\partial }^2{f}_1}{\partial x_3\partial x_5}& =\frac{{\partial }^2{f}_1}{\partial x_5\partial x_3}=\frac{{\beta }_1^{\ast }{\theta }_1\mu }{\mathrm{\Lambda }}+\frac{{\beta }_1^{\ast }{\theta }_3\mu }{\mathrm{\Lambda }},\frac{{\partial }^2{f}_1}{\partial x_4^2}=\frac{2{\beta }_1^{\ast }{\theta }_2\mu }{\mathrm{\Lambda }},\hfill \\ \hfill \frac{{\partial }^2{f}_1}{\partial x_4\partial x_5}& =\frac{{\partial }^2{f}_1}{\partial x_5\partial x_4}=\frac{{\beta }_1^{\ast }{\theta }_2\mu }{\mathrm{\Lambda }}+\frac{{\beta }_1^{\ast }{\theta }_3\mu }{\mathrm{\Lambda }},\frac{{\partial }^2{f}_1}{\partial x_5^2}=\frac{2{\beta }_1^{\ast }{\theta }_3\mu }{\mathrm{\Lambda }},\hfill \\ \hfill \frac{{\partial }^2{f}_2}{\partial x_1^2}& =-\frac{2{\beta }_1^{\ast }\mu }{\mathrm{\Lambda }},\frac{{\partial }^2{f}_2}{\partial x_2\partial x_3}=\frac{{\partial }^2{f}_2}{\partial x_3\partial x_2}=-\frac{{\beta }_1^{\ast }{\theta }_1\mu }{\mathrm{\Lambda }}-\frac{{\beta }_1^{\ast }\mu }{\mathrm{\Lambda }},\hfill \\ \hfill \frac{{\partial }^2{f}_2}{\partial x_2\partial x_4}& =\frac{{\partial }^2{f}_2}{\partial x_4\partial x_2}=-\frac{{\beta }_1^{\ast }{\theta }_2\mu }{\mathrm{\Lambda }}-\frac{{\beta }_1^{\ast }\mu }{\mathrm{\Lambda }},\frac{{\partial }^2{f}_2}{\partial x_2\partial x_5}=\frac{{\partial }^2{f}_2}{\partial x_5\partial x_2}=-\frac{{\beta }_1^{\ast }{\theta }_3\mu }{\mathrm{\Lambda }}-\frac{{\beta }_1^{\ast }\mu }{\mathrm{\Lambda }},\hfill \\ \hfill \frac{{\partial }^2{f}_2}{\partial x_3^2}& =-\frac{2{\beta }_1^{\ast }{\theta }_1\mu }{\mathrm{\Lambda }},\frac{{\partial }^2{f}_2}{\partial x_3\partial x_4}=\frac{{\partial }^2{f}_2}{\partial x_4\partial x_3}=-\frac{{\beta }_1^{\ast }{\theta }_1\mu }{\mathrm{\Lambda }}-\frac{{\beta }_1^{\ast }{\theta }_2\mu }{\mathrm{\Lambda }},\hfill \\ \hfill \frac{{\partial }^2{f}_2}{\partial x_3\partial x_5}& =\frac{{\partial }^2{f}_2}{\partial x_5\partial x_3}=-\frac{{\beta }_1^{\ast }{\theta }_1\mu }{\mathrm{\Lambda }}-\frac{{\beta }_1^{\ast }{\theta }_3\mu }{\mathrm{\Lambda }},\frac{{\partial }^2{f}_2}{\partial x_4^2}=-\frac{2{\beta }_1^{\ast }{\theta }_2\mu }{\mathrm{\Lambda }},\hfill \\ \hfill \frac{{\partial }^2{f}_2}{\partial x_4\partial x_5}& =\frac{{\partial }^2{f}_2}{\partial x_5\partial x_4}=-\frac{{\beta }_1^{\ast }{\theta }_2\mu }{\mathrm{\Lambda }}-\frac{{\beta }_1^{\ast }{\theta }_3\mu }{\mathrm{\Lambda }},\frac{{\partial }^2{f}_2}{\partial x_5^2}=-\frac{2{\beta }_1^{\ast }{\theta }_3\mu }{\mathrm{\Lambda }},\hfill \\ \hfill \frac{{\partial }^2{f}_3}{\partial x_3^2}& =2r{\sigma }_2,\frac{{\partial }^2{f}_5}{\partial x_3^2}=-2r{\sigma }_2,\hfill \\ \hfill \frac{{\partial }^2{f}_1}{\partial x_2\partial {\beta }_1^{\ast }}& =-1,\frac{{\partial }^2{f}_1}{\partial x_3\partial {\beta }_1^{\ast }}=-{\theta }_1,\frac{{\partial }^2{f}_1}{\partial x_4\partial {\beta }_1^{\ast }}=-{\theta }_2,\frac{{\partial }^2{f}_1}{\partial x_5\partial {\beta }_1^{\ast }}=-{\theta }_3,\hfill \\ \hfill \frac{{\partial }^2{f}_2}{\partial x_2\partial {\beta }_1^{\ast }}& =1,\frac{{\partial }^2{f}_2}{\partial x_3\partial {\beta }_1^{\ast }}={\theta }_1,\frac{{\partial }^2{f}_2}{\partial x_4\partial {\beta }_1^{\ast }}={\theta }_2,\frac{{\partial }^2{f}_2}{\partial x_5\partial {\beta }_1^{\ast }}={\theta }_3.\hfill \end{array}$$ 14

It thus follows that

$$\begin{array}{cc}\hfill \text{a}& =\sum _{i=2}^5{v}_2{w}_2{w}_i\frac{{\partial }^2{f}_2}{\partial x_2\partial x_i}+\sum _{i=2}^5{v}_2{w}_3{w}_i\frac{{\partial }^2{f}_2}{\partial x_3\partial x_i}+\sum _{i=2}^3{v}_2{w}_4{w}_i\frac{{\partial }^2{f}_2}{\partial x_4\partial x_i}\hfill \\ \hfill & +v_2{w}_5^2\frac{{\partial }^2{f}_2}{\partial x_5^2}+v_3{w}_3^2\frac{{\partial }^2{f}_2}{\partial x_3^2}+v_5{w}_3^2\frac{{\partial }^2{f}_2}{\partial x_3^2}\hfill \\ \hfill & =\frac{{\beta }_1\mu v_2\left(-\left(2\left(w_2+w_3+w_4\right)+w_5\right)\left({\theta }_1{w}_3+{\theta }_2{w}_4+w_2\right)-{\theta }_3{w}_5\left(w_2+w_3+w_4+2w_5\right)\right)}{\mathrm{\Lambda }}\hfill \\ \hfill & +2r{\sigma }_2\left(v_3-v_5\right)w_3^2\hfill \\ \hfill & ={\mathrm{\Theta }}_1-{\mathrm{\Theta }}_2={\mathrm{\Theta }}_2\left(\mathrm{\Delta }-1\right)\left(\frac{{\mathrm{\Theta }}_1}{{\mathrm{\Theta }}_2}=\mathrm{\Delta }\right),\hfill \\ \hfill \end{array}$$

where

$$\begin{array}{cc}\hfill {\mathrm{\Theta }}_1& =2r{\sigma }_2{v}_3{w}_3^2,\hfill \\ \hfill {\mathrm{\Theta }}_2=& \frac{{\beta }_1\mu v_2}{\mathrm{\Lambda }}\left(\left(2,\left(w_2,+,w_3,+,w_4\right),+,w_5\right),\left({\theta }_1,w_3,+,{\theta }_2,w_4,+,w_2\right),+,{\theta }_3,w_5,\left(w_2,+,w_3,+,w_4,+,2,w_5\right)\right)\hfill \\ \hfill & +2r{\sigma }_2{v}_5{w}_3^2.\hfill \end{array}$$

Note that if $\mathrm{\Delta }>1$, then $\text{a}>0$ and if $\mathrm{\Delta }<1$ then $\text{a}<0$. Lastly,

$$\begin{array}{cc}\hfill \text{b}=& {\displaystyle \sum _{i=2}^5{v}_2{w}_i\frac{{\partial }^2{f}_2}{\partial x_i\partial {\beta }_1^{\ast }}=\mu (\delta h_3{h}_4({\theta }_1+{\theta }_2)(1-\mathrm{\Phi })}\hfill \\ \hfill & +h_2({\gamma }_1{\theta }_3{\sigma }_1+h_3{h}_4(1-\mathrm{\Phi }))+\delta h_3{\theta }_3{\sigma }_2)(\delta ({\theta }_1({\gamma }_1(\mu +{\omega }_2)+h_4\mu )\hfill \\ \hfill & +{\sigma }_2({\gamma }_2{\theta }_2+h_3{\theta }_3))+h_2(h_3{h}_4(1-\mathrm{\Phi })+{\sigma }_1({\gamma }_1{\theta }_3+h_4{\theta }_2)))>0.\hfill \end{array}$$

We thus have the following result

Theorem 3

If$\mathrm{\Delta }>1$, then system (3) has a backward bifurcation at${\mathcal{R}}_0=1$. Otherwise, if$\mathrm{\Delta }<1$the endemic equilibrium is locally asymptotically stable for${\mathcal{R}}_0>1$but close to one.

We show the existence of a backward bifurcation through numerical example by creating bifurcation diagram around ${\mathcal{R}}_0=1$ (Fig. 1). To draw a bifurcation curve (the graph of $I_2^{\ast }$ as a function of ${\mathcal{R}}_0$), we fix the following parameters for illustrative purposes: $\mathrm{\Lambda }=0.25,\mu =0.03,{\beta }_1=0.5,{\beta }_2=0.4,{\beta }_3=0.4,{\beta }_4=0.2,\delta =0.7,{\sigma }_1=0.009,{\sigma }_2=0.04,r=0.5,{\omega }_1=0.09,{\omega }_2=0.06,{\gamma }_1=0.009,{\gamma }_2=0.09$.

Fig. 1.

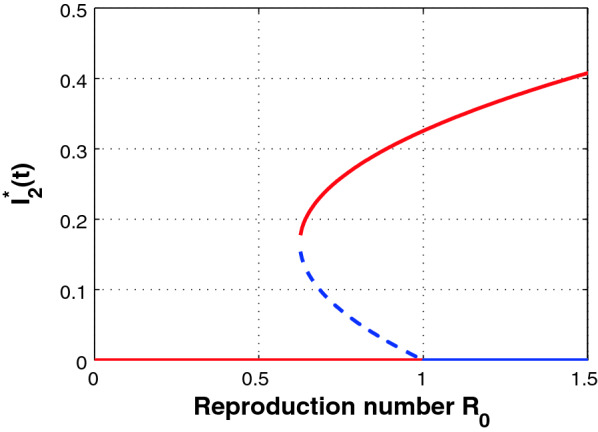
The figure showing a backward bifurcation. The solid lines denote stable states and the dotted lines denote unstable states

Remark

Epidemiologically, when a model exhibits backward bifurcation, this entails that it is not enough to only reduce the basic reproductive number to less than one in order to eliminate the disease.

Results and discussion

Numerical simulations

We carry out numerical simulations to support our theoretical findings.

Estimation of parameters

Parameter values used for numerical simulations are given in Table 1.

Table 1.

Parameter values used in numerical simulations

Parameter	Definition	Range	Value	Source
${\beta }_1$	Contact for individuals in S with those in $I_1$	0-1	0.912	[8]
${\beta }_2$	Contact for individuals in S with those in $I_2$	0-1	0.894	[8]
${\beta }_3$	Contact for individuals in S with those in $I_{A1}$	$0-1$	0.095	[8]
${\beta }_4$	Contact for individuals in S with those in $I_{A2}$	$0-1$	0.091	[8]
${\sigma }_1$	Progression from $I_1$ to $I_{A1}$	$0.01-1$	0.084	[8]
${\sigma }_2$	Progression from $I_2$ to $I_{A2}$	$0-1$	0.1	Assumed
$\delta$	Progression from $I_1$ to $I_2$	$0.01-1$	1.0	[8]
${\gamma }_1$	Progression from $I_{A1}$ to $I_{A2}$	$0.01-1$	0.096	[8]
${\gamma }_2$	Progression from $I_{A2}$ to $I_{A1}$	$0.1-1$	0.112	[8]
r	Effect of late initiation into ART	$0-1$	0.45	Assumed
${\omega }_1$	Disease related death of individuals in $I_2$	$0-1$	0.089	[7]
${\omega }_2$	Disease related death of individuals in $I_{A2}$	$0-1$	0.095	[7]
$\mathrm{\Lambda }$	Recruitment rate into S	$0-1$	0.0239	[12–14]
$\mu$	Natural death rate	$0-1$	0.0172	[14]

Numerical results

Figure 2 illustrates the effect of varying the parameter r on the prevalence of HIV. We note that increasing the parameter r results in an increase in the prevalence of HIV. In particular, increasing r from 0.1 up to 1.0 increases the prevalence rate of HIV with a level of approximately $28\%$. This is a reflection that late diagnosis of HIV contributes to an increase in HIV infections. Thus, more effort should be directed towards encouraging individuals to get tested for HIV and ensuring those who are positive are timely initiated into ART treatment.

Fig. 2.

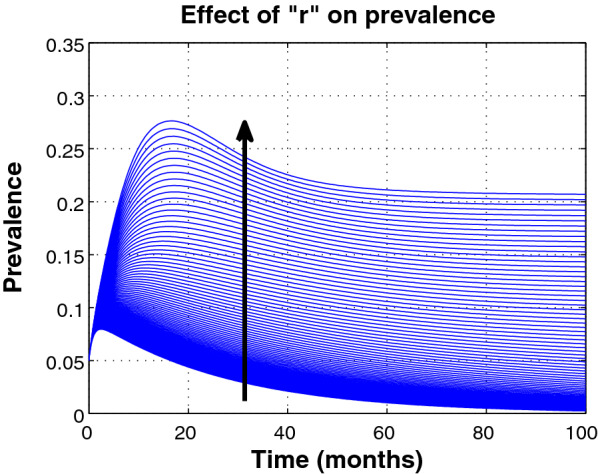
Effect of varying parameter r on the prevalence of HIV, starting from 0.1 up to 1.0 with a step size of 0.01

Conclusions

A mathematical model that describes the dynamics of HIV/AIDS has been formulated using nonlinear ordinary differential equations. The model takes into account the impact of late diagnosis on HIV/AIDS transmission dynamics. Initiation into ART treatment of individuals with a CD4⁺ T cell count in the range 200–350\μ L has been described by the function (1). The model developed in this paper fits well with settings in most underdeveloped countries where stigma of HIV remains prevalent. Inclusion of the treatment function (1) increases the realism of the model developed by [8] and leads to some interesting dynamical aspects such as the occurrence of backward bifurcation.

In this study, it has been shown that the classical ${\mathcal{R}}_0$—threshold is not the key to control the spread of HIV infection within a population. In fact HIV infection may persist in the population even with subthreshold values of ${\mathcal{R}}_0$. Our results suggest that considerable effort should be directed towards encouraging early initiation into ART in order to reduce HIV prevalence. For instance, strategies such as the implementation of HIV self-testing programs would be of great help in the fight against HIV.

Limitations

Like in any model development, the model is not without limitations. The model can be extended to include the contribution of pre-exposure prophylaxis (PrEP) and other control measures not considered in the work.

Abbreviations

AIDS

Acquired immune deficiency syndrome

HIV

Human immunodeficiency virus

ART

Antiretroviral therapy

Authors’ contributions

JM participated in the fomulation, analysis and drafting of the manuscript. All authors read and approved the final manuscript.

Funding

Not applicable.

Availability of data and materials

Estimation of parameters have been stated throughout the body of the paper and included in the reference section. The graphs were produced using the MATLAB software that is available from https://www.mathworks.com/products/matlab.html.

Ethics approval and consent to participate

No ethical approval was required for this project as this is secondary research.

Consent to publish

Not applicable.

Competing interests

The author declares there are no competing interests.