Abstract
Acid-fracturing operations are mainly applied in tight carbonate formations to create a highly conductive path. Estimating the conductivity of a hydraulic fracture is essential for predicting the fractured well productivity. Several models were developed previously to estimate the conductivity of acid-fractured rocks. In this research, machine learning methods were applied to 560 acid fracture experimental datapoints to develop several conductivity correlations that honor the rock types and etching patterns. Developing one universal correlation often results in significant error. To develop conductivity correlations, various data preprocessing methods were applied to remove the outliers and failed experiments. Features that did not contribute to precise predictions were removed through regularization. A machine learning classifier was built to predict the etching pattern based on the input data. We generated a multivariate linear regression model and compared it with other models generated through ridge regression. In addition to that, artificial neural network-based model was proposed to predict the fracture conductivity of several carbonate rocks such as dolomite, chalk, and limestone. The performance of the developed models was assessed using well-known metrics such as precision, accuracy, mean squared error, recall, and correlation coefficients. Cross-validation was also employed to assure accuracy and avoid overfitting. The classifier accuracy was 93%, while the regression model resulted in a relatively high correlation coefficient.
1. Introduction
Acid fracturing is a well productivity enhancement method performed on tight carbonate reservoirs. A hydraulic fracture is extended in the formation when the breakdown pressure is exceeded during the treatment. The formation minimum horizontal stress acts to close the hydraulic fracture once the pumping ceases. Fracture face asperities keep the fracture open against closure stresses which allows the fracture to conduct the reservoir fluids. Formation heterogeneity results in uneven dissolved fracture surfaces which improve the conductivity of the fracture.1,2 Conductivity is described as the capability of a fracture to deliver reservoir fluids to the wellbore; however, it decreases as the formation closure stress increases. A successful acid fracture job should result in sustained long-term conductivity.
Estimating acid fracture conductivity is important for improving an acid fracture design. Acid/rock reaction in a formation is a stochastic phenomenon that depends on many parameters. Thus, prediction of the resulting conductivity can be challenging. Different methods have been applied to predict acid fracture conductivity, which are summarized in Table 1. Empirical correlations based on experimental studies are most suitable as their parameters are easy to attain. Usually, theoretical derivations of an analytical model result in a complicated formula which requires many input parameters. Also, these parameters usually require tuning with experimental outcomes using regression analysis. On the other hand, artificial intelligence (AI) models require sizable, consistent, and accurate datasets in order to be feasible.
Table 1. Various Conductivity Correlations Developed through Different Approaches.
Nierode and Kruk5 proposed that among other parameters, the amount of rock dissolved should be used to estimate acid fracture conductivity. A recent study has also shown that acid-fracture fluid type could alter the pattern of rock removal which has a significant effect on the conductivity, even more so than the volume of the dissolved rock.14 For example, conductivity is higher when the acid fracture treatment creates channels rather than rough surfaces, given that they could withstand closure stress.15−23 The leaking of acid from the fracture into the surrounding rock matrix can also result in more heterogeneous fracture surfaces that enhance conductivity if the rock’s mechanical properties are unharmed.17
Pournik24 classified etching patterns of fractured rock samples after acid fracturing into five categories. The roughness etching pattern occurs when acid dissolves the rock randomly, leaving asperities spread on the fracture surface. The channeling etching pattern is defined by a V-shape where acid creates a defined path from the core inlet to the outlet. Cavity and turbulence dissolution patterns are similar in that pockets of dissolved spots are created by the acid reaction. The uniform etching pattern happens because of rock homogeneity or uniform or well-balanced reactivity with acid. Contact time, in a similar manner, can influence the etching pattern. Also, acid with different concentration magnitudes could affect the etching pattern and the amount of rock dissolved.25,26 Roughness is more likely to be created when even surfaces are being acidized, while acidization of uneven surfaces deepens valleys and smoothens peaks.27 Kamali and Pournik22 employed both theoretical and empirical methods to develop conductivity correlations for the roughness etching pattern, considering each rock type separately.
Few models accounted for the contribution of channels to conductivity, which provide a higher conductivity at a low stress and a long-term conductivity after fracture closure. Large channel dimensions make the fracture more conductive to fluids. Deng et al.4 captured their effect through numerical simulations, enhancing conductivity estimation. They categorized etching patterns into three classes: permeability distribution dominant, mineralogy distribution dominant, and competing effect of permeability and mineralogy distributions. To apply the developed correlations, six parameters are needed which could be hard to obtain or extract from field data. Almomen28 showed that acidizing rough fracture surfaces create a higher conductivity as compared to smooth ones at low closure stresses. Thus, ignoring such important parameters will yield simple models but could be inaccurate and biased.
In this work, machine learning algorithms were applied to estimate acid fracture conductivity based on the data collected from the large size standard API RP-61 conductivity cell (7 in. × 3 in. × 1.7 in.). Artificial neural network (ANN) and multivariate linear regression (MLR) models were utilized to develop empirical models to predict fracture conductivity in three different rock types, namely, limestone, chalk, and dolomite. Previous models were developed based on fewer data points and small size core samples. Also, we investigated the impact of treatment conditions and etching patterns on the generated conductivity, while it was previously ignored. Earlier work in the literature assumes that a larger conductivity can be obtained from a larger etched width. This was proven to be inaccurate as the acid fracture conductivity may be small even though the etching width is large due to rock weakening.
2. Data Gathering and Handling
We relied on the experimental data in this research as the published field data of acid fracture conductivity is rare. Also, in such field operations, there is no standard in terms of injection rate, injection time, and treatment volume based on which the acid fracture conductivity is evaluated. Generally, the field conditions are less controlled than the laboratory ones. Thus, tracking the effect of changing one condition on the resulting conductivity will be a challenge. An extensive literature review was applied to gather published data on the API acid fracture conductivity experiments.12,19,21,28−31 It is worth mentioning that the data collected are consistent as they are obtained from the same laboratory using the same experimental procedure. Table 2 illustrates the physical properties, meanings, and units of different features.
Table 2. Physical Meaning of Features Used in Conductivity Prediction.
| feature | symbol | physical meaning and unit |
|---|---|---|
| rock type | X1 | rocks etched by different acids |
| acid type | X2 | acid systems used to etch rocks |
| rock surface | X3 | initial rock surface before acid etching |
| etching pattern | X4 | manner of rock surface behavior after acid etching |
| temperature | X5 | temperature of etching acid in F |
| injection rate | X6 | rate of pumping acid through API conductivity cell in liters per minute |
| injection time | X7 | time for pumping acid through API conductivity cell in minutes |
| acid concentration | X8 | concentration of etching acid pumped through API conductivity cell as a percentage |
| stress | X9 | applied stress by loading frame in psi |
| conductivity | Y | resultant rock conductivity under stress in mD-ft |
The main goal of the acid fracture experiment was to measure conductivity at different formation closure stresses while mimicking field environments (e.g., rock type, acid type, injection rate, treatment volume). Different conditions resembled the field conditions but were scaled down using dimensionless numbers. Different conditions were tested in the laboratory to understand their effect on conductivity and estimate the optimum conditions at which the maximum conductivity is obtained. This will help later in optimizing the field treatment conditions. Treatment conditions (e.g., temperature, injection time) along with rock types and their initial surface conditions were tabulated. Then, conductivities at each load stress and etching pattern were compiled to complete the dataset, as illustrated in Table 3.32 Therefore, the data gathered were consistent as the data points were generated from the same modified API RP-61 conductivity cell using the same experimental standard procedure.33
Table 3. Sample of Showing the Input Data Used for AI Training.
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | Y |
|---|---|---|---|---|---|---|---|---|---|
| chalk | Gelled acid | rough | channeling | 175 | 1 | 30 | 15 | 3000 | 90 |
| chalk | straight | smooth | turbulence | 175 | 1 | 5 | 15 | 100 | 2778 |
| dolomite | gelled acid | smooth | Rough | 130 | 0.5 | 20 | 15 | 500 | 127 |
| dolomite | gelled acid | smooth | Rough | 130 | 0.5 | 20 | 15 | 1000 | 104 |
| limestone | gelled acid | rough | Rough | 175 | 1 | 30 | 15 | 5000 | 72 |
| limestone | emulsified | smooth | Rough | 200 | 1 | 15 | 15 | 1000 | 1597 |
Failed experiments and outliers were excluded to obtain the most appropriate data for creating the model. Table 4 includes a statistical summary of the different numerical features. Notice that the acid diffusion coefficient, as numerical input, was used for the ANN model, while the categorical input was used for the MLR model.
Table 4. Description of the Dataset Used for AI Modeling.
| statistical parameters | acid diffusion coefficient (cm2/s) | temperature, °F | exposure time, mins | closure stress, psi | fracture conductivity, mD-ft |
|---|---|---|---|---|---|
| (a) Dolomite | |||||
| mean | 9.0 × 10–6 | 146.67 | 259.09 | 3009.09 | 1127.78 |
| standard error | 2.0 × 10–7 | 2.85 | 11.22 | 195.78 | 120.03 |
| median | 1.0 × 10–5 | 130 | 300 | 3000 | 738 |
| mode | 1.0 × 10–5 | 130 | 150 | 1000 | 2341 |
| standard deviation | 2.02 × 10–6 | 28.39 | 111.66 | 1948.00 | 1194.24 |
| sample variance | 4.07 × 10–12 | 8.06 × 102 | 1.25 × 104 | 3.79 × 106 | 1.43 × 106 |
| kurtosis | 2.77 × 10–1 | –1.13 | –1.01 | –0.66 | 0.59 |
| skewness | −1.51 × 10 | 0.23 | 0.55 | 0.49 | 1.18 |
| range | 5.00 × 10−6 | 100.00 | 300.00 | 7500.00 | 4422.00 |
| minimum | 5.0 × 10–6 | 100.00 | 150.00 | 0.00 | 46.00 |
| maximum | 1.0 × 10–5 | 200.00 | 450.00 | 7500.00 | 4468.00 |
| (b) Chalk | |||||
| mean | 1.9 × 10–5 | 140.09 | 171.82 | 1688.18 | 1748.46 |
| standard error | 2.59 × 10–6 | 3.04 | 11.31 | 112.73 | 314.86 |
| median | 1.0 × 10–5 | 130.00 | 150.00 | 1750.00 | 165.50 |
| mode | 1.0 × 10–5 | 175.00 | 150.00 | 1000.00 | 72.00 |
| standard deviation | 2.7 × 10–5 | 31.8755 | 118.6269 | 1182.3419 | 3302.3062 |
| sample variance | 7.36 × 10–10 | 1.02 × 103 | 1.41 × 104 | 1.40 × 106 | 1.09 × 107 |
| kurtosis | 5.41 × 10 | –1.7 | 1.0 | –1.20 | 12.7 |
| skewness | 2.70 × 10 | 0.0 | 1.4 | 0.1 | 3.3 |
| range | 9.0 × 10–5 | 75.0 | 375.0 | 4000.0 | 20440.0 |
| minimum | 1.00 × 10–5 | 100.0 | 75.0 | 0.0 | 4.0 |
| maximum | 1.00 × 10–4 | 175.0 | 450.0 | 4000.0 | 20444.0 |
| (c) Limestone | |||||
| mean | 2.49 × 10–5 | 174.468 | 387.596 | 2993.617 | 1985.868 |
| standard error | 2.40 × 10–6 | 1.595 | 19.340 | 110.640 | 224.458 |
| median | 1.00 × 10–5 | 175 | 300 | 3000 | 482 |
| mode | 1.00 × 10–5 | 200 | 300 | 3000 | 72 |
| standard deviation | 3.68 × 10–5 | 24.456 | 296.477 | 1696.074 | 3440.870 |
| sample variance | 1.35 × 10–9 | 5.98 × 102 | 8.79 × 104 | 2.88 × 106 | 1.18 × 107 |
| kurtosis | 4.53 × 10–1 | –0.754 | 8.847 | –0.921 | 6.382 |
| skewness | 1.55 × 10 | –0.728 | 2.786 | 0.079 | 2.601 |
| range | 9.90 × 10–5 | 75.0 | 1605.0 | 6900.0 | 16823.0 |
| minimum | 1.00 × 10–6 | 125.0 | 75.0 | 100.0 | 15.0 |
| maximum | 1.00 × 10–4 | 200.0 | 1680.0 | 7000.0 | 16838.0 |
There were various types of predictors and features among the collected data, both categorical and numerical. The ranges of numerical values differed from one to another feature. For example, stress ranged from 0 to 7500 psi, while temperature from 100 to 275 F. The stress range was approximately 43 times larger than the temperature range. When further analyses were conducted (e.g., MLR), the attributed stress intrinsically influenced the result significantly because of its larger magnitude. However, this did not essentially mean that it is more important as a feature. The predictors considered were {X1, X2, ..., Xn}, where the superscript j is an index ranging from 1 to the total number of predictors n. Each predictor X contained m datapoints, xij, where the subscript i is an index ranging from 1 to the total number of points m. The objective of the normalization was to alter these features in the dataset to be in one common scale without changing the difference in the value range. Therefore, the normalization of the numerical features, prior to modeling, was accomplished by subtracting their means and scaling them to unit variance, as shown in the following equation:
 |
1 |
where zij is the z-score or normalized value of each data point, μj is the mean value of each predictor X, and σj is the standard deviation of the predictor.
3. Results and Discussion
3.1. Classification of Etching Patterns
Rock surface, rock type, and acid type were used as predictors for 80% of the data (78 experiments) in order to train the model with fivefold cross-validation. For testing, the last 20% of the data (19 experiments) was used. The classifier had a test error of 0.0833 and an overall accuracy of 94.7%. Figure 1 summarizes all precision and recall values. The overall accuracy of the classifier is shown in the corner square to the right of the figure. The rows represent the predicted class, while columns the actual class. The diagonal squares indicate the observations that were correctly classified. The off-diagonal squares are incorrectly classified observations. The number of observations and their percentages are shown in each square. The rightmost column includes the percentages of all observations predicted belonging to each class that was correctly or incorrectly classified. This metric is called precision. The bottom row includes the percentages of all observations belonging to each class that was correctly or incorrectly classified. This metric is called the true positive rate (i.e., recall).
Figure 1.
Confusion matrix of the etching pattern classifier (i.e., channeling, roughness, turbulence, and uniform).
Precision and recall become more important when the data are skewed or unbalanced. For instance, dolomite generated a roughness etching pattern in 90.6% of the experiments. There was an unbalance in the etching pattern generated. If an etching pattern classifier for dolomite only was set to always output roughness, the overall accuracy would be higher than 90%. Any other etching pattern would be misclassified. Thus, assessment of a classifier based on overall accuracy alone when there is a severe class imbalance is inaccurate.
3.2. Regression for Conductivity Prediction (MLR)
3.2.1. Dolomite
Data often contain predictors that do not have a major or any impact on the response. To obtain a non-redundant or simpler model, these predictors should be excluded from the model. Having a limited number of predictors, yet holding nearly complete variance of the data, is recommended.34 One approach to finding the most relevant predictors for response is to repeatedly train the model while adding predictors and observing loss. At a specific point, adding more predictors will not improve the accuracy but increase only the calculation time and memory consumption.
The rock surface, acid type, and etching pattern were converted into dummy variables to make the entire dataset homogeneous as numeric values. For example, a categorical predictor that contained several categories equal to K was converted into K – 1 predictors of zeros and ones.
Figure 2 shows the minimum number of predictors that are enough to get the least loss in the multivariate linear model for predicting the dolomite conductivity. Adding the etching pattern and temperature considerably decreased the loss and then remained almost constant after adding the rock surface and acid type.
Figure 2.
Minimum number of predictors to obtain the least loss for dolomite.
The features that resulted in the least loss in Figure 2 were utilized to obtain the first dolomite model. The predictors starting with “Stress” and ending with “RockSurface = Roughness” were chosen. MATLAB software function “x2fx.” was used to build the design matrix. One of the following four models should be selected at the beginning: “linear,” “interactions,” “quadratic,” or “pure quadratic.” The 10-predictor matrix was transformed into a design matrix using the “quadratic” model. Figure 3 shows the learning curve showing a high variance that cannot be resolved by regularization or simplification of the model. This usually means that more input data should be utilized. The actual and fitted value correlation coefficient was 94.9%, and the normalized MSE was around 0.03. This model contained many parameters (52) which is not practical for implementation. To obtain a simpler model with reasonable performance, other models were trained with different combinations of predictors. Using the first four predictors, starting with “Stress” and ending with “InjectionRate”, a simpler correlation was obtained whose bias and weights are presented in Table 5.
Figure 3.
Learning curve for dolomite showing the training and testing set error evolution.
Table 5. Dolomite Detailed Conductivity Model Showing Bias and Weights.
| parameter | value |
|---|---|
| bias | 0.7969 |
| X6 | 0.1103 |
| X7 | 0.5616 |
| X8 | –0.0107 |
| X9 | –0.2002 |
| X6 × X7 | 0.3348 |
| X6 × X8 | –0.0325 |
| X6 × X9 | –0.0738 |
| X7 × X8 | –0.1305 |
| X7 × X9 | –0.0548 |
| X8 × X9 | 0.0145 |
| (X6)2 | –0.1686 |
| (X7)2 | –0.6016 |
| (X8)2 | –0.0402 |
| (X9)2 | 0.0309 |
Figure 4 shows a plot of predicted versus actual dolomite conductivity values. The fitted values at high stresses were less than the experimental values, as expected.
Figure 4.
Actual vs predicted values of dolomite conductivity estimation.
The fitted and actual value correlation coefficient was 93.1%, and the normalized MSE was 0.05. Figure 5 shows the error distribution indicating a slightly asymmetric behavior.
Figure 5.
Error distribution of dolomite conductivity predictions.
3.2.2. Chalk
The minimum number of predictors sufficient to obtain the lowest loss in the multivariate linear model for predicting the chalk conductivity is shown in Figure 6. Hence, “Stress,” “InjectionTime,” “Temperature,” and “EtchingPattern = Turbulence” were chosen as predictors. The chalk conductivity model was obtained by training a polynomial regression model of the selected predictors, their quadratic values, and their interactions with one another.
Figure 6.
Lowest number of predictors to obtain the least loss for chalk.
Figure 7 shows the learning curve with a good model fit, as the two curves plateau at a low error value.
Figure 7.
Learning curve for chalk showing the training and testing set error evolution.
The regularization parameter selected was 0.001 as it resulted in the lowest cross-validation error.
The values predicted for chalk conductivity were then plotted against the actual ones (see Figure 8).
Figure 8.
Actual vs predicted values of chalk conductivity estimation.
The fitted and actual values of correlation coefficient were 90.6%. Chalk conductivity error distribution indicates asymmetric behavior, as seen in Figure 9.
Figure 9.
Error distribution of chalk conductivity predictions.
It is possible to train simpler models with fewer predictors for dolomite and chalk as they often develop a roughness etching pattern (see Table 6). Table 7 shows a simpler model for chalk conductivity with the same performance as the previous model discussed above.
Table 6. Tendency of a Rock Type To Develop a Certain Etching Pattern.
| channeling | rough | turbulence | uniform | total | |
|---|---|---|---|---|---|
| dolomite | 5 | 125 | 8 | 0 | 138 |
| 3.6% | 90.6% | 5.8% | 0% | 100% | |
| chalk | 6 | 100 | 11 | 0 | 117 |
| 5.1% | 85.5% | 9.4% | 0% | 100% | |
| limestone | 85 | 142 | 33 | 30 | 290 |
| 29.3% | 49% | 11.4% | 10.3% | 100% |
Table 7. Detailed Conductivity Model for Chalk Showing Bias and Weights.
| parameter | value |
|---|---|
| bias | 0.3769 |
| X5 | –0.1179 |
| X7 | 0.2851 |
| X9 | –0.3391 |
| X5 × X7 | –0.0672 |
| X5 × X9 | –0.0867 |
| X7 × X9 | 0.0232 |
| (X5)2 | –0.5476 |
| (X7)2 | –0.0567 |
| (X9)2 | 0.1459 |
3.2.3. Limestone
Predicting limestone conductivity can be challenging as acid/rock reaction generates all kinds of etching patterns. Thus, to develop a reasonable conductivity model, high conductivity values were evaluated first. A classifier was created based on an ensemble classification using the treatment and original surface conditions. The accuracy of the classifier was around 93%, as shown in Figure 10. The outcome of this classifier was then inserted into the polynomial regression model as an additional predictor.
Figure 10.
Confusion matrix of normal and high limestone conductivities.
The high conductivity values were labeled “Conductivity = High” and the normal values were labeled “Conductivity = Normal”. Four data points from the test dataset were misclassified by the confusion matrix. Error analysis was carried out to examine why this misclassification occurred. The channels could be thought of as open slots, the conductivity of which depended on the channel width. Wider channels usually have a higher conductivity as they are more open to flow. The channel’s V-shaped angle impacts its sustainability under stress. For example, if the V-shaped angle was acute, it would collapse at higher stresses than would an obtusely angled channel.
The minimum number of predictors sufficient to obtain the lowest loss in the multivariate linear model predicting the conductivity of limestone is shown in Figure 11. Hence, the predictor “Stress” was selected for the beginning and “AcidType = Straight” for the end. The loss curve began to increase as the number of predictors grew which could be an indicator of data overfitting.
Figure 11.
Lowest number of predictors to obtain the least loss for limestone.
Multiple limestone conductivity models were generated by training a polynomial regression model with different predictor combinations where the simplest is tabulated in Table 8. Figure 12 shows the learning curve showing a slightly high variance as the training curve plateaus, whereas the test error had a higher value. The regularization parameter that minimizes the cross-validation error was around 0.003.
Table 8. Detailed Conductivity Model for Limestone Showing Bias and Weights.
| parameter | value |
|---|---|
| bias | 0.2374 |
| conductivity = normal | –0.5451 |
| X5 | 0.4974 |
| X9 | –0.8598 |
| conductivity = normal × X5 | –0.4680 |
| conductivity = normal × X9 | 0.7245 |
| X5 × X9 | –0.1317 |
| AcidType = viscoelastic | –0.0700 |
| AcidType = straight | 0.1103 |
| (X9)2 | –0.0008 |
Figure 12.
Learning curve for limestone showing the training and testing set error evolution.
Figure 13 shows the actual versus predicted values of limestone conductivity. It is evident from the plot that the extreme values could not be predicted by the model.
Figure 13.
Actual vs predicted values for limestone conductivity estimation.
The fitted and actual values of correlation coefficient were around 92%. The error distribution of limestone conductivity was asymmetrical (see Figure 14) as high conductivity values could not be predicted. The classifier and the conductivity model were not trained to handle extremely high conductivity values as they were 2 to 3 orders of magnitude higher than the normal values. The overall error was around 0.686 due to the occurrence of these points.
Figure 14.
Error distribution of limestone conductivity predictions.
3.3. ANN Model Outcomes
Several numbers of experiments were performed to measure the fracture conductivity of dolomite, chalk, and limestone rocks. From these experiments, several data points were collected. Out of the total datasets, 70% of them were used to train the model and remaining 30% were used to test the model.
3.3.1. Dolomite
On a set of 70% of data for training, the ANN model predicted the natural log of fracture conductivity of dolomite rock with an R2 of 0.877 and a root mean square error (RMSE) of 0.057, while testing of the ANN model predicted the natural log of fracture conductivity of dolomite rock with an R2 of 0.897 and an RMSE of 0.103. The performance plots for the training and testing are shown in Figures 15 and 16.
Figure 15.
Measured and predicted values of fracture conductivity for dolomite rock during training and testing with RMSE.
Figure 16.
Training and testing cross-plot between experimentally measured and predicted fracture conductivities for dolomite.
The proposed equation of fracture conductivity of the dolomite rock is given by eq 2. The output of eq 2 will be in mD-ft.
 |
2 |
where
 |
3 |
where 
, σo(x) = x, w1, w2, b1, and b2 are the weights and biases of the fracture conductivity
of dolomite rock, given in Table 9. Dn is the normalized
value of the diffusion coefficient, Tn is the normalized value of the temperature, Etn is the
normalized value of the exposure time, and σn is
the normalized value of the closure stress. The equations to find Dn, Tn, Etn, and σn for dolomite rock are given in eqs 4–7.
 |
4 |
where D is the diffusion coefficient in cm2/s.
 |
5 |
where T is the temperature in F
 |
6 |
where Et is the exposure time in min and
 |
7 |
where σ is the closure stress in psi.
Table 9. Weights and Biases of the Proposed Conductivity Model for Dolomite.
| hidden layer neurons (Nh) | weights between input and hidden layers (w1) | weights between hidden and output layers (w2) | hidden layer bias (b1) | output layer bias (b2) | |||
|---|---|---|---|---|---|---|---|
| 1 | –0.541 | –2.654 | 0.455 | –1.765 | 2.032 | 3.084 | –0.584 |
| 2 | 1.823 | 0.728 | –0.308 | 2.064 | 1.200 | –2.155 | |
| 3 | –0.744 | 0.071 | –3.273 | 1.274 | –0.049 | 1.224 | |
| 4 | 0.396 | 3.026 | –0.462 | –2.078 | 0.460 | –0.711 | |
| 5 | –0.227 | –2.129 | 2.148 | 0.467 | –1.336 | 0.444 | |
| 6 | 0.565 | 0.450 | –2.782 | 0.774 | –0.914 | –0.828 | |
| 7 | 0.752 | 2.023 | –1.729 | 0.545 | –1.310 | 0.341 | |
| 8 | –1.731 | 0.041 | 0.084 | 1.785 | 0.540 | –1.618 | |
| 9 | –2.468 | 1.091 | 2.787 | 0.817 | –0.898 | –2.944 | |
| 10 | 0.633 | –0.274 | –2.087 | –1.739 | 0.529 | –2.856 | |
3.3.2. Chalk
On a set of 70% of data for training, the ANN model predicted the natural log of fracture conductivity of chalk with an R2 of 0.914 and an RMSE of 0.077, while testing of the ANN model predicted the natural log of fracture conductivity of chalk with an R2 of 0.952 and an RMSE of 0.107. The performance plots for the training and testing are shown in Figures 17 and 18.
Figure 17.
Measured and predicted values of fracture conductivity for chalk during training and testing with RMSE.
Figure 18.
Training and testing cross-plot between experimentally measured and predicted fracture conductivities for chalk.
The proposed equation of fracture conductivity of the chalk is given by eq 8. The output of eq 8 will be in mD-ft.
 |
8 |
where
 |
9 |
where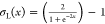 
, σo(x) = x, w1, w2, b1, and b2 are the weights and biases of the fracture conductivity
of dolomite rock, given in Table 10. Dn is the normalized
value of the diffusion coefficient, Tn is the normalized value of the temperature, Etn is the
normalized value of the exposure time, and σn is
the normalized value of the closure stress. The equations to find Dn, Tn, Etn, and σn for chalk are given in eqs 10–13.
 |
10 |
where D is the diffusion coefficient in cm2/s.
 |
11 |
where T is the temperature in oT
 |
12 |
where Et is the exposure time in min
 |
13 |
and where σ is the closure stress in psi.
Table 10. Weights and Biases of the Proposed Conductivity Model for Chalk.
| hidden layer neurons (Nh) | weights between input and hidden layers (w1) | weights between hidden and output layers (w2) | hidden layer bias (b1) | output layer bias (b2) | |||
|---|---|---|---|---|---|---|---|
| 1 | 0.057 | 2.091 | –0.632 | –2.305 | –0.308 | 1.775 | –0.831 |
| 2 | 1.913 | 1.082 | 2.088 | 0.543 | 0.103 | –0.914 | |
| 3 | –2.431 | 3.276 | –0.018 | –1.401 | 0.566 | –0.710 | |
| 4 | 1.059 | 1.453 | –0.119 | –2.460 | –0.193 | –0.236 | |
| 5 | 1.463 | –0.473 | 2.206 | 1.809 | –0.468 | –0.584 | |
| 6 | 0.091 | 1.550 | –1.001 | –0.313 | 0.375 | 1.378 | |
| 7 | –2.274 | 1.140 | –0.279 | –1.633 | –0.357 | –0.415 | |
| 8 | 0.866 | 0.223 | –1.150 | –3.090 | 0.329 | 1.476 | |
| 9 | –2.393 | 0.164 | –2.246 | 3.159 | –0.204 | –2.581 | |
| 10 | –0.223 | –1.150 | 2.175 | –2.182 | 0.336 | 1.987 | |
3.3.3. Limestone
On a set of 70% of data for training, the ANN model predicted the natural log of fracture conductivity of limestone with an R2 of 0.85 and an RMSE of 0.049, while testing of the ANN model predicted the natural log of fracture conductivity of chalk with an R2 of 0.845 and an RMSE of 0.091. The performance plots for the training and testing are shown in Figures 19 and 20.
Figure 19.
Measured and predicted values of fracture conductivity for limestone rock during training and testing with RMSE.
Figure 20.
Training and testing cross-plot between experimentally measured and predicted fracture conductivities for limestone.
The proposed equation of fracture conductivity of the limestone rock is given by eq 14. The output of eq 14 will be in mD-ft
 |
14 |
where
 |
15 |
where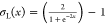 
, σo(x) = x, w1, w2, b1, and b2 are the weights and biases of the fracture conductivity
of dolomite rock, given in Table 11. Dn is the normalized
value of the diffusion coefficient, Tn is the normalized value of the temperature, Etn is the
normalized value of the exposure time, and σn is
the normalized value of the closure stress. The equations to find Dn, Tn, Etn, and σn for chalk are given in eqs 16–19.
 |
16 |
where D is the diffusion coefficient in cm2/s.
 |
17 |
where T is the temperature in F
 |
18 |
where Et is the exposure time in min
 |
19 |
and where σ is the closure stress in psi.
Table 11. Weights and Biases of the Proposed Conductivity Model for Limestone.
| hidden layer neurons (Nh) | weights between input and hidden layers (w1) | weights between hidden and output layers (w2) | hidden layer bias (b1) | output layer bias (b2) | |||
|---|---|---|---|---|---|---|---|
| 1 | 5.001 | 1.241 | –9.074 | –0.422 | –0.851 | –7.506 | 5.203 |
| 2 | 0.521 | –5.155 | 1.886 | –2.537 | –2.443 | 2.002 | |
| 3 | –1.235 | 0.932 | –3.035 | 1.092 | –3.206 | 1.261 | |
| 4 | –1.360 | 0.222 | 1.658 | 1.034 | –1.760 | –0.170 | |
| 5 | –0.687 | 5.472 | –1.242 | 2.609 | –2.516 | –1.738 | |
| 6 | 0.972 | 0.067 | 0.746 | 0.894 | –1.817 | 0.853 | |
| 7 | 1.012 | 0.938 | –0.481 | 0.593 | 2.745 | –0.512 | |
| 8 | 2.002 | –0.357 | –3.777 | 0.118 | –1.583 | 0.365 | |
| 9 | –5.494 | –2.375 | 0.527 | 0.870 | 1.636 | –3.967 | |
| 10 | –0.815 | –4.526 | –2.476 | –2.126 | 0.799 | –2.403 | |
4. Methods
Figure 21 shows the two goals for this research where the first was to classify the etching patterns based on the rock type and treatment conditions. A multiclass algorithm was required to label the different classes, depending on different conditions. The second objective was predicting the conductivity of the different rock types, using their most important features. MLR was a simple and robust approach to obtaining a predictive model. Another approach was also utilizing the ANN model to train the data and predict the conductivity.
Figure 21.
Flow diagram showing the objectives of the proposed work.
The workflow to develop new regression models for the prediction of the fracture conductivity of the different rocks is given in Figure 22. After gathering extensive laboratory experimental data, the dataset was collected, analyzed, and cleaned from misleading values such as negative or extreme values. Then, various machine learning algorithms were applied for both classification and regression models.
Figure 22.
Workflow diagram of the present study.
4.1. Classification of Etching Patterns
Ensemble templates can be used to train multiclass error-correcting output code models. The template used in this study has three arguments: method, number of learners, and learner. The specified approach was “GentleBoost,” the number of learners was 100, and the learner was a decision tree. As a classifier, the decision tree splits data based on a certain condition (node) into two groups (branches) in binary classification problems.35 For each variable, there is a splitting value (threshold) that yields the best split with a minimum error. After finding the first variable splitting value, the rest of the splitting values corresponding to other variables should be identified in a sequential process. The splitting continues for each branch until reaching a single data point (leaf). Multiclassification is similar to the binary classification, but with a minor modification. One class is regarded as positive and the rest are negative. The decision trees are weak learners and unstable, that is, the whole tree structure and the results may change a lot by changing the initial training data set. Ensemble learning methods such as boosting can mitigate this effect.
Ensemble learning is an aggregation of multiple options that decreases the possibility of choosing a poor model. It starts with giving more weight (boost) to the misclassification from the first tree. The next tree is constructed by the new boosted weights, and the process is repeated for the predefined number of learners.36
4.2. MLR
The importance of regression
as used in the present study is to reduce the cost function J(θ⃗)through gradient descent. The cost function
measures how wrong the model is when estimating the responses from
predictors. A gradient descent minimizes the cost function by finding
the weights, θj, that make 
equal to zero. The hypothesis hθ differentiates between linear and nonlinear regressions.
Directly using the feature values means a linear hypothesis, whereas
introducing a logarithm or power to the feature values makes the hypothesis
nonlinear. The hypothesis function is sensitive to slight changes
in the coefficients. The coefficients’ values change by a significant
amount as the training data change. Thus, regularized linear regression
was appropriate for this problem. Regularization is used to drop features
that do not contribute to a good prediction. The regularization term
has different forms, and the regression is named based on whether
it is ridge, lasso, or elastic net. Fitting a linear regression model
to data can result in coefficients with large variances. Regularization
reduces the variance of coefficients, yielding models with smaller
prediction errors. Here, ridge regression was used, and the cost function
is defined as in eq 20
 |
20 |
where J(θ⃗) is the cost function, m is the number of data points, y(i) is the actual response at the datapoint i, λ is the regularization parameter, n is the number of predictors, θj is the weight multiplied by the feature j, and hθ(x(i)) is the hypothesis. The hypothesis consisted of a combination of Xs multiplied by θs, depending on the design matrix.
4.3. ANN Model
An ANN technique was used to predict fracture conductivities of the three types of carbonate rocks. The ANN models were trained with 1 hidden layer and 10 neurons. Each model was developed with four input parameters, namely, diffusion coefficient (D), temperature (T), exposure time (Et), and closure stress (σ). Exposure time is the product of acid concentration in wt % and injection time in minutes. Exposure time (Et) is given by eq 21.
 |
21 |
Tangential sigmoidal “Tansig” was used as an activation function between the input layer and the hidden layer, and pure linear was used as an activation function between the hidden and output layers for each model. The rate of learning was constant at 0.15. Levenberg–Marquardt (LM) was used as an ANN learning algorithm. The general topography of the proposed ANN models is given in Table 12.
Table 12. Topography of Proposed ANN Models.
| parameters | values |
|---|---|
| number of input parameters | 4 |
| hidden layer | 1 |
| number of neurons in a hidden layer | 10 |
| learning algorithm | LM |
| rate of learning, α | 0.15 |
| transfer function of a hidden layer | tangential sigmoidal |
| transfer function of an outer layer | linear |
The models were evaluated based on the RMSE and maximum coefficient of determination (R2). The definitions of RMSE and R2 are given in eqs 22 and 23, respectively.
 |
22 |
 |
23 |
where Ymeasured is the measured value of tor and Ypredicted is the estimated value from the model. k is the total number of data points.
To avoid the model to get stuck on a local minimum, a total of 10,000 realizations were made to arrive at the most optimum ANN model. ANN is a stochastic algorithm which generates different results in each run. In order to fix this issue, the seeds were generated randomly. All the results were unique for each seed. To get the most accurate and generalized robust model, a multiobjective function was designed. In this study, a total of 10,000 realizations were made and, in every realization, the seed numbers were changed and the multiobjective function was evaluated. The seed number corresponding to the maximum value of the objective function was taken as the best model. The definition of the designed multiobjective function is expressed by eq 24
 |
24 |
where Rtraining2 is the R2 obtained during training on 70% of the dataset, Rtesting2 is the R2 obtained during testing on 30% of the dataset, RMSEtraining – 1 is the inverse of RMSE obtained during training on 70% of the dataset, and RMSEtesting – 1 is the inverse of RMSE obtained during testing on 30% of the dataset. The inverse of RMSE was taken to move the objective function in the same direction, as our objective was to get the maximum R2 and minimum RMSE.
5. Conclusions
Different acid fracture stimulation conditions result in different etching patterns. Considering field operations, these parameters can be adjusted to get favorable etching patterns. Conventional machine learning algorithms can be a robust and quick way to get an accurate estimation of conductivity. Also, predicting the etching pattern development on the rock surface with different stimulation conditions can improve the design. The etching pattern that results from acid fracturing has a more significant impact on limestone acid fracture conductivity than on that of chalk and dolomite. Both dolomite and chalk developed a roughness etching pattern in more than 85 and 90% of the acid etching experiments, respectively. Limestone developed a roughness etching pattern in less than 50% and a channeling etching pattern in 30% of the acid etching experiments. Limestone’s extremely high conductivity channels could not be fit by the model and caused increased errors. Most errors in acid fracture conductivity estimation happen at low stresses when the fracture behaves like an open slot, or at high stresses when the rock fails unexpectedly under closure stress.
The ANN models proposed in this study are used to predict the fracture conductivity of dolomite, chalk, and limestone rock. The developed equations using ANN do not require any AI software for execution. The models were tested within a range of values on which the models were trained. The range of tested values are quite reasonable in the oil and gas field. All AI models are data driven; they can be used within the range of input parameters on which they are trained. Using them beyond their range will result in unreliable results. Users of the proposed correlations are recommended to apply these models within the range of dataset given in Table 4. The developed correlations are not recommended to use beyond the range of input parameters on which they are developed.
The authors declare no competing financial interest.
References
- Williams B. B.; Gidley J. L.; Schechter R. S.. Acidizing Fundamentals; Henry L., Ed.; Doherty Memorial Fund of AIME, Society of Petroleum Engineers of AIME: New York, 1979. [Google Scholar]
- Asadollahpour E.; Baghbanan A.; Hashemolhosseini H.; Mohtarami E. The Etching and Hydraulic Conductivity of Acidized Rough Fractures. J. Pet. Sci. Eng. 2018, 166, 704–717. 10.1016/J.Petrol.2018.03.074. [DOI] [Google Scholar]
- Gangi A. F. Variation of whole and fractured porous rock permeability with confining pressure. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1978, 15, 249–257. 10.1016/0148-9062(78)90957-9. [DOI] [Google Scholar]
- Deng J.; Mou J.; Hill A. D.; Zhu D. A New Correlation of Acid-Fracture Conductivity Subject to Closure Stress. SPE Prod. Oper. 2012, 27, 158–169. 10.2118/140402-PA. [DOI] [Google Scholar]
- Nierode D. E.; Kruk K. F.. An evaluation of acid fluid loss additives retarded acids, and acidized fracture conductivity. Fall Meeting of the Society of Petroleum Engineers of AIME; Society of Petroleum Engineers, 1973. [Google Scholar]
- Akbari M.; Ameri M. J.; Kharazmi S.; Motamedi Y.; Pournik M. New correlations to predict fracture conductivity based on the rock strength. J. Pet. Sci. Eng. 2017, 152, 416–426. 10.1016/j.petrol.2017.03.003. [DOI] [Google Scholar]
- Walsh J. B. Effect of pore pressure and confining pressure on fracture permeability. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1981, 18, 429–435. 10.1016/0148-9062(81)90006-1. [DOI] [Google Scholar]
- Kamali A.; Pournik M.. Rough Surface Closure–A Closer Look at Fracture Closure and Conductivity Decline. ISRM Regional Symposium-EUROCK 2015; International Society for Rock Mechanics and Rock Engineering, January, 2015.confproc [Google Scholar]
- Nasr-El-Din H. A.; Al-Driweesh S. M.; Chesson J. B.; Metcalf A. S.. Fracture acidizing: what role does formation softening play in production response? SPE Annual Technical Conference and Exhibition; Society of Petroleum Engineers, January, 2006.confproc [Google Scholar]
- Eliebid M.; Hassan A. M.; Mahmoud M.; Abdulraheem A.; Elkatatny S.. Intelligent Prediction of Acid-Fracturing Performance in Carbonates Reservoirs. SPE Kingdom of Saudi Arabia Annual Technical Symposium and Exhibition; Society of Petroleum Engineers, August, 2018.confproc [Google Scholar]
- Gong M.Mechanical and hydraulic behavior of acid fractures: experimental studies and mathematical modeling. Doctoral Dissertation, University of Texas at Austin, 1997. [Google Scholar]
- Pournik M.; Zhu D.; Hill A. D.. Acid-fracture conductivity correlation development based on acid-etched fracture characterization. 8th European Formation Damage Conference; Society of Petroleum Engineers, January, 2009.confproc [Google Scholar]
- Motamedi-Ghahfarokhi Y.; Shahrabi M. J. A.; Akbari M.; Pournik M. New correlations to predict fracture conductivity based on the formation lithology. Energy Sources, Part A 2018, 40, 1663–1673. 10.1080/15567036.2018.1486896. [DOI] [Google Scholar]
- Pournik M.; Gomaa A. M.; Nasr-El-Din H. A.. Influence of acid-fracture fluid properties on acid-etched surfaces and resulting fracture conductivity. SPE International Symposium and Exhibition on Formation Damage Control; Society of Petroleum Engineers, January, 2010.confproc [Google Scholar]
- Van Domelen M. S.; Gdanski R. D.; Finley D. B.. The application of core and well testing to fracture acidizing treatment design: a case study. European Production Operations Conference and Exhibition; Society of Petroleum Engineers, January, 1994.confproc [Google Scholar]
- Ruffet C.; Fery J. J.; Onaisi A. Acid Fracturing Treatment: a Surface Topography Analysis of Acid Etched Fractures to Determine Residual Conductivity. SPE J. 1998, 3, 155–162. 10.2118/38175-pa. [DOI] [Google Scholar]
- Beg M. S.; Kunak A. O.; Gong M.; Zhu D.; Hill A. D. A Systematic Experimental Study of Acid Fracture Conductivity. SPE Prod. Facil. 1998, 13, 267–271. 10.2118/52402-pa. [DOI] [Google Scholar]
- Nieto C. M.; Pournik M.; Hill A. D. The texture of acidized fracture surfaces: implications for acid fracture conductivity. SPE Prod. Oper. 2008, 23, 343–352. 10.2118/102167-pa. [DOI] [Google Scholar]
- Melendez M. G.; Pournik M.; Zhu D.; Hill A. D.. The effects of acid contact time and the resulting weakening of the rock surfaces on acid fracture conductivity. European Formation Damage Conference; Society of Petroleum Engineers, January, 2007.confproc [Google Scholar]
- Antelo L. F.; Zhu D.; Hill A. D.. Surface characterization and its effect on fracture conductivity in acid fracturing. SPE Hydraulic Fracturing Technology Conference; Society of Petroleum Engineers, January, 2009.confproc [Google Scholar]
- Cash R. J.Acid fracturing carbonate-rich shale: a feasibility investigation of eagle ford formation. Doctoral Dissertation, Society of Petroleum Engineers, 2016. [Google Scholar]
- Kamali A.; Pournik M. Fracture closure and conductivity decline modeling – Application in unpropped and acid etched fractures. J. Unconv. Oil Gas Res. 2016, 14, 44–55. 10.1016/j.juogr.2016.02.001. [DOI] [Google Scholar]
- Lu C.; Bai X.; Luo Y.; Guo J. New study of etching patterns of acid-fracture surfaces and relevant conductivity. J. Pet. Sci. Eng. 2017, 159, 135–147. 10.1016/j.petrol.2017.09.025. [DOI] [Google Scholar]
- Pournik M.Laboratory-Scale Fracture Conductivity Created by Acid Etching; Texas A&M University, 2008. [Google Scholar]
- Pournik M.; Li L.; Smith B. T.; Nasr-El-Din H. A. Effect of acid spending on etching and acid-fracture conductivity. SPE Prod. Oper. 2013, 28, 46–54. 10.2118/136217-pa. [DOI] [Google Scholar]
- Aljawad M. S.; Aljulaih H.; Mahmoud M.; Desouky M. Integration of field, laboratory, and modeling aspects of acid fracturing: A comprehensive review. J. Pet. Sci. Eng. 2019, 181, 106158. 10.1016/j.petrol.2019.06.022. [DOI] [Google Scholar]
- Al-Momin A.; Zhu D.; Hill A. D.. The effects of initial condition of fracture surfaces, acid spending and acid type on conductivity of acid fracture. Offshore Technology Conference-Asia; Offshore Technology Conference, March, 2014.confproc [Google Scholar]
- Almomen A. M.The Effects of Initial Condition of Fracture Surfaces, Acid Spending, and Type on Conductivity of Acid Fracture. Doctoral Dissertation, Offshore Technology Conference, 2013. [Google Scholar]
- Hill A. D.; Pournik M.; Zou C.; Nieto C. M.; Melendez M. G.; Zhu D.; Weng X.. Small-scale fracture conductivity created by modern acid fracture fluids. SPE Hydraulic Fracturing Technology Conference; Society of Petroleum Engineers, January, 2007.confproc [Google Scholar]
- Penaloza A. N.Experimental Study of Acid Fracture Conductivity of Austin Chalk Formation. Doctoral Dissertation, Texas A&M University, 2013. [Google Scholar]
- Jin X.; Zhu D.; Hill A. D.; McDuff D.. Effects of Heterogeneity in Mineralogy Distribution on Acid Fracturing Efficiency; Society of Petroleum Engineers, January 29, 2019. [Google Scholar]
- Desouky M.Enhancement and Prediction of Long-Term Acid Fracture Conductivity. Master of Science Thesis, King Fahd University of Petroleum and Minerals, 2019. [Google Scholar]
- Zou C.Development and Testing of an Advanced Acid Fracture Conductivity Apparatus 2006 59 f. Master of Science Thesis, Texas A&M University, 2006. [Google Scholar]
- Kazakov N.; Miskimins J. L.. Application of multivariate statistical analysis to slickwater fracturing parameters in unconventional reservoir systems. SPE Hydraulic Fracturing Technology Conference; Society of Petroleum Engineers, January, 2011.
- Breiman L.; Friedman J.; Stone C. J.; Olshen R. A.. Classification and Regression Trees; CRC press, 1984. [Google Scholar]
- Freund Y.; Schapire R.; Abe N. A short introduction to boosting. J. Jpn. Soc. Artif. Intell. 1999, 14, 1612. [Google Scholar]