Transport Phenomena: Challenges and Opportunities for Molecular Catalysis in Metal–Organic Frameworks

Abstract

Metal–organic frameworks (MOFs) are appealing heterogeneous support matrices that can stabilize molecular catalysts for the electrochemical conversion of small molecules. However, moving from a homogeneous environment to a porous film necessitates the transport of both charge and substrate to the catalytic sites in an efficient manner. This presents a significant challenge in the application of such materials at scale, since these two transport phenomena (charge and mass transport) would need to operate faster than the intrinsic catalytic rate in order for the system to function efficiently. Thus, understanding the fundamental kinetics of MOF-based molecular catalysis of electrochemical reactions is of crucial importance. In this Perspective, we quantitatively dissect the interplay between the two transport phenomena and the catalytic reaction rate by applying models from closely related fields to MOF-based catalysis. The identification of the limiting process provides opportunities for optimization that are uniquely suited to MOFs due to their tunable molecular structure. This will help guide the rational design of efficient and high-performing catalytic MOF films with incorporated molecular catalyst for electrochemical energy conversion.

Introduction

Metal–organic frameworks (MOFs) are emerging as widely popular support structures to incorporate molecular catalysts for the electrochemical activation and conversion of small molecules.¹⁻³ Composed of discrete molecular building blocks (organic linkers and metal nodes),^4,5 MOFs have a wide range of synthetic tunability.^6,7 Varying the microscopic molecular structure produces materials with different pore sizes and chemical environments, perhaps allowing for augmentation of the active site of molecular catalysts.⁸ In addition, the permanent porosity and high internal surface area of many MOFs could result in very high active-site densities,⁹ which is necessary for the fast transformation of substrate into product per unit volume.¹⁰

However, when moving away from a homogeneous environment to heterogeneous porous films, chemical reactions become interfacial in nature as a consequence of immobilizing or heterogenizing the molecular catalyst into a three-dimensional support matrix. For the system to operate efficiently in such cases, both charge and substrate must be transported to the catalytic sites within the film at a faster rate than the intrinsic turnover rate of the catalytic reaction. We postulate in this Perspective that one critical, but often overlooked, aspect of utilizing MOFs for the molecular catalysis of electrochemical reactions is transport.

In MOF films with discrete redox-active molecular linkers, electron-hopping—formally governed by Fick’s laws of diffusion—delivers charge to the catalytic sites. Therefore, the diffusional transport of both charge and substrate needs to be appropriately accounted for in order to quantitatively characterize and optimize each potentially limiting process. Diffusion has the potential to be much slower compared to other processes occurring during catalysis, particularly chemical reaction rates, and this can be exacerbated in the confined environments of porous materials. Given the microporous nature of MOFs, transport phenomena are expected (and in a few exceptional cases have been qualitatively shown, as will be discussed) to have an enormous effect on the overall catalytic performance of electroactive MOF films. The observed reaction rate easily can be limited by mass or charge transport if these phenomena are not controlled or optimized. While experimentally examining MOF-based reactions, it is imperative to remember that when these reactions are coupled with diffusion,^11,12 substrates and/or catalytic intermediates will have spatially dependent concentration profiles, and their concentration throughout the film may not reflect the bulk concentrations of these species.

In the following sections, we will explore well-established electrochemical methods to quantify rates of charge transport, substrate diffusion, and the intrinsic catalytic reaction. Next, the question, “Where is the bottleneck for catalysis?” is posed and answered by examining each potentially limiting transport process in detail with numerical simulations, incorporating relevant data from the literature. Concepts of charge transport dynamics and catalytic reaction engineering from closely related fields are utilized to understand these issues on a fundamental level. Finally, looking to the future, the quantitative analysis and parameters detailed in the beginning sections are used to understand how to optimize catalytic performance and design new MOFs, which alleviate transport limitations. The reaction-diffusion kinetic models outlined here reveal important design rules, and indicate which features of the catalyst–support system to select and optimize in order to rationally control transport and ultimately reactivity. While the incorporation of transport phenomena into kinetic studies of MOF-based catalysis is under-represented in the literature, it is certainly not unique to MOFs. Many of the concepts of reaction-diffusion kinetics that will be discussed here apply widely to other micro- or mesoporous catalyst materials.^10,13−15 However, MOFs do offer a unique opportunity for rational control over mass and charge transport properties at the molecular level. This is enabled by the vast array of combinations for both the organic linkers and the connectivity between these building blocks via the inorganic nodes, as well as the synthetic tuning possible for both these functionalities. More research is certainly needed to translate molecular-level design of MOFs into targeted control over macroscopic transport properties, which is crucial to optimize catalysis for large-scale applications. However, the first step toward this goal, and consequently the focus of the following discussion, is to delineate and quantitatively characterize the influence of transport phenomena on chemical reactivity in MOFs by simple kinetic models, leading to specific design criteria for not only transport properties but also for important extrinsic parameters such as film thickness. This has implications for MOFs applied to the electrochemical conversion of small molecules for energy related processes (fuel-forming reactions, water oxidation etc.), but also potentially to recently revitalized electrochemical organic transformations and redox catalysis producing high-value organic products.¹⁶⁻¹⁸ We end by summarizing the opportunities and challenges for MOFs entering applications as high-performance catalytic films for this variety of possible electrochemical reactions.

Revisiting Reaction-Diffusion

The analysis of transport phenomena occurring in porous media and their effect on catalytic reactions has some important historical origins. The year 2019 celebrated the 80th anniversary of Prof. E. W. Thiele’s pioneering publication, “Relationship between Catalytic Activity and Size of Particle”.¹⁹ Therein, Thiele presented a model for reaction-diffusion occurring in porous catalyst particles or “grains” and outlined two regimes: (1) where the intrinsic kinetics of the catalyst solely limit the overall reaction rate, and (2) where internal substrate diffusion limits the overall reaction rate. An important part of these results accounts for the transition between these two scenarios in a quantitative manner and predicts the resulting behavior based on a small number of input parameters. This is accomplished by defining a single descriptor, a dimensionless control parameter that has come to be known as the Thiele modulus ϕ,

1

where R_a is the radius of the equivalent sphere, k_cat is the first-order rate constant of the catalytic reaction, and D_S is the diffusion coefficient of the substrate inside the particle. This very simply states that the efficiency of any chemical reaction occurring in concert with diffusion will be a function of a geometric length scale describing the physical system, the catalytic rate, and the diffusivity of the substrate. If the time scale required for substrate to diffuse through the particle is large compared to the reaction rate (ϕ > 1), the substrate will be consumed by the reaction before permeating through the entire particle. A boundary layer (also referred to as a reaction-diffusion layer) forms near the particle surface, which limits the amount of catalyst actively participating in the reaction—in other words, the catalysts in the interior of the particle are largely dormant (Figure 1). Thus, porous catalysts with large particle sizes and/or very fast reactions will have a significant diffusional resistance that lowers the observed reaction rate.^13,20,21 Therefore, an optimized catalytic material will inevitably have these parameters balanced appropriately, so that any limitations of transport by diffusion on the reaction rate are small or negligible. Thiele developed his model for catalyst particles of several different geometries, but the same underlying physical principle applies here to porous MOF film electrodes. In either case, overall efficiency is controlled by the ratio of the intrinsic catalytic reaction rate to a particular diffusion rate (this could be the diffusion of either charge or substrate through the MOF film). Efficiency, in this context, denotes how much of the catalyst is utilized during the reaction in the particle or film, i.e., the ratio of the amount of active catalyst to the total amount of catalyst contained in the MOF. This metric is canonically referred to as the “effectiveness factor” ²¹ and is easily quantified as the observed reaction rate divided by the maximum reaction rate in the absence of any diffusional gradients or transport limitations.^13,20,21 Practitioners in MOF-based catalysis of both chemical and electrochemical reactions are encouraged to read Thiele’s original paper—its message is indeed still as timely now as it was in 1939. We will see in later sections how the same physical principles captured by Thiele’s modulus can influence catalysis of electrochemical reactions mediated by molecular species covalently incorporated in MOF film electrodes. For convenience, the dimensionless parameters used in this Perspective are summarized in Table 1. It is important to highlight the outstanding independent contribution of Dr. Gerhard Damköhler, who arrived at the same relationship between mass transport and chemical reactions.²² In his honor, the Damköhler number (Da) is often used to represent the ratio between a particular reaction rate and a convective mass transport rate.²¹

Figure 1.

(a) Quantitative representation of a boundary or reaction-diffusion layer in a MOF particle (approximated as spherical) for a first-order reaction at steady state. Dimensionless concentration is displayed on the y-axis, where C_S is the substrate concentration inside the MOF particle (a function of the radial distance r), and C_S⁰ is the bulk substrate concentration (taken as constant outside the particle for simplicity). The dimensionless radial coordinate (R_a is the particle radius) is plotted on the x-axis. The arrow indicates increasing values of the Thiele modulus, ϕ > 1. (b) Expanded region showing reaction-diffusion layer, with thickness given by δ_rxn.

Table 1. Dimensionless Parameters^a.

^aA full list of all dimensional symbols and their definitions is given in the Symbols section.

Charge Transport Dynamics

Returning to electroactive MOF films, in this section we will introduce two primary microscopic charge transport mechanisms, band or ohmic conduction (migration) and electron-hopping conduction (formally diffusion), which carry electrons or holes to the covalently incorporated molecular catalysts. MOFs with discrete redox-active linkers (e.g., molecular metallocatalysts) most often exhibit an electron-hopping mechanism, which will be the main focus of the following discussion. Since electron hopping is formally a diffusion process (vide infra), these concepts will become important when considering the reciprocity between the rate of charge transport and catalysis and how the resulting reaction-diffusion behavior of the film can affect catalytic efficiency and kinetic measurements.

Band or ohmic conduction occurs when the electronic states of the MOF are highly delocalized and possibly strongly coupled to the electrode’s electronic states, due to through-bond or through-space conjugation of the organic linkers and/or metal nodes.²³ Electron movement in the film in this case is driven by migration as a result of electrical potential gradients. Experimentally, cyclic voltammograms (CVs) of such films display only capacitive current (faradaic waves are only observed if interaction with a substrate molecule causes the injected charge to be localized at a specific site).^24,25 An example of this behavior was demonstrated by a highly conjugated (electrical conductivity σ = 40 S cm^–1) Ni₃(hexaiminotriphenylene)₂ 2-D MOF reported by Dincă and co-workers for the oxygen reduction reaction (ORR).²⁶ Under a N₂ atmosphere, a large capacitive wave is observed, while conversely if O₂ is added to the cell, there is a clear increase in current corresponding to the faradaic signature of the charge transfer reactions occurring during catalysis.

Alternatively, a MOF film may have components that are redox-active within a given potential window but are not electronically coupled to one another through conjugation, where the electronic states of the MOF are now spatially localized and defined by standard potentials (E⁰). Thus, in this instance electron hopping will be the main charge transport mechanism, and electron movement is driven by a series of bimolecular self-exchange electron transfer reactions between the reduced form of the linker or node and the oxidized form of the linker or node in close proximity.²⁷ The voltammetric response of this type of MOF film exhibits faradaic waves even in the absence of substrate and has been characterized in many recent examples.²⁸⁻³⁴

Dahms³⁵ and Ruff³⁶⁻³⁸ first outlined the theory for electron transport via self-exchange reactions, including a contribution for the local physical displacement of the redox-active molecules. Andrieux and Savéant,²⁷ as well as Laviron,³⁹ developed an extension of this initial work by considering only stationary or fixed sites (most relevant to MOFs), with significant experimental contributions from Murray,⁴⁰ Anson,⁴¹ and Bard,^42,43 utilizing redox-polymer-modified electrodes. By definition, there is zero driving force for a self-exchange reaction; however, an activation barrier still is present, and a rate constant k_ex can be defined for the reaction between linkers in adjacent layers (Figure 2). For a given geometry, each electron “hop” occurring in a random direction is governed by a time-step set by k_ex. The overall process is in essence a random walk, and therefore can be formally modeled by the diffusion of fixed redox-active centers. Electron self-exchange or “hopping” through a molecular redox film responds to concentration gradients or, more accurately, chemical potential gradients created at the electrode surface by the applied potential.^40,44 Thus, similar to a freely diffusing species in solution, the change in concentration of each linker in a particular oxidation state within the film formally adheres to Fick’s laws.

Figure 2.

Electron-hopping mechanistic scheme for the reaction P + e^– ⇌ Q in a redox-active MOF film occurring between two layers, separated by an average hopping distance d.

An equivalent diffusion coefficient D_e for this electron-hopping mechanism was defined^27,39 and is shown in eq 2,

2

where C_P⁰ is the total redox-active linker concentration, d is the average hopping distance, normally taken as the distance between nearest neighbors in the lattice, and k_e (with k_e = 6k_ex) is the electron-transfer rate constant assuming self-exchange occurs only in the direction normal to the electrode surface with, however, six possible nearest-neighbor sites. The value (k_e/6)C_P is sometimes referred to as “k_hopping” (s^–1).^28,29,45

Counterion Diffusion–Migration

Further refinement of the above model takes into account that electron displacement is associated with the movement of counterions to maintain electroneutrality.⁴⁶⁻⁴⁸ Transient measurements (potential-step chronoamperometry) include macroscopic diffusion of charge-balancing mobile counterions, as a net flow of electrons is concomitant with a net displacement of mobile counterions within the film and across the film–solution interface, resulting in an apparent diffusion coefficient, D_e^app. Notably, Cottrell behavior has been repeatedly observed for these systems (the transient current after a large potential step is proportional to t^–1/2).^{28−30,34,49−51}

It has been recently demonstrated⁴⁴ that if the overall process involves ion-coupled electron transfer reactions (where an electro-inactive counterion participates in the self-exchange reaction), the maximum conductivity of the charge transport process will be dominated by the slower of two processes, characterized by either a purely ionic diffusion coefficient for mobile counterion displacement or an apparent diffusion coefficient for the ion-coupled charge-hopping process.⁴⁴ This may well be the case in MOFs, as reported recently by Morris and co-workers, where the purely ionic diffusion coefficient and the electron-hopping diffusion coefficient were independently determined for charge transport between ferrocene units anchored in NU-1000.³¹ In any case, the microscopic interpretation of D_e^app will be highly dependent on the microscopic charge transport mechanism or model.⁴⁰

Additionally, significant electrostatic interactions such as ion-pairing may exist within MOF pores. In a theoretical treatment of charge hopping in redox polymers, which have relatively nonpolar interiors with potentially very high concentrations of ionic species, it was shown that D_e^app decreases with increasing association constant for the ion-paired species between the redox-active component in the polymer backbone and the mobile redox-inactive counterion.^52,53 The effect of ion-pairing on charge transport in MOFs has recently been examined, and initial results support the dependence of D_e on the ion-pairing association constant.³¹

Cyclic Voltammetric Analysis of Electroactive MOF Films

Applying these theoretical treatments, it has been established that macroscopic electron transport through MOF films with discrete redox-active components proceeds formally as a diffusion process.^50,54 The voltammetric response of such a MOF film will therefore be very similar to that of a freely diffusing species in solution, however, with the very important difference that the formal diffusion of fixed redox-active linkers is occurring within a finite domain. This means the boundary condition at the solution–film interface needs to be considered and will give rise to both linear finite and semi-infinite diffusional responses depending on the rate of diffusion relative to the time scale of the voltammogram (set by the scan rate in CV) and the film thickness. Further, if electron transfer between the electrode and the first layer in the film is unconditionally at equilibrium during the scan, the boundary condition at the electrode–film interface obeys the Nernst equation. Alternatively, Butler–Volmer kinetics can describe the electron transfer reaction occurring at the electrode surface if the reaction is slow relative to the CV time scale. Transition between these complementary behaviors and the overall current–potential response are captured by two dimensionless parameters, originally defined by Matsuda and co-workers^55,56 and Savéant and co-workers:²⁷ the finite diffusion parameter, λ_e, and the kinetic parameter, Λ_s, given below,

3

where d_f is the film thickness, ν is the scan rate, D_e^app is the electron-hopping diffusion coefficient, F is the Faraday constant, and k_s is the standard rate constant for heterogeneous electron transfer. The competition between diffusion and interfacial electron transfer is expressed by Λ_s, and λ_e is the ratio of the film thickness to the diffusion layer thickness. First, taking limits of the finite diffusion parameter under Nernstian electrode kinetics (Λ_s > 1), when λ_e→∞, the diffusion layer thickness, over which there is a significant concentration gradient of reduced/oxidized linkers, becomes much smaller than the film thickness (thick films, fast scan rates). As a result, electron-hopping diffusion can be approximated as taking place in a semi-infinite domain. The current–potential response is a classical diffusion wave (Figure 3a; for examples of the concentration profiles of the reduced linker during the scan, see the Supporting Information) with a peak separation of 57 mV and peak current proportional to 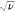. In the opposite limit of thin films or slow scan rates, as λ_e→0, the same material will display zero peak separation and peak current proportional to ν, characteristic of a symmetric “adsorption” or “surface” wave (Figure 3c). Here, the diffusion layer becomes large and starts to explore the finite geometry imposed by the film thickness—a situation of diffusion in a finite domain. Figure 3b shows an intermediate regime with λ_e = 2. A crucial feature of this analysis is that even if a symmetric adsorption wave is observed, the electron transport mechanism occurring through the MOF film is still formally diffusional with, however, a finite boundary condition representing the film–solution interface. Simulations of CVs demonstrating the two behaviors with different scan rates can be found in the Supporting Information. Slow interfacial electron transfer at the electrode–film interface (Λ_s < 1) gives rise to larger peak potential separation in either limit of λ_e, expected for electrochemical irreversibility (shown in the blue CVs in Figure 3, Λ_s = 0.2).

Figure 3.

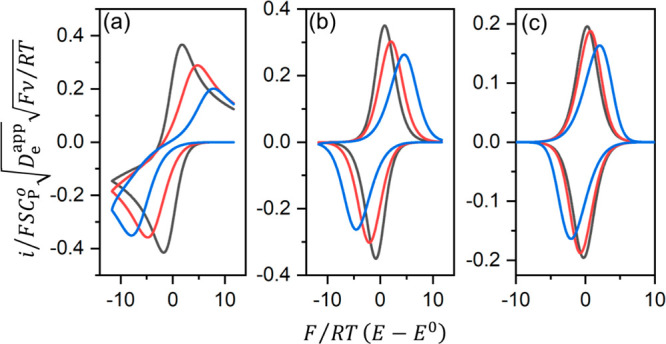
Simulated CVs of a molecular redox film using a range of values for the finite diffusion parameter λ_e: (a) = 7, (b) 2, and (c) 0.7, each with varying magnitudes of the heterogeneous electron transfer parameter Λ_s (black, 10; red, 1; blue, 0.2). Current i is normalized to the semi-infinite current (). The normalized electrode potential F/RT(E – E⁰) is plotted on the horizontal axis. Current–potential responses were generated numerically with finite difference method.

As expressed by λ_e, the transition between these two behaviors will occur on variation of either the scan rate or the film thickness, approximately when λ_e is equal to unity. Pushing the system from one regime to the other will provide a method to extract the diffusion coefficient, if the film thickness can be measured independently (e.g., SEM cross section imaging). For example, in a recent report from our lab, a Zr-based MOF film containing molecular Co catalysts (UU-100) showed that the CV peak current transitioned from proportionality with ν to proportionality with at ∼100 mV s^–1.³² Since the film thickness was known, it was possible to estimate D_e^app as being on the order of 10^–8 cm² s^–1, which matched well with the value obtained from potential-step chronoamperometry experiments. It should be noted that the CVs displayed in Figure 3 do not account for non-idealities such as significant intermolecular interaction between linkers that would lead to broadening of the faradaic waves,^57,58 which may be encountered in the case of many MOF-based electrodes.

Deviations from the CVs in Figure 3, for example in the observed peak current, could also occur as a result of inhomogeneous film thickness (roughness).^59,60 A method developed recently by Buesen et al. delivers a way to determine the film thickness under operating conditions (with the film in the solvated state).⁶⁰ The authors demonstrated that deviations from the ideal behavior described above could be used to estimate film roughness, quantified as an ensemble thickness distribution.⁵⁹ These are important parameters to measure and optimize (surface roughness, film thickness, and charge transport diffusion coefficients), since they are tied to the reaction-diffusion behavior of the system, as demonstrated by the Thiele modulus, and inevitably control catalytic performance, which we will see in the following sections.

Molecular Catalysis in MOF-Based Electrodes

The occurrence of diffusional transport of both charge and substrate presents a significant challenge in extracting kinetic parameters (rate constants or turnover frequencies, TOFs) and in identifying mechanistic pathways for molecular catalysis taking place in MOF films. Transport phenomena are often overlooked in the kinetic analysis of catalytic reactions occurring in MOFs, resulting in reporting of disguised kinetic parameters (TOFs, Tafel slopes, rate constant, or possibly reaction orders), due to unaccounted interference from mass or charge transport.¹² Fortunately, there are well-developed reaction-diffusion models from mature tangential fields such as electrochemically mediated catalysis within redox polymer-modified electrodes (with covalently or ionically bound transition metal complexes)⁶¹⁻⁶³ or using biocatalytic films,⁶⁴⁻⁶⁶ either of which may be relevant for analyzing MOF-based catalysts. This section outlines a steady reaction-diffusion kinetic model applicable to a simple one-electron, one-step catalytic reaction facilitated by a molecular catalyst incorporated in a MOF film, where the catalyst species is responsible for both the reaction with the substrate and shuttling of electrons through the film (Figure 4).^67,68

Figure 4.

One-electron, one-step catalytic mechanism occurring in a molecular heterogenized MOF film electrode, where P and Q are the oxidized and reduced forms of the catalyst linker, respectively, S is the substrate, and k is the second-order rate constant for the catalytic reaction (k_cat = kC_S⁰).

Primarily three phenomena will determine the overall performance and steady-state current response of any catalytic process taking place within an electroactive MOF:

• (1)the intrinsic catalytic reaction
• (2)permeation and diffusion of the substrate
• (3)diffusional transport of electrons

Additional considerations for electron transfer kinetics at the electrode–film interface or a finite rate of mass transport of the substrate across the film–solution interface appear as boundary conditions in the overall reaction-diffusion problem and have been treated previously.⁶⁸⁻⁷¹ If the substrate is depleted by the reaction and its concentration at the film–solution interface drops below its bulk value, ensuing mass transfer outside the film in solution can be treated as described previously for either rotating disk electrode voltammetry (RDEV) or CV.^63,68 However, for simplicity, here we consider the concentration of substrate outside the film to be constant and equal to its bulk value. In general, Fick’s laws hold for statistically homogeneous microporous materials, and a continuum model for diffusion and any coupled reactions is valid.¹⁴ This will certainly apply to MOFs as well; however, as for any microporous material, extensions or adjustments to Fickian diffusion may be considered if required by the particular experimental system at hand.^{13,14,29,30,72} The following discussion focuses on the two diffusional phenomena and the catalytic reaction mentioned above, since these give rise to relativity unfamiliar complications resulting from reaction-diffusion—mainly that the concentration of each species will have a spatial dependence within the film. This is a fundamental characteristic of reactions coupled to diffusion occurring in porous media, where the possible existence of boundary layers, outside of which concentrations of substrate and/or intermediates drop to zero, needs to be taken into account.

Early reports first identified the three primary rate-limiting phenomena,^73,74 for example by examining the mediated reduction of dibromoalkyl substrates by metalloporphyrin catalysts in multilayer films.⁷⁵ A detailed kinetic model (outlined for steady-state techniques, RDEV) was soon after introduced by Andrieux, Dumas-Bouchiat, and Savéant,⁶¹ which recently has been updated by Costentin and Savéant for analysis by cyclic voltammetry including the case when the substrate is depleted in solution outside the film (total catalysis).^67,68,76 The details of this model are briefly recalled in the next section in order to frame its application to molecular catalysis inside MOF films for the analysis that follows.

First of all, a steady-state situation will hold for the dynamical processes in the film when the catalytic reaction is fast as compared to the time scale of the experiment so that there is no accumulation of either reduced catalyst or substrate within the film.⁶⁸ A mass balance on the system in this situation entails that the maximum current will be proportional to either the flux of reduced catalyst at the electrode interface or the flux of substrate at the film–solution interface.⁶⁴ This situation is often referred to as pure kinetic conditions(68,77) and becomes important when analyzing reaction-diffusion phenomena of this type, as it simplifies the problem to a form where an analytical or semi-analytical solution for the current–potential response may be obtained. The rate of change of any species undergoing reaction-diffusion can be expressed as Fick’s second law plus a kinetic term accounting for the coupled chemical reaction. At steady state the time derivative is zero, giving

4

5

where x is the distance normal to the electrode surface with x = 0 located at the electrode–film interface, and k is the second-order rate constant of the catalytic reaction (see Figure 4). A simultaneous solution to these two equations given the appropriate boundary conditions will render the current–potential response.^61,67,68,76

The three rate-limiting factors can each be expressed simply as a characteristic current density:⁶²i_k, i_e, and i_s, for the catalytic reaction, charge transport, and substrate diffusion, respectively.

6

where κ_S is the equilibrium partition coefficient for substrate crossing the film–solution interface, C_P⁰ is the concentration of redox-active linkers, C_S is the bulk concentration of substrate, and d_f is the film thickness (other terms are defined the same as above). The characteristic current densities are obtained from the hypothetical maximum flux for each potentially limiting process, displayed in Figure 5, and these describe the overall capacity of the film to deliver charge and substrate to the active sites to carry out the catalytic reaction at a given rate.⁷⁸ They represent how the rate of each process (reaction or diffusion) scales under a given set of conditions and independent variables (eq 6). A single process or possibly two processes in parallel, reaction on one hand and a transport phenomenon on the other, may determine the overall observed current.

Figure 5.

Schematic illustration of limiting fluxes: F_Q for diffusion-like charge transport and F_S for substrate diffusion.⁷⁸ The catalytic reaction is represented by a maximum production or generation rate of product per unit surface area (mol cm^–2 s^–1), G_k. Concentration profiles for each process are displayed, which give the corresponding characteristic current densities (i_e, i_s, and i_k, respectively) from multiplication of the magnitude of each flux or rate by F.

Akin to Thiele’s prediction, the behavior is governed by the ratio of the catalytic rate to either the rate of electron diffusion or substrate diffusion, precisely given by ratios of the characteristic current densities. Therefore, two dimensionless control parameters can be defined,⁶³ noting their fundamental similarity to the Thiele modulus in eq 1:

7

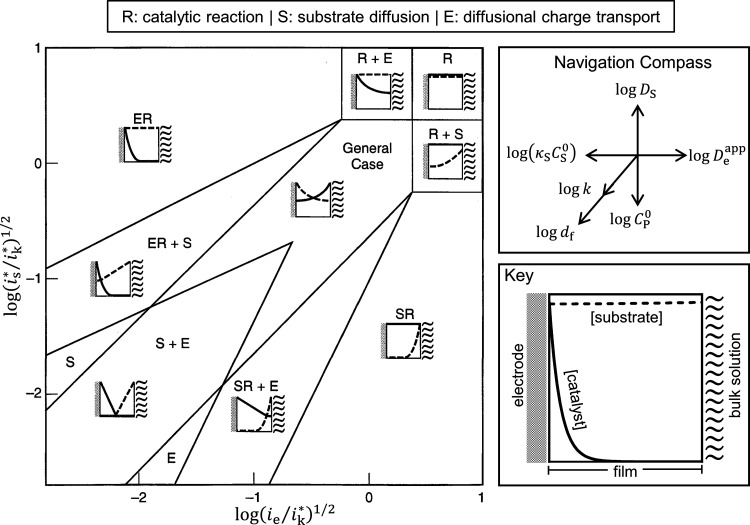
When one or both parameters are very large, transport limitations by substrate or electron-hopping diffusion are observed along with the appearance of boundary layers, which reduce the total amount of active catalyst within the film under operating conditions. Analytical solutions can be found in many limiting situations when there exists a linear gradient for either Q or S over a significant dimension of the film.^63,68 This results in the limiting regimes shown in the zone diagram in Figure 6.^63,68,69 It should be noted that there is no analytical solution for the general case (middle, Figure 6), and numerical methods to compute the solution to eq 4 and eq 5 must be employed.^79,80 In the original formalism,⁶¹ a nomenclature for the limiting process(es) was established, and the letters R, S, and E are assigned to the catalytic reaction, substrate diffusion, and diffusional charge transport being limiting, respectively. Combinations thereof represent mixed kinetic control by two or more phenomena.

Figure 6.

Kinetic zone diagram for limiting cases of a one-step, one-electron catalytic reaction occurring in a multilayer film.⁶⁹ Schematic concentration profiles of reduced catalyst Q (solid line) and substrate S (dotted line) are displayed in each zone. The definitions of i_s^* and i_k incorporate the possibility for substrate depletion at the film–solution interface and ensuing solution-phase mass transport outside the film.⁶³ The navigation compass on the top right shows the magnitude and direction in which each experimental variable will translate the system within the zone diagram. Adapted from ref (69) with permission from Elsevier Science.

Using Film Thickness as a Diagnostic Tool for Reaction-Diffusion

The main analytic tool to diagnose the kinetic limitation occurring within the film is variation of the film thickness.^67,68,76 This is the parameter that provides the most information and can in principle be varied systematically over a range of values. Very intuitively it can be expected that thicker films will lead to limitations by mass or charge transport. For a simple example, consider the case where electron-hopping diffusion is relatively fast (i_S ≪ i_e) compared to the rate at which substrate diffuses through the film, and κ_S is approximately unity (Figure 7).⁷⁶

Figure 7.

(a) Steady-state CVs with increasing film thickness from d_f = 10 nm (black) to d_f = 640 nm (orange). (b) Corresponding plot of steady-state plateau current density (j_pl, blue dots) vs d_f when i_s ≪ i_e with D_e^app = 1 × 10^–5 cm² s^–1, D_S = 1 × 10^–10 cm² s^–1, k = 10 M^–1 s^–1, C_S = 1 M, C_P⁰ = 0.1 M, and κ_S = 1.

Starting with very thin films, the measured catalytic plateau current will be proportional to the film thickness, as the catalytic reaction encompasses the entirety of the volume contained inside the film (zone R, eq 8). With thicker films, this current reaches a limiting value and no longer varies with d_f (zone SR, eq 9). Now, the catalytic reaction and substrate diffusion jointly limit the observed current density. Plotting the plateau current density versus the film thickness, will allow for estimating the intrinsic characteristics of the film. The slope in the limit of thin films is proportional to the intrinsic reaction rate constant k, where C_P⁰ and C_S are either known or can be measured. In the region where the current is invariant with d_f, the limiting current can be used to calculate D_S (eq 9), since k has been determined.^68,76

8

9

where S is the geometric surface area (cm²). Analogously, when substrate diffusion is much faster than electron hopping (i_s ≫ i_e) and the catalytic reaction is fast compared to diffusion-like charge transport (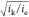 ≫ 1), the steady-state plateau current is given by⁶⁷

10

While the theoretical model presented here is well established,⁸¹ such an analysis has never, to the best of our knowledge, been done with catalytic MOF films.

Kinetic Analysis of MOF-Based Catalysis Relies on Identifying and Characterizing Boundary Layers

Above, we saw that the current saturates upon increasing the film thickness, perturbing the system into a regime where both reaction and diffusion are now both limiting the overall current. This situation arises principally because the reaction consumes the substrate before it diffuses into the interior of the film forming a boundary layer near the film–solution interface. This is important because the current density in zone SR (eq 9) is proportional to the thickness of the resulting boundary layer. As this becomes thinner, there are fewer active catalysts, and thus, lower overall catalytic efficiency. A scaling relationship of Fick’s second law can show how to (very simply) calculate reaction-diffusion layer thickness and total active catalyst concentration. Taking eq 5 when i_s ≪ i_e and ≫ 1 (zone SR) and again for simplicity assuming κ_S = 1,

11

If we assume concentrations scale with the corresponding total or bulk concentration of each species (at E ≪ E_P/Q⁰) and the distance perpendicular to the electrode surface is rescaled to the size of the reaction-diffusion layer (δ_rxn), then eq 11 becomes

After rearranging, the reaction-diffusion layer thickness is given by

12

The active portion of catalyst (m_Q^active, with units of moles) can then be found by integrating over the reaction-diffusion layer thickness:

Finally, this results in

13

Interestingly, since the reaction is first-order in substrate, in this situation increasing the bulk concentration of substrate outside the film does not in fact help alleviate the transport limitation by substrate diffusion (the active catalyst concentration is independent of C_S⁰). The complementary expression for when charge transport is jointly limiting with the catalytic reaction and substrate diffusion is fast (i_S ≫ i_e and ≫ 1, zone ER) is

14

In this case increasing the substrate concentration accelerates the reaction, causes the reaction-diffusion layer to decrease in thickness, and reduces the amount of active catalyst—all exacerbating the limitation by diffusional charge transport. It should be noted that these effects apply to the efficiency of the catalytic film in terms of the fraction of catalyst participating in the reaction, and ultimately put a limit on how thick the film can be made without having unused catalytic sites within the film. Since the reaction is first-order in substrate, increasing the bulk substrate concentration will, however, increase the overall current accordingly (see eqs 8, 9, and 10).

Falsified Kinetics and TOFs That Depend on Film Thickness

Since the chemical reactions occurring in MOFs are innately coupled to diffusive charge or mass transport, situations arise where measured kinetic parameters such as rate constants, reaction orders, TOFs, and activation energies do not reflect intrinsic values. Internal transport limitations by mass or charge diffusion will disguise kinetic values, resulting in what is designated from the traditional chemical engineering vernacular as “falsified kinetics”.²¹ In a classic example from basic chemical reaction engineering,^13,21 the apparent or measured reaction order n′ in substrate (C_S) can be related to the true reaction order n by

15

valid for the situation when substrate diffusion and the catalytic reaction are jointly limiting (i_S ≪ i_e and ≫ 1; zone SR, i.e., when the substrate is present in a thin boundary layer at the film–solution interface, and κ_S = 1). Conversely, in the case where electron diffusion is slow (i_e ≪ i_S and ≫ 1, zone ER), the apparent reaction order for substrate is given by

16

(i.e., when the reduced catalyst is present in a thin boundary layer at the electrode–film interface).^67,77 Unless transport limitations are identified or the system is pushed to a regime where only the catalytic reaction is limiting and all gradients are eliminated (see zone R, Figure 6), mechanistic conclusions normally sought from uncorrected kinetic measurements will certainly contain artifacts.

Similarly, using the expression defined in eq 14, recall that TOFs can depend on film thickness,^10,82

where TOF_max^true reflects the intrinsic reaction rate of the catalyst. This example is given for when i_S ≫ i_e and 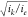≫ 1 (zone ER and κ_S = 1). Indeed, the apparent turnover frequency, TOF_max, will have different expressions in each limiting regime, and when transport limitations are present, TOF_max^app will underestimate TOF_max. Additionally, comparing different catalytic MOF films using conflicting TOF values may encumber kinetic benchmarking and comparison between such materials since the film thickness is not necessarily a parameter intrinsic to the material (i.e., it can be varied by using different synthetic routes or fabrication techniques). Consequently, given a new catalytic MOF, diagnosing the limiting regime (zone diagram, Figure 6) under operating conditions, identifying and quantifying any possible boundary layers that may arise, and extracting intrinsic parameters of the system (D_S, D_e^app, TOF_max) are important endeavors to advance the field of MOF-based catalysis.

One experimental example for CO₂ reduction (Figure 8)⁸³ demonstrates the impact of thick films and ensuing mass or charge transport limitations on the observed current density. Starting from the thinnest films examined, an increase in film thickness led to an approximately linear increase in the total current density (Figure 8), corresponding to the R limiting regime recalled from the zone diagram in Figure 6. Here the entire film is active since the reaction-diffusion layer is larger than the film thickness (i.e., ≪ 1 or 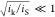), and the transport processes are able to supply charge or substrate across the entire film before being consumed by the reaction. In these limits, turnover frequencies measured in the usual way will yield TOF_max^true. For example, Kornienko et al. reported a TOF value from data taken under these conditions on the order of 0.06 s^–1 (Figure 8).⁸³

Figure 8.

Influence of film thickness on overall steady-state current density demonstrating interference from transport phenomena. CO₂ reduction to CO catalyzed by Al₂(OH)₂TCPP-Co (TCPP-H₂ = 4,4′,4″,4‴-(porphyrin-5,10,15,20-tetrayl)tetrabenzoate) films of different thickness (50 ALD cycles correspond to a film thickness approximately of 30–70 nm).⁸³ Adapted from ref (83) with permission from the American Chemical Society.

However, upon increasing the film thickness further, the MOF films exhibit a saturation in the total observed current density followed by a sharp decline (Figure 8).⁸³ The transition from the linear region to this peaked region is expected to correspond to the situation where on the time scale of the reaction, diffusional mass or charge transport are not able to supply electrons or substrate over the entire length of the film (i.e., > 1 or 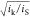> 1). Since now the film thickness has exceeded the size of the reaction-diffusion layer, a boundary layer would be expected at either the electrode–film interface or the film–solution interface depending on the relative rates of electron-hopping and substrate diffusion (as compared to the catalytic reaction) within the film. Further increase in the film thickness leads to a drop in current as the second diffusional process becomes limiting as well and the film most probably enters either the SR+E or ER+S situation.⁶⁸ In these limits, as soon as or 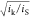becomes greater than unity, TOF_max^app ≠ TOF_max, and uncorrected kinetic values will be falsified, since the bulk concentration of catalyst is no longer reflective of the amount of active catalyst contained within the boundary layer. It should be noted, from this example it is not possible to conclude which transport process (either substrate diffusion or charge transport) initially limits the current as the film thickness is increased. This would require additional information, particularly the rate at which the substrate (CO₂ or possibly protons) diffuse through the MOF films. Additionally, the authors identified several other factors that may contribute to the observed effect on the current density and which may complicate the analysis of these data in terms of reaction-diffusion. For example, Al₂(OH)₂TCPP-Co films with the largest thickness may have an underlying layer of aluminum oxide between the conducting FTO surface and the MOF film, which is remaining from the film synthesis and fabrication.⁸³ If this layer is sufficiently thick, it would reduce the ohmic contact between the film and conducting substrate, producing lower currents. In short, while this example is one of the few reports to systematically examine the effect of MOF film thickness on catalysis and certainly reveals important effects associated with thick films, overall these results point toward a need for improved methods of film synthesis and fabrication methods for MOFs on electrodes with controllable film thickness and morphology.

Opportunities and Challenges

Understanding the fundamental kinetics of MOF-based catalysis using molecular active sites is still a major challenge for the field. Where is the bottleneck for catalysis, and how can the unique properties of MOFs be exploited for optimization? Incorporating the foundational principles from the reaction-diffusion models described above, this next section attempts to analyze each potentially limiting process in turn, with suggestions for increasing catalytic efficiency in ways that are uniquely suited to MOFs.

Limiting Electron Diffusion

As an illustrative example, a situation with limitations by electron-hopping diffusion is displayed in Figure 9. In this situation substrate transport is relatively fast (i_s ≫ i_e),⁶⁷ or the bulk concentration of the substrate is very high (for example when the substrate is the solvent). This may be encountered in practice with catalytic MOF films having large pores allowing facile substrate diffusion, but slow charge transport due to a large separation between redox-active linkers²⁸ (D_e^app = 10^–10–10^–14 cm² s^–1).² Catalytic steady-state current (at E ≪ E_P/Q) is plotted versus the dimensionless parameter = (Figure 9a), which is the ratio of the catalytic reaction rate to the rate of diffusional charge transport. An insightful alternative definition can be expressed based on a geometric length scale present in the problem (d_f) and a physical length scale for reaction-diffusion. Consequently, this parameter is also equivalent to the ratio of the film thickness to the thickness of the reaction-diffusion layer. As the electron-hopping diffusion coefficient decreases, the current (normalized to the reaction-limited current, i_R = FSkκ_SC_S⁰C_Pd_f) drops markedly. The blue and black dots in Figure 9 and the corresponding concentration profiles in Figure 9 represent electron-hopping diffusion coefficients in a realistic range for electroactive MOF films.^30,34,51,84 The current in this situation is controlled by both the catalytic reaction and electron diffusion and is no longer a function of film thickness, and the reaction is fast enough compared with diffusion to cause finite gradients of the reduced catalyst to form within the film. Thus, the reaction-diffusion layer is significantly smaller than the film thickness; and therefore, increasing the number of layers (increasing the thickness) is unproductive, because the outer region of the film will not participate in the catalytic reaction.⁶⁷ The y-axis in Figure 9 is a measure of catalytic efficiency (how much of the film is active in the reaction), and accordingly it can be seen that large values of 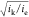cause a reaction-diffusion layer to form that reduces the efficiency of the system (i.e., diffusion is not able to support charge transport to all the catalytic sites on the time scale of the reaction, see concentration profiles in Figure 9b).

Figure 9.

(a) Variation of the steady-state plateau current (at E ≪ E_P/Q⁰) with = when substrate concentration is constant throughout the film (i_s ≫ i_e). (b) Corresponding concentration profiles of Q: d_f = 1 μm, C_P = 1 M, and kκ_SC_S⁰ = 10 s^–1, and D_e = (red) 1.3 × 10^–6 cm² s^–1, (green) 2 × 10^–7 cm² s^–1, (yellow) 5 × 10^–8 cm² s^–1, (blue) 5.5 × 10^–9 cm² s^–1, (black) 5 × 10^–10 cm² s^–1.

Limiting Substrate Diffusion

The situation of kinetically limiting substrate diffusion within the film in addition to charge transport is shown in Figure 10.⁶⁸ Representative conditions found for MOF films^34,54 were used to generate concentration profiles: D_e^app = 5 × 10^–10 cm² s^–1, d_f = 1 μm, C_P = 1 M, with various values of D_S. An important situation arises when ≫ 1 and ≫ 1. The observed current density is independent of the rate of the catalytic reaction and the only limitations are from substrate diffusion and/or charge transport. This is represented in Figure 10c, displaying zone S+E. In fact, when the transport processes are much slower than the reaction rate, the reaction-diffusion layer approaches the size of a monolayer, which can be located at either interface (either the electrode–film interface, zone S, or the film–solution interface, zone E).^61,64 The overall current density is plotted in Figure 10e for each value of D_S, corresponding to the concentration profiles in Figure 10a–d. Typical surface concentrations and electron-hopping transport parameters reported in literature indeed show that catalytic MOF films are able to reach the recognized minimum 10 mA cm^–2 needed for large-scale applications⁸⁵ with a moderately active catalyst (25 turnovers per second); however, with a typical film thicknesses d_f = 1 μm the efficiency is rather low (see the shaded region in Figure 10 indicating the size of the reaction-diffusion layer). Importantly, this assumes facile substrate transport through the film (Figure 10, D_S = 10^–5 cm² s^–1) more typical of a freely diffusing species in solution. As the substrate diffusion coefficient is decreased below 10^–7 cm² s^–1 while holding all other values constant, a sharp decline in steady-state current density is observed (Figure 10e). As an example of typical diffusion rates, the diffusivities of tertiary amines (triethylamine, tripropylamine, etc.) through solvent-filled pores of a Zn MOF ([Zn₂L_0.5(BPDC)₂]₃·9DMF·9H₂O) were quantified in the range of 10^–9–10^–10 cm² s^–1.⁸⁶ However, we note that alkyl amines may not be representative of typical small molecule substrates for energy conversion applications. Clearly there is room for the field and in particular for electrochemistry as a technique to aid in the quantitative measurement of diffusion rates of small molecules through MOFs under conditions relevant to catalysis (solvated). Overall, the simulated results presented here preliminarily suggest that a combination of substrate diffusion and charge transport may be kinetically limiting in many MOF-based catalytic films of average thickness (∼1 μm); however, certainly more experimental studies addressing catalysis and transport phenomena are needed to fully assign the kinetic behavior of many catalytic MOFs.

Figure 10.

Progressively slower substrate diffusion: simulated concentration profiles of oxidized catalyst P (red), reduced catalyst Q (black), and substrate S (blue) using finite difference method using D_e^app = 5 × 10^–10 cm² s^–1, d_f = 1 μm, C_P = 1 M, κ_SC_S⁰ = 0.1 M, and kκ_SC_S = 25 s^–1, with D_S from (a) 5 × 10^–5, (b) 5 × 10^–7, (c) 5 × 10^–9, to (d) 5 × 10^–11 cm² s^–1. Substrate concentration within the film (blue lines, C_S) is normalized to the substrate concentration at the film–solution interface (equal to κ_SC_S⁰). Below each concentration profile the normalized local current density (cyan) as a function of distance from the electrode (x) normalized to the film thickness is shown. The shaded region indicates the location of the reaction-diffusion layer inside the film. (e) Calculated steady-state current density (at E ≪ E_P/Q) corresponding to the concentration profiles in part (a) through (d) plotted as a function of with the value of D_S shown next to each point. Other parameters are the same as above (D_e^app = 5 × 10^–10 cm² s^–1, d_f = 1 μm, C_P = 1 M, κ_SC_S⁰ = 0.1 M, and kκ_SC_S = 25 s^–1).

Opportunities

Future efforts toward improving or designing molecular catalysis in MOF films should include utilizing reaction-diffusion models (such as the simple one recalled above) to characterize charge and mass transport rates. However, importantly, deployment of these types of porous catalyst materials at scale requires optimizing both catalyst reactivity and transport properties concurrently. Avoiding transport limitations might require decelerating the catalytic rate so that it is slower than diffusive transport by operating the catalytic MOF film at lower current densities. However, this is not very effective for fast conversion of substrate to product on a large scale. Conversely, running the overall process at higher current densities (where the catalytic reaction is much faster than the diffusional processes) quickly becomes inefficient as transport limitations restrict the amount of active catalyst via the formation of boundary layers. Finding the most efficient operating conditions between these two scenarios can only be done when the intrinsic chemical reactivity of the catalyst toward the substrate and the transport properties of the catalyst support matrix are examined, characterized, and optimized together. For MOF-based molecular catalysis, this means that modifying the reactivity of the molecular catalyst alone is not enough to progress toward realistic applications of these materials, and significant efforts must be made to design these systems so as to balance chemical reactivity with the diffusional transport phenomena outlined here.

Once the transport parameters (diffusion coefficients) and intrinsic reaction kinetics are measured and the rate-limiting process or processes is identified, a clear step forward is to improve these limitations by one of two methods. As shown above, MOF films are indeed able to reach high current densities of industrial relevance (10 mA cm^–2). However, often the efficiency (what fraction of the catalysts are active in the film) is less than ideal, making these systems difficult to scale-up to meet requirements for applications. The first and most straightforward strategy is to modify the film to an optimal thickness where ≈ 1 and ≈ 1.^15,67,68 Practical methods to make MOF films in a controlled manner are critical in this endeavor.^87,88 Optimizing film thickness is displayed in Figure 11 (green curve) assuming facile substrate transport for simplicity, where starting from D_e^app = 5 × 10^–10 cm² s^–1, a 1 μm film produces 10 mA cm^–2 of current. Decreasing the film thickness from 1 μm to 100 nm (process I in Figure 11a) improves the overall efficiency to where nearly all the catalysts are active, while maintaining the same current density. However, the rates of substrate and electron-hopping diffusion set an upper limit on how thick the film can be made (i.e., no larger than the reaction-diffusion layer thickness), and thus bounds the overall rate of product formation. Alternatively, tuning the molecular building blocks is a unique property of MOFs that can be used to modify macroscopic transport properties—something that is relatively more difficult to accomplish in other porous materials lacking molecularly discrete components. Using the same example (Figure 11a), increasing D_e from 5 × 10^–10 cm² s^–1 to 5 × 10^–8 cm² s^–1 (process II in Figure 11a) gives an even higher current density of about 20 mA cm^–2 and unity catalyst efficiency with the same 100 nm film (Figure 11, red curve). Now with faster charge transport properties, the catalytic MOF film can be made thicker (up to the point where 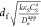≈ 1, process III in Figure 11a) without compromising efficiency, reaching a maximum of 100 mA cm^–2 with 1 μm thick films. Designing the pore environment to facilitate charge or substrate transport by synthetic tuning of the linkers or by well-established reticular chemistry^89,90 is thus a distinct advantage available to MOF materials. Ultimately, this will allow thicker films to be used, which do not display transport limitations, giving higher overall catalyst efficiency and higher rates of production.

Figure 11.

(a) Options for optimizing MOF-based molecular catalysis either by adjustment of the film thickness or by increasing one or more diffusion coefficients by modifying the pore structure/properties via linker design. The example shown here applies to when electron-hopping diffusion is much slower than substrate transport (i_s ≫ i_e). The shaded region below each curve signifies film thicknesses where the efficiency is less than unity and the amount of active catalyst is less than the amount of total catalyst. In (a), the observed current density is plotted versus the film thickness (d_f) for two different values of D_e^app, 5 × 10^–10 cm² s^–1 (green curve) and 5 × 10^–8 cm² s^–1 (red curve). Other parameters are the same as above: C_P = 1 M, κ_SC_S⁰ = 0.1 M, and kκ_SC_S = 25 s^–1. (b) Effect of different intrinsic catalyst turnover frequencies, kκ_SC_S⁰ = 25 s^–1 (green curve) and kκ_SC_S = 250 s^–1 (blue curve), on observed current density with D_e^app = 5 × 10^–10 cm² s^–1, C_P = 1 M, and κ_SC_S⁰ = 0.1 M. (c) Double logarithmic plot of catalyst efficiency (red curve, left axis) and observed current density normalized to the electron diffusion limited current density, 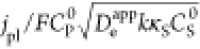(black curve, right axis), versus the dimensionless control parameter = . Optimal catalytic performance is obtained at the intersection of these two curves when = 1 (shaded circle).

It is interesting to note that the current densities in this simple example (≥10 mA cm^–2) could be achieved with a relatively slow intrinsic rate of turnover (25 s^–1) for the molecular catalyst covalently incorporated in the MOF. This is certainly due to the relatively high concentration of active sites within the MOF film (10–100 nmol cm^–2 is a typical range^32,34,83). If the intrinsic rate of the molecular catalyst were increased further, this would allow one to make thinner films utilizing less material and achieve higher current densities. This is shown in Figure 11 where an increasing in k_cat by an order of magnitude for the same charge transport rate (D_e^app = 5 × 10^–10 cm² s^–1 and d_f = 0.1 μm) increases the observed current density from 10 to 30 mA cm^–2 (process IV, Figure 11b). Reducing the film thickness (process V, Figure 11b) is then an option for achieving optimal efficiency. Overall, a common theme in all the examples presented here is the realization that reaction-diffusion leads to a balance between catalyst efficiency (amount of used catalyst within the film) and the total rate of production (observed current density), as depicted in Figure 11c. Optimal catalytic performance (highest efficiency and highest current density) is obtained when = 1 (Figure 11c, intersection between red and black curves).⁶⁷

Conclusion

Metal–organic frameworks are excellent candidates for support matrices in which to incorporate molecular catalysts. A major advantage to this strategy is the synthetic tunability of both the framework and the catalyst at the molecular scale. At present, however, a notable barrier to this realization and to the eventual application of these materials to catalytic processes at industrial scale is the coupling of transport phenomena to traditional chemical kinetics, as a consequence of immobilization of the molecular species in a finite 3D porous structure. However, once transport by diffusion is quantitatively analyzed and taken into account using simple and well-established reaction-diffusion kinetic models, first introduced by Thiele and Damköhler in the 1930s, optimizing the pore structure of the framework for facile diffusive transport could yield highly efficient catalytic materials as well as a deeper understanding of the intrinsic kinetics and mechanisms of the molecular catalyst under operating condition inside the MOF-film structure. MOFs are uniquely suited to this task due to the structure–property relationship between their molecular-level building blocks and their macroscopic physical and chemical properties. The kinetic information gained from the analysis presented here can be in turn used to inform molecular-level design that will best elevate metal–organic frameworks toward becoming suitable for applications as high-performance catalysts for the electrochemical activation and conversion of small molecules.

Glossary

Symbols

C_j

concentration of species j (M, mol cm⁻³)

C_P^o

total electroactive concentration of redox-active linker, P (M, mol cm⁻³)

C_S^o

bulk concentration of substrate (M, mol cm⁻³)

d_f

film thickness (cm)

d

average hopping distance (cm)

D_e

electron hopping diffusion coefficient (cm² s⁻¹)

D_e^app

apparent charge transport diffusion coefficient (cm² s⁻¹)

D_S

intra-MOF diffusion coefficient of substrate (cm² s⁻¹)

E

electrode potential (V)

E⁰

standard potential (V)

F_j

molar flux of species j (mol cm⁻² s⁻¹)

F

Faraday constant (C mol⁻¹)

G_k

production/consumption rate of chemical reaction per unit surface area (mol cm⁻² s⁻¹)

i

current (A)

i_pl

plateau or limiting steady state current (A)

i_s

characteristic current density for substrate diffusion within film (A cm⁻²)

i_e

characteristic current density for diffusional charge transport (A cm⁻²)

i_k

characteristic current density for catalytic reaction (A cm⁻²)

j

current density (A cm⁻²)

j_pl

plateau or limiting steady state current density (A cm⁻²)

k

second order rate constant of chemical step (M⁻¹ s⁻¹, cm³ mol⁻¹ s⁻¹)

k_cat

observed first order catalytic rate constant (s⁻¹)

k_e

self-exchange rate constant occurring only in direction normal to electrode (M⁻¹ s⁻¹, cm³ mol⁻¹ s⁻¹)

k_ex

self-exchange rate constant (M⁻¹ s⁻¹, cm³ mol⁻¹ s⁻¹)

k_s

standard interfacial rate constant (cm s⁻¹)

m_Q^active

moles of active catalyst in MOF film (mol)

n′

apparent reaction order in substrate

n

true reaction order in substrate

r

radial distance (cm)

R

gas constant (J mol⁻¹ K⁻¹)

R_a

MOF particle radius (cm)

S

surface area (cm²)

t

time (s)

TOF_max^app

maximum apparent turnover frequency (s⁻¹)

TOF_max^true

maximum true turnover frequency (s⁻¹)

x

distance in Cartesian coordinates perpendicular to electrode surface (cm)

δ_rxn

reaction-diffusion layer thickness (cm)

δ

diffusion layer thickness (cm)

κ_S

partition equilibrium constant for substrate crossing MOF film-solution interface

ν

scan rate (V s⁻¹)

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.0c02899.

• CV simulations and corresponding concentration profiles of electron-hopping diffusion occurring in a MOF film (MP4)

The authors declare no competing financial interest.