Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Jun 15;53(13):5599–5603. doi: 10.1021/acs.macromol.9b02647

The Role of Polyethylene Wax on the Thermal Conductivity of Transparent Ultradrawn Polyethylene Films

Xinglong Pan †, Albert H P J Schenning †,‡, Lihua Shen †,§, Cees W M Bastiaansen †,∥,*
PMCID: PMC7366500  PMID: 32684640

Abstract

graphic file with name ma9b02647_0005.jpg

Transparency and thermal conductivity of ultradrawn, ultrahigh-molecular-weight polyethylene films containing different contents of low-molecular-weight polyethylene wax (PEwax) are explored from experimental and theoretical viewpoints. It is shown that the addition of PEwax decreases light scattering in all directions, resulting from a reduction of defects while having little effect on crystallinity or chain orientation of ultradrawn films. In general, upon the addition of PEwax, the thermal conductivity of ultradrawn films increases with the highest conductivity being 47 (W m–1 K–1) and subsequently decreases at higher concentrations. The thermal conductivity also depends on draw ratio and number-average molecular weight (Mn) of the films. A model is presented which correlates the thermal conductivity of the films with the draw ratio and Mn, enabling explanation of the experimental results. Hence, the thermal conductivity of ultradrawn polyethylene films can be predicted as a function of Mn and draw ratio.

1. Introduction

Thermally conductive materials such as metals, ceramics, carbon materials, and polymer composites are receiving a lot of attention from both scientific and application points of view. Polymer composites are attractive due to their low density, ease of processing, and chemical stability.1−4 In these composites, the intrinsically low conductivity of polymers is enhanced by adding thermally conductive additives. However, most polymer composites are nontransparent due to light scattering and/or absorbance by additives, which limits their applications. Most polymers are amorphous or semicrystalline and their low thermal conductivity is usually attributed to phonon scattering.2,5 Generally, phonon transport in isotropic polymers is influenced by many factors including the number of side chains, the chemical composition, and morphology.2,3 The thermal conductivity of isotropic polymers is typically below 1 W/(m K),6 while anisotropic polymers with higher thermal conductivity can be obtained via a variety of techniques such as drawing.7−10

The thermal conductivity of ultradrawn PE films in the drawing direction increases nonlinearly with increasing draw ratio,11,12 while the transverse thermal conductivity slightly decreases.12 A model has been derived by Ronca et al. to describe the nonlinear thermal conductivity versus draw ratio of ultradrawn PE, which assumes that the thermal conductivity is governed only by the draw ratio.11 Xu et al. reported that thermal conductivity also depends on the length of the crystal phase.9 Furthermore, computer simulations suggest that the thermal conductivity of a single PE chain and bulk PE might also depend on chain length to some extent.6,13−15 However, experimental evidence for chain length dependence of the thermal conductivity in drawn polymer films has not been reported to date.

Recently, we reported on highly transparent, ultradrawn high-density polyethylene and ultrahigh-molecular-weight polyethylene (UHMWPE) nanocomposite films containing graphene and 2-(2H-benzotriazol-2-yl)-4,6-di-tert-pentylphenol (BZT) as additives16,17 with high thermal conductivity (∼75 W m–1 K–1).13 We now report on the use of polyethylene wax (PEwax) as an additive to obtain highly transparent, thermally conductive UHMWPE films. Upon the addition of PEwax, the thermal conductivity of the polymer films increases with the highest conductivity being 47 (W m–1 K–1), and it decreases again at higher concentrations. It is demonstrated that the thermal conductivity of ultradrawn films not only depends on the draw ratio but also on the number-average molecular weight (Mn) of polyethylene. A deterministic model is developed able to describe the Experimental Results. Hence, this model is useful to predict the thermal conductivity of drawn polymer films as a function of their Mn and draw ratio.

2. Experimental Section

2.1. Materials

UHMWPE (weight-average molecular weight (Mw) ∼ 4 × 103 kg/mol and a polydispersity index (PDI or Đ ∼ 7) was received from DSM (Geleen, The Netherlands). PEwax B (Mn ∼ 1000 g/mol, Đ ∼ 1.08) and PEwax C (Mn ∼ 3000 g/mol, Đ ∼ 1.08) were purchased from Baker Hughes Incorporated. PEwax D (Mn ∼ 4255 g/mol, Đ ∼ 3) was received from Mitsui Chemicals Incorporated (Japan). Paraffin oil and xylene were purchased from Thermo Fisher Scientific Incorporated (The Netherlands) and Biosolve BV (The Netherlands), respectively. All reagents were used without further purification.

2.2. Fabrication

First, UHMWPE powder (2 g), PEwax (0, 1, 2, and 5 wt % to UHMWPE/PEwax blend), and the antioxidant Irganox 1010 (0.1 wt % to UHMWPE) were added to xylene (200 mL). After degassing via ultrasonication for 30 min, the mixture was stirred at approximately 120 °C in an oil bath until the Weissenberg effect was observed. The solution was then cast into aluminum trays of approximately 144 cm2 after UHMWPE was completely dissolved. The solution-cast films were left at room temperature for several days to evaporate the xylene completely. Dry UHMWPE/PEwax (PE-wax) films were then cut into small strips and were stretched at ∼120 °C.

2.3. Analytical Techniques

The surface microstructure and roughness of the films were characterized by optical microscopy (Leica DM 2700M) and an Interferometer (FOGALE Nanotech Incorporated, France). The polarized transmittance of samples was measured in the range of 0–180° at 550 nm on a Shimadzu (Japan) UV-3102 PC spectrophotometer with a 1° interval. During UV–vis measurement, the samples were sandwiched between two glass slides and coated with a few drops of paraffin oil to reduce the surface scattering of the samples.16 Small-angle light scattering (SALS) patterns were measured using a He–Ne gas laser (wavelength: 632 nm) and Vv patterns were obtained with the polarizer and analyzer parallel. Differential scanning calorimetry (DSC) experiments were performed on a TA Instruments Q2000 calorimeter at a rate of 10 °C/min between 25 to 180 °C. Wide-angle X-ray scattering (WAXS) measurements were performed on a Ganesha lab instrument equipped with a Genix-Cu ultralow divergence source producing X-ray with a wavelength of 1.54 Å. Raman spectra were performed to characterize the crystallinity and chain orientation on a Raman Microscope (Witec Alpha 300 R). Thermal conductivity was measured by a setup based on the Angstrom method as previously reported.16

3. Results and Discussion

3.1. Thermally Conductive and Transparent Ultradrawn Films

Transparent ultradrawn UHMWPE (Mw ∼ 4 × 103 kg/mol) with different ratios of PEwax of different Mn (PEwax B, Mn ∼ 1000 g/mol; PEwax C, Mn ∼ 3000 g/mol, and PEwax D, Mn ∼ 4255 g/mol) were fabricated by solution-casting, followed by solid-state stretching. The Mw of the PE films decreases linearly upon adding PEwax (Figure S1; Figure S1A) while the Mn of the films shows a sharp, nonlinear decrease (Figure S1B). The polydispersity, Đ, displays an inverse, linear trend (Figure S1C), indicating that adding wax with low Mw and Mn has little effect on Mw of PE-wax films but a large effect on Mn, since short chains mainly contribute to Mn. To further characterize the structure of ultradrawn UHMWPE films before and after adding different PEwax, Raman spectra were recorded (Figures S2, S4). The intensity ratio of Raman bands at 1128 to 1060 cm–1 is representative of the orientation of ultradrawn films, while the ratio of integral areas of the Raman band at 1414 cm–1 to Raman the bands at 1293 and 1305 cm–1 represent the crystallinity of the films.18 The Raman results indicate that adding PEwax has no obvious effect on the crystallinity or the orientation of the films, while drawing increases the chain orientation and crystallinity, consistent with the results of DSC and WAXS experiments in Table S1 and Table S2.

First, the polarized visible light transmission was measured of the ultradrawn PE and PE-wax films containing 1 wt % PEwax (Figure 1A, Figure S5). The transparency of the PE-wax films is higher than that of the PE films and displays angular independence. The PE-wax films exhibit a higher visible light transmission (over 90%), while pure PE film shows a lower visible light transmission (84%). However, ultradrawn PE-wax films with different waxes or Mn did not show the obvious difference between optical transmission (Figure 1 and Figure S5). Small-angle light scattering (SALS) measurements reveal strong and weak light scattering in the pure PE and PE-wax films, respectively. Apparently, adding PEwax improves visible light transmission by decreasing defects inside the ultradrawn films, although there is no obvious difference in the surfaces of the ultradrawn films (Figures S2 and S4). In the past, the enhanced visible light transmission was attributed to the filling of microvoids with an elongated shape parallel to the drawing direction,17 and it is assumed that this is also the case here. The dependence of light transmission on the polarization direction is different from the PE-BZT and PE-BZT-graphene films reported earlier which show a difference of visible light transmission at different polarization directions (Figure S5).16 This difference might be attributed to the birefringence of the drawn polymer and the slight mismatch in refractive indexes between pure BZT, BZT/graphene, and PE in the direction perpendicular or parallel to drawing direction.17 The improved optical transmission of PE-wax films could be attributed to the decreasing voids inside drawn films and matched refractive indexes between PE and PEwax.

Figure 1.

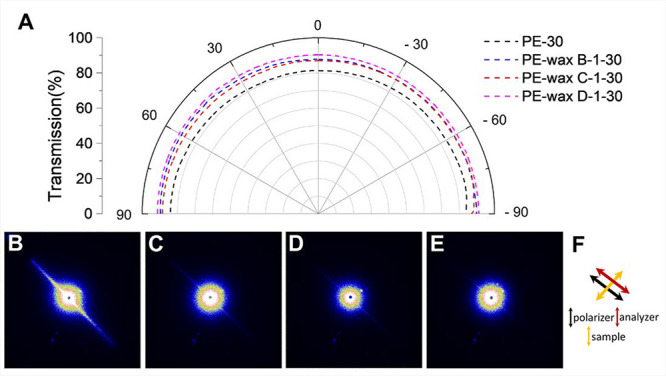
Figure 1

Open in a new tab

(A) Polarized visible light transmission of pure PE and PE-wax films at 550 nm (the angular axes represent the angle between the polarizer and the drawing direction of films). (B–E) SALS (Vv) patterns of PE, PE-wax B, PE-wax C, and PE-wax D films with 1 wt % wax and a draw ratio of 30. (F) Drawing directions of samples and polarizers in SALS images.

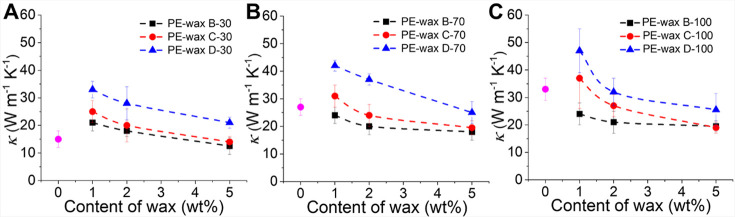
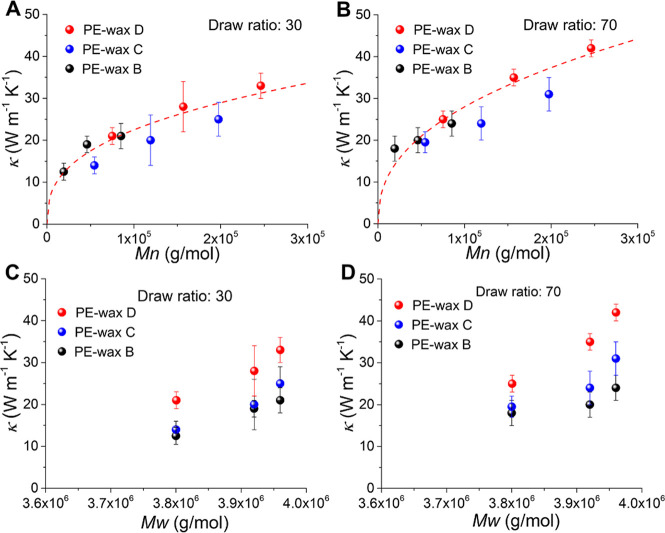
Next, the thermal conductivities of the different ultradrawn UHMWPE and PEwax films were measured (Figure 2A–C). In the case of PEwax films with a draw ratio of 30 (Figure 2A), the thermal conductivity of the films increased upon the addition of 1 wt % PEwax. PE-wax D films exhibit a higher thermal conductivity than the PE-wax C and PE-wax B films, suggesting that the molecular weight of the wax has an effect on the thermal conductivity. Upon increasing the PE-wax content, the films showed a nonlinear decrease in the thermal conductivity (Figure 2A). In general, upon increasing the draw ratio from 30 to 100, the thermal conductivity increases (Figure 2A–C) and the highest conductivity of 47 (W m–1 K–1) is observed for the PE-wax containing 1 wt % PEwax D with a draw ratio of 100 (Figure 2C and Figure 3A).

Figure 2.

Figure 2

Open in a new tab

Thermal conductivity of PE-wax films as a function of contents of PEwax with fixed draw ratios (A–C). The pink dot represents the data of pure PE films (without wax) with draw ratios of 30, 70, and 100.

Figure 3.

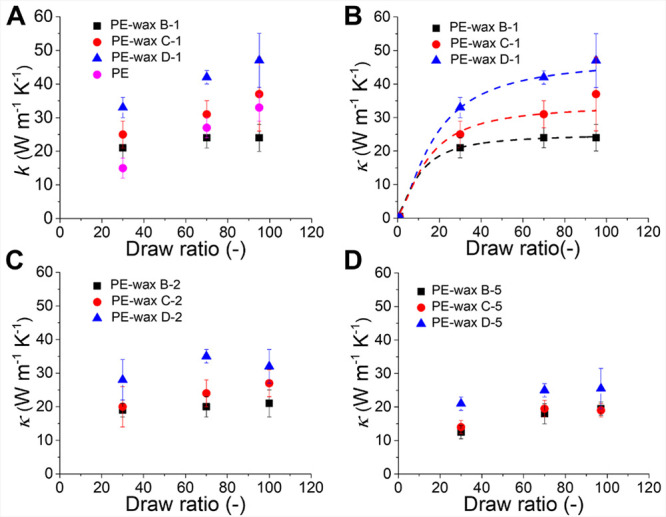
Figure 3

Open in a new tab

(A–D) Thermal conductivity of PE-wax films as a function of draw ratios. A: pure PE and PE with 1 wt % waxes. B–D: PE with 1, 2, and 5 wt % waxes. In Figure 3B, the dashed lines are the fitting curves using eq 1 and the value of thermal conductivity with a draw ratio of 1 is set as 0.5 W m–1 K–1.2,5,7

When displaying the thermal conductivity as a function of the draw ratio, a nonlinear relationship is observed (Figure 3A–D), consistent with previous publications.10,19 However, the thermal conductivity of ultradrawn films with high PEwax content did not increase further (Figure 3C,D).

The lower thermal conductivity of pure PE ultradrawn films could result from the phonon scattering (Figure 1) caused by defects such as nano- or microvoids inside the bulk PE films. Upon addition of 1% of PE-wax, these voids are filled, leading to less phonon scattering and enhanced thermal conductivity. However, PE-wax B films having a low molecular weight of PE-wax with a high draw ratio are an exception. The different PE-wax films show different thermal conductivity at the same draw ratio, and the films with the highest molecular weight PEwax (PE-wax D) outperform the other films. As the crystallinity and chain orientation in the PE-wax films is the same (vide supra), this reveals that the thermal conductivity also depends on the molecular weight of the wax.

To investigate the molecular weight dependence further, the thermal conductivity of PE-wax films with different PEwax concentrations was plotted as a function of the number-average molecular weight, Mn, and the weight-average molecular weight, Mw, at two draw ratios (Figure 3). The plots show that the thermal conductivity of ultradrawn films increases with increasing Mn, while there is no such relationship with Mw. PE-wax films with similar Mw and content of PEwax show different thermal conductivities, indicating the thermal conductivity of ultradrawn films is more related to Mn than Mw.

3.2. Model for Thermal Conductivity, Mn, and Draw Ratio

To shed light on the relationship between Mn, draw ratio, and thermal conductivity of PE-wax films, a model is developed based on the assumption that the extended-chain region mainly contributes to thermal conductivity in ultradrawn films and that the majority of regions in ultradrawn PE films are extended chain regions.10 Thus, only the effect of the extended-chain region is considered in our model.

The thermal conductivity (κ) in anisotropic polymers has been described by Ronca et al. (eq 1):11

3.2. 1

where λ is the draw ratio, κ1 and κ2 the thermal conductivities of perfectly oriented polymers parallel and perpendicular to the chain axis, respectively, and they are considered to be constant typically. It was found that eq 1 can also describe our data at a constant Mn in each PE-wax system assuming that the thermal conductivity on unstretched PE-wax films is low (Figure 3B). However, this equation is not able to describe the different thermal conductivity values for the different PE-wax films (Figure 4A,B).

Figure 4.

Figure 4

Open in a new tab

Thermal conductivity of PE-wax films with draw ratios of 30 and 70 as functions of Mn (A, B) and Mw (C, D). The red dashed lines are the curves fit using eq 4. When the draw ratio is 70 times, κ is close to κ1 and κ2 is ignored. The values of parameters in eq 4 are obtained based on the thermal conductivity at a draw ratio of 70. Thermal conductivity of PE-wax films with a draw ratio of 100 as functions of Mn and Mw was shown in Figure S7. The data of pure PE films are excluded due to their different morphology with PE-wax films.

As mentioned earlier, κ1 has been described in computer simulations as an exponential function of chain length (L).13,14 However, the thermal transport is different in a single PE chain than PE films,20 as PE chains are difficult to be extended completely in polymer films without entanglements and kinks.13 Therefore, in our model, κ1 is described by an exponential function of Mn instead of chain length.

3.2. 2

Here, B is a constant and its unit is W/(g/mol)γ m–1 K–1. γ indicates the competition between diffusive and ballistic phonon transport, where diffusive and ballistic phonon transport leads to γ = 0 and 1, respectively.13

By combining eqs 1 and 2, eq 3 describes both the dependence of the thermal conductivity as a function of Mn and the draw ratio:

3.2. 3

In the case of a specific draw ratio, the thermal conductivity is described roughly by Mn following the equation below, which is consistent with that in a perfect stretched PE chain.13

3.2. 4

The values of B and γ are approximately 0.206 ± 0.13 and 0.426 ± 0.052 by fitting the data in Figure 4A and B.

When Mn was fixed, eq 1 was obtained from eq 3 while eq 4 was achieved from eq 3 with a fixed draw ratio. Equation 3 fits our data as well (Figure S8). Equation 4 was verified using the ultimate thermal conductivity predicted by eq 1, revealing the good fitting between eq 1 and eq 4 in different systems (Table S4). These fitting results demonstrate the accuracy of our model and its feasibility in other polyethylene systems.

According to our model, the draw ratio is the main factor determining thermal conductivity at low draw ratios, while Mn mainly contributes to the increase in thermal conductivity at high draw ratios. This indicates that polyethylene films with a high Mn could exhibit a high thermal conductivity at high draw ratios. The increased thermal conductivity in ultradrawn films with the high Mn could be attributed to less short chains, resulting in weak photon scattering.14 However, chain entanglements, side chains, and defects inside of films show negative effects on thermal conductivity and these factors were not considered in our work (see also Supporting Information). The thermal conductivity of (isotropic and anisotropic) polymers is governed by intramolecular and intermolecular phonon transport. In most polymers, the intramolecular phonon transport along the macromolecular backbone is dominating, which results in a high theoretical thermal conductivity for extended polymer chains with an infinite molecular weight.6,9,10,14 In polymeric systems with a high molecular weight, the macroscopic thermal conductivity is usually restricted by intermolecular phonon transport between the chains, which is facilitated by orientation and chain extension and hindered by interfibrillar voids.1,2,15,20,21 Upon the addition of PE wax, the interfibrillar voids in ultradrawn PE are filled which decreases intermolecular phonon scattering and enhances thermal conductivity. With the increasing Mn of PE wax, the number of chain ends of PE wax decreases, resulting in less phonon scattering. Furthermore, the density and size of the PE domains might decrease when Mn of PE wax increases. This could explain the observed semiempirical relationship between the thermal conductivity and the Mn of PE wax.

4. Conclusions

Highly transparent PE-wax ultradrawn films were fabricated by solution-casting and solid-stretching method. It was found that adding PEwax improves the visible light transmission (>90%) of ultradrawn PE films via decreasing defects inside films, while adding PEwax has a little effect on the crystallinity and orientation of ultradrawn films. It is revealed that the thermal conductivity of ultradrawn PE-wax films not only depends on the draw ratio but also on the Mn of PE-wax films. Furthermore, the thermal conductivity of PE-wax films predicted by our model is in good agreement with experimental results. The model shows the relationship between thermal conductivity, Mn, and draw ratio and it is able to predict the thermal conductivity of drawn polymers by macroscopic parameters, such as Mn and draw ratio, which is vital for making transparent, high thermally conductive polymer films in optoelectronic devices where thermal management is crucial.

Acknowledgments

We thank Dr. Tom A. P. Engels, Ir. Simon J. A. Houben, and Ir. Rob C. P. Verpaalen for the helpful discussions, and A. B. P. Bus for practical support. This work was funded by the China Scholarship Council (CSC201706450053).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.macromol.9b02647.

  • Mn, Mw, and DPI of samples. Optical images of PE-30, PE-wax B-1-30, PE-wax C-1-30, PE-wax D-1-30, PE-70, PE-wax B-1-70, PE-wax C-1-70, and PE-wax D-1-70 films. Surface (bottom) structure and roughness of films. Raman spectra of PEwax B, PEwax C, PEwax D, and PE powder. DSC and WAXS results of samples. Thermal conductivity of samples as a function of Mw. Fitting curves of thermal conductivity of PE and PE-wax ultradrawn films. (PDF)

The authors declare no competing financial interest.

Supplementary Material

ma9b02647_si_001.pdf (2.1MB, pdf)

References

  1. Xu X.; Chen J.; Zhou J.; Li B. Thermal Conductivity of Polymers and Their Nanocomposites. Adv. Mater. 2018, 30, 1705544. 10.1002/adma.201705544. [DOI] [PubMed] [Google Scholar]
  2. Chen H.; Ginzburg V. V.; Yang J.; Yang Y.; Liu W.; Huang Y.; Du L.; Chen B. Thermal Conductivity of Polymer-Based Composites: Fundamentals and Applications. Prog. Polym. Sci. 2016, 59, 41–85. 10.1016/j.progpolymsci.2016.03.001. [DOI] [Google Scholar]
  3. Huang C.; Qian X.; Yang R. Thermal Conductivity of Polymers and Polymer Nanocomposites. Mater. Sci. Eng., R 2018, 132, 1–22. 10.1016/j.mser.2018.06.002. [DOI] [Google Scholar]
  4. Zhang Y.; Heo Y. J.; Son Y. R.; In I.; An K. H.; Kim B. J.; Park S. J. Recent Advanced Thermal Interfacial Materials: A Review of Conducting Mechanisms and Parameters of Carbon Materials. Carbon 2019, 142, 445–460. 10.1016/j.carbon.2018.10.077. [DOI] [Google Scholar]
  5. Han Z.; Fina A. Thermal Conductivity of Carbon Nanotubes and Their Polymer Nanocomposites: A Review. Prog. Polym. Sci. 2011, 36, 914–944. 10.1016/j.progpolymsci.2010.11.004. [DOI] [Google Scholar]
  6. Henry A.; Chen G. High Thermal Conductivity of Single Polyethylene Chains Using Molecular Dynamics Simulations. Phys. Rev. Lett. 2008, 101, 235502. 10.1103/PhysRevLett.101.235502. [DOI] [PubMed] [Google Scholar]
  7. Saeidijavash M.; Garg J.; Grady B. P.; Smith B.; Li Z.; Young R. J.; Tarranum F.; Bel Bekri N. High Thermal Conductivity through Simultaneously Aligned Polyethylene Lamellae and Graphene Nanoplatelets. Nanoscale 2017, 9, 12867–12873. 10.1039/C7NR04686C. [DOI] [PubMed] [Google Scholar]
  8. Zhu B.; Liu J.; Wang T.; Han M.; Valloppilly S.; Xu S.; Wang X. Novel Polyethylene Fibers of Very High Thermal Conductivity Enabled by Amorphous Restructuring. ACS Omega 2017, 2, 3931–3944. 10.1021/acsomega.7b00563. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Xu Y.; Kraemer D.; Song B.; Jiang Z.; Zhou J.; Loomis J.; Wang J.; Li M.; Ghasemi H.; Huang X.; et al. Nanostructured Polymer Films with Metal-like Thermal Conductivity. Nat. Commun. 2019, 10, 1771. 10.1038/s41467-019-09697-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Shen S.; Henry A.; Tong J.; Zheng R.; Chen G. Polyethylene Nanofibres with Very High Thermal Conductivities. Nat. Nanotechnol. 2010, 5, 251–255. 10.1038/nnano.2010.27. [DOI] [PubMed] [Google Scholar]
  11. Ronca S.; Igarashi T.; Forte G.; Rastogi S. Metallic-like Thermal Conductivity in a Lightweight Insulator: Solid-State Processed Ultra High Molecular Weight Polyethylene Tapes and Films. Polymer 2017, 123, 203–210. 10.1016/j.polymer.2017.07.027. [DOI] [Google Scholar]
  12. Choy C. L.; Wong Y. W.; Yang G. W.; Kanamoto T. Elastic Modulus and Thermal Conductivity of Ultradrawn Polyethylene. J. Polym. Sci., Part B: Polym. Phys. 1999, 37, 3359–3367. . [DOI] [Google Scholar]
  13. Duan X.; Li Z.; Liu J.; Chen G.; Li X. Roles of Kink on the Thermal Transport in Single Polyethylene Chains. J. Appl. Phys. 2019, 125, 164303. 10.1063/1.5086453. [DOI] [Google Scholar]
  14. Liu J.; Yang R. Length-Dependent Thermal Conductivity of Single Extended Polymer Chains. Phys. Rev. B: Condens. Matter Mater. Phys. 2012, 86, 104307. 10.1103/PhysRevB.86.104307. [DOI] [Google Scholar]
  15. Ouyang Y.; Zhang Z.; Xi Q.; Jiang P.; Ren W.; Li N.; Zhou J.; Chen J. Effect of Boundary Chain Folding on Thermal Conductivity of Lamellar Amorphous Polyethylene. RSC Adv. 2019, 9, 33549–33557. 10.1039/C9RA07563A. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Pan X.; Shen L.; Schenning A. P. H. J.; Bastiaansen C. W. M. Transparent, High-Thermal-Conductivity Ultradrawn Polyethylene/Graphene Nanocomposite Films. Adv. Mater. 2019, 31, 1904348. 10.1002/adma.201904348. [DOI] [PubMed] [Google Scholar]
  17. Shen L.; Nickmans K.; Severn J.; Bastiaansen C. W. M. Improving the Transparency of Ultra-Drawn Melt-Crystallized Polyethylenes: Toward High-Modulus/High-Strength Window Application. ACS Appl. Mater. Interfaces 2016, 8, 17549–17554. 10.1021/acsami.6b04704. [DOI] [PubMed] [Google Scholar]
  18. Shrestha R.; Li P.; Chatterjee B.; Zheng T.; Wu X.; Liu Z.; Luo T.; Choi S.; Hippalgaonkar K.; De Boer M. P.; et al. Crystalline Polymer Nanofibers with Ultra-High Strength and Thermal Conductivity. Nat. Commun. 2018, 9, 1664. 10.1038/s41467-018-03978-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Xu Y.; Wang X.; Zhou J.; Song B.; Jiang Z.; Lee E. M. Y.; Huberman S.; Gleason K. K.; Chen G. Molecular Engineered Conjugated Polymer with High Thermal Conductivity. Sci. Adv. 2018, 4, 3031. 10.1126/sciadv.aar3031. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Henry A.; Chen G.; Plimpton S. J.; Thompson A. 1D-to-3D Transition of Phonon Heat Conduction in Polyethylene Using Molecular Dynamics Simulations. Phys. Rev. B: Condens. Matter Mater. Phys. 2010, 82, 114308. 10.1103/PhysRevB.82.144308. [DOI] [Google Scholar]
  21. Hennig J. Anisotropy and Structure in Uniaxially Stretched Amorphous High Polymers. J. Polym. Sci., Part C: Polym. Symp. 1967, 16, 2751–2761. 10.1002/polc.5070160528. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ma9b02647_si_001.pdf (2.1MB, pdf)

Articles from Macromolecules are provided here courtesy of American Chemical Society

RESOURCES