Background Reduction in STED-FCS Using a Bivortex Phase Mask

Abstract

Fluorescence correlation spectroscopy (FCS) is a valuable tool to study the molecular dynamics in living cells. When used together with a super-resolution stimulated emission depletion (STED) microscope, STED-FCS can measure diffusion processes on the nanoscale in living cells. In two-dimensional (2D) systems like the cellular plasma membrane, a ring-shaped depletion focus is most commonly used to increase the lateral resolution, leading to more than 25-fold decrease in the observation volume, reaching the relevant scale of supramolecular arrangements. However, STED-FCS faces severe limitations when measuring diffusion in three dimensions (3D), largely due to the spurious background contributions from undepleted areas of the excitation focus that reduce the signal quality and ultimately limit the resolution. In this paper, we investigate how different STED confinement modes can mitigate this issue. By simulations as well as experiments with fluorescent probes in solution and in cells, we demonstrate that the coherent-hybrid (CH) depletion pattern created by a bivortex phase mask reduces background most efficiently and thus provides superior signal quality under comparable reduction of the observation volume. Featuring also the highest robustness to common optical aberrations, CH-STED can be considered the method of choice for reliable STED-FCS-based investigations of 3D diffusion on the subdiffraction scale.

Fluorescence correlation spectroscopy (FCS) is a technique that, with conventional microscopy, allows the observation of molecular diffusion at the scale of a couple of hundreds of nanometers.^1,2 Traditional FCS implementation makes use of confocal optics and is as such limited by the diffraction limit to length-scales of approximately 200 nm. This precludes insights into molecular nanoscale organization, for instance in the plasma membrane. Fortunately, the resolution of FCS microscopes can be increased by means of stimulated emission depletion (STED) to access the diffusion information on the subdiffraction scale (STED-FCS³). In STED microscopy, the excitation laser beam is overlaid with a high-intensity depletion laser beam that exhibits a central intensity minimum, inducing stimulated emission in the areas of its high intensity and thus reducing the effective observation volume to the very center of the excitation focus.

In an ideal STED configuration, photons are emitted only in the center of the focus, in a super-resolved volume. However, in practice, spurious background noise is emitted from outside of this area, either because of re-excitation of fluorophores by the STED laser or because of an imperfect overlap between the excitation and depletion beams.⁴ Methods such as stimulated emission double depletion (STEDD),⁵ background subtraction by polarization switching⁶ or separation of photons by lifetime tuning (SPLIT)^7,8 have been developed to circumvent these issues. STEDD and polarization switching involve substantial hardware modifications from the standard STED imaging setup, limiting their widespread dissemination. STEDD and SPLIT also require photon-timing detection electronics, which may not be ubiquitously available, and impose a careful offline calibration of the dyes’ fluorescence lifetime, thus, precluding measurements in samples where the fluorescence lifetime varies spatially. For these reasons, it can be preferable to improve the physical depletion pattern of background photons using the STED laser, with minimal alterations to the most frequently used (commercial) setups.

The most common STED depletion pattern is a ring-shaped focus constraining the lateral resolution but leaving the axial resolution unchanged (2D-STED, Figure 1, left). This depletion pattern has been extensively used to study two-dimensional systems, like cellular membranes,⁹⁻¹³ but faces severe limitations when studying three-dimensional diffusion due to varying axial cross sections and high background originating from undepleted areas^10,14 that leads to an increase in the apparent number of molecules in the observation volume.^10,15 Out-of-focus contributions can, in principle, be reduced by using a total-internal-reflection-fluorescence (TIRF) microscopy configuration (TIRF-STED-FCS¹⁶), but this limits the spatial range of achievable measurements and precludes most investigations deeper inside the cellular cytoplasm. Alternatively, a bottle-shaped depletion beam can be employed to essentially constrain the axial resolution (z-STED). However, this configuration is more sensitive to optical aberrations,^17,18 which can only be mitigated with advanced implementation of adaptive optics.¹⁹ Even aberration-free z-STED-FCS, though, exhibits spurious contributions from undepleted areas that damp the amplitude of the autocorrelation function, bias measurements of the numbers of molecules, and reduce the signal-to-noise ratio.^3,10 A combination of both 2D and z-STED depletion patterns (3D-STED) has also been used in STED-FCS,^5,10 but did not significantly reduce background contributions. To obtain an FCS signal of adequate quality under such conditions, extremely bright and photostable fluorescent probes are needed or excessively long acquisition times required, which both pose severe limitations to final applicability of the technique.

Figure 1.

STED confinement modes. Top: Schematics of the phase patterns of the masks (left, black to white: phase shift from 0 to 2π) used to generate the corresponding STED depletion patterns (right, axial cross sections of back-reflected images of gold beads, scale bar: 500 nm). Bottom: experimental images of 40-nm fluorescent beads, acquired in confocal (left) and with the different STED confinement modes, at a STED laser power of 55 mW. Scale bar: 200 nm.

More recently, the contrast in STED imaging has been increased using a superposition of two mutually coherent ring-shaped foci created by a bivortex phase mask²⁰ named coherent-hybrid (CH) STED (Figure 1, right). Anticipating signal-to-noise improvements also in STED-FCS, we here investigated the spatial distribution of background in STED-FCS experiments performed with common STED confinement modes (2D-, z-, and 3D-STED), as well as with CH-STED. We characterized the performance and sensitivity to optical aberrations of each of these confinement modes in STED-FCS and showcased their use in biological specimens.

Origin of Background in STED-FCS in 3D

Simulations

Recent work showed that the relatively poor signal-to-background ratio (SBR) obtained with 2D-STED-FCS when studying 3D diffusion was due to low-intensity contributions originating from undepleted areas of the excitation focus.^10,14 To extend this study to different STED confinement modes, we first obtained better insight into spatial origins of signal and background by simulating the excitation and depletion foci of our system. To this end, we calculated the three-dimensional intensity distributions of the excitation and depletion beams using vectorial diffraction theory, as detailed in the Methods section. The resulting effective intensity distributions in confocal and different STED confinement modes are symmetric with respect to the optical axis and therefore conveniently represented in cylindrical coordinates (see axial cross sections (rz-planes) in Figure 2a, left). In this representation, however, not all pixels contribute equally to the overall intensity, as the value of the integral along the azimuthal axis increases with distance from the optical axis. A more informative representation of signal and background contributions is thus obtained by integrating the intensity distribution along the azimuthal axis (Figure 2a, right). In this representation, low intensity contributions far away from the optical axis that significantly contribute to overall background levels are highlighted. This showed that significant undepleted background levels remained with 2D-, z- and 3D-STED (Figure 2b–d). On the contrary, CH-STED efficiently suppressed low intensity contributions (Figure 2e) thanks to a good overlap between the excitation and depletion foci.

Figure 2.

Simulation of spatial distribution of signal and background in STED-FCS. (a) Visualization of spatially varying intensity contributions in a confocal observation spot, for the axial cross-section of the intensity distribution (left) and integrated along the azimuthal axis (right), as sketched below, with the log scale color legend plotted on the left. (b–e) Similar visualizations of spatially varying intensity contributions for 2D-STED (b), z-STED (c), 3D-STED (d), and CH-STED (e).

From these simulations, we could estimate the expected STED laser power-dependent signal-to-background ratio (SBR) for each confinement mode. We therefore assigned the regions of high and low intensity to signal and background, respectively, using the contour at 1/e² of the maximum intensity as the threshold, as applied previously in STED-FCS.¹⁴ The outcome (Supporting Information, Figure S2) confirmed that the SBR was highest with CH-STED, corroborating the visual impression from Figure 2 and promising superior signal quality of CH-STED in actual FCS measurements. Due to the simplistic thresholding model and neglect of other noise-contributing factors (e.g., scattering of and re-excitation by STED light), though, the obtained SBR values are only to be compared qualitatively.

Experimental Measurement of Background

We next compared the depletion modes experimentally using supported lipid bilayers (SLBs). SLBs exhibit two-dimensional diffusion, and by measuring with (STED-)FCS at different axial positions of the focus with respect to the membrane plane (Figure 3a,b), we determined the out-of-focus uncorrelated background contributions as would arise in the case of 3D diffusion. For distances to the focal plane ranging from 0 to 1100 nm, we measured both the average number of molecules in the observation surface and the average transit time, which is proportional to the size of the observation surface (see eq 3 in the Methods section). Undepleted background light damps the amplitude of the FCS curves, leading to an apparently higher average number of molecules in the observation surface, but leaves lateral transit times unchanged. As a result, the relative variations of number of molecules and lateral transit times with depth can be used to estimate SBR (see derivation in the Methods section):

1

where N and N₀ are the average number of molecules in the observation surface measured, respectively, at depths z and 0, and τ and τ₀ are the lateral transit times at depths z and 0. Estimating the size of the observation surface at each depth from the extracted transit time (eq 9) and knowing the average photon counts I at each depth, we could reconstruct the depth-dependent profile of FCS observation volumes (Figure 3c–f, left). Finally, we assessed the spatial origin of background by separating photons between signal and background using eqs 1 and 11 (Figure 3c–f, right).

Figure 3.

Experimental determination of background in STED-FCS using supporting lipid bilayers (SLBs). (a) Principle of the experiment: FCS measurements on planar SLBs at various axial positions of the focus (z) were used to probe the intensity (I), size of the observation surface (obtained from the fitted transit time τ_xy), and average number of molecules within (N), from which signal and background contributions were estimated (see Methods, Estimation of Background with SLBs, for details). (b) Side-view of SLBs in confocal, CH-STED, and z-STED modes. Right: axial intensity profiles. (c–f) Reconstruction of the effective observation volume and signal to background ratio for confocal (c), 2D-STED (d), z-STED (e), and CH-STED (f). Intensity profiles (left) were calculated as described in eq 9. Right: axial position-dependent values of total intensity (blue), signal (green), and background (magenta), as determined from eq 10 and as indicated in the legend in panel (f); values represent the averages of two repeated measurements. STED laser power: 55 mW.

We found only minor background contributions at large depths in the confocal mode (Figure 3c), as expected from an observation volume properly filtered by the pinhole set to 1 Airy unit. The effective observation volume was nevertheless slightly elongated, with a Lorentzian-like shape along the optical axis. We attributed this elongation to the remaining system aberrations that slightly distort the focus far away from the focal plane, leading to a pronounced focus elongation when imaging extended objects like SLBs, but not considerably when imaging point objects like fluorescent beads (Supporting Information, Figure S1). For 2D-STED, significant background contributions were detected at distances to the focal plane beyond 300 nm (Figure 3d), which is consistent with the results of simulations (Figure 2b) and previous work on the subject¹⁴ and corresponds to residual undepleted light from the excitation focus. Smaller relative background values were measured in z-STED (Figure 3e) due to the undepleted side lobes that can be readily visualized in imaging (Figure 3b), peaking at a distance 700–900 nm from the focal plane. CH-STED (Figure 3f) exhibited small background values at depths higher than 300 nm, likely originating from the undepleted area around the optical axis where the intensity of the CH-STED depletion pattern is low. These background values were, however, much smaller than for any other confinement mode.

Both the simulations as well as this depth-profiling experiment nicely illustrated that, for all confinement modes, background originated from areas of less-effective fluorescence depletion far from the focal plane. This was in our comparison most efficiently suppressed in CH-STED, potentiating better STED-FCS performance when measuring 3D diffusion in solution.

Results

Influence of Bivortex Radius Parameter

The shape of the CH depletion pattern and, thus, of the effective observation volume can be tuned by varying the size of the bivortex parameter ρ of the CH-STED phase mask (Figure 4a).²⁰ A smaller bivortex parameter corresponds to a larger deviation from the vortex pattern, meaning a better axial confinement, at the expense of a lower lateral confinement. To study the impact of CH radius on STED-FCS performance, we measured the diffusion of Abberior Star Red dyes in solution. A mixture of water in glycerol (1:1) was used to slow down the diffusion enough that the decay times of the diffusion and triplet components were discernible also in the STED mode (lateral transit times down to approximately 40 μs for the highest STED powers) at our temporal sampling rate (1 MHz). Aberration correction was performed prior to data acquisition, and the resulting correction was used for all the measurements. We acquired a series of STED-FCS measurements for a range of values of the inner radius parameter (Figure 4b) at two different STED laser powers to ensure that any effect observed was not power-specific. Fitting the curves with the model from eq 2 allowed extraction of both the observation volume (calculated from transit times) and of the number of molecules (Figure 4b,c). Unsurprisingly, STED-FCS recordings with a low bivortex parameter exhibited a lower resolution (Figure 4c), but also showed much lower values of the average number of molecules in the observation volume (Figure 4d), which indicated a pronounced decrease in background levels. Indeed, for low CH radius, the number of molecules decreased with STED laser power (green curve below magenta curve), as expected in the absence of background, while the opposite effect was observed for large CH radii and 2D-STED (ρ = 1), indicating increased background levels at high STED powers, as previously reported.^3,10

Figure 4.

Influence of the bivortex parameter ρ on CH-STED-FCS measurements, as experimentally determined from measurements of Abberior Star Red in water/glycerol solution. (a) The inner radius ρ of the central π phase step of the STED phase mask (top) determines the concavity of the effective depletion pattern. Bottom: pictures of the xz cross sections of the depletion pattern imaged using scattering gold beads. Scale bar: 300 nm. (b) Representative normalized FCS curves in confocal and CH-STED modes with different bivortex parameters ρ (STED laser power: 32 mW). (c, d) Average size of the effective observation volume (c) and average number of molecules in the observation volume (d) determined from STED-FCS recordings for different values of the parameter ρ and at two different STED laser power, as indicated in the legend in panel (e), and normalized with the confocal value. (e, f) Estimation of background contributions in STED-FCS curves. (e) Variation of the observed number of molecules in the observation volume with size of the observation volume for different values of the parameter ρ within the range 0.7–1.0 in steps of 0.05. If no undepleted background is present, the normalized observation volume and number of molecules are equal (gray line). (f) ρ-Dependent variation of the nRMSD (indicator of noise in FCS curves). Error bars: standard deviation, n = 6. Excitation power: 17 μW.

We then set out to quantify background contributions in CH-STED. Unlike in the case of 2D diffusion (SLBs), we did not assume that background noise was negligible for 3D diffusion even for confocal FCS recordings, because of the focal side-lobes of the excitation laser (Figure 2a), which are even more pronounced in real experimental systems due to residual optical aberrations. Instead, as a measure of the amount of undepleted background, we compared the relative decrease in average number of molecules in the observation volume with that of the observation volume (Figure 4e), which are expected to be strictly proportional in the absence of any background. This showed that lower CH-STED radii depleted the background most effectively. As an alternative measure of undepleted background, we calculated the root-mean-square of the fitting residuals normalized to the amplitude²¹ (nRMSD; Figure 4e), which confirmed that lower CH-STED radii led to lower background levels.

Throughout the rest of this paper, and unless specified otherwise (see section Results, Resistance against Aberrations), we set ρ to an intermediate value of 0.85 to benefit from both good resolution and low background levels, which also corresponds to the conditions used previously for CH-STED imaging.²⁰

Comparison between STED Confinement Modes in Solution

To compare the STED-FCS performance of different confinement modes for characterizing 3D diffusion, we conducted STED-FCS experiments in a solution of freely diffusing Abberior Star Red dyes. At a given STED laser power, the resulting FCS curves acquired with CH-STED featured the highest amplitudes (Figure 5a), which could either originate from better signal confinement or better noise suppression. Fitting the FCS curves with the model from eq 2 allowed extraction of observation volumes and average number of molecules in the observation volume (Figure 5b,c). This confirmed that z- and 3D-STED offer the best resolution (Figure 5b), but that CH-STED minimizes the average number of molecules in the observation volume, suggesting a more efficient background suppression. This was confirmed by plotting relative decreases in average number of molecules with that of the observation volumes (Figure 5d) and by lower residuals in the FCS curves (Figure 5e).

Figure 5.

STED-FCS with different confinement modes in an aqueous solution of freely diffusing Abberior Star Red dyes. (a) Representative FCS curves at a STED laser power of 55 mW, for different confinement modes, as indicated in the legend. (b, c) STED laser power-dependent effective observation volume (b) and average number of molecules in the observation volume (c), normalized with values determined from confocal recordings, and (d) their pairwise scatterplot. STED-FCS recordings without any background would follow the dotted gray line (proportionality between number of molecules in the observation volume and size of the observation volume). (e) Variation of nRMSD with STED laser power, for different STED confinement modes as indicated in the legend. Error bars: s.d., n = 6. Excitation power: 8 μW.

Resistance against Aberrations

To assess the robustness of STED-FCS measurements with different confinement modes, we used the wavefront shaping capabilities of the SLM to quantify the effects of optical aberrations introduced as low-order Zernike modes, which had previously been reported to be most often present while imaging common biological specimens.²² We introduced either 0, 0.5, or 1 rad rms of each mode using the SLM, corresponding respectively to no aberrations, to the maximum amplitude of aberrations we experienced in our microscope across this study (see Supporting Information, Figure S5) and to highly aberrating situations that can be encountered, for instance, when focusing deep inside a medium with a refractive index mismatch¹⁹ or when focusing deep through an optically inhomogeneous specimen. For each aberration value, we acquired a set of STED-FCS measurements of freely diffusing Abberior Star Red dye in a water/glycerol solution. From the parameters of fits to the obtained FCS curves (Figure 6a,b), relative variations in the average number of molecules within the observation volume and effective size of the observation volume were used as indicators of the sensitivity of each STED confinement mode to aberrations (Figure 6c–f). The CH radius was set to a value of 0.75, smaller than in the rest of this study, to maximize the difference between CH-STED and 2D-STED.

Figure 6.

Effect of common aberrations on the depletion pattern on STED-FCS experiments. (a–c) Spherical aberration. (a, b) FCS curves of Abberior Star Red in water/glycerol solution, obtained with different confinement modes, without (a) and with (b) 1 rad rms of spherical aberration introduced in the depletion beam. Insets: images (xz) of the corresponding depletion patterns obtained with a sample of scattering gold beads (scale bar: 1 μm). (c) Relative variation of size of the observation volume (x-axis) and average number of molecules in the observation volume (y-axis) upon various amounts of introduced spherical aberration (indicated by the size of the marker) for different STED-FCS confinement modes, as indicated in the legend in panel (f). Aberrations either reduce the resolution or increase the strength of background contributions, as indicated by the arrows. The inset represents the phase distribution of 1 rad rms of spherical aberration. (d–i) Corresponding effects of (d, g) astigmatism (e, h) coma, and (f, i) tilt on STED-FCS parameters (d–f) and gold bead images (g–i) in xy (top) and xz (bottom) planes for the depletion patterns with 1 rad rms of the corresponding aberrations. In panel (i), the white dotted line represents the position of the excitation focus. STED laser power: 16 mW.

In accordance with previous work on the effect of aberrations on STED depletion patterns,^17,23 we found that spherical aberrations were detrimental to z-STED but had very limited effects in 2D-STED (Figure 6c). Surprisingly, spherical aberrations slightly decreased the average number of molecules in the observation volume in 2D-STED, which can be attributed to an elongation of the depletion pattern (insets in Figure 6a,b), leading to a better overlap between excitation and depletion foci. We also found that as predicted in ref (20), CH-STED was much more resistant to spherical aberrations than z-STED (Figure 6c).

Similar to the spherical aberration, astigmatism (Figure 6d) had a more damaging effect on z-STED than on 2D and CH-STED. Coma aberration revealed to be particularly detrimental to CH-STED (Figure 6e), as well as for 2D-STED, but not to z-STED. Coma aberration typically occurs when the coverslip is tilted. The exact amount depends on the immersion medium, as more aberrations appear when the index mismatch between the coverslip and the immersion medium is large. For example, previous research suggests that when using a water immersion objective together with a standard, 170 μm thick coverslip, a tilt of 2° of the coverslip would cause approximately 3 rad rms of coma aberrations.²⁴ In the case of using an oil immersion objective, however, the effect should be much less pronounced. In our system, we never measured coma values larger than 0.2 rad rms (see Supporting Information, S5), for which CH-STED would still show lower background than 2D- and z-STED.

Finally, the impact of tilt, which in this situation corresponds to a misalignment between excitation and depletion foci, is useful to be assessed to estimate the impact of chromatic aberrations²⁵ or thermal and mechanical drift.¹⁹ We found that 2D-STED was the most sensitive to tilt, followed by z-STED and CH-STED, which can be linked to the respective sizes of their central areas, with a smaller central area leading to a higher vulnerability to misalignment (Figure 6f).

To help illustrate these results, we defined the degree of sensitivity to aberrations as follows: a given STED depletion pattern is defined to have a high sensitivity to a given aberration mode if 0.5 rad rms of this mode increases either the number of molecules in the observation volume or the size of the observation volume by more than 50%. If instead 1 rad rms of this mode leads to such an increase, the sensitivity to this mode is defined as intermediate. Otherwise, the sensitivity is low. Results are presented in Table 1.

Table 1. Sensitivity of STED Confinement Modes to Common Optical Aberrations.

	spherical	astigmatism	coma	tilt
2D	low	high	intermediate	intermediate
CH	low	low	high	low
z	intermediate	intermediate	low	intermediate

STED-FCS in Living Cells

To evaluate the applicability of each STED confinement mode to measurements of 3D diffusion in biological specimens, we measured 3D diffusion of the expressed GFP-SNAP construct, labeled with the bright, photostable, and STED-compatible membrane-permeable organic dye silicon-rhodamine, in the cytoplasm of human fibroblasts (Figure 7a,b). This experimental system is a convenient model for mobility studies of cytoplasmic proteins. We analyzed the protein’s diffusion using z-, 3D-, and CH-STED-FCS, resulting most importantly in changes of values of effective observation volume V, average number of molecules N in the observation volume, and the noise estimation parameter nRMSD with increasing power of the STED laser (Figure 7c–e). 2D-STED was not assessed, as results already showed much poorer signal and spatial resolution in solution than the other confinement modes (see Figure 5).

Figure 7.

Diffusion of the protein GFP-SNAP, labeled with a membrane-permeable fluorescent dye SNAP silicon-rhodamine (SiRo), in the cytoplasm of living cells recorded with STED-FCS and different confinement modes. (a) Exemplary confocal xy images of a cell where STED-FCS experiments were performed. Left: green channel (GFP); Right: red channel (SiRo, used for STED-FCS). (Scale bar: 5 μm). (b) Representative STED-FCS curves of SiRo-tagged GFP (normalized with confocal amplitude) obtained in cells with different confinement modes, as indicated in the legend, at a STED laser power of 32 mW. (c) Observation volumes at different STED laser powers and with different STED patterns, normalized with the confocal value, (d) average number of molecules in the observation volume normalized with confocal values, and (e) noise in correlation curves, measured as nRMSD for different confinement modes as a function of STED laser power (mean ± s.d, n ≥ 12 curves from 3 cells).

In our experiments, we found that the anticipated decrease in observation volume with STED laser power was very similar for all confinement modes, with a slightly more pronounced decrease for z-STED recordings (Figure 7c). On the other hand, CH-STED offered the lowest values of N (Figure 7d), indicating lower contributions of noncorrelating fluorescence signal, as anticipated from results with model systems (Figure 5c). To further evaluate the noise levels, we calculated the nRMSD of each curve (Figure 7e). Noise levels, that is, nRMSD values, were the lowest for CH-STED, followed closely by z-STED, and the highest when using 3D-STED, consistently with measurements in solution (compare Figure 5d,e).

It should be noted that these results were obtained with adaptive correction of system- and specimen-induced aberrations, without which larger differences between z-STED and CH-STED would be expected. In the presence of 0.5 rad rms of spherical aberrations (typically measured even at shallow depth in the presence of an oil/water interface, see Figure S5), our measurements of the sensitivity of depletion patterns to spherical aberrations (Figure 6c) indicate that a similar performance would be obtained with CH-STED (observation volume increased by only 2%), while the performance of z-STED would be notably deteriorated (observation volume increased by approximately 14%).

Discussion

STED-FCS has become a widely adopted tool for investigations of nanoscale diffusion properties of molecules in 2D environments, like plasma membranes,⁹⁻¹² yielding invaluable insights into their dynamic nanoarchitecture. The application of STED-FCS in 3D environments, however, such as nucleus and cytosol, has been very scarce. The challenge of getting satisfactory FCS signal quality from the reduced focal volumes using traditional 2D- and z-STED patterns stems from nondepleted residual fluorescence, largely exacerbated by optical aberrations commonly present in biological systems. Attempting to overcome these issues, sophisticated experimental approaches, relying on the introduction of additional laser pulses,⁵ have been developed, requiring the acquisition of time-tagged photon streams, or by advanced dynamic aberration corrections.¹⁹ On the contrary, we here aimed at improving STED-FCS in 3D environments by a technically simpler approach, adopting the alternative depletion pattern designed to reduce the background fluorescence in imaging via bivortex, CH-STED.²⁰ This implementation is straightforwardly introduced in setups incorporating an SLM (available also in certain commercial implementations of STED), as it only requires the modulation of the STED laser with a bivortex phase mask.

We investigated the effects of four different STED confinement modes (2D-, z-, 3D-, and CH-STED) on the performance of STED-FCS experiments, both theoretically using simulations and experimentally in a variety of systems. Our study confirms that the background from undepleted volumes can significantly deteriorate signal levels in STED-FCS, which largely depends on the depletion pattern used. We found that undepleted background noise was particularly high in 2D- and 3D-STED, while it was reduced with z-STED and the lowest with CH-STED (Figure 5). We also found that CH-STED was generally less sensitive to optical aberrations than z-STED, especially to spherical aberrations, which are most common in biological experiments (Figure 6). Finally, we compared 3D-, z-, and CH-STED-FCS on diffusion of a fluorescently-labeled protein in the cellular cytosol, where again CH-STED provided an excellent compromise between resolution and reduced noise levels. Therefore, considering its experimental simplicity, CH-STED can be considered a depletion pattern of choice for STED-FCS experiments of 3D diffusion. Only when the highest attainable resolution is required, z-STED or 3D-STED combined with advanced aberration correction¹⁹ can offer better reduction of the observation volume.

In practice, the demonstrated background reduction is helpful to attain the required signal-to-noise levels, which can otherwise be enhanced primarily by increasing the power of the excitation laser, prolonging the acquisition time, or by choosing a brighter dye, all of which may pose practical limitations to the experiment at hand. Of note, CH-STED-FCS reduces the background without making any assumptions on the properties of the fluorophores imaged, as opposed to other background reduction methods for STED-FCS.^5,7 As an example, CH-STED-FCS could be used together with probes with varying fluorescence lifetimes²⁶ while using these with SPLIT or STEDD would complicate experimental designs. Though we did not record the dyes’ lifetime in our study, CH-STED is fully compatible when this rich molecular information is sought. CH-STED can also easily be used together with other background subtraction methods to further increase signal levels of STED-FCS experiments.

We showed that CH-STED is a tool of choice to facilitate STED-FCS experiments in 3D environments. The broader understanding of the origin of background in STED-FCS gained in this study will also help design new depletion patterns that optimize background reduction. In STED systems with a double-pass configuration, for example, we expect a combination of z- and CH-STED to join the great resolution of the former and the background suppression capabilities of the latter for optimized STED-FCS in 3D.

Together with increasingly accessible and versatile self-labeling strategies, which allow tagging of proteins with the brightest available organic dyes that are more suitable for STED and FCS than most of the existing fluorescent proteins, these advances hold promise for exciting new applications in the context of cellular 3D nano-organization. In particular, STED-FCS could importantly elucidate the diffusional properties and, hence, molecular mechanisms underlying the recently much-debated liquid–liquid phase separation,²⁷⁻²⁹ its implications for cellular processes, and involvement in diseases.

Methods

Microscope

Experiments were performed using a custom STED microscope built around a RESOLFT microscope by Abberior Instruments equipped with an oil immersion objective lens (Olympus UPLSAPO, 100×/1.4 oil), as described in previous publications¹⁹ and as sketched in Figure 8. The depletion STED laser (Spectra-Physics Mai Tai, pulse-stretched by a 40 cm glass rod and a 100 m single-mode fiber) was pulsing at a frequency of 80 MHz at a wavelength of 755 nm. The STED laser beam was separated in two arms using a polarization beam splitter, with the amount of light going in each arm being controlled by rotating the plane of the incident linear polarization using a λ/2 phase plate. In the first arm, a spatial light modulator (SLM, Hamamatsu LCOS X10468-02) was used to generate 2D-, z-, and CH-STED patterns. In the second arm, a vortex phase plate (VPP-1a, RPC Photonics, Rochester, NY) was used to create a 2D depletion pattern, which was overlaid with a z-STED pattern generated by the SLM to create 3D-STED. System aberrations in the depletion arm, including the SLM, were removed by scanning a sample of scattering gold beads, using the sensorless method and using image standard deviation as an image quality metric. A 640 nm laser pulsing at a frequency of 80 MHz was used for excitation, at powers ranging from 4 to 17 μW measured in the back focal plane of the objective. Fluorescence light was collected back by the objective, filtered with a pinhole with a size approximately equal to 1 magnified Airy disk, and detected with an avalanche photodiode.

Figure 8.

Sketch of the microscope. Excitation (green) and depletion (magenta) lasers are focused by an oil immersion objective (OBJ). The depletion laser beam is split in two orthogonal polarizations and later recombined using a polarization beam splitter (PBS 1 and 2). One component is modulated in phase by the SLM (gray box) that generates different phase patterns (inset), while the other is modulated by a vortex phase plate (VPP). Excitation, depletion, and detection (orange) beam paths are recombined using dichroic beamsplitters (DBS 1 and 2).

Samples

Dye Solutions

Freely diffusing dyes in solution were prepared by diluting Abberior Star Red dyes (Abberior, Germany) to a concentration of 50 nM in a 1:1 water/glycerol solution. Glycerol was used to slow down diffusion speeds to facilitate the analysis of FCS data.

Fluorescent Beads

Slides of immobilized 40-nm far-red fluorescent nanoparticules used for STED imaging were purchased from Abberior Instruments (Germany).

Supported Lipid Bilayers

Supported lipid bilayers were prepared as described previously.³⁰ The coverslips were cleaned with piranha acid (3:1 sulfuric acid and hydrogen peroxide) and stored in water for no more than 2 weeks before the experiment. A total of 25 μL of 1 mg/mL POPC (1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine; Avanti Polar Lipids, AL, U.S.A.) lipid solution in chloroform/methanol with 0.01 mol % of fluorescent Abberior Star Red-labeled phosphatidylethanolamine (PE; Abberior) was spin-coated onto a clean dry coverslip at 3200 rpm for 30 s. The lipid film was rehydrated with SLB buffer (10 mM HEPES and 150 mM NaCl pH 7.4) and washed several times to remove nonplanar lipid structures.

Cells

Cells were prepared using the same protocol as in ref (19). Human fibroblasts (GM5756T, Moser, Baltimore, U.S.A.) were maintained in a culture medium consisting of DMEM with 4500 mg glucose/L, 110 mg sodium pyruvate/L supplemented with 10% fetal calf serum, l-glutamine (2 mM), and penicillin–streptomycin (1%). The cells were cultured at 37 °C/5% CO₂. Cells were grown in a 35 mm imaging dish with a glass coverslip bottom (ibidi GmbH, Germany) and transfected with 2.5 μg DNA per dish of a plasmid expressing a fusion protein of GFP and SNAP-tag using Lipofectamine 3000 transfection reagent (Invitrogene, Carlsbad, U.S.A.). A total of 24 h after transfection, the cells were incubated together with SNAP-Cell 647-SiR (New England Biolabs (U.K.) Ltd., Hitchin, U.K.) for 40 min and washed twice with culture medium, with a waiting time between washings of 20 min. The culture medium was finally substituted with L-15 medium (Sigma-Aldrich, Dorset, U.K.), and each sample was visualized at 37 °C for no longer than 1 h.

Depletion Patterns

We investigated the performances of four depletion patterns: 2D-, z-, CH-, and 3D-STED (Figure 1). 2D-, z-, and CH-STED patterns were generated with the SLM, while the 3D-STED pattern was created as an overlay of an SLM-generated z-STED pattern and a phase-plate-generated 2D-STED pattern. For 3D-STED, 80% of the STED laser power was in the z-STED arm and 20% in the 2D-STED, except in cells where 50% of the STED laser power was in each arm. The inner radius of the CH-STED mask can be changed to modify the shape of the corresponding depletion pattern. We initially set the value of this parameter to 0.85 (85% of the pupil radius size), as was used in a previous implementation.²⁰ The influence of the CH-STED radius parameter is discussed in the Results section.

FCS

FCS curves were either obtained directly from a correlator card (Flex02–08D, correlator.com) or by acquiring fluorescence intensity timetraces with a frequency comprised between 0.25 and 1 MHz that were correlated offline using the Python package multipletau.³¹ Acquisition times were set to 10 s.

FCS parameters were obtained by fitting FCS curves with standard diffusion model, assuming Gaussian-shaped observation volumes³² (Supporting Information, Figure S2):

2

where N refers to the average number of molecules in the effective observation volume, T is the average triplet amplitude, τ_T is the triplet correlation time, τ_xy is the average lateral transit time, α is a factor characterizing deviation (values different from 1) from the Gaussian shape of the observation volume or anomalous diffusion, and K is the aspect ratio of the observation volume, defined as K = ω_z/ω_xy, and ω_xy and ω_z are, respectively, the lateral and axial 1/e² radii. The lateral transit time τ_xy and ω_xy size are related to the diffusion coefficient D:^1,2,32

3

Triplet correlation times τ_T were determined from confocal recordings and set to the constant value of 5 μs in cells and SLBs and of 11 μs for Abberior Star Red in solution. Triplet correlation times in solution were larger than the usually reported value (5 μs). This was probably due to the fact that a 5 μs triplet correlation time is usually found for dyes in water, while here we used a water/glycerol solution. In solution, where transit times were the shortest, we determined the triplet correlation amplitude T from confocal recordings and set to a constant value, as it was previously determined that triplet correlation amplitude depends predominantly on the power of the excitation and not the depletion laser.²¹ Triplet correlation amplitude was thus set to 0.16 in experiments with an excitation power of 8 μW and 0.25 in experiments with an excitation power of 17 μW (see Supporting Information, Figure S6).

As a measure of noise in experimental FCS curves, we calculated the root-mean-square values of the fitting residuals up to a lag time of 50 μs (smaller than transit times in most cases), normalized by the amplitude (nRMSD), as applied before.²¹ This method has among the others the advantage of being independent of dye concentration in the range of concentrations used in this study.²¹

A general procedure for STED-FCS data analysis can be found in ref (11). The factor α was also determined from confocal recordings and was set to 1 (describing free diffusion) in every sample except for cells, where α was set to 0.8 to account for anomalous subdiffusion caused by the crowded environment in the cell cytoplasm^11,33 (see Supporting Information, Figure S7). Since typical molecular brightness of conventional fluorophores is not high enough to independently determine the lateral transit time τ_xy and the aspect ratio K,^3,10 we calibrated the variations of the aspect ratio with the lateral size for each STED confinement mode, and fitted the observation volumes with a prescribed shape, as described in ref (19) (see Supporting Information, Figure S1). In cells, we minimized the effects of cell–cell variations by normalizing STED-FCS results with confocal values. For each series of measurements made of one confocal FCS and three STED curves at different STED laser power, we normalized the average number of molecules in the observation volume and the size of the observation volume in STED with the confocal value.

Estimation of Background Contributions with SLBs

To estimate background contributions with SLBs, FCS measurements were performed on SLBs, at different axial positions of the excitation and STED focus with respect to the membrane. At each position, two or three FCS curves were recorded with an acquisition time of 10 s. Resulting curves were fitted with the model from eq 2 to extract the average number of molecules in the observation surface and the average transit time. The average photon count was also recorded. From these three quantities, we could estimate background levels as follows. Undepleted background increases the apparent number of molecules in the observation surface:^10,14,15

4

where N is the number of molecules in the observation surface estimated with FCS, N_real is the actual number of molecules in the observation volume, and SBR is the signal-to-background ratio, defined as SBR = I_signal/(I_signal + I_background), where I_signal refers to the average photon count of the photons contributing to the correlating signal and I_background is the average photon count of photons contributing to the uncorrelating background.

At a depth z, N can be directly obtained from the amplitude of FCS curves. The actual number of molecules, N_real, in the observation surface is a function of the concentration of fluorescent molecules per surface unit c and of the size of the observation surface S:

5

The concentration c is unknown, but its determination is not necessary: assuming that there is no undepleted background at depth 0, when the SLB is in the focal plane of the objective, we have N_real,0 = N₀, where N_real,0 is the actual number of molecules in the observation surface at depth 0, and N₀ is the average number of molecules in the observation surface at depth 0, measured by FCS. Equation 5 at any depth z can then be divided by the values measured at depth 0:

6

where ω_xy,0 is the size of the observation surface at depth 0, which was determined as the plane of measurements with the highest photon counts. At a depth z, the number of molecules can be calculated from eqs 3 and 6 as

7

Finally, at each depth, we can calculate the SBR:

8

This quantity assumes that N_fcs is systematically larger than N, which is always true according to the theory (eq 4). However, in situations where very low background is present, statistical variations in the measurements of N and τ can lead N_fcs to be slightly smaller than N. In this case, we considered N_fcs and N equal and set the SBR to an infinite value. Determination of the absolute size of the observation surface results directly from eq 3:

9

where ω_{xy,0,confocal} is the lateral size of the confocal spot in the focal plane, measured to be 102 nm (corresponding to a full width at half-maximum of 240 nm) by imaging a sample of fluorescent beads, and τ_{xy,0,confocal} is the lateral transit time as determined in SLBs with confocal FCS. Knowing the lateral size of the observation surface ω_xy and the average photon counts I(z) at each depth, we could reconstruct the Gaussian intensity g(x,y,z) profile of each focus as

10

Knowing the SBR at each depth from eq 8, we estimated at each depth the fraction of photons contributing to the signal and the fraction contributing to background:

11

Adaptive Optics

The employed depletion patterns show different sensitivity to optical aberrations.^17,23,34 To ensure optimal performance and thus fair comparison of the confinement modes, we first corrected sample-induced optical aberrations, as well as residual system-induced aberrations, using the sensorless adaptive optics approach described in ref (19). While measuring z-STED FCS (the most aberration-prone mode), we corrected low-order Zernike modes (modes 5–11, following the convention defined by Noll³⁵) in each sample by minimizing the average number of molecules in the observation volume. The correction optimizes the shape of the depletion beam for all confinement modes, but can result in their slight misalignment.³⁶ Hence, once the correction was determined using z-STED-FCS, coalignment between excitation and depletion pattern of interest (2D or CH) was ensured by optimizing tip and tilt, again using the average number of molecules in the observation volume as a quality metric. During aberration correction procedures, STED laser power was set to 16 mW. Aberration amplitudes were measured in radians root-mean-square (rad rms, see Methods and Supporting Information) and measured at 755 nm.

Simulations

The intensity distributions of the excitation and depletion lasers were calculated using the vectorial diffraction theory, as described, for instance, in ref (36). We integrated the Debye-Wolf integral in the vicinity of the focal point of the objective:

12

where E describes the electric field at the point x, y, z (the focal point corresponds to the point where x, y, and z are equal to 0). α is the semiaperture angle, with NA = n sin α, n is the refraction index of the propagation medium, k = 2πn/λ, λ is the wavelength, T(θ, Φ) describes the phase function of the STED phase mask (set to 1 to model the excitation focus), and 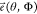describes the field distribution which, in the desired case of circularly polarized light, can be explicited as

13

where A(θ) describes a Gaussian illumination profile. Depletion patterns were simulated at a wavelength of 755 nm, and excitation was calculated at 640 nm, both wavelengths used in our system. The refractive index n was set to 1.518 (oil) and NA to 1.4.

The detection profile was defined as a convolution of the excitation profile with a pinhole with a size of 1 Airy unit. Pixel size was set to 10 nm. To minimize computing time, only two-dimensional (xz) profiles were calculated. Integration was performed in cylindrical coordinates, using the invariance of the calculated foci along the azimuthal coordinate to calculate three-dimensional integrals from two-dimensional simulation data.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsphotonics.0c00388.

• Calibration of the FCS fitting method, determination of shape of observation volume with images of fluorescent beads, SBR in simulated data, FCS curves in solution, aberrations measured in the system, determination of triplet correlation parameters in solution, and determination of factor α in cells (PDF)

The authors declare no competing financial interest.