The Lac Repressor hinge helix in context: the effect of the DNA binding domain and symmetry

Abstract

The Lac system of genes has been an important model system in understanding gene regulation. When the dimer lac repressor protein binds to the correct DNA sequence, the hinge region of the protein goes through a disorder to order transition. The hinge region is disordered when binding to nonoperator sequences. This region of the protein must pay a conformational entropic penalty to order when it is bound to operator DNA. Structural studies show that this region is flexible. Previous simulations showed that this region is disordered when free in solution without the DNA binding domain present. Our simulations corroborate that this region is extremely flexible in solution, but we find that the presence of the DNA binding domain proximal to the hinge helix and salt make the ordered conformation more favorable even without DNA present.

1. Introduction

The lac system has been a model of gene regulation since 1952 .^1–12 The lac repressor regulates the expression of a set of genes involved in lactose metabolism in the bacterium Escherichia coli (E. coli). When lactose is either no longer in the system or no longer the favorable source of energy in the system, a binding signal modulates the affinity of the lac repressor protein for the operator. The repressor then binds to the operator region of the operon and the gene’s expression is suppressed.¹³

The lac repressor is a protein of 360 amino acids that assembles into a homotetramer. The three-dimensional structure of the lac repressor provides important atomic level clues as to how the repressor performs its biological role. The structure of fragments of the DNA-binding domain (DBD)¹⁴ and regulatory domain (RD) when bound to inducer have been determined.^15–17 The structure of the DBD showed that the repressor contained the helix-turn-helix (HTH) motif that is common in other proteins that bind specifically to DNA. These early studies were only able to characterize the pieces of the protein and were unable to do so for the full protein where the RD and DBD were linked by the hinge helix (HH) region.

M. Lewis et. al were able to obtain the full three-dimensional structure bound to operator-like DNA in 1996 using x-ray crystallography to obtain an image of the alpha carbons of the full molecule with resolution 2.7Å (PDB 1LBG).¹⁷ Work continued on the repressor protein bound to the operator using other methods to get better resolution.^18–20 Previous experiments had determined there must be a structural change to the protein when no longer bound to operator DNA,^{3, 21, 22} but characterizing this through crystallography or NMR was difficult. Kaptein et al made a single mutation to the HH, V52C, and were able to solve the structure of the head piece structure (HP62), the DBD+HH, bound to operator and non-operator DNA using NMR spectroscopy (Figure 1).^{23, 24} This mutation showed no sign of altering the affinity of the protein for the operator site or change to the binding, it simply made the protein fluctuate less. This sequence change allowed a view of the structure bound to non-operator DNA and showed that it was disordered.

Figure 1:

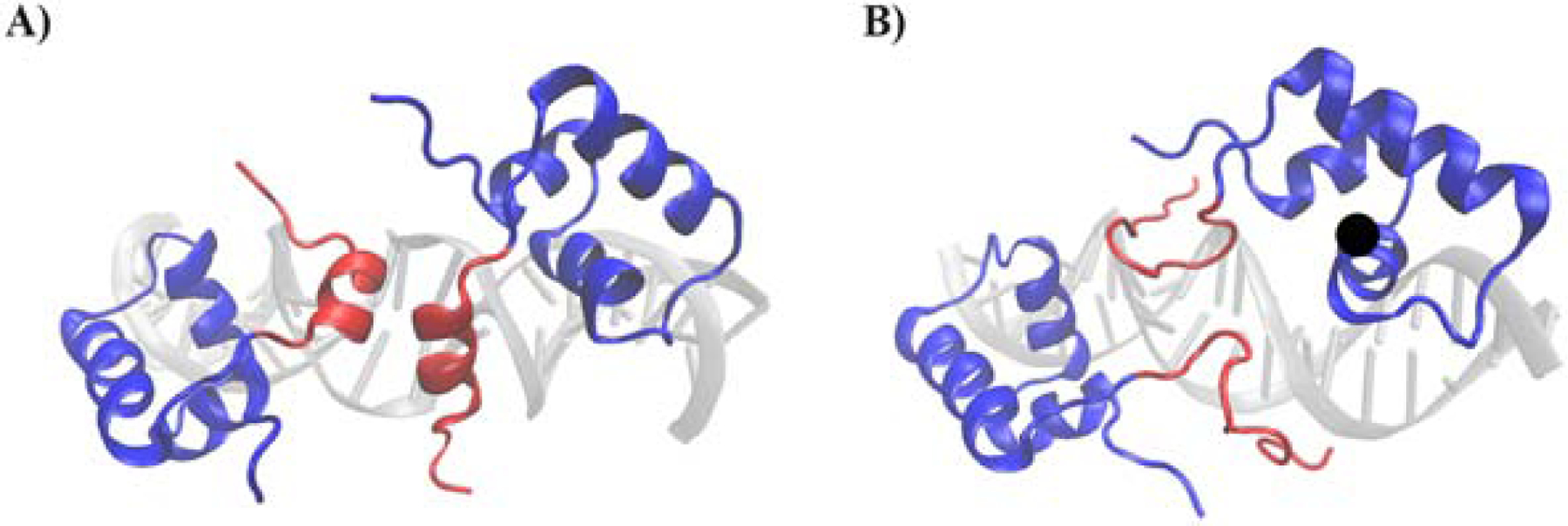
A rendering of PDB 1L1M(A) and 1OSL (B) using VMD showing the lac repressor protein’s conformation when bound to operator and non-operator DNA respectively. The HH is shown in red and the DBD is shown in blue.

Proteins and protein domains with a less well-defined structure are referred to as intrinsically disordered proteins (IDP) or intrinsically disordered regions (IDR). These types of proteins were first characterized in the mid-1990s and have been extensively studied.^25–31 The secondary structures of many proteins are disordered under physiological conditions, but they can adopt specific structures in a particular functional state.²⁶ This type of folding is often coupled with binding to the protein’s target.³² The HH of the lac repressor protein is one of these IDRs.

Although a disordered structure has been determined for the hinge helix when bound to non-operator DNA, there is still very little information on the protein when free in solution. Part of this is due to limitations of current experimental techniques to characterize disordered proteins in solution. Simulations have been performed on the hinge-helix peptide in solution³³ and confirmed the tendency towards disorder of this region of the protein. Here we use computational simulation techniques to investigate the structure and conformational free energy of this system in solution when the DBD is present. To investigate the effect on the protein conformation of the ion atmosphere around DNA, which is known to substantially increases the salt concentration over bulk, we consider up to 0.4M salt.³⁴

2. Methods

We performed metadynamics simulations starting from minimized crystal coordinates in order to compute the free energy surface for the hinge-helix with the full DNA-binding domain as a function of a set of collective variables (CVs). We chose to sample the root mean square deviation (RMSD) from the starting coordinates as our original CV and subsequently reweight the sampling to other CVs for further analysis. The studies were performed in two different ionic concentration conditions, 0.0M and 0.4M.

2.1. System Preparation

To compare the differences between the ordered and disordered states of the HH region, two metadynamics simulations were performed. We monitored the simulations to ensure that each was traversing the entire range of the collective variable. For both simulations the starting structure was the V52C mutant of the full homodimer DBD+HH (residues 1–62).²³ Many previous experiments and simulations have been performed using either the PurR-GCG construct or the V52C mutant to aid dimer formation.^{33, 35} In order to compare most closely with previous simulations,³³ both systems used the PDB structure 1L1M.²³ This structure is a dimer consisting of the first 62 N-terminal residues of each monomer, crystalized to operator DNA.

To prepare the structures for simulation the DNA was removed from the starting crystal structure. Then hydrogen atoms were added using PSFGen in Visual Molecular Dynamics (VMD).³⁶ The peptides were then solvated in explicit TIP3P³⁷ water molecules. Then ions were randomly added to the two systems in order to match desired concentrations, 0.4 M and 0 M (neutral). The high ion system had a total of 52159 atoms while the low ion system had 52667 atoms.

All systems were minimized for 21000 steps then equilibrated for 640 ps in an NVT ensemble at 300 K. A weakly coupled Langevin thermostat³⁸ was used to maintain constant temperature. Electrostatic interactions were computed using the particle-mesh Ewald algorithm (PME).³⁹ The PME grid spacing was 1.0 Å.

2.2. Metadynamics Variables

The free energy landscape representing the HH unfolding pathway in the presence of the DBD was investigated using metadynamics,^{40, 41} an enhanced sampling method to calculate the free-energy surface as a function of a few selected collective variables (CVs). We tested a number of different collective variables including RMSD from the crystal structure, radius of gyration, endto-end distance (E2E), and helical content. Each of these CVs has desirable and undesirable characteristics.⁴² We concluded RMSD from the crystal structure was an adequate compromise and allowed other variations via reweighting (below). We used the RMSD of residues 50–58 from each monomer from the starting structure of each respective simulation. The systems were run using NAMD 2.10³⁸ and the CHARMM36 force field.^{37, 43} The VMD package³⁸ provided some analysis and visualization.

To begin metadynamics for systems 1 and 2, a Gaussian height of 1.0 kcal/mol was used. The systems were able to traverse the entire range of the CV at least 5 times at the initial Gaussian height. The height was subsequently reduced according to the schedule shown in Table 1 in order to get a more accurate and smooth final potential of mean force (PMF).^{38, 44, 45}

Table 1:

The change in average ion density versus RMSD for each of the HH amino acids based on line of least squares fit from the first and last point of RMSD, 0.058 and 9.911Å respectively.

Amino Acid	Starting Avg. Ion Count	Ending Avg. Ion Count	Change in Avg. Ion Count
Asn 50	0.2023	0.0880	−0.1143
Arg 51	0.4352	0.1850	−0.2502
Cys 52	0.0833	0.0526	−0.0307
Ala 53	0.0459	0.0794	+0.0335
Gln 54	0.1521	0.1687	+0.0166
Gln 55	0.2918	0.1578	−0.1399
Leu 56	0.0474	0.1272	+0.0798
Ala 57	0.0281	0.1887	+0.1606
Gly 58	0.0858	0.2010	+0.1152

For each subsequent height the systems transited the entire range of the CV multiple times, at least 1 trip/10 ns, until the results showed regularity allowing for convergence. Every 50 ps we collected an intermediate output PMF file. Once all runs were complete, all PMFs from each Gaussian height were averaged using the block method (4 blocks/ns). Then every four points along the RMSD were averaged. The variance from the average PMF for each height is shown in Supporting Information Figure S1. System 1 was sampled for a total of 300 ns while system 2 was sampled for a total of 340 ns.

The systems were analyzed using VMD with plugins from PLUMED,⁴⁶ NAMD,³⁸ and METAGUI.^{47, 48} Analysis using METAGUI 3 was used to cluster the metadynamics data based on RMSD. Once clustered PLUMED was used to calculate the torsion angles of residues 51–58, and E2E distances of the HHs (N-Asn50 to O-Gly58) of each frame in those clusters. Using the 16 torsion angles of each frame, the number of consecutive helical residues (−90 <φ<−35 and −70<ψ<−15)⁴⁹ was calculated. The metadynamics calculation was then reweighted to E2E distance using the original PMF and the populations of each variable per RMSD cluster. The reweighting followed the usual procedure for a biased distribution.

$$h_i^{\mathrm{*}}=\frac{\sum _{j=0}^n{h}_i\left(x_j\right)e^{-\beta V\left(x_j\right)}}{\sum _{j=0}^{n}Q\left(x_j\right)e^{-\beta V\left(x_j\right)}}$$ (1)

where V(x_j) is the value of the original PMF at an RMSD of x_j, h_i(x_j) is the number of frames with the new E2E CV at value i in RMSD cluster x_j, Q(x_j) is the bin size of the cluster at RMSD x_j and h_i* is the reweighted value for the new CV value for i.

3. Results

3.1. Metadynamics PMF Analysis

The results from the metadynamics simulations, shown in Figure 2(A,B), display a large difference between the two systems in different ion concentrations. These PMFs were calculated by averaging the PMFs of the simulation steps after achieving the smallest Gaussian height, 0.3 kcal/mol.

Figure 2:

(A,B), Graphs of the potential of mean force during the metadynamics simulations based on the collective variable of root mean squared deviation in high ion and low ion solutions respectively. In the low ion solution the difference in energy between the starting structure and the most energetically favorable structure is over 60 kcal/mol as shown in the insert of A. The larger graph of A shows the PMF on the same scale as the high ion system of B

Considering the system without ions, the free energy difference between the starting structure and the lower region of the basin is around 60 kcal/mol. The wide basin from ~3–9 Å is rough and in the range of about 0–5 kcal/mol. Comparing points less than an Angstrom apart shows there are large jumps of 2–3 kcal/mol instead of a smooth basin with a single minimum. This makes it more likely for the protein to stay in a single local conformation for an extended period of time. There are quite a few local minima that are similar, less than 1 kcal/mol difference, along this basin.

The PMF of the system with high ion concentration is quantitatively different. The free energy difference between the structure with both monomers being fully helical and the minimum is 12 kcal/mol, rather than over 60 kcal/mol. But at ~0.5 Å, when one of the helices has started to partially unwind, the free energy has already dropped by about 3.5 kcal/mol. Near an RMSD of ~1.2 Å when one helical turn has fully unwound or both are partially unwound, the structure is another 4 kcal/mol more favorable. These two plateaus indicate meta-stable structures. The free energy surface has a minimum from 5–5.5 Å where both helices are unwound but not stretched out. However, the entire bottom of the basin from 2–9 Å is within a 4 kcal/mol difference and relatively smooth with only one large feature. This indicates that a transition between these many states would be accessible on the few ns timescale.

3.2. Ion Concentrations

The RMSD PMFs demonstrated that there were clear differences between the two systems. In a previous study, ion concentration was found to be significant in determining the dynamics and thermodynamics of the isolated HH.³³ Looking at the low ion concentration system in the current study, there are only 4 ions in the ~50,000 atom system and at no time are they within 5Å of the HH residues (50–58). In the high ion system, many statistically significant ionic interactions with the HH occur and we will focus our analysis there. We considered proximal ion density versus RMSD.

The ion density within 4 or 5 Å of all HH residues is relatively featureless and flat along the RMSD (slopes of −0.007 ions/Å). The density does not change depending on the conformation (RMSD) of the HH region. When ion density around individual residues is investigated, some trends can be seen. The ion densities within 5 Å of three of the residues (Cys52, Ala53, Gln54) remain fairly constant and do not change depending on the RMSD. (Table 1) These three residues are known to mostly interact with the other HH monomer by making protein-protein contacts.^{19, 50} For the polar residues Asn50, Arg51, and Gln55 there is a greater concentration of ions within 5Å of the residue when the HH has a lower RMSD, which is when the HH is more helical (Table 1). The concentration for these 3 residues steadily increases as the RMSD decreases. The charged arginine at residue 51 is expected to have a high density of ions surrounding it due to its positive charge, but it is interesting to see how the folding of the HH region affects the result. The asparagine at position 50 has the lowest slope and densities of the 3 residues; its increase in ion density is probably related to its proximity to arginine 51. The third residue with an inverse relationship between ion density and RMSD is glutamine 55. This molecule is facing away from the DNA binding surface and interacting with the core domain.^{19, 50}

When the protein is in the helical conformation, but without DNA or the core domain present, residue 55 is facing out into solution. The three end residues of the HH (Table 1) show a positive correlation, the greater the RMSD the greater the ion density surrounding them. As the RMSD increases, the HH becomes less tightly coiled. This allows the ends of the HH to extend farther into the solution, allowing more ions to be near, due to not having as much steric hindrance from the rest of the surrounding protein. At these higher RMSDs, residues 56–58 also are better hydrated having more (Supplemental Figure 2) solution accessible surface.

3.3. Reweighted E2E Results

To further investigate the conformational free energy surface for this system, the PMFs for both systems were reweighted based on end-to-end (E2E) distance, as described in equation 1. The distances considered are from the first heavy atom of residue 50 to the last heavy atom of residue 58 for both monomers. Thus, we chose the nitrogen of Asn50 to the oxygen on Gly58. In crystal form, the length of both of these distances is 14Å. In our starting structure, those distances are 14.5Å and 11.5Å, denoted as (14.5, 11.5), for monomer 1 and 2 respectively. Since these two monomers are independent and have nonsymmetric conformations, we consider the re-weighted energetic profile as the E2E distance of monomer 1 versus the E2E distance of monomer 2 versus the free energy of the system.

Figure 3 shows the minima for both systems are near the helical the starting structure. For the system in high ion concentration the minimum is seen at (14.75, 11.25), while the system in low ion concentration has minimum at (14.25, 11.25). (Figure 3, A and B) When looking at the structures of the protein with E2E distances near these minima, ± .25Å, the majority of the structures are helical, similar to the starting structure, but some can be found with an RMSD up to 3.07Å.

Figure 3:

A,B – Free energy versus end to end distances of the two monomers for the high ion and low ion systems respectively.

The re-weighted PMF in terms of end-to-end distances of the helices gives a different perspective from the RMSD from the crystal structure. While neither CV may be optimal both give insight into the collection of the most energetically favorable structures.

We find a persistence of a lack of symmetry despite the sequence identity. Both systems favor asymmetric conformations with monomers exploring different lengths and thus different structures. Monomer 1 is usually longer than monomer 2 in Figure 3. Conformations where the opposite is true are less favorable.

4. Discussion and Conclusions

The trait of coupled folding and binding is common in protein-DNA recognition.^51–54 LacI repressor has been an often studied model of this sort of recognition pathway.^{11, 18} This pathway has many complexities that contribute to its function as reflected in the inter-protein interactions, protein-solution interactions, and protein-DNA interactions. To better understand the details of the protein conformational energetic changes, we have looked at the mechanism of the range of protein conformations without the added influence of DNA to determine the protein’s propensity for the required shape. In this work, we have presented a quantitative analysis of the structural transition of the LacI HH, in the presence of the DBD, from helical to disordered conformation in two different solution conditions. The high salt solution is a model for the counterion-condensed atmosphere the protein would be in when binding to DNA.

Previously it has been noted that the protein should be disordered in solution, without considering its free energy profile to transition from this state.^{3, 21, 22} We found that the HH prefers to be in a disordered conformation when free in solution, with or without salt, regardless of the presence of the DBD. The free energy required to make the transition to the helical state is however considerably lowered when the DBD is present and ions are added to the system. This is mechanistically consistent with the understanding that the area surrounding DNA is highly saturated with ions³⁴ and so would promote helical propensity. Thus, when the protein gets closer to any DNA, an environment with a higher ion concentration, the cost of helix formation is lowered. The amount of free energy needed by the operator sequence to secure that change is then reasonable in comparison to the HH alone in solution.³³ We note that all simulation studies show a dependence on force fields and recent studies have shown issues when considering unstructured domains with force fields designed for folded proteins.⁵⁵

Previous studies^{56,57, 58} have shown that an increase in ionic strength shifts the equilibrium towards helical stability in alanine rich peptides. They found that concentrations below 0.15M had a linear effect while higher concentrations followed a more exponential dependence. We saw the effect ion concentration has on charged or polar residues, specifically the importance of Arg51 and Gln55. According to previous studies^{19, 50} Asn50, Arg51, and Gln55 all associate with the core domain while bound to operator DNA. This means that when the HH is helical and the core domain is not present, they are facing out towards the solution and able to interact with the most ions. Future studies will be required to study whether this trend of high ion-protein interaction still holds when the core domain is present or if the protein-protein interactions out compete them. Residues 52 and 53 are consistently surrounded by the two lowest ion concentrations, this correlates with both having strong monomer-monomer interactions.⁵⁰ Residue 52 was specifically chosen as the one to be mutated (V52C) because it was the only one that had no direct interactions with DNA or the core domain.³⁵ It only interacts with the other HH.

The PMFs reweighted based on end-to-end distances gave additional insight into the 3-dimensional structure of the protein when free in solution. Although the RMSD PMFs gave markedly different numbers between the ordered and disordered structures, the reweighted E2E PMFs of the two systems are quite similar to each other. This points toward possible favored structural characteristics in solution even with a broad conformational distribution. Despite the environments being different, without DNA present these two systems both favored structures with similar end-to-end lengths. Further investigations into what specific characteristics other than this are favored should be pursued. More information on the structure of the protein in solution could help our understanding of the protein as a whole.

Our results show a clear difference between the free energy landscape in low and high ion concentrations. This gives a better idea of the free energetic changes as the protein moves through solution to recognize DNA. These results build upon Spronk’s work⁵⁹ that showed the dimer to be necessary for helical formation. When comparing to our previous work³³ of the single HH alone in solution, adding the rest of the DBD complex significantly lowers the free energy penalty between the ordered and disordered conformations when in a solution similar to that surrounding DNA. The physical principles that emerge from this study add to our understanding of IDPs, specifically intrinsically disordered regions that change conformation upon binding DNA.

Supplementary Material

2

Supporting Figure 1: Average variance of PMFs at each Gaussian height for simulations versus RMSD from starting helical structure. A) is of the high ion system, B) is of the low ion system.

3

Supporting Figure 2: The average number of water molecules within 5 Angstroms of the specific protein residue versus the RMSD of the HHs. Red = Leucine 56, Green = Alanine 57, Blue = Glycine 58

Highlights.

• When the Lac repressor protein binds to the correct DNA sequence, the hinge region of the protein goes through a disorder to order transition.

• Previous simulations showed that this region is disordered when free in solution without the DNA binding domain present but those studies lacked the DNA binding domain and the saline environment.

• Our simulations find that the presence of the DNA binding domain proximal to the hinge helix and salt make the ordered conformation more probable even without DNA present.