The heterogeneous landscape and early evolution of pathogen-associated CpG dinucleotides in SARS-CoV-2

Abstract

SARS-CoV-2 infection can lead to acute respiratory syndrome in patients, which can be due in part to dysregulated immune signalling. We analyze here the occurrences of CpG dinucleotides, which are putative pathogen-associated molecular patterns, along the viral sequence. Carrying out a comparative analysis with other ssRNA viruses and within the Coronaviridae family, we find the CpG content of SARS-CoV-2, while low compared to other betacoronaviruses, widely fluctuates along its primary sequence. While the CpG relative abundance and its associated CpG force parameter [1] are low for the spike protein (S) and comparable to circulating seasonal coronaviruses such as HKU1, they are much greater and comparable to SARS and MERS for the 3’-end of the viral genome. In particular, the nucleocapsid protein (N), whose transcripts are relatively abundant in the cytoplasm of infected cells and present in the 3’UTRs of all subgenomic RNA, has high CpG content. We speculate this dual nature of CpG content can confer to SARS-CoV-2 high ability to both enter the host and trigger pattern recognition receptors (PRRs) in different contexts. We then investigate the evolution of synonymous mutations since the outbreak of the COVID-19 pandemic. Using a new application of selective forces on dinucleotides to estimate context driven mutational processes, we find that synonymous mutations seem driven both by the viral codon bias and by the high value of the CpG force in the N protein, leading to a loss in CpG content. Sequence motifs preceding these CpG-loss-associated loci match recently identified binding patterns of the Zinc Finger anti-viral Protein (ZAP) protein.

1. Introduction

The innate immune system and RNA processing machinery recognizes “non-self” patterns and motifs in viruses that are rarely seen in the hosts they infect. These patterns can differ between species [2]. When a virus enters a new host, it can present pathogen-associated molecular patterns (PAMPs) in its new host that are rarely seen in circulating strains that have adapted to that host’s immune environment over evolutionary timescales. The emergence of SARSCoV-2, therefore, provides a rare window into innate immune signaling that may be relevant for understanding immune-mediated pathologies of SARS-CoV-2, anti-viral treatment strategies, and the evolutionary dynamics of the virus, where evidence for selective pressures on viral features can reflect what defines “self” in its new host. As a case in point, the 1918 influenza pandemic was likely caused by a strain that originated in water fowl and entered the human population after possible evolving in an intermediate host. That viral genome presented CpG dinucleotides within a context and level of density rarely found in the human genome where they are severely underespressed, particularly in a set of genes coding for the proteins associated with antiviral innate immunity [3, 2, 4, 1]. Over the past century the 1918 H1N1 lineage evolved in a directed manner to lower these motifs and gain UpA motifs, in a way that could not be explained by its amino acid usage of codon bias [5, 1]. It has since been found that these motifs can engage the pattern recognition receptors (PRRs) of the innate immune system [6, 7], and directly bind the Zinc Finger anti-viral Protein (ZAP), both in a CpG dependent manner [8, 9, 10]. Hence, the interrogation of emergent viruses from this perspective can predict novel host virus interactions.

COVID-19 presents, thus far, a different pathology than that associated with the 1918 H1N1, which was disproportionately fatal in healthy young adults. It has been characterized by a large heterogeneity in the immune response to the virus [11, 12, 13] and likely dysregulated type I interferon signaling [14, 15]. Various treatments to attenuate inflammatory responses have been proposed and are currently under analysis or being clinically tested [16]. It is therefore essential to quantify pathogen-associated patterns in the SARS-CoV-2 genome for multiple reasons. The first is to better understand the pathways engaged by innate immune agonism and the specific agonists to help build better antiviral therapies. Another is to better predict the evolution of motif content in synonymous mutations in SARS-CoV-2, as it will help understand the process and timescales of attenuation in humans. Third is to offer a principled approach for optimizing vaccine strategy for designed strains [17, 18] to better reflect human-genome features.

In this work we will use the framework developed in [1] to carry out a study of non-self associated dinucleotide usage in SARS-CoV-2 genomes. The statistical physics framework is based on the idea of identifying the abundance or scarcity of dinucleotides given their expected usage based on host features. In [1] some of us introduced a parameter, which we call the selective force, that characterizes the deviation with respect to a null model in which the number of dinculeotides is the one statistically expected under a set of constraints. For instance, the selective force on CpG dinucledoties is zero if the number of CpG is exactly the one expected, is positive when it is larger than what is expected and negative otherwise. Such a force generalizes the dinucleotide relative abundance introduced in [2], not only when choosing the nucleotide bias as the null model, but also to a null model built on other features such as a fixed amino acid sequence and reference codon bias. CpG forces could be related to the evolutionary constraint to lower or increase CpG number under the pressure of host PRRs that recognize a pathogen. Such formalism has further been applied to identify non-coding RNA from repetitive elements in the human genome expressed in cancer that can also engage PRRs [19], to characterize the CpG evolution through synonymous mutations in H1N1 [1], and to characterize local and non-local forces on dinucleotides across RNA viruses [7].

We perform an analysis of the landscape of CpG and UpA motifs and associated selective forces in SARS-CoV-2 in comparison with other genomes in the coronavirus family in order to understand specific PAMPs associated features in the new SARS-CoV-2 strains (Sec. 2.1). We also focus on the heterogeneity of CpG motif usage along the SARS-CoV-2 genome (Sec. 2.1 and 2.2). Finally we use a model of the viral gene evolution under human host pressure, characterized by the CpG force, to study synonymous mutations, and in particular those which change CpG content, observed since the SARS-CoV-2 entered the human population (Sec. 2.3). The latter approach points out at hotspots where new mutations will likely attenuate the virus, while evolving in contact with the human host.

2. Results

2.1. SARS-CoV-2 heterogeneous landscape of CpG force

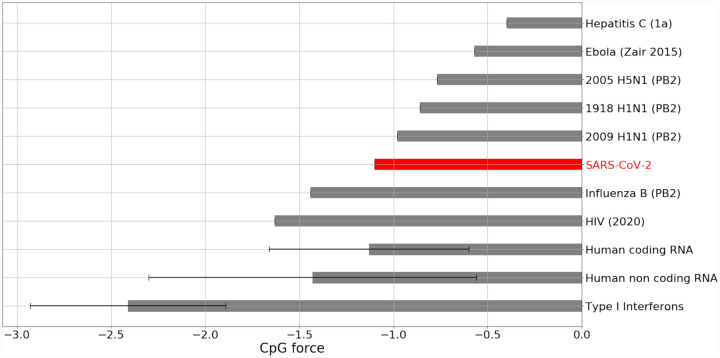
We analyze dinucleotide forces across the SARS-CoV-2 genome, in particular those on CpG and UpA motifs¹. As a first check, in Fig. 1 we compare the total CpG forces of SARS-CoV-2 with other ssRNA viruses (Influenza B, 1918 and 2009 H1N1, H5N1, Ebola, type 1 HIV, type 1a Hepatitis C), and the forces in human transcriptome for coding, non coding region [19] as well as the RNA for type I interferons. Fig. 1 shows that the total SARS-CoV-2 force on CpG motifs is larger than influenza B but smaller than the H1N1 strains, H5N1, Ebola virus, therefore putting SARS-CoV-2 in an intermediate region of CpG forces.

Figure 1: Comparison of CpG forces for SARS-CoV-2 genome with human coding DNAs and non-coding RNAs and other ssRNA viruses.

The average value and variances are shown for human RNA. Type 1 Interferons coding transcripts are shown separately to highlight their very low CpG force. For human influenza the longest gene (PB2) has been chosen. Data from Gencode [20] and NCBI [21], see SI.1.

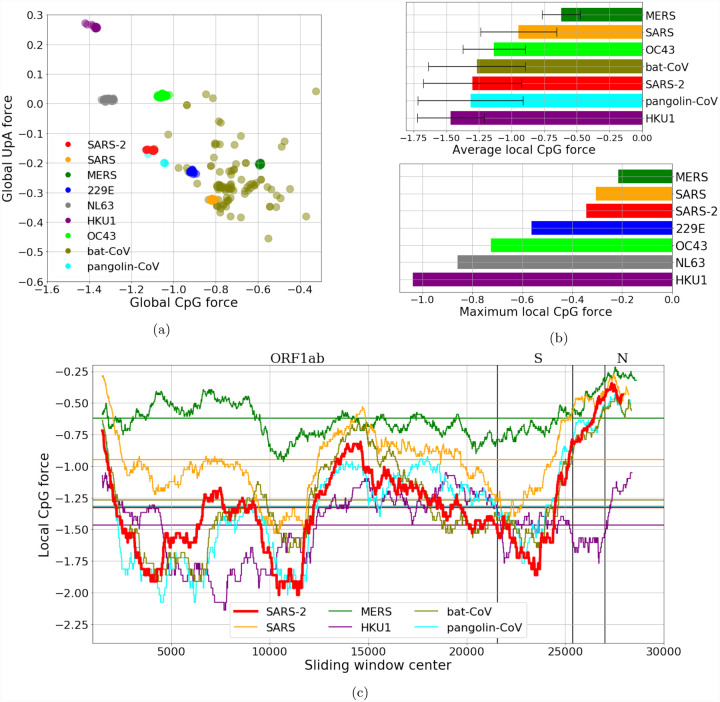
Next we explore more in detail the CpG forces within the Coronaviridae family, with a particular emphasis on the genera Alphacoronavirus and Betacoronavirus, and on those viruses which infect humans [22]. We have first compared the global forces on CpG and UpA dinucleotides, computed across the whole genome without any constraint on amino acid or codon usage. To calculate such forces we need a reference nucleotide bias, to give a null model for nucleotide usage (See Methods Sec. 4.1, 4.2). We will in the following use as nucleotide bias, the one calculated from the human genome [23]. This is the natural choice since we ultimately want to predict regions sensed by PRRs as non-self, which may engage the human innate immune response. We have verified that the specific choice of such bias does not change qualitatively the results in the comparative analysis, as long as the same set of reference frequencies is used to compute the forces across viral genomes. For instance, we obtain similar results in terms of the rank order of viruses, using the average frequencies of nucleotides in coronavirus genomes.

The resulting comparison is summarized in Fig. 2a: in this case MERS shows the highest CpG force among the human coronaviruses, followed by SARS, while some bat coronaviruses have stronger CpG force. It is worth noticing that SARS-CoV-2 is among the viruses with smallest global CpG force and some hCoV that circulate in humans with less pathogenicity have a global CpG force comparable or higher than that of SARS-CoV-2, so there is not a straightforward correlation between global CpG force and the pathology of a coronavirus in humans. For the force on UpA dinucleotides, it is clear already from this comparison that it is anti-correlated with the CpG force, as we expect for the complementarity between such motifs². Due to the fact that the genes and the global length of viruses in the Alphacoronavirus and Betacoronavirus genera are quite similar, the comparison of CpG forces gives the same outcome than the direct comparison of the number of CpG along the sequence, see Supp. Fig. SI.3.

Figure 2: CpG and UpA forces and their local fluctuations in the coronaviriadae family.

(a):CpG Forces computed on the whole genome. Species are well clustered, due to the large conservation of the sampled sequences, except for the strains originating in bats which is a grouping of several diverse strains. The anticorrelation of the CpG and the UpA force is due to their complementarity. (b, c, d): Local analysis in sliding windows of 3 kb along the genome. Local forces along the genome (b, c): while the average CpG force of SARS-CoV-2 is relatively low, the variance along the genome is high with greater CpG forces in certain regions (such as the coding region for protein N) and lower CpG forces in other (e. g. coding region for protein S). (b)-lower panel: maximum value of the local CpG force showing that values for SARS-CoV-2 moves closer to the most dangerous viruses. The bat sequence analyzed in panels (b) and (c) is RaTG13, while the pangolin sequence has been sequenced at Guangdong, in 2019. Data from VIPR [24] and GISAID [25], see Methods Sec. 4.5 and SI.1.

To go beyond the global analysis we have performed a local analysis on CpG motif usage, by looking to the local forces in fixed-length windows along the genome (similar results are also obtained by looking directly at the CpG content in the same windows). This is done in Fig. 2c for SARS, MERS, SARS-CoV-2, hCoV-HKU1 and two representative sequences of bat and pangolin coronaviruses, which are chosen because of their closeness (in Hamming distance) to SARS-CoV-2 (the bat-coronavirus sequence is RaTG13, the pangolin-coronavirus sequence has been sequenced at Guangdong, in 2019).

It is evident that in some regions, especially at the 5’ and 3’ ends of the sequence, the SARS-CoV-2, SARS and MERS (together with the bat and pangolin viruses) have a peak in CpG forces, which is absent in the hCoV-HKU1 (as well as in the other hCoVs, see Supp. Fig. SI.4). The high CpG content at the extremities can have an important effect on the activation of the immune response via sensing, as the life cycle of the virus is such that the initial and final part of the genome are those involved in the subgenomic transcription needed for viral replication [26, 27]. During the infection many more RNA fragments with these regions are present in the cytoplasm, than the other regions of the viral genome. In this sense, despite the relatively low CpG content of SARS-CoV-2 compared to other coronaviruses, there is can be a high concentrations of CpG rich RNA due to the higher transcription of these regions.

To complement this analysis, in Fig. 2b (upper bar plot) we make a direct comparison among the average local CpG forces and standard deviations of the coronaviruses analyzed. This shows more clearly that, while the SARS-CoV-2 has an intermediate overall CpG level, its variance is very high, comparable with that of SARS and of two examples of bat and pangolin coronaviruses. This suggests a comparison among the coronaviruses based on the part of the sequence with the highest CpG and UpA force, which is presented in Fig. 2b (lower bar plot). In this case, the results are much closer to what may be expected: MERS and SARS, viruses that are likely less well adapted to a human host, have the highest local peaks in CpG content, followed by SARS-CoV-2 and then by seasonal strains that circulate in humans. These results are corroborated by the same qualitative picture which comes from the analysis of CpG motif density, as shown in Suppl. Fig. SI.3c. It is interesting to notice that high and very high levels of proinflammatory cytokines/chemokines (such as IL-6 and TNF-α) have been observed in, respectively, SARS and MERS and, at times, SARS-CoV-2 infection [28, 11].

2.2. Forces in coding regions constrained by codon and amino acid usage

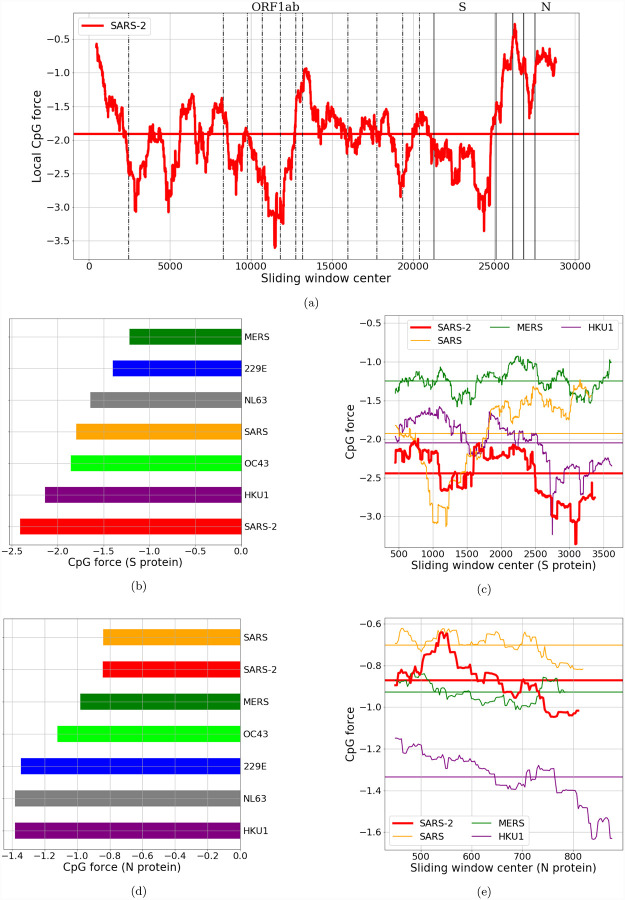
We have seen in Fig. 2c that in all the coronavirus genomes there are regions with large deviations in CpG content with respect to the average (whatever we use to measure this content, be it density or force), and that SARS-CoV-2 has a particularly high variance when compared with other coronaviruses circulating in humans. However, most of the viral genome codes for proteins, so the analysis should take this feature into account. The advantage of the method of dinucleotide forces is that its statistical physics framework allows such constraints to be introduced in a straightforward manner (Methods Sec. 4.2). In Fig. 3a we perform the local analysis of forces on dinucleotides with the coding constraints, by using as reference codon usage bias the human one, along all the coding regions of the SARS-CoV-2 genome, and in Figs. 3b, 3c, 3d and 3e, we focus on the genome regions coding for the nucleocapside (N) and spike (S) proteins [29, 30, 17].

Figure 3: CpG local Forces on SARS-CoV-2 coding regions constrained by codon and amino acid usage.

(a): Local Forces, on sliding windows over 900 nucleotides, on all the coding regions of SARS-CoV-2 (pre-processed to ensure the correct reading frame, see Methods Sec. 4.5). The horizontal line denotes the average force. Many large fluctuations coincide with boundaries of protein domains, suggesting that recombination could have had a role in creating theses CpG force fluctuations. In panels (b) and (d): bar plots for average local forces for structural proteins in the Coronaviridae family. The two largest structural proteins, N and S, have very different forces in SARS-CoV-2. Each bar is obtained by averaging the CpG force over several sequences (from VIPR [24] and GISAID [25], see SI.1), and the standard deviation of the average (not shown) is lower than 0.025. (c) and (e): local forces for N and S compared with the same proteins of other beta-coronaviruses. Horizontal lines denote the average forces.

A first, relevant observation is that the high variability which we discussed in Fig. 2c is confirmed by this analysis, and in particular the 3’ peak of high CpG density and force is still present. Moreover, in Fig 3a some of the small non-coding regions which are excluded from the figure (as they are not used for the computation of the local force) are pointed out with black solid lines. It seems that large changes in local force happen in the vicinity of these lines, thus hinting at a possible role of recombination in the generation of this complex and heterogeneous local CpG-force landscape, though such a hypothesis would have to be confirmed by phylogenetic analysis.

To compare several strains of coronaviruses, we focus on the structural proteins, which are always present and quite similar across the Coronaviridae family. Notice that all these proteins are coded for after the ORF1ab coding region in Fig. 2c. We computed the CpG force with coding constraints for each structural protein. The first protein (in the standard 5’-to-3’ order) is the S protein, and it corresponds to the low-peak in CpG force and density for SARS-CoV-2 in Fig. 2c. The S protein has to bind with ACE2 human receptor and TMPRSS2 [30]. It is also the longest structural protein. In Fig. 3e the CpG force along the region coding for S (S ORF) computed. SARS-CoV-2 shows the lowest average of CpG force among the human-infecting betacoronaviruses, see Fig. 3b, and also locally it has a force lower than most of the other beta-CoVs. A fascinating (as well as speculative) reason that could explain the low CpG force on the S protein, is again recombination: the S protein coding region may come (at least in part) from other coronaviruses that better bound human entry receptors [31].

The second longest structural protein is the N protein. Fig. 3c shows the local computation of CpG forces under coding constraints restricted to this protein, coded for in a region (N ORF) of about 1.2 kb close to the 3’-end of the viral genomes. In this case it is apparent that the CpG force in the SARS-CoV-2 is much higher, immediately below that of SARS and above that of MERS. This is confirmed by the comparison of the total CpG force computed for N across the human-infecting members of the Coronaviridae family, presented in Fig. 3d. This high CpG content, together with the large concentration of N transcripts and similar sequences as a part of all other subgenomic RNAs [27], could confound the “global” prediction that SARS-CoV-2 presents low levels of dinucleotide patterns to receptors that can recognize them, which may be relevant to innate recognition of the virus.

In the comparative analysis of structural proteins in the Coronaviridae family, the E protein is the one showing the largest difference in CpG forces between coronaviruses that circulate in humans (see Supp. Fig. SI.5b). However, the fact that the E protein is short (coded for in about 228 nucleotides) makes the computation of the local forces less stable (that is, small variations in CpG number may correspond to large force variations). The M protein is also quite short (coded for in about 669 nucleotides) and has smaller CpG force differences among species (see Supp. Fig. SI.5c). We therefore focus in the next section on the two longest structural proteins, S and N, to check for the ability of our model to explain (and possibly predict) the CpG changes via synonymous mutations in protein coding regions.

2.3. A quantitative model for early evolution of CpG motifs in SARS-CoV-2

As seen in the previous sections, SARS-CoV-2 has regions which have higher CpG content (and forces) than strains that have been circulating in humans, while the number of CpGs (and the corresponding force) is much lower in other regions. It is therefore interesting to ask to what extent the CpG force model is able to predict any bias in the synonymous mutations already detectable in the few months of evolution since the first SARS-CoV-2 genome was sequenced (data from GISAID [25], reference sequence Wuhan, 26-12-2019, last updated sequence 2020-05-08, see Methods Sec. 4.5) and, consequently, could allow us to predict putative mutational hotspots in the viral evolution.

Barring confounding effects, we would expect that some regions, such as the N ORF, will be driven by host mimicry towards a lower number of CpG motifs. Other regions, such as the the S ORF, have already low CpG content and would feel no pressure to keep the CpG content at that level, so random mutations would likely increase their CpG numbers. These predictions are in good agreement with the observed mutations in current SARS-CoV-2 data, as shown in Fig. 4a. We see that the N and S subsequences undergo synonymous mutations that decrease (blue) or increase (red) their numbers of CpG. We also show the local CpG force, constrained by codon and amino acid usage (same as Fig. 3a), along the sequence. Most of the mutations that decrease the number of CpG are located at the 3’-end of the sequence, in correspondence with the high peak in CpG force in the N ORF region. Conversely, mutations that increase the number of CpG are found in ORF1ab, in the low-CpG-force regions and in the S ORF region.

Figure 4: Analysis of the synonymous mutations from one among the first sequenced SARS-CoV-2 genomes (Wuhan, 26-12-2019).

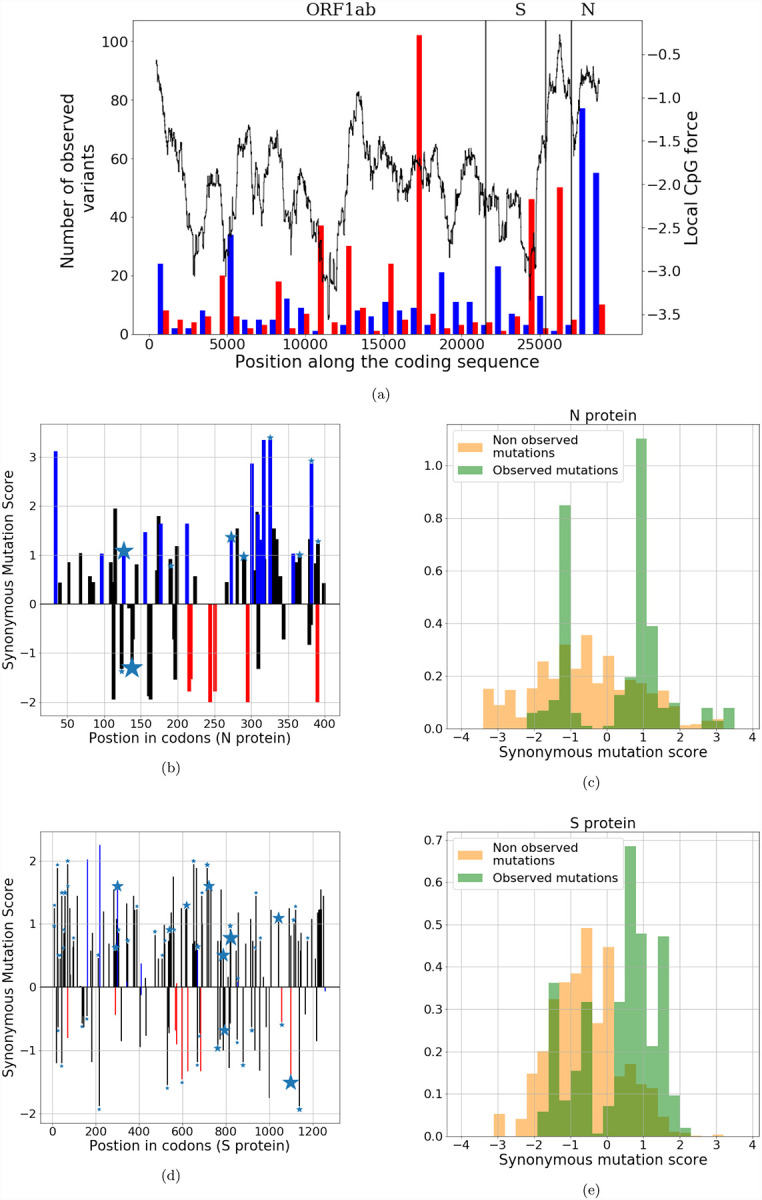
(a): CpG-changing mutations. Red and blue bars show the numbers of mutations that, respectively, increased and decreased the mean CpG content over 900 b windows (left scale). The black curve shows the CpG force along the sequence (right scale). (b),(d) for N and S protein: bars show the synonymous mutation score (SMS) associated to mutations along the sequence. Color code for mutations: black–no change in CpG; blue–increase in CpG, red–decrease in CpG. Stars show mutations observed at least 5 times in sequence data; the size of the star is proportional to the number of observations. (c),(e): histograms of SMS for observed mutations (in green) and for non-observed putative mutations (in yellow) in the N and S proteins. Data from GISAID [25], see Methods Sec. 4.5.

We first focus on the N protein. The locations of synonymous mutations and multiplicities (the number of sequences in which they are found to occur) are indicated by star symbols of corresponding sizes in Fig. 4b. We observed a total number of M_s = 342 synonymous variants (with 67 unique mutations). Out of these M_s variants 129 and 10, respectively, lower and increase CpG, while the remaining 203 leave CpG content unchanged. It is remarkable than more than 92% of the mutations that affect the CpG count decrease it.

When restricting the analysis on the 129 mutated sequences in which the CpG count decreases, the losses take place in at 14 different loci. The nucleotide motifs preceding these loci are listed in the top 14 lines of Table 1, together with their positions along SARS-CoV-2 (Wuhan, 26/12/2019) and their number of occurrences in the sequence data. 7 out of 14 of these motifs, which represent 80 out of the 129 observed CpG losses, are of the type CnxGxCG, where nx is a spacer of n nucleotides and were identified as ZAP binding patterns in [9]. The binding affinity of ZAP to the motifs strongly depends on the spacer length, n, with top affinity for n=7 [9]. Notice that 3 out of the 7 CpG-suppression related motifs in SARS-CoV-2 correspond to n=7. Other motifs of the type CnxGcCG are also present in SARS-CoV-2, but their CpG is not lost in sequence data, see last 3 lines of Table 1; the dissociation constants associated to their spacer lengths are on average larger than the ones of the motifs showing CpG loss.

Table 1:

Analysis of nucleotidic motifs preceding CpG in the N protein. The top 6 lines show subsequences of SARS-CoV-2 (Wuhan, 26/12/2019) of the type CnxGxCG, where the spacer nx includes n=4, 5, 7 or 8 nucleotides, for which the CpG dinucleotide was lost in some of the mutated sequences. These motifs were shown to be binding patterns for the ZAP protein in [9]; the dissociation constants were measured for repeated A spacers, with values (in μM) K_d(4) = 0.33 ± 0.05, K_d(5) = 0.49 ± 0.10, K_d(7) = 0.12 ± 0.04, K_d(8) = 0.64±0.14, [9]. The next 7 lines show the other 3 CpG lost through mutations and their 10 preceding nucleotides, which do not correspond to motifs tested in [9]. The last 6 lines show other subsequences in the N protein, known as binding motifs of ZAP from [9], but for which no loss of CpG is observed in the sequence data.

Motif	n	Position of CpG	Nb. of sequences with CpG loss
CATTGGCCG	4	905	2
CGGAATGTCG	5	953	2
CATATT GACG	5	1074	1
CGCAGTGGGGCG	7	104	2
CTAACAAAGACG	7	384	68
CTGGCAATGGCG	7	642	2
CGTGGTGGTGACG	8	294	3
ATGCTGCAATCG	-	471	1
AGAAGGGAGGCG	-	533	1
CACAAGCTTTCG	-	822	29
TTGCCCCCAGCG	-	930	4
CAGCGTTCTTCG	-	945	1
GTCACACCTTCG	-	980	7
CAAGCCTTACCG	-	1148	6
CGGCAGACG	4	829	0
CTACCA GACG	5	277	0
CACGTAGTCG	5	571	0
CAAAACAACGTCG	8	121	0
CGAGGACAAGGCG	8	213	0

For the S protein (see Fig. 4d and star sizes) we observed M_s = 516 synonymous variants (with 152 unique mutations). Among these unique mutations, 42 and 63, respectively, lower and increase the CpG content. Therefore, only 40% of the mutations that affect the CpG count decreases it.

These results seem to support the existence of early selection pressure to lower CpG occurrence in N ORF, but not in S ORF. Moreover, according to our model, mutations are not only driven by the local CpG force, but also by viral codon bias computed on the reference sequence³. It is therefore theoretically possible (and in full accord with our model) that, even in low CpG force regions, a mutation decreasing the CpG number is favorable due to the biases introduced by the distribution of synonymous codons. We developed a computational framework to estimate the odds of transition to a mutated sequence from SARS-CoV-2 (Wuhan, 26-12-2019) based on the CpG-force model (Methods Sec. 4.3). For a synonymous mutation that does not change CpG, our synonymous mutation score (SMS), defined in Methods Sec. 4.3, will only depend on the change in codon biases due to the mutation. Additionally, mutations affecting CpG content bring contributions to the transition probabilities that depend on the local CpG force. In Fig. 4 we show our predictions for synonymous mutations in the N (4b, 4c) and the S (4d, 4e) proteins. Figs. 4b and 4d show SMS along, respectively, the N and S sequences and the mutations, respectively, lowering (blue), increasing (red), or leaving unchanged (black) the CpG content. We observe that the majority of mutations (taking into account multiplicity, labeled by stars in the figure) in SARS-CoV-2 correspond to high SMS, in agreement with our model.

To make our arguments more quantitative, we tested the ability of our model to discriminate between observed and non-observed mutations. In Figs. 4c and 4e we show the histograms of the SMS corresponding to observed synonymous variants (in green) and to putative mutations that would leave amino-acid content unchanged but have not been observed so far (in yellow).

The distribution of SMS for observed mutations is shifted to higher values compared to their counterparts for non-observed mutations, both for the proteins N and S. Hence, our model is able to statistically discriminate between non-observed and observed synonymous mutations (ANOVA F-test: 107 for N and 408 for S). Note that for the null mutational models in which synonymous mutational rate are uniform, the score distribution for observed and unobserved mutations is equally peaked at zero (ANOVA F-test=1). A simpler model for the SMS using codon bias only, without force (Suppl. Fig. SI.6) is also able to discriminate between observed and non-observed mutations, albeit with a smaller score for protein N (ANOVA F-test=42) and a comparable result for S (ANOVA F-test=411), further demonstrating that S ORF synonymous mutations are likely due to a neutral reversion to the mean, while N ORF mutations may contain an additional pressure. Notice that similar results are obtained if we consider unique mutations (dropping any information about multiplicity), (ANOVA F-test=37 (N protein), 145 (S protein) see Suppl. Fig. SI.7).

We have further performed comparative tests of our model, in which mutations are driven by codon bias and CpG forces, with simpler models using: i) only the transition versus transversion rate (with ratio 4:1), [32] (trs-trv bias) (Methods Sec. 4.4.), ii) the transition versus transversion rate and CpG force, iii) a uniform rate (null model described above), and iv) a uniform rate and CpG force. The results of these additional tests are shown in Suppl. Fig. SI.8. The ANOVA F-test and p-values are shown in Table 2 and confirm that while the uniform rate and the transition versus transversion bias are not enough to separate the score distributions between observed and unobserved mutations, for the N ORF adding a CpG force gives a very clear separation, in the two cases, while for the S ORF we observe a still present but less marked separation. We checked the consistency of our results at different times since our first analysis (dated 2020-04-22, see Suppl. Table 3).

Table 2:

Anova F-test with the corresponding p-values for distributions of synonymous mutation scores (SMS) computed from observed and non-observed mutations in S ORF and N ORF and for different models of synonymous mutations (uniform bias, transition versus transversion bias (trt-trv), virus codon bias, with, and without CpG force). In the uniform case, we did not specify the p-value since all mutations have the same SMS.

	F-test (S ORF)	F-test (N ORF)	p-value (S ORF)	p-value (N ORF)
Uniform bias	1	1	-	-
Uniform bias + CpG force	79	240	1 · 10−18	5 · 10−50
trt-trv bias	0.6	5 · 10−6	> 0.05	> 0.05
trt-trv bias + CpG force	53	159	4 · 10−13	1 · 10−34
Virus codon bias	411	42	< 10−50	1 · 10−10
Virus codon bias + CpG force	408	107	< 10−50	3 · 10−24

Consequently, mutation data seem to confirm the hypothesis that the CpG force drives the evolution of synonymous mutations to lower number of CpG motifs in the N ORF. For the S ORF, which already has quite low CpG number, the situation is less clear: the observed tendency to CpG increase through synonymous mutations is compatible with the presence of a force pushing up this number, but is equally well explained by the viral codon bias model. This uncertainty is expected from the relatively small number of mutations with a CpG change in S protein region in the sequences collected so far.

3. Discussion

The present work contains three main directions in the early analysis of SARS-CoV-2 genomes and dinucleotide motifs, particularly CpG, usage. First, a comparative analysis with other genomes in the Coronaviridae family, which has stressed that a peculiarity of SARS-CoV-2 with respect to the other coronavirus genomes is a globally lower CpG content (though not particularly low compared to other RNA viruses) accompanied by large fluctuations along the genome. Notably the segment coding for the S protein has a much lower CpG content and force. Other regions, in particular the region after the slippage site in ORF1ab and the initial and final part of the genome including the N ORF, are characterized by a larger density of CpG motifs (and corresponding CpG force), which are comparable to the SARS and MERS viruses in the Betacoronavirus genus.

Interestingly the initial and final part of the genome are implied in the full-genome and subgenomic viral replication. In particular, the coding region of the N protein and its RNA sequence, present in the 3’ untranslated region (UTRs) of all SARS-CoV-2 subgenomic RNAs, has been shown in [27] to be the most abundant transcript in the cytoplasm. The high concentration of this feature could contribute to a dysregulated innate immune response. SARSCoV-2, due to its complex replication machinery, does not express its RNA at uniform concentration. A mechanism generating different densities of PAMPs being presented to the immune system at different points in the viral life cycle can affect immune recognition and regulation. The precise way this can contribute to immuno-pathologies associated with COVID-19 and how this is related to the cytokine signaling dysfunction associated with severe cases, need further experimental investigation. The sharp heterogeneity of the CpG abundance along the SARS-CoV-2 genome is also compatible with viral recombination, in agreement with the hypothesis stated in [31]. The degree to which this heterogeneity in any way reflects zoonotic origins should be further carried out using phylogeny. A first analysis of the evolution of synonymous mutations since the outbreak of COVID-19 shows that mutations increasing CpG content have occurred in the middle and low CpG content regions, in particular the S protein region. Conversely, mutations lowering the number of CpG have taken place in regions with higher CpG content, in particular, the N protein region. The sequence motifs preceding the loci of the CpG removed by mutations match some of the strongly binding patterns of the ZAP protein [9].

Natural sequence evolution seems to be compatible for protein N with our model, in which synonymous mutations are driven by the virus codon bias and the CpG forces leading to a progressive loss in CpG. These losses are expected to lower the CpG forces, until they reach the equilibrium values in human host, as is seen in coronaviruses commonly circulating in human population [33]. More data, collected at an unprecedented pace [34, 25, 24], and on a longer evolutionary time are needed to confirm these hypothesis. SARS-CoV-2 has a low mutation rate for an RNA virus due to the presence of a proofreading mechanism in its replication [35]. An integrative study of the transmissivity of the SARS-CoV-2 and its mutation rate could be performed to predict the time scale at which such natural evolution driven by host mimicry would bring the virus to an equilibrium with its host [5, 1].

While the results presented here are preliminary due to the early genomics of this emerging virus, they point to interesting future directions to identifying the drivers of SARS-CoV-2 evolution and building better antiviral therapies.

4. Methods

4.1. CpG density versus local and global forces

The aim of this section is to give an overview of the methods used throughout this work, and to explain why for some analyses we used one method rather than the others.

We want to characterize the CpG content of a given genome. The different methods that we used to achieve this result, discussed with their usage cases and their limits, are the following:

• A first possibility is to simply count the number of dinucleotide motifs (or to compute their density), along the whole genome. This simple count can be useful to see if there is an evolution of the motif number over time, or to study local fluctuations along a sequence to identify regions in which a motif is abundant or scarce, but it is not suitable to make comparisons among viruses of different families, mainly because of the different length and usage biases of viral genomes. However, since we focused mostly on the Coronaviridae family, these differences are not so important, and indeed we can see in Suppl. Fig. SI.3 that some of our results are also apparent from the motif density analysis.

• The force defines the abundance or scarcity of a motif given its expected usage based on the nucleotide bias. It can be computed on the whole or part of the genome. In this work we always use, to calculate the force, the human nucleotide bias as reference bias. In Sec. 4.2 we detail the force calculation. An important remark is that the force is directly related to the relative abundance $\frac{f(ab)}{f(a)f(b)}$ of a motif of nucleotides a and b with respect to their bias, (f(ab) is the frequency of the motif and f(a), f(b) the reference biases of nucleotides a and b) [2], see Eq. 4 and SI Sec. SI.2. This method gives results qualitatively similar to the CpG-density methods for the local analysis. However it allows, in principle, also comparisons among more different genomes, as was done in Fig. 1.

• As shown in Sec. 4.2, the calculation of the force can be extended to constrain variability of nucleotidic sequences at fixed codons, and using as reference bias the codon bias. This way of computing forces takes into account the fact that the virus has to code for certain specific proteins in its genome. We always used here the human codon bias as reference to compute this force with codon constraints. Calculating forces at fixed codon usage allows us to confirm also in this framework the identification of high- and low-CpG force regions in Sec. 2.2 and it was crucial to investigate the dynamics of the synonymous mutations in viral evolution, Sec. 2.3.

4.2. Force-based model

The model at the core of many of the analyses made here is taken from [1]. Here we briefly review the model, together with its simplified version which does not take into account the codon constraint. Let us start from the latter. Given a motif m and a sequence s₀ = {s₁, …, s_N} of length N, we consider the ensemble of all sequences with length N, which we denote with S, and we suppose the probability of observing s out of this ensemble to be

$$p(s)=\frac{1}{Z}\left(\prod _{i=1}^{N}f\left(s_i\right)\right)e^{x{N}_m(s)}.$$ (1)

Here, f(s_i) is the nucleotide bias, that the i-th nucleotide is s_i (for example, we always used in this work the human frequency of nucleotides as f(s_i)), x is the force we want to compute, and N_m is the number of times the motif m appears in the sequence. Z is the normalization constant, that is

$$Z=\sum _{s\in \mathcal{S}}\left(\prod _{i=1}^{N}f\left(s_i\right)\right)e^{x{N}_m(s)}.$$ (2)

Therefore the force x is a parameter which quantifies the lack (if negative) or abundance (if positive) of occurrences of m with respect to the number of occurrences due to the local probabilities f(s_i). We can fix x by requiring that the number of motifs in the observed sequence, N_m(s₀) = n₀, is equal to the average number of motifs computed through the model, 〈n〉, that is

$$\langle n\rangle =\sum _{s\in \mathcal{S}}\left(\prod _{i=1}^{N}f\left(s_i\right)\right)N_m(s)e^{x{N}_m(s)}.$$ (3)

Notice that this is exactly equivalent to the request that x maximizes the probability of having observed s₀.

Let us focus now on the specific case of a dinucleotide motif, that is our motif m consists of the pair ab, where a and b are two consecutive nucleotides (for example, a = C and b = G for the CpG motif). In this case, within an approximation discussed in the SI, Sec. SI.2, the force computed as above turns out to be the logarithm of the relative abundance index, that is

$$x\simeq \text{log}\left(\frac{f(ab)}{f(a)f(b)}\right),$$ (4)

where f(ab) is the number of motifs ab divided by the total length of the sequence N. In Suppl. Fig. SI.1 we tested the accuracy of this approximation in our specific case.

Our model can be improved to take into account the fact that not all the possible sequences with length N can be observed if the genome is coding for one (or more) protein(s). If we restrict the ensemble of sequences to those coding for the same protein, we obtain the model with the codon constraints that we used for several of our analyses here. In this case, we write each sequence s as a series of codons, and its probability is defined as

$$p(s)=\frac{1}{Z}\left(\prod _{i=1}^{N/3}f\left(c_i\right)\right)e^{x{N}_m(s)},$$ (5)

where now the bias takes the form of a codon usage bias, and the normalization constant Z changes accordingly into a sum over all possible synonymous sequences. The force x can be computed, analogously with the procedure for the simpler case, by requiring that the number of motifs observed in s₀ is equal to the model average (although this creates some technical difficulties, which have been overcome in [1]).

4.3. Definition of synonymous mutation score

We use the model introduced above in Eq. 1 to assign a score, which we call synonymous mutation score (SMS), to each possible synonymous mutation of a reference sequence. We consider a system evolving for a small time scale, and a mutation which changes the i-th codon c_i into a synonymous $c_i^{\prime }$. The transition probability, that is the probability of observing the mutation, for such evolution can be decomposed in the product of two evolution operators: The first $T\left(N_{CG}\to N_{CG}^{\prime }\right)$ representing the change in the number of CpG motifs in the mutated sequence, and the second $T\left(c_i\to c_i^{\prime }\right)$ representing the gain in mutating the particular codon in position i.

The first operator can be computed from the dynamical equation introduced in [1] for the evolution of the CpG number N_CG of a sequence under a initial force x through a equilibrium force x_eq:

$$\tau \frac{d{N}_{CG}}{dt}=\left(x_{eq}-x\right).$$ (6)

The equilibrium force is the force computed on a viral strain which is supposed to be to the equilibrium with the human innate immune system, because it has evolved in the human host since a long time. Eq. 6 was used in [1] to describe the evolution of the CpG numpber in H1N1, taking as the equilibrium force the one of the Influenza B strain. In analogy with this approach we take here as f_eq the average force calculated for the given segment or coding region on the seasonal hCoVs (that is hCoV-229E, hCoV-NL63, hCoV-HKU1, hCoV-OC43). τ is a parameter determining the characteristic time scale for synonymous mutations. Based on Eq. (6) we define the transition operator for CpG number as

$$T\left(N_{CG}\to N_{CG}^{\prime }\right)\propto e^{\left(x_{eq}-x\right)\Delta N_{CG}},$$ (7)

where $\Delta N_{CG}=N_{CG}^{\prime }-N_{CG}$. Notice that for all the synonymous mutations leaving unchanged the CpG number the above operator is one. The codon mutational operator is

$$T\left(c_i\to c_i^{\prime }\right)\propto \left(\frac{f\left(c_i^{\prime }\right)}{f\left(c_i\right)}\right),$$ (8)

where f(c_i) is the frequency of codon c_i from the chosen codon usage bias. Putting together these two terms allows us to estimate how likely a specific synonymous mutation is to happen. The synonymous mutation score (SMS) accompanying a mutation is defined as the logarithm of this quantity,

$$\text{SMS}=\left(x_{eq}-x\right)\Delta N_{CG}+\text{log}\left(\frac{f\left(c_i^{\prime }\right)}{f\left(c_i\right)}\right).$$ (9)

4.4. Uniform codon usage bias with transversion penalties

It is well known that transversions (i. e. mutations of purines in pyrimidines and vice-versa) are suppressed with respect to transitions (i. e. mutations of purines in purines or pyrimidines in pyrimidine).

We introduce here a simple way to account for penalties for transversions in the uniform codon bias. We suppose that a mutation with n transversions happens 4 times less than a mutation with n − 1 transversions. Therefore, starting from a uniform probability of mutating a codon c into a synonymous codon c′, we insert the transvertion penalty and obtain that this probability becomes

$$p\left(c\to c^{\prime }\right)=\frac{1}{\mathcal{N}}{\left(\frac{1}{4}\right)}^{t\left(c,c^{\prime }\right)},$$ (10)

where t(c, c′) is the number of transvertions needed to mutate c into c′. Here $\mathcal{N}$ is a normalization constant, such that

$$\sum _{c^{\prime }}p\left(c\to c^{\prime }\right)=1,$$ (11)

the sum runs over the synonymous of c (without including c). Then we can define, for a fixed set of synonym codons, a transition matrix

$$T_{c,c^{\prime }}=p\left(c\to c^{\prime }\right).$$ (12)

The codon usage bias, for synonyms mutations with transversion penalties, is the stationary probability distribution of the Markov chain having the matrix defined in Eq. 12 as transition operator. This stationary distribution is therefore given by the unique vector of probabilities b(c) such that

$$b\left(c^{\prime }\right)=\sum _{c}b(c)T_{c,c^{\prime }}.$$ (13)

By solving this set of equations, together with the requests that ${\sum }_{c}b(c)=1$, for each set of synonymous codons, we obtain our codon usage bias. We have repeated this calculation for all amino acids.

We used this modified bias, which is not very different from the uniform one, to perform ANOVA F-tests together with other codon usage biases, see Table 2 and Suppl. Fig. SI.8.

4.5. Data Analysis

SARS-CoV-2 sequences are taken from GISAID [25]. We collected each sequence present in the database, which was obtained by 2020-05-08. Before any of our analyses, we discarded all the sequences where one or more nucleotides were wrongly read. This left us with 4259 SARS-CoV-2 sequences. To obtain Fig. 2 we considered, in addition to the SARS-CoV-2 sequences are taken from GISAID, other Alphacoronavirus and Betacoronavirus sequences (whole genomes and genes) which have been obtained from VIPR [24]. The pre-processing consisted again of discarding all the sequences with one error or more. After this process we collected 341 SARS, 48 MERS, 20 hCoV-229E, 48 hCoVNL63, 14 hCoV-HKU1, 124 hCoV-NL63, 166 bat-CoVs and 5 pangolin-CoVs whole genomes. For Fig. 2a and for Fig. 2b (lower panel) we used the largest number possible of sequences, up to a maximum of 100. For Fig. 2b (upper panel) and Fig. 2c we chose a single sequence for each species. However, we checked that the result is qualitatively the same if we use other sequences from the same species for human coronaviruses.

To obtain the plots in Fig. 3 and Fig. 4, we considered as reference SARS-CoV-2 sequence the one which has been collected on 26-12-2019 (ID: EPI ISL 406798). Sequences has been processed to ensure the correct reading frame. This means, for instance, that the ORF1ab gene is read in the standard frame up to the ribosomal shifting site, and it is read in the shifted frame from that site up to the end of the polyprotein. To produce the bar plots in Figs. 3b and 3d we collected genes data on VIPR. Then we discarded as usual all the sequences with one or more errors, and we computed for each gene an average of up to 20 different sequences (coming from the same species). For some structural proteins we did not find 20 different genes but in any case the standard deviation of the averages presented in Figs. 3b and 3d is smaller than 0.025 (and, for most of the viruses, much smaller). More detailed information about the genomes used in this work are given in Supplementary SI.1.