Association between weather data and COVID-19 pandemic predicting mortality rate: Machine learning approaches

Abstract

Nowadays, a significant number of infectious diseases such as human coronavirus disease (COVID-19) are threatening the world by spreading at an alarming rate. Some of the literatures pointed out that the pandemic is exhibiting seasonal patterns in its spread, incidence and nature of the distribution. In connection to the spread and distribution of the infection, scientific analysis that answers the questions whether the next summer can save people from COVID-19 is required. Many researchers have been exclusively asked whether high temperature during summer can slow down the spread of the COVID-19 as it has with other seasonal flues. Since there are a lot of questions that are unanswered right now, and many mysteries aspects about the COVID-19 that is still unknown to us, in-depth study and analysis of associated weather features are required. Moreover, understanding the nature of COVID-19 and forecasting the spread of COVID-19 request more investigation of the real effect of weather variables on the transmission of the COVID-19 among people. In this work, various regressor machine learning models are proposed to extract the relationship between different factors and the spreading rate of COVID-19. The machine learning algorithms employed in this work estimate the impact of weather variables such as temperature and humidity on the transmission of COVID-19 by extracting the relationship between the number of confirmed cases and the weather variables on certain regions. To validate the proposed method, we have collected the required datasets related to weather and census features and necessary prepossessing is carried out. From the experimental results, it is shown that the weather variables are more relevant in predicting the mortality rate when compared to the other census variables such as population, age, and urbanization. Thus, from this result, we can conclude that temperature and humidity are important features for predicting COVID-19 mortality rate. Moreover, it is indicated that the higher the value of temperature the lower number of infection cases.

1. Introduction

The Coronavirus disease (COVID-19), caused by SARS-CoV-2, initially came to attention in a series of patients with pneumonia of unknown etiology in Wuhan city, China, and thereafter spread to many other countries of the world through people travel from China [1]. Because of geographical proximity and significant travel connections, epidemiological modeling of the epicenter predicted that regions in Southeast Asia, and specifically Bangkok would follow Wuhan, and China in the epidemic [2]. More recently, the World Health Organization has declared this as a pandemic and probably it will remain for long and people have to adjust how to tackle and avoid it until proved vaccine becomes available (WHO 2020). For many, the biggest concern is not how large the problem but what will happen in the coming months and which areas and populations are mostly at risk [3].

The correlation between weather variables in the affected regions and the spread of COVID-19 earned special attention in the upgoing research publications. Recently, researchers found that a notable association between the weather variables (temperature and humidity) and the regions that have major COVID-19 outbreaks. Moreover, these regions are located at the same temperature zone in the northern hemisphere [4].

Even though the pandemic is becoming a global issue, the most infected areas include outbreak epicentres such as parts of Northeastern United States, China’s central province of Hubei, South Korea, Japan, Iran, Italy, Spain, Germany, and England, all of which share an average temperature of 5C to 11C and 47% to 79% humidity in January and February 2020. For Italy, regions with a temperature higher than 15 degrees Celsius and 75% humidity have less spread of COVID-19 cases.

Therefore, we hypothesise that the spread of the virus will decrease in the area with higher temperature and humidity than areas with average records. From our experimentation, the thresholds for temperature and humidity are fixed at 15 degrees Celcius and humidity at 75% respectively. These thresholds for the temperature and humidity parameters varied from one to another country. These numbers will be subtracted from the maximum values of temperature and the overall humidity during the day.

Moreover, understanding the nature of coronavirus and forecasting its spread requires more investigation and come up with the real impact of weather variables (temperature and humidity) on the transmission of the virus. To address this problem, the largest datasets integrating COVID-19 infections and weather have been collected. In this work, machine learning algorithms and OLS model estimate the impact of weather on the transmission of COVID-19 by extract the relationship between the number of confirmed cases in many regions and the temperature as well as humidity.

Compared to the previous work of the other researchers, this study includes more features that can influence the spread of the virus. The additional features that are included are associated with weather and climatic conditions.

Nuno [5] explored the spread of the COVID-19 in the Rio de Janeiro state, Brazil, that has a large population. The researcher has applied Susceptible-Infectious-Quarantined-Recovered (SIQR) model based on the collected available data from March 5, 2020 to April 26, 2020. The parameters that are estimated by the model are: ($I_0=24,\beta =0.32,\eta =\alpha =0.018,k_0=0.033$ and $\gamma =0.02$). The author has suggested, the relaxation of social isolation policies and predicted the period to relax lockdown safely that starts from June 11, 2020, onwards.

Melin et al. [6] conducted a study to analyze the spatial evolution of coronavirus pandemic around the world using unsupervised neural network namely self-organizing maps. The researchers concluded that the clustering abilities of self-organizing maps enable to group countries based on COVID-19 confirmed cases.

The main contribution of our work includes:

• •Find the best predictive model for daily confirmed cases in countries with the highest number of COVID-19 cases in the world.
• •Predict the number of confirmed cases to have more readiness in healthcare systems and make forecast using advanced machine learning algorithms.
• •To validate the propose model, we have includes more number of weather and climatic condition features that can influence the spread of the COVID-19 virus.

This paper is organized as follows: Section 2 presents the related works. Section 3 introduces our new methodology and the proposed approaches. Section 4 presents the experimental observations. Finally, the conclusions and possible future works are introduced in Section 5.

2. Related works

Dangi et al. [7] proposed a short term weather forecasting based method on wavelet denoising and catboost algorithm to predict the upcoming COVID-19 outbreak in 35 major cities in India (March and April 2020) by correlating the temperature factor of five major cities in the world. This study is based on population density and the correlation of temperature with selected cities where the COVID-19 outbreak has already become a pandemic.

Sajadi et al. [4] proposed a simplified model that presents a zone at an increased risk of COVID-19 spread. Using weather modelling, it predicts the regions that are most likely at higher risk of significant community spread of COVID-19 in the upcoming weeks, allowing for the concentration of public health efforts to contain the spread of the infectious virus.

Demongeot et al. [8] have illustrated that the virulence of coronavirus diseases due to viruses such as SARS-CoV and MERS-CoV decreases in humid and hot weather climatic condition. The presumed temperature dependence of infectivity by the new coronavirus namely COVID-19 has got a high interest in the domain of medical area. Likewise, our work aims to identify crucial parameters such as potentially temperature-dependent parameters, like the contagion coefficient increasing with cold, dry weather from the COVID-19 spread dynamics.

Marvi and Arfeen [9] have examine the relationship between average temperature and rate of spread of COVID-19 across various regions around the globe. Their finding manifests a bounded relationship between factors under consideration, that is, the spread rate of the virus has found to be slower in regions with extreme temperatures.

A study that uses statistical method was conducted by Xu et al. [10] that uses comprehensive datasets of the global spread of COVID-19 pandemic until late April 2020, spanning for more than 3700 locations worldwide. These researchers, construct and validate their proposed method to estimate the number of infected cases in various locations. They have suggested that the output of their study can be an input in controlling the spread of the virus considering various features such as detection delay, population density, and time-variant responses. It also uses some weather variable to predict the spread of the virus and then provide year-round, global projections.

Several studies, both laboratory [11], epidemiological analysis [12], and mathematical modelling [13], point to the role of ambient temperature on the survival and transmission of viruses. A tremendous number of researches support both ambient temperature and humidity in the role of transmission and infection motivated this study to examine the influence of environmental factors on COVID-19. We sought to determine whether climate could be a factor in the spread of this disease.

In the last few months, in association with the outbreak of coronavirus, a notably large number of research papers were published in many journals. Here, we have summarized the recently published papers along with their core contributions. Crokidakis [5] explored the Susceptible-Infectious-Quarantined Recovered (SIQR) model to check out if public policies of social isolation work in overcoming the pandemic. Contreras et al. [14] conducted an empirical study using a general multi-group SEIRA model that enables to demonstrate the spread of COVID-19 among the heterogeneous population. Mohammed et al. [15] studied non-linear mathematical models to find approximate solutions by applying the fractional Adams Bashforth (AB) method. Chakraborty and Ghosh [16] proposed two-fold approaches namely generating short term forecasting and risk assessment for COVID-19. Mandal et al. [17] proposed a mathematical model considering the quarantine class and governmental intervention measures to address the transmission of COVID19. Melin et al. [18] proposed an ensemble neural network model with a fuzzy response for the COVID-19 based on time series approach.

Many research conducted works related to weather impact on spread and distribution of COVID-19 appear to be ill-defined and not well grounded. There has been little discussion on the relationship between the weather variables and the COVID-19 outbreak in terms of which temperature threshold will slowdown the COVID-19. Moreover, previous works have only been limited to use a predictive statistical model and experimental results are less accurate. Despite this interest, no one to the best of our knowledge has studied and provided evidence for the relationship between several weather variables and the spread of COVID-19, finding a negative association between temperature and humidity and transmission

3. Methodology

In the subsequent subsection, we are going to introduce the hypothesis of our model, data collection and description of software and hardware that are using.

3.1. Data collection

According to the WHO, several environmental factors can influence the spread of communicable diseases that can cause epidemics. The most important of these are water supply, sanitation facilities, food, and climate. The underlying theory is the number of cases and the spread of previous infectious viruses demonstrate seasonal patterns, affected by climate, and so Covid-19 should display similarity in this aspect. Furthermore, temperature and humidity changed throughout seasons, have an effect on the number of virus incidents.

The dataset is collected from official case reports of various countries, beginning with the data collected and compiled by Kaggle and the Johns Hopkins Center for Systems Science [19]. The COVID-19 data obtained from the beginning of the epidemic in the time between December 12, 2019 to April 22, 2020. We collect different types of data on the spread of COVID-19 country-wise. For instance, in Italy (21 states), the United States (3144 counties and 5 territories), and use country-level aggregates for the rest of the world.

Moreover, weather data is collected from historical weather database [20], [21]. For each location for which that have infection data with features such as country, longitude, latitude, date, confirmed, deaths, recovered, and active cases. While for the weather data we collected minimum and maximum daily temperature, humidity, precipitation, snowfall, moon illumination, sunlight hours, ultraviolet index, cloud cover, wind speed and direction, and pressure data. Besides, we used population density data from Demography. Table 1 shows a sample of the collected data. Figs. 1 a and 1 b present Worldwide confirmed and deaths cases over time.

Table 1.

Features used to train the proposed models.

Date	Country	State	Confirmed	Deaths	Recovered	Active	Population	Fertility	Age	Urban percentage	icu	Humidity	Sun Hour	TempC	Wind speed
2020-03-21	France	Guadeloupe	53	0	0	53	65,244,628	1.9	42.0	0.82	6.5	73.0	6.3	10.0	19.0
2020-03-21	France	Mayotte	7	0	0	7	65,244,628	1.9	42.0	0.82	6.5	73.0	6.3	10.0	19.0
2020-03-21	France	Reunion	45	0	0	45	65,244,628	1.9	42.0	0.82	6.5	73.0	6.3	10.0	19.0
2020-03-21	France	Saint Barthelemy	3	0	0	3	65,244,628	1.9	42.0	0.82	6.5	73.0	6.3	10.0	19.0
2020-03-21	France	St Martin	4	0	0	4	65,244,628	1.9	42.0	0.82	6.5	73.0	6.3	10.0	19.0
2020-03-21	UK	Cayman Islands	3	1	0	2	67,814,098	1.8	40.0	0.83	2.8	51.0	10.5	9.0	8.0
2020-03-21	UK	Channel Islands	32	0	0	32	67,814,098	1.8	40.0	0.83	2.8	51.0	10.5	9.0	8.0
2020-03-21	UK	Gibraltar	10	0	2	8	67,814,098	1.8	40.0	0.83	2.8	51.0	10.5	9.0	8.0
2020-03-21	UK	Montserrat	1	0	0	1	67,814,098	1.8	40.0	0.83	2.8	51.0	10.5	9.0	8.0

Fig. 1.

Worldwide data over time.

To analyze the weather and temperature data of the respective countries since the outbreak of the virus. We have composed a dataset as follows: url{https://www.kaggle.com/winterpierre91/covid19-global-weather-data} [19], [20] and Load the cleaned data from url{https://www.kaggle.com/imdevskp/corona-virus-report} [22], [23]. The file contains the cumulative count of confirmed, death and recovered cases of COVID-19 from different countries from 22nd January 2020. The assumption here is, there a correlation between certain weather metrics and the speed of the number of infections/deaths.

3.2. Methods

In this work, we developed machine learning models used to investigate and understand the real effect of temperature and humidity on the spread of COVID-19 [24], [25]. The following machine learning models such as linear models (Linear Regression, Lasso Regression, Ridge Regression [26], Elastic Net, Least Angle Regression, Lasso Least Angle Regression, Orthogonal Matching Pursuit, Bayesian Ridge, Automatic Relevance Determination, Passive Aggressive Regressor, Random Sample Consensus, TheilSen Regressor, Huber Regressor) are used. Moreover, ensemble learning-based modes such as Random Forest, Extra Trees Regressor, AdaBoost Regressor, Gradient Boosting Regressor [27] are also explored. Extreme Gradient Boosting (XGBoost), Light Gradient Boosting Machine (LightGBM) [28], and CatBoost Regressor [29]), Kernel Ridge, Support Vector Machine (SVM), K-Nearest Neighbors Regressor (KNN) [30], Multi-level Perceptron (MLP) [31], and Decision Tree [32] for prediction on the spread of coronavirus.

These algorithms were selected as they are the most widely used for predicting the spread of COVID-19 and other prediction related analysis. Each of the models were trained with the features such as Population Density, Fertility Rate, Median Age, Intensive Care Unit (ICU) beds per 1000 People, Infection Ratio, Urban Percentage, Temperature, Humidity, Hours of Sunlight, and Wind Speed. Fig. 2 shows the general steps for the proposed methods.

Fig. 2.

The general steps for the proposed models.

4. Experimental results and interpretation

To carry out the forecasting of the spread of COVID-19, the presented methods shall be trained on a huge volume of the dataset. The amount of dataset plays a vital role in the training step and affects the performance of the proposed algorithms. The whole dataset that divided into two separate parts namely the training and the testing sets. The training datasets are used during model development and the test sets which are not previously seen by the model are used for validation [24], [31].

We have analyzed the correlation between weather variables and the spread of COVID-19 in the case of Italy. We have used temperature and humidity variables in this case as shown in Fig. 2. The dataset is collected from the Meteoblue website [33]. The number of confirmed COVID-19 cases (dependent variable) will be log-transformed to make it follow a normal distribution as per the assumption of statistical analysis since the original data is skewed highly in selected states. To estimate the relationship, we have used the standard regression model namely the naive Ordinary Least Squares (OLS) model [34]. The reason why the Naive OLS estimation is utilized in this work is because of its simplicity and ease of interpretation. Eqs. 1 and 2 present how the OLS estimator works to predict the correlation between weather variables and the spread of COVID-19.

$$\begin{array}{ccc}& & \mathbf{\text{Model}}\mathbf{\text{1}}\mathbf{\text{(for}}\mathbf{\text{Infected}}\mathbf{\text{cases:)}}\text{log}\text{(Number}\text{of}\text{cases}\text{on}\text{May}\text{17)}\hfill \\ & & =\alpha \left(\text{Temperature}\text{-}\text{15C}\right)+\beta \left(\text{Humidity}\text{-}\text{75\%}\right)+\text{error}\text{term}\hfill \end{array}$$ (1)

$$\begin{array}{ccc}& & \mathbf{\text{Model}}\mathbf{\text{2}}\mathbf{\text{(for}}\mathbf{\text{Growth}}\mathbf{\text{rate:)}}\text{log}\text{(Cases}\text{on}\text{May}\text{17/}\text{Cases}\text{on}\text{Mar}\text{3)}\hfill \\ & & =\alpha \left(\text{Temperature}\text{-}\text{15C}\right)+\beta \left(\text{Humidity}\text{-}\text{75\%}\right)+\text{error}\text{term}\hfill \end{array}$$ (2)

The number of confirmed cases: Model 1 estimates the relationship based on the number of confirmed cases as of March 16th, 2020, and the temperature and humidity of the regions in Italy’s map. The hypothesis that is being considered in this case is that high temperature and humidity has corresponded to a decreased number of reported COVID-19 cases when it is interpreted based on the log-transformation in the linear model. For every one-unit increase in the independent variables (temperature and humidity), the number of COVID-19 cases decreases by about 67%. It is experimentally proved that the weather variables, temperature and humidity have an inverse relationship to the number for confirmed cases. For every one-unit increase in the independent variable, the number of COVID-19 cases decreases by about 16%. Fig. 3 shows the relationship between the weather variables temperature and humidity to the number of confirmed cases in all regions of Italy as of March 16th, 2020.

Fig. 3.

Correlation between weather variables (temperature and humidity) and number of COVID-19 confirmed on March 16, 2020 for Italy.

The naive OLS estimates the relationship based on the number of confirmed cases in Italy as of May 17, 2020. For every one-unit increase in the independent variable temperature, the number of COVID-19 cases increases by about 143%. and for every one-unit increase in the independent variable humidity, the number of COVID-19 cases increases by about 8%. Interpretation of log-transformation in a linear model for humidity is shown in Fig. 4 that presents the relationship between temperature and humidity based on the number of confirmed cases in all regions of Italy as of May 17, 2020.

Fig. 4.

Correlation between weather variables (temperature and humidity) and number of COVID-19 confirmed on May 17, 2020 for Italy.

The performance of the proposed model is evaluated using $R-square$ metric and experimental results shows that the R-square of the model is within the range of 86% and 88% with some variation in the number of confirmed COVID-19 cases. A one-unit increase in temperature in the Italian map of regions with above 15-degree Celcius and 80% humidity will lead to 143% increase in the number of COVID-19 cases in comparison to regions that are below this threshold. Fig. 5 a shows the scatter plot between the number of confirmed cases and temperature in Italy on the date 17/05/2020. A one-unit increase in humidity in the Italian region with above 75% humidity and 15 ^∘ Celsius also lead to 8% increase in the number of COVID-19 cases in comparison to regions that are below this threshold. Fig. 5b shows a scatter plot between the number of confirmed cases and humidity on the date 17/05/2020 for Italy.

Fig. 5.

Scatter plot for the number of confirmed cases.

Growth rate: Model 2 estimates the relationship based on the number of growth rate as of May 17th, 2020, and the temperature and humidity of the regions in Italy’s map. Based on the second model 2 one-unit increase in temperature in Italy’s regions with above 15 ^∘ Celsius and 75% humidity leads to 45% increase in the number of COVID-19 cases in comparison to regions that are below this threshold. Moreover, a one-unit increase in humidity in Italy’s region with above 75% humidity and 16 ^∘ Celsius lead to 5% increase in the number of COVID-19 cases in comparison to regions that are below this threshold (see Fig. 6 ).

Fig. 6.

Scatter plot of the number of growth rate.

Table 2 presents the experimental results considering various values of the temperature and humidity features. The temperature values are set to five different values that are 15, 20, 25, 30 and 35. Similarly, the humidity is set to three different values that are 70, 75 and 80 respectively. In the experimentation, each temperature value is validated on each humidity value. For instance, the value of the temperature 15 was validated for its effect on the spread of Covid-19 on each of the three humidity values. Moreover, other temperature values were validated on each humidity values. From the experimental results, it is indicated that the higher the value of temperature, the lower number of infection cases. Similarly, the same effect is applied for growth rate, that is, as the temperature increases the value of growth rate of the infection decreases. Hence, the relationship between temperature and R ² have a positive correlation as the performance of the model increases when the value of temperature increases. On the other hand, when the values of temperature and humidity increases, the number of infected cases and the growth rate of the infection decreases.

Table 2.

The experimental results of the different values for temperature and humidity.

Model(1/2)	Temp.	Humidity	Alpha	Beta	Temp. Effect	Humidity Effect	R2	Adj R2
Infected cases	15	70	0.861434	0.087399	136.655189	9.133222	0.889706	0.878096
Growth rate	15	70	0.347038	0.056481	41.487019	5.810663	0.939840	0.933507
Infected cases	15	75	0.890908	0.078644	143.734231	8.181937	0.881435	0.868954
Growth rate	15	75	0.374966	0.057369	45.494151	5.904673	0.934377	0.927469
Infected cases	15	80	0.906039	0.066578	147.450062	6.884406	0.873540	0.860228
Growth rate	15	80	0.401863	0.057235	49.460689	5.890449	0.927305	0.919653
Infected cases	20	70	1.450845	0.120595	326.671899	12.816847	0.669052	0.634215
Growth rate	20	70	0.630435	0.077356	87.842768	8.042613	0.802427	0.781630
Infected cases	20	75	1.398349	0.069157	304.850990	7.160394	0.633080	0.594457
Growth rate	20	75	0.655225	0.065638	92.557478	6.783971	0.750911	0.724691
Infected cases	20	80	1.220575	0.003514	238.913541	0.352016	0.618146	0.577951
Growth rate	20	80	0.637707	0.046733	89.213732	4.784182	0.703043	0.671785
Infected cases	25	70	-1.191378	-0.223587	-69.619758	-20.035463	0.220440	0.138381
Growth rate	25	70	-0.232620	-0.046521	-20.754566	-4.545522	0.062890	-0.035753
Infected cases	25	75	-1.290774	-0.276363	-72.494214	-24.146228	0.420579	0.359588
Growth rate	25	75	-0.307090	-0.075870	-26.441568	-7.306374	0.208000	0.124632
Infected cases	25	80	-1.225998	-0.277625	-70.653529	-24.241925	0.579262	0.534974
Growth rate	25	80	-0.310293	-0.084043	-26.676799	-8.060824	0.351543	0.283284
Infected cases	30	70	-1.169891	-0.136057	-68.959909	-12.720687	0.847642	0.831605
Growth rate	30	70	-0.402274	-0.032372	-33.120269	-3.185389	0.656796	0.620669
Infected cases	30	75	-1.077191	-0.137452	-65.944914	-12.842340	0.867964	0.854066
Growth rate	30	75	-0.377918	-0.037119	-31.471337	-3.643827	0.677836	0.643924
Infected cases	30	80	-0.987054	-0.135130	-62.732701	-12.639745	0.885003	0.872898
Growth rate	30	80	-0.349860	-0.039597	-29.521294	-3.882344	0.698319	0.666563
Infected cases	35	70	-0.719808	-0.075775	-51.315407	-7.297566	0.936220	0.929507
Growth rate	35	70	-0.258704	-0.011015	-22.794884	-1.095416	0.794235	0.772576
Infected cases	35	75	-0.686391	-0.076581	-49.661064	-7.372178	0.940009	0.933694
Growth rate	35	75	-0.252149	-0.013923	-22.287095	-1.382684	0.797535	0.776223
Infected cases	35	80	-0.653181	-0.076517	-47.961237	-7.366293	0.943451	0.937499
Growth rate	35	80	-0.243749	-0.016176	-21.631597	-1.604607	0.801278	0.780360

Based on the experimental results as shown in Table 2, we have proved that climatic conditions such as temperature and humidity contribute to the spread of the virus. Based on the results of the models, one can draw a conclusion that when the temperature is low and humidity is also low, infection rate increases. On the other hand, when both temperature and humidity are high, the infection rate of COVID-19 decreases. However, it is very important to note that when a country has more hours of sunlight, more people may go outside and interact with social groups so that there is a high risk of virus transfer among people. The percentage of people living in an urban area also has an impact as it signifies a higher density of people, making it easier to transmit the virus. Thus, other variables which are not considered in our work can be analyzed carefully as they may have an effect on the spread of the virus. In terms of population, for example, the more people there are in a country, the more likely they are to get infected. Moreover, the age factor also matters that older people may be more likely susceptible to the infection.

From our experimental results, we have observed that temperature and humidity features are not sufficient in providing accurate results as shown in Fig. 2. To address this limitation, we created a more generalized machine learning model which considers more number of features instead of taking temperature and humidity only. This model helps to conduct proper analysis and understand the real effect of weather variables on the spread of COVID-19. The list of commonly used machine learning models in the data-driven analysis are shown in Table 3 . These models help to understand the actual relationship between the number of confirmed cases and the weather variables. We selected these models as they are the most used in machine learning tasks such as prediction based on learning from existing datasets. In this study, we have employed the following features for the experiment such as population density, fertility rate, median age, ICU beds per 1000 People, infection ratio, urban percentage, temperature, humidity, hours of sunlight, and wind speed as shown in Table 1.

Table 3.

Experimental results of the state-of-the-art algorithms for prediction of confirmed cases on global COVID-19 datasets.

Model	MAE	MSE	RMSE	R2	RMSLE	MAPE
K Neighbors Regressor	369.837	1.49381e+07	3782.07	0.0456	1.501	4.1186
Extra Trees Regressor	365.563	1.51515e+07	3811.82	0.0307	1.3096	3.3704
Random Forest	368.821	1.52086e+07	3823.22	0.0245	1.3027	3.3131
Decision Tree	385.084	1.52274e+07	3819.96	0.0162	1.4723	7.605
Support Vector Machine	374.921	1.54591e+07	3853.44	0.01	1.5798	4.0062
Huber Regressor	380.769	1.56759e+07	3882.29	-0.0054	1.8197	2.9956
Ridge Regression	383.174	1.56992e+07	3885.28	-0.007	1.7949	2.0534
Least Angle Regression	383.169	1.56992e+07	3885.28	-0.007	1.7949	2.0548
Linear Regression	383.169	1.56992e+07	3885.28	-0.007	1.7949	2.0548
Bayesian Ridge	383.242	1.56999e+07	3885.36	-0.0071	1.7958	2.0343
AdaBoost Regressor	385.502	1.5716e+07	3887.52	-0.0083	1.7628	1.4017
Orthogonal Matching Pursuit	386.552	1.5721e+07	3888.17	-0.0086	1.8743	1.6181
Lasso Regression	391.905	1.57419e+07	3890.79	-0.01	2.4943	0.8246
Elastic Net	391.69	1.57415e+07	3890.73	-0.01	2.4081	0.8149
Lasso Least Angle Regression	391.905	1.57419e+07	3890.79	-0.01	2.4943	0.8246
CatBoost Regressor	482.418	9.60296e+07	6272.84	-3.5039	1.3871	2.6725
Light Gradient Boosting Machine	474.62	7.08946e+07	6155.48	-7.7306	1.3274	2.6168
Extreme Gradient Boosting	5618.07	1.96674e+11	143,720	-13574.3	1.5256	2.5724
Passive Aggressive Regressor	7795.09	3.02021e+11	184,794	-20857.5	2.5097	95.2851
Gradient Boosting Regressor	8468.15	3.52228e+11	191,742	-35165.9	1.5391	4.9954

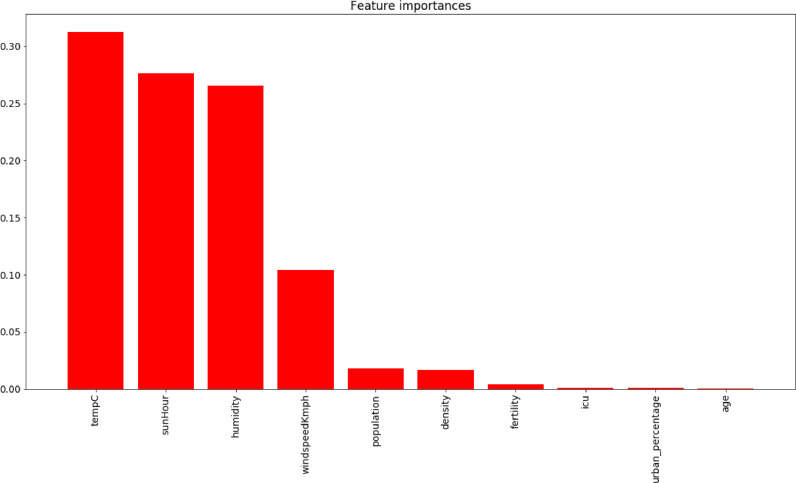
The regression models are implemented by using each country’s input variables which are a combination of weather features (Humidity, Wind speed, Temperature, Sunny Hours), population variables (Population, Density, Fertility, Age, Urban percentage) and health center resources related variables (ICU) to predict the number of infections and death rates. In this case, some features play major roles when compared to the other features and this is proved using random forest feature selector algorithm and is given in ranked feature importance as shown in Fig. 7 . From Fig. 7, it is presented that many variables are positively correlated to the number of COVID-19 infections such as temperature, hours of sunlight, humidity, wind speed, and population. Moreover, Fig. 8 shows the variables that are positively correlated to the number of deaths such as temperature, hours of sunlight, wind speed, and humidity.

Fig. 7.

Feature importance for infected cases of Covid-19 cases (17/05/2020).

Fig. 8.

Features importance for Deaths of Covid-19 cases (17/05/2020).

From the experimental result, when inspecting the death rate, it appears to be the weather features are more important than census features such as population, age, and urban percentage. The standard deviation of prediction error should be taken into account, but from the results, it can be concluded that temperature and humidity are important features for predicting COVID-19 death rate. Furthermore, with the current regression model, it does not seem that ICU beds per 1000 people are as important as expected.

Table 3 presents the experimental results for the regression models using the 10-fold cross-validation (CV) procedure to predict the number of COVID-19 confirmed cases, where the performance of these models is evaluated using various performance evaluation metrics such as R2, MSE, RMSE, RMSLE, MAPE, and MAE. The highest performance was registered using the metrics MSE, and RMSE are obtained by the KNN regressor (1.49381e+07, 3782.07). When evaluated using MAE, the Extra Trees algorithm scores 365.563 and RMSLE obtained by Random Forest is 1.3027. The models with the least performance are found to be Gradient Boosting Regressor and Passive-Aggressive Regressor.

Table 4 presents the experimental results for the comparison of the state of art models for death cases. The highest performance was registered by the Decision Tree algorithm when evaluated using MAE, MSE, RMSE, and RMSLE metrics. Moreover, the Extra Trees Regressor algorithm scores better result when evaluated using MAPE. The least performing algorithms, in this case, are Huber Regressor and Lasso Least Angle Regression.

Table 4.

Experimental results of the state-of-the-art algorithms for prediction of deaths cases on global COVID-19 datasets.

Model	MAE	MSE	RMSE	R2	RMSLE	MAPE
Decision Tree	15.8633	35927	184.686	0.0438	0.7716	0.8981
K Neighbors Regressor	16.4205	37962.9	189.354	0.0027	0.8287	0.8133
Extra Trees Regressor	16.4825	38652.8	190.594	-0.0055	0.8154	0.7975
Support Vector Machine	16.4789	38674.6	190.67	-0.0066	0.8236	0.7979
Random Forest	16.4963	38681.7	190.69	-0.0068	0.8244	0.804
Extreme Gradient Boosting	16.5124	38,690	190.71	-0.007	0.8459	0.8403
Passive Aggressive Regressor	16.6054	38687.4	190.704	-0.007	0.8717	0.8497
CatBoost Regressor	16.5044	38689.1	190.708	-0.007	0.8352	0.8203
Light Gradient Boosting Machine	16.5017	38688.5	190.706	-0.007	0.8312	0.8161
Gradient Boosting Regressor	16.5124	38690.1	190.71	-0.007	0.846	0.8404
Linear Regression	16.542	38696.7	190.726	-0.0072	0.8722	0.891
AdaBoost Regressor	16.5551	38696.3	190.725	-0.0072	0.8697	0.889
Least Angle Regression	16.542	38696.7	190.726	-0.0072	0.8722	0.891
Orthogonal Matching Pursuit	16.5433	38698.1	190.73	-0.0072	0.8785	0.8994
Ridge Regression	16.542	38696.7	190.726	-0.0072	0.8722	0.891
Bayesian Ridge	16.5421	38696.7	190.726	-0.0072	0.8723	0.8914
Lasso Regression	16.5757	38703.3	190.743	-0.0074	0.9122	0.9685
Elastic Net	16.5737	38703.1	190.743	-0.0074	0.9104	0.9656
Lasso Least Angle Regression	16.5757	38703.3	190.743	-0.0074	0.9122	0.9685
Huber Regressor	16.5366	38705.3	190.748	-0.0074	0.9287	1

From the experimental results, in the case of death rate, it is experimentally proved that the weather variables are more important when compared to other factors such as census feature including population, age, and urban percentage. Thus, from the experimental result, we can conclude that temperature and humidity are important features for predicting COVID-19 death rates, and it does not seem that the ICU beds per 1000 people are an important feature as shown in Fig. 8.

This study includes awareness and understanding of factors that can decrease or increase the spread rate of the disease which helps people to prepare and plan better for daily activities, based on weather and meteorological forecast. Hence, it is a wise option to continue lockdown and social distancing until the vaccine created or temperature rises to help to reduce the number of infected cases.

5. Conclusion

In this work, we are motivated to study the impact of a climatic condition such as weather variables, census features such densely populated area and the capacity of health centres in accommodating the number of infected cases due to COVID-19. We have developed predictive models for the spread of COVID-19 on different features taken from climatic conditions such as (temperature and humidity), census and health centre resources features. We have used several machine learning models whereby each of these models are trained on the specified climate, census and health centre features. To validate the proposed method, we have used publicly available datasets from Kaggle and the dataset was executed on various machine learning algorithms. The performance of the regressor models is measured using standard performance metrics. From the experimental results, it is shown that the weather variables are more relevant in predicting the mortality rate when compared to the other variables such as population, age, and urbanization. The contribution of this study is to prove the factors that can influence the spread of the virus. It is possible to note here that this study can be used as an input to create general awareness and understanding about factors influences the spread of the pandemic which helps governments to plan and act to overcome the disaster that can follow due to COVID-19. Moreover, it is advisable to continue lockdown and social distancing until the vaccine created or temperature rises to help to reduce the number of infected cases.

In our future work, we will look at how to improve the performance of the selected models by considering additional weather features such as wind speed and rainfall. We are also planning to update this study with more analyses and cases continuously by fine-tuning the prediction and visualization methodology. Moreover, multiple ensemble neural network models can be considered for analyzing the relationship between COVID-19 and weather variables. The spatial autocorrelation in the data for the other countries requires more analysis. For instance, how the tropical countries are dealing with the COVID-19, whether temperature and humidity can help in the fight against coronavirus and decreasing the number of cases.

CRediT authorship contribution statement

Zohair Malki: Supervision, Project administration. El-Sayed Atlam: Methodology, Writing - review & editing. Aboul Ella Hassanien: Supervision, Project administration. Guesh Dagnew: Data curation, Writing - original draft. Mostafa A. Elhosseini: Visualization, Investigation, Writing - review & editing. Ibrahim Gad: Formal analysis, Methodology, Software.

Declaration of Competing Interest

The authors declare that there is no conflict of interest