Dynamics of motor cortical activity during naturalistic feeding behavior

Abstract

Objective.

The orofacial primary motor cortex (MIo) plays a critical role in controlling tongue and jaw movements during oral motor functions, such as chewing, swallowing and speech. However, the neural mechanisms of MIo during naturalistic feeding are still poorly understood. There is a strong need for a systematic study of motor cortical dynamics during feeding behavior.

Approach.

To investigate the neural dynamics and variability of MIo neuronal activity during naturalistic feeding, we used chronically implanted micro-electrode arrays to simultaneously recorded ensembles of neuronal activity in the MIo of two monkeys (Macaca mulatta) while eating various types of food. We developed a Bayesian nonparametric latent variable model to reveal latent structures of neuronal population activity of the MIo and identify the complex mapping between MIo ensemble spike activity and high-dimensional kinematics.

Main results.

Rhythmic neuronal firing patterns and oscillatory dynamics are evident in single-unit activity. At the population level, we uncovered the neural dynamics of rhythmic chewing, and quantified the neural variability at multiple timescales (complete feeding sequences, chewing sequence stages, chewing gape cycle phases) across food types. Our approach accommodates time-warping of chewing sequences and automatic model selection, and maps the latent states to chewing behaviors at fine timescales.

Significance.

Our work shows that neural representations of MIo ensembles display spatiotemporal patterns in chewing gape cycles at different chew sequence stages, and these patterns vary in a stage-dependent manner. Unsupervised learning and decoding analysis may reveal the link between complex MIo spatiotemporal patterns and chewing kinematics.

1. Introduction

Central nervous system control of orofacial behaviors such as biting, tongue protrusion, speaking, chewing, and swallowing involves neural circuits in the brainstem and neocortex (Martin et al 1995, Sessle et al 2013, Moore et al 2014). Better understanding of the role of the orofacial primary motor cortex (MIo) in control and coordination of orofacial behaviors not only promises to enhance treatments of a range of disorders ranging from dysphonia to dysphagia, but it also provides an opportunity to study motor control outside of the well-studied reach and grasp system. Natural feeding involves sequences of behaviors—ingestion, manipulation, food transport, chewing, swallowing—making it an ideal system for investigation of how changes in behaviors employing the same musculoskeletal structures are related to changes in neural activity. Studies of naturalistic feeding in non-human primates have yielded rich data on jaw kinematics (Reed and Ross 2010, Iriarte-Diaz et al 2011, 2017, Nakamura et al 2017), and muscle activity (Hylander and Johnson 1994, Lassauzay et al 2000, Hylander et al 2004, 2005, Vinyard et al 2008, Kravchenko et al 2014, Ram and Ross 2017), but studies of neural mechanisms underlying cortical control of orofacial behaviors have emphasized simple, discrete behaviors such as tongue protrusion and biting (Kawamura 1974, Gossard et al 2011, Arce-McShane et al 2014, 2016). This paper presents data on spiking activity in populations of neurons in the MIo during rhythmic chewing stages of naturalistic feeding sequences by Macaca mulatta.

Single neuronal responses in the motor cortex are complex, and there is disagreement about which movement parameters are represented (Afshar et al 2011, Churchland et al 2012). For instance, there is a considerable body of work that suggests that the MI does not represent any variables, but rather acts as a controller that does not need explicit representations (Todorov 2000, Scott 2008, Shenoy et al 2013). In contrast, population codes are more robust and modeling the neural population activity using a dynamical system or latent variable approach is an active research area in computational neuroscience (Yu et al 2009, Churchland et al 2012, Ames et al 2014, Michaels et al 2016, Feeney et al 2017, Whiteway and Butts 2017). Neural responses are variable in both firing rate and temporal dynamics. At the population level, various statistical tools have been developed to extract the single-trial variability that correlates with behavior (Churchland et al 2007, Yu et al 2009, Afshar et al 2011). One popular approach is to use supervised learning to establish encoding models (such as generalized linear models) for individual motor neurons, and then apply the encoding model to decode behavioral variables (such as kinematics). However, this approach requires restrictive statistical assumptions for the encoding model. In addition, the high-dimensionality of behaviors and high degree of heterogeneity in unit firing activity, make it unrealistic to assume that a common encoding model applies to all neurons; therefore, the under-fitting or over-fitting problems induced by oversimplified or over-complex parametric models may occur in the encoding analysis.

An alternative approach generates unbiased assessments of neuronal population activity using unsupervised learning (Yu et al 2009, Chen et al 2014, Kao et al 2015, Gao et al 2016, Sussillo et al 2016, Wu et al 2017, Zhao and Park 2017), without the information of dynamics of the movement kinematics. This approach has several advantages over traditional approaches for studies of naturalistic feeding behavior: feeding sequences vary in duration, in number of jaw gape cycles, and in number of swallows; neuronal population activity is expected to include cyclical dynamics at multiple timescales; these statistical models can take into account time warping—time dilation or contraction for a representation of the same content—during rhythmic chewing. We propose a discrete latent variable method based on a Bayesian hidden Markov model (HMM) to characterize the MIo ensemble spike activity. We derived a new divergence measure and a sequence alignment method to quantify the population response variability at multiple timescales during feeding—complete chewing sequences (trials), different chewing stages within sequences, and gape cycle phases. The neural response variability could be either intrinsic or driven by noise. Here, we use the term ‘variability’ instead of ‘noise’ to distinguish from the extrinsic noise in the spiking activity (e.g. random jittering). Our proposed new methodology enables us to tackle these computational challenges. A high-level schematic of motor population data analysis is shown in figure 1. Our results suggest that these techniques can capture relationships between neuronal population dynamics in a way that mirrors current understanding of naturalistic feeding behavior in the laboratory. The HMM approach also yields comparable or improved decoding accuracy compared to two tested continuous-valued latent variable models.

Figure 1.

Schematic diagram of the latent state model (HDP-HMM) on motor population spikes. The analyses (text in the dashed boxes) consist of five computational tasks: (i) estimate the state transition matrix (m × m) and state-filed matrix (m × C) associated with the HDP-HMM; (ii) infer the latent state sequences {S_t} associated with the population spike activity {y_t}; (iii) compute the time-averaged dissimilarity (divergence) measure between the inferred state sequences; (iv) compute the mutual information between the latent state sequences and (clustered) behavior sequences; and (v) decode the chewing kinematics.

2. Materials and methods

2.1. Behavioral task and experimental recording

All of the surgical and behavior procedures were approved by the University of Chicago IACUC and conformed to the principles outlined in the Guide for the Care and Use of Laboratory Animals. Two adult female macaque monkeys (Macaca mulatta) were trained to feed themselves with their right hands while seated in a primate chair with their heads restrained by a halo coupled to the cranium through chronically implanted head posts. Two-dimensional (2D) tongue and jaw kinematics were captured using digital videoradiography of tantalum markers implanted in the tongue and jaw (Nakamura et al 2017). Markers were manufactured by hand by taking polyethylene spheres, melting a small area on one part of the sphere to create a flat region, and then conforming retro-reflective tape to the surface of the sphere. Optical markers were anchored to the mandible of the animals using a bone screw system chronically implanted in the bones of the face. These screws protrude percutaneously, and the mandible and cranium each had two–three markers attached to it (Ross et al 2010). Depending on specific animals, there were a varying number (eight–ten) of markers implanted. Each marker’s movement was associated with the horizontal and vertical positions and velocity; the positions of the markers in the anterior-, middle-, posterior-tongue, jaw, hyoid and thyroid cartilage were expressed as 2D coordinates. While the animals fed, two-dimensional lateral view videoradiographic recordings of jaw and tongue movements were made at 100 Hz using an OEC 9600 C-arm fluoroscope retrofitted with a Redlake Motion Pro 500 video camera (Redlake MASD LLC, San Diego, CA). The 2D tongue and jaw movement data were extracted from the videoradiographic images using MiDAS 2.0 software (Xcitex, Boston, MA) (Ross et al 2010) or custom written MATLAB (MathWorks, Natick, MA) code. The marker coordinates were bi-directionally low-pass filtered with a 4th order Butterworth filter with a 15 Hz cutoff frequency.

At the start of each feeding trial (sequence), the animal was presented with a single food item (Iriarte-Diaz et al 2011) (table 1). Monkey O ate 11 food types (almond, green bean, carrot, apple, hazelnut, potato, pear, kiwi, blueberry, mango and date) among 38 trials (Dataset 1). Monkey A ate nine food types (almond, potato, yam, date, kiwi, grape, peanut, dry apricot, dry peach) among 34 trials in one session (Dataset 2), and 12 food types (almond, persimmon, peach, almond with shell, date, apricot, yam, potato, kiwi, banana, zucchini, grape) among 64 trials in another session (Dataset 3).

Table 1.

Summary of experimental recordings from two monkeys.

Recording	# Trials	# Single units	# Food types
Monkey O (Dataset 1)	38	142	11
Monkey A (Dataset 2)	34	78	9
Monkey A (Dataset 3)	64	75	12

Feeding bouts in the wild and recording sessions in the laboratory are divided into feeding sequences (trials) starting with ingestion of a piece of food and ending in a final swallow (Ross and Iriarte-Diaz 2014) (figure 2). Each feeding sequence consists of a series of coordinated jaw and tongue movement cycles. Jaw movement cycles, gape cycles, are defined by the cyclic elevation and depression of the mandible from maximum gape to maximum gape. Gape cycles are assigned to different types depending on the feeding behavior: ingestion cycles, in which food is passed into the oral cavity; stage 1 transport cycles, when food is moved from the ingestion point to the molars for mastication; manipulations, when food is repositioned in the oral cavity prior; chewing cycles when food is broken down between the molars; and swallows, when food is transported from the oral cavity and oropharynx into the esophagus (Ross and Iriarte-Diaz 2014). Videoradiographic files were used to identify chewing gape cycles for our analysis.

Figure 2.

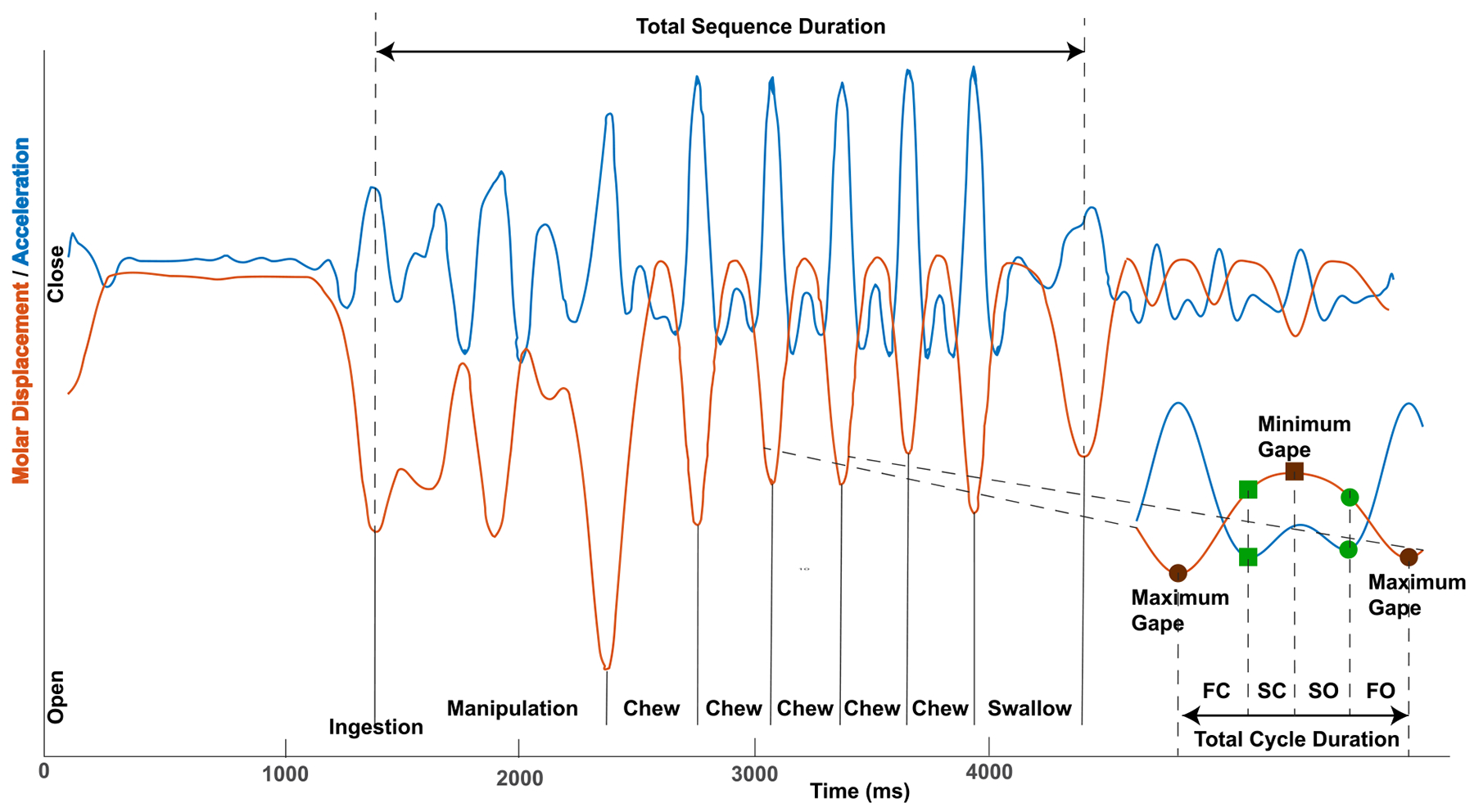
Definitions of feeding sequence, gape cycle and gape cycle phases. The red line shows open-close motor displacements (gape) of the lower jaw during a complete feeding sequence from ingestion to final swallow. The second derivative of the displacement, the blue line, is used to define the four chew cycle phases. Most chewing gape cycles are made up of Hiiemae’s four gape cycle phases: fast close, FC; slow close, SC; slow open, SO; fast open, FO (Hiiemae and Crompton 1985). The four gape cycle phases are delineated by jaw and tongue kinematic events associated with changes in sensory afferent input that are key events in sensorimotor control (Lund 1991): SC starts when the teeth contact the food and mandibular closing movements slow; SC ends and SO begins when the mandible stops moving upwards and begins moving downwards (min-gape); SO ends when the mandible starts depressing quickly (SO-FO transition, in theory when tongue has captured the food item ready for transport); and FO ends when the mandible changes from depression to elevation (max-gape).

Each chewing gape cycle was sub-divided into Hiiemae’s four gape cycle phases (Bramble and Wake 1985, Hiiemae and Crompton 1985)—fast close (FC), slow close (SC), slow open (SO), fast open (FO)—delineated by jaw and tongue kinematic events associated with salient changes in sensory information used in sensorimotor control cite (Lund 1991). FC ends and SC starts when the teeth contact the food and mandibular vertical elevation slows; SC ends and SO begins at minimum gape (min-gape) when the mandible stops moving upwards and begins moving downwards; SO ends and FO begins when the mandible starts depressing quickly, when the tongue has captured the food item ready for transport; FO and FC starts at maximum gape (max-gape) when mandible vertical movement changes from depression to elevation.

Multiple single unit spiking activities were recorded from a 100-electrode 2D Utah array (electrode length of 1.5 mm, 10 × 10 grid, 400 μm inter-electrode spacing) chronically implanted in the MIo on the left side of each monkey (figure 3). The MIo is located at the lateral end of the pre-central gyrus, delimited by the central sulcus posteriorly and the arm/hand area medially. The boundary of orofacial and arm/hand areas was determined by surface stimulation of the cortex that elicited only tongue, jaw or lip twitches, but no arm or hand twitches evoked. Spiking activity from up to 96 channels was recorded at 30 kHz. Spike waveforms were sorted offline using a semi-automated method incorporating a previously published algorithm (Vargas-Irwin and Donoghue 2007). The signal-to-noise ratio (SNR) for each unit was defined as the difference in mean peak to trough voltage over all spikes divided by twice the mean standard deviation computed over all sample points of the spike. All the units with SNR < 3 were discarded for the current study.

Figure 3.

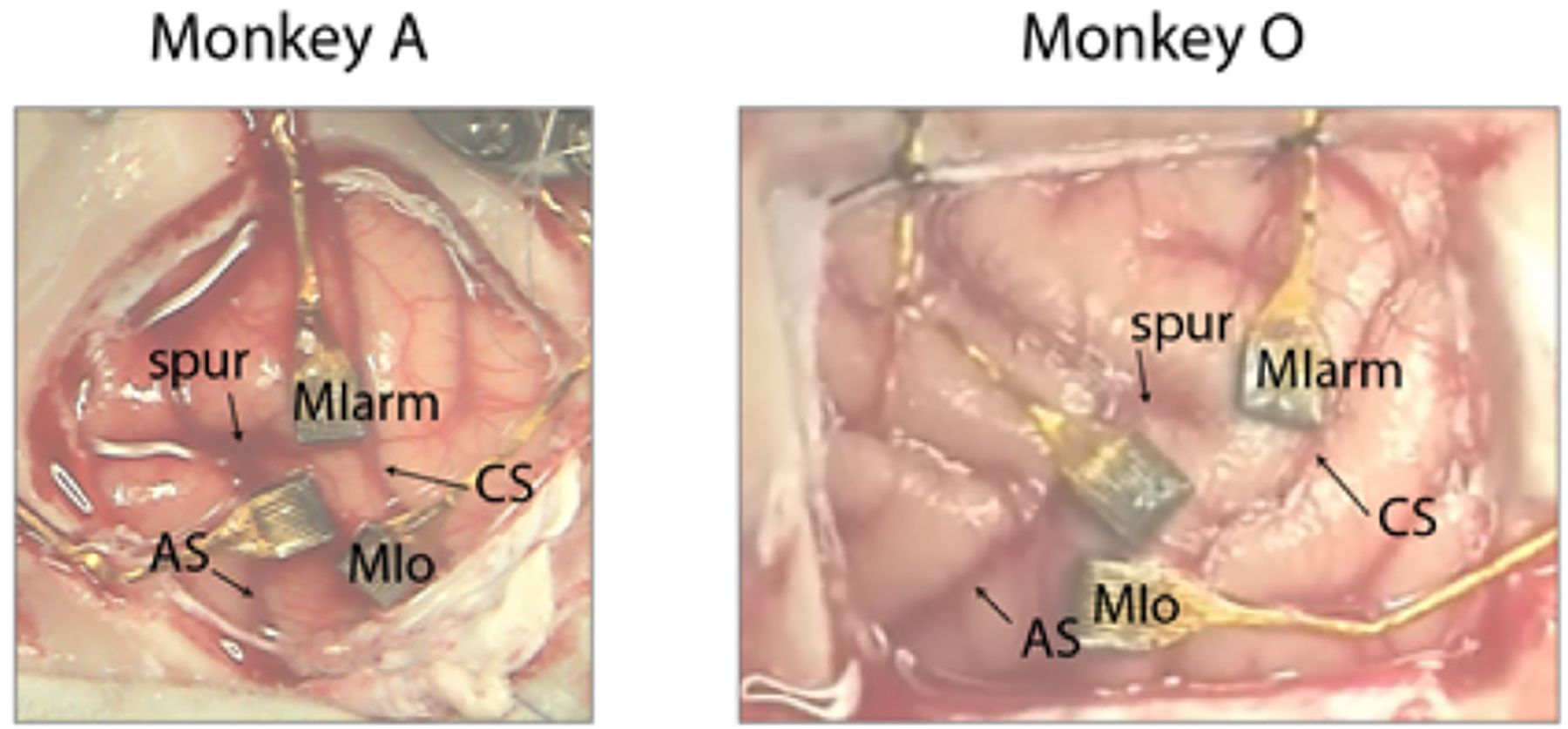
Array implant locations in Monkey A (left) and Monkey O (right). The current paper presents data collected from the MIo arrays in each animal.

2.2. Principal component analysis (PCA) and temporal clustering for kinematics

We preprocessed each kinematic measure with zero mean, and applied principal component analysis (PCA) to the high-dimensional kinematic variables (position plus velocity, six dimensions per marker). The PCA was efficiently computed via eigenvalue decomposition of a high-dimensional covariance matrix. We further extracted the dominant principal components associated with the top largest eigenvalues that explained at least 90% cumulative variance.

As a dimensionality reduction method, temporal clustering projects high-dimensional time series (e.g. kinematics or other behavioral measures) into a low-dimensional discrete space. Here we used an unsupervised, bottom-up temporal clustering method known as aligned cluster analysis (ACA) and hierarchical aligned cluster analysis (HACA) (Zhou et al 2013) to label the motor behavioral measures. By combining the ideas of kernel k-means and dynamic time alignment kernel, ACA finds a partition of our high-dimensional jaw and tongue kinematic time series into m disjoint segments, such that each segment belongs to one of k clusters. HACA extends ACA by providing a hierarchical decomposition of time series at different temporal scales and further reduces the computational complexity. Therefore, ACA and HACA provide a bottom-up framework to find a low-dimensional embedding for time series using efficient optimization (coordinate descent and dynamic programming) methods (open source software: www.f-zhou.com/).

2.3. Task modulation of MIo single units

To analyze the single unit activity of the MIo, we computed the mean firing rate (FR) during feeding (FR_feed), as compared to the FR during baseline (FR_baseline) before food ingestion. Similar to the modulation index metric defined in Arce-McShane et al (2014):

$$\text{Modulation}\text{index}=\frac{{\text{FR}}_{\mathit{\text{feed}}}-{\text{FR}}_{\mathit{\text{baseline}}}}{{\text{FR}}_{\mathit{\text{baseline}}}}.$$ (1)

Single units were deemed task-modulated when FR_feed was significantly different from FR_baseline (paired t test, p < 0.01). The baseline was defined as the period prior to the feeding behavior, and FR_feed was averaged over the complete feeding period.

Among the task-modulated units, we further computed the tuning curve of individual units with respect to the four gape cycle phases (SO, FO, FC, SC), averaged across multiple gape cycles and food types. The tuning curve was first interpolated uniformly (with 20 points) within a normalized time frame [0, 1], and then temporally smoothed (5-point Gaussian kernel, SD 2.5).

We also computed the spike spectrum by using the multitaper method of the Chronux toolbox (http://chronux.org) (Bokil et al 2016). We used the function mtspectrmpt.m and the tapers setup [TW, K], where TW is the time-bandwidth product, and K = 2 × TW − 1 is the number of tapers. We determined the TW parameter based on the neuronal firing rate, with a range from 7 to 15. We used smaller TW for neurons with a high firing rate, and larger TW in the case of a low firing rate. A larger TW value implies a higher degree of smoothing. The maximum frequency range was adjusted according to the average firing rate of individual units.

2.4. Bayesian nonparametric hidden Markov model (HMM)

First, we assumed that the latent state process follows a first-order finite discrete-state Markov chain {S_t} ∈ {1, 2, … , m}. We further assumed that the raw (non-smoothed) spike counts of individual MIo units at the tth temporal bin (bin size 50 ms), y_t, conditional on the latent state S_t, follow a Poisson probability distribution with associated tuning curve functions Λ = {λ_c,i}:

$$p\left(y_{1:T},S_{1:T}\mid \theta \right)=p\left(S_1\mid \pi \right)\prod _{t=2}^{T}p\left(S_t\mid S_{t-1},P\right)\prod _{t=1}^{T}p\left(y_t\mid S_t,\Lambda \right)$$ (2)

where θ = {π, P, Λ}, P = {P_ij} denotes an m-by-m state transition matrix, with P_ij representing the transition probability from state i to j ; π = {π_i} denotes a probability vector for the initial state S₁; and $p\left(y_t\mid S_t,\Lambda \right)={\prod }_{c=1}^C\text{Poisson}\left(y_{c,t}\mid {\lambda }_{c,S_t}\right)$ (where C denotes the total number of observed units). This probability model is defined by a HMM.

To accommodate automatic model selection for the unknown parameter m, the hierarchical Dirichlet process (HDP)-HMM extends the finite-state HMM with a nonparametric HDP prior, and inherits a great flexibility for modeling complex data. For inference of HDP-HMM, we sampled a distribution over latent states, G₀, from a Dirichlet process (DP) prior, G₀ ~ DP(γ, H), where γ is the concentration parameter and H is the base measure. We also placed a prior distribution over the concentration parameter, γ ~ Gamma(a_γ, 1). Given the concentration, we sampled from the DP via the ‘stick-breaking process’: the stick-breaking weights in β were drawn from a beta distribution:

$${\tilde{\beta }}_i~\text{Beta}(1,\gamma ),{\beta }_i={\tilde{\beta }}_i\prod _{j=1}^{i-1}\left(1-{\tilde{\beta }}_j\right)$$ (3)

where ${\beta }_1={\tilde{\beta }}_1$, ${\sum }_{i=1}^{\infty }{\beta }_i=1$, and Beta(a, b) defines a beta distribution with two shape parameters a > 0 and b > 0. For inference, we used a ‘weak limit’ approximation in which the DP prior is approximated with a symmetric Dirichlet prior

$$\begin{gathered} \gamma ~\text{Gamma}\left(a_{\gamma },1\right) \\ {\alpha }_0~\text{Gamma}\left(a_{{\alpha }_0},1\right) \\ \mathit{\beta }\mid \gamma ~\text{Dirichlet}(\gamma /\mathit{M},\dots ,\gamma /\mathit{M}), \\ \mathit{\pi }\mid {\alpha }_0,\mathit{\beta }~\text{Dirichlet}\left({\alpha }_0{\beta }_1,\dots ,{\alpha }_0{\beta }_M\right), \\ {P}_{i,:}\mid {\alpha }_0,\mathit{\beta }~\text{Dirichlet}\left({\alpha }_0{\beta }_1,\dots ,{\alpha }_0{\beta }_M\right) \end{gathered}$$

where M denoted a truncation level for approximating the distribution over the countably infinite number of states.

We updated the conjugate posterior of parameters in a closed form using Gibbs sampling

$$\begin{gathered} {\lambda }_{c,i}\mid y,S_{1:T}~\text{Gamma}\left({\alpha }_c^0+\sum _{t=1}^T{y}_{c,t}\mathbb{I}\left[S_t=i\right],{\beta }_c^0+\sum _{t=1}^T\mathbb{I}\left[S_t=i\right]\right). \\ \mathit{\pi }\mid {\alpha }_0,\mathit{\beta }~\text{ Dirichlet }\left({\alpha }_0\mathit{\beta }+1_{S_1}\right), \\ {P}_{i,:}\mid {\alpha }_0,\mathit{\beta }~\text{Dirichlet}\left({\alpha }_0\mathit{\beta }+n_i\right), \\ {n}_{i,j}=\sum _{t=1}^{T-1}\mathbb{I}\left[S_t=i,S_{t+1}=j\right], \end{gathered}$$

where 1_j is a unit vector with a one in the jth entry.

Upon the completion of MCMC (Markov chain Monte-Carlo) inference, we sampled from the posterior distributions and obtained the estimates of m-by-m state transition matrix and m-by-C state field matrix (figure 1). At each column of the state field matrix, the sparsity of the vector describes how much each neuron contributes to each state in encoding; whereas at each row, the sparsity of the vector describes how much information is encoded per state from all neurons. This may help understand whether firing patterns are always population-wide, or whether specific state transitions are driven by individual neurons.

We also jointly updated the latent states using a forward filtering, backward sampling algorithm to obtain a full sample from p(S_1:T |θ). For firing rate hyperparameters $\left\{{\alpha }_c^0,{\beta }_c^0\right\}$, we used one of two methods (Linderman et al 2016): (i) Hamiltonian Monte-Carlo sampling for the joint posterior $\left\{\text{log}{\alpha }_c^0,\text{log}{\beta }_c^0\right\}$, and (ii) sampling the scale hyperparameter ${\beta }_c^0$ (using a gamma prior) while fixing the shape hyperparameter, ${\alpha }_c^0=1$. Results from each sampling technique were similar. Finally, we obtained the posterior estimates of unknown states and parameters {m, S_1:T, π, P, Λ} and their respective hyperparameters. A Python software package for the Bayesian nonparametric HMM is available online (https://github.com/slinderman/pyhsmm_spiketrains).

To test the generalization of the HMM, we ran an additional decoding analysis on the held-out data. Similar to the previously described method (Linderman et al 2016), based on the inferred model parameters, we ran a maximum a posteriori (MAP) or maximum likelihood (ML) estimator to infer the state sequences from the held-out data. We used a ‘divide-and-conquer’ strategy and mapped the behavioral variables (e.g. one-dimensional kinematics) to the latent states. The approximate one-to-one state-to-kinematics mapping was found to be a greedy algorithm.

2.5. Quantifying the similarity between two state sequences

Let KL(λ_a‖λ_b) denote the Kullback–Leibler (KL) divergence between two univariate Poisson distributions with firing rate λ_a and λ_b. Since the KL divergence is asymmetric, we used the averaged divergence metric $\frac{1}{2}\left(\text{KL}\left({\lambda }_a\Vert {\lambda }_b\right)+\text{KL}\left({\lambda }_b\Vert {\lambda }_a\right)\right)$. Once the latent states of HMM were inferred, given the C × m Poisson firing rate matrix Λ, we defined a new divergence metric, $\mathcal{l}$ (unit: spikes per second), which characterized the dissimilarity between two latent states while accounting for the variability in individual neuronal firing rates:

$$\begin{gathered} \mathcal{l}\left(S_1,S_2\right)=\frac{1}{2C}{w}^{\top }\left(\text{KL}\left({\lambda }_1\Vert {\lambda }_2\right)+\text{KL}\left({\lambda }_2\Vert {\lambda }_1\right)\right) \\ =\frac{1}{2C}\sum _{c=1}^C{w}_c\left({\lambda }_{c,1}-{\lambda }_{c,2}\right)\text{log}\frac{{\lambda }_{c,1}}{{\lambda }_{c,2}} \end{gathered}$$ (4)

where ^⊤ denotes the transpose operator; λ₁ and λ₂ are two firing rate vectors of C neurons associated with states S₁ and S₂, respectively; w = [w₁, … , w_C] denotes the weighting coefficients according to the relative neuronal firing rates: $w_c=\frac{{\lambda }_{c.1}}{2{\sum }_{k=1}^c{\lambda }_{k.1}}+\frac{{\lambda }_{c.2}}{2{\sum }_{k=1}^c{\lambda }_{k.2}}$ such that ${\sum }_{c=1}^C{w}_c=1$. Therefore, equation (4) computes the difference between two states S₁ and S₂ based on the similarity of their associating tuning curves, weighted by relative firing rate contributions. The purpose of weighting is to reduce the impact of neurons with higher firing rates. When w is uniformly distributed, it corresponds to the unweighted setup. However, the qualitative relationship on the dissimilarity measure was robust regardless of the weighting or unweighting operation.

In light of Λ, we computed an m × m divergence matrix with the (i, j)th entry that defines the divergence between states S_i and S_j. The diagonal elements of the matrix are all zeros. From all nonzero values of $\mathcal{l}\left(S_i,S_j\right)$ (unit: spike per second), we further constructed its cumulative distribution function (CDF) and defined the ‘dissimilarity’ by the distribution percentile value (range: 0–1, unitless). We concluded that the neural activity represented at the state level was similar if the divergence value was low. We used two similarity criteria: (i) the relative divergence percentile was below 25% in the CDF curve, and (ii) the divergence was smaller than the average divergence measure. In addition, the relative similarity statistic in terms of percentile allowed for comparison between different recordings.

For two state sequences with equal length T, we computed the mean divergence as follows: $\frac{1}{T}{\sum }_{t=1}^T\mathcal{l}\left(S_t,S_t^{\prime }\right)$. The lower the mean divergence, the more similar are two state sequences or two underlying population representations. When the lengths of two sequences differed, we employed a dynamic time warping (DTW) algorithm to align two temporal sequences (MATLAB function: dtw.m). Specifically, the sequences were warped in the time dimension to determine a measure of their ‘similarity’ independent of certain nonlinear variations in time, where the similarity was assessed by the symmetric KL divergence metric. Finally, once two sequences were aligned, we further computed the mean divergence by temporal average.

All statistical comparisons were conducted with nonparametric rank-sum tests of differences between two samples using p < 0.05 significance level, unless otherwise noted.

2.6. Hierarchical clustering of latent states

Based on the similarity measure, we built a hierarchical clustering tree of latent states. Hierarchical clustering groups data over a variety of scales by creating a cluster tree or ‘dendrogram’, a multilevel hierarchy in which clusters at one level are joined as clusters at the next level. The clustering procedure consisted of three steps: (i) define the similarity or dissimilarity between every pair of data points or strings in the data set; (ii) group the data or strings into a binary, hierarchical cluster tree; (iii) determine where to cut the hierarchical tree into clusters. Using the KL divergence metric, we applied a hierarchical clustering algorithm (MATLAB function: clusterdata.m) to define the similarity between latent states.

2.7. Mutual information

To map neural representations to behavior, we quantified their statistical dependency between the inferred neural state sequences and temporally clustered kinematic sequences.

Given two random discrete sequences $\mathcal{S}$ and ${\mathcal{S}}^{\prime }$, we computed the Shannon entropy, conditional entropy (unit: bits): $H(\mathcal{S})$, $H({\mathcal{S}}^{\prime })$, $H\left(\mathcal{S}\mid {\mathcal{S}}^{\prime }\right)$ and normalized mutual information (NMI):

$$\text{NMI}\left(\mathcal{S},{\mathcal{S}}^{\prime }\right)=\frac{H(\mathcal{S})-H\left(\mathcal{S}\mid {\mathcal{S}}^{\prime }\right)}{\sqrt{H(\mathcal{S})H\left({\mathcal{S}}^{\prime }\right)}}$$ (5)

where 0 ⩽ NMI ⩽ 1. A high NMI value indicates the strong statistical dependency or correspondence between two sequences. Using a resampling method, we computed the NMI statistic. In addition, we randomly shuffled the sequence labelings independently 1000 times and computed the shuffled NMI distribution (‘null distribution’), from which we computed the Monte-Carlo p-value and Z-score (by approximating the shuffle distribution as Gaussian). A low Monte-Carlo p -value (p < 0.05) indicates the high degree of statistical significance.

In addition, we used the nearest-neighbor method proposed in Ross (2014) to compute the mutual information between a discrete random sequence and a (one or multi-dimensional) continuous random signal (the open source MATLAB code is available in the online supporting information of cited reference).

2.8. Continuous latent variable models for neural population codes

To compare with standard unsupervised methods for population codes, we also considered two continuous latent variable models for dimensionality reduction and prediction. The first one is a static statistical model known as factor analysis (FA). In FA, the spike count observations were treated as independent and identically distributed (iid) samples. For simplicity, we assumed the reduced model dimensionality is known as m, which is much smaller than the number of observed neurons. The model selection can be determined by statistical criteria such as cross validation. Due to model identification ambiguity, we reordered the estimated latent variables (‘factor’) using a rescaling strategy (Yu et al 2009). Specifically, we applied singular value decomposition (SVD) to the estimated loading matrix C: C = USV^⊤ (where U and V are orthogonal matrices with orthonormal columns, S is a nonnegative diagonal matrix), and rescaled the latent variable {x₁, … , x_m} by ${\tilde{x}}_i=(\mathit{SV})x_i(i=1,\dots ,m)$, such that the latent trajectories $\left\{{\tilde{x}}_1,\dots ,{\tilde{x}}_m\right\}$ were sorted by their explained variance represented in the singular values in S. To plot the neural latent variable, we showed the rotated latent trajectories accordingly. We further ran a standard linear regression analysis between the inferred m-dimensional latent factors and individual chewing kinematic variables. The optimal model order m could be determined by the cross-validated decoding error.

The second method is a dynamic statistical model known as the Poisson linear dynamical system (PLDS), which can viewed as a dynamic extension of FA or a generalized version of linear dynamical systems (Buesing et al 2012, Macke et al 2012). In the PLDS, the Poisson-distributed spike count observations are assumed to be modulated by Gaussian–Markov latent variables. Details of the PLDS and inference algorithms have been described elsewhere Macke et al (2015) and Chen et al (2017). Similar to FA, we also assumed that the model dimensionality m was known. We ran an expectation–maximization (EM) algorithm to infer the model parameters and continuous state latent variables and then evaluated the predictive performance on held-out data.

2.9. Decoding analysis

For HDP-HMM, the decoding analysis was similar to the approach described in Linderman et al (2016). From the training trials, we first estimated the latent states and parameters of HDP-HMM; and the mapping between the latent states and kinematics variable was further identified by the median statistics. In the testing trials, we estimated the latent states and predicted the kinematic variables based on the mapping, and then compared them with the ground truth.

For FA or the PLDS, the decoding analysis was similar to the approach described in Aghagolzadeh and Truccolo (2016). We first inferred the latent state variables from the training data, and then ran a linear regression analysis between the continuous latent states and kinematics. In the testing stage, we used the regression model to predict the kinematics from the inferred the latent state variables.

All decoding results were reported based on cross-validation or leave-one-trial-out analyses.

2.10. Computer simulation

In order to validate our proposed method for neural population data analysis, we generated synthetic neural spike trains from artificial motor cortical neurons with assumed ground truth tuning curves. Specifically, we simulated four classes of trajectory paths that are associated with the following move ment kinematics $u_t\triangleq \left[x_t,y_t,{\dot{x}}_t,{\dot{y}}_t\right]\in {ℝ}^4$ (Wu and Srivastava 2011):

$$\begin{gathered} x_t^{(1)}=-\text{cos}(0.5\pi t),y_t^{(1)}=\text{sin}(0.5\pi t) \\ {x}_t^{(2)}=-\text{cos}(0.5\pi t),y_t^{(2)}=-\text{sin}(0.5\pi t) \\ {x}_t^{(3)}=0.5(\text{cos}(\pi t)+1){\Theta }_t,y_t^{(3)}=0.5\text{sin}(\pi t) \\ {x}_t^{(4)}=0.5(\text{cos}(\pi t)+1){\Theta }_t,y_t^{(4)}=-0.5\text{sin}(\pi t) \end{gathered}$$

where the superscript denotes the index of trajectory class, and Θ_t is a step function. The trajectories of kinematics are temporally smooth over 2 s. In addition, we assumed that the firing rate of the cth neuron, λ_c,t, is nonlinearly modulated by a four-dimensional instantaneous kinematic vector [x_t, y_t, ${\dot{x}}_t$, ${\dot{y}}_t$]. For the ith trajectory path (i = 1, 2, 3, 4), the firing rate of the cth neuron had the following log-linear form:

$${\lambda }_{c,t}^{(i)}=b_c\text{exp}\left(a_c^{\top }\left[x_t^{(i)},y_t^{(i)},{\dot{x}}_t^{(i)},{\dot{y}}_t^{(i)}\right]\right)$$ (6)

where $a_c\in {ℝ}^4$ denotes the modulation coefficients of the c-th neuron. The resulted firing rate varied in both time and trajectory type. We used the following setup in the current study: 40 neurons, 50 trials (2 s per trial), with 40 trials for training and the remaining ten trials for testing. We binned neuronal spikes with 100 ms bin size to obtain 21 spike count observations per trial. In this computer simulation example, there was no unique mapping between kinematic sequences {u_t} and neural spike train observations. The inference goal was to unfold the representation of neural population dynamics that explains the kinematics.

3. Results

3.1. Kinematics of chewing behavior

PCA of the jaw and tongue kinematics during feeding recovered various (three–five) numbers of principal components that explained more than 95% of the variance in these high-dimensional kinematics in all single trials or feeding sequences, whether with the position kinematics alone, or together with the position, velocity, and acceleration kinematics.

Chewing sequences (trials) varied in duration from 7.1 to 45.3 s. It took monkeys more gape cycles to finish harder (e.g. almond, date, hazelnut, peanut) than softer (e.g. green bean, potato, carrot, apple, pear, kiwi, blueberry, mango) foods. Depending on the food type or size, it took animals one–four swallows to complete each feeding trial, with the majority of trials having one or two swallows (e.g. one swallow: 15/38 in Dataset 1 and 19/34 in Dataset 2; two swallows: 17/38 in Dataset 1 and 11/34 in Dataset 2). Gape cycles also had different durations, varying from 300 ms to 550 ms (6–11 bins for 50 ms bin size), reflecting a chewing frequency of around 2.5–3 Hz. Chew frequency varied with food type and the process of food intake. Chew gape cycle duration was altered by changing the velocity of jaw opening and the duration of the occlusal phase.

Across all trials, the durations of the four gape cycle phases (i.e. SO, FO, FC, SC) varied significantly. For instance, using a bin size of 50 ms, the numbers of temporal bins for SO, FO, FC, SC were 167, 862, 459, 614, respectively in Dataset 1; and 693, 983, 639, 1197, in Dataset 2.

3.2. Characterization of single MIo unit responses

Among all MIo units (n = 142 in Dataset 1, n = 78 in Dataset 2, n = 75 in Dataset 3), many units (78/142 in Dataset 1, 77/78 in Dataset 2, 74/75 in Dataset 3) showed significant modulation during chewing relative to the baseline. Each chewing sequence consists of multiple gape cycles, of varying length (figure 4(A)). To reveal the role of MIo units in generation and fine control of orofacial movements, we displayed the tuning curves of all MIo units over the full gape cycle by averaging their spike activity over all cycles (figure 4(B)). The tuning curves were computed over the complete gape cycle phases and then displayed at a normalized scale. Spike spectra of single units also exhibit significant oscillatory frequencies that modulate the spiking activity (figure 4(C)). Interestingly, the tuning curves and spike spectra of MIo units varied across food types, especially between foods with high stiffness and low toughness (e.g. almond in figures 4(A)–(C) and food with low stiffness and high toughness (e.g. potato in figures 4(D)–(F). This is likely due to the fact that the animal had to generate different forces according to the food type, and each force had distinct temporal dynamics. The units that showed significant modulation in equation (1) were task-modulated. We focused on the spike spectrum of units with firing rate above 2 Hz (n = 106 in Dataset 1, n = 43 in Dataset 2, n = 42 in Dataset 3), and those units with >2 Hz firing rate were mostly task-modulated (70 in Dataset 1, 43 in Dataset 2, 42 in Dataset 3). Specifically, a large percentage of those units (34/70 in Dataset 1, 27/43 in Dataset 2, 26/42 in Dataset 3) showed strong oscillatory modulation during rhythmic chewing; around 80% of those subunits showed a dominant oscillatory frequency around 2.2–3.5 Hz (27/34 in Dataset 1, 22/27 in Dataset 2, 22/26 in Dataset 3), roughly matching the period of a full gape cycle (300–500 ms).

Figure 4.

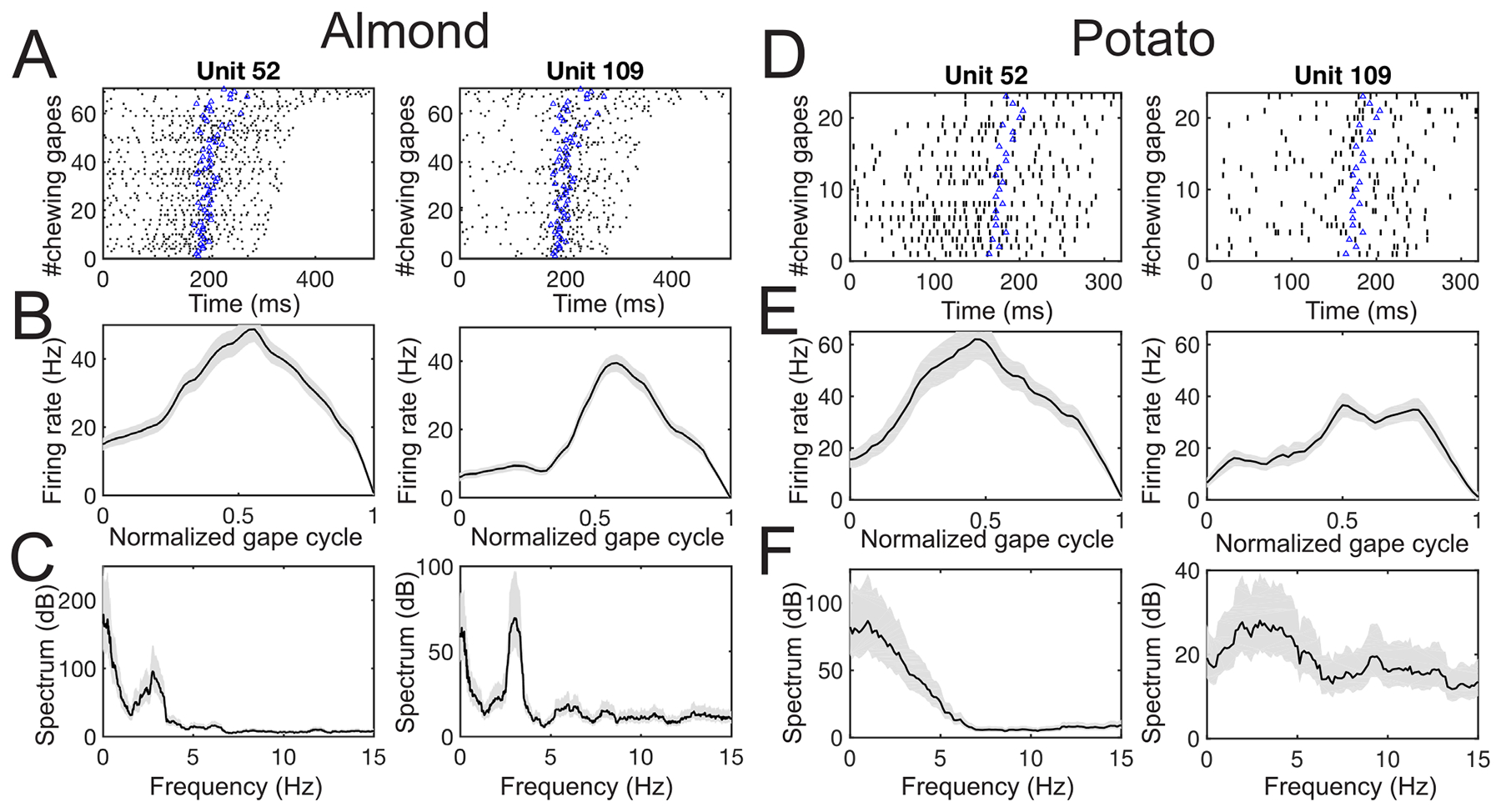
Characterization of two representative MIo single units (Monkey O, Dataset 1) in two single trials. (A) Spike rasters of all chewing gape cycles (from the maximum gape to the consecutive maximum gape) within a single almond trial. Each row corresponds to one gape cycle. The rasters are ordered bottom to top by increasing cycle duration. The blue triangle in each row marks the time where the minimum gape occurs in each gape cycle. (B) Tuning curve of chewing gape within a normalized gape cycle. Shaded area marks the SEM. (C) Spike spectrum. Shaded area marks the confidence interval. (D)–( F) Same as (A)–(C), except for potato-type trials. Note the lack or less stronger 3 Hz oscillation in both spike spectra in panel (F).

Next, we examined the unit response with respect to swallowing among all food types. Aligning the spike rasters and peri-event time histogram (PETH) of single units at swallowing onset (note that some trials or feeding sequences may include two or more swallow cycles) revealed that subsets of MIo units changed their firing rates before or around the swallow onset (figures 5(A) and (B)). In Dataset 1, 37.8% and 13.6% of units increased or decreased their firing rates before the swallow onset, respectively. In Dataset 2, the corresponding percentages were 39.7% and 7.7%, respectively. In Dataset 3, the percentage statistics were 40.0% and 8.0%, respectively. These results suggest that single MIo units show modulated activity with respect to chewing and swallowing in a temporally precise manner.

Figure 5.

Characterization of four representative MIo single units (Monkey O, Dataset 1) with respect to the swallow onset in all experimental trials. (A) Spike rasters before and after the swallow onset (time 0). (B) Corresponding peri-event time histogram (PETH) for panel (A). In the first two examples, we observed an increase in spike activity before the swallow event; whereas in the last two examples, the firing rate dropped before the swallow onset. All error bars are the SEM.

3.3. Validation of simulated neural population dynamics

Computer simulations were used to validate the ability of our approach to extract meaningful latent state dynamics relevant to the underlying behavior (where the 2D trajectory path and velocity profiles are shown in figures 6(A) and (B), respectively). We used our proposed HDP-HMM and unsupervised learning to characterize the simulated population spike data from multiple trials (Materials and Methods). We randomly drew samples from the neuronal tuning curves on each trial (figure 6(C)). From the inferred state-firing rate matrix, we computed the divergence metric matrix for m = 52 inferred states (figure 6(D)), and further assessed the similarity between states or state sequences within training or testing data. In this example, we concluded that the state sequences were ‘similar’ or consistent if the divergence metric between two state sequences was low in the sense that (i) its absolute value was below the chance level, and (ii) its divergence percentile was below 25% in the CDF curve (figure 6(E)). Typically, two states were ‘similar’ if their pairwise divergence metric or percentile was small (figure 6(G)). The similarity of two state sequences could be assessed by the mean-averaged divergence or percentile statistics once two sequences were aligned. Across test trials, we computed the mean divergence percentile between all pairwise trials, and further calculated the inter- or intra-type trial statistics. Specifically, the mean intra-type divergence measures for the four trajectory paths were 1.60, 1.50, 1.60 and 0.80, respectively (corresponding to the divergence percentiles 3.8%, 3.6%, 3.8% and 2.4%, respectively. Lower percentile implies higher similarity, with 0 meaning perfect similarity). In contrast, the inter-type divergence percentiles were higher (varying from 30% to 70%). This result was robust with respect to various ranges of parameters a_c and b_c in equation (6). To compute the between/within-trial dissimilarity, we computed the time-averaged dissimilarity measures between the inferred state sequences; the measure was presented as a trial-by-trial dissimilarity matrix. As a comparison between the model-based and model-free dissimilarity measure, we also computed the averaged KL divergence directly based on the raw spike counts. In this example, the empirical trial-type variability yielded qualitatively similar pattern.

Figure 6.

Computer simulations and validation. (A) Simulated movement trajectory (x_t, y_t), with four colors representing different paths. (B) Velocity of $\left({\dot{x}}_t,{\dot{y}}_t\right)$ for different paths. Solid and dashed lines denote the x and y directions, respectively. (C) Temporal profile of neuronal firing rate (spikes per second). (D) Divergence metric matrix among 52 inferred latent states (unit: spike per second). (E) Cumulative distribution of all nonzero pairwise divergence between the latent states. (F) Correspondence map between 52 latent states (sorted by decreasing occupancy) and 48 clustered behavioral states (derived from two-level spatiotemporal clustering of kinematics). (G) Similarity dendrogram: hierarchical clustering of latent states according to the divergence metric matrix (panel (C)). Two sequences 26-40-6-1-14 and 25-49-15-7-4 correspond to the inferred latent state sequences from two selected gape cycles. (H) Quantification of dissimilarity of population responses in terms of divergence percentile between four types of trajectories. Dark pixel represents high dissimilarity of high divergence percentile. The first panel corresponds to the result derived from m = 52, and the 2nd to 5th panels correspond to the results using fixed m = 30, 40, 60, 70, respectively. (I) Difference of divergence measures between m = 52 and fixed m = 30, 40, 60, 70.

To investigate whether the derived dissimilarity measure was robust with respect to the number of states m, we also prefixed the number of states m = 30, 40, 60, 70 and repeated the analysis. We found that the change of m did not affect the shape of the CDF curve (the greater the value m, the smoother the CDF curve), nor the quantitative dissimilarity measure between different trajectory types (figure 6(H)). The difference of dissimilarity measure between using different values of m is shown in figure 6(I).

To link the inferred latent states to behavior, we used ACA and HACA clustering algorithms to derive a discrete behavioral sequence from high-dimensional kinematics. From the correspondence map between the clustered behavioral sequence and inferred latent states, we found that the majority of behavioral clusters were captured by a few dominant HMM latent states (figure 6(F)), whereas the most occupied HMM states represented multiple behavioral clusters. This implies that the same states can represent different sets of kinematics, or the same kinematics may be represented by distinct states in different contexts. The ‘one-to-many’ or ‘many-to-one’ correspondence may be ascribed to high-dimensional kinematics as well as limited neural recording samples. In general, discretization of continuous spaces lead to the ‘curse of dimensionality’ problem. Our proposed unsupervised learning provides an ‘adaptive sampling or representation’ strategy to examine the discrete behavioral spaces without defining them a priori.

In addition, we computed the NMI between the inferred latent state sequence and the clustered behavioral sequence. For the given four trajectory paths, the inferred NMI statistics were 0.66, 0.48, 0.60, and 0.75, respectively. All NMI statistics were statistically significant (Monte-Carlo p < 10⁻⁴). We have also examined the mutual information between the discrete latent states and continuous 4-dimensional kinematic variables, yielding the mutual information for four trajectories path as 0.86, 0.44, 0.72, and 1.01, respectively. This result had a similar trend as the NMI statistics.

Therefore, the computer simulation experiment demonstrated that our unsupervised learning approach was capable of uncovering neural dynamics including variability of neural population responses. The inferred latent structure, expressed in the form of neural sequences or trajectories, showed high statistical dependence with the kinematics. In fact, we could employ an ‘NMI-guided encoding’ strategy in that the computed NMI statistic was used to determine the most relevant behavioral measures (e.g. selecting the position, velocity, acceleration, their combinations, and across various time lags).

In summary, the computer simulation results validate the capability of our method to characterize neural variabilities of within and between-trial types at a population level consistent with behavioral variabilities. Our method can reveal interesting relationship (through mutual information) between the abstract latent states and observed kinematic variables.

3.4. Inferring neural population dynamics of rhythmic chewing

The goal of our analysis was to extract latent states that drive the neural spatiotemporal patterns represented in the spike trains. We analyzed the ensembles of sorted units recorded from the MIo area, and binned the spike trains with a bin size of 50 ms. Snapshots of population spike rasters during consecutive chewing gapes are shown in figure 7(A). For each dataset, we used all trials (i.e. feeding sequences) and focused on the periods of rhythmic chewing, excluding the ingestion, manipulation, and stage 1 transport cycles. We used the standard hyperparameter setup for the HDP-HMM and ran MCMC to infer the model parameters and the number of latent states from the data. Upon convergence, the inferred number of states m was stabilized (e.g. 39–42 for Dataset 1, 66–68 for Dataset 2, 86–88 for Dataset 3). We also derived the state-firing rate matrix, divergence metric matrix and the associated divergence CDF curve (figures 7(B) and (C)). In the example in figure 7, the median divergence measure was about 0.25 spike per second. It is worth emphasizing that the shape of the divergence CDF curve was robust with respect to the number of states m. As a sanity check, we varied the number of states (m ± 15) and ran the inference algorithm for the finite-state HMM for each dataset. The derived CDF curve’s shape was nearly identical (figure 7(C), dashed lines), suggesting that the divergence percentile statistic was robust with respect to the number of states and the model.

Figure 7.

Inferring neural population dynamics of rhythmic chewing (Monkey A, Dataset 2). (A) Spike rasters of MIo population during consecutive chewing gapes in one single trial (food: date). Vertical dashed line indicate the phase transition moments of max-gape (‘triangle’) and min-gape (‘diamond’). (B) Divergence metric matrix among the latent states derived from all experimental trials. (C) Cumulative distribution of all nonzero pairwise divergence statistics derived from panel (B). Solid line denotes the result from m = 66, dashed and dotted lines denote the results from m = 50 and m = 80, respectively.

Once the latent state sequences were inferred from the recorded neural population spike activity, we aligned latent state sequences at each gape cycle of rhythmic chewing that consists of four chewing phase transition times: FC-SC, min-gape (SC → SO), SO-FO, max-gape (FO → FC) (figure 2). We further characterized neural population dynamics and variability at multiple levels or timescales: between sequences of chews on different food types; between chewing sequence stages within chewing sequences; and between chewing phase transitions within gape cycles. We uncovered a periodic spatiotemporal pattern from population spike activity, consistent with the chewing kinematics and single unit activity. In what follows, we present these characterizations and statistics across these levels.

3.5. Neural variability at distinct chewing stages displays temporally structured patterns

Since the chewing behavior was rhythmic and many single MIo units showed rhythmic modulation in spiking activity, we investigated how the population spiking patterns varied at different stages of rhythmic chewing. Independent of trial durations and number of gape cycles, we split evenly the chewing sequences of each trial into an early stage (Stage 1), an intermediate stage (Stage 2, immediately before the first swallow), and a late stage (Stage 3, immediately after the first swallow). Each stage consisted of roughly the same number of full chewing gape cycles (i.e. one third of chewing gape cycles).

In each single feeding sequence (trial), it was difficult to distinguish between the gape-wise ensemble spike activity in a high-dimensional space among multiple gape cycles (e.g. see figure 8(A) for multi-unit rasters of spiking activity during two consecutive chewing gape cycles in Stages 1, 2, and 3). Instead, we resorted to latent state mapping and quantified the dissimilarity between the inferred latent state sequences in selected gape cycles, where the dissimilarity was represented by the divergence percentile (figure 8(B)). Interestingly, this example showed less variability in consecutive chewing gapes within the same stage. Next, we extended the method to every gape cycle within a trial (figure 8(C)). As seen from the block structure of figure 8(C), subsets of neighboring trials displayed striking similarity in a locally clustered structure. Finally, we pulled together the dissimilarity measures across all trials and computed the group statistics between stages (figure 8(D)). Dissimilarity or divergence statistics between stages are shown in table 2.

Figure 8.

Variability comparison of neural population dynamics of chewing gapes at different stages in two monkeys. (A) Selective two consecutive chewing gapes at Stage 1, Stage 2 and Stage 3 within one almond(shell) trial (left: Monkey O, Dataset 1; right: Monkey A, Dataset 2). Panels (B)–(D): top: Monkey O, Dataset 1; bottom: Monkey A, Dataset 2. (B) Dissimilarity (mean divergence measure) of six gapes in panel (A), characterized by a 6 × 6 matrix. Light color represents a high similarity. (C) Dissimilarity (mean divergence measure) percentile of total n gapes in a full single feeding trial, characterized by an n × n matrix. Dashed lines indicate the boundary between the three chewing stages. (D) Comparison of within and inter-stage group statistics of variability in population response during chewing across all feeding trials. In both cases, the intra-stage (Stage 2 versus Stage 2) had smallest divergence statistics, whereas the inter-stage (State 3 versus Stage 2) had the largest divergence statistics. These two groups were significantly different (p < 0.01, two-sample KS test; p < 0.01, rank-sum test).

Table 2.

Comparison of the median divergence (spike per second) and divergence percentile (in bracket) between chewing stages 1–3 (early, intermediate, late stages, respectively).

	Dataset 1			Dataset 2			Dataset 3
	Stage 1	Stage 2	Stage 3	Stage 1	Stage 2	Stage 3	Stage 1	Stage 2	Stage 3
Stage 1	0.060 (0.158)	0.059 (0.157)	0.069 (0.237)	0.065 (0.025)	0.092 (0.061)	0.109 (0.089)	0.071 (0.040)	0.109 (0.123)	0.134 (0.198)
Stage 2	0.059 (0.157)	0.058 (0.149)	0.065 (0.193)	0.092 (0.061)	0.074 (0.037)	0.108 (0.088)	0.109 (0.123)	0.083 (0.064)	0.128 (0.176)
Stage 3	0.069 (0.237)	0.065 (0.193)	0.063 (0.178)	0.109 (0.089)	0.108 (0.088)	0.085 (0.051)	0.134 (0.198)	0.124 (0.176)	0.109 (0.127)

To compare the within-stage and between-stage dissimilarity, we used Stage 2 as a control. The reason of this choice is because Stage-2 structure was the more stable than Stage-1 and Stage-3 structure across gape cycles within the same trials. First, we computed the within-stage dissimilarity of Stage 2 versus Stage 2 (denoted as Div_2,2). Next, we computed the between-stage dissimilarity of Stage 2 versus Stage 1 (denoted as Div_2,1) and Stage 2 versus Stage 3 (Div_2,3). In Dataset 1, there was a significant difference between Div_2,2 and Div_2,1 (p = 0.03, KS test; p = 0.42, rank-sum test), and between Div_2,2 and Div_2,3 (p = 1.4 × 10⁻¹¹, KS test; p = 3.8 × 10⁻¹¹, rank-sum test). In Dataset 2, there was a significant difference between Div_2,2 and Div_2,1 (p = 1.8 × 10⁻⁴⁹, KS test; p = 2.6 × 10⁻⁵⁸, rank-sum test), and between Div_2,2 and Div_2,3 (p = 3.2 × 10⁻¹¹⁰, KS test; p = 3.2 × 10⁻¹¹⁰, rank-sum test). In Dataset 3, there was a significant difference between Div_2,2 and Div_2,1 (p = 1.4 × 10⁻⁸², KS test; p = 2.4 × 10⁻⁹², rank-sum test), and between Div_2,2 and Div_2,3 (p = 7.6 × 10⁻¹⁴⁴, KS test; p = 5.4 × 10⁻¹⁶⁷, rank-sum test).

Furthermore, we found that structured stage-wise chewing patterns varied between feeding sequences and animals. Overall, there was a large degree of variability across sequences (trials). However, similar patterns were also found among the same food type (e.g. persimmon, Dataset 3). Among three datasets examined, we identified more qualitatively clustered patterns of gape dynamics in Monkey A’s recordings (see examples in figure 9).

Figure 9.

Illustrated examples of chewing gape variability during food-specific single trials (Monkey A). Top row: dry apricot, dry peach, dry apricot, date (Dataset 2). Bottom row: persimmon, persimmon, persimmon, kiwi (Dataset 3). In all panels, horizontal and vertical lines indicate the boundary between the three chewing stages.

3.6. Neural variability in chewing dynamics with respect to food types

Food size and material properties are known to affect within-subject variability of chewing cycle kinematics (Reed and Ross 2010), so we hypothesized that food type would have an impact on the neural variability. Within each dataset (recording session) we investigated stage-dependent variability of neural population dynamics with respect to food types. To assure comparable trial length and number of chewing cycles, we only analyzed the food types that had repeated (i.e. at least two or more) trials. There were a total of seven repeated food types (almond, green bean, carrot, apple, potato, pear, kiwi) in Dataset 1, a total of eight repeated food types (almond, date, yam, kiwi, potato, grape, dry peach, dry apricot) in Dataset 2, and a total of ten repeated food types in Dataset 3 (figure 10(A)). Within recording sessions, we ranked the foods based on average chew cycle duration (figure 10(A)) then grouped two foods that had the longest chewing duration as Type-L, and two foods that had the shortest chewing duration as Type-S. Generally, harder foods required longer chewing sequence durations than softer foods, and bigger foods required longer chewing sequence durations than smaller foods.

Figure 10.

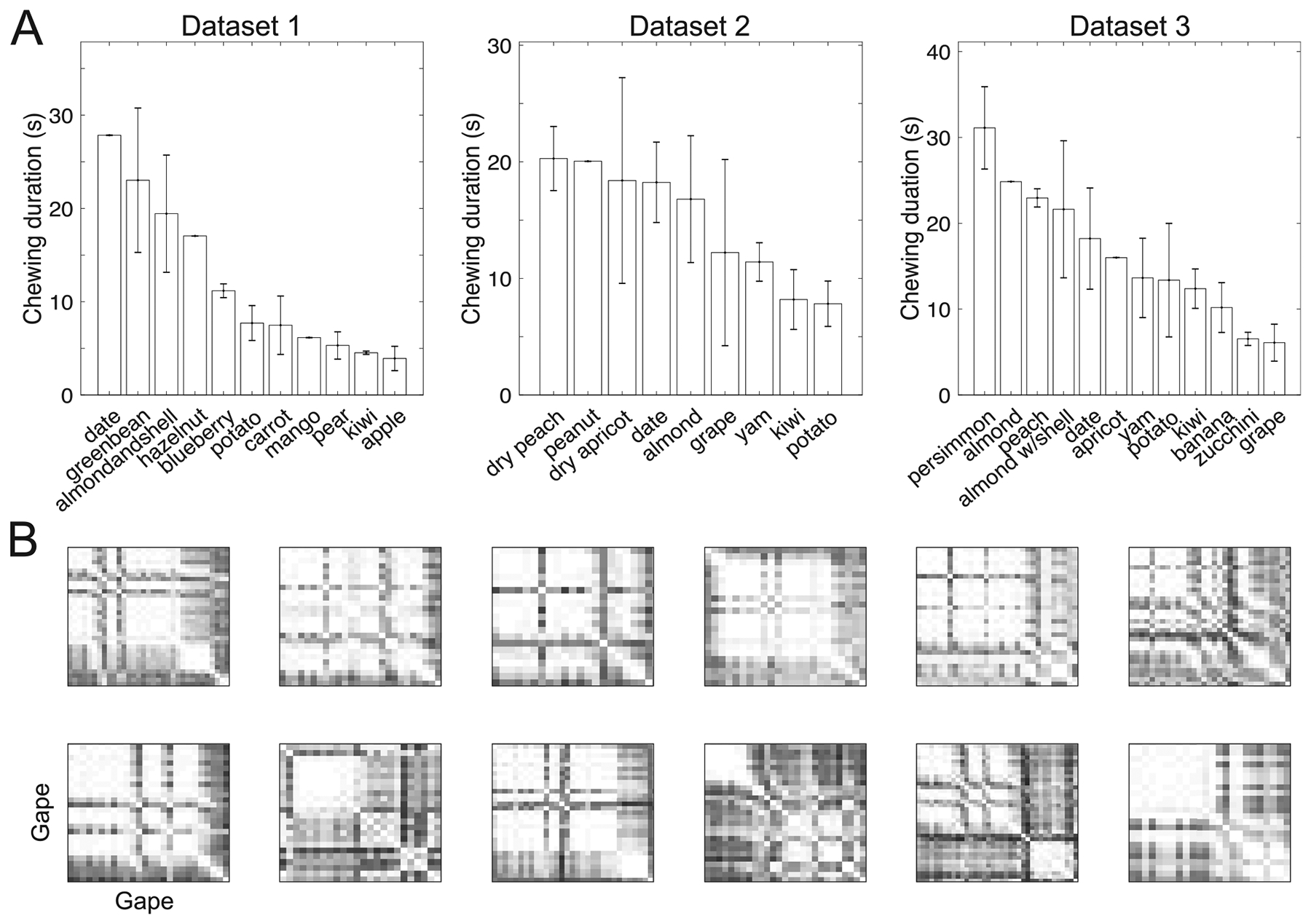
Variability in chewing of inter- and intra-food. (A) Duration of chewing gapes among all food types in each dataset. (B) Illustration of dissimilarity of chewing dynamics for the same food (kiwi) at multiple single trials (Dataset 3). Each matrix shows the dissimilarity (mean divergence measure) percentile of all chewing gapes within a single trial.

Next, we selected three representative foods: almond, potato, and kiwi, which had long, medium and short durations, respectively (figure 10(A)). In terms of chewing dynamics at stage 2, the most dissimilar chewing dynamics between foods was almond versus kiwi, followed by potato versus kiwi and almond versus potato.

We further analyzed the dissimilarity of chewing dynamics within the same food at different trials. For the given food, we sorted the trials by their durations, and then quantified the within-trial variability. However, no relationship was found between trial-variability and trial duration. As an illustration, we selected 12 kiwi trials from Dataset 3 (mean ± SD trial length: 12.4 ± 2.3 s) and computed the chewing gape dissimilarity within each single trial (figure 10(B)). Using the data of Stage 2, we compared the dissimilarity distribution between different trials. Among comparisons of all possible 66 pairs, 53 pairs showed no statistical difference (rank-sum test, p > 0.05). Therefore, the patterns of chewing dynamics within the same food type were mostly similar between chewing gapes.

3.7. Neural variability in chewing phase transitions

Turning our attention to the variability at the finest timescale, we examined the representation variability during the four gape cycle phase transitions—min-gape, max-gape, SO-FO, FC-SC. First, we examined the state histogram of those phase transitions within the same food (see an illustrated example for all almond trials, figure 11(A)) and then among all food types (figure 11(B)). Interestingly, there were distinct state occupancy patterns among the four gape cycle phase transitions (see histograms in figure 11(A)) suggesting that different gape cycle phase transitions are associated with variation in neural states.

Figure 11.

Variability comparison of four gape phase transitions (Monkey O, Dataset 1). (A) and (B) Histograms of state occupancy for four chewing phase transition moments during feeding, in the cases of one representative food type: almond (A) and all food types (B). There are distinct state occupancy patterns among four gape phase transitions. (C) Mean divergence percentile (dissimilarity metric) between four phase transitions derived from one food (almond, left) and all foods (right). Low value shows high similarity. Higher similarity values in the diagonal are visible. The values above the statistical significance threshold (with respect to the off-diagonal statistics) are marked in bold font. (D) Histograms of dissimilarity (i.e. divergence percentile) for inter-transition variability of min-gape versus max-gape (left) and FC-SC versus SO-FO (right). (E) Cumulative distribution function (CDF) curves of dissimilarity of inter-transition variability and respective self-transition variabilities associated with panel (D).

From the histograms, we computed the weighted average divergence measure (in percentile) and obtained the corresponding 4-by-4 dissimilarity matrices (figure 11(C)). Lower dissimilarity values in the diagonal elements suggest that neural states vary less within transitions than across transitions, both within the single food—almond (left panel) and across all foods (right panel). Among the off-diagonal elements in the dissimilarity matrix, the inter-transition variability of min-gape versus max-gape was the highest, whereas the inter-transition variabilities of SO-FO versus min-gape and FC-SC versus max-gape were relatively lower. Minimum gape is the time when the teeth are in maximum occlusion and are transmitting force to the food whereas maximum gape is when the jaws are maximally depressed and the tongue is manipulating the food item. These very different sensorimotor tasks probably explain these divergent neural states and variability. A similar explanation likely applies to the high divergence (or dissimilarity) between FC-SC and SO-FO: the first is the time when the teeth first encounter the food during closing, and the second when the tongue picks up the food during opening. To assess the significance of dissimilarity, we put together the divergence metrics from all sample points in the diagonal as the control group, and compared with the off-diagonal group. If the divergence measure from the off-diagonal group (e.g. min-gape versus max-gape) was significantly greater than their respective intra-variabilities of control group (by the signed-rank test and two-sample KS test), we would conclude that the dissimilarity was significant. Only the dissimilarity values that showed statistical significance in both tests (p < 0.01) were treated significant.

Next, we closely examined these two chewing phase transitions that showed the greatest dissimilarity in figure 11(C). Across all trials, the distributions of these dissimilarity indices had a relatively narrow range. See figure 11(D) for a single trial illustration. Similarly, we also compared their CDF plots (e.g. figure 11(E)) and their median statistics. In these examples, the dissimilarity of min-gape versus max-gape was significantly greater than that of max-gape versus max-gape and min-gape versus min-gape; the dissimilarity of FC-SC versus SO-FO was significantly greater than that of SO-FO versus SO-FO and FC-SC versus FC-SC. All pairwise comparisons showed statistically significant differences (p < 10⁻¹⁰, both rank-sum test and two-sample KS test).

Finally, we examined the relationship between the latent states representing gape phase transitions and chewing kinematics. As seen in figure 11(A), for the almond trials, the gape transition of max-gape and min-gape could be represented by several latent states, namely their state occupancies had a sparsely distributed pattern. For instance, in max-gape, the two dominant modes of state occupancy are states 9 and 18, whereas the two domain modes of state occupancy in min-gape are states 6 and 12.

Take the max-gape as an illustrated example, we explored the difference between the first two dominant states. Specifically, their divergence percentile was 0.721, indicating that the neural population activities they represent were quite different. We then examined if this difference was linked to the chewing kinematics. We conducted the analysis using either almond trials only or all food trials. First, we compared the appearance of two dominant states in time at each trial (normalized from 0 to 1). We found that state 18’s appearance in the second half of trial was less frequent than that of state 9 (figure 12(A)) (p = 2.1 × 10⁻⁵, rank-sum test). When data from all trials were considered, the same conclusion was found (figure 12(B)) (p = 8.8 × 10⁻⁷, rank-sum test). Second, we investigated whether these two latent states also reflected distinct kinematic patterns; or in other words, what type of kinematic variables was better characterized by the latent states. To do so, we conducted PCA on all kinematic data of samples that were marked as max-gape, and reported the scores on the first two principal components (PCs) associated with the latent states 18 and 9. Specifically, we used 12 selected kinematics variables in three different ways: (i) both position and velocity combined; (ii) position data alone; and (iii) velocity data alone. As shown in (figure 12(C)), when case (iii) was considered, there was significant difference between two state’s PC scores (shown in the range of [min, max] value) on both PC1 (p = 7.1 × 10⁻⁶, rank-sum test) and PC2 (p = 1.9 × 10⁻⁹). However, when cases (i) and (ii) were considered, we only found significant difference in PC1 scores (p = 1.2 × 10⁻⁵ and p = 1.8 × 10⁻⁴, respectively). This result suggests that states 9 and 18 represented more velocity variability than position variability. Again, using data from all trials led to a similar conclusion (figure 12(D)). The same principle of analysis can be applied to min-gape, SO-FO and FC-SC.

Figure 12.

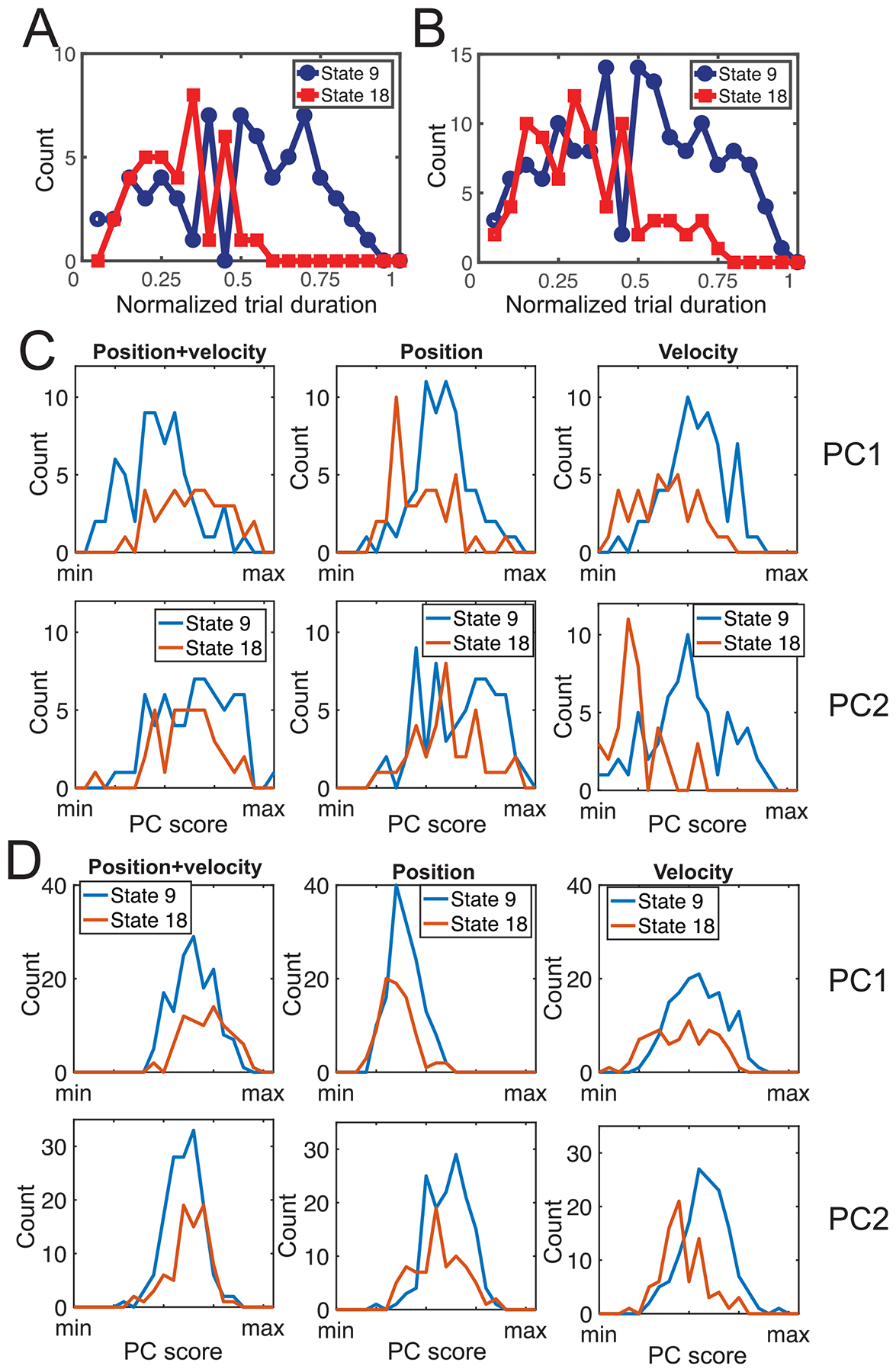
Relationship of latent state representation for max-gape and position/velocity kinematic variables. (A) and (B) Appearance statistics of two dominant latent states (9 and 18) in time of each trial in almond trials (A) and all food trials (B). (C) and (D) Comparison of distribution of principal component (PC) scores derived from PCA on chewing kinematic variables in almond trials (C) and all food trials (D). PC1 and PC2 denote the first and second dominant principal components, respectively.

3.8. Mapping between neural representations and kinematics

Our unsupervised learning framework provides a mapping between the inferred latent states and population spike activity. To link the neural activity with behavior, we examined the relationship between latent representations and kinematics. Unlike the computer simulation where the ground truth was known, we did not know the exact mapping between population responses and kinematics. In addition, regarding their temporal relationship, we did not know whether two sequences were synchronously aligned, time-lagged or time-led.

We first assumed that high-dimensional chewing kinematics could be represented by a low-dimensional behavioral sequence. We applied the HACA method to perform temporal clustering for the kinematic variables. We selected the position and/or velocity kinematics from representative markers in the cranium and mandible coordinate systems during the rhythmic chew period. Temporal clustering results for each trial yielded a clear segmentation (four parts) within each gape cycle. Next, we aligned the latent state sequence with kinematic cluster sequences during rhythmic chewing (see figure 13 for illustrations, where distinct color coding represents different kinematic clusters). Comparing state sequences with jaw and tongue kinematic profiles revealed a temporal relationship—behavioral clusters correspond to four well-defined mastication cycles. To further quantify these relationships, we computed the bootstrapped NMI statistics between the latent state sequence with the clustered kinematic sequence during each trial. There was a wide range of mutual information among all trials (NMI range: 0.24–0.65). Nearly all trials (37/38 in Dataset 1; 34/34 in Dataset 2) showed significant NMI (Monte-Carlo p < 10⁻³).

Figure 13.

(A) and (B) Correspondence of inferred state and behavioral sequences in consecutive multiple gape cycles during rhythmic chewing. Top panel: Inferred latent state sequence. The vertical solid line indicates the timing of swallow. Middle and bottom panels: two selected kinematic variables (mandible vertical axis and tongue horizontal axis). Different colors or symbols represent kinematic clusters. Panels (A) and (B) are taken from two single feeding trials of hazelnut and almond(shell), respectively.

3.9. Predictive power of the model

We further investigated the predictive power of the HDP-HMM for the kinematic variable. We first validated the idea using previously described computer simulated data. We used 30 trials of each type for estimating the model and 15 trials of each type for testing. Upon the completion of model inference based on unsupervised learning, we used a ‘divide-and-conquer’ strategy to decode the four 1D kinematic variables (Methods). The median decoding error of 60 held-out trials for [x_t, y_t, ${\dot{x}}_t$, ${\dot{y}}_t$] are 0.092, 0.105, 0.060, 0.116 (in a.u.), respectively, accounting for <5% variance of individual kinematic variables. See figure 14(A) for a snapshot illustration.

Figure 14.

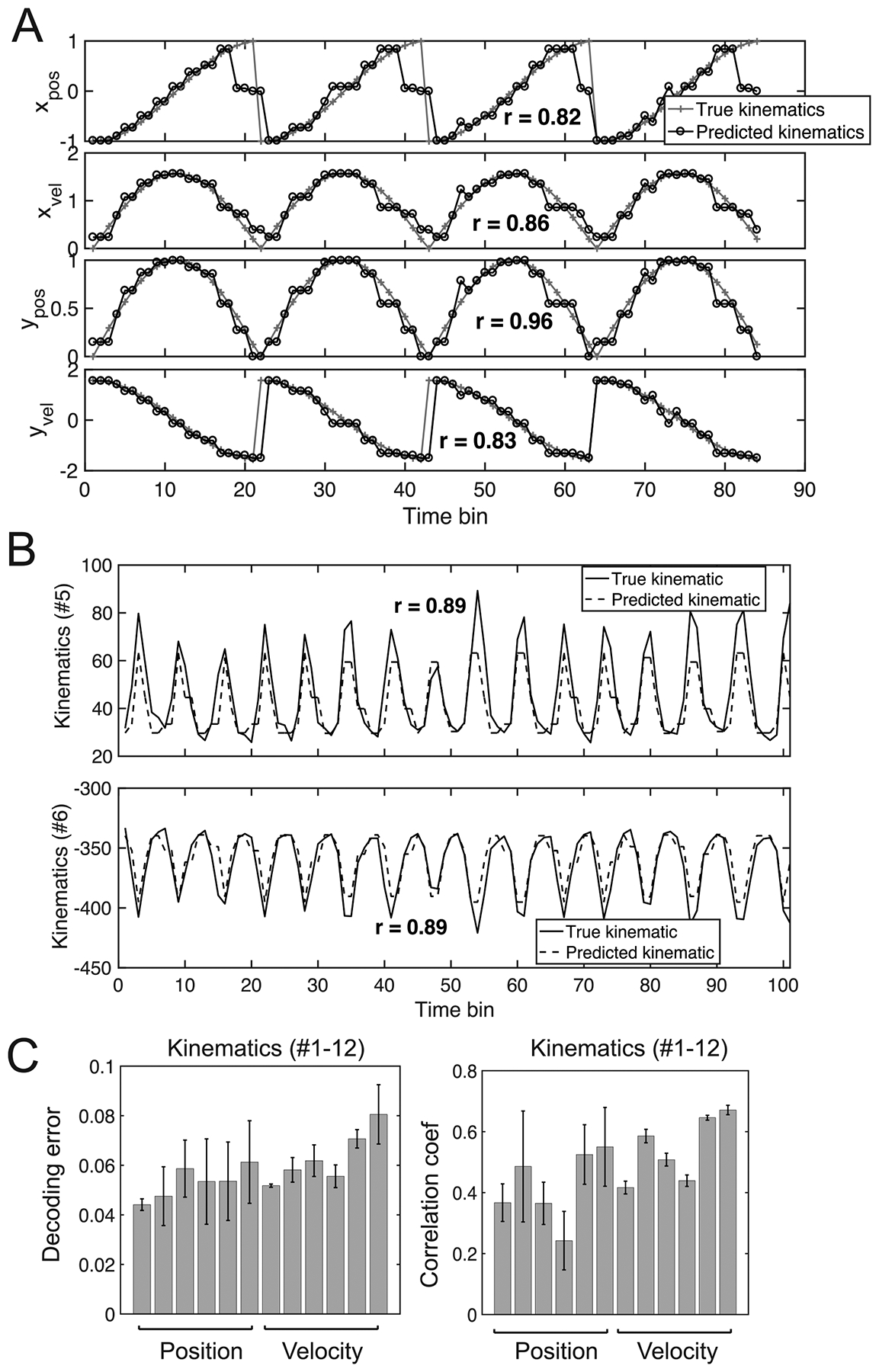
An illustration of population decoding analysis for movement kinematics. (A) Snapshots of predicted 4-dimensional kinematics variables [x_t, y_t, ${\dot{x}}_t$, ${\dot{y}}_t$] used in computer simulations. Four repeated trials with the same kinematics are shown in time. In each panel, the correlation coefficient r between the actual and predicted kinematics is shown. (B) Snapshots of predicted two selected position kinematics (#5 and #6) within a single trial (bin size: 50 ms, Monkey O, Dataset 1). (C) Assessment of normalized decoding error and correlation coefficients (mean ± SEM) for 12 kinematics (#1–6 position, #7–12 respective velocity), averaged across all trials and time.

Next, we tested the predictive power of the model on experimental data. In Dataset 1, we selected 12 kinematics variables (#1–6 position and #7–12 respective velocity) and ran the decoding analysis based on three-fold cross-validated assessment (figure 14(B)). For each decoding kinematics, we computed the normalized decoding error and correlation coefficients. Overall, the mean decoding accuracy varied between different kinematics variables across all trials (figure 14(C), correlation coefficients r = 0.41–0.75). For Dataset 2, the derived median decoding errors for #one–six position variables were 0.080, 0.098, 0.119, 0.094, 0.083, and 0.141, respectively.

Together, these decoding results suggest that (i) our proposed method can uncover latent neural population dynamics without the knowledge of kinematics or the relationship between kinematics and population spike activity; (ii) our proposed method can reveal subtle neural variability at the stage level of each chewing trial and at chewing phase transitions; and (iii) our proposed method can reveal an accurate mapping between latent states and complex chewing kinematics, and their relationship in time.

In order to confirm that the latent structure inferred from our method was meaningful, we also conducted additional analyses on the surrogate (or ‘shuffled’) dataset. Specifically, we first randomly shuffled the binned firing rates in both time and trial, and then repeated the decoding analysis. Our premise is that if there was no intrinsic structure in the neural data, the derived neural variability and decoding results would be poor as compared to those results inferred from the raw data. As a demonstration, we ran the analysis on the computer simulated data (where the ground truth was known). We found that the median decoding error for [x_t, y_t, ${\dot{x}}_t$, ${\dot{y}}_t$] greatly degraded (0.31, 0.27, 0.65, 0.35, respectively). A similar degraded trend was also found in the trial-type variability analysis.

3.10. Robustness of representation in dynamics and variability

Finally, we investigated whether our results were sensitive to the exact choice of neuronal population. In other words, how many neurons in a subset of the entire population were sufficient to capture the dynamics or variability of population responses during rhythmic chewing? We used Dataset 1 and uniformly sampled 50% and 70% units (corresponding to C = 70 and 98 units, respectively) from the whole population. We compared the median and CDF curves of divergence measure as well as the variability patterns (figures 15(A) and (B)). Although the selected number of units affected the inferred number of states m, the inferred patterns or structures were rather robust. Results on the CDF curve, stage-wise chewing variability and chewing phase transitions variability remained qualitatively similar for three distinct population sampling percentages. As seen in figure 15(A), the median statistics were significantly different (rank-sum test) between Stage 2 versus Stage 2 and State 3 versus Stage 2. Again, Stage 2 versus Stage 2 was chosen as the control because it’s the most stable stage during food trials. Overall, we observed a similar trend in the median statistics between different unit sample sizes (especially 70% versus 100%), but the exact significance statistics might change due to the sample size.

Figure 15.

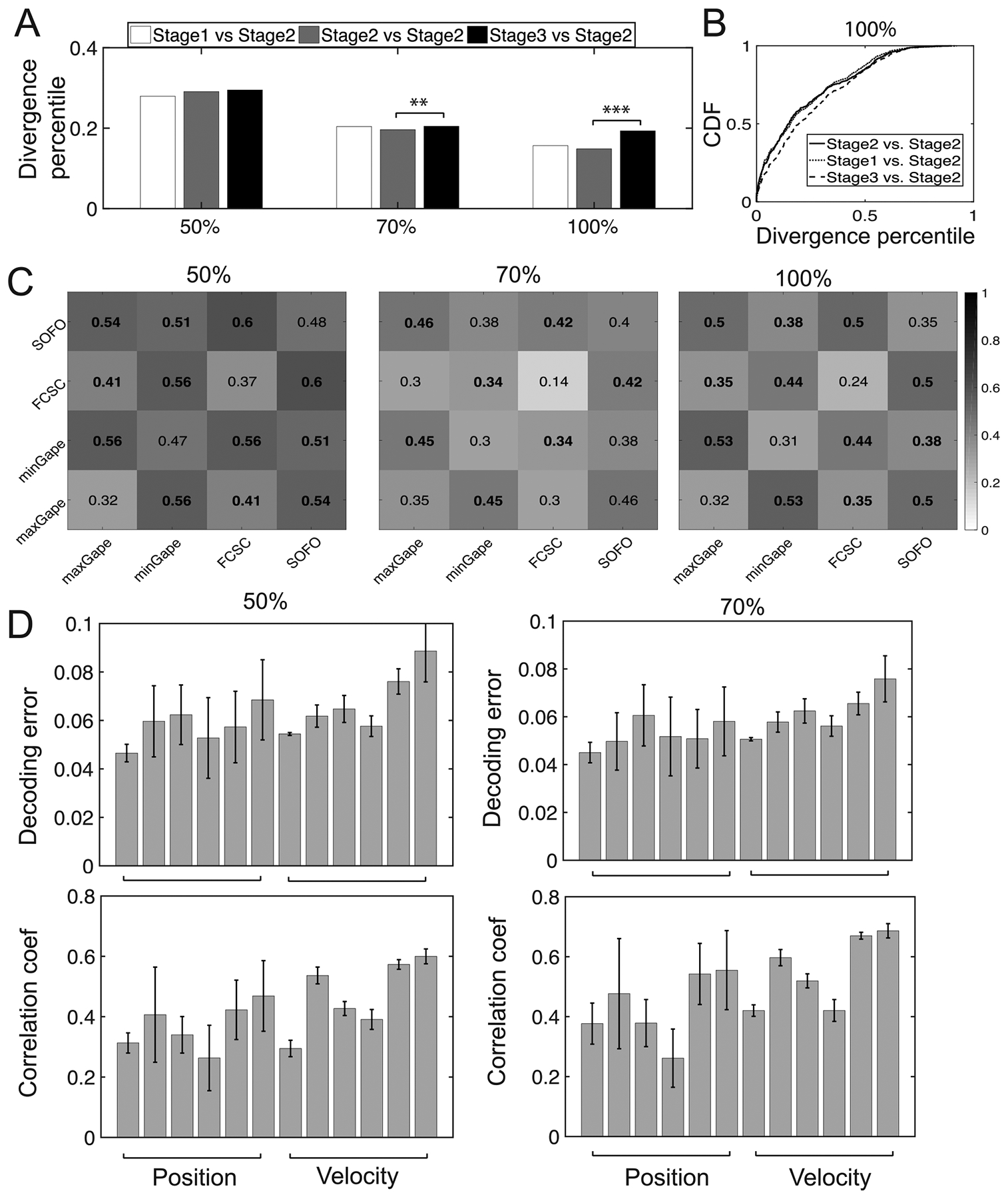
Result robustness with respect to cell sampling percentages 50%, 70% and 100% (Monkey O, Dataset 1). (A) Comparison of median statistics of divergence percentile (rank-sum test: ** p < 0.01, *** p < 0.001) at stage-wise chewing periods. (B) Comparison of their CDF curves for the 100% condition. Two-sample KS test: 2–2 versus 1–2, p = 0.03; 2–2 versus 3–2, p = 1.4 × 10⁻¹¹). (C) Comparison of four transitions between chewing phases derived from all food trials. Numbers indicate the median divergence percentile. Lower values in diagonal elements are common in three panels. Similar to figure 11(C), the values above the statistical significance threshold (with respect to off-diagonal divergence statistics) are marked in bold font. (C) Decoding error (similar to figure 14) based on subsampled cell populations.

Furthermore, we ran the decoding analysis based on the sub-sampled units (on Dataset 1). In comparing figures 15(D) with 14(C), we found that the decoding accuracy was stable with respect to the cell number, suggesting the robustness of representation in population codes.

3.11. Comparison with FA and PLDS

Compared to two tested continuous-valued latent variable models (FA and the PLDS), our proposed Bayesian-HMM method provides a complementary perspective for examining the motor cortical activity.

First, the latent trajectory derived from our method is a discrete sequence, whereas the (unscaled or scaled) latent factors in FA or the PLDS are continuous (figure 16(A)). In this case, we could derive a Euclidean distance-based dissimilarity measure based on the derived latent trajectories (assuming Gaussian distributed). When the correct latent model dimensionality m = 4 was used, the FA results were qualitatively similar to the ones derived from the HMM (figure 16(B)). However, the dissimilarity patterns derived from FA and the PLDS changed dramatically when a different model dimensionality was used (figure 16(C)). In contrast, our method was more robust with respect to the model dimensionality (figure 6(H)).

Figure 16.

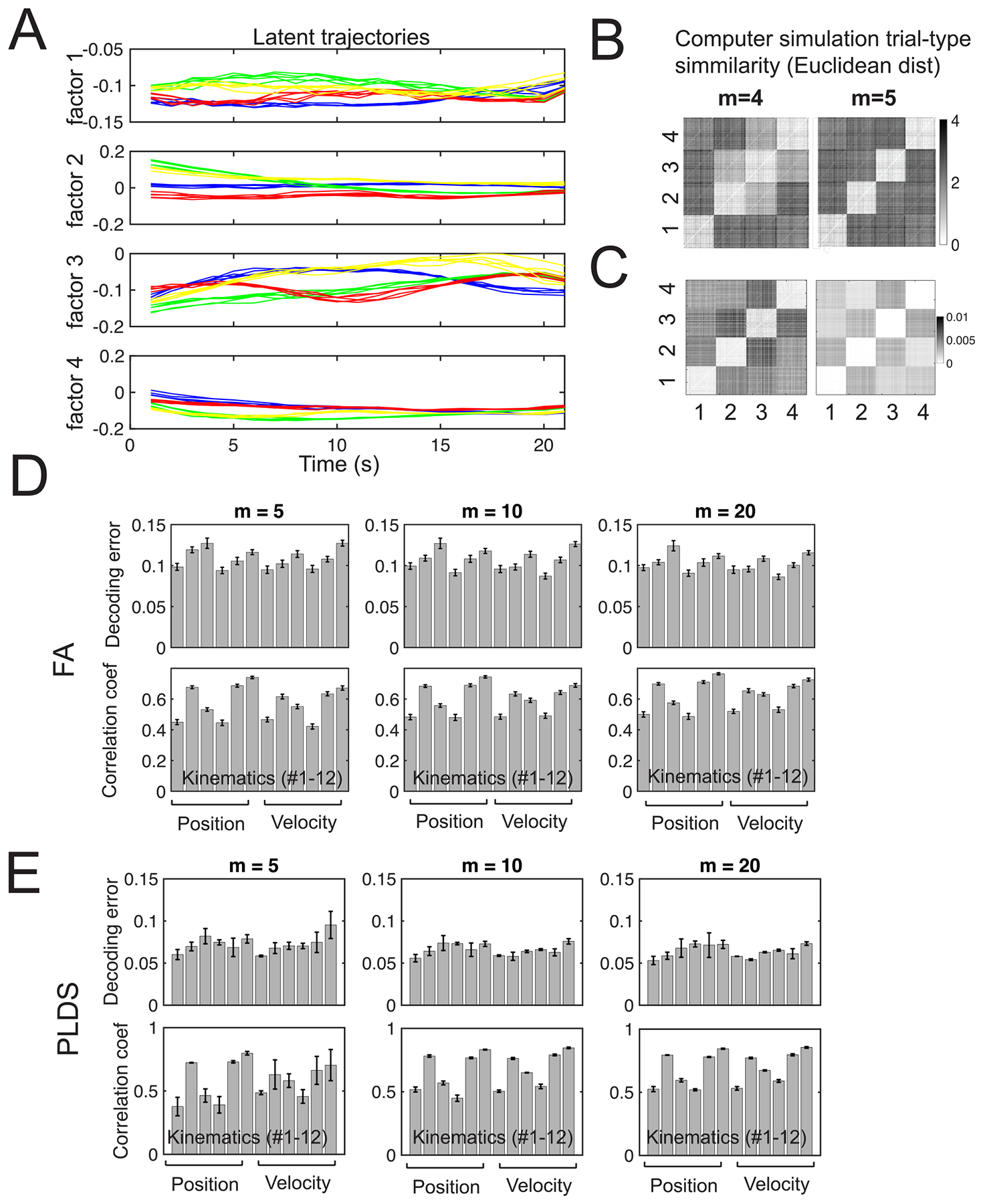
(A) Color-coded 1D latent trajectories of four scaled latent factors (i.e. continuous-state trajectories) derived from the PLDS (m = 4) for the computer simulated data. Curves with the same color represent the five trials selected from the same path type shown in figure 6. (B) and (C) Trial-by-trial dissimilarity measured by averaged Euclidean distance between latent factors for m = 4 and m = 5 based on the FA (B) and PLDS (C) models. (D) and (E) Decoding error and correlation coefficients derived from FA and PLDS based on three different sizes of latent state dimensionality (m = 5, 10, 20) for the experimental MIo data (Monkey O, Dataset 1). Compared to figure 14(C), the PLDS-based decoding had a comparable accuracy, and the FA-based decoding performance degraded. Note that increasing dimensionality of latent state m did not change the saturated decoding performance.

Second, although the HMM and PLDS are both dynamic and built upon the Poisson spiking assumption, only the HMM decoding analysis is based on the maximum likelihood (figure 14); whereas FA and the PLDS rely on regression analysis in decoding. Furthermore, FA ignores the temporal dynamics in the motor population codes. As shown in figure 16(D), the FA-based decoding performance degraded compared to the HMM-based performance (figure 14(C)). In contrast, the PLDS-based approach had comparable performance (figure 16(E)).

Third, to quantify the mutual information between kinematics and latent state sequences, our approach computes the mutual information between two sets of discrete random variables. In contrast, the FA or the PLDS approaches would need to compute the mutual information between two multidimensional continuous random variables (i.e. latent factors versus kinematics).

Fourth, unlike FA or the PLDS, our approach provides a unique way to examine the spatiotemporal mapping between state transition and motor behavior at a fine timescale, such as the gape transition analysis shown in figure 12.

Finally, we would like to point out that the dissimilarity can be computed directly on the raw spike count data using either Poisson (KL divergence) or Gaussian (Euclidean distance) assumption. In fact, the variability results derived from raw spike count data show qualitatively similar trends in our computer simulated data. However, model-based versus model-free methods may also yield different statistical significance results; we believe that the model-based characterization is more robust to noise and cell sample size. A systematic investigation and comparison of different methods will be explored elsewhere.

4. Discussion

A number of nonhuman primate studies have studied naturalistic feeding behaviors (Reed and Ross 2010, Iriarte-Diaz et al 2011, 2017, Nakamura et al 2017). However, very few studies have carried out systematic investigation on the physiology, dynamics, and variability of motor cortical activity during such feeding behavior.

In this paper, we characterized spiking dynamics in populations of neurons in the orofacial region of the primary motor cortex (MIo) during chewing using a novel unsupervised learning paradigm based on a latent variable model and Bayesian inference. The 2D jaw and tongue kinematic data were represented in reduced dimensionality using a hierarchical clustering method that recovered discrete kinematic states closely approximating the traditional four phase subdivision of the gape cycle (Bramble and Wake 1985, Hiiemae and Crompton 1985). These phases are delineated by kinematic events (changes in vertical movement velocity and direction) associated with significant changes in sensory feedback, so we expected that these transitions would be associated with changes in neural state in MIo.

During chewing sequences on a variety of foods, modulation in activity of many MIo neurons was reflected in changes in dynamic states across chewing sequence stages, between gape cycles, and with transitions in gape cycle phases. Our delineation of three chew sequence stages—Stage 1, early chews; Stage 2, intermediate chews (typically before the first swallow); and Stage 3, late chews (typically after the first swallow)—aimed to control for variation in chew sequence duration between trials, even on the same food. Our findings indicated that neural states were indeed more similar within stages than between them, and Stage 1 and Stage 3 were less similar to Stage 2 compared to within Stage-2 comparison. Note that Stage 1 includes the first chews on the food item, and Stage 3 typically includes the first chews after the first swallow, which we hypothesize are on a new part of the ingested food item that was secreted in the oral vestibule prior to the swallow, then recovered for a new chew sequence (figure 8). This pattern of dissimilarity between stages may be food-specific. As shown in figure 9, neural states during Stages 1 and 3 are similar during date chewing, and between Stage 1 and the start of Stage 3 during persimmon chewing. However, it is also clear that there can be substantial variation in neural states dissimilarity matrices between chewing sequences on the same food (persimmon example in figure 9). This suggests that MIo neural state activity varies in a sequence specific manner, possibly reflecting the moment-to-moment variation in food bolus properties and position. As expected, there were changes in neural states around transitions between gape cycle phases (figure 11). The largest differences were seen between maximum gape and minimum gape, then between FC-SC and SO-FO, times when the changes in sensory feedback and motor control goals differed. For example, the sensory information signaling maximum gape (spindles, joint, skin stretch receptors) is very different from that signaling minimum gape (periodontal afferents), whereas the kinematic control at maximum gape (start of jaw elevation against no food resistance) is different from that at minimum gape (generation of high bite forces between occluding teeth, which guide the kinematics).

4.1. Related work on neural population dynamics

Two different classes of methods have been used in analyzing neural population activity: supervised and unsupervised learning. The supervised learning approach assumes a neural encoding model across all neurons and fits the model parameters with observed spike data. The performance of the supervised learning approach depends on the fidelity of the assumed model and the amount of training data. Model misspecification and overfitting are the two most serious problems in population decoding analysis. In contrast, the philosophy of unsupervised learning is ‘structure first, content later’—namely, the inference approach makes no prior assumptions about population spike activity in relation to the kinematics or other aspects of behavior (Chen et al 2016, Chen and Wilson 2017); the inferred latent structure or neural representation is compared with the observed behavioral correlates in the post-hoc analysis.

To date, many latent variable models and unsupervised learning paradigms have been developed for uncovering neural population dynamics. The HMM, FA and PLDS are all examples of latent variable models. The latent variable approach can be viewed as a subclass of ‘neural trajectory’ methods that aim to uncover the low-dimensional neural trajectory. Methods are either based on trial averaging, such as PCA or other subspace methods (Churchland et al 2012, Ames et al 2014, Cunningham and Yu 2014), or based on single-trial dynamics, such as the mixture of trajectory models (Yu et al 2007), Gaussian process factor analysis (GPFA) (Yu et al 2009, Zhao and Park 2017), Gaussian process dynamical models (Lawrence 2004, 2005), latent factor analysis via dynamical systems (LFADS) (Sussillo et al 2016) and other generalized nonlinear latent variable models (Wu et al 2009, Lawhern et al 2010, Pandarinath et al 2015, Gao et al 2016, Michaels et al 2016, Wu et al 2017). For instance, these models and unsupervised learning methods have been used to analyze motor cortical data (Kao et al 2015, Aghagolzadeh and Truccolo 2016). In contrast to these continuous latent-variable models, the HMM and its variants belong to discrete latent-variable models, where the latent states are associated with distinct spatiotemporal temporal patterns (Kemere et al 2008, Chen et al 2014, Linderman et al 2016). Given the measured motor population spike activity, unsupervised decoding analysis is aimed to unfold the latent state trajectory that drives the motor population dynamics, and to further reveal the link between the inferred ‘neural trajectories’ and behavioral correlates.

Our proposed Bayesian HDP-HMM has several important features: (i) it is dynamic (whereas PCA and FA are static) and can automatically infer the state dimensionality m; (ii) it estimates not only the latent state sequences, but also the state tuning curve (Λ) for each neuron (whereas the PLDS or GPFA cannot). The knowledge of Λ allows us to capture the dissimilarity between state sequences (whereas other continuous latent variable dynamic models can only capture the similarity of latent trajectories in the abstract state space); and (iii) it allows us to examine the state representation occupancy in time and their neural representations with respect to chewing kinematics at a fine timescale.

In comparison with the continuous latent variable models, the inferred HDP-HMM model order m was sometimes comparable to the number of neurons C; however, the discrete state occupancy was not uniform. In terms of information coding efficiency, we could compute the Shannon entropy to characterize the ‘complexity’ of the state space. Therefore, the term of ‘dimensionality reduction’ has a broader meaning. In addition, dimensionality reduction also implies data smoothing and denoising. Characterizing the neural variability in the reduced model space instead of the raw data space would allow us to account for temporal dependency and noise in the raw spike observations.

4.2. Neural response variability

Variability, or variance is a term specifically reserved for a random variable or noise. Neural variability is an important phenomenon that is observed in a wide range of neuroscience experiments, occurring at both single cell and population levels (including neuroimaging) (Stein et al 2005, Czanner et al 2008, Menzer et al 2010, Wu et al 2011). Understanding the variability of neural responses is key to unveil the circuit mechanisms or neural coding principles operating in a model system. The unexplained neural variability can be derived from multiple extrinsic and/or intrinsic sources, such as behaviors, and uncontrolled internal variables mediating attention, degree of arousal, expectation or context (Churchland et al 2010, Cohen and Kohn 2011, Masquelier 2013, Ecker et al 2014, Churchland 2015).

Our work can be viewed as the first effort of modeling rhythmic chewing using a discrete-state dynamical system. In the first step, we used statistical models to infer latent state sequences or trajectories. In the second step, we assessed the quantitative relationship between the inferred state sequences and behavioral measures. The abstract latent states are associated with specific neural spatiotemporal patterns during chewing. Therefore, characterizing the variability of population patterns is equivalent to characterizing the variability or dissimilarity between neural state sequences. The pairwise similarity of two arbitrary states is computed by the inferred state-dependent firing patterns. Our proposed paradigm offers to quantify the population response variability across multiple timescales. In our experiments, we documented various degrees of neural variability across stages in chewing sequences and across phase transitions in individual gape cycles. In addition, we observed inter-subject variability across animals as well as inter-recording variability within the same animal. Furthermore, our results were insensitive to the number of inferred states, or the subset of neurons selected in the population. Therefore, our approach provides a robust characterization of neural variability at the population level for rhythmic chewing and other motor behaviors (such as locomotion).

Dimensionality reduction methods have been applied to understand how the high-dimensional neural population activity gives rise to sensory or motor functions of the brain. Regarding the scaling properties of dimensionality reduction, an important question is whether neural representations would change if the number of neurons or the recording time is substantially modified. Some theoretical and experimental studies have recently become available (Gao and Ganguli 2015, Williamson et al 2016, Gallego et al 2017). Our analyses suggest that random subsets of neural population produce qualitatively similar results (figure 15). In addition, changes in recording duration may affect the inferred number of latent states; yet our results are also robust with respect to the number of latent states (e.g. figures 6(H) and 7(C)).

4.3. Common structures underlying chewing behaviors

In comparison to the reaching-and-grasping movement, rhythmic chewing behaviors could be also complex and highly variable (e.g. chewing duration, left/right chewing, swallowing, etc), even for the same food type. However, the complexity may not be easily observed from the measured kinematics. Despite the high degree of neural variability within or between food trials, there is also consistent population firing patterns or abstract state representation at a fine timescale. While assessing the state occupancy representing chewing gape phase transitions, we have seen similar state representations within specific food trials as across all trials (figures 11(A) and (B)). In addition, the dominant latent states have distinct occupancy in each chewing trial. More importantly, these dominant states contributed differently to encoding the measured chewing kinematics (figure 12). Those patterns are also relatively consistent. Therefore, our proposed HMM approach is capable of characterizing the subtle differences in chewing kinematics by different neural state representations. In addition, although we only investigated on the relationship between population codes and chewing kinematics, it would be informative to study the neural correlate with respect to chewing kinetics (such as force and torque).

4.4. Implications

The role of MIo in control of naturalistic feeding behavior is poorly understood, in part because of the difficulty of testing hypotheses about relationships between synchronous, oscillatory changes in neural activity, muscle activity and jaw and tongue kinematics in multiple dimensions. Our comparisons of neural state sequences with chewing behavior at multiple time scales suggests that it is possible to relate MIo population level activity to chewing kinematics using a latent state HMM approach and obtain results that are explicable with reference to current models of sensory feedback and motor control during feeding in nonhuman primates. The high degree of variation between chewing sequences on the same food suggests that the MIo cortex plays an important role in ongoing monitoring and modulating feeding behavior. The variation in neural states between gape cycle phases suggests that this control and monitoring occurs at the time scale of the individual chew. The importance of fine control of bite force and jaw displacement during feeding should not be underestimated: because the adult teeth are not replaced during life, reduction of rates of tooth wear and avoidance of tooth breakage are important control parameters.