Evaluating the Utility of Coarsened Exact Matching for Pharmacoepidemiology Using Real and Simulated Claims Data

Abstract

Coarsened exact matching (CEM) is a matching method proposed as an alternative to other techniques commonly used to control confounding. We compared CEM with 3 techniques that have been used in pharmacoepidemiology: propensity score matching, Mahalanobis distance matching, and fine stratification by propensity score (FS). We evaluated confounding control and effect-estimate precision using insurance claims data from the Pharmaceutical Assistance Contract for the Elderly (1999–2002) and Medicaid Analytic eXtract (2000–2007) databases (United States) and from simulated claims-based cohorts. CEM generally achieved the best covariate balance. However, it often led to high bias and low precision of the risk ratio due to extreme losses in study size and numbers of outcomes (i.e., sparse data bias)—especially with larger covariate sets. FS usually was optimal with respect to bias and precision and always created good covariate balance. Propensity score matching usually performed almost as well as FS, especially with higher index exposure prevalence. The performance of Mahalanobis distance matching was relatively poor. These findings suggest that CEM, although it achieves good covariate balance, might not be optimal for large claims-database studies with rich covariate information; it might be ideal if only a few (<10) strong confounders must be controlled.

Abbreviations

ATT

average treatment effect among the treated

CEM

coarsened exact matching

FS

fine stratification by propensity score

IEP

index exposure prevalence

MDM

Mahalanobis distance matching

NSAID

nonsteroidal antiinflammatory drug

PSM

propensity score matching

rMSE

square root of mean squared error

“Coarsened exact matching” (CEM) is a design strategy that has been shown to produce good covariate balance between exposure groups and, thus, to reduce the impact of confounding in observational causal inference (1, 2). The strategy is simply matching simultaneously by a set of potential confounders that have been “coarsened,” reducing the number of potential matching values for a given covariate to increase the number of matches achieved.

It has been demonstrated that CEM may outperform certain adjustment techniques that are common in pharmacoepidemiology with respect to covariate balance and effect bias (3, 4). For example, King et al. (3, 4) demonstrated that, unlike CEM, propensity score matching (PSM) can sometimes increase covariate imbalance (although such increases in imbalance due to PSM appear unlikely to manifest in a typical pharmacoepidemiologic study (5)). Because CEM has been implemented infrequently within the context of pharmacoepidemiologic analyses of claims data, and because CEM has properties that make it a desirable choice for causal inference (1, 2), the utility of CEM for such analyses should be explored.

Here, we compare CEM with PSM, Mahalanobis distance matching (MDM), and fine stratification by propensity score (FS) with respect to covariate balance, confounding control, and effect-estimate precision, using real and simulated claims-based cohorts that represent typical pharmacoepidemiologic claims scenarios (i.e., scenarios involving many potential confounders of an association between a drug and a health outcome (6–8)). Throughout, we estimate the exposure effect among the index-exposed (i.e., the average treatment effect among the treated (ATT)), although the analysis weights described below for CEM and FS could be tuned to target other estimands.

PSM was selected because of its popularity in pharmacoepidemiology. MDM was selected because it is a scalar-based matching technique that, like CEM (and unlike PSM), operates in the original covariate space. FS was selected because, similar to CEM, it relies on stratification to derive analysis weights and can achieve good covariate balance, retaining more study subjects than the matching techniques. Like CEM, these 3 techniques are semiparametric design techniques, which might be less susceptible to outcome model misspecification, compared with a fully parametric technique (3, 9). To our knowledge, these techniques have not been compared, simultaneously, within the context of claims-based analyses, although some separate comparisons in various settings have been performed (3–5, 10–14).

METHODS

Coarsened exact matching

Let X be the vector of observed covariates. Let “covariate balance” indicate equivalency of the empirical distributions of the covariates in X between exposure groups (1). CEM entails the following steps.

1. Coarsen the covariates in X, ensuring that units with the same value for the coarsened covariate are substantively indistinguishable (e.g., categorizing continuous body mass index into clinically relevant categories such that units in the same category are practically equivalent with respect to body mass index). Empirical “autocoarsening” has been proposed when substantive knowledge is scarce (1, 15).

2. Implement exact matching with the coarsened data—all index-exposed and reference-exposed units (i.e., units with and without the exposure of interest, respectively) that appear in the same bin of the multiway array created by the coarsening strategy are considered “exactly matched.” Although it is a matching procedure, CEM might equally be considered to be a multidimensional stratification approach.

3. Eliminate units that appear in bins that do not contain units of opposite exposure status (i.e., unmatched units). Such bins represent regions of nonpositivity that, if not excluded from the analysis, could bias exposure effect estimates (16, 17).

4. Estimate the ATT in the matched data set. In each matched set, index-exposed units receive a weight of 1, and reference-exposed units are weighted in proportion to the distribution of index-exposed units in the matched set (i.e., because unequal numbers of index-exposed and reference-exposed units may appear across bins—thus, the empirical distribution of X might not be equivalent between the matched exposure groups) (1, 2, 10). The weight applied to each reference-exposed unit is (1, 2):

   

   Of note, the risk ratio form of the ATT weighted via this scheme is equivalent to the common measure of association, the standardized morbidity ratio (18).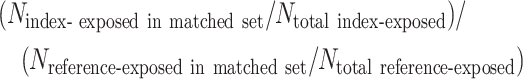

With CEM, balance for each covariate is ensured—limited only by the coarseness of the categorization—and is never worse than in the original data set. A coarsening strategy resulting in finer strata will achieve better balance for that covariate (1–4). For scalar-based matching techniques, such as PSM, covariate balance for each variable is not guaranteed. Balance can be checked after matching, at which point it might be decided that the process should be performed again (e.g., using a different caliper criterion). Moreover, CEM guarantees balance for higher-order terms (e.g., multiway interactions of covariates) (1). In contrast, for example, no such guarantee is inherent in a propensity score methodology—even in the rare situation in which such terms are included in the propensity score model (1, 19, 20).

Comparison techniques

Here we describe PSM, MDM, and FS only briefly, because these techniques are not new to pharmacoepidemiology.

By PSM, we mean the specific case of 1:1 PSM without replacement (5, 21, 22), which is popular in biomedical fields such as pharmacoepidemiology (23–28). The appeal of PSM might be due to the ability to match on a scalar summary of X, which could involve many covariates in a typical claims study, and to other benefits that have been outlined extensively (5–8, 26–34). MDM operates similarly to PSM, except that it is based on the Mahalanobis distance, which, unlike the distance between propensity scores, is measured in the actual covariate space—a characteristic shared by CEM (1–5).

FS is simply stratification by propensity score using a large number of propensity score strata (10, 11, 35, 36). The same unit-level weights described for CEM might be applied when estimating the ATT. FS overcomes a potential drawback of matching: the exclusion of unmatched units that might have been chosen as matches. Losing these units decreases precision of the effect estimate (10). With FS, the only exclusions are from the nonoverlapping tails of the propensity score distribution; within the range of overlap, every unit falls into a propensity score stratum and is counted in the analysis.

Empirical examples

We used a cohort of 49,653 low-income Medicare beneficiaries, at least 65 years of age, who were enrolled in the Pharmaceutical Assistance Contract for the Elderly database in New Jersey over the years 1999–2002 and who initiated treatment with nonselective nonsteroidal antiinflammatory drugs (NSAID) or selective cyclooxygenase-2 inhibitors (“NSAID cohort”) (37, 38). Approximately 35% of patients were nonselective NSAID (index exposure) initiators. The outcome of interest was occurrence of gastrointestinal complications (552 cases). Three covariate sets were used for the NSAID cohort analyses. The “small” covariate set comprised 19 continuous and binary covariates that were selected based on clinical importance. The second and third covariate sets (“standard” and “large,” respectively) included binary covariates (representing concomitant medications, comorbidities, and other medical encounters) selected by a high-dimensional propensity-score algorithm (39), in addition to the 19 predetermined covariates: The 50 covariates with the highest bias-based ranks were included in the standard covariate set, and the 100 covariates with the highest bias-based ranks were included in the large covariate set. The distribution of the small set of prematched covariates in the NSAID cohort is shown in Web Table 1 (available at https://academic.oup.com/aje).

We used another cohort with information on 886,996 completed pregnancies that was generated from the Medicaid Analytic eXtract over the years 2000–2007—the mothers in this cohort either did or did not use statins during the first trimester of pregnancy (“statin cohort”) (10, 40, 41). Approximately 0.13% of mothers in this cohort filled a statin (index exposure) prescription during the first trimester of pregnancy. The outcome of interest was congenital malformation (31,489 cases). The statin cohort included 20 categorical covariates, selected based on clinical importance. The distribution of prematched covariates in the statin cohort is shown in Web Table 2. This cohort was selected because of its unique rare exposure and because the importance of propensity score–based methods for identifying comparable exposure groups in pharmacoepidemiology has been demonstrated in this cohort in previous work (10).

For each data set, we applied all 4 methods described above to account for confounding. For CEM, we applied the R (R Foundation for Statistical Computing, Vienna, Austria) CEM package’s default autocoarsening strategy, which attempts to divide the range of values for the numerical covariates in X into the number of bins required to approximate a normal density (Sturges rule) (1, 15). We chose the autocoarsening strategy to emulate the scenario in which substantive knowledge regarding the best coarsening strategy for the few continuous covariates in a typical claims data set is sparse. For the NSAID-cohort PSM and FS analyses, all continuous variables were categorized to relax linearity assumptions for the propensity score model. For PSM and MDM, we used a nearest-neighbor matching algorithm. To emulate previous analyses of these data, we applied a 0.025 absolute propensity-score distance caliper for PSM but allowed all exposed units to be matched for MDM (5). We performed MDM for all 3 NSAID cohort–based data sets for the sake of example, even though in practice, MDM is not warranted for high-dimensional scenarios, in which it is slow to implement and suboptimal with respect to covariate balance (4, 5, 42–44). Thus, we expected to observe worse covariate balance from MDM in the larger NSAID cohort–based analyses. For FS, we trimmed regions of nonoverlap between index-exposed and reference-exposed propensity score distributions and generated 50 strata based on quantiles of the index-exposed propensity score distribution.

We measured covariate balance in the resulting analytical data sets using the Mahalanobis balance metric, which has been used in previous methodological assessments in pharmacoepidemiology (5, 45). The Mahalanobis balance is calculated as the Mahalanobis distance between the vectors of covariate means in the 2 exposure groups. Higher Mahalanobis balance values indicate worse covariate balance.

We then estimated risk ratios corresponding to the ATT and corresponding 95% Wald confidence intervals generated from log-binomial regression models. The outcomes of interest were occurrence of gastrointestinal complications and congenital malformation for the NSAID cohort and statin cohort, respectively.

For all CEM and FS scenarios, units were weighted using the scheme described above before calculating the Mahalanobis balance, risk ratio, and corresponding standard error.

Description of simulated data sets

A series of plasmode-simulated data sets were generated using the NSAID cohort. In plasmode simulation, the true effect of exposure on outcome is set to a known value, using the estimated associations between covariates and outcome from the original data to inform the outcome simulation model (46–48). This technique is particularly apt for methodologic research in claims data because it maintains observed complex data structures.

Simulation scenarios were constructed by simulating outcome (gastrointestinal complications, 20% event rate in all scenarios), using all of the covariates included in a given scenario to predict outcome. The true risk ratio for each scenario was set at 1. Each scenario comprised 1,000 simulated cohorts of 25,000 units and represented a variation of index exposure prevalence (IEP; 5%, 10%, 20%, 30%, and 40%) and covariate set size (“very small,” “small,” “standard,” and “large”). The very small covariate set comprised the 8 predetermined covariates that were expected to be most associated with gastrointestinal complications (Web Table 1), and the small, standard, and large covariate sets were the same as those used in the analysis of the real NSAID cohort. Two additional small covariate scenarios included a product term representing the interaction between continuous age and continuous Charlson Comorbidity Index score (49) in the outcome generation model. In one scenario, the coefficient on the product term maintained its original estimated value from the real data (“default”). In the other scenario, the strength of the product term was increased by 200% (“exaggerated”). For both product-term scenarios, IEP was set at 20%. We generated product-term scenarios because, unlike the other methods, CEM guarantees balance on such terms (within the limits of the coarsening strategy) (1, 43). We summarize our simulation scenarios in Web Table 3.

Analysis of simulated data sets

We applied the same methods used for the analysis of the real data sets. For the scenarios that included a product term, we performed CEM using a manual coarsening strategy for the age and Charlson comorbidity score variables to ensure that any lack of balance on those variables was not due to use of inappropriate coarsening boundaries. Specifically, we coarsened the age variable into groups of 5 years, and we coarsened the Charlson comorbidity score variable into the following groups: 0, 1, 2, 3, ≥4 (both categorizations were used in previous analyses of these data (5)). We performed MDM only for the very small and small covariate set scenarios, because MDM is not warranted for high-dimensional scenarios.

We compared the following metrics among the methods (45, 50): 1) average proportional decrease in Mahalanobis balance (compared with starting Mahalanobis balance); 2) bias = [average adjusted ln(risk ratio) value] – [true ln(risk ratio)]; 3) variance of the adjusted ln(risk ratio) values; and 4) square root of mean squared error (rMSE) = √[bias² + variance].

RESULTS

Analysis of real data sets

We present the results of the analysis of real data sets in Table 1. CEM always produced essentially perfect covariate balance (Mahalanobis balance values never greater than 0.020), although PSM and FS still demonstrated notable improvement in covariate balance, compared with crude balance. MDM was worst with respect to covariate balance in each NSAID cohort analysis, with Mahalanobis balance values increasing from 0.207 to 0.681 as covariate set size increased. For the statin cohort analysis, MDM performed better with respect to covariate balance compared with PSM and FS (Mahalanobis balance values: 0.244, 1.632, 0.586, respectively).

Table 1.

Results of Analysis of Real Data Sets, Pharmaceutical Assistance Contract for the Elderly Data Set (Nonsteroidal Antiinflammatory Drug Cohort, 1999–2002) and Medicaid Analytic eXtract Data Set (Statin Cohort, 2000–2007), United States

Original Data Set	No. of Units Analyzed	No. of Outcomes Analyzed	RR	95% CI	95% CI Width a	MB
NSAID, small
Crude	49,653	552	0.92			0.558
CEM	16,139	106	1.68	1.09, 2.58	2.36	0.017
PSM	34,150	355	1.05	0.86, 1.29	1.51	0.089
MDM	35,222	361	1.05	0.86, 1.29	1.51	0.207
FS	49,634	552	1.08	0.90, 1.31	1.45	0.026
NSAID, standard
Crude	49,653	552	0.92			0.641
CEM	3,226	10	2.55	0.64, 10.09	15.73	0.014
PSM	33,368	339	1.12	0.90, 1.38	1.53	0.087
MDM	35,222	318	1.39	1.11, 1.74	1.56	0.541
FS	49,626	552	1.12	0.93, 1.36	1.47	0.051
NSAID, large
Crude	49,653	552	0.92			0.654
CEM	1,763	6	1.71	0.31, 9.48	30.58	0.020
PSM	33,174	340	1.09	0.88, 1.34	1.53	0.089
MDM	35,222	309	1.49	1.19, 1.87	1.57	0.681
FS	49,626	552	1.12	0.92, 1.37	1.48	0.057
Statin
Crude	886,996	31,489	1.79			5.127
CEM	11,321	307	1.13	0.54, 2.36	4.35	0.000
PSM	2,302	144	1.03	0.75, 1.41	1.88	1.632
MDM	2,304	147	0.99	0.72, 1.35	1.87	0.244
FS	809,732	29,072	1.03	0.82, 1.31	1.60	0.586

Abbreviations: CEM, coarsened exact matching; CI, confidence interval; FS, fine stratification by propensity score; MB, Mahalanobis balance; MDM, Mahalanobis distance matching; NSAID, nonsteroidal antiinflammatory drug; PSM, propensity score matching; RR, risk ratio.

^a The 95% CI width was calculated by dividing the upper 95% CI endpoint by the lower 95% CI endpoint (using all available digits).

CEM always produced the least precise effect estimate (highest 95% confidence interval widths). Conversely, FS always was optimal with respect to precision (lowest 95% confidence interval widths). PSM and MDM produced effect estimates with similar levels of precision.

Analysis of simulated data sets

Noninteraction scenarios.

CEM and FS generally maintained the highest average proportional decrease in Mahalanobis balance among the 4 methods (Figure 1). CEM performed worse than FS only with respect to covariate balance improvement in the 5% and 10% index-exposure-prevalence standard (Figure 1C) and large (Figure 1D) covariate set scenarios. Generally, PSM performed worst with respect to covariate balance improvement, especially in the lowest IEP scenarios. For the very small covariate set scenarios (Figure 1A), MDM performed as well as CEM, except in the 40% IEP scenario. For the small covariate set scenarios (Figure 1B), MDM generally performed worst among the methods with respect to balance improvement. For both the very small and small scenarios, MDM produced a consistently decreasing trend in covariate balance improvement with increasing IEP. Finally, in general, covariate balance improvement for all 4 methods became worse, for a given IEP, as covariate set size increased.

Figure 1.

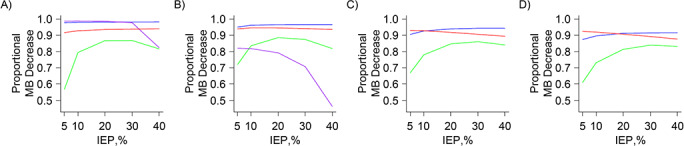
Results of plasmode analysis, noninteraction scenarios—average proportional decrease in Mahalanobis balance. A) Very small covariate set scenarios. B) Small covariate set scenarios. C) Standard covariate set scenarios. D) Large covariate set scenarios. Blue: coarsened exact matching trends; green: propensity score matching trends; purple: Mahalanobis distance matching trends; and red: fine-stratification-by-propensity-score trends. IEP, index exposure prevalence; MB, Mahalanobis balance.

Perhaps the key finding is that CEM generally produced the highest rMSE among the 4 methods, with the highest values seen in the standard (Figure 2C) and large (Figure 2D) covariate set scenarios. The exceptions were the very small covariate set scenarios (Figure 2A), in which CEM performed as well as the other 3 methods. In the small covariate set scenarios (Figure 2B), the rMSE from CEM was highest with 5% IEP and generally declined as IEP increased. For PSM, MDM, and FS, the rMSE generally decreased as IEP increased (Figure 3). For a given IEP, there was a slight upward trend in rMSE as covariate set size increased for these 3 methods. In most scenarios, FS produced the lowest rMSE. PSM and FS always produced similar rMSE values for the higher IEP scenarios, but FS always produced lower rMSE values, compared with PSM, in the lower IEP scenarios. For the very small covariate set scenarios (Figure 3A), MDM performed as well as PSM, and for the small covariate set scenarios (Figure 3B), MDM always produced the highest rMSE.

Figure 2.

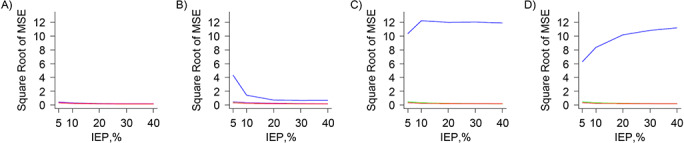
Results of plasmode analysis, noninteraction scenarios—square root of mean squared error (MSE), including coarsened exact matching results. A) Very small covariate set scenarios. B) Small covariate set scenarios. C) Standard covariate set scenarios. D) Large covariate set scenarios. Blue: coarsened exact matching trends; green: propensity score matching trends; purple: Mahalanobis distance matching trends; and red: fine-stratification-by-propensity-score trends. IEP, index exposure prevalence.

Figure 3.

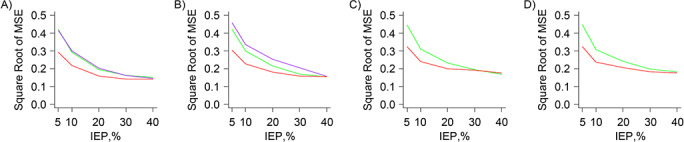
Results of plasmode analysis, noninteraction scenarios—square root of mean squared error (MSE), excluding coarsened exact matching results. A) Very small covariate set scenarios. B) Small covariate set scenarios. C) Standard covariate set scenarios. D) Large covariate set scenarios. Green: propensity score matching trends; purple: Mahalanobis distance matching trends; and red: fine-stratification-by-propensity-score trends. IEP, index exposure prevalence.

It was clear that variance drove the high rMSE values for CEM, because the CEM variance trends (Web Figure 1) were similar to the CEM rMSE trends (Figure 2). The strong influence of variance on the rMSE trends was also seen for PSM, FS, and MDM, among which the FS variance trends were lowest (Web Figure 2). The CEM bias trends generally were much higher than the PSM, FS, and MDM bias trends (Web Figure 3), with the exception of the very small covariate set scenarios (Web Figure 3A), in which CEM performed as well as the other 3 methods. The latter 3 bias trends were relatively similar across all scenarios, with PSM and FS yielding the lowest bias values overall (Web Figure 4).

Interaction scenarios.

The trends among all metrics for the default and exaggerated product-term scenarios (Table 2) were similar between the 2 scenarios and compared with the trends seen for the noninteraction scenarios.

Table 2.

Simulation Metrics for Plasmode Analysis Results^a, Small Covariate Set, 20% Index-Exposure-Prevalence Interaction Scenarios

Scenario b	Bias	Variance	Square Root of MSE	AMB
Defaultc
Crude	−0.103
CEM	0.327	0.226	0.577	0.967
PSM	0.067	0.040	0.210	0.886
MDM	0.131	0.041	0.242	0.792
FS	0.070	0.027	0.178	0.946
Exaggeratedc
Crude	−0.091
CEM	0.341	0.220	0.580	0.967
PSM	0.079	0.040	0.214	0.886
MDM	0.143	0.038	0.242	0.792
FS	0.080	0.023	0.172	0.946

Abbreviations: AMB, average proportional decrease in Mahalanobis balance; CEM, coarsened exact matching; FS, fine stratification by propensity score; MDM, Mahalanobis distance matching; MSE, mean squared error; PSM, propensity score matching.

^a Using a data set based on data from the Pharmaceutical Assistance Contract for the Elderly (nonsteroidal antiinflammatory drug cohort), United States, 1999–2002.

^b The product term represented the interaction between age and score on the Charlson Comorbidity Index.

^c The “default” scenario maintained the original product term and the “exaggerated” scenario was based on a product term that was 200% greater than the default product term.

We demonstrate the extent to which CEM improved covariate balance between the index-exposed and reference-exposed groups within the context of the interaction between age and Charlson comorbidity score in Table 3. This table shows the absolute differences between the exposure groups with respect to the average of the average age (or weighted average age for CEM and FS) within each coarsened category of Charlson comorbidity score, and vice versa, across plasmode simulations (default product-term scenario only). CEM yielded the lowest difference values among the 4 methods and, unlike the other 3 methods, never produced a difference value that was higher than the corresponding difference value in the original simulated cohort. Thus, as expected, CEM led to much better covariate balance in the product term compared with the other 3 methods.

Table 3.

Plasmode Analysis Results^a, Small Covariate Set, 20% Index-Exposure-Prevalence Interaction Scenarios, Balance Improvement Within the Context of the Interaction Between Age and Charlson Comorbidity Score^b

Difference in Average	Original	CEM c	PSM	MDM	FS c
Average age, years
Within score 0	2.09	0.05	0.38	0.47	0.28
Within score 1	2.03	0.11	0.25	0.42	0.15
Within score 2	1.66	0.11	0.06	0.45	0.14
Within score 3	1.93	0.01	0.16	0.94	0.07
Within score ≥4	1.43	0.02	0.25	0.99	0.31
Average score
Within age <70	0.16	0.00	0.06	0.28	0.04
Within age 70–74	0.23	0.00	0.07	0.22	0.06
Within age 75–79	0.15	0.00	0.01	0.15	0.01
Within age 80–84	0.20	0.01	0.05	0.01	0.05
Within age 85–89	0.06	0.01	0.12	0.15	0.12
Within age 90–94	0.01	0.01	0.12	0.10	0.12
Within age ≥95	0.18	0.00	0.00	0.04	0.00

Abbreviations: CEM, coarsened exact matching; FS, Fine stratification by propensity score; MDM, Mahalanobis distance matching; PSM, propensity score matching.

^a The values in this table are absolute differences between index-exposed and reference-exposed groups with respect to the average of the average age within each coarsened category of score on the Charlson Comorbidity Index, and vice versa, across the plasmode simulations; default product-term scenario only.

^b Using a data set based on data from the Pharmaceutical Assistance Contract for the Elderly (nonsteroidal antiinflammatory drug cohort), United States, 1999–2002.

^c The average age and average score values were weighted (at the unit level) for the CEM and FS scenarios.

DISCUSSION

Overall, the analyses of real and simulated data sets led to the same conclusions. CEM generally was optimal with respect to covariate balance and FS generally was optimal with respect to bias and precision (and still maintained excellent covariate balance). PSM tended to perform almost as well as FS with respect to all simulation metrics, especially for higher exposure prevalence scenarios. The performance of MDM generally never surpassed that of FS and PSM, with the exception of some of the very small simulation covariate set scenarios, for which MDM performed almost as well as CEM with respect to covariate balance and almost as well as PSM with respect to all other simulation metrics.

The optimal performance of CEM with respect to covariate balance was effectively guaranteed by the high number of binary covariates in our data—here, CEM amounted to exact matching (1–4, 12). The high performance of FS with respect to covariate balance was also not surprising. Because 50 strata were used, the maximum distance between index-exposed and reference-exposed units within a given stratum usually was very low—even lower than the PSM absolute propensity-score distance caliper of 0.025. Therefore, the low “implied calipers” associated with FS corresponded to high covariate balance overall (5). Moreover, because it already has been shown that FS tends to outperform PSM with rare IEP, the differences between FS and PSM with respect to covariate balance improvement in the lowest IEP scenarios were not surprising (10). The fact that all 4 methods generally performed worse with respect to covariate balance improvement, for a given IEP, as covariate set size increased, is attributable to the difficulties of achieving covariate balance in higher dimensions (4, 5).

In the analysis of simulated data sets, the very high rMSE values associated with CEM were due to the extreme loss of study size, and the corresponding decrease in the number of outcomes, that occurred during creation of the matched data sets. This extreme loss of study size might explain the discrepancy between the CEM average proportional decrease in Mahalanobis balance trends and the CEM bias trends, which would be expected to coincide (i.e., improvement in covariate balance for confounders should be complemented by decreased bias in the effect estimate). In other words, the decrease in effective study size and number of outcomes across simulations was so consequential that the resulting sparse data led to elevated bias trends (51). This extreme loss of study size was also clear in the analysis of the real NSAID cohort: In the small covariate set scenario, the matched data set produced by CEM comprised 16,139 units and 106 outcomes, representing a decrease in study size and number of outcomes of approximately 70% and 80%, respectively (Table 1). These numbers decreased dramatically as covariate set size increased.

The decrease in study size associated with CEM is intuitive because CEM was effectively exact matching in our scenarios. This phenomenon also explains the finding that CEM performed best with respect to rMSE in the very small and small covariate set scenarios with higher IEP: Matching exactly on a small vector of covariates with many exposed units led to better retention of outcomes and, thus, to lower rMSE. Conversely, the large analytical cohorts resulting from FS (leading to low variance) and the consistently low bias values associated with FS were responsible for the low rMSE values observed for FS. Thus, overall, FS was optimal among the 4 methods with respect to rMSE. Notably, PSM was more similar to FS with respect to rMSE as IEP increased—a result also seen in previous work (10).

The overall suboptimal performance of MDM, especially with respect to covariate balance, might be attributed to known issues with MDM in high-dimensional space (5, 42–44, 52). The fact that covariate balance improvement for MDM worsened with higher IEP in both the very small and small covariate set scenarios was not surprising given that no matched-set pruning was performed. Thus, overall, with increasing IEP, the matched data set’s Mahalanobis balance value approached the original data set’s Mahalanobis balance value. A similar logic applies to the decreasing bias trends for MDM: Overall, because bias was already relatively low in the original simulated data set, the bias from MDM approached the bias from the original data set as IEP increased. It is worth noting that MDM performed almost as well as PSM with respect to variance, mainly because of the lack of matched-set pruning for MDM.

Although in our analyses CEM was always optimal with respect to covariate balance, the ultimate objective is to obtain a valid and precise effect estimate. The high levels of balance achieved by CEM in our study generally were not complemented by low rMSE values because CEM produced heavy losses in study size and outcomes to achieve this balance. If not for this problem, there would be less motivation to pursue a dimension-reduction technique, such as a propensity score–based method.

Therefore, in these types of pharmacoepidemiologic analyses, or in any epidemiologic analysis based on high-dimensional data comprising many binary covariates, CEM might not be the optimal choice. Instead, FS or PSM might be preferred. CEM (and MDM) might be warranted only when the vector of important confounders is relatively small (e.g., fewer than 10), comprises multiple continuous covariates, or both—unusual scenarios for the typical pharmacoepidemiologic analysis of claims (6–8). This suggestion also is supported by recent work comparing CEM with propensity score–based methods (12–14). CEM also should be considered if it is of interest to ensure tight control of balance on covariates involved in important higher-order terms. Finally, to take advantage of the balancing properties of CEM, stratification might be applied to a smaller set of the most important confounders within a large vector to ensure tight control over these confounders before applying a propensity score–based method to balance the remaining covariates within each stratum (2, 3, 53).

Importantly, although we covered a wide range of scenarios, our simulated data were based on one real cohort, exemplifying only one type of complex exposure-covariate structure from claims data. Also, we implemented the 4 methods in the common manner (e.g., use of a 0.025 absolute propensity-score distance caliper for PSM), not necessarily in an optimal manner. Future work might be warranted to fill the gaps left by these limitations.