Polarized evanescent waves reveal trochoidal dichroism

Significance

The ability of certain materials to discriminate between two opposite light polarizations is the basic principle behind several technologies such as liquid crystal displays and three-dimensional glasses. While there are numerous forms of light polarization, only linear and circular polarizations, which have wave motion in a flat sheet or helix, respectively, are typically used. Here, we utilize trochoidal polarizations with cartwheeling wave motion. We demonstrate that single gold nanorod dimers can discriminate between trochoidal fields rotating in opposite directions, which we term trochoidal dichroism. Trochoidal dichroism forms an additional classification of polarized light–matter interaction and could inspire the development of optical studies uniquely sensitive to molecules with cartwheeling charge motion, potentially relevant for probing key light-harvesting antennas.

Abstract

Matter’s sensitivity to light polarization is characterized by linear and circular polarization effects, corresponding to the system’s anisotropy and handedness, respectively. Recent investigations into the near-field properties of evanescent waves have revealed polarization states with out-of-phase transverse and longitudinal oscillations, resulting in trochoidal, or cartwheeling, field motion. Here, we demonstrate matter’s inherent sensitivity to the direction of the trochoidal field and name this property trochoidal dichroism. We observe trochoidal dichroism in the differential excitation of bonding and antibonding plasmon modes for a system composed of two coupled dipole scatterers. Trochoidal dichroism constitutes the observation of a geometric basis for polarization sensitivity that fundamentally differs from linear and circular dichroism. It could also be used to characterize molecular systems, such as certain light-harvesting antennas, with cartwheeling charge motion upon excitation.

Dichroism is the differential absorption of orthogonal light polarizations by matter and enables optical characterization of molecular geometry. Circular dichroism (CD) suffers from low sensitivity due to its reliance on far-field radiation, whose wavelength is typically orders of magnitude larger than the molecular features it is used to probe. An effective route for improving optical sensitivity is the use of highly confined, structured, light such as evanescent waves (1–5), interference fields (6–8), and focused Gaussian beams (7, 9).

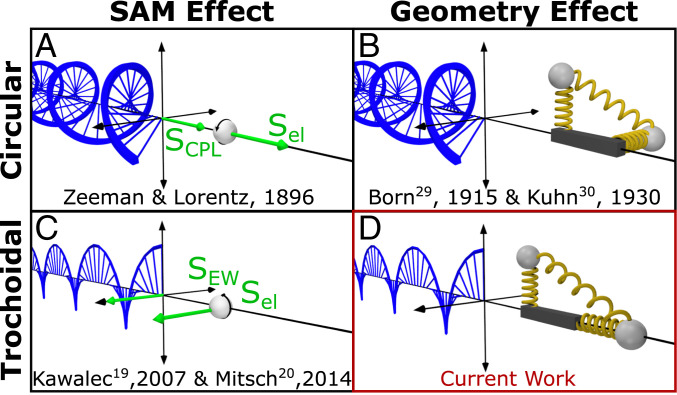
Confined light has distinct polarization properties from free-space radiation. In particular, laterally confined light can support longitudinal electromagnetic oscillations, which enable rich near-field polarization phenomena (9–12). The longitudinal oscillations of an evanescent wave result in a spin-angular momentum (SAM) component that is perpendicular, or transverse, to the light propagation direction. Transverse SAM components first gained interest in 2009 (13, 14) and have since been found in evanescent waves to be helicity-independent yet locked to the propagation direction of light (10, 15), enabling spin-dependent unidirectional propagation (16–18). Kawalec et al. (19) and Mitsch et al. (20) have found that the transverse SAM of confined light can enable electronic transitions of atoms within a magnetic field (Fig. 1C), exactly analogous to the Zeeman effect observed with circularly polarized light (Fig. 1A). These studies provided some of the first experimental evidence of the existence of longitudinal oscillations and transverse SAM in evanescent waves. Further, Junge et al. (21) demonstrated transverse spin-momentum locking in evanescent waves, convenient for nondestructive interference of counterpropagating light in microresonators. Finally, as predicted by Yang and Cohen (7), and experimentally demonstrated by Mathevet and Rikken (22), transverse SAM in an external magnetic field can give rise to magnetic field-induced CD signals.

Fig. 1.

SAM and geometry drive distinct polarization-dependent light-matter interactions. (A) Circularly polarized light has a longitudinal SAM vector (S_CPL) that couples to electrons with coaligned spins (S_el). (B) The Born-Kuhn model for CD of two charged masses (gray spheres) attached to two coupled, orthogonal springs displaced along a third orthogonal axis. (C) Trochoidal polarizations produce a transverse SAM vector (S_EW) that similarly couples to electrons with coaligned spins. (D) A modified Born-Kuhn model for trochoidal dichroism where one oscillator is aligned along the direction of light propagation.

The transverse SAM of confined light is also associated with cycloidal, or more generally, trochoidal field motion (10, 12). Trochoidal field motion is both planar and rotational, producing a cartwheeling motion, which results from significant phase delays between transverse and longitudinal oscillations. However, the differential extinction of orthogonal trochoidal polarizations by an analyte based on its geometry, the corresponding analog to CD (Fig. 1B), has not yet been observed (Fig. 1D). In this study, we develop a model metamaterial system composed of coupled dipole scatterers and observe unique differential scattering with trochoidal fields of opposite rotational directions. The measurement of trochoidal differential scattering is directly analogous to circular differential scattering (23, 24), successfully employed to characterize the optical activity of single chiral nanoparticles (25–27). While CD is historically defined as the differential absorption of left- and right-handed circular polarizations, as only absorption is relevant for small molecules, a CD spectrometer’s measurement is based on differential extinction (23). The scattering component of the extinction can significantly contribute to the CD of larger objects such as nanoparticles and macromolecules (23, 28). The trochoidal differential scattering we characterize here is therefore a significant component of an effect we name trochoidal dichroism.

Result and Discussion

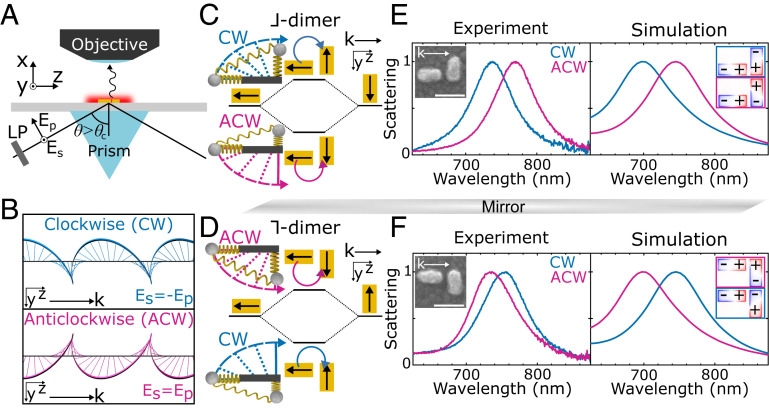
We use total internal reflection (TIR) of light with orthogonal linear polarizations, E_s = ±E_p (±45°) (Fig. 2A), to generate an evanescent wave with significant trochoidal character (SI Appendix, Supplementary Text and Fig. S1). Clockwise (CW) trochoidal motion results from E_s = −E_p (−45°) incident polarization and anticlockwise (ACW) field motion from E_s = E_p (45°) (Fig. 2B). The corresponding phase delays between the sample-plane transverse and longitudinal oscillations are −67° and 113° (SI Appendix, Supplementary Text). In addition to the ACW and CW trochoidal fields produced in the sample plane (Fig. 2B), TIR of E_s = ± E_p polarizations also yields a trochoidal field spinning perpendicular to the sample plane (SI Appendix, Fig. S1), with a transverse SAM component parallel to the plane (S_y). However, S_y is not expected to significantly contribute to trochoidal dichroism in this work as it cannot effectively couple to the sample and its sign is determined by the propagation direction which is held constant in our measurements (10). Therefore, by using TIR of E_s = ± E_p polarizations, we characterize trochoidal dichroism that arises mainly due to the differential interaction of matter with the vertical transverse SAM component (S_x).

Fig. 2.

Orthogonal and offset nanorods are a model system for observing trochoidal differential scattering. (A) Experimental TIR geometry. LP: linear polarizer, E_s, E_p: incident electric field components, $\theta$: angle of incidence. (B) Isolated in-sample-plane components of the evanescent wave for E_s = −E_p and E_s = E_p incident polarizations, tracing CW and ACW trochoids, respectively. (C) Plasmon hybridization for the ⅃-dimer. The light-induced electric dipoles are shown with black arrows and are excited opposite with respect to the electric field, with the curved arrow solely indicating the trochoidal polarization. Excitation from a CW (ACW) trochoidal field gives a high (low) energy antibonding (bonding) mode. In the corresponding spring system, attached masses are positively charged and are attracted toward the trochoidal electric field drawn with dashed lines and curved arrows. (D) Plasmon hybridization for the mirror-image ⅂-dimer. Normalized measured and simulated scattering spectra of the (E) ⅃-dimer and (F) ⅂-dimer under CW and ACW trochoidal excitation. (Insets) Correlated scanning electron microscopy (SEM) images with scale bars of 100 nm and charge distributions calculated at the scattering maxima for CW and ACW trochoidal excitation, matching the black arrows in C and D.

To demonstrate trochoidal dichroism, we probe the differential scattering of CW and ACW trochoidal fields with a model system based on the Born–Kuhn model for CD (29, 30). In this model, left- and right-handed circularly polarized light perform differential work on a chiral spring system composed of orthogonal, coupled, harmonic oscillators with attached charges that are displaced along a third orthogonal axis (Fig. 1B). In the trochoidal analog (Fig. 1D), the same two oscillators are instead displaced in the plane containing the two oscillators. Importantly, the second harmonic oscillator’s motion is collinear with the light propagation direction, k, to enable coupling with longitudinal oscillations. Trochoidal fields with CW and ACW rotational directions couple differently to the spring isomers, giving rise to trochoidal dichroism.

To realize such a model system, we utilize two orthogonal gold nanorods with a planar offset. The spectral response of gold nanorods is dominated by the coherent oscillation of conduction band electrons known as the localized surface plasmon resonance, accurately approximated as a damped harmonic oscillation (31). Plasmon hybridization between two adjacent nanorods dictates their collective interaction with light, similar to the principles of molecular orbital theory (32). Inspired also by Yin et al., who used coupled plasmonic oscillators to describe CD (33), we develop a plasmonic system for the trochoidal analog of the Born–Kuhn model. Specifically, we lithographically fabricate two nanorods with orthogonally aligned axes, aspect ratios of 2, lengths of 80 nm, heights of 40 nm, and an interparticle gap of 20 nm (Fig. 2 and SI Appendix, Fig. S2).

The coupling of the hybridized plasmon modes to CW or ACW trochoidal excitations depends on dimer shape and orientation relative to k. We first consider a system in which one nanorod is placed parallel to k and the other is perpendicular, forming a ⅃-shaped dimer (Fig. 2C). The significant separation of the nanorods relative to the wavelength of light causes each nanorod to experience distinct phases of the electric field. Based on plasmon hybridization theory, the electric-field vectors align with both nanorods under CW trochoidal excitation, exciting the higher-energy antibonding mode (Fig. 2C). Similar considerations predict that ACW field motion excites the lower-energy bonding mode (Fig. 2C). Mirroring the ⅃-dimer over the (x, z) plane containing k forms a ⅂-dimer, and the opposite polarization-dependent mode excitation is expected (Fig. 2D).

To test these predictions, we record single-particle scattering spectra of both ⅃- and ⅂-dimers, quantitatively confirming that the bonding and antibonding plasmon modes are selectively excited with CW and ACW trochoidal fields. As both modes have a significant net electric dipole, they are both readily observable in the scattering spectra (34). CW trochoidal excitation yields a single-particle scattering maximum at 740 nm (Fig. 2E) for the ⅃-dimer, while under ACW trochoidal excitation, the resonance is redshifted to 770 nm. Electromagnetic simulations validate the assignments of antibonding and bonding modes (Fig. 2E) and suggest that changes in dimer dimensions can further enhance the spectral shift (SI Appendix, Fig. S3). In particular, charge distributions calculated at the scattering maxima visualize the antibonding and bonding plasmon modes excited with CW and ACW trochoidal fields, respectively (Fig. 2 E, Inset), in excellent agreement with the plasmon hybridization sketched in Fig. 2C. These results are reproduced with the mirror-image ⅂-dimer, but with ACW trochoidal polarization now exciting the higher-energy antibonding plasmon (Fig. 2F). Additionally, single-particle spectra and simulations verify that the resonance energy of an individual nanorod indeed lies between the two hybridized dimer modes and is independent of trochoidal excitation (SI Appendix, Fig. S4). Finally, the trochoidal polarization-dependent differential excitation of bonding and antibonding plasmon modes is well-reproduced in simulated absorption spectra (SI Appendix, Fig. S5).

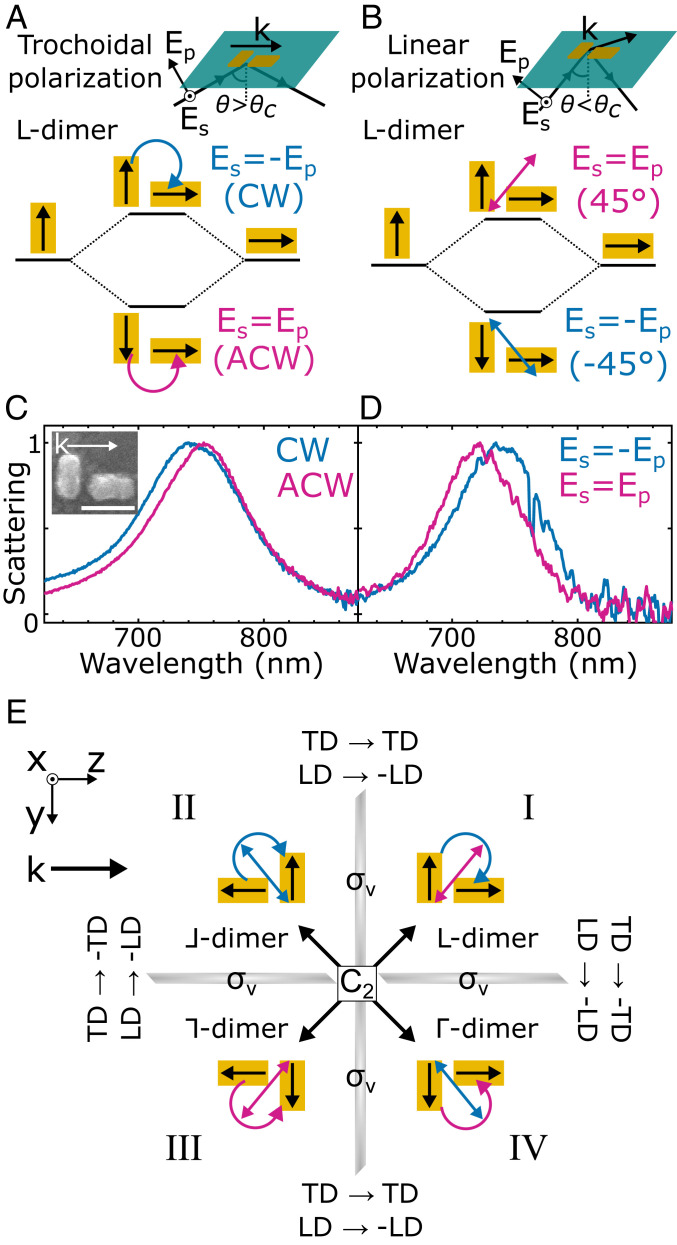
Our results cannot be explained by linear dichroism, as can be demonstrated when examining geometric isomers that show opposite trochoidal and linear dichroism. Because the dimers have anisotropic geometries and our trochoidal excitation has linear components (SI Appendix, Figs. S1 and S6), a minor contribution from linear dichroism is expected. While ⅃- and ⅂-dimers have trochoidal and linear dichroism of the same sign (SI Appendix, Figs. S6 and S7), the L-dimer, formed by mirroring the ⅃-dimer over the (x, y) plane, does not (Fig. 3). With k unchanged, CW trochoidal excitation resulting from TIR of E_s = −E_p (−45°) has electric-field vectors aligned with both nanorods, exciting an antibonding mode (Fig. 3A). The net dipole of this antibonding mode is oriented along the 45° axis (Fig. 3B). In contrast, if the excitation did not possess trochoidal character, E_s = −E_p (−45°) incident polarization would excite the bonding mode oriented along the −45° axis (Fig. 3B). Indeed, CW trochoidal excitation from TIR of E_s = −E_p yields a single-particle scattering resonance that is 10 nm blueshifted relative to ACW trochoidal excitation (Fig. 3C), well outside the experimental error in resonance shifts (SI Appendix, Fig. S4). Scattering spectra collected with identical polarizations but incident at an oblique angle (SI Appendix, Fig. S8) reveal a 15-nm redshift for E_s = −E_p (Fig. 3D). This opposite mode excitation when changing between trochoidal and purely linear polarizations demonstrates that our results are not due to linear dichroism, which is well reproduced by electromagnetic simulations (SI Appendix, Fig. S9). In total, each geometric isomer can be related to another by mirror (σ_v) and 180° rotation (C₂) symmetry operations (Fig. 3E). Performing a mirror operation over the (x, y) plane maintains trochoidal dichroism but gives opposite linear dichroism, enabling a clear distinction between the two dichroisms for both L-dimers and Γ-dimers (SI Appendix, Fig. S10).

Fig. 3.

L-dimers have trochoidal and linear dichroism of opposite sign. (A) Plasmon hybridization for the L-dimer with trochoidal excitation resulting from TIR of E_s = E_p (45°) and E_s = −E_p (−45°). Excitation from a CW (ACW) trochoidal field gives a high- (low-) energy antibonding (bonding) mode. (B) Plasmon hybridization for the L-dimer with oblique E_s = ±E_p incident polarizations. E_s = E_p (E_s = −E_p) linearly polarized light excites the high- (low-) energy antibonding (bonding) mode. Note that while magenta and blue arrows indicate the ±45° linear polarization of the incident light, the polarization once projected onto the sample plane is ±70° (SI Appendix, Supplementary Text). (C) Normalized single-particle scattering spectra of an L-dimer under CW and ACW trochoidal excitation. (Inset) Correlated SEM image. (Scale bar, 100 nm.) (D) Normalized scattering spectra of the same L-dimer under oblique incident excitation. Consistent results are observed also with normal incidence excitation (SI Appendix, Fig. S11). The increase in noise is due to the reduced sensitivity of oblique incidence scattering spectra (35). (E) Summary of symmetry operations relating each geometric isomer to another and the effect on trochoidal and linear dichroism (TD and LD). Each mirror operation (σ_v) gives opposite linear dichroism, but mirroring over the (x, y) plane maintains trochoidal dichroism. Therefore, the two effects are consistently distinguishable across L-dimers and Γ-dimers (quadrants I and IV) (SI Appendix, Fig. S12). These isomers have reduced resonance shifts relative to those of ⅃- and ⅂-dimers (quadrants II and III) (SI Appendix, Fig. S12), likely resulting from competing contributions of both dichroisms. However, trochoidal dichroism dominates (SI Appendix, Fig. S6 and S12).

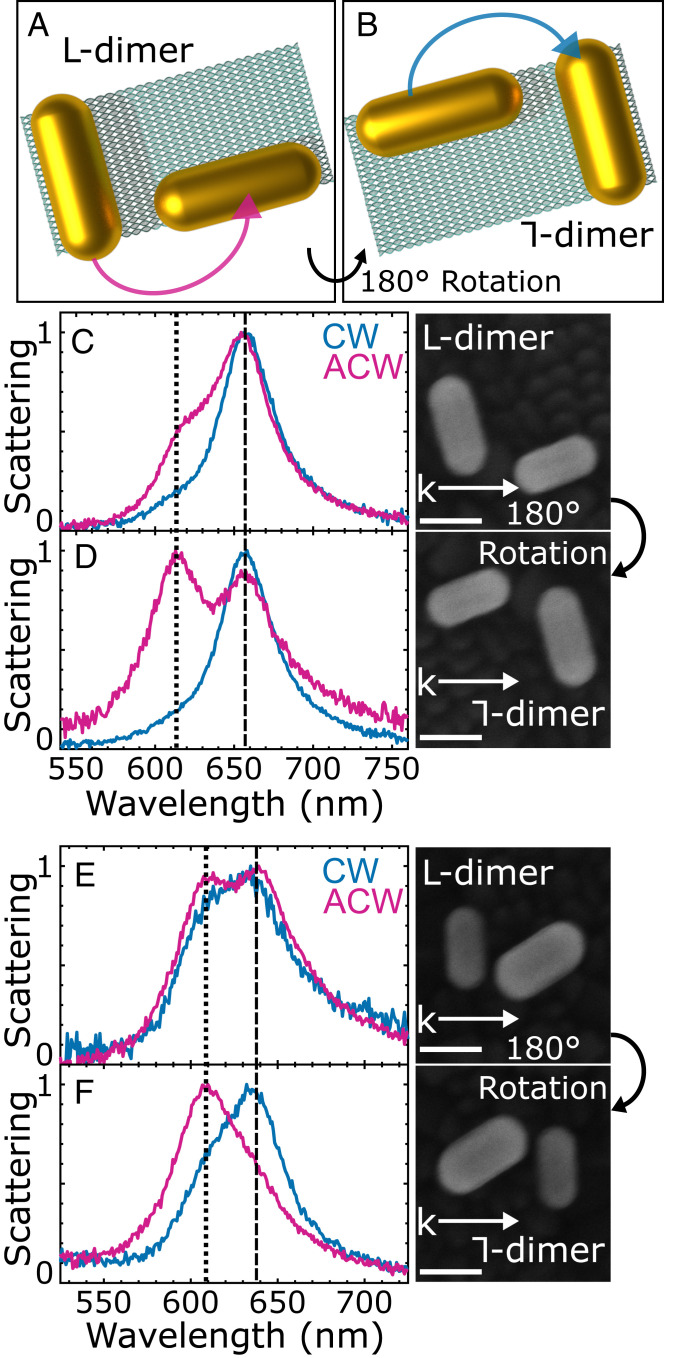
We further investigate trochoidal differential scattering in self-assembled colloidal nanorod dimers that deviate from the ideal model geometry. We take advantage of DNA origami templates (36–38), formed into rectangles by scaffold single-stranded DNA that is pinned in place by short staple strands (SI Appendix, Fig. S13). Capture DNA strands extend from the template to place gold nanorods in an approximately orthogonal arrangement with a planar offset (Fig. 4A). L-dimers from self-assembled gold nanorods are characterized under CW and ACW trochoidal excitations at two different sample orientations: 0° and rotated 180° relative to k (Fig. 4 A and B). The C₂ rotation maintains any linear dichroism contributions while giving opposite trochoidal dichroism, enabling their distinction (Fig. 3E, quadrant I $\to$ III).

Fig. 4.

Observation of trochoidal differential scattering in self-assembled gold nanorod dimers (A) Schematic of self-assembled dimers utilizing DNA origami, forming an approximate L-dimer. (B) Sample rotation of 180° forms a ⅂-dimer, reversing the trochoidal dichroism and promoting opposite mode excitation. (C and E) Normalized scattering spectra of the L-dimers at 0° sample orientation with CW and ACW trochoidal excitation. SEM images depict dimer orientation relative to k. (Scale bar, 50 nm.) (D and F) Normalized scattering spectra of the same dimers after 180° rotation. Dashed and dotted lines identify bonding and antibonding modes, respectively. As for the ideal dimers in Figs. 2 and 3, the trochoidal polarization of the incident field allows for mode selective excitation of hybridized nanorod dimer plasmons.

We find that observing trochoidal differential scattering is indeed not limited to only precisely engineered lithographically fabricated models. Deviations from the model-dimer geometry arise in the self-assembled dimers due to particle size heterogeneity, drying of the assembly on a substrate for spectroscopy, and a lack of control over the final orientation of the dimers relative to a fixed k. Relaxing the structural requirements enables components of both CW and ACW trochoidal excitations to map onto the bonding and antibonding modes, resulting in the partial excitation of both modes with each polarization. However, the relative excitation of each mode strongly depends on the direction of trochoidal rotation. Specifically, for the L-dimers, ACW trochoidal excitation predominantly excites a bonding mode (Fig. 4 C and E dashed line), directly analogous to the engineered model shown in Fig. 3C. Upon 180° sample rotation, yielding approximate ⅂-dimers, ACW trochoidal polarization predominantly excites the antibonding plasmon (Fig. 4 D and F dotted line), exactly analogous to Fig. 2F. These results are in excellent agreement with the mode-selective excitations seen for the model dimers presented above. Furthermore, the relative mode excitations are well-matched by theory (SI Appendix, Fig. S14) and the linear dichroism is indeed maintained upon C₂ rotation (SI Appendix, Fig. S15).

Conclusion

In conclusion, the observed dependence of the dimers’ optical properties on the rotational direction of the trochoidal field constitutes an additional form of light–matter interaction: trochoidal dichroism. Consistent with theoretical work (7) on confined light polarization states, trochoidal polarizations may be able to probe molecular rotational symmetries to which CD is less sensitive. Relevant mutants of photosynthetic chlorosomes of green sulfur bacteria are composed of chlorophylls that self-assemble into cylinders with charge delocalization around closely stacked rings (39, 40). Trochoidal dichroism, being optimized for a planar rotation of charges, may be able to effectively probe structure–function relationships in light-harvesting antennas, in a complementary fashion to CD. Further, any achiral molecule with perpendicular electric and magnetic dipoles experiences a planar rotation of charge upon excitation. The rotational direction of the charge is dependent on molecular orientation and could potentially be probed with trochoidal dichroism. Finally, while the longitudinal spin of surface waves can be observed through chiral structures (27), and helicity-invariant transverse spin can be observed through spin-orbit coupling (16), here we are sensitive to the diagonal polarization-dependent transverse spin component of evanescent waves (10). Thus trochoidal dichroism, as observed through far-field scattering, completes the ability to optically probe the full spin-basis set of a confined electromagnetic wave.

Materials and Methods

Electron-Beam Lithography.

The lithographic nanorod dimers were fabricated with a designed width of 40 nm, a length of 80 nm, and a height of 40 nm of gold with a 2-nm Ti adhesion layer and an interparticle gap of 20 nm. Single nanorods were fabricated with the same designed dimensions. The dimer arrays each contained 32 structures, which were divided into four subarrays containing dimers at different interparticle orientations (SI Appendix, Fig. S2). Indium tin oxide (ITO)-coated float glass (Delta Technology Ltd. CG-50IN-S107) was used as a transparent conductive substrate. The substrates were cleaned through sequential 10-min sonication in a 2% V/V solution of Hellmanex detergent, water, and ethanol. Slides were gently dried with a stream of N₂ and then spin-coated with a poly(methyl methacrylate) electron resist (Kayaku Advanced Materials PMMA 950 A4) at 3,000 rpm for 60 s. The slides were then baked for 2 min at 180 °C. Patterns were written into the resist with a Nanometer Pattern Generation System on an FEI Quanta 650 scanning electron microscope (SEM). The beam voltage was 30 kV, with a beam current of 40 pA, a spot size of 2.1, and a working distance of 7 mm. Samples were then developed in a 1:3 methyl isobutyl ketone/isopropanol solution for 70 s, followed by a 60-s rinse in isopropanol and gentle drying with N₂. The samples were then placed in an electron-beam evaporator, where a 2-nm Ti adhesion layer was deposited, followed by a 40-nm layer of gold. Excess material was removed by soaking the sample in acetone overnight, followed by gentle sonication and drying with N₂.

DNA Origami-Based Self-Assembly.

Rectangular DNA origami (∼60 nm × 100 nm; SI Appendix, Fig. S13) was prepared by annealing a mixture of a circular single-stranded M13mp18 DNA with a set of short helper strands, each ∼32 nucleotides, as well as capture strands for positioning the nanorods. All DNA was purchased from Integrated DNA Technologies. Complete sequences of the helper and capture strands are given in SI Appendix, Tables S1 and S2. M13mp18 DNA was annealed with helper and capture strands at a 1:10 molar ratio in a TE-Mg²⁺ buffer (14 mM magnesium chloride) in a thermocycler programmed for a cooling ramp from 85 to 25 °C overnight. The assembled DNA structures were purified using a 30-kDa Amicon filter under centrifugation at 8,000 rpm for 15 min. The concentration was estimated by measuring the absorption at 260 nm. Gold nanorods, 25 nm × 70 nm, were purchased from Nanopartz and modified with thiolated single-stranded DNA following published protocols (41). To produce gold nanorod dimers, DNA-decorated nanorods were mixed with the purified DNA origami template with a molar ratio $\ge$5, followed by annealing from 45 to 30 °C, cycled four times over 12 h. The assembled nanorod dimers were purified through Agarose gel electrophoresis and recovered using a Bio-Rad Freeze 'N Squeeze spin column under centrifugation at 13,000 rpm for 5 min. Gold nanorod dimers were deposited onto indexed ITO glass and flushed three times in deionized water, then dried under N₂ flow. Finally, the deposited dimers were exposed to an O₂ plasma for 2 min to partially remove the DNA to allow high-resolution SEM imaging.

Single-Particle Scattering Spectroscopy.

Single-particle scattering measurements were performed with an inverted dark-field microscope (Zeiss, Axio Observer m1). Light from a quartz tungsten halogen lamp (Newport 66884) was coupled by fiber-optic cable to a home-built optical rail system. The light was collimated with a plano-convex lens (Thorlabs AC254-030-A) and filtered with a 304–785-nm bandpass filter (Thorlabs FGS550) to protect the film linear polarizer from undue heating. The light was then polarized with a linear polarizer (Thorlabs LPVIS100) set to either $\pm$45° from the parallel polarized (E_p) axis (Fig. 2A and SI Appendix, Fig. S1). The polarized light was focused with a plano-convex lens (Thorlabs AC254-030-A) onto an equilateral prism. TIR conditions were achieved with an input angle of 55°. Free-space, oblique incidence dark-field excitation was achieved with an input angle on the prism of ∼27°. The scattered light from the nanostructures was collected with either a 50× magnification air-space objective lens (Zeiss, numerical aperture of 0.8) for TIR experiments or a 40× magnification air-space objective lens (Zeiss, numerical aperture of 0.6 with an extralong working distance) for oblique incidence experiments. The collected light was passed through the microscope and then directed to a hyperspectral detection system that has been described previously (42). Briefly, the output light was directed into a spectrograph (Acton SpectraPro 2150i) and the dispersed light was detected with a back-illuminated charge-coupled device camera (Princeton Instruments PIXIS 400BR). The spectrograph and camera were both mounted on a scanning stage driven by a linear actuator (Newport LTA-HL). The data collection was performed in a hyperspectral fashion, with a slit aperture allowing for the collection of multiple spectrally resolved image slices as the spectrograph was scanned over the field of view. Normal incidence measurements were performed with light from a tungsten-halogen lamp (Zeiss, Axioline HAL 100) which was filtered and polarized with the same optics described above. The light was focused on the sample with an oil-immersion condenser (Zeiss, adjustable numerical aperture of 0.7–1.4) in bright-field mode (incident angle of 0°) with the numerical aperture set to 0.7. The scattered light was collected with a 74× reflecting objective (Beck Optronic Solutions, 0.65 numerical aperture) with a direct beam block aligned with the incident excitation, allowing dark-field imaging. Light scattered to a high angle was collected by the objective lens and detected with the same hyperspectral procedure described above. Spectra with lower signal-to-noise ratios, such as the oblique incidence measurements, were subjected to a five-point moving boxcar average.

Numerical Simulations.

Finite-difference time-domain (FDTD) simulations were performed using the Lumerical FDTD package. The simulation model consisted of nanorods with a length of 85 nm, a width of 35 nm, and a height of 40 nm with a 2-nm Ti adhesion layer. The simulated gap between the nanorods was 15 nm and the nanorods were arranged to form ⅃, ⅂, and L-dimers. All simulation parameters were tuned to be within 5 nm of the design parameters to achieve a reasonable resonance match with the experimental spectra. Remaining deviations from the experimentally measured spectra likely originate from the poor crystallinity of lithographically fabricated structures and increased plasmon damping from the Ti adhesion layer that is not captured in the bulk dielectric functions. The dielectric functions of gold and Ti were extracted from Johnson and Christy (43) and Palik (44), respectively, and fit to a Drude–Lorentz model for the time-domain calculations. The substrate was glass (refractive index n = 1.52) with 160 nm of ITO (n ∼ 1.7) (45). Perfectly matched layers were used to avoid any reflections from the boundaries. For TIR, the incident angle from the substrate medium was 55° from the sample normal. For oblique incidence simulations, the incident angle was 39°. As in experiments, $E_s=\pm E_p$ was used as the incident polarization. The charge plots were calculated using the electric field obtained from the FDTD simulations. The charge distribution varied over the height of the dimers because the presence of a substrate changes the charge distribution compared to vacuum. To account for this variance when calculating the two-dimensional charge plots, the charge distributions were summed over the entire height of the dimers.

Data Availability.

Scripts used to analyze data and all data presented in the figures are available in an online directory at https://rice.box.com/s/rv65ydbiuxaiokxuucgkpjryxs9pelfi.