Unusual activated processes controlling dislocation motion in body-centered-cubic high-entropy alloys

Significance

This work demonstrates dislocation dynamics in body-centered-cubic (BCC) high-entropy alloys (HEAs). The local composition inhomogeneity in these concentrated solutions leads to an unconventional rate-controlling mechanism that governs dislocation mobility. The activated process becomes nanoscale detrapping, of kinks on screw dislocations and of trapped segments of edge dislocations, presenting an activation barrier of similar magnitude for both dislocation types. Their sluggish mobility explains the elevated strength and strain hardening in BCC HEAs.

Abstract

Atomistic simulations of dislocation mobility reveal that body-centered cubic (BCC) high-entropy alloys (HEAs) are distinctly different from traditional BCC metals. HEAs are concentrated solutions in which composition fluctuation is almost inevitable. The resultant inhomogeneities, while locally promoting kink nucleation on screw dislocations, trap them against propagation with an appreciable energy barrier, replacing kink nucleation as the rate-limiting mechanism. Edge dislocations encounter a similar activated process of nanoscale segment detrapping, with comparable activation barrier. As a result, the mobility of edge dislocations, and hence their contribution to strength, becomes comparable to screw dislocations.

Plastic strain in metals and alloys is carried by dislocations (1). Their movement is driven by an applied external stress, which balances out the lattice friction that resists dislocation glide on the slip plane (1). Dislocation mobility can be distinctly different for different types of dislocations. In metals of the face-centered-cubic (FCC) structure, screw and edge dislocations glide easily over a low Peierls barrier, with similarly high speeds (2). In contrast, in body-centered-cubic (BCC) metals the velocity of screw dislocations is orders of magnitude slower than that of edge dislocations, because the glide of screw dislocations needs to overcome a sizable energy barrier in a kink-pair process (3, 4). Only when the activation barrier in this thermally activated process is overcome by elevated deformation temperature (5, 6), or smeared out by sufficiently high imposed stress (7), can the screw dislocations reach a mobility comparable to edge dislocations. Therefore, in BCC metals at temperatures T < 0.2T_m (T_m is the melting point) the motion of screw dislocations is rate-limiting, rendering a flow stress considerably higher than FCC metals, as well as a much stronger dependence of the strength on temperature and strain rate.

However, the recent advent of high-entropy alloys (HEAs) calls into question the universality of this rate-controlling mechanism, and of the contrast between the edge and screw dislocations in BCC structure. An HEA comprises multiple principal elements, leading to a rugged atomic and energy landscape for dislocations (for discussions on FCC HEAs, see ref. 8). BCC HEAs may thus be an outlier of the dislocation behavior summarized above for conventional BCC metals. While HEAs are currently attracting considerable attention (9, 10), most reports so far have focused on compositions and measurements of their mechanical data (8, 10), rarely revealing unprecedented dislocation mechanisms (8). In this work, we show that unconventional dislocation dynamics emerge in model BCC HEAs; this is in fact a striking example demonstrating that these concentrated HEAs can indeed be special, requiring materials science concepts mechanistically different from those known for traditional metals and solid solutions.

In the following, we use atomistic simulations to unravel the dislocation mobility of edge and screw dislocations, using Co_16.67Fe_36.67Ni_16.67Ti₃₀ as a model BCC HEA, in direct comparison with α-Fe and with a Fe-5 at. % Al solid solution as the conventional BCC counterpart. The BCC HEA is constructed as a random solid solution with no intentionally introduced local chemical order (Materials and Methods and SI Appendix, Fig. S1). We discover that, different from conventional BCC metals, in HEAs inhomogeneity-imposed trapping of nanoscale segments of the moving dislocation (and the nucleated kinks in the screw case) constitutes the primary resistance to dislocation motion. This is an unusual activated process that takes over the rate-limiting role in dislocation mobility, in lieu of kink-pair nucleation, resulting in elevated strength. The detrapping required to escape from locally favorable environments also slows down edge dislocations such that they glide with a speed approaching that of screw dislocations and become a major player in controlling strength.

Results

We first explore the expansion of a dislocation loop under a constant external shear stress, τ, in these three BCC systems at temperature T = 300 K using molecular dynamics (MD) simulations (Materials and Methods). The circular loop embedded has a radius of 15 nm, residing on the ($1\overline{1}0$) plane. For α-Fe in Fig. 1A, an applied shear stress τ ∼400 MPa sets off the motion of the edge segments with a rather high mobility. In comparison, the screw segments barely move at this stress level. The loop therefore evolves toward a rectangular shape. The dislocation loop in the Fe-5 at. % Al solution behaves in a similar way (SI Appendix, Fig. S2).

Fig. 1.

Expansion of dislocation loop in (A) α-Fe under 400 MPa and (B and C) Co_16.67Fe_36.67Ni_16.67Ti₃₀ HEA under 600 and 950 MPa at 300 K. The loop radius is 15 nm. (A) For α-Fe, when the applied stress reached ∼400 MPa, the edge segment moved on ($1\overline{1}0$) plane, whereas the screw segment remained almost stationary. Due to this large difference in mobility (quantified in the next figure), the loop quickly turns rectangular, dominated by the action of the edge segments. (B) On the contrary, in Co_16.67Fe_36.67Ni_16.67Ti₃₀ the entire loop starts to expand at almost the same time. The mobility is very low at 600 MPa and increases pronouncedly when the stress reached 950 MPa. The mobilities of the edge and screw segments are very close such that the dislocation loop roughly retains its round shape. The expansion progresses in a sluggish and nonconserved manner due to the strong local trapping that roughens the dislocation line.

The Co_16.67Fe_36.67Ni_16.67Ti₃₀ BCC-HEA behaves very differently. The initial dislocation loop slowly evolves to become curved locally, after relaxing at 300 K. Both the edge and screw segments start to move noticeably at τ ∼600 MPa (Fig. 1B) with a low velocity. The mobility difference between the edge and screw segments is insignificant. As a result, the dislocation loop expands while roughly retaining its original round shape (Fig. 1B). The same is true at very high stresses, e.g., τ = 950 MPa shown in Fig. 1C. The mobility is elevated considerably at this high stress. Contrary to the smooth glide in α-Fe and Fe-5 at. % Al, the dislocation in this HEA glides in a rather rugged way: local (nanometer-scale) segments on the moving dislocation line become strongly curved, bulging forward in between regions that act like trapping sites (to be discussed later). With intermittent detrapping, the dislocation line crawls forward, and a high density of debris (vacancies and interstitials) is produced in its wake. We also performed another set of simulations using a constant strain rate (SI Appendix, Fig. S3). The critical stresses needed for the movement of edge and screw dislocations are very close. Note here that the behavior in Fig. 1 appears to be generic; see another example showing a similar contrast between BCC Nb and BCC-HEA Ti_33.3Zr_33.3Nb_33.3 in SI Appendix, Fig. S4.

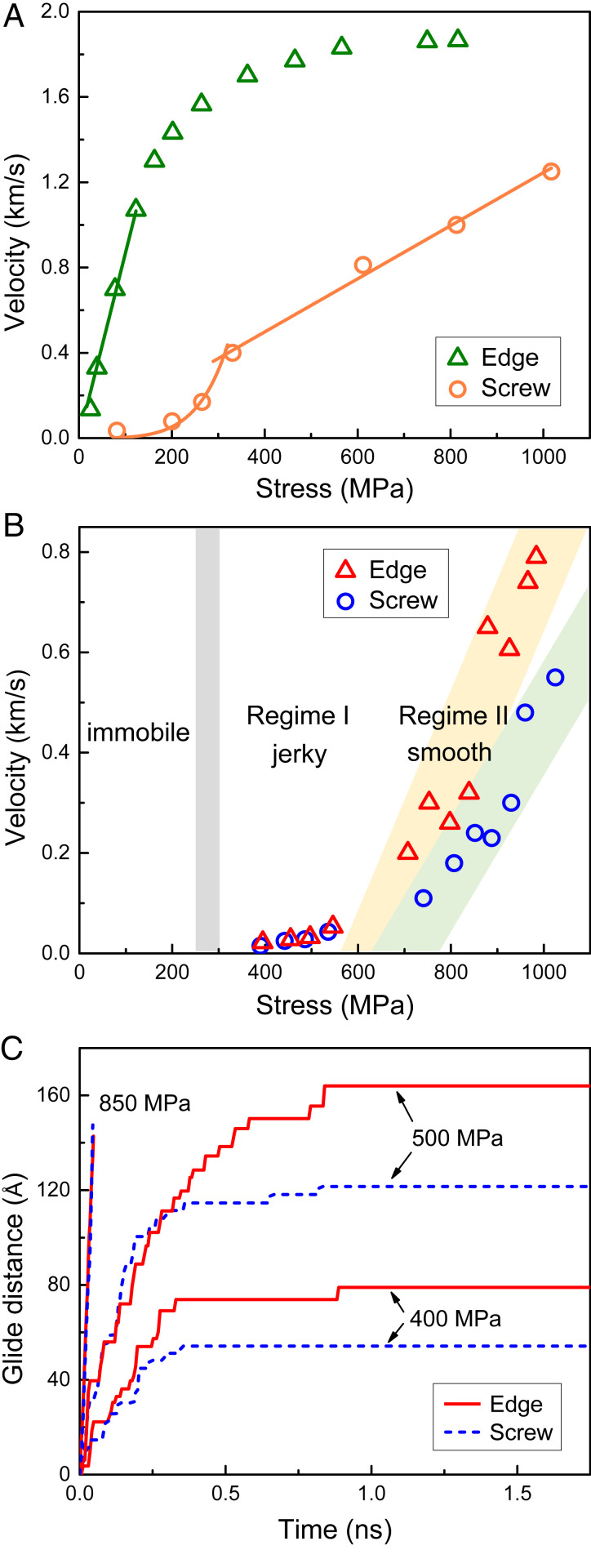
Next we quantitatively map out the dislocation velocity (v) in α-Fe versus Co_16.67Fe_36.67Ni_16.67Ti₃₀, across a range of applied shear stress up to τ ∼1 GPa at 300 K (Materials and Methods and SI Appendix, Figs. S5 and S6). The stress levels in MD simulations are higher than those in laboratory experiments, to drive sufficiently large dislocation displacements that can be easily monitored within the MD timeframe. Nevertheless, we believe that the trend and regimes depicted in Fig. 2 should remain generally valid. For the α-Fe case, Fig. 2A plots v versus τ for edge and screw dislocations, respectively. As expected for such a normal BCC metal, the edge dislocation and the screw dislocation behave quite differently (SI Appendix, Supplementary Note 1). For edge dislocations, v starts to linearly increase with τ at fairly low stresses, eventually saturating at high τ; see open triangles shown in Fig. 2A. This means that the athermal stress for instantaneous runaway is very low for the edge dislocation. The v of screw dislocation, on the other hand, shows an exponential dependence on τ at low stresses, apparently controlled by a thermally activated process, which is known to be the kink-pair mechanism (3, 4). Over a range of τ, the v of screw dislocation is slower than that of the edge dislocation by roughly one order of magnitude. Beyond a much higher stress (τ ∼300 MPa), the screw dislocation eventually also switches into the instantaneous glide mode, where v linearly scales with τ (SI Appendix, Fig. S7). A drag coefficient, B, can be defined from the Peach–Koehler force, τb = Bv, where b is the magnitude of the dislocation Burgers vector (Materials and Methods), and directly obtained from the inverse slope of a linear fit to the data (4, 11) in Fig. 2A. In this instantaneous motion regime, B is one order of magnitude larger for the screw dislocation (2.1 × 10⁻⁴ Pa⋅s) than the edge dislocation (2.6 × 10⁻⁵ Pa⋅s) at 300 K. The comparison of B at other temperatures is presented in SI Appendix, Fig. S8. In terms of v, take τ ∼400 MPa as an example, the mobility of the screw dislocation is lower than the edge by a factor of 3.6 (0.5 vs. 1.8 km/s) at 300 K. This obvious difference is consistent with the round-to-rectangular shape change of the expanding loop observed in Fig. 1A. As compared in Fig. 2A, we observe that only when τ reaches GPa level (which is rarely relevant in normal BCC deformation), can the mobility of the screw dislocation approach that of the edge dislocation.

Fig. 2.

(A) The dislocation velocity v versus stress τ for edge and screw dislocation at 300 K in α-Fe. The drag coefficient B is determined from the inverse of the slope in the linear regime. (B) The variation of v as a function of τ for both edge and screw dislocations at T = 300 K in Co_16.67Fe_36.67Ni_16.67Ti₃₀ alloy. (C) The typical glide distance–time curves with different stresses at 300 K. Below the stress threshold (250∼300 MPa, gray line in B), the dislocation is almost immobile. In the first regime (regime I) above the threshold, dislocation glides in a discontinuous manner (see curves at τ ∼400 and 500 MPa in C). Only when the stress applied is very high, as shown in the yellow and green shadows in B, can dislocation move continuously (see curves at τ ∼850 MPa in C). In the high-stress regime (regime II), velocity shows roughly a linear increase with increasing τ. The effective drag coefficients B^eff, obtained by linear fitting of the data, is ∼1.2 × 10⁻⁴ Pa⋅s for edge dislocation and ∼1.6 × 10⁻⁴ Pa⋅s for screw dislocation in Co_16.67Fe_36.67Ni_16.67Ti₃₀ alloy. In addition, the speed for the transverse shear wave along the [111] direction is estimated to be v_s^[111] = 3 km/s for α-Fe and 2 km/s for Co_16.67Fe_36.67Ni_16.67Ti₃₀ alloy (Materials and Methods).

We now examine the situation for the Co_16.67Fe_36.67Ni_16.67Ti₃₀ BCC-HEA, using Fig. 2 B and C. Fig. 2B plots v as a function of τ for both the edge and screw dislocations at 300 K. We see there is a stress threshold (τ = 250 to 300 MPa, gray line in Fig. 2B), below which all dislocations are immobile. This clearly demonstrates that the HEA is much stronger than α-Fe. Above this threshold, there are two regimes. As seen in Fig. 2B, with increasing τ the velocity rises exponentially in regime I, characteristic of thermally activated slip assisted by external stress, and then approximately linearly in regime II, indicative of instantaneous dislocation glide. Regime I spans a τ range several hundred MPa wide, in which three features are noteworthy. First, unlike α-Fe, both the edge and screw dislocations now show similar v-τ relation, implying that they share a similar activation mechanism. In fact, both the edge and screw dislocations move at similar v (well within a factor of 2, see Fig. 2B) for a given τ, further indicating that they now are controlled by a similar thermally activated process. The small v difference between edge and screw is consistent with the nearly equal expansion speed of the edge and screw segments of the dislocation loop in Fig. 1B. Second, for the screw dislocation in this regime I, even though the v-τ relation for the HEA looks like that for the α-Fe case, it functions in a τ range considerably higher, suggesting that a different activation mechanism is at play. Third, Fig. 2C presents the typical glide distance–time curves at 300 K. We observe that both the edge and screw dislocations move in a jerky manner in regime I. Such an intermittent motion (Fig. 2C), corresponding to the segmented crawl seen in Fig. 1, is not seen in normal BCC, once again suggestive of an unusual activated mechanism. This interesting activated process will be illustrated and explained below, together with an assessment of the energy barrier encountered. Although our current simulations only cover a short time (2.0 ns), we have managed to estimate the velocity by linearly fitting glide displacement with time. As seen in Fig. 2C, screw and edge dislocations move at similar velocities, differing by less than a factor of 2.

Regime II is for still higher τ, where the motion of both the edge and screw dislocations in the HEA changes from jerky to smooth (see the curve at τ = 850 MPa in Fig. 2C). This is the high-stress regime in which the dislocation velocity scales roughly linearly with stress; see the yellow and green shadowed regions shown in Fig. 2B for the edge and screw dislocations, respectively. The data scatter in each shadowed bar arises from compositional fluctuation in the samples we simulated. While we have seen such a linear regime for normal BCC metals earlier (Fig. 2A), for the HEA a linear fit will not go through the origin [FCC equiatomic concentrated NiFe alloys behave the same way (12)]. The slope of the fit gives an effective drag coefficient, B^eff, which is ∼1.2 × 10⁻⁴ Pa⋅s for the edge dislocation and ∼1.6 × 10⁻⁴ Pa⋅s for the screw dislocation, also close to each other in this regime II. This explains the similar speed observed for the edge and screw segments of the expanding dislocation loop at 950 MPa in Fig. 1C.

The next order of business is to understand what is happening in the activated process underlying the stick–slip forward motion of local dislocation segments. To this end, we map out the energy landscape for dislocation motion, to gauge how the presence of the inhomogeneous distribution of the multiple elements trips the dislocation, acting as short-distance obstacles to change the dynamics of dislocations traveling in the lattice. In a solution with concentrated multiple constituents as in an HEA, many properties [such as the stacking faults energy (13)] can vary spatially from location to location. Using the climbing image nudged elastic band (CINEB) method (14), we have calculated the energy landscape confronting the gliding screw and edge dislocations, as shown in Figs. 3 and 4, respectively. The main feature common to both the edge and screw dislocations is that the minimum energy path is very rugged, with variable saddle points that constitute energy barriers a fraction of 1 eV in height. The examples shown in the figure are for a dislocation line with an initial length of ∼15 nm, and the sampling was done by moving the dislocation across a distance of about 1 nm.

Fig. 3.

The minimum energy pathway for the movement of a screw dislocation in the Co_16.67Fe_36.67Ni_16.67Ti₃₀ HEA. (A) The energy landscape is quite rugged for screw dislocation. The energy barriers observed correspond to activated events that control the dislocation movement, i.e., the rate-limiting processes. (B) The initial screw dislocation contains a high density of kinks, on three equivalent {110} planes, that get trapped locally. With reference to the initially created straight dislocation (the dashed black line), the trapped dislocation segments on three {110} planes are marked by three different colors (red, blue, and green solid lines), in this projection view. A cross-kink is formed when two differently oriented kinks meet, as indicated by the black arrow in position B, a. The movement of the screw dislocation requires detrapping of the kinks and cross-kinks from lower-energy local environments. The red, blue, and green arrows indicate the propagation directions of corresponding kinks. As an example, from position B, a to B, c, the kink propagation requires detrapping to overcome a barrier (∼0.25 eV, see saddle point in position B, b). As another example, from position B, d to B, g the activation barrier for detrapping the cross-kink is ∼0.4 eV.

Fig. 4.

The minimum energy pathway for the movement of an edge dislocation in the Co_16.67Fe_36.67Ni_16.67Ti₃₀ HEA. (A) The energy landscape is quite rugged like that of screw dislocation. (B) The glide of the edge dislocation also has to undergo detrapping on the nanoscale. The dashed line marks the curved edge dislocation. The pink solid lines show the profiles of dislocation line gliding to the new position. The locally trapped segments need to bulge forward to detrap, as indicated by the pink arrows.

We now compare this activation barrier with that in conventional BCC metals, in which kink-pair nucleation is the rate-limiting event for screw dislocation motion below the athermal stress, whereas the kink spread on the dislocation line is very fast with an exceptionally low barrier (3, 4). The activation energy for the kink nucleation process depends on stress and temperature (SI Appendix, Fig. S9). In contrast, we found that kink nucleation in Co_16.67Fe_36.67Ni_16.67Ti₃₀ HEA is promoted by local composition fluctuations. Some kinks are generated spontaneously upon relaxation of the screw dislocation, on three equivalent {110} planes along the initially [111]-oriented straight dislocation line (see examples in SI Appendix, Fig. S10). Apparently, the atomic configurations with kinks are energetically more favorable in some local regions. This is understandable, because the heterogeneity in local composition and arrangements of the multiple elements makes each local region different, with or without the presence of the dislocation. The screw dislocation can adopt a kinked configuration that lowers the overall energy upon a favorable composition fluctuation (15). However, the easier kink nucleation in an HEA does not mean that screw dislocations would now be highly mobile. Rather, the screw motion can encounter considerable difficulty during kink propagation. This is because the local energetically favorable environments now exert a strong trapping effect to retard kink propagation that would create unfavorable environments. In other words, the sweep of the nucleated kinks, easy in conventional BCC metals, is now challenged by the local trapping in the mixture HEA solution, as reflected by the barriers seen in Fig. 3A. The trapping force comes from the energy cost associated with a dislocation segment cutting through a locally favorable environment, leaving in its wake a less energetically favorable configuration. In an HEA, the heavily concentrated elements almost always fluctuate from location to location, and the composition undulation is often enhanced by local atomic rearrangements that are driven by the reduction of lattice strain or the establishment of local chemical order (preference for, or avoidance of, certain bonds). The inhomogeneity is therefore throughout the lattice and local trapping is ubiquitous all over the path of the traversing dislocation, leading to a rugged energy landscape for the movement of a screw dislocation. As seen in Fig. 3A, the barriers for dislocation motion vary from one location to another, but are generally in the range from 0.1 to 0.4 eV. In other words, while kinks nucleate readily, they are no longer so mobile as in conventional BCC metals. The mobility of the screw dislocations in HEAs is now primarily limited by the propagation of the nucleated kinks. Also, the easily nucleated kinks on different {110} planes enhance the probability to form cross-kinks (Fig. 3B and SI Appendix, Fig. S10), which cause extra pinning against dislocation motion. All these are distinctly different from conventional BCC metals, where kink nucleation is the rate-limiting event whereas the kink spread on the dislocation line is very fast with a low barrier (3, 4). The kinks, cross-kinks, and their detrapping action/events are illustrated in detail in Fig. 3B and its legend, with corresponding barriers shown by the saddle points in Fig. 3A. Note that in pure BCC metals, the energy landscape for dislocation motion is smooth. Therefore, the rugged energy landscape we observed above should stem from the intrinsic compositional inhomogeneities in HEAs (8); these concentration fluctuations/undulations become increasingly pronounced with increasing number of constituent elements, which are all highly concentrated in the mixture solution.

In fact, even for edge dislocations, normally highly mobile in BCC metals, the nanoscale local trapping also holds down their propagation in the HEA. We show in Fig. 4A for Co_16.67Fe_36.67Ni_16.67Ti₃₀ HEA that the local barriers facing edge dislocations range from ∼0.1 to 0.3 eV, similar to those for screws earlier and drastically larger than that in α-Fe (∼2.8 meV/nm) (16). Indeed, as seen in Fig. 4B, some nanoscale dislocation segments are badly curved even for a short-distance movement, because they are reluctant to escape from local inhomogeneities where they have settled in to reduce low-energy, much like the trapped kinks on screw dislocations discussed above. The nanoscale segment detrapping (NSD) events (8) are illustrated in detail in Fig. 4B and its legend, with corresponding barriers shown by the saddle points in Fig. 4A. The short dislocation line in Fig. 4, only 15 nm in length, is far from sampling all of the possible trapping–detrapping events. Nevertheless, the present simulations suffice to illustrate that edge dislocation motion in BCC HEAs requires NSD the same way as screw dislocations. Both types of dislocations glide on the slip plane in a stick–slip manner, one nanoscale segment at a time (see Fig. 2C, as well as the intermittent detrapping actions in Movie S1 for screw dislocation and Movie S2 for edge dislocation). As the effective energy barriers for detrapping of screw kinks and edge segments are similar (Figs. 3 and 4), the mobilities of screw and edge dislocations are not very different in Co_16.67Fe_36.67Ni_16.67Ti₃₀ (Fig. 2). These also explain the observed loop expansion behavior in Fig. 1B.

The implications of the minimum energy path in Figs. 3 and 4 can be summarized as follows. For both screw and edge dislocations, we observed a rugged energy landscape that the dislocation has to traverse. The magnitude of the barrier height is of the order of a few tenths of an eV, similar for both edge and screw dislocations. These barriers can be mapped to events occurring along the dislocation line, for detrapping that enables kink spreading in the screw case, and for depinning of strongly curved dislocation segments in the edge case. The obvious trapping due to favorable local chemical environment is absent in conventional BCC metals, where the smooth sailing of edge dislocation in the lattice and the spreading of nucleated kinks on screw dislocation both encounter minimal energy barrier.

Discussion

To recapitulate, we have used α-Fe as a model for normal BCC metals to show that for a wide range of practically relevant resolved shear stresses, edge dislocation runs far faster than screw dislocation. As an example, as shown in Fig. 2, at τ < 200 MPa edge dislocation moves at ∼1.4 km/s, whereas screw dislocation can only reach < 0.1 km/s. This expected large contrast is because screw dislocation motion is rate-limited by kink nucleation, whereas edge velocity already enters the “linear with τ” regime. Only at very high driving stresses (>1 GPa), when the intrinsic kink mechanism no longer matters, can the two types of dislocations behave alike, and their speed contrast diminishes.

The HEA case is clearly different. At below ∼250 MPa, dislocations do not even move, a result of clear solid-solution strengthening due to the multiple principal elements. When the threshold stress is exceeded, both edge and screw start moving, and they move at similar speed, in the same jerky manner via the NSD mechanism (8). This is an unusual dislocation behavior: Different from normal BCC, the edge and screw dislocations can now behave alike well before they both enter the phonon drag regime with linear τ–v dependence. Putting it another way, we have discovered that across a stress regime (see regime I above) where trapping effect on dislocation glide is dominant, edge and screw dislocations can have similar behavior. Here the trapping is no longer from kink pair on screws but from NSD needed to sustain glide. It is NSD that renders both edge and screw dislocations intermittent in their slip mode. As seen from the displacement–time curves (Fig. 2C) and the rough dislocation line (Figs. 1B, 3B, and 4B), the motion of both screw and edge is mediated by the forward crawl of nanoscale segments undergoing stick–slip.

Note again that the regime discussed above (regime I) is for a stress range below regime II. The latter, on the other hand, is toward the high-stress (τ > 600 MPa in Fig. 2) end, where edge and screw are expected to behave in a similar way, even for α-Fe and BCC metals. In other words, in regime II the high stress overrides the trapping mechanism, including the kink-pair mechanism in normal BCC metals and the NSD mechanism (mixture solution hardening) in HEAs. For HEAs, both the screw and edge dislocations would return toward smooth and straight at the ultrahigh stresses in regime II. By including this regime in our discussion, our results present the whole picture of dislocation mobility for BCC HEAs, delineating the boundaries of each regime that can be compared with conventional BCC metals. As a specific example, the motion of edge and screw in α-Fe encounters different barriers (almost negligible for edge, but kink-pair for screw); this makes them different starting from low stresses and they enter the linear τ–v regimes at different stress levels. In HEAs, we have shown that both edge and screw dislocations need to overcome a similar barrier for NSD such that they behave similarly and also reach the linear regime almost at the same time/stress.

Finally, let us go back to regime I and make a quantitative comparison between the contribution from the NSD mechanism with that from phonon drag. In elemental metals, when the resistance to dislocation motion primarily arises from the scattering of lattice vibration (phonons) (2, 17), it is the phonon damping force, τ_phonon = B_phononv/b, that balances the Peach–Koehler force on the dislocation. The B_phonon is proportional to the phonon density and linearly depends on temperature at T > Θ (Θ is the Debye temperature). In solid-solution alloys, besides the resistance from phonon damping, the solute atoms add an extra pinning force τ_pinning against dislocation motion, such that τ = τ_phonon + τ_pinning. For a dilute solution, the pinning effect is not an overwhelming contribution due to the low probability of the dislocations encountering the separate individual solute atoms. For HEAs, it is known that the phonon spectrum broadens (18), and the chemical complexity in the Co_16.67Fe_36.67Ni_16.67Ti₃₀ HEA is found to shift the phonon density of states profile toward the low-frequency side (SI Appendix, Fig. S11), signaling a higher dragging force τ_phonon against dislocation motion, when compared with α-Fe and Fe-5 at. % Al. However, the B_phonon/T calculated following the model of Leibfried (19) tells us that the phonon drag is only a minor contributor in regime I for our HEA (SI Appendix, Supplementary Note 2 for the quantitative evaluation of τ_phonon). This supports our claim that the pinning effect from NSD should play the dominant role in controlling dislocation motion in regime I for the HEAs.

As discussed earlier, the trapping arises from the appreciable inhomogeneity in local composition of the elements, which is a consequence of the complex interactions in a concentrated HEA solution. The composition inhomogeneity with undulations can be due to statistical fluctuation, local chemical order, and elastic distortion/strain (20). To probe into the concentration inhomogeneity that imposes trapping effect on the moving dislocation in our HEA, we checked the spatial distribution of each species around the dislocation lines. Relative to other species, Ti appears to segregate around the cross-kinks on the screw dislocation as well as the trapping sites observed for the edge dislocation. Note that Ti is the element that has a larger atomic radius than the other three and could produce a larger lattice distortion in the BCC solution. Thus, the compositional fluctuation seems to be accentuated by the tendency for Ti to stay out of the way, which may help lower the lattice strain and associated energy (SI Appendix, Fig. S12 and Supplementary Note 3). Dislocation shear ruins such favorable local configurations; its motion therefore encounters a dragging force. A pronounced concentration undulation was also observed when the larger Pd replaces Mn in the Cantor alloy, and the strength was elevated as a result of the enhanced concentration inhomogeneity (20).

Before concluding, we note several important implications. First, unlike in normal BCC metals, edge dislocations in BCC-HEAs no longer move smoothly and fast. The mobility difference between screw and edge dislocations diminishes. As such, edge dislocations can no longer be disregarded when it comes to the rate-limiting dislocation processes. In fact, the activation of edge dislocation motion can become an equal contributor to the flow stress as that of screws. This is different from conventional BCC metals, where the strength is governed solely by screw dislocations. In fact, an edge-dislocation-based model has already been proposed recently for interpreting the solid-solution strengthening in BCC refractory HEAs (21). Second, an appreciable activation barrier is present for detrapping from locally favorable regions (inhomogeneity on nanometer- or subnanometer scale), which can be regarded as yet another “high-entropy” effect, in this case arising from the high variability of local configuration and composition almost inevitable in a heavily concentrated solution of multiple principal elements. The detrapping on nanoscale, needed now both for kink propagation in the screw case and segment detrapping in the edge case, constitutes an unconventional activated process that is rate-controlling. The sizable barrier suggests an elevated dependence of the flow stress on deformation temperature and strain rate. If more local chemical order is introduced into these HEA solutions via prolonged processing or tuning of alloying elements (20), the activation barriers, and hence the stress needed to move dislocations, may be even higher. Third, the local-variability-facilitated kink nucleation may increase the density of cross-kinks to produce an extra pinning effect on screw dislocations, making it difficult for them to move but easier for them to stall and accumulate. Meanwhile, the rugged motion of edge dislocations also increases the probability of dislocation–dislocation interactions. These mechanisms should enhance dislocation multiplication, and hence may contribute to the pronounced strain hardening in BCC HEAs (22–24). All in all, our findings extend from the postulations in refs. 15 and 25–27, and demonstrate that dislocation behaviors in BCC HEAs can be clearly different from those in traditional simple BCC alloys (possible scenarios where BCC HEAs can be very similar to normal BCC are discussed in SI Appendix, Note 3 and Fig. S13).

Materials and Methods

The Interatomic Potentials.

For the study of dislocation behaviors in α-Fe, we used two embedded atom method (EAM) potentials developed by Zhou et al. (28) and Mendelev et al. (29). The simulation results obtained using the two potentials are similar. In this paper, we show the results using the potential by Zhou et al. (28). The interatomic interaction of Fe-Al is described by the second nearest-neighbor modified EAM developed by Kim et al. (30). The interatomic interaction in Co-Fe-Ni-Ti is described by a model EAM potential by Zhou et al. (28). At present, the EAM potential developed by Zhou et al. (28) is the most reliable empirical potential (needed to simulate dislocation behavior on relatively large scale), for BCC concentrated solid-solution alloys. This is because considerable prior work has tested this potential, including study of dislocation behaviors, in several HEAs. First, the values of lattice parameter, elastic constants, and unstacking fault energy predicted by this EAM potential are close to those obtained from density-functional theory (DFT) calculations in BCC Ti-Zr-Nb complex concentrated alloys (see details in ref. 27). Second, this potential can even reproduce a compact core structure of a 1/2<111> screw dislocation, consistent with that found in first-principles calculations. Third, Rao et al. have tested the Co-Fe-Ni-Ti potential we used for describing the properties in a BCC Co_16.67Fe_36.67Ni_16.67Ti₃₀ HEA (26). The elastic constants are calculated to be close to that of Fe-36Ni. The unstable stacking fault energies were found to be comparable to pure V. The 1/2<111> screw dislocation core described is nonplanar, spreading on several {110} planes like pure BCC metals. Fourth, this model potential has been recently used to study the dislocation behavior (31) and mechanical deformation-induced surface roughness (32) in an FCC Co₃₀Fe_16.67Ni_36.67Ti_16.67 high-entropy alloy. However, the specific potential we used, while predicting a qualitative difference from a conventional BCC metal, should be taken as an empirical HEA model and not literally the real-world Co_16.67Fe_36.67Ni_16.67Ti₃₀. For example, the observed nonsmooth energy landscape is meant to capture the general trend but not necessarily the exact degree of ruggedness in a corresponding laboratory HEA.

The Calculation of Chemical Short-Range-Order Parameters.

The pairwise multicomponent short-range-order (SRO) parameters are defined as ${\alpha }_{ij}^m=(p_{ij}^m-C_j)/({\delta }_{ij}-C_j)$, where δ_ij = 1 if i = j and 0 otherwise, $p_{ij}^m$ is the probability of finding a j-type atom near the i-type atom in shell m and C_j is the average concentration of j-type atom in the system. We calculated the values of SRO parameters ${\alpha }_{ij}^1$ for the nearest neighbor (m = 1). SI Appendix, Fig. S1 shows the values for each pair in the solid solution Co_16.67Fe_36.67Ni_16.67Ti₃₀. The parameter values are all close to zero, indicating that our BCC HEA is close to a random solid solution without significant local chemical order or segregation.

The Expansion of Dislocation Loops.

We investigated the expansion of dislocation loops in three BCC systems, i.e., α-Fe, Fe-5 at. % Al solid solution, Co_16.67Fe_36.67Ni_16.67Ti₃₀ complex alloy. The simulation box is oriented as x-[$111$], y-[$1\overline{1}0$], and z-[$11\overline{2}$]. The sample has dimensions of 60 nm × 5 nm × 56 nm, containing around 1.4 million atoms. Periodic boundary conditions were applied in all dimensions. The dislocation loop was created by displacing the two adjacent slabs in xz plane with a Burgers vector b = a/2[111] along the x direction, where a is the lattice constant. The radius of dislocation loops is 15 nm. The shear stress was applied in steps of 50-MPa increment at T = 300 K. The simulations were carried out under the constant stress with the isothermal–isobaric ensemble (33). All of the simulations were carried out using the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) code (34).

The Calculation of Drag Coefficients.

To characterize the dislocation dynamics, we calculated the drag coefficients B for both 1/2<111>/{110} edge dislocation and 1/2<111> screw dislocation in these three BCC systems (SI Appendix, Figs. S5 and S6). The samples have the dimensions of 24 nm × 36 nm × 24 nm. The system is oriented of x-[$11\overline{2}$], y-[$\overline{1}10$], z-[$111$] for the screw dislocation and x-[$111$], y-[$1\overline{1}0$], z-[$11\overline{2}$] for the edge dislocation. Periodic boundary conditions were applied in the x and z directions, and the free-boundary condition was applied in the y direction. Several atomic layers at upper and lower surfaces were fixed rigidly as the loading grips. To drive dislocations motion, we applied the constant shear stress to the system by adding a constant force in the rigid layers. The velocities of dislocations were obtained when the dislocations glided steadily. The drag coefficient is determined as the inverse of the slope by fitting the v-τ data in the linear regime. The simulations were carried out at different temperatures using the Nosé–Hoover thermostat (35).

The Calculation of Phonon Density of States.

The phonon density of states was calculated using the add-in package in LAMMPS (36). In this method, the dynamical matrix is constructed by observing the displacements of atoms based on the fluctuation-dissipation theory. The density of states is further obtained by integrating the phonon dispersion relation in the q-mesh space.

The Minimum Energy Path Calculations.

To explore the activation barriers facing dislocation motion in the Co_16.67Fe_36.67Ni_16.67Ti₃₀ alloy, we calculated the energy landscape of the movement of the 1/2<111> screw dislocation and 1/2<111>/{110} edge dislocation by using the CINEB method (14). The length of both dislocations is around 15 nm. The moving distance is less than 1 nm. The minimum energy pathway was searched without applying external stress. Our calculations are considered to be converged when the potential force on each replica is less than a stropping force tolerance of 0.01 eV/Å. The energy landscape is not influenced pronouncedly even if using a convergence tolerance of 0.001 eV/Å, one order of magnitude smaller, as shown in SI Appendix, Fig. S14. The results we presented here are obtained with an initial path along which the intermediate replicas are interpolated in a linear fashion between the first and last replicas. To check how the initial path may influence the optimized energy landscape, we added a random displacement (perturbation) to the atomic coordinates of intermediate replicas with a maximum value of 0.3 Å. As shown in SI Appendix, Fig. S15, although the energy landscape profile is slightly altered, the barrier height for detrapping dislocations remains practically the same (with a magnitude of several tenths of an eV).

The Calculation of Sound Speed.

The sound velocity along [111] direction is determined by v_s^[111] = [(C₁₁-C₁₂+C₄₄)/3ρ]^1/2, where C_ij is the elastic constant and ρ is the density. The elastic constants are C₁₁ = 229.9 GPa, C₁₂ = 135.5 GPa, and C₄₄ = 116.6 GPa for α-Fe and C₁₁ = 164.3 GPa, C₁₂ = 133.3 GPa, and C₄₄ = 95.0 GPa for Co_16.67Fe_36.67Ni_16.67Ti₃₀. The sound speeds were then estimated to be around 3 km/s for α-Fe and 2 km/s for Co_16.67Fe_36.67Ni_16.67Ti₃₀.

Data Availability.

Data generated or analyzed during this study are included in this article and its SI Appendix files.