Significance
The mitotic spindle machinery is a bipolar structure that segregates sister chromatids during cell division. Spindle assembly relies on the self-organization of motor proteins and microtubule filaments—dynamic polymers that constitute the spindle building blocks. How motors ensure a bipolar spindle-like structure is not understood. Here we build a liquid crystal droplet description of the spindle that quantitatively accounts for pole focusing as a function of dynein activity. Our results show how active forces driven by molecular motors can shape liquid crystalline droplets.
Keywords: mitotic spindle, Xenopus laevis, dynein, liquid crystals, active matter
Abstract
The metaphase spindle is a dynamic structure orchestrating chromosome segregation during cell division. Recently, soft matter approaches have shown that the spindle behaves as an active liquid crystal. Still, it remains unclear how active force generation contributes to its characteristic spindle-like shape. Here we combine theory and experiments to show that molecular motor-driven forces shape the structure through a barreling-type instability. We test our physical model by titrating dynein activity in Xenopus egg extract spindles and quantifying the shape and microtubule orientation. We conclude that spindles are shaped by the interplay between surface tension, nematic elasticity, and motor-driven active forces. Our study reveals how motor proteins can mold liquid crystalline droplets and has implications for the design of active soft materials.
Cell division relies on the self-organization of the mitotic spindle, a highly dynamic nonequilibrium structure that segregates chromosomes to the two daughter cells. This structure is composed of an aligned array of microtubules—dynamic polymers that nucleate, grow, and shrink—and energy transducing proteins such as molecular motors (1) that generate forces and fluxes within the structure. In vitro reconstitution approaches have advanced our basic understanding of how microtubule-motor mixtures self-organize (2–6). Motor activity can bundle, cluster, and slide microtubules. These processes generate nonequilibrium patterns in bulk mixtures such as asters, vortices (2, 6), or even turbulent-like flows (3) that can be recapitulated by active liquid crystal descriptions (7–9). The self-organization of molecular motors and microtubules in spindles has been the subject of intense investigation (10–14). Nevertheless, how motor-driven forces determine the characteristic bipolar shape of the spindle remains poorly understood (11, 15–18).
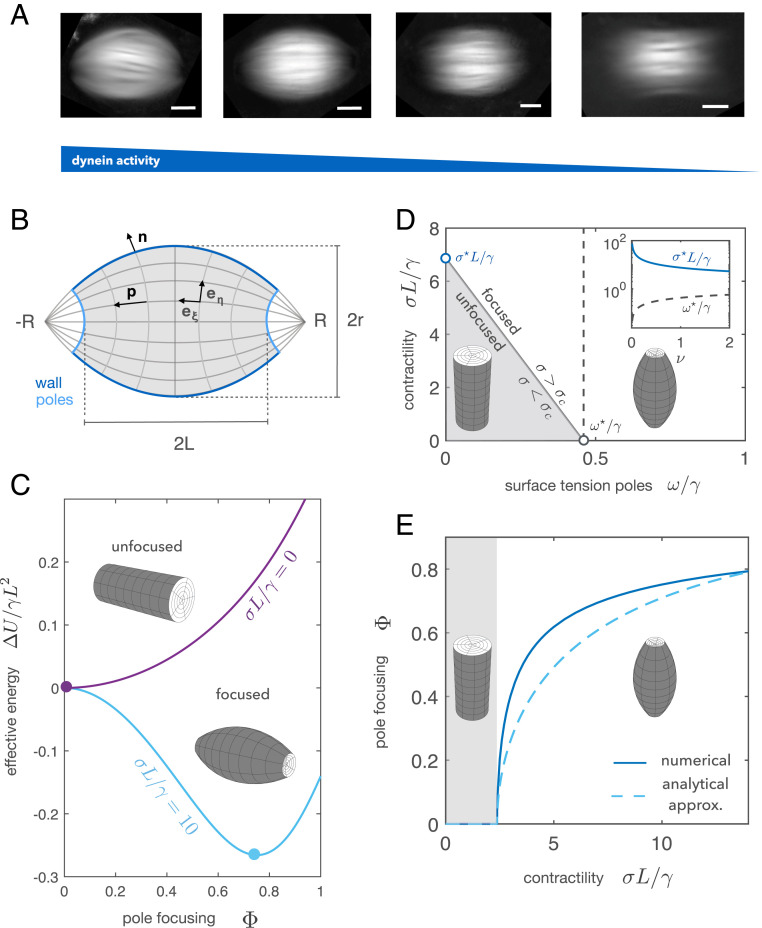
Mitotic motors are known to critically influence spindle shape and microtubule orientation (18–22). Inhibition of dynein leads to unfocused poles and flag-like microtubule structures (Fig. 1A) (20, 23), whereas inhibition of kinesin-5 leads to monopolar spindles (18, 24). How the interplay of motor-induced forces and the liquid crystalline order governs spindle shape is unclear. Here we combine theory and experiments to understand how motor activity shapes Xenopus egg extract spindles. By considering the spindle as a liquid crystal droplet, we find that its characteristic bipolar shape emerges through a barreling-type instability as a consequence of dynein activity. The mechanism resembles the process by which an elastic beam acquires a barrel-like shape under the action of compressive forces (25). We experimentally test our theory by characterizing the evolution of the spindle shape and microtubule orientation under the titration of a dynein inhibitor. Overall, our results are consistent with spindle pole focusing being a consequence of a mechanical instability driven by dynein-mediated forces.
Fig. 1.
Theory of spindle pole focusing. (A) Averaged retardance images of egg extract spindles under different concentrations of the dynein inhibitor p150-CC1. Images correspond to different titration days. (Scale bars: 20 m.) (B) The spindle is described as a tactoid of length , width , and pole-to-pole distance . The two dimensionless parameters describing the spindle shape are the pole focusing parameter and the aspect ratio . The spindle is parameterized using bispherical coordinates , and the director field follows the coordinate (SI Appendix). (C) Dimensionless energy of the spindle relative to the cylindrical configuration as a function of the pole focusing parameter for two different values of the stress . The shape is found by minimizing . (D) Phase diagram of how spindle shape changes as a function of the contractile stress and the surface tension at the poles . (Inset) Evolution of and as a function of the dimensionless volume . (E) Bifurcation diagram considering dynein contractility as the control parameter: Below a certain critical contractility the cylindrical configuration is stable. Once the contractility exceeds the threshold value , the structure undergoes axisymmetric buckling, acquiring a barrel-like shape. The solid curve corresponds to the full solution, and the dashed curve corresponds to the analytical solution expanding the energy up to quartic order in (SI Appendix). The study is done in the limit of constant volume () with parameters , , , and .
Differential Surface Tension and Bulk Contractility Control Spindle Pole Focusing
To understand how motor forces lead to spindle pole focusing, we formulate a coarse-grained theory considering the spindle as a liquid crystal with director , characterizing the local axis of microtubule orientation, and microtubule density . We consider the spindle as a tactoid (26–31) using a prescribed bispherical orientational field as depicted in Fig. 1B. For an equilibrium nematic liquid crystal, the bulk free energy reads (7, 9, 32)
| (1) |
where and are the Frank elastic constants (32), is a compression modulus, and corresponds to density fluctuations around a preferred density (7). The first two terms account for splay and bending deformations of a bulk nematic, respectively, while the last term penalizes density fluctuations. We do not include a saddle-splay term since it merely renormalizes the splay contribution for a bispherical director field (28). At the interface with the surrounding cytoplasm, we adopt the following expression for the surface free energy (28):
| (2) |
where is the normal vector to the interface, is the surface tension, and is an anchoring strength describing how microtubules anchor to the spindle surface (28, 31). The anchoring strength is chosen such that for normal and tangential anchoring to the surface, the resulting surface tension values are and , respectively. In general, motor activity is known to influence material properties such as the viscosity (8, 33) or the surface tension (34), as compared to the passive case. Hence, in general the surface tensions and depend on motor activity. In addition to contributing to surface tension, motor proteins can also generate active stresses in the bulk (7–9, 18). These can be written as
| (3) |
where the strength of the active stress is characterized by the coefficient . The sign of defines the extensile () or contractile () nature of the active stress (7–9). Motivated by in vitro studies, we consider the overall motor activity to be dominated by dynein and thus to be contractile (4, 35, 36). In general, active stresses can drive internal flows. In our approach, we neglect the role of viscous stresses arising from internal microtubule flows since they are not affected by dynein inhibition and the velocity gradients are small near the poles (SI Appendix, Fig. S1, and Materials and Methods). We parameterize the spindle by its length , width , and the distance between the virtual poles (Fig. 1B). Such parameterization allows us to continuously move from a tactoid to a cylinder, reproducing the shapes observed under the titration of dynein activity (Fig. 1A). The spindle shape is determined by two parameters: the pole focusing parameter and the aspect ratio . Additionally, we consider the spindle length to remain constant under changes in spindle shape. This constraint is motivated by recent evidence suggesting that spindle length is mainly set by microtubule nucleation gradients and tubulin mass balance but not by mechanics (37, 38).
Given the previous considerations, it can be shown that the curves are independent of the active stress (SI Appendix). This allows us to reduce the problem to the minimization of an effective work function that includes passive and active contributions. For simplicity, we consider the case where the spindle volume is conserved and further show that compressibility effects do not significantly change the physics of the problem within the parameter regime relevant for the spindle (SI Appendix, Fig. S2). Close to the cylindrical configuration, i.e., when the virtual pole-to-pole distance is much larger than the spindle length (Fig. 1B), the effective work function can be expanded for small pole focusing parameter . The problem can then be mapped to a Landau theory (39), where plays the role of the order parameter,
| (4) |
and the different coefficients can be explicitly determined (SI Appendix). In particular, changes sign as a function of the surface tension at the poles and the bulk contractility parameter . Provided that , axisymmetric buckling [alias barreling (25)] occurs (Fig. 1 C–E) whenever or exceed a critical value and the cylindrical configuration () becomes unstable (Fig. 1D and Movie S1). Taking as our control parameter, the spindle undergoes a barreling transition at the critical stress (Fig. 1E and SI Appendix):
| (5) |
where . Our theory shows that contractile stresses as well as differential surface tension can focus spindle poles via a barreling-type instability. Contractility may focus the poles either exerting normal stresses () or in-plane stresses () at the spindle poles, whereas nematic elasticity () and the surface tension at the spindle walls () oppose active forces.
Dynein Controls a Barreling-Type Instability in Spindles
Our theory predicts that spindle pole focusing is driven by a barreling-type instability. To verify this prediction, we experimentally quantified the changes in shape and microtubule orientation in spindles during the transition from closed to open poles by using an LC-Polscope (Materials and Methods) and titrating the dynein inhibitor p150-CC1 (23). The transition was found to be reversible and poles focused by adding back fresh extract (Materials and Methods and SI Appendix, Fig. S3).
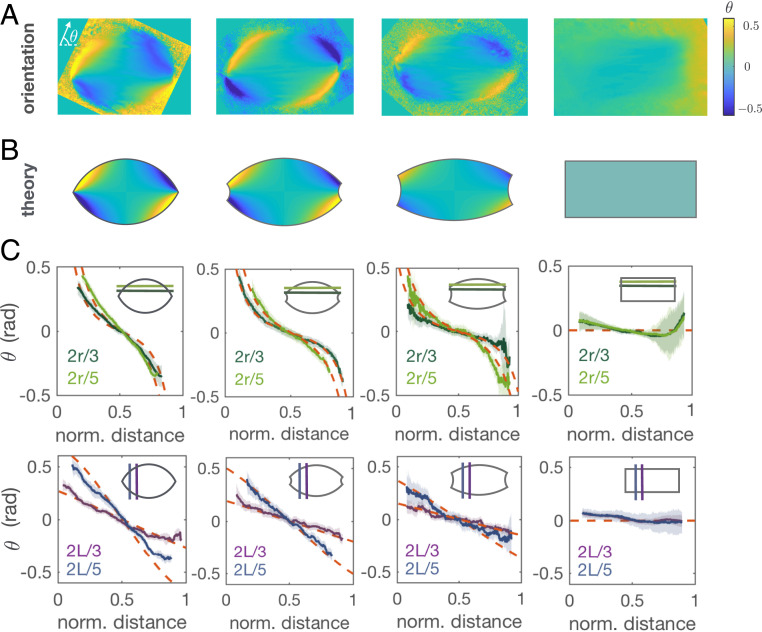
We characterized spindle shapes using the retardance images (Fig. 1A) to obtain the distance between the virtual poles (), spindle length (), and spindle width () (Materials and Methods and SI Appendix, Fig. S4). The steady state spindle length and width were not significantly affected by the inhibition of dynein and read 14 m and 9 m (, mean SD), respectively. Although spindles elongated right after the addition of p150-CC1, their steady state length after 30 min of inhibitor addition was not significantly affected during the titration (SI Appendix, Fig. S5, Left), consistent with microtubule nucleation mainly determining spindle size (37, 38). At the same time, the steady state spindle volume remained constant (SI Appendix, Fig. S5, Right) in agreement with previous studies where spindle volume recovers after external deformations (40). The evolution of the microtubule orientational field was quantified using the slow axis component of the LC-Polscope (Fig. 2A) and showed good agreement to the prescribed orientational field (Fig. 2 B and C). This result is a strong evidence that microtubule orientation in spindles is determined by passive liquid crystal elasticity and validates our choice of orientational field (14).
Fig. 2.
The microtubule orientational field in the spindle corresponds to a bispherical orientational field. (A) Averaged orientational fields corresponding to the different spindles in Fig. 1A where is the orientation angle respect to the spindle long axis. (B) Prescribed orientational field according to the shape parameters measured using the retardance signal. The angle range is chosen for visualization purposes. (C) Comparison between the prescribed orientational field in B (red dashed lines) and the averaged experimental orientational field in A (solid lines) for different sections along the spindle long axis (Upper) and along the spindle short axis (Lower). The shaded error bars correspond to SD.
To compare our theory to the experiments, we first estimated the different parameters. We calculated the mean spindle volume using the measured shape parameters for the tactoidal shape, which lead to a mean volume (, mean SEM) (Materials and Methods) and a corresponding dimensionless volume . To estimate the ratio of surface tensions , we used that in the absence of dynein activity () the spindle is found in an unfocused configuration, implying for our measured dimensionless volume (Fig. 1D). To deform the structure, contractility needs to be comparable to the surface tension at the spindle walls, and thus, we expect as shown in Fig. 1D. Using the values Pa and pN/m estimated from fluctuation spectroscopy (14), we obtain . Using for simplicity the one-constant approximation , nematic elasticity needs to be for the poles to be almost completely focused with the previous contractility value (SI Appendix, Fig. S6). Relaxing the approximation does not change the results significantly (SI Appendix, Fig. S6, Inset). With the values given above we estimate the nematic elasticity to be pN. Finally, microrheology studies on spindles suggest that the Young’s elastic modulus is on the order of kilopascals (41). Taking the compressibility modulus of the same order as the Young’s modulus, kPa, leads to a value , suggesting that the constant volume assumption is a good approximation. This is indeed confirmed when we compare the dependence of the aspect ratio with the pole focusing parameter of our model to the one found experimentally (SI Appendix, Fig. S3 and Fig. 3, Inset). SI Appendix, Table S1 summarizes all of the parameters used.
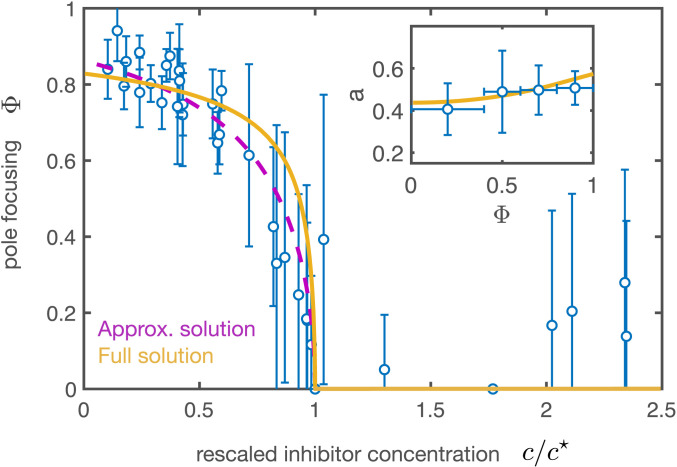
Fig. 3.
Bifurcation diagram under the titration of a dynein inhibitor. Pole focusing parameter as a function of the rescaled concentration of p150-CC1 inhibitor () with respect to the critical inhibitor concentration for the corresponding extract day. The circles correspond to the averaged experimental results using data from 10 different titrations during 7 different extract days ( spindles). Error bars indicate SD. The purple dashed curve and the yellow solid curve correspond to the dashed and solid curves in Fig. 1E, respectively, using , where is the dynein stress at zero inhibitor concentration. , and . The vertical error bars denote SD. (Inset) Aspect ratio a as a function of the pole focusing parameter (mean SD, spindles). The theoretical curve (yellow) stems from the constant volume condition and has no fitting parameters (SI Appendix). The parameters used for the theoretical curves are the same as in Fig. 1.
In Fig. 3 we compare the experimental results with the theoretical bifurcation curves (analytical and numerical curves in Fig. 1E) for our estimate of parameters. The theoretical curves are plotted assuming the active stress is a linear decreasing function of the inhibitor concentration (legend of Fig. 3). Given the fact that the critical concentration of the inhibitor depended on the extract used, we plotted versus the rescaled inhibitor concentration for each titration (Materials and Methods) (Fig. 3). Overall, we found good agreement between experiments and theory and thus conclude that a barreling-type instability captures the process of pole focusing in spindles.
Discussion
We have shown that pole focusing in spindles is a consequence of a mechanical instability driven by dynein activity. Dynein has been reported to generate active contractile stresses in disordered networks as a consequence of its accumulation at microtubule minus-ends (4, 35, 36). Our results are consistent with dynein focusing spindle poles by either generating bulk contractile stresses or increasing the surface tension at the poles, where dynein is known to be enriched (42). However, our experiments cannot distinguish these two scenarios.
Although we have shown that dynein drives pole focusing, it is less clear what drives pole unfocusing in the absence of dynein. Our model provides three different ways to unfocus the spindle poles: via active dipolar extensile stresses (), increasing nematic elasticity () (SI Appendix, Fig. S6), or decreasing the surface tension at the poles () (Fig. 1D). A potential candidate to account for these effects is kinesin-5, a tetrameric plus-ended motor that generates poleward flows by sliding antiparallel microtubule overlaps (42, 43). One possibility is that kinesin-5 motors generate extensile stresses in the spindle, similarly to artificial tetrameric motor clusters in in vitro active nematic systems (3). However, microtubule overlaps dramatically decrease close to the poles (13). Consistent with this picture, unfocusing of spindle poles can be achieved in the presence of a kinesin-5 inhibitor (FCPT), forcing tight binding of kinesin-5 onto microtubules and blocking its ATP activity (44). We thus propose that kinesin-5 might unfocus spindle poles by bundling microtubules in the spindle, thus increasing nematic elasticity and/or decreasing the effective surface tension at the poles.
Our study also provides an explanation to the puzzling problem of a bipolar structure under the double inhibition of kinesin-5 and dynein motors (13, 18, 45). In this case, spindle shape is set by a combination of differential surface tension and nematic elasticity, which in general can lead to a tactoidal shape with partially focused poles (Fig. 1D; ). Kinesin-5 bundles microtubules, thus leading to a flag-like configuration of the spindle in the absence of dynein activity. When dynein is added to the system, it focuses the poles by overcoming the stresses generated by kinesin-5, thus resuming a spindle-like shape. This raises the question of why the competition between kinesin-5 and dynein motors is necessary to set spindle shape given that a spindle-like structure is achieved in the absence of the two types of motors. A possible answer is that kinesin-5 poleward flux is essential for the proper microtubule organization in Xenopus extract spindles (13, 46, 47). However, as a side product of this activity, kinesin-5 induces pole unfocusing in the absence of dynein. Thus, we propose that dynein activity is essential to maintain a spindle-like structure to overcome pole unfocusing driven by kinesin-5, in line with recent studies in mammalian spindles (48).
We argue that our results generally apply to spindles made of microtubules that are shorter than the overall spindle size. While it was previously thought that this was only the case for large spindles such as in Xenopus (13, 49), recent work shows that this is also true for smaller spindles in other organisms such as Caenorhabditis elegans and sea urchin (50, 51). This suggests that the approach presented may be applicable to a wide range of spindles. More generally, our work shows that the spindle behaves as an active nematic droplet, similarly to in vitro condensates such as actin (31, 52, 53) or microtubule (54) tactoidal droplets. Further work will be needed to elucidate to what extent the physics of active nematic droplets can be used to understand cell division (52, 55, 56).
Materials and Methods
Cytoplasmic Extract Preparation, Spindle Assembly, and Biochemical Perturbations.
Cytostatic factor (CSF)-arrested Xenopus laevis egg extract was prepared as described previously (57, 58). In brief, unfertilized oocytes were dejellied and crushed by centrifugation. After adding protease inhibitors (Leupeptin, Pepstatin, Chymostatin [LPC]) and Cytochalasin D (CyD) to a final concentration of 10 g/mL each to fresh extract, we cycled single reactions to interphase by adding frog sperm (300 to 1,000 sperm/L final concentration) and calcium solution (10 mM , 250 mM KCl, 2.5 mM to 0.4 mM final concentration), with a subsequent incubation of 1.5 h. While fresh CSF extract containing LPC and CyD was kept on ice, all incubation steps were performed at 18 to 20 °C. The reactions were driven back into metaphase by adding 1.3 volumes of fresh CSF extract (containing LPC and CyD). Spindles formed within 30 min of incubation. We inhibited dynein with p150-CC1, purified according to ref. 59 and added to the reactions to the desired final concentration, and incubated for an additional 20 min. Prior to imaging, Höchst 33342 was added to the reactions to a final concentration 16 g/mL, to visualize DNA. For each titration, four different concentrations of p150-CC1 were used in 30 L reactions using the same extract batch, in the range from 1 to M. Backward titrations were set in parallel to the forward titrations, and increasing amounts of crude metaphase extract were added after 30 min to the different dynein-inhibited reactions. Titrations were repeated for different extract days. Six microliters of the previous extract reactions were dropped on MatTek glass bottom dishes and covered with 1 mL mineral oil to prevent the evaporation of the drops. In these conditions, spindles were remarkably stable and could be imaged continuously for more than 30 min. The critical dynein inhibitor concentration showed variability depending on the extract day; therefore, we estimated the critical concentration for each day and normalized the inhibitor concentration with respect to this value.
LC-Polscope.
Spindles were imaged using an LC-Polscope (on a Ti Eclipse microscope body) with an sCMOS camera (Hamamatsu Orca Flash 4.0) using a 60 1.2 NA water immersion objective. An open chamber was used to avoid possible mechanical stresses which could affect the degree of pole focusing. For data acquisition we used Manager (60). The exposure time was set to 200 ms. A total number of 362 spindles were analyzed. In order to estimate the shape parameters we followed a similar characterization as in ref. 30 and fit two intersecting circles forming a tactoid to the spindle retardance images. The threshold retardance value to define the spindle length was the background level for each spindle (SI Appendix, Fig. S4). Close to the completely unfocused configuration the position of the virtual poles was difficult to estimate; thus, we considered a spindle to be unfocused below a threshold value of the pole focusing parameter of 0.4. The room temperature was kept at 19 °C.
Speckle Microscopy.
Speckle microscopy on spindles was done by adding Atto 565 frog tubulin in egg extracts to a final concentration of nM and imaging using a Nikon spinning disk microscope (Ti Eclipse), an EMCCD camera (Andor iXon DU-888 or DU-897), a 60x 1.2 NA water immersion objective, and the software AndorIQ for image acquisition. The tubulin speckles were further analyzed using TrackMate (61) and classified according to which pole they moved to. The speed and density of speckle tracks in each population was obtained, and the center of mass velocity was computed.
Data Availability.
The experimental data are available from the 4TU.Centre for Research Data Repository: DOI: 10.4121/uuid:5a5ec254-b9df-4144-821b-de11f6f61b58.
Supplementary Material
Acknowledgments
We thank F. Decker, B. Dalton, F. Berndt, K. Ishihara, E. Rieckhoff, and T. Quail for critical reading of the manuscript. We also thank K. Ishihara for providing the construct to purify the protein p150-CC1 and J. Sharpe and J. Baumgart for useful discussions. We kindly thank Heino Andreas for frog maintenance. We acknowledge funding from European Molecular Biology Organization (Long-Term Fellowship 483-2016 to D.O.) and Human Frontier Science Program (Career Development Award 000 74/2014 to J.B.).
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
Data deposition: The experimental data are available from the 4TU.Centre for Research Data Repository (DOI: 10.4121/uuid:5a5ec254-b9df-4144-821b-de11f6f61b58).
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2002446117/-/DCSupplemental.
References
- 1.Howard J., et al. , Mechanics of Motor Proteins and the Cytoskeleton (Sinauer Associates, Inc., Sunderland, MA, 2001). [Google Scholar]
- 2.Nédélec F. J., Surrey T., Maggs A. C., Leibler S., Self-organization of microtubules and motors. Nature 389, 305–308 (1997). [DOI] [PubMed] [Google Scholar]
- 3.Sanchez T., Chen D. T. N., DeCamp S. J., Heymann M., Dogic Z., Spontaneous motion in hierarchically assembled active matter. Nature 491, 431–434 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Foster P. J., Fürthauer S., Shelley M. J., Needleman D. J., Active contraction of microtubule networks. Elife 4, e10837 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Norris S. R., et al. , Microtubule minus-end aster organization is driven by processive HSET-tubulin clusters. Nat. Commun. 9, 2659 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Roostalu J., Rickman J., Thomas C., Nédélec F., Surrey T., Determinants of polar versus nematic organization in networks of dynamic microtubules and mitotic motors. Cell 175, 796–808 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Marchetti M. C., et al. , Hydrodynamics of soft active matter. Rev. Mod. Phys. 85, 1143 (2013). [Google Scholar]
- 8.Prost J., Jülicher F., Joanny J.-F., Active gel physics. Nat. Phys. 11, 111–117 (2015). [Google Scholar]
- 9.Jülicher F., Grill S. W., Salbreux G., Hydrodynamic theory of active matter. Rep. Prog. Phys. 81, 76601 (2018). [DOI] [PubMed] [Google Scholar]
- 10.Burbank K. S., Mitchison T. J., Fisher D. S., Slide-and-cluster models for spindle assembly. Curr. Biol. 17, 1373–1383 (2007). [DOI] [PubMed] [Google Scholar]
- 11.Dumont S., Mitchison T. J., Force and length in the mitotic spindle. Curr. Biol. 19, R749–R761 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Loughlin R., Heald R., Nédélec F., A computational model predicts Xenopus meiotic spindle organization. J. Cell Biol. 191, 1239–1249 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Brugués J., Nuzzo V., Mazur E., Needleman D. J., Nucleation and transport organize microtubules in metaphase spindles. Cell 149, 554–564 (2012). [DOI] [PubMed] [Google Scholar]
- 14.Brugués J., Needleman D., Physical basis of spindle self-organization. Proc. Natl. Acad. Sci. U.S.A. 111, 18496–18500 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Gatlin J. C., Matov A., Danuser G., Mitchison T. J., Salmon E. D., Directly probing the mechanical properties of the spindle and its matrix. J. Cell Biol. 188, 481–489 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Reber S., Hyman A. A., Emergent properties of the metaphase spindle. Cold Spring Harbor Perspect. Biol. 7, a015784 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Prosser S. L., Pelletier L., Mitotic spindle assembly in animal cells: A fine balancing act. Nat. Rev. Mol. Cell Biol. 18, 187–201 (2017). [DOI] [PubMed] [Google Scholar]
- 18.Oriola D., Needleman D. J., Brugués J., The physics of the metaphase spindle. Annu. Rev. Biophys. 47, 655–673 (2018). [DOI] [PubMed] [Google Scholar]
- 19.Verde F., Berrez J.-M., Antony C., Karsenti E., Taxol-induced microtubule asters in mitotic extracts of Xenopus eggs: Requirement for phosphorylated factors and cytoplasmic dynein. J. Cell Biol. 112, 1177–1187 (1991). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Merdes A., Ramyar K., Vechio J. D., Cleveland D. W., A complex of NuMA and cytoplasmic dynein is essential for mitotic spindle assembly. Cell 87, 447–458 (1996). [DOI] [PubMed] [Google Scholar]
- 21.Compton D. A., Focusing on spindle poles. J. Cell Sci. 111, 1477–1481 (1998). [DOI] [PubMed] [Google Scholar]
- 22.Goshima G., Nédélec F., Vale R. D., Mechanisms for focusing mitotic spindle poles by minus end-directed motor proteins. J. Cell Biol. 171, 229–240 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Gaetz J., Kapoor T. M., Dynein/dynactin regulate metaphase spindle length by targeting depolymerizing activities to spindle poles. J. Cell Biol. 166, 465–471 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Skoufias D. A., et al. , S-trityl-L-cysteine is a reversible, tight binding inhibitor of the human kinesin Eg5 that specifically block mitotic progression. J. Biol. Chem. 281, 17559–17569 (2006). [DOI] [PubMed] [Google Scholar]
- 25.Goriely A., Vandiver R., Destrade M., Nonlinear euler buckling. Proc. R. Soc. London A Math. Phys. Eng. Sci. 464, 3003–3019 (2008). [Google Scholar]
- 26.Zocher H., Heller W., Schillerschichten als Reaktionsprodukte der langsamen Eisenchlorid-Hydrolyse. Z. Anorg. Allg. Chem. 186, 75–96 (1929). [Google Scholar]
- 27.Buining P. A., Lekkerkerker H. N. W., Isotropic-nematic phase separation of a dispersion of organophilic boehmite rods. J. Phys. Chem. 97, 11510–11516 (1993). [Google Scholar]
- 28.Prinsen P., van der Schoot P., Shape and director-field transformation of tactoids. Phys. Rev. E 68, 021701 (2003). [DOI] [PubMed] [Google Scholar]
- 29.Barry E., Hensel Z., Dogic Z., Shribak M., Rudolf O., Entropy-driven formation of a chiral liquid-crystalline phase of helical filaments. Phys. Rev. Lett. 96, 018305 (2006). [DOI] [PubMed] [Google Scholar]
- 30.Oakes P. W., Viamontes J., Tang J. X., Growth of tactoidal droplets during the first-order isotropic to nematic phase transition of F-actin. Phys. Rev. E 75, 061902 (2007). [DOI] [PubMed] [Google Scholar]
- 31.Weirich K. L., et al. , Liquid behavior of cross-linked actin bundles. Proc. Natl. Acad. Sci. U.S.A. 114, 2131–2136 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Prost J., The Physics of Liquid Crystals (Oxford University Press, 1995), vol. 83. [Google Scholar]
- 33.Oriola D., Alert R., Casademunt J., Fluidization and active thinning by molecular kinetics in active gels. Phys. Rev. Lett. 118, 088002 (2017). [DOI] [PubMed] [Google Scholar]
- 34.Salbreux G., Jülicher F., Mechanics of active surfaces. Phys. Rev. E 96, 032404 (2017). [DOI] [PubMed] [Google Scholar]
- 35.Foster P. J., Yan W., Fürthauer S., Shelley M. J., Needleman D. J., Connecting macroscopic dynamics with microscopic properties in active microtubule network contraction. New J. Phys. 19, 125011 (2017). [Google Scholar]
- 36.Tan R., Foster P. J., Needleman D. J., McKenney R. J., Cooperative accumulation of dynein-dynactin at microtubule minus-ends drives microtubule network reorganization. Dev. Cell 44, 233–247.e4 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Oh D., Yu C.-H., Needleman D. J., Spatial organization of the Ran pathway by microtubules in mitosis. Proc. Natl. Acad. Sci. U.S.A. 113, 8729–8734 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Decker F., Oriola D., Dalton B., Brugués J., Autocatalytic microtubule nucleation determines the size and mass of Xenopus laevis egg extract spindles. eLife 7, e31149 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Landau L. D., On the theory of phase transitions. Ukr. J. Phys. 11, 19–32 (1937). [Google Scholar]
- 40.Takagi J., Itabashi T., Suzuki K., Shimamoto Y., Kapoor T. M., Ishiwata S., Micromechanics of the vertebrate meiotic spindle examined by stretching along the pole-to-pole axis. Biophys. J. 106, 735–740 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Itabashi T., et al. , Probing the mechanical architecture of the vertebrate meiotic spindle. Nat. Methods 6, 167–172 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Uteng M., Hentrich C., Miura K., Peter B., Surrey T., Poleward transport of Eg5 by dynein-dynactin in Xenopus laevis egg extract spindles. J. Cell Biol. 182, 715–726 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Valentine M. T., Fordyce P. M., Krzysiak T. C., Gilbert S. P., Block S. M., Individual dimers of the mitotic kinesin motor eg5 step processively and support substantial loads in vitro. Nat. Cell Biol. 8, 470–476 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Groen A. C., et al. , A novel small-molecule inhibitor reveals a possible role of kinesin-5 in anastral spindle-pole assembly. J. Cell Sci. 121, 2293–2300 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Mitchison T. J., et al. , Roles of polymerization dynamics, opposed motors, and a tensile element in governing the length of Xenopus extract meiotic spindles. Mol. Biol. Cell 16, 3064–3076 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Desai A., Maddox P. S., Mitchison T. J., Salmon E. D., Anaphase A chromosome movement and poleward spindle microtubule flux occur at similar rates in Xenopus extract spindles. J. Cell Biol. 141, 703–713 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Miyamoto D. T., et al. , The kinesin Eg5 drives poleward microtubule flux in Xenopus laevis egg extract spindles. J. Cell Biol. 167, 813–818 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Hueschen C. L., Galstyan V., Amouzgar M., Phillips R., Dumont S., Microtubule end-clustering maintains a steady-state spindle shape. Curr. Biol. 29, 700–708.e5 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Crowder M. E., et al. , A comparative analysis of spindle morphometrics across metazoans. Curr. Biol. 25, 1542–1550 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Redemann S., et al. , C. elegans chromosomes connect to centrosomes by anchoring into the spindle network. Nat. Commun. 8, 15288 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Lacroix B., et al. , Microtubule dynamics scale with cell size to set spindle length and assembly timing. Dev. Cell 45, 496–511 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Weirich K. L., Dasbiswas K., Witten T. A., Vaikuntanathan S., Gardel M. L., Self-organizing motors divide active liquid droplets. Proc. Natl. Acad. Sci. U.S.A. 116, 11125–11130 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Scheff D. R., et al. , Tuning shape and internal structure of protein droplets via biopolymer filaments. Soft Matter, 10.1039/C9SM02462J (2020). [DOI] [PubMed]
- 54.Edozie B., et al. , Self-organization of spindle-like microtubule structures. Soft Matter 15, 4797–4807 (2019). [DOI] [PubMed] [Google Scholar]
- 55.Giomi L., DeSimone A., Spontaneous division and motility in active nematic droplets. Phys. Rev. Lett. 112, 147802 (2014). [DOI] [PubMed] [Google Scholar]
- 56.Leoni M., Manyuhina O. V., Bowick M. J., Marchetti M. C., Defect driven shapes in nematic droplets: Analogies with cell division. Soft Matter 13, 1257–1266 (2017). [DOI] [PubMed] [Google Scholar]
- 57.Murray A. W., Cell cycle extracts. Methods Cell Biol. 36, 581–605 (1991). [PubMed] [Google Scholar]
- 58.Hannak E., Heald R., Investigating mitotic spindle assembly and function in vitro using Xenopus laevis egg extracts. Nat. Protoc. 1, 2305–2314 (2006). [DOI] [PubMed] [Google Scholar]
- 59.King S. J., Brown C. L., Maier K. C., Quintyne N. J., Schroer T. A., Analysis of the dynein-dynactin interaction in vitro and in vivo. Mol. Biol. Cell 14, 5089–5097 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Edelstein A. D., et al. , Advanced methods of microscope control using Manager software. J. Biol. Methods 1, 10 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Tinevez J.-Y., et al. , TrackMate: An open and extensible platform for single-particle tracking. Methods 115, 80–90 (2017). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The experimental data are available from the 4TU.Centre for Research Data Repository: DOI: 10.4121/uuid:5a5ec254-b9df-4144-821b-de11f6f61b58.