The capillary Kir channel as sensor and amplifier of neuronal signals: Modeling insights on K⁺-mediated neurovascular communication

Significance

Local brain activity is rapidly accompanied by a vascular response to increase blood perfusion. How neuronal activity is sensed by the vasculature is not fully understood. This process, known as neurovascular coupling, constitutes the physiological basis of functional neuroimaging scans and its disruption is associated with cognitive disorders and stroke. We have recently demonstrated the active involvement of capillary endothelial cells in neurovascular communication through the activity of Kir channels. Here, using a computational modeling approach, we investigate the biophysical determinants of capillary-mediated neurovascular coupling. Simulations show how capillary Kir channels sense neuronal activity and initiate and amplify electrical signals—through a process that resembles electrical activity in excitable cells—to produce a robust vasodilatory response.

Abstract

Neuronal activity leads to an increase in local cerebral blood flow (CBF) to allow adequate supply of oxygen and nutrients to active neurons, a process termed neurovascular coupling (NVC). We have previously shown that capillary endothelial cell (cEC) inwardly rectifying K⁺ (Kir) channels can sense neuronally evoked increases in interstitial K⁺ and induce rapid and robust dilations of upstream parenchymal arterioles, suggesting a key role of cECs in NVC. The requirements of this signal conduction remain elusive. Here, we utilize mathematical modeling to investigate how small outward currents in stimulated cECs can elicit physiologically relevant spread of vasodilatory signals within the highly interconnected brain microvascular network to increase local CBF. Our model shows that the Kir channel can act as an “on–off” switch in cECs to hyperpolarize the cell membrane as extracellular K⁺ increases. A local hyperpolarization can be amplified by the voltage-dependent activation of Kir in neighboring cECs. Sufficient Kir density enables robust amplification of the hyperpolarizing stimulus and produces responses that resemble action potentials in excitable cells. This Kir-mediated excitability can remain localized in the stimulated region or regeneratively propagate over significant distances in the microvascular network, thus dramatically increasing the efficacy of K⁺ for eliciting local hyperemia. Modeling results show how changes in cEC transmembrane current densities and gap junctional resistances can affect K⁺-mediated NVC and suggest a key role for Kir as a sensor of neuronal activity and an amplifier of retrograde electrical signaling in the cerebral vasculature.

Neuronal activity leads to a rapid increase in local cerebral blood flow (CBF) by dilating penetrating (parenchymal) arterioles (PAs) and surface (pial) arteries. The process which underlies this functional hyperemia is referred to as neurovascular coupling (NVC) and allows blood supply to respond to the metabolic demands in the brain (1). NVC is essential for normal brain function and is disrupted in several cognitive disorders and stroke (2). Functional hyperemia also constitutes the physiological basis for functional neuroimaging techniques that are widely used to probe brain function (3).

Despite significant research efforts, how neuronal activity is sensed by the vasculature is far from being fully understood and the communicating cells and chemical messengers involved are still under debate. It is now recognized that NVC mechanisms involve a variety of mediators including nitric oxide, arachidonic acid metabolites, and K⁺ ions that are released from neurons or glial cells (4–9). An emerging paradigm is that astrocytes are the bridges between neurons and the vasculature to mediate much of the hyperemic response (4, 8, 10–12). However, this view has been challenged by data questioning whether astrocytes mediate an arteriolar response in functional hyperemia (13–16). Studies also suggest that vasoactivity may originate from deeper layers of the cortex (17, 18) and that vasodilatory signals may ascend along the cerebral microcirculation to dilate surface arteries (17). Whether retrograde vasodilatory signaling can account for disparate findings regarding the involvement of astrocytes in NVC needs to be further examined (17).

K⁺ is a byproduct of every neuronal action potential (AP) (19, 20), and following neuronal stimulation, Ca²⁺ mobilization in astrocytic endfeet may open large conductance calcium-activated potassium (BK_Ca) channels (4, 5) to increase the K⁺ efflux. Thus, neuronal activity can lead to an increase in perivascular/interstitial K⁺. Regardless of its neuronal or astrocytic origin, an increase in extracellular potassium concentration ([K⁺]_o) can activate vascular inward rectifying potassium (Kir) channels, resulting in vessel hyperpolarization, dilation, and a subsequent increase in local CBF (4, 21).

The arteriolar smooth muscle has been considered as the primary target of NVC mediators. Recent studies, however, put the endothelial layer at center stage in NVC. Data suggest that retrograde vasodilatory signals propagate through the endothelial layer to dilate feeding arteries (17, 22), and evidence of coupling between neuronal activity and the vasculature at the capillary level has been presented (22, 23). We have recently proposed that brain capillaries act as a neuronal activity-sensing network which initiate electrical (hyperpolarizing) signals that ascend to dilate upstream arterioles and increase local CBF (22). In support of this proposition, we have shown that local K⁺ release at distal capillary sites evokes significant and Kir2.1-dependent hyperpolarization and dilation of the feeding PA, and that hyperemic responses to whisker stimulation are significantly attenuated in endothelial cell (EC)-specific Kir2.1 knockout mice (EC Kir2.1^−/−) in vivo. Our data suggest extracellular K⁺ as a critical mediator for capillary-level NVC and the Kir2.1 channel as the key molecular player for sensing neuronal activity-dependent elevations in [K⁺]_o and translating them into retrograde hyperpolarizing signals.

Although our previous work provided strong experimental evidence for capillary-to-arteriole communication during NVC, the requirements and determinants of this signal conduction remain elusive, and are only accessible, at this time, in silico. The effectiveness of this capillary-initiated vasodilatory signaling will depend on whether the number of capillary EC (cEC) Kir channels activated is sufficient to produce a robust local hyperpolarization, and also on the vessels’ conduction properties that will determine the rate of signal dissipation as it spreads in a highly intertwined brain microvascular network. In this study, we utilized a mathematical framework to investigate the underlying mechanisms that enable capillaries to sense neuronally induced changes in [K⁺]_o and transmit vasodilatory signals effectively to upstream contractile vascular segments (i.e., transitional capillaries with contractile pericytes or PAs). Through integration of model with experimental data, we examine the mechanistic basis for retrograde electrical signaling in the cerebral microcirculation. Model simulations suggest that K⁺ can evoke AP-like responses in the endothelial layer through the activation of Kir channels, enabling capillary-initiated signals to ascend upstream the vascular network and orchestrate rapid and refined regional blood flow control. Results highlight the role of Kir channel as a critical regulator of the hyperemic response.

Results

Modeling cEC Electrophysiology.

We investigate electrical signaling in the brain microcirculation by first developing a mathematical model for a single cEC. Patch data in freshly isolated mouse cerebral cECs revealed the presence of functional Kir2.1 and TRPV4 channels in these cells (22, 25). In contrast to ECs from all other vascular beds examined up to this date, they do not express small (SK) and intermediate (IK) conductance calcium-activated K⁺ channels. To examine the role of these newly characterized channels (i.e., Kir2.1 and TRPV4) in capillary electrophysiology, we form minimal mathematical representations (namely models I and II) by reducing a detailed mathematical model of a cEC (adapted from ref. 24 and Fig. 1 A, Left). This minimalistic approach incorporates explicit descriptions for the current through Kir and TRPV4 channels, while all other transmembrane currents are linearized and lumped into a nonspecific background current (I_bg) with a conductance, G_bg (Fig. 1 A, Right). The proposed simplification allows us to focus on the key role of Kir/TRPV4 on K⁺-mediated dynamics in capillaries and overcome limitations arising from the absence of functional data for other membrane channels in cECs.

Fig. 1.

(A) Single-cell models of cEC electrophysiology. A detailed model of cEC incorporates currents through Kir (I_Kir), TRPV4 (I_TRPV4), nonselective cation (NSC) and chloride (Cl) channels, sodium–potassium (NaK) and plasma membrane-calcium ATPase (PMCA) pumps, sodium–calcium (NCX) exchanger, and the NaKCl cotransport. Other channels such as hyperpolarization-activated cyclic nucleotide-gated (HCN) channels (I_f), or piezo channels (I_piezo) may be present as suggested by expression data (55). A minimal representation of the cEC includes explicit descriptions for I_Kir and I_TRPV4, while the rest of the transmembrane currents are lumped into a nonspecific background current (I_bg). Kir and TRPV4 activity can be modulated by the levels of PIP₂. (B) Simulations of electrical signal propagation are performed in realistic angioarchitectures reconstructed from the vibrissa primary sensory cortex of a mouse (26). cECs are coupled in series through gap junctions to create multicellular capillary segments and networks. Conduction in arterioles accounts for the number of ECs and coupled SMCs at each longitudinal position. Each EC–SMC unit is modeled by including a background current, I_bg,PA = G_bg,PA(V_m – E_bg,PA), based on an effective membrane conductance of the two-cell system and a net Kir current [I_Kir,PA = G_Kir,PA (V_m – E_K)]. Gap junctional currents between neighboring cells in capillaries (I_gj) and in arterioles (I_gj,PA) are based on V_m gradients. PAs and pial arteries are shown in red, veins in blue, and capillaries in gray.

A first minimal model of a cEC (model I) contains an explicit mathematical description for the Kir current (I_Kir) and the I_bg:

$$I_{Kir}=\frac{{\overline{G}}_{Kir}\sqrt{{\left[K^{+}\right]}_o}\left(V_m-E_K\right)}{1+\exp \left(\frac{{\text{V}}_{\text{m}}-{\text{V}}_{0.5}}{\text{k}}\right)}$$ [1]

$$I_{bg}=G_{bg}\left(V_m-E_{bg}\right),$$ [2]

where E_bg is the reversal potential for I_bg; E_K = RT/F ln([K⁺]_o/[K⁺]_i) is the Nernst potential for K⁺ where R, T, and F are the universal gas constant, temperature, and the Faraday’s constant, respectively; and V_0.5 and k are parameters that describe a sigmoidal inhibition of Kir with membrane depolarization (i.e., V_m for half-maximal inactivation and the steepness factor, respectively). The Boltzmann-type formula (Eq. 1) captures the I_Kir’s inward rectification and the negative slope conductance as V_m approaches more depolarized potentials (i.e., the inhibition of I_Kir as V_m depolarizes yields the characteristic N-shaped relationship depicted in Fig. 2B). The channel’s conductance increases with [K⁺]_o $\left(G_{Kir}={\overline{G}}_{Kir}\sqrt{{\left[K^{+}\right]}_o}\right)$, capturing the activation of the channel by extracellular K⁺. Using a standard Hodgkin–Huxley-type formalism, the time-dependent changes in V_m are predicted from Eq. 3:

$$C_m\frac{d{V}_m}{dt}+I_{tot}=0,$$ [3]

where C_m is the membrane capacitance and $I_{tot}=I_{Kir}+I_{bg}$.

Fig. 2.

Single-cEC V_m response to [K⁺]_o. (A) Simulated V_m responses (model I) to step increases (blue lines) and decreases (red lines) in [K⁺]_o show jumps between hyperpolarized and depolarized V_m and hysteresis. Solid and dotted traces correspond to $G_{bg}/{\overline{G}}_{Kir}$ ratios of 0.7 and 0.3 (mM^1/2), respectively. (B–E) Stability analysis. Representative I_Kir and (−I_bg) traces are depicted as a function of V_m at increasing (3, 5, and 8 mM) [K⁺]_o. Intersection points denote steady states (stable: solid circles, unstable: open circle) where the total current is zero. (B) At low [K⁺]_o the outward Kir current is small and the cell rests at a depolarized V_m. (C) Increasing [K⁺]_o leads to a rightward and upward shift of the I_Kir curve as a result of the increase in G_Kir and E_K. As the [K⁺]_o increases past a critical concentration, the system undergoes a saddle-node bifurcation and three steady states emerge. The depolarized and hyperpolarized stable steady states (solid red circles) are separated by an unstable steady state in between (threshold V_m, open circle). (D) Further increase in [K⁺]_o drives the system past a second saddle-node bifurcation. The presence now of only one hyperpolarized steady state will force the cell to jump to a hyperpolarized V_m close to E_K. (E) Stability diagram shows the parameter space where bistability (depicted in C) exists. Blue/red color map shows the ΔV_m threshold at points within the bistable region, for transition to a hyperpolarized/depolarized state. (F) Patch-clamp recordings of isolated cECs (Inset) with 6 mM and 60 mM [K⁺]_o bath concentrations (n = 24) were used to estimate Kir and background conductances (${\overline{G}}_{Kir}=0.18\pm 0.1$ nS/mM^0.5 and G_bg = 0.06 ± 0.04 nS). (G) Minimal model (model II) examines Kir-TRPV4 dynamics. Stochastic openings of a single TRPV4 channel yield transient depolarizations. At intermediate [K⁺]_o, transient fluctuations between two polarization levels are predicted as the system crosses a bifurcation point during TRPV4 opening. V_m fluctuations are dampened at higher levels of stimulation as the TRPV4 current is not sufficient to transition the system to the depolarized state.

To examine the contribution of TRPV4 to cEC dynamics, we separate the TRPV4 current (I_TRPV4) from the lumped background current in model I (model II). We account for the stochastic opening of TRPV4 and the resulting transient depolarizing current as described in ref. 25. The simplifying assumptions in the minimal modeling approach (models I and II) are validated against the detailed EC model (SI Appendix, Fig. S1).

Multicellular Model of Microvascular Networks.

cECs were coupled through gap junctions to construct multicellular capillary networks. Current flow between adjacent cECs is estimated based on the electrical gradient and the cEC-to-cEC coupling resistance (R_gj). Capillary networks were constructed with a geometry that approximates isolated ex vivo preparations (22) (see Fig. 4 A, Inset) or were adapted from larger reconstructed microvascular networks in the brain cortex (26) (Fig. 1B). Conduction of electrical signals in PAs is accounted by considering three ECs coupled to three SMCs at each longitudinal position (Fig. 1 B, Inset). Each PA EC–SMC unit has an effective leak conductance reflecting the net transmembrane resistance (G_bg,PA = 1/R_m,PA, where R_m,PA is the effective membrane resistance of the PA EC–SMC unit) and a total Kir conductance (G_Kir,PA). Each EC–SMC unit is coupled to an adjacent unit through gap junctions (coupling resistance, R_gj,PA).

Fig. 4.

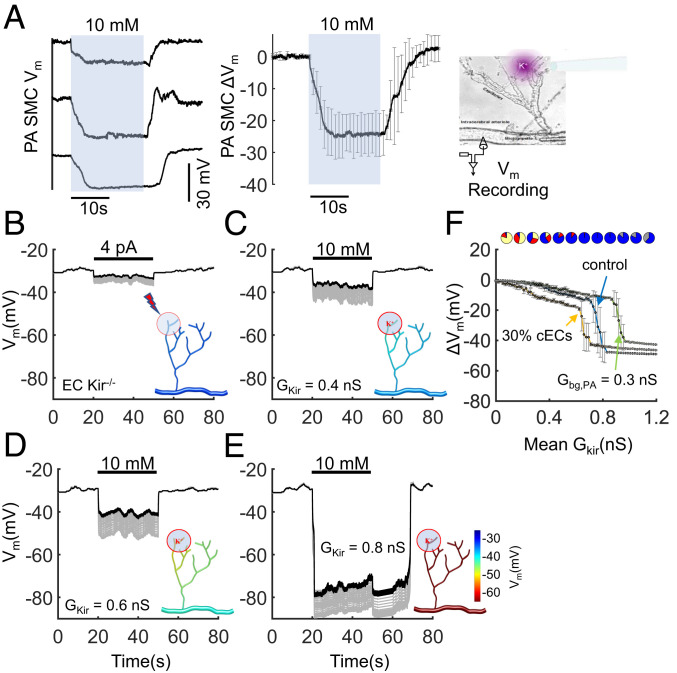
K⁺-induced electrical signaling in an ex vivo capillary-PA preparation. (A) Smooth muscle V_m recordings in an isolated and pressurized PA with the attached capillary network (Inset) when 10 mM K⁺ is picospritzed onto the capillary ends. (Left) Representative traces from three mice. (Right) The average (± SD) of six recordings from five mice. (B–E) Model simulations in a corresponding, microvascular network (Inset) that contains 45 cECs (represented by model II) and a 200-µm segment of a PA consisting of 30 coupled EC–SMC units. A localized region at one end of the capillary network is stimulated by injecting 4 pA of current in B (to simulate a response in the absence of EC Kir [EC Kir^−/− mice]), or via application of 10 mM K⁺ to 7 cECs in C–E. In C–E G_Kir in each cEC is assigned from a normal distribution with SD of 0.2 nS and the mean G_Kir progressively increases from 0.4 to 0.6 and 0.8 nS. In E, the activity of cEC Kir and TRPV4 is dynamically regulated (i.e., gradual decrease in Kir and increase in TRPV4 conductance with time constants of 3 and 6 min, respectively). (F) Summary data for the predicted level of PA hyperpolarization (at ∼120 µm away from the capillary–PA junction), shown as mean ± SD of 30 simulations with random Kir distributions. cECs are represented with model I. Control conditions (n = 7 cECs [∼15%] stimulated; G_bg,PA = 0.2 nS); leftmost trace (n = 15 cECs [∼30%] stimulated; G_bg,PA = 0.2 nS); rightmost trace (n = 7 cECs [∼15%] stimulated; G_bg,PA = 0.3 nS). Pie charts indicate the resting distribution of cECs based on the classification in Fig. 2E.

Kir Mediates Sustained cEC Hyperpolarization in Response to a K⁺ Challenge.

We used mathematical modeling to investigate the ability of cECs to sense an increase in [K⁺]_o by responding through Kir activation. Model I captures the salient features of Kir dynamics in an isolated cEC during a K⁺ challenge (Fig. 2A). A moderate increase in [K⁺]_o (i.e., from 3 to 8 mM) opens Kir channels and produces a sustained hyperpolarization. Simulations show jumps of V_m from a depolarized to a hyperpolarized potential when [K⁺]_o increases past a critical concentration level ([K⁺]_o ≥ 5 mM in this figure), in agreement with an “all or none” V_m response in cultured ECs (27) and diameter responses in PAs, as well as in coronary and cerebral arteries, when increasing [K⁺]_o (10, 22, 28–30). The critical concentration for the hyperpolarizing V_m jump depends on the $G_{bg}/{\overline{G}}_{Kir}$ ratio, as can be observed in solid vs. dashed blue traces (corresponding to solid vs. dashed green arrows in the heat map of Fig. 2E, respectively). Decreasing [K⁺]_o back to resting levels can either return the cEC V_m to the depolarized resting potential (solid red line) or leave the cell at a hyperpolarized potential (dashed red line). This behavior is attributed to the presence of two bifurcation points (i.e., saddle-node bifurcations), yielding a system that can exhibit hysteresis during a K⁺ challenge/washout cycle and bistability within a K⁺ concentration window (Fig. 2 B–E). As a consequence of this bistability, small biological variability in channel densities can yield a binomial distribution of hyperpolarized and depolarized resting membrane potentials, as observed in cultured ECs (31, 32).

cECs Can Have a Bistable V_m.

The stability diagram in Fig. 2E summarizes the system’s dynamic behavior as we move around in the parameter space. The diagram depicts the K⁺ concentration window for bistability as the ratio of $G_{bg}/{\overline{G}}_{Kir}$ changes. As [K⁺]_o increases or $G_{bg}/{\overline{G}}_{Kir}$ decreases, the threshold V_m (unstable steady state; open circle in Fig. 2C) gets closer to the depolarized steady state (the solid red circle at depolarized V_m in Fig. 2C). This lowers the ΔV_m threshold, ΔV_Hyp (and the corresponding current threshold, ΔI_Hyp) for jumping from the depolarized to the hyperpolarized steady state while increasing the ΔV_m threshold, ΔV_Dep, for transition in the opposite direction (SI Appendix, Fig. S2). We separate the bistability region in hyperpolarization-favoring (blue) and depolarization-favoring (red) areas based on the magnitude of ΔV_m thresholds required for transition toward one or the other direction (Fig. 2E). cECs can thus be classified into four groups according to their Kir conductance relative to the total transmembrane conductance: cells that have a single depolarized (yellow region) or hyperpolarized (gray region) steady state, depolarization-favoring (red region), and hyperpolarization-favoring (blue region) bistable cells (Fig. 2E).

Studies have previously provided evidence for Kir-mediated bistable membrane potentials in ECs and SMCs (32, 33). We examined whether the Kir current density in cECs is sufficient to create a bistable system at physiological [K⁺]_o. cECs were enzymatically isolated from mouse brain slices (SI Appendix, SI Materials and Methods) and whole-cell patch data were used to estimate the Ba²⁺-sensitive (G_Kir) and -insensitive (G_bg) transmembrane conductances (Fig. 2F) (22, 34). Channel conductances [${\overline{G}}_{Kir}=0.18\pm 0.1$ nS/mM^0.5; G_bg = 0.06 ± 0.04 nS (n = 24); mean C_m of 8 pF] place cECs within/near the predicted bistability region at physiological [K⁺]_o (refer to SI Appendix, Supplementary Information Text and Fig. S2 for the effect of model parameters on predicted V_m bistability window). Dynamic regulation of the number of active channels per cell can change the percentage of bistable cells in a population of cECs. Overall, theoretical analysis and experimental data suggest that the presence of a dominant Kir current in cECs can create a “bistable switch” in V_m, a characteristic of electrical excitability and a necessary condition for regenerative, AP-like propagation of electrical signals (35).

TRPV4 Mediates Transient V_m Responses during a K⁺ Challenge.

Stochastic openings of TRPV4 can produce transient depolarizations in V_m (36). At moderate levels of K⁺ stimulation (i.e., from 3 to 5 mM), the TRPV4 bursting activity can drive the system past the bifurcation points (i.e., transitioning a cEC from gray to yellow in Fig. 2E), producing large transient V_m jumps (Fig. 2G and SI Appendix, Fig. S3C). These results are in line with experimental data where isolated ECs and arterioles exhibit fluctuations between two polarization levels upon stimulation with intermediate K⁺ concentrations (∼5 to 8 mM) (27, 32, 37). This experimentally observed instability suggests a bistable system, which can be reproduced in silico when accounting for the stochastic opening of TRPV4. The stochastic V_m fluctuations are dampened with further increasing [K⁺]_o (i.e., ≥8 mM), as the TRPV4 current is not sufficient to drive the cell past the threshold to transition to the stable depolarized V_m (Fig. 2G and SI Appendix, Fig. S3D).

Bistable Cells Amplify Electrical Signals and Promote Hyperpolarizing Jumps in Capillary Segments.

AP firing, as described by Hodgkin–Huxley-type dynamics, is due to the voltage dependency of the Na⁺ channel’s (Na_v) activation gate that initially creates [i.e., prior to the Na_v inactivation or the delayed voltage gated potassium channel [K_v] activation) a bistable V_m (SI Appendix, Fig. S4)]. Thus, from a dynamics point of view, V_m bistability allows for the “all-or-none” response and the regenerative propagation of a depolarizing front along neurons during an AP. By the same token, Kir-induced bistability can facilitate excitability and regenerative propagation of electrical signals along the endothelium (35). In Fig. 3A, we formulated a model of a capillary segment by placing cECs (model I) in series and coupled them via gap junctions with a cell-to-cell electrical resistance, R_gj. Model simulations show that at low Kir current densities (G_Kir = 0.2 nS), a local K⁺ stimulus produces a small local hyperpolarization that spreads passively and attenuates along the capillary segment with a length constant $\mathrm{\lambda }=\sqrt{\raisebox{1ex}{$r_m$}\!\left/ \!\raisebox{-1ex}{$r_i$}\right.}$ ($r_i=R_{gj}/L_{EC}$ and $r_m=R_m{L}_{EC}$ are the axial and membrane resistivities per unit length, respectively, and L_EC and R_m are the cEC length and membrane resistance). At higher Kir conductances relative to the background current (G_Kir = 0.4 nS, still within the range of values obtained from single cEC patch clamp recordings), that is, when cECs are bistable, the model predicts significant local hyperpolarization (stimulated cells jump close to E_K) that spreads without attenuation (i.e., an “excitable” system; Fig. 3 A and B).

Fig. 3.

Electrical conduction in a capillary segment in response to local elevations of [K⁺]_o. cECs (model I) were coupled in series to form a model of a capillary segment. (A) An array of 20 axially connected and identical cECs are stimulated at the left end (n = 2 cells) with 10 mM K⁺. V_m responses are depicted at rest (dashed line) and following stimulation, for G_Kir = 0.2 nS and 0.4 nS with R_gj = 10 MΩ. Bistable cECs (G_Kir = 0.4 nS; blue region in Fig. 2E) can produce substantially higher local hyperpolarization, compared to passive cECs (G_Kir = 0.2 nS; yellow region in Fig. 2E), which propagates without attenuation. (B) Time course of the V_m responses presented in A. The system resets to the resting depolarized V_m after stimulus termination when low levels of G_Kir are assumed (G_Kir = 0.2 nS; yellow cECs), but it does not when higher G_Kir (G_Kir = 0.4 nS; blue cECs) promotes a hyperpolarizing V_m jump upon stimulation. Traces for the stimulated cells are shown in green and for the last cell in red. (C) TRPV4 activity (model II) can facilitate resetting in the excitable system. (D–F) Level of distal (400 μm/20 cells from stimulus site) hyperpolarization (ΔV_m) color-coded for a long (n = 200 cells) (D) and a short (n = 20 cells) (F) capillary segment. Depending on G_Kir and R_gj, passive conduction, facilitated hyperpolarization, or excitability with or without regenerative propagation of a hyperpolarizing front is predicted. In a long capillary segment, increasing R_gj (arrow in D) can increase distal hyperpolarization by promoting regenerative conduction (E). (G) Time course of a hyperpolarizing jump in a short, well-coupled (R_gj = 10 MΩ) segment upon stimulation of two or four cells at one end. (H and I) Regenerative propagation of the hyperpolarizing front in a long segment (n = 200 cells) with R_gj of 100 MΩ (H) and 1 GΩ (I).

The “passive” system resets following stimulus termination in our capillary model (Fig. 3B; G_Kir = 0.2 nS), that is, V_m returns to its basal value upon removal of the stimulus. However, removing the stimulus could not reset V_m in the excitable system (Fig. 3B; G_Kir = 0.4 nS), as the local bistable cells did not depolarize by the return of [K⁺]_o to resting levels due to hysteresis (Fig. 2A, dotted line). Furthermore, as theoretical analysis in ref. 35 indicates, an infinitely long capillary (i.e., capillary length [L] >> λ) with identical and bistable ECs can promote regenerative conduction of either a hyperpolarizing (blue ECs) or a depolarizing (red ECs) front, but not both. Thus, the model capillary cannot return to the resting V_m values upon stimulus termination under the excitable conditions in Fig. 3B. Similar to an AP, delayed inactivation/activation of channels may be required to depolarize the capillary back to resting V_m (discussed in later sections).

TRPV4 Activity Can Facilitate the System’s Return Following Stimulus Termination.

Model simulations in Fig. 3C suggest that the presence of TRPV4 channels can provide a resetting mechanism for the excitable capillary segment in Fig. 3 A and B. Basal TRPV4 channel activity (SI Appendix, Fig. S5), at levels that have been observed experimentally (25), was capable of turning back the “bistable switch” in an excited capillary segment. The depolarizing effect of stochastic TRPV4 transients along the capillary segment enables capillary depolarization to resting V_m levels after stimulus termination (i.e., the current threshold for transitioning to the depolarized V_m is reduced after the stimulus is removed). Basal TRPV4 activity can, thus, conditionally facilitate (i.e., depending on the required threshold current) the return of the capillary to the depolarized resting potential upon stimulus termination. More robust resetting can be achieved by the presence of delayed activated currents (SI Appendix, Fig. S6), or by a progressive down-regulation of Kir activity and/or up-regulation of TRPV4 upon stimulation as observed, for example, during plasma membrane phosphatidylinositol 4,5-bisphosphate (PIP₂) hydrolysis or reduction of adenosine 5′-triphosphate (ATP) (25, 34). This would slowly transition cECs from hyperpolarization-favoring (blue) during stimulus initiation to depolarization-favoring (red or yellow), enabling capillary V_m to return to resting potential and protect the system against a prolonged excitability.

Weak Intercellular Coupling Promotes Regenerative Electrical Conduction.

Whether a K⁺ challenge can produce a hyperpolarizing jump (i.e., whether a capillary is “excitable”) depends on the ratio of G_Kir/G_bg, the stimulus strength (i.e., number of cells stimulated), and the coupling between neighboring cECs (Fig. 3 D and F). Interestingly, the minimum required G_Kir for excitability decreases as the resistance (R_gj) between adjacent ECs increases under the conditions of Fig. 3D (i.e., long capillary segment; L >> λ). Thus, for the given level of stimulation and Kir activity, significant local and distal hyperpolarization can be achieved only if R_gj is increased within an optimal range (green arrow in Fig. 3D and traces in Fig. 3E) (35). Our model predicts that electrical signals can propagate along the endothelium even if R_gj is in the GΩ range [compared to the R_gj in the MΩ range that enables robust but passive propagating responses in arteries (38, 39)]. This behavior is attributed to the enhanced efficacy of K⁺, as a stimulus onto cECs, in eliciting a voltage response from a cEC when R_gj is higher (i.e., current loss to neighboring cells is reduced and opening of Kir channels induces a larger local change in V_m), which allows for local hyperpolarization above the ΔV_m threshold (ΔV_Hyp) for “turning the bistable switch.” Once V_m passes the threshold value, the cEC jumps to a hyperpolarized potential and drives hyperpolarization of its neighboring cell, causing a domino-like effect along the capillary (regenerative conduction), analogous to the propagation of APs in neurons.

Capillary Length, Coupling Resistance, and Amplification of Hyperpolarization.

Simulations in short (relative to λ) capillary segments revealed different V_m dynamics (Fig. 3F) compared to long segments (Fig. 3D). Significant hyperpolarization can be achieved with lower G_Kir, and R_gj in the megaohm range. Stimulation of a few cECs, and the resulting small initial hyperpolarization, is enhanced by the opening of Kir channels along the length of the capillary segment. This Kir-mediated facilitation results in higher levels of local and distal hyperpolarization (facilitated hyperpolarization), and the fidelity of this response increases with an elevation in Kir density/activity. This mode of positive feedback by Kir channels has been theoretically analyzed and experimentally observed in neurons (40) and in arteries (41–43). Further increase in G_Kir above a threshold value, but below what is required for regenerative conduction in Fig. 3D, promotes a hyperpolarizing jump in V_m upon K⁺ stimulation (excitable region in Fig. 3F). This Kir-mediated segment excitability differs from the regenerative conduction described in long segments by the absence of a propagating hyperpolarizing front, that is, the last cEC jumps to the hyperpolarized V_m before the stimulated cECs (notice the crossover of the red [last cell] vs. green [stimulated cells] traces in Fig. 3G compared to Fig. 3 H and I), and by its dependence on the size of the capillary. Stimulation of a sufficient number of cECs may allow such a spatially confined excitability in a capillary network. Thus, depending on the length, stimulus strength, gap junctional resistance, and channel densities, focal stimulation of a capillary segment may result in 1) a relatively small local V_m change that spreads passively and dissipates with distance (passive system), 2) a more pronounced local and distal hyperpolarization as the conducted signal is facilitated by the partial opening of Kir channels in neighboring cells (facilitated conduction), 3) a segment excitability without the regenerative propagation of a hyperpolarizing front (excitable system), and 4) a full-blown regenerative propagating hyperpolarizing front (regenerative conduction).

Conduction Velocity.

In a capillary with passive characteristics (i.e., constant R_m), the ratio of λ to the characteristic time constant τ = C_mR_m (∼130 ms) (i.e., $v=\lambda /\tau =L_{EC}/\left(C_m\sqrt{r_i{r}_m}\right)$; ∼0.6 to 6 mm/s) governs the time to record a detectable V_m change at a distal cell upon local stimulation. Distal V_m will continue to rise and approach a new steady-state value within milliseconds as dictated by τ. In Fig. 3 G–I we examine the conduction velocity in capillary segments under conditions that promote the opening of distal Kir channels (i.e., nonpassive conductions). In a short capillary segment (L = 200 μm; R_gj = 10 MΩ), distal cells respond fast upon K⁺ stimulation ($\lambda /\tau$ at rest is ∼6 mm/s) and detectable V_m changes are predicted at the distal end within tens of milliseconds (Fig. 3G). Thus, cECs in a short and well-coupled capillary segment responds nearly simultaneously to the K⁺ stimulus. However, the time for the capillary segment to rise to the new steady-state V_m depends on the stimulus strength (number of cells stimulated) and can become significantly slower than τ. This behavior suggests that the response dynamics of distal cECs are not limited by the time to charge the cells’ membrane capacitance, but rather by the rate of progressive Kir channel recruitment as V_m hyperpolarizes. Experimental data in small isolated capillary networks (Fig. 4A) demonstrate such characteristics, providing evidence for a Kir-mediated amplification of the propagating electrical signal.

In long capillary segments (L = 4,000 μm; R_gj = 100 MΩ to 1 GΩ; $\lambda /\tau =2\hspace{0.5em}\text{to}\hspace{0.5em}0.6$ mm/s), distal cells respond with a delay (reflecting the delayed arrival of the hyperpolarizing front) followed by a fast transition to a hyperpolarized V_m (Fig. 3 H and I). The conduction velocity of the hyperpolarizing front is $v\approx 40$ cECs/s or ≈ 0.8 mm/s for R_gj of 1 GΩ (Fig. 3I), and increases to 120 cECs/s ≈ 2.4 mm/s, if R_gj = 100 MΩ (Fig. 3H). The latter is still three orders of magnitude less than typical conduction velocities in unmyelinated neuronal axons, owing to approximately three orders of magnitude larger membrane (r_m) and axial (r_i) resistivities of a capillary to those of axons (SI Appendix, Table S1).

Evidence for Regenerative Hyperpolarization in the Brain Microcirculation—an Inverted Sustained AP.

We have recently provided ample evidence that elevation of K⁺ around capillaries transmits electrical signals to upstream arterioles (22). Picospritzing 10 mM K⁺ onto a few capillary ends in an ex vivo preparation of a PA with attached capillaries (Cap-PA) (Fig. 4 A, Right, Inset) (SI Appendix, SI Materials and Methods) caused significant hyperpolarization (up to 30 mV) and maximal dilation of the PA, hundreds of microns away from the stimulus site (Fig. 4A). However, the magnitude of outward Kir current in cECs (often below the limit of detection in patch-clamp experiments) suggests that K⁺ stimulation of a few cECs can only generate up to a few picoamperes of hyperpolarizing current. By comparison, equivalent conducted responses in small arterioles typically require several nanoamperes of stimulating current (38, 44, 45). This disparity in stimulatory current requirement cannot be explained by differences in size or in the number of cells between arteries and capillaries. How does the stimulation of a few cECs produce robust dilations in upstream feeding arteries?

We formulated a model capillary-PA network that resembles the Cap-PA preparation and examined the effect of increasing [K⁺]_o on cECs located on one end of the capillary branch (∼15% of total cECs in the network). Simulations assume a heterogeneous population of cECs with variable number of active Kir channels to account for biological variability, similar to values observed experimentally (Fig. 2F). As the mean G_Kir increases, the majority of the cell population shifts from passive (yellow) to depolarization-favoring (red) to hyperpolarization-favoring (blue), as shown in the respective pie charts in Fig. 2F. A heterogeneous capillary network behaves passively when most cells are passive or depolarization-favoring and remains insensitive to K⁺ stimulation (Fig. 4C). This response is comparable to that of a capillary network without Kir channels (EC Kir^−/−) which is locally stimulated with an equivalent current injection (Fig. 4B). Thus, the model predicts a limited hyperpolarization of the feeding PA (black trace) under passive conditions, significantly below the observed 20- to 30-mV arteriolar response observed experimentally (Fig. 4A). The effect from an equivalent local stimulation in vivo is expected to be even lower since the current would disperse in both upstream and downstream directions and to every connected side branch. Thus, comparison of ex vivo and in silico data suggests that amplification of the capillary-initiated electrical signaling, by a mechanism intrinsic to the microvascular network, is essential to explain our experimental observations.

When a higher Kir density is assumed (mean G_Kir = 0.6 nS), the majority of cECs become bistable, and the K⁺ challenge produces a local hyperpolarization that is enhanced by the Vm-induced opening of cECs along the capillary network (Fig. 4D). A network containing mostly bistable and hyperpolarization-favoring (i.e., blue) cECs (Fig. 4E) produces significant local response upon stimulation (V_m jumps close to E_K), and the predicted level of PA hyperpolarization is comparable to the experimentally observed SMC responses in Fig. 4A. Furthermore, the V_m traces in Fig. 4E can account for the slow increase in V_m hyperpolarization observed in Fig. 4A as Kir channels are progressively recruited. Additionally, consistent with the observations in Fig. 4A, the return of the system to its resting V_m in Fig. 4E is delayed, since the bistable system can stay at a hyperpolarized potential following stimulus termination until the relative Kir activity drops below the threshold for turning the “bistable switch.” At Kir activity levels below the requirement for excitability, amplification of hyperpolarization (facilitated conduction) and a passive return (i.e., without the need of TRPV4 or dynamic changes in channel conductances) to resting levels following stimulus termination is observed (Fig. 4D).

Fig. 4F presents summary data from simulations using the Cap-PA model as the mean G_Kir varies from 0 to 1.2 nS, with cECs modeled using model I. In a relatively well-coupled network (R_gj = 10 MΩ), sufficient Kir activity (G_Kir = 0.8 nS) promotes a V_m jump to values close to E_K upon K⁺ stimulation (10 mM) even with only 15% of total cECs stimulated. As the leakiness of the PA increases, or the number of stimulated cells decreases, higher Kir activity is required to promote significant PA hyperpolarization through network excitability. Collectively, simulation results suggest that even with conservative estimates for critical parameter values (R_gj = 10 MΩ, n = 15 cells [30% of total cEC stimulated], r_m,PA = 5 GΩcm), the observed PA SMC hyperpolarization in the experiments (up to 30 mV) cannot be explained unless the capillary-initiated signal is significantly amplified by bistable ECs as it is conducted toward the PA, that is, an excitable system.

Binary vs. Graded Responses of Capillary Modules to K⁺ Stimulus.

Simulations using realistic angioarchitectures allow us to relate the ex vivo data to in vivo function. We used a small segment of an in vivo capillary network reconstruction from the vibrissa primary sensory cortex of a mouse (adapted from ref. 26) with its feeding PA and a draining parenchymal venule (PV) to examine how neuronal signals are integrated in capillaries to produce hyperpolarization (dilation) of the feeding arteriole (Fig. 5C). Simulations assume a heterogeneous population of cECs with variable number of active Kir channels to account for biological variability. We examine the effect of changing the mean G_Kir in the capillary network—probing the system’s ability to dynamically regulate Kir activity, as occurs through PIP₂/ATP depletion (25, 34). Simulations in Fig. 5A show that stimulating a small number of randomly distributed cECs (∼10 to 14% of total cECs, highlighted in white) with 10 mM K⁺ can hyperpolarize the feeding PA. When the mean cEC G_Kir is small (i.e., 0.1 nS; yellow cECs), a passive capillary network is insensitive to K⁺ stimulation. As the mean G_Kir (and the percentage of bistable cECs) increases, so does the sensitivity of the microvasculature to local K⁺ stimulation. In a relatively well-coupled network (R_gj = 50 MΩ), graded increases in PA hyperpolarization are predicted as the number of stimulated cECs increases (Fig. 5A; mean G_Kir = 0.4 and 0.5 nS). Above a mean G_Kir threshold (>0.5 nS, where majority of cECs are hyperpolarization-favoring bistable), a highly sensitive capillary module allows maximum hyperpolarization when a sufficient number of cells (≥12% of cECs) are stimulated, and the module operates in a binary (on/off) mode. Summary results for the model network are presented in Fig. 5B. Depending on the level of Kir activity, the microvascular network can exhibit graded or “all-or-none” responses as the number of stimulated cells increase, and for a given stimulatory scenario, modulation of G_Kir can regulate the fidelity of the response. In larger microvascular network simulations, graded responses can be achieved by summation of binary inputs from multiple activated capillary network regions (SI Appendix, Fig. S7).

Fig. 5.

Binary or graded electrical responses in microvascular networks. (A) Predicted V_m hyperpolarization (color-coded) in a capillary network reconstruction from the vibrissa primary sensory cortex of a mouse with its feeding PA and draining venule, stimulated with 10 mM of [K⁺]_o (stimulated sites are highlighted with white circles). Vascular geometry from ref. 26. A heterogeneous population of cECs with different Kir densities is assumed (normal distribution of cEC G_Kir with SD of 0.2 nS). Simulations for different mean cEC G_Kir and various number of randomly selected cECs stimulated (as a percentage of total in the network) are presented. At low levels of mean G_Kir (0.1 nS, first column), the system is insensitive to K⁺ stimulus for the number of stimulated cells examined. Increasing the mean G_Kir level (0.4 and 0.5 nS, second and third columns) places more cECs in the bistable region, and the level of evoked PA hyperpolarization is enhanced as the number of stimulated cECs increase. Further increase in the mean G_Kir makes the capillary network highly sensitive to K⁺ stimulus (fourth column, mean G_Kir = 0.6 nS, majority of cells are hyperpolarization-favoring). Surpassing a threshold number of stimulated cells results in a hyperpolarizing jump for the entire capillary network, which in turn increases the level of PA hyperpolarization. (B) Summary data for the mean PA hyperpolarization in A. Pie charts show the distribution of cECs at mean G_Kir levels of 0.1, 0.4, 0.5, and 0.6 nS, respectively. Data are shown as mean ± SD averaging results from 30 trials with randomly distributed Kir densities and stimulated cECs. (C) Schematic of the network used for the simulations in A and B where capillaries are depicted in gray, the feeding PA in red, and the draining PV in blue. Simulations use model I for cECs and R_gj = 50 MΩ.

Retrograde Electrical Signaling through Capillaries and PAs.

We used simulations in larger realistic microvascular network reconstructions to test whether a focal stimulation deep in the cortex can be conducted to the surface microcirculation to cause a robust dilation and a pronounced increase in local CBF. We first examined the propagation of electrical activity upon direct focal stimulation of a PA. In simulations of Fig. 6A we stimulate a PA segment (100 μm in length), approximately located in cortical layer IV or layer VI, with 10 mM K⁺. Under control conditions, we assume a relatively modest Kir activity in both capillaries and PAs (i.e., G_Kir = 0.3 nS, G_Kir,PA = 0.65 nS). The model predicts only a few millivolts of arteriolar hyperpolarization in this scenario. The fidelity of local K⁺ stimulation and the efficiency of electrical conduction along the PA were significantly affected by the level of cEC coupling in the surrounding capillaries; this is attributed to the increased dissipation of the electrical signal at capillary branching points as R_gj decreases. Results also demonstrate dependence on the location of focal stimulation. A higher number of branching points in the deeper layers of the cortex leads to attenuated hyperpolarization and less-efficient electrical conduction when the PA is stimulated in approximately layer VI vs. in layer IV (Fig. 6B). Despite the inhibitory effect of the capillary network on the retrograde signaling through the PA, conditions could be identified (G_Kir,PA = 2.4 nS; R_gj = 100 MΩ) that would promote PA excitability and significant hyperpolarization of the feeding surface arteries. Overall, simulation results suggest that significant upstream hyperpolarization upon focal PA stimulation with K⁺ requires sufficient Kir channel density to amplify the stimulatory current and a high coupling resistance at branching capillaries to limit the dissipation of the conducting current toward the capillary network.

Fig. 6.

Ascending [K⁺]_o-mediated hyperpolarization along penetrating arterioles in a reconstructed microvascular network. A 1,000- × 500- × 500-µm³ reconstructed network containing ∼8,000 cECs, feeding PAs, and draining PVs is utilized to investigate the effect of focal K⁺ stimulation on microvascular network hyperpolarization. Vascular geometry from ref. 26. Each cEC is modeled using model I. (A) V_m response is presented color-coded following stimulation of a PA segment (100 μm) located approximately in cortical layers IV or VI with 10 mM K⁺ (highlighted white box). Simulations show level of PA hyperpolarization as G_Kir,PA and R_gj increase, and when the surrounding cECs (within a 4-nL volume; 50 cECs) are also exposed to 10 mM [K⁺]_o. (B and C) Summary data comparing the average level of PA hyperpolarization upon focal stimulation of the PA at two different depths (layer IV vs. layer VI) (B), or a focal PA simulation with or without stimulation of surrounding capillaries (C).

Stimulating cECs in addition to PA ECs can facilitate vasodilatory signals to ascend toward the surface circulation. Simulations show that K⁺-induced stimulation of surrounding cECs, in addition to a direct stimulation of the PA segment, increases the local stimulatory current, and as a result increases ascending hyperpolarization through the PA (Fig. 6A). Furthermore, under conditions that promote regenerative conduction in the capillary network, such as increased Kir density and low gap junctional coupling, stimulation of a few cECs can elicit robust retrograde electrical signaling in the brain. In Fig. 7 we tested whether stimulation of cECs deep in the cortex can be transmitted to the upstream PAs and surface pial arteries. Approximately 200 cECs within a 10-nL tissue volume were stimulated with 10 mM K⁺. In Fig. 7 A, Middle, a significant Kir channel density (G_kir = 0.6 nS) resulted in local excitability (∼30 mV of hyperpolarization) and the hyperpolarizing signal remained confined in the stimulated area. The hyperpolarizing influence on the PA was rather modest (a few millivolts) and local. Increasing the number of stimulated capillary regions could produce robust PAs hyperpolarization (SI Appendix, Fig. S7). In Fig. 7A, Right, as well as in Fig. 7B, we examined the effect of preferentially distributing capillary Kir channels closer to PAs while maintaining a similar average Kir density in the capillary network. Simulations assume a gradient in capillary Kir conductance (G_Kir reduces from 1.2 nS in capillaries close to PA to 0.3 nS in capillaries close to the venular end of the network) and an increased R_gj (400 MΩ) to promote regenerative conduction. Simulation results show that the same stimulatory scenario as before yields a significant local hyperpolarization that regeneratively ascends through the capillary network toward the surface microvasculature (Fig. 7). Thus, the electrical signal can efficiently propagate through the capillary network as a result of conditions that promote regenerative conduction, allowing stimulations deep in the cortex to be transmitted over long distances and affect tone of upstream PAs and surface pial arteries. The regenerative electrical signaling was spatially confined (Fig. 7, top view) and preferentially directed toward PAs and surface arteries by the gradient in Kir density.

Fig. 7.

Kir-mediated control of electrical conduction in microvascular networks. (A) Simulations of electrical signal propagation in a reconstructed network containing ∼25,000 cells within a 500-nL volume. K⁺ stimulation of cECs deep within the cortex (white dots, Left) results in local excitability (Middle) or in regenerative electrical conduction toward the surface vessels (Right). Vascular geometry from ref. 26. Two hundred cECs within approximately a 10-nL volume are stimulated with 10 mM of K⁺. Higher R_gj and preferential distribution of Kir channels in the vicinity of PAs (Right) promote regenerative (AP-like) conduction of electrical signals (Middle: R_gj = 50 MΩ, G_kir = 0.6 nS; Right: R_gj = 400 MΩ, G_kir = 1.2 to 0.4 nS [decreasing 0.1 nS per generation from the arteriolar to the venular end of the network]). (B) Time course of ascending electrical signaling under conditions promoting regenerative conduction. Similar to A, preferential distribution of Kir in cECs near PAs promotes regenerative propagation of electrical signals (R_gj = 100 MΩ, G_kir is 1.2 nS in the vicinity of PA and 0.3 nS away from the PA). Network V_m distribution is depicted at different time points from stimulus initiation (t = 0; 10 mM of K⁺). A hyperpolarizing front ascends toward the surface vasculature without attenuation, while it remains spatially confined near the feeding PA (top view, Bottom Right). Each cEC in the network is represented by model I.

Discussion

Capillary ECs in the brain have been extensively studied in the context of the blood–brain barrier, yet very little is known about their electrophysiological properties. The high capillary density in the brain allows for a close proximity of cECs to every neuron, thus uniquely positioning them to monitor neuronal activity. However, whether the capillary endothelium is capable of sensing neuronal activity and transmitting signals to cause upstream vasodilation—a question with profound implications for global NVC mechanisms—has received little research attention. Recent experimental evidence indicates that capillaries may act as a sensory web to detect neuronal activity through Kir channel-mediated sensing of local elevations in [K⁺]_o (22). These changes can be communicated by a hyperpolarizing electrical signal from capillaries to PAs through the endothelial layer. Together with direct activation of arteriolar (SMC and EC) Kir channels by K⁺ from astrocytes and/or neurons, the capillary-initiated electrical signals can produce stable vasodilation and hyperemia. Model analysis in this study elucidates the biophysical determinants of K⁺ sensing by cECs and the parameters/mechanisms that regulate retrograde electrical signal transmission from capillaries to upstream feeding arteries in the brain.

The Capillary Kir Channel as a Sensor of K⁺.

Activation of Kir family members by V_m and [K⁺]_o has been well characterized and likely reflects unblocking of the channels by internal polyamines (46). As [K⁺]_o increases, the current–voltage relationship shifts in an upward and rightward direction (Fig. 2 B–D) due to an increase in G_Kir, E_K, and V_0.5 (Eq. 2). Consequently, the Kir activity at resting V_m increases. For example, at resting conditions (V_m ≈ −30 mV), increasing [K⁺]_o from 3 mM to 10 mM causes an ∼100-fold increase in Kir chord conductance (from ∼0.0006 nS to ∼0.07 nS). However, this 100-fold increase in conductance yields only a small (subpicoampere) increase in the outward, hyperpolarizing current at resting potentials. The K⁺-induced Kir opening, however, can be self-amplifying since the cell hyperpolarizes in response to the increased I_Kir, which can further increase activity through channel opening by V_m hyperpolarization. Mathematical analysis (Fig. 2) quantifies this effect and shows how small increases in [K⁺]_o can exert a profound hyperpolarizing effect as a result of a bifurcation that promotes a hyperpolarizing jump when a threshold [K⁺]_o is crossed. Thus, the Kir channel acts essentially as an “on–off” switch to rapidly and profoundly hyperpolarize the cell membrane in capillaries and arterioles when extracellular K⁺ increases.

Kir-Mediated Control of Microvascular V_m.

ECs are classified as electrically nonexcitable cells; however, studies have often revealed nontypical V_m dynamics: Two resting potentials have been observed in cultured EC monolayers (31, 32), and isolated ECs may exhibit spontaneous transitions between a hyperpolarized and a depolarized potential when bath K⁺ increases (24, 27). Similarly, all-or-none responses to increasing [K⁺]_o (10, 22, 28–30, 47) and spontaneous transitions between two polarization levels (37) have been documented in isolated cerebral arteries, and evidence for V_m bistability in cerebral SMCs has also been presented (33). Although the presence of Kir current is a prerequisite for these responses, the underlying mechanisms and physiological relevance have not been elucidated. Model simulations performed in this study show how bistable cells can amplify incoming electrical signals and under certain conditions promote excitability and regenerative conduction (Figs. 3F and 5–7).

Are ECs Capable of Carrying APs?

The inward rectification of the Kir by channel pore blockers provides the characteristic N-shaped current–voltage relationship that resembles, albeit inverted, the V_m dependence of the Na_v activation gate that underlies neuronal APs (SI Appendix, Fig. S4). This nonlinear dependence on voltage allows for the creation of bistable systems in capillaries and neurons that can promote hyperpolarizing and depolarizing jumps upon threshold excitation (Fig. 2 and SI Appendix, Fig. S4). Model simulations demonstrate that AP-like electrical responses are possible in capillaries when there is sufficient Kir density (Fig. 3).

Experiments have provided evidence of bistability in ECs (27) and mechanisms exist to modulate Kir activity (i.e., regulation by [K⁺]_o and PIP₂/ATP) (25, 34) and thus adjust/regulate the percentage of bistable ECs in a microvascular network. Most importantly, experiments in capillary networks have shown threshold excitation and robust all-or-none responses (supplementary figure 5 in ref. 22)—the salient features of an AP. Unlike neuronal APs, the inverted (i.e., hyperpolarizing) burst of electrical activity in cECs is mediated by K⁺ efflux rather than Na⁺ influx and does not spontaneously reset, allowing for a prolonged and stimulus-dependent duration of activity. Compared to neurons, capillaries form a low-intensity system with transmembrane current densities on the order of 0.5 pA/pF, almost 1,000-fold lower that typical current densities in mammalian axons (20). Higher membrane (r_m = 30 MΩcm) and axial (r_i = 5 to 500 GΩ/cm for R_gj = 10 MΩ to 1 GΩ) resistances yield much lower conduction velocities in capillaries (millimeters per second) compared to neurons (meters per second) (Fig. 3 H and I). Thus, the predicted vascular AP resembles a low-intensity, inverted, neuronal AP which can be sustained during stimulation and has a much slower conduction velocity.

Evidence for Kir-Mediated Amplification of Electrical Signaling.

K⁺ stimulation of a few cECs can yield robust Kir-mediated hyperpolarization and dilation of the feeding PA several hundred microns away in an ex vivo preparation and in vivo (22). The levels of evoked hyperpolarization are remarkable when one considers the small outward Kir currents recorded in isolated cECs and the small number of cECs stimulated in the experiments (22). Model analysis here consolidates experimental data in isolated cECs with integrated responses in capillary networks and shows that the evoked arteriolar hyperpolarization cannot be explained by a passive electrical spread from the stimulated capillary segment to the PA (Fig. 4 B and C). We thus propose that the significant arteriolar hyperpolarization in the ex vivo Cap-PA preparation, as well as in the in vivo data (22), suggests amplification of electrical signals in the cerebral microcirculation. Simulations reveal a significant potential of Kir channels for amplifying conducted electrical signals, providing the means to induce significant upstream dilations in response to small local stimulatory currents (Figs. 4–7).

Analog vs. Digital Mode of Microvascular Network Hyperpolarization.

Simulations show that a progressive increase in Kir activity can transition a capillary segment (Fig. 3) or a microcirculatory region (Fig. 5) from insensitive to K⁺ stimuli (passive system) to one of intermediate sensitivity with responses graded to the level of stimulation (facilitated conduction) to a sensitive and binary (on/off) sensory web (excitable with/without propagating front). Thus, dynamic modulation of Kir by [K⁺]_o, PIP₂, or membrane potential can regulate the system’s fidelity/sensitivity and the ability to work in a digital or analog fashion. Binary responses in capillary regions can be integrated to hyperpolarize feeding arteries at levels that increase as more regions are stimulated. Under this scenario, the blood flow response can be graded by the number of activated regions (SI Appendix, Fig. S7).

Space-Clamped Excitability or AP-Like Propagation.

Parametric analysis in models depicting capillary segments or networks revealed conditions that can promote hyperpolarizing jumps upon K⁺ stimulation. Conditions that promote excitability were identified in short, well-coupled capillary segments after local stimulation (Fig. 3F), in isolated networks (Fig. 5A), and in larger vascular architectures (SI Appendix, Fig. S7) when a small percentage of locally distributed cECs were stimulated. Experimental data provide evidence for capillary excitability in isolated ex vivo microvascular networks stimulated locally by 10 mM K⁺ (Fig. 4A). Model simulations show how these hyperpolarizing jumps can be achieved with lower Kir densities than what is required for regenerative (AP-like) conduction, and how they could reset following stimulus termination by basal levels of TRPV4 activity (Fig. 3C). This process could be supported by delayed changes in transmembrane currents (including, e.g., I_f, I_Cl, I_Piezo, or I_NaK) which would slowly shift the balance of depolarizing and hyperpolarizing forces during stimulation (SI Appendix, Text and Fig. S6). For instance, the upstream conduction of a vasodilatory response can increase flow and pressure to downstream vascular regions—relative to their pressure at rest, prior to stimulation. Pressure increases can activate mechanosensitive channels, such as EC Piezo1 channels, shifting the balance of hyperpolarizing/depolarizing currents and resetting V_m. Down-regulation of Kir and/or up-regulation of TRPV4 activity following the hyperpolarizing stimulus could also enable resetting (Fig. 4E).

Higher Kir density can promote regenerative conduction of electrical signals and translate picoamperes of stimulatory signal into robust dilatory responses several hundred microns away. This condition would provide maximum sensitivity to the capillary network and the ability to modulate blood flow based on neuronal activity almost at the single neuron level, as local stimulation of few cECs can drive V_m responses in feeding PA and even in surface pial arteries (Fig. 7). Capillary network operation under this mode requires high G_Kir and an active mechanism for network resetting following stimulus termination. As in the excitable conditions, the mechanism that would allow such a response is not known. Delayed activation/inactivation of channels (I_f, I_Cl, I_Piezo, or I_NaK), changes in ionic concentrations ([K⁺]_o, [Na]_i), mechanical (pressure and shear), or chemical stimuli may contribute to the resetting of an AP-like conducted response (SI Appendix, Fig. S6). Additionally, ECs exhibit local calcium transients which reflect local release of neurotransmitters, EC Gq-protein-coupled receptor (GqPCR) activation, and PIP₂ depletion (25, 48). These events likely reflect “stop signs” for hyperpolarizing signals via attenuating Kir activity (while enhancing depolarizing TRPV4 activity) and thus could shape the spatiotemporal characteristics of the vasodilatory signaling.

Since a regenerative electrical signal can travel without attenuation in the highly interconnected brain capillary network, a mechanism should exist for spatial confinement. Furthermore, for efficient CBF control the electrical signal needs to be directed preferentially toward the upstream feeding arterioles. Evidence for heteromeric connexin channels that allow unidirectional conduction of electrical signals has been presented and may provide a mechanism for guiding such signaling in the vasculature (49, 50). In representative simulations, we show how a regenerative electrical signal can ascend toward the upstream feeding vessels when a Kir density/activity gradient from the venular to the arteriolar side of the capillary network exists (Fig. 7). Thus, excitability with (Fig. 7) or without (SI Appendix, Fig. S7) an AP-like propagation can be spatially confined and allow vasodilatory signals to travel significant distances and preferentially ascend toward upstream feeding arterioles and surface arteries.

PA vs. Capillary-Mediated NVC.

Simulations using realistic representation of the microvascular geometry provide a way to test the physiological relevance of stimulating PAs and/or capillaries under different scenarios. Model simulations suggest that conduction along PAs can be significantly inhibited by current losses to branching capillaries, particularly in the deeper layers of the cortex where there is a higher density of capillaries branching off the PAs (Fig. 6). The model predicts that a level of electrical coupling between ECs in the capillaries similar to that in the PAs (i.e., R_gj = R_gj,PA = 10 MΩ) can have a strong inhibitory effect on electrical signal propagation along the PAs (Fig. 6A). For weakly coupled capillaries, however, focal stimulation of a PA segment and the resulting local hyperpolarization can ascend along the arteriole and potentially reach the surface microcirculation. This would require a strong local hyperpolarizing current (i.e., activation of calcium activated potassium [K_Ca] channels) or a significant PA Kir density to amplify weaker stimulatory currents.

Our model simulations corroborate previous experimental findings for the presence of an alternative/parallel mechanism, aside from already-known mechanisms of NVC through arteriolar SMCs, to communicate neuronal activity to the vasculature by stimulating cECs (22). The resulting hyperpolarizing signal could propagate through the capillary network and feed into and dilate upstream PAs. Simulations identify conditions where stimulation of a small population of cECs can promote hyperpolarization of their feeding PA (Fig. 5). Furthermore, regenerative conduction of electrical signals can provide physiologically relevant spread of hyperpolarization through the microcirculation (Fig. 7), allowing signals initiated deep in the cortex to ascend and reach the surface microcirculation to evoke robust local CBF increase.

Model Limitations.

We use minimal models to simulate electrical communication in the cerebral microcirculation. More detailed representations of ECs, pericytes, and SMCs should be developed as electrophysiological data become more readily available. The modeled capillary does not account for the presence of pericytes. The PA model assumes that a coupled EC/SMC pair is isopotential and neglects nonlinearities arising from the activity of Ca²⁺- and voltage-activated channels. Values for several of the model’s parameters need to be more accurately quantified, as estimated values vary significantly in the literature (SI Appendix, Supplementary Information Text). A parametric analysis shows that retrograde electrical signaling is sensitive to several parameters (i.e., G_Kir, G_bg, R_gj, ΔV_Kir, and [K⁺]_o), which can represent critical points of regulatory control (SI Appendix, Fig. S2). The parameter space that enables 1) robust hyperpolarization in isolated cells/capillaries, 2) local hyperpolarizing jumps in capillary networks, and 3) long-range regenerative conduction in microvascular networks becomes progressively more restricted. Experimental studies should test whether mean parameter values fall within the required parameter space and whether biological variability allows for robustness in predicted responses. Whether electrical signals can regeneratively propagate over long distances in microvascular networks needs to be confirmed experimentally. Efficient blood flow control would require tight spatiotemporal control of such signaling, including mechanisms that would promote directional propagation and robust resetting to resting potentials upon stimulus termination. The mechanisms that would allow such control have not been determined. Experiments should test whether changes in ionic concentrations, delayed activation of channels, or mechanical/chemical stimuli contribute to resetting. TRPV4/Kir activity modulation by mechanical forces or by NVC mediators (e.g., prostaglandin E2 [PGE₂] and epoxyeicosatrienoic acids [EETs]) needs to be examined for its contribution in shaping the spatiotemporal characteristics of the vasodilatory response.

Summary

In this study, we utilized mathematical modeling to determine the biophysical determinants of capillary-mediated signaling during NVC. The Kir channel can act as an “on–off” switch in cECs to hyperpolarize the cell membrane as the interstitial K⁺ increases. This enables capillaries to sense K⁺ released by neuronal activity and initiate retrograde hyperpolarizing signaling toward upstream feeding arteries. Model analysis consolidates experimental data in isolated cECs with integrated responses in capillary networks and shows that the evoked arteriolar hyperpolarization cannot be explained by a passive electrical spread from the stimulated capillary segment to the PA, suggesting an intrinsic amplification mechanism. We propose that robust amplification is possible under conditions that enable an AP-like response in the microvascular network. Simulations in reconstructed microvascular networks show how such a mechanism can provide a physiologically relevant spread of electrical signaling. Stimulation of cECs within a region can promote a robust hyperpolarization of the local capillary network, in a binary on/off fashion, and the activity in different regions can be integrated to produce graded vasodilatory responses in the upstream feeding arterioles. Higher Kir densities will increase the sensitivity of the system and could allow small stimulatory signals to regeneratively propagate over significant distances along the microcirculatory network. A Kir density gradient could restrict this conduction and preferentially direct the signal toward upstream feeding vessels, thus better matching increases in blood supply to regions of activity. Previous experimental observations suggest a role for the Kir channel as a sensor of neuronal activity and controller of retrograde signaling in the cerebral vasculature. In this study, we outline plausible mechanisms underlying Kir-mediated responses and paradigms for electrical conduction in the cerebral microcirculation. Further experimentation is needed to investigate the contribution and biophysical limits of the proposed mechanisms in endothelium-mediated NVC. New quantitative data will enhance model development, which in turn will provide an integrated view and a comprehensive understanding of CBF control at the microscale.

Methods

Minimal Model of Single cEC.

A minimal model of cEC electrophysiology (model I) comprises an explicit description for the whole-cell Kir current (I_Kir), while all other transmembrane currents are lumped into a nonspecific linear background current (I_bg) (Eqs. 1–3). Model parameters (C_m, ${\overline{G}}_{Kir}$, G_bg, and E_bg) were determined from patch data in freshly isolated mouse cerebral cECs (Fig. 2F). ${\overline{G}}_{Kir}$ was estimated by fitting current–voltage data at V_m values negative to the E_K and G_bg by fitting current data at positive V_m values. Conductances were corrected for leak currents and E_bg was determined from the cEC resting V_m (−30 mV). The slope factor, k, and half-maximal inactivation voltage, V_0.5, account for the level of inward rectification and determine the magnitude and shape of the outward Kir current. Experimental data show that V_0.5 drifts with E_K, as [K⁺]_o changes (i.e., V_0.5 = E_K + ΔV_Kir) (51, 52). Reported values for the voltage offset, ΔV_Kir, vary significantly in the literature and estimates include both negative and positive values (SI Appendix, Supplementary Information Text). The value assumed as control in this study provides sufficient outward current for reproducing experimentally observed K⁺-mediated responses.

Stochastic TRPV4 Model.

In model II, we separate the TRPV4 current (I_TRPV4) from the lumped background current in model I to examine the contribution of stochastic TRPV4 currents in the dynamics of cEC V_m. Model II accounts for the activity of TRPV4 channels and the resultant transient depolarizing current with bursting kinetics as characterized in mouse cECs (25). cECs show infrequent single-channel openings with a whole-cell open probability of NP_o ≈ 0.04 at rest (25). We simulate the TRPV4 using a three-state discrete-time Markov chain model (36, 53). More specifically, we assume that the TRPV4 channel can reside in any of the following three states: 1) blocked (B, intraburst short-closed state), 2) open (O), and 3) shut (S, interburst long-closed state), using the following mechanism:

$$B\begin{array}{c}{k}_2\\ \rightleftarrows \\ k_1\end{array}O\begin{array}{c}{k}_3\\ \rightleftarrows \\ k_4\end{array}S,$$

where k₁ through k₄ indicate the transition rates from one state to the other and quantities 1/(k₃ + k₁), 1/k₂, 1/k₄, and (1 + k₁/k₂)/k₃ determine the mean open time, mean blocked time, mean shut time, and burst length, respectively (36). Experimental recordings of single cEC TRPV4 openings in ref. 25 show bursts of stochastic TRPV4 openings with a mean open time (∼90 ms), a mean blocked time (∼33 ms), a mean shut time (∼4 min), and a mean burst duration (∼20 s), from which the transition rates can be estimated. The above mechanism results in the following transition rate matrix (Q) (36):

$$Q=\left[\begin{array}{ccc}-\left(k_3+\hspace{0.17em}{k}_1\right)& k_1& k_3\\ k_2& -k_2& 0\\ k_4& 0& -k_4\end{array}\right].$$

The state transition probability matrix (T) is the matrix exponential of the Q matrix (53). Here, we used the built-in MATLAB discrete-time Markov chain (dtmc) function to generate temporal traces of TRPV4 openings in each cEC, with a time increment of 0.1 ms. The Na⁺, K⁺, and Ca²⁺ currents through an open TRPV4 channel are modeled via a Goldman–Hodgkin–Katz equation with the general form

$$I_{TRPV4,S}\left(t,V_m,S_i\right)=P_{TRPV4,S}\frac{z_s^2{F}^2}{RT}{V}_m\frac{S_i-S_0{e}^{\frac{-z_s{V}_{m}F}{RT}}}{1-e^{\frac{-z_s{V}_{m}F}{RT}}},$$ [4]

where I_TRPV4,S is the current carried by each cation S (i.e., Ca²⁺, K⁺, and Na⁺), S_i is the intracellular and S₀ the extracellular concentration of S, $z_s$ is the valence of the ion, F is the Faraday constant, R is the universal gas constant, T is the temperature in Kelvin, and P_TRPV4,S is the ionic permeability [P_TRPV4,Ca = 10⁻⁷ cm/s and P_TRPV4,Ca:P_TRPV4,K:P_TRPV4,Na = 7.1:1.4:1 (36), which provides a single channel conductance of 92 pS, in line with our prior estimate (25)]. The time-dependent net current [I_TRPV4(t)] is the sum of the currents carried by each ion through an open TRPV4 channel, multiplied by the number of open channels, N(t), that is, $I_{TRPV4}\left(t\right)=N\left(t\right)\sum _S{I}_{TRPV4,S}$.

Modulation of Kir and TRPV4 Currents by PIP₂.

Stretch and putative NVC mediators, including PGE₂, activate G_qPCR-dependent pathways that result in the hydrolysis of plasma membrane PIP₂ into diacylglycerol and inositol 1,4,5-trisphosphate. We have demonstrated that depletion of PIP₂ gradually inhibits the Kir channels and conversely increases the activity of TRPV4 channels with time constants on the order of minutes (25, 34). In simulations performed in Fig. 4E, we have incorporated the effect of the dynamic regulation of Kir and TRPV4 through an exponential decrease in I_Kir, and an exponential increase in I_TRPV4, with their respective time constants upon K⁺ stimulation.

Multicellular Models of Microvascular Networks.

cECs are coupled through incorporation of gap junctions to construct multicellular capillary networks. In simulations of Fig. 3, a capillary segment of serially connected cECs is examined. In simulations performed in Figs. 3–7, cECs are connected such that the resultant geometry approximates the isolated ex vivo preparations in Fig. 4 and in ref. 22 or matches larger reconstructed microvascular networks adapted from ref. 26. The procedure used for large network simulations was as follows. 1) Vectorized data for vessel strands between bifurcation points, discretized in smaller segments, were obtained from ref. 26. Data provided length, radius, and connectivity information for each segment. 2) Each strand was resegmented to approximately match the average EC length in capillaries (20 µm) and parenchymal and pial vessels (33 µm). A weighting factor (representing number of cells per segment) was further estimated to scale conductances and gap junctional resistances in each segment and account for length variability in our segmentation. 3) An in-house algorithm was developed to extract the adjacency matrix from the data, indicating segment to segment connectivity. 4) Self-loops and stranded components were removed from the graph network. Current flow between adjacent cECs was estimated based on the electrical gradient and the cEC-to-cEC coupling resistance (R_gj):

$$I_{gj,i}=\sum _n\frac{1}{R_{gj,i,n}}\left(V_{m,i}-V_{m,n}\right),$$ [5]

where n is the index of cells connected to cell(i), I_gj,i is the gap junctional current flowing from cell(i) to cell(n) with a gap junctional resistance R_gj,I,n. R_gj has not been measured in capillaries; we thus examine R_gj values ranging from 10 MΩ to 1 GΩ based on estimates for coupling resistances between ECs in arteries and the axial cytoplasmic resistance, as estimated based on length and cross-sectional area (38, 39). PAs are modeled using PA EC and SMC membrane resistivities (R_m,EC, R_m,_SMC), Kir conductances (G_Kir,_EC G_Kir,_SMC), and the myoendothelial gap junctional resistance (R_ME), as previously described (38, 54). Three ECs are coupled to three SMCs at each longitudinal position and are assumed isopotential. For each EC–SMC pair, we account for a total Kir conductance (G_Kir,_PA = G_Kir,_EC + G_Kir,_SMC) and a background conductance G_bg,_PA as the inverse of the resting transmembrane resistance, R_m,PA. The latter is estimated from the parallel connection of R_m,EC with R_ME and R_m,SMC combined in series:

$$R_{m,PA}=\frac{\left(R_{m,SMC}+R_{ME}\right)R_{m,EC}}{\left(R_{m,SMC}+R_{ME}+R_{m,EC}\right)}.$$ [6]

Each unit is coupled to adjacent EC–SMC units with a resistance, R_gj,PA. PVs are modeled similarly to PAs with negligible Kir conductance. Pial arteries and pial veins are treated the same as PAs and PVs, respectively, but with assuming five ECs in the circumferential direction to account for the larger diameter of these vessels compared to PAs. Boundary conditions were imposed at each vessel crossing the simulation domain. We assumed an effective resistance, equal to the input resistance of a semiinfinite cable (i.e., $R_{in}=\sqrt{R_{gj}{R}_m}$, where R_gj and R_m are vessel-specific), connecting each boundary segment to resting V_m. Thus, effectively we assume that each boundary vessel extends to infinity. All simulations were performed in MATLAB 2018b using ode15s, suitable for solving stiff initial value ordinary differential equations.

Data Availability.

All codes and scripts associated with this study can be accessed on GitHub at https://github.com/ntsoukias/ (Capillary-Kir-Model).