Abstract
COVID-19 infection is growing in a rapid rate. Due to unavailability of specific drugs, early detection of (COVID-19) patients is essential for disease cure and control. There is a vital need to detect the disease at early stage and instantly quarantine the infected people. Many research have been going on, however, none of them introduces satisfactory results yet. In spite of its simplicity, K-Nearest Neighbor (KNN) classifier has proven high flexibility in complex classification problems. However, it can be easily trapped. In this paper, a new COVID-19 diagnose strategy is introduced, which is called COVID-19 Patients Detection Strategy (CPDS). The novelty of CPDS is concentrated in two contributions. The first is a new hybrid feature selection Methodology (HFSM), which elects the most informative features from those extracted from chest Computed Tomography (CT) images for COVID-19 patients and non COVID-19 peoples. HFSM is a hybrid methodology as it combines evidence from both wrapper and filter feature selection methods. It consists of two stages, namely; Fast Selection Stage (FS2) and Accurate Selection Stage (AS2). FS2relies on filter, while AS2 uses Genetic Algorithm (GA) as a wrapper method. As a hybrid methodology, HFSM elects the significant features for the next detection phase. The second contribution is an enhanced K-Nearest Neighbor (EKNN) classifier, which avoids the trapping problem of the traditional KNN by adding solid heuristics in choosing the neighbors of the tested item. EKNN depends on measuring the degree of both closeness and strength of each neighbor of the tested item, then elects only the qualified neighbors for classification. Accordingly, EKNN can accurately detect infected patients with the minimum time penalty based on those significant features selected by HFSM technique. Extensive experiments have been done considering the proposed detection strategy as well as recent competitive techniques on the chest CT images. Experimental results have shown that the proposed detection strategy outperforms recent techniques as it introduces the maximum accuracy rate.
Keywords: COVID-19, Classification, KNN, Feature selection
1. Introduction
Undoubtedly, new Coronavirus appeared in 2019 (also called COVID-19) has negatively affected human life all over the world. It belongs to a family of viruses that usually causes respiratory tract disease as well as fatal infections such as Severe Acute Respiratory Syndrome (SARS) and Middle East Respiratory Syndrome (MERS) [1], [2]. Unfortunately, COVID-19, which has not been previously identified in humans, has the ability to move from the animal species to the human population, and then it can rapidly spread [3], [4]. According to recent studies, it is shown that once coronavirus begins to spread, it will take less than four weeks to quash the medical system (e.g., hospital) [3], [4]. Hence, early detection of COVID-19 patients is a vital process to quarantine the infected people.
Data mining is an effective tool that can be used to predict medical conditions as well as enabling caregivers to accurately make medical decisions [5]. It can perform complicated computational processes such as determining patterns in large dataset, hence data mining can be successfully applied to detect and extract meaningful information and patterns for medical classification. More precisely, it can be used to accurately detect COVID-19 infections based on medical datasets [5]. In fact, classification is one of the data analysis processes that assigns COVID-19 patients to their corresponding classes [6]. Based on data mining, there are many classification methods such as; decision tree, KNN, Bayesian method, artificial neural networks, support vector machine, etc. [6].
KNN proves a high efficiency and excellent capability to solve difficult pattern classification problems. Generally, KNN is a useful and rapid technique [7]. Hence, it is desirable to classify and evaluate COVID-19, specifically in the epidemic region to save the medical professionals’ precious time. However, it can be trapped. KNN trapping may be due to several reasons. Some of them are due to the characteristics of KNN itself, while the others are due to the environment and the classification problem it solves. The most effective reasons of KNN trapping are; (i) the existence of outliers in the training examples, (ii) KNN is a distance based classifier as it employs on other heuristic in taking its decision, (iii) its performance is sensitive to the value of K (e.g., there is no clear rule to decide the optimal value of K).
Due to the seriousness of COVID-19 that results from its rapid spread and the inability to quick and accurate diagnose, it is important to provide fast and accurate diagnostic methods to combat the disease in real time. Really, classification methods can be used to diagnose COVID-19 patients based on the extracted features from CT images. Feature extraction process should be performed on CT images before using detection model. The main objective of feature extraction is to transform or convert CT image into its set of features that help the classification technique to make correct decisions [8], [9]. Recently, there are various methods employed for feature extraction such as; texture features, co-occurrence matrix, Gabor features, wavelet transform based features, etc. [10], [11]. In fact, Gray Level Co-occurrence Matrix (GLCM) is the most widely and robust way used for image analysis applications that describes the image texture [12]. The extracted features may contain many irrelevant or redundant features, thus, eliminating those non-informative features is a vital process before starting to learn the classification model. Selecting the meaningful features enables the classification method to accurately classify COVID-19 patients with the minimum time penalty. There are numerous feature selection approaches grouped to three basic classes, which are; filter, wrapper, and hybrid approach [13], [14], [15].
Genetic Algorithm (GA) is a search heuristic that is inspired by Charles Darwin’s theory of natural evolution [16]. This algorithm reflects the process of natural selection where the fittest individuals are selected for reproduction in order to produce offspring of the next generation. GA has several advantages as an optimization technique such as; (i) it can find fit solutions in a very less time, (ii) the random mutation guarantees to some extent that we see a wide range of solutions, and (iii) GA coding is quite easy compared with other algorithms which perform the same job. Hence, GA can be successfully applied as a wrapper feature selection method.
The originality of this paper is concentrated in introducing a new COVID-19 Patients Detection Strategy (CPDS) to detect infected patients. CPDS consists of two phases, which are; (i) Data Pre-processing Phase (DP2) and (ii) Patient Detection Phase (PDP). During DP2, the historical data of COVID-19 patients is collected, and then represented in a suitable form for the diagnostic model. Two main processes are performed in DP2 to accomplish such aims, which are; feature extraction and feature selection. Both processes are performed using data mining techniques to build an informative pattern of data for the next phase (e.g., PDP). Feature extraction is performed by using GLCM method to extract set of features from CT images, and then the effective features are selected from those extracted features by using a proposed Hybrid Feature Selection Methodology (HFSM). HFSM combines both filter and wrapper approaches, in which it composes of two stages, namely; Fast Selection Stage (FS2), which relies on several filter methods and Accurate Selection Stage (AS2), which uses using GA as a wrapper method. HFSM aims to utilize the benefits of both filter and wrapper methods for overcoming their drawbacks. In fact, filter methods can provide fast selection, but it lack high fidelity as; (i) it ignores feature dependencies and (ii) the selection needs to be performed only once.
To compensate filter methods faults, wrapper methods such as GA can provide accurate selection as it considers feature dependencies as well as the interaction with the used classifier. However, but it cannot provide fast selection compared with filter methods. Consequently, HFSM can select the most informative subset of features as; (i) it can provide fast selection by using filter methods, (ii) it can provide accurate selection by using wrapper method, and (iii) it takes in the consideration the feature dependencies and the interaction with the classifier. On the other hand, during the second phase (e.g., PDP), fast and accurate detection of COVID-19 patients based on the selected features is provided by the proposed Enhanced KNN (EKNN) classifier. Like traditional KNN, EKNN considers the K nearest neighbors to the tested item in the feature space. However, those neighbors will have different votes according to the degree of closeness to the tested item as well as the degree of the neighbor membership to its class, which is called Item Strength (IS). The more the closeness and the strength of the neighbor, the more the importance of its vote. In fact, EKNN involves the benefits of the classical KNN and overcomes its problems in which; (i) EKNN is a simple, easy to be implemented, and straightforward and (ii) it overcomes the drawbacks of the traditional KNN as it uses solid heuristics for choosing the involved neighbors for classifying the tested case. Each of the proposed techniques (e.g., HFSM and EKNN) has been evaluated through excessive experiments. Experimental results have shown that the proposed CPDS strategy outperforms recent ones in which it introduces the best detection accuracy with the minimum time penalty.
This paper is organized as follows; Section 2 describes a problem definition about COVID-19. Section 3 discusses the K-nearest neighbors trapping problem. Section 4 provides the previous efforts about COVID-19 patients classification. Section 5 focuses on the proposed corona patients’ classification strategy. Section 6 depicts the experimental results. Finally, conclusions are presented in Section 7.
2. Problem definition
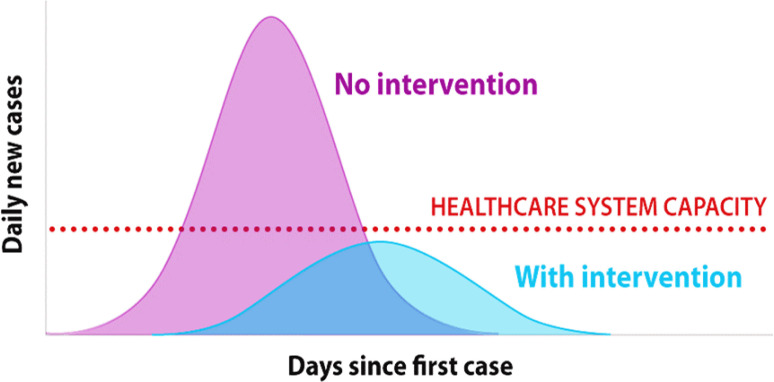
Once coronavirus was first found in Wuhan, China, it grown at rapid rate around the whole world [1], [4]. By February, the capacity of hospitals was filled, and ambulances became unavailable due to the large number of patients. Really, the waiting list to get an ambulance stretched into the hundreds. Medical practitioners had not yet gotten a handle on what they were dealing with. Social distancing measures were not taken until it was too late. Hence, it is an extremely important to early detect COVID-19 patients due to unavailability of specific drugs for disease cure and control. A graphic representation of the rapid spike in infections called the epidemic curve is shown in Fig. 1.
Fig. 1.
A graphic representation of the rapid spike in infections.
To describe the outbreak of the novel coronavirus pandemic, a simple approximate mathematical model can be used to understand how the virus spreads among the population. The susceptible individuals can be infected through either direct contact with infectious individuals or indirect contact with an environment affected by the virus. It is assumed that, at an initial stage of the COVID-19 epidemic, the proportion of the population with immunity to COVID-19 is negligible. In the first stage of an infectious epidemic, a small number of infected people begins to transmit the disease to a large population.
The mathematical model that defines the COVID-19’s problem is based on four parameters which are; (i) basic reproductive number () that represents the expected number of new infectious cases per infectious case, (ii) case fatality rate () that represents the proportion of cases who die within the symptomatic period, (iii) incubation period (p) that represents the time from infection to symptom, and (v) duration of disease (x) that represents the time from symptom to recovery or death. Actually, to predict the number of COVID-19 cases, only two parameters are used which are; basic reproductive number () and incubation period (p). Assume that, after one incubation period (p), one infectious case produces new infectious cases. The cumulative total number of cases at this time is 1+N. After two incubation periods (2P), there are No2 cases produced by the previous cases. The total number of cases is 1+No+No2. Assuming that the predicted number of cases on is , hence, total number of cases can be expressed by (1).
| (1) |
Where is the predicted total number of cases, the predicted number of incident cases on , and t is the time expressed in the number of incubation periods. Table 1 illustrates the application of the model to calculate the predicted number of COVID-19 cases, using and p=5 days.
Table 1.
Predicted number of COVID-19 cases using and p = 5 days.
| Number of incubation period (t) | Predicted incident cases (Q) | Predicted total cases (Q) | |
|---|---|---|---|
| 0 | 0 | 1(= ) | 1 |
| 1 | 5 | 3 (= ) | 4 (=1+3) |
| 2 | 10 | 9 (= ) | 13 (=1+3+9) |
| 3 | 15 | 27 (= ) | 40 (=1+3+9+27) |
Additionally, to predict number of COVID-19 deaths, assuming that after one disease duration x, the cases are removed with death or recovery. percentage of them die while 1- percentage recover. Consequently, the predicted number of deaths on and the predicted total number of deaths can be calculated by (2), (3).
| (2) |
| (3) |
Where is the predicted number of deaths on , is the predicted total number of deaths, and t is the time expressed in the number of incubation periods. Table 2 illustrates the application of the model to calculate the predicted number of COVID-19 deaths, using , p=5 days, =10%, and x=14 days.
Table 2.
Predicted number of COVID-19 deaths using , p = 5 days, = 10% and x = 14 days.
| Number of incubation period (t) | Day | Predicted incident cases (Q) | Predicted new deaths( M) | Predicted total deaths (M) |
|---|---|---|---|---|
| 0 | 0 (= t*p) | 1 | 0 | 0.0 |
| 1 | 5 | 3 | 0 | 0.0 |
| 2 | 10 | 9 | 0 | 0.0 |
| 14 | 0 | 0.1 (= 1*Fr) | 0.1 | |
| (= t*p+x) | ||||
| 3 | 15 | 27 | 0 | 0.1 |
| 19 | 0 | 0.3 (= 3*Fr) | 0.4 | |
According to Table 2, cases from day 0 are removed on day 14, after one disease duration (14 days). The one case from day 0 is expected to produce 0.1 death (1*10%) and 0.9 recovered people. Likewise, the three cases from day 5 are expected to produce on day 19 (after 14 days) 0.3 death and 2.7 recovered people. The value of x can be determined from patient’s epidemiological studies. The optimal value of can be determined in a particular situation, given the optimal values of , p and x, can be determined by trying multiple values to see which combination of , , p and x produces the predicted total number of COVID-19 deaths that most closely matches the observed total number of COVID-19 deaths. Finally, it can be concluded from the illustrated model that COVID-19 can spread very quickly in the absence of interventions.
3. K-Nearest neighbors trapping problem
The detection of coronavirus (COVID-19) patients is now a critical task for the medical practitioner as it spreads very quickly among people and approaches millions of people worldwide. Accordingly, it is very much essential to quickly identify the infected people to prevent such exponential virus spread and also proper treatments for patients can be taken. The k-nearest neighbors (KNN) is one of the efficient and simplest methods for item classification [7]. In KNN, training examples are expressed as points in the feature space in several separate classes. To predict the label of a new item , initially, it is projected in the problem feature space. Then, the distances between and the K-nearest examples are calculated. Then, is classified by a majority vote of its neighbors. In spite of its simplicity and high efficiency, traditional KNN can be easily trapped. KNN trapping may take place in two different situations. The first if when there is no confidence in the classifier decision. This may happened if the probabilities that the tested item is targeted several classes are almost the same or very closed to each other. The second situation of KNN trapping takes place when the decision of the classifier is to target the tested item to two or more classes. This occurs when two or more classes have highest identical contribution (e.g., the same number of examples) within the K-nearest neighbors of the testing item.
Definition 1 KNN Trapping —
Given a set of target classes C={c, c, …. c}, KNN classifier can be trapped if there exists a set C C in which the classes belong to C have identical maximum contribution in the K nearest examples to the tested item or almost the same contribution.
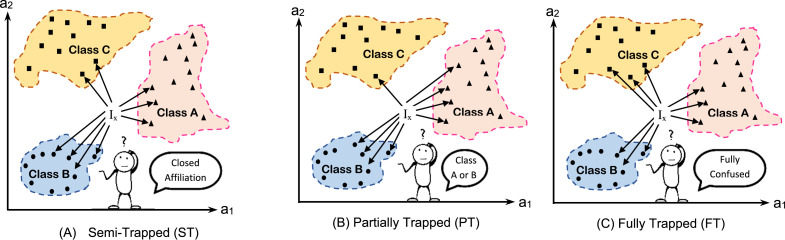
For illustration, assuming K=9, three target classes (A, B, and C), and two dimensional feature space, Fig. 2 shows several examples of KNN trapping. As illustrated in such figure, three different types of trapping can be considered, which are; (i) semi-trapping, which happened if the K nearest neighbors of the are distributed in so closed values among several classes, which minimize the confidence of the classifier decisions. As considered in Fig. 2(A), the testing item is classified to class B as the maximum neighbors in the K considered ones are belonging to class B. However, if one or more neighbors of the K considered ones are outliers, the decision will fully change. In the semi-trapping, the decision can be taken as the target class is identified, but there is no much confidence in the classifier decision as it can be simply changed if there are outliers in the elected K neighbors.
Fig. 2.
Different types of KNN trapping.
Fig. 2(B) illustrates the second type of KNN trapping in which a subset of the target classes have the same maximum contribution in the K-nearest neighbors of the tested examples. As shown in such figure, the classifier is partially trapped as it is confused. It cannot give a decision to classify the tested item to class A or class B since both have the same maximum number of examples (equal to 4) in the set of K-nearest neighbors to the tested item. On the other hand, Fig. 2(C) depicts the third type of KNN trapping in which the classifier is fully confused. There is no decision to take as all target classes have the same vote. Another drawback of the traditional KNN is that it is a distance based classifier [7]. It depends mainly on the calculated distance between the tested item and the considered examples in the problem feature space. No other criteria or heuristic is considered in KNN which cause the classifier to be easily trapped, which is not acceptable in the current epidemic situation of coronavirus wide spread. In many cases, the infected people are not recognized, and accordingly, they do not get suitable treatment on time. Those infected and unrecognized people spread the virus to healthy people due to communicable nature of coronavirus.
4. Related work
In this section, the previous research efforts about COVID-19 patients classification will be reviewed. In [2], an automatic prediction of COVID-19 was performed by applying Deep Convolution Neural Network (DCNN). The implementation of DCNN depended on pre-trained transfer model (ResNet50) in addition to chest X-ray images. As illustrated in [17], the proposed method to classify COVID-19 patients depended on machine learning techniques. Actually, classification process was performed after forming four different datasets by taking patches from 150 CT images with size as 16 × 16, 32 × 32, 48 × 48, and 64 × 64. In [17], the feature extraction process was performed on CT images by using five extraction methods to extract the features that accurately could separate the infected patches. Then, Support Vector Machine (SVM) as a classification method was implemented based on these extracted features to classify the patients. The experimental results in [17] shown that Gray Level Size Zone Matrix with SVM (GLSZM-SVM) was performed well.
As depicted in [18], Deep Learning based Methodology (DLM) was proposed for detecting coronavirus using X-ray images. DLM depended on two main processes, which are; feature extraction process and classification process. Firstly, DLM extracted deep features from X-ray images by using pre-trained Convolutional Neural Network (CNN). Then, it could classify the patients based on these extracted features by using SVM classifier. Although SVM was a powerful method, it was not suitable for large dataset and could not perform its task well when the dataset included more noise. In [19], it was hypothesized that Deep Learning Algorithm (DLA) has the ability to extract COVID-19’s specific graphical features to introduce a clinical diagnosis prior to pathogenic testing. This method tried to save critical time for the disease diagnosis. The experimental results in [19] proven the effectiveness of DLA to extract graphical features to diagnose COVID-19 patients.
As illustrated in [20], the analysis of COVID-19 was demonstrated by using a probabilistic method that involved a classification technique. This classification method could classify COVID-19 patients based on most important features of CT images. Hence, feature extraction process was applied on CT images and then the selection process was performed on these extracted features before using the proposed classification technique called Stack Hybrid Classification (SHC) method. SHC depended on ensemble methods that integrate several models for improving prediction performance. According to the experimental results in [20], the proposed method was better than the classical classification methods. In [21], the proposed framework of pre-trained deep learning classifiers (COVIDX-Net) was provided to automatically diagnose COVID-19 based on X-ray images. This proposed method depended on using seven different architectures of deep CNN models. Although the efficiency of these models to classify positive cases of COVID-19, their corresponding performance was worst to classify the normal cases correctly. Therefore, it requires another model in CAD systems to determine healthy cases of patients against COVID-19 in X-ray images. A brief comparison about previous works on COVID-19 classification techniques is shown in Table 3.
Table 3.
Comparison about previous works on COVID-19 classification techniques.
| Used technique | Description | Advantages | Disadvantages |
|---|---|---|---|
| Deep Convolutional Neural Network (DCNN) [2] | DCNN is a classification technique that was used for the detection of coronavirus infected patient based on three different convolutional Neural Network models. | Transfer learning allows the training of data with fewer datasets and requires less calculation costs. | One of the biggest limitations to transfer learning is the problem of negative transfer. Transfer learning only works if the initial and target problems are similar enough for the first round of training to be relevant. |
| Gray Level Size Zone Matrix with SVM (GLSZM-SVM) [17] | GLSZM-SVM is a hybrid method that extracted the features by using GLSZM and then used SVM to classify these extracted features. | SVM is a powerful classification method. | SVM was not suitable for large dataset and could not perform its task well when the dataset included more noise. |
| Deep Learning based Methodology (DLM) [18] | Deep features were extracted using pre-trained CNN and SVM was used for classification. | Pre-trained model is effective power in features extraction and SVM is a powerful classification method. | SVM was not suitable for large dataset and could not perform its task well when the dataset included more noise. |
| Deep Learning Algorithm (DLA) [19] | DLA has the ability to extract COVID-19’s specific graphical features to introduce a clinical diagnosis prior to pathogenic testing. This method tried to save critical time for the disease diagnosis. | It demonstrated the principle of using artificial intelligence to extract the radiological features for a timely and accurate diagnosis of COVID-19. | This method cannot provide the optimal accuracy. |
| Stack Hybrid Classification (SHC) method [20] | SHC is a COVID-19’s classification method that depended on ensemble methods that integrate several models for improving prediction performance. | The proposed SHC model is better than the traditional classification approaches to classify COVID-19 patients. | This method is slow. |
| Deep learning framework (COVIDX-Net) [21] | COVIDX-Net is the frame work included seven different architectures of deep convolutional neural network models to classify the patient status either negative or positive COVID-19 case. | Efficient to classify positive cases. | Cannot classify the normal cases correctly. Therefore, it requires another model in CAD systems to determine the health status of patients against COVID-19 in X-ray images. |
5. The proposed COVID-19 patient detection strategy
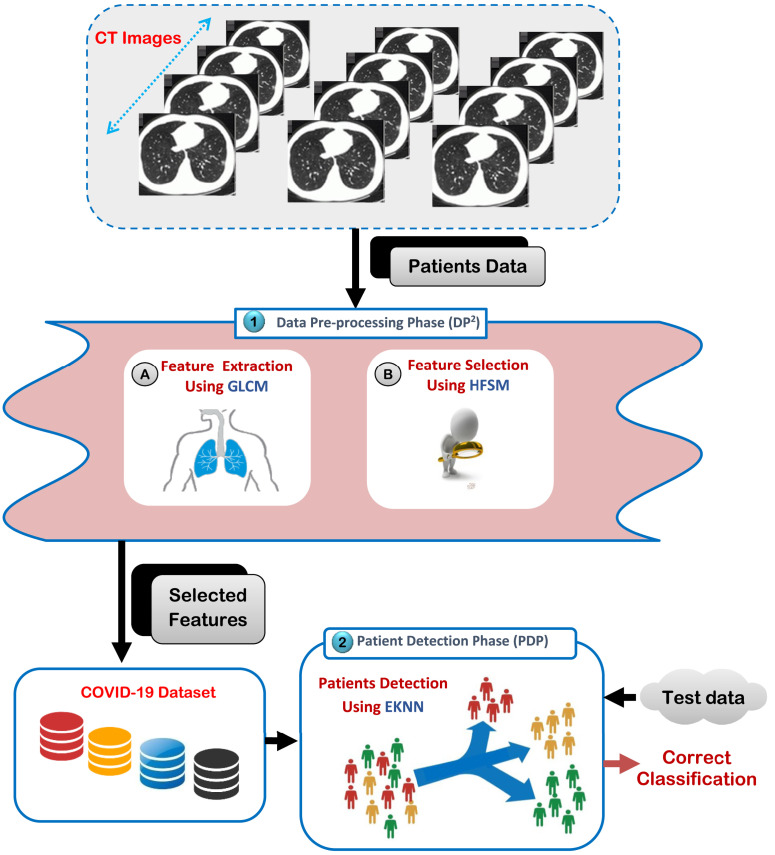
Automatic medical diagnosis has become very important, especially when it is needed to make quick decisions for serious infectious diseases such as COVID-19 disease [22], [23], [24]. Corona patients must be diagnosed remotely because their contact with people increases the number of victims daily. Thus, direct contact with corona patients may threaten the life of doctors and the nursing staff and expose them to death. To overcome this global and dangerous challenge, it is a vital process to analyze patients data and then accurately detect them with the minimum time penalty. In this paper, an intelligent detection strategy called Corona Patients Detection Strategy (CPDS) has been introduced in healthcare system to provide more accurate and fast diagnostic results. As illustrated in Fig. 3, the proposed detection strategy is composed of two phases, which are; (i) Data Pre-processing Phase (DP2) and (ii) Patient Detection Phase (PDP). The main task in DP2 phase is to extract a set of features from CT image by using GLCM and then eliminate irrelevant features by using Hybrid Feature Selection Methodology (HFSM) as a new feature selection method to provide informative data to the next PDP. In PDP phase, fast and accurate detection of infected patients can be performed on the selected features from PDP phase by using Enhanced K-Nearest Neighbors (EKNN).
Fig. 3.
Corona patients detection strategy.
5.1. The proposed feature selection strategy
Irrelevant features existence is one of the main causes of classifier overfitting [7], [25], [26]. Hence, feature selection should be performed during DP2 phase before starting to train the classification method. The reason is that feature selection process can improve the performance of the classification model that leads to faster and more cost-effective models [7], [25], [26]. Generally, the filter approaches are much faster than the wrapper approaches and they easily scale to very high-dimensional datasets [27]. On the other hand, filter approaches ignore the interaction between feature subset search and classifier and they unable to take into account features dependencies when compared to wrapper approaches [27]. In this section, a simple but effective methodology called Hybrid Feature Selection Methodology (HFSM) will be provided to select the main subset of features that can characterize COVID-19. HFSM, as a new feature selection method, is a hybrid technique that integrates between filter and wrapper methods. It consists of two main stages, which are; (i) Fast Selection Stage (FS2) using many filter methods and (ii) Accurate Selection Stage (AS2) using Genetic Algorithm (GA) as a wrapper method.
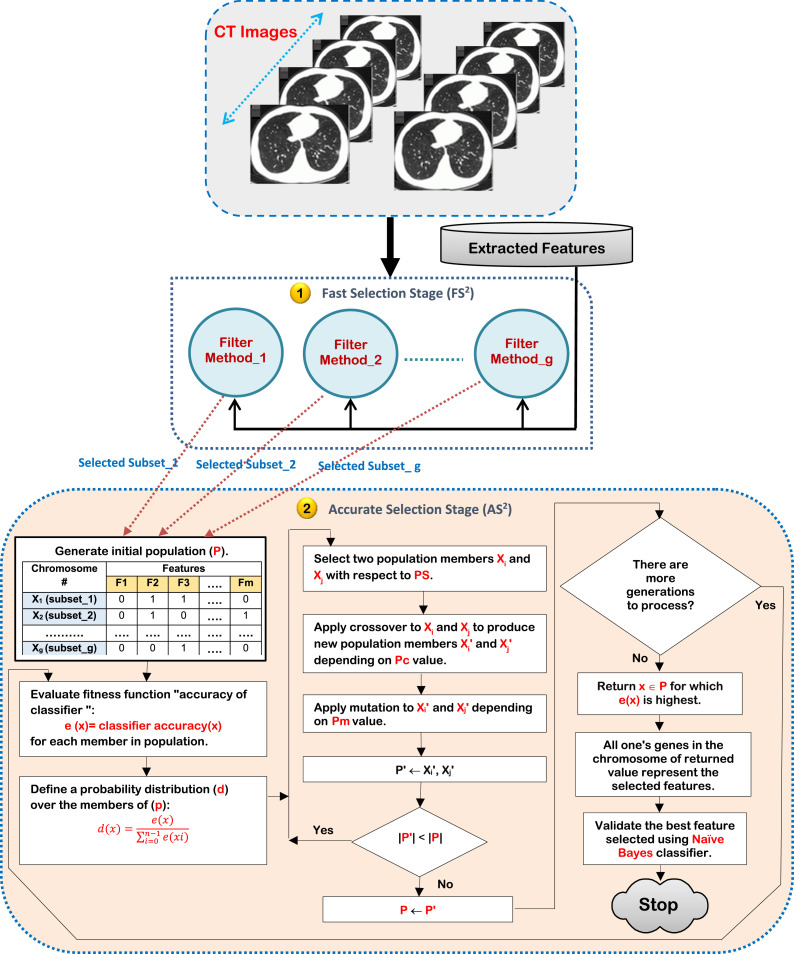
In FS2, many filter methods will be implemented separately on the same COVID-19’s dataset to quickly select a different subset of features according to each method. Then, the results of filter methods will be used as an initial population for GA in AS2 to select the best subset of features accurately. Although GA can accurately select the informative features, it suffers from the computational time and its convergence is very much dependent on the initial population used. Thus, the results of fast selection methods in FS2 should be used as an initial population for GA in AS2 to reduce its computational time and to give it the ability to select an optimal subset of features. Finally, the best subset of features will improve the performance of COVID-19’s classification model. To implement HFSM, assume that there are ‘m’ dimensional Feature Space; FS={f 1 , f }. Additionally, the input training data of ‘h’ objects (patients) can be expressed by A={T 1 , T } and the testing data of ‘q’ objects can be expressed by Q= {E 1 , E }. Each object of A and Q is expressed as an ordered set of ‘m’ features; (f 1 , f2 , f3 , …., f )=[f , f , f , …, f ] and (f 1 , f2 , f3 , …., f )=[f , f , f , …, f ]. Hence, each object and can be expressed in an ‘m’ dimensional space of features. For the considered CPDS problem, it is an important to reduce m-dimensions or eliminate the irrelevant features in COVID-19’s dataset to avoid overfitting and enhance the performance of the classification model. Fig. 4 illustrates the sequential steps of HFSM method using ‘g’ filter methods.
Fig. 4.
The sequential steps of HFSM method.
Firstly, COVID-19’s dataset after performing feature extraction process on CT images should be passed to FS2 to implements ‘g’ filter methods on it in parallel manner. Then, the results of these filter methods will be passed to AS2 for generating the initial population of GA. In Fig. 4, it is noted that the number of chromosomes in initial population equals ‘g’ that is the same number of filter methods in FS2. Additionally, the values of chromosomes are the results of filter methods in FS2. Secondly, GA iterations will be performed until a termination condition is satisfied. At the end, the best chromosome provide the best subset of features that should be evaluated by using classifier such as Naïve Bayes (NB) as a standard classifier [14]. Generally, GA is an evolutionary algorithm that performs a global search to optimally solve the problem depending on its fitness value [16]. Hence, GA can provide near-optimal solutions for fitness function of an optimization problem.
Initially, GA begins with a group of individuals (chromosomes) which are called a population (P). In fact, each chromosome is composed of a sequence of genes that would be bits, characters, or numbers [16]. A subset of features is represented in each chromosome as a binary string in which its length is the same number of features presented in the COVID-19’s dataset. The value of chromosome bits may be zero or one. While zero in the th position in the chromosome denotes the elimination of the th feature in the particular subset, one denotes the selection of the th feature [16]. An example for clarification, a single chromosome is represented in Table 4, assuming m=10, thus; FS={f 1 , f2 , f3 ,…., f 10 }. There are three biologically inspired GA operators, called selection, crossover, and mutation, which are used to produce a new generation of chromosomes [16]. Selection operator selects good chromosome (subset of input features). Crossover operator combines good chromosomes to attempt to produce better offspring’s in the new generation. Mutation operator changes a chromosome locally to try to create a better chromosome. Actually, the population is evaluated in each generation to terminate the algorithm in which the three GA operators are continued for a fixed number of generations or until a termination condition is satisfied [16].
Table 4.
An example of single chromosome.
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
Finally, implementing GA as a feature selection technique requires many essential steps as shown in Fig. 4. In AS2, the genetic evaluation (fitness) function represents an accuracy of the employed classifier such as NB classifier to select the most characterized features to COVID-19. Fitness function measures the fitness degree of each chromosome (subset of input features) based on an accuracy index of the classifier. The best chromosome (subset of input features) is the one that introduces the highest fitness (accuracy) value. In the initial population of GA (P), there are ‘g’ chromosomes include the results of ‘g’ filter methods in FS2 as initial solutions. Each chromosome (X) consists of binary bits in which one donates the presence of feature and zero donates the absence of feature. The fitness value of each chromosome should be provided by calculating the accuracy of NB classifier. Then, the three GA operators should be performed.
In selection process, the probability of selection value (Ps) is assigned for the chromosomes in P to select the best two parents. In crossover process, the probability of the crossover value (Pc) is assigned for both parents to indicate if the crossover process will be performed between them or not to produce new offsprings in the next generation. In mutation process, the probability of mutation value (Pm) is assigned for every offspring to indicate if the mutation process will be performed on every offspring or not. The steps from selection process will be repeated until the size of the new population is the same size in the initial population. Then, the number of generations will be examined to terminate the algorithm. According to the number of generations, the previous steps from evaluation step will be repeated in the case if there are more generations, else, the chromosomes in the population will be evaluated as a final results by using only evaluation step. In the end, the best subset of features is represented in the chromosome that provide the highest fitness value. HFSM is illustrated in algorithm 1.
To clarify the idea, assume that there are four filter methods in FS2, which are; Information Gain (IG) [7], [25], [26], Chi-square (CHI) [28], [29], [30], Fisher score (F) [31], and Correlation Based Feature Selection (CBFS) [32]. Additionally, consider that the number of features in COVID-19’s dataset is six (m=6); FS={f 1 , f2 , f3 , f4 , f5 , f6 }. After implementing IG, CHI, F, and CBFS on the dataset, it is assumed that the subset of selected features according to these methods are; {f 1 , f3 , f5 , f6 }, {f 3 , f4 , f6 }, {f 1 , f2 , f3 , f4 , f6 }, and {f 1 , f2 , f5 , f6 } respectively. Hence, these four subsets of features are used as four chromosomes ( , X2 , X3 , X4) in the initial population (P) of GA in AS2. Then, GA is implemented according to many assumptions in Table 5. According to the presented assumptions in Table 5, it is assumed that GA is implemented through two iterations providing new population that includes an new values at four chromosomes; ={0,1,1,1,1,0}, X 2 ={1,1,0,1,1,1}, X 3 ={0,0,0,0,1,1}, and ={1,1,1,0,0,1}. After evaluating , X2 , X3, and , it is considered that achieves the highest fitness value, thus, is the best chromosome that provides the best subset of features. Finally, the most effected features in COVID-19’s dataset are; {f 1 , f2 , f3 , f6 }.
Table 5.
The assumptions for employing GA in AS2.
| No. | Assumption | Value |
|---|---|---|
| 1 | No. of generation to process | 2 |
| 2 | Population size | 4”No of filter methods in FS2”(g) |
| 3 | Probability of Selection “Ps” | various value for each selected chromosome |
| 4 | Probability of Crossover “Pc” | 0.9 |
| 5 | probability of mutation “Pm” | 0.1 |
| 6 | Individual size or Chromosome size “X” | 6” No. of features” (m) |
| 7 | Fitness function | Accuracy of NB classifier |
| 8 | Initial population |
={1, 0, 1, 0, 1, 1} ={0, 0, 1, 1, 0, 1} ={1, 1, 1, 1, 0, 1} ={1, 1, 0, 0, 1, 1} |
5.2. Enhanced K-Nearest neighbor (EKNN)
In this section, a new instance of KNN classifier will be introduced, which is called Enhanced KNN (EKNN). The proposed EKNN solves the drawbacks of the traditional KNN by adding solid heuristics in choosing the neighbors of the tested item, only qualified neighbors are considered for classifying the tested item. Like traditional KNN, EKNN considers the K nearest neighbors to the tested item in the feature space. However, those neighbors will have different votes according to the degree of closeness to the tested item as well as the degree of the neighbor membership to its class, which is called Item Strength (IS). The more the closeness and the strength of the neighbor, the more the importance of its vote. The proposed EKNN is applied into two steps, namely; training and testing, which will be explained in more details through the next subsections.
5.2.1. EKNN Training
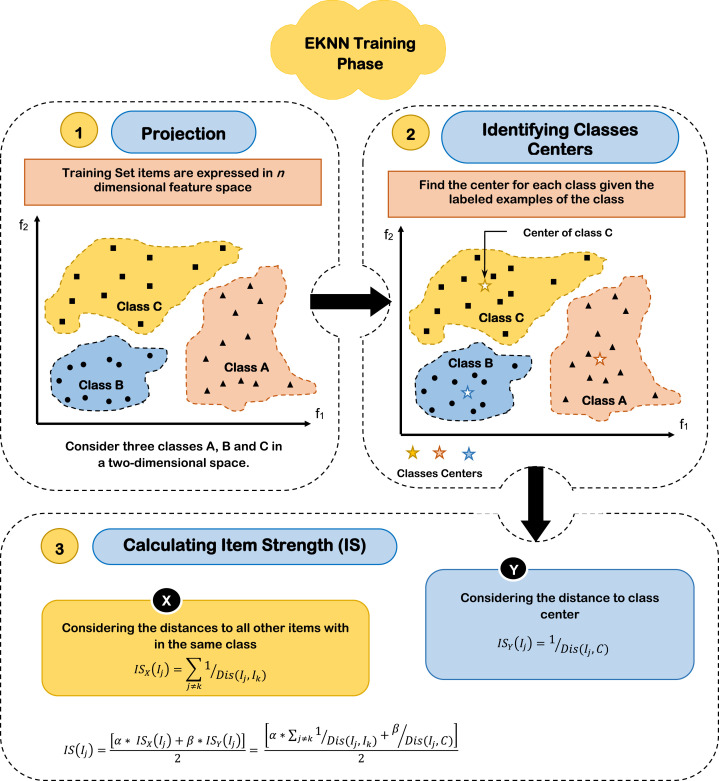
During the training phase of the proposed EKNN, the strength of each item (Training example) is calculated. Item strength is a measure for the degree of relationship of the item to its hosting class. Assuming n features, m considered target classes, for calculating the strength of each item, initially, all items are projected into the considered n dimensional feature space. Then, the center of each class containing t examples in n dimensional feature space for can be accomplished using (4).
| (4) |
Where C is the class center in the considered n dimensional feature space, t is the number of examples within the class, and is the value of the th dimension of the th example. Finally, the strength of item can be calculated using (5).
| (5) |
Where IS(I ) is the strength of item , which is the weighted average of two values. The former measures the strength of the item based on its closeness to the other items (examples) within its class and denoted as; (I ). On the other hand, the later value considers the closeness of the item to the class center as an indication of its degree of affiliation to the class and accordingly its strength, which is denoted as; (I ). As depicted in (5), and are weighting factors that express the relative impact of (I ) and (I ), where 0< 1 and 0< 1. Generally, (I ) and (I ) can be calculate by (6), (7) respectively.
| (6) |
| (7) |
Where (I ) and (I ) are the strength of the item considering the closeness to the class items and class center respectively. Dis(I ,I ) is the Euclidian distance between the items and and Dis(I ,C) is the Euclidian distance between the item and the class center. Calculating the distance between two points and in the n dimensional feature space can be calculated using (8).
| (8) |
Where and is the value of the th dimension of the points and respectively in the n dimensional feature space. Then, substituting in (5), the strength of the item can be calculated by (9).
| (9) |
An important issue is how to estimate the optimal values of and . As tunable parameters, the optimal values of and can be calculated empirically by assigning them different values in a per-defined scenario, then calculate the resultant accuracy of EKNN classifier considering a set of test items. The optimal values of and are those that give the maximum classification accuracy. A suggested scenario is to start with initial values of and , for example and , the values of and will be increased using a constant positive step keeping the values of and greater than 0 and less than or equal 1. Estimating the optimal values of and is illustrated in Section 6.1. An illustrative example showing the details of EKNN training considering three target classes {A, B, C}, two dimensional feature space (assuming two features and ) is depicted in Fig. 5.
Fig. 5.
EKNN training phase.
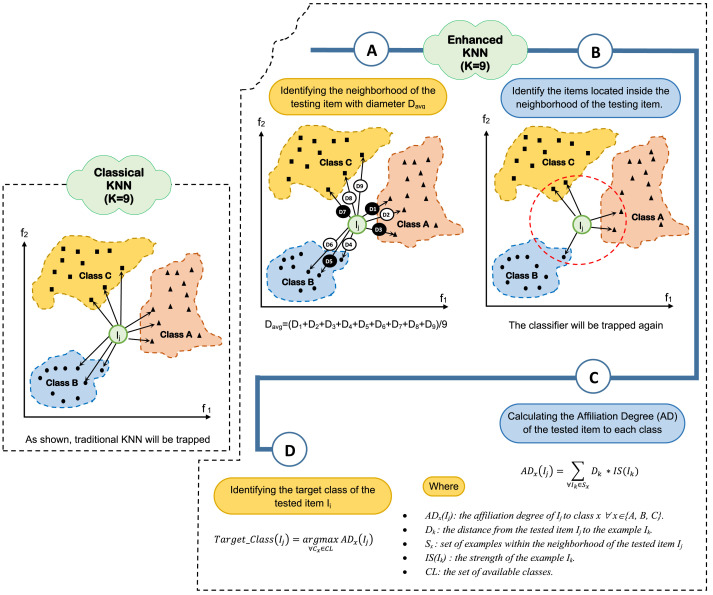
5.2.2. EKNN Testing
In the current situation of the exponential spread of COVID-19, there exists a critical need for rapid and accurate predictions of coronavirus infections. The proposed EKNN takes this issue into account by guaranteeing a simple but fast and effective testing for patients. During the testing phase of the proposed EKNN, considering a set of finite m target classes CL={c 1 , c2 , ….c }, initially, the tested item (person) is projected in the n dimensional feature space. Then, the K-nearest neighbors are identified. The distance from the tested item to each neighbor of the K nearest ones is calculated, then the average distance () is then calculated. A circular neighborhood is identified whose radius equals . Only the examples within the identified neighborhood will be considered for classifying the new item. The Affiliation Degree (AD) of the tested item to each class is calculated using (10).
| (10) |
Where (I ) is the affiliation degree of the tested item to class x x {A, B, C}, is the distance from the tested item to the example , S is the set of examples within the neighborhood of the tested item , and IS(I ) is the strength of the example . Finally, the tested item is targeted to the class to which it has the maximum affiliation degree as illustrated in (11).
| (11) |
Where CL is the set of considered target classes. An illustrated example showing the followed steps during EKNN testing is depicted in Fig. 6 considering three target classes {A, B, C}, two dimensional feature space (assuming two features and ).
Fig. 6.
Illustrative example showing the followed steps during EKNN testing phase.
6. Experimental results
In this section, the main contributions that were provided in the proposed Corona Patients Detection Strategy (CPDS) will be evaluated. Those contributions are; (i) HFSM for feature selection and (ii) EKNN as a new classification procedure. Firstly, feature extraction process will be performed using GLCM method to extract set of features from CT images before implementing HFSM method and then EKNN method. Secondly, the proposed HFSM will be implemented on the extracted features to select the most significant features. Finally, the proposed CPDS that combines both HFSM and EKNN will be executed to accurately detect COVID-19 patients with the minimum time penalty. Our implementation is based on COVID_CT dataset [33], [34]. COVID_CT is an internet based dataset that contains CT images from patients. It has been employed to allow reproduction of the results introduced in this paper in which it is divided into two sets, namely; training and testing. The training set is used for model learning. Then, the testing set is used to measure the goodness of the proposed model.
Several tunable parameters have been used in HFSM and EKNN. Some of them are set empirically, namely; and . As mentioned in Section 5.2.1, the optimal values of and are calculated empirically assuming the initial values of and (e.g., and ) as well as the step of change (e.g., ) are set to 0.1. Hence, the values assigned to and are in the set {0.1, 0.2, 0.3, …., 0.9, and 1.0}. EKNN is then tested using 100 patients. The optimal values of and , which gives the maximum classification accuracy was 0.7 and 0.9 respectively. The applied parameters with the corresponding implemented values are depicted in Table 6.
Table 6.
The applied parameters with the corresponding used values.
| Parameter | Description | Applied value |
|---|---|---|
| Ps | Probability of selection | Random (0Ps1) |
| Pc | Probability of crossover | Random (0Pc1) |
| Pm | Probability of mutation | Random (0Pm1) |
| K | No. of neighbors | 5 |
| Weighting factors | 0.7 | |
| 0.9 |
6.1. Evaluation metrics
During the next experiments, accuracy, error, precision, and sensitivity are four evaluation parameters will be calculated. Then, F-measure and micro-average related to precision and recall will be measured as additional parameters to clear the application results. To calculate the values of these measurements, a confusion matrix is applied as presented in Table 7. Noticeably, various formulas are used as a summarization of the confusion matrix as depicted in Table 8 [35], [36].
Table 7.
Confusion matrix.
| Predicted label |
|||
|---|---|---|---|
| Positive | Negative | ||
| Known label | Positive | True Positive (TP) | False Negative (FN) |
| Negative | False Positive (FP) | True Negative (TN) | |
Table 8.
Confusion matrix formulas.
| Measure | Formula | Intuitive meaning |
|---|---|---|
| Precision (P) | TP / (TP + FP) | The percentage of positive predictions those are correct. |
| Recall / Sensitivity (R) | TP / (TP + FN) | The percentage of positive labeled instances that were predicted as positive. |
| Accuracy (A) | (TP + TN) / (TP + TN + FP + FN) | The percentage of predictions those are correct. |
| Error (E) | 1-Accuracy | The percentage of predictions those are incorrect. |
| Macro-average | “for Precision” | The average of the precision and recall of the system on different c classes. |
| “for Recall” | ||
| Micro-average | (TP1 + TP2) / (TP1 + TP2 + FP1 + FP2) “for precision” | The summation up to the individual true positives, false positives, and false negatives of the system for different classes and the apply them to get the statistics |
| (TP1 + TP2) / (TP1 + TP2 + FN1 + FN2) “for Recall” |
||
| F-measure | 2*PR/(P+R) | The weighted harmonic mean of Precision and Recall |
6.2. Testing the proposed hybrid feature selection methodology (HFSM)
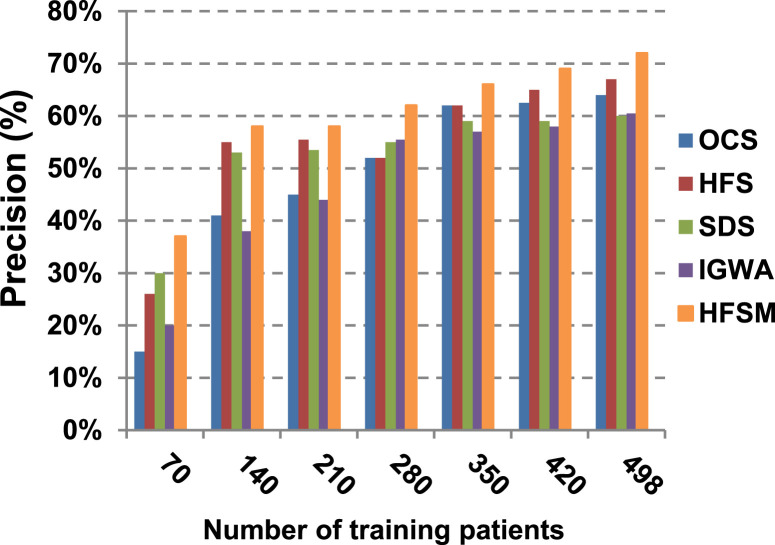
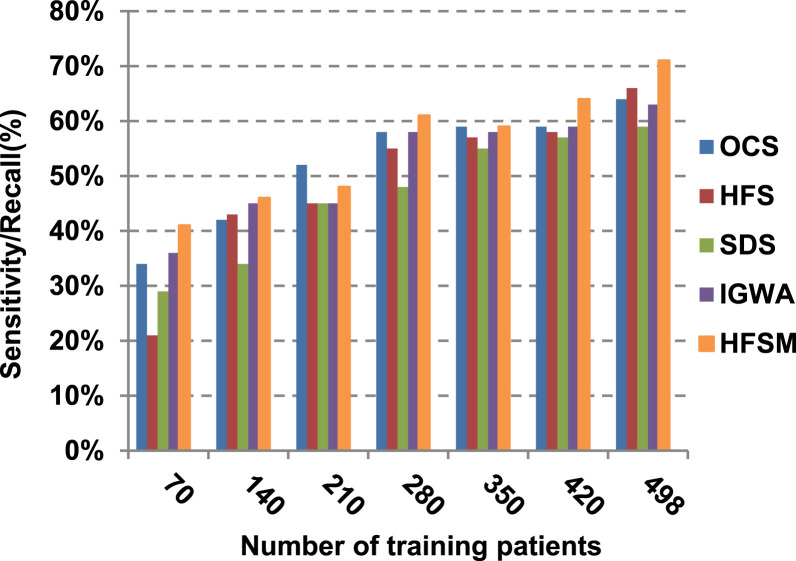
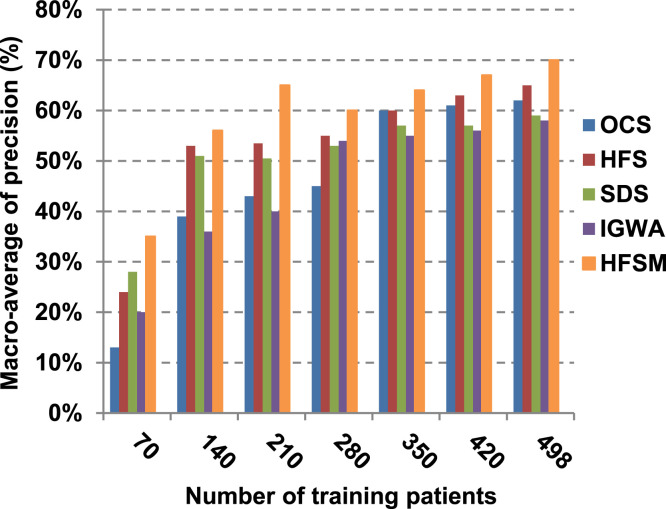
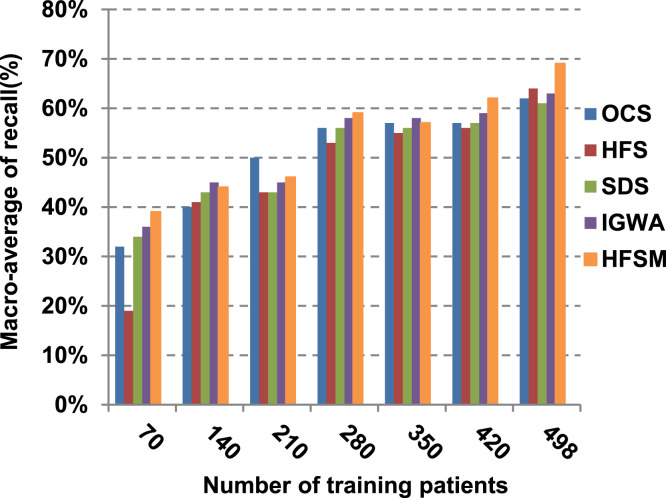
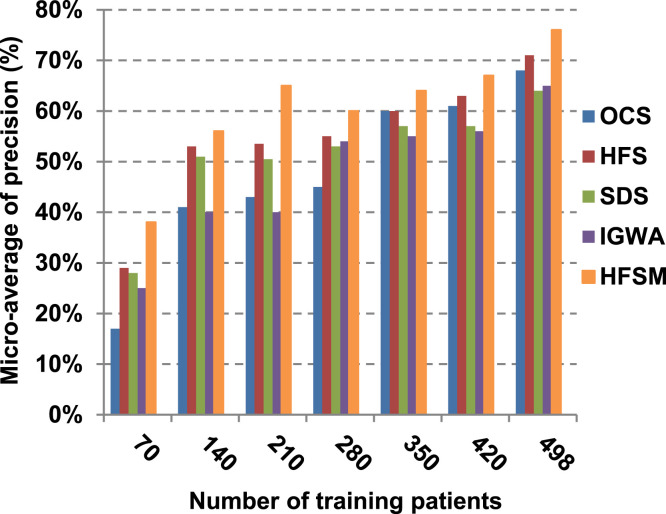
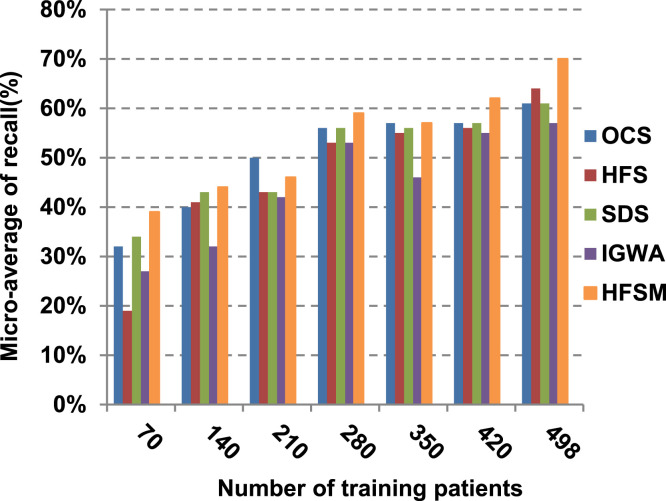
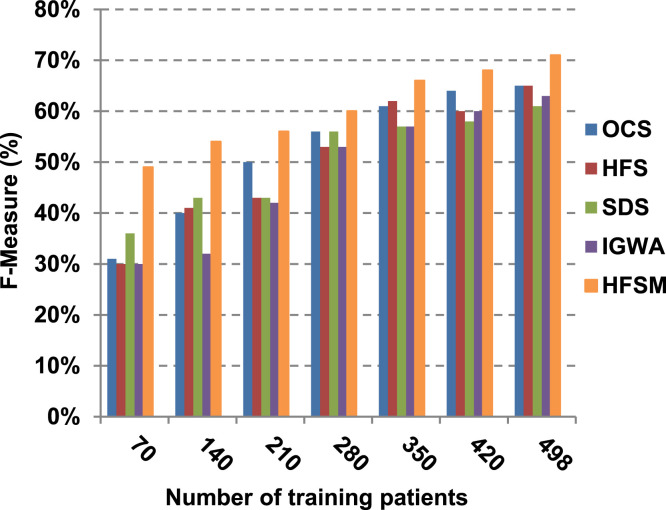
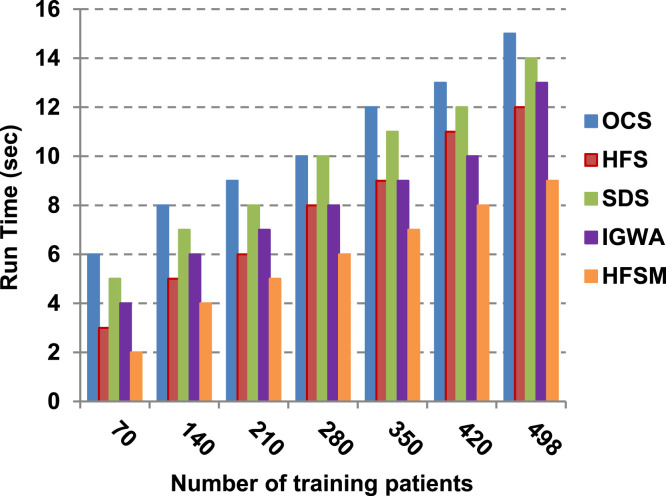
This paper introduces a hybrid feature selection methodology (HFSM) which combines both filter and wrapper methods. To prove the effectiveness of the proposed feature selection method, many features selection techniques are compared to the proposed features selection technique HFSM based on NB classifier as a standard classifier. The most recent feature selection techniques used for evaluation are presented in Table 9. Results are depicted in Fig. 7, Fig. 8, Fig. 9, Fig. 10, Fig. 11, Fig. 12, Fig. 13, Fig. 14, Fig. 15, Fig. 16. The first four measurements in Fig. 7, Fig. 8, Fig. 9, Fig. 10 which are; accuracy, error, precision and recall illustrate the performance of HFSM against many of recent methods. The final application results are measured by the last six measurements in Fig. 11, Fig. 12, Fig. 13, Fig. 14, Fig. 15, Fig. 16. These measurements are macro-average precision, macro-average recall, micro-average precision, micro-average recall, F-measure, and run time.
Table 9.
The most recent features selection techniques used for evaluation.
| Features selection technique | Description |
|---|---|
| Improvised Gray Wolf Algorithm (IGWA) [37] | In [37], IGWA is developed as an improvement over the traditional Gray Wolf Optimizer (GWO) algorithm. It is developed for multiple feature selection as the original GWO that can only be implemented on the mathematical function. Results presented in [37] show that the optimal feature set selected by IGWA gives the highest accuracy using different classifier. |
| Stochastic Diffusion Search (SDS) Based Feature Selection [38] | In [38], SDS for feature selection is employed to identify optimal feature subsets. In the initial stages, every agent is assigned to combining the feature subset from their respective search spaces (all the possible combinations of these features). Every agent now employs an independent and random split of the dataset for forming both training and testing subsets |
| Hybrid Feature Selection (HFS) approach [39] | In [39], HFS approach for feature selection using PCA and Relief method. PCA is a dimensionality reduction technique which is based on eigenvalue decomposition of a data matrix and it is a mathematical tool used for enhancing the accuracy of predictive models. Relief is a robust algorithm that deals well with incomplete, noisy and missing data.so this feature selection approach works well with multi-class problems and finds the conditional dependencies between features as well. Results presented in [39] find that the hybrid approach drastically reduced dimension on all datasets, thereby, enhancing the efficiency of the classifier and decrease in computation cost and time. |
| Opposition-based Crow Search (OCS) algorithm [40] | In [40], OCS is an optimization algorithm where most of the significant features are selected. OCS has been developed as an improvement over the Traditional Crow Search (CS) algorithm by adding the contrast operation to develop efficiency. For every initiated solution, the adjacent opposite operation also starts working. If the solutions are compared, better solution can be selected to obtain the optimal solution. Results presented in [40] find that OCS improves the classification result and increased the accuracy, specificity and sensitivity in the diagnosis of medical images. |
Fig. 7.
Accuracy of features selection methods using NB.
Fig. 8.
Error of features selection methods using NB.
Fig. 9.
Precision of features selection methods using NB.
Fig. 10.
Sensitivity of features selection methods using NB.
Fig. 11.
Macro-average of precision for features selection methods using NB.
Fig. 12.
Macro-average of recall for features selection methods using NB.
Fig. 13.
Micro-average of precision for features selection methods using NB.
Fig. 14.
Micro-average of recall for features selection methods using NB.
Fig. 15.
F-Measure of the different features selection methods using NB.
Fig. 16.
Run time of the different features selection methods using NB.
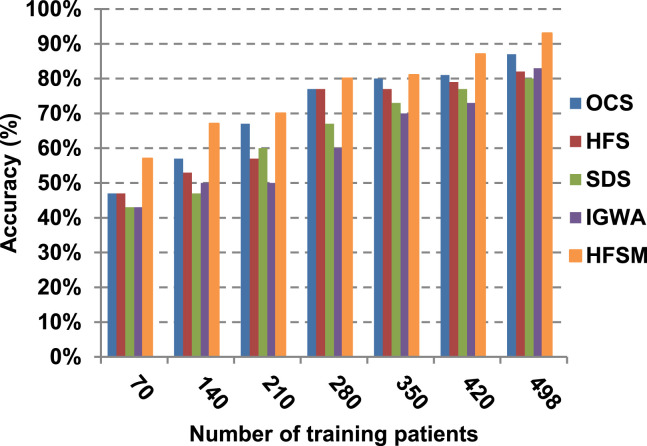
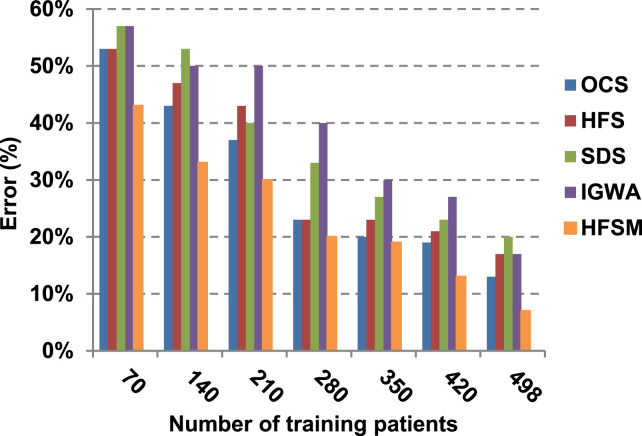
As illustrated in Fig. 7, Fig. 8, Fig. 9, Fig. 10, it is concluded that the performance of all methods is promoted by increasing the number of the patients inside training dataset. The maximum “Precision”, “Recall”, and “Accuracy”, while the minimum “Error” are obtained at maximum number of training patients (e.g., 498 patients). The reason is very simple; by increasing the number of training patients, the amount of data collected in addition to classification rules will definitely increase. Accordingly, classification accuracy is also enhanced, as the classifiers were better trained. It is also noted that; the proposed selection method called HFSM introduces the best performance against of others methods. Accordingly, both True Positive (TP) and True Negative (TN) are maximized, while False Positive (FP) and False Negative (FN) are minimized. This promotes the accuracy, precision, and recall of the proposed selection method while demoting its error. On the other hand, SDS introduces the worst performance. This happened because SDS method eliminates an effective feature then NB classifier is learned using training patients with the least effective subset of features. When training patients = 498, HFSM introduces about 0.72 precision, while it is 0.6 for SDS. At training patients equals 498, recall value for SDS is worth than HFSM which are 0.59, and 0.71 respectively. SDS’s accuracy is 0.80 while it is 0.93 for HFSM when training patients equals 498, which means that SDS suffers from a higher error rate than HFSM. For SDS and HSFM, the error reaches 0.20 and 0.07 respectively.
The final application results in Fig. 11, Fig. 12, Fig. 13, Fig. 14, Fig. 15, Fig. 16 show that the highest macro-average precision is related to HFSM with value reaches to 0.7, while the lowest measurement value is related to IGWA with value reaches to 0.58 at training patients equals 498. According to the macro-average recall at training patients equals 498, the highest value equals 0.69 at HFSM, but the lowest value related to SDS with value equals 0.61. When training patients equals 498, HFSM introduces about 0.76 micro-average precision value, while it is 0.64 for SDS. Moreover, micro-average recall value for OCS and SDS are worth than HFSM at training patients equals 498 which are 0.61, 0.61, and 0.7 respectively. The worst value of F-measure is 0.61 related to SDS and the best value is 0.71 related to HFSM at training patients equals 498. Additionally, implementing HFSM is faster than OCS at training patients equals 498 with run time reaches to 9 and 15 (seconds) respectively.
6.3. Testing the proposed COVID-19 patients detection strategy (CPDS)
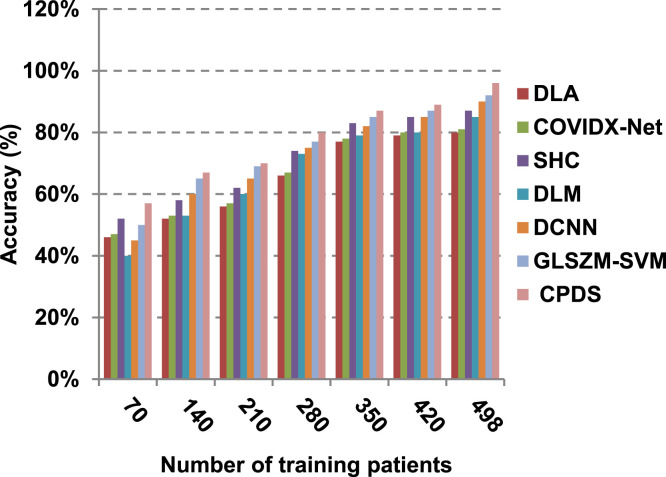
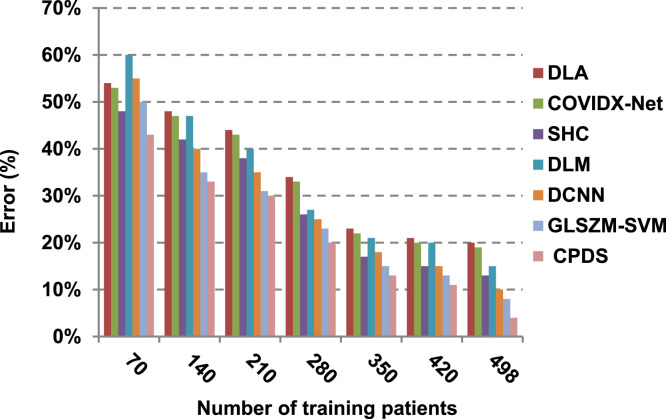
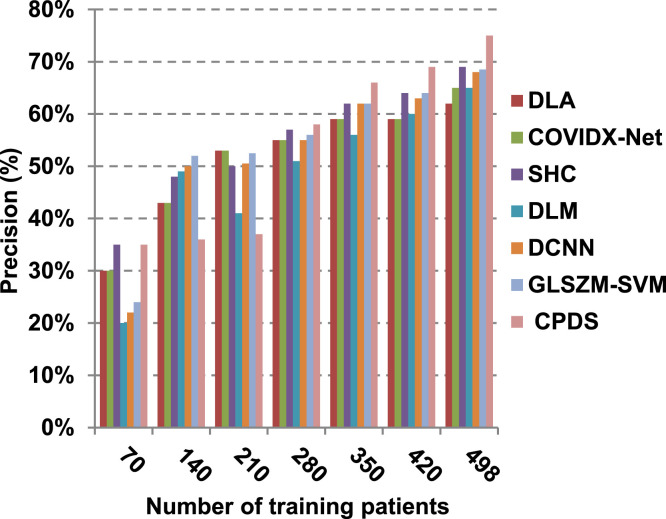
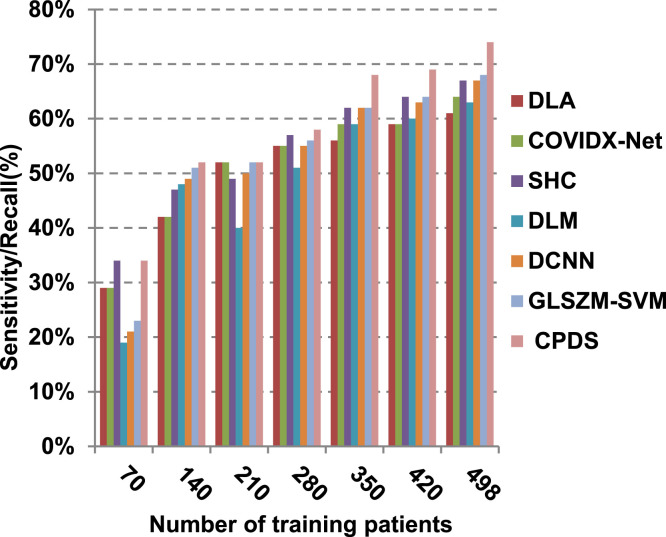
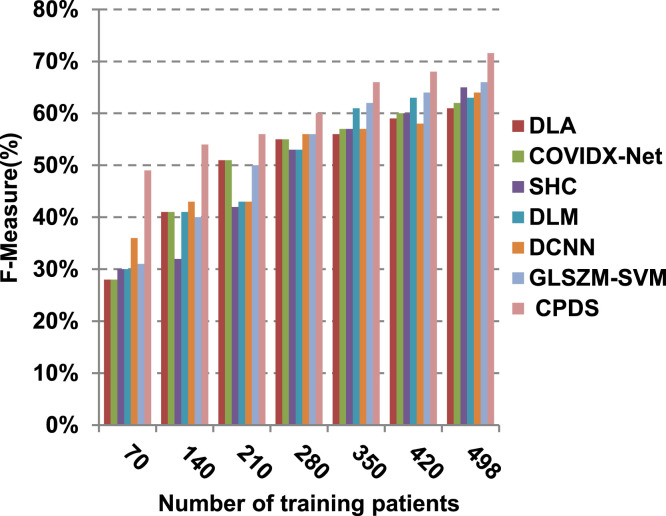
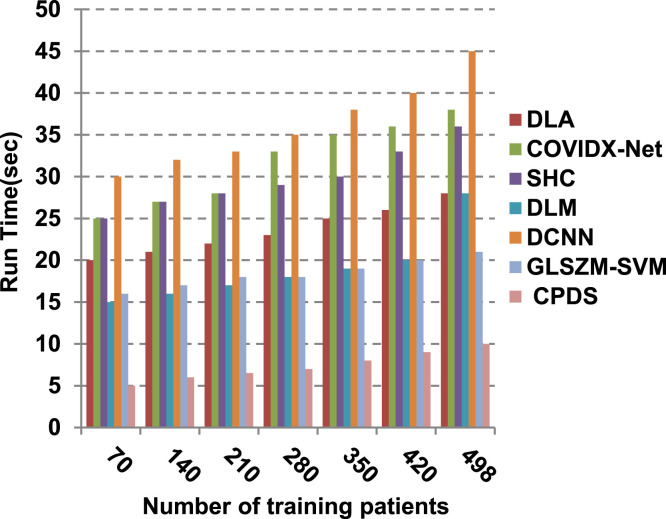
Finally, in this subsection, it is the time to test the whole proposed CPDS keeping all the proposed feature selection, and classification methodologies working together. To argue the effectiveness of our proposed strategy, it is compared against some of the recently used COVID-19 classification methods as presented in Table 3. Those recent methods are DCNN [2], GLSZM-SVM [17], DLM [18], DLA [19], SHC [20], and COVIDX-Net [21]. All capabilities proposed are used in our CPDS, hence, HFSM is employed for feature selection, and EKNN is used for classification. Results are shown in Fig. 17, Fig. 18, Fig. 19, Fig. 20, Fig. 21, Fig. 22, Fig. 23, Fig. 24, Fig. 25, Fig. 26. As illustrated in Fig. 17, Fig. 18, Fig. 19, Fig. 20, Fig. 21, Fig. 22, Fig. 23, Fig. 24, Fig. 25, Fig. 26, the proposed CPDS demonstrates the best performance. Error of CPDS is reduced, while its accuracy, precision, recall, macro-average, micro-average, and F-measure are promoted. This proves the effectiveness of HFSM and EKNN, which are the main parts of the proposed CPDS as they can effectively work together. Additionally, CPDS proved that it is faster than other methods.
Fig. 17.
Accuracy of the different classification techniques.
Fig. 18.
Error of the different classification techniques.
Fig. 19.
Precision of the different classification techniques.
Fig. 20.
Sensitivity of the different classification techniques.
Fig. 21.
Macro-average precision of the different classification techniques.
Fig. 22.
Macro-average recall of the different classification techniques.
Fig. 23.
Micro-average precision of the different classification techniques.
Fig. 24.
Micro-average recall of the different classification techniques.
Fig. 25.
F-Measure of the different classification techniques.
Fig. 26.
Run time of the different classification techniques.
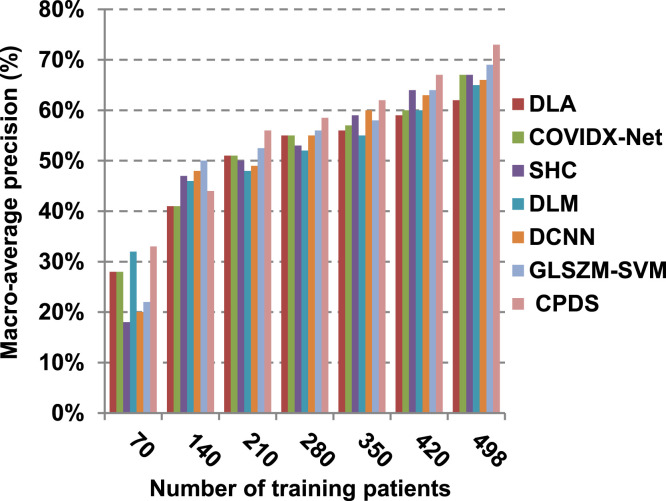
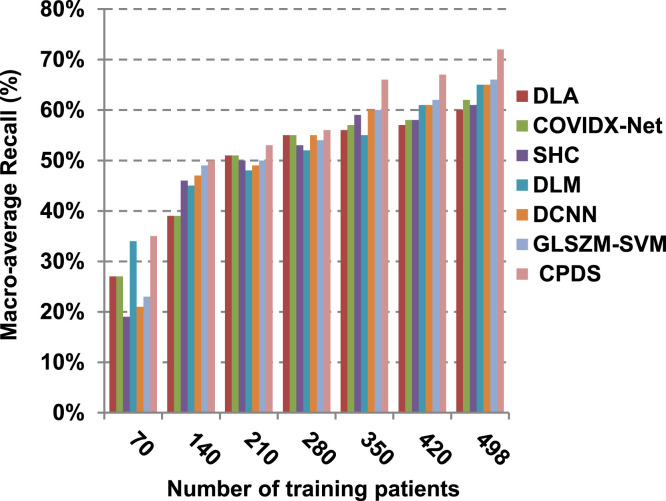
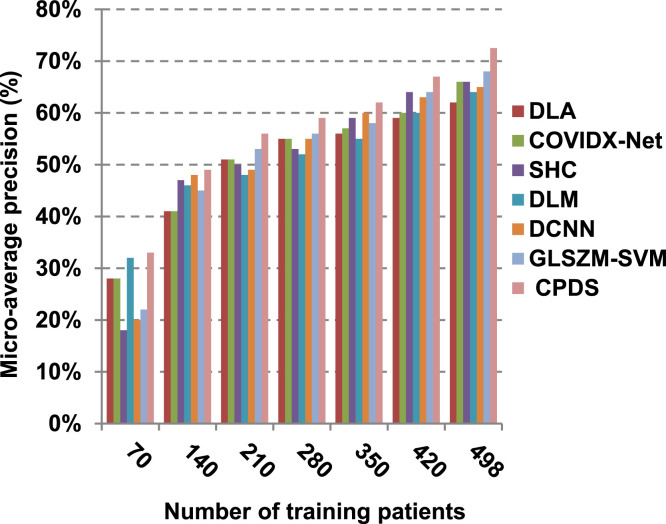
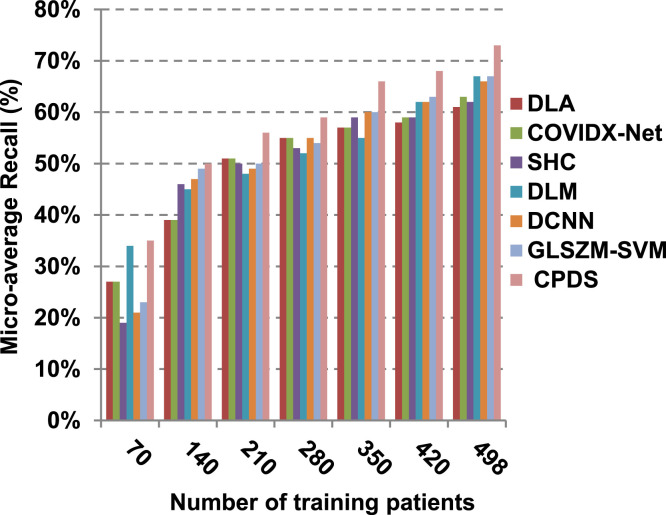
According to Fig. 17, Fig. 18, Fig. 19, Fig. 20, DLA introduces about 0.80 accuracy, while it is 0.96 for CPDS at training patients equals 498. The reason is that EKNN gives accurate detect infected patients with the minimum time penalty which is based on the most effective nearest neighbor’s based on the most significant features selected by HFSM. Thus, DLA provides the maximum error value that equals 0.2, but CPDS provides the minimum value that equals 0.04. CPDS provides about 0.75 precision, while it is 0.62 for DLA at training patients equals 498. Recall value of CPDS is 0.74, but it is 0.61 for DLA when training patients equals 498. Consequently, Fig. 17, Fig. 18, Fig. 19, Fig. 20 illustrate that CPDS is much better than GLZSM-SVM, DCNN, DLM, SHC, COVIDX-Net, and DLA. Results of the final application in Fig. 21, Fig. 22, Fig. 23, Fig. 24, Fig. 25 illustrate that macro-average precision of CPDS is 0.73, while it is 0.62 for DLA at training patients equals 498. Additionally, CPDS provides about 0.72 macro-average recall while it is 0.6 for DLA when training patients equals 498. CPDS provides the highest micro-average precision with value reaches to 0.725, while DLA provides the lowest measurement value equals 0.62 at training patients equals 498. Moreover, micro-average recall value of CPDS is 0.73, but it is 0.615 for DLA at training patients equals 498. When training patients equals 498, CPDS provides about 0.716 F-measure, while it is 0.61for DLA. Consequently, Fig. 21, Fig. 22, Fig. 23, Fig. 24, Fig. 25 illustrate that CPDS is much better than GLSZM-SVM, DCNN, DLM, SHC, COVIDX-Net, and DLA.
As depicted in Fig. 26, in spite of time complexity of both the wrapper feature selection and KNN classification algorithm, CPDS provides fast classification compared with other competitors. This happened because other competitors rely on deep learning concept. It is known that deep learning is computationally expensive, requires a large amount of memory and computational resources. Moreover, it suffers from high time penalty. On the other hand, CPDS is more simple, flexible, and able to manage problems with inaccurate data. Additionally, it relies on a perfect hybrid feature selection methodology that elects only those effective features. As feature selection takes place only one time, it does not affect the classification speed of CPDS during the testing (diagnose) process. Such accurate feature selection methodology results in reducing the dimensionality of the employed feature space, which in turn minimizes the time taken by EKNN for diagnose. Moreover, electing the most suitable neighbors by EKNN accelerates the diagnose process as it does not consider all neighbors of the tested item. Hence, CPDS represents a fast and accurate decision-making system for detecting COVID-19 patients aiming to protect the healthcare system from becoming overwhelmed.
For summarizing the discussion introduced through this section, it can be concluded that the proposed COVID-19 Patients Detection Strategy (CPDS) outperforms recent detection strategies due to the following reasons;
-
i.
The proposed CPDS perfectly elects the best set of features to express the problem in hand as it relies on a strong hybrid feature selection strategy that combines evidence from both filter and wrapper methods.
-
ii.
CPDS is also immune to KNN trapping problem as it uses an enhanced version called EKNN. Unlike traditional KNN, EKNN classifies an item based on only item’s qualified neighbors. This guarantees the maximum classification accuracy and minimizes the classification time.
-
iii.
Compared to recent techniques, EKNN can accurately detect infected patients with the minimum time penalty based on those significant features selected by HFSM as well as considering only the most effective neighbors of the tested item by EKNN.
7. Conclusions
COVID-19 infectious disease shocked the world and still threatens the lives of billions of people. Accordingly, early detection of COVID-19 patients is an important process for disease cure and control. The literature review work shows that an optimum technique could not be defined yet. Thus our challenge is to find a suitable fast and accurate detection strategy. In this work, we have presented an accurate and intelligent detection strategy which can potentially provide smart medical diagnosis . In our detection strategy, COVID-19 Patients Detection Strategy (CPDS) is built upon two essential parts, which are; features selection, and new classification model. The proposed feature selection methodology is called Hybrid Feature Selection Methodology (HFSM), which combines between the benefits of both filter and wrapper selection methods. HFSM elects the most informative and effective features from the features extracted from chest CT images. On the other hand, the proposed classification methodology is called Enhanced K-Nearest Neighbor (EKNN). Experimental results have shown that the proposed feature selection technique provides fast and accurate results comparing to the existing methods in terms of accuracy, error, precision, and sensitivity/recall. HFSM provides precision, recall, accuracy, and error values reach to 0.72, 0.71, 0.93, and 0.07 respectively. The proposed CPDS achieved 96% of accuracy that is higher than other recent methodologies. Finally, the proposed CPDS based on HFSM and EKNN provides fast and more accurate results than the existing techniques in terms of accuracy, precision, sensitivity, and execution time.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
The authors are so pleased to introduce their great thanks to all staff members of Nile higher institute for engineering and technology for the great support. Most of the work introduced in this paper has been done in the great laboratories of the institution. Special thanks of gratitude to doctor Salah Abd Elghafar Mansour for his endless support and kindness.
Footnotes
The code (and data) in this article has been certified as Reproducible by Code Ocean: (https://codeocean.com/). More information on the Reproducibility Badge Initiative is available at https://www.elsevier.com/physical-sciences-and-engineering/computer-science/journals.
References
- 1.Chung M., Bernheim A., Mei X., Zhang N. CT Imaging features of 2019 Novel Coronavirus (2019-nCoV) Radiology. 2019;275(1):202–207. doi: 10.1148/radiol.2020200230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Narin A., Kaya C., Pamuk Z. 2020. Automatic detection of Coronavirus disease (COVID-19) using X-ray images and deep convolutional neural networks.arXiv:2003.10849 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Kong W., Agarwal P. Chest imaging appearance of COVID-19 infection. Radiology. 2020;2(1):1–22. doi: 10.1148/ryct.2020200028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Conghy T., Pon B., Anderson E. 2020. When does hospital capacity get overwhelmed in USA? Germany? A model of beds needed and available for Coronavirus patients. trent.st. [Google Scholar]
- 5.Thamilselvan P., Sathiaseelan J. A comparative study of data mining algorithms for image classification. Int. J. Educ. Manag. Eng. (IJEME) 2015;5(3):1–9. [Google Scholar]
- 6.G. Gayathri, S. Satapathy, A Survey on techniques for prediction of asthma, in: Smart Intelligent Computing and Applications, Springer, pp. 751–758.
- 7.Ayyad S., Saleh A., Labib L. Gene expression cancer classification using modified K-nearest neighbors technique. BioSystems. 2019;176:41–51. doi: 10.1016/j.biosystems.2018.12.009. [DOI] [PubMed] [Google Scholar]
- 8.Shariaty F., Hosseinlou S., Rud V. Automatic lung segmentation method in computed tomography scans. J. Phys.: Conf. Ser. IOP Conf. 2019:1–7. [Google Scholar]
- 9.Lingayat N., Tarambale M. A computer based feature extraction of lung nodule in chest X-ray image. Int. J. Biosci. Biochem. Bioinform. 2013;3(6):624–629. [Google Scholar]
- 10.Mohan G., Subashini M. MRI Based medical image analysis: Survey on brain tumor grade classification. Biomed. Signal Process. Control. 2018;39:139–161. [Google Scholar]
- 11.Kanagaraj G., Kumar P. Pulmonary tumor detection by virtue of GLCM. J. Sci. Ind. Res. 2020;79:132–134. [Google Scholar]
- 12.Zotin A., Hamad Y., Simonov K., Kurako M. Proceedings of the 23rd International Conference on Knowledge-Based and Intelligent Information & Engineering Systems, vol. 159. Elsevier; 2019. Lung boundary detection for chest X-ray images classification based on GLCM and probabilistic neural networks; pp. 1439–1448. [Google Scholar]
- 13.Rabie A., Saleh A., Abo-Al-Ez K. A new strategy of load forecasting technique for smart grids. Int. J. Modern Trends Eng. Res. (IJMTER) 2015;2(12):332–341. [Google Scholar]
- 14.Saleh A., Rabie A., Abo-Al-Ezb K. A data mining based load forecasting strategy for smart electrical grids. Adv. Eng. Inf. 2016;30(3):422–448. [Google Scholar]
- 15.Rabie A., Ali S., Saleh A., Ali H. A new outlier rejection me thodology for supporting load forecasting in smart grids based on big data. Clust. Comput. 2019:1–27. doi: 10.1007/s10586-019-02942-0. [DOI] [Google Scholar]
- 16.khare P., Burse K. Feature selection using genetic algorithm and classification using weka for Ovarian Cancer. Int. J. Comput. Sci. Inf. Technol. (IJCSIT) 2016;7(1):194–196. [Google Scholar]
- 17.M. Barstugan, U. Ozkaya, S. Ozturk, Coronavirus (COVID-19) Classification using CT Images by Machine Learning Methods, arXiv preprint arXiv:2003.09424.
- 18.Sethy P., Behera S. 2020. Detection of Coronavirus Disease (COVID-19) Based on Deep Features; pp. 1–9. preprints, https://www.preprints.org/manuscript/202003.0300/v1. [Google Scholar]
- 19.Wang S., Kang B., Ma J. 2020. A deep learning algorithm using CT images to screen for Corona Virus Disease (COVID-19) pp. 1–26. medRxiv preprint, [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Farid A., Selim G., Khater H. 2020. A Novel Approach of CT Images Feature Analysis and Prediction To Screen for Corona Virus Disease (COVID-19) pp. 1–9. Preprints https://www.preprints.org/manuscript/202003.0284/v1. [Google Scholar]
- 21.Hemdan E., Shouman M., Karar M. 2020. COVIDX-Net: A framework of deep learning classifiers to diagnose COVID-19 in X-ray images. arXiv preprint arXiv:2003.11055. [Google Scholar]
- 22.Cortegiani A., Ingoglia G., Ippolito M., Giarratano A., Einav S. A systematic review on the efficacy and safety of chloroquine for the treatment of COVID-19. J. Critic. Care. 2020:1–5. doi: 10.1016/j.jcrc.2020.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Felice F., Polimeni A., Valentini V. The impact of Coronavirus (COVID-19) on head and neck cancer patients’ care. Radiother. Oncol. 2020;147:84–85. doi: 10.1016/j.radonc.2020.03.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Allam M., Nandhini M. A study on optimization techniques in feature selection for medical image analysis. Int. J. Comput. Sci. Eng. (IJCSE) 2017;9:75–82. [Google Scholar]
- 25.Gu S., Cheng R., Jin Y. Feature selection for high-dimensional classification using a competitive swarm optimizer. Soft Comput. 2018;22(3):811–822. [Google Scholar]
- 26.Ayyad S., Saleh A., Labib L. A new distributed feature selection technique for classifying gene expression data. Int. J. Biomath. 2019;12(2):1–34. [Google Scholar]
- 27.Shah S., Shabbir H., Rehman S., Waqas M. A comparative study of feature selection approaches: 2016-2020. Int. J. Sci. Eng. Res. 2020;11(2):469–478. [Google Scholar]
- 28.Li Y. Text feature selection algorithm based on chi-square rank correlation factorization. J. Interdiscipl. Math. 2017;20(1):153–160. [Google Scholar]
- 29.Rajab K. New hybrid features selection method: A case study on websites phishing. Secur. Commun. Netw. 2017:1–10. [Google Scholar]
- 30.Vinutha H., Poornima B. An ensemble classifier approach on different feature selection methods for intrusion detection. Inf. Syst. Des. Intell. Appl. 2018;672:443–451. [Google Scholar]
- 31.Djellali H., Zine N., Azizi N. Modelling and Implementation of Complex Systems. vol. 1. Springer; Cham: 2016. Two stages feature selection based on filter ranking methods and SVMRFE on medical applications; pp. 281–293. (Lecture Notes in Networks and Systems). [Google Scholar]
- 32.Alyam R., Alhajja J., Alnajran B. Proceedings of the 2017 International Conference on Informatics, Health & Technology (ICIHT) IEEE; Riyadh, Saudi Arabia: 2017. Investigating the effect of correlation based feature selection on breast cancer diagnosis using artificial neural network and support vector machines. [Google Scholar]
- 33.https://github.com/UCSD-AI4H/COVID-CT.
- 34.Zhao J., Zhang Y., He X., Xie P. 2020. COVID-CT-Dataset: A CT scan dataset about COVID-19. arXiv preprint, arXiv:2003.13865v1. [Google Scholar]
- 35.Abualigah L. Studies in Computational Intelligence. Springer; Boston, MA, USA: 2019. Feature selection and enhanced krill herd algorithm for text document clustering; pp. 1–7. [Google Scholar]
- 36.Abualigah L., Khader A. Unsupervised text feature selection technique based on hybrid particle swarm optimization algorithm with genetic operators for the text clustering. J. Supercomput. 2017;73:4773–4795. [Google Scholar]
- 37.Gupta N., Gupta D., Khanna A., Filho P., Albuquerque V. Evolutionary algorithms for automatic lung disease detection. Measurement. 2019;140:590–608. [Google Scholar]
- 38.Shanth S., Rajkumar N. Lung cancer prediction using stochastic diffusion search (SDS) based feature selection and machine learning methods. Neural Process. Lett. 2020 doi: 10.1007/s11063-020-10192-0. [DOI] [Google Scholar]
- 39.Jain D., Singh V. A two-phase hybrid approach using feature selection and adaptive SVM for chronic disease classification. Int. J. Comput. Appl. 2019:1–13. doi: 10.1080/1206212X.2019.1577534. [DOI] [Google Scholar]
- 40.Raj R., Shobana S., Pustokhina I., Pustokhin D., Gupta D., Shankar K. Optimal feature selection-based medical image classification using deep learning model in Internet of medical things. IEEE Access. 2020;8:58006–58017. [Google Scholar]