Highlights
-
•
Light scattering by complex-shaped large particles is investigated in laboratory.
-
•
The scattering matrix of airborne ragweed pollen is measured as a case study.
-
•
A (VIS, IR) polarimeter has hence been built and validated on spherical particles.
-
•
The (VIS, IR) spectral dependence of the ragweed scattering matrix is revealed.
Keywords: Scattering, Ragweed pollen, Scattering matrix, Polarimetry, Spectroscopy
Abstract
Ragweed or Ambrosia artemisiifolia pollen is an important atmospheric constituent affecting the Earth's climate and public health. The literature on light scattering by pollens embedded in ambient air is however rather sparse: polarization measurements are limited to the sole depolarization ratio and pollens are beyond the reach of numerically exact light scattering models mainly due to their tens of micrometre size. Also, ragweed pollen presents a very complex shape, with a small-scale external structure exhibiting spikes that bears some resemblance with coronavirus, but also apertures and micrometre holes. In this paper, to face such a complexity, a controlled-laboratory experiment is proposed to evaluate the scattering matrix of ragweed pollen embedded in ambient air. It is based on a newly-built polarimeter, operating in the infra-red spectral range, to account for the large size of ragweed pollen. Moreover, the ragweed scattering matrix is also evaluated in the visible spectral range to reveal the spectral dependence of the ragweed scattering matrix within experimental error bars. As an output, precise spectral and polarimetric fingerprints for large size and complex-shaped ragweed pollen particles are then provided. We believe our laboratory experiment may interest the light scattering community by complementing other light scattering experiments and proposing outlooks for numerical work on large and complex-shaped particles.
1. Introduction
Pollens are important atmospheric constituents with multitude of impacts. Through allergenic diseases, pollen exposure leads to pollinosis [1], clinically characterized by bronchial asthma or rhinoconjunctivis with annual periodicity. Ragweed pollen or Ambrosia artemisiifolia represents one of the major seasonal allergens in Europe and Northern America [2], [3], [4] and induces asthma about twice as often as other pollens [5]. To figure out, 15.8 million persons in Europe are clinically ragweed sensitised, for an economic cost in Europe of about 7 billion euros [6]. This pollen allergenicity is further enhanced by atmospheric pollution by particulate matter [7], which modifies the pollen morphological structure [8]. Pollens also contribute to the Earth's climate through light scattering and extinction and by acting as cloud condensation and ice nuclei [9], hence influencing regional precipitations [10], [11]. At a local scale, the infra-red downwelling flux can be increased by up to eight times the monthly mean at high pollen concentrations [12]. Hence, climate warming promotes the spread of ragweed in central Europe [13] and ragweed production and growth is directly impacted by rising atmospheric carbon dioxide concentrations [14]. Due to climate change, the ragweed pollen season starts earlier and has an increased duration [15]. Moreover, each ragweed plant produces millions of pollen grains that can be transported over large distances and be observed far from source regions [5], up to a continental scale [16]. Hence, atmospheric transport models have been developed to forecast pollen concentrations [17] by considering meteorological data, emission maps and pollen counts [18].
With about twenty micrometres volume equivalent diameter, ragweed pollen grains are rather large particles [19]. The ragweed shape is overall spherical but exhibits a smaller scale complex external structure with spikes, apertures and sub-micrometre holes, as well as an heterogeneous cell content [20]. As recently underscored by Liu et al. [21], accounting for this complex geometry is key for radiative transfer applications involving pollens. To study the size and the morphology of ragweed, the most widely-used methodology is the historical approach, based on optical and scanning electron microscopy after gravitational deposition on a substrate [22]. Deep learning recently considerably improved this methodology [23]. In the last two decades, complementary optical methodologies have been developed, based on laser-induced fluorescence, interferometry, or / and light scattering. In laser-induced fluorescence, the pollens lifetime and emission spectra are recorded from the UV to the NIR spectral range to allow identifying fingerprints [24], [25], [26]. Pollens holography allows image-based recognition [27], [28]. Moreover, as published by M. Berg and G. Videen [29], a cluster of ragweed pollen particles can be imaged in-situ using digital in-line holography to discern the ragweed single-particle size and shape. The sensitivity of light scattering to the pollens size and shape has been studied for several decades when pollen grains are embedded in aqueous solutions [30], [31], [32]. More recently, light scattering by pollens has been studied when pollens are in a fixed orientation as deposited on a holder in [33], [34], [35] or more recently in [36]. Concerning airborne pollens, forward and side scattering have been compared in [37] and the spectral dependence of forward light scattering patterns has been studied in [38], without however considering the light polarization property, which may be vary during the scattering process for non-spherical particles [39], as for ragweed pollen particles. The light depolarization ratio of several pollens has been evaluated in the atmosphere in [40], [41], [42], [43]. However, such polarization measurements remain sparse and the measured atmospheric depolarization ratio may differ [44], [45] from that specific to ragweed since pollens are usually present in the atmosphere in the form of particle mixtures. Furthermore, these polarization measurements are limited to the sole particles depolarization ratio, while the ragweed ability to scatter light should be specified for each polarization state by providing its scattering matrix. Likewise, due to their large size, and the small-scale morphological structures of ragweed pollen grains are beyond the reach of numerically exact light-scattering models [46], [47]. Historically, the Lorenz-Mie theory has been applied to study the influence of the membrane thickness and the pollen refractive index on the scattered light intensity using a core/shell model [48]. However, as well-known [49], the spherical model cannot reproduce the polarization properties of ragweed complex-shaped grains. Interestingly, the ragweed overall spherical shape with regular spikes bears some resemblance with that of coronavirus, which has been recently studied using T-Matrix numerical code by D. Petrov [50]. However, applying this numerical code to ragweed pollen particles a priori remains challenging due to their larger size. Also, surface roughness should be considered for such large particles. In this context, controlled laboratory measurements of the ragweed pollen scattering matrix may help to discuss the underlying assumptions inherent to such light scattering numerical models for pollens.
On account of the above literature, the scattering matrix of ragweed pollen particles should be evaluated by taking into account their large size and their complex shape, which is key for radiative transfer applications [21]. The novelty of our contribution is then twofold. Firstly, a controlled-laboratory experiment has been developed to precisely evaluate the scattering matrix of ragweed pollen particles embedded in ambient air. It is based on a newly-built laboratory polarimeter, operating in the infra-red spectral range to account for the large size of ragweed pollen particles. As a second novelty, this ragweed scattering matrix is evaluated also in the visible spectral range at 532 nm wavelength, to reveal precise spectral and polarimetric fingerprints for ragweed. The paper is organised as follows. Section 2 details our laboratory methodology to precisely evaluate the ragweed scattering matrix at two wavelengths with corresponding sources of uncertainties. Section 3 is dedicated to the characterization of the size and the shape of our ragweed samples, based on scanning electron microscopy images and evaluation of their size distribution. The evaluation of the ragweed scattering matrix at two wavelengths is presented in Section 4. The paper ends with a conclusion and proposes outlooks.
2. Light scattering by ragweed pollen
2.1. Scattering matrix formalism
We here consider elastic scattering of an electromagnetic radiation (wavelength λ, polarization state π) by an ensemble of ragweed pollen particles embedded in ambient air. While the wavelength is preserved during the elastic scattering process, the polarization states of the incident and scattered radiations (respective wave-vectors k 0(λ) and k(λ)) may differ and be analysed in the framework of the scattering matrix formalism [39]. In this formalism, the polarization states of the incident and scattered radiations are described by the incident and scattered Stokes vectors (S 0) = [I0, Q0,U0,V0]t and (S) = [I, Q, U, V]t, where I corresponds to the light intensity, Q and U are parameters describing the linear polarization state, while V refers to circular polarization. The wave-vectors (k 0, k) define the scattering angle, used as a reference plane for the Stokes vectors. By assuming ragweed pollen particles to be randomly oriented and to have their mirror particles in equal number in the particles ensemble, the incident and scattered Stokes vectors relate as:
| (1) |
where d is the distance from the ragweed pollen particles to the light detector. In Eq. (1), the dimensionless scattering matrix elements Fij(λ) (i,j from 1 to 4) depend on the wavelength of the radiation, the scattering angle, the size, the shape and the refractive index of the ragweed pollen particles. If ragweed pollen particles were spherical, the scattering matrix elements would simplify [51] since for homogeneous spherical particles, F 11(λ) = F 22(λ) and F 33(λ) = F 44(λ). The scattering matrix elements can be normalized with respect to the scattering phase function F 11(λ):
| (2) |
which at most equal unity, as detailed in light scattering textbooks [52].
2.2. Laboratory (VIS, IR) light scattering experimental setup for ragweed
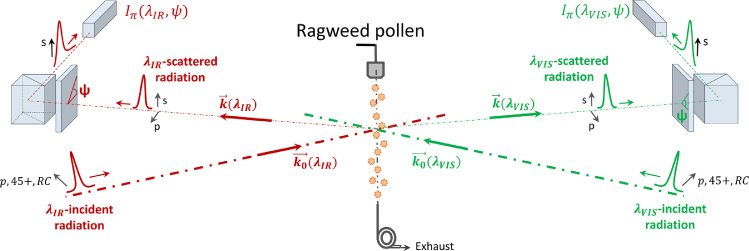
Fig. 1 schemes our laboratory light scattering experimental set-up, based on two laboratory polarimeters operating at wavelength λVIS = 532 nm and λIR = 1064 nm respectively, to account for the spectral dependence of the ragweed pollen scattering matrix. Ragweed pollen particles are embedded in laboratory ambient air as described in Section 3.1. While the λVIS-polarimeter is similar to our previous work [53], the λIR-polarimeter is new and has been specifically designed to evaluate light scattering by ragweed pollen grains, which exhibit a size in the tens of micrometres range. Special care has been taken to precisely define the Stokes vector of the incident radiation at each wavelength. The polarization state of the scattered radiation is analysed with a quarter-wave plate (QWP) and a retro-reflecting polarizing beam-splitter cube (PBC). At wavelength λIR, the intensity of the s-polarization component of the scattered radiation is measured with an Si avalanche photodiode cooled at 0 °C. To minimize wavelength cross-talks, a selective interference filter is inserted before the photodiode. After minimizing the polarization and wavelength cross-talks (see Section 2.4), to add precision in the evaluation of the scattering matrix elements, the scattered light intensity is measured for a complete rotation of the QWP. The radiation scattered by ragweed pollens grains is discriminated from light scattering by laboratory ambient air by achieving time-resolved measurements synchronized with the laser pulse, hence addressing the time-of-flight 2d/c taken by a laser pulse to reach the detector after light scattering. The scattered intensity by ragweed pollens grains is then evaluated by subtracting the intensity scattered by laboratory ambient air from the total intensity scattered by ragweed and ambient air. As underscored in Fig. 1, both polarimeters evaluate the scattering matrix elements of the same ragweed sample and operate at a scattering angle of 178°, close to 180°, which can be interesting for remote sensing applications. The scattering angle slightly differs from strict backscattering to allow the Eq. (1) scattering matrix elements to be a priori independent from F 22(λ). Indeed, at strict backscattering, only F 11(λ) and F 22(λ) would appear in Eq. (1) since F 33(λ) = −F 22(λ), F 44(λ) = F 11(λ) − 2F 22(λ), while F 12(λ) = F 34(λ) = 0.
Fig. 1.
Scheme of our laboratory experimental set-up for ragweed scattering matrix evaluation at two wavelengths (λVIS = 532 nm and λIR = 1064 nm). The 178° scattering angle has been exaggerated to ease the reading. Ragweed pollens grains are embedded in laboratory ambient air as described in Section 3.1.
2.3. Methodology for evaluating the ragweed scattering matrix elements
The light intensity scattered by ragweed pollen grains is evaluated by accounting for the successive Mueller matrices encountered in Fig. 1 by the (λVIS, λIR) laser pulses. If P 0(λ) is the incident laser power at wavelength λ and the polarization state of the incident radiation is defined with a polarizer [P], the detected scattered intensity at wavelength λ is given by:
| (3) |
Where η(λ) is the electro-optics efficiency of the light detector and (P j) = [1, 0, 0, 0] is a unitary projector as the light detector is solely sensitive to the first component of the scattered Stokes vector, i.e. the light intensity. [QWP] and [PBC] are the Mueller matrices of the quarter-wave plate and the reflecting PBC respectively. The π-subscript is used in Eq. (3) to refer to the polarization state of the incident radiation defined by the Stokes vector [P](S 0). To evaluate the five normalized ragweed scattering matrix elements fij(λ) = Fij(λ)/F 11(λ), three successive incident polarization states are required, for example π = (p, 45+, RC), corresponding to the following Stokes vectors [P](S 0) = [1, 1, 0, 0], [1, 0, 1, 0] and [1, 0, 0, 1] respectively. If ψ represents the angle between the QWP-fast axis and the scattering plane, using [54] for [QWP] and [PBC], the detected scattered intensity I π(λ,ψ) for incident polarization state π is given by:
| (4) |
Where I 11(λ = )η(λ)P 0(λ)F 11(λ)/4d 2 and ψ is counted counter-clockwise for an observer looking from the PBC to the ragweed pollen particles. Interestingly, the a π(λ), b π(λ),c π(λ),d π(λ) coefficients are combinations of the normalized scattering matrix elements fij(λ) and depend on the polarization state of the incident radiation, as referred to by the π-subscript. After a few calculations detailed in Miffre et al. [53], the normalized scattering matrix elements then express as:
| (5a) |
| (5b) |
| (5c) |
| (5d) |
| (5e) |
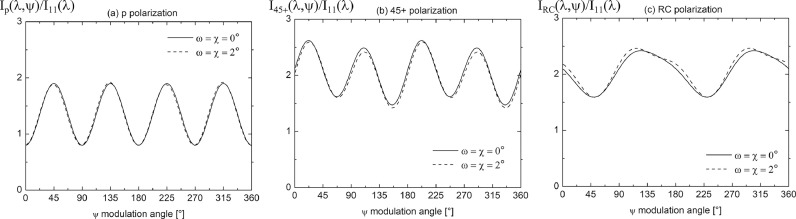
Where, to ease the reading, the dependence of a π(λ), b π(λ),c π(λ),d π(λ) with wavelength λ has been omitted. Hence, the normalized scattering elements f 33(λ) and f 44(λ) can be retrieved using incident polarization states (45+) and (RC) respectively, while the normalized scattering matrix elements f 12(λ) and f 34(λ) can be retrieved either from (45+) or (RC) incident polarization state. From the evaluation of f 12(λ), incident polarization state (p) allows retrieving f 22(λ). By adjusting the detected scattered intensity with Eq. (4) over a complete rotation of the QWP, the coefficients a π(λ) to d π(λ) can be precisely determined, allowing precise evaluations of the normalized scattering matrix elements by applying Eqs. (5). Fig. 2 shows the variations of I π(λ,ψ)/I 11(λ) for given scattering matrix elements at incident polarization states π = (p, 45+, RC) when varying the modulation angle ψ. Following Eqs. (4, 5), the minima in Fig. 2(a), which are equal to 2(1 − f 22), are null for spherical particles and the (p)- polarization curve is π/2-periodic as coefficients bp(λ) and dp(λ) are zero. In Fig. 2(b) corresponding to 45+ -incident polarization state, the detected scattered intensity I 45+(λ)/I 11(λ) is π-periodic as b 45+(λ) is not null. The difference between two successive maxima or minima in Fig. 2(b) is proportional to f 34(λ). In Fig. 2(c) corresponding to RC-incident polarization state, the detected scattered intensity IRC(λ,ψ)/I 11(λ) is also π-periodic, with minima equal to 2(1 − f 44(λ)).
Fig. 2.
Numerical simulation of the detected scattered light intensity Iπ(λ,ψ)/I11(λ) as a function of the ψ modulation angle of the QWP following Eq. (4), for f22(λ)= 0.6, f33 (λ) = − 0.5, f44(λ) = − 0.2, f12(λ) = −0.05 and f34(λ) = −0.05, at incident polarization states π = (p, 45+, RC) from panels (a) to (c). As detailed in Section 2.4, dashed curves show the modification induced in I(λ, ψ)/I11(λ) when considering a 2° deviation in both ω(λ) and χ(λ) for the incident polarization state.
2.4. Accuracy on ragweed scattering matrix elements fij(λ)
Special care has been taken to precisely evaluate the uncertainties on the retrieved scattering matrix elements fij(λ) at wavelength λ.
-
•
Statistical errors on fij(λ) may arise from fluctuations in the probed scattering volume of the ragweed pollen particles number concentration. If the ragweed pollen number concentration is stable over a complete rotation of the QWP (see Section 4.2), fluctuations over a one second timescale may occur and add noise to the detected scattered intensity. As explained in [53], we overcame this difficulty by normalizing the detected scattered light intensity with a polarization insensitive photodetector.
-
•
Systematic errors may occur if the incident polarization states differ from strict (p, 45+, RC) polarization states, or / and, through possible mismatch between the s-polarization axis of the emitted and detected scattered radiations, that may lead to undesirable polarization cross-talks. Also, wavelength cross-talks may occur between the VIS and IR-detectors.
To quantify these systematic errors, we follow the polarization state of the electromagnetic radiation from the laser source to the light detector. The incident Stokes vector can be described by a vector in the Poincare sphere describing all possible polarization states by its longitude 2χ and latitude 2ω [54]. These angles, which quantify the deviation from considered incident polarization states π = (p, 45+, RC), modify a π(λ) to d π(λ) coefficients (i.e. Eqs. (5) no longer apply). To minimize this remaining ellipticity, two successive PBC have been used to precisely set the polarization state of the incident radiation at wavelength λ to (p), then (45+, RC) using wave-plates. On the detector side, as the retro-reflecting PBC is imperfect (Rs > 99.5 %, Tp > 90 %), the fraction RsTp of the s-polarization component of the light intensity is measured, together with an undesired fraction RpTs originating from the p -component of the scattered radiation. To minimize this polarization cross-talk CT = RpTs/RsTp and allow the s-polarization component of the scattered radiation to be detected (with efficiency Tp), a second PBC has been inserted in the detector after the retro-reflecting PBC. Likewise, wavelength cross-talks between the VIS and IR-detectors have been minimized by using narrow interference filters at wavelengths λVIS and λIR, presenting an optical density of 5 at the complementary wavelength (i.e. at wavelength λVIS for the λIR-polarimeter). To be quantitative, we quantified the error in Δfij(λ) on fij(λ) at first order in χ(λ), ω(λ) and CT(λ):
| (6a) |
| (6b) |
| (6c) |
| (6d) |
| (6e) |
Where, to ease the reading, the wavelength dependence of χ(λ), ω(λ) and CT(λ) has been omitted. Following Eqs. (6), at negligible polarization cross-talk, the error on fij(λ) is majored by 2χ(λ) or 2ω(λ) since fij(λ) are below unity. The error on f 44(λ) is then at most equal to 2χ(λ). Fig. 2 displays in dashed lines the variation of the detected scattered intensity when considering a 2° deviation in both χ(λ) and ω(λ) assuming negligible polarization cross-talk. As to be seen in Fig. 2(a) minima, the error on f 22(λ) is independent from χ(λ) and ω(λ). Moreover, when f 34(λ) = 0.05 and f 33(λ) = −0.4, a 1%-relative accuracy is achieved on f 33(λ) (resp. f 44(λ)) if ω(λ) (resp. χ(λ)) remains below 2.3. The angles χ(λ) and ω(λ) can be precisely evaluated in our experiment by taking benefit from complementary polarization states (45−) and (LC) since 2χ(λ) = a 45+/(a 45+ + c 45+) − a 45−/(a 45− + c 45−) while 2ω(λ) = aRC/(aRC + cRC) − aLC/(aLC + cLC).
3. Ragweed pollen samples
3.1. Ambrosia artemisiifolia pollen
Our ragweed (Ambrosia artemisiifolia) samples are from Stallergenes Greer supplier. Dry ragweed powder has been embedded in laboratory ambient air using a solid pollen generator supplied with dried compressed air (RH < 10%), before injecting the ragweed pollens grains in the light scattering volume as schemed in Fig. 1. The size and the shape of our ragweed samples have been characterized as detailed below. Less than 5% fluctuations in the ragweed pollen number concentration were observed in the coarse mode of the size distribution. In complement, to validate the ability of the λIR-laboratory polarimeter to precisely evaluate scattering matrices, spherical water droplets, which follow Mie theory, have also been embedded in ambient air using a commercial atomizer.
3.2. Ragweed pollen particles scanning electron microscopic images
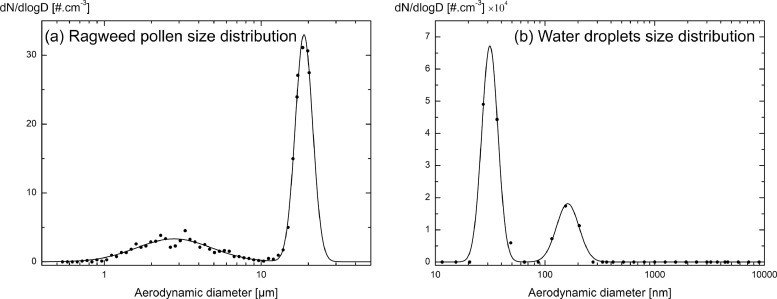
To characterize the size and the shape of pollens, scanning electron microscopy (SEM) was used, following the historical methodology [20]. Since pollen are dielectric material, to apply SEM, the ragweed pollen particles were deposited on an adhesive SEM tape, metallized with thin copper coating to increase the conductivity of the grains' surface. Fig. 3 presents our scanning electron microscope images, observed with a magnification factor of 3250 (panel (a), then 10 000 (panel b) to highlight the surface roughness of the pollen membrane. In agreement with the literature [19], our ragweed samples exhibit a volume equivalent diameter of 21 µm and an overall spherical shape, covered by regular spikes (echinus) of about 1 µm length. One of the three characteristic black apertures of ragweed, which are smaller than 2 µm, is visible at the pollen wall in the lower part of Fig. 3(a). In agreement with the literature, this pollen wall exhibits a perforate structure, i.e. covered with around 100 nm diameter holes to be seen in Fig. 3(b).
Fig. 3.
Scanning electron microscopy (SEM) images of our Ambrosia Artemisiifolia samples embedded in ambient air, once deposited on an adhesive substrate with a 3250 magnification (a), 10 000 magnification (b). One of the three characteristic black apertures is visible in panel (a), while the surface roughness to be seen in panel (b) corresponds to around 100 nm diameter holes.
3.3. Ragweed pollen particles size distribution
To evaluate the size of our ragweed samples, in complement to the above SEM images, an aerodynamic particle sizer (APS) was used. This commercial instrument evaluates the aerodynamic diameter through a time-of-flight measurement. Fig. 4 (a) presents the retrieved ragweed size distribution, which exhibits a coarse mode at seventeen micrometres, but also finer particles attributed to sub-pollen particles [55]. The aerodynamic diameter can be lower than the volume equivalent diameter since ragweed pollen grains are non-spherical and exhibit a dynamic shape factor above unity [56]. Likewise, the size distribution of our spherical water droplets embedded in ambient air was measured with a scanning mobility particle sizer coupled to an optical particle sizer, as displayed in Fig. 4(b).
Fig. 4.
(a) Particle size distribution of our generated ragweed pollen particles, as measured with an aerodynamic particle sizer (upper measured size equal to 20 µm). (b) Particle size distribution of water droplets to be used in Section 4.1 to validate the λIR-laboratory polarimeter.
4. Results and discussion
Following Sections 2 and 3, the scattering matrix of ragweed pollen is evaluated in laboratory at wavelengths (λVIS, λIR) with corresponding error bars. The (λVIS, λIR)-polarimeters are first validated on spherical water droplets that follow the analytical Lorenz-Mie theory.
4.1. (VIS, IR) experimental set-up validation on spherical water droplets
By applying Fig. 1 experimental set-up on spherical water droplets, we recorded the variations of the detected scattered intensity I π(λ,ψ) for successive incident polarization states π = (p, 45+, RC) at wavelength λVIS in Fig. 5 (a) and wavelength λIR in Fig. 5(b). To account for potential particles number fluctuations, the detected scattered intensity has been normalized by that of a polarization insensitive photodetector. At both wavelengths, the (p)-polarization curve exhibits null minima, consistent with spherical particles for which f 22(λ) = 1. Similarly, in the (45+)-polarization curve, the difference between two successive minima is not distinguishable, meaning that f 34(λ) is very close to zero for our spherical particles. For each incident polarization state π = (p, 45+, RC), coefficients from a π(λ) to d π(λ) are evaluated by adjusting the experimental data points with Eqs (5) to provide the scattering matrix presented in Table 1 at both wavelengths with corresponding error bars. Indeed, use of complementary incident polarization states π = (s, 45−, LC) allowed to evaluate 2ω = 2χ = 0.01 at both wavelengths. Within our experimental error bars, the retrieved normalized scattering matrix elements agree with numerically exact solutions the Maxwell's equations, obtained by applying the Lorenz-Mie theory [49], which provides f 22(λ) = − f 33(λ) = − f 44(λ) = 1 and f 12(λ) = f 34(λ) = 0 for the size distribution shown in Fig. 4(b) by taking into account the complex refractive index of water at both wavelengths. Hence, the newly-developed (λVIS, λIR)-polarimeters precisely reveal the scattering matrix of spherical water droplets embedded in ambient air at two both wavelengths.
Fig. 5.
Detected light intensity Iπ(λ,ψ) scattered by water droplets as a function of the modulation angle ψ of the QWP at wavelength λVIS (panel (a), data in green) and wavelength λIR (panel (b), data in red) for successive incident polarization states π = (p, 45+, RC) at 178° scattering angle. The detected scattered intensity, expressed in arbitrary units (a.u.) as P0(λ) is wavelength dependant, is adjusted with Eq. (4) to retrieve the scattering matrix elements fij(λ) = Fij(λ)/F11(λ) using Eqs. (5).
Table 1.
(λVIS, λIR)-evaluation of the scattering matrix elements fij(λ) = Fij(λ)/F11(λ) for spherical water droplets at 178° scattering angle, retrieved by adjusting the Fig. 5 experimental data points with Eqs. (5).
| VIS-wavelength (λVIS = 532 nm) | IR-wavelength (λIR = 1064 nm) |
|---|---|
4.2. Spectral dependence of the scattering matrix elements of ragweed
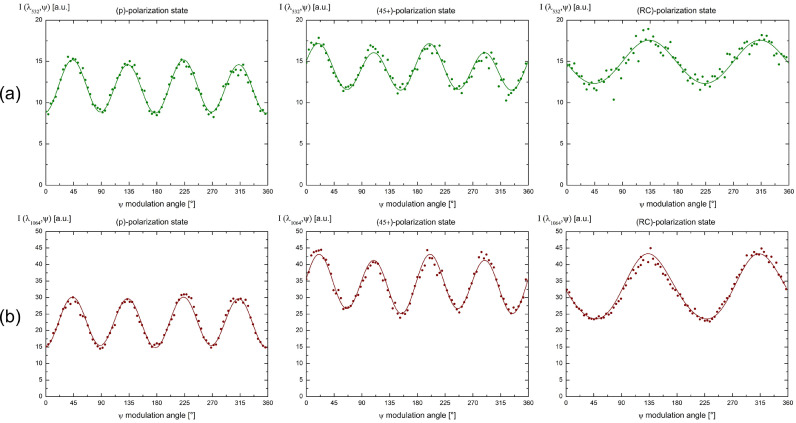
Fig. 6 is the analogue of Fig. 5 but dedicated to ragweed pollen particles. In contrary to Section 4.1, the minima in the (p)-polarization curve (left panel), which are related to the scattering matrix element 1 − f 22(λ), no longer vanish, in agreement with the ragweed overall nonspherical shape. Likewise, the minima in the (RC)-polarization curve (right panel) are constant and related to the scattering matrix element 1 − f 44(λ). In the (45+)-polarization curve (middle panel), at wavelength λIR, a difference exists between two successive local minima or maxima, meaning that f 34(λIR) is non-zero for ragweed pollen particles, as for several biological species [31]. As for water droplets in Fig. 5, the reproducibility of these extrema is clearly observed in Fig. 6, which means that the size and the shape distribution of our ragweed samples did not vary during the experimental acquisition. Coefficients a π(λ) to d π(λ) were then retrieved by adjusting our experimental data points at both wavelengths (λVIS,λIR) with Eq. (4) to retrieve the normalized scattering matrix elements fij(λ) presented in Table 2 by applying Eq. (5). The conditions of applicability of the single-scattering approximation (SSA) may there be questioned. Mishchenko et al. [57] underscored that for the SSA to be applicable, a large average inter-particle distance 〈d〉 (i.e. k1〈d〉 >> 30, where k1 is the wave vector in the surrounding medium) and low particle volume concentrations ρ (low packing densities ρ << 1%) should be considered. In our laboratory light scattering experiment, from the ragweed particles size distribution shown in Fig. 4, we calculate a particle volume concentration of ρ = 3.9 × 10−8 ≪ 1. Moreover, according to [58], at volume fraction ρ, the mean distance between neighbour particles for monodisperse particles with radius r is 〈d〉 = 0.554 × (4π/(3ρ))1/3r. Even if one considers ρ = 3.9 × 10−6 , monodisperse grains with effective radius r = 10.5 µm correspond to 〈d〉 = 0.6 mm, which leads to k1〈d〉 ≃ 7000 ≫ 30. As a result, the single-scattering approximation is fairly safe in our laboratory experiment where the particles are moving in a thin (2.5 mm) wide beam, so that the volume element is optically thin. The error bars in Table 2 result from the evaluation of 2ω(λVIS) = 0.03 and 2χ(λVIS) = 0.02, and 2ω(λIR) = 2χ(λIR) = 0.01. Interestingly, our error bars remain lower than the observed spectral variations of the scattering matrix elements. Hence, due to negligible wavelength cross-talks, the spectral dependence of the ragweed scattering matrix elements is revealed within our experimental error bars : the diagonal scattering matrix elements f 22(λ),f 33(λ) and f 44(λ) are larger at wavelength λIR than at wavelength λVIS. Equally, the off-diagonal element f 34(λ) increases from λVIS to λIR, except for f 12(λ), which exhibits no spectral variation between both wavelengths λVIS and λIR. As a conclusion, the retrieved scattering matrix elements presented in Table 2 provide precise spectral and polarimetric fingerprints of ragweed pollen.
Fig. 6.
Same as Fig. 5 for ragweed pollen particles.
Table 2.
Same as Table 1 for ragweed pollen particles.
| VIS-wavelength (λVIS = 532 nm) | IR-wavelength (λIR = 1064 nm) |
|---|---|
To interpret the observed spectral dependence of ragweed scattering matrix elements, two main arguments can be put forward. Firstly, the ragweed complex refractive index is a priori wavelength dependent, though the literature is, to our knowledge, not well documented, especially at wavelength λIR. At wavelength λVIS, values of the Pinus refractive index between 1.50 and 1.53 have been reported [59] using optical diffraction tomography and similar values were obtained for the refractive index of the cell of a yew pollen grain [60]. Secondly, ragweed pollen grains are large-sized particles and present periodic structures, the interference of waves scattered by the large particle surface and the spikes may appear, which may play a role in the observed spectral dependence of the scattering matrix elements. Also, the interference of waves scattered by different spikes may also reveal itself in the phase and spectral dependences of the scattering matrix elements. It is however far beyond the scope of this paper to investigate these possible explanations. Still as is, our retrieved scattering matrix elements may interest the light scattering numerical community for ragweed pollen grains exhibit fairly large size parameters (around 120 at wavelength λVIS) and are beyond the reach of numerically exact light-scattering methods. Light scattering by ragweed is a priori difficult to model numerically as ragweed pollen particles are complex-shaped particles with regular spikes, apertures, holes and surface roughness. As underscored by M. Kahnert et al. [61] in their review on model particles in atmospheric optics, several numerical approaches have been considered to evaluate light scattering by complex-shaped particles. Very recently, D. Petrov [50] applied the T-matrix numerical code on coronavirus-shaped particles which exhibit characteristic spikes, as for ragweed. Applying this new numerical method to ragweed pollen particles is interesting but a priori challenging due to their larger size [62], [63]. To account for surface roughness, the size parameter (micrometre range, wavelength λVIS) is too small for applying geometrical optics, but geometrical optics may eventually be used in conjunction with a random-tilting method (M. Kahnert, private communication), as successfully applied for large ice particles presenting surface roughness [64]. These considerations underscore the complexity of a precise numerical modelling of light scattering by ragweed pollen particles, which further reinforce the importance of controlled-laboratory experiments allowing to precisely retrieve the ragweed scattering matrix at wavelengths (λVIS, λIR). Hence, to tackle the important issue of light scattering by large and complex-shaped particles, more laboratory work has to be proposed, at other scattering angles and at other laser wavelengths. Still as is, our retrieved scattering matrices may help to constrain such light scattering numerical models.
5. Conclusion and outlooks
In this paper, a controlled-laboratory experiment is proposed to precisely evaluate the scattering matrix of ragweed pollen particles embedded in ambient air. Ragweed pollen, or Ambrosia artemisiifolia, is indeed one of the major pollens whose impact on public health and on the Earth's climate is appealed to increase in the forthcoming decades, due to global warming. In this context, the goal of this paper is to improve the knowledge on this important pollen, by quantifying its ability to scatter light at two wavelengths. This task is complex as ragweed is beyond the reach of numerically exact light scattering models, due its tens of micrometres size. Moreover, the shape of ragweed pollen particles is also complex, with a small-scale non-spherical feature exhibiting spikes, apertures and holes, as observed in Section 3 with scanning electron microscopy. To face such a complexity, we took benefit in Section 2 from the scattering matrix formalism to build a controlled-laboratory experiment, based on two polarimeters, allowing precise evaluation of the ragweed scattering matrix at two wavelengths, in the visible and infra-red spectral ranges. The infra-red spectral range was chosen to account for the large size of ragweed pollen particles and the newly-built polarimeter at wavelength λIR has been validated on spherical water droplets following Lorenz-Mie theory. Then, the polarimeters were operated on ragweed pollen particles embedded in ambient air. Special care has been taken to evaluate the systematic and statistical uncertainties on the retrieved scattering matrix elements by taking into account potential polarization and wavelength cross-talks. Interestingly, our experimental error bars are sufficiently low to reveal the spectral dependence of the ragweed scattering matrix: all ragweed scattering matrix elements except f 12 are higher at wavelength λIR than at wavelength λVIS. As a result, precise spectral and polarimetric ragweed fingerprints are here provided.
The outlooks of this work are numerous. First of all, the ragweed scattering matrix elements may also be evaluated in the UV-spectral range to improve our sensitivity to the small-scale irregularities exhibited at the ragweed grains' surface. Moreover, evaluating the ragweed scattering matrix elements at wavelengths larger than 1 µm would ensure the size parameters of the ragweed spikes to be within 1 or 2. As underscored in several papers [65], [66], [67], the features of exactly these sizes are responsible for characteristic details in the phase and spectral dependences of the intensity and polarization. We may also extend this evaluation to other scattering angles, including exact backscattering for remote sensing observations. Our laboratory experimental set-up allows scattering angles measurements from 176.0° to 180.0° [53] and the dependence of the ragweed scattering matrix elements with the scattering angle will be studied in a dedicated contribution, as this question may provide important information on the object under study itself [68]. Addressing the phase function would also be interesting but challenging within our experimental set-up [53]. As well, other pollens can be likewise studied by applying the same methodology to investigate how light scattering is modified by different grain morphologies. Finally, our laboratory findings can be applied by the light scattering numerical community to further improve their numerical models by investigating complex-shaped particles with spikes such as ragweed, or even coronavirus as recently tackled by [50]. Indeed, the near but non-spherical overall ragweed shape, with regular spikes, bears resemblances with that of other biological particles. Hence, our methodology may be potentially applied to study such biological objects. This however represents a laboratory intensive work. Still, precise modelling of light scattering by ragweed represents a challenging task due to its large size and complex shape. We hope our experimental contribution at two wavelengths will help to further tackle the important issue of the light scattering by complex-shaped and large particles.
CRediT authorship contribution statement
Danaël Cholleton: Formal analysis, Investigation, Software, Visualization, Writing - original draft, Writing - review & editing. Emilie Bialic: Writing - original draft, Project administration. Antoine Dumas: Writing - original draft, Project administration. Pascal Kaluzny: Project administration, Supervision. Patrick Rairoux: Conceptualization, Writing - original draft, Project administration, Supervision. Alain Miffre: Conceptualization, Formal analysis, Investigation, Methodology, Supervision, Writing - original draft, Writing - review & editing.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
CNRS is acknowledged for financial support and the Lyon Centre Technologique des Microstructures for their help in electronic microscopy.
References
- 1.Taketomi E.A., Sopelete M.C., de Sousa Moreira P.F., de Assis Machado Vieira F. Pollen allergic disease: pollens and its major allergens,". Braz J Otorhinolaryngol. 2006;72(4):562–567. doi: 10.1016/S1808-8694(15)31005-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Taramarcaz P., Lambelet C., Clot B., Keimer C., Hauser C. Ragweed (Ambrosia) progression and its health risks: will Switzerland resist this invasion? Swiss Med Wkly. 2005;12 doi: 10.4414/smw.2005.11201. [DOI] [PubMed] [Google Scholar]
- 3.C. Bohren, "Ambrosia artemisiifolia – a motivation for European-wide control," 6 (2008).
- 4.Smith M., Cecchi L., Skjøth C.A., Karrer G., Šikoparija B. Common ragweed: a threat to environmental health in Europe. Environ Int. 2013;61:115–126. doi: 10.1016/j.envint.2013.08.005. [DOI] [PubMed] [Google Scholar]
- 5.Thibaudon M., Šikoparija B., Oliver G., Smith M., Skjøth C.A. Ragweed pollen source inventory for France – The second largest centre of Ambrosia in Europe. Atmos Environ. 2014;83:62–71. [Google Scholar]
- 6.Schaffner U., Steinbach S., Sun Y., Skjøth C.A., de Weger L.A., Lommen S.T. Biological weed control to relieve millions from Ambrosia allergies in Europe. Nat Commun. 2020;11(1):1–7. doi: 10.1038/s41467-020-15586-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.H. Behrendt and W.-.M. Becker, "Localization, release and bioavailability of pollen allergens: the influence of environmental factors," 7(n.d.). [DOI] [PubMed]
- 8.Myszkowska D. Aerobiological studies – current state and future challenges. Alergoprofil. 2020;16(1):8–14. [Google Scholar]
- 9.Pope F.D. Pollen grains are efficient cloud condensation nuclei. Environ Res Lett. 2010;5(4) [Google Scholar]
- 10.Wozniak M.C., Solmon F., Steiner A.L. Pollen Rupture and Its Impact on Precipitation in Clean Continental Conditions. Geophys Res Lett. 2018;45(14):7156–7164. [Google Scholar]
- 11.Gute E., Abbatt J.P.D. Ice nucleating behavior of different tree pollen in the immersion mode. Atmos Environ. 2020;231 [Google Scholar]
- 12.Spänkuch D., Döhler W., Güldner J. Effect of coarse biogenic aerosol on downwelling infrared flux at the surface. J Geophys Res Atmos. 2000;105(D13):17341–17350. [Google Scholar]
- 13.Mang T., Essl F., Mosef D., Dullinger S. Climate warming drives invasion history of Ambrosia artemisiifolia in central Europe. Preslia. 2018;90(1):59–81. [Google Scholar]
- 14.Wayne P., Foster S., Connolly J., Bazzaz F., Epstein P. Production of allergenic pollen by ragweed (Ambrosia artemisiifolia L.) is increased in CO2-enriched atmospheres. Ann Allergy Asthma Immunol. 2002;88(3):279–282. doi: 10.1016/S1081-1206(10)62009-1. [DOI] [PubMed] [Google Scholar]
- 15.Ziska L., Knowlton K., Rogers C., Dalan D., Tierney N., Elder M.A. Recent warming by latitude associated with increased length of ragweed pollen season in central North America. Proc Natl Acad Sci. 2011;108(10):4248–4251. doi: 10.1073/pnas.1014107108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Sofiev M., Belmonte J., Gehrig R., Izquierdo R., Smith M., Dahl Å., Siljamo P. Airborne Pollen Transport. In: Sofiev M., Bergmann K.-C., editors. Allergenic pollen. Springer; Netherlands: 2013. pp. 127–159. [Google Scholar]
- 17.Makra L., Matyasovszky I., Thibaudon M., Bonini M. Forecasting ragweed pollen characteristics with nonparametric regression methods over the most polluted areas in Europe. Int J Biometeorol. 2011;55(3):361–371. doi: 10.1007/s00484-010-0346-9. [DOI] [PubMed] [Google Scholar]
- 18.Zink K., Kaufmann P., Petitpierre B., Broennimann O., Guisan A., Gentilini E. Numerical ragweed pollen forecasts using different source maps: a comparison for France. Int J.Biometeorol. 2017;61(1):23–33. doi: 10.1007/s00484-016-1188-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Robbins R.R., Dickinson D.B., Rhodes A.M. Morphometric Analysis of Pollen from Four Species of Ambrosia (compositae) Am J Bot. 1979;66(5):538–545. [Google Scholar]
- 20.Hesse M., editor. Pollen terminology: an illustrated handbook. Springer; 2009. [Google Scholar]
- 21.Liu C., Yin Y. Inherent optical properties of pollen particles: a case study for the morning glory pollen. Opt Express. 2016;24(2):A104. doi: 10.1364/OE.24.00A104. [DOI] [PubMed] [Google Scholar]
- 22.Hirst J.M. An automatic volumetric spore trap. Ann Appl Biol. 1952;39(2):257–265. [Google Scholar]
- 23.Daood A., Ribeiro E., Bush M. Pollen Grain Recognition Using Deep Learning, In: Bebis G., Boyle R., Parvin B., Koracin D., Porikli F., Skaff S., Entezari A., Min J., Iwai D., Sadagic A., Scheidegger C., Isenberg T., editors. Advances in visual computing. Springer International Publishing; 2016. pp. 321–330. Lecture Notes in Computer Science. [Google Scholar]
- 24.Pan Y.-.L., Hill S.C., Pinnick R.G., House J.M., Flagan R.C., Chang R.K. Dual-excitation-wavelength fluorescence spectra and elastic scattering for differentiation of single airborne pollen and fungal particles. Atmos Environ. 2011;45(8):1555–1563. [Google Scholar]
- 25.Kiselev D., Bonacina L., Wolf J.-.P. A flash-lamp based device for fluorescence detection and identification of individual pollen grains. Rev Sci Instrum. 2013;84(3) doi: 10.1063/1.4793792. [DOI] [PubMed] [Google Scholar]
- 26.Könemann T., Savage N., Klimach T., Walter D., Fröhlich-Nowoisky J., Su H. Spectral Intensity Bioaerosol Sensor (SIBS): an instrument for spectrally resolved fluorescence detection of single particles in real time. Atmos Meas Tech. 2019;12(2):1337–1363. [Google Scholar]
- 27.Giri R., Morello C., Heinson Y.W., Kemppinen O., Videen G., Videen G., Videen G. Generation of aerosol-particle light-scattering patterns from digital holograms. Opt Lett. 2019;44(4):819–822. doi: 10.1364/OL.44.000819. [DOI] [PubMed] [Google Scholar]
- 28.Sauvageat E., Zeder Y., Auderset K., Calpini B., Clot B., Crouzy B. Real-time pollen monitoring using digital holography. Atmos Meas Tech. 2020;13(3):1539–1550. [Google Scholar]
- 29.Berg M.J., Videen G. Digital holographic imaging of aerosol particles in flight. J Quant Spectrosc Radiat Transf. 2011;112(11):1776–1783. [Google Scholar]
- 30.Bickel W.S., Davidson J.F., Huffman D.R., Kilkson R. Application of polarization effects in light scattering: a new biophysical tool. Proc Natl Acad Sci. 1976;73(2):486–490. doi: 10.1073/pnas.73.2.486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Bickel W.S., Stafford M.E. Light scattering by irregularly shaped particles. Springer; Boston, MA: 1980. Biological Particles as Irregularly Shaped Scatterers; pp. 299–305. [Google Scholar]
- 32.Sloot P.M.A., Hoekstra A.G., van der Liet H., Figdor C.G. Scattering matrix elements of biological particles measured in a flow through system: theory and practice. Appl Opt. 1989;28(10):1752. doi: 10.1364/AO.28.001752. [DOI] [PubMed] [Google Scholar]
- 33.Surbek M., Esen C., Schweiger G., Ostendorf A. Pollen characterization and identification by elastically scattered light. J Biophotonics. 2011;4(1–2):49–56. doi: 10.1002/jbio.200900088. [DOI] [PubMed] [Google Scholar]
- 34.Iwai T. Polarization Analysis of Light Scattered by Pollen Grains of Cryptomeria japonica. Jpn J Appl Phys. 2013;52(6R) [Google Scholar]
- 35.Raman P., Fuller K.A., Gregory D.A. Polarization signatures of airborne particulates. Opt Eng. 2013;52(7) [Google Scholar]
- 36.Nouri S.A., Gregory D.A., Fuller K. Development of an angle-scanning spectropolarimeter: preliminary results. J Quant Spectrosc Radiat Transf. 2018;206:342–354. [Google Scholar]
- 37.Matsuda S., Kawashima S. Relationship between laser light scattering and physical properties of airborne pollen. J Aerosol Sci. 2018;124:122–132. [Google Scholar]
- 38.Holler S., Fuerstenau S.D., Skelsey C.R. Simultaneous two-color, two-dimensional angular optical scattering patterns from airborne particulates: scattering results and exploratory analysis. J Quant Spectrosc Radiat Transf. 2016;178:167–175. [Google Scholar]
- 39.Mishchenko M.I., Travis L.D., Lacis A.A. Cambridge University Press; 2002. Scattering, absorption, and emission of light by small particles. [Google Scholar]
- 40.Roy G. Lidar polarization discrimination of bioaerosols. Opt Eng. 2010;49(11) [Google Scholar]
- 41.Sicard M., Izquierdo R., Alarcón M., Belmonte J., Comerón A., Baldasano J.M. Near-surface and columnar measurements with a micro pulse lidar of atmospheric pollen in Barcelona. Atmos Chem Phys. 2016;16(11):6805–6821. [Google Scholar]
- 42.Sassen K. Boreal tree pollen sensed by polarization lidar: depolarizing biogenic chaff. Geophys Res Lett. 2008;35(18) [Google Scholar]
- 43.Noh Y.M., Müller D., Lee H., Choi T.J. Influence of biogenic pollen on optical properties of atmospheric aerosols observed by lidar over Gwangju, South Korea. Atmos Environ. 2013;69:139–147. [Google Scholar]
- 44.Miffre A., David G., Thomas B., Rairoux P. Atmospheric non-spherical particles optical properties from UV-polarization lidar and scattering matrix. Geophys Res Lett. 2011;38(16):L16804. [Google Scholar]
- 45.Mehri T., Kemppinen O., David G., Lindqvist H., Tyynelä J., Nousiainen T. Investigating the size, shape and surface roughness dependence of polarization lidars with light-scattering computations on real mineral dust particles: application to dust particles’ external mixtures and dust mass concentration retrievals. Atmos Res. 2018;203:44–61. [Google Scholar]
- 46.Hoekstra A.(ed.) Novosibirsk; Russia: 2007. pp. 3–6. (Optics of Biological Particles: Proceedings of the NATO Advanced Research Workshop on Fluorescence and Other Optical Properties of Biological Particles for Biological Warfare Agent Sensors). October 2005, NATO Science Series Series II, Mathematics, Physics and Chemistry No. 238 (Springer, 2007). [Google Scholar]
- 47.Mackowski D., Kolokolova L., Sparks W. T-matrix approach to calculating circular polarization of aggregates made of optically active materials. J Quant Spectrosc Radiat Transf. 2011;112(11):1726–1732. [Google Scholar]
- 48.Meyer R.A. Light scattering from biological cells: dependence of backscatter radiation on membrane thickness and refractive index. Appl Opt. 1979;18(5):585. doi: 10.1364/AO.18.000585. [DOI] [PubMed] [Google Scholar]
- 49.Bohren C.F., Huffman D.R. Wiley-VCH; 1983. Absorption and scattering of light by small particles. [Google Scholar]
- 50.Petrov D. Photopolarimetrical properties of coronavirus model particles: spike proteins number influence. J Quant Spectrosc Radiat Transf. 2020;248 doi: 10.1016/j.jqsrt.2020.107005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Mishchenko M.I. Electromagnetic scattering by nonspherical particles: a tutorial review. J Quant Spectrosc Radiat Transf. 2009;110(11):808–832. [Google Scholar]
- 52.Hovenier J.W., Van Der Mee C., Domke H. Springer; Netherlands: 2004. Transfer of polarized light in planetary atmospheres; p. 318. Astrophysics and Space Science Library. [Google Scholar]
- 53.Miffre A., Cholleton D., Rairoux P. Laboratory evaluation of the scattering matrix elements of mineral dust particles from 176.0° up to 180.0°-exact backscattering angle. J Quant Spectrosc Radiat Transf. 2019;222–223:45–59. [Google Scholar]
- 54.Shurcliff W.A. Polarized Light: Production and Use. 1962 [Google Scholar]
- 55.Bacsi A., Choudhury B., Dharajiya N., Sur S., Boldogh I. Subpollen particles: carriers of allergenic proteins and oxidases. J Allergy Clin Immunol. 2006;118(4):844–850. doi: 10.1016/j.jaci.2006.07.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.DeCarlo P.F., Slowik J.G., Worsnop D.R., Davidovits P., Jimenez J.L. Particle Morphology and Density Characterization by Combined Mobility and Aerodynamic Diameter Measurements. Part 1: theory, Aerosol Sci Technol. 2004;38(12):1185–1205. [Google Scholar]
- 57.Mishchenko M.I., Liu L., Videen G. Conditions of applicability of the single-scattering approximation. Opt Express. 2007;15(12):7522. doi: 10.1364/oe.15.007522. [DOI] [PubMed] [Google Scholar]
- 58.Bansal P.P., Ardell A.J. Average nearest-neighbor distances between uniformly distributed finite particles. Metallography. 1972;5(2):97–111. [Google Scholar]
- 59.Kim G., Lee S., Shin S., Park Y. Three-dimensional label-free imaging and analysis of Pinus pollen grains using optical diffraction tomography. Sci Rep. 2018;8(1) doi: 10.1038/s41598-018-20113-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Charrière F., Marian A., Montfort F., Kuehn J., Colomb T., Cuche E. Cell refractive index tomography by digital holographic microscopy. Opt Lett. 2006;31(2):178. doi: 10.1364/ol.31.000178. [DOI] [PubMed] [Google Scholar]
- 61.Kahnert M., Nousiainen T., Lindqvist H. Review: model particles in atmospheric optics. J Quant Spectrosc Radiat Transf. 2014;146:41–58. [Google Scholar]
- 62.Petrov D., Shkuratov Y., Videen G. Electromagnetic wave scattering from particles of arbitrary shapes. J Quant Spectrosc Radiat Transf. 2011;112(11):1636–1645. [Google Scholar]
- 63.Petrov D., Shkuratov Y., Videen G. Light scattering by arbitrary shaped particles with rough surfaces: sh-matrices approach. J Quant Spectrosc Radiat Transf. 2012;113(18):2406–2418. [Google Scholar]
- 64.Macke A., Mueller J., Raschke E. Single Scattering Properties of Atmospheric Ice Crystals. J Atmos Sci. 1996;53(19):2813–2825. [Google Scholar]
- 65.Tishkovets V.P., Petrova E.V., Jockers K. Optical properties of aggregate particles comparable in size to the wavelength. J Quant Spectrosc Radiat Transf. 2004;86(3):241–265. [Google Scholar]
- 66.Mishchenko M.I., Dlugach J.M. Adhesion of mineral and soot aerosols can strongly affect their scattering and absorption properties. Opt Lett. 2012;37(4):704–706. doi: 10.1364/OL.37.000704. [DOI] [PubMed] [Google Scholar]
- 67.Tishkovets V.P., Petrova E.V. Spectra of light reflected by aggregate structures of submicron particles. J Quant Spectrosc Radiat Transf. 2020;252 [Google Scholar]
- 68.Nagdimunov L., Kolokolova L., Mackowski D. Characterization and remote sensing of biological particles using circular polarization. J Quant Spectrosc Radiat Transf. 2013;131:59–65. [Google Scholar]