Synchronization and control of capillary flows in rectangular microchannel with spacers

Abstract

Liquid control in microchannels is quite important in microfluidic devices used in, for example, lab-on-a-chip and point-of-care applications. Capillary microfluidics, being self-powered, is especially advantageous for use in passive devices, and has attracted significant attention. In this paper, capillary flows in rectangular microchannels with spacers are studied experimentally and theoretically; in particular, capillary flow synchronization (or waiting) behavior is identified and investigated. Based on changes of channel walls, two basic synchronization modes are proposed for flows isolated by spacers in a channel. Experimental results show that the velocities of faster capillary flows are reduced by the liquid pinning effect and that the time delay between two capillary flows is automatically balanced. The synchronization behavior of capillary flows is explained by analyzing the time delay, contact angle variation, and capillary forces. In addition, the quantity of liquid flowing out of the waiting channels is estimated and verified. Then a model for the change in contact angle during synchronization is derived and verified. Finally, we conceive a series of studies of the control of capillary flows for different spacer designs and conduct an experiment to study the dynamic behaviors of a number of capillary flows by adding many spacers in a microchannel. This study expands the applications of capillary microfluidics.

I. INTRODUCTION

Automatic and accurate control of liquid in microfluidic devices is significant on chemical, biological and medical applications, and this promotes the development of lab on a chip, point-of-care, etc. Operations such as liquid transport, positioning, and mixing typically rely on active control systems that need external energy sources.^1–4 This increases the cost and complexity of fabrication. Capillarity is commonly used in microfluidic systems and does not require an external energy source. With passive devices, fluid flow is self-driven and accomplished using capillary forces and surface wettability.⁵ Capillary microfluidics has promoted the development and application of pumps, valves, microreactors, sensors, electronics cooling, bio-chemical analysis, etc.^6–12

Elastocapillary^13–16 and magnetocapillary¹⁷ phenomena can be utilized to develop effective methods for liquid control in capillary microfluidics. Anoop and Sen¹³ studied capillary flow enhancement in a system of rectangular polymer microchannels, in which one of the channel walls was a deformable polymer membrane. They studied the physics of elastocapillary interaction between a capillary flow and an elastic membrane, and found that incorporation of the membrane can lead to significant improvements in capillary flow performance. George et al.¹⁴ considered the manipulation of a liquid plug inside a rectangular microchannel with a deformable membrane wall. They found that when the plug approaches the membrane, the elastocapillary flow causes the membrane to be pulled near the plug. The plug is transported by a differential pressure that develops across the plug as a result of the increase in the radius of curvature of the trailing meniscus of the plug. Reddy et al.¹⁵ reported on the interaction of opposing elastocapillary flows in parallel microchannels across a thin membrane. At the crossing point, the interaction between the capillary flows through the thin membrane leads to a significant retardation of the capillary flow. Reddy et al. found that the ratio of the capillary force to the mechanical restoring force governs the meniscus velocity at the crossing point. Samy et al.¹⁶ studied bio-inspired liquid transport produced by the elastocapillary interaction of a thin membrane with a liquid meniscus. They proposed a simple theoretical model based on the Euler–Bernoulli law to predict membrane deformation profiles. Banerjee et al.¹⁷ reported the influence of stationary and moving permanent magnets on the magnetocapillary flow of the ferrofluid in a microchannel. With a stationary magnet placed at the microchannel exit, a sudden increase in the meniscus velocity was observed as the ferrofluid meniscus came under the influence of the magnet.

Microchannel surface wettability has significant effects on capillary flows.^18–21 Hydrophobic patterns, open-channel microfluidics, stop valves, etc., have been developed to control liquid flows for various applications.^4,6,22–24 Suk and Cho⁴ controlled capillary flow velocities at specific positions within a microchannel using an array of hydrophobic patterns. Kim and Whitesides²¹ studied the imbibition of wetting fluids in rectangular polydimethylsiloxane (PDMS) channels to control channel surfacee hydrophilicity. Lade Jr. et al.²² presented a study of the capillary coating process that considered the influence of drying in open microchannels. The study had potential applications to electronic and catalytic devices. Majhy et al.⁶ reported the capillary flow of oil in an open superoleophilic channel and demonstrated the application of a channel with integrated electrodes to impedance-based sensing of oil from an oil–water emulsion. Sneha Maria et al.²⁵ fabricated a microchannel with different wetting by oxygen plasma exposure, and studied capillary flow of blood in the channel in order to achieve plasma separation and on-chip detection of glucose in plasma.

The surface geometry (posts, ridges, etc.) can also affect capillary flows, as it can induce dynamic contact angle and contact line changes.^26,27 In microchannels with posts and ridges, pinning on posts edges can suppress capillary filling,^28,29 and the ridges perpendicular to the flow direction introduce contact line pinning which can slow capillary filling, whereas the ridges parallel to the flow direction provide extra surface which can enhance filling.²⁹ Various devices have been designed to achieve functional operations. Safavieh and Juncker³⁰ designed pre-programmed, self-powered microfluidic circuits based on capillary elements (capillary valves, pumps, etc.) to control liquid flows. Melin et al.²⁷ studied a surface tension- and geometry-based liquid-triggered microvalve for on-chip liquid flow control. Useful functions including fluidic AND gates, contactless on-chip liquid sample control, etc. were demonstrated using microfluidics. Hyun et al.³¹ achieved diode-like unidirectional liquid flow in open capillary channels like a diode. The researchers fabricated a microfluidic junction between two open channels with different sizes, such that liquids could flow only from the large channel to the small channel. Arango et al.³² presented “electrogates” for stop–and–go control of liquid flow in capillary microfluidics by combining liquid pinning with electrowetting.

Most studies of liquid control in capillary microfluidics have considered only flow in a single channel, however, liquid control studies about capillary flows in two or more channels of a microfluidic device are lacking. In this paper, we study the dynamic behaviors and relation of capillary flows in a microchannel based on the liquid pinning effect. Spacers are supposed to fabricated in a microchannel, then small channels can be isolated by the spacers and the corresponding capillary flows can be obtained in the microchannel. The basic problem is about the dynamic behaviors and relation of two capillary flows. For a common microchannel with a rectangular cross section and no changes in its upper and lower walls, capillary flow is affected by changes in the remaining one or two walls, which correspond to two modes. Thus, we designed two microfluidic devices to study capillary flow behavior via experiment and analysis.

II. MATERIALS AND METHODS

A. Experimental section

The microfluidic devices were fabricated from PDMS via soft lithography. As shown in Fig. 1(a), three small channels were isolated by placing two spacers in each microchannel. One microchannel (hereafter referred as microfluidic device 1) had one narrow and two wide small channels, with widths of 0.35 mm and 0.75 mm, respectively. The other microchannel (referred as microfluidic device 2) had one wide and two narrow small channels, with widths of 1.25 mm and 0.325 mm, respectively. Ethanol was used as the test liquid because it interacts with the PDMS surface in a hydrophilic manner.³³ In experiments, the microfluidic device was placed horizontally and ethanol was dripped into the channel inlet using a dropper. A microscope (Olympus CKX41) with a CCD camera (400 fps) was used to observe liquid-gas interfacial movement during capillary flow. The observation areas are enclosed by blue, dotted lines in Fig. 1(a). The positions and shapes of the interfaces were analyzed to determine the experimental results.

FIG. 1.

(a) Schematic showing the experimental setup and two types of microfluidic devices. The positions and shapes of the liquid-gas interfaces in (b) device 1 and (c) device 2 at various times. The scale bar is 500 μm.

Figures 1(b) and 1(c) show the positions and shapes of the liquid-gas interfaces in devices 1 and 2, respectively. In device 1, the capillary flow moves faster in the narrow, small channel than that in the wide, small channels. When it arrives at the end of the two spacers, the difference in the wall configuration leads to contact–line pinning that slows the flow.²⁸ The interfacial shape changes from concave to convex. Small quantity of liquid flows out of the channel during deceleration. Later, the capillary flows in the two small, wide channels catch up with the leading flow, the interfaces link, and the liquids finally move together. In device 2, the capillary flows in the two narrow, small channels move faster than that in the wide, small channel, much like in device 1. However, only one wall changes. The narrow, small channels can be seen as waiting channels. Thus, their behavior can be referred to as a waiting or synchronization phenomenon of different capillary flows that operates via liquid pinning. The velocity of the faster capillary flow is reduced, and the time delays of the two flows are automatically balanced.

B. Theory of capillary flows

The fluid flow in microchannels is described by the Navier–Stokes equations. For Newtonian, incompressible, steady, laminar fluid flows with low Reynolds number, the Navier–Stokes equations can be simplified. The simplified solution shows that the relationship between the pressure drop Δp and the flow rate Q satisfies the Hagen–Poiseuille law,³⁴ Δp = R_hydQ, where R_hyd is the hydraulic resistance. For the rectangular cross-section microchannel with length L, width w and depth h (w > h), the hydraulic resistance is³⁴

$$R_{\mathrm{hyd}}={\displaystyle \frac{12\mu L}{(1-0.63h/w)}{\displaystyle \frac{1}{h^{3}w},}}$$ (1)

where μ is the dynamic viscosity. Here we conducted analysis based on the momentum equation of capillary flow. For a horizontally placed microchannel, the gravity can be neglected, and the momentum equation is³⁵

$${\displaystyle \frac{\mathrm{d}I}{\mathrm{d}t}=F_{\sigma }-F_{\mu },}$$ (2)

where I is the liquid momentum, t is time, F_σ is the capillary force, and F_μ is the viscous force. In fact, this momentum equation of capillary flow can be derived from the Navier–Stokes equations by integrating the momentum equation over the liquid volume.^36–38 Liou et al.³⁶ derived the momentum equation of capillary flow in nonuniform cross-sectional capillaries based on the Navier–Stokes equations. Their derived model is validated by comparing the solutions for a circular cylindrical tube and rectangular cross-section microchannels.

According to the situation which forces are dominant, capillary flow can be divided into four stages:³⁵ (1) the purely inertial time stage, (2) the visco-inertial time stage, (3) the purely viscous time stage, and (4) the viscous and gravitational time stage. For a horizontally placed rectangular cross–section microchannel, gravity is neglected as the stage (2). With width w and depth h (w > h), the liquid momentum is I = ρwhxv; the viscous force is $F_{\mu }=\frac{12\mu wxv}{(1-0.63h/w)h}$; the capillary force is F_σ = 2(w + h)σcos(θ),³³ where x is the flow distance; the velocity $v=\frac{\mathrm{d}x}{\mathrm{d}t}$; ρ is the liquid density, σ is the surface tension and θ is the contact angle. The momentum equation is

$${\displaystyle \frac{\mathrm{d}(\rho whxv)}{\mathrm{d}t}+{\displaystyle \frac{12\mu w}{(1-0.63h/w)h}xv=2\sigma (w+h)\cos (\theta ).}}$$ (3)

If we assume that C₁= 12μ/[ρ(1−0.63h/w)h²] and C₂= 2σ(1/w + 1/h)cos(θ)/ρ, the solution of Eq. (3) is

$$x=\sqrt{{\displaystyle \frac{2C_2}{C_1}\left(t+{\displaystyle \frac{1}{C_1}{\mathrm{e}}^{-C_{1}t}-{\displaystyle \frac{1}{C_1}}}\right)}}.$$ (4)

Based on Eq. (4), xv = C₂(1−e^−C1t)/C₁, so F_μ = 2(w + h)σcos(θ)× (1−e^−C1t), F_μ/F_σ = (1−e^−C1t), and F_σ is constant, while F_μ increases with t. When F_μ is approximately equal to F_σ, the inertial force, F_σ−F_μ, can be ignored, and the relationship between x and t fits the Lucas–Washburn model (i.e., x ∝ t^1/2).^39,40 For ethanol, ρ = 789 kg/m³, μ = 0.001 Pas, σ = 0.022 N/m, and θ ≈ 25.5° (here, θ is the dynamic contact angle⁴¹ measured during our experiment). We then assume that the depth h = 100 μm. As shown in Fig. 2(a), at various aspect ratios w/h, F_μ/F_σ increases with t until it approaches 1 and then remains unchanged. Thus, the ratio of inertial and capillary forces, (F_σ−F_μ)/F_σ, approaches 0. Finally, the flow distance x is proportional to t^1/2.

FIG. 2.

(a) F_μ/F_σ dependence on t for various w/h. The time difference Δt changes (b) as a function of the flow distance x for various k (=w_II/w_I) and (c) as a function of k for various x.

For two microchannels (I and II) that contain ethanol and have depths h = 100 μm and widths w_I= 1 mm and w_II= kw_I, the time difference Δt between the two capillary flows at the same x can be calculated using Eq. (4). For this calculation, Δt = t_II−t_I, where t_I and t_II are the capillary flow durations of microchannels I and II. The Δt results [Figs. 2(b) and 2(c)] show that capillary flows may not be always faster in narrower channels than in wider channels, as this depends on the flow distance x and the ratio k (=w_II/w_I). When 0.1 < k < 0.2052, Δt starts off negative before becoming positive. The capillary flow in the wider microchannel (w_I) is slower at the start but accelerates to exceed that in the narrower channel (w_II). When k ≈ 0.2052, the capillary flow in the wider microchannel (w_I) is slower than that in the narrower channel (w_II) at first, and Δt tends to be constant at last. When 0.2052 < k < 1, the capillary flow in the wider microchannel (w_I) is always slower than that in the narrower channel (w_II). We note that Δt is maximized when k ≈ 0.3405 and then gradually decreases. When k = 1, w_I= w_II and Δt = 0. When k < 1, the capillary flow in the wider microchannel (w_II) is slower than that in the narrower channel (w_I). In experiments, the ratios of the narrow and wide small channels are 0.467 (device 1) and 0.26 (device 2). These ratios are both in the range 0.2053–1 and the experimental results (Fig. 1) are consistent with the theoretical determination that the capillary flows in wider channels are always slower.

The time difference Δt between two capillary flows at the same flow distance can be calculated. Assume that the capillary numbers of the flows in two channels are Ca_I and Ca_II. For the same liquid, the relationship between Δt (=t_II–t_I) and capillary numbers can be got by the following equations:

$$\{\begin{array}{c}{x}_I=\sqrt{{\displaystyle \frac{2C_{21}}{C_{11}}\left(t_I+{\displaystyle \frac{1}{C_{11}}{\mathrm{e}}^{-C_{11}{t}_I}-{\displaystyle \frac{1}{C_{11}}}}\right)}};\\ x_I{v}_I={\displaystyle \frac{C_{21}(1-{\mathrm{e}}^{-C_{11}{t}_I})}{C_{11}};}\\ v_{\mathrm{I}}={\displaystyle \frac{\mathrm{d}{x}_{\mathrm{I}}}{\mathrm{d}{t}_{\mathrm{I}}},C{a}_{\mathrm{I}}={\displaystyle \frac{\mu v_{\mathrm{I}}}{\sigma }.}}\end{array}$$ (5)

$$\{\begin{array}{c}{x}_{II}=\sqrt{{\displaystyle \frac{2C_{22}}{C_{12}}\left(t_{II}+{\displaystyle \frac{1}{C_{12}}{\mathrm{e}}^{-C_{12}{t}_{II}}-{\displaystyle \frac{1}{C_{12}}}}\right)}};\\ x_{II}{v}_{II}={\displaystyle \frac{C_{22}(1-{\mathrm{e}}^{-C_{12}{t}_{II}})}{C_{12}};}\\ v_{\mathrm{II}}={\displaystyle \frac{\mathrm{d}{x}_{\mathrm{II}}}{\mathrm{d}{t}_{\mathrm{II}}},C{a}_{\mathrm{II}}={\displaystyle \frac{\mu v_{\mathrm{II}}}{\sigma },}}\end{array}$$ (6)

where

$$\{\begin{array}{c}{C}_{11}={\displaystyle \frac{12\mu }{\rho \left(1-{\displaystyle \frac{0.63h}{w_{\mathrm{I}}}}\right)h^2};}\\ C_{12}={\displaystyle \frac{12\mu }{\rho \left(1-{\displaystyle \frac{0.63h}{w_{\mathrm{II}}}}\right)h^2};}\\ C_{21}={\displaystyle \frac{2\sigma \cos (\theta )}{\rho }\left({\displaystyle \frac{1}{w_{\mathrm{I}}}+{\displaystyle \frac{1}{h}}}\right);}\\ C_{22}={\displaystyle \frac{2\sigma \cos (\theta )}{\rho }\left({\displaystyle \frac{1}{w_{\mathrm{II}}}+{\displaystyle \frac{1}{h}}}\right).}\end{array}$$ (7)

The time difference Δt can be got as a function of Ca_I and Ca_II using the above equations. For the same liquid, Fig. 3 shows the phase diagram of Δt, where the parameters are ρ = 789 kg/m³, μ = 0.001 Pas, σ = 0.022 N/m, h = 100 μm, and the dynamic contact angle θ ≈ 25.5°. The widths of the two channels are w_I= 0.35 mm and w_II= 0.75 mm. The results show that the capillary flow in the wider microchannel (w_II) is always slower than that in the narrower channel (w_I), and this is consistent with the experimental results. In addition, the absolute value of Δt decreases gradually with the increasing of Ca_I and Ca_II, i.e., the time difference of the two capillary flows decreases gradually.

FIG. 3.

The phase diagram of the time difference Δt as a function of Ca_I and Ca_II.

III. RESULTS AND DISCUSSION

A. Contact angle and capillary force analysis

The dynamic contact angle, measured experimentally, was investigated in this paper. The contact angle (θ) is formed at the advancing edge of the liquid, as shown in Fig. 4, so it is the advancing contact angle.^32,42 When liquid arrives at the end of the spacers, it will flow out of the waiting channel during deceleration because of inertia. Meanwhile, the actual advancing contact angles will change to θ₁ or θ₂ on relevant walls (in the x–z plane) during synchronization, as shown in Fig. 4, where θ₁ and θ₂ correspond to the two types of microfluidic devices described in this manuscript. The corresponding capillary forces are also marked in the figure.

FIG. 4.

The advancing contact angle (θ) and the contact angles (θ₁ and θ₂) at the ends of spacers. The corresponding capillary forces are marked.

In fact, when the three-phase contact line meets a mathematically sharp solid edge as shown in Fig. 5(a), the advancing contact angle should be studied based on the condition of equilibrium (i.e., the Young–Dupré equation),^43,44

$$\theta \le {\theta }_i\le ({180}^{°}-\mathrm{\Phi })+\theta ,i=1,2,$$ (8)

where Φ is the edge angle, the i (=1, 2) corresponds to the two types of microfluidic devices in the manuscript. According to the Gibbs criterion,^43,44 the liquid front can pass over the sharp edges when its advancing contact angle (θ_i) exceeds a critical value (θ_cr),

$${\theta }_{cr}=({180}^{°}-\mathrm{\Phi })+\theta .$$ (9)

FIG. 5.

(a) Schematic of the liquid–gas interface when it moves on the spacer end surface and the corresponding capillary force. Critical positions are at the sharp edges. (b) Schematic of the advancing contact angle change.

The liquid front will become pinned if the advancing contact angle θ_i < θ_cr. Here, the edge angle Φ is 90° in this study, so the advancing contact angle θ_i must reach 90° + θ  if the liquid is to pass over the first right angle, and 180° + θ if it is to pass over the second right angle, as shown in Fig. 5(b).

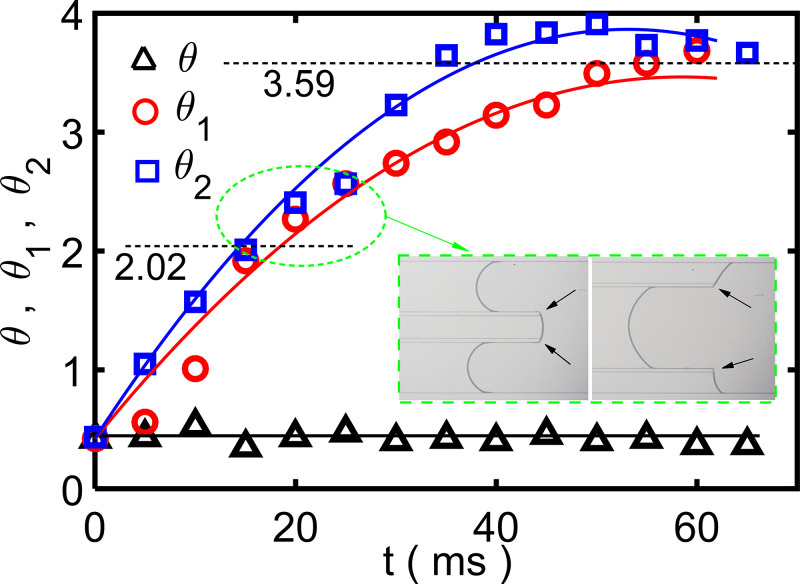
The contact angles determined in the experiment are shown in Fig. 6. Theoretically speaking, the angle marked θ_i–t in Fig. 6 should have the same characteristics as the angle given in Fig. 5(b), which has stable periods of θ_i. The first stable period corresponds to the case where the three–phase contact lines in the x–z plane are on the spacer end surfaces, as shown in the inset figures of Fig. 6. The experimentally determined dynamic contact angle θ ≈ 25.5°. Thus, the advancing contact angle θ_i must reach 90° + θ (=115.5°; ≈2.02 rad) to pass over the first right angle, and 180° + θ (=205.5°; ≈3.59 rad) to pass over the second right angle. These two critical values are marked in Fig. 6, but the characteristics are not obvious. This may be because there are errors in the experimental measurement, or because the spacer width (50 μm) is small that the stable period of θ_i lasts for only a very short time.

FIG. 6.

The contact angles (θ, θ₁, and θ₂) results as functions of time t. The solid lines are fitting curves. The two critical contact angles (2.02 and 3.59) are marked. Inset figures show the three–phase contact lines (in the x–z plane) which are on the spacer end surfaces.

When the advancing contact angle changes, the magnitude and direction of the capillary force change correspondingly. Experimental results show that the advancing contact angles θ₁ and θ₂ both change from acute (hydrophilic) to obtuse (corresponding to hydrophobic) angles. This indicates that the relevant capillary forces on the walls in the deep plane gradually change from promotive forces to impeditive forces, as shown in Figs. 4 and 5.

We wish to determine the capillary force by investigating the change in contact angle, so as to explain the synchronization or waiting phenomenon of capillary flows. Therefore, we need to determine the relationship for θ_i–t. The experimental results show that the characteristic of the contact angle shown in Fig. 5, which has stable periods of θ_i, is not clear. We conducted a simplified analysis, which neglected the details of the contact angle change at the edges, and obtained the θ_i–t relationship [Eq. (10)] by numerical fitting, based on the experimental results. The fitting curves are shown as solid lines in Fig. 6,

$$\{\begin{array}{c}\theta =0.4452;\\ {\theta }_1=0.4198+104.1t-889.8t^2;\\ {\theta }_2=0.4233+129.6t-1220t^2.\end{array}$$ (10)

As shown in Fig. 7(a), w₁ and w₂ are the widths of the waiting channels. In device 1, the capillary force on the walls in the x–z plane changes to 2hσcos(θ₁), while that on the walls in the x–y plane does not change because the contact angle remains unchanged. The resultant force is still 2w₁σcos(θ) in the flow direction. The total capillary force changes from F_σ1 (=2(w₁ + h)σcos(θ)) to

$$F_{\sigma 1}^{\mathrm{\prime }}=2w_1\sigma \cos (\theta )+2h\sigma \cos ({\theta }_1).$$ (11)

FIG. 7.

(a) The capillary forces on relevant walls of devices 1 and 2 in the x–y plane. The inset figures show the shapes of the liquid–gas interfaces in the x–z plane. (b) The result of $F_{\sigma i}^{\mathrm{\prime }}/F_{\sigma i}$ as a function of time t.

Similarly, the relevant total capillary force in device 2 changes from F_σ2 [=2(w₂+h)σcos(θ)] to

$$F_{\sigma 2}^{\mathrm{\prime }}=2(w_2+h)\sigma \cos (\theta )+h\sigma \cos ({\theta }_2).$$ (12)

The relative results $F_{\sigma i}^{\mathrm{\prime }}/F_{\sigma i}$ (i = 1, 2) [Fig. 7(b)] indicate that the capillary force decreases with the change in the contact angle, slowing the capillary flow. This explains the experimentally observed capillary flow synchronization phenomenon. In addition, the contact angles of the two walls (in the x–z plane) of the waiting channel in device 1 both change. Thus, the total capillary force decreases both faster and by a larger margin in device 1 than in device 2 [see Fig. 7(b)].

B. Estimating the liquid flow output

The volume of liquid that flows out of the waiting channel during deceleration is substantially smaller than that in the channel, so the corresponding momentum and viscous force can be ignored. If we assume a length L, the simplified liquid momentum I′ ≈ ρwhLv and viscous force $F_{\mu }^{\mathrm{\prime }}\approx \frac{12\mu wLv}{(1-0.63h/w)h}$. Upon integrating the total capillary force $F_{\sigma }^{\mathrm{\prime }}$, the momentum equation becomes

$${\displaystyle \frac{\mathrm{d}(\rho whLv)}{\mathrm{d}t}+{\displaystyle \frac{12\mu wLv}{(1-0.63h/w)h}=F_{\sigma }^{\mathrm{\prime }}.}}$$ (13)

So,

$$v={\displaystyle \frac{1}{L}{\mathrm{e}}^{-C_{1}t}\left(\int {\displaystyle \frac{F{{}^{\mathrm{\prime }}}_{\sigma }}{\rho wh}{\mathrm{e}}^{C_{1}t}\mathrm{d}t+C}\right),}$$ (14)

where C is a constant. For device 1, we have the momentum (≈ρw₁hLv), viscous force ($\approx \frac{12\mu w_{1}Lv}{(1-0.63h/w_1)h}$), and $F_{\sigma 1}^{\mathrm{\prime }}=2w_1\sigma \cos (\theta )+2h\sigma \cos ({\theta }_1)$. The velocity v(t) can then be calculated using Eq. (14) based on the fitting result from θ₁. The flow distance x(t), which can be seen as the equivalent distance for liquid in the waiting channel, can be calculated by integrating v(t). The equivalent liquid volume V(t) can then be calculated via

$$V(t)=x(t)\times w_1\times h.$$ (15)

Similarly, the equivalent liquid volume in device 2 can be calculated based on the corresponding momentum equation. In experiments, when the interface begins to change from the initial state (the stable interface shape in the waiting channel), the area S(t) of the output liquid as shown in the inset figure of Fig. 8 can be determined by measuring the experimental results. One can then calculate the liquid volume using S(t) × h. Comparisons of the liquid volumes between theory and experiment are shown in Fig. 8. Agreement between the two results indicates that the analysis is reasonable and can predict the amount of the liquid that flows out of the waiting channels. We can see that the error increases with time because the momentum and viscous force cannot be ignored when large quantities of liquid flow out.

FIG. 8.

Comparisons of the liquid volumes V(t) for devices 1 and 2 as determined theoretically and experimentally. The inset figures mark the relevant area changes of liquid in the x–y plane.

C. The varied contact angle model

For capillary flow in the waiting microchannel of device 1, we develop a theoretical analysis model of the contact angle change during synchronization that can be used for control. A simplified analysis was done by ignoring the effect of the spacer width to determine the contact angle changes at the ends of the spacers. The simplified schematic in Fig. 9(a) shows the positions and shapes of the liquid-gas interfaces during synchronization. When the interface begins to change from its initial state, the area S(t) (in the x–y plane) of the liquid that flows out of the waiting channel can be represented using the color schematics in Figs. 9(b)–9(d) based on the contact angle ranges θ ≤ θ₁ < π/2, π/2 ≤ θ₁ < π, and π ≤ θ₁ ≤ π + θ, respectively. The area S(t) can thus be derived as

$$S={\displaystyle \frac{w_1^2}{4}\left[{\displaystyle \frac{\pi -2\theta -\sin (2\theta )}{1+\cos (2\theta )}-{\displaystyle \frac{\pi -2{\theta }_1-\sin (2{\theta }_1)}{1+\cos (2{\theta }_1)}}}\right].}$$ (16)

FIG. 9.

(a) Schematic of the positions and shapes of the capillary flow liquid-gas interface in the waiting channel of devices 1. Color schematics of the area S(t) (in the x–y plane) of the liquid flowing out of the waiting channel according to the contact angle ranges (b) θ ≤ θ₁ < π/2, (c) π/2 ≤ θ₁ < π, and (d) π ≤ θ₁ ≤ π + θ.

Particularly,

$$\underset{\theta \to \pi /2}{\lim }S={\displaystyle \frac{w_1^2}{4}{\displaystyle \frac{\pi -2\theta -\sin (2\theta )}{1+\cos (2\theta )}.}}$$ (17)

The liquid volume can be obtained,

$$V={\displaystyle \frac{w_1^{2}h}{4}\left[{\displaystyle \frac{\pi -2\theta -\sin (2\theta )}{1+\cos (2\theta )}-{\displaystyle \frac{\pi -2{\theta }_1-\sin (2{\theta }_1)}{1+\cos (2{\theta }_1)}}}\right].}$$ (18)

Figure 10 shows the comparison of the experimental V vs θ₁ results and the analytical V vs θ₁ results from Eq. (18), and they agree with each other. By calculating the derivative with respect to time, we can determine $\frac{\mathrm{d}V}{\mathrm{d}t}$ and $\frac{{\mathrm{d}}^{2}V}{\mathrm{d}{t}^2}$, from Eqs. (15) and (18), respectively. These can be combined with Eq. (13) to derive a differential equation for the contact angle θ₁ (i.e., the relation θ₁–t can be obtained from V–t via V–θ₁),

$$C_3{\displaystyle \frac{{\mathrm{d}}^2{\theta }_1}{\mathrm{d}{t}^2}+C_4{\left({\displaystyle \frac{\mathrm{d}{\theta }_1}{\mathrm{d}t}}\right)}^2+C_1{C}_3{\displaystyle \frac{\mathrm{d}{\theta }_1}{\mathrm{d}t}={\displaystyle \frac{{F^{\mathrm{\prime }}}_{\sigma }}{\rho L{w}_1^2\mathrm{h}},}}}$$ (19)

where

$$\{\begin{array}{c}{C}_3={\displaystyle \frac{1+\cos (2{\theta }_1)+\left({\theta }_1-{\displaystyle \frac{\pi }{2}}\right)\sin (2{\theta }_1)}{{[1+\cos (2{\theta }_1)]}^2},}\\ C_4={\displaystyle \frac{3\sin (2{\theta }_1)+(2{\theta }_1-\pi )[2-\cos (2{\theta }_1)]}{{[1+\cos (2{\theta }_1)]}^2},}\\ {F^{\mathrm{\prime }}}_{\sigma }=2w_1\sigma \cos (\theta )+2h\sigma \cos ({\theta }_1).\end{array}$$ (20)

FIG. 10.

A comparison of the experimental and theoretical V vs θ₁ results.

Thus, θ₁ can be obtained by solving Eq. (19). It is a function of the parameters ρ, μ, σ, L, w₁, h, θ, and t. The dimensional analysis result shows a clear relationship between these parameters as follows:

$${\theta }_1=f\left({\displaystyle \frac{w}{L},{\displaystyle \frac{h}{L},{\displaystyle \frac{\mu t}{\rho L^2},{\displaystyle \frac{\sigma t^2}{\rho L^3},\theta }}}}\right).$$ (21)

D. Synchronization and control of capillary flows

Based on this investigation, we have obtained a general idea of the basic principle of the synchronization of capillary flows. Next, we conceived a series of control studies of capillary flows, in a study of spacer position change, as shown in Fig. 11. Our design incorporated spacers with regular spacing [Figs. 11(a) and 11(b)], two types of liquid [Fig. 11(c)], and multisegment spacers in the flow direction [Fig. 11(d)]. There will be a confluence area at the end of the microchannel. In the of multisegment spacer design, we can change the parameters, including the width between the spacers and the microchannel wall, the spacing between adjacent spacers (δ), and the spacer length (Δ). The possible positions of the liquid–gas interfaces are shown with colored, dashed lines, where each color corresponds to a different flow case. In addition, we designed a new microfluidic device and conducted capillary flow experiments. A number of capillary flows were obtained by adding many spacers in a microchannel; in this way, the dynamic behaviors of more capillary flows could be studied. The microfluidic device was fabricated from PDMS by soft lithography, and ethanol was used as the test liquid.

FIG. 11.

Schematic of capillary flow control studies. Spacers in (a) and (b) are designed with regular spacing, (c) two types of liquid, and (d) multisegment spacers in the flow direction.

Figure 12 shows the positions and shapes of the liquid–gas interfaces at different time points. The different capillary flows show obvious waiting or synchronization phenomena, based on the liquid pinning effect. As well as the pinning and interface linking effects, we observed an enhance filling phenomenon. When there are walls parallel to the flow direction, they provide extra surfaces that can enhance filling.²⁹ These results show that a cluster of capillary flows at the inlet can be controlled by designing such parameters as spacer position. Based on the liquid pinning effect, there will be waiting or synchronization during the flow. This means that capillary flows can be readjusted to form new cluster flows.

FIG. 12.

The positions and shapes of the liquid–gas interfaces of multiple capillary flows at different moments. The capillary flows are readjusted to form a new cluster ones finally. The scale bar is 500 μm.

IV. CONCLUSION

This study considered synchronization and control of capillary flows isolated by spacers in rectangular microchannels using the liquid pinning effect. Two basic synchronization modes were investigated. The experimental results showed that the velocities of faster capillary flows were reduced and the time delay between two capillary flows was automatically balanced. Time differences between capillary flows, contact angle variation, and capillary forces were analyzed to explain this synchronization behavior. The amount of liquid that flowed out of the waiting channel was estimated and verified experimentally. A model for the contact angle change during synchronization was derived and verified experimentally based on the liquid flow analysis. In addition, there will be more design space for various liquids and more capillary flows via this work, which is thus useful for promoting detection and allowing reactions to proceed spontaneously.

AUTHORS' CONTRIBUTIONS

L.Z. and Z.Z. contributed equally to this work.

DATA AVAILABILITY

The data that support the findings of this study are available within the article.