Re-evaluating the conventional wisdom about binding assays

Abstract

Analytical technologies based on binding assays have evolved substantially since their inception nearly 60 years ago, but our conceptual understanding of molecular recognition has not kept pace. Indeed, contemporary technologies such as single-molecule and digital measurements have challenged, or even rendered obsolete, core concepts behind conventional binding assay design. Here, we explore the fundamental principles underlying molecular recognition systems, which we consider in terms of signals generated through concentration-dependent shifts in equilibrium. We challenge certain orthodoxies related to binding-based detection assays, including the primary importance of a low dissociation constant (K_D) and the extent to which this parameter constrains dynamic range and limit of detection. Lastly, we identify key principles for designing binding assays optimally suited for a given detection application.

Molecular Quantification via Concentration Dependent Shifts in Equilibrium

The first published implementation of a binding-based molecular assay was an immunoassay (see Glossary) for insulin detection in 1960 [1]. Over the following 60 years, analytical technologies based on binding assays have evolved substantially. Molecular detection platforms based on enzyme-linked immunosorbent assays (ELISAs), as well as newer commercial technologies, such as Luminex and NanoString, are core components of today’s diagnostic armamentarium. In general, binding assays generate signal through concentration-dependent shifts in equilibrium that result from the interaction of the target molecule with an affinity reagent. Typically, either the target or affinity reagent is directly coupled to a moiety that generates an observable readout upon binding. For example, myriad immunosensors [2] have been developed that couple the interaction between antibody and antigen to an observable output based on an electronic [3], optical [4], or mechanical [5] signal, or even on the production and amplification of a quantifiable DNA sequence [6–8]. In all of these cases, an increase in target concentration shifts the equilibrium toward the formation of more antibody-antigen complexes, increasing the signal. Microarray technology likewise quantifies gene expression in a manner where the equilibrium fraction of target molecules bound to the array surface—and thus the fluorescence signal generated at their cognate array feature—is proportional to their concentration in the bulk solution [9–11].

A conventional understanding of molecular recognition principles has been used for decades to describe microarray and immunoassay technologies. However, the advent of contemporary molecular detection technologies, such as single-molecule measurements, for example, digital ELISA [12], droplet digital PCR [13], Simoa [14,15], and DNA-PAINT [16], has rendered important aspects of this understanding either unnecessarily restrictive or even obsolete. For instance, it is commonly assumed that the useful detection range of an affinity reagent spans an 81-fold change in target concentration centered around the equilibrium dissociation constant (K_D). This heuristic is still useful for conventional immunoassays, but it may be overly limiting in the broader context of molecular detection assays because it implies that one can only quantify target concentrations as low as K_D/9 and as high as 9 ∗ K_D (i.e., a dynamic range of 81). There is also a prevalent notion that a lower K_D is always “better” because it results in a lower limit of detection (LOD); however, there are many scenarios in which this would be detrimental to the assay. This is not to say that the conventional wisdom about molecular recognition is wrong, but rather that stringent adherence to prior conventions limits what could otherwise be achieved with newly available technologies. Here, we aim to reevaluate the conceptual frameworks used when developing binding assays and to provide an intuitive understanding of molecular recognition, empowering researchers to make better use of contemporary technologies for quantitative analysis of biological systems. A number of excellent articles have already shown how to shift and manipulate binding curves from a physicochemical perspective [17]. Therefore, we endeavor to approach the topic from a stance that is agnostic to the specific assay chemistry or implementation. After providing a brief background on the fundamental principles of affinity-based assays, we use simple mathematical reasoning and literature examples to argue against some long-held preconceptions of molecular recognition.

Single-Site Molecular Recognition

Although more complicated examples of molecular recognition, such as population shift [18–20], allostery [21–23], and proximity assays [24], have proven extremely powerful, many novel insights about assay development can still be gleaned from a simple model of bimolecular association. In the standard model of bimolecular association, the binding strength between an affinity reagent, A, and a target molecule, T, is characterized by the binding affinity, which is quantified in terms of K_D (eq. 1).

$$A+T\stackrel{K_{\text{D}}=\frac{[A][T]}{[A\cdot T]}}{\leftrightarrow }A\cdot T$$ (1)

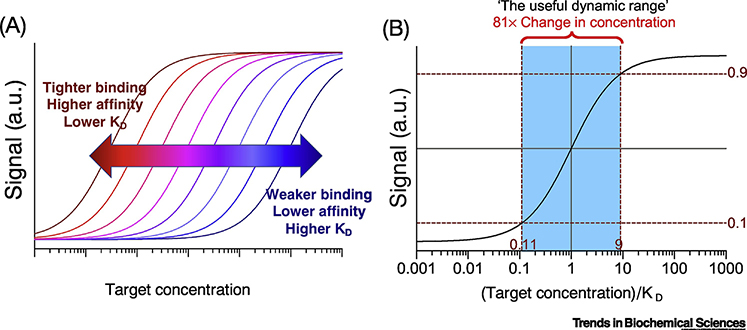
Binding affinity plays a crucial role in determining what range of target concentrations yields an observable signal (Figure 1A). A typical antibody-antigen interaction has a K_D of ~1 nM [25]. An affinity reagent is generally considered high affinity when K_D < 10 nM and low affinity when K_D > 1 μM, although, as we will discuss, this is not necessarily the best conceptual approach. The binding curve is commonly defined in terms of the Langmuir isotherm [26–28], an equation that characterizes the amount of binding as a function of target concentration (eq. 2), although this approach is not without limitations (Box 1). Several key assumptions underlie the simplicity of the Langmuir isotherm: i) single-site binding, ii) single K_D, iii) one component is in excess, and iv) no off-target reactions. If these assumptions hold, one can derive the fraction of affinity reagent bound to target as

$$f=\frac{[A\cdot T]}{{[A]}_{\text{total}}}=\frac{[T]}{K_{\text{D}}+[T]}$$ (2)

for conditions in which [A] << [T]. This simple equation has informed much of our conventional understanding of molecular recognition—e.g., that 50% of affinity reagent molecules are bound to target when the target concentration is equal to the K_D (Figure 1B), which defines the center of the detection range around the affinity. In this context, the useful detection range has conventionally been defined as the range of target concentrations at which 10–90% of the affinity reagents are bound to target [17]. A cocktail-napkin analysis reveals that the detection range in this model spans target concentrations from 0.11–9.0 × K_D, representing an 81-fold concentration window (Figure 1b). This implies that an affinity reagent with a K_D of 1 nM can only quantitatively detect targets in the range of 111 pM to 9 nM. However, the utility of this heuristic is called into question by the myriad examples of affinity reagents being used to quantify target concentrations far below their K_D.

Figure 1 |. Conventional understanding of binding curves.

(a) Increasing affinity (i.e., lowering K_D) shifts binding curves leftward relative to target concentration, whereas lowering affinity (i.e., increasing K_D) leads to a rightward shift in the binding curve. (b) The “useful detection range” (blue) is considered to encompass the target concentrations over which 10–90% of the affinity reagent molecules are target-bound. This yields detectable target concentrations that span 0.11–9.0 × K_D.

Box 1 |. When can we use the Langmuir isotherm and when does it fall apart?

A core, but often overlooked, assumption enabling the use of the Langmuir isotherm is that one component of the system must be in vast excess of the other so binding does not cause depletion of one of the species. If the target is much more abundant than the affinity reagent (i.e., [T] ≫ [A]), then changes in the target concentration lead to changes in the fraction of affinity reagent that is bound to the target:

$$[A\cdot T]=\frac{{[T]}_{\text{total}}}{{[T]}_{\text{total}}+K_{\text{D}}}{[A]}_{\text{total}}$$ (i)

In this case, the resultant signal is non-linear in terms of target concentration but linear in terms of affinity reagent concentration. In contrast, if the affinity reagent is present at a much higher concentration than the target (i.e., [A] ≫ [T]), then the fraction of bound target remains constant while the total amount of target varies:

$$[A\cdot T]=\frac{{[A]}_{\text{total}}}{{[A]}_{\text{total}}+K_{\text{D}}}{[T]}_{\text{total}}$$ (ii)

Here, the signal is non-linear in terms of affinity reagent concentration and linear in terms of target concentration. Since it is typically easier to couple a detection modality (e.g., a fluorescent or bioluminescent tag) to an affinity reagent than to the target, the background signal scales with [A] in most experimental setups. Therefore, the affinity reagent-limited scenario usually exhibits a more favorable signal-to-noise ratio than the target-limited scenario. However, a practical consideration of imposing the condition that [T] ≫ [A] is that in order to measure low target concentrations, affinity reagent concentration must be even lower. Thus, in the absence of signal amplification, the detection limit is constrained by the detection modality rather than the affinity reagent.

The conventional Langmuir isotherm no longer holds if affinity reagent and target concentrations are comparable. In this case, the amount of target-affinity reagent complexes is a non-linear function of the concentrations of both components[53]:

$$[A\cdot T]=\frac{1}{2}\left({[A]}_{\text{total}}+K_{\text{D}}+{[T]}_{\text{total}}-\sqrt{{\left({[A]}_{\text{total}}+K_{\text{D}}+{[T]}_{\text{total}}\right)}^2-4{[A]}_{\text{total}}{[T]}_{\text{total}}}\right).$$ (iii)

If [A] = [T] = K_D, rather than observing the intuitive 50% binding, one would instead observe ~38.2% binding. The concentrations must be raised to [A] = [T] = 2K_D to achieve 50% binding.

The Langmuir isotherm can be a powerful tool for rationalizing and analyzing binding data, especially because it conveniently distills a binding curve into a single parameter. However, the misuse of the equation can lead to misinterpretations and erroneous conclusions.

What is a “Good” K_D?

Other misconceptions related to molecular recognition stem from our own implicit biases. One such bias is the concept of an objectively “better” K_D; we are biased towards thinking that a lower K_D is intrinsically superior because we predominantly work under conditions where the K_D is higher than the concentration of the target we are trying to detect. In practice, the concept of a “better” K_D is only relevant in the context of a desired detection range. Many researchers, however, fall into the trap of optimizing for lower and lower LODs—and by proxy, lower and lower K_D—without regard for the biological scenario in which the assay is to be used.

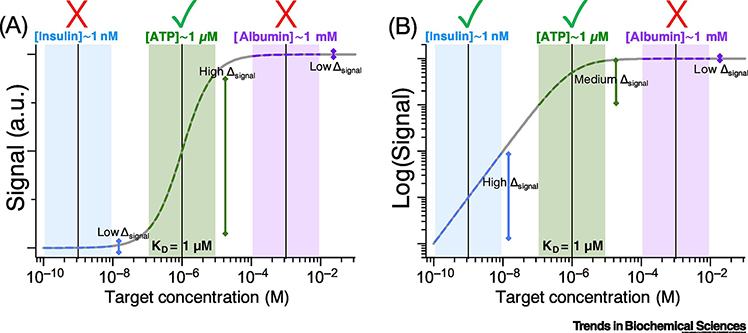
We often overlook the fact that quantifying albumin concentrations in the 1 mM range using an affinity reagent with K_D = 1 μM is as challenging as, or, as we will discuss later, possibly even more challenging than, quantifying insulin concentrations in the 1 nM range using a reagent with the same affinity (Figure 2A). If the K_D is too high, there will be too little signal over the desired detection range; if the K_D is too low, the signal will be saturated. In either case, one loses the ability to differentiate changes in target concentration via shifts in equilibrium. What matters is matching the detection range to the clinical scenario at hand. Therefore, a good effective K_D or detection range can only be defined in terms of a given biological context. For example, an affinity reagent with a K_D of 1 μM is perfect for detecting ATP in blood, since its basal level is on the order of 20 nm to 1 μM [29]. In contrast, an affinity reagent with K_D = 1 pM towards ATP would be functionally useless because any reasonable deviation in ATP concentration would not result in an observable change in binding. Unfortunately, it remains common in the realm of biosensor development to report K_D without any mention of the clinically relevant detection range.

Figure 2 |. The right K_D for the job.

a) Detecting 1 nM insulin with an affinity reagent with K_D = 1 μM is just as challenging as detecting 1 mM albumin. If the affinity is too high or too low, the output signal will not change appreciably with changes in target concentration. b) The greater sensitivity of contemporary single-molecule and digital detection assays means that one can, with sufficiently low background, quantitatively detect 1 nM insulin more easily than 1 mM albumin or even 1 μM ATP using an affinity reagent with a K_D of 1 μM. In this scenario, a logarithmic scale for detection is more useful than the linear scale employed in a.

The 10–90% concentration window is ultimately arbitrary, and was established based on the typical precision of measurements in the past. Below 10% occupancy, the signal response curve still exhibits an appreciable slope; however, quantification in this region requires much more precise, high-resolution measurements that have only recently become possible. For this reason, in the next section, we will differentiate between traditional ensemble measurements that have outputs that are best characterized on a linear scale, as opposed to high-resolution digital measurements that are best characterized on a logarithmic scale.

Logarithmic Detection Modalities and the Influence of Background Signal

The advent of sophisticated detection modalities with extremely high resolution and considerably lower levels of background should encourage a reconsideration of how best to define signal output. In contrast to traditional readouts like bulk fluorescence or electrochemistry, which report ensemble averages of the number of bound affinity reagent molecules, single-molecule and digital assays report individual molecular counts. Since these outputs are quantitative over orders of magnitude, it is more useful to define the y-axis on a logarithmic scale. This has the important result that the quantification of analytes at concentrations arbitrarily lower than K_D becomes possible, assuming zero background signal. This is in stark contrast to the conventional thinking that the functional detection range is strictly proscribed relative to the K_D. Moreover, the error associated with the calculated concentration decreases with the logarithm of the signal—that is, measurements get more precise at lower concentrations (Figure 2B). Hypothetically, the LOD for a purely digital measurement with zero background is limited solely by Poisson statistics. We further discuss the limitations of detecting targets at ultra-low concentrations in Box 2.

Box 2 |. A note on detection at ultra-low concentrations.

There are additional considerations for the detection of molecules at ultra-low concentrations, i.e., <1,000 molecules per sampling volume, particularly in terms of detection probability and binding kinetics. First, we describe how, as target concentration approaches zero, the probability of the target being absent from the sampling volume becomes non-negligible. Secondly, we want to briefly touch on the limitations of binding kinetics at ultra-low concentrations.

We have thus far considered primarily the situation where [A]<<[T] to minimize background signal. However, this becomes problematic as [T] approaches zero, because you must also lower [A] to maintain [A]<<[T], which results in a decrease in the maximum obtainable signal. Fortunately, equations (i) and (ii) in Box 1 become equivalent in the limit that [A] and [T] are both much lower than K_D, and the signal response is still linear with respect to [T] and [A]. At very low concentrations, there is a non-negligible probability that your target of interest will not be in your sample volume. For instance, at a concentration of 5 aM there are an average of 3 molecules per microliter. According to the Poisson distribution, if you draw a single microliter of sample, there is a 5% chance there will be zero molecules in the draw, a 15% chance that there will be one molecule, a 22.4% chance that there will be two molecules, a 22.4% chance that there will be three molecules, a 16.8% chance that there will be four molecules, a 10% chance that there will be five molecules, and so on. This underlies the concept of “limiting dilution”, which was first introduced in 1990 for the detection of ultra-low concentrations [49]. This is also the principle underlying droplet digital PCR [50] and digital ELISA [12]. Many digital assays not only exhibit this principle but rely on it explicitly in order to estimate concentrations approaching single molecules.

In terms of binding kinetics at ultra-low concentrations, we first note that the rate of binding from the bulk solution to a 2D surface, e.g., an electrode, can be exceedingly slow at ultra-low concentrations. Squires et al. have written a detailed perspective on this phenomenon [51], and here we want to focus on how the rate of reaching equilibrium in the bulk is limited as target concentrations approach zero.

As target concentration decreases, the rate at which the system approaches equilibrium decreases. However, this rate doesn’t approach zero as target concentration approaches zero; rather, it approaches a constant that is a function of the on-rate, off-rate, and concentration of the affinity reagent. The time to reach equilibrium is determined by the kinetic parameters and the concentration of affinity reagent only and is not a function of the concentration of the low concentration target.

We derive that briefly as follows. For A + T ⟷ A ∙ T, when [T]<<[A], the production of A ∙ T as a function of time is given by [52]

$$[\text{A}\cdot \text{T}](\text{t})=\frac{{\text{T}}_0{\text{A}}_0{\text{k}}_{\text{on}}}{{\text{A}}_0{\text{k}}_{\text{on}}+{\text{k}}_{\text{off}}}\left(1-{\text{e}}^{-\left({\text{A}}_0{\text{k}}_{\text{on}}+{\text{k}}_{\text{off}}\right)\text{t}}\right).$$ (iv)

If we approximate the kinetics of reaching equilibrium as how long it takes to reach 99% of the equilibrium value (i.e., $\frac{[\text{A}\cdot \text{T}](\text{t})}{[\text{A}\cdot \text{T}](\text{inf})}=0.99$), then the time to reach equilibrium is given by:

$${\text{t}}_{99\%}=\frac{4.605}{{\text{A}}_0{\text{k}}_{\text{on}}+{\text{k}}_{\text{off}}}$$ (v)

Clearly, this value can be decreased by increasing the concentration of the affinity reagent and does not depend on the target concentration. There is ultimately a tradeoff between kinetics and background signal, in which increasing the affinity reagent concentration will increase the kinetics but could also increase the background signal. The specifics of this tradeoff will depend on the particular chemical implementation used in the assay.

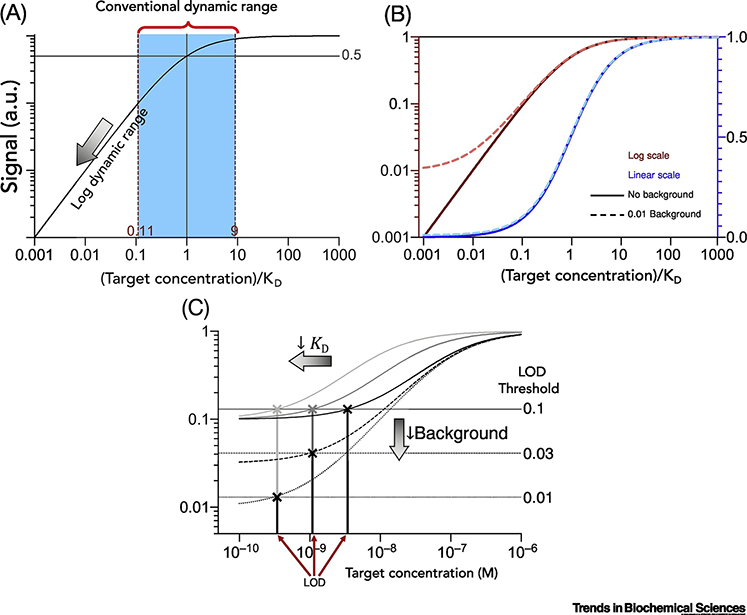
In the absence of background signal, the log dynamic range extends indefinitely, retaining quantitative resolution over arbitrarily low concentrations (Figure 3A). This means that in theory, the ability to detect low concentrations can be completely decoupled from K_D. In practice, background signal strongly influences the LOD [30] and the detection range of an assay. Background signal can often be decreased through assay design or optimization, whereas binding affinity is generally, with some exceptions [17,18,20,23], a fixed property of an affinity reagent-target pair. Moreover, a background signal of 1% has a large impact on a log linear range but a negligible effect on the conventional linear range (Figure 3B). Therefore, the minimization of background signal is more attractive for improving LOD than relying on decreasing K_D. Specifically, assuming a constant coefficient of variation (CV) for background signal, decreasing the background signal will have the same effect on the LOD as reducing K_D by the same factor (Figure 3C).

Figure 3 |. Logarithmic detection and background signal.

(A) If the y-axis can be plotted on a log-scale, which is appropriate for detection modalities that can distinguish between small changes in binding fraction, then the log-linear detection range extends below the conventional detection range (blue) that is defined in Figure 1B. In the absence of background signal, the log detection range includes indefinitely low target concentrations and the center of the log detection range is no longer located at [Target] = K_D. (B) Background signal has a larger impact on a logarithmic output than a linear output. The extent to which the log detection range extends below K_D is a strong function of background signal. Adding a background signal of 1% does not appreciably affect the dynamic range for a linear output, but it greatly reduces the dynamic range for a log output. (C) Decreasing K_D (dark to light solid lines) has the same effect on LOD as decreasing the background signal by the same factor (solid to dashed to dotted black lines). Horizontal lines represent the background signals equivalent to 1, 3, and 10% plus three standard deviations, assuming 10% coefficient of variation. In contrast, K_D and background signal can have different effects on the detection range. Decreasing K_D does not appreciably change the extent of the detection range, whereas decreasing background signal greatly extends the log detection range.

Sophisticated detection modalities with considerably lower levels of background and digital outputs enable us to quantify molecules at concentrations vastly below K_D, thereby rendering the traditional notion of an 81-fold dynamic range centered around the K_D obsolete. Instead, it is more useful to define a log-linear detection range where, given a sufficiently sensitive detection modality and low enough background, it should be possible to detect analytes at concentrations arbitrarily lower than the K_D. A corollary of this rationale is that the burden of optimizing LOD should not be placed solely on decreasing the K_D of the affinity reagent itself but also on the development of low-background assays with detection modalities that can discriminate small changes (e.g., 0.1–0.01%) in the fraction of bound affinity reagents. Detection modalities that are capable of this level of resolution typically involve the counting of single-molecule events, such as droplet digital PCR [13], DNA sequencing [31,32], digital ELISA [14], or single-molecule imaging [33]. With a sufficiently low background signal and a logarithmic detection modality, it is possible to detect and quantify target concentrations many orders of magnitude below K_D. An interesting ramification of this rationale is that the K_D of the affinity reagent must be higher than the physiological range of target concentration in order to ensure an appropriate log-linear detection range. Indeed, it is actually worse to have a K_D lower than the relevant concentration range.

A Case Study

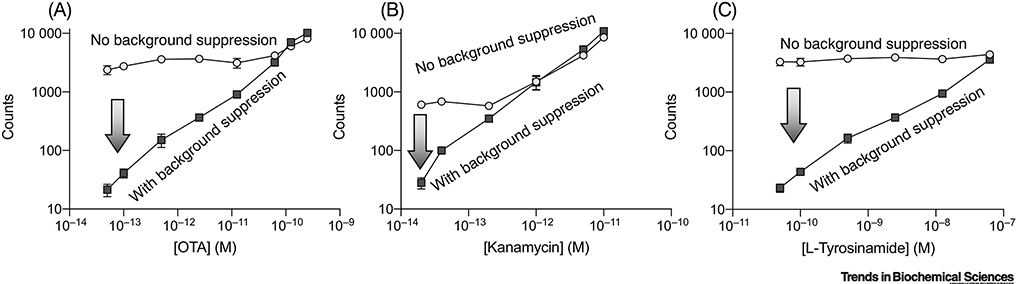
This concept of extending the dynamic range through the selection of an appropriate detection modality and the elimination of background signal is exemplified by recent work from Li and colleagues [34], where they were able to consistently quantify analytes at concentrations that are orders of magnitude below K_D. The authors used a three-state population-shift mechanism, which they termed recognition-enhanced metastably-shielded aptamer probes (RMSApt). The affinity reagents are designed in such a way that they can initiate a rolling circle amplification (RCA) reaction [35,36] when bound to the target molecule. They are coupled to a solid surface, so that individual RCA products can be imaged and counted. This assay inherently exhibited high background signal, because aptamers not bound to target could also initiate an RCA reaction. The authors solved this problem by introducing an enzymatic “locking” mechanism that results in the non-equilibrium depletion of unbound aptamers, functionally eliminating background signal. Impressively, the authors observed quantitative detection ranges and LODs that consistently extend many orders of magnitude below the reported aptamer K_D. These improvements in quantitative sensitivity appear to be very robust and were demonstrated with three different affinity reagents. An ochratoxin A (OTA) aptamer with a reported K_D of 500 nM [37] exhibited a LOD of 38.8 fM and a detection range of 100 fM to 1 nM (Figure 4A); a kanamycin aptamer with a reported K_D of ~80 nM [38] exhibited a LOD of 8.9 fM and a detection range of 10 fM to 10 pM (Figure 4B); and a tyrosinamide aptamer with a reported K_D of 45 μM [39] exhibited a LOD of 47.5 pM and a detection range of 10 pM to 100 nM (Figure 4C). The authors consistently demonstrate the quantification of concentrations orders of magnitude below K_D!

Figure 4 |. Digital detection and low background single render the concept of an 81-fold dynamic range centered around the K_D obsolete.

The recognition-enhanced metastably-shielded aptamer probe (RMSApt) system [34] exemplifies how a digital readout with little to no background signal on a log output scale can dramatically extend an assay’s functional detection range. RMSApt essentially eliminates background signal through an enzymatic locking mechanism, achieving LODs and quantitative detection ranges that are orders of magnitude below reported affinities of the aptamers for their targets: a) ochratoxin A (OTA), b) kanamycin, and c) L-tyrosinamide. Importantly, a digital readout by itself (circles) is not sufficient to achieve these results; rather, a mechanism of background suppression (squares) must also be included. Data has been replotted from Ref. 36 with permission from the authors.

Although these results initially seem impossible in light of traditional understanding of molecular recognition, they should not be surprising considering the impact that background signal and the use of a digital detection modality have on the functional detection range. The high resolution is conferred in part by the ability to image and count individual binding events, which enables discrimination between small changes in the fraction of bound aptamers, and in part by the functional elimination of background through an enzymatic locking mechanism, which enables detection at concentrations far below K_D. These features ultimately result in dynamic ranges that far exceed the conventional 81-fold change in concentration. In this scenario, the ability to distinguish between small percentages of binding events is limited only by the number of viewable RCA products, which is in turn constrained by Poisson noise at the low end of target concentration and by image saturation at the high end. Thus, the ability to perform a high-sensitivity assay should not be exclusively dictated by access to high-affinity binding reagents but should also exploit a high-resolution detection modality and the ability to minimize background signal.

The previous example required the introduction of an irreversible reaction to the assay. This is not a necessity; many other methods can achieve similar outcomes. In another excellent example [40], the authors were able to detect and quantify fewer than 100 molecules/μL simply by requiring that three antibodies bind to the target simultaneously in order to generate a signal. This equilibrium-based approach greatly reduced the probability of background signal generation and conferred ultra-high resolution. Other digital approaches based on molecular confinement [12,41] have also illustrated the concepts discussed here, achieving successful quantitation at target concentrations far below the affinity of the binder.

The Challenge of Specificity

If the detection of analytes at concentrations orders of magnitude below the K_D is possible, is the effort [42,43] to develop high affinity reagents unnecessary? This question seems to be particularly salient given the potential performance that can be achieved with a moderate-affinity binder and a focus on decreasing the background signal. However, there remains another important driving force underlying the need for high-affinity detection reagents: specificity. Previously, we have only considered background signal arising from spurious molecular interactions of the affinity reagent itself, e.g., in RMSApt, the initiation of an RCA reaction by an aptamer not bound to any molecule. However, interference can also arise from the false positive signal caused by binding to off-target molecules. Every biomolecule has an effective binding affinity to every other biomolecule, even though, in most cases, this affinity is exceedingly low. Since most biomolecules can form multiple hydrogen bonds with one another, many off-target molecules will still produce a measurable K_D for a given affinity reagent, even if this affinity is many orders of magnitude weaker than that for the intended target. Since the concentrations of target molecules can be many orders of magnitude lower than the concentrations of off-target molecules [44], achieving high specificity through biomolecular recognition is critical. Whereas background signal can often be reduced through assay design, in practice, we have little to no control over the concentrations of off-target molecules or their effective binding affinity to the detection reagent. Even if one can still detect low target concentrations with modest affinity binders, the ability to distinguish between target and off-target molecules decreases as the affinity for the target molecule decreases or as the concentration of off-target molecules increases. This becomes problematic if we do not understand the limitations imposed by imperfect specificity.

Therefore, we would like to conclude this perspective with a brief discussion on the limitations imposed by specificity. Imagine a scenario where an affinity reagent has a K_D1 of 1 μM for a desired target, T₁. Assuming [T₁] ≫ [A], the log-linear signal is given by

$$\log (f)\approx \log \left(T_1\right)-\log \left(K_{\text{D}1}\right).$$ (3)

Upon the addition of an off-target molecule, T₂, for which the affinity reagent exhibits an affinity of K_D2, then the total signal is now approximately

$$f_{\mathit{total}}\approx \frac{T_1}{K_{\text{D}1}}+\frac{T_2}{K_{\text{D}2}},$$ (4)

assuming [T₂] ≫ [A], [T₁] ≪ K_D1, and [T₂] ≪ K_D2. The log-linear range is now

$$\log (f)\approx \log \left(T_1+\frac{K_{\text{D}1}}{K_{\text{D}2}}{T}_2\right)-\log \left(K_{\text{D}1}\right).$$ (5)

In this scenario, measurements of T₁ in the presence of T₂ will be off by a factor of $\frac{K_{\text{D}1}}{K_{\text{D}2}}{T}_2$. This implies that the impact of off-target specificity becomes problematic if T₁/T₂ does not greatly exceed K_D1/K_D2. This reinforces the need for high-affinity (i.e., low K_D) reagents. For example, consider the detection of a target that is present at 1 nM in whole blood. Albumin is the off-target protein with the highest concentration in blood (~5 mM) [45]. If albumin binds weakly to the affinity reagent with K_D2 ~500 mM, then K_D1 would need to be less than 9 nM for the error resulting from off-target binding to albumin to be less than 10%. As such, the concentrations and cross-reactivity of off-target molecules impose a lower limit on the affinity that is acceptable for an affinity reagent in a given context. This complication is often overlooked, perhaps because addressing it would require the impractical task of profiling each reagent’s K_D for all possible off-target molecules. Perhaps confirmation bias is also at play; we have a tendency to seek confirming rather than disconfirming information [46]. This bias is exacerbated when unwarranted assumptions—such as the assumption that affinity reagents are highly specific—make disconfirming evidence seem unlikely. Fortunately, specificity can be increased through assay design. For example, by requiring multiple binding events to produce a signal [6,40,47], the probability of two binding events occurring on the same off-target molecule is greatly reduced. Therefore, specificity can be improved by requiring dual (or higher-order [40]) recognition for signal generation, an approach that has the added benefit of reducing background signal and therefore extending the log-linear detection range.

Concluding Remarks

A rigorous understanding of the core principles underlying binding assays is needed to guide the generation of affinity reagents that are best suited for the development of effective biosensors. Some of the conventional wisdom related to binding assays may be stifling the innovation that could be possible with novel technologies. For instance, we have discussed the limiting effects of over-reliance on K_D as a measure of biosensor performance and how our own biases cause us to overlook important factors like specificity because they are challenging to quantify. By considering binding assays in terms of concentration-dependent shifts in equilibrium, we have embarked on a critical assessment of the key features of these systems, with the goal of identifying important considerations for future biosensor development. First, we explored how the K_D of a given reagent for its target should only be judged as “better” or “worse” depending on the context in which it is to be employed. We showed that high-resolution measurements can be made even with a low affinity binder, and that by making use of a digital detector (in which binding events are counted rather than averaged in an ensemble) and a low-background assay design, one can extend the log-linear detection range to far lower target concentrations that are independent of K_D and limited only by Poisson noise. This is in stark contrast to the conventional view that an affinity reagent can only achieve quantitative detection at concentrations with a lower limit of ~K_D/9. This implies that less effort should be spent developing high affinity binders and more on assay development. However, we also show that the upper limit of useful K_D′s for an affinity reagent is imposed by its specificity; higher concentrations of off-target molecules and stronger binding to these molecules necessitates the use of detection reagents with higher affinity for the target.

We conclude by noting that metrics such as K_D, LOD, detection range, and specificity aren’t the end of the story (see Outstanding Questions). Even with perfect molecular quantification, diagnostic assays are still limited by biological variability, which impacts clinical sensitivity and specificity [48]. Although the extent to which assay development should focus on LOD, sensitivity, specificity, or resolution will depend on the context in which the assay is to be used, the design of an optimal assay will inevitably entail achieving the right K_D, a method of background suppression, signal amplification, a digital readout, and dual recognition (or some other mechanism to ensure specificity). It is our hope that the concepts presented here will instill an appreciation of the unexplored opportunities for pushing the capabilities of our ever-increasing technological armamentarium in biomarker discover, molecular quantification, and even diagnostic medicine.

OUTSTANDING QUESTIONS.

• How does resolution come into play, and should there be a standardized definition?

• What other technologies can take advantage of this approach?

• We have approached this concept from viewpoint that is agnostic to the particular chemical implementation. Is there a universal way to approach these principles in practice?

• Is it possible to use the same high-resolution argument to quantify concentrations much higher than K_D, perhaps in the context of a “signal-off” assay?

• Assays involving digital detection typically require some sort of molecular confinement followed by amplification and counting. As single molecule technologies are advanced, will these “requirements” for digital detection still hold?

• How does improving molecular quantification improve fundamental life science research, and how can it be extended to translational fields such as clinical diagnostics?

• How will the ability to quantify molecules are ultralow concentrations change biomarker discovery? Are there any previously undetected, ultralow-concentration molecules that are diagnostically relevant?

HIGHLIGHTS.

• Binding assays utilize concentration-dependent shifts in equilibrium to achieve target quantification; binding assays, such as ELISAs, are indispensable in the diagnostic armamentarium

• Binding assays have been primarily characterized by the dissociation constant (K_D) of the affinity reagent; there are many other parameters that are important in describing the performance of an assay, such as limit of detection (LOD) and detection range

• Long held heuristics used to describe binding assays fail to describe the results of many modern detection technologies, such as digital and single molecule readouts, and we argue that these heuristics are unnecessarily restrictive.

• This Opinion article does not aim to challenge the existing conventional wisdom about molecular recognition, but rather to point out that stringent adherence to prior conventions limits what could otherwise be achieved with contemporary detection technologies.

GLOSSARY

Affinity Reagent

A molecule that binds to a specific target molecule of interest for the purpose of detection or quantification. An affinity reagent can be an antibody, peptide, nucleic acid, or small molecule

Aptamer

A specific type of affinity reagent that is made of DNA or RNA. They are produced through repeated rounds of directed evolution

Binding Assay

A method of molecular quantification that involves the binding of a one molecule to another, i.e. receptor to ligand, antibody to antigen, etc. The addition of target molecule shifts the equilibrium towards a higher fraction of target-bound molecules

Binding Curve

A response function that characterizes the amount of binding as a function of target concentration

Detection Range

The range of concentrations over which the assay output signal has a large derivative with respect to target concentration. This is conventionally considered to be the concentrations over which the binding curve corresponds to between 10% to 90% of that total signal. e.g. for K_D = 1uM, the conventional detection range is 111 pM to 9 nM

Dynamic Range

The ratio between the highest and lowest concentrations in the detection range. This is conventionally considered to be 81 regardless of K_D

Dissociation Constant (K_D)

An equilibrium constant that characterizes the strength of binding between two molecules. It has units of concentration and is inversely proportional to binding affinity

Immunoassay

A method of molecular quantification that utilizes antibody-antigen interactions to achieve detection

Limit of Detection (LOD)

The lowest concentration that is statistically discernable from background signal

Sensitivity

In this context, sensitivity refers to the ability of an assay to distinguish between small changes in concentration

Specificity

In this context, specificity refers to the ability of an assay to discriminate between non-cognate and cognate molecules