Multimode ultrasound viscoelastography for three-dimensional interrogation of microscale mechanical properties in heterogeneous biomaterials

Abstract

Both static and time-dependent mechanical factors can have a profound impact on cell and tissue function, but it is challenging to measure the mechanical properties of soft materials at the scale which cells sense. Multimode ultrasound viscoelastography (MUVE) uses focused ultrasound pulses to both generate and image deformations within soft hydrogels non-invasively, at sub-millimeter resolution, and in 3D. The deformation and strain over time data are used to extract quantitative parameters that describe both the elastic and viscoelastic properties of the material. MUVE was used in creep mode to characterize the viscoelastic properties of 3D agarose, collagen, and fibrin hydrogels. Quantitative comparisons were made by extracting characteristic viscoelastic parameters using Burger’s lumped parameter constitutive model. Spatial resolution of the MUVE technique was found to be approximately 200 μm, while detection sensitivity, defined as the capability to differentiate between materials based on mechanical property differences, was approximately 0.2 kPa using agarose hydrogels. MUVE was superior to nanoindentation and shear rheometry in generating consistent microscale measurements of viscoelastic behavior in soft materials. These results demonstrate that MUVE is a rapid, quantitative, and accurate method to measure the viscoelastic mechanical properties of soft 3D hydrogels at the microscale, and is a promising technique to study the development of native and engineered tissues over time.

1. Introduction

The importance of mechanical factors in regulating cell and tissue function is clear. However, the ability to meaningfully leverage the principles of mechanobiology requires more and better information about the structure and function of the cellular microenvironment. Cells sense and respond to their mechanical environment through receptors and signaling pathways that coordinate such functions as differentiation, proliferation, migration, and matrix remodeling [1]. Mechanical behavior must therefore be considered when developing biomaterials to guide cell function, either as platforms to study cellular processes or as components of restorative therapies. Importantly, the fields of cell-matrix interactions and cellular mechanobiology have evolved over the past decade [2–4], from a focus on the passive mechanical properties of the extracellular environment to a growing realization that the dynamic and complex nature of extracellular mechanics must be considered. In particular, recent work has demonstrated that nonlinear elastic [5–7] and viscoelastic [8–10] behaviors of the extracellular matrix affect cells in ways that transcend the simple elastic response.

While the impact of both passive and dynamic mechanical signals on cell behavior is undisputed, our understanding of mechanobiology is hampered by a lack of information about the local physical properties of the cellular microenvironment on length scales that cells sense [11,12]. Native tissues are composed of cells surrounded by a network of fibrillar glycoproteins and hydrated proteoglycans. This composite structure gives rise to scale-dependent heterogeneity as well as complex mechanical properties and behaviors. A variety of biomaterial systems have been developed to mimic key aspects of the structure of native extracellular matrix, including hydrogels composed of natural proteins [13–15], polysaccharide matrices [16] and synthetic polymers [17]. Such materials are used widely in studying cellular mechanobiology. However, the mechanical properties of heterogeneous materials can depend on the resolution at which they are examined, such that microscale structure-function relationships can be distinct from the macroscale mechanical properties. In addition, the high water content and combination of solid and fluid elements in these materials results in time-dependent and viscoelastic behavior.

A variety of methods have been applied to measure mechanical properties of native tissues and hydrogel biomaterials. However, microscale testing of soft materials with high water content can be challenging. Most studies have used conventional, macroscale techniques such as tensile [18,19] and compressive testing [20,21], or shear rheology [22–24], which cannot discriminate microscale heterogeneity in materials, nor can they provide insight into interior architectures. A much smaller number of studies have probed microscale properties. For example, atomic force microscopy and nanoindentation have been applied to mature bone but only sparingly to tissues and hydrogel materials [25–27]. However, these techniques suffer from high variability and provide only two-dimensional (2D) surface maps of material properties. Optical trapping of particles embedded in hydrogel matrices has been used for oscillatory dynamic mechanical analysis [28], but provides deformations only on the nanoscale and is only feasible for small, thin samples. Notably, all of these techniques require physical contact or manipulation of the samples, which hinders longitudinal assessment of developing tissues. Non-invasive methods like magnetic resonance elastography (MRE) have been developed for quantification of viscoelastic properties by measuring shear wave propagation, which is often initiated by external excitation or tissue palpation. MRE has been applied for 3D mapping of viscoelasticity in organs including breast, brain and liver [29,30].

Here we demonstrate a novel ultrasound-based approach that can noninvasively characterize the complex microscale mechanical properties of heterogeneous, three-dimensional (3D), soft biomaterials over time. Our approach capitalizes on the ability of ultrasound waves to penetrate and interact with components in a material at depth and without contact. Besides imaging material morphology and structure (recently reviewed in Refs. [31,32]), conventional ultrasound elastography uses either direct physical compression or remote deformation using acoustic radiation force for visualization of relative tissue stiffness (e.g. to identify tumors) [33–38]. A few studies have reported the use of acoustic radiation force to assess relative elastic and viscoelastic properties of a sample [39–42], but have been limited to measuring only bulk properties of samples suspended in solution.

Our technique, called multimode ultrasound viscoelastography (MUVE), uses interleaved ultrasound pulses at two distinct center frequencies to both deform and image soft hydrogel samples at microscale resolution. Focused ultrasound pulses at low frequency (e.g. 1–3 MHz) are used to noninvasively apply a controlled body force (e.g. acoustic radiation force) to selected regions within the sample. Concurrent ultrasound imaging at high frequency (e.g. 10–50 MHz) allows measurement of time-dependent sample deformation or strain at any desired location within the sample, as well as creation of 3D spatial maps of the interior features of the sample. The strains in the sample over time and location are then used to generate a set of quantitative parameters that describe both the elastic and viscoelastic properties of the material. Here we report on the application of MUVE to characterizing both the bulk and local mechanical properties of commonly used hydrogel biomaterials, and demonstrate the ability to discriminate between phases in multiphase materials. We characterize the spatial resolution and detectivity of the technique, and compare MUVE to other commonly-used mechanical measurement methods. This work highlights the distinct ability of MUVE to noninvasively probe the local mechanical properties of soft biomaterials at depth using induced deformations at the cellular scale.

2. Materials and methods

2.1. Synthesis of HA-Agarose microbeads

Agarose solution (50.0 mg/ml) was prepared by dissolving agarose powder (Sigma Aldrich, St. Louis, MO) in deionized water. Nano-grade hydroxyapatite (HA) solution was prepared at 200 mg/ml in Dulbecco’s modified Eagle’s medium-low glucose (DMEM; Life Technologies, Grand Island, NY) and sonicated for an hour before use. HA-agarose beads were fabricated by an oil-in-water emulsion method. 1 ml mixture of 80% agarose solution, 5% HA solution, and 15% deionized water was injected into 75 ml polydimethylsiloxane (PDMS; PMX-200,100cS; Xiameter) under constant stirring using an impeller. Emulsification was carried out at 37 °C for 5 min and then on ice for 30 min. To obtain HA-agarose beads of 10–1000 μm diameters, the stirring speed was set to 400 and 500 rpm. HA-agarose beads in PDMS were collected through centrifugation and washing with phosphate buffered saline.

2.2. Fabrication of hydrogel constructs

To illustrate MUVE’s capability of delineating multi-phase multimaterial constructs, 40.0 mg/ml HA-agarose beads were embedded in 5.0 mg/ml HA-doped agarose, 2.0 mg/ml HA-doped collagen, and 2.0 mg/ml HA-doped fibrin hydrogels. To determine the size resolution, 40.0 mg/ml HA-agarose beads with various diameters were embedded in 5.0 mg/ml HA-doped agarose gel (Fig S1). HA-doped agarose gel of 5.0, 10.0, 20.0, 30.0 and 40.0 mg/ml containing 40.0 mg/ml HA-agarose beads were tested to determine the detectable contrast in hydrogel composition. For comparing MUVE, nanoindenter, and shear rheometer, HA-doped agarose hydrogels (5.0,10.0, 20.0, 30.0, and 40.0 mg/ml) and HA-doped fibrin hydrogels (2.0, 6.0 and 10.0 mg/ml) were tested. All hydrogel constructs contained 10.0 mg/ml nano-grade HA.

HA-doped agarose hydrogels were prepared as discussed previously [43]. Briefly, 50.0 mg/ml agarose stock solution was mixed with deionized water and 5% 200 mg/ml HA stock solution to obtain selected final agarose concentration. 250 μl of the mixture was injected into a custom mold. HA-agarose beads were transferred into the mixture, and the mixture was allowed to gel at 4 °C for 30 min. Agarose hydrogel constructs were 9 mm in diameter and 3–4 mm in height.

HA-doped fibrin and collagen hydrogels were fabricated as discussed previously [44]. HA-doped collagen hydrogels were synthesized by mixing 50% 4.0 mg/ml collagen Type I (MP Biomedicals, Solon, OH) in 0.02 N acetic acid, 20% 5X-concentrated Dulbecco’s modified Eagles’ medium (5X-DMEM; Invitrogen, Carlsbad, CA), 10% fetal bovine serum (FBS; Invitrogen), 5% DMEM, and 5% 200 mg/ml HA stock solution, and 10% 0.1 N NaOH (Sigma Aldrich). HA-doped fibrin hydrogels were generated by mixing 83% fibrinogen stock solution (4.0,12.0, and 20.0 mg/ml), 10% FBS, 2% 50 UT thrombin (Sigma Aldrich) and 5% HA stock solution. 250 μl of the HA-collagen or HA-fibrin mixture were injected into a 48 well plate, and HA-agarose beads were transferred into the mixture to make multi-phase constructs. The mixture was incubated at 37 °C for 30 min for gelation. HA-collagen and HA-fibrin constructs were 10 mm in diameter and 2–3 mm in thickness.

2.3. Multimode ultrasound viscoelastography

2.3.1. Experimental setup, data acquisition, and analysis

As described previously [43], the MUVE setup consisted of a 2 MHz FUS transducer (H148; Sonic Concepts, Woodinville, WA; 62.5 mm focal distance, −6 dB focal length of 8.0 mm, −6 dB beam width of 1.5 mm) collinearly aligned with a 10 MHz imaging transducer (Olympus, Waltham, MA; focal distance at 55 mm, −6 dB beam width of 1 mm). The FUS transducer was driven by a waveform generator (33220A; Agilent, Santa Clara, CA) and a power amplifier (75A250; Amplifier Research, Souderton, PA) to deliver a series of pulses (1 Hz PRF with 99% duty cycle and 0.7 MPa acoustic pressure) for an 180 s total duration. The imaging transducer was driven by a pulser/receiver (5900 PR; Olympus) to send and acquire signals at 1 Hz or 50 Hz PRF. The imaging pulses were initiated 20 s before the FUS pulses and terminated 150 s after the FUS pulses. Synchronization of the FUS and imaging pulses was achieved using a pulse/delay generator (Model 565; BNC, San Rafael, CA). Back-scattered signals acquired by the imaging transducer were recorded at 250 MSamples/s and stored on an oscilloscope (54380B, Agilent, Santa Clara, CA) for offline analysis. The ultrasound set-up used in this study allowed measurement of deformation to an approximate depth of 8 mm, which is determined by the axial focal length of the pushing transducer. The penetration depth depends on the acoustic attenuation of the sample and the center frequency of the ultrasound transducer. With higher attenuation and higher probe center frequency, the acoustic stress diminishes.

Hydrogel constructs were first imaged using a high-resolution VEVO 770 imaging system (VisualSonics Inc. Toronto, Canada) to obtain grayscale B-mode and 3D images, as well as raw back-scattered data for attenuation measurements (Table S1) [45]. Then samples were placed in a custom holder with agar gel padding for mechanical testing with MUVE. A time series of RF signals were acquired and Hilbert transform was applied to generate M-mode images. Two-step cross-correlation [46] was used to compare signals to the baseline signals before compression to determine displacements within the sample. Displacement values were assigned to each pixel to create displacement color maps (Fig. S2).

2.3.2. Mechanical parameter extraction

Displacements near the surface of the construct and near the surface of the HA-agarose bead were extracted and presented as displacement-time curves to illustrate mechanical property differences between the hydrogel and bead. To account for differences in sample attenuation coefficient and resulted differences in acoustic radiation force, compliance was computed by normalizing strain with the stress induced by acoustic radiation force. The ARF acts as a body force in the construct, and the induced stress in the ARF cylinder with radius R₀ and length l₀ was computed as:

$${\sigma }_0=\frac{\underset{V}{\int }Fdv}{S_{FUS}}=\frac{{\int }_0^{R_0}{\int }_0^{l_0}F(r,z^{\prime })2\pi rdrd{z}^{\prime }}{S_{FUS}},$$ (1)

where S_FUS is the FUS bean cross sectional area and the ARF, F[N/m³], at a location with radius r and depth z was calculated under a plane wave assumption as:

$$F(r,z)=\frac{2\alpha (r,z)I^{\prime }(r,z)}{c}=\frac{2\alpha (r,z)I(r,z)e^{-2\alpha (r,z)•z}}{c},$$ (2)

where α[m⁻¹] is the absorption coefficient, c[m/s] is the speed of sound in the sample, and $I^{\prime }\left[W/m^2\right]$ is the in situ acoustic intensity approximated by the free field intensity I(r,z) multiplied by the attenuation factor. Stress calculations were based on the initial sample dimensions.

The mechanical properties were quantified by determining selected parameters: the maximum strain (max|ε(t)|), residual strain (res|ε(t)|, creep time constant (τ_c), recovery time constant (τ_R) and instantaneous elastic modulus (R₁). Maximum compliance was defined as the highest value of compliance in creep and residual compliance was defined as the steady-state compliance at the end of recovery. Creep and recovery time constants were derived by fitting the creep and recovery compliance over time with exponential functions. To avoid subjectivity, the instantaneous elastic modulus was derived by fitting the creep compliance with Burger’s four-parameter model [47] (Fig. S3):

$${\epsilon }_{creep}(t)=\frac{{\sigma }_0}{R_1}+\frac{{\sigma }_{0}t}{{\eta }_1}+\frac{{\sigma }_0}{R_2}\left[1-\exp \left(-\frac{R_2}{{\eta }_2}t\right)\right].$$ (3)

Limit of Detection (LOD) – To determine the limit of detection for spatial resolution, the diameter of the microbead was estimated as the distance between the depth where the displacement drops to 5.24 μm (mean displacement at the surface of HA-agarose bead) and the bottom of the construct. The true diameter was determined as the distance between the first positive peak corresponding to the HA-agarose bead surface and the first peak corresponding to the bottom of the bead in the RF signal. Linear regression of the estimated size against the true size was determined, and the limit of detection was defined as

$$LOD=3\frac{s}{b},$$ (4)

where s is the standard deviation of the regression and b is the slope of the regression [48].

To determine the LOD for detectivity, the difference between the displacement at the surface of the construct and at the surface of the HA-agarose bead was computed and plotted against the agarose concentration difference between the hydrogel and the bead. Linear regression was applied and LOD was computed as in Eq. (4).

2.4. Nanoindentation

Nanoindentation on HA-doped agarose hydrogels and HA-doped fibrin hydrogels was performed using Hysitron Tribolndenter (Hysitron, MN) with a flat-punch probe. A load function of 0.8 s pre-loading, 40.0 s hold time and 0.8 s unload time to mimic the step stress function applied with MUVE (Table S2). A peak force of 2.0–40 μN was applied to the constructs to generate displacement over 1 μm and under 5 μm. Compliance was computed as strain normalized by the peak stress. Maximum compliance (max|J(t)|), creep time constant (τc), and instantaneous elastic modulus (R1) were calculated as described in the previous section. Creep during the hold-time was used for obtaining R1 by fitting data to the Burger’s model to reduce the effect of the slower loading speed compared to MUVE.

2.5. Shear rheometry

The storage modulus (G′), and the loss modulus (G″) were determined using AR-G2 rheometer (TA Instruments, New Castle, DE). A 20 mm parallel plate (500 μm apart) and a Peltier stage were used for performing the shear rheometry analysis. Agarose and fibrin gels were casted in-situ by quickly injecting 250 μL of freshly prepared hydrogel mixture directly in the parallel plates. Tests were conducted (n ≥ 3) at 37 °C for a 15 min time sweep at 1% strain and angular frequency of 1 rad s⁻¹. The storage modulus and los modulus values were calculated by taking the average values of the linear portion of the curves.

2.6. Statistical analysis

Results were presented as mean ± standard deviation. Student’s two-tailed t-test for unpaired samples was performed to determine differences between groups. Analysis ofvariance (ANOVA) followed with Tukey’s Honest significant difference (Tukey’s HSD) test was performed with results involving more than two groups. Differences were considered statistically significant at p < 0.05.

3. Results and discussion

3.1. Multimode ultrasound viscoelastography (MUVE)

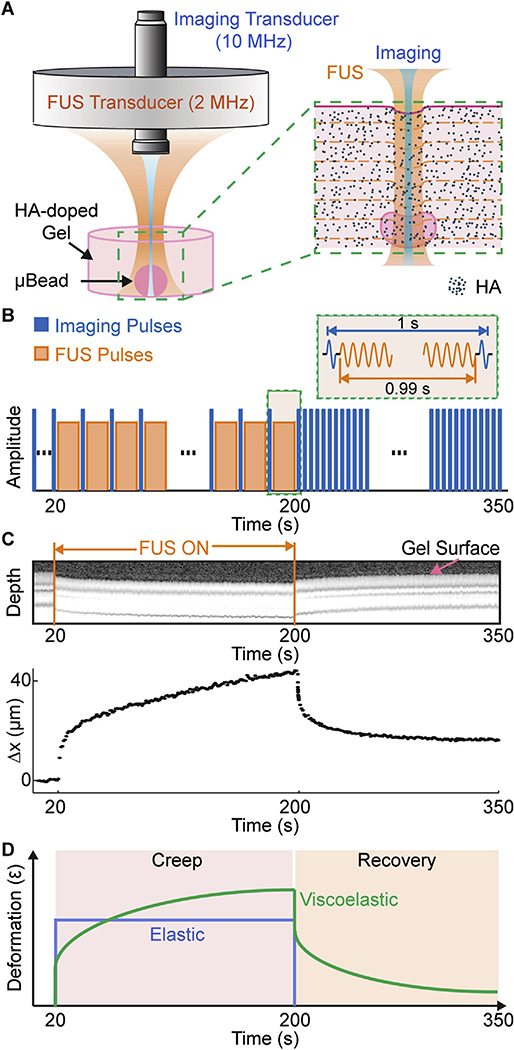
MUVE uses co-linearly aligned ultrasound pulses at separate frequencies to both deform and image soft biomaterial samples (Fig. 1A). An annular focused ultrasound (FUS) transducer (2 MHz) is used to apply “pushing” pulses to the sample. The acoustic radiation force (ARF) associated with the “pushing” pulses deforms the sample within a confined volume determined by the focused ultrasound beam profile. A high frequency imaging transducer (10 MHz) is nested in the annular space of the pushing transducer for high resolution pulse-echo imaging and detection of the ARF-induced deformation in the sample over time. Since the ARF is a body force and is applied locally, it acts throughout the volume of the applied ultrasound beam and is weakly influenced by the boundaries.

Fig. 1.

A) Schematic diagram of transducer set-up and expanded view of sample in MUVE. B) Schematic trace of the protocol for interleaving pushing (FUS) and imaging pulses during MUVE for creep testing. C) M-mode (Motion-mode) grayscale image and corresponding peak displacement versus time curve of agarose hydrogel sample showing deformation during application of FUS. D) Schematic of deformation versus time traces for elastic and viscoelastic materials during creep testing.

We implemented MUVE for testing in creep mode, in which a constant force is applied to the sample and deformation is monitored over time, using interleaved pushing and imaging pulses (Fig. 1B). Ultrasound M-mode imaging was applied before, during, and after sample deformation. FUS was applied to deform the sample for a period of 180 s to simulate a creep test. To maintain an essentially constant force, the pulse repetition frequency (PRF) was set to 1 Hz at a duty cycle of 99.99%, leaving a short “off” interval of 10 ms for pulse-echo imaging at 1 s intervals to detect sample deformation At the end of the pushing phase, imaging was continued for a further 150 s to monitor recovery in the sample after removal of the force. The ultrasound imaging data generated in this way clearly showed sample dimensions and the deformation in the materials over the duration of the creep test (M-mode images, Fig. 1C). The characteristic deformation over time curve of a sample provides insight into the viscoelastic behavior of the material (Fig. 1D). Purely elastic materials (blue curve) deform instantaneously to a degree determined by their stiffness, and maintain a constant deformation until the load is removed, at which point they recoil fully to their original dimensions. In contrast, viscoelastic materials (green curve) continue to deform over time under a constant load (this behavior is termed “creep”), and also exhibit time-dependent and incomplete recovery when the load is removed. Viscoelastic behavior in hydrogels and tissues is caused by rearrangement of fluid and solid components in the material structure over time.

3.2. Material properties of multiphase biomaterials

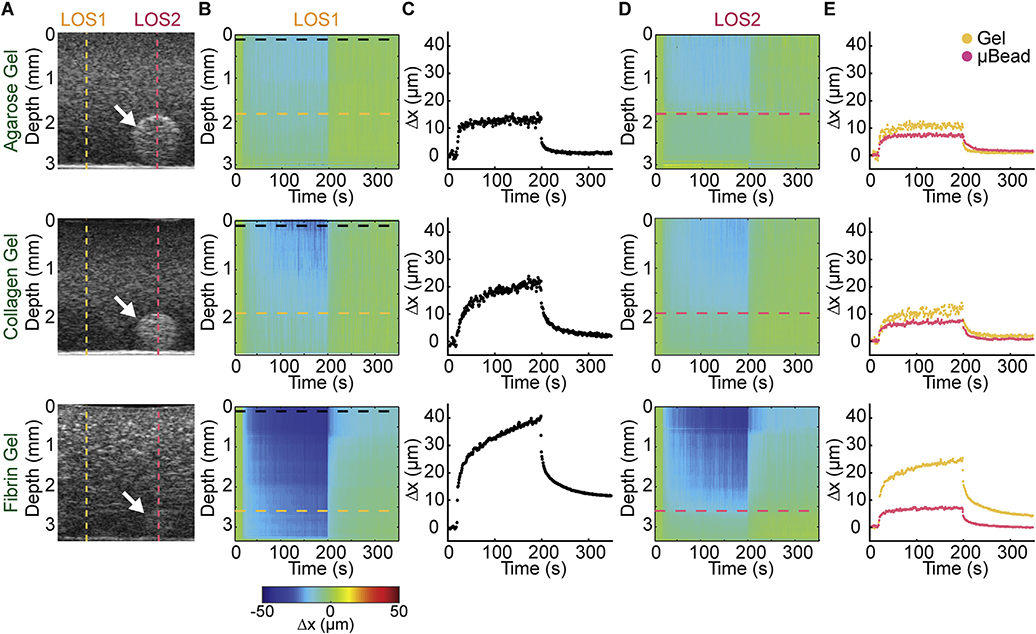
An advantage of MUVE is that it can be used to spatially characterize multiphase biomaterials. To demonstrate this ability, we prepared constructs consisting of commonly-used hydrogel biomaterials (agarose, collagen, and fibrin) doped with hydroxyapatite (HA) to enhance scattering of the ultrasound signals. These constructs also had embedded within them a high concentration agarose microbead, which was included in the constructs at the time of gel formation, serving as an inclusion with properties distinct from the surrounding hydrogel. Grayscale B-mode ultrasound imaging in 2D (Fig. 2A) and 3D (Fig. S1) showed diffuse distribution of the HA throughout the constructs. In each of the three different matrices, the denser agarose microbead (white arrows) can be visualized. MUVE characterization was performed in these constructs at a line of sight (LOS) adjacent to the microbead (LOS1, dashed yellow line), as well as at a line of sight that included the microbead (LOS2, dashed red line). Heat maps that represent deformation as a function of depth and time (2B) and the corresponding displacement-time curves at the surface of the construct (Fig. 2C) at LOS1 (adjacent to the microbead) revealed the properties of the bulk matrix. The applied creep test produced deformation in each of the materials over the 180 s pushing phase, followed by relaxation of the matrix when the pushing force was removed. Force-induced displacement in the matrix showed characteristic behavior of each of the hydrogel materials. Agarose exhibited essentially elastic behavior, with instantaneous deformation of about 10 μm, little creep over time, and recovery to close to the initial dimensions. In contrast, the fibrillar collagen and fibrin hydrogels exhibited a marked creep response, as characterized by increasing deformation over time after application of the constant acoustic force. Collagen and fibrin both showed a relatively rapid recovery response, and collagen recovered to close to its prestrained dimensions, while fibrin did not.

Fig. 2.

A) Grayscale images of HA-doped agarose, collagen and fibrin hydrogels containing HA-doped agarose bead (white arrow). Dashed lines indicate a line of sight (LOS) through a location in the sample without (yellow line) and with (red line) the microbead. B) Displacement color maps corresponding to LOS without microbead (LOS1). C) Peak displacement profile of the sample at the surface of the construct in LOS 1 (without microbead). D) Displacement color map corresponding to a location with the microbead (LOS2). E) Peak displacement profiles at the depth of the microbead surface of the LOS without (yellow trace, LOS1) and with (red trace, LOS2) the microbead. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Deformation heat maps generated at LOS2 (including the microbead) (Fig. 2D) showed decreased deformation at the location of the microbead, due to its high concentration and therefore relatively stiffer matrix compared to the surrounding matrix. This demonstrates MUVE’s capability to detect heterogeneity in mechanical properties in the depth direction (in the same LOS). In each case, the microbead can be distinguished from the surrounding matrix material by examining its response to the pushing pulse and the resulting displacement-over-time curve (Fig. 2E, in which both the yellow and red traces were taken at the depth of the microbead). In the agarose hydrogel, both the microbead and the surrounding gel exhibited little creep-characteristic behavior, but the stiffer 40 mg/mL microbead deformed less than the surrounding 5 mg/mL gel. In the collagen and fibrin materials, the agarose microbead can again easily be identified from the surrounding gel, both through its lower degree of deformation and by its distinctly more elastic behavior, as demonstrated by the shape of the displacement over time curve. It is important to note that even when the microbead is indistinguishable from the surrounding matrix in grey-scale B-mode imaging (eg. Fibrin matrix in Fig. 2A), MUVE was able to detect it based on its distinct mechanical properties (Fig. 2E).

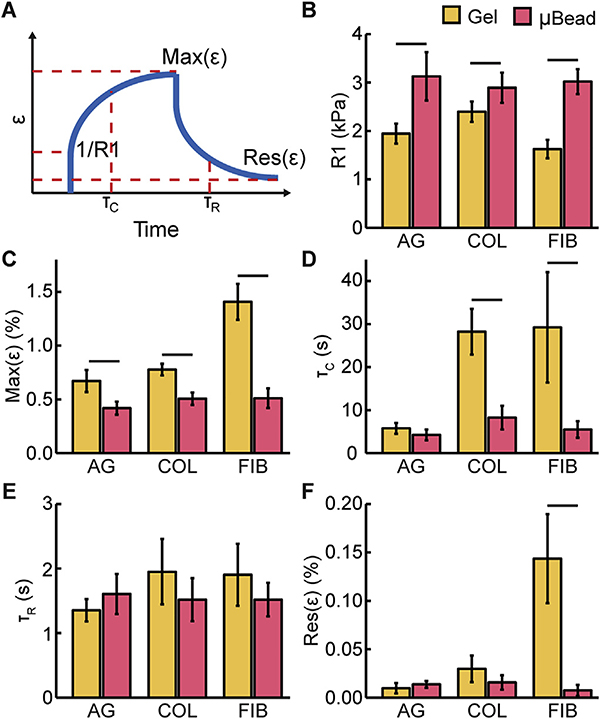
We obtained strain-time curves from the deformation over time data to allow extraction of a set of objective parameters that quantitatively describe viscoelastic material behavior (shown schematically in Fig. 3A and Fig. S3). The panels in Fig. 3B–F shows these extracted parameters from a series of experiments similar to those presented in Fig. 2, in which we compared responses at the depth of the bead surface across different LOS with and without the microbead. An instantaneous elastic modulus (R1, Fig. 3B) can be derived by fitting Burger’s Viscoelastic Model [47]. This parameter represents the initial elastic response of the material, which is reflective of the elastic modulus. MUVE showed that fibrin was the least stiff, and that the agarose and collagen materials had similar stiffness at the concentrations used. As would be expected, these quantitative results also show that the embedded high concentration agarose microbead was stiffer than the surrounding matrix and its properties were independent of the surrounding material. The maximum strain (Max(ε), Fig. 3C) is a measure of the degree of creep after instantaneous deformation and reflects time-dependent behavior of the materials. Fibrin exhibited a significantly greater creep response than the agarose and collagen gels. These data also show that creep over time of the embedded microbead was significantly less than the surrounding gels, and was again essentially invariant across the embedding matrices.

Fig. 3.

A) Schematic showing parameters used to characterize material properties. Parameters derived from creep tests on agarose, collagen, and fibrin hydrogels performed at LOS without (yellow bars) and with (red bars) the microbead at the depth of microbead surface: B) instantaneous elastic modulus (R1), C) maximum strain (Max(ε)), D) creep time constant (τ_C), E) recovery time constant (τ_R), F) residual strain (Res(ε)). Lines above bars indicated p < 0.05 with student’s two-tailed t-test, n = 4. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Curve fitting of the strain-versus-time plots was used to extract time constants for the rate of transition to the creep and recovery phases of the mechanical tests. The larger creep time constant (τ_C, Fig. 3D) for collagen and fibrin corresponded to a more gradual transition to the extended state, relative to the agarose bulk gel and microbead, indicating more viscous influence on material behavior. Interestingly, the recovery time constant (τ_R, Fig. 3E) was similar across materials, and was relatively rapid compared to the creep response. However, the residual strain (Res(ε), Fig. 3F) showed that both agarose and collagen underwent essentially complete recovery to their original dimensions, whereas fibrin exhibited plastic (non-recovered) deformation.

Taken together, these data demonstrate how MUVE can be used to spatially quantify both bulk and regional properties in soft hydrogel matrices in 3D. The displacements produced in these experiments were in the range of 5–50 μm, which is at the scale that cells sense through cell-surface receptors and the cytoskeleton [49]. Importantly, the technique can probe regions inside materials and characterize spatial variation in material properties both in the depth direction and across multiple locations, as demonstrated by the ability to identify and measure the properties of microbeads embedded in surrounding matrices. Complete 3D mapping of the viscoelastic properties for the entire construct would require more sampling locations, which leads to longer data acquisition time. The time cost can be reduced by using more advanced systems featuring array transducers and parallel testing. For more precise computation of the dynamic stress field and mechanical properties in heterogeneous constructs, established 3D inverse finite element analysis can also be applied to account for heterogeneity [50,51]. Finally, all of this testing can be performed under physiological conditions (temperature, pH) and both the deformation and imaging of the sample is entirely noninvasive, allowing longitudinal nondestructive imaging of samples over time, which has been shown in our previous work on cellular constructs [43].

3.3. Spatial resolution and detection sensitivity

The ability to discriminate between materials or between regions within a material based on their mechanical properties is important in characterizing heterogeneity and structure in multiphase materials. The spatial resolution of MUVE depends primarily on the resolution of the pulse-echo ultrasound imaging system being used to acquire signals. The lateral resolution is determined by the lateral beam width, and is about 450 μm for the 10 MHz system used in this study. The axial resolution can be estimated based on the axial resolution of ultrasound elastography [52]. In this study, the axial resolution was estimated to be about 225 μm.

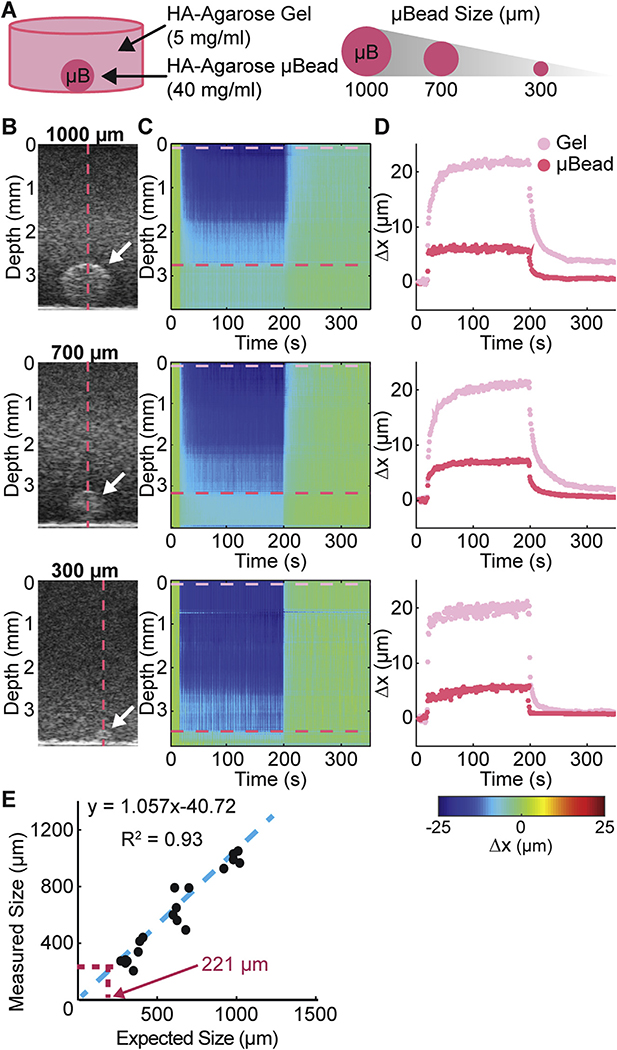
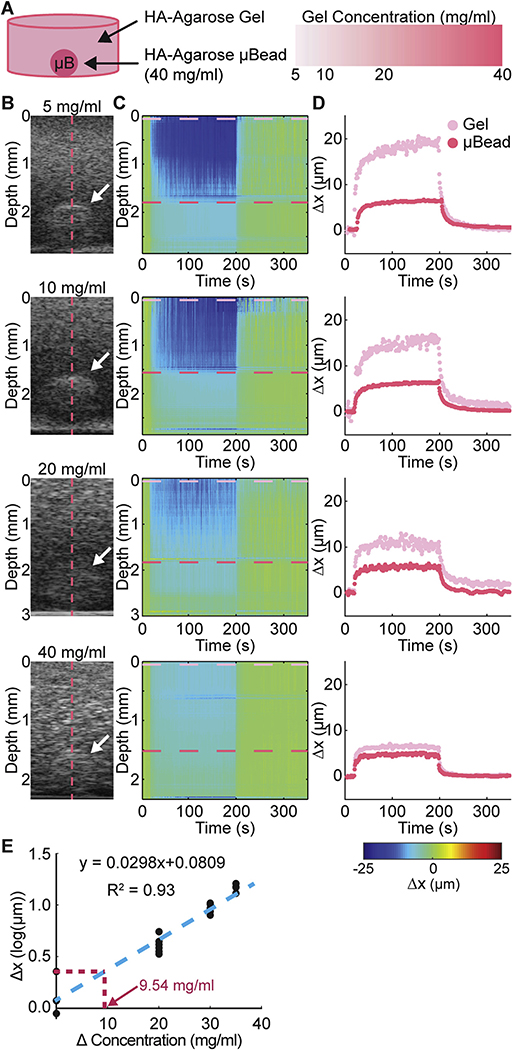
To experimentally validate the axial resolution of our system, we used a two-phase hydrogel construct to determine the spatial resolution at which MUVE can differentiate between high concentration agarose microbeads of specified sizes (from 300 to 1000 mm in diameter) embedded in a surrounding low concentration agarose gel (Fig. 4A). The high concentration agarose microbeads could be detected using B-mode imaging (white arrows in Fig. 4B), though as the size decreased, it became difficult to discriminate the microbead from the surrounding matrix. Importantly, heat maps of sample deformation during the application of MUVE (Fig. 4C) revealed the location of the microbead, as evidenced by smaller deformation of the more concentrated microbead matrix. In addition, deformation over time traces (Fig. 4D) clearly revealed the distinct behavior of the high concentration agarose microbead (red trace) and the surrounding agarose gel (magenta trace). As expected, both materials exhibited the characteristic pseudo-elastic behavior of agarose. However, the degree of deformation in the stiffer microbead was significantly smaller than the surrounding hydrogel. A plot of microbead diameter as measured by MUVE versus the nominal microbead diameter (Fig. 4E) showed strong agreement (R = 0.93). The limit of MUVE’s spatial resolution was estimated using the standard deviation and linear regression of this curve [48], and indicated that the current MUVE system can discriminate objects on a size scale of approximately 221 μm, close to the theoretical value of 225 μm.

Fig. 4.

A) Schematic of sample configuration showing high concentration agarose microbead embedded within a surrounding hydrogel. Microbead size was varied to determíne the spatial resolution of MUVE. B) Grayscale image of sample and microbead (white arrow). C) Color map of deformation through depth of the sample over time. D) Peak displacement profile of the surrounding hydrogel (pink trace) and the embedded microbead (red trace). E) Plot of measured size of microbead versus actual size, showing theoretical size resolution of MUVE. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Detection sensitivity refers to the capability of MUVE to differentiate between materials based on compositional or mechanical property differences. It depends on the minimal detectable difference in displacements due to local spatial variation of material properties, and is also influenced by the signal-to-noise ratio (SNR) of the system. At a given SNR, the displacement of a material depends on its mechanical properties and the applied force. Since the deforming ARF is constant in our system, any differences in displacements are caused by variations in the mechanical properties of the sample. Therefore, the detection sensitivity can be derived based on the minimal detectable displacement difference.

We assessed the detection sensitivity of MUVE experimentally using agarose constructs of varying concentration (from 5 to 40 mg/mL), that contained an embedded high concentration agarose microbead (40 mg/mL, 1000 μm diameter, Fig. 5A). As the difference in matrix concentration between the microbead and the surrounding matrix decreased from 35 mg/mL to 0 mg/mL, the contrast in grayscale (B-mode) images decreased as expected (Fig. 5B), since the acoustic impedance mismatch between the materials diminishes as the concentrations become more similar. Deformation of the sample during MUVE application as shown in heat maps (Fig. 5B) revealed a similar trend. Similarly, deformation over time traces (Fig. 5C) showed a narrowing of the distance between the trace for the microbead (red trace) and the trace for the surrounding gel (magenta trace) as the difference in matrix concentration between the two phases became smaller. The displacement traces exhibited the characteristic shape for agarose, with a relatively rapid initial deformation and recovery response, and a low degree of creep. Linear regression of the difference in peak displacement versus the difference in agarose concentration between the microbead and surrounding gel (Fig. 5D) showed a strong positive correlation (R = 0.93). Linear regression was used to estimate that the minimum concentration difference that MUVE can detect in this system is about 10 mg/mL, which corresponds to approximately 0.2 kPa for agarose. In this case, matrix deformation caused directly by MUVE was converted into mechanical properties data, which in turn is reflective of sample composition.

Fig. 5.

A) Schematic of sample configuration showing high concentration agarose microbead embedded within a surrounding hydrogel. Microbead concentration was varied to determine the detectivity of MUVE. B) Grayscale image of sample and microbead (white arrow). C) Color map of deformation through depth of the sample over time. D) Peak displacement profile of the surrounding hydrogel (pink trace) and the embedded microbead (red trace). E) Plot of measured deformation difference versus actual concentration, showing theoretical detectivity of MUVE. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

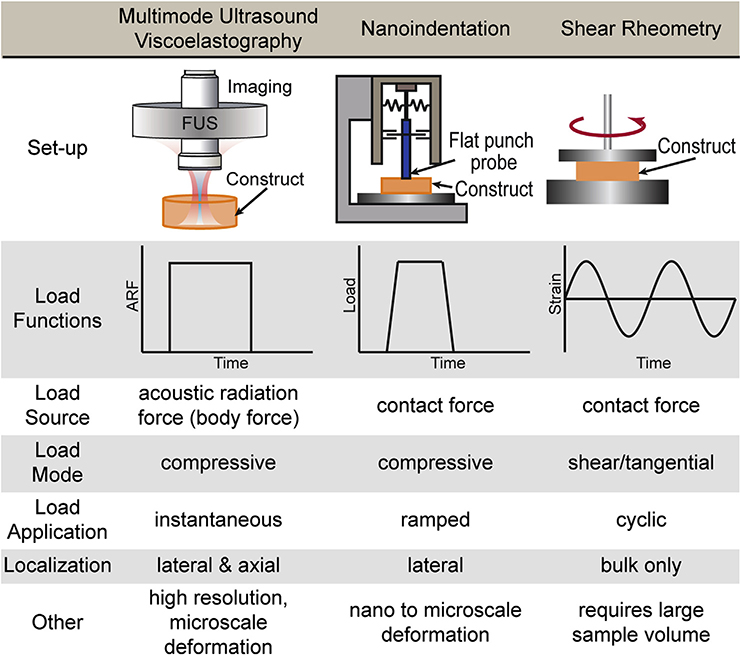
3.4. Comparison of MUVE with other techniques

We directly compared MUVE with two other techniques commonly used to characterize biomaterials: nanoindentation and shear rheometry (Fig. 6). Each of these methods differs in how the load function is applied and generates a distinct set of parameters. Nanoindentation is typically used only to determine a compressive material modulus under small strains generated by compression at the sample surface. Often a reduced elastic modulus is reported [53], which takes into account system parameters, but is difficult to reconcile with very soft samples such as hydrogels. On some instruments, this technique can also be used to run creep tests at microscale deformations. However, the application of load is necessarily gradual and only 2D surface maps of material properties can be generated [54]. Shear rheometry applies tangential force, typically in torsion, and measures only bulk properties [22]. The storage and loss moduli it obtains reflect the elastic and viscous components of material behavior, respectively. Nanoindentation and related compressive techniques, as well as shear rheometry, require contact with the sample and are therefore difficult to use for longitudinal studies of a specific sample.

Fig. 6.

Table comparing key features of MUVE, nanoindentation, shear rheometry as methods for characterizing the mechanical properties of soft biomaterials.

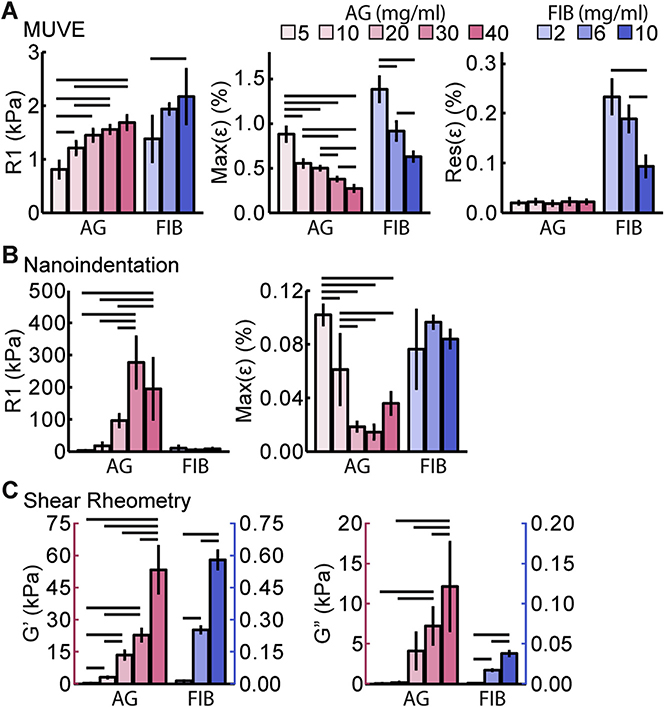
Direct comparison of MUVE, nanoindentation, and shear rheometry was performed through mechanical characterization of agarose and fibrin hydrogels over a range of concentrations. Results using MUVE (Fig. 7A, strain-time curves shown in Fig. S4A, C and E) show clear concentration-dependent increases in the stiffness parameter (R1) in both materials. The maximum strain value (Max(ε)), a measure of the degree of creep response, decreased in a concentration-dependent manner in both materials, suggesting that at higher matrix concentrations both agarose and fibrin behaved more like elastic materials. The residual strain (Res (ε))was very low in agarose and was constant across concentrations, reflecting more elastic behavior. Fibrin exhibited a markedly higher residual strain than agarose, which decreased with increasing concentration, again suggesting that a higher concentration leads to a more elastic matrix.

Fig. 7.

Mechanical property parameters of agarose (AG, pink bars) and fibrin (FIB, blue bars). hydrogels at a range of concentrations: A) instantaneous elastic modulus (R1), maximum strain (Max(ε)), and residual strain (Res(ε)) as determined by MUVE (n = 4), B) instantaneous elastic modulus (R1) and maximum strain (Max(ε)) as determined by nanoindentation (n ≥ 3), C) storage (G′) and loss (G″) modulus as determined by shear rheometry (n 2≥ 3). Lines above bars indicate p < 0.05 with ANOVA followed by Tukey’s HSD test. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Analogous creep tests using nanoindentation (Fig. 7B, strain-time curves shown in Fig. S4B, D and F) resulted in a less clear relationship between concentration and the stiffness parameter (R1) in agarose gels, and the method had insufficient sensitivity to distinguish between the fibrin concentrations tested. The maximum strain (Max(ε)) values measured by nanoindentation dropped sharply with increasing agarose concentration, but again this method could not distinguish between fibrin concentrations based on this parameter. Because nanoindentation requires sample contact with the probe, it cannot be used to measure residual strain. The variability and relatively low sensitivity of nanoindentation compared to MUVE when probing soft materials can be attributed to several factors. Because it is a contact-dependent method, adhesion between the probe tip and the sample surface can make it difficult to determine the zero strain position, leading to inaccuracy [55,56]. This is a particular problem with fibrin materials because of their adhesive nature and high compliance. The rate of strain application is another main difference between creep testing using nanoindentation and MUVE. The full range of deformation of most nanoindentation techniques is small (approx. 5 μm), and often a level of pre-loading is required to determine the zero position. These limitations in working range necessitate a lower stress ramping rate, shorter creep duration and a lower maximum load for softer materials. These conditions are not ideal for satisfying the assumptions associated with the constitutive models for creep tests [57] and limit the sensitivity of the method. In contrast, MUVE applies an essentially instantaneous stress on the sample and can measure both the zero strain position and subsequent strains noninvasively.

Measurement of macroscopic material properties using shear rheometry (Fig. 7C) revealed clear positive relationships between concentration and both storage (G′) and loss (G″) moduli in both materials. These trends reflect that both material stiffness and viscous dissipation increase with concentration in hydrogel matrices. Hydrogels are biphasic materials consisting of a solid network structure intermixed with a fluid component, and these two phases respond differently to shear and compression. The solid network tends to be more resistant in shear and tension than in compression, particularly when the network consists of fibrillar structures as in fibrin hydrogels. Under shear load, the solid network extends and supports most of the load, allowing the network and the fluid to move together with limited interstitial flow. Under compression, the network is buckled and the load is transferred to the fluid phase. This induces relative motion between the network and the solution, which causes interphase drag that is reflected in the time-dependent mechanical properties of the material [23]. These differences in microstructural deformation under shear and compression have been shown to affect overall macroscopic mechanical properties, such that very different properties data may be obtained depending on the testing mode [23]. In general, more compliant hydrogel materials are affected more strongly by the mode of mechanical testing [58].

3.5. Summary and conclusions

These studies show that MUVE can be used to investigate and quantify mechanical behaviors and properties that are characteristic of soft biomaterials. The method can measure mechanical properties, as well as distinguish between materials based on their mechanical behavior. MUVE can provide quantitative data directly from stress-strain relationships, and more complex analysis is possible by fitting appropriate constitutive models and examining the relative contributions of elastic and viscous components and applying finite element analysis with a 3D inverse problem approach. Importantly, the magnitude of the applied deformations is on a scale relevant to cells and their contacts with the extracellular matrix.

A key feature of MUVE is that the acoustic radiation force it generates is a body force acting on all scattering elements within the beam path. This allows MUVE to spatially interrogate the interior of 3D materials and map regional heterogeneity at the microscale. The application of ultrasound pulses is also essentially instantaneous, providing a more ideal creep test that better reflects material properties. Importantly, both the imaging and deforming pulses are applied noninvasively and maintain physiological conditions, such that MUVE is particularly useful for materials containing living cells and nondestructive longitudinal studies. We have previously used spectral ultrasound imaging to longitudinally monitor the composition of biomaterials and engineered tissue constructs [45,59]. In addition, the acoustic radiation force used to create compression during MUVE could also be used to apply defined forces to cells within hydrogel constructs, as a means of mechanically inducing desired phenotype changes. Therefore, by combining separate imaging and pushing transducers, it is potentially possible to apply controlled mechanical stimulation to a sample, while also monitoring the composition and mechanical properties and their spatial distribution. Taken together, these capabilities of advanced ultrasound systems offer a host of possibilities for soft biomaterials characterization and the development of novel mechanobiology-based approaches.