A Well-Mixed E. coli Genome: Widespread Contacts Revealed by Tracking Mu Transposition

SUMMARY

The three-dimensional structures of chromosomes are increasingly being recognized as playing a major role in cellular regulatory states. The efficiency and promiscuity of phage Mu transposition was exploited to directly measure in vivo interactions between genomic loci in E. coli. Two global organizing principles have emerged: First, the chromosome is well-mixed and uncompartmentalized, with transpositions occurring freely between all measured loci; second, several gene families/regions show ‘clustering’: strong three-dimensional co-localization regardless of linear genomic distance. The activities of the SMC/condensin protein MukB and nucleoid-compacting protein subunit HU-α are essential for the well-mixed state; HU-α is also needed for clustering of 6/7 ribosomal RNA-encoding loci. The data are explained by a model in which the chromosomal structure is driven by dynamic competition between DNA replication and chromosomal relaxation, providing a foundation for determining how region-specific properties contribute to both chromosomal structure and gene regulation.

eTOC blurb

Using phage Mu transposition to measure the chromosomal conformation in live E. coli under physiological conditions reveals a well-mixed E. coli genome with no hard regional boundaries, but with some specific robust contacts among co-regulated gene groups.

INTRODUCTION

The problem of compacting genomes while still performing cellular processes is common to all life forms, but the functional interplay between chromosomal structure and function remains an area of intense research. Bacterial chromosomes range anywhere from 0.5 to 8 Mb in length and are compacted nearly 1000-fold to fit within the nucleoid (Postow et al., 2004, Travers and Muskhelishvili, 2005, Wang and Rudner, 2014). Genomic compaction is thought to occur through the combined activity of nucleoid-associated proteins (NAPs) and condensation through molecular crowding (Hadizadeh Yazdi et al., 2012, Pelletier et al., 2012, Youngren et al., 2014). NAPs such as H-NS, HU, Fis, and the SMC-like MukBEF complex, are capable of binding DNA to introduce bends, loops, and bridges in the chromosome (Rybenkov et al., 2014, Badrinarayanan et al., 2015, Marbouty et al., 2015, Valens et al., 2016, Lioy et al., 2018), and are generally the best understood modulators of genome folding (Thanbichler et al., 2005, Le et al., 2013).

Our current view of the genomic structure of E. coli is derived from fluorescent microscopy, site-specific recombination, and 3C/Hi-C experiments (Niki et al., 2000, Valens et al., 2004, Wang et al., 2006, Fisher et al., 2013, Schmitt et al., 2016, Lioy et al., 2018). The first indication of organized chromosomal regions came from fluorescent in situ hybridization (FISH) of Ori and Ter domains of E. coli (Niki et al., 2000), revealing that loci within the Ori domain are positioned at the mid cell and segregate toward the poles after replication (Fig. S1A,B) (Wang et al., 2006, Espeli et al., 2008, Reyes-Lamothe et al., 2012), whereas loci located within Ter stay located at the mid cell, and after division, remain at the nascent cell poles (Kleckner et al., 2018).

Experiments based on λ att site recombination suggested the existence of additional organization beyond Ori and Ter (Valens et al., 2004). Relying on recombination frequencies between λ att sites placed around the chromosome, four large structured ‘macrodomains’ (MDs) were proposed – Ori, Ter, L and R – where there was more recombination within each domain than between them; two ‘non-structured’ NS domains were proposed to flank Ori (Fig. S1A). Recent advances in chromosome conformation capture (3C) techniques have also led researchers to propose the existence of Chromosomal Interaction Domains (CIDs), which are contiguous blocks on the chromosome wherein two loci within the same CID interact more frequently than loci from different CIDs (Cagliero et al., 2013, Le and Laub, 2016, Lioy et al., 2018). A survey of diverse bacteria showed the presence of roughly 20 CIDs across the genome of each species studied (Marbouty et al., 2015, Val et al., 2016). The boundaries of the CIDs in C. crescentus correlate with high gene expression (Le et al., 2013). 3C experiments have shown that many of the CIDs can coalesce to form large macrodomains ranging from 0.5 to 1.4 Mb in B. subtilis and C. crescentus (Le et al., 2013, Le and Laub, 2016).

Every methodology has its limitations. Fluorescence techniques (FROS) are useful in locating the cellular position of genomic loci, but their sensitivity for monitoring interactions between the loci is limited (Espeli et al. 2008). The λ recombination methodology is limited by its site-specificity in that it can only monitor artificially placed sites similar to FISH/FROS. HiC analysis of the E. coli genome observed a strong characterization of the Ter region, but not necessarily the L, R or NS domains to the extent reported by λ recombination (Cagliero et al. 2013; Lioy, 2018). In addition, 3C and related approaches may be limited by the use of formaldehyde crosslinking to solidify interactions between chromosomal loci, which might alter chromosomal conformation itself.

In this study, an alternative methodology was developed and applied for probing bacterial chromosomal structure, employing the transposable phage Mu. This approach combines the utility of sampling multiple independent sites simultaneously, with high promiscuity in choosing locations, conducted entirely in vivo with no external perturbations or crosslinking agents. Mu is capable of integrating its DNA indiscriminately and with high frequency into the genome of its E. coli host (Mizuuchi, 1992, Chaconas et al., 1996, Nakai et al., 2001, Harshey, 2014). Mu transposes by a nick-join pathway, where single-strand cleavages generated at each end of the Mu genome (Mu ends) by the transposase MuA are joined to similar cleavages made 5 bp apart on the target DNA. The resulting branched Mu-target joint is resolved by replication through Mu during the lytic cycle, amplifying Mu copies in a process called replicative transposition (Fig. 1A). Joining of the Mu donor and target strands is entirely dependent on MuA-mediated DNA interaction between the Mu genome and the target site, and as such is governed by physical ability of those sites to interact. MuA has a fairly degenerate 5 bp target recognition consensus of 5’-CYSRG. Target capture is aided by MuB, a non-specific DNA-binding protein and AAA+ ATPase.

Figure 1. Mechanism of Mu transposition, and initial genomic location of Mu prophages.

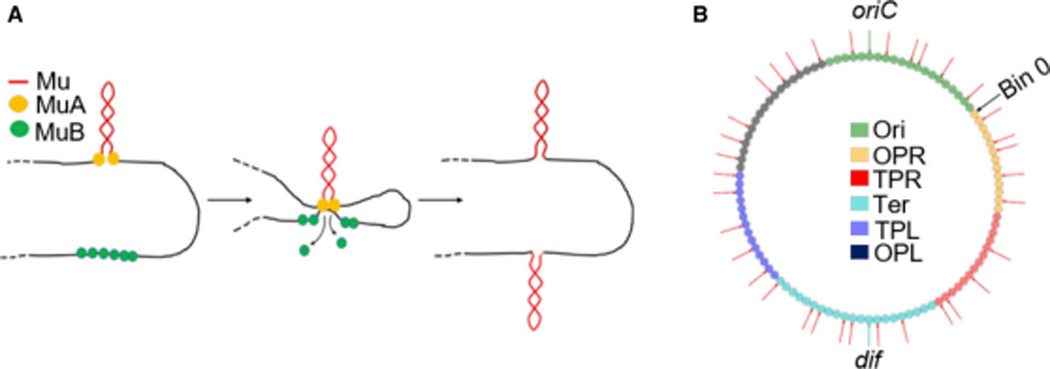
(A) Simplified cartoon of Mu replicative transposition. (B) Locations on the E. coli genome of the 35 Mu prophages (red arrows) used in this study. oriC and dif are sites where replication initiates and terminates. The genome was partitioned into 100 equally sized bins (0–99; small circles). The different bin colors refer to the regions shown in the legend. The original NS regions flanking Ori are named Ori proximal left (OPL) and Ori proximal right (OPR), and the original Left and Right regions flanking Ter, Ter proximal left (TPL) and Ter proximal right (TPR), to avoid confusion when talking about the general left and right arms of the chromosome.

The work presented here follows 35 independent Mu prophages located throughout the genome through one round of transposition. The data show that in a clonal population, Mu is able to sample the entirety of the genome regardless of the starting genome location with roughly equal probability, suggesting widespread contacts between all regions of the chromosome and arguing against the strong compartmentalization that has been inferred from some (but not all) Hi-C experiments. Statistical modeling of the data reveals a distance independent 3-D co-localization of several functional gene classes. The condensin complex MukBEF and the NAP HUα were identified as being crucial for these properties. A simple polymer model was used to interpret these findings and provide a global framework for understanding the effects of NAP activity and specific contacts on the chromosomal structure of E. coli.

RESULTS AND DISCUSSION

Mu Samples Every Region of the Genome, Transposing across Macrodomain Boundaries and Replichores

Mu was placed at sites all around the E. coli chromosome by generating 35 prophage strains as shown in Figure 1B, and a single round of transposition was induced in each strain (see STAR Methods and Movies S1 and S2 for details). For analysis, the genome was partitioned into 100 equally sized bins (each bin ~46.4 kb) to monitor transposition from the starting location/bin to the 99 other bins. Given the random nature of Mu transposition, each cell in the clonal population is expected to have experienced a different transposition event. Representative insertion profiles of the first hop for nine different prophages located across the E. coli chromosome are shown in Figure 2A. The data clearly show that, irrespective of its starting bin, Mu transposes to every bin of the genome at the resolution presented here, with roughly equal frequencies. Similar profiles were obtained for the remaining 26 prophages (data available; see STAR Methods). Given that Mu transposition depends on contacts between transposase-bound Mu ends and MuB-bound target DNA (Fig. 1A), these insertion profiles demonstrate that there are roughly equal physical interactions between every chromosomal region, allowing Mu to transpose globally within the nucleoid.

Figure 2. Normalized Mu insertion counts and regional efficiency of transposition.

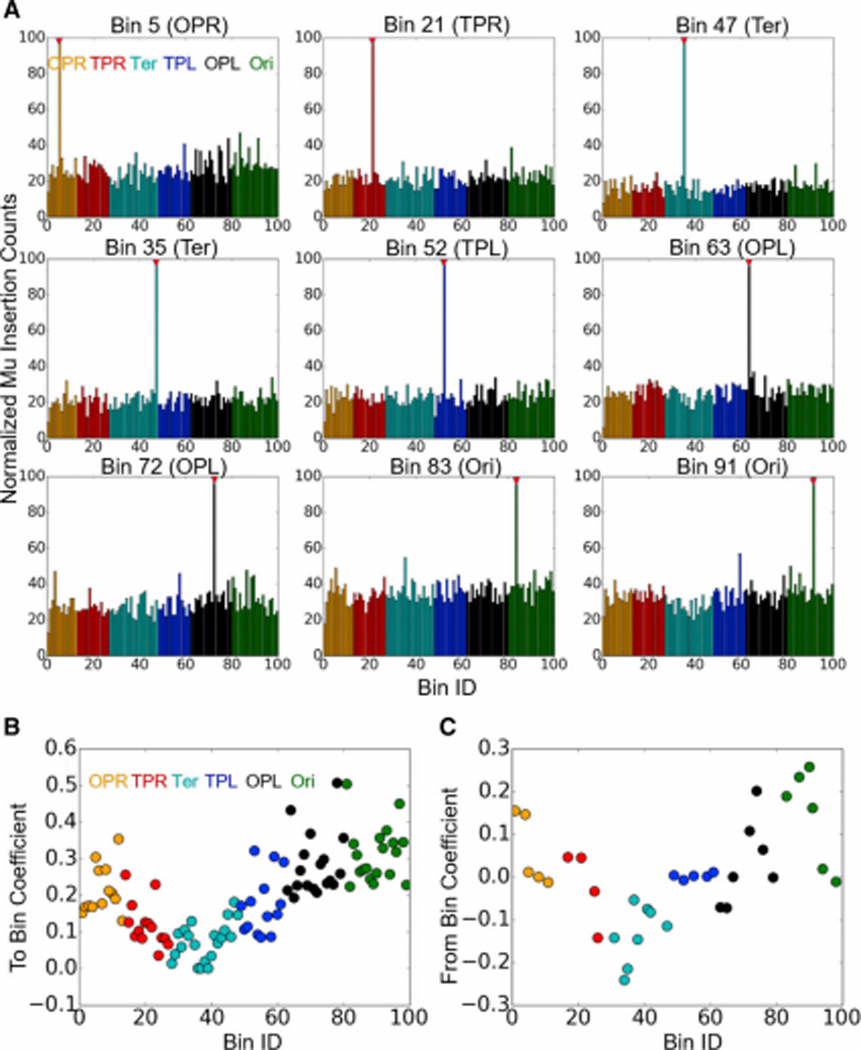
(A) Mu insertion counts for nine representative prophages located around the E. coli genome after one round of transposition. The number of insertions have been normalized to the read depth of each bin. Initial Mu positions (red triangles) were given an arbitrarily large value to emphasize their location along the x-axis. (B) Coefficients of the To Bin and From Bin contributions to the LASSO model. For all 100 bins, Mu’s ability to insert into that bin irrespective of its starting locations is measured by the To Bin coefficient. Positive values mean that it is easier to insert into that Bin compared to the global average. Similarly, From Bin coefficients measure Mu’s ability to leave that and insert into the remaining 99 bins.

The data in Fig. 2A also highlight that Mu transposes freely across MD boundaries originally defined by the lack of phage λ att site recombination (Valens et al., 2004, Espeli et al., 2008) (Fig. S1A). An alternative set of MD boundaries were observed using high throughput 3C experiments (Lioy et al., 2018), although other previously reported 3C data sets under similar conditions did not show the classic MD structure (Cagliero et al., 2013); likewise, the data in Fig. 2A show no barriers at the 3C-identified MD locations. Given the presence of discrepant data regarding the nature of MDs, these will be refered to as chromosomal regions instead, maintaining the locations of the original boundaries for convenience and continuity, but using a slightly modified nomenclature described in Fig. 1B.

The transposition data are derived from an asynchronous population in which many cells have partially replicated chromosomes, with Ori and its flanking regions having moved towards the cell poles, while Ter and its flanking regions are often still unreplicated and located at the mid cell (Fig. S1C). A higher frequency of interactions would be expected between the replichore arms during segregation, compared to unreplicated regions (see Fig. S1B). The transposition frequencies from all 35 strains are consistent with the expected increase in trans-replichore interactions for replicated portions of the chromosome (Fig. S1D-E), with a break point at the quarter-positions relative to oriC, reflecting the average replication state of cells in the population (Fig. S1C).

A striking feature of the view from Mu is that there are no detectable hard boundaries in the genome. If a Mu prophage was close to an expected MD boundary (based on the definitions of Valens et al. 2004), it crossed that boundary with impunity (Fig. 2A). We deduce that the conformations of the chromosomes across a population of cells in similar growth states is highly heterogeneous, since if these conformations were uniform, some bin-bin interactions would be necessarily excluded from our data as no single conformation would permit Mu transposition between all pairwise combinations of bins. The data reveal that linear distance on the genome provides no information on contact frequencies over length scales of tens of kb or longer, consistent with the overall conformation of the chromosome being well-mixed – i.e., an E. coli population will at any point contain an ensemble of conformations in which any given locus is roughly equally likely to be in contact with any other locus, regardless of genomic distance or intervening features.

Model-Based Statistical Analysis Confirms a Well-Mixed Genome

To identify significant contacts implied by the efficiency of Mu transposition, a penalized regression model (LASSO) was employed, to highlight terms that contribute information to the observed contacts. Three major classes of contribution were considered: First, (linear) genomic distance between bins; second, the intrinsic reactivity of each bin as both a donor and recipient of Mu, and third, specific pairwise interactions between bins, which would reflect the presence of long-range contacts. The different abundances of DNA from different genomic bins were corrected using an offset term (see STAR Methods).

The fits across 35 donor bins reveal several global trends in the data: First, in wild type cells, the contribution of linear genomic distance to Mu transposition frequency is essentially non-existent, yielding no more than a 2.5% difference in transposition frequency between the nearest and farthest bins (based on the fitted LASSO coefficients). This finding indicates that the overall chromosomal structure follows a ‘small world’ layout where any given chromosomal segment may interact with any other segment, rather than being confined to its immediate linear vicinity or by MD boundaries. Second, the contributions of the ‘donor’ and ‘recipient’ bin terms demonstrate that Mu transposition is particularly inefficient into or out of the Ter region, and particularly efficient into or out of the Ori region of the chromosome (Fig. 2B, C). Even with the lower donor/recipient terms exhibited by Ter, however, Mu was able to insert into every bin within Ter regardless of starting location. This observation readily implies that the difficulty of Mu insertion into Ter is not indicative of the region being refractory to Mu insertion, but rather that Ter is less well-mixed with the other regions of the chromosome. The role of the Ter region in excluding MukBEF (Nolivos et al., 2016), a complex responsible for the well-mixed genome reported in this study (see below) may account for this property. These findings are consistent with numerous 3C-type experiments showing both that the Ter region is more isolated from the chromosome and that has unique structural characteristics shaped by the activity of MatP (Mercier et al., 2008, Cagliero et al., 2013, Lioy et al., 2018). The relatively high reactivity of Ori may be due to special organizational features related to its mobility over the course of the cell cycle, or (within the context of the kinetic model discussed below) the fact that Ori will on average have had more time post-replication to relax due to being replicated first.

Mu Transposition Reveals ‘Clustering’ of Distant Chromosomal Loci

The LASSO model terms described above accounts for global effects due to DNA abundance, linear genomic distance, and intrinsic properties of the bins themselves with regards to Mu transposition. When the contributions of genomic abundance and donor/recipient effects are removed, the small world well-mixed view of the chromosome becomes readily apparent, as transposition frequencies become nearly uniform (Fig. S2). The last class of terms included in the model were those for specific interactions between bin pairs, which directly represent pairwise bin combinations that have significantly higher or lower transposition rates than can be explained by the global terms described above. Due to the direct contact-based mechanism of Mu transposition, we interpret the presence of significant interaction terms as indicating higher or lower rates of physical contact between the indicated bins, analogous to the contact frequencies inferred from normalized HiC data. As shown in Figure 3A, numerous significant and informative interaction terms survive in our fully fitted model (Figure 3 is also available as an interactive html file provided in Document S1).

Figure 3. Locations of significant bin interactions implied by Mu transposition data.

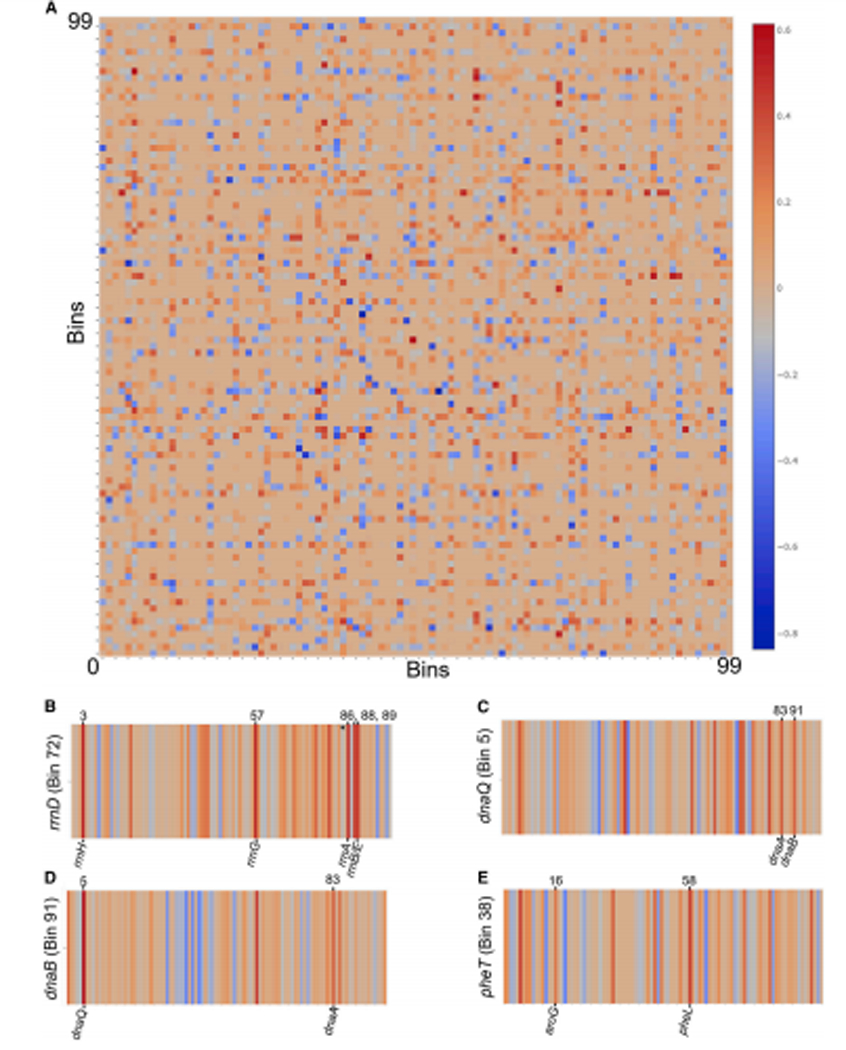
(A) Pairwise Bin:Bin interaction coefficient matrix. The x- and y-axes correspond to the 100 Bins representing the chromosome. Each pixel in the matrix is colored to indicate the coefficient value for that specific Bin:Bin interaction. Positive values of interaction indicate a higher degree of interaction compared to the global average. (B-E) Enlarged views of the rows of the matrix from panel A corresponding to Bins 5, 38, 72, and 91 (as labeled); color scale is identical to panel A. The asterisk in Bin 72 is used to indicate the low-level interaction with Bin 84 (rrnC).

Several of the significant interactions correspond to bins containing genes that are distant in linear genomic space but expected to be co-regulated. For example, Bin 72 (Fig. 3B) shows the fitted interaction profile for a prophage located in the same bin as the rrnD operon (~10 kb away). For this Mu donor location, the bins containing the rrnA, B, E, G, and H operons show significantly positive interaction terms, suggesting physical co-localization. These findings support earlier work in which fluorescent imaging showed spatial co-localization of six of the seven rRNA operons in E. coli (Gaal et al., 2016). Interestingly, the interaction between Bin 72 and Bin 84 (the latter containing the rrnC operon; marked with an asterisk in Fig. 3B) does not have a significant interaction. This exception is surprising, but consistent with the findings of Gaal et al. where all but the rrnC operons are in close proximity.

Similar trends emerged with other co-regulated gene clusters within the contact matrix (Fig. 3A). Besides the rrn clusters, a predominant gene cluster to emerge is one specifying the replisome machinery (Fig. 3C, Fig. 3D) as seen in Bins 5 (dnaQ), 83 (dnaA and dnaN), and 91 (dnaB). Even though dnaQ and dnaA are nearly 1 Mb apart in linear distance on the chromosome, the bins containing these genes co-localize within the nucleoid. A similar evidence of clustering was observed in the phenylalanine biosynthesis pathway. Bin 38 contains the pheT gene and is seen to strongly cluster with Bins 16 and 58 containing the aroG and pheL genes, respectively (Fig. 3E). Higher resolution probing may detect many more of such clustering events. Notably absent from the contact map provided here is any hint of the classic MDs, which would be expected to form boxes of high interaction frequency centered on the diagonal. At the same time, strong and specific off-diagonal interactions were observed between loci that are located in different MDs, as highlighted in Figure 3B-E. Thus, while the conformation of the chromosome is ‘well-mixed’ with respect to large-scale conformation, the data indicate that there several specific pairwise interactions between distant loci that are consistently preserved within the broader context of the mostly-random structure of the chromosome.

Microscopy Corroborates Gene Clustering Identified by Mu Transposition

To corroborate the observations of clustered gene groups noted in Figure 3, co-localization of specific genes was tested via fluorescence microscopy using the parS/ParB FROS approach. Two different par sites (parSP1 and parST1) were placed in the parent strain MG1655 (devoid of Mu), close to a pair of genes being interrogated. These sites can be visualized by co-expression of their cognate fluorescent ParB proteins (P1 CFP-ParB and T1 GFP-ParB). Using this approach, the co-localization of rrnD and rrnG loci were readily detected (Fig. S3), consistent with the Mu transposition results and earlier experiments (Gaal et al., 2016). The same methodology was then applied to test two families of clusters inferred solely from the Mu transposition data.

As noted above, there was a strong co-localization of several genes involved in DNA replication. The bins containing dnaA and dnaB (Bins 83 and 91) are too close to be distinguished by microscopy using FROS (Fig. 4A) (Heintzmann and Ficz, 2006), so the par sites were placed next to dnaA and dnaQ in one strain, and next to dnaB and dnaQ in another strain. As controls, two strains with par site markers at similar linear distances to the dna gene pairs, but at positions that were not identified as being clustered, were evaluated.

Figure 4. Fluorescent microscopy confirms gene clustering predicted from Mu transposition analysis.

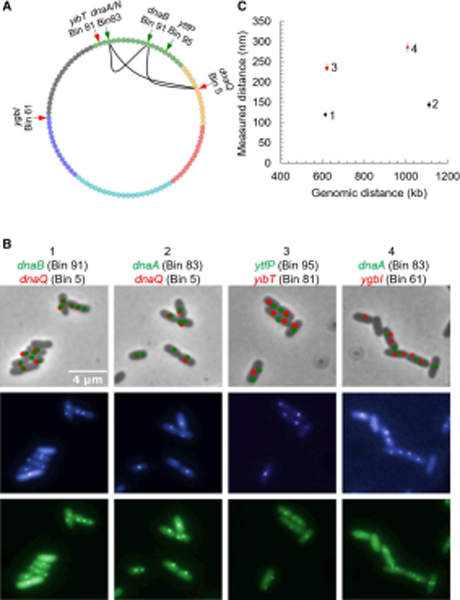
(A) In the cartoon, arrows point to positions of the various parS sites placed near the indicated genes in the listed chromosome bins, and visualized with GFP- (green arrow) and CFP-ParB (red arrow). (B) The top bright field panels represent CFP puncta in red and GFP puncta in green, from fluorescence data obtained from the two panels immediately underneath. Panel 1 shows data for DW151, where parS sites were positioned next to dnaB and dnaQ in the indicated bins, ~615 kb apart. Panel 3 is a control for panel 1, where the parS sites are 622 kb apart, located near ytfP and yjbT genes (DMW153). Panel 2 has parS sites located near the replisome genes dnaA and dnaQ located 1.1 Mb from one another (DMW155). Panel 4 is a control for panel 2, where the parS sites are ~1.0 Mb apart located near the genes dnaA and ygbI (DMW157). (C) The measured physical distances between the pairwise labeled parS loci were calculated and compared between the controls and dna genes. The identifying numbers (1–4) correspond to the panel numbers in B. Error bars represent the 95% confidence interval assuming normality. 1 (N=408) and 2 (N=514) appear to be much closer than their respective controls 3 (N=523) and 4 (N=569).

Figure 4B shows representative imaging data for parSP/parST locations near the clustered loci dnaQ and dnaB (panel 1) as compared with the ytfP and yibT control (panel 3). The former were measured as being (on average) 120 nm apart, whereas the latter were 235 nm apart (Fig. 4C). Similarly, parSP/parST pairs located near dnaA and dnaQ showed an average distance of 144 nm (Fig. 4B, panel 2), whereas the control dnaA/ygbI yielded distances of 286 nm. The differences in distances between each clustered locus pair and the corresponding control were statistically significant using a Wilcoxon rank sum test (p < 0.005), and the negative control locus pairs further match the average distance expected by chance within an ellipse with a long axis of 1 μm and short axis of 0.5 μm (270 nm; see Fig. S3C). To our knowledge, the physical co-localization of these strongly co-regulated dna genes has not been observed previously. It is notable, however, that a re-analysis of an early E. coli high-throughput 3C data set also suggested general three-dimensional co-localization of coregulated genes (Xie et al., 2015).

A second family of clustered genes, pheL (Bin 58) and aroG (Bin 16) was interrogated next. The transposition data indicated that both Bins 58 and 16 were co-localized with Bin 38 (Ter), which contains pheT. All three genes are encoded in operons involved in the synthesis of phenylalanine (Pittard and Yang, 2008), making this another example of clustering of co-functional genes. Par sites were placed within 1 kb of pheL and aroG located on the left and right chromosomal arms (Fig. 5A,B). A bimodal distribution of the nearest aroG - pheL distance was observed, which appears to be determined by the number of aroG foci present in the cell (Fig. 5C). In cells where aroG has been replicated (2 GFP foci), there was a much higher degree of co-localization between aroG and pheL; one GFP focus would be co-localized with the CFP focus while the other was separated on the other side of the cell, whereas no contact was apparent in cells with a single aroG copy. This result indicates that co-localization of aroG and pheL is dependent on the extent of replication for any given cell, and the enhanced contact frequency observed in the LASSO analysis reflects the averaging of many distinct conformations present in our heterogeneous cell population. Figure 5D highlights the distribution of the four types of localization, based on the replication status of aroG and pheL. To test the generality of the replication-dependent clustering observed for aroG and pheL, the GFP-labeled rrnD and CFP-labeled rrnG loci were followed because rrnD is near the origin and thus replicated by the majority of cells in the asynchronous experimental population, whereas rrnG will frequently not be replicated (Fig. S1E). Consistent with these expectations, data in Figure S3A show that the bulk of the population has two GFP foci and one CFP focus for every cell. In such cells, the CFP focus is localized with one of the two GFP loci, consistent with the pheL/aroG observations (Fig. 5). However, unlike the case with cells harboring single pheL and aroG foci, in cells harboring single GFP and CFP rrn foci, these foci still co-localize, as indicated by the lack of a bimodal distribution (Fig. S3B). These data suggest two categories of clustering – replication-dependent and replication-independent, which are likely driven by different biological mechanisms.

Figure 5. Two genes for phenylalanine synthesis show co-localization only after replication.

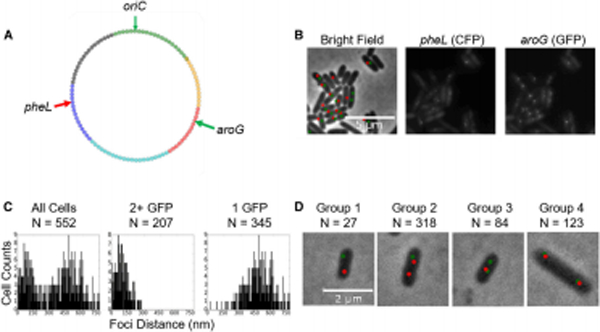
(A) Locations of the aroG and pheL genes tracked using fluorescent microscopy. (B) The left bright field panel represents CFP puncta in red and GFP puncta in green from fluorescence data gathered from the two neighboring panels, where the CFP locus is near pheL (Bin 58), and GFP near aroG (Bin 16) in DMW160. (C) The distance between an aroG (GFP) locus and its nearest pheL (CFP) neighbor takes on a bimodal distribution. The distribution of distances for 2+ foci is significantly lower than a random distribution obtained by drawing pairs of distances from the 1-focus distribution and keeping the lowest draw from each pair (p < 10⁻⁵⁹, Wilcoxon rank sum test). (D) The CFP/GFP localization pattern was distributed among 4 distinct groups with following numbers of aroG and pheL markers respectively: Group 1 – 1:1, Group 2 – 1:2, Group 3 – 2:1, Group 4 – 2:2. Sample sizes are indicated in the figure.

Genome Compaction Contributes to Both Chromosomal Mixing and Clustering

The co-localization of several gene classes detected by Mu may arise either as a direct result of forces (e.g., shared DNA-binding proteins) that bind and compact the specific loci involved, or reflect a broader intrinsic feature of the chromosomal regions in which those genes are found. The former hypothesis was ruled out by experiments presented and discussed in Fig. S4A, in which highly interacting loci were transplanted without corresponding rearrangements of clustering patterns, observations also supported by gene product network maps (Fig. S4B). The data are consistent with those of Gaal et al. that co-localization of rrn operons is driven by properties of flanking chromosomal regions rather than transcription of the ribosomal RNAs themselves. These findings suggest that clustering may arise during normal cellular processes of genome replication/compaction, and that these positions were likely exploited by evolutionary forces to position some genes in clustered regions for facilitating efficient co-regulation.

To test the role of genome compacting mechanisms in clustering, Mu transposition was monitored in strains with deletions of genes encoding architectural functions. Because of its well-documented rrn clustering behavior, Mu insertions from Bin 72 were initially tracked to monitor the effects of deletion of several NAPs on rRNA operon clustering. Deletions in genes encoding several general or specific NAPs – fis, hupB, hns, ihfA and matP - showed little to no effect on transposition patterns (Fig. S5). HU is a heterodimeric subunit (encoded by hupA and hupB), but can function as a homodimer of the A(α) or B(β) subunit (Dillon and Dorman, 2010). Mu requires HU for transposition, but either α or β homodimers are sufficient (Fig. S5) (Huisman et al., 1989).

A striking change in Mu insertion patterns (monitored from Bin 72) was seen in strains with deletions of mukB or, to a slightly lesser extent, hupA (Fig. 6A). MukB is an essential subunit of the SMC-like MukBEF complex, a functional homolog of the loop-extruding condensins in eukaryotes (Dillon and Dorman, 2010, Rybenkov et al., 2014, Terakawa et al., 2017, Ganji et al., 2018, Lioy et al., 2018). Because of the more pronounced change in insertion patterns for the mukB mutant compared to hupA, the mukB patterns were monitored from the 6 chromosomal regions (Fig. 1B). Contrary to wild-type cells, Mu insertion frequencies exhibited a distance-dependent behavior in the hupA and mukB strains, where linear genomic distance became a dominant predictor of interaction frequencies. Figure 6B shows the results of a simple regression fit, for transpositions across different genomic distances in each strain of interest. The loss of ‘small world’ behavior in these mutant genotypes is sufficient to cause a 3.5-fold drop in average contact frequencies between opposed points on the chromosome in the mukB strains, and a 2.2-fold drop in the hupA strain. Thus, MukBEF and HU-α, proteins that compact the genome, also promote widespread genomic contacts.

Figure 6. MukBEF and HU-α both contribute to chromosomal mixing, and HU-α to rrn clustering.

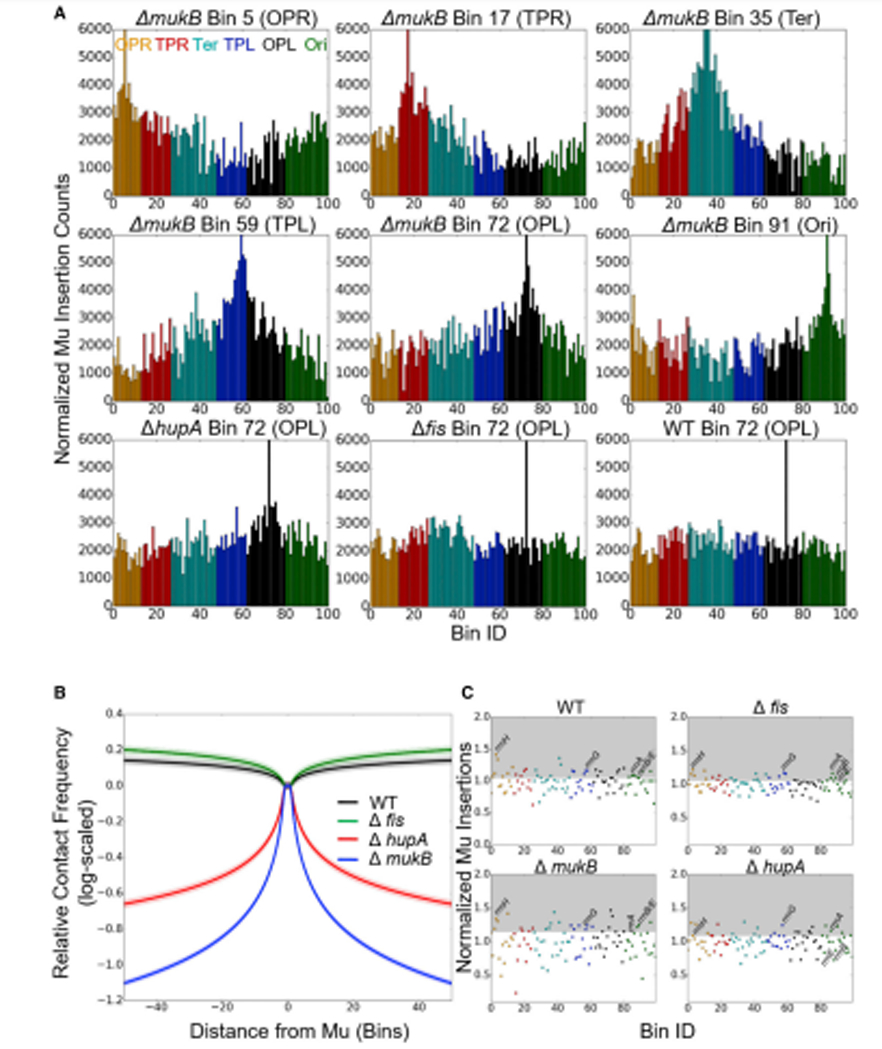
(A) Effect of disabling the function of HU-α and MukBEF on Mu insertion patterns. Mu insertion counts were from a target-enrichment protocol for Mu transposition sequencing (see STAR Methods); they are normalized to the respective sequencing depths of each bin in a non-Mu-containing population grown under identical conditions. (B) Genomic distance effects are strengthened in both the mukB and hupA deletion mutants. Shown are robust linear regression fits of the genomic distance dependence of (log-scaled) contact rates as a function of distance from Mu. (C) Mu insertions analyzed by a high pass filter highlight the effect of gene deletions on clustering. For each point, the ratio between the interaction rate of a specified bin with the Bin 72 Mu location was plotted, and an 11-bin rolling median on the same quantity centered on that bin. The grey region represents the value needed to be included in the upper quartile of interaction rates.

The unique sensitivity of the Mu transposition method in identifying region-specific long-range contacts also permits assessment of the effects of architectural protein deletions on clustering. As seen in Figure 6C, while deletion of fis has no notable effect on clustering, the hupA mutant has lost some meaningful rrn clusterings (at least as assessed by contacts with the rrnD-containing Bin72). Wilcoxon rank-sum tests of the difference in median between interactions of Bin72 with other rrn loci-containing bins yields p values <0.01 for all genotypes except hupA, and 0.74 for the hupA mutant. The loss of significant rrn clustering in the hupA genotype is driven by loss of contacts between Bin 72 and the bins containing rrnB and rrnE, which fall below the 25^th percentile of contact frequencies rather than above the 75^th percentile in the corresponding WT sample. In contrast, ribosomal RNA operon clustering of the mukB deletion appears similar to that observed for WT cells, and shows significant enrichment relative to background (p=0.005, Wilcoxon rank sum test). MukBEF is therefore not involved in the formation of long distance contacts between rrn operons. Note that despite the presence of several Fis binding sites in rrn promoters, Fis does not participate in clustering [(Gaal et al., 2016) and Fig. 6].

Given the profound loss of the well-mixed chromosomal conformation in both mukB and hupA mutants, we sought to obtain additional information on the large-scale effects of both deletions on chromosomal structure. Loss of MukB has previously been shown to cause decondensation of the nucleoid (Kumar et al., 2017), whereas comparatively little evidence is available regarding the effects of loss of HU-α; the HU subunits generally complement each other without observable phenotypes (Wada et al., 1988, Macvanin and Adhya, 2012). Analysis of the distributions of nucleoids from WT, mukB, and hupA cells showed that the mukB cells exhibit substantial nucleoid decondensation (consistent with prior findings), whereas the size distributions of WT and hupA nucleoids are virtually indistinguishable (Fig. S6).

The data thus indicate that MukBEF and HU-α are both responsible for generating the well-mixed chromosome, although it is not clear whether they act in tandem or through complementary mechanisms. HU-α appears to play an additional role in establishing the stable, long-range contacts between ribosomal RNA operons that are fixed features of the E. coli chromosome. The small-world organization of the chromosome is not simply a constant property of a well-compacted nucleoid (as might have been expected given prior knowledge of the effects of MukB on nucleoid compaction), as loss of hupA leads to loss of long-range contact formation without nucleoid decompaction. The requirement for HU-α but not for the HUβ subunit for both clustering and global genome access, reveals a physiologically important difference between these closely related proteins, which were previously assumed to be interchangeable.

Simulated Relaxation Dynamics of the Chromosome Provide a Kinetic Mechanism for the Balance of Short- and Long-Range Contacts.

To provide further insight into what physical processes might shape the contact map patterns observed in the Mu transposition data, we made use of a simple polymer model of the bacterial chromosome; an example conformation of the genome using the model is shown in Figure 7A. In contrast with many other modeling efforts on bacterial chromosomes [(Umbarger et al., 2011, Hacker et al., 2017, Yildirim and Feig, 2018); see STAR Methods for a detailed comparison], the model was not designed to reproduce any precise contact map, nor were inter-bead contacts parameterized on the basis of the Mu transposition data. Rather, the genome was divided into 965 ~4.8 kb regions (beads), interacting via harmonic potentials with adjacent beads, and through a Lennard-Jones potential with all other beads (see Fig. 7B). Folding of the chromosome was simulated starting from a fully circular structure, working from the ansatz that at some point during replication, the chromosome will be functionally extended due to a combination of replication, origin re-localization, decatenation, and cell division.

Figure 7. Polymer modeling recapitulates key aspects of E. coli chromosomal structure.

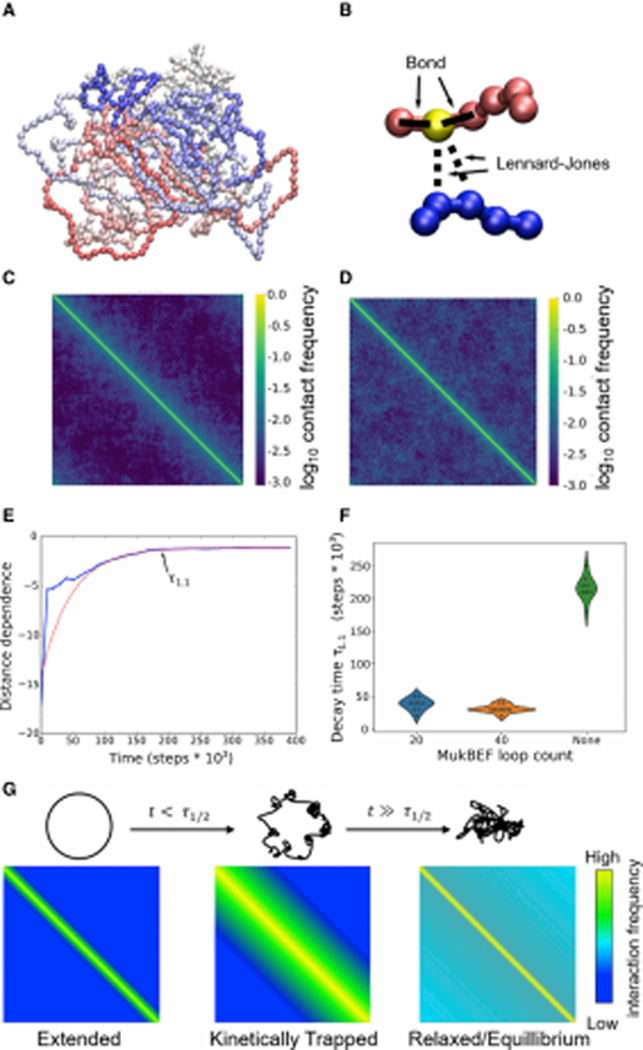
(A) Example conformation of the model at apparent equilibrium after relaxation from a fully extended ring shape. Coloring runs from blue to red showing linear position along the genome. (B) Schematic of two distant regions of the model chromosome and the interactions acting upon the yellow highlighted bead. (C) Contact matrix obtained by averaging contact maps from 50 short (10⁶ timestep) simulations; see STAR Methods. (D) Contact matrix obtained by averaging the last halves of 20 long (2.5 * 10⁷ timestep) simulations, showing the eventual equilibrium state reached by the system as it relaxes. Note that in all contact maps, the strong yellow stripe along the diagonal represents self-contacts (which thus have a frequency of 1.0 by definition). (E) Change in the dependence of contact frequencies from a representative polymer simulation over time. Distance dependences are obtained at each timepoint by fitting a logistic regression to predict contact frequency as a function of log(genomic distance); thus, a more negative distance dependence indicates stronger effects of linear distance. The red dashed line shows a single exponential fit to the observed decay curve beginning after 100,000 steps. _T1.1 indicates the time needed to reach within 10% of the asymptotic value. (F) Violin plots showing the distributions of relaxation times (_T1.1) for the distance dependence (as shown in panel E) in the absence vs. presence of MukBEF-induced loop extrusion. (G) Model for the progression of chromosomal states and contact maps in the polymer model. Schematic of the chromosomal conformation (top) and corresponding contact matrices (bottom) at the beginning of the simulations (left), after an amount of time shorter than the required relaxation time (middle), or after sufficient time for the conformation to reach equilibrium (right).

The contact maps observed in folding simulations using this simple polymer model reproduce two important classes of maps that are observed in various experimental data sets. Over short simulation times, the contact maps (Fig. 7C) are dominated by short-range interactions, and closely resemble the landscapes seen in Mu transposition experiments in mukB and hupA cells, as well as qualitatively resembling (aside from the lack of MDs and CIDs) the distance dependence observed by others in HiC-type experiments (Lioy et al., 2018). After the chromosome is allowed to reach equilibrium, the initial distance dependence is lost, and contact frequencies with distant beads become uniform (Fig. 7D). Thus, for a simple ring polymer approximation of the E. coli chromosome, the equilibrium structure is in fact the ‘well-mixed’ structure that is observed via Mu transposition. In interpreting these simulation results, it is important to note that the model used here is intentionally very simple, and reflects the behavior of a featureless polymer with broad topological and structural similarities to the E. coli chromosome (see the “Characteristics of the Polymer Model” heading in STAR Methods for more details). It is nevertheless remarkable that a well-mixed conformation is in fact achieved by a simple ring polymer without the need for any bias toward long-range interactions. Deviations from this structure in experimental data sets must arise from either a specific process altering the structure of the chromosome that is not represented in the model (e.g., formation of specific contacts or conformational barriers), changes in the average strength of nucleoid cohesion that lead to a change in the chromosome’s equilibrium state (Fig. S7D), or non-equilibrium effects where the chromosomal conformations of the population of cells being observed has not yet had time to relax fully to the small-world state (a kinetic trap in nucleoid folding after replication/division) – that is, changes in the overall behavior of the contact map may in fact arise from either thermodynamic or kinetic effects.

While the data on the mukB mutant in isolation might have been interpreted as a phase transition in the nucleoid structure (Fig. S7D-E), the data regarding the DNA distribution in hupA nucleoids (Fig. S6) instead favors a kinetic argument, as the small-world contact map can be lost without causing nucleoid decompaction. The data suggest that MukBEF and HU act to catalyze relaxation from a short-range ordered state (as in Fig. 7C) to a well-mixed state (as in Fig. 7D), promoting mixing by avoiding kinetic trapping and allowing the nucleoid to relax to the well-mixed state. Indeed, the FROS data presented in Figure 5 provide strong evidence for the presence and importance of non-equilibrium effects on chromosomal structure: the pheL and aroG loci are co-localized in cells that had recently replicated the pheL locus (38% of the population), but not those with only a single copy of pheL (which must have undergone a longer waiting time since the last time pheL was replicated).

To test the feasibility of the proposed mechanism that MukBEF enhances mixing by accelerating relaxation kinetics of the chromosome (in addition to its well-known role in nucleoid compaction), a MukBEF-like loop extrusion activity was implemented in the polymer simulation, in which ‘loops’ were randomly formed (and subsequently broken; see STAR Methods for details) at regular intervals, and the relaxation rates of the chromosome with vs. without dynamic loop formation were then compared. As shown in Figure 7E-F, simulated nucleoids with dynamic MukBEF loops showed relaxation times toward abundant long-range contacts that were substantially faster than those without dynamic loops. Thus, in the simplified chromosomal model described above, MukBEF-like activity alone is sufficient to accelerate equilibration of the chromosome. The kinetic hypothesis offers an explanation for several aspects of the experimental findings described above regarding the effects of MukB without any need to explicitly participate in forming long-range contacts (indeed, MukBEF-mediated loop extrusion would intuitively be expected to promote more short-range order in addition to overall compaction, as discussed in more detail in the “Effects of MukB loop extrusion on chromosomal relaxation” heading of STAR Methods ). The contribution of functional HU-α to chromosomal mixing is not yet entirely clear; it may arise either due to some mechanistic interplay with the MukBEF complex or through other effects of HU binding (such as containment of negative supercoiling) (Lal et al., 2016) that ultimately enhance the rate of chromosomal relaxation.

The kinetic model for chromosomal ordering described here also offers an explanation for the distinction between replication-dependent (e.g., pheL-aroG) and replication-independent (e.g., rrn clustering) interactions. We hypothesize that the pheL – aroG interaction is characteristic of a metastable conformation (Fig. 7G, middle panel) that occurs transiently, but is subsequently lost during relaxation of the chromosome to an equilibrium state (Fig. 7G, right panel). In contrast, the replication-independent interactions are apparently sufficiently strong that they persist throughout the cell cycle, and are either not broken or swiftly re-form after replication of the regions of the chromosome involved in any particular interaction. It is possible to envision a third category of interactions, which form preferentially in the equilibrated state, and would only be observed after longer time periods since the most recent replication event. No instances of such behavior have been directly observed. The potential kinetic distinctions between different categories of interactions outlined here may provide a useful test in the future of the hypothesis of kinetic control of the chromosomal conformations.

Comparison of Mu Transposition Results with Other Methods for Genome-Wide Chromosomal Structure Measurement

Compared with recent 3C data sets (Cagliero et al., 2013, Lioy et al., 2018), Mu transposition-based mapping shows several distinct differences, including revelation of a well-mixed chromosome unconstrained by linear distance and an apparent lack of substantial barriers to contact between any arbitrary locations on the chromosome (although, as shown in Fig. S7A, a similar picture emerges upon re-analysis of one such experiment; re-analysis of that data set also showed the presence of co-localization of co-regulated genes consistent with the clustering that was noted above (Xie et al., 2015)). The Mu transposition and microscopy data described above also revealed and corroborated several clustering interactions between distant chromosomal loci not observed in genomic 3C maps. It is important to consider possible causes for the discrepancies between the methods, and what useful data might be extracted from each. Current Mu data sets lack a sufficient density of donor sites to permit comparison with the CID structures inferred from 3C experiments; probing at this level of structure will be a promising future application for higher-throughput variants of the Mu procedure, but at present, we cannot make any statements regarding discrepancy or concordance with CIDs or other fine-grain features of the Hi-C and high-throughput 3C data, and focus instead on the prevalence of local vs. long-range contacts, and large-scale “macrodomain” structures, between the methods.

The most obvious difference between 3C/Hi-C experiments and mapping of contacts based on Mu transposition is that the former methods require crosslinking of growing cells with formaldehyde. Additional factors include choice of endonucleases, ligation times, and different methods of data treatment (Cagliero et al., 2013, Le and Laub, 2016, Schmitt et al., 2016). As detailed in Figure S7B-C, simulation results using the polymer model employed above show that at least in that coarse-grained model, the sequential formation of bonds between chromosomal components in spatial proximity (as occurs with formaldehyde crosslinking) is sufficient to force the chromosome into an alternative conformation dominated by short-range contacts, and under appropriate initial conditions can lead to spurious formation of macrodomain-like structures.

The above findings on the effects of mukB or hupA deletions on long-range ordering are consistent with the conclusion drawn from high throughput 3C experiments (Lioy et al., 2018), that MukBEF, together with HU, contributes to long-distance contacts. The 3C contact map shows a less dramatic distinction between the wild type and mukB/hupAB mutant; this is likely because the 3C maps are dominated by short-range local contacts even in WT cells. Conversely, the Mu transposition profiles only become dominated by similar short-range interactions upon the deletion of mukB or hupA, suggesting that the 3C map may be biased toward reporting of contacts between proximal loci (possibly due to the use of formaldehyde crosslinking over the course of sample preparation).

Taken together, one possible interpretation of the differences between Mu-based and 3C-based interaction maps in E. coli is that the former represents a population average of the direct chromosomal contacts at the time of Mu induction, whereas 3C will report the presence of highly connected regions in the vicinity of any long-range chromosomal contacts present at the time when crosslinking begins, which are amplified due to self-reinforcing crosslinking. The utility of the methods thus may differ depending on the biological problem of interest.

Summary

We have provided a map of genome organization in E. coli through the use of Mu transposition as an in vivo tool to monitor DNA-DNA contacts. Mu insertion profiles show convincing evidence that long-range genomic interactions are frequent, and that the genome is broadly well-mixed and devoid of hard regional boundaries. Statistical analysis of the transposition provided evidence of extensive ‘clustering’ or spatial proximity of distant bins, frequently those containing genes of similar function. The SMC-like complex MukBEF and the nucleoid-associated protein HU-α play significant and positive roles in promoting mixing and relaxation of the chromosome, and in their absence the genome’s small-world properties and many specific long-distance clusters are lost. By combining genome-wide transposition data with insights from a simple physical model, we show that the overall conformational distribution of the chromosome can be explained by a constant tension between order imposed by genome replication, and relaxation toward a highly disordered state that is encouraged by the loop-extruding and genome-condensing properties of the nucleoid-associated protein complexes MukBEF and HUα. We hypothesize that this tension, superimposed on the global structural requirements of cell division and a small number of specific, high-affinity long distance interactions, gives rise to the overall chromosomal architecture of an E. coli population.

The findings presented here provide a set of fundamental governing principles of the E. coli chromosome: that as a rule, the chromosome follows small-world properties where all genomic loci are able to intermix spatially, but that chromosomal replication induces a transiently ordered state in which linear distance does matter. We are now able to lay the foundation for future work determining the precise physical forces driving functional clustering, and the regulatory consequences of the observed co-localizations. It is reasonable to speculate that similar patterns of conformational dynamics – kinetically controlled relaxation to a well-mixed conformational ensemble -- apply more generally across the tree of life.

STAR Methods

Lead Contact and Materials Availability

For further information and requests of resources, inquiries should be directed to the Lead Contact, Rasika Harshey (rasika@austin.utexas.edu). All strains and plasmids generated in this study are available from the Lead Contact without restriction.

Experimental Model and Subject Details

Bacterial Strains and Plasmids

All experimental strains used are derivatives of MG1655 and listed in the Key Resources Table. E. coli DH5α was used as a host to grow and purify plasmids. All MG1655 gene deletion strains were created by transducing these alleles from the Keio collection (Baba et al., 2006) using phage P1, with the exception of mukB. Initial parS strains and the pFH2973 plasmid containing the fluorophore labeled ParB proteins were generously gifted to us from Olivier Espeli and Rick Gourse. Additional parS mutants where generated using the methodology reported in earlier work (Espeli et al., 2008). Oligonucleotides used in this study are all provided in Table S1.

Key Resources Table

REAGENT or RESOURCE		SOURCE	IDENTIFIER
Chemicals, Peptides, and Recombinant Proteins
Terminal Transferase (TdT)		New England Biolabs	M0315S
HinP1		New England Biolabs	R0124S
AlwNI		New England Biolabs	R0514S
BglII		New England Biolabs	R0144S
T4 DNA ligase		New England Biolabs	M0202S
Phusion Polymerase		New England Biolabs	M0530S
2’-deoxy-cytidine-5´-triphosphate (dCTP)		New England Biolabs	N0446S
2’,3’-dideoxy-cytidine-5’-triphosphate (ddCTP)		Thermo Scientific	45–001-339
4′,6-Diamidine-2′-phenylindole dihydrochloride (DAPI)		Sigma Aldrich	10236276001
FM 4–64 Dye		Invitrogen	T13320
Critical Commercial Assays
Wizard Genomic DNA Purification Kit		Promega	A1120
Quick Ligation Kit		New England Biolabs	M2200L
Qiaquick PCR Cleanup Kit		Qiagen	28106
Axygen™ AxyPrep Mag™ PCR Cleanup Kits		Thermo Scientific	14–223-227
Deposited Data
Genemoic Sequencing Data		This Study	https://www.ncbi.nlm.nih.gov/sra/PRJNA597349
Experimental Models: Organisms/Strains
E. coli : CW45 : MP1999 with cat at nt 35040 of Mu		(Choi et al. 2010)	CW45
E. coli : DMW11 : MG1655 with Mu:cat at nt 4203381 (Bin 91)		This study	DMW11
E. coli : DMW14 : MG1655 with Mu:cat at nt 3425548 (Bin 83)		This study	DMW14
E. coli : DMW15 : MG1655 with Mu:cat at nt 263131 (Bin 5)		This study	DMW15
E. coli : DMW16 : MG1655 with Mu:cat at nt 517329 (Bin 11)		This study	DMW16
E. coli : DMW18 : MG1655 with Mu:cat at nt 3547885 (Bin 76)		This study	DMW18
E. coli : DMW19 : MG1655 with Mu:cat at nt 1947582 (Bin 41)		This study	DMW19
E. coli : DMW21 : MG1655 with Mu:cat at nt 50316 (Bin 1)		This study	DMW21
E. coli : DMW22 : MG1655 with Mu:cat at nt 3339450 (Bin 72)		This study	DMW22
E. coli : DMW24 : MG1655 with Mu:cat at nt 2555144 (Bin 55)		This study	DMW24
E. coli : DMW25 : MG1655 with Mu:cat at nt 1247622 (Bin 25)		This study	DMW25
E. coli : DMW26 : MG1655 with Mu:cat at nt 1733701 (Bin 37)		This study	DMW26
E. coli : DMW27 : MG1655 with Mu:cat at nt 398930 (Bin 8)		This study	DMW27
E. coli : DMW30 : MG1655 with Mu:cat at nt 1235556 (Bin 26)		This study	DMW30
E. coli : DMW32 : MG1655 with Mu:cat at nt 2856391 (Bin 61)		This study	DMW32
E. coli : DMW33 : MG1655 with Mu:cat at nt 792226 (Bin 17)		This study	DMW33
E. coli : DMW34 : MG1655 with Mu:cat at nt 225365 (Bin 4)		This study	DMW34
E. coli : DMW37 : MG1655 with Mu:cat at nt 2738859 (Bin 59)		This study	DMW37
E. coli : DMW38 : MG1655 with Mu:cat at nt 4554492 (Bin 98)		This study	DMW38
E. coli : DMW41 : MG1655 with Mu:cat at nt 2937424 (Bin 63)		This study	DMW41
E. coli : DMW42 : MG1655 with Mu:cat at nt 4209762 (Bin 90)		This study	DMW42
E. coli : DMW44 : MG1655 with Mu:cat at nt 3447802 (Bin 74)		This study	DMW44
E. coli : DMW47 : MG1655 with Mu:cat at nt 2219564 (Bin 47)		This study	DMW47
E. coli : DMW48 : MG1655 with Mu:cat at nt 2440295 (Bin 52)		This study	DMW48
E. coli : DMW51 : MG1655 with Mu:cat at nt 2286196 (Bin 49)		This study	DMW51
E. coli : DMW54 : MG1655 with Mu:cat at nt 4053514 (Bin 87)		This study	DMW54
E. coli : DMW57 : MG1655 with Mu:cat at nt 1657887 (Bin 35)		This study	DMW57
E. coli : DMW58 : MG1655 with Mu:cat at nt 3700134 (Bin 79)		This study	DMW58
E. coli : DMW59 : MG1655 with Mu:cat at nt 4385978 (Bin 94)		This study	DMW59
E. coli : DMW61:MG 1655 with Mu:cat at nt 995741 (Bin 21)		This study	DMW61
E. coli : DMW63 : MG1655 with Mu:cat at nt 3119489 (Bin 67)		This study	DMW63
E. coli : DMW64 : MG1655 with Mu:cat at nt 1590702 (Bin 34)		This study	DMW64
E. coli : DMW66 : MG1655 with Mu:cat at nt 3045056 (Bin 65)		This study	DMW66
E. coli : DMW69 : MG1655 with Mu:cat at nt 1799218 (Bin 38)		This study	DMW69
E. coli : DMW71 : MG1655 with Mu:cat at nt 1465154 (Bin 31)		This study	DMW71
E. coli : DMW72 : MG1655 with Mu:cat at nt 1939066 (Bin 42)		This study	DMW72
E. coli : DMW104 : MG1655, aidB:parSP1-cat		(Nielsen et al., 2006)	DMW104
E. coli : DMW106 : MG1655, araC:parST1-kan		(Nielsen et al., 2006)	DMW106
E. coli : DMW110 : MG1655, ycdN:parST1-cat		(Nielsen et al., 2006)	DMW110
E. coli : DMW112 : MG1655, feaR:parSP1-kan		(Nielsen et al., 2006)	DMW112
E. coli : DMW134 : MG1655, ycdN:parST1-cat, yfgE:parSP1-kan		(Nielsen et al., 2006)	DMW134
E. coli : DMW138 : MG1655, ycdN:parST1-cat, yfgE:parSP1-kan, Mu:cat at nt 3867127 (Bin 83)		This study, DMW134	DMW138
E. coli : DMW150 : MG1655 dnaQ:parSP1-kan		This study	DMW150
E. coli : DMW151 : MG1655 dnaQ:parSP1-kan, dnaB:parST1		This study, DMW150	DMW151
E. coli : DMW152 : MG1655 yibT:;parSP1-kan		This study	DMW152
E. coli : DMW153 : MG1655 yibT:parSP1, ytfP:parST1		This study, DMW151	DMW153
E. coli : DMW155 : MG1655 dnaQ:parSP1-kan, dnaA:parST1		This study, DMW150	DMW155
E. coli : DMW156 : MG1655 dnaA:parST1-cat		This study	DMW156
E. coli : DMW157 : MG1655 dnaA:parST1-cat, ygbI:parSP1-kan		This study, DMW156	DMW157
E. coli : DMW159 : MG1655 aroG:parST1-cat		This study	DMW159
E. coli : DMW160 : MG1655 aroG:parST1-cat, pheL:parSP1-kan		This study, DMW156	DMW160
E. coli : DMW191 : DMW22 ΔIhf:kan		This study	DMW191
E. coli : DMW192 : DMW22 Δfis:kan		This study	DMW192
E. coli : DMW193 : DMW22 ΔhuB:kan		This study	DMW193
E. coli : DMW194 : DMW22 ΔmatP:kan		This study	DMW194
E. coli : DMW200 : DMW22 ΔhupA:kan		This study	DMW200
E. coli : DMW201 : DMW22 ΔhupA/B:kan		This study	DMW201
E. coli : DMW204 : DMW22 ΔmukB:kan		This study	DMW204
E. coli : DMW205 : DMW15 ΔmukB:kan		This study	DMW205
E. coli : DMW206 : DMW33 ΔmukB:kan		This study	DMW206
E. coli : DMW207 : DMW57 ΔmukB:kan		This study	DMW207
E. coli : DMW208 : DMW37 ΔmukB:kan		This study	DMW208
E. coli : DMW209 : DMW11 ΔmukB:kan		This study	DMW209
E. coli : DMW220 : MG1655 rrnD:parSP1-kan, rrnG:parST1		(Gaal et al., 2016)	DMW220
E. coli : DMW221 : DMW24 Mu:cat Δnt 5138–7233 parSP1:kan at nt 5238		This study	DMW221
E. coli : DMW235 : DMW69 ΔpheL:frt		This Study	DMW235
E. coli : DMW236 : DMW69 ΔpheL:frt, pheL:kan at nt 522930		This Study	DMW236
E. coli : DMW237 : DMW69 ΔpheL:frt, pheL:kan at nt 1418108		This Study	DMW236
Oligonucleotides
Please see Table S1 for oligonucleotide primers		This Study	N/A
Plasmids
pFH2973 (CFP-Δ30ParBP1/ eGFP-Δ23ParBT1 expression vector, AmpR)		(Nielsen et al., 2006)	N/A
pKD46		(Datsenko and Wanner, 2000)	N/A
pKD4		(Datsenko and Wanner, 2000)	Addgene 45605
pDW33 (pKD4 pheL:kan, AmpR, KanR)		This study	N/A
Software and Algorithms
MAPS (Python)		This Study	https://github.com/dmwalker/MuSeq
Spot_detect.py (Python)		This Study	https://github.com/dmwalker/MuSeq
LASSO Regression Analysis (R)		This Study	https://github.com/dmwalker/MuSeq
Microscopy Analysis (Python)		This Study	https://github.com/dmwalker/MuSeq
DL-POLY Classic		(Todorov et al., 2006)	https://www.ccp5.ac.uk/DL_POLY_CLASSIC
Polymer simulation analysis (Python)		This study	https://github.com/dmwalker/MuSeq
BWA-MEM		Li H., 2013	https://sourceforge.net/projects/bio-bwa/
MATLAB		The Mathworks Inc	https://mathworks.com/products/matlab.html

Mu::parSP1 construction:

Mu::parSP1 strains were generated by amplifying the parS site from DMW220 using the oligonucleotides Mu_parS_f and Mu_parS_R. The PCR product was concentrated using the Qiaquick PCR cleanup kit, and electroporated into a Mu lysogen containing pKD46. The parS::kan and Mu::cam cells were identified by initial selection for by kanamycin resistance (Kan^R) and chloramphenicol resistance (Cam^R), respectively, followed by confirmation by DNA sequencing. The parSP1 site was placed inside the semi-essential region of Mu, where it replaced nucleotides (nt) 5138 to 7233. The parSP1 site was then transferred to a fresh Mu lysogen (DMW24) using P1 transduction to generate DMW221.

mukB deletion:

Partial mukB deletion was generated by eliminating a PstI-PstI region within the coding sequence of mukB by inserting a Kan^R gene via recombineering, both to disrupt mukB and to infer selection. This was done by first amplifying the Kan^R gene from pKD4 (Datsenko and Wanner, 2000) using the oligonucleotides mukBF and mukBR to provide homology sequences with the mukB gene. The PCR product was then electroporated into Mu lysogens containing the Amp^R plasmid pKD46, which provides lambda Red recombination functions (Datsenko and Wanner, 2000). After selection for Kan^R, pKD46 was cured from the strain through successive streaking on Kan plates and testing for Amp sensitivity. mukB deletion strains were grown at room temperature (~21 °C) and had a significantly slower growth curve compared to other strains.

pheL constructs:

Oligonucleotides (See Table S1) pKD4_pheLf and pKD4_pheLr were used to amplify pheL and its promoter off the MG1655 chromosome spanning from nt position 2737579 to 2737744 with an additional 5’ AlwNI restriction site and a 3’ BglII restriction site for the construction of plasmid pDMW33. The resulting PCR product was 178 bp in length. Both the plasmid pKD4 and the pheL PCR product were digested with the restriction enzymes AlwNI and BlgII simultaneously. The restriction digest products were gel purified and ligated together using T4 DNA ligase. The ligation product was electroporated into DH5α and selected for Kan^R. Plasmid construction was confirmed via gel size shift and sequencing. pheL was moved into separate locations within the E. coli chromosome at nt positions 522930 and 1418108 by amplifying the pheL:kan construct from pDW33. The PCR product for each amplification was inserted into a MG1655 strain containing pKD46 and successful constructs were selected by Kan^R. Subsequently the pheL:kan gene was transduced via P1 phage into fresh DMW235. Oligonucleotides pheL_Bin10f and pheL_Bin10r were used to amplify the pheL:kan construct for recombineering into nt position 522930, and oligonucleotides pheL_Bin30f and pheL_Bin30r were used for recombineering into nt position 1418108.

Media and Growth Conditions

E. coli cells were grown in a M9-Cas minimal media consisting of M9 salts with 50 μg/mL casamino acids, 0.2% glucose, 100 μg/mL thiamine, and appropriate antibiotics. All cells were incubated at 30 ˚C unless otherwise stated for temperature induction.

Method Details

Experimental Design and Justification for Mu as a Probe

Transposition of Mu is absolutely dependent on MuA/MuB-mediated DNA-DNA interactions, where the ends of Mu insert into a random target DNA locus (Fig. 1A). The high efficiency and low target specificity of Mu transposition allow us to explore the frequency of such interactions within the E. coli genome. To ensure that the presence of the prophage did not cause gross changes in chromosomal topology, the positions of two fluorescent parS/ParB reporters (Nielsen et al., 2006) placed on each arm of the chromosome were monitored in the presence or absence of a prophage. The average distance between the two reporters was independent of the prophage. To induce Mu transposition, the experimental set up used the inactivation of a thermosensitive Mu repressor that otherwise keeps the prophage silent. Using the statistical analysis of the Mu transposition sites from whole genome sequencing data, a 10-minute timeframe was determined to be sufficient for Mu to go through only one round of transposition at the inducing temperature. Using parS-labeled Mu (Mu::parS), only one GFP focus per cell was observed in an uninduced population, and two foci on average after 10 minutes of induction (Movies S1, S2), corroborating the genome sequencing data at the single cell level and demonstrating that the most common experimental outcome was a single transposition event. Mu::parS has a sub-diffusive trajectory, both before and after Mu induction (Movies S1, S2), consistent with other tracked loci on the chromosome (Espeli et al., 2008); thus Mu does not acquire ballistic or super diffusive properties during transposition. The replication status of the cells at the time of Mu induction was also deduced using parS sites placed at four different locations on the genome and fluorophore-labeled ParB; at the time of Mu induction, the genome was partially replicated with ~95% of cells having two Ori loci moved towards the cell poles from the mid cell (Fig. S1C). Similar growth and induction conditions were used for all 35 prophages to determine the sites of Mu insertion after the first round of transposition.

Generation of Mu Lysogens

10 mL of M9-Cas media were inoculated with 10 μL of the overnight MG1655 subculture. The 10 mL culture was grown at 30 ˚C while shaking until an OD of ~0.4 was reached. Cell counts were estimated using a Biorad SmartSpec Plus spectrophotometer. Mu::cat was added to the MG1655 culture to an MOI of 0.1 and set to shaking at 30 ˚C for 30 minutes. Sterile sodium citrate was added to the reaction to a concentration of 250 mM. The reaction was spun down at 3000 rpm in a tabletop centrifuge and resuspended in 200 μL of 0.5% NaCl, 250 mM sodium citrate solution. The solution was plated on LB Cam plates and incubated for 30 ˚C for 18 hours. Lysogens were selected for Cam^R.

Identification of Mu prophage locations

Single colonies were selected for overnight growth in 5 mL LB broth shaking at 30 ˚C. Genomes were purified using the Wizard genome purification kit. The genomic DNA was diluted to 40 ng/uL and sheared by sonication. The sheared DNA was run through a Qiagen PCR cleanup column to remove <100 bp fragments and ssDNA. The sheared DNA was then extended on the 3’ end using terminal deoxynucleotdyl transferase (TdT) with a 16:1 ratio of dCTP and ddCTP. The TdT reaction was then PCR amplified using a nested PCR protocol. Each PCR reaction consisted of an initial melting temp at 95 ˚C for 1 min followed by 25 cycles of 95 ˚C for 20 s, 58 ˚C for 20 s, and 72 ˚C for 1 min. A final extension of 72 ˚C for 2 min was performed and the reaction product was held at 4 ˚C until collected. The first round of PCR (PCR1) consisted of the extension oligonucleotides rand_polyG paired with either Mu_L213 or Mu_R137. The template DNA for PCR1 was the TdT reaction product. The second round of PCR used the product from PCR1 as the template with the extension oligonucleotides being rand_seq paired with either Mu_L213 or Mu_R137. The PCR product was sequenced by the departmental core facility using the appropriate Mu end oligonucleotide (Mu_L213 or Mu_R137), and the sequencing results where aligned with the MG1655 genome using Command Line Basic Local Alignment Search Tool. The first 200 reads are expected to align to Mu, while the first segment that aligns with MG1655 is taken to be the phage position.

Phage Induction

Mu lysogens where grown shaking ON at 30 ˚C from single colonies in M9-Cas/Cam. Ten microliters of overnight growth where used to inoculate 10 mL of fresh M9-Cas/Cam in a 250 mL Erlenmeyer flask. The 10 mL cultures were incubated at 30 ˚C shaking until an O.D. of ~0.4 was reached (typically 3 hours). The culture was then temperature shifted to 42 ˚C for 10 minutes. The cells were fixed with −20 ˚C 95% ethanol and stored in 95% ethanol at −20 ˚C until the genomes were purified. Lysogen genomic DNA (gDNA) was purified through use of the Wizard kit. Purified genomes were stored in a 10 mM Tris pH 8.0, 1 mM EDTA buffer at −20 ˚C until submitted for sequencing.

Genomic Sequencing and Alignment

Individual gDNA samples were submitted to the Genomic Sequencing and Analysis Facility (GSAF) at the departmental core facility for sequencing. Libraries were prepped by GSAF using a low-cost high throughput library preparation method; the input material was either plain genomic DNA (for the original data sets discussed in Figs. 2,3 and associated text) or enriched pools targeting the Mu insertion sites (for the data discussed in Fig. 6) Sequencing was performed on an Illumina Hi-Seq platform using 2X150 paired end reads targeting 20 million reads per sample. Initial Alignments where performed on the Lonestar5 super-computing cluster provided by the Texas Advanced Computing Center (TACC) using a modified Burrows-Wheeler Alignment algorithm (BWA-MEM). The fastq files for all sequencing can be found online in the Sequence Reads Archive (See Key Resources Table).

Mu Target Enrichment Protocol

For Mu target enrichment, purified genomic DNA was digested with HinP1. The digested DNA was ligated with the Y-linker sequence y_link using a Quick ligation kit. Ligation was quenched with the addition of EDTA to 20 mM. Ligation product was purified and concentrated using magnetic beads (Axygen). The ligation product was then PCR amplified using the oligos Mu_L31 and y_linkrev and the same PCR thermocycler program as describe earlier. PCR product was verified on a 1% Agarose gel and purified using magnetic beads. Purified product was frozen at −20 ˚C until submission for sequencing.

Microscopy

parB-GFP/CFP Imaging:

MG1655 strains with integrated parS sites and the plasmid (pFH2973) carrying IPTG-inducible parBSP1-yGFP and parBST1-CFP were grown as described above until an OD ~0.4 was reached. IPTG was added to the cultures at a concentration of 100 uM, and left shaking at 30 ˚C for 1 hr. One mL of cells were spun down, and resuspended in 200 uL of M9-Cas and placed on a 1.5% agar pad.

Nucleoid and Membrane staining:

Strains DMW22, DMW200, and DMW204 were grown in M9Cas to an OD ~ 0.6 mL. At appropriate optical densities, 5 mL of cell culture were spun down and resuspended in 400 uL of 0.1 M PBS (pH 7.4). Cells were then fixed in 6.4 mL of 74% ice cold methanol for a final concentration of 70% methanol. Cells were spun down and washed twice in PBS, and finally resuspended into 600 uL of PBS. FM 4–64 dye was added to the cell solution to 0.5 μg ml⁻¹ and stained for 1 min at room temperature in the dark for cell membrane visualization. Cells were deposited in a chamber created by attaching a poly-L-lysine coated coverslip to a glass microscope slide by double-sided tape and incubated for 10 minutes at room temperature before being washed twice with 40 uL of PBS. Nucleoid staining was achieved by washing the cells with 40 uL of 300 nM DAPI (4′,6-diamidino-2-phenylindole) followed by a wash with PBS after 30 s of staining.

All microscopy was carried out on an Olympus BX53 Fluorescent Microscope under 100x magnification, and images where acquired using the Cell Sense software. GFP, CFP, RFP and UV filters were used to view GFP, CFP, FM4–64, and DAPI fluorescence, respectively.

Network Mapping

Regulatory pathways (including metabolism, DNA/RNA synthesis, DNA repair etc) and their constituent genes were identified using the genomic database (Keseler et al., 2017). The genome was partitioned into 100 equally sized bins as in Figure 1B. For any bin of interest (Bin i), all genes and their corresponding regulatory pathways where identified. For all pathways contained within Bin i, genes related to that pathway where searched for in the remaining 99 bins. Any bins that contained a gene sharing a pathway with Bin i, were connected with a blue edge in the circular networking map. Similarly, any bin with a positive Bin:Bin interaction coefficient with respect to Bin i as determined from LASSO regression had a green edge drawn between those bins.

Polymer Modeling

Polymer simulations were implemented in DL-POLY CLASSIC (Todorov et al., 2006), using a chromosome with 965 beads (each representing roughly 4.8 kbp of DNA). Each bead had a covalent bond to its immediate neighbors treated using a restrained harmonic potential (rhrm in DL-POLY), with an equilibrium distance of 128 AU (arbitrary units), saturation distance of 500 AU, and force constant of 1.69 RT/AU. In addition, all beads interacted via a pairwise Lennard-Jones nonbonded potential, with ε = 0.84 RT and σ = 128 AU, with a 500 AU cutoff.

Standard simulations were performed beginning from a circular conformation of the chromosome with an initial radius of 10,000 AU, and propagated under constant temperature conditions at 310 K using a Nose-Hoover thermostat. Simulations were performed using a nominal timestep of 10 ps, although the model is sufficiently coarse that the time is likewise better thought of as an arbitrary unit. Simulation durations were 25 million steps for non-crosslinking simulations, or 12.5 million steps for crosslinking simulations (as the latter were performed after the very short relaxation times of the systems had become apparent).

In the simulations emulating formaldehyde crosslinking, additional covalent bonds were added once every 50,000 steps, and had parameters equivalent to those of all other covalent bonds in the system. Each bond addition was constrained to only occur between beads within 250 AU of each other. In the case of simulations with pre-formed bonds between non-adjacent beads, the starting structure was perturbed by causing the radius of the circle to vary from 5,000 to 10,000 AU, with the minima occurring at the points of beads that were bonded to each other. An important consideration is that these simulations provide a model of the effects of crosslinking represent an extreme case in which the entire chromosome is in a fully extended/circular state at the precise moment when crosslinking begins. In an asynchronous population of cells, the more reasonable expectation would be that some fraction of the population would have their chromosomes in either a globally or locally extended conformation at the point when crosslinking begins, whereas the rest would be in an equilibrium structure (perhaps roughly resembling that in Fig. 7D, with additional off-diagonal contacts). In such a case, the contact map thus obtained by a 3C experiment would be a simple mixture of the contributions from cells that were in kinetically trapped vs. equilibrium conformations at the time of crosslinking, with the equilibrium contribution becoming increasingly prominent for slower-growing cells.

For the simulations demonstrating the effects of MukBEF-like loop extrusion on relaxation times, we performed simulations for 400,000 steps beginning from a circular starting conformation, in which a new set of ‘loops’ was formed once every 5000 steps. Loop formation consisted of selecting a random set of 20 or 40 bead pairs, among beads that were separated by two to five bonds. Over the next 5000 step leg of the simulation, each of those bead pairs were subject to an additional attractive force of magnitude 53900/r² RT/AU, with r the distance between the beads in AU. The attractive force between two nearby but nonadjacent beads serves here as a crude model of loop extrusion, in which a chromosomal region between two anchor points would be expected to be ‘looped out’ from the anchor formed by those points. For the purposes of Figure 7E-F, the mixing state of the chromosome was analyzed by fitting a logistic regression at each simulation snapshot for the fraction of possible contacts formed at each linear genomic distance, as a function of the natural logarithm of that distance; the fitted distance dependence coefficient was used to assess the formation of local vs. long-distance contacts. Because the decay curves could not be fitted by a simple exponential (Fig. 7E), a nonparameteric approach was used to identify the relaxation rates, defining the asymptotic value reached by the interaction coefficient as the median observed over the last 10% of the simulation, and then define the decay time _T1.1 as the time required for the coefficient to reach a value within 10% of the asymptotic value. Note that even if the same threshold (that required for the +MukBEF cases) were applied for all simulations, the observed values of _T1.1 for the with-MukBEF cases are still on average less than half of those for the no-MukBEF cases (data not shown).

Comparison with other Coarse-grained Modeling Approaches for Bacterial Chromosomes.

While numerous other groups have presented models of the chromosomes of E. coli and other bacteria at varying resolutions (Umbarger et al., 2011, Jung et al., 2012, Le et al., 2013, Hacker et al., 2017, Yildirim and Feig, 2018), in general the focus both of explicit modeling efforts and of mental models implicit in explanations of chromosomal structure has been on equilibrium states. One notable exception is the work of Jung and colleagues (Jung et al., 2012) who studied both relaxation kinetics and equilibrium structure of model chromosomes using a ring polymer model similar to that employed here. Several important distinctions between the assumptions in the models, however, lead to substantially different conclusions regarding the E. coli chromosome; the model of Jung and colleagues treats the chromosomal components as purely repulsive spheres interacting with both each other and a confining cylinder (the latter providing compaction), whereas here compaction is treated as arising implicitly from weak attractive forces between beads, without a confining shell (the attractive forces in the present model simply act as a stand-in for confinement by the cell membrane, protein factors promoting nucleoid compaction, and exclusion of ribosomes and other non-DNA cellular components). Perhaps a more important difference, Jung et al. model the E. coli chromosome with fewer beads which are relatively large compared with the diameter of the cylindrical confining shell (D = 4.8 bead radii); as a result, the chromosome in their model using E. coli-like parameters is forced into a linearly ordered conformation along the length of the cell, which is incompatible with the well-mixed conformation implied by the Mu transposition data. In contrast, the polymer model employed here provides an equilibrium state that is consistent with the qualitative features of our contact maps, a purely kinetic explanation for the effects of loss of MukB function, and additional insight into possible causes for the differences between contact maps observed via Mu transposition and HiC-like approaches.

It is also essential to note, in our consideration of both the kinetic and equilibrium properties of chromosomal conformations, that the ‘well-mixed’ property of the chromosome demonstrated by the Mu transposition data arises purely at the population level, and does not bear any requirements on the speed of Mu transposition or diffusion of Mu-containing loci. Indeed, the diffusive mobility of Mu-containing loci does not differ substantially from that of bulk DNA (Movie S2), ruling out the possibility that the observed contact map arises due to some super diffusive motion of the Mu-integrated locus itself. Instead, both the experimental and theoretical contact maps shown here arise due to averaging of the conformations of large numbers of cells – in any individual cell, a particular Mu origin location will only have access to the relatively small number of other chromosomal loci that it is in contact with over the timescale required for expression and assembly of MuA. The ‘small-world’ property of the Mu contact maps arises because over an ensemble of cells, a Mu donor site will be found with roughly even frequencies to be in contact with any particular other part of the chromosome (with the exception of the specific instances of clustering considered elsewhere in the text).

Characteristics of the Polymer Model

In order to assess the robustness and applicability of the polymer model simulations employed here, a series of trajectories was generated in which the well depth of the main Lennard-Jones (LJ) potential was scanned through a 1000-fold range of values (see Figure S7D). Three rough domains of behavior are apparent: at low interaction potential strengths, the system is never driven to form noncovalent interactions at any meaningful rate, and thus the contact map is dominated by the diagonal. At a well depth of ~0.5 RT, the system appears to undergo a phase transition into a well-mixed state, in which any given locus can interact randomly with any other locus. This state shows the presence of a compact nucleoid, but is flexible and permits rapid conformational search. As the well depth continues to increase, the system undergoes a second phase transition to a glassy state in which the contact map is dominated by nearby neighbors, due to either kinetic or thermodynamic trapping into a state where only local contacts (those between nearby beads) are formed with any regularity. The relatively dynamic behavior of the middle phase relative to the glassy high-LJ phase can be further demonstrated by taking a collection of conformations from the medium-LJ state and switching them to the high-LJ state and vice versa (Figure S7E); the high-LJ state remains trapped near its starting conformations and thus retains the well-mixed initial conditions, whereas switching high-LJ conformations to the middle-LJ state causes rapid transition to a well-mixed conformation. Thus, the high-LJ state undergoes little meaningful motion over the timescales simulated here, raising the strong possibility that the short-range contact maps observed for high LJ constants in Figure S7D are primarily due to trapping in the first conformation taken on by the system after initial collapse.

Of the regimes explored here, the middle one appears most appropriate for coarse modeling of the E. coli nucleoid due to several considerations: It is compacted (as the nucleoid should be) yet flexible and dynamic (again as the nucleoid should be); the phases occurring with weaker or stronger values of the Lennard-Jones force constant represent either severely decondensed structures, or those for which the chromosome is essentially static. To maintain consistency with both the Mu experimental data and the general desiderata outlined above, we use a well depth of 0.84 RT in all other simulations presented in this work, squarely in the middle of the well-mixed phase of the system.

Effects of MukB loop extrusion on chromosomal relaxation in the polymer model

Several simulation studies have recently demonstrated that processive loop extrusion activities akin to those suspected of MukBEF can enhance chromosome compaction and dynamic processes such as segregation (Goloborodko et al., 2016), and that its activity in E. coli likely plays a major role in the specific compacted structure taken on by the nucleoid (Mäkelä and Sherratt, 2019). For the purposes of the present model, MukBEF activity was treated in a more coarse-grained fashion, in which loops encompassing up to six beads were formed (by adding an attractive potential between the beads at the base of the loop) and subsequently broken. Two prominent effects on the behavior of the modeled nucleoid were apparent: the kinetics of relaxation from a fully extended state toward a small-world like state were substantially accelerated (Fig. 7E-F), but conversely, the asymptotic distance dependence of contact rates was somewhat stronger in the presence of MukBEF activity than in its absence, with values for the fitted distance dependence over the last 10% of 400,000 step simulations of around −1.1 in the absence of MukBEF loop extrusion, or −3.0 in its presence. The latter finding is consistent with other simulation studies demonstrating that loop extrusion can contribute to chromosomal domain formation (Fudenberg et al., 2016), as well as the intuitive expectation that a protein complex promoting cohesion between nearby portions of the chromosome would promote local contacts. The experimental finding that MukBEF activity is in fact necessary for the formation of a well-mixed chromosome, and that in the absence of MukBEF short-range contacts predominate, is counter-intuitive when considered only from the standpoint of the final structures that might be reached in the presence vs. absence of MukB. This finding can be understood as arising either due to acceleration of relaxation of the chromosome away from more extended states and toward better mixed states (the kinetic model proposed in the Main Text) and thus raises the fraction of the population that is able to form long range contacts, the possibility that in the absence of MukBEF the chromosome is too diffuse to form any detectable contacts, or some interplay not captured in our simple model between MukBEF and other chromosomal organizing factors.

Quantification and Statistical Analysis

Identification of Mu locations after the first transposition

Mu locations were identified using the custom software entitled Mu Analysis of Positions from Sequencing (MAPS). In short, MAPS identifies the transposition sites for Mu the genomic sequence by aligning the genomic sequencing fastq files to both to the MG1655 genome from genbank (genid: 545778205) and the Mu phage genome (genid: 6010378) using BWA tools. PCR duplicates are discarded using SAMTOOLS. Reads corresponding to both MG1655 and either of the Mu ends are pulled from the alignment files for further processing. This pool of sequences were then aligned once again with BWA against the MG1655 genome (genid: 545778205). The lowest value nucleotide of the MG1655 genome observed before transitioning into the Mu genome was taken to be the location of insertion. The average error in estimating Mu location sites is estimated to be around 300 bp as that is the average template length created during sequencing library preparation. Nearly 50% of all Mu locations sampled correspond to the location of the initial prophage, confirming that Mu has transposed only once in the initial induction experiment.

LASSO Regression Analysis

We performed penalized Poisson regression using the R package glmnet (Friedman et al., 2010) to fit the observed interaction counts for all bin-bin pairs in each data set. The model incorporated indicator variables for each bin of origin, destination bin, and bin-bin interaction pair, as well as a regression parameter accounting for genomic distance on the genome (expressed as log(1+d), for d the distance in bins between the source and destination of the Mu phage). In addition, to each count bin c_i,j representing the transition count from bin i to bin j, an offset term of log(q_i * q_j) was included, where q_i is the relative abundance of genomic material from bin i in an untargeted sequencing experiment, thus accounting for any effects on Mu transposition frequencies arising solely from the relative abundances of different donor and acceptor bins (that is, the products of the bin abundances are treated as an exposure term). Thus, the overall form of the model for the number of transpositions from any bin i to any other bin j, ci,j, is given by

$$c_{ij}~\text{Poisson}\left({\alpha }_{i,j}+{\beta }_{intercept}+{\beta }_{\text{dist}}{d}_{i,j}+{\beta }_{\text{From}\text{bin}\text{i}}+{\beta }_{\text{Tobin}j}+{\beta }_{i,j}\right)$$ (1)

Here α_i,j represents the abundance constant described above, d_i,j is the log-scaled distance between bins i and j as described above, and the β values are regression parameters to be fitted (in all, 2 + m + n + m*n for a system with the contacts divided into n bins for which m donor Mu integrants were tested). The penalized log-likelihood

$$\frac{1}{N}L(\beta \mid D)+\lambda \sum _{k=1}^N\left|{\beta }_k\right|$$ (2)

was maximized in order to obtain the fitted β coefficients, where L represents the Poisson likelihood, D are the observed count data and known independent variables, and N is the total number of free parameters (all β values appearing in Equation 1 above). We used 100-fold cross validation (as implemented in the cv.glmnet function) to identify optimal values for the penalty parameter λ, and report the fit with the highest (most restrictive) value for λ yielding a cross-validated deviance within 1 standard error of the best fit; results of this fitted model are shown in the text. The processed data serving as input to the model fit (all_interaction_counts_withnorm.csv), as well as the R code used to implement the model (run_classic_lasso.R), are available from the project Github page.

In the case of the follow-up analysis of targeted insertions in the presence of various genetic perturbations, a restricted version of the model was fitted above for each data set, assuming that the abundance terms α_i,j matched those used in the analysis of the wild type data, and fitted the following joint model for all of the genotype/Mu bin combinations g described in Figure 6 and the accompanying text:

$$c_{i,j,g}~Poisson\left({\alpha }_{i,j}+{\beta }_{g\text{dist}}{d}_{i,j}+{\beta }_{\text{From}\text{bin}i}+{\beta }_{\text{To}\text{bin}j}+{\beta }_{i,j}+{\beta }_{g\text{intercept}}+{\beta }_{g,j}\right)$$ (3)

The model was fitted according to the same procedure as described above. Included in the data used to fit the model were both all of the original data from wild type cells obtained via untargeted sequencing (the same data set used in Figures 2–3), and the targeted resequencing data for a single WT bin72 Mu donor and the other genotype/donor location combinations shown in Figure 6. The indicator g refers to any single batch of data; the untargeted sequencing data were all treated as having identical values of g (and all β_g,j, terms for this g level were constrained to 0), but the WT bin72 targeted-sequencing data was treated as an independent g. Note that the identity for the donor bin is thus implicit in the value of g in the last term of Equation 3, and that separate intercept terms and distance coefficients are likewise fitted for all values of g.

Microscope Foci and Nucleoid Tracking

Analysis of individual foci tracking was done using a custom python script (spot_detect.py). In brief: for a field of cells, foci where isolated by increasing Otsu threshold (Otsu, 1979) on each channel for GFP or CFP. The positional information for each set of foci were calculated. For each GFP the nearest CFP distance was calculated and stored. Histograms of the distances between GFP and CFP were generated to visualize the distribution of distances for a given population of cells. Image fields were restricted to those containing between 120 and 200 cells for analysis. For nucleoid tracking acting on the DAPI channel, cells were segmented by calculating the Otsu threshold (Otsu, 1979) and merging contiguous regions exceeding that threshold (using tools from the mahotas library (Coelho, 2013)). Image fields which were too dense to segment using this method were discarded. Statistics were calculated for all regions (objects) called via the approach above. To exclude ‘cells’ consisting of severely out-of-plane portions or objects containing multiple cells, the principal axes for each called object were calculated, as well as the cell’s maximum extent along those axes. Only objects with a length of at least 2.8 μm along their long axis, and between 313 nm and 1.56 μm along the short axis, were included in the bulk analysis shown in Supplementary Figure S6.

Supplementary Material

2

Movie S1. Visualization of ParB-bound Mu prophage prior to induction of transposition, Related to Figure 1 and Methods S1. A Mu prophage located in Bin 55 was labeled with a parS site to which ParB-GFP is bound. As reported by ParB, the phage behaves as a stable, sub-diffusive locus on the chromosome prior to induction. There is only one focus per cell, as expected from a single copy of the prophage on the chromosome. Cells were imaged as described in STAR Methods, with 300 ms intervals between each frame. The frames periodically shift between fluorescence and bright-field to ensure focus.

3

Movie S2. Visualization of ParB-bound Mu prophage after a single round of transposition, Related to Figures 1, 2 and STAR Methods. The fluorescently labeled Mu prophage strain described in Movie S1 legend, was induced for transposition by shifting temperature to 42 ºC for 10 minutes. Fluorescent Mu foci have doubled per cell, as expected after one round of transposition. These foci show sub-diffusive behavior even after induction of transposition.

4

Figure S1. Replication-Segregation cycle of E. coli, the replication status of the experimental population, and cross-replichore transposition frequencies, Related to Fig. 2 and STAR Methods. (A) Representation of the E. coli macrodomains and their disposition during the cell cycle. The timely relocalization of the Ori region from the mid cell toward the cell poles during replication is a well-studied phenomenon (Lau et al., 2003, Nielsen et al., 2007, Espeli et al., 2008, Reyes-Lamothe et al., 2012, Wang and Rudner, 2014, Youngren et al., 2014, Badrinarayanan et al., 2015, Kleckner et al., 2018). Prior to initiation of replication, Ori and Ter are co-localized to the midpoint of the cell. oriC and dif are sites where replication originates and terminates, respectively. (B) During replication, duplicated Ori domains migrate towards the poles to their future cell midpoints. The four macrodomains – Ori, Ter, Right, Left – are color coded as indicated by the legend (Valens et al., 2004). NS – Non-structured regions. (C) Monitoring the replication status of the E. coli genome under the experimental conditions used for inducing Mu transposition. The parS/ParB system described under Methods was used, with one parS site present per cell. These sites were placed in four different regions of the chromosome color-coded as indicated in the cartoon legend. The four panels show typical microscope images of the fluorophore labeled ParB bound to its respective parS site located in the chromosomal region as indicated by the arrows coming from the cartoon above. The cells were observed just prior to Mu induction. Ori (green), as well as Ori’s flanking regions (orange and black) have moved towards the cell poles (see Fig. 1B for new nomenclature of the colored regions). Ter (cyan), as well as its immediate flanking regions (red and blue) are still unreplicated and located at the mid cell. Greater than 90% of observed cells have replicated Ori puncta and harbor a single Ter punctum. Additionally, a large majority (> 66%) have replicated Ori-proximal OPL and OPR puncta and have single Ter-proximal TPL and TPR puncta; thus, the majority of the population are in the midst of DNA replication. Cells observed: Ori: N = 327; OPL: N= 226: Ter: N=455; TPR: N= 588. (D) Cross-replichore Mu transposition is favored in the replicated regions of the chromosome. Mu transposition between two loci equidistant from oriC (trans pair or TP) was followed with a third locus that is the same genomic distance from the prophage as the Ori pair but does not cross oriC (cis pair or CP). The figure shows an example analysis for a Mu lysogen starting at Bin 65. Bin 65 and Bin 5 are equidistant from oriC and form a TP. These bins are both are 20 bins away from oriC and a total of 40 bins away from each other. Bin 25 is the CP for Bin 65 because both Bin 5 and Bin 25 are 40 bins away from Bin 65. (E) A polar plot of the ratio between TP and CP interaction for 34 of the 35 prophages (the prophage in Bin 38 had similar TP and CP values). Positive values favor TP interactions, while negative values favor the CP interactions. Dotted radial lines indicate positions where Mu prophages were located. Bin names are indicated for a few bins to help orient the reader. Both actively replicating and newly replicated genomic regions should have higher rates of TP interactions compared to the corresponding CP interactions due to TP co-localization during replication-segregation. The results show a near-uniform trend where for 34/35 prophages, OP interactions are favored for loci in Ori and its immediate flanking regions OPL and OPR, with Bin 87 (right of oriC) as a single outlier. Bins found within Ter, TPL, and TPR (Bins 14–63) either favor CP or show no preference for TP or CP interactions. There is a break point at the quarter-positions relative to oriC, reflecting the average replication state of cells in the experimental population (C).

Figure S2: Mu inserts across the genome equally, displaying a ‘small world’ genome after controlling for bin-wise characteristics, Related to Figure 2. (A) Raw Mu insertion counts display a heavy preference for inserting into Ori over other regions. (B) When accounting for the abundance of Ori in a cellular population undergoing partial replication, the insertion frequencies across the genome level out. (C) Further accounting for the donor and recipient effects of specific bins (fitted using data from all 35 Mu origin sites) flatten out the Mu insertion profile completely, and gives evidence of a well-mixed chromosome where inserting into any region is equally likely. Mu profiles for all three panels are for the wild-type Bin 72 insertions.

Figure S3. Co-localization of two rrn loci as observed by Gaal et al. 2016, Related to Figure 3 and 5. (A) The merged brightfield images (left) show merged fluorescent foci from the GFP and CFP channels (shown individually on the right). rrnD (Bin 72) was labeled with parSP1-GFP (middle) and rrnG (Bin 57) with parST1-CFP (right). Magnification of the merged brightfield image (red square) shows more clearly the distances between the foci. (B) The observed/calculated distances between the foci are shown with their relative counts, N= 327. Distances calculated are Euclidian distances on a 2D plane, where the focus’ location is estimated by the mean of a 2D Gaussian fit. The majority of foci pairs are only 150 nM or less apart, consistent with data reported by Gaal et al. 2016. Note the lack of a bimodal distribution of distances, suggesting that the genes are always clustered, unlike the replication dependent aroG and pheL pairs in Fig. 5. (C) The expected inter-focus distance for two randomly placed foci in a 1 μm cell is around 270 nm, N=10000 (right). The observed clusters in B are well below the average for randomly placed foci pairs.

Figure S4. Clustering reflects intrinsic properties of chromosomal regions, Related to Figures 3, 4 and 5. To test if clustering of genes is a direct result of regulatory proteins that bind and compact the specific loci involved, a clustered gene was separately deleted and moved to alternate locations, with the expectation that if gene regulation was important for clustering, the precise chromosomal locations of the gene should not matter, but rather, that clustering should follow the new gene location. (A) Mu insertion profiles in strains with altered chromosomal locations of pheL. The pheL gene within Bin 58 was used, because it is marked with strong interactions with both Bin 16 and 38, where other genes for phenylalanine biosynthesis are located. The insertion profiles of Mu in Bin 38 were monitored under three scenarios: a pheL deletion mutant (∆pheL), pheL (along with its promoter) moved from Bin 58 to Bin 10 (opposite side of the chromosome from Bin 58; Bin10:pheL), and pheL plus its promoter moved from Bin 58 to Bin 30 (located within Ter, but closer to the Mu located in Bin 38; Bin30:pheL). Insertion counts were divided by a rolling median with a window-size of 11 bins centered on the bin of interest to highlight the abundance of certain bins relative to their genomic neighbors. Bins within the grey background represent the top quartile of interactions for that specific experiment. In all three panels, Mu is located in Bin 38. Normalized insertion counts for bins of interest are highlighted with bin labels directly underneath. Relative amounts of Mu insertions into the specific bins indicated were compared to the average number of insertions across the genome. In all tested pheL constructs Bins 16 and 58 remain in the top quartile of interactions, indicative of clustering with Bin 38. Conversely, there is no increase in interactions for Bins 10 and 30 (where pheL was moved) with Bin 38. In interpreting these data, it is important to note that the choice of moving pheL was made specifically to test the hypothesis that clustering of Bins 16 and 58 was driven solely by the presence of the co-regulated pheL and aroG genes in those bins. The possibility that some different pair of specific genes residing in those bins is in fact solely responsible for the observed co-localization cannot be excluded; however, the data do permit us to directly falsify the tested hypothesis that the clustering was driven by pheL/aroG alone, and provide evidence against the broader notion that clustering might be driven solely by locus-specific interaction between co-regulated genes. We instead favor the possibility that gene location has been subjected to selective pressure within the framework of the overall conformation of the chromosome. These observations are in agreement with Gaal et al., who observed that deletion of an rrn gene, or inhibition of transcription did not affect clustering (Gaal et al., 2016), and that moving the gene to other locations did not make it part of the cluster (Gourse, personal communication). (B) Network maps highlight that not all regulatory pathways exhibit clustering events. To explore the finding in A further, a network map was developed for each starting prophage showing the connections (edges) between the bins that share regulatory pathways (see STAR Methods). The network maps of four representative Mu lysogens are shown. Each bin is a node and each blue line (edge) connects nodes that share regulatory pathways. Green edges are nodes predicted to be clustered by LASSO regression. Orange edges connect nodes that are both predicted to be clustered by LASSO regression and have regulatory pathway connections. In most cases there are vastly more blue edges than green edges, except for Bin 35. This bin was also the only bin where the analysis identified every clustering between all shared pathways. If the bin clustering observed by Mu were based on the criteria of shared regulatory pathways, then clustering would be much more widespread. Thus, co-regulation per se does not dictate clustering.

Figure S5. NAP deletion mutants display similar Mu insertion profiles to wild-type E. coli, Related to Figure 2 and 6. Starting Mu locations were all in Bin 72. The ability of Mu to integrate across the genome was monitored in the indicated strains that had loss of a single NAP function: H-NS, MatP, β subunit of heterodimer HU, α subunit of heterodimer IHF and full deletion of the HU heterodimer, in order. Mu insertion counts for the hupAB mutant were from a target enrichment protocol of Mu transposition sequencing, marked with an asterisk.

Figure S6. Fluorescence microscopy showing the nucleoid conformations of WT, hupA, and mukB cells, Related to Figure 6. (A) Merged images showing DAPI (blue; DNA stain) and FM 6–46 (red; membrane stain) for cells of the indicated genotypes grown under conditions matching those of Mu induction. Cells were viewed with 100x magnification. DAPI-stained images were obtained using 126 ms exposure time, and FM 6–46-stained membranes were imaged using 900 ms exposures. (B) Four-fold magnifications of representative fields of view for each genotype shown in panel A. (C) Violin plots showing the distribution of cell-wise nucleoid compaction (assessed by the ratio of the maximum pixel intensity for DAPI in that cell to the mean DAPI intensity in that cell). . ‘***’: p<0.001, Wilcoxon rank-sum test.

Figure S7. Effects of 3C/Hi-C experimental and computational methodology on contact maps, Related to Figure 7. (A) Renormalization of high throughput 3C data from Cagliero et al. is consistent with a small world chromosomal structure. Shown are log phase junction counts from Cagliero et al. (Cagliero et al., 2013), as re-quantified by Xie et al. (Xie et al., 2015), either in their raw form (Original), or (Normalized) after dividing each bin by the product of the sums for all interactions involving the two participating bins (which is used here as a proxy for genomic DNA abundance). For the present analysis the genome is divided into 100-kilobase bins. The absence of a strong diagonal or macrodomains should be noted. (B) Effects of crosslinking on relaxed conformations of the E. coli chromosome based on polymer modeling. Relaxed conformations (last half of 4*10⁷ step trajectories) of the chromosome averaged across 10 simulations in which formaldehyde crosslinking, but no other constraints, were imposed on the chromosome, demonstrating a contact map biased toward short-range contact formation. (C) As in panel B, for cells that initially had six loops formed between distant locations on the chromosome (indicated by arcs above the contact matrix); thus, in addition to a bias toward short-range contacts, domain-like behavior is observed among the beads that were between the initial contact points. (D) Behavior of the polymer model for the chromosome when simulated using a range of well depths for the Lennard-Jones interaction. For each sub-panel, the top conformation shows a representative snapshot for a given well depth ε (in units of characteristic energy RT, with R the gas constant and T the temperature of the system). Beneath the snapshot a contact map is shown, obtained by averaging the interaction frequencies (using a 300 arbitrary unit cutoff) on 20 independent, 5*107 step simulations (showing an average of 10 evenly spaced snapshots over the last 2*106 steps; after addition of a pseudocount of 0.0001 to each bin frequency). Note that the contacts along the diagonal (yellow stripe) are set to a value of 1.0 by definition. Three phases of the system are apparent, dependent upon the Lennard-Jones well depth; in particular, the middle phase (ε = 0.538 – 2.150) showing a fluid globule for the chromosome and a small-world contact map. The other phases show either a completely diffuse genomic conformation (low ε), or a crystallized conformation with no apparent motion after initial collapse (high ε). (E) For the same 20 trajectories shown for panel D at ε = 0.538 and ε = 17.203, the conformations at the ends of the trajectories were taken and then simulated for an additional 5*10⁶ steps at the opposite Lennard-Jones well depth (thus, the ε = 0.538 endpoints were subsequently run at ε = 17.203 and vice versa); averages of 5 snapshots over the last 2*10⁶ steps are then shown. Switching the well-mixed conformation to stronger interactions causes a loss of mobility but retains mixing over the simulated timescale, whereas the crystallized, local-only conformation of the high-interaction state rapidly dissipates when the interactions are weakened. Color scale is identical to panel D. The findings here demonstrate several important aspects of the model: that the well-mixed state is an equilibrium characteristic of the middle phase of ε values regardless of initial conditions, that in the middle phase the system rapidly explores the range of relevant conformations for the model chromosome, and that in contrast, the high- ε state is dominated by kinetic trapping at the nearest local minimum of the system over the simulated timescales.

Highlights.

• Mu describes a boundary-less E. coli genome making widespread chromosomal contacts

• Within the well-mixed genome, many co-regulated loci, e.g. rrn and dna, are ‘clustered’

• Condensin complex MukBEF and NAP HUα are responsible for the dynamic genome

• Polymer modeling explains the observed data based on relaxation kinetics